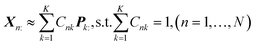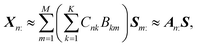Open Access Article
Open Access ArticleA data-driven sequencer that unveils latent “codons” in synthetic copolymers†
Yusuke
Hibi
 *,
Shiho
Uesaka
and
Masanobu
Naito
*,
Shiho
Uesaka
and
Masanobu
Naito
 *
*
Data-driven Polymer Design Group, Research and Services Division of Materials Data and Integrated System, National Institute for Materials Science, 1-2-1, Sengen, Tsukuba, Ibaraki 305-0047, Japan. E-mail: hibi.yusuke@nims.go.jp; naito.masanobu@nims.go.jp
First published on 20th March 2023
Abstract
The recent emergence of sequence engineering in synthetic copolymers has been innovating polymer materials, where short sequences, hereinafter called “codons” using an analogy from nucleotide triads, play key roles in expressing functions. However, the codon compositions cannot be experimentally determined owing to the lack of efficient sequencing methods, hindering the integration of experiments and theories. Herein, we propose a polymer sequencer based on mass spectrometry of pyrolyzed oligomeric fragments. Despite the random fragmentation along copolymer main-chains, the characteristic fragment patterns of the codons are identified and quantified via unsupervised learning of a spectral dataset of random copolymers. The codon complexities increase with their length and monomer component number. Our data-driven approach accommodates the increasing complexities by expanding the dataset; the codon compositions of binary triads, binary pentads and ternary triads are quantifiable with small datasets (N < 100). The sequencer allows describing copolymers with their codon compositions/distributions, facilitating sequence engineering toward innovative polymer materials.
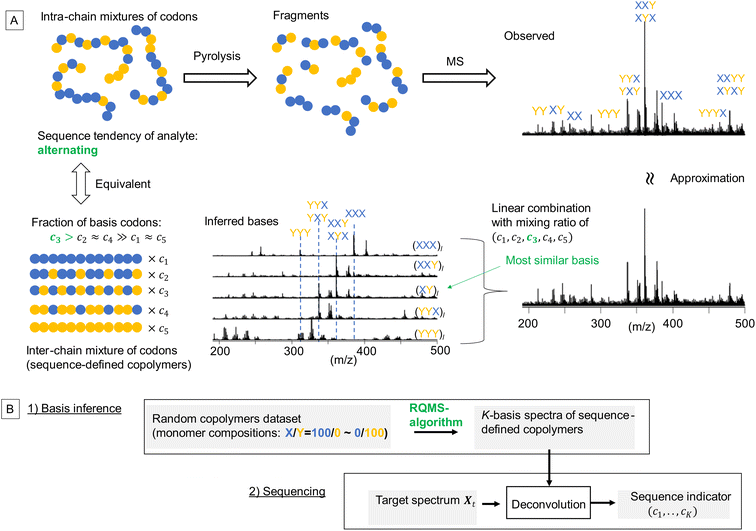
The properties/functions of biopolymers are encoded in their well-defined sequences. In contrast, in synthetic copolymers, such sequence–property correlations are obscured, since the properties are averaged over the polydisperse sequences.1 Nevertheless, outstanding functions originating from sequence-specific short segments stochastically generated via random copolymerization have been recently reported.2–4 These discoveries imply that the properties of random copolymers are deemed to be encoded into their short sequences, herein called “codons”. From theoretical approaches, the impact of codon structures on the copolymer properties has been well studied using machine-learning and molecular dynamics simulations, where aperiodic and complex codons were designed as optimal repeating segments to achieve the target polymer properties.5,6 However, owing to the lack of efficient methods for sequence distribution analysis, i.e., sequencing7 (also see the ESI “Definition of sequencing”†), a significant gap remains between theories and experiments: first, embedding such designed codons into the main chains is very challenging even with state-of-the-art sequence-controlled polymerization techniques;1 second, the codon–property correlations cannot be experimentally investigated, because conventional copolymer characterization using the monomer reactivity ratio can estimate the codon compositions only at the ground-state sequence distribution,8 but not at controlled sequence distribution. This means that the impact of the controlled sequence on material performances cannot be quantitatively evaluated although various sequence-controlled polymerization methods have been developed thanks to the continuous effort from the polymer synthesis community. The well-known sequencing method utilizes nuclear magnetic resonance spectroscopy (NMR); depending on the adjacent monomer-unit species, the electronic environment surrounding the central monomer unit varies, inducing peak shifts. However, such shifts are often subtle and coupled with tacticity in most monomer combinations, allowing only qualitative analysis, e.g., see our previous attempts;9,10 therefore, NMR sequencing can only estimate the codon compositions of binary triads in very limited monomer combinations, which is insufficient and ineffective.7 As the complexity of codons increases with the length and monomer component number according to the system of interest, a data-driven approach accommodating this increasing complexity by expanding the dataset is attractive. Notably, if the codon composition of growing copolymers can be estimated in real time during the polymerization, the polymerization conditions could be autonomously tuned via reinforced learning11 so that the fraction of the theoretically designed codons would be maximized.
Toward practical sequence-engineering, herein, we propose a polymer sequencer quickly quantifying complex codon compositions in diverse multi-monomer systems based on ambient gas-phase mass spectrometry (MS)12 of pyrolyzed oligomeric fragments (Fig. 1A). The observed fragment pattern potentially reflects the codon compositions; however, direct peak-wise characterization is ineffective, because the peak intensities are strongly biased owing to different ionization efficiencies and regioselective thermal cleavages of chemically inequivalent main chains. Our key strategy towards codon quantification is to interpret the observed fragment pattern as that generated from a certain mixture of K-basis sequence-defined copolymers repeating single-codon species (Fig. 1A, here K = 5 for quantifying the simplest binary triad codons). The actual copolymer ensemble is an intra-chain mixture of codons; yet, via fragmentation, they can be likened to an inter-chain mixture whose fraction (c1,…,cK) represents the codon composition in the actual analyte. This interpretation is equivalent to assuming that any observed spectrum of the X/Y-copolymers can be approximated by a linear combination of K-basis spectra. To intuitively understand this key concept, consider an alternating-like copolymer ensemble as an example (Fig. 1A). Its spectrum should be most similar to that of the ideal alternating copolymer (XY)l with strong peaks of XYX and YXY codons. However, due to the imperfection of the alternating sequence, the XYX peak appeared much stronger than the YXY peak, indicating a significant contribution from the (XXY)l basis as well. Also, small peaks of blocky codons such as XXX and YYY were observed, indicating a small contribution from (XXX)l and (YYY)l basis spectra. Therefore, this observed spectrum would be best approximated by mixing the basis spectra of sequence-defined copolymers with different mixing ratios which would quantitatively indicate the sequence tendency of the analyte ensemble. If we can observe all the basis spectra, this process would be a routine spectral deconvolution. The difficulty is that sequence-defined copolymers are not synthesizable in reality, and thus, the basis spectra are not measurable. We overcome this issue by a data-driven approach; based on a lot of easily synthesizable random copolymers with different monomer compositions, each of which is interpretable as a mixture of sequence-defined copolymers, we would infer the basis spectra. The critical challenge here is thus summarized by the following question: can we infer the basis spectra of the pure constituents (i.e., references) only from the observed spectra of mixed samples? If this basis inference would become feasible, we can conduct quantitative compositional analysis on MS without using references—we therefore named this framework reference-free quantitative MS (RQMS)—which would solve the sequencing task as well via subsequent spectral deconvolution (Fig. 1B). Notably, the complexity of accessible codons is defined by the inferred basis number, and the inferable basis number is determined by the dataset size of random copolymer spectra; binary triad, binary pentad and ternary triad codons were quantifiable with five, nine, and 13 basis spectra, respectively, inferred from 30, 80 and 84 samples of random copolymers (see Fig. S1† for the basis number selection). Therefore, the larger dataset is fed, the more complex codon information RQMS would output, which goes beyond the analytical limitation of the conventional NMR sequencing as later shown.
In the remaining part of this paper, we first theoretically construct an RQMS algorithm. We then verify the RQMS accuracy with a benchmark compositional analysis of ternary homopolymer films. This is because the verification of RQMS sequencing result itself is very challenging owing to the lack of alternative sequencing methods. Via the benchmark test, we demonstrate that RQMS can conduct accurate compositional analysis without using the pure constituent spectra nor any prior knowledge about the constituents. We then apply RQMS for the sequencing purpose. The inferred basis spectra of sequence-defined copolymers look like real measured spectra with the corresponding codon peaks at consistent peak positions. Finally, we compare the RQMS sequencing result to the NMR and theoretically predicted sequence for verifying the accuracy of RQMS sequencing.
Development of RQMS
In this section, a spectrum is represented by a D-dimensional row vector,![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +1×D (D: channel number), storing the non-negative signal intensities at D-channels. The observed spectral set of the N-mixed samples is then represented by X ∈
+1×D (D: channel number), storing the non-negative signal intensities at D-channels. The observed spectral set of the N-mixed samples is then represented by X ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +N×D, where N-spectra are vertically stacked. The spectrum of the nth sample is located at the nth row, and represented as Xn:. The unmeasurable K-basis spectral set is then represented by P ∈
+N×D, where N-spectra are vertically stacked. The spectrum of the nth sample is located at the nth row, and represented as Xn:. The unmeasurable K-basis spectral set is then represented by P ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +K×D. Our mission is to infer the bases P from the observed spectral set X under the assumption that every observed spectrum Xn: can be approximated by linear combination of K-basis spectra:
+K×D. Our mission is to infer the bases P from the observed spectral set X under the assumption that every observed spectrum Xn: can be approximated by linear combination of K-basis spectra:where C ∈
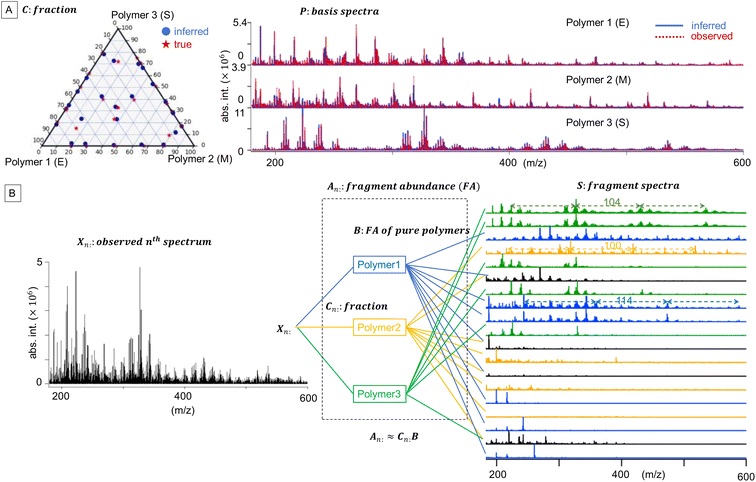
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +N×K represents the basis fractions, whose (n, k)-element represents the fraction of the kth basis in the nth sample, satisfying the sum-to-one condition in every sample. This can be simply written as X ≈ CP in the matrix form, which is called non-negative matrix factorization13–15 (NMF). This non-negative constraint is requested because both fractionation and spectral intensity cannot be negative. In this context, NMF is a mathematical expression of compositional analysis that simultaneously identifies bases P and their quantities C. If the dataset does not contain all K-basis spectra P, it corresponds to RQMS. The most significant difference between conventional quantitative MS and RQMS is that RQMS does not require the actual measurement of all basis spectra P. To verify RQMS accuracy, we designed a ternary film system composed of poly(ethyl methacrylate) (E), poly(methyl methacrylate) (M), and polystyrene (S). The dataset (data S2) consisted of 24 binary and ternary mixtures, whose highest fractions did not exceed 80 wt% (therefore, reference-free). The accuracy of the RQMS algorithm can be evaluated by checking if the output C and P are well consistent with the true composition and the observed pure E/M/S spectra. This was actually achieved, as shown in Fig. 2A. Even a biased dataset without samples beyond 40 wt% S-fraction gave an accurate estimation (Fig. S2†). However, direct and single-step NMF, X ≈ CP, yielded inaccurate results (Fig. S3†). This is because pyrolysis-MS does not measure polymers themselves, but measure their pyrolyzed fragments; therefore, the spectrally distinct and independent components are not K-polymers but their pyrolyzed M-fragments (K ≪ M). This problem is particularly acute when the basis polymers contain common sub-structures such as the polymer backbone, which can often occur in practical polymer science. In our benchmark test, E and M have identical methacrylic backbones, which would generate the same fragments (the black spectra in Fig. 2B). To conduct fragment-based NMF, we assume a latent hierarchical structure (Fig. 2B), where the kth basis polymer generates the mth fragment spectrum Sm: with a fragment abundance (FA) of Bkm (k = 1,…,K, m = 1,…,M), where S ∈
+N×K represents the basis fractions, whose (n, k)-element represents the fraction of the kth basis in the nth sample, satisfying the sum-to-one condition in every sample. This can be simply written as X ≈ CP in the matrix form, which is called non-negative matrix factorization13–15 (NMF). This non-negative constraint is requested because both fractionation and spectral intensity cannot be negative. In this context, NMF is a mathematical expression of compositional analysis that simultaneously identifies bases P and their quantities C. If the dataset does not contain all K-basis spectra P, it corresponds to RQMS. The most significant difference between conventional quantitative MS and RQMS is that RQMS does not require the actual measurement of all basis spectra P. To verify RQMS accuracy, we designed a ternary film system composed of poly(ethyl methacrylate) (E), poly(methyl methacrylate) (M), and polystyrene (S). The dataset (data S2) consisted of 24 binary and ternary mixtures, whose highest fractions did not exceed 80 wt% (therefore, reference-free). The accuracy of the RQMS algorithm can be evaluated by checking if the output C and P are well consistent with the true composition and the observed pure E/M/S spectra. This was actually achieved, as shown in Fig. 2A. Even a biased dataset without samples beyond 40 wt% S-fraction gave an accurate estimation (Fig. S2†). However, direct and single-step NMF, X ≈ CP, yielded inaccurate results (Fig. S3†). This is because pyrolysis-MS does not measure polymers themselves, but measure their pyrolyzed fragments; therefore, the spectrally distinct and independent components are not K-polymers but their pyrolyzed M-fragments (K ≪ M). This problem is particularly acute when the basis polymers contain common sub-structures such as the polymer backbone, which can often occur in practical polymer science. In our benchmark test, E and M have identical methacrylic backbones, which would generate the same fragments (the black spectra in Fig. 2B). To conduct fragment-based NMF, we assume a latent hierarchical structure (Fig. 2B), where the kth basis polymer generates the mth fragment spectrum Sm: with a fragment abundance (FA) of Bkm (k = 1,…,K, m = 1,…,M), where S ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +M×D represents the M-fragment spectra, and B ∈
+M×D represents the M-fragment spectra, and B ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +K×M represents the FA of the basis polymers. The observed spectrum of the nth sample then can be written as a linear combination of S:
+K×M represents the FA of the basis polymers. The observed spectrum of the nth sample then can be written as a linear combination of S:where A ≈ CB ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +N×M represents the sample-wise FA. Our developed RQMS algorithm first conducts fragment-based NMF, X ≈ AS, and subsequently second NMF, A ≈ CB, summarized as X ≈ AS ≈ CBS = CP, outputting the sample-wise fraction C and basis-polymer spectra P. The actual implementation is slightly more complicated, as depicted in Fig. S4 and S5.†
+N×M represents the sample-wise FA. Our developed RQMS algorithm first conducts fragment-based NMF, X ≈ AS, and subsequently second NMF, A ≈ CB, summarized as X ≈ AS ≈ CBS = CP, outputting the sample-wise fraction C and basis-polymer spectra P. The actual implementation is slightly more complicated, as depicted in Fig. S4 and S5.†
Because both NMFs are low-rank approximations, the fundamental driving force toward the optimum solution is identical: e.g., A and S are determined so that the squared residuals of X and AS are minimized while adhering to the non-negative constraints, i.e., 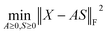 . A solution (A*,S*) derived from this criterion is, however, not unique even for a given component number M, as any non-singular Q ∈
. A solution (A*,S*) derived from this criterion is, however, not unique even for a given component number M, as any non-singular Q ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) M×M satisfying A*Q ≥ 0, Q−1S* ≥ 0 gives another solution (A*Q, Q−1S*).16 Imposing additional constraints is thus necessary to approach a better solution. Soft orthogonal constraints14,17,18 on the fragment spectra S are particularly effective for narrowing down the solution candidates, accounting for low yet non-zero possibilities that different fragments occupy common channels (full formulation in the ESI Computational Methods section†). NMF is called “unique” when Q is limited to the identity or permutation matrices.16 Importantly, the first NMF, X ≈ AS, is not unique because this is a spectral interpretation with no correct answer, whereas the second NMF, A ≈ CB, should be unique to determine the polymer fraction C with a single correct answer.19 The second NMF uniqueness can be ensured by minimizing the volume of the simplex, which is spanned by row-vectors of B and contains all the datapoints, i.e., row-vectors of A.15,20,21 The connection between the two non-unique and unique NMFs is key to the RQMS algorithm. For robustly outputting (C, B) from any “good enough” A, which is a non-unique solution of the first NMF, the factorization residual of the second NMF is evaluated using Riemannian metrics,22,23 considering the non-orthogonality of S (Fig. S6†). The component number M for the first NMF is unknown and thus statistically determined via automatic relevance determination (ARD),14,24 whereas K for the second NMF should be appropriately given depending on the analytical purpose (Fig. S1†). Two formulations were thus separately derived, as presented in the ESI Computational Methods section.†
M×M satisfying A*Q ≥ 0, Q−1S* ≥ 0 gives another solution (A*Q, Q−1S*).16 Imposing additional constraints is thus necessary to approach a better solution. Soft orthogonal constraints14,17,18 on the fragment spectra S are particularly effective for narrowing down the solution candidates, accounting for low yet non-zero possibilities that different fragments occupy common channels (full formulation in the ESI Computational Methods section†). NMF is called “unique” when Q is limited to the identity or permutation matrices.16 Importantly, the first NMF, X ≈ AS, is not unique because this is a spectral interpretation with no correct answer, whereas the second NMF, A ≈ CB, should be unique to determine the polymer fraction C with a single correct answer.19 The second NMF uniqueness can be ensured by minimizing the volume of the simplex, which is spanned by row-vectors of B and contains all the datapoints, i.e., row-vectors of A.15,20,21 The connection between the two non-unique and unique NMFs is key to the RQMS algorithm. For robustly outputting (C, B) from any “good enough” A, which is a non-unique solution of the first NMF, the factorization residual of the second NMF is evaluated using Riemannian metrics,22,23 considering the non-orthogonality of S (Fig. S6†). The component number M for the first NMF is unknown and thus statistically determined via automatic relevance determination (ARD),14,24 whereas K for the second NMF should be appropriately given depending on the analytical purpose (Fig. S1†). Two formulations were thus separately derived, as presented in the ESI Computational Methods section.†
Basis inference for binary triad sequencing
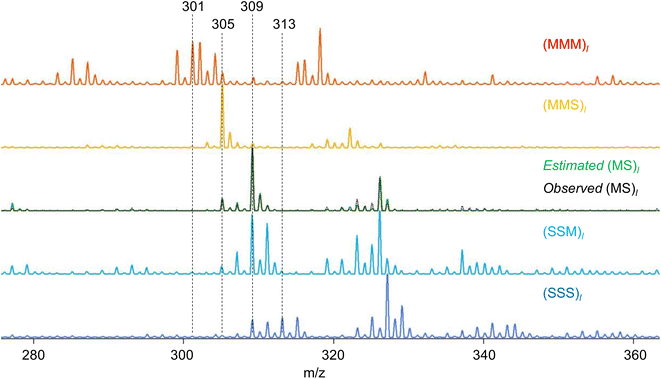
RQMS sequencing consists of two steps: inferring K-basis spectra P of sequence-defined copolymers composed of the single-codon species and deconvoluting the targeted spectrum Xt into P (Fig. 1B). As forementioned, the simplest binary and triad sequencing requires five-basis spectra of (XXX)l, (XXY)l, (XY)l, (YYX)l, and (YYY)l. As two of the five bases are synthesizable and, thus, referenceable homopolymers, the inference of the other bases should be reliable even if the dataset is biased, as demonstrated in the benchmark test (see Fig. S2†). For sequencing, a “biased” dataset indicates that at least one of the K-basis codons does not occupy a sufficiently high fraction in any samples.Since the accuracy of the RQMS algorithm has been ascertained in the benchmark test, the reliability of RQMS sequencing now depends on the validity of the linear combination model assuming that any copolymers can be approximated by linearly mixed sequence-defined copolymers (Fig. 1A). To verify this assumption, we began with M/S triad sequencing because the alternating copolymer (MS)l is exceptionally synthesizable25 (also see Fig. S7†), which allowed us to compare the inferred and measured (MS)l spectra. A dataset of 30 M/S random copolymers quickly prepared via free-radical copolymerization (data S3) was subjected to RQMS, outputting five-basis spectra (Fig. 3). They were attributable to (MMM)l, (MMS)l, (MS)l, (SSM)l, and (SSS)l based on the proton-adducted triad peaks at 301, 305, 305/309, 309, and 313 m/z reflecting the molecular weight difference between M (100) and S (104). The peak distributions are rational; e.g., (MMS)l generates only MSM and MMS triads at 305 m/z with the absence of the other triad peaks at 301, 309 and 313 m/z. Furthermore, the inferred and observed (MS)l spectra showed good consistency. (MS)l theoretically consists of an equivalent number of MSM and SMS triads; nevertheless, regioselective thermal cleavages and individually different ionization efficiencies biased the peak intensities (SMS ≫ MSM). Such coefficients were inexplicitly learned and embedded into the basis spectrum by the RQMS algorithm, allowing the precise basis inference. Note that the observed (MS)l spectrum was not included in the dataset and never used for the basis inference. This elucidated that the spectra of sequence-defined copolymers were accurately inferable only from a random copolymer dataset. No explicit instructions specifically oriented to sequencing were implemented in the RQMS algorithm, justifying the assumed linear combination model for reducing sequencing to compositional analysis (Fig. 1A).
Basis inference for ternary triad sequencing
For triad sequencing, J-multi (J ≥ 3) monomer systems require the basis number K = JC3 + 3JC2 + JC1. The three terms correspond to ternary, binary, and unary triad codons. We here demonstrate M/S/poly(butyl acrylate) (B) ternary triad sequencing, based on a dataset of 4 terpolymers and 80 binary copolymers (data S4). The output 13 basis spectra, including ternary-alternating (MSB)l basis, were rational spectra with consistent peak positions (Fig. S8†). In contrast to NMR sequencing, which is limited to J = 2, RQMS sequencing has no limitations for J thanks to the data-driven nature.Binary pentad sequencing
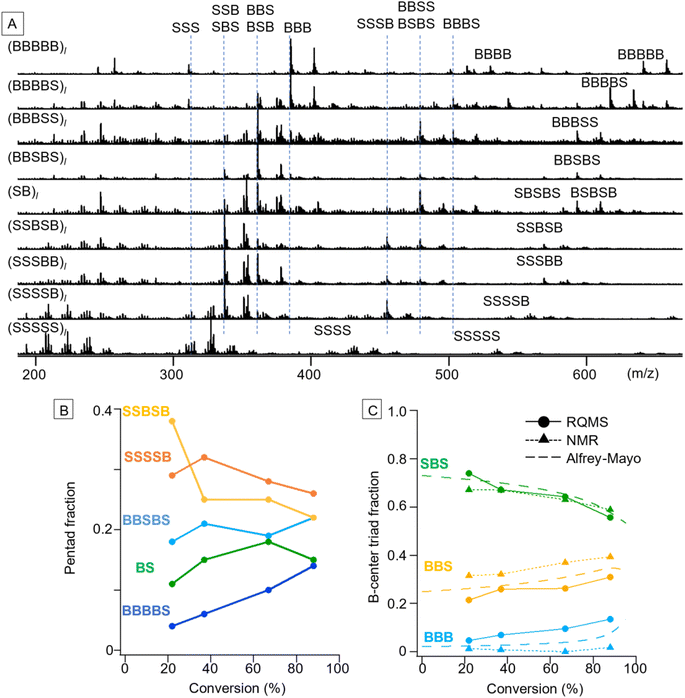
S/B binary pentad sequencing necessitated a more careful dataset design based on the monomer-reactivity ratio (Fig. S9†). Based on the 80 S/B binary copolymers (data S5), RQMS output nine basis spectra of pentad codons with reasonable peaks (Fig. 4A). The output tetrad/triad distributions were also appropriate; e.g., (BBBSS)l and (BBSBS)l spectra showed a pentad peak at identical positions (593 m/z for the proton adduct and 607 m/z for the ammonium adduct), but showed triad peaks at different positions owing to the presence or absence of the BBB triad (385 m/z). As another example, (SB)l had two pentads of BSBSB (607 m/z) and SBSBS (569 m/z), a single tetrad of BSBS (479 m/z) and two triads of BSB (361 m/z) and SBS (337 m/z).After the basis inference, spectral deconvolution is conducted by sequentially projecting the target spectrum Xt onto the inferred basis spectra (see the ESI “Sequential projection of a target pyrolysis-MS spectrum”† for the detailed procedure). The basis spectra are peculiar to the monomer combinations and invariant to polymerization conditions such as catalytic systems. Therefore, a different polymerization technique can be employed for the target copolymer synthesis from the one used for dataset preparation; e.g., the dataset and target copolymers, respectively, can be synthesized by simple free-radical copolymerization and living copolymerization. Furthermore, impurity signals on the target spectrum would be automatically filtered out when being projected onto the basis spectra, allowing semi-real-time direct sequencing from the polymerization solution without any chemical purification. By coupling with reversible addition–fragmentation chain-transfer (RAFT) polymerization using 2-(dodecylthiocarbonothioylthio)-2-methylpropionic acid (DDMAT) as a RAFT agent,1,26 varying codon distributions along the main chain were monitored (Fig. 4B and C). We selected S/B copolymers as targets, since their B-centered triad fractions can be obtained via NMR as well by decoupling their tacticity,27 allowing result verification (Fig. S10†). Reflecting the lower monomer reactivity of B as compared to S, the fractions of B-rich codons such as BBBBS and BBSBS increased as the copolymerization progressed (Fig. 4B). To verify this pentad sequencing result, the RQMS pentad fractions were downgraded to B-centered triad fractions (Fig. 4C, also see the ESI “Downgrading the S/B pentad-fraction”†), so that the RQMS sequencing result can be compared with NMR observations and theoretical predictions from the Alfrey–Mayo equation based on the monomer-reactivity ratio (rS, rB) = (0.70, 0.17)28 (see the ESI “Prediction of sequence distribution from the monomer reactivity ratio”†). The modulation of the B-centered triad fraction throughout the polymerization was consistent between the RQMS and theoretical prediction (Fig. 4C, the gap was within 5%), suggesting the validity of RQMS sequencing. On the other hand, a significant gap between RQMS and NMR was observed for BBS and BBB codon fractions. We cannot explicitly conclude which method was more accurate; however, NMR sequencing seems to have failed to capture the increasing trend of the BBB codon at the final polymerization stage, which was predicted by theory reflecting the lower monomer reactivity of B as compared to S. This could be attributable to the large peak fitting error in the NMR spectrum as shown in Fig. S10,† which may overestimate the BBS fraction and underestimate the BBB fraction.
Conclusions
In this paper, we proposed a sequencer determining the codon compositions of synthetic copolymers where polymer properties/functions could be encoded. Despite the lack of pure constituent codon spectra, unsupervised learning of random copolymer spectra allowed identification and quantification of the codons in the analyte. Unlike the conventional NMR sequencing, our method seems to have no restrictions on the applicable monomer combinations; nevertheless, sequencing of depolymerization-susceptible copolymers would be challenging. This is because a perfect depolymerization into single-monomer units would leave no clues of the original sequence. Such depolymerization would rarely occur in reality, since pyrolysis is conducted under ambient air. However, we already found that sequencing of methacrylic copolymer with a very bulky side-chain, such as adamantane groups, was challenging owing to the depolymerization issue even if pyrolysis was conducted under air. To aid such a problematic monomer chemistry, we are further developing an analytical system and algorithms. In this paper, we demonstrated that in versatile vinyl monomer systems the simplest codon compositions of binary triads were accurately determined with very small datasets (N ∼ 30). Thanks to the data-driven feature, the compositions of higher complex codons, e.g., binary pentads and ternary triads, were also accessible with the expanded datasets (N ∼ 80), which was beyond the analytical limit of conventional NMR sequencing. More complex codons would be accessible by further expanding the dataset. For stress-free preparation of a large dataset, feeding continuously changed monomer composition into a flow polymerization reactor seems very promising.29 Since random copolymers now become describable with their codon compositions, codon–property correlations can be quantitatively analyzed in the framework of material informatics.30 Furthermore, our semi-real-time sequencing directly applicable to growing copolymers in a polymerization solution would allow practical sequence-controlled polymerization in tandem with autonomous self-optimizing reactors.11 Overall, the proposed sequencer would facilitate sequence engineering towards innovative polymer materials.Data availability
All spectral datasets used in this study are available at https://doi.org/10.26434/chemrxiv-2022-mw76d-v2.Author contributions
Y. H. conceived the research, prepared the samples, developed the software, analyzed the data, and wrote the manuscript. S. U. conducted the pyrolysis-MS and NMR measurements. M. N. supervised the research.Conflicts of interest
Y. H. and M. N. are the owners of patent applications on RQMS and RQMS sequencing.Acknowledgements
The Core Research for Evolutional Science and Technology program of Japan Science and Technology Agency under Grant JPMJCR19J3 (to M. N.) is acknowledged.References
- J. F. Lutz, M. Ouchi, D. R. Liu and M. Sawamoto, Science, 2013, 341, 1238149 CrossRef PubMed.
- M. W. Urban, D. Davydovich, Y. Yang, T. Demir, Y. Zhang and L. Casabianca, Science, 2018, 362, 220–225 CrossRef CAS PubMed.
- T. Jiang, A. Hall, M. Eres, Z. Hemmatian, B. Qiao, Y. Zhou, Z. Ruan, A. D. Couse, W. T. Heller, H. Huang, M. O. de la Cruz, M. Rolandi and T. Xu, Nature, 2020, 577, 216–220 CrossRef CAS PubMed.
- M. Shin, H. Kim, G. Park, J. Park, H. Ahn, D. K. Yoon, E. Lee and M. Seo, Nat. Commun., 2022, 13, 2433 CrossRef CAS PubMed.
- M. A. Webb, N. E. Jackson, P. S. Gil and J. J. de Pablo, Sci. Adv., 2020, 6, eabc6216 CrossRef PubMed.
- T. Zhou, Z. Wu, H. K. Chilukoti and F. Müller-Plathe, J. Chem. Theory Comput., 2021, 17, 3772–3782 CrossRef CAS PubMed.
- H. Mutlu and J. F. Lutz, Angew. Chem., Int. Ed., 2014, 53, 13010–13019 CrossRef CAS PubMed.
- F. R. Mayo and F. M. Lewis, J. Am. Chem. Soc., 1944, 66, 1594–1601 CrossRef CAS.
- Y. Hibi, M. Ouchi and M. Sawamoto, Angew. Chem., Int. Ed., 2011, 50, 7434–7437 CrossRef CAS PubMed.
- Y. Hibi, S. Tokuoka, T. Terashima, M. Ouchi and M. Sawamoto, Polym. Chem., 2011, 2, 341–347 RSC.
- M. Rubens, J. H. Vrijsen, J. Laun and T. Junkers, Angew. Chem., Int. Ed., 2019, 58, 3183–3187 CrossRef CAS PubMed.
- J. H. Gross, Anal. Bioanal. Chem., 2014, 406, 63–80 CrossRef CAS PubMed.
- D. D. Lee and H. S. Seung, Nature, 1999, 401, 788–791 CrossRef CAS PubMed.
- M. Shiga, K. Tatsumi, S. Muto, K. Tsuda, Y. Yamamoto, T. Mori and T. Tanji, Ultramicroscopy, 2016, 170, 43–59 CrossRef CAS PubMed.
- X. Fu, K. Huang, B. Yang, W. K. Ma and N. D. Sidiropoulos, IEEE Trans. Signal Process., 2016, 64, 6254–6268 Search PubMed.
- D. Donoho and V. Stodden, Advances in Neural Information Processing Systems 16, MIT Press, Cambridge, Massachusetts, 2003 Search PubMed.
- C. Ding, T. Li, W. Peng and H. Park, Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining, 2006, pp. 126–135, DOI:10.1145/1150402.1150420.
- K. Kimura, Y. Tanaka, M. Kudo, D. Phung and H. Li, J. Mach. Learn. Res., 2014, 39, 129–141 Search PubMed.
- H. Laurberg, M. G. Christensen, M. D. Plumbley, L. K. Hansen and S. H. Jensen, Comput. Intell. Neurosci., 2008, 764206 Search PubMed.
- M. D. Craig, IEEE Trans. Geosci. Rem. Sens., 1994, 32, 542–552 CrossRef.
- L. Miao and H. Qi, IEEE Trans. Geosci. Rem. Sens., 2007, 45, 765–777 Search PubMed.
- W. Liu and N. Zheng, Pattern Recogn. Lett., 2004, 25, 893–897 CrossRef.
- T. Yoshida, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2011, vol. 6804 LNAI, pp. 214–219 Search PubMed.
- V. Y. F. Tan and C. Févotte, IEEE Trans. Pattern Anal. Mach. Intell., 2013, 35, 1592–1605 Search PubMed.
- H. Hirai, T. Tanabe and H. Koinuma, J. Polym. Sci., Polym. Chem. Ed., 1979, 17, 843–857 CrossRef CAS.
- G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2012, 65, 985–1076 CrossRef CAS.
- A. S. Brar and C. V. V. Satyanarayana, Polym. J., 1992, 24, 879–887 CrossRef CAS.
- L. K. Kostanski and A. E. Hamielec, Polymer, 1992, 33, 3706–3710 CrossRef CAS.
- M. H. Reis, C. L. G. Davidson IV and F. A. Leibfarth, Polym. Chem., 2018, 9, 1728–1734 RSC.
- T. S. Lin, C. W. Coley, H. Mochigase, H. K. Beech, W. Wang, Z. Wang, E. Woods, S. L. Craig, J. A. Johnson, J. A. Kalow, K. F. Jensen and B. D. Olsen, ACS Cent. Sci., 2019, 5, 1523–1531 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06974a |
| This journal is © The Royal Society of Chemistry 2023 |