Thermodynamic mechanism of controllable growth of two-dimensional uniformly ordered boron-doped graphene†
Yuansen
Zhu
,
Xiaoshu
Gong
,
Liang
Ma
 * and
Jinlan
Wang
* and
Jinlan
Wang

School of Physics, Southeast University, Nanjing 211189, China. E-mail: liang.ma@seu.edu.cn
First published on 21st December 2022
Abstract
Two-dimensional (2D) boron-doped graphene (B–G) exhibits remarkable properties for advanced applications in electronics, sensing and catalysis. However, the synthesis of large-area uniformly ordered 2D B–G remains a grand challenge due to the low doping level and uncontrolled distribution of dopants or even the phase separation from the competitive growth of boron polymorphs and graphene. Here, we theoretically explored the mechanism of the epitaxial growth of 2D uniformly ordered B–G on a metal substrate via ab initio calculations. We show that, by establishing the substrate-mediated thermodynamic phase diagrams, the controllable growth of 2D ordered B–G with different B/C stoichiometry can be achieved on appropriate substrates within distinct chemical potential windows of the feedstock by beating the competitive growth of graphene and other impurity phases. It is suggested that a suitable substrate for the controllable epitaxial growth of 2D ordered B–G can be efficiently screened based on the symmetry match and interaction between 2D B–G and the surfaces. Importantly, by carefully considering the chemical potential of boron/carbon as a function of temperature and partial pressure of the feedstock with the aid of the standard thermochemical tables, the optimal experimental parameters for the controllable growth of 2D ordered B–G are also suggested accordingly. This work provides a comprehensive and insightful understanding of the mechanism of controllable growth of 2D B–G, which will guide future experimental design.
New conceptsThe growth of large-area 2D uniformly ordered boron-doped graphene (B–G) is a grand challenge due to the low doping level and phase separation issue. Here we show that, by establishing the substrate-mediated thermodynamic phase diagrams, the controllable growth of 2D ordered B–G with different B/C stoichiometry can be achieved on a pre-selected substrate within distinct chemical potential windows of the feedstock by beating the competitive growth of graphene and other impurity phases, where a suitable substrate is efficiently screened based on the symmetry match and surface interaction with 2D B–G. More importantly, the optimal experimental parameters for the controllable growth of 2D ordered B–G are also suggested according to the standard thermochemical tables. This work not only provides a comprehensive and insightful understanding of the mechanism of controllable growth of 2D B–G but also can be reasonably extended to guide the controllable growth of other 2D doped systems. |
Introduction
Doping of heteroatoms with different electron configurations can efficiently tailor the chemical and electronic properties of two-dimensional (2D) graphene, which will lead to diverse applications of doped graphene.1,2 Since boron (B) has one valence electron less than the carbon host but similar atomic radii, B doping in graphene will act like an electron deficiency or hole additive and thus has been suggested to be an efficient way to tune the electronic properties of graphene while avoiding significant structural changes.3–5 Previous studies have confirmed the characteristics of p-type semiconductors of boron doped graphene (B–G)6,7 and explored the potential usage of B–G in electronic devices,8 where B doping is usually conducted through ex situ processes experimentally.9It was shown that B–G can be applied as a channel material for high-performance field effect transistors (FETs) or as cathode material for high-power lithium-ion batteries.8,10 B–G also exhibits great prospects in the fields of photocatalysis and photo-electronics. For example, the reduction of highly active and selective oxygen to H2O2 with B–G as the catalyst can achieve higher productivity than the most advanced carbon oxide catalysts in industrial production.11 B–G can also be adopted as an efficient metal-free electrocatalyst for the electrochemical reduction of nitrogen in aqueous solution.12 In addition, complexes of B–G and TiO2 nanoparticles have shown potential application in CO2 photo-reduction since the holes in B–G can be effectively transferred to TiO2.13 Furthermore, it was also experimentally demonstrated that B doping in graphene could lead to a much-enhanced sensitivity for detecting trace amounts of molecules of toxic gases.14 Besides, ab initio molecular dynamics simulations elucidate that B doping can significantly improve the gas adsorption performance of graphene, thus promoting the hydrogen storage capacity.15
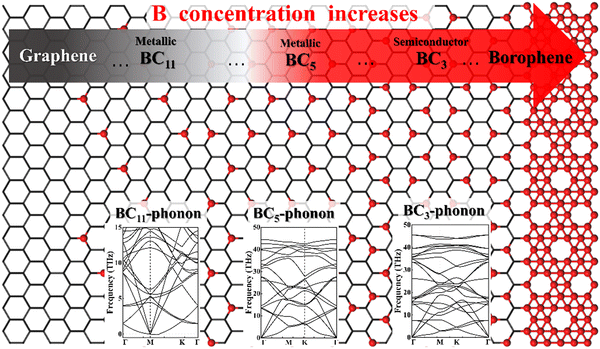
Obviously, the properties and applications of B–G are highly dependent on the doping concentration and distribution of B atoms.7 For instance, it was theoretically predicted that 2D uniformly ordered BC5 shows metallic characters while BC3 behaves as a semiconductor. Therefore, the preparation of large area high-quality 2D uniformly ordered B–G structures with effective control over the concentration and distribution of B doping is crucial for their real application. However, the substitutional doping of B atoms into the honeycomb-like carbon sp2 network of graphene is rather difficult due to the strong C–C bonds. Density functional theory (DFT) calculations revealed that displacing C atoms from the graphene lattice with boron atoms is associated with a large activation energy barrier of ∼1.3 eV.16 In addition, it is suggested theoretically that the presence of three or more boron atoms within a single six-member ring leads to conspicuous deformations, while one or two boron atoms per hexagonal ring were found to be able to form stable heteroatomic nanostructures.17 For this reason, the experimentally realized doping level of B atoms in graphene is fairly low. Moreover, a significant characteristic of the boron element is its polymorphism.18,19 Actually, a variety of planar or quasi-planar boron clusters with medium sizes have been predicted, such as B12, B13, B19 and B36, where the B12 appears as the energetically more preferred one.20–26 Hence, due to the competitive formations of graphene and boron polymorphs, phase separation is highly expected in the growth of B–G, which will lead to the uncontrolled doping concentration and distribution of B atoms.27
A few initial attempts at the synthesis of B–G have been conducted recently with some prototype devices based on B–G being demonstrated. For example, B–G nanoribbons have been prepared via surface assisted reaction by using organic-boron as the precursor28 or via the reactive microwave plasma method by using B(CH3)3 as the precursor.8 The chemical vapor deposition (CVD) method, which was widely employed to produce large-area high quality graphene, has also been used for the growth of B–G.10,12,15,28,29 However, the controllable growth of large-area 2D uniformly ordered B–G film has not yet been experimentally realized due to the low doping level and phase separation issues, which severely hinder the theoretical and experimental studies of 2D ordered B–G. A comprehensive mechanistic study with atomic-level insight into the controllable growth of 2D uniformly ordered B–G is urgently needed. Here, we theoretically explore the mechanism of the controllable growth of two uniformly ordered phases of 2D B–G, namely, BC3 and BC5, on catalytic metal surfaces based on ab initio DFT calculations. Our study indicates that the controllable growth of 2D uniformly ordered BC3 and BC5 can be reasonably realized by choosing an appropriate substrate and carefully adjusting the experimental conditions.
Method and models
All the DFT calculations were performed by using the Vienna Ab initio Simulation Package (VASP).30,31 The Perdew–Burke–Ernzerhof (PBE) functional32 was used to describe the exchange and correlation, and the electronic interaction was described by the projector augmented wave (PAW) potential. The Monkhorst–Pack k-point sampling32 parameters were carefully tested to produce convergent results. The DFT-D3 scheme was applied to treat the interlayer van der Waals (vdW) interactions.33 All structures were fully optimized until the force component on each atom was less than 0.02 eV Å−1 with an energy convergence of 10−4 eV. The energy cutoff of the plane-wave basis was 400 eV.When calculating the formation enthalpy of 2D B–G on both C2V and C6V surfaces, slab models consisting of three atomic layers with bottom layer atoms fixed were constructed to mimic the epitaxial substrate. The supercells of 2D B–G and epitaxial substrates are carefully constructed to ensure that the lattice mismatch is less than ∼5%.34 In addition, the 2D B–G was slightly stretched or compressed to match that of the substrates. The initial distance between the 2D B–G sheets and surfaces was set to 3.00 Å during the calculations. A vacuum space of >15 Å was set to separate images along the vertical direction of the supercell to avoid suspicious interactions between adjacent images.
Results and discussion
There are a variety of possible ordered phases of 2D B–G with distinct B/C stoichiometry. However, it is suggested by the previous literature that the presence of three or more boron atoms within one six-member ring leads to conspicuous deformations.17 In other words, over high B/C ratio (high B concentration) renders the 2D B–G system highly hole-rich and therefore highly active/unstable. In contrast, 2D ordered B–G compounds with low B concentration are predicted to show better stability. Indeed, our calculations reveal that there is no imaginary frequency band in the phonon spectrum of BC3 and BC5, both of which are representative examples of 2D uniformly ordered 2D B–G with low B concentration. We thus mainly focus on BC3 and BC5 in the present work. In addition, another 2D B–G compound, BC11, with lower boron concentration as well as negligible phonon spectrum imaginary frequency bands was also considered (Fig. 1). Thermodynamic competitions among distinct phases of 2D B–G with different B/C ratios are expected to play vital roles during epitaxial CVD growth. Moreover, the elementary substance of carbon and boron, graphene and B12 molecules, would also be the competitive phases to disturb the controllable growth of ordered 2D B–G. To figure out the thermodynamic competitions, which depend on the chemical potential of the carbon and boron source, we define the formation enthalpy (ΔH) of dangling 2D B–G at 0 K as (1): | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 or 1
5 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11. μC(graphene)/μB(B12) is the chemical potential of the carbon/boron atoms in graphene/B12 molecules. The ΔH of graphene/B12 at 0 K equals zero based on such a definition. In order to stimulate the growth of 2D B–G, the chemical potential of carbon and boron μC/μB from the feedstock35 must satisfy the following eqn (2) as required in thermodynamics:
11. μC(graphene)/μB(B12) is the chemical potential of the carbon/boron atoms in graphene/B12 molecules. The ΔH of graphene/B12 at 0 K equals zero based on such a definition. In order to stimulate the growth of 2D B–G, the chemical potential of carbon and boron μC/μB from the feedstock35 must satisfy the following eqn (2) as required in thermodynamics: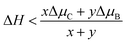 | (2) |
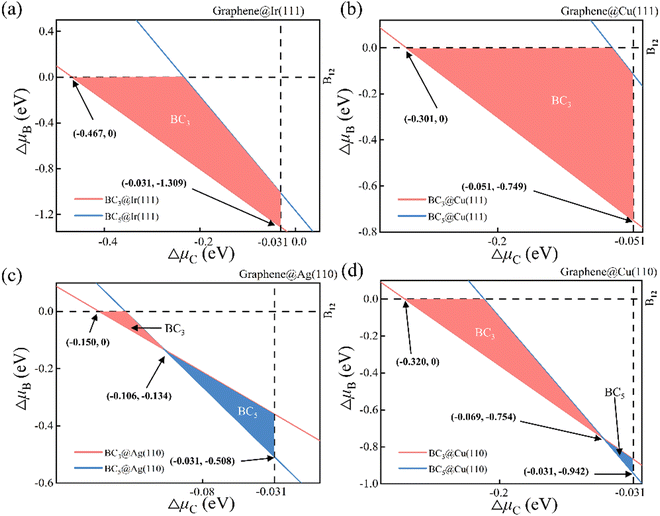
The phase diagram of suspending BC3 and BC5 under vacuum is attained accordingly as shown in Fig. S1 (ESI†) based on the thermodynamic conditions of eqn (2). Each line in the phase diagram divides the μC − μB phase space into two sectors, where the upper sector favors the formation of the corresponding 2D B–G while the lower sector is unfavorable for the formation. Obviously, the unmarked upper sector of the phase diagram allows the formation of both BC3 and BC5 while the unmarked lower part rejects both. The marked in-between sector of the phase diagram may lead to the selective formation of either BC3 or BC5. The areas painted in pink and blue denote the selective formation windows of BC3 and BC5, respectively. Note that the reference phase of carbon and boron, namely the graphene (vertical dash line μC = 0) and B12 (horizontal dash line μB = 0), may also be formed in the condition of μC > 0 eV and μB > 0 eV, respectively. Thus, the graphene and B12 molecule will serve as main competitors to disturb the growth of 2D B–G. The formation of graphene and B12 will inevitably introduce solid impurities in 2D B–G and may even cause the phase separation issue. The thermodynamic phase diagram of suspending 2D B–G indicates that controllable growth of BC3 and BC5 is feasible within certain chemical potential windows of μC and μB, which may be achieved by selecting proper epitaxial substrates and carefully tuning the experimental parameters.
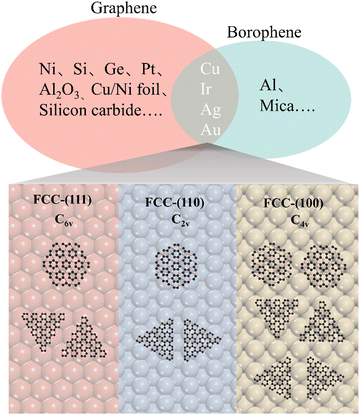
It is known that an epitaxial substrate is very important for the CVD growth of 2D materials in terms of surface interaction and symmetry match.36,37 Since the interaction between the substrate and carbon or boron atoms would be different, it is thus reasonably suggested that the intersection group of substrates used for both graphene and borophene growth could be more suitable for the epitaxial growth of 2D B–G. According to this simple theoretical assumption, four metal substrates Cu, Au, Ag,38 Ir27 have been successfully picked out from the intersection group to serve as the potential epitaxial substrates for the growth of 2D B–G, as shown in Fig. 2. Furthermore, a previous report suggested that the interplay between the symmetries of the epitaxial substrates and 2D materials is of vital significance to determine the crystal orientation, morphology and domain size in the epitaxial growth of 2D materials.39 Consequently, the symmetry match between possible epitaxial substrates and 2D B–G must be well concerned to attain the single crystal growth of 2D B–G. Surfaces with six-fold or two-fold symmetry may be employed for the epitaxial growth of the single crystal of 2D B–G in light of the theoretical analysis of the symmetry rules of preferential alignment of 2D materials on epitaxial substrates,39 as BC3 presents six-fold symmetry while BC5 exposes three-fold symmetry. As shown in Fig. 2, BC3 tends to unidirectionally align on either six-fold or two-fold surfaces whereas two/four energetically equivalent antiparallel orientations appear for the nucleation of BC3/BC5 on four-fold symmetric epitaxial surfaces due to the symmetry mismatch, which is more unfavorable for the single crystal growth. Accordingly, the single crystal growth of BC3 and less crystalline orientation growth of BC5 could be possible on the six-fold and two-fold epitaxial substrates. What's more, Al is excluded as a result of the incompatibility between Al and the common boron source B2H6. Thus, we consider the face-centered cubic (fcc) Cu(111), Ag(111), Au(111) and Ir(111) surfaces with six-fold symmetry and Cu(110), Ag(110), Au(110) and Ir(110) surfaces with two-fold symmetry to act as the potential epitaxial surfaces for the growth of 2D B–G in this work.
The strong surface interaction will be beneficial for the epitaxial growth of 2D B–G. Therefore, we extract the vdW interaction (EvdW) between 2D B–G and epitaxial surfaces via DFT calculations, which is defined as:
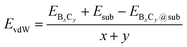 | (3) |
By considering the symmetry of both 2D B–G and metal surfaces, we calculated the vdW interactions of various configurations where the 2D B–G shows different rotation angles θ = 0° (zigzag (ZZ)//substrate 〈110〉) and 30° (armchair (AC)//substrate 〈110〉) with respect to the 8 types of substrate except for the case of BC5-30° on the Ir(111) surface as the corresponding supercell is too large to be computationally affordable. Here the lattice mismatch is defined as eqn (4):
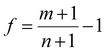 | (4) |
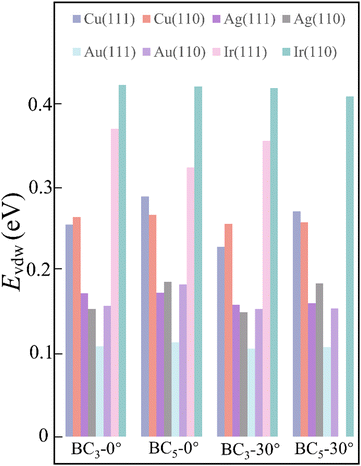 | ||
| Fig. 3 The vdW interaction between 2D B–G and various metal surfaces with rotation angle of 0° and 30°, respectively. | ||
To investigate the thermodynamic equilibrium of 2D B–G on epitaxial surfaces, eqn (1) can be modified as:
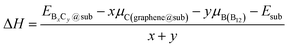 | (5) |
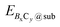 and Esub represent the energies of the substrate with and without the 2D B–G, respectively.
and Esub represent the energies of the substrate with and without the 2D B–G, respectively.
The thermodynamic phase diagrams of 2D B–G on different metal surfaces are shown in Fig. 4 and Fig. S2 (ESI†) according to eqn (2) and (5). It is suggested that the selective growth of BC3 is feasible on Cu(111), Ir(111), Ir(110) and Au(111) surfaces while the growth of BC5 may only be feasible on the Ag(111) surface. Note that the controllable growth of both BC3 and BC5 can be achieved on Cu(110), Ag(110) and Au(110) surfaces by beating the competition growth of graphene, where the product's transition between BC3 and BC5 on Cu(110), Ag(110) and Au(110) surfaces occurs around certain μC and μB (see Fig. 4(c), (d) and Fig. S2d, ESI†). Our calculations demonstrated that the eight investigated surfaces are all possible for the single crystal growth of BC3 or BC5 with appropriate μB and μC.
So far, B–G has been experimentally synthesized by using reactive microwave plasma with B(CH3)3 as the precursor,8 by the surface chemical reaction with organoboron as the precursors28 or via simultaneous reduction of boron-doped graphene oxide at high annealing temperatures,40etc. However, none of these methods can accurately control the coordination environment of boron compared to chemical vapor deposition (CVD), which is a more effective method for the synthesis of B–G films, such as growing on polycrystalline copper foils using a mixture of CH4, H2 and B2H6 gases at 1000 °C.41 The doped graphene film produced by CVD is utilized mainly for the thin film-based electronic devices, which prefer a clean and pollution-free environment. Therefore, the CVD manufacturing process of using gas as the feedstock of doping atoms and carbon is more preferred, which can reduce the difficulty of cleaning the generated impurities. Here, B2H6 and CH4 are considered as the feedstock of boron and carbon in our calculations, respectively.
Actually, in practical CVD growth the μC or μB will be variable in a wide range as a function of temperature and pressure of the feedstock. Nevertheless, the previously mentioned formation enthalpy of 2D B–G is calculated by using the static energy of the graphene sheet and B12 molecule at 0 K as the reference of μC and μB, which cannot be utilized to directly guide the experimental study. To fill this gap, it would be highly desirable to provide the optimal experimental conditions for the controllable growth of high-quality 2D B–G by probing the thermal equilibrium between the grown 2D B–G and feedstock. To this end, we manage to establish the relationship between the chemical potential of carbon/boron and the typical experimental growth parameters, temperature and partial pressure of the feedstock, based on the NIST-JANAF thermochemical tables. At the given partial pressure (P) and temperature (T), the chemical potential of carbon from the hydrocarbon (CH4) feedstock, by using the chemical potential of graphene per atom as the reference, can be defined as (see ESI† for more details):
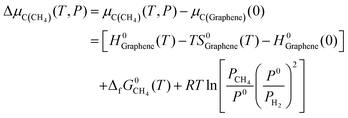 | (6) |
Similarly, at the given partial pressure and temperature, the chemical potential of boron from the feedstock of B2H6, by taking the energy of the B12 molecule per atom as the reference, is expressed as (see ESI† for more details):
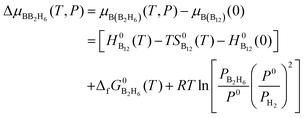 | (7) |
Thus, the optimal experimental conditions for the controllable growth of high quality 2D B–G can be easily obtained according to eqn (6) and (7). As presented in Fig. 5, the selective growth of 2D B–G can be achieved under appropriate temperatures and moderate partial pressure by using CH4 and B2H6 as feedstocks. It is found that the appropriate experimental parameters can be straightforwardly figured out from the chart for realizing the controllable growth of targeted 2D B–G. In other words, the experimental condition data where the selective growth of BC3 and BC5 on distinct surfaces can be realized, where the required temperature range can be easily grabbed at a certain partial pressure. Taking the case of BC3 on Ag(110) as an example, the selective growth can be realized when the partial pressure of B2H6 ∼ 10−6 MPa and that of CH4 ∼ 107 MPa under the temperature range of 750–1000 K.
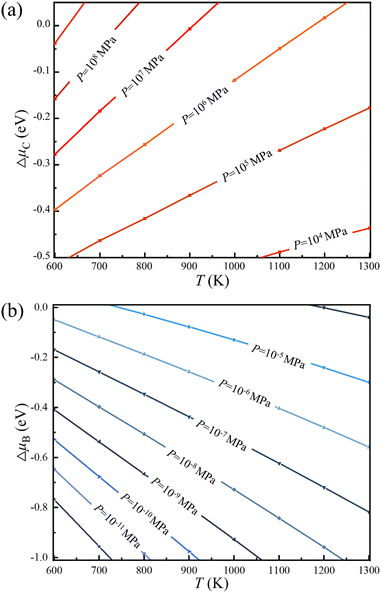 | ||
| Fig. 5 Chemical potential of (a) carbon and (b) boron under specific experimental parameters of temperature and partial pressure (PH2 = 10 MPa), respectively. | ||
Conclusion
To conclude, we theoretically investigate the thermodynamic mechanism of epitaxial growth of 2D uniformly ordered B–G, BC3 and BC5, on metal substrates by means of DFT calculations. It is suggested that the controllable growth of 2D ordered B–G on metal substrates can be achieved under distinct chemical potential windows of B/C feedstock by carefully considering the interfacial interaction and symmetry match between 2D B–G films and the metal substrates. Our results indicate that the 2D BC3 can be grown on almost all the investigated substrates except for the Ag(111) surface while the selective growth of BC5 may be possible on Cu(110), Ag(110), Ag(111) and Au(110) surfaces. Furthermore, the optimal experimental parameters, including the temperature and partial pressure, for the controllable growth of 2D ordered B–G are also proposed by taking the thermal equilibrium between the 2D B–G and feedstock into consideration. Our study provides useful guidelines for the future experimental design of the epitaxial controllable growth of 2D ordered B–G.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Natural Science Foundation of China (No. 22222302, 22033002, 21903014), the National Key Research and Development Program of China (2021YFA1500703), the “Shuang Chuang” Talent Program (JSSCRC2021489) and the Basic Research Program (grant no. BK20190328) of Jiangsu Province, and the Fundamental Research Funds for the Central Universities (2242021K10009). The authors acknowledge the computational resources from the Big Data Center of SEU and the National Supercomputing Center in Tianjin.References
- X. Xu, C. Liu, Z. Sun, T. Cao, Z. Zhang, E. Wang, Z. Liu and K. Liu, Chem. Soc. Rev., 2018, 47, 3059–3099 RSC.
- X. Wang, G. Sun, P. Routh, D.-H. Kim, W. Huang and P. Chen, Chem. Soc. Rev., 2014, 43, 7067–7098 RSC.
- X. Li, L. Fan, Z. Li, K. Wang, M. Zhong, J. Wei, D. Wu and H. Zhu, Adv. Energy Mater., 2012, 2, 425–429 CrossRef CAS.
- S. Agnoli and M. Favaro, J. Mater. Chem. A, 2016, 4, 5002–5025 RSC.
- C. N. R. Rao, K. Gopalakrishnan and A. Govindaraj, Nano Today, 2014, 9, 324–343 CrossRef CAS.
- T. B. Martins, R. H. Miwa, A. J. R. da Silva and A. Fazzio, Phys. Rev. Lett., 2007, 98, 196803 CrossRef CAS PubMed.
- A. Lherbier, X. Blase, Y.-M. Niquet, F. Triozon and S. Roche, Phys. Rev. Lett., 2008, 101, 036808 CrossRef PubMed.
- Y.-B. Tang, L.-C. Yin, Y. Yang, X.-H. Bo, Y.-L. Cao, H.-E. Wang, W.-J. Zhang, I. Bello, S.-T. Lee, H.-M. Cheng and C.-S. Lee, ACS Nano, 2012, 6, 1970–1978 CrossRef CAS PubMed.
- J. Wu, M.-T. F. Rodrigues, R. Vajtai and P. M. Ajayan, Adv. Mater., 2016, 28, 6239–6246 CrossRef CAS PubMed.
- Z.-S. Wu, W. Ren, L. Xu, F. Li and H.-M. Cheng, ACS Nano, 2011, 5, 5463–5471 CrossRef CAS PubMed.
- Y. Xia, X. Zhao, C. Xia, Z.-Y. Wu, P. Zhu, J. Y. Kim, X. Bai, G. Gao, Y. Hu, J. Zhong, Y. Liu and H. Wang, Nat. Commun., 2021, 12, 4225 CrossRef CAS PubMed.
- X. Yu, P. Han, Z. Wei, L. Huang, Z. Gu, S. Peng, J. Ma and G. Zheng, Joule, 2018, 2, 1610–1622 CrossRef CAS.
- M. Xing, F. Shen, B. Qiu and J. Zhang, Sci. Rep., 2014, 4, 1–7 Search PubMed.
- R. Lv, G. Chen, Q. Li, A. McCreary, A. Botello-Méndez, S. V. Morozov, L. Liang, X. Declerck, N. Perea-López, D. A. Cullen, S. Feng, A. L. Elías, R. Cruz-Silva, K. Fujisawa, M. Endo, F. Kang, J.-C. Charlier, V. Meunier, M. Pan, A. R. Harutyunyan, K. S. Novoselov and M. Terrones, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14527–14532 CrossRef CAS PubMed.
- S. Nachimuthu, P.-J. Lai, E. G. Leggesse and J.-C. Jiang, Sci. Rep., 2015, 5, 1–8 Search PubMed.
- L. Tsetseris and S. T. Pantelides, Carbon, 2014, 67, 58–63 CrossRef CAS.
- V. V. Chaban and O. V. Prezhdo, Nanoscale, 2016, 8, 15521–15528 RSC.
- B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668 CrossRef CAS PubMed.
- T. Ogitsu, E. Schwegler and G. Galli, Chem. Rev., 2013, 113, 3425–3449 CrossRef CAS PubMed.
- J.-i Aihara, J. Phys. Chem. A, 2001, 105, 5486–5489 CrossRef CAS.
- J. E. Fowler and J. M. Ugalde, J. Phys. Chem. A, 2000, 104, 397–403 CrossRef CAS.
- W. Huang, A. P. Sergeeva, H.-J. Zhai, B. B. Averkiev, L.-S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206 CrossRef CAS PubMed.
- Z. A. Piazza, H.-S. Hu, W.-L. Li, Y.-F. Zhao, J. Li and L.-S. Wang, Nat. Commun., 2014, 5, 3113 CrossRef PubMed.
- I. A. Popov, Z. A. Piazza, W.-L. Li, L.-S. Wang and A. I. Boldyrev, J. Chem. Phys., 2013, 139, 144307 CrossRef PubMed.
- A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W.-L. Li, C. Romanescu, L.-S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358 CrossRef CAS PubMed.
- H.-J. Zhai, B. Kiran, J. Li and L.-S. Wang, Nat. Mater., 2003, 2, 827–833 CrossRef CAS PubMed.
- X. Liu, Q. Li, Q. Ruan, M. S. Rahn, B. I. Yakobson and M. C. Hersam, Nat. Mater., 2022, 21, 35–40 CrossRef CAS PubMed.
- S. Kawai, S. Saito, S. Osumi, S. Yamaguchi, A. S. Foster, P. Spijker and E. Meyer, Nat. Commun., 2015, 6, 8098 CrossRef CAS PubMed.
- D. Wei, Y. Liu, Y. Wang, H. Zhang, L. Huang and G. Yu, Nano Lett., 2009, 9, 1752–1758 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Liu and J. Zhang, Chem. Rev., 2020, 120, 2123–2170 CrossRef CAS PubMed.
- M. W. Chase, J. Phys. Chem. Ref. Data, 1996, 25, 551–603 CrossRef CAS.
- R. Dong, X. Gong, J. Yang, Y. Sun, L. Ma and J. Wang, Adv. Mater., 2022, 34, 2201402 CrossRef CAS PubMed.
- H. Fang, B. Wang, X. Zhang, Y. Guo, L. Ma and J. Wang, Comput. Mater. Sci., 2021, 198, 110688 CrossRef CAS.
- B. Kiraly, E. V. Iski, A. J. Mannix, B. L. Fisher, M. C. Hersam and N. P. Guisinger, Nat. Commun., 2013, 4, 2804 CrossRef.
- J. Dong, L. Zhang, X. Dai and F. Ding, Nat. Commun., 2020, 11, 5862 CrossRef CAS PubMed.
- D.-Y. Yeom, W. Jeon, N. D. K. Tu, S. Y. Yeo, S.-S. Lee, B. J. Sung, H. Chang, J. A. Lim and H. Kim, Sci. Rep., 2015, 5, 9817 CrossRef CAS PubMed.
- L. Zhao, M. Levendorf, S. Goncher, T. Schiros, L. Pálová, A. Zabet-Khosousi, K. T. Rim, C. Gutiérrez, D. Nordlund, C. Jaye, M. Hybertsen, D. Reichman, G. W. Flynn, J. Park and A. N. Pasupathy, Nano Lett., 2013, 13, 4659–4665 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00507g |
| This journal is © The Royal Society of Chemistry 2023 |