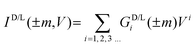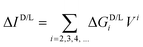Transverse magnetoconductance in two-terminal chiral spin-selective devices†
Md Anik
Hossain
 a,
Sara
Illescas-Lopez
a,
Sara
Illescas-Lopez
 b,
Rahul
Nair
ac,
Juan Manuel
Cuerva
b,
Rahul
Nair
ac,
Juan Manuel
Cuerva
 b,
Luis
Álvarez de Cienfuegos
b,
Luis
Álvarez de Cienfuegos
 bd and
Sandipan
Pramanik
bd and
Sandipan
Pramanik
 *a
*a
aDepartment of Electrical and Computer Engineering, University of Alberta, Alberta, T6G 1H9, Canada. E-mail: spramani@ualberta.ca
bDepartamento de Química Orgánica, Universidad de Granada, Unidad de Excelencia Química Aplicada a Biomedicina y Medioambiente, C. U. Fuentenueva, Avda. Severo Ochoa s/n, E-18071, Granada, Spain
cSchool of Electronics Engineering, Vellore Institute of Technology, Chennai, 600127, India
dInstituto de Investigación Biosanitaria ibs. Avda. De Madrid, 15, E-18016, Granada, Spain
First published on 25th January 2023
Abstract
The phenomenon of chirality induced spin selectivity (CISS) has triggered significant activity in recent years, although many aspects of it remain to be understood. For example, most investigations are focused on spin polarizations collinear to the charge current, and hence longitudinal magnetoconductance (MC) is commonly studied in two-terminal transport experiments. Very little is known about the transverse spin components and transverse MC – their existence, as well as any dependence of this component on chirality. Furthermore, the measurement of the CISS effect via two-terminal MC experiments remains a controversial topic. Detection of this effect in the linear response regime is debated, with contradicting reports in the literature. Finally, the potential influence of the well-known electric magnetochiral effect on CISS remains unclear. To shed light on these issues, in this work we have investigated the bias dependence of the CISS effect using planar carbon nanotube networks functionalized with chiral molecules. We find that (a) transverse MC exists and exhibits tell-tale signs of the CISS effect, (b) transverse CISS MC vanishes in the linear response regime establishing the validity of Onsager's relation in two-terminal CISS systems, and finally (c) the CISS signal remains present even in the absence of electric magneto chiral effects, suggesting the existence of an alternative physical origin of CISS MC.
New conceptsIn this paper, the following new concepts have been introduced: (a) in a chiral spin selective device, spin components exist along directions transverse to the charge current. Existing models of chirality induced spin selectivity (CISS) always assume that the spin components are longitudinal, i.e. parallel or antiparallel to carrier velocity. Our study shows that this is not necessarily the case. (b) We show that in a chiral spin selective device, Onsager's reciprocity principle holds in the linear response region. In the current literature, there is significant controversy on this topic. Here, we establish the validity of this principle by directly probing the linear response range. (c) CISS has a physical origin that is independent of electromagnetochiral anisotropy. Some recent studies have suggested that CISS may originate from electromagnetochiral anisotropy effects in a chiral medium. Our experiments show that this is not the case. The CISS phenomenon is extremely important for multiple disciplines such as chemistry, solid-state physics, device electronics and spintronics. However, many aspects of it still remain less understood. The new concepts described above are expected to clarify some of these aspects, and are expected to have direct implications for CISS based spintronics device design and operation. |
Chirality refers to entities that are non-superimposable mirror images of each other. Traditionally, chirality has played a fundamental role in the areas of chemistry and biology, because many organic molecules are chiral and their interactions are governed by their respective chiralities.1 The interplay between chirality and magnetic field, and their manifestation in various optical and transport processes have also been explored in the past few decades.2 The connection between the chirality of a medium and the spin of a charge carrier in that medium is a relatively recent endeavour.3,4 It has been found by various optical, transport and electrochemical experiments that there exists a correlation between carrier spin and medium chirality, and that the passage of a spin unpolarized carrier population through a chiral medium can impart a chirality-dependent spin polarization to the carriers.3,4 This phenomenon, commonly dubbed as “Chirality induced spin selectivity” or CISS, has profound implications in the areas of condensed matter, device physics and spintronics, as well as various electron transfer processes in chemical and biological systems.3,4
In the CISS effect, the chiral medium can be considered as a spin filter material, in which the generated spin polarization is expected to have a component parallel or antiparallel to the direction of the charge current (depending on the chirality).3,5 In the context of solid state devices, CISS is often studied using a two-terminal geometry, in which a chiral layer is contacted by a ferromagnetic and a non-magnetic electrode.6–10 As the ferromagnet magnetization m is switched between parallel and antiparallel to the current via a global magnetic field B, it offers different transmission probabilities to the carrier spins, resulting in different currents (I+ ≠ I−). This difference is typically reported as the CISS signal and is quantified by various parameters such as differential conductance (ΔG),10 relative change in resistance with respect to some reference resistance (ΔR/R),9 or relative change in current with respect to some reference current (ΔI/I).7,8,11 The sign of these quantities flips for the opposite chirality. In two-terminal transport experiments, such observations are commonly attributed to the manifestation of the CISS effect.
Due to the collinearity of spins and current, a longitudinal measurement geometry is typically used in two-terminal setups in which m (and B) are collinear with I. The carriers can have a net transverse spin component as well, although very little is known about those components and their chirality dependence. Ref. 12 showed by theoretical calculations that the final emerging spin polarization has a non-trivial dependence on the details of the molecules, coupling to the leads, energy of the incoming electrons, etc. As such, the topic of CISS MC in a transverse geometry (B and m perpendicular to I) remains underexplored.
Critical analysis of the CISS MC effect described above has been a topic of significant discussion in recent years.13–18 According to Onsager's reciprocity principle, in a two terminal device with only one magnetic contact, two terminal current I must remain unchanged under magnetization reversal i.e. I (+m, V) = I (−m, V), where V is the applied bias in the linear response regime. Therefore, no CISS MC can exist in two-terminal devices with only one magnetic contact, at least in the linear regime.13,14 This restriction implies that experimentally observed CISS MC must be a higher order nonlinear effect, where Onsager's restriction does not necessarily apply.19 Recent experiments have indeed noted the importance of transport nonlinearity in the bias range where the CISS signal manifests.8 However, the existence of CISS in the linear response range remains controversial.17,18 Some experimental work shows zero CISS signal at low bias,7 whereas some other experiments appear to report non-zero CISS effect in this range, and hence apparent violation of the Onsager reciprocity condition.8,10,11
Validity of the reciprocity principle can be directly checked by determining linear response conductances for +m and −m, which, however, has not been reported in CISS systems. This is presumably due to very low current values in the low bias range, which is a common characteristic of molecular systems, since these materials are essentially insulators in terms of their bulk electronic properties. We note that the CISS signal has been detected in chiral crystals using alternative schemes such as the inverse spin Hall effect.20,21 In the current study, however, our focus is on the two terminal geometry with one ferromagnetic contact because of its wide use in the literature as a CISS detection technique, as well as due to the potential practical importance of this simple geometry in logic and memory applications.22,23
Despite significant advances in recent years, the underlying physical mechanism of CISS remains elusive.3,4 In purely molecular systems, the magnitude of the CISS effect is significantly higher than the spin–orbit and hyperfine coupling strengths of the constituent molecules, and has weak dependence on temperature. Such features have not been adequately described by any microscopic theory, suggesting the absence of a critical ingredient in the theoretical models, and has motivated the search for alternative explanations.4,15,16 In particular, ref. 15 has suggested a possible explanation of the CISS MC, which relies on electric magnetochiral anisotropy (EMChA) coupled with high resistance of the chiral molecular layers typically present in CISS experiments. The phenomenon of EMChA manifests in chiral materials and introduces a resistance term of the form χD/LI·B, where D and L indicate the handedness of the chiral material, with χD = −χL.2,24,25 The resistance of the chiral conductor therefore depends on the relative orientation of bias current I and magnetic field B, and hence exhibits an asymmetric diode-like behavior as a function of the applied bias, for a fixed magnetic field. If the magnetic field is reversed, the diode-like response will also get inverted with respect to bias, resulting in an MC effect. We note that in the case of CISS, however, the I–V response for a fixed B is antisymmetric relative to bias, and not diode-like as in EMChA.3
According to ref. 15, in a typical two-terminal CISS experiment, since the chiral material offers different resistances between positive and negative magnetic fields due to EMChA, it can potentially affect the accumulated charge on the insulating layer, thereby changing the effective potential barrier between the electrodes. This can result in an MC effect that is typically observed in the CISS experiments. As described above, in most CISS experiments B is parallel (or antiparallel) to I, which may result in a non-zero EMChA contribution, and the validity of the above model for these experimental setups remains to be established.6,8–10,26,27 Most importantly, when B and I are perpendicular, the EMChA contribution should be zero and there should not be any EMChA-induced MC asymmetry between +B and −B for a fixed bias and chirality. If any CISS effect that is independent of EMChA exists, it should manifest in this configuration. To avoid or minimize any potential contribution of EMChA, it is therefore necessary to perform the transport experiments in a transverse configuration in which B is perpendicular to I.
Results and discussion
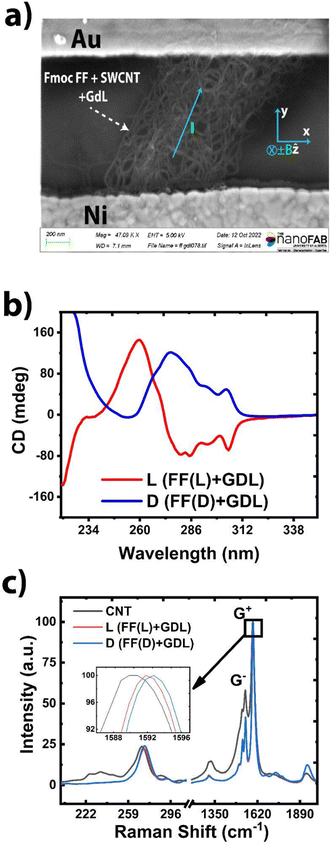
To investigate the above aspects of CISS MC, we have considered planar two-terminal devices with one magnetic electrode (Ni) and one non-magnetic electrode (Au), in the presence of a transverse (out of plane) magnetic field B (Fig. 1(a)). The role of the chiral layer is played by a network of carbon nanotubes (CNTs), functionalized with chiral dipeptide molecules (diphenylalanine or FF, L/D) attached with an Fmoc (Fluorenylmethyloxycarbonyl) functional group. In addition, there are trace amounts of D-glucono-δ-lactone (or, GdL) present in the system, which affects the supramolecular chirality of the medium and hence any chirality-dependent transport phenomenon.28,29 The molecular structures are schematically shown in Fig. S1 (ESI†). Compared to the vertically stacked molecular layers commonly reported in the literature, the planar device has several advantages. For example, (a) it is free of any pinhole shorts, and avoids any spurious effect that can affect the transport data, (b) due to high conductivity compared to the molecules, the low bias linear range conductance can be directly measured, and finally (c) high conductivity of CNTs also reduces any charge accumulation and associated EMChA effects discussed above. Furthermore, the data is significantly less prone to measurement fluctuations, thereby avoiding the need to perform statistical averages of a large number of measurements, except in the limit of very low bias. The CNT-peptide hybrid structure is stable and shows reproducible transport characteristics over periods of several months. Since the magnetic field is perpendicular to the plane, it is normal to all current paths in the plane, and eliminates any EMChA effect. Ni magnetization is also perpendicular to the plane, which enables the measurement of any transverse CISS MC.Synthesis of Fmoc-FF functionalized CNTs has been described in detail in the past.28–30 Briefly, a basic aqueous solution of Fmoc-FF was prepared and a CNT suspension was created in this solution via sonication. Next, the pH is lowered by the addition of GdL, which results in the collapse of the peptide molecules and the formation of a three-dimensional peptide hydrogel network, encapsulating CNTs. The network formation takes place via π–π and hydrogen bonding between the peptide molecules as well as between the peptide molecules and CNT sidewalls.31 Since the FF side chain is chiral, its interaction with the CNTs is expected to induce chirality dependent effects in charge transport.
Fmoc-FF (L) and (D) are chiral molecules that have a relationship with each other of non-superimposable mirror images, that is, they are enantiomers. In the presence of GdL, these peptides self-assemble giving rise to fibrillar aggregates presenting also supramolecular chirality. The CD spectra of these fibrillar aggregates (Fig. 1(b); HT spectra in Fig. S2, ESI†) are nearly mirror images showing the preservation of the enantiomeric relationship in these supramolecular aggregates. Therefore, the chirality of GdL is practically not interfering in the supramolecular packing of the peptides. CD spectra of these peptides have already been reported,32,33 showing the Cotton effect at 220 nm (π → π* transition of the amino acids) and at 270–315 nm (π → π* transition of the fluorenyl groups), which indicate superhelical arrangements. We have previously shown that this supramolecular chirality is the one that dictates any chirality dependent effect in the transport phenomena.8,29 For the rest of the paper we will refer to Fmoc-FF(L) + GdL as “L” and Fmoc-FF(D) + GdL as “D”.
The device is fabricated by transferring a slice of the gel between photolithographically patterned Ni–Au contacts and subsequent vacuum annealing, which results in a xerogel structure, containing CNTs, contacted by the electrodes, as shown in Fig. 1(a). It is to be noted that Au/Ni contact pads are always covered with photoresist in order to prevent atmospheric oxidation. The photoresist protection is removed just before drop-casting the chiral materials. This procedure minimizes Ni oxidation.
Charge transport in CNT networks has been extensively studied in the past few decades and it is well-established that it can be captured by a “heterogeneous” model.34–39 As shown in Fig. 1(a), the tube interconnections, molecular attachments, etc. act as potential barriers, localizing charge carriers in the nanotubes. Carriers therefore experience multiple potential barriers as they traverse from one contact to the other.34 At low temperatures, carrier transport takes place via phonon-assisted tunneling, whereas, at higher temperatures, it becomes thermionic emission over the top of the barriers. Earlier studies have shown that transport in such systems can be modeled by variable range hopping (VRH).28,35,39–41 In our system, charge transport is essentially the same, however, non-helical chiral molecules (monomers) are attached on the CNT walls, and the monomers can organize in helical supramolecular structures.29 The chiral potential arising from this supramolecular structure induces CISS spin polarization on the electrons while they travel through the CNTs.28,29 It is to be noted that in our system, the current flows through the CNTs. The chiral molecules themselves behave as insulators, especially on the length scale used in this study, and hence direct conduction through these molecules is unlikely.
Fig. 1(c) shows typical Raman characterization of Fmoc-FF (L, D) + GdL functionalized CNTs. The primary peak (or, the G+ peak) occurs at ∼1590 cm−1 and originates from the longitudinal vibration of the hexagonal graphitic lattice of CNTs.42 The shoulder peak (or, the G− peak), occurs at ∼1550 cm−1, and originates due to the tangential vibrations of the carbon atoms, and is unique to the CNTs due to their cylindrical geometry.42 Molecular attachments on the sidewalls suppress the tangential vibrations and hence the relative intensity of the G− and G+ peaks can be considered as an indicator of molecular attachment. As seen from Fig. 1(c), compared to the non-functionalized CNTs, the G− peak is significantly suppressed after functionalization with Fmoc-FF. Other evidence of functionalization includes the shift of the G+ peak location (Fig. 1(c) inset), which occurs due to fractional charge transfer between the CNTs and the molecules.42 Other relevant peaks are the defect peak (or, D peak) at ∼1350 cm−1, which primarily occurs due to the broken ends of the CNTs, and can contribute to the potential barriers during charge transport, as discussed above. Finally, radial breathing modes (RBM) are observed at ∼275 cm−1, which occurs due to molecular vibrations that cause radial expansion and contraction of the tubes.
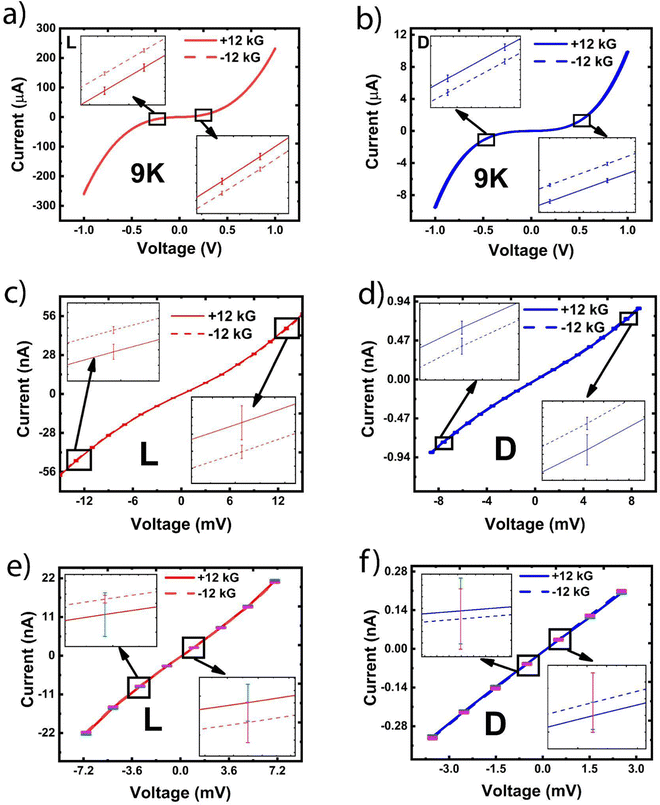
Fig. 2(a and b) show the low temperature I–V characteristics of samples with opposite chiralities, taken at ±12 kG, and represent the fundamental chirality dependent behavior of the CNT networks. Each curve is the average of ten scans with error bars shown in the insets. For all bias values, positive or negative, the current magnitude at −12 kG is lower than that at +12 kG for the L samples (insets of Fig. 2(a)). The opposite behavior has been observed for the D samples in Fig. 2(b). As discussed earlier, such responses are commonly considered as the signature of the CISS effect, and clearly it manifests in the transverse geometry in which the magnetic field B is perpendicular to the sample plane. In this geometry, B is perpendicular to all the current paths in the sample, thus eliminating the EMChA effect. Nevertheless, the presence of a clear CISS signal indicates that it originates from a different mechanism other than EMChA. The observed chirality dependence and current asymmetry between ±12 kG rules out any spurious contribution from the Hall effect. As discussed later in this article, the observed effect does not originate from the Au/chiral medium interface either.
In these samples, the CISS signal is strongest (and signal-to-noise ratio the highest) at low temperatures,28,29 and this is consistent with many studies in the literature that reported data from large area devices.8,10 The magnitude of the CISS signal is also consistent with such studies.7,9,10 As shown in our earlier work, the CISS signal weakens (and signal-to-noise ratio worsens) as the temperature is increased.28,29 In this study, therefore, we present data from the low temperature measurements where the signal-to-noise ratio is the highest.
In a geometry such as Fig. 1(a), using the standard CISS picture, chirality-induced spins are expected to lie in the x–y plane. This is because spin unpolarized carriers are injected from Au into the planar CNT network and the helical supramolecular structures around the CNTs induce chirality dependent spins. Since the Ni electrode is magnetized in the out-of-plane direction, it is expected to transmit the planar spin components equally for both +z and −z magnetizations, resulting in the same current and hence zero CISS signal. Conversely, +z (or −z) spins are injected from Ni into the planar CNT network. Since the CNTs are oriented in different directions in the x–y plane, so are the superhelices around the CNTs. As such, +z (or −z) spins have equal probability to transmit through this medium, resulting in zero CISS signal. However, as seen from Fig. 2(a and b), the currents are different and the response is chirality dependent. This indicates the presence of an out-of-plane component of spin generated by the chiral medium, even though there is no net current in the z direction.
In general, the average carrier velocity along the transverse direction should be zero, because there is no net bias in this direction and the positive and negative velocity components should cancel out. However, supramolecular chirality of the medium may “favor” one spin component, while suppressing the other, resulting in a spin dipole in the transverse direction. This can lead to chirality-dependent response in the transverse MC measurements.
As described in ref. 43, the magnetization direction of the FM film dictates the tilt angle of the attached chiral/helical molecules via spin–spin interactions. In the case of out-of-plane magnetization, the tilt angle (defined as the angle between the surface normal and the helical axis) is small, whereas it is large for the in-plane magnetization. Since in our case FM magnetization is out-of-plane, it can be argued that the chiral axis of the molecules is close to the normal direction, making it the preferred CISS direction and leading to an out-of-plane CISS effect.
However, this explanation is unlikely in the present case. In the case of the molecules,43 they spontaneously aggregate via self-assembly forces. FM magnetization affects the orientation of the molecules during this self-assembly process. In our case, however, the chiral molecules (especially the chiral side chains) are strongly attached to the CNT walls via π–π interaction, and the CNTs are arranged in the form of a planar network, and hence the orientations of the molecules are not freely changeable. Furthermore, in ref. 43 a thin layer of Au was used on top of FM in order to facilitate the adsorption of the molecules. No such scheme was used in our case. Thus, it is unlikely that magnetization induced molecular organization determines the preferred CISS direction in our case.
Ferromagnetic thin films, upon adsorption of chiral molecules, may exhibit a reoriented magnetization direction,43 which can therefore result in a spin detection axis that is different from the surface normal. However, such magnetization reorientation effects are limited to very thin FM layers (∼1–2 nm),43 when chiral molecules are freely self-assembled on top via an interfacial Au layer, as described above. Such effects are unlikely in our case because of the much thicker FM layer (∼100 nm), the absence of any interfacial Au layer on top of FM and most importantly, due to binding of the molecules with CNTs rather than the metals.
The I–V curves show strong nonlinear behavior, especially in the bias range of ± 1 V, and exhibit antisymmetric dependence on the bias, as discussed later in this paper. As mentioned earlier, for a given chirality, Onsager's reciprocity relation should preclude any difference in the I–V curves between +12 kG and −12 kG, as V → 0 (linear response range). To check whether the observed transverse CISS MC satisfies this principle, we proceed as follows.
In Fig. 2(c and d), we show the I–V characteristics for both chiralities at ±12 kG in a smaller voltage range of ∼±10 mV. Even in this small voltage range, the I–V characteristics indicate signs of non-linearity. Compared to Fig. 2(a and b), we note from the insets that the I–V curves at ±12 kG are much closer to each other. The error bars, however, are still distinct and non-overlapping, implying a non-zero difference between the ±12 kG scans.
Next, in Fig. 2(e and f), we show the I–V characteristics for both chiralities at ±12 kG in an even smaller voltage range of ∼±5 mV. The I–V curves are almost linear in this range. The insets show significant overlap between the ±12 kG scans, implying that the current values are virtually identical in both cases. The above analysis clearly shows that the current difference ΔI = I (+12 kG, +V) – I (−12 kG, +V) approaches zero as V → 0 (linear range).
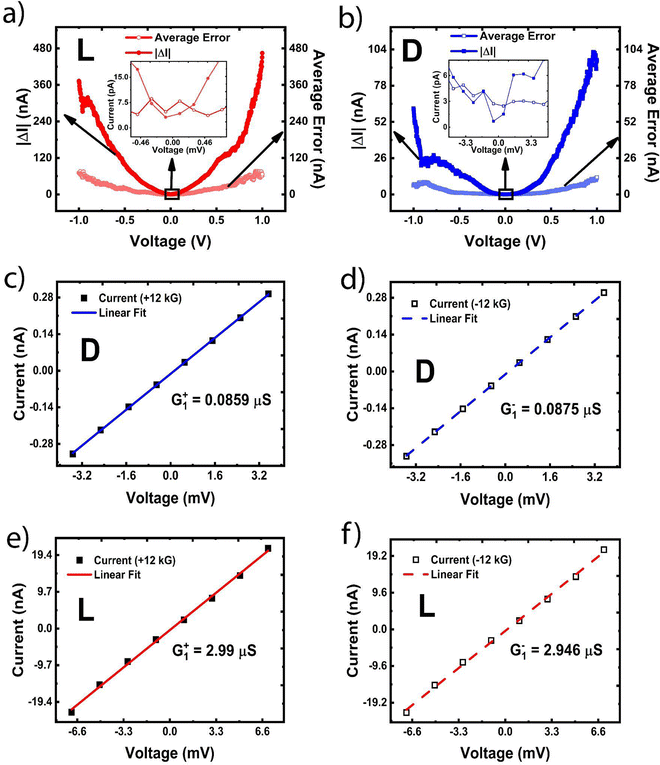
The above behavior is summarized in Fig. 3(a and b), which show the magnitude of the current difference (|ΔI|) as a function of bias for the L and D samples, respectively. We also show the average error (computed as the average of the standard deviation values for ± 12 kG scans) as a function of bias, which serves as the “noise floor” for our measurements. At higher bias, |ΔI| is clearly above the intrinsic noise level of the samples, whereas as the bias approaches zero, |ΔI| decreases monotonically. As shown in the insets, |ΔI| falls below the average error level in the low bias linear range, and becomes virtually undetectable. This clearly shows that as V → 0, ΔI → 0, which is consistent with Onsager's reciprocity relation. We note that the instrumental limit of measuring current is ∼0.1 pA (lower limit), which is much lower than the linear range current values in these samples.
Linear region conductance values can be estimated as follows. Since the I–V characteristics discussed above are nonlinear, following ref. 19 we can expand them in a power series of V:
In the linear range (small voltage), the above equation simply becomes ID/L(±m, V) = GD/L1(±m)V. Fig. 3(c and d) show the low bias I–V characteristics (average of ten scans) of the D sample taken at +12 kG and −12 kG, respectively. In the low bias range, the data points can be indeed fitted with straight lines with slopes of GD1(+12 kG) = 85.9 nS and GD1(−12 kG) = 87.5 nS. Fig. 3(e and f) show similar analysis for the L chiral sample and again we find linear fits with slopes GL1(+12 kG) = 2.99 μS and GL1(−12 kG) = 2.946 μS. However, as discussed above, the differences between GD/L1(+m) and GD/L1(−m) are not statistically significant, because the I–V curves have significant overlap with each other (Fig. 2(e and f)). Therefore, we conclude that ΔG1 = GD/L1(+m) − GD/L1(−m) → 0 as V → 0, hence satisfying Onsager's reciprocity relation in a CISS system.
The above analysis (Fig. 2 and 3) clearly shows the connection between transport non-linearity and CISS MC in a two terminal device with one ferromagnetic contact. The CISS effect vanishes in the linear range and gradually emerges as the bias is increased and as the transport becomes more nonlinear. Ref. 14 highlighted the importance of energy dependent transport and energy relaxation within the device for the MC effect to manifest. Such a condition is naturally met in our systems where transport is via phonon-assisted tunneling from site to site as described above.
Linear response typically refers to small “perturbation” of the equilibrium by a small voltage V, so that the current response is linear with respect to the applied voltage.44 A sufficient condition for linearity is qV < kBT, which is not strictly satisfied under our experimental conditions, because the minimum applied bias is ∼1 mV (I–V), which is slightly higher than 0.78 mV (thermal voltage at 9 K). Although this is a sufficient condition, it is not a necessary condition. In fact, the response can be considered linear regardless of the temperature if the I–V relation remains linear or the slope of dV/dI is unaffected by bias.44 This is definitely the case in Fig. 3(c–f).
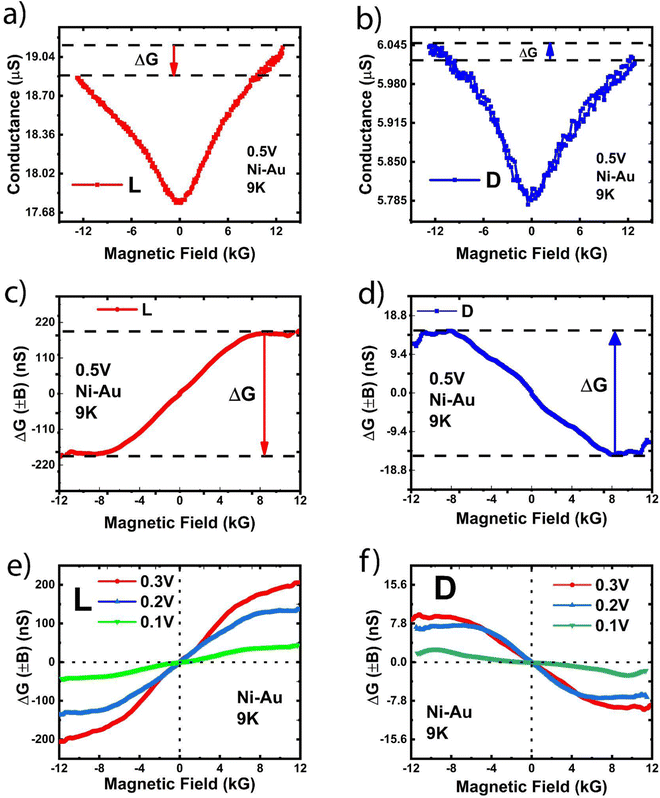
The transverse CISS effect and its bias dependence can also be examined via direct MC measurements. Fig. 4(a and b) show typical MC curves, taken at 0.5 V bias, which clearly falls in the non-linear range of transport as discussed above. A positive background MC (symmetric relative to B) is present which often appears in CNT networks at low temperatures due to magnetic field dependent hopping phenomena.35,39,45,46 Most importantly, consistent with the I–V data, the conductances at +12 kG and −12 kG are unequal. In the case of L samples, the conductance at −12 kG is lower than that at +12 kG, whereas the opposite behavior is observed for the D samples.
To eliminate the symmetric positive MC background, in Fig. 4(c and d) we show the conductance change ΔG (B), defined as ½[G(B) − G(−B)], which saturates around ± 8 kG, where the magnetization of the Ni contact is also saturated. We note that the conductance change as a function of B is sensitive to the magnetization change at the ferromagnetic interface, instead of the bulk, and interfacial magnetization can change gradually with B. This could explain the gradual change of ΔG (B) around the origin as B is varied. As shown in Fig. 4(c and d), the L and D samples have opposite resistance switching behavior. Since the Ni contact is magnetized out-of-plane, according to the conventional description of CISS, the detected conductance change must correspond to the spin components in the out-of-plane direction. Clearly, they exhibit the signature chirality dependent behavior as well.
To investigate the effect of bias on ΔG (B), we have taken MC measurements at multiple bias values of 0.3 V, 0.2 V and 0.1 V, as shown in Fig. 4(e and f). ΔG shows a decreasing trend as bias is reduced. This is clearly consistent with the earlier discussion (Fig. 2 and 3) where we showed that the CISS effect gradually disappears as the bias is reduced.
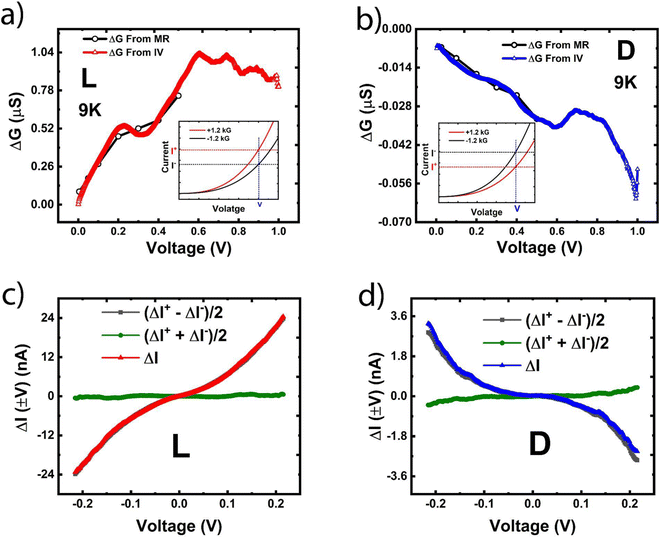
Fig. 5(a and b) show ΔG as a function of bias, computed from the I–V characteristics at ±12 kG as well as from the MC measurements. In the case of I–V characteristics, each voltage bias V (non-linear range) results in two distinct current states ID/L (±12 kG, V) as shown schematically in the insets (following Fig. 2(a and b)). Conductance difference ΔG is computed as ID/L (+12 kG, V)/V − ID/L (−12 kG, V)/V. As can be seen from Fig. 5(a and b), the magnitude of ΔG decreases as the bias is reduced. The ΔG values computed from the MC measurements match closely with those computed from the I–V measurements, and confirm the validity of Onsager's reciprocity principle in the linear range. As discussed above, any apparent non-zero ΔG value at zero bias is below the noise floor of our measurements and hence is not meaningful.
As discussed before, the transverse geometry effectively nullifies the EMChA in our setup. In order to detect the presence of any trace amounts of this effect, we take a closer look at the functional dependence of the CISS signal ΔI on bias, in the intermediate bias range of ∼0.2 V. As discussed earlier, EMChA can introduce a second order contribution to the current, resulting in a diode-like behavior, which should manifest in the intermediate bias range. Since G1(+m) = G1(−m), using the power series expansions discussed above, we can compute ΔID/L, defined as ID/L (+m, +V) − ID/L (−m, +V), which will have the following form:19
In Fig. 5(c and d) we show the even and odd components of ΔI computed as (ΔI(+V) + ΔI(−V))/2 and (ΔI(+V) − ΔI(−V))/2, respectively. The even component is negligible and is almost non-existent in the intermediate bias range, which indicates the absence of any trace amounts of EMChA in our setup. Thus, the CISS effect exists even when EMChA is vanishingly small, and hence this is unlikely to be the driving mechanism behind CISS. The underlying mechanism should have an odd functional dependence on the bias. Any small second-order contribution at higher bias may arise due to dissimilar contacts (Au and Ni) used in the measurement.
Finally, a comment about the role of the Au/chiral medium interface is in order. Apparent local ferromagnetism has been reported in gold surfaces capped with certain organic molecules.47,48 This could arise from surface bonds between the molecules and gold. If we consider the Au surface to be ferromagnetic, then, combined with the Ni ferromagnet it represents a “spin valve” structure. The magnetoconductance response of such structures exhibits characteristic valleys when the two magnetizations are antiparallel. However, in our case we do not see that. Ref. 23 showed ferromagnetic hysteresis using Au with chiral molecules on top. We note that the thickness of the Au contact in this study is small (∼15 nm), and hence a layer of adsorbed chiral molecules on its surface imparts soft ferromagnetism via spin–spin interaction. In contrast, our Au contacts are significantly thicker (∼100 nm) and the chiral molecules are primarily bonded with the CNTs, and hence such effects are expected to be negligible.
Furthermore, in our case, we anneal the sample under vacuum before any transport measurements. This step ensures good ohmic contact and produces reproducible transport data. This indicates that the carriers are directly injected into the CNTs, rather than some ill-defined interface or “bad contacts”. The VRH transport behavior also suggests that the transport data originates from the bulk, rather than the Au interface. Thus, the observed phenomena must originate from spin polarization accrued during bulk transport, rather than interfacial injection.
A final proof of the fact that the observed response originates from the bulk of the sample rather than the interface follows from our earlier work where we showed that the device response depends on the supramolecular chirality of the medium.29 Supramolecular chirality is a long-range “global” order, rather than a short range “local” interfacial phenomenon. This proves that the device behavior reported in our work does not originate from the Au/chiral medium interface.
In conclusion, we have investigated the bias dependence of the CISS effect using carbon nanotubes functionalized with chiral dipeptide molecules. A transverse measurement configuration was chosen (unlike most common longitudinal configurations), in which the magnetic field is perpendicular to the transport direction. This allows us to investigate transverse CISS MC and its chirality dependence. This aspect of the CISS effect has often been overlooked, because most studies focus on the longitudinal MC effects. In addition, the transverse geometry also eliminates any contribution from the EMChA effect. We showed that transverse MC exists, and exhibits tell-tale signatures of the CISS effect, and it persists even in the absence of EMChA. Finally, our bias dependent studies directly probed the linear response region, and clearly showed that the transverse CISS effect vanishes in the linear response regime (consistent with Onsager's reciprocity principles), and gradually manifests at higher bias as the transport characteristics become increasingly non-linear. The non-linear CISS signal has an odd functional dependence on the applied bias, which may help identify the possible underlying mechanism of CISS. The above observations are expected to be key ingredients for a self-consistent theory of CISS MC.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This study was supported by project PID2020-118498GB-I00 funded by MCIN/AEI/10.13039/501100011033 and project P18-FR-3533 funded by FEDER/Junta de Andalucía-Consejería de Transformación Económica, Industria, Conocimiento y Universidades (Spain). S. P. acknowledges support from NFRFE-2019-01298 (New Frontiers in Research Fund – Exploration) and NSERC (Natural Sciences and Engineering Research Council of Canada), project RGPIN-2018-05127. M A. H. acknowledges the help of Seyedamin Firouzeh during FESEM imaging and Md. Wazedur Rahman for his guidance during the initial experimental setup and fabrication process of the contacts.References
- G. A. Hembury, V. V. Borovkov and Y. Inoue, Chem. Rev., 2008, 108, 1–73 CrossRef CAS PubMed.
- M. Atzori, C. Train, E. A. Hillard, N. Avarvari and G. L. J. A. Rikken, Chirality, 2021, 33, 844–857 CrossRef CAS PubMed.
- C. D. Aiello, J. M. Abendroth, M. Abbas, A. Afanasev, S. Agarwal, A. S. Banerjee, D. N. Beratan, J. N. Belling, B. Berche, A. Botana, J. R. Caram, G. L. Celardo, G. Cuniberti, A. Garcia-Etxarri, A. Dianat, I. Diez-Perez, Y. Guo, R. Gutierrez, C. Herrmann, J. Hihath, S. Kale, P. Kurian, Y.-C. Lai, T. Liu, A. Lopez, E. Medina, V. Mujica, R. Naaman, M. Noormandipour, J. L. Palma, Y. Paltiel, W. Petuskey, J. C. Ribeiro-Silva, J. J. Saenz, E. J. G. Santos, M. Solyanik-Gorgone, V. J. Sorger, D. M. Stemer, J. M. Ugalde, A. Valdes-Curiel, S. Varela, D. H. Waldeck, M. R. Wasielewski, P. S. Weiss, H. Zacharias and Q. H. Wang, ACS Nano, 2022, 16, 4989–5035 CrossRef CAS PubMed.
- F. Evers, A. Aharony, N. Bar-Gill, O. Entin-Wohlman, P. Hedegård, O. Hod, P. Jelinek, G. Kamieniarz, M. Lemeshko, K. Michaeli, V. Mujica, R. Naaman, Y. Paltiel, S. Refaely-Abramson, O. Tal, J. Thijssen, M. Thoss, J. M. van Ruitenbeek, L. Venkataraman, D. H. Waldeck, B. Yan and L. Kronik, Adv. Mater., 2022, 34, 2106629 CrossRef CAS PubMed.
- B. Gohler, V. Hamelbeck, T. Z. Markus, M. Kettner, G. F. Hanne, Z. Vager, R. Naaman and H. Zacharias, Science, 2011, 331, 894–897 CrossRef CAS PubMed.
- Z. Xie, T. Z. Markus, S. R. Cohen, Z. Vager, R. Gutierrez and R. Naaman, Nano Lett., 2011, 11, 4652–4655 CrossRef CAS PubMed.
- V. Kiran, S. P. Mathew, S. R. Cohen, I. H. Delgado, J. Lacour and R. Naaman, Adv. Mater., 2016, 28, 1957–1962 CrossRef CAS PubMed.
- C. Kulkarni, A. K. Mondal, T. K. Das, G. Grinbom, F. Tassinari, M. F. J. Mabesoone, E. W. Meijer and R. Naaman, Adv. Mater., 2020, 32, 1904965 CrossRef CAS PubMed.
- H. Lu, J. Wang, C. Xiao, X. Pan, X. Chen, R. Brunecky, J. J. Berry, K. Zhu, M. C. Beard and Z. V. Vardeny, Sci. Adv., 2019, 5, eaay0571 CrossRef CAS PubMed.
- T. Liu, X. Wang, H. Wang, G. Shi, F. Gao, H. Feng, H. Deng, L. Hu, E. Lochner, P. Schlottmann, S. von Molnár, Y. Li, J. Zhao and P. Xiong, ACS Nano, 2020, 14, 15983–15991 CrossRef CAS PubMed.
- H. Al-Bustami, S. Khaldi, O. Shoseyov, S. Yochelis, K. Killi, I. Berg, E. Gross, Y. Paltiel and R. Yerushalmi, Nano Lett., 2022, 22, 5022–5028 CrossRef CAS PubMed.
- S. Dalum and P. Hedegård, Nano Lett., 2019, 19, 5253–5259 CrossRef CAS PubMed.
- X. Yang, C. H. van der Waals and B. J. van Wees, Phys. Rev. B, 2019, 99, 024418 CrossRef CAS.
- X. Yang, C. H. van der Waals and B. J. van Wees, Nano Lett., 2020, 20, 6148–6154 CrossRef CAS PubMed.
- J. Xiao and B. Yan, arXiv, 2022, preprint, arXiv:2201.03623 DOI:10.48550/arXiv.2201.03623.
- Y. Liu, J. Xiao, J. Koo and B. Yan, Nat. Mater., 2021, 20, 638–644 CrossRef CAS PubMed.
- R. Naaman and D. H. Waldeck, Phys. Rev. B, 2020, 101, 026403 CrossRef CAS.
- X. Yang, C. H. van der Waals and B. J. van Wees, Phys. Rev. B, 2020, 101, 026404 CrossRef CAS.
- K. H. Huisman and J. M. Thijssen, J. Phys. Chem. C, 2021, 125, 23364–23369 CrossRef CAS PubMed.
- A. Inui, R. Aoki, Y. Nishiue, K. Shiota, Y. Kousaka, H. Shishido, D. Hirobe, M. Suda, J. Ohe, J. Kishine, H. M. Yamamoto and Y. Togawa, Phys. Rev. Lett., 2020, 124, 166602 CrossRef CAS PubMed.
- K. Shiota, A. Inui, Y. Hosaka, R. Amano, Y. Ōnuki, M. Hedo, T. Nakama, D. Hirobe, J. Ohe, J. Kishine, H. M. Yamamoto, H. Shishido and Y. Togawa, Phys. Rev. Lett., 2021, 127, 126602 CrossRef CAS PubMed.
- O. B. Dor, S. Yochelis, S. P. Mathew, R. Naaman and Y. Paltiel, Nat. Commun., 2013, 4, 1–6 Search PubMed.
- H. Al-Bustami, G. Koplovitz, D. Primc, S. Yochelis, E. Capua, D. Porath, R. Naaman and Y. Paltiel, Small, 2018, 14, 1801249 CrossRef PubMed.
- G. L. J. A. Rikken, J. Fölling and P. Wyder, Phys. Rev. Lett., 2001, 87, 236602 CrossRef CAS PubMed.
- V. Krstić, S. Roth, M. Burghard, K. Kern and G. L. J. A. Rikken, J. Chem. Phys., 2002, 117, 11315–11319 CrossRef.
- A. K. Mondal, N. Brown, S. Mishra, P. Makam, D. Wing, S. Gilead, Y. Wiesenfeld, G. Leitus, L. J. W. Shimon, R. Carmieli, D. Ehre, G. Kamieniarz, J. Fransson, O. Hod, L. Kronik, E. Gazit and R. Naaman, ACS Nano, 2020, 14, 16624–16633 CrossRef CAS PubMed.
- S. Mishra, A. K. Mondal, E. Z. B. Smolinsky, R. Naaman, K. Maeda, T. Nishimura, T. Taniguchi, T. Yoshida, K. Takayama and E. Yashima, Angew. Chem., 2020, 132, 14779–14784 CrossRef.
- Md. W. Rahman, M. C. Mañas-Torres, S. Firouzeh, J. M. Cuerva, L. Álvarez de Cienfuegos and S. Pramanik, ACS Nano, 2021, 15, 20056–20066 CrossRef CAS PubMed.
- Md. W. Rahman, M. C. Mañas-Torres, S. Firouzeh, S. Illescas-Lopez, J. M. Cuerva, M. T. Lopez-Lopez, L. Á. de Cienfuegos and S. Pramanik, ACS Nano, 2022, 16, 16941–16953 CrossRef CAS PubMed.
- R. Contreras-Montoya, G. Escolano, S. Roy, M. T. Lopez-Lopez, J. M. Delgado-López, J. M. Cuerva, J. J. Díaz-Mochón, N. Ashkenasy, J. A. Gavira and L. Á. de Cienfuegos, Adv. Funct. Mater., 2019, 29, 1807351 Search PubMed.
- B. G. Cousins, A. K. Das, R. Sharma, Y. Li, J. P. McNamara, I. H. Hillier, I. A. Kinloch and R. V. Ulijn, Small, 2009, 5, 587–590 CrossRef CAS PubMed.
- Y. Zhang, H. Gu, Z. Yang and B. Xu, J. Am. Chem. Soc., 2003, 125, 13680–13681 CrossRef CAS PubMed.
- V. Jayawarna, M. Ali, T. A. Jowitt, A. F. Miller, A. Saiani, J. E. Gough and R. V. Ulijn, Adv. Mater., 2006, 18, 611–614 CrossRef CAS.
- A. B. Kaiser, G. Düsberg and S. Roth, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1418–1421 CrossRef CAS.
- M. Jaiswal, W. Wang, K. A. S. Fernando, Y.-P. Sun and R. Menon, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 113401 CrossRef.
- G. Baumgartner, M. Carrard, L. Zuppiroli, W. Bacsa, W. A. de Heer and L. Forró, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 6704–6707 CrossRef CAS.
- J. E. Fischer, H. Dai, A. Thess, R. Lee, N. M. Hanjani, D. L. Dehaas and R. E. Smalley, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, R4921–R4924 CrossRef CAS.
- K. Yanagi, H. Udoguchi, S. Sagitani, Y. Oshima, T. Takenobu, H. Kataura, T. Ishida, K. Matsuda and Y. Maniwa, ACS Nano, 2010, 4, 4027–4032 CrossRef CAS PubMed.
- G. T. Kim, E. S. Choi, D. C. Kim, D. S. Suh, Y. W. Park, K. Liu, G. Duesberg and S. Roth, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 16064–16069 CrossRef CAS.
- M. W. Rahman, S. Firouzeh and S. Pramanik, Nanotechnology, 2021, 32, 455001 CrossRef CAS PubMed.
- Md. W. Rahman, S. Firouzeh, V. Mujica and S. Pramanik, ACS Nano, 2020, 14, 3389–3396 CrossRef CAS PubMed.
- M. S. Dresselhaus, G. Dresselhaus, R. Saito and A. Jorio, Phys. Rep., 2005, 409, 47–99 CrossRef.
- N. Sukenik, F. Tassinari, S. Yochelis, O. Millo, L. T. Baczewski and Y. Paltiel, Molecules, 2020, 25, 6036 CrossRef CAS PubMed.
- S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, Cambridge, 1995 Search PubMed.
- V. L. Nguen, B. Z. Spivak and B. I. Shklovskii, J. Exp. Theor. Phys., 1985, 62, 1021 Search PubMed.
- J.-L. Pichard, M. Sanquer, K. Slevin and P. Debray, Phys. Rev. Lett., 1990, 65, 1812–1815 CrossRef PubMed.
- M. Agrachev, S. Antonello, T. Dainese, M. Ruzzi, A. Zoleo, E. Aprà, N. Govind, A. Fortunelli, L. Sementa and F. Maran, ACS Omega, 2017, 2, 2607–2617 CrossRef CAS PubMed.
- J. De La Venta, E. Fernandez Pinel, M. A. Garcia, P. Crespo, A. Hernando, O. R. De La Fuente, C. De Julián Fernández, A. Fernández and S. Penadés, Mod. Phys. Lett. B, 2007, 21, 303–319 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1: Molecular structures of Fmoc-FF (L/D) and gluconolactone (GdL). Fig. S2: HT spectra of Fmoc-FF (L/D) hydrogels formed in the presence of GdL. See DOI: https://doi.org/10.1039/d2nh00502f |
| This journal is © The Royal Society of Chemistry 2023 |