Open Access Article
Open Access ArticleOperando monitoring of gas bubble evolution in water electrolysis by single high-frequency impedance†
Kamran
Dastafkan
 a,
Shuhao
Wang
ab,
Shuang
Song
a,
Shuhao
Wang
ab,
Shuang
Song
 c,
Quentin
Meyer
c,
Quentin
Meyer
 a,
Qiang
Zhang
a,
Qiang
Zhang
 b,
Yansong
Shen
b,
Yansong
Shen
 c and
Chuan
Zhao
c and
Chuan
Zhao
 *a
*a
aSchool of Chemistry, The University of New South Wales, Sydney, New South Wales 2052, Australia. E-mail: chuan.zhao@unsw.edu.au
bBeijing Key Laboratory of Green Chemical Reaction Engineering and Technology, Department of Chemical Engineering, Tsinghua University, Beijing 100084, China
cSchool of Chemical Engineering, University of New South Wales, Sydney, NSW 2052, Australia
First published on 8th August 2023
Abstract
Gas bubble management is highly demanded in water electrolysis and the lack of real-time monitoring of gas bubbles has slowed down the progress. Here, we demonstrate operando single frequency impedance measurement as an electrochemical means to detecting gas bubble evolution during water splitting reactions. At optimum high frequencies, where the contribution of faradaic charge transfer and mass transport as well as the phase component of the impedance are minimized, the dynamic variation of the resistance response can be correlated to the effect of gas bubbles. The amplitude of the resistance fluctuations indicates the impact of gas bubble evolution on the available active surface in a non-periodic pattern, where a bigger amplitude points to a larger number of gas bubbles and their sluggish growth and detachment over electrodes. Accordingly, the dynamic resistance variation varies with surface wettability and electrode configuration from flat two-dimensional to porous three-dimensional electrodes. Coupling this technique with operando optical microscopy unravels the correlation of the dynamic variation amplitude with gas bubble characteristics, i.e., size and release rate. The approach is applied to a bifunctional hetero-hierarchical Ni(OH)2@N-NiC catalyst to confirm the operando monitoring of ultrafast hydrogen and oxygen bubble evolution due to its superaerophobicity and anisotropic morphology. This facile operando approach is applied for monitoring gas bubble evolution in non-transparent full water electrolyser cells, and is useful for developing gas-repelling electrodes, as well as a range of gas evolving applications beyond.
Broader contextGas bubble management is a central issue in water electrolysis where the adverse effects of gas bubbles, resulting in large overpotentials and unstable current densities, lead to a loss of energy efficiency up to 40% in industry. The lack of real-time monitoring of gas bubbles has been a bottleneck in the progress thus far. Optical imaging and evaluation of current/potential response are often conducted to observe gas bubble behaviour in standard Lab-scale conditions. However, these methods respond poorly at large current densities and to non-transparent water electrolyser devices. Here, we introduce operando monitoring of gas bubble evolution using single frequency impedance spectroscopy. By fixing the impedance at a high frequency, minimizing the phase component and the effect of faradaic charge transfer on the electrode resistance, dynamic resistance variation can be recorded. Such resistance variation adopts different patterns over different surfaces and is highly impacted by surface wettability and electrode morphology. A systematic investigation is conducted on the dynamic resistance variation over bare electrodes with flat surfaces as well as catalyst-coated electrodes with unique morphologies during hydrogen and oxygen evolution reactions, as well as in alkaline and anion-exchange membrane water electrolysers. To correlate the dynamic resistance variation to gas bubble evolution, we couple the single frequency impedance with optical microscopy and use the fast Fourier transform of the resistance variation. The method is universal and the successful application in water electrolyser devices shows that it can predict gas bubble evolution behavior under industrial testing conditions. |
Introduction
Currently, there is a gap between lab-scale and industrial-scale water electrolysis, which to a large extent is effectuated by catalytic efficiency and electrode state of health. Aside from catalyst intrinsic activity studied at the kinetically-controlled regions in oxygen and hydrogen evolution reactions (OER and HER), the catalytic efficiency loss originates from the limited gas bubble evolution (GBE)1,2 involving the nucleation of micro-bubbles, growth into macro-bubbles, and dissipation into electrolyte or gas collecting containers. Being hydrophobic, gas bubbles tend to stick to the electrode surface and block the active sites, thereby reducing the accessible surface for electrolytes.3 The contribution of GBE to ohmic, mass transport, and faradaic charge transfer resistances results in large overpotentials and unstable current responses.4,5 Gas bubble release rate not only influences the surface-electrolyte contact via diffusion but also affects the uniformity of gas product transportation via convection.6 The increase in the size of gas bubbles induces a stretch force entailing the physical loss of catalysts.7 These adverse effects are exacerbated at large current densities, delivered at industrially-relevant conditions in water electrolyzers,8,9 and give rise to an energy loss of up to 40% in the water electrolysis industry.10–12Buoyancy and surface adhesion forces at the triple phase boundary of catalyst–electrolyte–gas bubbles should at least match for GBE to happen.13,14 While continuous coalescence of gas bubbles occurs due to adhesion force, upward transportation occurs via buoyancy, and hence gas bubbles could be trapped within the void space of the catalyst structure.1,6 Thus, active surface accessibility and the resistance originated by GBE vary by the surface structure and catalyst inner space.6,8 This becomes a concern in using porous three-dimensional (3D) electrodes such as metal foams. Generally, approaches to mitigate the gas bubble effect include regulating surface wettability and nano-structuring to reduce the surface tension and the adhesion force of gas bubbles.15,16 Generating a hydrophilicity/aerophobicity gradient and directional nano-structuring have recently been exerted by bioinspired structures, woodpile structures, and dual-gradient architectures.8,17–24
The progress in studying GBE for the OER and HER has been slow largely due to the limited electrochemical monitoring of gas bubbles in operando. To date, optical recording of underwater GBE remains the most suitable method for capturing the GBE dynamics, i.e., size, growth, and release rate of gas bubbles. However, this is limited by the constant need for costly setups of optical recording devices such as high-speed/resolution cameras and optical microscopy, which become impractical at larger current densities and temperatures25 applied in non-transparent water electrolysers. Currently, the impact of GBE is mostly studied electrochemically based on the current response, where the current oscillations emerge by the nucleation, growth, and detachment of gas bubbles.26 Eckert et al.27 reported an in situ gas bubble dynamics recording and observed a transient current with oscillations due to single hydrogen bubble evolution over a Pt microelectrode. Kim et al.8 used scanning electrochemical microscopy (SECM) to monitor current oscillations delivered by gas bubbles over a 3D stack-printed Ir catalyst during the OER. Taking the fast Fourier transform (FFT) of the current spectra identified characteristic frequency features with higher detected frequency amplitudes referring to faster GBE. The voltage response fluctuations have also been used to address the gas bubble issue. Iwata et al.28 reported a periodic voltage response variation over time by introducing superhydrophobicity to a nickel foam electrode. Different surface coverage of polytetrafluoroethylene deposited on the electrode indicated the correlation of voltage transient signal variation with gas bubble evolution during the OER.
However, the voltage/current responses capture different electrochemical processes simultaneously, i.e., charging current and/or the current associated with redox processes of the electrodes themselves including metal deposition and/or dissolution.29 The reproducibility of the voltage/current response variation has not been demonstrated yet, as vigorous GBE at large current densities, often forming a froth layer on the surface, causes signal overlap which leads to non-periodic and bulky chronopotentiometric/amperometric curves. Thus, voltage/current response variation ensues from more factors than just gas bubbles, making the interpretation difficult particularly for 3D porous electrodes and device applications.
Here, we demonstrate an operando monitoring of GBE using facile single frequency impedance at an optimum high frequency over bare model electrodes and catalyst-coated electrodes for the HER, OER, and full electrolyser cells. To attribute the dynamic variation of the resistance response to the GBE, the minimum phase angle (<1 degree) for each electrode is approached by conducting AC impedance at relevant potentials and the corresponding frequency is determined from phase-frequency spectra obtained from Nyquist measurements. This frequency is high enough to minimize the contributions of both faradaic processes and the phase component of the impedance, so that detecting the effect of gas bubbles on the accessible surface could be studied. To link the dynamic resistance variation with GBE, the technique is coupled with optical microscopy in an in situ electrochemical cell. By taking the FFT patterns of the data, the amplitude of the resistance variation is analyzed, the magnitude of which refers to the difference in the number of gas bubbles and their evolution between different electrodes. Image processing further relates the resistance fluctuations to GBE in real time. A bifunctional hetero-hierarchical catalyst grown over Ni foam (Ni(OH)2@N-NiC/NF) is developed as an advanced electrode to showcase the accelerated GBE during the HER and OER using single frequency impedance. The dynamic resistance variation depicts minimum amplitudes and optical microscopy reveals minimum gas bubble size and ultrafast release rate for Ni(OH)2@N-NiC/NF due to the anisotropic morphology, multi-directional surface hierarchies, and surface superaerophobicity. This highlights the use of this method in developing gas-repelling electrodes and catalysts via operando GBE monitoring.
Results
Monitoring GBE over model electrodes
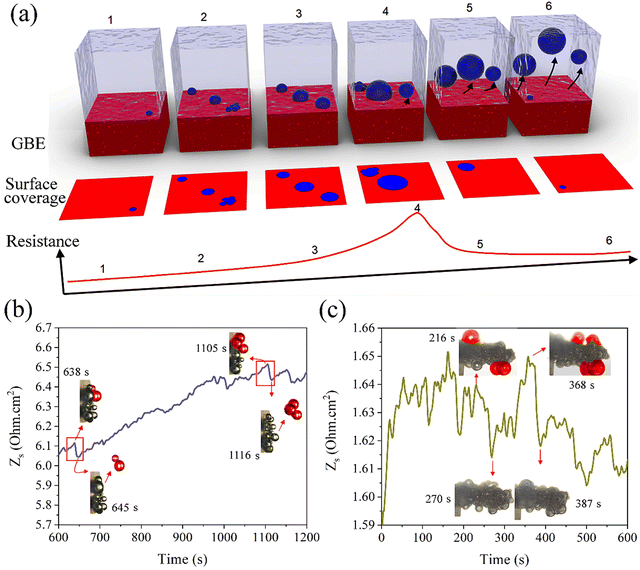
The single frequency impedance measures the impact of gas bubbles on the change in resistance (R) which is inversely proportional to the electrode surface (A):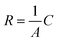 , where C is a constant describing the applied electrolytic cell conditions.30 At a frequency high enough to reach a minimum phase (i.e., <1 degree), the contributions of interfacial charge transfer, mass transport of reactants and ionic species, and the phase component of impedance to the dynamic change in the surface resistance are minimized. Thus, the resistance variation can be correlated to the change in the accessible surface caused by the evolving gas bubbles. Operando monitoring of the resistance variation over time allows for demonstrating the difference between electrodes for the number of gas bubbles and how fast their evolution is over the surface. The longer the lifetime and the bigger the size of the gas bubbles blocking the surface, the higher the electrode resistance. Using single frequency impedance, detecting large amplitudes of resistance fluctuations, referring to the growth and release patterns of gas bubbles, alludes to more sluggish GBE and vice versa. Therefore, this method can serve as an electrochemical means to detect GBE and as a guide to developing advanced electrodes with desirable surface and morphology properties for gas bubble management in water electrolysis. Here, the key point in detecting GBE is to find the proper frequency of the minimum phase, which can be easily obtained from conventional AC impedance measurements. However, the optimum value of the single frequency should be determined individually for different electrodes as well as for the same electrode at different electrolytic conditions. Here, the resistance is normalized by the electrode geometric surface area and the recorded fluctuations are induced by GBE (Fig. 1a). To examine GBE over 2D and 3D electrodes, a bare macrodisc glassy carbon electrode (GCE) and a Ni foam (NF) electrode are used as model working electrodes, respectively, and placed in a home-made in situ three-electrode electrochemical cell with a transparent window for simultaneous optical imaging using an optical microscope (Fig. S1, ESI†).
, where C is a constant describing the applied electrolytic cell conditions.30 At a frequency high enough to reach a minimum phase (i.e., <1 degree), the contributions of interfacial charge transfer, mass transport of reactants and ionic species, and the phase component of impedance to the dynamic change in the surface resistance are minimized. Thus, the resistance variation can be correlated to the change in the accessible surface caused by the evolving gas bubbles. Operando monitoring of the resistance variation over time allows for demonstrating the difference between electrodes for the number of gas bubbles and how fast their evolution is over the surface. The longer the lifetime and the bigger the size of the gas bubbles blocking the surface, the higher the electrode resistance. Using single frequency impedance, detecting large amplitudes of resistance fluctuations, referring to the growth and release patterns of gas bubbles, alludes to more sluggish GBE and vice versa. Therefore, this method can serve as an electrochemical means to detect GBE and as a guide to developing advanced electrodes with desirable surface and morphology properties for gas bubble management in water electrolysis. Here, the key point in detecting GBE is to find the proper frequency of the minimum phase, which can be easily obtained from conventional AC impedance measurements. However, the optimum value of the single frequency should be determined individually for different electrodes as well as for the same electrode at different electrolytic conditions. Here, the resistance is normalized by the electrode geometric surface area and the recorded fluctuations are induced by GBE (Fig. 1a). To examine GBE over 2D and 3D electrodes, a bare macrodisc glassy carbon electrode (GCE) and a Ni foam (NF) electrode are used as model working electrodes, respectively, and placed in a home-made in situ three-electrode electrochemical cell with a transparent window for simultaneous optical imaging using an optical microscope (Fig. S1, ESI†).
Firstly, Nyquist and the corresponding Bode-phase plots are obtained for the alkaline HER in 1 M KOH above the onset potential over bare GCE and NF electrodes at −1.45 and −0.15 V, respectively (Fig. S2, ESI†). A high frequency of 10 kHz, determined from the Bode plots giving a minimum phase angle (<1 degree), was applied to the electrodes at the applied potentials. The dynamic resistance variation is recorded in operando (Fig. 1b and c), with the sluggish GBE captured in real time over the flat surfaces of the GCE and NF scaffolds via operando optical microscopy (Movies S1 and S2, ESI†), correlating the resistance variation to the slow growth and release of large hydrogen bubbles. Here, due to a large number of gas bubbles impacting the surface area and the resistance being detected simultaneously, many signals corresponding to the change in the resistance overlap, which along with a constant sampling rate (2 s) of the single frequency impedance results in an accumulative resistance variation followed by a sudden decrease in a random fashion. In comparison, smooth resistance curves are recorded for both electrodes at low frequencies, i.e., 0.1 Hz, which deals with faradaic processes (Fig. S3, ESI†). Also, bigger amplitudes of resistance variation are recorded on the 3D NF electrode, which delivers larger current densities and deals with a larger gas bubble coalescence (Fig. 1c).
Besides frequency, other parameters influencing the dynamic resistance variation including current density and surface area are investigated for the HER over a bare NF electrode in a standard three-electrode half-cell. The corresponding Bode-phase plot from AC impedance spectroscopy reveals that a higher frequency of 20 kHz is the optimum single frequency in the standard half-cell (Fig. S4, ESI†). Firstly, the correlation with GBE is tracked by applying incrementing current densities on NF (0.25 cm2), where a significant amplitude is evident at −100 mA cm−2 (Fig. S5, ESI†). At lower current densities (50 mA cm−2) corresponding to the kinetically-controlled region of the HER, NF has a weak catalytic activity and hence a small number of evolving gas bubbles at the surface. At larger current densities (500 mA cm−2), the faster gas bubble detachment slightly reduces the amplitude. Enlarging the electrode surface area (2.5 cm2) slightly suppresses the resistance variation as comparably a smaller portion of the Ni surface is blocked by gas bubbles, which dissipate faster at a higher applied voltage required for a larger surface area (Fig. S6, ESI†). Interestingly, the dynamic resistance response for the HER and OER reactions over NF at the same current density of 100 mA cm−2 reveals slightly larger amplitudes for the HER (Fig. S7, ESI†). The stoichiometric ratio between O2 and H2 gases during water splitting renders more H2 bubbles produced during the HER; however, generally H2 bubbles are smaller than O2 bubbles.31 Thus, a combination of effects is in play to render a different dynamic resistance variation between the HER and OER reactions. At a moderate current density of 100 mA cm−2, a stronger impact is shown by more H2 bubbles on resistance variation. This difference is likely to become smaller at larger current densities, where the resistance variation is suppressed with the accelerated gas bubble detachment by providing a larger energy input. These results highlight the need to optimize the electrolytic conditions and consider the nature of the reaction to monitor GBE.
Monitoring GBE over catalyst-coated electrodes
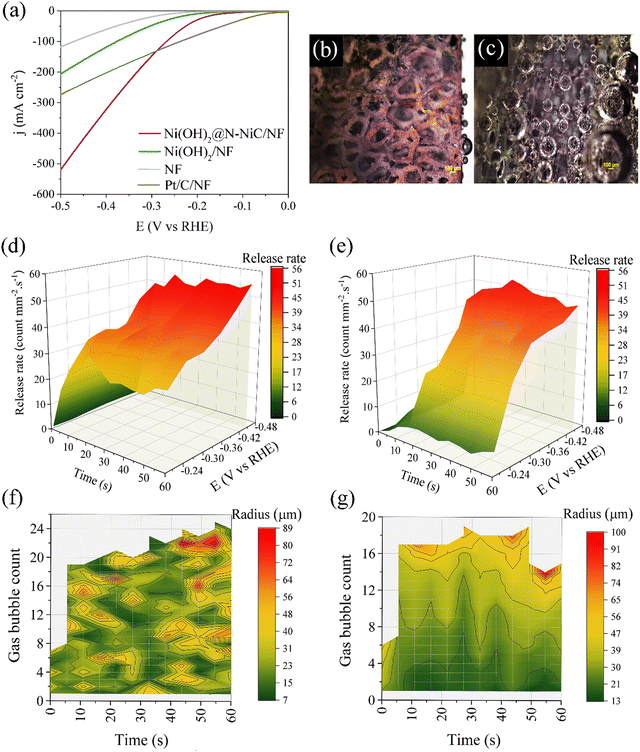
Typically, the non-homogeneous distribution of catalytic active sites on the surface and morphological differences cause non-homogeneous GBE. Correspondingly, the operando single frequency impedance monitoring of GBE should distinguish the magnitude and density of resistance fluctuations over distinct structures and morphologies. We further applied this method to monitor GBE over catalyst-coated electrodes for the HER. A hetero-hierarchical nanostructure, composed of Ni(OH)2 and N-NiC phases on the NF surface (Ni(OH)2@N-NiC/NF) is used as a case study (see Methods, Fig. S8 and Supplementary Note 1, ESI†),32 exhibiting a remarkably improved alkaline HER performance compared to Ni(OH)2 with typical nanosheets (Fig. 2a). Nano-structuring of the NF surface resulted in multi-directional surface hierarchies over Ni(OH)2@N-NiC/NF. Formation of nanoscale hetero-interfaces between oxide and non-oxide phases of Ni catalysts as well as anisotropic growth orientation zones at the surface hierarchies induce surface wettability, a key factor for preparing gas-repelling surfaces and gas bubble maneuvers.33,34A fast surface-wetting transition from the Cassie–Baxter state to the Wenzel state can be considered during the HER over Ni(OH)2@N-NiC/NF (Supplementary Note 2, ESI†).13,35 The unique surface morphology induces superaerophobicity, illustrated by the lack of an appreciable underwater gas bubble adhesion force during the advancing of an air bubble (A, process 1), its contact with the surface (C, process 2) and it receding from the electrode surface (R, process 3) (Fig. S9a, ESI†). In contrast, Ni(OH)2/NF and NF impose about 27.1 and 39.0 μN adhesion force with apparent bubble deformation during the receding process (Fig. S9b and c, ESI†). Similarly, a larger underwater gas bubble contact angle of 171.4° compared to 139.0° and 130.4° for Ni(OH)2/NF and NF, respectively, reveals the desired superwettability of Ni(OH)2@N-NiC/NF (Fig. S9, ESI†). The impact of multi-directional surface hierarchies on GBE is further illustrated by particle-scale numerical simulations using the multiphase Lattice Boltzmann (LBM) method,36 confirming less gas bubble adhesion to the surface and accelerated dissipation over Ni(OH)2@N-NiC/NF (Fig. S10, S11 and Supplementary Note 3, ESI†).
To verify the effects of surface wettability and anisotropic morphology on the GBE over Ni(OH)2@N-NiC/NF via monitoring by operando single frequency impedance, the GBE dynamics during the HER are probed by operando optical microscopy (Fig. S12, ESI†). Considering the similar GBE behavior and surface wettability of Ni(OH)2/NF with the bare NF, the growth and release rate of hydrogen bubbles is compared to Ni(OH)2/NF. Firstly, distinctively smaller gas bubbles and faster release are recorded over Ni(OH)2@N-NiC/NF (Fig. 2b, c and Fig. S13, S14, ESI†).
Secondly, time- and potential-dependent GBE is evaluated in operando, where a rapid rise in release rate is illustrated at the beginning of the HER at all potentials followed by a relatively maintained fast bubble dissipation in the 3D surface plot of Ni(OH)2@N-NiC/NF (Fig. 2d and Supplementary Note 4, ESI†). In contrast, Ni(OH)2/NF does not show appreciable bubble removal at low potentials as well as at the early stage of HER at moderate potentials (Fig. 2e). Also, a larger number of smaller bubbles is detected at every time interval at different potentials in the 3D contour plots of Ni(OH)2@N-NiC/NF (Fig. 2f and Fig. S15a, b, ESI†). In contrast, less bubble count with several similar sizes yet overall larger bubbles are captured at various regions of Ni(OH)2/NF surface at every time interval (Fig. 2g and Fig. S15c, d, ESI†).
The GBE is monitored on Ni(OH)2@N-NiC/NF and Ni(OH)2/NF as a free standing electrode for the HER in a standard electrochemical half-cell via the single frequency impedance technique at 20 kHz, determined by the corresponding Bode-phase plots (Fig. S16 and Supplementary Note 5, ESI†). Significantly reduced dynamic resistance variation is observed at a current density of −100 mA cm−2 (Fig. 3a and Fig. S17, ESI†). In comparison, the recorded resistance fluctuations for Ni(OH)2/NF and NF refer to the gas bubble effect. The FFT patterns of the dynamic resistance variations are extracted to illustrate how the detected GBE via single frequency impedance is patterned during the HER (see Methods, ESI†).37,38 The wider simulated FFT envelop, the bigger amplitudes of the dynamic resistance variation, and the fitted FFT peaks refer to the significant resistance amplitudes repeated at various periods. Also, the stronger envelop and fitted FFT peaks at smaller frequencies along the frequency range, the more sluggish GBE, as they reflect longer times for the bubble detachment which appears as a sudden decrease in the resistance amplitude. A fast relaxation in FFT with weak amplitudes is obtained for Ni(OH)2@N-NiC/NF (Fig. 3b). The FFT peaks are far less significant, pointing to a fast GBE with much smaller gas bubbles. Whereas the FFT patterns of Ni(OH)2/NF and NF display ample larger amplitudes along the frequency range, pointing to the longer-lived surface-bound gas bubbles of various sizes (Fig. 3c and d). For instance, two peaks at 0.014 and 0.025 Hz in the FFT pattern of Ni(OH)2/NF correspond to gas bubbles evolving at the repeating intervals of 71.4 and 40.0 s, and the characteristic FFT peak for NF correlates with gas bubbles evolving at every 47.6 s. The distinct difference in dynamic resistance variations and the corresponding FFT patterns follow with increasing the HER potential, with no apparent change for Ni(OH)2@N-NiC/NF compared to the larger amplitudes and FFT patterns of Ni(OH)2/NF at 0.445 V vs. RHE (Fig. S18 and S19, ESI†).
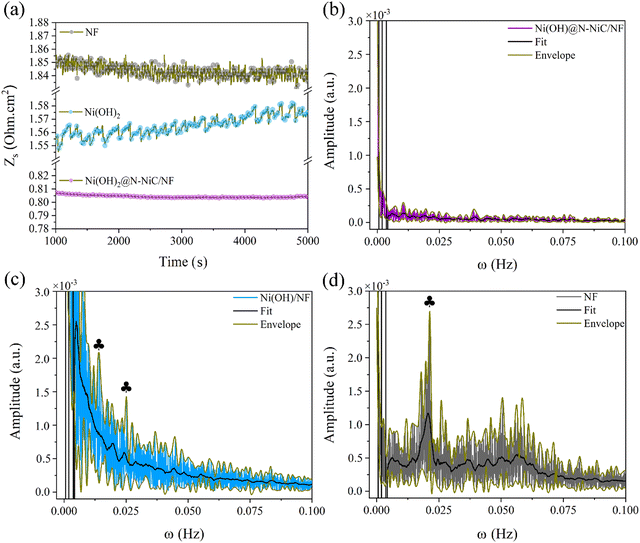 | ||
| Fig. 3 (a) Dynamic resistance variation at 20 kHz and −100 mA cm−2 and the corresponding FFT plots of (b) Ni(OH)2@N-NiC/NF, (c) Ni(OH)2/NF, and (d) NF. | ||
Given the consistent observations by single frequency impedance and optical microscopy, the two techniques are again coupled using an in situ electrochemical cell with a cross-section view of Ni(OH)2@N-NiC/NF and Ni(OH)2/NF electrodes under the microscope chamber (Fig. S20, ESI†). A high frequency of 10 kHz was required using the in situ cell with different geometric electrode sizes. Again, compared to Ni(OH)2/NF, the hetero-hierarchical Ni electrode exhibits suppressed dynamic resistance variation with smaller amplitudes, in agreement with smaller gas bubbles rapidly evolving and dissipating (Movies S3–S5, ESI†). A fluctuation-free resistance response is obtained at a low frequency of 0.1 Hz, confirming the operando GBE monitoring at the optimum high frequency (Fig. S21, ESI†). Similar to the bare NF electrode, the resistance value increases over time at low frequencies, alluding to the impact of faradaic processes on the surface.
Intriguingly, oxygen GBE monitoring via single frequency impedance at 20 kHz in a standard three-electrode half-cell also reveals dramatically decreased dynamic resistance variation over Ni(OH)2@N-NiC/NF at 100 mA cm−2 (Fig. S22, ESI†). A stable and fast-quenched FFT profile is obtained compared to the multiple larger amplitudes along the frequency range for Ni(OH)2/NF and NF (Fig. S23, ESI†). Accelerated GBE is beneficial to alkaline OER performance at large current densities, where Ni(OH)2@N-NiC/NF surpasses the benchmark IrO2/NF electrode (Fig. S24, ESI†). The distinct impact of multi-directional surface hierarchies on accelerating GBE during the OER also follows with incrementing potentials (Fig. S25, S26 and Supplementary Note 6, ESI†).
Monitoring GBE in water electrolysers
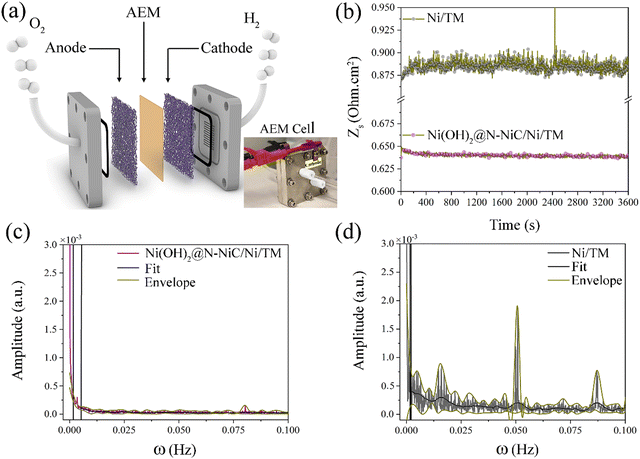
To demonstrate the practical application of this method, GBE monitoring via single frequency impedance is investigated in electrolyser devices. Firstly, when assembled as both the anode and cathode in an alkaline water electrolyser, Ni(OH)2@N-NiC/NF exhibits an improved performance compared to Ni(OH)2/NF‖Ni(OH)2/NF and NF‖NF electrolysers (Fig. S27a, ESI†), and an almost perturbation-free dynamic resistance variation at 20 kHz and a large current density of 500 mA cm−2 (Fig. S28, ESI†). Here, the resistance fluctuations in electrolyser full-cells are rendered by the change in the sum of surface resistance, i.e., ohmic, of both the anode and cathode, caused by the evolving oxygen and hydrogen bubbles. Given that the HER produces more gas products and faster but with smaller size of hydrogen bubbles, the resistance variation at the cathode is expected to have a slightly bigger impact on the overall dynamic resistance variation, which is similar to detecting more hydrogen gas bubbles on cathodes via voltage signal noise and acoustic emission techniques.39 However, the FFT patterns of bare NF and Ni(OH)2/NF electrodes in an alkaline electrolyser full-cell show more similar amplitudes to those recorded during the OER at increased potentials in the three-electrode half-cell, and notably smaller than the FFT patterns of these electrodes during the HER. This could be due to the cancellation effect of the combined noises and fluctuations at the anode and cathode.Electrochemical monitoring of GBE is further investigated in the zero-gap membrane electrode assembly in an anion exchange membrane (AEM) water electrolyser at 20 °C (Fig. 4a and Fig. S27b, ESI†). Titanium mesh (TM) with a smoother surface than NF is used as a support to avoid damaging the membrane, while an ultrathin metallic Ni film is coated onto TM via electrodeposition to render similar conductivity in 1 M KOH electrolyte fed at both anodic and cathodic flow fields (see Methods). To minimize the effect of electrolyte flow on the resistance response, a slow flow rate (<2 mL min−1) was applied. A smaller value of the optimum high frequency of minimum phase (10 kHz) is required to conduct single frequency impedance, and overall smaller absolute resistance values are recorded by the AEM electrolyser compared to the alkaline electrolyser as the membrane electrode assembly configuration is known to significantly improve the transport of gas bubbles. Similarly, much less dynamic resistance variation with significantly smaller amplitudes is observed for Ni(OH)2@N-NiC/N/TM as both the anode and cathode compared to the Ni/TM‖Ni/TM AEM electrolyser (Fig. 4b–d), even though the Ni/TM electrode exhibits a more periodic resistance variation and fewer characteristic peaks in the corresponding FFT pattern compared to the NF‖NF alkaline water electrolyser (Fig. S28d, ESI†). This implies that the presented method is also suitable to monitor GBE on different electrodes in AEM water electrolysers, which generally show a mitigated gas bubble effect on the electrocatalytic performance compared to the traditional alkaline water electrolysers. All in all, the significance of the unique surface morphology and surface superaerophobicity in boosting gas bubble transport during practical water electrolysis is evident for Ni(OH)2@N-NiC/N/TM.
Discussion
Tracking dynamic resistance variation via a single high frequency impedance at an optimum high frequency of minimum phase is demonstrated as a universal alternative for operando GBE monitoring during water electrolysis. By attributing the change in the surface resistance to the change in the surface area of the electrodes due to the evolving gas bubbles, the method can detect different GBE effects for various electrodes with varying degrees of surface wettability and different surface morphologies in lab-scale electrochemical half-cells and industrial-scale water electrolyser full-cells. Using FFT numerical analysis, the amplitude of dynamic resistance variation can predict if the number of gas bubbles and their evolution is different between various electrodes.First, bare electrodes with flat surfaces such as GCE and porous NF with 3D scaffolds are tested for the HER in alkaline media to demonstrate the concept of this approach. Parallel image processing by coupling to optical microscopy correlates the resistance variation with varying amplitudes with GBE. The faster the resistance variation and the smaller the amplitude, the faster GBE. This is exemplified with a catalyst-coated Ni electrode with superaerophobicity and multi-directional anisotropic hierarchical regions at the surface in standard half-cells and water electrolyser cells. Individually conducted operando optical microscopy at different HER potentials verifies the correlation between dynamic resistance variation and GBE dynamics, where accelerated growth and detachment of smaller-sized gas bubbles are observed for Ni(OH)2@N-NiC/NF. Not only during the HER but also during the OER and full water electrolysis, Ni(OH)2@N-NiC/NF exhibits almost perturbation-free resistance responses and insignificant amplitudes at different applied potentials and current densities.
The distinct dynamic resistance variations illustrated for different Ni electrodes in alkaline and AEM water electrolysers indicate that this method is particularly suitable to detect different GBE behaviors in non-transparent devices for practical water electrolysis, where optical recording/visualization cannot be used. This method is facile and applicable to larger electrodes using shelves potentiostat workstations, whereas optical recording is limited to smaller areas on electrodes with a fewer number of gas bubbles along with the inherent difficulty to visualize GBE at large current densities, where a bubble forth layer forms at the surface of the electrodes. Besides, this approach is useful to examine water electrolysis performance prior to the aggravating impact of gas bubbles on stability decline by optimizing the extents of current density and electrolyte flow rate, and thus maintaining a GBE regime to sustain the state of the health of electrodes. Unlike the fluctuations in the voltage/current response, which are generated due to more factors other than GBE, i.e., charging current or the current associated with metal dissolution and re-deposition, the dynamic resistance variation captured at optimum high frequency of minimum phase can be correlated to the effect of gas bubbles on the active surface. Such correlation can be followed for a range of electrode configurations, surface morphologies, and surface wettabilities. Using the implications made by resistance variation amplitudes as an electrochemical guide, advanced gas-repelling electrodes and membrane electrode assembly for gas bubble management in water electrolysers can be developed.
However, currently single frequency impedance cannot directly resolve the gas bubble effect, i.e., promoting gas bubble management in water electrolyzers, and cannot quantitatively predict GBE dynamics, i.e., size, growth and release rate of gas bubbles, for which high resolution/speed optical recording remains the best method, which is not yet applicable to water electrolysers. Also, the resistance response fluctuations do not reflect the periodicity in GBE dynamics. Here, the impact of a large number of gas bubbles on the electrode surface is detected simultaneously by the change in the electrode resistance, leading to the signal overlap, and also the relatively low sampling rate in current electrochemical workstations shields them from detecting more data over time. Thus, non-periodic patterns are mostly observed for different electrodes, although with distinct amplitudes and variation profiles. Besides, with the increase in the number of gas bubbles, i.e., with increasing the current density, a large gradient of bubble size and release rate entails more non-periodic patterns. Currently, numerical simulation via FFT processing is important to grasp the difference in GBE behavior based on the resistance variation amplitude. Future innovative designs in electrolyser devices allowing for optical observations of GBE dynamics, as well as in potentiostat workstations with flexible sampling rates allowing for a higher resolution of the resistance response can boost this method in identifying GBE.
Methods
Synthesis of Ni(OH)2@N-NiC/NF and Ni(OH)2/NF
Ni foam was initially cleansed with HNO3 (5 M) in an ultrasonic bath for half an hour, then washed thoroughly with water and ethanol, and kept dried in a vacuum oven before use. The hetero-hierarchical nanostructure is synthesized according to a previously reported solvothermal procedure.32 Firstly, a piece of clean NF (1 × 3 cm2) was placed in a homogeneous mixture of water and Ethylenediamine (EDA) with a volume ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (v
2 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v%) and with 5 mM of Ni(NO3)2·6H2O. A light pink solution appears upon the addition of an ionic Ni supplement. A portion of the transparent resultant solution (5 mL) was transferred to a 20 mL stainless steel autoclave and subjected to the solvothermal reaction at 180 °C for 5 h. The solvothermal-reacted NF was rinsed with water and ethanol several times and dried under vacuum. Then, the solvothermal-reacted NF was treated by post-thermal annealing in a nitrogen atmosphere at a mild temperature of 400 °C for 2 h. The resultant NF was kept under vacuum before use. The preparation of the monophasic Ni(OH)2/NF electrode was the same except for the addition of EDA into the solvothermal bath.
v%) and with 5 mM of Ni(NO3)2·6H2O. A light pink solution appears upon the addition of an ionic Ni supplement. A portion of the transparent resultant solution (5 mL) was transferred to a 20 mL stainless steel autoclave and subjected to the solvothermal reaction at 180 °C for 5 h. The solvothermal-reacted NF was rinsed with water and ethanol several times and dried under vacuum. Then, the solvothermal-reacted NF was treated by post-thermal annealing in a nitrogen atmosphere at a mild temperature of 400 °C for 2 h. The resultant NF was kept under vacuum before use. The preparation of the monophasic Ni(OH)2/NF electrode was the same except for the addition of EDA into the solvothermal bath.
Operando GBE electro-microscopy
Single frequency impedance-time measurement and optical microscopy were coupled using a house-built in situ electrochemical cell, which was placed under an optical microscope chamber and connected to a 760E CHI potentiostat. A glassy carbon electrode (GCE, 0.08 cm2) as well as NF, Ni(OH)2/NF, and Ni(OH)2@N-NiC/NF (0.5 cm2) electrodes were mounted on a holder as working electrodes. A saturated calomel electrode (SCE) and graphite rod were used as the reference and counter electrodes, respectively. Impedance-time measurement was conducted at a fixed frequency of 10 kHz, an amplitude of 0.01 V, and a sampling rate of 2 s, at the applied potentials of −1.45 V vs. RHE for GCE, −0.15 V vs. RHE, and equivalent potentials to deliver a fixed current density of −27 mA cm−2 for Ni electrodes. A (×2) lens magnification was fixated on the cross-section view of the working electrodes in 1 M KOH electrolyte and GBE was recorded. The image processing of GBE at different time intervals was analyzed by NIS-Elements D software.Three-electrode system electrochemical measurements
Electrochemical tests were performed in a standard three-electrode system using CHI 760E Electrochemical Workstations (CHI instruments). The Ni electrodes (0.25 cm2) were directly used as working electrodes. SCE and graphite plate were used as the reference and counter electrodes, respectively. The recorded potentials were converted to a reversible hydrogen electrode (RHE) system using the following equation.| ERHE = ESCE + 0.241 V + 0.059pH | (1) |
Operando optical microscopy
The growth and detachment of the evolved hydrogen gas bubbles during the HER process were captured in operando by a Nikon SMZ25 (Japan) optical microscope. A house-built in situ electrochemical cell was used with Ni(OH)2@N-NiC/NF and Ni(OH)2/NF electrodes (0.25 cm2), graphite rod, and SCE as the working, counter, and reference electrodes, respectively. The in situ cell was placed under a microscope lens and bias potentials between −0.195 and −0.445 V vs. RHE were applied via the chronoamperometry technique using a 760E CHI potentiostat. The GBE was recorded at a lens magnification of 4. NIS-Elements D software was used to detect the average values of gas bubble population per surface area, diameter, and release rate at different time intervals at different potentials.Shan-and-Chen-type multicomponent multiphase lattice Boltzmann method
A multicomponent, multiphase lattice Boltzmann method (LBM) is developed based on a combination of the Shen-Chen model40 and the immersed boundary method41 to investigate single gas bubble size and transport as a function of surface geometry in both random and periodic paradigms. The LBM method overcomes numerical challenges with the Navier–Stokes equation and is appropriate for flow through complex geometries. The open-source program Palabos was used to carry out the simulations.42 A single-component density distribution function fi(x,t) is introduced for each of the two fluid components, fi(x,t) with i = 1 for the gas bubble (fluid 1) and i = 2 for the liquid electrolyte (fluid 2). The interactions between the fluids and electrode surface are solved using the immersed moving boundary technique based on the local solid fraction in each lattice cell, known as the partially-solid scheme.37 A series of 3D simulations are carried out with a pure gas bubble of fluid 1 (ρ1) placed inside a 45 × 45 × 45 cuboidal volume of fluid 2 (ρ2) with periodic boundaries. An electrode surface with a size of 30 × 30 × 10 is immersed in fluid 2 (ρ2). The gas bubble transport with varying sizes is calculated based on surface geometry. The input parameters used for the LBM model are outlined in Table S1 (ESI†).AEM electrolyser system assembly
The AEM electrolyser is composed of Ni(OH)2@N-NiC/Ni/TM (1 cm2) as both the cathode and anode, and an anion exchange membrane (5 × 5 cm2, X37-50, dioxide materials). Titanium mesh with a smooth surface was used as the gas diffusion layer instead of NF to prevent damaging the membrane. Metallic Ni was coated onto TM via cathodic deposition with graphite plate and SCE counter and reference electrodes, respectively, as at −2.0 V (vs. SCE) for 600 s at 20 °C in an electrolyte bath containing NiSO4 (0.5 M) and H3BO3 (0.5 M). The membrane electrode assembly was sandwiched between two stainless steel plates with flow channels. The alkaline electrolyte (1 M KOH) was pumped through both anode and cathode chambers using low flow rates (<2 mL min−1) to minimize the effect of electrolyte circulation on the resistance variation. AEM tests were taken at 20 °C and the polarization curves were obtained at a scan rate of 5 mV s−1.Data availability
The supporting data in this work are presented in the paper and/or the Supplementary Information. Source data are available from the corresponding author upon request.Author contributions
K. D. designed and carried out the experiments, collected data, and wrote the manuscript. S. W. and Q. Z. performed operando optical microscopy. S. S. and Y. S. carried out LBM simulations. K. D. and Q. M. collected, analyzed, and interpreted single frequency EIS data. C. Z. supervised the work. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Electron Microscope Unit at UNSW Mark Wainwright Analytical Centre (MWAC) and Professor Lei Jiang at Technical Institute of Physics and Chemistry, China for assisting with adhesion force measurements. The study was supported by Australian Research Council (FT170100224, DP210103892, IC200100023, DP220100306).References
- L. Wang, et al., Increasing gas bubble escape rate for water splitting with nonwoven stainless steel fabrics, ACS Appl. Mater. Interfaces, 2017, 9, 40281–40289, DOI:10.1021/acsami.7b12895.
- H. Li, et al., Systematic design of superaerophobic nanotube-array electrode comprised of transition-metal sulfides for overall water splitting, Nat. Commun., 2018, 9, 2452, DOI:10.1038/s41467-018-04888-0.
- A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. Fernández Rivas, Influence of bubbles on the energy conversion efficiency of electrochemical reactors, Joule, 2020, 4, 555–579, DOI:10.1016/j.joule.2020.01.005.
- K. Dastafkan, Q. Meyer, X. Chen and C. Zhao, Efficient oxygen evolution and gas bubble release achieved by a low gas bubble adhesive iron-nickel vanadate electrocatalyst, Small, 2020, 16, e2002412, DOI:10.1002/smll.202002412.
- K. Dastafkan, Y. Li, Y. Zeng, L. Han and C. Zhao, Enhanced surface wettability and innate activity of an iron borate catalyst for efficient oxygen evolution and gas bubble detachment, J. Mater. Chem. A, 2019, 7, 15252–15261, 10.1039/c9ta03346g.
- T. Kou, et al., Periodic porous 3D electrodes mitigate gas bubble traffic during alkaline water electrolysis at high current densities, Adv. Energy Mater., 2020, 10(46), 2002955, DOI:10.1002/aenm.202002955.
- Q. Song, et al., General strategy to optimize gas evolution reaction via assembled striped-pattern superlattices, J. Am. Chem. Soc., 2020, 142, 1857–1863, DOI:10.1021/jacs.9b10388.
- Y. J. Kim, et al., Highly efficient oxygen evolution reaction via facile bubble transport realized by three-dimensionally stack-printed catalysts, Nat. Commun., 2020, 11, 4921, DOI:10.1038/s41467-020-18686-0.
- X. Yu, et al., “Superaerophobic” nickel phosphide nanoarray catalyst for efficient hydrogen evolution at ultrahigh current densities, J. Am. Chem. Soc., 2019, 141, 7537–7543, DOI:10.1021/jacs.9b02527.
- M. Wang, Z. Wang, X. Gong and Z. Guo, The intensification technologies to water electrolysis for hydrogen production – A review, Renewable Sustainable Energy Rev., 2014, 29, 573–588, DOI:10.1016/j.rser.2013.08.090.
- K. Zeng and D. Zhang, Recent progress in alkaline water electrolysis for hydrogen production and applications, Prog. Energy Combust. Sci., 2010, 36, 307–326, DOI:10.1016/j.pecs.2009.11.002.
- A. Hodges, et al., A high-performance capillary-fed electrolysis cell promises more cost-competitive renewable hydrogen, Nat. Commun., 2022, 13, 1304, DOI:10.1038/s41467-022-28953-x.
- Z. Lu, Y. Li, X. Lei, J. Liu and X. Sun, Nanoarray based “superaerophobic” surfaces for gas evolution reaction electrodes, Mater. Horiz., 2015, 2, 294–298, 10.1039/c4mh00208c.
- W. Yang and S. Chen, Recent progress in electrode fabrication for electrocatalytic hydrogen evolution reaction: A mini review, Chem. Eng. J., 2020, 393, 124726, DOI:10.1016/j.cej.2020.124726.
- X. Shan, et al., An Engineered superhydrophilic/superaerophobic electrocatalyst composed of the supported CoMoSx chalcogel for overall water splitting, Angew. Chem., Int. Ed., 2020, 59, 1659–1665, DOI:10.1002/anie.201911617.
- D. Kim, X. Qin, B. Yan and Y. Piao, Sprout-shaped Mo-doped CoP with maximized hydrophilicity and gas bubble release for high-performance water splitting catalyst, Chem. Eng. J., 2021, 408, 127331, DOI:10.1016/j.cej.2020.127331.
- X. Tang, et al., Bioinspired nanostructured surfaces for on-demand bubble transportation, ACS Appl. Mater. Interfaces, 2018, 10, 3029–3038, DOI:10.1021/acsami.7b14453.
- J. Li, et al., Breathing-mimicking electrocatalysis for oxygen evolution and reduction, Joule, 2019, 3, 557–569, DOI:10.1016/j.joule.2018.11.015.
- P. Hou, et al., Delicate control on the shell structure of hollow spheres enables tunable mass transport in water splitting, Angew. Chem., Int. Ed., 2021, 60, 6926–6931, DOI:10.1002/anie.202016285.
- Q. Hu, et al., Integrating well-controlled core-shell structures into “superaerophobic” electrodes for water oxidation at large current densities, Appl. Catal., B, 2021, 286, 119920, DOI:10.1016/j.apcatb.2021.119920.
- S. J. Gross, K. M. McDevitt, D. R. Mumm and A. Mohraz, Mitigating bubble traffic in gas-evolving electrodes via spinodally derived architectures, ACS Appl. Mater. Interfaces, 2021, 13, 8528–8537, DOI:10.1021/acsami.0c20798.
- Z. Long, et al., A multi-bioinspired dual-gradient electrode for microbubble manipulation toward controllable water splitting, Adv. Mater., 2020, 32, e1908099, DOI:10.1002/adma.201908099.
- D. Kim, X. Qin, B. Yan, H. Hong and Y. Piao, Nano/microscale integrated mushroom-shaped hydrophilic CoP@Ni-CoP with optimized gas bubble release for high-performance water splitting catalysis, ACS Appl. Energy Mater., 2020, 3, 9769–9784, DOI:10.1021/acsaem.0c01374.
- G. Liu, W. S. Y. Wong, M. Kraft, J. W. Ager, D. Vollmer and R. Xu, Wetting-regulated gas-involving (photo)electrocatalysis: biomimetics in energy conversion, Chem. Soc. Rev., 2021, 50, 10674–10699, 10.1039/d1cs00258a.
- K. Dastafkan, S. Wang, C. Rong, Q. Meyer, Y. Li, Q. Zhang and C. Zhao, Cosynergistic molybdate oxo-anionic modification of FeNi-based electrocatalysts for efficient oxygen evolution reaction, Adv. Funct. Mater., 2021, 32, 2107342, DOI:10.1002/adfm.202107342.
- Y. Wang, E. Gordon and H. Ren, Mapping the nucleation of H2 bubbles on polycrystalline Pt via scanning electrochemical cell microscopy, J. Phys. Chem. Lett., 2019, 10, 3887–3892, DOI:10.1021/acs.jpclett.9b01414.
- X. Yang, F. Karnbach, M. Uhlemann, S. Odenbach and K. Eckert, Dynamics of single hydrogen bubbles at a platinum microelectrode, Langmuir, 2015, 31, 8184–8193, DOI:10.1021/acs.langmuir.5b01825.
- R. Iwata, L. Zhang, K. L. Wilke, S. Gong, M. He, B. M. Gallant and E. N. Wang, Bubble growth and departure modes on wettable/non-wettable porous foams in alkaline water splitting, Joule, 2021, 5, 887–900, DOI:10.1016/j.joule.2021.02.015.
- D. Y. Chung, et al., Dynamic stability of active sites in hydr(oxy)oxides for the oxygen evolution reaction, Nat. Energy, 2020, 5, 222–230, DOI:10.1038/s41560-020-0576-y.
- D. Kiuchi, H. Matsushima, Y. Fukunaka and K. Kuribayashi, Ohmic resistance measurement of bubble froth layer in water electrolysis under microgravity, J. Electrochem. Soc., 2006, 153, E138–E143, DOI:10.1149/1.2207008.
- R. H. Hacha, A. G. Merma, H. J. B. Couto and M. L. Torem, Measurement and analysis of H2 and O2 bubbles diameter produced by electroflotation processes in a modified Partridge-Smith cell, Powder Technol., 2019, 342, 308–320, DOI:10.1016/j.powtec.2018.09.062.
- K. Dastafkan, X. Shen, R. K. Hocking, Q. Meyer and C. Zhao, Monometallic interphasic synergy via nano-hetero-interfacing for hydrogen evolution in alkaline electrolytes, Nat. Commun., 2023, 14, 547, DOI:10.1038/s41467-023-36100-3.
- T. Kou, S. Wang and Y. Li, Perspective on high-rate alkaline water splitting, ACS Mater. Lett., 2021, 3, 224–234, DOI:10.1021/acsmaterialslett.0c00536.
- G. Liu, et al., Wetting-regulated gas-involving (photo)electrocatalysis: biomimetics in energy conversion, Chem. Soc. Rev., 2021, 50, 10674–10699, 10.1039/d1cs00258a.
- W. Xu, Z. Lu, X. Sun, L. Jiang and X. Duan, Superwetting electrodes for gas-involving electrocatalysis, Acc. Chem. Res., 2018, 51, 1590–1598, DOI:10.1021/acs.accounts.8b00070.
- S. Song, S. Wang, P. Le-Clech and Y. Shen, LBM-DEM simulation of particle deposition and resuspension of pre-deposited dynamic membrane, Powder Technol., 2022, 407, 117637, DOI:10.1016/j.powtec.2022.117637.
- A. R. Zeradjanin, E. Ventosa, A. S. Bondarenko and W. Schuhmann, Evaluation of the catalytic performance of gas-evolving Electrodes using Local Electrochemical Noise Measurements, ChemSusChem, 2012, 5, 1905–1911 CrossRef CAS PubMed.
- J. T. H. Kwan, A. Nouri-Khorasani, A. Bonakdarpour, D. G. McClement, G. Afonso and D. P. Wilkinson, Frequency analysis of water electrolysis current fluctuations in a PEM flow cell: insights into bubble nucleation and detachment, J. Electrochem. Soc., 2022, 169, 054531 CrossRef CAS.
- G. Swiegers, A. L. Hoang, R. E. Owen, G. Tsekouras and D. J. L. Brett, Bubble detection on the cathode and anode of a high-performing capillary-fed water electrolysis cell, ChemRxiv, Cambridge Open Engage, Cambridge, 2023.
- X. W. Shan and H. D. Chen, Lattice boltzmann model for simulating flows with multiple phases and components, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 1815–1819 CrossRef PubMed.
- D. R. Noble and J. R. Torczynski, A lattice-Boltzmann method for partially saturated computational cells, Int. J. Mod. Phys. C, 1998, 9, 1189–1201 CrossRef.
- J. Latt, et al., Palabos: parallel lattice boltzmann solver, Comput. Math. Appl., 2021, 81, 334–350 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental procedures and data. See DOI: https://doi.org/10.1039/d3ey00182b |
| This journal is © The Royal Society of Chemistry 2023 |