Open Access Article
Open Access ArticleIn silico characterization of nanoparticles†
Björn
Kirchhoff
 *a,
Christoph
Jung
*a,
Christoph
Jung
 abc,
Daniel
Gaissmaier
abc,
Daniel
Gaissmaier
 abc,
Laura
Braunwarth
a,
Donato
Fantauzzi
a and
Timo
Jacob
abc,
Laura
Braunwarth
a,
Donato
Fantauzzi
a and
Timo
Jacob
 *abc
*abc
aInstitute of Electrochemistry, Ulm University, Albert-Einstein-Allee 47, 89081 Ulm, Germany. E-mail: nawi.ec@uni-ulm.de; Fax: +49 731 5025409; Tel: +49 731 5025401
bHelmholtz-Institute Ulm (HIU) Electrochemical Energy Storage, Helmholtz-Straße 16, 89081 Ulm, Germany
cKarlsruhe Institute of Technology (KIT), P.O. Box 3640, 76021 Karlsruhe, Germany
First published on 26th April 2023
Abstract
Nanoparticles (NPs) make for intriguing heterogeneous catalysts due to their large active surface area and excellent and often size-dependent catalytic properties that emerge from a multitude of chemically different surface reaction sites. NP catalysts are, in principle, also highly tunable: even small changes to the NP size or surface facet composition, doping with heteroatoms, or changes of the supporting material can significantly alter their physicochemical properties. Because synthesis of size- and shape-controlled NP catalysts is challenging, the ability to computationally predict the most favorable NP structures for a catalytic reaction of interest is an in-demand skill that can help accelerate and streamline the material optimization process. Fundamentally, simulations of NP model systems present unique challenges to computational scientists. Not only must considerable methodological hurdles be overcome in performing calculations with hundreds to thousands of atoms while retaining appropriate accuracy to be able to probe the desired properties. Also, the data generated by simulations of NPs are typically more complex than data from simulations of, for example, single crystal surface models, and therefore often require different data analysis strategies. To this end, the present work aims to review analytical methods and data analysis strategies that have proven useful in extracting thermodynamic trends from NP simulations.
1 Introduction
Deployment of heterogeneous catalysts in nanoparticulate form has various benefits. Not only do nanoparticles (NPs) promise high mass activity due to the more favorable surface-to-volume ratio compared to catalysts with grain sizes in the micro- or millimeter range, NPs can also express heightened or outright different catalytic properties compared to the bulk material as a result of finite- and quantum-size effects and due to the availability of a plethora of chemically distinct surface reaction sites. However, synthesis of shape- and size-controlled NPs is challenging, and Ostwald ripening as well as other degradation effects can impact the longevity of NP catalysts.1 In order to streamline material optimization cycles, interest has therefore been growing in computational approaches that can predict favorable catalyst candidate structures for a reaction of interest. More and more, computational science is asked to establish structure-activity relationships for model NP catalysts in the 1 to 5 nm range and to investigate degradation mechanisms.Historically, computational investigation of NP properties was usually carried out by performing density functional theory (DFT) calculations of single crystal model surfaces that correspond to the surface facets of a NP of interest.2–6 However, results from surface models are often not transferable to NPs for several reasons. Firstly, the number of chemically different surface sites on a NP is larger than on single crystal surface models. In particular, the highly reactive, undercoordinated edge and vertex sites are hard to represent using a surface model.7 Furthermore, when using stepped model surfaces to mimic the lower coordination of NP edge sites, one finds that such models contain both convex and concave surface structures while NPs typically only contain one type.8 Another disparity between surface models and actual NPs is that quantum-size effects can affect the properties of clusters and small NPs in non-systematic ways.9,10 In fact, not all properties observed for NPs will converge to the bulk limit as the system size increases.11 Surface models are therefore unsuitable to study certain NP properties, even if the surface model is used as a stand-in for very large NPs. Finally, investigation of catalyst degradation processes using surface models and DFT can be arduous given the computational limitations with regards to system size and time scale that such processes typically occur at.
Nevertheless, the surface model approach remained the default option for a long time to model the behavior of extended facets of NPs because accurate simulations of NPs with hundreds or thousands of atoms are computationally demanding. Recent advances in computational methodology have changed this circumstance. Force field-based methods such as ReaxFF12,13 or semi-empirical methods such as xTB14 and Sutton-Chen type potentials15–18 have brought down costs for calculations of NPs significantly while retaining reasonable accuracy. Similarly, highly scalable codes enable electronic structure calculations of model sizes previously thought inaccessible using DFT. Advances in the field of hybrid simulations such as the QMMM ansatz also push the limits of system size.19–23
With computational costs for NP simulations brought down, one important question remains: how best to extract useful information from the model systems and simulations? Analyzing properties and the reactivity of NPs is not as straight forward as analyzing a single crystal surface for example. The abundance of different binding sites will naturally lead to noisier results. Oftentimes, molecular dynamics (MD) or Monte Carlo (MC) based simulations are used to study NP model systems. Such simulations can create large data sets that require specialized data analysis strategies to extract the desired information.
This work aims to review methods of data analysis that we found useful in our research in this field24–26 to extract information about thermodynamic properties and structure-activity relationships from simulations of NP catalysts. Exemplary studies applying the presented methods are highlighted when appropriate, without the intention to be exhaustive in this regard.
Many of the methods discussed in this review will be illustrated using atomic configurations of 3 nm octahedral Pt NP structures in various states of oxidation. These structures are taken from an openly accessible data set available under the https://doi.org/10.5281/zenodo.6322004 which our group recently published alongside a study comparing electrochemical oxidation trends of Pt NPs of various shapes.26 Additionally, we have made available a git repository of a Jupyter book that serves as a tutorial on how to implement many of the methods presented below using Python3: https://bjk24.gitlab.io/in-silico-review/intro.html. The code is written to directly interact with the data set for oxidized octahedral NPs. More information on the required setup to follow the tutorial and execute the code for yourself can be found on the website linked above.
Of course, almost all of the presented methods are already very efficiently implemented in existing software packages for daily use. However, such programs are typically closed-source or at least hard to decipher due to radical optimization for speed. We therefore encourage readers, who we anticipate are scientists first and programmers second, to run and modify our more straight forward test script suite to familiarize themselves with the implementation of these methods and with code-driven data analysis in general.
The remainder of this review is structured as follows: Section 2 shortly summarizes open-source software solutions that enable users to generate atomic configurations of NPs. Section 3 is concerned with analytical methods aimed at extracting information from individual structures while Section 4 presents methods aimed at analyzing entire data sets. Some concluding remarks are given in Section 5. All figures original to this work used the Visual Molecular Dynamics (VMD) software27 and the Tachyon renderer28 to visualize atomic configurations. If not indicated otherwise, Pt atoms are grey while oxygen atoms are red.
2 Generating nanoparticle model systems
Many commercial computational chemistry software suites allow users to generate NP configurations. Here, three open-source alternatives are mentioned to reduce the activation barrier for newcomers.• Atomic simulation environment (ASE): ASE is a Python3-based framework for molecular and materials simulations that interfaces with many commercial and open-source computational codes.29 The ase.cluster class provides various means for generating NPs based on user-provided information about the lattice type and constants as well as Miller indices of the surfaces that should be cut. Pre-configured methods exist to generate typical NP shapes such as octahedra. A method for Wulff constructions exists as well which requires users to supply the formation energy of different types of surface facets. The method will then create a NP shape that minimizes the overall surface energy.
• WulffPack: WulffPack is a powerful python3 package used to generate NPs using Wulff construction.30 WulffPack features built in methods to visualize the generated NPs and interfaces with ASE to export atomic coordinates.
• Nanocut: nanocut is a python3 package that can be used to generate NPs by providing cell and Miller index information. The program can also generate periodic surfaces and crystals, nanotubes, and nanowires.31 The ability to chain sequences of cutting procedures allows users to realize unusual shapes. At the time of writing, development appears to have halted. Nanocut may still be worth a look for users who find other alternatives too restrictive as compatibilty issues should be quick to fix due to the open-source nature of the project.
3 Analyzing single structures
3.1 Quantifying the surface coverage of nanoparticles
In computational surface science, coverage is typically given in terms of monolayers, i.e. with respect to the number of atoms within the top layer of the underlying periodic surface model. This is often a convenient measure because it directly relates to single-crystal experiments for example. In case of NPs, however, a monolayer is somewhat ill-defined due to the inhomogeneous nature of the available surface sites. Experimental data on NPs, for example from X-ray spectroscopy methods, can give insight into the relative occurrence of different chemical species or oxidation states in a material. Hence, giving coverage as a ratio of x = number of adatoms/number of substrate atoms is found to be more useful.24,32–34 Senftle and co-workers for example have characterized the degree of oxidation of a Pd NP via its O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd ratio.32 This method of designating coverage will be used throughout this review.
Pd ratio.32 This method of designating coverage will be used throughout this review.
3.2 Coordination number-based approaches
Moreover, CNs have been shown to be useful as a descriptor for catalytic activity. In 2009, Jiang and co-workers showed that the CNs of surface atoms on small NPs linearly correlate with metal d-band centers,36 priming CNs as descriptors for reactivity.37 Mpourmpakis and co-workers exploited this relationship further: they used CNs to characterize the interactions between small gold clusters (Au16 to Au45) and CO molecules.38 From these results, the group extrapolated a transferable concept that uses the CN and the bonding angle of an adspecies on the particle surface as descriptors for the binding energy. This approach therefore allows for the prediction of NP reactivity without requiring expensive electronic structure calculations. Certainly, this concept cannot be generalized to any surface and adspecies as it neglects various aspects such as surface rearrangement and crowding effects. To address some of these limitations, the group introduced a refined descriptor approach based on the relationship between CO binding energy and surface CN that takes into account interdependence of NP structure and adsorbate coverage in a follow-up study.39
Two interesting applications are highlighted in the following to further illustrate the usefulness of CNs for catalysis research. Using O atoms and CO molecules as probes, Kleis et al. employed CNs to identify the point of transition at which the adsorption properties on cuboctahedral Au NPs will converge to the extended surface behavior.10 By relating adsorption energy values to CNs, the group was able to show that for particles with more than 561 atoms (diameter of ca. 2.7 nm), the adsorption energy on a (111)-indexed Au NP facet becomes invariant against the extent of the facet and is close to the number obtained for an extended Au(111) model surface. In another example, Ouyang et al. chose a Au(997) surface to simulate a NP system and used CNs to study O and NO adsorption.6 The group identified the relative activity of different adsorbed oxygen species towards NO reduction which they found to be “island O” > “terrace O” > “O near step-edge sites”.
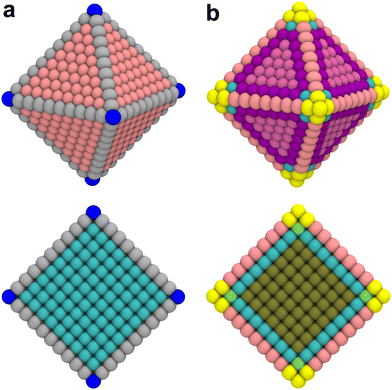
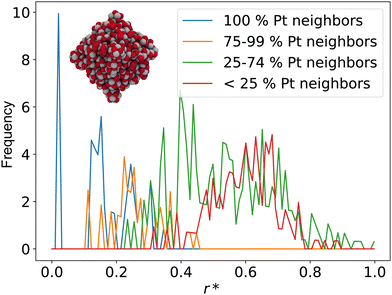
A noteworthy limitation of CNs is their low sensitivity for microscopic features. For example, the ABC-layered structure of a Pt(111) surface gives rise to two different threefold adsorption sites, HCP and FCC. It is well known that these two sites interact differently with certain adspecies such as oxygen; however, since CNs only take into account the first coordination sphere, adatoms adsorbed at HCP and FCC sites are assigned the same CN. Furthermore, when CNs are used with NPs, they do not capture edge or kink site effects. As shown in Fig. 1a, all facet atoms barring those located exactly on the edges and vertices are assigned values of the corresponding single crystal surface.
The study by Kleis et al. discussed above established that a certain particle size is required before facet atoms express properties analogous to the corresponding single crystal surface.10 CNs as a categorization tool are too coarse-grained to capture such effects. This limitation is further exemplified in the cross section view in Fig. 1a. The cross section illustrates that CNs immediately converge to the bulk value of an FCC crystal at the first layer below the surface. This step-like change does not reflect the more gradual – albeit still fast – decay of surface properties with increasing depth.
 were introduced by Calle-Vallejo and co-workers in 2014.40 The
were introduced by Calle-Vallejo and co-workers in 2014.40 The  of a specific atom constitutes the average of the CNs of its nearest-neighbor atoms, see eqn (1):
of a specific atom constitutes the average of the CNs of its nearest-neighbor atoms, see eqn (1):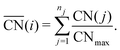 | (1) |
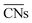 are distinct for different types of three-fold adsorption sites or bridge positions on ABC-layered surfaces. Similarly,
are distinct for different types of three-fold adsorption sites or bridge positions on ABC-layered surfaces. Similarly, 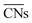 give a more nuanced picture of the different adsorption sites on NPs, see Fig. 1b.
give a more nuanced picture of the different adsorption sites on NPs, see Fig. 1b.
Calle-Vallejo and co-workers have shown the usefulness of 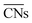 in several studies. The group used
in several studies. The group used 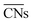 to study the interplay between adsorption energetics and adsorbate-induced core–shell deformation.41 They show that the deformation cost is site-independent and can be assumed constant for a specific adspecies. In 2015, the group used
to study the interplay between adsorption energetics and adsorbate-induced core–shell deformation.41 They show that the deformation cost is site-independent and can be assumed constant for a specific adspecies. In 2015, the group used 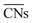 to devise a relationship for adsorption properties of oxygen species on transition-metal surfaces that does not require expensive electronic structure calculations.42 The relationship they propose relies on knowledge of the valence of the adatom, which can be obtained from electron-counting rules, and the chemical environment of the active site, which they represent via
to devise a relationship for adsorption properties of oxygen species on transition-metal surfaces that does not require expensive electronic structure calculations.42 The relationship they propose relies on knowledge of the valence of the adatom, which can be obtained from electron-counting rules, and the chemical environment of the active site, which they represent via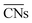 . The approach can be used to predict surface features that satisfy the energetic requirements of each intermediate of a given reaction mechanism, which Calle-Vallejo et al. confirmed against benchmark DFT calculations. The group successfully applied this approach to inform the experimental modification of a Pt(111) surface which produced a material with threefold enhanced ORR activity.43 Tymoczko et al. further used this approach to explain the heightened experimental HER activity of a Cu–Pt(111) near-surface alloy.44
. The approach can be used to predict surface features that satisfy the energetic requirements of each intermediate of a given reaction mechanism, which Calle-Vallejo et al. confirmed against benchmark DFT calculations. The group successfully applied this approach to inform the experimental modification of a Pt(111) surface which produced a material with threefold enhanced ORR activity.43 Tymoczko et al. further used this approach to explain the heightened experimental HER activity of a Cu–Pt(111) near-surface alloy.44
Recently, Calle-Vallejo et al. used 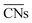 to clarify why simulation results from single crystal model surfaces are oftentimes not transferable to NPs.8 In particular, they note that Pt surfaces contain both convex and concave sites while typical NP systems like cuboctahedra contain only convex sites that are less active towards the ORR. They find that active sites with
to clarify why simulation results from single crystal model surfaces are oftentimes not transferable to NPs.8 In particular, they note that Pt surfaces contain both convex and concave sites while typical NP systems like cuboctahedra contain only convex sites that are less active towards the ORR. They find that active sites with 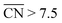 promote ORR activity, where
promote ORR activity, where 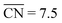 corresponds to Pt atoms in an extended Pt(111) surface.
corresponds to Pt atoms in an extended Pt(111) surface.
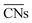 are ill-defined in case of alloy catalysts for which not only the number but also the elemental nature of neighboring atoms are important to describe the properties of a specific site. Similarly,
are ill-defined in case of alloy catalysts for which not only the number but also the elemental nature of neighboring atoms are important to describe the properties of a specific site. Similarly, 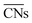 cannot be used to study systems for which strain is the dominant factor governing chemical reactivity.
cannot be used to study systems for which strain is the dominant factor governing chemical reactivity.
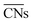 outlined above, Ma and Xin extend the coordination number approach to orbitals. Orbitalwise coordination numbers (CNα, where α refers to the orbital α = s, d)45 are based on the electronic structure by way of moment characteristics of the projected density of states. Ma and Xin define CNα in eqn (2) as
outlined above, Ma and Xin extend the coordination number approach to orbitals. Orbitalwise coordination numbers (CNα, where α refers to the orbital α = s, d)45 are based on the electronic structure by way of moment characteristics of the projected density of states. Ma and Xin define CNα in eqn (2) as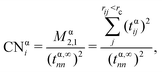 | (2) |
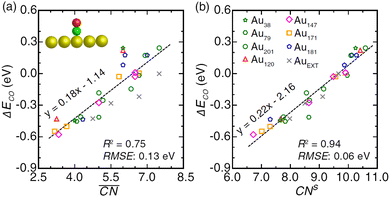
Ma and Xin tested the CNα descriptor against 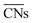 for CO adsorption on small Au clusters of 38 to 181 atoms, see Fig. 2.
for CO adsorption on small Au clusters of 38 to 181 atoms, see Fig. 2.
The CNα-based model, which in this case relied on s electron hopping integrals (CNs) exclusively, is found to correlate better with DFT-PBE results (R2 = 0.94) than the model based on 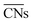 (R2 = 0.75). Wang et al.47 used this approach to study larger Au NPs optimized using the embedded-atom method (EAM).48 Adsorption energy results on individual sites were evaluated using s-orbital dependent coordination numbers. Wang et al. further included a microkinetics model to predict CO oxidation rates as a function of particle size. They found improved agreement between experiments and the CNα based model over using classical or
(R2 = 0.75). Wang et al.47 used this approach to study larger Au NPs optimized using the embedded-atom method (EAM).48 Adsorption energy results on individual sites were evaluated using s-orbital dependent coordination numbers. Wang et al. further included a microkinetics model to predict CO oxidation rates as a function of particle size. They found improved agreement between experiments and the CNα based model over using classical or 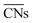 .
.
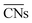 offer greater resolution than classic CNs, they can still be too coarse-grained for highly disordered systems such as transition metal oxides for which different oxidation states of surface metal atoms, surface defects, and other non-trivial electronic properties complicate the picture. Adjusted coordination numbers (ACNs) were proposed by Fung and co-workers in 2017 as a descriptor for transition metal oxides in particular.49 Here, the ACN of an oxygen atom located at the surface of the system is calculated based on its own coordination number, CNO, and the sum over the coordination numbers of nearest-neighbor metal centers,
offer greater resolution than classic CNs, they can still be too coarse-grained for highly disordered systems such as transition metal oxides for which different oxidation states of surface metal atoms, surface defects, and other non-trivial electronic properties complicate the picture. Adjusted coordination numbers (ACNs) were proposed by Fung and co-workers in 2017 as a descriptor for transition metal oxides in particular.49 Here, the ACN of an oxygen atom located at the surface of the system is calculated based on its own coordination number, CNO, and the sum over the coordination numbers of nearest-neighbor metal centers, 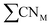 , as presented in eqn (3):
, as presented in eqn (3):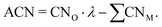 | (3) |
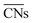 and are therefore advantageous for describing the local chemical environment of low-coordination, surface-bound species such as oxides in more detail. In their publication, Fung et al. calibrated ACNs for bulk Co3O4, V2O3, NiO, and C–H bond activation barriers.49
and are therefore advantageous for describing the local chemical environment of low-coordination, surface-bound species such as oxides in more detail. In their publication, Fung et al. calibrated ACNs for bulk Co3O4, V2O3, NiO, and C–H bond activation barriers.49
3.3 Partial charge analysis
| ψi = cijϕj + cikϕk, | (4) |
| 1 = cij2 + cik2 + cijcikSjk, | (5) |
Mulliken charges suffer from a major limitation. Computational codes using the LCAO approach represent atoms through basis sets of different makeup and size. Basis sets may include varying numbers of basis functions to represent an orbital. The total atomic charge extracted via Mulliken's approach depends on the basis set size and has no basis set limit.55 Mulliken occupancies typically do not sum up to the total number of electrons in the system and can even be negative in rare cases.55 Finally, Mulliken analysis cannot be used with plane wave calculations directly.
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , ρmol(
, ρmol(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ), to the charge density of the “promolecule”, ρpro(
), to the charge density of the “promolecule”, ρpro(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ), which is constructed from the individual non-interacting atomic densities, results in the deformation density ρd(
), which is constructed from the individual non-interacting atomic densities, results in the deformation density ρd(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ), as shown in eqn (6):58
), as shown in eqn (6):58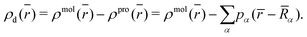 | (6) |
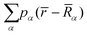 is the sum over the spherically averaged ground state electron densities of all free atoms α, centered at the location of nucleus
is the sum over the spherically averaged ground state electron densities of all free atoms α, centered at the location of nucleus ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) α. For an uncharged molecule, the effective charge of an atom qα can be obtained using eqn (7),
α. For an uncharged molecule, the effective charge of an atom qα can be obtained using eqn (7),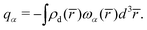 | (7) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) denotes the relative share that atom α contributes to the density at site
) denotes the relative share that atom α contributes to the density at site ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) .
.
De Proft and co-workers extensively tested the Hirshfeld scheme on a series of functionalized organic molecules.59 They note that while overall trends for charges are in good agreement with measurements, the magnitude of charges and dipoles is frequently underestimated. This conclusion is corroborated by other benchmark studies.60–62 Furthermore, Hirshfeld charges can be affected unfavourably by atomic fragments exerting electron withdrawal or excess electrons in an atom's vicinity, as often observed by contradictory charges on hydrogen atoms.58,63 Saha et al. proposed refinements to overcome these limitations.58
Unlike in case of the Mulliken approach, NPA produces only physically meaningful, non-negative occupations and the overall charge will sum up to the total number of electrons in the system. Weinhold and co-workers showed that NPA can significantly improve results over Mulliken and Löwdin analysis by varying the exponent of a 2p basis function in the SCF calculation of H2 and relating the resulting energy changes to charge results obtained from the different partial charge analysis methods.65
The NPA and Mulliken schemes share the limitation of not being directly applicable to plane wave calculations. Furthermore, dipole moments are overestimated significantly using NPA, which is discussed to be a result of the far-reaching tails of (diffuse) basis functions.62,69
Fundamentally, Bader analysis separates the system by creating curved surfaces that run through minima in the charge density. The volume segments enclosed by these surfaces are referred to as Bader regions. The total charge of each Bader region is obtained by integration. Bader charge analysis has been shown to systematically overestimate charges and dipole moments.60,62,69
 | (8) |
The electronegativity equalization method (EEM) was first introduced by Mortier et al. (1985)97–99 based on Sanderson's principle of electronegativity equalization states.100 With its easily adaptable equations and transferable parameters, the model provides an efficient analysis of charge distributions at a low computational cost. EEM has been validated and successfully applied for applications including organic molecules,101–109 inorganic solids,110–116 biomolecular systems,117–122 metal-organic frameworks,123–125 and electrochemical systems.126–128 Further improvements and formalisms evolved from the original EEM principle. Derivative methods include the atom-bond electronegativity equalization (ABEEM),129 charge equilibration (QEq and CHEQ),130,131 fluctuating charges (FlucQ),132 chemical potential equalization (CPE),133 and split charge equilibration (SQE) approaches.134
Our group recently used EEM partial charge analysis to characterize oxidized cuboctahedral platinum NPs with to identify the prevalent type of oxide in this system which at first glance appears amorphous.24 An exemplary EEM partial charge distribution is shown in Fig. 3. To provide context for the obtained partial charge distribution, 3 nm spherical particles cut from bulk PtO, α-PtO2, β-PtO2, and Pt3O4 are analyzed and the maxima of the oxygen partial charge distributions are shown as dotted lines in Fig. 3. Comparison to the reference particles indicates that the oxygen atoms in the oxidized octahedral NP most likely correspond to Pt3O4.
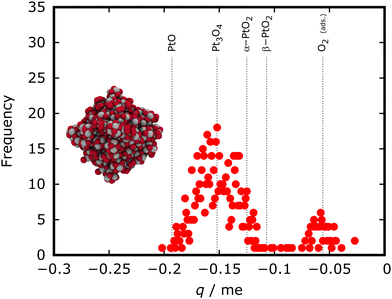 | ||
| Fig. 3 Distribution of EEM partial charges on oxygen atoms for a fully oxidized (pO = 1 mbar, 500 K) 3 nm octahedral Pt NP obtained using the ReaxFF-GCMC simulation approach. Dotted reference lines indicate the oxygen partial charge distribution maxima obtained from spherical 3 nm reference particles cut from bulk oxide materials. The analysis indicates that the oxide composition of the particle is most closely related to a Pt3O4 reference particle. Adapted from Kirchhoff et al.24 | ||
Notably, EEM-based approaches suffer from cubic scaling of the dipole polarizability with the system size135,136 and often predict fractional molecular charges for systems with well-separated molecules.137 Fractional charges result in a conductor-like charge distribution throughout the system and an ill-defined description of oxidized and reduced species.
Verstraelen et al. addressed these limitations by proposing the atom-condensed Kohn–Sham density functional theory approximated to second-order (ACKS2) scheme.138,139 Here, the EEM formalism is expanded by additional variables and quadratic energy terms to overcome the unrealistic long-range charge smearing. ACKS2 provides a more realistic description of charge delocalization. All parameters of the ACKS2 model have direct physical meaning and can be obtained from DFT calculations.138,140
Recent applications of the ACKS2 approach, among others, are the pseudoclassical treatment of explicit electrons in reactive force field simulations,141–143 proton-transfer reactions in subcritical and supercritical water systems,144 and charge-transfer processes in electrolytes of Li-ion batteries.143,145,146
3.4 Radial atomic density distributions
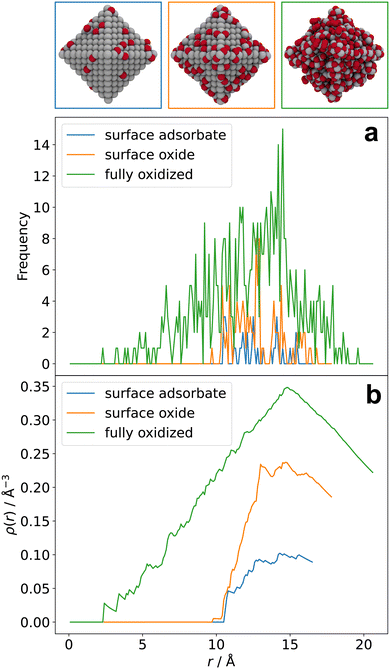
Radial atomic density distributions visualize the distribution of a particular chemical species in a complex heteroatomic material. Senftle and co-workers used it to illustrate different stages of oxidation of a Pd NP,32 hydrogen uptake of a Pd NP,33 as well as Pd carbide formation.34 To obtain such a distribution, atoms of the respective chemical species are counted in volume segments radially outward from the center of the system. In Fig. 4a, radial atomic density distributions are used to show the distribution of oxygen atoms in barely oxidized (blue), surface-oxidized (orange), and fully oxidized (green) 3 nm cuboctahedral Pt NPs. While oxygen atoms are mostly located in the outer shell of the particle at surface oxidation conditions (blue and orange), oxidation all the way to the core can be observed beyond this point (green). Broadening of the green distribution indicates expansion of the NP as a result of oxidation.Integration over the volume segments and normalization of the results gives the distributions shown in Fig. 4b. Compared to Fig. 4a, this way of presentation is less noisy and allows for large amounts of data to be presented at once. For example, Fig. 4b presents integrated distributions for the three aforementioned barely oxidized (blue), surface-oxidized (orange), and fully oxidized (green) structures. While Fig. 4b still retains information about the oxidation-dependent expansion of the particles, the regular radial atomic density distribution in Fig. 4a can be easier to read depending on what information is most important to visualize; for example, it is immediately obvious from the absolute Frequency value in Fig. 4a that the highest density of O atoms in the configuration obtained at 400 K is found between 12 and 14 Å, whereas this information is contained in the slope of the corresponding data in Fig. 4b.
3.5 Oxidation state analysis
When atomic (partial) charges are not available, for example in force field calculations, the oxidation state of an atom in a metallic NP can be roughly estimated by the number of its metal-metal bonds. A density of oxidation states can thus be obtained by showing the number of atoms within a specific oxidation state (i.e. number of metal-metal bonds) as a function of the radial distance r from the particle center. Hong and van Duin147 used this technique to monitor the formation of different types of oxides during a ReaxFF-driven reactive molecular dynamics (MD) simulation of an aluminium NP in the presence of oxygen. Fig. 5 shows an application of the method to a strongly oxidized 3 nm octahedral Pt NP.3.6 Radial distribution function
A radial distribution function (RDF, g(r)) is obtained by calculating distances between all pairs of atoms in a system and presenting them as a volume-normalized density (ρ = N/V). Usually, the density is obtained by counting all distances that fall into r + dr sphere segments originating from the center of the system. The RDF is therefore entirely dependent on the atomic configuration of the system.The g(r) can be measured in X-ray148,149 or neutron scattering experiments.149–152 Theory can play an integral role in the analysis of scattering data. For example, hybrid quantum mechanical/molecular mechanical (QM/MM) simulations have been successfully used to predict RDFs and assist in the interpretation of the experimental result.149,153,154
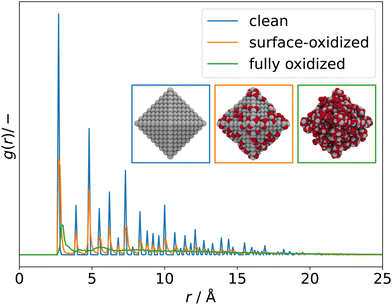
Going back to our guinea pig, the 3 nm octahedral Pt NPs, the g(r) can be used to quantify the degree of amorphicity in a series of increasingly oxidized structures. Fig. 6 illustrates RDFs of an almost clean octahedral particle (blue) as well as of a surface-oxidized (orange) and of a fully oxidized particle (green).
The RDFs become more and more liquid-like as oxidation proceeds and long-range ordering is lost.
A recent example of RDFs applied to NP systems was published by Thomä et al. who experimentally measured the RDF response of the water solvation shell around faceted iron oxide NPs.155 The group used calculated RDFs of different bonding situations of water to assign the correct structures to the measured bands. In another recent computational study, Zeng et al. used RDFs to monitor the structure and response to heating of a core–shell aluminium/aluminium oxide NP and its surrounding water shell over the course of a ReaxFF reactive MD simulation.156
3.7 Common neighbor analysis
Common neighbor analysis (CNA) was introduced by Honeycutt and Andersen in 1987.157 CNA seeks to identify reoccurring structural patterns in atomic configurations. CNA is based on earlier works by Blaisten-Barojas158 and Haymet159 and was further developed and first implemented into code by Clarke, Faken, and Jónsson.160,161 In CNA, each pair of atoms in a structure is assigned a triple of indices, jkl.‡ The three indices represent the number of nearest neighbors common to both atoms (j), the number of bonds between common neighbors (k), and the number of bonds in the longest chain formed by the k bonds between common neighbors (l). These triples are unique for characteristic structural motifs such as FCC, HCP, BCC, or icosahedral arrangements of atoms. Large structures can therefore be characterized based on the occurrence of smaller sub-structures with fingerprint triples. While relatively insensitive to small displacements of atoms, the method will quickly highlight larger changes in a crystal structure caused, for example, by local melting, and can therefore be used to analyze phase transitions. In their original publication, Honeycutt and Andersen annealed small Lennard-Jones clusters of 13 to 309 atoms in MD simulations and used CNA to identify the dominant structural feature (FCC, HCP, or icosahedral) of the relaxed structures.CNA can be understood as a partitioning of the RDF of the system. The RDF, g(r), of a structure can be represented as a sum of RDFs of each jkl triple, gjkl(r), so that
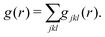 | (9) |
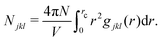 | (10) |
As exemplary applications, CNA has been used to describe solid-liquid phase transitions such as melting of small clusters,162,163 strain and deformation in metallic systems,164 and properties of glasses.165 CNA routines can be found in many computational tools, such as the open-source Atomic Simulation Environment (ASE).29
3.8 X-Ray diffraction spectrum
(Powder) X-ray diffraction (XRD) spectra of NPs can be calculated from a given structure using the Debye scattering equation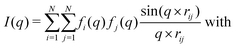 | (11) |
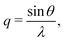 | (12) |
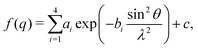 | (13) |
Fig. 7 compares powder XRD spectra of barely oxidized (blue), surface oxidized (orange), and fully oxidized (green) 3 nm octahedral Pt NPs. Band broadening is observed already for the barely oxidized system as a result of its nanometer size.168 As oxidation proceeds, bands broaden even further and the overall intensity I reduces, indicating that the NP becomes increasingly disordered. Similar to RDFs, with which this approach has in common the dependence on atomic pair distances, the calculated powder XRD spectra can therefore be used to quantify the degree of amorphicity in a series of structures aside from determining the characteristic diffraction peaks.
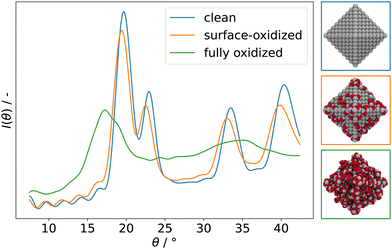 | ||
| Fig. 7 Simulated powder XRD spectra of clean (blue), surface-oxidized (orange), and fully oxidized (green) 3 nm octahedral Pt NPs. Assuming Cu-Kα incidence radiation. | ||
Examples for successful use of simulated XRD spectra in literature are abundant. To name a few, Chiche and co-workers showed that calculated XRD spectra can be used in combination with measurements to reveal detailed structural information.169 By comparing simulated and experimental XRD spectra of MgO and bohemite, the group showed that the simulated spectra contain detailed information about size and shape of the studied 3–7 nm NPs. They note that XRD in such cases outperforms TEM measurements which fail to provide morphological details for particles in this size range. Naicker et al. used simulated XRD spectra to monitor the characteristic rutile, anatase, and brookite bands during MD simulations of TiO2 NPs to study the surface rearrangement.170 Vogel and co-workers cross-referenced simulated and measured powder XRD spectra to characterize the reversible uptake of H in Pd NPs.171 Similarly, Gilbert and co-workers used simulated powder XRD spectra in combination with extended X-ray absorption fine structure (EXAFS) and wide-angle X-ray scattering (WAXS) spectroscopy techniques to study the increase in crystallinity in ZnS NPs upon hydration.172
3.9 Solvent-accessible surface area and interaction heatmaps
The Solvent-Accessible Surface Area (SASA) method can be used to create heatmaps of the interaction strength of probe atoms or molecules with a nanoparticle structure. The SASA method is rooted in biomolecular applications and computational protein structure prediction173,174 and was originally proposed by Richmond in 1984.175 To calculate the SASA, the van der Waals (vdW) radius of each surface atom in a structure is extended by a certain distance, for example by the vdW radius of the probe.174 By systematically placing probe atoms (e.g. oxygen, hydrogen, or a water molecule) on the extended vdW surface, an interaction heatmap visualizing the strength of interaction of the structure with the probe is obtained.Fig. 8 shows the interaction heatmap for an oxygen probe atom with an oxidized 3 nm octahedral Pt NP.
By assigning interaction points to the respective nearest surface atoms and averaging the interaction energy results assigned to each atom, the interaction strength of each surface atom can be estimated. This approach is exemplified in Fig. 9 for a pristine 3 nm octahedral Pt NP, using an oxygen probe atom. In this specific case, the NP edges are revealed to interact most strongly with the oxygen probe, suggesting that adsorption on these sites is preferred during early stages of the oxidation.24,25 The SASA heatmap approach therefore constitutes an intuitive way of visualizing surface reactivity even for complex systems.
3.10 Two-phase thermodynamics
The Two-Phase Thermodynamics (2PT) method enables the calculation of the density of states (DoS) of liquids from molecular dynamics trajectories, thus allowing the identification of translational, rotational and intramolecular vibrational modes.176–178 The 2PT method can aid in the interpretation of complex data obtained using surface infrared or Raman spectroscopy methods, in particular for studying the solid-electrolyte interface.179,180In the 2PT scheme, the velocity autocorrelation function (VACF) is calculated via the time-dependent atomic velocities, giving access to the DoS function. The total DoS is then separated into a diffusive gas-like component and a solid-like component. The components are treated separately via hard sphere thermodynamics and quantum statistics, enabling calculation of the entropy and the heat capacity.
The 2PT scheme has been used successfully in literature. In a reactive MD based study, Cheng et al. identified intermediates of the CO2 reduction reaction by their characteristic bands in the vibrational DoS.180 The group included explicit solvation and the electrode potential in their simulations. Pascal and co-workers evaluated the translational, rotational and vibrational entropic contributions of confined water using the 2PT method from MD simulations. They studied the wetting behavior of hydrophilic carbon nanotubes and report that water in the nanotube is found to be more stable despite the confinement.181 Persson and co-workers introduced a spatially resolved 3D variant of the 2PT method.179 Using MD simulations, the group studied local contributions to the solvation enthalpy, entropy, and free energy of hydrophilic and hydrophobic small molecular solutes under the influence of ions and the hydrogen bonding network.
4 Analyzing sets of calculations
4.1 Normalized formation energy
To study the stability of different NP structures as a function of particle size, the total energy per atom, Eatom, can be set in relation with the the NP size to obtain stability trends. Such analysis was performed, for example, by Huang et al. on Pt NPs of various shapes from 20 to 100 nm.18 Another useful variant of this analysis is to show Eatom as a function of the cubic root of the number of atoms in the system, N−1/3. Kirchhoff et al. used this type of analysis to study the stability of cuboctahedral, octahedral, spherical, dodecahedral, and cubic Pt NPs in a size range of ca. 1–10 nm.24 The results are reproduced in Fig. 10. Displaying the energy per atom as a function of N−1/3 linearizes the data. This allows for intuitive comparison of the stability of, in this example, different NP shapes. Differences between the particles are most distinct at small sizes and values converge to the bulk Eatom for the ReaxFF force field that they were obtained with, which is 5.77 eV atom−1.182 This linearized presentation also reveals slight alterations in the facet composition. For example, small differences in the relative size of (111) and (100) facets of cuboctahedral particles show as deviations from the otherwise linear behavior since the surface-to-volume ratio is not constant anymore. The same observation can be made for slightly trunctated octahedral or dodecahedral particles or when the edges of the cubic particle start to round off, for example as a result of surface reactions that take place.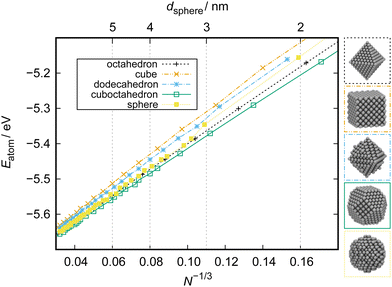 | ||
| Fig. 10 Stability of cuboctahedral, octahedral, spherical, dodecahedral, and cubic Pt NPs as a function of particle size obtained from ReaxFF calculations. N: number of atoms in a particle. The key diameter of the spherical particle, dsphere, is given on top. Bottom: Illustration of NP structures of ca. 3 nm size. Adapted from Kirchhoff et al.24 | ||
4.2 Adsorption isotherms and isobars
Adsorption isobars and isotherms can reveal information about the structure of a system in the presence of an adspecies at different thermodynamic conditions. Adsorption isobars or isotherms are constructed by showing the surface coverage as a function of either the partial pressure of the adspecies or the system temperature while keeping constant the other respective other value. For example, Senftle et al. constructed hydrogen adsorption isotherms to explore the uptake of hydrogen in Pd as a function of Pd cluster size.33A data set for this type of analysis can be achieved in different ways. One route is to manually generate structures of increasing coverage and diverse arrangements of an adspecies x and to calculate the thermodynamic stability of each structure at various different chemical potentials μx(p,T) in order to find the most stable coverage for each condition. Alternatively, schemes like the grand-canonical Monte Carlo (GCMC) algorithm32–34 can be used to generate diverse data sets of structures at certain μ(p,T) conditions using a stochastic sampling approach.
Returning to the data set of oxidized 3 nm octahedral Pt particles, which was generated using a reactive force field and the GCMC scheme at oxygen chemical potentials μO(p,T) corresponding to 200–1200 K at UHV (pO = 10−10 mbar) and NAP (pO = 1 mbar),26 adsorption isobars can be constructed as shown in Fig. 11. The coverage convention introduced in Section 3.1 is used. The individual data points shown in Fig. 11 correspond to the structures with the most favorable energy of formation at the corresponding μO(p,T).
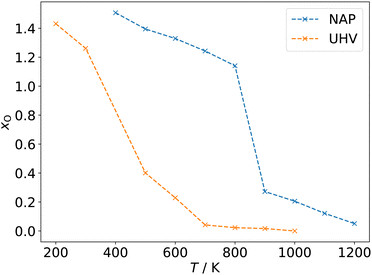 | ||
| Fig. 11 Adsorption isobars for a 3 nm octahedral Pt particles oxidized at UHV (pO = 10−10 mbar) and NAP (pO = 1 mbar) conditions and 200–1200 K temperature. The degree of oxidation is quantified as the quotient between oxygen and platinum atoms in the system (xO = NO/NPt). Adapted from Kirchhoff et al.26 | ||
Fig. 11 reveals that the oxidation process in case of this particular model system can be broadly divided into three steps: phase 1, surface adsorption at high temperatures marked by a slow increase of the NO/NPt ratio; phase 2, quick increase of NO/NPt marking full oxidation of the particle; and phase 3, decoration of the oxidized particles by additional dioxygen species on the surface.24 This trend is most obvious in case of the more aggressive NAP conditions.
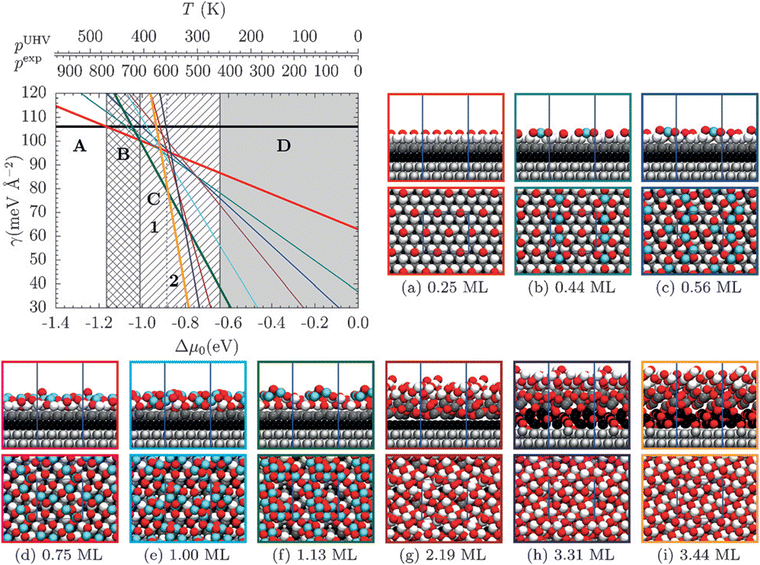
4.3 Adsorbate phase diagrams
The thermodynamic adsorption phase diagram can be regarded as a generalized case of an adsorption isotherm and isobar (Section 4.2). To construct a phase diagram, the energy of formation is displayed as a function of the chemical potential μ(p,T) of the adspecies. The formerly separated quantities of temperature and pressure are thus combined in this case. An exemplary phase diagram for adsorption of oxygen on Pt(111) published by Fantauzzi and co-workers183 is given in Fig. 12. This type of analysis can be used to predict the approximate coverage under given thermodynamic conditions and can thus be used to supplement experimental assessments184 and predict new structures.183Adsorbate phase diagrams can quickly become complex as the number of variables increases, for example in case of co-adsorption of multiple chemical species. Ferguson and co-workers have therefore developed a visualization tool entitled Surface Phase Explorer (SPE) to facilitate visualization of multidimensional phase diagrams.185
Finally, phase diagrams can be brought into the realm of electrochemistry using the Extended Ab Initio Thermodynamics (EAITD) approach.3,186,187 This approach makes use of the computational standard hydrogen electrode and therefore assumes that the reaction H2 ↔ 2H+ + 2e− is in equilibrium (assuming pH 0, 298 K, 1 atm pressure).188 The SHE can be applied to all electrochemical reactions that involve proton transfer reactions. For our exemplary data set of oxidized 3 nm octahedral Pt NPs, we can construct a thermodynamic cycle based on the assumption that all oxygen atoms must come from the water splitting reaction, H2O ↔ H2 + ½O2, to introduce H2 into the reaction. The potential-dependent energy of formation for each oxidized particle, ΔEsystemF(Δϕ), can then be calculated as
| ΔEsystemF(Δϕ) = Esystemtot − Ereftot − NO(μO + 2eΔϕ) with | (14) |
| μO = μH2O − μH2, | (15) |
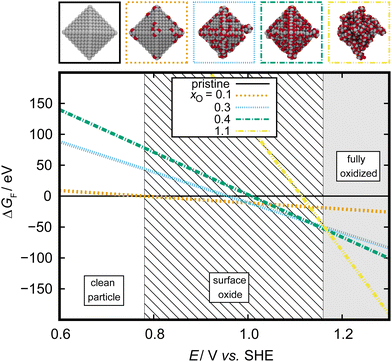 | ||
Fig. 13 Electrochemical phase diagram depicting the most stable adsorbate structures on a 3 nm octahedral Pt NP. Adsorbate structures are characterized by their O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio, xO, as outlined in Section 3.1. Adapted from Kirchhoff et al.26 Pt ratio, xO, as outlined in Section 3.1. Adapted from Kirchhoff et al.26 | ||
5 Conclusions
The present work reviewed analytical methods useful for extracting thermodynamic information from computational simulations of NP systems. As computational methods continue to improve and costs for high-performance computing are brought down by the year, simulations of large NP model systems instead of stand-ins such as periodic surface models will become the norm. Many established analytical methods, such as partial charge analysis or radial distribution functions, can easily be scaled for application to NP systems. On the other hand, the more complex nature of NPs requires new methods and approaches to analyze structure-activity relationships in particular. The authors hope that the present work will serve as a starting point for computational researchers working with NP structures.Author contributions
BK: conceptualization, methodology, data curation, visualization, writing – original draft. CJ: writing – review & editing. DG: writing – review & editing. DF: conceptualization, supervision. HJ: supervision. TJ: writing – review & editing, supervision, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
BK acknowledges funding from the Professional Graduate and Training Center Ulm (ProTrainU). Further, the authors gratefully acknowledge support by the DFG (german science foundation) through the collaborative research centers SPP-2248 (project ID 441209207) as well as SFB-1279 (project ID 316249678), SFB-1316 (project ID 327886311), TRR-234 (364549901). The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the DFG through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster).References
- J. C. Meier, C. Galeano, I. Katsounaros, J. Witte, H. J. Bongard, A. A. Topalov, C. Baldizzone, S. Mezzavilla, F. Schüth and K. J. J. Mayrhofer, Beilstein J. Nanotechnol., 2014, 44–67 CrossRef.
- N. Tian, Z.-Y. Zhou and S.-G. Sun, J. Phys. Chem. C, 2008, 112, 19801–19817 CrossRef CAS.
- P. Kaghazchi, F. C. Simeone, K. A. Soliman, L. A. Kibler and T. Jacob, Faraday Discuss., 2009, 140, 69–80 RSC.
- G. A. Tritsaris, J. Greeley, J. Rossmeisl and J. K. Nørskov, Catal. Lett., 2011, 141, 909–913 CrossRef CAS.
- T. Zhu, E. J. M. Hensen, R. A. van Santen, N. Tian, S.-G. Sun, P. Kaghazchi and T. Jacob, Phys. Chem. Chem. Phys., 2013, 15, 2268 RSC.
- G. Ouyang, K.-J. Zhu, L. Zhang, P.-F. Cui, B.-T. Teng and X.-D. Wen, Appl. Surf. Sci., 2016, 387, 875–881 CrossRef CAS.
- I. V. Yudanov, R. Sahnoun, K. M. Neyman and N. Rösch, J. Chem. Phys., 2002, 117, 9887–9896 CrossRef CAS.
- F. Calle-Vallejo, M. D. Pohl, D. Reinisch, D. Loffreda, P. Sautet and A. S. Bandarenka, Chem. Sci., 2017, 8, 2283–2289 RSC.
- Y. Volokitin, J. Sinzig, L. J. de Jongh, G. Schmid, M. N. Vargaftik and I. I. Moiseevi, Nature, 1996, 384, 621–623 CrossRef CAS.
- J. Kleis, J. Greeley, N. A. Romero, V. A. Morozov, H. Falsig, A. H. Larsen, J. Lu, J. J. Mortensen, M. Dułak, K. S. Thygesen, J. K. Nørskov and K. W. Jacobsen, Catal. Lett., 2011, 141, 1067–1071 CrossRef CAS.
- F. Viñes, J. R. B. Gomes and F. Illas, Chem. Soc. Rev., 2014, 43, 4922–4939 RSC.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- Y. Han, D. Jiang, J. Zhang, W. Li, Z. Gan and J. Gu, Front. Chem. Sci. Eng., 2016, 10, 16–38 CrossRef CAS.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS.
- A. P. Sutton and J. Chen, Philos. Mag. Lett., 1990, 61, 139–146 CrossRef.
- Y. Qi, T. Çağin, W. L. Johnson and W. A. Goddard, J. Chem. Phys., 2001, 115, 385–394 CrossRef CAS.
- N. Tian, Z.-Y. Zhou and S.-G. Sun, J. Phys. Chem. C, 2008, 112, 19801–19817 CrossRef CAS.
- R. Huang, Y.-H. Wen, Z.-Z. Zhu and S.-G. Sun, J. Mater. Chem., 2011, 21, 11578–11584 RSC.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- B. T. Thole and P. T. van Duijnen, Theor. Chim. Acta, 1980, 55, 307–318 CrossRef CAS.
- M. J. Field, P. A. Bash and M. Karplus, J. Comput. Chem., 1990, 11, 700–733 CrossRef CAS.
- X. Lu, D. Fang, S. Ito, Y. Okamoto, V. Ovchinnikov and Q. Cui, Mol. Simul., 2016, 42, 1056–1078 CrossRef CAS PubMed.
- A. O. Dohn, Int. J. Quantum Chem., 2020, 120, e26343 CrossRef CAS.
- B. Kirchhoff, L. Braunwarth, C. Jung, H. Jónsson, D. Fantauzzi and T. Jacob, Small, 2019, 16, 1905159 CrossRef PubMed.
- L. Braunwarth, C. Jung and T. Jacob, Top. Catal., 2020, 1647–1657 CrossRef CAS.
- B. Kirchhoff, C. Jung, H. Jónsson, D. Fantauzzi and T. Jacob, J. Phys. Chem. C, 2022, 126, 6773–6781 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- J. Stone, MSc thesis, Computer Science Department, University of Missouri-Rolla, 1998.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys. Cond. Matter, 2017, 29, 273002 CrossRef.
- J. Rahm and P. Erhart, J. Open Source Softw., 2020, 5, 1944 CrossRef.
- F. Uekermann, S. Fiedler and B. Aradi, nanocut, version 12.12; 2019, https://bitbucket.org/aradi/nanocut, accessed March 3, 2022.
- T. P. Senftle, R. J. Meyer, M. J. Janik and A. C. T. V. Duin, J. Chem. Phys., 2013, 139, 044109 CrossRef PubMed.
- T. P. Senftle, M. J. Janik and A. C. T. van Duin, J. Phys. Chem. C, 2014, 118, 4967–4981 CrossRef CAS.
- T. P. Senftle, A. C. T. van Duin and M. J. Janik, Catal. Commun., 2014, 52, 72–77 CrossRef CAS.
- I. J. Robertson, M. C. Payne and V. Heine, Europhys. Lett., 1991, 15, 301–306 CrossRef CAS.
- B. Hammer and J. K. Nørskov, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- T. Jiang, D. J. Mowbray, S. Dobrin, H. Falsig, B. Hvolbæk, T. Bligaard and J. K. Nørskov, J. Phys. Chem. C, 2009, 113, 10548–10553 CrossRef CAS.
- G. Mpourmpakis, A. N. Andriotis and D. G. Vlachos, Nano Lett., 2010, 10, 1041–1045 CrossRef CAS PubMed.
- M. G. Taylor, N. Austin, C. E. Gounaris and G. Mpourmpakis, ACS Catal., 2015, 5, 6296–6301 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- F. Calle-Vallejo, P. Sautet and D. Loffreda, J. Phys. Chem. Lett., 2014, 5, 3120–3124 CrossRef CAS PubMed.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189 CrossRef CAS PubMed.
- J. Tymoczko, F. Calle-Vallejo, W. Schuhmann and A. S. Bandarenka, Nat. Commun., 2016, 7, 10990 CrossRef CAS PubMed.
- X. Ma and H. Xin, Phys. Rev. Lett., 2017, 118, 036101 CrossRef PubMed.
- J. P. Gaspard and F. Cyrot-Lackmann, J. Phys. C: Solid State Phys., 1973, 6, 3077–3096 CrossRef CAS.
- S. Wang, N. Omidvar, E. Marx and H. Xin, Phys. Chem. Chem. Phys., 2018, 20, 6055–6059 RSC.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443–6453 CrossRef CAS.
- V. Fung, F. F. Tao and D.-e Jiang, J. Phys. Chem. Lett., 2017, 8, 2206–2211 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1841–1846 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 2338–2342 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 2343–2346 CrossRef CAS.
- T. J. Zielinski, E. Harvey, R. Sweeney and D. M. Hanson, J. Chem. Ed., 2005, 82, 1880 CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- P. Politzer and R. R. Harris, J. Am. Chem. Soc., 1970, 92, 6451–6454 CrossRef CAS.
- S. Saha, R. K. Roy and P. W. Ayers, Int. J. Quantum Chem., 2009, 109, 1790–1806 CrossRef CAS.
- F. D. Proft, C. V. Alsenoy, A. Peeters, W. Langenaeker and P. Geerlings, J. Comput. Chem., 2002, 23, 1198–1209 CrossRef PubMed.
- I. Choudhuri and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 5884–5892 CrossRef CAS PubMed.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- C. F. Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210 CrossRef CAS PubMed.
- E. R. Davidson and S. Chakravorty, Theor. Chim. Acta, 1992, 83, 319–330 CrossRef CAS.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736–1740 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073 CrossRef CAS.
- P.-O. Löwdin, Phys. Rev., 1955, 97, 1474–1489 CrossRef.
- P.-O. Löwdin, Phys. Rev., 1955, 97, 1490–1508 CrossRef.
- F. Martin and H. Zipse, J. Comput. Chem., 2005, 26, 97–105 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press, Oxford; New York, 1990 Search PubMed.
- R. F. W. Bader and C. F. Matta, J. Phys. Chem. A, 2004, 108, 8385–8394 CrossRef CAS.
- P. L. A. Popelier, Theor. Chim. Acta, 1994, 87, 465–476 CrossRef CAS.
- B. B. Stefanov and J. Cioslowski, J. Comput. Chem., 1995, 16, 1394–1404 CrossRef CAS.
- P. L. A. Popelier, Comput. Phys. Commun., 1998, 108, 180–190 CrossRef CAS.
- B. Silvi and C. Gatti, J. Phys. Chem. A, 2000, 104, 947–953 CrossRef CAS.
- P. L. A. Popelier, Theor. Chem. Acc., 2001, 105, 393–399 Search PubMed.
- N. O. J. Malcolm and P. L. A. Popelier, J. Comput. Chem., 2003, 24, 437–442 CrossRef CAS PubMed.
- N. O. J. Malcolm and P. L. A. Popelier, J. Comput. Chem., 2003, 24, 1276–1282 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- F. M. Bickelhaupt, N. J. R. van Eikema Hommes, C. Fonseca Guerra and E. J. Baerends, Organometallics, 1996, 15, 2923–2931 CrossRef CAS.
- G. Voronoi, J. Reine Angew. Math., 1908, 1908, 198–287 CrossRef.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541 CrossRef CAS PubMed.
- J. W. Storer, D. J. Giesen, C. J. Cramer and D. G. Truhlar, J. Comput.-Aided Mol. Des., 1995, 9, 87–110 CrossRef CAS PubMed.
- J. Li, T. Zhu, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 1998, 102, 1820–1831 CrossRef CAS.
- P. Winget, J. D. Thompson, J. D. Xidos, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2002, 106, 10707–10717 CrossRef CAS.
- J. M. Brom, B. J. Schmitz, J. D. Thompson, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 6483–6488 CrossRef CAS.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, Theor. Chem. Acc., 2005, 113, 133–151 Search PubMed.
- R. M. Olson, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2007, 3, 2046–2054 CrossRef CAS PubMed.
- J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2014, 10, 2802–2812 CrossRef CAS PubMed.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468 CrossRef CAS PubMed.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2012, 8, 2844–2867 CrossRef CAS PubMed.
- N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747 RSC.
- T. A. Manz, RSC Adv., 2017, 7, 45552–45581 RSC.
- N. G. Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707 RSC.
- W. J. Mortier, K. Van Genechten and J. Gasteiger, J. Am. Chem. Soc., 1985, 107, 829–835 CrossRef CAS.
- W. J. Mortier, S. K. Ghosh and S. Shankar, J. Am. Chem. Soc., 1986, 108, 4315–4320 CrossRef CAS.
- K. A. Van Genechten, W. J. Mortier and P. Geerlings, J. Chem. Phys., 1987, 86, 5063–5071 CrossRef CAS.
- R. T. Sanderson, Science, 1951, 114, 670–672 CrossRef CAS PubMed.
- T. Verstraelen, V. Van Speybroeck and M. Waroquier, J. Chem. Phys., 2009, 131, 044127 CrossRef PubMed.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- W. J. Mortier, S. K. Ghosh and S. Shankar, J. Am. Chem. Soc., 1986, 108, 4315–4320 CrossRef CAS.
- Z.-Z. Yang and C.-S. Wang, J. Phys. Chem. A, 1997, 101, 6315–6321 CrossRef CAS.
- P. Bultinck, R. Vanholme, P. L. A. Popelier, F. De Proft and P. Geerlings, J. Phys. Chem. A, 2004, 108, 10359–10366 CrossRef CAS.
- P. Bultinck, W. Langenaeker, P. Lahorte, F. De Proft, P. Geerlings, M. Waroquier and J. P. Tollenaere, J. Phys. Chem. A, 2002, 106, 7887–7894 CrossRef CAS.
- Y. Zhong, G. L. Warren and S. Patel, J. Comput. Chem., 2008, 29, 1142–1152 CrossRef CAS PubMed.
- J. E. Davis, G. L. Warren and S. Patel, J. Phys. Chem. B, 2008, 112, 8298–8310 CrossRef CAS PubMed.
- R. S. Varekova, Z. Jirouskova, J. Vanek, S. Suchomel and J. Koca, Int. J. Mol. Sci., 2007, 8, 572–582 CrossRef CAS.
- K. A. Van Genechten, W. J. Mortier and P. Geerlings, J. Chem. Phys., 1987, 86, 5063–5071 CrossRef CAS.
- G. O. A. Janssens, B. G. Baekelandt, H. Toufar, W. J. Mortier and R. A. Schoonheydt, J. Phys. Chem., 1995, 99, 3251–3258 CrossRef CAS.
- A. Ostadhossein, A. Rahnamoun, Y. Wang, P. Zhao, S. Zhang, V. H. Crespi and A. C. T. van Duin, J. Phys. Chem. Lett., 2017, 8, 631–640 CrossRef CAS PubMed.
- D. Akbarian, D. E. Yilmaz, Y. Cao, P. Ganesh, I. Dabo, J. Munro, R. Van Ginhoven and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2019, 21, 18240–18249 RSC.
- R. Heidler, G. O. Janssens, W. J. Mortier and R. A. Schoonheydt, Microporous Mater., 1997, 12, 1–11 CrossRef CAS.
- K. Smirnov and D. Bougeard, Chem. Phys., 2003, 292, 53–70 CrossRef CAS.
- J. Wen, T. Ma, W. Zhang, G. Psofogiannakis, A. C. van Duin, L. Chen, L. Qian, Y. Hu and X. Lu, Appl. Surf. Sci., 2016, 390, 216–223 CrossRef CAS.
- C.-M. Ionescu, S. Geidl, R. Svobodová Vařeková and J. Koča, J. Chem. Inf. Model., 2013, 53, 2548–2558 CrossRef CAS PubMed.
- Y. Ouyang, F. Ye and Y. Liang, Phys. Chem. Chem. Phys., 2009, 11, 6082–6089 RSC.
- A. Baeten and P. Geerlings, THEOCHEM, 1999, 465, 203–207 CrossRef CAS.
- J. L. Banks, G. A. Kaminski, R. Zhou, D. T. Mainz, B. J. Berne and R. A. Friesner, J. Chem. Phys., 1999, 110, 741–754 CrossRef CAS.
- T. Verstraelen, E. Pauwels, F. De Proft, V. Van Speybroeck, P. Geerlings and M. Waroquier, J. Chem. Theory Comput., 2012, 8, 661–676 CrossRef CAS PubMed.
- S. Patel, A. D. Mackerell Jr. and C. L. Brooks III, J. Comput. Chem., 2004, 25, 1504–1514 CrossRef CAS PubMed.
- C. E. Wilmer and R. Q. Snurr, Chem. Eng. J., 2011, 171, 775–781 CrossRef CAS.
- L. Huang, K. L. Joshi, A. C. T. V. Duin, T. J. Bandosz and K. E. Gubbins, Phys. Chem. Chem. Phys., 2012, 14, 11327–11332 RSC.
- L. Huang, T. Bandosz, K. L. Joshi, A. C. T. van Duin and K. E. Gubbins, J. Chem. Phys., 2013, 138, 034102 CrossRef PubMed.
- A. Ostadhossein, S.-Y. Kim, E. D. Cubuk, Y. Qi and A. C. T. van Duin, J. Phys. Chem. A, 2016, 120, 2114–2127 CrossRef CAS PubMed.
- Y. K. Shin, M. Y. Sengul, A. S. M. Jonayat, W. Lee, E. D. Gomez, C. A. Randall and A. C. T. V. Duin, Phys. Chem. Chem. Phys., 2018, 20, 22134–22147 RSC.
- M. Raju, P. Ganesh, P. R. C. Kent and A. C. T. van Duin, J. Chem. Theory Comput., 2015, 11, 2156–2166 CrossRef CAS PubMed.
- Z.-Z. Yang and C.-S. Wang, J. Phys. Chem. A, 1997, 101, 6315–6321 CrossRef CAS.
- A. K. Rappe and W. A. Goddard, J. Phys. Chem., 1991, 95, 3358–3363 CrossRef CAS.
- Y. Zhong and S. Patel, J. Phys. Chem. B, 2010, 114, 11076–11092 CrossRef CAS PubMed.
- S. W. Rick, S. J. Stuart and B. J. Berne, J. Chem. Phys., 1994, 101, 6141–6156 CrossRef CAS.
- D. M. York and W. Yang, J. Chem. Phys., 1996, 104, 159–172 CrossRef CAS.
- R. A. Nistor, J. G. Polihronov, M. H. Müser and N. J. Mosey, J. Chem. Phys., 2006, 125, 094108 CrossRef PubMed.
- G. Lee Warren, J. E. Davis and S. Patel, J. Chem. Phys., 2008, 128, 144110 CrossRef CAS PubMed.
- R. A. Nistor and M. H. Müser, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104303 CrossRef.
- J. Cioslowski and B. B. Stefanov, J. Chem. Phys., 1993, 99, 5151–5162 CrossRef CAS.
- T. Verstraelen, P. W. Ayers, V. Van Speybroeck and M. Waroquier, J. Chem. Phys., 2013, 138, 074108 CrossRef CAS PubMed.
- T. Verstraelen, S. Vandenbrande and P. W. Ayers, J. Chem. Phys., 2014, 141, 194114 CrossRef PubMed.
- P. Gütlein, L. Lang, K. Reuter, J. Blumberger and H. Oberhofer, J. Chem. Theory Comput., 2019, 15, 4516–4525 CrossRef PubMed.
- M. M. Islam, G. Kolesov, T. Verstraelen, E. Kaxiras and A. C. T. van Duin, J. Chem. Theory Comput., 2016, 12, 3463–3472 CrossRef CAS PubMed.
- B. Evangelisti, K. A. Fichthorn and A. C. T. van Duin, J. Chem. Phys., 2020, 153, 104106 CrossRef CAS PubMed.
- M. M. Islam and A. C. T. van Duin, J. Phys. Chem. C, 2016, 120, 27128–27134 CrossRef CAS.
- H. Manzano, W. Zhang, M. Raju, J. S. Dolado, I. López-Arbeloa and A. C. T. van Duin, J. Chem. Phys., 2018, 148, 234503 CrossRef PubMed.
- M. J. Hossain, G. Pawar, B. Liaw, K. L. Gering, E. J. Dufek and A. C. T. van Duin, J. Chem. Phys., 2020, 152, 184301 CrossRef CAS PubMed.
- K. A. O’Hearn, M. W. Swift, J. Liu, I. Magoulas, P. Piecuch, A. C. T. van Duin, H. M. Aktulga and Y. Qi, J. Chem. Phys., 2020, 153, 084107 CrossRef PubMed.
- S. Hong and A. C. van Duin, J. Phys. Chem. C, 2015, 119, 17876–17886 CrossRef CAS.
- E. B. Sirota, H. D. Ou-Yang, S. K. Sinha, P. M. Chaikin, J. D. Axe and Y. Fujii, Phys. Rev. Lett., 1989, 62, 1524–1527 CrossRef CAS PubMed.
- A. K. Soper, J. Phys.: Condens. Matter, 2007, 19, 335206 CrossRef CAS PubMed.
- N. S. Gingrich and L. Heaton, J. Chem. Phys., 1961, 34, 873–878 CrossRef CAS.
- J. L. Yarnell, M. J. Katz, R. G. Wenzel and S. H. Koenig, Phys. Rev. A: At., Mol., Opt. Phys., 1973, 7, 2130–2144 CrossRef CAS.
- F. Li and J. S. Lannin, Phys. Rev. Lett., 1990, 65, 1905–1908 CrossRef CAS PubMed.
- A. O. Dohn, E. Biasin, K. Haldrup, M. M. Nielsen, N. E. Henriksen and K. B. Møller, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 244010 CrossRef.
- A. O. Dohn, E. Biasin, K. Haldrup, M. M. Nielsen, N. E. Henriksen and K. B. Møller, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 059501 CrossRef.
- S. L. J. Thomä, S. W. Krauss, M. Eckardt, P. Chater and M. Zobel, Nat. Commun., 2019, 10, 995 CrossRef PubMed.
- H. Zeng, X. Cheng, C. Zhang and Z. Lu, J. Phys. Chem. C, 2018, 122, 9191–9197 CrossRef CAS.
- J. D. Honeycutt and H. C. Andersen, J. Phys. Chem., 1987, 91, 4950–4963 CrossRef CAS.
- E. Blaisten-Barojas, Kinam, 1984, 6A, 71–84 Search PubMed.
- A. D. J. Haymet, Chem. Phys. Lett., 1984, 107, 77–82 CrossRef CAS.
- A. S. Clarke and H. Jónsson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 3975–3984 CrossRef CAS PubMed.
- D. Faken and H. Jónsson, Comput. Mater. Sci., 1994, 2, 279–286 CrossRef CAS.
- C. Cleveland, W. Luedtke and U. Landman, Phys. Rev. Lett., 1998, 81, 2036–2039 CrossRef CAS.
- C. L. Cleveland, W. D. Luedtke and U. Landman, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 5065–5077 CrossRef CAS.
- M. R. Sørensen, M. Brandbyge and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3283–3294 CrossRef.
- Y. Q. Cheng and E. Ma, Prog. Mater. Sci., 2011, 56, 379–473 CrossRef CAS.
- D. T. Cromer and J. B. Mann, Acta Crystallogr., 1968, 24, 321–324 CrossRef CAS.
- P. J. Brown, A. G. Fox, E. N. Maslen, M. A. O’Keefe and B. T. M. Willis, International Tables for Crystallography, American Cancer Society, 2006, pp. 554–595 Search PubMed.
- C. F. Holder and R. E. Schaak, ACS Nano, 2019, 13, 7359–7365 CrossRef CAS PubMed.
- D. Chiche, M. Digne, R. Revel, C. Chanéac and J.-P. Jolivet, J. Phys. Chem. C, 2008, 112, 8524–8533 CrossRef CAS.
- P. K. Naicker, P. T. Cummings, H. Zhang and J. F. Banfield, J. Phys. Chem. B, 2005, 109, 15243–15249 CrossRef CAS PubMed.
- W. Vogel, W. He, Q.-H. Huang, Z. Zou, X.-G. Zhang and H. Yang, Int. J. Hydrogen Energy, 2010, 35, 8609–8620 CrossRef CAS.
- B. Gilbert, H. Zhang, F. Huang, J. F. Banfield, Y. Ren, D. Haskel, J. C. Lang, G. Srajer, A. Jürgensen and G. A. Waychunas, J. Chem. Phys., 2004, 120, 11785–11795 CrossRef CAS PubMed.
- E. Durham, B. Dorr, N. Woetzel, R. Staritzbichler and J. Meiler, J. Mol. Model., 2009, 15, 1093–1108 CrossRef CAS PubMed.
- B. Lee and F. Richards, J. Mol. Biol., 1971, 55, 379-IN4 CrossRef PubMed.
- T. J. Richmond, J. Mol. Biol., 1984, 178, 63–89 CrossRef CAS PubMed.
- S.-T. Lin, M. Blanco and W. A. Goddard, J. Chem. Phys., 2003, 119, 11792–11805 CrossRef CAS.
- S.-T. Lin, P. K. Maiti and W. A. Goddard, J. Phys. Chem. B, 2010, 114, 8191–8198 CrossRef CAS PubMed.
- T. A. Pascal, S.-T. Lin and W. A. Goddard III, Phys. Chem. Chem. Phys., 2011, 13, 169–181 RSC.
- R. A. X. Persson, V. Pattni, A. Singh, S. M. Kast and M. Heyden, J. Chem. Theory Comput., 2017, 13, 4467–4481 CrossRef CAS PubMed.
- T. Cheng, A. Fortunelli and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 7718–7722 CrossRef CAS PubMed.
- T. A. Pascal, W. A. Goddard and Y. Jung, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11794–11798 CrossRef CAS PubMed.
- D. Fantauzzi, J. Bandlow, L. Sabo, J. E. Mueller, A. C. T. V. Duin and T. Jacob, Phys. Chem. Chem. Phys., 2014, 16, 23118–23133 RSC.
- D. Fantauzzi, S. Krick-Calderón, J. E. Mueller, M. Grabau, C. Papp, H.-P. Steinrück, T. P. Senftle, A. C. T. van Duin and T. Jacob, Angew. Chem., Int. Ed., 2017, 56, 2594–2598 CrossRef CAS PubMed.
- D. Fantauzzi, J. E. Mueller, L. Sabo, A. C. T. V. Duin and T. Jacob, ChemPhysChem, 2015, 16, 2797–2802 CrossRef CAS PubMed.
- G. A. Ferguson, V. Vorotnikov, N. Wunder, J. Clark, K. Gruchalla, T. Bartholomew, D. J. Robichaud and G. T. Beckham, J. Phys. Chem. C, 2016, 120, 26249–26258 CrossRef CAS.
- T. Jacob, J. Electroanal. Chem., 2007, 607, 158–166 CrossRef CAS.
- S. Venkatachalam and T. Jacob, Density functional theory applied to electrocatalysis, John Wiley & Sons, Ltd., 2010 Search PubMed.
- S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966 CrossRef CAS.
Footnotes |
| † An online, Jupyter book based tutorial is available which outlines how to implement many of the methods presented here: https://bjk24.gitlab.io/in-silico-review/intro.html. The code is built to interact with a recently published data set of oxidized NP structures (DOI: https://doi.org/10.5281/zenodo.6322004).26 All figures in this manuscript involving the oxidized 3 nm octahedral NPs were obtained using these scripts and data set. We recommend interested readers to execute and modify the provided code examples to deepen their understanding of these various evaluation methods. |
| ‡ Note that use of quadruples is proposed in the original publication by Honeycutt and Andersen.157 We focus on the more commonly used triples representation introduced by Clarke and Jónsson in 1993.160 |
| This journal is © the Owner Societies 2023 |