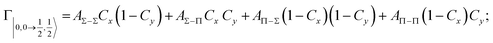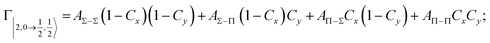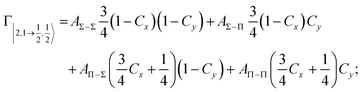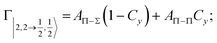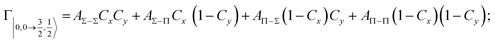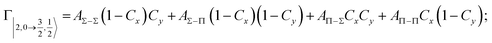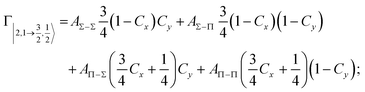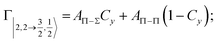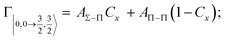Open Access Article
Open Access ArticleThe role of precursor states in the stereo-dynamics of elementary processes
Stefano
Falcinelli
 *a,
David
Cappelletti
*a,
David
Cappelletti
 b,
Franco
Vecchiocattivi
b,
Franco
Vecchiocattivi
 a and
Fernando
Pirani
a and
Fernando
Pirani
 ab
ab
aDipartimento di Ingegneria Civile ed Ambientale, Università di Perugia, 06125 Perugia, Italy. E-mail: stefano.falcinelli@unipg.it; Tel: +39-075-5853835
bDipartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, 06123 Perugia, Italy
First published on 19th May 2023
Abstract
The present perspective review focuses on the role of the precursor state, controlling the dynamical evolution of elementary processes, whose structure and stability are often difficult to characterize on quantitative grounds. In particular, such a state depends on the critical balance of weak intermolecular forces operative at long and intermediate separation distances. In this paper, a complementary problem has been properly addressed, concerning the suitable formulation of the intermolecular forces involved, defined in terms of a limited number of parameters and applicable in the whole space of the relative configurations of interacting partners. Important help to the solution of such a problem has been provided by the phenomenological method which adopts semi-empirical and empirical formulas to represent the basic features of the leading interaction components. Such formulas are defined in terms of a few parameters directly or indirectly related to the fundamental physical properties of the interacting partners. In this way, the basic features of the precursor state controlling its stability and its dynamical evolution have been defined in an internally consistent way for several elementary processes, having apparently different natures. Particular attention has been paid to the chemi-ionization reactions: they are treated as prototype oxidation processes for which all electronic rearrangements affecting stability and evolution of the precursor state, coincident with the reaction transition state, have been characterized in great detail. The obtained information appears to be in the perspective of general interest for many other elementary processes, difficult to investigate in the same detail since many other effects mask their basic features.
1. Introduction
Characterization and modeling of intermolecular interactions is a hot topic of current research (see, for instance, ref. 1–5). In particular, the proper assessment of the critical balance of attractive and repulsive interaction components is required to control all static properties of matter and to define the fundamental role of weakly bound precursor states in the dynamical evolution of elementary processes. Note that from a chemical point of view, such precursor states define the structure and energy of pre-reactive adducts. For chemical reactions with low barriers or barrier-less reactions, such as those considered in the second part of this perspective-review, the precursor state plays a direct-crucial role being coincident with the reaction transition state (TS). In many other cases, it indirectly controls the TS formation in specific configurations.Strongly anisotropic long-range intermolecular forces can selectively induce in a “natural” way a molecular orientation degree, even during single collision events occurring at low kinetic energy. Under such conditions, the capture of reagents and formation of the precursor state in specific structures favor in some cases and hinder in others, the dynamical evolution towards the final states of reactive processes.6 In particular, trapping and evolution of the precursor state dominate, especially at low temperatures:7–13 they directly affect the reactivity, determining Arrhenius and anti-Arrhenius behaviors in the temperature dependence of the processes.3,6
Therefore, the complete characterization of the precursor state features represents a fundamental question to be addressed adequately in chemistry and many other research fields of interest in biochemistry, biophysics, drug science, and material engineering.2 An essential starting point is the proper characterization of the intermolecular forces driving its formation and its subsequent evolution. In particular, for any molecular dynamics simulation, analytical formulations of the intermolecular potential energy represent a basic requirement to describe static and dynamical properties of systems interacting under various conditions of applied interest.
The perturbation theory suggests the partition of the intermolecular potential energy and identification of the leading components at intermediate and large separation distances.14 In particular, exchange repulsion, dispersion and induction attractions, charge transfer and electrostatic contributions are identified as the leading components, whose combination determines all crucial features of precursor states. In the analysis of the experimental findings (see below), we have found that it is appropriate to substitute the combination of exchange repulsion with dispersion attraction, with a unique component, called van der Waals (vdW). In this way, the roles of the charge transfer, a basic contribution of chemical nature, of induction, including polarization of external electronic clouds, and of the electrostatic contributions, which play an important role when anisotropic partners are interacting, have been better emphasized.
We pursued characterization and modeling of the leading interaction components, operative in several prototypical weakly bound systems, by performing scattering experiments and analyzing empirical findings that detail the interactions driving the collision events.15 The analysis of the experimental observables represented the starting point of the so-called phenomenological method, which adopts semi-empirical and empirical formulas to represent the leading components of the intermolecular interaction in analytical form. Accordingly, potential energy surfaces (PES) and related force fields (FFs) have been formulated in the whole space of the relative configurations of the interacting partners. In some specific cases, the predictions of the phenomenological method have been tested and combined with the results of state-of-the-art ab initio calculations, often permitting improvements and further generalizations of the method itself (see, for instance, ref. 16 and 17).
More in detail, high-resolution projectile-target elastic and inelastic scattering experiments have been performed, in the Perugia laboratory, with two apparatus exploiting the molecular beam (MB) technique, applied under high resolution conditions both in angle and in velocity.15,18 Integral cross-sections have been measured as a function of the collision velocity, and differential cross-sections have been measured as a function of the scattering angle. In both cases, the modulations of the observables due to quantum interference effects have often been resolved. They arise from the wave behavior of involved partners which undergoes, during each collision event, a perturbation by the intermolecular interaction, resulting in interference phenomena analogous to those of the light that passes through obstacles. Such quantum effects provide unique information on the range, strength and anisotropy of the interaction potential, especially in the case of intermolecular forces forming weakly bound adducts for collision.14
The analysis of the experimental findings obtained for several prototype systems suggested an improved Lennard Jones (ILJ) function, which is valid for the representation, under various conditions, of weak interactions determined by the balance of some leading components.15–18 The basic parameters of the potential function are as follows: the equilibrium distance (or bond length), the well depth (or bond energy) and an additional quantity, related to the partner's softness (see the Appendix). This new potential formulation removes most of the inadequacies of the venerable LJ model, reducing the strength of its excessive short-range repulsion and fully correcting the too strong long-range attraction. The ILJ formulation has also been extended to systems involving ions and to account for the molecular orientation effect. The appropriate representation of the balance of exchange repulsion, dispersion and induction attractions, provided by the ILJ function, is basic to isolate the role of charge transfer and of electrostatic effects.
For many weakly bound systems, investigated at a high level of detail and in an internally consistent way, important semi-empirical and empirical relationships have also been found, representing the dependence of global strength of attraction and repulsion (of formed intermolecular bond length and energy) on fundamental physical properties of interacting partners (see ref. 15, 19 and references therein). Such relationships, called correlation formulas (see the Appendix), favored the discovery of general laws that adopt as scaling factors of strength and range of the various components such as: electronic polarizability, electric charge, permanent electric multipole, electron affinity and ionization potential of atoms/molecules involved. These scaling laws help to represent appropriately the leading components of the interaction, and particularly the balance that controls all intermolecular bond features in the whole space of the configurations accessible to a weakly interacting complex, and to predict their behavior in unknown systems.
Therefore, the analysis of the experimental data, combined with the ILJ formulation and the adoption of scaling laws, represented the foundations of the above-mentioned phenomenological method. Such a method is essential to predict the behavior of unknown systems with increasing complexity, suggesting new experiments and the type of new theoretical calculations that can be used as tests and improvement of the phenomenological method.
This perspective-review presents an analysis of the fundamental features of the precursor state affecting the stereo-dynamical evolution of some basic elementary processes of interest in several research fields, that have been the objective of studies carried out in various laboratories. The first part (Section 2) focuses on phenomena whose precursor state is controlled by intermolecular forces that are mostly non covalent. The selective role of interaction components having a chemical origin, as the electron/charge transfer (CT), is discussed in the second part (Section 3), while the role of the precursor state, determined by the critical balance of intermolecular forces having both chemical and physical nature, is analyzed in the third part (Section 4). Particular attention will be paid to recent advances in understanding the stereo-dynamics of chemi-ionization reactions (CHEMI), that, being barrier-less processes stimulated by pronounced electronic rearrangements, exhibit a precursor state coincident with the TS.20 Such reactions are treated as prototype oxidation processes following a new general theoretical approach recently proposed by our research group and involve atoms and molecules reacting with highly excited species formed in collisions with electrons and/or cosmic rays.20 Therefore, CHEMI participate in the balance of elementary processes occurring under ultra-cold,8–13 thermal and hyper-thermal temperature conditions20 in several environments of interest for fundamental and applied research. The highlights on the role of the precursor state, emphasized by our study of CHEMI, must be considered of general interest for many other elementary chemical reactions for which the assessment of the role of this state is partially or fully obscured. We are also working to obtain for some prototype CHEMI, for which a complete study is favored, the topology of their stereo-dynamics, that is the detailed dependence of the reactivity on all quantities controlling their microscopic evolution. From this study, still in progress, we hope to obtain in perspective further general information for many other processes that are difficult to assess directly.
2. Some reference elementary processes
All the phenomena presented in this section are essentially controlled by weak interaction components, basically of non-covalent nature, that dominate at intermediate and large intermolecular distances.2.1. Transport in planetary atmospheres and plasmas
The phenomenological method has been exploited to evaluate transport phenomena in planetary atmospheres and plasmas, which are determined by the contributions of several interacting systems, including also those formed by highly unstable neutral and ionic species and controlling two-body collisions under a variety of conditions. For instance, the Mars atmosphere is mainly composed of CO2 (95.3%), N2 (2.7%), Ar (1.6%) and a small fraction of O2 (0.4%) at a total pressure of about 7 mbar. An impact of a shuttle on such an atmosphere generates plasmas in the proximity of its walls where several chemical-physical processes are promoted. They involve molecular dissociations, chemical reactions leading to the formation of other atomic and molecular species and free radicals, ionization phenomena with the production of single and multiple charged positive ions and also negative ions. Therefore, for the determination of the collision integrals, which are key quantities necessary to evaluate transport coefficients in the plasma, namely determining diffusion, thermal and charge conductivities and viscosity, it is necessary to know the interaction driving the collision events of many interacting pairs, that can involve both stable and highly unstable species. This hard problem has been solved with the adoption of the phenomenological method. A similar analysis has been performed also for the Jupiter atmosphere. All details are given in ref. 21–24 and references therein.2.2. Supersonic expansions and molecular alignment of gas phase reactants
Weakly bound adducts, formed by anisotropic vdW interactions in collisions of faster He and Ne atoms with heavier molecules, control the stereo-dynamics of elastic and inelastic phenomena that promote molecular focusing and acceleration, molecular relaxation and molecular alignment during the supersonic expansion leading to the formation of seeded and continuous molecular beams. A basic role is played by the precursor state formed in the second part of the expansion, where two-body collision events (see Fig. 1 for the case of lighter noble gas-heavier diatomic molecules) dominate. Such collisions occur at different orbital angular momentum values, that in a classical picture relate to different impact parameters, and involve the molecule in a specific initial rotational state. In the formed seeded beams, molecules are accelerated and rotation relaxed. Moreover, diatomic molecules show the propensity to fly in the “edge on” configuration, that is having “zero” as helicity state at the end of the expansion (Fig. 1), they fly preferentially rotating slowly in a plane parallel to the beam propagation direction.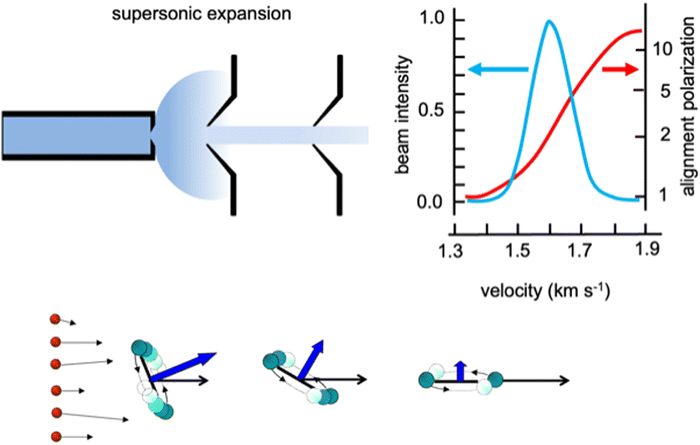 | ||
| Fig. 1 Upper part: A schematic representation of the supersonic expansion leading to the formation of a collimated and continuous seeded supersonic beam. Velocity distribution obtained for a beam of O2 seeded in He and alignment degree, defined as the ratio between molecules flying rotating parallel to the velocity vector, in the “edge on” state, and those rotating perpendicular to it, in the “broadside” state, characterized as a function of the final molecular speed.25 Lower part: A cartoon emphasizing the role of He–O2 collisions, occurring at different orbital angular moment values (or impact parameters b) determining molecular focusing (high b) molecular bending (intermediate b) and molecular acceleration and relaxation (low b) with the formation of molecules in low lying rotational states and flying in the “edge on” configuration. | ||
We investigated in detail the behavior of O2 and N2 in continuous beams seeded with He and Ne25–27 and found that such molecules effectively align in the “edge on” configuration with an average alignment degree comparable to that observed for other molecules, probed in seeded beams with different experimental techniques.28–33 However, our experiments, performed with an accurate mechanical velocity selection of the molecules in the formed seeded beams, emphasized a novel aspect of the phenomenon concerning the pronounced dependence of the alignment degree on the final molecular speed within the same seeded beam velocity distribution. In particular, molecules flying in the fast tail of the narrow distribution are strongly aligned, while those in the slow tail are exhibiting random orientations (see the upper part in Fig. 1). This represents an important finding, reflecting basic features of the weakly interacting atom-molecule precursor state, as, in particular, its selective dependence on the initial rotational state of the involved molecule and above all on the orbital angular momentum values mainly probed during the two-body collisions.34,35 Such features directly control molecular acceleration and relaxation, promoted by elastic and inelastic collisions, leading to the final speed.
Within a collaboration between Perugia and Trento groups, it has been also demonstrated, by exploiting simultaneously spectroscopic and scattering probes, that benzene in seeded beams shows the molecular propensity to fly like frisbees.35,36
A “simple” mechanical velocity section of the formed continuous seeded beams has been exploited to sample molecules at a different rotational alignment degree and then to investigate, within a Perugia–Genoa collaboration, the dependence of the stereo-dynamics of elementary processes, both in the gas phase and at the surface, on the molecular alignment.37–40 Complementary studies, focused on the stereo-dynamics of elastic and inelastic phenomena, controlled by precursor states formed at the gas–surface interphase, are summarized in Section 2.3. They indicate that the anisotropy of molecule-surface long-range forces tends to emphasize some selectivity of molecular collisions.
2.3. Physisorption states
Weak long-range interactions determine the precursor states that control the microscopic evolution of elementary physical-chemical processes occurring at the gas–surface interphase.41–43 Potential energy surfaces, given in analytical form, have been used to investigate, by semi-classical molecular dynamics calculations, the scattering, under a variety of conditions of applied interest, of gaseous diatomic molecules, such as H2, O2, N2 and CO in well-defined initial vibration-rotation (vi, ji) states, from graphite surfaces.44–47 The role of the precursor state, whose formation is controlled by the physisorption potential well arising from the long-range dispersion forces, has been properly emphasized. The collision dynamics, dominated by the coupling between translational and rotational internal degrees of freedom of molecule, indicates that, at low-medium collision energies, it can be also affected by the energy exchange with the surface phonons. The final states (vf, jf) of molecules, back-scattered elastically and inelastically, have been characterized and carefully analyzed. The most important results on the collision stereo-dynamics suggest that after the interaction with the graphite surface, molecules are back-scattered mainly in a direction very close to the specular one. Moreover, while vi is usually preserved, the final jf states, characterized for O2, N2 and CO, exhibit non-Boltzmann distributions with the main peak nearby jf = ji and a secondary maximum at very high jf. These and other features of rotational distributions suggest a close correlation between the initial rotational configuration of impinging molecules and the final state achieved after the scattering. These findings, complementary to those from molecular beam experiments (see Section 2.2), cast light on the relevant selectivity of elastic and inelastic collision events that control the stereo-dynamics of several elementary processes occurring both in gaseous and condensed phases for low energy (as those met in the interstellar medium) as well as for high energy (as those of interest for aerospace applications). The investigation of further molecule-surface systems, involving other surfaces, such as silica,48,49 kept at different temperatures, represents an important perspective to understand better the selectivity of phenomena, occurring at the gas–surface interphase and is of great relevance for plasmas.2.4. Clusters
In the last years, an important application of the phenomenological method focused on the formulation of the FF in systems involving benzene, benzene derivatives, and larger poly-aromatic hydrocarbons, like coronene (COR). The latter are important components of the interstellar medium and represent intermediates in the soot formation. An investigation of the structure and energy of systems at increasing complexity has been performed within a Madrid, Coimbra, Lisbon, Barcelona and Perugia collaboration.50–54 Such research provided a semi-empirical formulation of the multidimensional two-body PES, tested and improved by the comparison with results of ab initio calculations. For the smaller clusters, tests of the predicted interaction and geometry optimizations have been performed by using the density functional theory at the PBE-D3(BJ) level (see Table 2 and Fig. 5 of ref. 51), that has been previously found to be accurate for the description of the interaction in benzene clusters. The obtained PES have been used in an evolutionary algorithm, suitable to discover the leading properties of molecular clusters in their low-lying structures. In the case of small (COR)n clusters, columnar structures are found to be the most stable up to n = 5, while for n ≥ 6, various types of multi-stack and hand-shake arrangements are characterized as putative global minima (see the upper panel in Fig. 2).51 The observed arrangements are relevant pieces of nanostructures and represent the precursor state of the following nucleation leading to the formation of carbonaceous particles. It has been also demonstrated that the nanostructures substantially change if the coronene clusterization occurs in the presence of an alkaline ion (see the lower panel in Fig. 2) and, as a consequence, the following nucleation is affected.53 This suggestion is supported by the behavior of flames, where the addition of alkali metal salts promotes the formation of carbonaceous particles having different sizes (see ref. 53 and references therein). Related to this topic, an interesting perspective is the study of the selectivity of multilayer membranes, such as those formed by graphynes, for separation and storage of gaseous molecules.55–57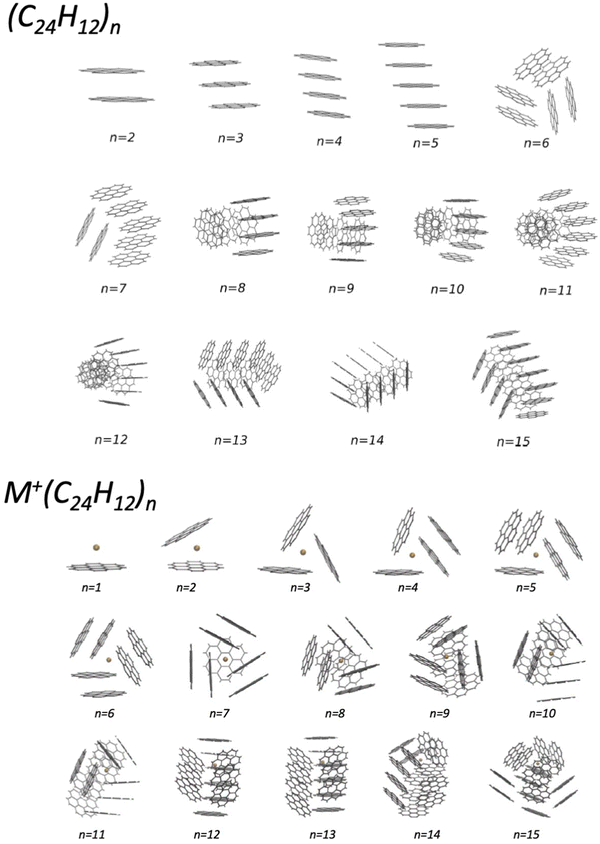 | ||
| Fig. 2 Putative global minimum structures of (COR)n (upper panel) and of K+(COR)n clusters (lower panel) with n = 1–15. They have been obtained by exploiting a detailed global optimization study with an evolutionary algorithm (see the text).51,53 | ||
3. The role of the charge transfer
Another important topic of modern research focuses on the features of the precursor state of elementary processes, determined by the critical balance of weak intermolecular forces of physical and chemical nature, that controls their collision stereo-dynamics. The chemical reactivity is often triggered by electron-charge transfer phenomena (CT) emerging in the precursor state, whose strength and selectivity are not trivial to characterize. Five years ago, we presented a perspective article in this journal, where the role of the CT in several phenomena was properly emphasized.58 In the present perspective review, some basic aspects must be again summarized, especially stressing those of relevance for the investigations presented in the next section.The study of many gas phase elementary processes, in the absence of the solvent and under single collision events, directly highlighted the role of the CT (see ref. 58–73 and references therein). It allowed the assessment of the phenomena controlled by the resonant CT, such as harpooning processes between a low ionization potential alkaline metal and a high electron affinity halogen atom/halogenated molecule, or the Coulomb explosion of some molecular dications, formed by the absorption of synchrotron light.58,73 Phenomena affected by the CT in perturbation limit, such as meta-stability of other molecular dications73 and structure and stability of noble gas halides,68,71,72 have been also identified. The noble gas halides provide CT excimers which are the basis of powerful UV laser development.68,69
A crucial open question still to be properly addressed is the planning of experiments probing in detail the CT component in the perturbation limit, since it is often elusive to advanced theoretical methods, being indirectly enclosed in other interaction contributions, such as induction, dispersion and electrostatic effects. In the past, we investigated in detail the interaction of high electron affinity open shell fluorine, chlorine and oxygen atoms with closed shell partners, where the CT just operates in the perturbation limit.15
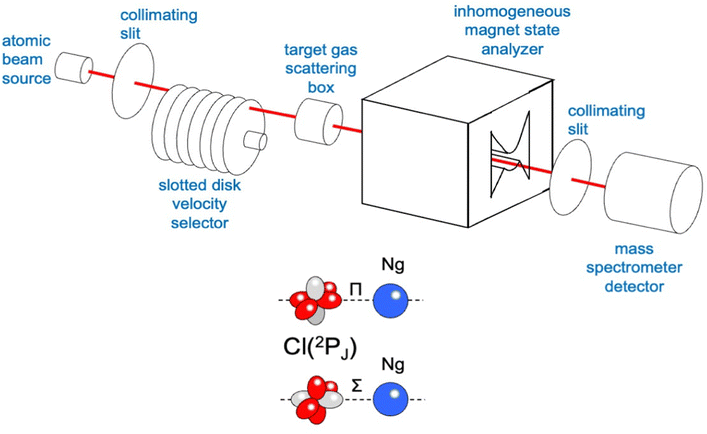
The used apparatus, schematized in Fig. 3, is basically the same as adopted for integral cross section measurements as a function of the collision velocity.15 A microwave discharge source has been used to generate the atomic beam, detected by a mass spectrometer kept in line with the beam direction. A Stern-Gerlach magnetic selector in Rabi configuration has been also inserted along the beam path, providing information on the electronic state of generated atoms and their distribution on the accessible spin–orbit levels identified by the electronic quantum number J. It also permitted the atomic magnetic sublevels populations to be varied in a controlled way. Cross section experiments, performed by inserting a gas target into the scattering chamber, resolved the different stabilities of collision complexes with Σ and Π symmetries, which, in the case of chlorine and fluorine projectile atoms, correspond, respectively, to their half-filled orbital aligned parallel and perpendicular to the separation distance with an interacting partner (see the lower part in Fig. 3).15,58
In the case of Cl–Kr, cross sections have been measured at different selector field strengths, controlling different magnetic sublevel populations of projectile atoms.74 Under such conditions, a modulation of the “glory” quantum interference, determining an oscillatory pattern over-imposed to the smooth component of the cross section, has been resolved (see left panels in Fig. 4).
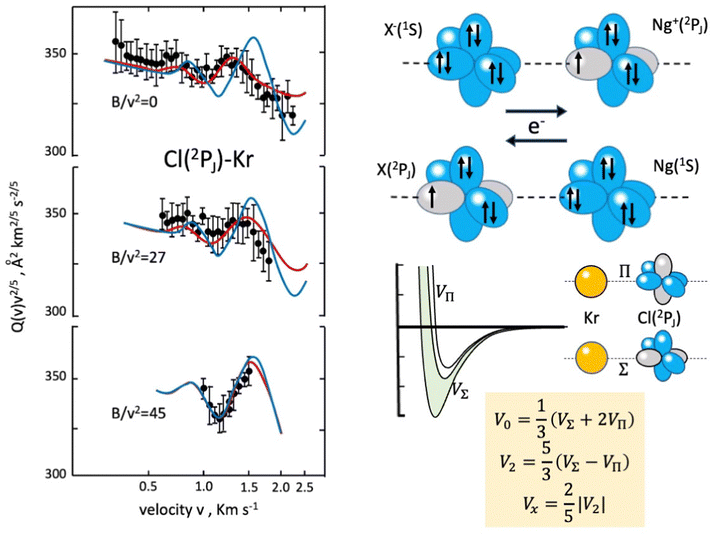 | ||
| Fig. 4 Experimental scattering studies performed on the KrCl system. B represents the intensity of the magnetic field in the state selector. The configuration interaction by the CT is depicted in the right upper panels. Some features of obtained interaction are given in the right lower panels, where the spherical V0, the anisotropic V2 interaction components and the bond stabilization Vx by the CT are properly defined. In order to emphasize the role of the interaction anisotropy, blue and red lines (left panel) represent calculated cross sections with only the V0 component and with the complete interaction, respectively.74 | ||
The analysis of the experimental findings provided both VΣ and VΠ interactions of the collision complex (see right panels in Fig. 4). Moreover, the application of the phenomenological method indicates that VΠ is a pure vdW interaction, while VΣ is stabilized by an additional interaction component, emerging at intermediate separation distances. The same method suggests that in the Σ configuration, additional bond stabilization effects arise from the configuration interaction between the ground neutral and the excited ionic state of the same symmetry differing for one electron exchange (see right upper panels in Fig. 4). Therefore, an important (chemical) CT contribution in the perturbation limit affects the system. The analysis of this and of many other prototype systems has been basic to obtain relationships between bond stabilization by the CT and ionization potential of the electron donor and the electron affinity of the electron acceptor. In this way, the strength of the CT stabilization effect has been related to the energy gap between the two coupled states and obtained relations represent additional scaling laws useful to map the transition from vdW to one electron chemical bond.71,72 More in detail, while F–He and Cl–He, because of the high energy gap, are essentially vdW systems, He2+, Ne2+, and Ar2+, affected by the resonant CT (being the energy gap null), are binding by one electron chemical bond, for which the prototype system is H2+. In this mapping, many systems with a limited energy gap, such as KrCl, XeF, (NeAr)+ and (ArXe)+, occupy an intermediate position.15,70–72 All this information has been fundamental to rationalize on quantitative grounds, and in an internally consistent way, most of the experimental findings of reactions discussed in the next section.
The experimental-theoretical investigation of basic features of the weak intermolecular hydrogen and halogen bond provided further and innovative details of the role of the CT. In particular, the phenomenological method suggested how to carry out, in an internally consistent way, a sequence of high-resolution scattering experiments, performed under the same conditions, involving both the systems of interest and reference cases binding by pure vdW forces. The target has been to probe both the absolute scale of the interaction and its change along homologous series of systems.75,76 In this way, we resolved changes in the quantum interference effects, accompanying the scattering observables, associated with the role of the CT in hydrogen bonds and of the CT, polar flattening and σ hole on halogen bonds. The predictions of the phenomenological method have been tested, and in some cases improved, by comparing basic experimental findings with results of ab initio calculations (see ref. 75,76 and references therein). Moreover, the integrated experimental-theoretical approach addressed ab initio calculations towards the evaluation of important details of the electron/charge displacement within the interacting adducts promoted by the intermolecular interactions. This approach permitted evaluation of the proportionality constant between the amount of transferred charge and the strength of the CT component, selectively affecting specific configurations of the interacting systems. For major details see ref. 19,75 and references therein. Note that weak intermolecular hydrogen and halogen bonds determine the precursor state of nanostructures of interest in several areas of materials engineering, biochemistry and chemistry.77–79
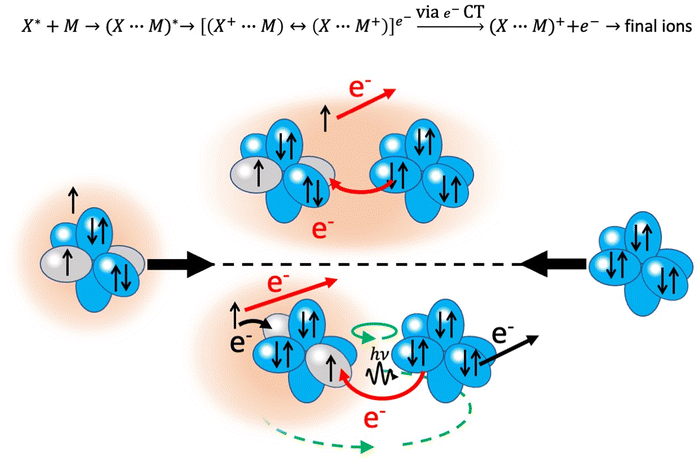
4. Chemiionization reactions
An important class of reactions, driven by the balance of physical and chemical intermolecular forces leading to precursor states, close or coincident with the reaction TS, are chemi-ionizations (CHEMI), also known as collisional autoionization or Penning ionization phenomena (see ref. 9–12, 80–107 and references therein). They were discovered about hundred years ago by Penning,108 a manager of Philips agency, and such reactions contribute to the balance of phenomena that occur in the interstellar medium, plasmas and planetary atmospheres.109 Such reactions usually involve a neutral species (X*) highly excited in a metastable state and another atomic/molecular partner M as reagents.93,94 The precursor state, schematized in the upper part of the Fig. 5 as (X⋯M)*, can be imaged as formed by a Rydberg electron whose floppy cloud is wrapping an ionic core, described as mixing of two limit electronic configurations completely different in energy and coupled by the CT. The reaction is triggered by the full relaxation of the system in the lowest state through a vertical transition, and the energy release is sufficient to eject an external electron with a defined kinetic energy and to form other ionic products, such as the associated ion XM+, the parent ion M+, usually called the Penning ion, and its fragmentation species.93,94If the excited species is a metastable helium or neon atom, the reaction occurs with all molecules available in nature and also with Ar, Kr and Xe. In the latter case, prototype atom-atom CHEMI are promoted, to which we address initially our attention since they have been the target of several experimental and theoretical investigations.11,12,82–84,87,88,91–95,97,105,109–113 Their full characterization represents the appropriate starting points to investigate reactions involving molecules. In particular, it is interesting to emphasize that such metastable atoms exhibit a change in their nature within the interacting adduct: at a long separation distance from the partner to be ionized, they behave like low ionization potential alkali metals, while at short distances, that is when they disclose their ionic core, behave like high electron affinity species (see below for important implications).
Therefore, the proper assessment of the basic electronic rearrangements, determining structure, stability and reactivity of the precursor state of CHEMI, is a target of general interest for the control of the stereo-dynamics of these and many other elementary processes, including those where such rearrangements are difficult to characterize since they are by other effects.
4.1. Atom–atom CHEMI
The lower part of Fig. 5 shows the approach of the Ne*(3P) reagent to another Ng atom. If the precursor state, formed at low collision energies, is a diatom weakly interacting at a long separation distance, the perturbed metastable atom can break the validity of the optical selection rules. The reaction can be promoted by a virtual photon exchange between reagents, assuming the character of a photo-ionization process (see ref. 82,83,88, and references therein). On the contrary, if the precursor state, formed at high collision energies and short separation distances, is a true molecule, the increased overlap between the valence orbitals promotes a direct electron transfer process. In particular, it is stimulated by the CT and classified as an elementary exothermic oxidation reaction.110–113As nuclear processes, also CHEMI, are driven by an optical potential W defined in eqn (1) as a combination of a real (Vt) and an imaginary (Γ) part.93,94 The real part controls the dynamical approach of reagents, while the imaginary part, also known as resonance width, triggers the passage from neutral reagents to ionic products through an electronic rearrangement and defines the opacity of the system.
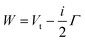 | (1) |
The strength of both the real and imaginary components varies with the centre-of-mass separation and relative orientation of interacting partners.
Typical CHEMI are barrier-less reactions of interest in fundamental research, addressed to assess the coherent control of reactivity events at low temperature and to explore the quantum nature of matter.8–13,98 They are also the target of applied research, including astrochemistry and cold chemistry, combustion, flames, plasmas, lasers, electric discharges and soft ionization processes.109 However, a unifying and internally consistent rationalization of these processes is still in progress.
Our contribution to this topic started with the realization of scattering experiments. The phenomenological method has been also used to define all basic chemical-physical features of the precursor-transition state controlling the reaction dynamics. The predictions of the treatment have been tested on the experimental observables obtained in our laboratory and in other laboratories.101,110–113
The phenomenological method suggests that the precursor state, formed by collisions of reagents, represents a sort of electromagnetic trap, where the quantum confinement of the system affects all valence electrons rearrangements driving the reaction.114 Electronic rearrangements are stimulated by the fundamental components of the intermolecular forces operative in the trap, as those promoting electronic polarization, charge transfer, spin–orbit effects, including their perturbations on the involved open-shell species, and coupling/decoupling of angular momentum arising from electronic and other contributions. The upper part in Fig. 6 emphasizes, in the case of Ne*(3P) approaching another Ng, the role of the electronic polarization in the formation of the reaction precursor state. The intermediate panel indicates that the internal ionic state formed by reagents in the entrance channel and the state of ionic products in the exit channel couple through a configuration interaction by the CT of the same type operative in noble gas halide systems (see Section 3). Moreover, to rationalize the role of electronic angular momentum couplings, the collision complex must be identified as a system rotating at variable separation distance. In particular, the case of atom–atom reactions can be confined in proper sequences of Hund's cases of rotating diatomic molecules (see lower panel in Fig. 6).115,116
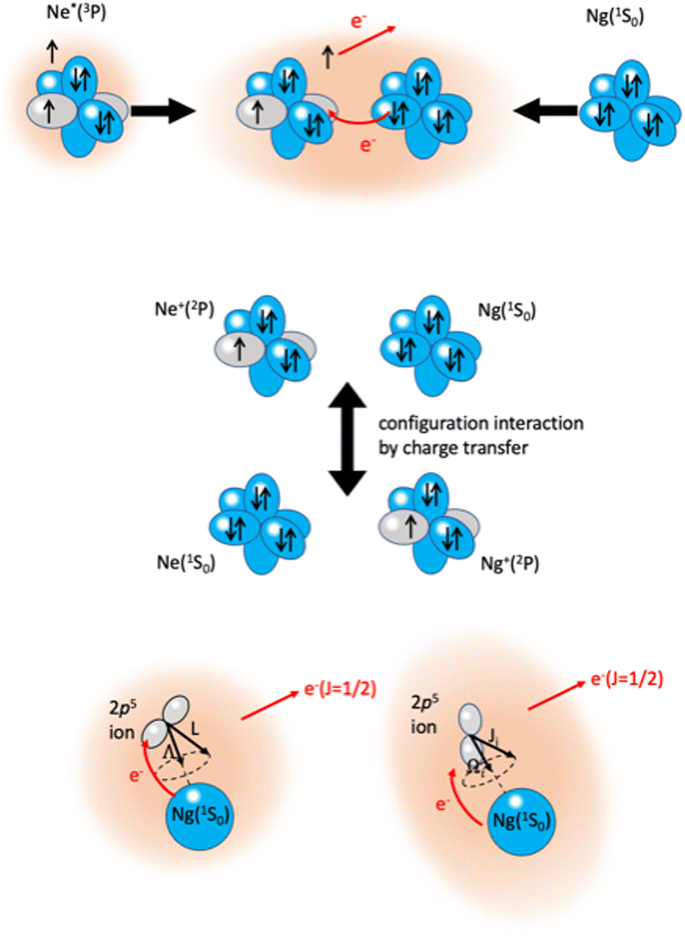 | ||
| Fig. 6 Upper part: The electromagnetic trap, formed by collisions of reagents, representing the precursor state of atom–atom CHEMI. Intermediate part: The internal ionic states coupled by configuration interaction by CT. Lower part: Collisions complex, confined in Hund's cases (a) and (c), according to the quantum numbers adopted to define the electronic angular momentum couplings. The interatomic distance interval where the system changes angular momentum coupling schemes, with the transition from |J,Ω〉 to |Λ,Ω〉 representations, is a region of “confusion” for the angular momentum coupling where non-adiabatic effects are effective15,74,110 (see also below). | ||
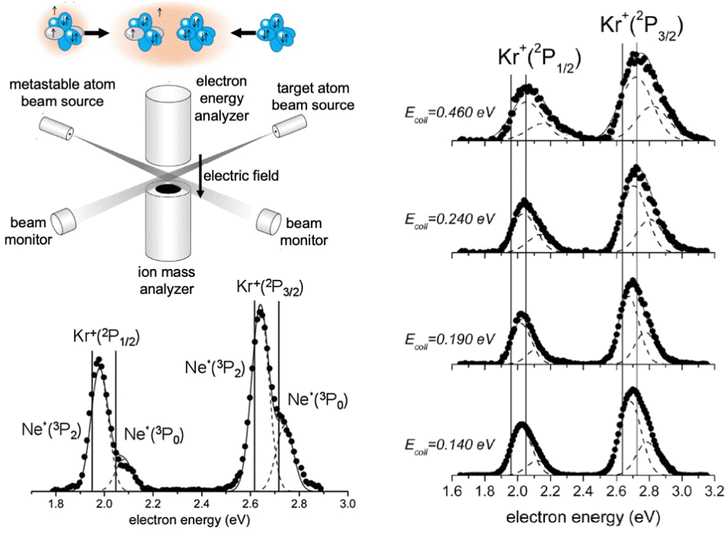
The apparatus used in our laboratory94,99,100,103,104,111–113 consists of (see Fig. 7) a noble gas beam source, from which the emerging atoms are excited by collisions with electrons or the passage through a microwave discharge, and they cross the molecular beam of the target gas at a right angle. A hemispherical electron analyzer, that is placed above the crossing region, provides the so-called Penning Ionization Electron Spectra (PIES), that define the intensity and kinetic energy of emitted electrons. The type and intensity of all other ionic products are provided by a mass spectrometer, located below the crossing region, from whose detections total, partial ionization cross sections and branching ratios BRs are obtained.
For krypton and xenon targets measured PIES resolved the different energetic and probability of reaction channels opened by spin–orbit levels of Ne*(3PJ) reagent and forming Kr+ and Xe+(2PJ) ionic products.110–112Fig. 7 illustrates the results for krypton. The dependence on the collision energy of the peak position, and of the peak area ratios, provided additional information on the efficiency change of the active channels. Therefore, the PIES represents a sort of transition state spectroscopy, and the origin of this important finding has been also suggested by many other authors investigating other CHEMI.88,92 It has been also confirmed by the PIES measured in our laboratory for the ionization of water, ammonia and hydrogen sulfide by their collisions with Ne* at a defined kinetic energy.100,101,103 In particular, the two main peaks, observed in CHEMI of water, relate to the formation of water ions in the ground and in the first excited state that occurs through different reaction channels whose precursor states are exhibiting different energy and symmetry.
The ample phenomenology achieved in our laboratory on the anisotropic behavior of high electron affinity open shell species, such as the halogen atoms,15,58,71,72,74 suggests that entrance and exit channels of CHEMI represent a unique manifold of quantum states, which are accessible to the system during the valence electron rearrangements promoted by the intermolecular forces. Such rearrangements are accompanied by adiabatic and non-adiabatic effects110–113 that control, respectively, collision dynamics and reactivity. In particular, adiabatic effects account for the adiabatic conversion of atomic quantum states, |J,Ω〉, where Ω defines (see also the lower part of Fig. 6) the absolute projection J along R, into molecular states of Σ and Π symmetry. The adiabatic effects determine the anisotropic behavior both of the real part of the optical potential in the entrance channels and of the interaction in the exit channels.110,111,113Fig. 8 plots the adiabatic potentials V|J,Ω〉 referred to as entrance and exit channels of Ne*–Ar, Ne*–Kr and Ne*–Xe systems. They have been obtained in an internally consistent way and all details of the potential formulation and parametrization are given in ref. 20 and 117. The reported plot permits a useful comparison of strength and anisotropy of the interaction and also emphasizes the different roles of the spin–orbit coupling, which changes by more than a factor of ten when passing from Ar+ to Xe+ as an ionic product.
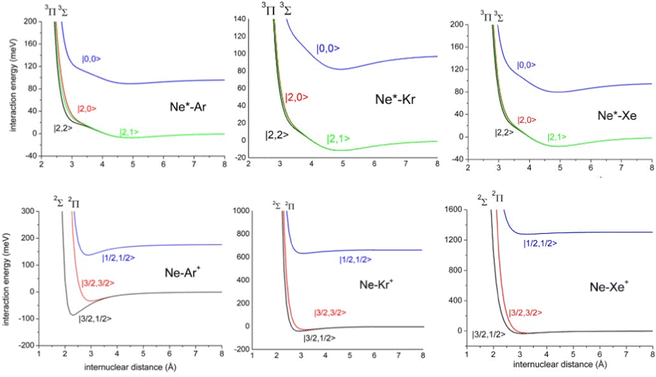 | ||
| Fig. 8 Adiabatic interaction potentials V|J,Ω〉 operative in the entrance and exit channels of atom–atom CHEMI (for details on their formulation see ref. 20 and 117). Such potentials correlate the atomic states with their spin–orbit levels, operative at a long internuclear distance, with molecular states of Σ and Π symmetry formed at short distances. | ||
Non-adiabatic effects, promoting the passage from entrance to exit channels, are triggered by specific features of the same electronic rearrangements. Therefore, real and imaginary parts of the optical potential must be interdependent and not independent as usually assumed in the past. Along these guidelines, we attempted to formulate also the state-to-state Γ components. Our analysis suggests the existence of two coefficients, extracted from the interaction potential formulation, that properly link adiabatic and non-adiabatic effects. Such coefficients, labeled as Cx and Cy, quantify, respectively, the Σ character degree in each entrance and exit channel at each separation distance. They represent marker-tracings of the electronic evolution with its dependence on the separation distance of interacting partners, suggesting if the precursor state is confined in the structure of two separate reagents, in that of a weakly interacting complex, in that of a formed molecule, or in the transition between two limiting structures. After all, each marker-tracing is the equivalent of the indicator in acid-base reactions, since the indicator provides information on the prevalence of acidic or basic character and on the equivalence point. Therefore, Cx and Cy map the adiabatic passage from atomic to molecular states and also define the regions where non-adiabatic effects of specific nature emerge.
From the Cx behavior, reported in the upper part of Fig. 9 for selected entrance channels of the prototype Ne*+ Kr CHEMI, it appears that an important region is the asymptotic one, where Cx assumes 1/3 and 2/3 values. In such regions, the reagents are so distant that intermolecular forces vanish and no reaction occurs. The first critical region is where Cx starts to vary, stimulating the reactions of two atoms perturbed by weak long-range forces. The other two critical regions are where Cx strongly varies and where it assumes 1 or 0, as a constant value. Here, chemical forces emerge. The precursor state passes from a diatomic to a molecular structure with a defined electronic symmetry. In the last two regions a different reaction mechanism, essentially driven by anisotropic CT contributions, arises and becomes dominant. In the same part of the figure is also reported the behavior of Cy, that defines the corresponding transition of the system in the exit channels.
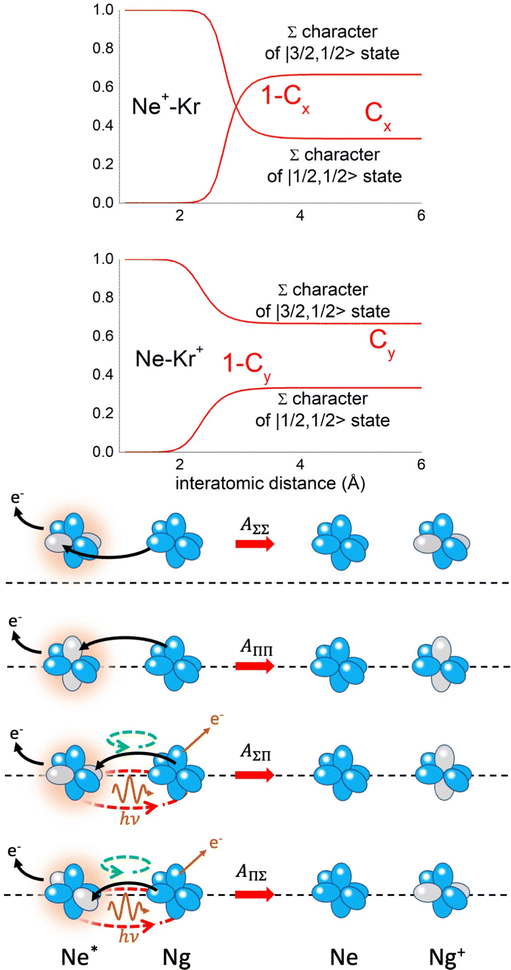 | ||
| Fig. 9 Upper part: (a) Vertical axes give values of the Σ character in the entrance (Cx) and exit (Cy) channels as a function of the internuclear distance R. The Π character is defined as a complement to 1 of the Σ one. All states accessible to the system are indicated by |J,Ω〉 quantum numbers. The entrance channels are identified by the states of the ionic precursor formed by the Ne*(3PJ) reagent (see the Upper part in Fig. 6). For both entrance and exit channels, the |3/2,3/2〉 states are not included since they exhibit a pure Π character at all R. Lower part: Cartoon representing the main features of Σ–Σ, Π–Π, Σ–Π, and Π–Σ couplings promoted by non-adiabatic effects operative during the collisions. As in Fig. 5, the arrows in the precursor states indicate the movement of the electrons accompanying the electronic rearrangements. | ||
Accordingly,110–114,117 we identified two different reaction mechanisms:
– Direct mechanism that involves a homogeneous electron exchange with non-adiabatic coupling terms, called AΣ–Σ and AΠ–Π and depicted in the lower part of Fig. 9, on the basis of a well-defined molecular character of initial and final states. Such mechanism is mostly triggered by the selectivity of the configuration interaction by the CT, strongly varying with R since related to the overlap between valence orbital exchanging electrons.
– Indirect mechanism that, stimulated by a heterogeneous electron transfer, is controlled by AΣ–Π and AΠ–Σ non-adiabatic coupling terms (see again the lower part in Fig. 9). It is basically promoted by polarization, perturbed spin–orbit couplings and Coriolis contributions, the latter related to centrifugal effects depending on the orbital angular momentum that accompanies any collision event. These interaction components generate a mixing of atomic/molecular states of different symmetry. Having AΣ–Π and AΠ–Σ a less pronounced radial dependence with respect to AΣ–Σ and AΠ–Π, the indirect mechanism dominates at large separation distances, where the critical balance of interaction components of chemical and physical nature tends to break the validity of the optical selection rules, and the reaction can transform in a photo-ionization process (see the lower panel in Fig. 5). The possibility of a virtual photon exchange between reagents has been suggested several years ago in pioneering works on CHEMI.82,83,87
According to our formulation,117 the state-to-state imaginary Γ components are defined as a weighted sum of AΛ–Λ′ coupling terms whose relative weights depend on Cx and Cy coefficients. Explicit relations are as follows:
Results obtained for Ne* + Ar, Ne* + Kr and Ne*+ Xe reactions are given in Fig. 10. The plot provides again a useful comparison from which it appears that the Γ components show an evident state-to-state dependence and those of Ne*–Xe are slightly stronger with respect to the corresponding ones of Ne*–Ar and Ne*–Kr cases.
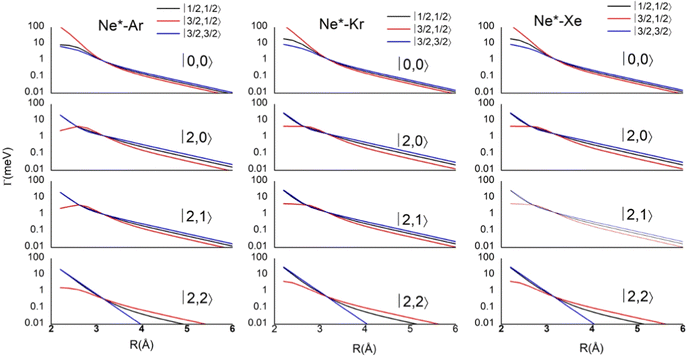 | ||
| Fig. 10 Radial dependence of state-to-state Γ components, defined in terms of |J,Ω〉 quantum numbers of Ne*(3PJ) neutral reagent and of Ar+, Kr+ and Xe+ ionic products in their 2PJ electronic states. | ||
Real and imaginary components of the optical potential so formulated allowed us to calculate, as a function of the collision energy E, state-to-state ionization cross sections, and BRs, defining, respectively, the absolute and relative reaction probability of selected channels. The comparison with the experimental findings represented an important test of the adopted theoretical methodology.
Calculations of scattering properties have been useful to show the anisotropy of state-to-state ionization cross sections and to emphasize that while the collision energy variation of each state-revolved result depends on the real part component of the optical potential, operative along the selected channel, its absolute value is controlled by the imaginary component operative along the same channel.93,94
Calculated state-to-state total ionization cross sections for Ne*–Ar reagents are compared in Fig. 11 with data reported by Gregor and Siska some years ago,87 measured without state selection in a wide collision energy range and indicated here as black points. The statistical average over all entrance channels, accessible in Gregor and Siska's experiments, provides results in good agreement with measured values. Similar data have been obtained for Ne*–Kr and Ne*–Xe reagents.113,117
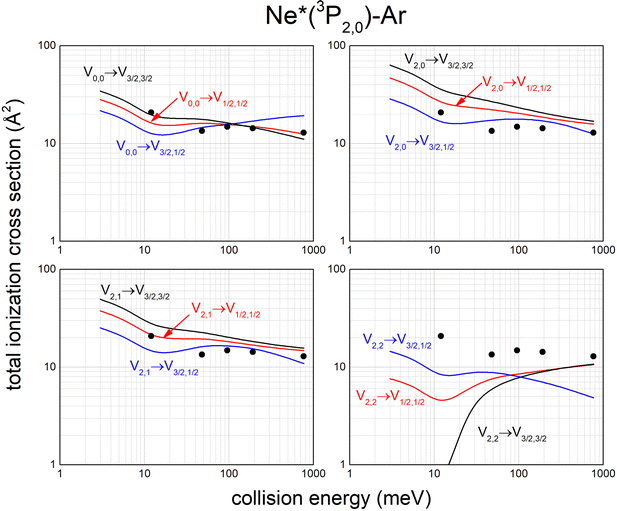 | ||
| Fig. 11 Calculated state-to-state total ionization cross section for Ne*–Ar as a function of the collision energy and comparison with experimental results87 (see text). | ||
The same analysis provides also the associative/Penning ratios, concerning the relative formation probability as products of an ionic aggregate (as the associated NeAr+) with respect to an atomic ion (as the Penning Ar+). It is important to note that each ratio depends on the position of the potential well in the exit channel, which acts as trapping of the formed associated ion, with respect to the region of the entrance channel where the reaction is effectively triggered. Predicted ratios, reported in Fig. 12, are consistent with results, measured in Perugia laboratories in an extended collision energy range,88 and referred to state averaged conditions (black points). They are also in agreement with ratios measured in Lausanne by the Osterwalder group (reported as open circles), adopting beams of Ne*(3P2) atoms state selected in their |J,Ω〉 quantum states.11,105 The detailed comparison is useful to emphasize again the state-to-state dependence of the associative/Penning ratio and the correctness of predicted values.
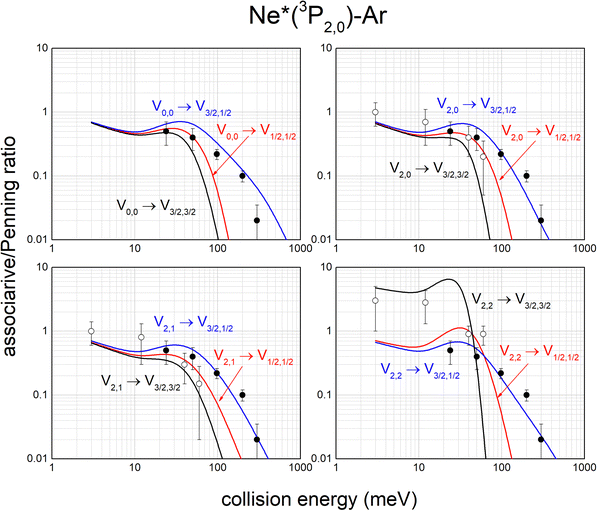 | ||
| Fig. 12 State-to-state associative/Penning ratios predicted for Ne*–Ar. The comparison involves results (black points) obtained in old experiments88 referred to state averaged conditions. Data, more recently measured with Ne*(3P2) beams selected in Ω = 2, 1, 0 quantum states,11,105 are also reported (open circles) for further comparison (see text). | ||
4.2. Atom–molecule CHEMI
Recently, our study focused on the stereo-dynamics controlling CHEMI of molecules M,118 and of particular interest are those involving N2 and O2 since they determine the chemistry in space and planetary ionospheres, affecting the transmission of radio and satellite signals.119 Compared to the atom–atom reactions, their description is complicated since real and imaginary parts depend also on the molecular orientation. Moreover, the associated ion NeM+ tends to pre-dissociate if the M+ moiety is formed vibration-rotationally excited.120,121The phenomenological method suggests that an important structure of the precursor state of the Ne*+ N2 reaction must be that reported in Fig. 13 (lower part), which appears rather different with respect to that promoting Ne*–Ng CHEMI (see the upper part of Fig. 6).
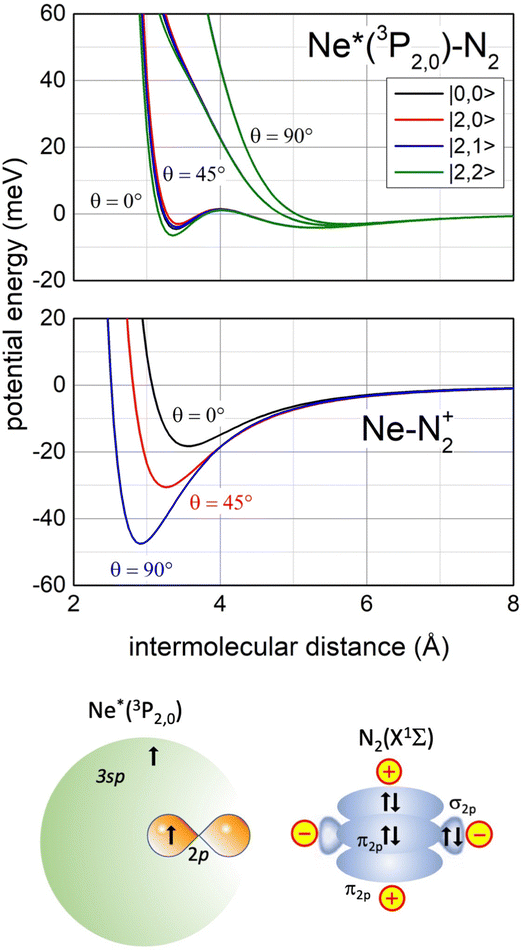 | ||
| Fig. 13 Upper panel: The real part Vt of the optical potential with its dependence on the intermolecular distance, on the orientation angle θ of N2 and on the |J,Ω〉 quantum state of Ne*(3PJ) reagent. Intermediate panel: The anisotropic interaction potential in the exit channels. Lower panel: A basic configuration of the precursor state of Ne*(3PJ) + N2 CHEMI in the collinear configuration of reagents (for more details see ref. 119). | ||
In particular, the permanent electric quadrupole moment of N2 determines, with respect to an isotropic Ng atom, a different polarization of the floppy cloud of 3s electrons on Ne* reagent. Such polarization controls the selectivity of the CT and also accounts for a strongly anisotropic electrostatic effect between the bare Ne+ ionic core and the molecular quadrupole.
The extension/generalization of the phenomenological method permitted us to obtain in analytical form both the real and the imaginary part of the optical potential.122 Note that for the formation of the ionic product N2+ in the ground 2Σ+g state, that is in the absence of spin–orbit contributions, only two non-adiabatic coupling terms, ADM and AIM, are effective. However, such terms must enclose a molecular orientation dependence. On these grounds, we obtained a real component exhibiting a marked dependence on the molecular orientation and a limited dependence on the atomic sublevel involved (see Fig. 13), while the imaginary components behave in an opposite way (see Fig. 14).121 Within the same method, we obtained also the interaction in the exit channel, reported in Fig. 13.
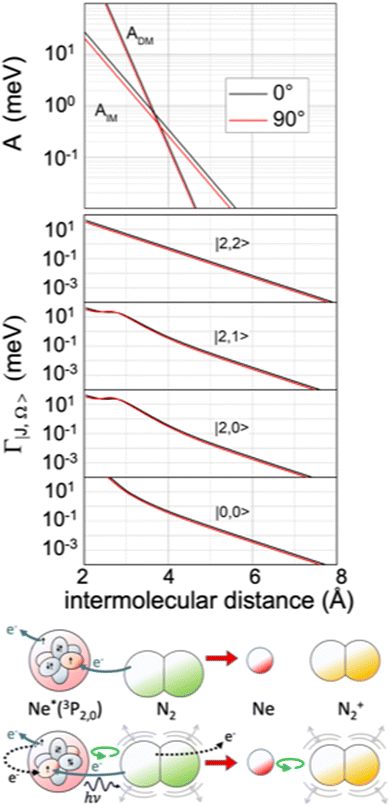 | ||
| Fig. 14 Upper panel: The radial dependence of non-adiabatic coupling terms ADM and AIM controlling the direct and indirect reaction mechanisms, respectively, for the perpendicular and parallel approach of N2 to Ne*. Intermediate panel: The radial dependence of the imaginary component Γ for the perpendicular and parallel approach of N2 to Ne*, including its dependence on the atomic |J,Ω〉 quantum state of Ne*(3PJ) reagent. Lower panel: A cartoon of direct and indirect mechanisms for a parallel configuration of the precursor state. The arrows of different colors indicate again the different electronic rearrangements accompanying the two mechanisms (see also Fig. 5 and 9). | ||
Important tests of the potential formulation reliability have been performed comparing predictions with available experimental findings, all summarized in Fig. 15:
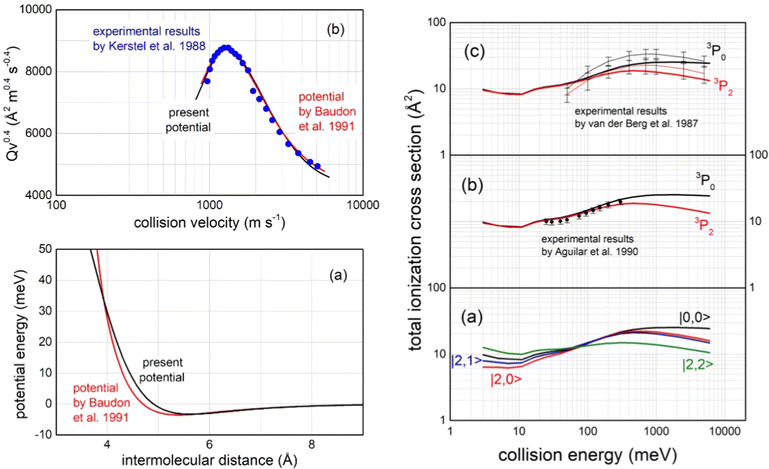 | ||
| Fig. 15 Left panel (a): The long-range behaviour of isotropic (spherically averaged) real part of the optical potential in the entrance channels, compared with that previously obtained by a multi-property analysis.124 Left panel (b): Total integral cross sections Q, measured as a function of the collision velocity v,123 plotted as Qv2/5 to emphasize the “glory” interference pattern, compared with calculations, carried out within the semi-classical JWKB approximation124 by the present optical potential for Ne*(3P2,0) atoms scattered by N2. Right panels: (a) Calculated state-dependent total ionization cross sections as a function of the collision energy; (b) comparison of calculations with data measured125 with a statistical population of Ne*(3P2) and Ne*(3P0) reagents; (c) comparison with experimental data126 obtained resolving the different reactivity of Ne*(3P2) and Ne*(3P0) reagents, where thin black and red lines are interpolations of experimental data. Vertical bars represent the experimental uncertainties. | ||
– The first comparison, reported in the left upper panel of such figure, regards the total (elastic + inelastic) integral cross sections, measured in the Eindhoven laboratory123 with the resolution of a maximum in the collision velocity dependence. Such observable, due to the “Glory” quantum interference effect, probes in detail the features of the average potential well depth in the entrance channels, located at about 5.5 Å, as shown in the upper panel in Fig. 13;
– The second test concerns the comparison in the entrance channels of the present isotropic interaction component with that provided thirty years ago by the use of a multi-property analysis124 including total (elastic + inelastic) integral and differential cross sections, probing simultaneously both the well region and the first part of the repulsion (left lower panel in Fig. 15);
– The third test focuses on the total ionization cross section measured, as a function of the collision energy E, both in Perugia125 and in Eindhoven laboratories126 (right panels in Fig. 15), which probe in detail strength and anisotropy of the optical potential at intermediate and short separation distances.
– The fourth test regards the different dependence on E of the total ionization cross section for the two spin–orbit levels of Ne*(3PJ) reagent. The larger increase for the 3P0 state, with respect to 3P2, as observed in Eindhoven experiments126 and emphasized by our calculated state-to-state results (see right panels in Fig. 15), arises from the most pronounced increase, as R decreases, of the Cx marker-tracing for such reagent.
For this reaction, associative/Penning ratios have been measured in the Perugia laboratory, using effusive beams (upper panel in Fig. 16).127 Under such conditions, all reaction channels, triggered by direct and indirect mechanisms, are effective. In the Lausanne laboratory, ratios have been measured exploiting a beam of Ne*(3P2) atoms, the state selected in their |J,Ω〉 quantum states, that crosses a seeded beam containing rotationally relaxed N2 molecules.12,128 Results measured for the selected |2,2〉 entrance channel show the highest ratio.128
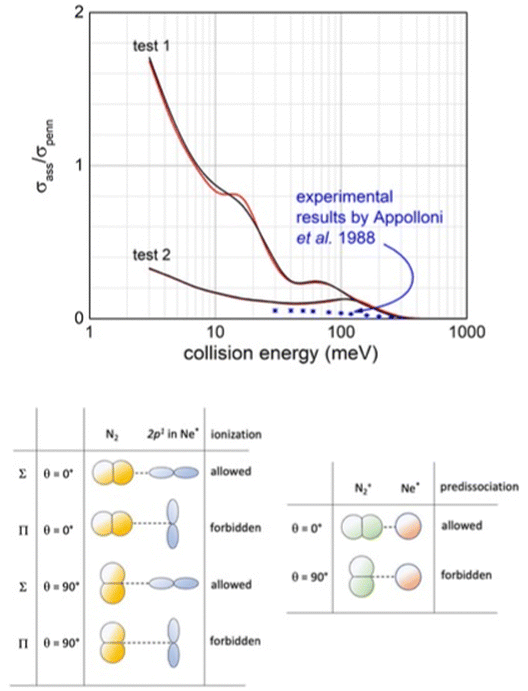 | ||
| Fig. 16 Upper panel: Comparison, as a function of the collision energy, between predicted associative/Penning ratio for Ne*(3P2) (red line) and Ne*(3P0) (black line) reagents and data measured127 using a statistical population of atomic fine levels. Lower panel: Schematic view of precursor state structures promoting reaction and associated ion formation. Note that while the HOMO orbital of N2, from which the electron is removed, does not exhibit any nodal plane perpendicular to the bond axis (passing for its centre of mass), the half-filled p orbital of Ne* atom exhibits a nodal plane.119 Therefore, in all configurations characterized by overlap null between orbitals exchanging the electron, as in the second and fourth cases, the ionization by direct mechanism is forbidden and the reaction can occur only by an indirect mechanism (see text). Moreover, associate ions are efficiently formed, without pre-dissociation, only if N2 maintains the perpendicular configuration both in the entrance and exit channels. | ||
Our analysis, accounting for the symmetry of atomic and molecular orbital involved (see lower panel in Fig. 16), emphasizes that the most effective configurations for the direct mechanism are those with the half-filled orbital 2p of the Ne* atom and N2 aligned parallel in the precursor state. Under such conditions, the produced NeN2+ associated ion shows the proper symmetry to stimulate the pre-dissociation, especially if N2+ moiety forms in vibrationally excited states, as confirmed by previous experimental findings.120,121 However, the pre-dissociation is hindered if N2 in the precursor state is perpendicularly aligned.
The pronounced differences shown in Fig. 16, between predictions, carried out omitting pre-dissociation (upper panel, test 1), and observables suggest that a consistent fraction of associated NeN2+ ions undergo pre-dissociation as a consequence of the vibrational/rotational excitation of the formed N2+ moiety within (NeN2)+. As for many other inelastic events, the possibility of internal degree excitation of nascent N2+ strongly depends on the geometry of the precursor state assumed during ionization. The excitation is favoured for collinear or near collinear configurations. For the present CHEMI, an improved agreement with the experimental data is obtained when assuming that only approaches with orientation close to the perpendicular configuration are effective for the formation of the associated ion without pre-dissociation (see test 2 in the upper panel in Fig. 16). Under such conditions, the predicted results are also in the right scale of quantum state averaged data from ref. 105. Moreover, Ne* in the |2,2〉 quantum state involves the half-filled atomic orbital aligned perpendicularly to R. The direct mechanism is forbidden and the reaction occurs only via an indirect mechanism for which most efficient collisions are those with N2 aligned parallel or near parallel to R.122
Recently, our interest focused on Ne* + HCl, and Ne*+ HBr reactions that show a strong stereo-selectivity.129 In particular, they promote the formation of parent ions in the ground electronic state, via precursor states having perpendicular configurations, and the formation of parent ions in the first excited electronic state, via precursor states in parallel configurations. The latter can trigger also proton transfer phenomena with the formation of NeH+ + X (Cl, Br) products. The different reaction channels are opened within angular cones exhibiting a different orientations and acceptance. Major details on the stereo-dynamics of such atom–molecule reactions have been reported in a recent paper.129
5. Conclusions and perspectives
The present perspective review emphasizes the role of the precursor state, controlling the dynamical evolution of elementary processes, whose structure and stability depend on the critical balance of weak intermolecular forces, of physical and chemical nature, operating at long and intermediate separation distances. The focus is on the strength, anisotropy and radial dependence of such forces that currently are difficult to correctly evaluate on quantitative grounds. Moreover, molecular dynamics simulations to be reliable require the use of an internally consistent representation of the force field in the whole space of the relative configurations of interacting partners. In the investigations presented in this paper, important help has been provided by the phenomenological method that adopts semi-empirical and empirical formulas to represent the basic features of the leading interaction components. Such formulas are defined in terms of a few parameters, directly or indirectly related to the fundamental physical properties of the interacting partners (see the Appendix). Important tests of the phenomenological method, to be further improved and generalized in the next future, have been performed by comparing its predictions with experimental information, obtained in our and in other laboratories, and, in some specific cases, with results of ab initio calculations. Furthermore, the NASA laboratories recently exploited such a method to determine transport properties in gaseous mixtures, for temperatures up to some thousands of Kelvin, and of interest in several scientific fields.130The possibility to implement the semi-empirical long-range interactions in ab initio reactive surface (as described in ref. 65 and 131) and the importance of the long-range and spin–orbit effects on the molecular dynamics have been demonstrated to give important predictions132,133 competitive (and probably in some case more accurate) than completely ab initio heavier calculations,134,135 especially of interest in ultra-cold regimes.
The possibility of rationalizing in an internally consistent way phenomena of a rather different nature, through a detailed representation of the precursor states controlling their stereo-dynamical evolution, represents one of the main topics supported by this perspective-review. The methodology presented, including the guidelines of its application, is discussed in detail for CHEMI. Such reactions, that occur under a variety of conditions in several environments, can be considered the inverse of electron attachment processes136 that are of relevance also for plasmas of nuclear fusion.137 As stressed above, the obtained results appear to be of general interest to define the role of the precursor state in the stereo-dynamics of many other reactive processes, concerning especially those occurring at low temperatures, that play a central role in cold chemistry and are difficult to characterize. In particular, phenomena occurring in interstellar environments, where highly excited atoms are formed with high probability by collisions with cosmic rays, can be mentioned as elementary processes of great relevance from both fundamental and speculative points of view.
The next steps for a further generalization of the methodology, on which our work is in progress, concern:
– An extended assessment of the relevance of the molecular alignment/orientation, also known as “molecular polarization”. Basic methodologies founded on the use of external strong fields have been proposed in the past to obtain molecular polarization (see ref. 138–144 and references therein). At present, such methods are still in progress to select polar molecules in their internal states.145–149 Moreover, molecular polarization can be also induced in a “natural way” within sufficiently high electric field gradients generated by strongly anisotropic intermolecular forces.150–156 This phenomenon should emerge especially during collision events at low temperature, involving ions and molecules with pronounced permanent electric multi-pole, slowly rotating and flying at low speed.
– The molecular polarization promoted by anisotropic intermolecular forces drives the formation of the precursor state in specific structures that can favor or hinder the following evolution towards the final states of elementary processes. This can be of interest to rationalize opposite temperature dependence, such as Arrhenius/Anti Arrhenius behaviors, manifested by several phenomena occurring at low temperature.3,6
– The selective role of the centrifugal barriers limits the orbital angular momentum components effectively promoting the reaction. In particular, such a role has been often invoked to describe some selectivity in ion–molecule reactions exploiting capture models,145–147,149,154–156 but in a more general vision, it is expected to control probability, structure and stability of the reaction precursor states, formed at low kinetic energy and under specific values of the orbital angular momentum of the collision complexes. Note also that a recent review suitably emphasizes some important limitations of the capture models when, in addition to the basic role of the long-range attraction, important short-range features of the interaction come into play.157
In conclusion, exploiting the favorable case of prototype CHEMI, we hope to obtain in the near future the full topology of their stereo-dynamics,139,158 with guidelines of general interest for the control of the microscopic evolution of several elementary processes, more difficult to characterize and of interest in many other chemical–physics fields. Intriguing results obtained very recently for CHEMI seem to confirm this possibility.159,160
Author contributions
S. F., F. V. and F. P. conceived and designed the study. All authors developed the proposed model with related calculations and analysed the experimental data. All authors participated in the writing and editing of the paper.Conflicts of interest
There are no conflicts to declare.Appendix: correlation formulas-scaling laws
The phenomenological approach, with related scaling laws, is solidly based on molecular beam scattering experiments carried out with open and closed shell atoms and molecules as projectiles and targets.15,40,58,76 The use of high angular and energy resolution conditions, allowed resolving for many colliding systems quantum interference effects in the scattering that appear as oscillatory patterns over-imposed to smooth cross-section components.18 The analysis of the experimental findings associated with systems, where pure vdW interactions operate, suggested the representation of the equilibrium distance Rm in the interacting complex and of its binding energy Dm by correlation formulas, given in terms of polarizability α1 and α2 of the partners involved. Specifically: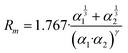 | (A1) |
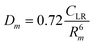 | (A2) |
The values of the CLR coefficient have been extracted161,162 from the analysis of the average integral cross-section value, measured in absolute scale for many systems with the same methodology, and they represent the global dispersion attraction, Vdisp(R), in the range of R mainly probed by the scattering experiments. The obtained values for CLR depend on the balance of several long-range attraction contributions (induced dipole-induced dipole, induced dipole-induced quadrupole, induced quadrupole-induced quadrupole, etc.) multiplied by damping functions f due to the emergence of overlap effects.14,15,162 Accordingly, it is convenient to define:
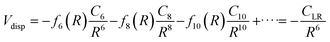 | (A3) |
C LR values obtained by experiments and accounting for the effective strength of the attraction in the range of R mainly probed by the scattering experiments (1.5Rm≤ R ≤ 2Rm) have been also represented by the following semi-empirical formula,162 where Ne1 and Ne2 are effective electron numbers contributing to the polarizability of each partner:
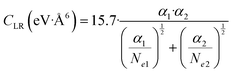 | (A4) |
Numerical coefficients in eqn (A1), (A2), and (A4) have been obtained on the phenomenological ground.15,161,162 It is of relevance to note that eqn (A1) reflects the fact that Rm depends on the balance between repulsion, represented as a sum of size contributions of the two partners and given as the cube root of their polarizability, and attraction, proportional to the product of polarizabilities (as suggested in eqn (A4)) and that such equation has been recently confirmed, for symmetric noble gas dimmers, by a refined quantum mechanical treatment.163 Moreover, eqn (A2) indicates that Dm corresponds to approximately 70% of the attraction in Rm defined by CLR and its reduced effect is ascribable to the role of size repulsion.
Such correlation formulas have been also extended to systems involving neutral partners with completely different structures, ions, open shell atoms, and free radicals (see ref. 15 and 19, and references therein).
The analysis of several experimental findings, coming from scattering, spectroscopic, transport and ion mobility experiments suggested the adoption of an Improved Lennard Jones (ILJ) formulation of non-covalent interactions,18 where most of the inadequacies of traditional Lennard Jones model, due to an excessive repulsion and to a too strong attraction, are removed. ILJ takes the general form:18
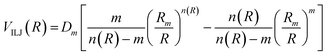 | (A5) |
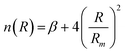 accounts for the falloff of the repulsion and modulates the radial dependence of the attraction. In particular, β controls the shape of the interaction potential well.
accounts for the falloff of the repulsion and modulates the radial dependence of the attraction. In particular, β controls the shape of the interaction potential well.
For neutral-neutral systems, for which m = 6, ILJ provides at large R, a dispersion attraction that accounts properly for the critical balance of the various damped contributions of eqn (A3) and whose relative strength changes with R:
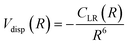 | (A6) |
Moreover, the same formulation provides asymptotically the value of the dipole–dipole C6 dispersion coefficient, defined as:
| C6 = Dm·R6m | (A7) |
For a detailed comparison between predicted C6 and accurate values from literature, obtained from experimental and theoretical methods, see ref. 18.
For ion-neural systems, for which m = 4, the leading ion-neutral induction attraction C4 coefficient takes the form:
| C4 = Dm·R4m | (A8) |
For ion–ion systems, for which m = 1, according to the Coulomb law, the leading attraction C1 coefficient is formulated as
| C1 = Dm·Rm | (A9) |
The ILJ function has been also extended to include the anisotropy of the interaction. The extension has been performed in atom molecule and molecule–molecule systems by adopting Legendre polynomials and spherical harmonic expansions for Rm, Dm and β quantities (see ref. 5, 16, 122 and references therein).
For systems affected by electrostatic effects, arising from permanent charge and permanent electric multipole interactions, related attractive-repulsive components are usually evaluated by the anisotropic charge distributions associated with the two interacting partners.4–6,14,16,17,50–57
Finally, the experimental investigation of several families of systems discussed in Section 3, affected by CT under various conditions, suggested the representation of the stabilization contribution by charge transfer VCT by simple formulas. In all cases VCT, being dependent on the overlap integral between orbital exchanging the electron, can be represented as an exponential decreasing function of the separation distance R,
| VCT(R) = ACT·e−γ·R | (A10) |
| VCT(R) = βCT(R) | (A11) |
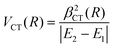 | (A12) |
The last equation comes from the concept of bond stabilization by the CT, introduced previously on phenomenological grounds (see ref. 19, 20, 71, 72, and references therein), whose role is attenuated by the absolute difference in energy between the coupled states, reported in the denominator. For details on the role of VCT(R) on the structure and stability of systems involving high electron affinity open-shell atoms, see Section 3 and ref. 71,72. For its contribution to the selectivity of CHEMI see Section 4 and ref. 20, 110 and 117.
Acknowledgements
This work was supported and financed by the Fondo Ricerca di Base, 2019, dell’Università degli Studi di Perugia (Project Titled: Produzione di metano per reazione di idrogenazione di CO2 con e senza catalisi in fase solida mediante l’uso di energie rinnovabili). Support from Italian MIUR and University of Perugia (Italy) is acknowledged within the program Dipartimenti di Eccellenza 2018-2022.References
- D. Cappelletti and S. Falcinelli, Editorial for the Special Issue on Long-range Intermolecular Interactions in Chemistry and Physics (in honour of Prof. Fernando Pirani), Chem. Phys. Lett., 2022, 786, 139190 CrossRef CAS.
- A. James, C. Jones, A. Melekamburath, M. Rajeevan and R. Srinivasamurthy, Swathi, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1599, 1–29 Search PubMed.
- Q. Hong, Q. Sun, M. Bartolomei, F. Pirani and C. Coletti, Phys. Chem. Chem. Phys., 2020, 22, 9375–9387 RSC.
- Q. Hong, M. Bartolomei, F. Esposito, C. Coletti, Q. Sun and F. Pirani, Phys. Chem. Chem. Phys., 2021, 23(29), 15475–15479 RSC.
- Q. Hong, Q. Sun, F. Pirani, M. A. Valentín-Rodríguez, R. Hernández-Lamoneda, C. Coletti, M. I. Hernández and M. Bartolomei, J. Chem. Phys., 2021, 154, 064304 CrossRef CAS PubMed.
- D. Ascenzi, A. Cernuto, N. Balucani, P. Tosi, C. Ceccarelli, L. M. Martini and F. Pirani, Astron. Astrophys., 2019, 625(A72), 1–9 Search PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2017, 358, 356–359 CrossRef CAS PubMed.
- O. Dulieu and A. Osterwalder, Cold Chemistry. Molecular Scattering and Reactivity Near Absolute Zero, Royal Society of Chemistry, Cambridge, 2018 Search PubMed.
- A. B. Henson, S. Gersten, Y. Shagam, J. Narevicius and E. Narevicius, Science, 2012, 338, 234–238 CrossRef CAS PubMed.
- E. Lavert-Ofir, Y. Shagam, A. B. Henson, S. Gersten, J. Kłos, P. S. Zuchowski, J. Narevicius and E. Narevicius, Nat. Chem., 2014, 6, 332–335 CrossRef CAS PubMed.
- S. D. S. Gordon, J. J. Omiste, J. Zou, S. Tanteri, P. Brumer and A. Osterwalder, Nat. Chem., 2018, 10, 1190–1195 CrossRef CAS PubMed.
- S. D. S. Gordon, J. Zou, S. Tanteri, J. Jankunas and A. Osterwalder, Phys. Rev. Lett., 2017, 119, 053001 CrossRef PubMed.
- P. Paliwal, N. Deb, D. M. Reich, A. van der Avoid, C. P. Koch and E. Narevicius, Nat. Chem., 2021, 13, 94–98 CrossRef CAS PubMed.
- G. C. Maitland, M. Rigby, E. B. Smith and W. A. Wakeham, Intermolecular Forces: Their origin and determination, Clarendon Press, Oxford, 1987 Search PubMed.
- F. Pirani, G. S. Maciel, D. Cappelletti and V. Aquilanti, Int. Rev. Phys. Chem., 2006, 25, 165–199 Search PubMed.
- D. Cappelletti, F. Pirani, B. Bussery-Honault, L. Gomez and M. Bartolomei, Phys. Chem. Chem. Phys., 2008, 10(36), 4281–4293 RSC.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez, F. Pirani, G. Giorgi and K. Yamashita, J. Phys. Chem. Lett., 2014, 5, 751–755 CrossRef CAS PubMed.
- F. Pirani, S. Brizi, L. F. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10(36), 5489–5503 RSC.
- F. Nunzi, G. Pannacci, F. Tarantelli, L. Belpassi, D. Cappelletti, S. Falcinelli and F. Pirani, Molecules, 2020, 25, 2367 CrossRef CAS PubMed.
- S. Falcinelli, J. M. Farrar, F. Vecchiocattivi and F. Pirani, Acc. Chem. Res., 2020, 53(10), 2248–2260 CrossRef CAS PubMed.
- M. Capitelli, D. Cappelletti, G. Colonna, C. Corse, A. Laricchiuta, G. Liuti, S. Longo and F. Pirani, Chem. Phys., 2007, 338, 62–68 CrossRef CAS.
- A. Laricchiuta, G. Colonna, D. Bruno, R. Celiberto, C. Gorse, F. Pirani and M. Capitelli, Chem. Phys. Lett., 2007, 445, 133–139 CrossRef CAS.
- D. Bruno, C. Catalfano, M. Capitelli, G. Colonna, O. De Pasquale, P. Diomede, C. Gorse, A. Laricchiuta, S. Longo, D. Giordano and F. Pirani, Phys. Plasmas, 2010, 17, 112315 CrossRef.
- G. Colonna, A. D’Angola, L. D. Pietanza, M. Capitelli, F. Pirani, E. Stevanato and A. Laricchiuta, Plasma Sources Sci. Technol., 2018, 27, 015007 CrossRef.
- V. Aquilanti, D. Ascenzi, D. Cappelletti and F. Pirani, Nature, 1994, 371, 399–401 CrossRef.
- V. Aquilanti, D. Ascenzi, D. Cappelletti, S. Franceschini and F. Pirani, Phys. Rev. Lett., 1995, 74, 2929–2932 CrossRef CAS PubMed.
- V. Aquilanti, D. Ascenzi, D. Cappelletti, R. Fedeli and F. Pirani, J. Phys. Chem., 1997, 101, 7648–7656 CrossRef CAS.
- M. P. Sinha, C. D. Calwell and R. N. Zare, J. Chem. Phys., 1974, 61, 491–503 CrossRef CAS.
- D. P. Pullmann, B. Friedrich and D. R. Herchbach, J. Chem. Phys., 1990, 93, 3224–3236 CrossRef.
- B. Friedrich, D. P. Pullmann and D. R. Herchbach, J. Phys. Chem., 1991, 95, 8118–8129 CrossRef CAS.
- M. J. Weida and D. J. Nesbitt, J. Chem. Phys., 1994, 100, 6372–6385 CrossRef CAS.
- S. Harich and A. M. Wodke, J. Chem. Phys., 1997, 107, 5983–5986 CrossRef CAS.
- V. Aquilanti, M. Bartolomei, F. Pirani, D. Cappelletti, F. Vecchiocattivi, Y. Shimizu and T. Kasai, Phys. Chem. Chem. Phys., 2005, 7, 291–300 RSC.
- V. Aquilanti, D. Ascenzi, M. de Castro Vitores, F. Pirani and D. Cappelletti, J. Chem. Phys., 1999, 111, 2620–2632 CrossRef CAS.
- D. Ascenzi, M. Scotoni, P. Tosi, D. Cappelletti and F. Pirani, Front. Chem., 2019, 7, 390 CrossRef CAS PubMed.
- F. Pirani, D. Cappelletti, M. Bartolomei, V. Aquilanti, M. Scotoni, M. Vescovi, D. Ascenzi and D. Bassi, Phys. Rev. Lett., 2001, 86, 5035 CrossRef CAS PubMed.
- L. Vattuone, A. Gerbi, M. Rocca, U. Valbusa, F. Pirani, F. Vecchiocattivi and D. Cappelletti, Angew. Chem., Int. Ed., 2004, 43, 5200–5203 CrossRef CAS PubMed.
- A. Gerbi, L. Savio, L. Vattuone, F. Pirani, D. Cappelletti and M. Rocca, Angew. Chem., Int. Ed., 2006, 45, 6655–6658 CrossRef CAS PubMed.
- L. Vattuone, A. Gerbi, D. Cappelletti, F. Pirani, R. Gunnella, L. Savio and M. Rocca, Angew. Chem., Int. Ed., 2009, 48, 4845–4848 CrossRef CAS PubMed.
- L. Vattuone, L. Savio, F. Pirani, D. Cappelletti, M. Okada and M. Rocca, Prog. Surf. Sci., 2010, 85, 92–160 CrossRef CAS.
- B. Jackson, J. Chem. Phys., 1988, 88, 1383–1393 CrossRef CAS.
- B. Jiang, M. Yang, D. Xie and H. Guo, Chem. Soc. Rev., 2016, 45, 3621–3640 RSC.
- H. Chadwick and R. D. Beck, Annu. Rev. Phys. Chem., 2017, 68, 39–61 CrossRef CAS PubMed.
- M. Rutigliano and F. Pirani, Chem. Phys., 2018, 504, 38–47 CrossRef CAS.
- M. Rutigliano and F. Pirani, J. Phys. Chem. C, 2019, 123, 11752–11762 CrossRef CAS.
- M. Rutigliano and F. Pirani, J. Phys. Chem. C, 2020, 124, 10470–10482 CrossRef CAS.
- M. Rutigliano and F. Pirani, J. Phys. Chem. C, 2021, 125, 9074–9084 CrossRef CAS.
- M. Rutigliano and F. Pirani, Plasmas Sources Sci. Technol., 2022, 31, 094006 CrossRef.
- M. Rutigliano and F. Pirani, Molecules, 2022, 27, 7445 CrossRef CAS PubMed.
- J. M. C. Marques, F. B. Pereira, J. L. Llanio-Trujillo, P. E. Abreu, M. Albertí, A. Aguilar, F. Pirani and M. Bartolomei, Philos. Trans. R. Soc., A, 2017, 375, 20160198 CrossRef PubMed.
- M. Bartolomei, F. Pirani and J. M. C. Marques, J. Phys. Chem. C, 2017, 121, 14330–14338 CrossRef CAS.
- M. Bartolomei, R. Pérez de Tudela, K. Arteaga, T. González-Lezana, M. I. Hernández, J. Campos-Martínez, P. Villarreal, J. Hernández-Rojas, J. Bretón and F. Pirani, Phys. Chem. Chem. Phys., 2017, 19, 26358–26368 RSC.
- M. Bartolomei, F. Pirani and J. M. C. Marques, Phys. Chem. Chem. Phys., 2019, 21, 16005–16016 RSC.
- C. F. O. Correia, J. M. C. Marques, M. Bartolomei, F. Pirani, E. Maçôas and J. M. C. Martinho, Phys. Chem. Chem. Phys., 2021, 23, 1500–1509 RSC.
- Y. Bramastya Apriliyanto, N. Faginas Lago, A. Lombardi, S. Evangelisti, M. Bartolomei, T. Leininger and F. Pirani, J. Phys. Chem. C, 2018, 122, 16195–16208 CrossRef.
- E. García-Arroyo, J. Campos-Martínez, M. Bartolomei, F. Pirani and M. I. Hernández, Phys. Chem. Chem. Phys., 2022, 24, 15840–15850 RSC.
- Y. Bramastya Apriliyanto, N. Faginas-Lago, S. Evangelisti, M. Bartolomei, T. Leininger, F. Pirani, L. Pacifici and A. Lombardi, Molecules, 2022, 27, 5958 CrossRef PubMed.
- S. Falcinelli, P. Candori, F. Pirani and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2017, 19, 6933–6944 RSC.
- D. R. Herschbach, Adv. Chem. Phys., 1966, 10, 319–392 Search PubMed.
- R. Grice and D. R. Herschbach, Mol. Phys., 1974, 27, 159–175 CrossRef CAS.
- C. T. Rettner and R. N. Zare, J. Chem. Phys., 1982, 77, 2416–2429 CrossRef CAS.
- R. L. Jaffe, M. D. Pattengill, F. G. Mascarello and R. N. Zare, J. Chem. Phys., 1987, 86, 6150–6170 CrossRef CAS.
- P. Tosi, O. Dmitrijev, Y. Soldo, D. Bassi, D. Cappelletti, F. Pirani and V. Aquilanti, J. Chem. Phys., 1993, 99, 985–1003 CrossRef CAS.
- M. De Castro, R. Candori, F. Pirani, V. Aquilanti, M. Garay and A. G. Urena, J. Chem. Phys., 2000, 112, 770–780 CrossRef CAS.
- V. Aquilanti, S. Cavalli, F. Pirani, A. Volpi and D. Cappelletti, J. Phys. Chem. A, 2001, 105, 2401–2409 CrossRef CAS.
- R. Candori, S. Cavalli, F. Pirani, A. Volpi, D. Cappelletti, P. Tosi and D. Bassi, J. Chem. Phys., 2001, 115, 8888–8898 CrossRef CAS.
- L. Pei, E. Carrascosa, N. Yang, S. Falcinelli and J. M. Farrar, J. Phys. Chem. Lett., 2015, 6, 1684–1689 CrossRef CAS PubMed.
- M. Krauss, J. Chem. Phys., 1977, 67, 1712–1719 CrossRef CAS.
- P. C. Tellinghuisen, J. Tellinghuisen, J. A. Coxon, J. E. Velazco and D. W. Setzer, J. Chem. Phys., 1978, 68, 5187–5198 CrossRef CAS.
- P. Dehmer, Comments At. Mol. Phys., 1983, 13, 205–227 CAS.
- V. Aquilanti, D. Cappelletti and F. Pirani, Chem. Phys. Lett., 1997, 271, 216–222 CrossRef CAS.
- F. Pirani, A. Giulivi, D. Cappelletti and V. Aquilanti, Mol. Phys., 2000, 98, 1749–1762 CrossRef CAS.
- M. Alagia, B. G. Brunetti, P. Candori, S. Falcinelli, M. Moix Teixidor, F. Pirani, R. Richter, S. Stranges and F. Vecchiocattivi, J. Chem. Phys., 2006, 124, 204318 CrossRef CAS PubMed.
- V. Aquilanti, D. Cappelletti, V. Lorent, E. Luzzatti and F. Pirani, J. Phys. Chem., 1993, 97, 2063–2071 CrossRef CAS.
- D. Cappelletti, E. Ronca, L. Belpassi, F. Tarantelli and F. Pirani, Acc. Chem. Res., 2012, 45, 1571–1580 CrossRef CAS PubMed.
- F. Pirani, D. Cappelletti, S. Falcinelli, D. Cesario, F. Nunzi, L. Belpassi and F. Tarantelli, Angew. Chem., Int. Ed., 2019, 58, 4195–4199 CrossRef CAS PubMed.
- A. C. Legon, Phys. Chem. Chem. Phys., 2010, 12, 7736–7747 RSC.
- Z. M. Han, G. Czap, C. L. Chiang, C. Xu, P. J. Wagner, X. Y. Wei, Y. X. Zhang, R. Q. Wu and W. Ho, Science, 2017, 358, 206–210 CrossRef CAS PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- T. M. Sugden, Annu. Rev. Phys. Chem., 1962, 13(1), 369–390 CrossRef CAS.
- H. Nakamura, Jpn. J. Appl. Phys., 1969, 26, 1473–1479 CrossRef CAS.
- W. H. Miller, J. Chem. Phys., 1970, 52, 3563–3572 CrossRef CAS.
- W. H. Miller and H. Morgner, J. Chem. Phys., 1977, 67, 4923–4930 CrossRef CAS.
- V. Hoffmann and H. Morgner, J. Phys. B: At. Mol. Phys., 1979, 12, 2857–2874 CrossRef CAS.
- H. Morgner and A. Niehaus, J. Phys. B: At. Mol. Phys., 1979, 12, 1805–1820 CrossRef CAS.
- H. Conrad, G. Ertl, J. Küppers, W. Sesselmann and H. Haberland, Surf. Sci., 1980, 100, L461–L466 CrossRef CAS.
- R. W. Gregor and P. E. Siska, J. Chem. Phys., 1981, 74, 1078–1092 CrossRef CAS.
- H. Hotop, J. Electron Spectrosc. Relat. Phenom., 1981, 23, 347–365 CrossRef CAS.
- K. Ohno, H. Mutoh and Y. Harada, J. Am. Chem. Soc., 1983, 105, 4555–4561 CrossRef CAS.
- A. Niehaus, Ber. Bunsenges Phys. Chem., 1983, 77, 632–640 Search PubMed.
- A. Aguilar-Navarro, B. Brunetti, S. Rosi, F. Vecchiocattivi and G. G. Volpi, J. Chem. Phys., 1985, 82, 773–779 CrossRef CAS.
- A. Benz and H. Morgner, Mol. Phys., 1986, 57, 319–336 CrossRef CAS.
- P. E. Siska, Rev. Mod. Phys., 1993, 65, 337–412 CrossRef CAS.
- B. G. Brunetti and F. Vecchiocattivi, in Ion Clusters, ed C. Ng, T. Baer, I. Powis, Springer, New York, 1993, pp. 339–445 Search PubMed.
- K. Ohno, H. Yamakado, T. Ogawa and T. Yamata, J. Chem. Phys., 1996, 105, 7536–7542 CrossRef CAS.
- Y. Harada, S. Masuda and H. Ozaki, Chem. Rev., 1997, 97, 1897–1952 CrossRef CAS PubMed.
- B. A. Jacobs, W. A. Rice and P. E. Siska, J. Chem. Phys., 2003, 118, 3124–3130 CrossRef CAS.
- C. A. Arango, M. Shapiro and P. Brumer, Phys. Rev. Lett., 2006, 97, 193202 CrossRef PubMed.
- B. G. Brunetti, P. Candori, D. Cappelletti, S. Falcinelli, F. Pirani, D. Stranges and F. Vecchiocattivi, Chem. Phys. Lett., 2012, 539–540, 19–23 CrossRef CAS.
- B. G. Brunetti, P. Candori, S. Falcinelli, F. Pirani and F. Vecchiocattivi, J. Chem. Phys., 2013, 139, 164305 CrossRef PubMed.
- S. Falcinelli, A. Bartocci, P. Candori, F. Pirani and F. Vecchiocattivi, Chem. Phys. Lett., 2014, 614, 171–175 CrossRef CAS.
- J. Jankunas, B. Bertsche, K. Jachymski, M. Hapka and A. Osterwalder, J. Chem. Phys., 2014, 140, 244302 CrossRef PubMed.
- S. Falcinelli, A. Bartocci, S. Cavalli, F. Pirani and F. Vecchiocattivi, Chem. – Eur. J., 2016, 22, 764–771 CrossRef CAS PubMed.
- S. Falcinelli, M. Rosi, S. Cavalli, F. Pirani and F. Vecchiocattivi, Chem. – Eur. J., 2016, 22, 12518–12526 CrossRef CAS PubMed.
- J. Zou, S. D. S. Gordon, S. Tanteri and A. Osterwalder, J. Chem. Phys., 2018, 148, 164310 CrossRef PubMed.
- S. D. S. Gordon and A. Osterwalder, Phys. Chem. Chem. Phys., 2019, 21, 14306–14310 RSC.
- L. Ploenes, P. Straňák, H. Gao, J. Küpper and S. Willitsch, Mol. Phys., 2021, 119(17–18), e1965234 CrossRef.
- F. M. Penning, Naturwissenschaften, 1927, 15, 818 CrossRef CAS.
- S. Falcinelli, F. Pirani and F. Vecchiocattivi, Atmosphere, 2015, 6(3), 299–317 CrossRef.
- S. Falcinelli, F. Vecchiocattivi and F. Pirani, Phys. Rev. Lett., 2018, 121, 163403 CrossRef CAS PubMed.
- S. Falcinelli, F. Vecchiocattivi and F. Pirani, J. Chem. Phys., 2019, 150, 044305 CrossRef PubMed.
- S. Falcinelli, F. Pirani, P. Candori, B. G. Brunetti, J. M. Farrar and F. Vecchiocattivi, Front. Chem., 2019, 7, 445 CrossRef CAS PubMed.
- A. Bartocci, L. Belpassi, D. Cappelletti, S. Falcinelli, F. Grandinetti, F. Tarantelli and F. Pirani, J. Chem. Phys., 2015, 142(18), 184304 CrossRef PubMed.
- S. Falcinelli, F. Vecchiocattivi, S. Cavalli and F. Pirani, Eur. Phys. J. D, 2021, 75, 94 CrossRef CAS.
- E. E. Nikitin and R. N. Zare, Mol. Phys., 1994, 82, 85–100 CrossRef CAS.
- S. Falcinelli, F. Vecchiocattivi and F. Pirani, J. Phys. Chem. A, 2021, 125, 1461–1467 CrossRef CAS PubMed.
- S. Falcinelli, F. Vecchiocattivi and F. Pirani, Commun. Chem., 2020, 3, 64 CrossRef CAS PubMed.
- S. Falcinelli, F. Vecchiocattivi, J. M. Farrar and F. Pirani, J. Phys. Chem. A, 2021, 125, 3307–3315 CrossRef CAS PubMed.
- S. Falcinelli, F. Vecchiocattivi, J. M. Farrar, B. G. Brunetti, S. Cavalli and F. Pirani, Chem. Phys. Lett., 2021, 778, 138813 CrossRef CAS.
- D. M. Sonnenfroh and S. Leone, Int. J. Mass Spectrom. Ion Processes, 1987, 80(21), 63–82 CrossRef CAS.
- J. H. Noroski and P. E. Siska, Chem. Phys. Lett., 2009, 475, 208–214 CrossRef CAS.
- S. Falcinelli, F. Vecchiocattivi and F. Pirani, Sci. Rep., 2021, 11, 19105 CrossRef CAS PubMed.
- E. R. T. Kerstel, M. F. M. Janssens, K. A. H. van Leuwen and H. C. W. Beijerinck, Chem. Phys., 1988, 119, 325–341 CrossRef CAS.
- J. Baudon, P. Feron, C. Miniatura, F. Perales, J. Reinhardt, J. Robert, H. Haberland, B. Brunetti and F. Vecchiocattivi, J. Chem. Phys., 1991, 95, 1801–1807 CrossRef CAS.
- A. Aguilar, B. Brunetti, M. Gonzalez and F. Vecchiocattivi, Chem. Phys., 1990, 145, 211–218 CrossRef CAS.
- F. T. M. Van den Berg, F. T. M. Schonenberg and H. C. W. Beijerinck, Chem. Phys., 1987, 115, 359–379 CrossRef CAS.
- L. Appolloni, B. Brunetti, F. Vecchiocattivi and G. G. Volpi, J. Phys. Chem., 1988, 92, 918–921 CrossRef CAS.
- J. Zou, S. D. S. Gordon and A. Osterwalder, Phys. Rev. Lett., 2019, 123, 133401 CrossRef CAS PubMed.
- S. Falcinelli, F. Vecchiocattivi, B. G. Brunetti, M. Parriani, G. Gigliotti, S. Stranges and F. Pirani, RSC Adv., 2022, 12, 7587–7593 RSC.
- G. B. Chatzigeorgis, J. B. Haskins and J. B. Scoggins, Phys. Fluids, 2022, 34, 087106 CrossRef.
- V. Aquilanti, S. Cavalli, D. De Fazio, A. Volpi, A. Aguilar and J. M. Lucas, Chem. Phys., 2005, 308, 237–253 CrossRef CAS.
- D. De Fazio, V. Aquilanti and S. Cavalli, J. Chem. Phys., 2006, 125, 133109 CrossRef PubMed.
- D. De Fazio, J. M. Lucas, V. Aquilanti and S. Cavalli, Phys. Chem. Chem. Phys., 2011, 13, 8571–8582 RSC.
- D. De Fazio, V. Aquilanti and S. Cavalli, Front. Chem., 2019, 7, 328 CrossRef CAS PubMed.
- D. De Fazio, V. Aquilanti and S. Cavalli, J. Phys. Chem. A, 2020, 124, 12–20 CrossRef CAS PubMed.
- D. E. Atems and J. M. Wadehra, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 5201–5207 CrossRef CAS PubMed.
- N. Bacal, Nucl. Fusion, 2006, 46, S250–S259 CrossRef.
- R. N. Zare, Ber. Bunsenges. Phys. Chem., 1982, 86, 422–425 CrossRef CAS.
- R. N. Zare, Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics, Wiley-Interscience, New York, 1988, pp. 1–335 Search PubMed.
- S. Stolte, Ber. Bunsenges. Phys. Chem., 1982, 86, 413–421 CrossRef CAS.
- B. Friedrich and D. R. Herschbach, ZPhys-e.D: At., Mol. Clusters, 1991, 18, 153–161 CAS.
- R. N. Zare, Science, 1998, 279, 1875–1879 CrossRef CAS PubMed.
- F. Wang, J.-S. Lin and K. Liu, Science, 2011, 331, 900–903 CrossRef CAS PubMed.
- F. Filsinger, U. Erlekam, G. von Helden, J. Küpper and G. Meijer, Phys. Rev. Lett., 2008, 100, 133003 CrossRef PubMed.
- Y.-P. Chang, K. Długołęcki, J. Küpper, D. Rösch, D. Wild and S. Willitsch, Science, 2013, 342, 98–101 CrossRef CAS PubMed.
- D. Rösch, S. Willitsch, Y.-P. Chang and J. Küpper, J. Chem. Phys., 2014, 140, 124202 CrossRef PubMed.
- A. Kilaj, H. Gao, D. Rösch, U. Rivero, J. Küpper and S. Willitsch, Nat. Commun., 2018, 9, 2096 CrossRef PubMed.
- J. Wang, A. Kilaj, L. He, K. Długołęcki, S. Willitsch and J. Küpper, J. Phys. Chem. A, 2020, 124, 8341–8345 CrossRef CAS PubMed.
- A. Kilaj, J. Wang, P. Straňák, M. Schwilk, U. Rivero, L. Xu, O. A. von Lilienfeld, J. Küpper and S. Willitsch, Nat. Commun., 2021, 12, 6047 CrossRef CAS PubMed.
- A. W. Gisler and D. J. Nesbitt, Faraday Discuss., 2012, 157, 297–305 RSC.
- A. Li, Y. Li, H. Guo, K.-C. Lau, Y. Xu, B. Xiong, Y.-C. Chang and C. Y. Ng, J. Chem. Phys., 2014, 140, 011102 CrossRef PubMed.
- L. F. Roncaratti, D. Cappelletti and F. Pirani, J. Chem. Phys., 2014, 140, 124318 CrossRef PubMed.
- L. F. Roncaratti, D. Cappelletti, P. Candori and F. Pirani, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 012705 CrossRef.
- A. Cernuto, P. Tosi, L. M. Martini, F. Pirani and D. Ascenzi, Phys. Chem. Chem. Phys., 2017, 19, 19554–19565 RSC.
- A. Cernuto, F. Pirani, L. M. Martini, P. Tosi and D. Ascenzi, ChemPhysChem, 2018, 19, 51–59 CrossRef CAS PubMed.
- V. Richardson, E. Valença Ferreira de Aragão, X. He, F. Pirani, L. Mancini, N. Faginas-Lago, M. Rosi, L. M. Martini and D. Ascenzi, Phys. Chem. Chem. Phys., 2022, 24, 22437–22452 RSC.
- A. Tsikritea, J. A. Diprose, T. P. Softley and B. R. Heazlewood, J. Chem. Phys., 2022, 157, 060901 CrossRef CAS PubMed.
- R. B. Bernstein, D. R. Herschbach and R. D. Levine, J. Phys. Chem., 1987, 91(21), 5365–5377 CrossRef CAS.
- S. Falcinelli, F. Vecchiocattivi and F. Pirani, Commun. Chem., 2023, 6(1), 30 CrossRef CAS PubMed.
- S. Falcinelli, M. Parriani, F. Vecchiocattivi and F. Pirani, Eur. Phys. J. D, 2023, 77, 65 CrossRef CAS.
- G. Liuti and F. Pirani, Chem. Phys. Lett., 1985, 122, 245–250 CrossRef CAS.
- R. Cambi, D. Cappelletti, G. Liuti and F. Pirani, J. Chem. Phys., 1991, 95, 1852–1861 CrossRef CAS.
- D. V. Fedorov, M. Sadhunkhn, M. Stöhr and A. Tkatchenko, Phys. Rev. Lett., 2018, 121, 183401 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2023 |