Open Access Article
Open Access ArticleThe computational road to reactivity scales
Maike
Vahl
 and
Jonny
Proppe
and
Jonny
Proppe
 *
*
Institute of Physical and Theoretical Chemistry, Technische Universität Braunschweig, Gaußstraße 17, 38106 Braunschweig, Germany. E-mail: j.proppe@tu-braunschweig.de
First published on 6th January 2023
Abstract
Reactivity scales are useful research tools for chemists, both experimental and computational. However, to determine the reactivity of a single molecule, multiple measurements need to be carried out, which is a time-consuming and resource-intensive task. In this Tutorial Review, we present alternative approaches for the efficient generation of quantitative structure–reactivity relationships that are based on quantum chemistry, supervised learning, and uncertainty quantification. First published in 2002, we observe a tendency for these relationships to become not only more predictive but also more interpretable over time.
1 Reactivity scales in a nutshell
Reactivity is a kinetic concept and defined as a molecule's propensity to undergo a chemical reaction: “A species is said to be more reactive or to have a higher reactivity in some given context than some other (reference) species if it has a larger rate constant for a specified elementary reaction.”1 Reactivity scales, on the other hand, interrelate the reactivity of different molecules in a quantitative way.2 They are useful research tools in several aspects, three of which we would like to highlight:Insight. By integrating reactivity scales into the analysis of time-resolved experimental data, relative heights of reaction barriers can be estimated, which facilitates the elucidation of reaction mechanisms.
Efficiency. The search for optimal starting materials is usually a time-consuming and resource-intensive process. By combining reactivity scales with chemical intuition, one can speed up this process through targeted selection.
Reliability. Reactivity scales can also serve as experimental benchmarks when assessing the performance of computational models. Better computational models yield better predictions.
This Tutorial Review does not cover all kinds of reactivity scales. Instead, we focus on two of the most prevalent kinds of reactivity complementing each other: electrophilicity and nucleophilicity.
The genesis of reactivity scales dates back to Lewis's electron theory of valency and the general acid–base theory of Lowry and Brønsted (both mid-1920s) on the basis of which Ingold introduced the concepts of electrophiles and nucleophiles in the 1930s.3
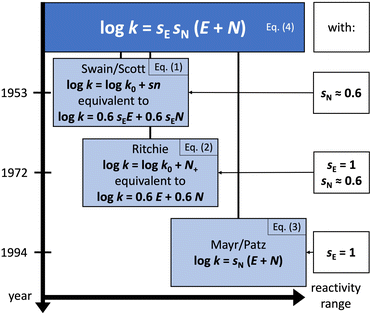
In 1953, Swain and Scott, who studied SN2 reactions at the time, presented the first systematic approach to constructing a nucleophilicity scale.4
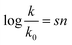 | (1) |
In 1972, Ritchie proposed a nucleophilicity scale for reactions with carbocations and diazonium ions.5
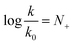 | (2) |
Contrary to the work by Swain and Scott, (i) the right-hand side of the equation is independent of the nature of the electrophile, and (ii) the reference rate constant k0 is electrophile-specific with water serving as the reference nucleophile. The latter feature allowed Ritchie to widen the range of accessible nucleophilicity values. The relationship shown in eqn (2) is also referred to as “constant-selectivity relationship”, because the difference N(1)+ − N(2)+ = log(k1/k2), reflecting the reactions of two nucleophiles with the same electrophile, is independent of the reactivity of that electrophile. (We recommend ref. 3 for a more detailed account of the early history of reactivity scales.)
These pioneering achievements ultimately led to the Mayr–Patz equation (MPE),3
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sN(E + N) k = sN(E + N) | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k0. Indeed, eqn (1)–(3) are special cases of the general equation of electrophile–nucleophile combinations,2
k0. Indeed, eqn (1)–(3) are special cases of the general equation of electrophile–nucleophile combinations,2log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sEsN(E + N) k = sEsN(E + N) | (4) |
The MPE [eqn (3)] was developed on the basis of a rich body of data on reactions involving benzhydrylium ions (Fig. 2) and π-nucleophiles (including alkenes, arenes, allylsilanes, etc.). Contrary to the work by Ritchie, Mayr and Patz relaxed the assumption of constant selectivity by introducing the sensitivity factor sN. Therefore, the order of selectivity of two nucleophiles reacting with a weak electrophile may be reversed when reacting with a strong electrophile (see Table 1 and Fig. 3).
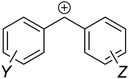 | ||
| Fig. 2 Lewis structure of a generic benzhydrylium ion. Substituents Y and Z are to be placed at meta and/or para positions to avoid mixing of electronic and steric effects. | ||
| N7 (sN = 1.00, N = 1.70) | N40 (sN = 1.46, N = 0.49) | |
|---|---|---|
| E15 (E = 0.00) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 1.70 k = 1.70 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 0.72 k = 0.72 |
| E20 (E = 3.59) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 5.29 k = 5.29 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 5.96 k = 5.96 |
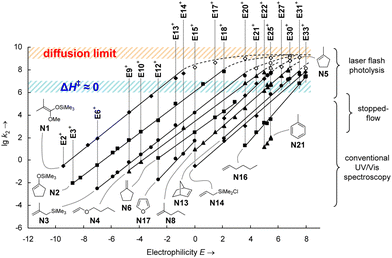 | ||
Fig. 3 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (here, lg k (here, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2) as a function of the electrophilicity parameter E as defined in eqn (3). Each line refers to a series of reactions of a single nucleophile with various electrophiles. The nucleophilicity parameter N can be determined from the intersection of a line with the abscissa (log k2) as a function of the electrophilicity parameter E as defined in eqn (3). Each line refers to a series of reactions of a single nucleophile with various electrophiles. The nucleophilicity parameter N can be determined from the intersection of a line with the abscissa (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 0 ⇒ E = − N). Nonparallel lines indicate nucleophiles with different values of the sensitivity factor sN. Reprinted with permission from J. Ammer, C. Nolte and H. Mayr, J. Am. Chem. Soc., 2012, 134, 13902–13911. Copyright 2012 American Chemical Society. k = 0 ⇒ E = − N). Nonparallel lines indicate nucleophiles with different values of the sensitivity factor sN. Reprinted with permission from J. Ammer, C. Nolte and H. Mayr, J. Am. Chem. Soc., 2012, 134, 13902–13911. Copyright 2012 American Chemical Society. | ||
Moreover, the scales of electrophilicity and nucleophilicity developed by Mayr and coworkers were no longer bound; by combining strong (weak) electrophiles with weak (strong) nucleophiles, it could be ensured that all reactions are observable (k > 10−5 M−1 s−1) without reaching the diffusion limit (k < 108 M−1 s−1). It is this leap in adaptability that has warranted the persistence of Mayr's reactivity scale approach for the past three decades.
Meanwhile, the applicability of the MPE has also been confirmed for other types of carbocations and for Michael acceptors, as well as for a diverse range of nucleophiles including amines, enamines, alcohols, enol ethers, ylides, phosphines, hydride donors, and organometallic compounds.7 Mayr's Database of Reactivity Parameters (https://www.cup.lmu.de/oc/mayr/reaktionsdatenbank2/) currently holds values of reactivity parameters for 352 electrophiles (E) and 1251 nucleophiles (sN, N).8,9
It is this broad application space that eventually caught the attention of computational chemists in 2002.10,11 Two directions have been followed since then: quantum chemical calculations of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (Section 2) and regression of reactivity parameters on chemical descriptors (Section 3). The overall workflow embedding both experimental and computational approaches to constructing reactivity scales is shown in Fig. 4. A recent development involves uncertainty quantification of both Mayr–Patz-type reactivity parameters (E, N, sN) and log
k (Section 2) and regression of reactivity parameters on chemical descriptors (Section 3). The overall workflow embedding both experimental and computational approaches to constructing reactivity scales is shown in Fig. 4. A recent development involves uncertainty quantification of both Mayr–Patz-type reactivity parameters (E, N, sN) and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k to increase the reliability of the reactivity scale approach (Section 4). In Section 5, we discuss limitations of the computational reactivity scale approach and conclude with a look ahead.
k to increase the reliability of the reactivity scale approach (Section 4). In Section 5, we discuss limitations of the computational reactivity scale approach and conclude with a look ahead.
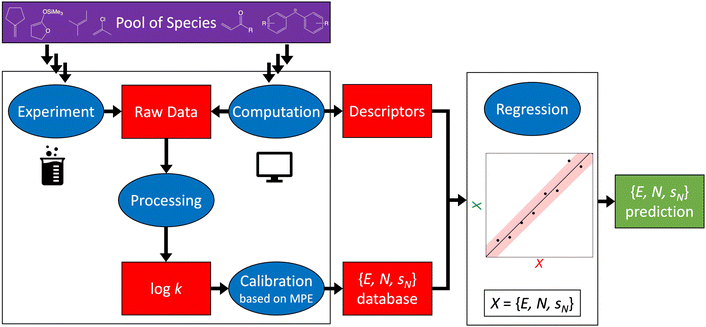 | ||
Fig. 4 Schematic workflow illustrating the possible approaches to constructing reactivity scales. A pool of species (electrophiles and nucleophiles) defines the starting point. Raw kinetic data on electrophile–nucleophile reactions can be obtained by means of both experiment (Box 1) and computation (Section 2), which is processed to yield a rate constant – here, in the form of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k – of the reaction under study. From the resulting set of log k – of the reaction under study. From the resulting set of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values, Mayr–Patz-type reactivity parameters, which are subsequently stored in Mayr's database,8,9 can be determined through calibration (Box 2). Once a sufficient number of reactivity parameters exists, more efficient access to new reactivity parameters is possible via regression of the more expensive database parameters on computationally generated chemical descriptors (Section 3). k values, Mayr–Patz-type reactivity parameters, which are subsequently stored in Mayr's database,8,9 can be determined through calibration (Box 2). Once a sufficient number of reactivity parameters exists, more efficient access to new reactivity parameters is possible via regression of the more expensive database parameters on computationally generated chemical descriptors (Section 3). | ||
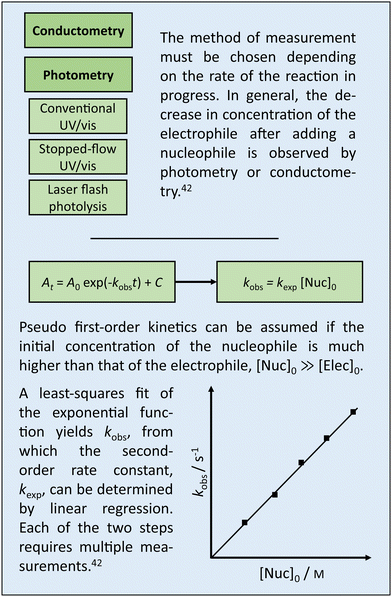
Box 1 Experimental determination of log k. |
Box 2 Reactivity parameters from log k. |
2 Computational prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) k
k
Box 1 summarizes established approaches to determining log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k in wet laboratories. This section, on the other hand, discusses approaches to determine log
k in wet laboratories. This section, on the other hand, discusses approaches to determine log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k by means of quantum chemical calculations. The motivation is twofold. Calculations have the potential to (i) accelerate research as they are more resource-efficient and simpler to automate than experiments, and (ii) deepen understanding as they can resolve details that are hidden in experimental data.
k by means of quantum chemical calculations. The motivation is twofold. Calculations have the potential to (i) accelerate research as they are more resource-efficient and simpler to automate than experiments, and (ii) deepen understanding as they can resolve details that are hidden in experimental data.
The Eyring equation [eqn (5)] is the common link between the molar activation free energy in solution – obtained by quantum chemical calculations –, 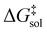 , and the rate constant, k.12
, and the rate constant, k.12
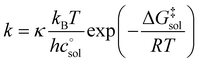 | (5) |
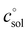 , and κ denote Boltzmann's constant, Planck's constant, the gas constant, absolute temperature, the standard state in solution (1 M), and a transmission coefficient, respectively. The transmission coefficient κ takes values between zero and one and is sometimes referred to as fudge factor because of its ad hoc nature. It is usually set to one, which implies the no-recrossing assumption. That is, once the transition state has been passed along the reaction coordinate, the product inevitably forms without passing through the transition state again.
, and κ denote Boltzmann's constant, Planck's constant, the gas constant, absolute temperature, the standard state in solution (1 M), and a transmission coefficient, respectively. The transmission coefficient κ takes values between zero and one and is sometimes referred to as fudge factor because of its ad hoc nature. It is usually set to one, which implies the no-recrossing assumption. That is, once the transition state has been passed along the reaction coordinate, the product inevitably forms without passing through the transition state again.
The molar activation free energy in solution, in turn, is a multilevel composite quantity.
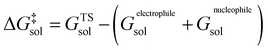 | (6) |
On the highest level, it is composed of the molar solution free energies of the reactants and the transition state (TS) connecting the isolated reactants with the adduct to be formed. Each of these components can be decomposed into three major terms.
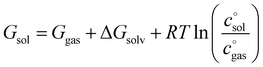 | (7) |
The first term, the molar free energy in the gas phase, Ggas, is obtained from a combination of electronic-structure calculations and equilibrium statistical mechanics. The second term, ΔGsolv, takes the change of free energy into account when embedding the molecule in gas phase into a solvent environment. It is usually obtained by a parametrised implicit solvation model.13 The third term, 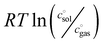 , is a crucial constant taking into account the change of the standard state when transitioning from gas phase to solution phase. The standard state of the solution is set to
, is a crucial constant taking into account the change of the standard state when transitioning from gas phase to solution phase. The standard state of the solution is set to 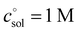 , whereas an ideal gas is assumed for the standard state of the gas phase at 293.15 K (20 °C) and 1 atm:
, whereas an ideal gas is assumed for the standard state of the gas phase at 293.15 K (20 °C) and 1 atm: 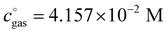 . Neglecting this correction term leads to an offset of almost 2 kcal mol−1 in barriers of bimolecular reactions.
. Neglecting this correction term leads to an offset of almost 2 kcal mol−1 in barriers of bimolecular reactions.
The internal energy U and the entropy S are the variables determining the free energy.
| Ggas = Ugas + RT − TSgas | (8) |
The dominant contribution to the internal energy is the electronic energy of the ground state, E(0)el, which is obtained from electronic-structure calculations.
| Ugas = [E(0)el + E(0)vib + Ethermvib + Ethermrot + Ethermtrans]gas | (9) |
Other factors determining the internal energy are the zero-point vibrational energy, E(0)vib, obtained from frequency calculations (requiring the Hessian of the electronic energy), and thermal contributions due to vibration, rotation, and translation obtained from equilibrium statistical mechanics.14 It is assumed here that the first electronic excitation energy is much greater than kBT, i.e., all excited states are assumed to be inaccessible at any temperature.
The entropy is also composed of electronic, vibrational, rotational, and translational contributions derived from equilibrium statistical mechanics.14
| Sgas = [Sel + Svib + Srot + Strans]gas | (10) |
Because the harmonic approximation to Svib leads to numerical instabilities when low-frequency vibrations are present, it has become established to employ a quasi-harmonic approximation15 instead where the low-lying modes are treated as rotational contributions.
The “jigsaw puzzle of quantum chemistry”
It is a challenging task to predict log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k from quantum chemical calculations.16,17 Many of the variables involved in the aforementioned equations cannot, in practical terms, be determined with arbitrary accuracy. Assumptions and approximations are necessary to render their calculation feasible. For instance, electronic and zero-point-vibrational energies require the choice of an electronic-structure method and a basis set; the free energy of solvation, ΔGsolv, is usually obtained from parametrised implicit solvation models; and vibrational and rotational motion are most often approximated by harmonic oscillators and rigid rotors, respectively.
k from quantum chemical calculations.16,17 Many of the variables involved in the aforementioned equations cannot, in practical terms, be determined with arbitrary accuracy. Assumptions and approximations are necessary to render their calculation feasible. For instance, electronic and zero-point-vibrational energies require the choice of an electronic-structure method and a basis set; the free energy of solvation, ΔGsolv, is usually obtained from parametrised implicit solvation models; and vibrational and rotational motion are most often approximated by harmonic oscillators and rigid rotors, respectively.
On the other hand, the equations relating these variables to each other are approximations, too. For instance, the Eyring equation follows from canonical transition state theory (TST), which is not an exact theory.18 A deviation of one order of magnitude in the rate constant can be expected from this simplification alone.19 Furthermore, it is assumed that translational, rotational, vibrational, and electronic motion are separable; basis sets, convergence thresholds, integration grids, truncation and rounding all introduce numerical noise; and the existence of conformational degrees of freedom is fully neglected in these equations.
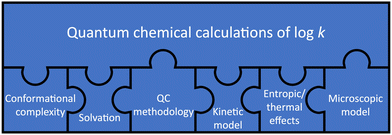
These limitations suggest that quantum chemical calculations of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k require careful consideration of several aspects, which we represent as puzzle pieces in Fig. 5, in the style of work on homogeneous catalysis by Harvey et al.16 These aspects are also highlighted in a recent review by Jorner et al., who discuss a related topic (organic reactivity in the context of machine learning).20 The jigsaw puzzle suggests that accurate quantum chemical calculations of log
k require careful consideration of several aspects, which we represent as puzzle pieces in Fig. 5, in the style of work on homogeneous catalysis by Harvey et al.16 These aspects are also highlighted in a recent review by Jorner et al., who discuss a related topic (organic reactivity in the context of machine learning).20 The jigsaw puzzle suggests that accurate quantum chemical calculations of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k are not possible if one piece of the puzzle is not considered correctly or at all.
k are not possible if one piece of the puzzle is not considered correctly or at all.
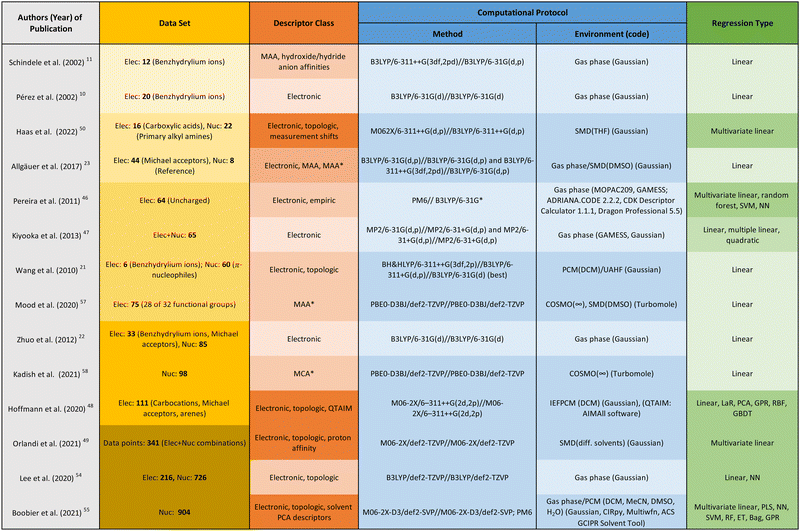
In the following, the different puzzle pieces are explained in the context of the computational studies highlighted in this section, an overview of which is provided in Table 2.21–27 For a more detailed account of general molecular reactions in solution, we refer to the best-practice guide for thermochemistry/kinetics calculations by Harvey and colleagues.16
| Publication | Data set | Remarks |
|---|---|---|
| Wang et al.21 | π-Nucleophiles | The first to have used calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values to determine N. Demonstration of the importance of steric interactions. k values to determine N. Demonstration of the importance of steric interactions. |
| Zhuo et al.22 | Benzhydrylium ions, Michael acceptors, diverse nucleophiles | Derivation of MPE via FMO theory and quantification of E and N via LUMO and HOMO energies. |
| Allgäuer et al.23 | Michael acceptors | Additional experimental prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. k. |
| Jangra et al.24 | Cycloadditions of aryldiazomethanes with Michael acceptors | Additional experimental prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. k. |
| Mayer et al.25 | Reaction of phenolate ions with benzhydrylium ions and quinone methides | Regioselectivity study of phenolate reactions, C vs. O attack, including the prediction of kinetic or thermodynamic reaction control. Additional experimental prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. k. |
| Li et al.26 | Heteroallenes | Additional experimental prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. k. |
| Zhang et al.27 | Reactions of iminium ions with diphenyldiazomethane and aryldiazomethanes | Additional experimental prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. k. |
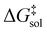 leads to a shift of 0.75 units in log
leads to a shift of 0.75 units in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. While no approximate XC functional offers universal chemical accuracy, contemporary approximations are capable to reach or even pass this limit for well-defined classes of chemical systems.29,30
k. While no approximate XC functional offers universal chemical accuracy, contemporary approximations are capable to reach or even pass this limit for well-defined classes of chemical systems.29,30
Among the selected XC functionals in the reviewed field are hybrid functionals21,22,24–27 and double-hybrid functionals.23 Dispersion corrections were considered occasionally.27 Stationary points of the potential energy surface (reactants, adducts, and transition states) were verified by frequency calculations in all studies. In the majority of cases, transition states were verified to be connected with reactants and adducts through IRC (intrinsic reaction coordinate) following.22–27
Despite the known difficulties XC functionals introduce, such as self-interaction and static-correlation errors,31 KS-DFT remains the method family of choice. While post-Hartree–Fock wave function methods, with CCSD(T) often being referred to as gold standard, offer several advantages over KS-DFT (e.g., systematic improvability, generally higher accuracy), their computational scaling is often much steeper, also because larger basis sets are required to obtain converged properties.32 To ensure high-quality results from KS-DFT calculations, best-practice guides have been published.33,34
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k is much weaker than the choice of the XC functional, though.
k is much weaker than the choice of the XC functional, though.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k.21,23–27 Since rate constants are exponential functions of reaction barriers, even small errors introduced by quantum chemical calculations can lead to rate constants that differ by orders of magnitude. As long as thermal relaxation is fast with respect to reaction time scales, and if quantum effects such as proton tunneling can be neglected, canonical TST and, hence, the Eyring equation are reasonable approximations. More sophisticated approaches based on microcanonical TST,18,38 the master equation,38 or quantum rate theories18 should be considered otherwise. The application of these approaches is often limited to the description of reactions of small molecules in the gas phase because of their extreme computational cost. There exist corrections to TST taking account of quantum effects such as tunneling, which in many, but not all, cases lead to results that agree reasonably well with quantum mechanical rate theories.16 These approaches, however, are not practical for the study of reactivity scales that are based on reactions of bulky electrophiles and nucleophiles in solution.
k.21,23–27 Since rate constants are exponential functions of reaction barriers, even small errors introduced by quantum chemical calculations can lead to rate constants that differ by orders of magnitude. As long as thermal relaxation is fast with respect to reaction time scales, and if quantum effects such as proton tunneling can be neglected, canonical TST and, hence, the Eyring equation are reasonable approximations. More sophisticated approaches based on microcanonical TST,18,38 the master equation,38 or quantum rate theories18 should be considered otherwise. The application of these approaches is often limited to the description of reactions of small molecules in the gas phase because of their extreme computational cost. There exist corrections to TST taking account of quantum effects such as tunneling, which in many, but not all, cases lead to results that agree reasonably well with quantum mechanical rate theories.16 These approaches, however, are not practical for the study of reactivity scales that are based on reactions of bulky electrophiles and nucleophiles in solution.
Zhuo et al. took an alternative route to calculating log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k.22 They computed Mayr–Patz-type reactivity parameters from frontier orbital energies to arrive at log
k.22 They computed Mayr–Patz-type reactivity parameters from frontier orbital energies to arrive at log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. For this approach to work, the parameters need to be calculated in a recursive fashion. That is, each parameter is a function of all previously determined parameters. As a consequence, the error introduced to the first parameter by the quantum chemical treatment propagates to all of the following parameters, rendering the method increasingly inaccurate. The authors claim that this method is equivalent to the approach followed by Mayr and co-workers, which is not true (cf. Box 2). In a recent study, frontier molecular orbitals have been revisited for the calculation of the nucleophilicity parameter of enamines.39
k. For this approach to work, the parameters need to be calculated in a recursive fashion. That is, each parameter is a function of all previously determined parameters. As a consequence, the error introduced to the first parameter by the quantum chemical treatment propagates to all of the following parameters, rendering the method increasingly inaccurate. The authors claim that this method is equivalent to the approach followed by Mayr and co-workers, which is not true (cf. Box 2). In a recent study, frontier molecular orbitals have been revisited for the calculation of the nucleophilicity parameter of enamines.39
3 Computational prediction of reactivity scales
Box 2 describes how the reactivity parameters E, N, and sN are determined on the basis of experimental (or, alternatively but yet hypothetically, computational) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k data.6,42,43 This section, on the other hand, discusses approaches to determine these parameters by means of regression analysis. The motivation to do so stems from the fact that determining reactivity parameters from log
k data.6,42,43 This section, on the other hand, discusses approaches to determine these parameters by means of regression analysis. The motivation to do so stems from the fact that determining reactivity parameters from log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k is expensive for two reasons. First, accurate measurements – both physical (Box 1) and virtual (Section 2) – are expensive per se, and second, multiple measurements are required to determine a single parameter. Using relatively inexpensive, computable descriptors that correlate well with these parameters, the aforementioned drawbacks can be mitigated. We define descriptors as representations (descriptions) of molecules, electrophiles or nucleophiles in the present work, the specific forms of which will be discussed later in this section.
k is expensive for two reasons. First, accurate measurements – both physical (Box 1) and virtual (Section 2) – are expensive per se, and second, multiple measurements are required to determine a single parameter. Using relatively inexpensive, computable descriptors that correlate well with these parameters, the aforementioned drawbacks can be mitigated. We define descriptors as representations (descriptions) of molecules, electrophiles or nucleophiles in the present work, the specific forms of which will be discussed later in this section.
The regression analyses reviewed in this section (see also Fig. 6) have in common that the descriptors function as independent variables (x), whereas the reactivity parameters of Mayr's database function as dependent variables (y). Regression of y on x yields a model that can be used to make efficient predictions (f(x) = ŷ) of otherwise expensive-to-obtain reactivity parameters for new molecules based on descriptors representing them.
The regression model can comprise a single variable (x) or multiple variables (x = (x1,x2,…,xM)), depending on the dimensionality of the applied descriptor, and its flexibility can range from low (linear) to high (arbitrarily nonlinear).44 While nonlinear and multivariate models require more training data (pairs of x and y), they have the potential to yield more accurate predictions. The downside of nonlinear models is that they are more difficult to interpret than linear models. In addition, multivariate models are more prone to overfitting training data compared to univariate models, which diminishes both predictive power and understanding.
A general/multivariate linear model is linear with respect to its coefficients c0,c1,c2,…,cM.
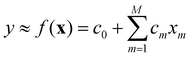 | (11) |
The variables can be arbitrarily nonlinear without affecting the linearity of the model. In a polynomial model, for instance, where xm = xm, all variables are constructed from a single variable x. The form of eqn (11) still qualifies the model as being linear. The coefficient c0 is known as bias. In the case of M = 1, a univariate linear model is obtained, where c0 and c1 are referred to as intercept and slope, respectively.
Nonlinear models of contemporary prominence are neural networks (NNs),44 support vector machines, (SVMs)44 and Gaussian processes (GPs).45 These model types are associated with the term machine learning.44 They are trained – like any regression model – in a supervised fashion. That is, in addition to the input values (x), the target values (y) are presented to the model. Regression is a subdomain of supervised learning. Among other nonlinear models, NNs, SVMs, and GPs have been examined in the descriptor-based regression analysis of reactivity parameters.46–50 A particular model class we would like to highlight is the class of kernel models to which GPs belong. The kernel model shown in eqn (12) resembles the general linear model shown in eqn (11).
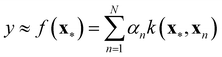 | (12) |
Although the kernel model appears to be linear, we note important differences. First, the sum runs over the index n, with N representing the number of training points, instead of the index m, with M representing the number of coefficients. Indeed, a data point of interest (x*) is compared to all training points (x1,x2,…,xN) via the kernel function k(x*,xn), which, for this very reason, is also referred to as similarity measure. The kernel itself carries its own coefficients, termed hyperparameters, which require optimisation on their own. Therefore, kernel models are effectively nonlinear. If the kernel is exponential (e.g. Gaussian), the regression function f(·) can assume any shape,45 which renders this type of model highly flexible and the bias term (“α0”) superfluous. GPs, in addition, provide the standard deviation of the predictions they make. This feature not only is interesting for assessing the reliability of particular predictions, it can also be exploited to systematise the selection of new training points for the sake of model improvement in a data-economic fashion (active learning51), as we did in previous work on dispersion corrections in collaboration with the Reiher group at ETH Zürich.52
Over the last 20 years, the correlation of many different descriptors to one of the three reactivity parameters has been studied extensively. The descriptors discussed here can be assigned to different classes. The first and most prominent class contains electronic descriptors mostly based on conceptual density functional theory (CDFT),53 which include (i) global molecular descriptors and (ii) atomic descriptors.10,21–23,46–50,54,55 They are defined by mathematical combinations of LUMO and HOMO energies within in the frontier molecular orbital (FMO) approximation. The atomic descriptors additionally account for local effects by using local functions such as the Fukui function and dual descriptor. Examples for (i) are the electrophilicity index ω and the electron affinity μ+FMO, as well as the local electrophilicity 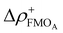 and the minimum composite Fukui function μ for (ii). Atomic descriptors based on the quantum theory of atoms in molecules (QTAIM)56 are also presented.48 The quantum chemical calculation of electronic descriptors is relatively expensive. However, these descriptors provide fundamental insight that can be applied to many other problems and thus offer great benefits.
and the minimum composite Fukui function μ for (ii). Atomic descriptors based on the quantum theory of atoms in molecules (QTAIM)56 are also presented.48 The quantum chemical calculation of electronic descriptors is relatively expensive. However, these descriptors provide fundamental insight that can be applied to many other problems and thus offer great benefits.
The second class of descriptors includes different affinities. Most prominent examples are methyl anion affinities (MAA) as well as methyl cation affinities (MCA) and proton, hydride and hydroxide affinities.11,23,57,58 These descriptors are obtained from quantum chemical calculations of reaction energies. They are more expensive than the electronic descriptors of the first class as reaction energies require the characterisation of both a reactant state (isolated species) and a product state (adduct). While affinities do not provide conceptual insight, they involve complete information of the electron density, explaining their strong correlation with reactivity parameters.
Topological descriptors define the third class and include, amongst others, spatial parameters such as buried volume, bond lengths, and more.48–50,54,55 The fourth class of descriptors contains empirical ones from cheminformatics such as the fractional negative surface area (FNSA) descriptor, as well as measurement shifts from NMR or IR spectroscopy and specific solvent descriptors.46,50,55
In addition to the choice of the descriptor class and the descriptor itself, the selection of training data is crucial for the creation of a representative model. The number of electrophiles and nucleophiles with known reactivity parameters, as well as their diversity, has a major impact on the generalisation and application capabilities of the model created. The more diverse the data set for training the model, the greater the applicability after successful training. In recent years, the data set size has been expanded to a number of reference structures greater than 750 to learn correlations between different descriptors and reactivity parameters, which enable highly accurate predictions of reactivity. Saini et al.59 report their best result using a NN for 752 structures, while Tavakoli et al.60 use methyl anion/cation affinities in solution (MAA* and MCA*, see below) as inputs for over 2421 structures to train a graph attention network. A graph neural network was trained by Nie et al.61 on nearly 900 nucleophiles from Mayr's database, in which electronic and, additionally, solvent descriptors were employed.
To provide an overview of the regression studies reviewed in this section, the following aspects are listed in the table of Fig. 6: the data set used for training and testing, the selected descriptors, the computational protocol applied for obtaining those descriptors, and the examined types of regression.
The publications are ordered by increasing complexity and diversity of the data set used, as indicated by the yellow colour gradient in the data set column, leading to more complex and diverse data sets in dark yellow. In the same way, the columns describing the descriptor class (orange) and regression type (green) are coloured. The column representing the computational protocol (blue) distinguishes between the method, environment, and code used. Light blue represents gas phase calculations, and dark blue represents calculations involving implicit solvation.
A discussion of the correlation results as well as their generalisability is beyond the scope of this work and can be found in the respective publications. Instead, we developed a colour scheme, which we propose as a rule of thumb for assessing the quality of a regression analysis, both in terms of correlation result and generalisability: the higher the number of darker colours in the different columns for a study, the higher the generalisation capabilities for the combination of descriptor and regression model.
In our opinion, the following advances of the past few years are particularly noteworthy. Mood et al. found that the correlation between the methyl anion affinity (MAA*) and the electrophilicity parameter E can be greatly improved or made possible in the first place by taking into account solvent effects for structurally diverse data sets.57 Kadish et al. found the same qualitative results for the methyl cation affinity (MCA*) and the nucleophilicity parameters N.58 Previously, correlation studies on individual structure classes concluded that solvent effects can be neglected as these were found to be approximately constant within a given class.10,11,21 However, as soon as structurally diverse data sets are applied, good correlation results can no longer be expected without taking solvent effects into account. Another highlight is the work by Hoffmann et al., who created a way to systematise the choice of descriptor and regression model through comprehensive study and comparison of many different examples in both categories.48 Last but not least, Orlandi et al. were able to use multivariate linear regression not only to significantly improve the prediction of the nucleophilicity parameter, but also to create an interpretable model. The main influence on the nucleophilicity N comes from the proton affinity of the nucleophile as well as the solvation energy of both the nucleophile and the adduct. Steric effects also have an effect on N, but to a minor extent.49 Boobier et al. came to a very similar conclusion in their study including 904 nucleophiles.55 A possible explanation for the weak steric influence could be a bias in the database, as the majority of its nucleophiles does not suffer from significant steric hindrance.
4 Uncertainty quantification
So far, we reviewed the various known computational approaches to determining reactivity parameters (E, N, sN) of polar species and the bimolecular rate constants of their reactions (in the form of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k). This section addresses the question what the uncertainty, or accuracy, of those predictions is. While the aforementioned studies provided measures of the average error/performance of their prediction models, these measures neglect that prediction errors are generally nonuniformly distributed.
k). This section addresses the question what the uncertainty, or accuracy, of those predictions is. While the aforementioned studies provided measures of the average error/performance of their prediction models, these measures neglect that prediction errors are generally nonuniformly distributed.
This nonuniformity of errors is taken into account, in a qualitative way, in Mayr's database8,9 by a star-rating system. Each species listed in the database is assigned up to five stars, depending on the number and status (either reference or non-reference, see Box 2) of reaction partners that were employed to determine the reactivity parameter(s) of that species. The more stars, the higher the expected accuracy of the corresponding parameter(s). Five stars are reserved for reference species. Therefore, the most accurate predictions of rate constants derived from eqn (3) can be expected for reactions of reference electrophiles with reference nucleophiles. As a consequence, computational models trained on reference species tend to yield better predictions than those trained on a more diverse set of species, which reflects Mayr's uncertainty principle of reactivity: prediction accuracy (of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) and chemical diversity cannot be maximised at the same time.
k) and chemical diversity cannot be maximised at the same time.
Inspired by the qualitative star-rating approach, we developed an uncertainty quantification (UQ) framework6 to estimate the uncertainty associated with the prediction of a specific parameter/rate constant. Case-specific uncertainties carry more information about the underlying problem than average measures of error/performance.
For instance, a desired nucleophile (in terms of reactivity) may be expensive or difficult to synthesise in contrast to a less suitable nucleophile that is readily available. In such a scenario, it would be preferable to know whether the predicted difference in reactivity is statistically significant in order to decide whether the extra work or money is worth the effort. By transforming the associated reactivity parameters into probability distributions by our UQ framework, the aforementioned significance can be quantified by calculating the normalised overlap integral (NOI) of their distributions. The possible values of the NOI range from zero (no overlap at all) to unity (identical distributions).
Another field of application is optimal design,62 which is concerned with the challenge of achieving a certain goal with a minimum number of experiments. Given the amount of resources that are required to determine a single log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k value, optimal design is certainly a task of interest. The probability distributions generated by our UQ framework can function as decision-making tool in this context. The larger the uncertainty of log
k value, optimal design is certainly a task of interest. The probability distributions generated by our UQ framework can function as decision-making tool in this context. The larger the uncertainty of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for a specific electrophile–nucleophile combination is, the more information is gained by measuring log
k for a specific electrophile–nucleophile combination is, the more information is gained by measuring log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for this combination. By visualising an uncertainty matrix spanned by the reference electrophiles and reference nucleophiles of Mayr's database, we could derive a rule for selecting new combinations of benzhydrylium ions and π-nucleophiles in a systematic fashion.6 Verification by experimental colleagues is pending.
k for this combination. By visualising an uncertainty matrix spanned by the reference electrophiles and reference nucleophiles of Mayr's database, we could derive a rule for selecting new combinations of benzhydrylium ions and π-nucleophiles in a systematic fashion.6 Verification by experimental colleagues is pending.
Besides synthesis planning and optimal design, case-specific uncertainties open up new possibilities for benchmark studies of computational models. Benchmarking is a crucial assessment tool for computational chemists.63 Its success depends on the availability of highly accurate reference data, whose generation is typically resource-intensive and time-consuming and, therefore, poses a critical bottleneck for exploring broader domains of chemical space. As our framework enables the quantification of uncertainty in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for electrophile–nucleophile combinations for which experimental log
k for electrophile–nucleophile combinations for which experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values do not yet exist, the resulting predictions can be employed as pseudo-benchmarks.
k values do not yet exist, the resulting predictions can be employed as pseudo-benchmarks.
While these novel possibilities may sound appealing, UQ only generates added value to synthesis planning, optimal design and benchmarking if high accuracy of the uncertainty estimates can be ensured. Therefore, it is important to estimate and assess uncertainty in concert. By reporting our uncertainty estimates as 95% confidence intervals, it is straightforward to determine their overall validity. We find that 99% (instead of 95%) of the actual prediction errors are located within their corresponding 95% confidence interval, suggesting a tendency to overestimate the prediction uncertainty. A more elaborate analysis by Pernot confirms this trend.64 It also reveals that the overestimation increases with decreasing magnitude of the uncertainty estimates. The finding by Pernot is an interesting starting point for further investigation as the relative magnitude of individual contributions to the overall uncertainty correlates with its absolute magnitude. That is, the smaller the magnitude of the overall uncertainty, the larger the relative magnitude of the model error (the other contribution being parameter uncertainty).
Taking into account the latest findings, we are currently working on a second version of our UQ framework, the first version of which is available as a Python package (MAYRUQ: https://gitlab.com/jproppe/mayruq) under an open-access license.65
5 Where will the road take us?
Scales of electrophilicity and nucleophilicity have been strongly rooted in physical organic chemistry for decades. They link the reactivity of molecules – in the form of empirical parameters – to the bimolecular rate constant of polar reactions. Here, we reviewed computational approaches to constructing reactivity scales, including (i) the quantum chemical calculation of such rate constants, (ii) the estimation of reactivity parameters by means of regression analysis, and (iii) the quantification of uncertainty for these quantities. In this last section, we discuss general aspects of the computational approach, including both limitations and ideas for future directions.As reactivity parameters are the key to predicting rate constants of polar reactions, their efficient estimation is of particular interest in cases where high-frequency data streams are processed in order to investigate chemical reactions. This scenario is not hypothetical. Reaction network exploration,66–68 which seeks to identify reaction mechanisms with microscopic detail, is an active field of research processing extensive amounts of data. Such an undertaking is only feasible in a recursive manner where each elementary reaction of a given search generation is assessed in terms of its kinetic and thermodynamic relevance.69 If labelled irrelevant, it will no longer be considered in future generations in order to save resources. The hundreds, thousands, or even more transition state optimisations required to evaluating kinetic importance (in the form of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) present a critical bottleneck of this procedure.
k) present a critical bottleneck of this procedure.
We envision a workflow in which those quantum chemical characterisations of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k are primarily replaced by Mayr–Patz estimates [eqn (3)] in combination with efficient regression-based predictions of reactivity parameters. The efficiency of these predictions is bound by the ease with which the chemical descriptors to be correlated with the reactivity parameters can be generated. At present, most of the descriptors applied in this context result from expensive quantum chemical calculations. However, in the past decade, a considerable number of inexpensive but information-rich chemical descriptors have been developed, which can be constructed from the positions and charges of a system's atomic nuclei alone.70
k are primarily replaced by Mayr–Patz estimates [eqn (3)] in combination with efficient regression-based predictions of reactivity parameters. The efficiency of these predictions is bound by the ease with which the chemical descriptors to be correlated with the reactivity parameters can be generated. At present, most of the descriptors applied in this context result from expensive quantum chemical calculations. However, in the past decade, a considerable number of inexpensive but information-rich chemical descriptors have been developed, which can be constructed from the positions and charges of a system's atomic nuclei alone.70
Besides efficiency, reliability is a key aspect when considering the replacement of quantum chemical calculations with regression-based predictions. As these predictions cannot be more accurate than the data they have been trained on (“garbage in, garbage out”, a popular saying among computer scientists), it is crucial to ensure high accuracy of the reactivity parameters listed in Mayr's database.8,9 It is known that the accuracy of these parameters is not uniformly distributed across the database. For instance, reactivity parameters of reference species yield more reliable predictions of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k than those of non-reference species (cf. Box 2). We identify two general strategies toward enhancing the overall accuracy of database/training parameters, which are partially interdependent. The first strategy is to extending the pool of reference species. This may appear like a simple task requiring nothing more than a repetition of the least-squares optimisation task presented in Box 2. However, a successful reparametrisation also depends on the number and distribution of available log
k than those of non-reference species (cf. Box 2). We identify two general strategies toward enhancing the overall accuracy of database/training parameters, which are partially interdependent. The first strategy is to extending the pool of reference species. This may appear like a simple task requiring nothing more than a repetition of the least-squares optimisation task presented in Box 2. However, a successful reparametrisation also depends on the number and distribution of available log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values. Therefore, the second strategy addresses the acquisition of new log
k values. Therefore, the second strategy addresses the acquisition of new log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k data. To avoid redundant experimental work, optimal-design approaches coupled with uncertainty quantification can guide the planning of new experiments.6
k data. To avoid redundant experimental work, optimal-design approaches coupled with uncertainty quantification can guide the planning of new experiments.6
In time-resolved (non-equilibrium) contexts, such as molecular dynamics simulations, different challenges arise since log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k is an intrinsically time-averaged quantity. In pioneering work on this topic, Hoffmann et al. examined the impact of structural fluctuations on the electrophilicity parameter of Michael acceptors.71 They provided evidence that the prediction of electrophilicity can be improved (with respect to the values listed in Mayr's database) and even made temperature-dependent, allowing for better comparability with actual experimental data.
k is an intrinsically time-averaged quantity. In pioneering work on this topic, Hoffmann et al. examined the impact of structural fluctuations on the electrophilicity parameter of Michael acceptors.71 They provided evidence that the prediction of electrophilicity can be improved (with respect to the values listed in Mayr's database) and even made temperature-dependent, allowing for better comparability with actual experimental data.
While the prediction of experimental observables is an undoubtedly desirable task, it does not deepen our understanding of organic reactivity per se. Recent studies by Hoffmann et al.,48 Van Vranken and co-workers,57,58 and Orlandi et al.,49 which present attempts to systematise the search for factors governing reactivity, mark a starting point in this direction. We conclude with a quote by Herbert Mayr, which we consider a signpost guiding theoretical chemists along the computational road to reactivity scales: “We still consider the long linearity of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus E correlations, which we find again and again, as a challenge to theory. It should be noted that this amazing linearity is completely independent of the validity or nonvalidity of [the Mayr–Patz equation]. […] I repeat my appeal to theoreticians. There is a lack in our understanding of organic reactivity.”7
k versus E correlations, which we find again and again, as a challenge to theory. It should be noted that this amazing linearity is completely independent of the validity or nonvalidity of [the Mayr–Patz equation]. […] I repeat my appeal to theoreticians. There is a lack in our understanding of organic reactivity.”7
Author contributions
Maike Vahl: conceptualisation, investigation, visualisation, writing – original draft, writing – review and editing. Jonny Proppe: conceptualisation, investigation, project administration, supervision, writing – original draft, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding by Germany's joint federal and state program supporting early-career researchers (WISNA) established by the Federal Ministry of Education and Research (BMBF).Notes and references
- P. Muller, Pure Appl. Chem., 1994, 66, 1077–1184 CrossRef.
- H. Mayr, Tetrahedron, 2015, 71, 5095–5111 CrossRef CAS.
- H. Mayr and M. Patz, Angew. Chem., Int. Ed. Engl., 1994, 33, 938–957 CrossRef.
- C. G. Swain and C. B. Scott, J. Am. Chem. Soc., 1953, 75, 141–147 CrossRef CAS.
- C. D. Ritchie, Acc. Chem. Res., 1972, 5, 348–354 CrossRef CAS.
- J. Proppe and J. Kircher, ChemPhysChem, 2022, 23, e202200061 CAS.
- H. Mayr, Angew. Chem., Int. Ed., 2011, 50, 3612–3618 CrossRef CAS.
- H. Mayr and A. R. Ofial, SAR QSAR Environ. Res., 2015, 26, 619–646 CrossRef CAS PubMed.
- H. Mayr and A. R. Ofial, Mayr's Database of Reactivity Parameters, https://www.cup.lmu.de/oc/mayr/reaktionsdatenbank2/, last accessed on 24 August 2022.
- P. Pérez, A. Toro-Labbé, A. Aizman and R. Contreras, J. Org. Chem., 2002, 67, 4747–4752 CrossRef PubMed.
- C. Schindele, K. N. Houk and H. Mayr, J. Am. Chem. Soc., 2002, 124, 11208–11214 CrossRef CAS PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- J. W. Ochterski, Thermochemistry in Gaussian, Gaussian, Inc, 2000 Search PubMed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- J. N. Harvey, F. Himo, F. Maseras and L. Perrin, ACS Catal., 2019, 9, 6803–6813 CrossRef CAS.
- J. Proppe, T. Husch, G. N. Simm and M. Reiher, Faraday Discuss., 2016, 195, 497–520 RSC.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- A. S. Petit and J. N. Harvey, Phys. Chem. Chem. Phys., 2011, 14, 184–191 RSC.
- K. Jorner, A. Tomberg, C. Bauer, C. Sköld and P.-O. Norrby, Nat. Rev. Chem., 2021, 5, 240–255 CrossRef CAS.
- C. Wang, Y. Fu, Q.-X. Guo and L. Liu, Chem. – Eur. J., 2010, 16, 2586–2598 CrossRef CAS PubMed.
- L.-G. Zhuo, W. Liao and Z.-X. Yu, Asian J. Org. Chem., 2012, 1, 336–345 CrossRef CAS.
- D. S. Allgäuer, H. Jangra, H. Asahara, Z. Li, Q. Chen, H. Zipse, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2017, 139, 13318–13329 CrossRef PubMed.
- H. Jangra, Q. Chen, E. Fuks, I. Zenz, P. Mayer, A. R. Ofial, H. Zipse and H. Mayr, J. Am. Chem. Soc., 2018, 140, 16758–16772 CrossRef CAS PubMed.
- R. J. Mayer, M. Breugst, N. Hampel, A. R. Ofial and H. Mayr, J. Org. Chem., 2019, 84, 8837–8858 CrossRef CAS PubMed.
- Z. Li, R. J. Mayer, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2020, 142, 8383–8402 CrossRef CAS PubMed.
- J. Zhang, Q. Chen, R. J. Mayer, J.-D. Yang, A. R. Ofial, J.-P. Cheng and H. Mayr, Angew. Chem., Int. Ed., 2020, 59, 12527–12533 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6648–6653 CrossRef CAS PubMed.
- P. Morgante and R. Peverati, Int. J. Quantum Chem., 2020, 120, e26332 CrossRef CAS.
- M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed; Angew. Chem., 2022, 134, e202205735 Search PubMed.
- E. Dzib and G. Merino, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1583 CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 609–620 CrossRef CAS PubMed.
- G. N. Simm, P. L. Türtscher and M. Reiher, J. Comput. Chem., 2020, 41, 1144–1155 CrossRef CAS PubMed.
- D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed.
- Y. Li, L. Zhang and S. Luo, ACS Omega, 2022, 7, 6354–6374 CrossRef CAS PubMed.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren, J. L. Knight, J. W. Kaus, D. S. Cerutti, G. Krilov, W. L. Jorgensen, R. Abel and R. A. Friesner, J. Chem. Theory Comput., 2016, 12, 281–296 CrossRef CAS PubMed.
- H. Mayr, T. Bug, M. F. Gotta, N. Hering, B. Irrgang, B. Janker, B. Kempf, R. Loos, A. R. Ofial, G. Remennikov and H. Schimmel, J. Am. Chem. Soc., 2001, 123, 9500–9512 CrossRef CAS PubMed.
- J. Ammer, C. Nolte and H. Mayr, J. Am. Chem. Soc., 2012, 134, 13902–13911 CrossRef CAS PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning, Springer, New York, 2006 Search PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, Cambridge (MA), United States, 2006 Search PubMed.
- F. Pereira, D. A. R. S. Latino and J. Aires-de-Sousa, J. Org. Chem., 2011, 76, 9312–9319 CrossRef CAS PubMed.
- S.-i Kiyooka, D. Kaneno and R. Fujiyama, Tetrahedron, 2013, 69, 4247–4258 CrossRef CAS.
- G. Hoffmann, M. Balcilar, V. Tognetti, P. Héroux, B. Gaüzère, S. Adam and L. Joubert, J. Comput. Chem., 2020, 41, 2124–2136 CrossRef CAS.
- M. Orlandi, M. Escudero-Casao and G. Licini, J. Org. Chem., 2021, 86, 3555–3564 CrossRef CAS PubMed.
- B. C. Haas, A. E. Goetz, A. Bahamonde, J. C. McWilliams and M. S. Sigman, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2118451119 CrossRef CAS PubMed.
- B. Settles, Active Learning, Morgan & Claypool, San Rafael (CA), United States, 2012, vol. 18 Search PubMed.
- J. Proppe, S. Gugler and M. Reiher, J. Chem. Theory Comput., 2019, 15, 6046–6060 CrossRef CAS PubMed.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
- B. Lee, J. Yoo and K. Kang, Chem. Sci., 2020, 11, 7813–7822 RSC.
- S. Boobier, Y. Liu, K. Sharma, D. R. J. Hose, A. J. Blacker, N. Kapur and B. N. Nguyen, J. Chem. Inf. Model., 2021, 61, 4890–4899 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- A. Mood, M. Tavakoli, E. Gutman, D. Kadish, P. Baldi and D. L. Van Vranken, J. Org. Chem., 2020, 85, 4096–4102 CrossRef CAS PubMed.
- D. Kadish, A. D. Mood, M. Tavakoli, E. S. Gutman, P. Baldi and D. L. Van Vranken, J. Org. Chem., 2021, 86, 3721–3729 CrossRef CAS PubMed.
- V. Saini, A. Sharma and D. Nivatia, Phys. Chem. Chem. Phys., 2022, 24, 1821–1829 RSC.
- M. Tavakoli, A. Mood, D. Van Vranken and P. Baldi, J. Chem. Inf. Model., 2022, 62, 2121–2132 CrossRef CAS PubMed.
- W. Nie, D. Liu, S. Li, H. Yu and Y. Fu, J. Chem. Inf. Model., 2022, 62, 4319–4328 CrossRef CAS PubMed.
- F. Pukelsheim, Optimal Design of Experiments, Society for Industrial & Applied Mathematics, Philadelphia, PA, 2006 Search PubMed.
- R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018 CrossRef CAS PubMed.
- P. Pernot, J. Chem. Phys., 2022, 156, 114109 CrossRef CAS PubMed.
- J. Proppe, Uncertainty Quantification of Reactivity Scales, https://gitlab.com/jproppe/mayruq, last accessed on 24 August 2022.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- J. P. Unsleber and M. Reiher, Annu. Rev. Phys. Chem., 2020, 71, 121–142 CrossRef CAS PubMed.
- M. Steiner and M. Reiher, Top. Catal., 2022, 65, 6–39 CrossRef CAS PubMed.
- J. Proppe and M. Reiher, J. Chem. Theory Comput., 2019, 15, 357–370 CrossRef CAS PubMed.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815 CrossRef CAS PubMed.
- G. Hoffmann, V. Tognetti and L. Joubert, Chem. Phys. Lett., 2019, 724, 24–28 CrossRef CAS.
Footnote |
† The left-hand sides of eqn (3) and (4) refer to the logarithm of a quantity that is not dimensionless (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k). As long as it is ensured that the reactivity parameters strictly correspond to a specific set of units (here, [k] = M−1 s−1), this expression is unambiguous. k). As long as it is ensured that the reactivity parameters strictly correspond to a specific set of units (here, [k] = M−1 s−1), this expression is unambiguous. |
| This journal is © the Owner Societies 2023 |