Triplet-to-singlet exciton transfer in hyperfluorescent OLED materials

Abstract

Hyperfluorescent organic light-emitting diodes combine two kinds of dopants to maximize device efficiency: one molecule exhibiting thermally activated delayed fluorescence (TADF) and another molecule with a high fluorescence rate and narrow emission spectrum. The postulated role of a TADF sensitizer is to enable up-conversion of triplet to singlet excitons through the reverse intersystem crossing mechanism, which is followed by a Förster energy transfer to the fluorescent emitter. However, a second mechanism based on the direct triplet-to-singlet exciton transfer between TADF molecules is a priori possible, but its role in hyperfluorescence has not been investigated. Here we employ first-principles electronic-structure and kinetic Monte Carlo simulations to study the hyperfluorescence mechanism in four pairs of TADF/fluorescent emitters. We demonstrate how the triplet-to-singlet energy transfer mechanism is, in some cases, the main driver for the quantum efficiency boost observed in hyperfluorescent devices.

---

1 Introduction

Recent advances in organic light-emitting diodes (OLEDs) have relied on the phenomenon of thermally activated delayed fluorescence (TADF).^1,2 It is due to the necessity to overcome the efficiency limitation that results from the fact that only 25% of electrically generated excitons are singlets, the remaining 75% being composed of generally non-emissive triplet excitons.³ In this sense, molecules that present TADF can harvest some of the triplet excitons through reverse intersystem crossing (rISC).⁴ In this process, the triplet exciton is converted into a singlet one with the assistance of thermal energy, which allows it to overcome the singlet–triplet energy gap. Such up-converted triplet excitons are then able to decay radiatively, producing delayed fluorescence.⁵

Attempts at the optimization of the rISC process have resulted in molecular designs that take advantage of S₁ states with charge-transfer character to reduce the exchange interaction and consequently the singlet–triplet gap.⁶ This approach, however, comes with a cost: charge transfer states typically display low oscillator strengths, which translates into low fluorescence rates.⁷ This shortcoming makes excitons more prone to decay via nonradiative pathways, reducing the luminescence quantum yield of devices.

Such apparent incompatibility between efficient TADF and efficient fluorescence has prompted the development of the so-called hyperfluorescent devices.^8–12 In this approach, both TADF molecules and fluorescent emitters are employed as dopants in a host matrix. The working principle is that after triplet excitons undergo rISC in the TADF molecules, the newly generated singlets may diffuse and transfer to a fluorescent emitter by means of Förster resonance energy transfer (FRET). However, this transfer is conditioned on the existence of an overlap between the TADF molecule's fluorescence spectrum and the emitter's absorption spectrum,¹³ which puts some constraints on the selection of appropriate TADF/emitter pairs. When the pairing is successful, it is possible to take advantage of both the triplet harvesting mechanism of TADF molecules and the better luminescence properties of emitters, resulting in more efficient devices. In this sense, some design rules for the TADF dopants used in hyperfluorescence have been proposed,^14,15 and some theoretical works have aimed at providing insight on the mechanism and how it could be optimized.^16–18

In spite of recent advances, there is an often-overlooked phenomenon whose role in hyperfluorescence has not been subject to investigation, namely the mechanism of direct triplet-to-singlet (TTS) exciton transfer. In this process, a triplet exciton is able to undergo FRET, hopping to a nearby molecule and converting into a singlet exciton in the process.^19,20 OLEDs that take advantage of this mechanism by using organometallic sensitizers with strong room-temperature phosphorescence have already been demonstrated.²¹ More recently, TTS transfers have also been engineered to develop systems that present long-persistent luminescence.^22,23 In a further example, a donor–acceptor system that displayed both singlet and triplet FRET has also been demonstrated, showing that cooperation between these two exciton transfer channels can be possible.²⁴

Fundamentally, triplet-to-singlet FRET is only possible if the triplet state in question is not pure, that is, if it mixes with singlet states²⁵ through spin–orbit coupling. This is so because in the case of TTS, the aforementioned spectral overlap requirement of the FRET mechanism has to be satisfied by the donor's phosphorescence and the acceptor's absorption spectra and phosphorescence is a forbidden process for triplet pure states. Appreciable coupling is also a necessary condition for both efficient rISC and phosphorescence. Thus, it stands to reason that this particular process could play a relevant role in the behavior of TADF molecules as well and is worthy of investigation. More generally, the estimation of the individual contributions from different exciton transfer mechanisms to overall device performance is fundamental and has been the subject of experimental investigation.^26,27

In this work, we analyze four systems composed of TADF and fluorescent emitter dopants dispersed in host matrices (Fig. 1) that were used by Adachi and collaborators.⁸ It is done by combining a set of theoretical tools that we have previously developed for optical spectra simulations, estimation of exciton diffusion lengths, and calculations of TADF rates.^28,29 This multiscale modeling approach enables us to estimate the rates for the key processes occurring in hyperfluorescent OLED materials, i.e., FRET, ISC, rISC, fluorescence, and phosphorescence. Importantly, FRET rates are calculated not only for transfers from TADF molecules to fluorescent emitters but also for those in the opposite direction and those that take place among homodimers. Including these processes is necessary to account for the effects of exciton diffusion. The interplay between these different phenomena is investigated using kinetic Monte Carlo (KMC) simulations, which have been extensively used for modeling exciton dynamics.^30–34 Results from experimental optical characterization are used to tune the non-radiative decay rates, after which simulations under OLED operational conditions are conducted. These simulations allow us to quantify the contribution of each triplet conversion mechanism to the overall performance. We show that TTS exciton transfers may account for a significant portion of the harvested triplets, but the actual number varies significantly for different TADF/emitter pairs. This realization adds a new dimension to the problem of optimizing performance in hyperfluorescent devices.

Fig. 1 Systems analyzed in this work: (a) 10-phenyl-10H,10′H-spiro[acridine-9,9′-anthracen]-10′-one (ACRSA)³⁵ paired with 2,5,8,11-tetra-tert-butylperylene (TBPe) in a bis-(2-(diphenylphosphino)phenyl)ether oxide (DPEPO) matrix (b) 3-(9,9-dimethylacridin-10 (9H)-yl)-9H-xanthen-9-one (ACRXTN)⁸ paired with 9,10-bis[N,N-di-(p-tolyl)-amino]anthracene (TTPA) in a 1,3-bis(N-carbazolyl)benzene (mCP) matrix (c) 2-phenoxazine-4,6-diphenyl-1,3,5-triazine (PXZ-TRX)³⁶ paired with 2,8-ditert-butyl-5,11-bis(4-tert-butylphenyl)-6,12-diphenyltetracene (TBRb) in a 3,3-di(9H-carbazol-9-yl)biphenyl (mCBP) matrix (d) 2,4,6-tri(4-(10Hphenoxazin-10H-yl)phenyl)-1,3,5-triazine (Tri-PXZ-TRZ)³⁷ paired with tetraphenyldibenzoperiflanthene (DBP) in a 4,4′-bis(9-carbazolyl)-1,1′-biphenyl (CBP) matrix.

2 Methods

2.1 Electronic structure calculations

The electronic structure properties of all molecules were calculated using density functional theory (DFT). The long-range corrected functional ωB97X-D was used throughout along with the 6-31G(d,p) basis set. For each molecule, the range separation parameter of the functional was non-empirically tuned following the procedure outlined in ref. 38 and results are shown in Table S1 of the ESI† file. Once the functionals were tuned, geometry optimizations and normal mode analyses were performed for all the TADF molecules in the S₁ and T₁ states and for all the fluorescent emitters in the S₀ and S₁ states.

Absorption, fluorescence, and phosphorescence spectrum simulations were performed according to the nuclear ensemble method,^28,39 which is outlined in the ESI† file. One of the shortcomings of the nuclear ensemble approach to spectrum simulations is that it lacks vibrational resolution, with only the envelope of the band being more reliably described. This is due to the fact that each of the ensemble's geometries contributes equally to the overall spectrum with a Gaussian curve of same standard deviation, given by the thermal energy at 300 K. Incidentally, it has been observed⁴⁰ that some vibrational structure is able to be reproduced when the number of samples is reduced, but this, in turn, increases the uncertainty in the values of the absorption cross-section and of the differential emission rate. From the point of view of rate calculations, however, reducing the uncertainty of the physical quantities is more important since the rates are derived from Förster radii estimations that depend on the calculation of spectral overlaps and emission lifetimes.

All excited-state calculations were performed using the Tamm–Dancoff (TDA) approximation,⁴¹ as it is known to mitigate issues of triplet instability⁴² as well as being appropriate for spectrum simulations.⁴³ The polarizable continuum model⁴⁴ was used in all calculations except for the tuning procedure due to its tendency to result in underestimated excitation energies.⁴⁵ A dielectric constant ε = 3 and a refractive index of 1.8 were assumed.¹⁷

Spectrum simulations were used to estimate Förster radii, exciton transfer rates, and emission rates following ref. 29. Intersystem crossing rates were similarly obtained using the NEMO software⁴⁶ with the methodology described in ref. 28 and outlined in the ESI† file. This approach constitutes an extension of the nuclear ensemble method that aims at determining intersystem crossing rates while accounting for vibrational effects, as these have been shown to be important.^4,47 Electronic structure calculations were performed with the QChem 5.2 software.⁴⁸

2.2 Kinetic Monte Carlo simulations

Kinetic Monte Carlo simulations were performed on a 50 × 50 × 50 cubic lattice with the Xcharge software.⁴⁹ Each site was randomly assigned either as a TADF molecule or a fluorescent emitter. The relative amount of each material follows the experimental concentrations used in ref. 8 and are presented in the ESI.† Similarly, inter-site distances are set by employing a model (also detailed in the ESI†) that considers the proportion of host, guest and dopant molecules used in each experimental setup along with their molecular weights. Molecules in the simulation are considered to be randomly oriented to reflect the amorphous nature of the systems under study. This also justifies the use of an orientation factor of 2/3 in the calculation of Förster rates. Finally, each site is also assigned fluorescence and phosphorescence energy values sampled from the corresponding simulated spectra.

Singlet and triplet excitons are generated randomly in the lattice and allowed to move through Förster transfers, decay radiatively (fluorescence or phosphorescence) or nonradiatively, and undergo intersystem crossing according to their calculated rates. The selection of the actual process that takes place at each time step is made by a weighted random selection algorithm that is repeated until the exciton recombines. Each simulation is run with a total of 100 000 excitons.

3 Results

The starting point of the analysis concerns the evaluation of spectral overlaps between the emission spectra (fluorescence and phosphorescence) of the TADF molecules and the absorption spectra of the fluorescent emitters they are paired with. To this end, we have calculated absorption and fluorescence spectra for all molecules analyzed here. In addition, we have also computed phosphorescence spectra for the TADF molecules. A comparison between calculated and experimental peak energies is presented in the ESI† (Table S5, ESI†) and demonstrates an overall good agreement, in particular for the fluorescence energies of the organic emitters. For TADF molecules, we observe that calculations tend to overestimate the fluorescence energy. It is justified by the fact that these correspond typically to emission from S₁ states with a strong charge-transfer character that undergo a further stabilization under solvation that the PCM calculations fail to account for completely.

Fig. 2 shows the simulated emission spectra of TADF molecules along with the absorption spectra of fluorescent emitters. It can be seen that in all cases, there is a significant overlap between both the fluorescence and phosphorescence spectra of the TADF molecules and the absorption spectra of the emitters. It indicates that both Förster transfers of singlet exciton and TTS transfers can take place from the TADF molecule to the emitter in all pairs. It is also worth investigating whether the opposite transfer (from the emitter to the TADF dopant) is allowed. This is a potential loss mechanism, as excitons transferred to the emitters could transfer back to the TADF dopant, whose lower fluorescence rate would make it more likely for nonradiative decay to take place. Fig. S1 (ESI†) shows that also in all cases there is overlap between the fluorescence spectra of the emitters and the absorption spectra of the TADF molecules. These overlaps are, however, clearly less intense than those shown in Fig. 2, which suggests that backward transfers should be less efficient.

Fig. 2 Comparison between simulated absorption spectra of the fluorescent emitters with the simulated fluorescence and phosphorescence spectra of the TADF molecules that compose each TADF/emitter pair.

The observation of the spectra allows us to infer the kinds of Förster transfers that could take place for each pair, but the expected efficiency of each of these transfers requires the calculation of the corresponding Förster radii. The Förster radius is the intermolecular distance at which the probability of exciton transfer equals that of radiative decay. As such, it corresponds to a measure of the relative efficiency of exciton transfers with respect to the radiative decay process associated with it (fluorescence for usual Förster transfers and phosphorescence for TTS transfers).

The Förster radii can be estimated from the simulated spectra and are shown in Table 1 for transfers between TADF molecules and their paired fluorescent emitters. Radii for three kinds of transfer are shown: singlet exciton transfers from TADF to emitter molecules (S^T₁ → S^E₁); TTS transfers from TADF to emitter molecules (T^T₁ → S^E₁), and backward singlet transfers from emitters to TADF molecules (S^E₁ → S^T₁). Förster radii for both singlet and TTS transfers from TADF molecules to fluorescent emitters are similar for all pairs. Still, backward transfers display radii roughly half as large as those for transfers in the opposite direction, as expected from the lower spectral overlaps. Importantly, all Förster radii shown in Table 1 exceed the estimated average distances between adjacent molecules of either TADF or emitter kind, which range from 10 to 20 Å (see Table S4, ESI†). It means that exciton transfer probabilities exceed those of radiative emission in all cases. It is also true for the Förster radii for transfers between emitters, as shown in Table S6 (ESI†).

Table 1 Estimated Förster radii for singlet (S₁) and triplet (T₁) exciton transfers between TADF molecules (superscript T) and the fluorescent emitters (superscript E) they are paired with

TADF/emitter	Förster radius (Å)
	S^T1 → S^E1	T^T1 → S^E1	S^E1 → S^T1
ACRSA/TBPe	55.5	47.5	21.2
ACRXTN/TTPA	34.0	36.6	24.2
PXZ-TRZ/TBRb	54.4	58.4	21.4
Tri-PXZ-TRZ/DBP	77.3	73.8	39.2

---

The fact that the TTS transfers display significant efficiency suggests that this phenomenon could also play a role in hyperfluorescence as a second mechanism for triplet harvesting besides rISC. However, because of the rather large intermolecular distances found in OLEDs, triplet exciton diffusion mediated by Dexter transfer is inefficient.⁵⁰ As such, TTS transfers from TADF to emitter molecules could only take place if triplet excitons were generated in TADF molecules adjacent to a fluorescent emitter, which is expected to occur rarely given the low concentration of the fluorescent emitter dopants (Table S4, ESI†). On the other hand, exciton transfers between TADF molecules are expected to take place (see Fig. S2, ESI†). Table 2 shows the calculated Förster radii for singlet and triplet transfers between TADF molecules. Comparison between these values and average intermolecular distances indicate that both transfer mechanisms are more likely than radiative emission, and since TADF molecules are present in much larger concentrations than the emitter dopants, the above-mentioned objection against assigning TTS transfers as a viable method for triplet recycling no longer holds. It is conceivable then that triplet excitons generated in TADF dopants could perform TTS transfers to nearby TADF molecules, after which singlet diffusion ensues until Förster transfers to fluorescent emitters can take place. This process could constitute an effective mechanism for triplet harvesting that bypasses the diminished triplet mobility and may inflate estimates of rISC rates if unaccounted for.

Table 2 Förster radii for singlet and TTS exciton transfers between TADF molecules

Molecule	Förster radius (Å)
	S1 → S1	T1 → S1
ACRSA	22.7	20.7
ACRXTN	35.9	33.7
PXZ-TRZ	35.4	30.9
Tri-PXZ-TRZ	41.7	39.0

---

To investigate the effect of TTS transfers on the performance of hyperfluorescent materials, we start by estimating the key rates relevant to the photophysics of the systems. In the case of TADF molecules, these include fluorescence and phosphorescence, as well as ISC and rISC rates. These are presented in Table 3 and were calculated following the methodology developed in ref. 28 and summarized in the ESI† file. We note that, as expected, fluorescence rates are between 3 and 6 orders of magnitude higher than phosphorescence rates. Nevertheless, they are lower than the fluorescence rates of the corresponding emitter pairs, as can be seen from Table 3. Furthermore, ISC rates were overall similar for the different TADF molecules analyzed here. On the other hand, rISC rates varied more significantly, ranging from 1.99 × 10³ s⁻¹ for ACRXTN to 1.83 × 10⁵ s⁻¹ for Tri-PXZ-TRZ. Such differences suggest that the relative importance of the TTS exciton transfer mechanism to overall luminescence quantum yields may vary between TADF molecules.

Table 3 Estimated fluorescence, phosphorescence, ISC, and rISC rates for the TADF molecules analyzed in this work

TADF	Fluorescence (s^−1)	Phosphorescence (s^−1)	ISC (s^−1)	rISC (s^−1)
ACRSA	4.58 × 10^6	4.19 × 10^3	3.11 × 10^9	4.16 × 10^4
ACRXTN	5.47 × 10^7	9.87 × 10^1	1.00 × 10^9	1.99 × 10^3
PXZ-TRZ	8.50 × 10^7	2.92 × 10^1	3.00 × 10^8	2.90 × 10^3
Tri-PXZ-TRZ	4.99 × 10^7	6.30 × 10^1	1.18 × 10^8	1.83 × 10^5

---

Once all relevant rates have been estimated, we resort to KMC simulations to investigate how the different phenomena affect the behavior of the systems. These simulations account for all transfer and conversion mechanisms as well as for all different deactivation pathways for both singlet and triplet excitons. One such deactivation pathway, nonradiative decay, is harder to estimate from ab initio calculations, as this process suffers from the influence of solid state packing. To determine nonradiative decay rates, we perform preliminary simulations reproducing photoluminescence quantum yield measurements in the four different films. In these simulations, only singlet excitons resulting from light absorption are generated in the lattice. A value k_nr is set for the nonradiative decay of singlet excitons. For triplet excitons, this k_nr value is divided by 10³ to reflect their lower nonradiative decay rates compared with singlet excitons. Finally, the k_nr rate is varied, and the photoluminescence quantum yield (Φ_PL) is calculated for each simulation. The results of this procedure are seen in Fig. 3a, which shows how sensitive the calculated quantum yields for the different films are to the nonradiative decay rates. Whereas for the ACRXTN/TBPe film, the quantum yield decreases sharply for rates larger than 10⁴ s⁻¹, the Tri-PXZ-TRZ/DBP film shows much less sensitivity, requiring rates at excess of 10⁵ s⁻¹ to impact its quantum yields significantly. The two remaining films display a very similar behavior, with quantum yield curves caught between the first two more extreme cases.

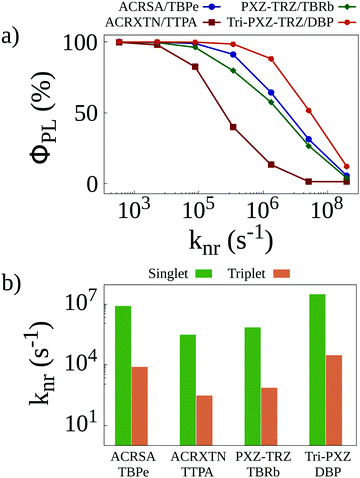Fig. 3 (a) Photoluminescence quantum yields as a function of the non-radiative decay rate for singlet excitons calculated for simulations with initially only singlet excitons. (b) Non-radiative decay rates that better reproduce experimentally obtained quantum yields⁸ as a function of the energy of the emission peak of the four TADF/emitter pairs.

By comparing the curves in Fig. 3a with experimentally obtained quantum yield values,⁸ we are able to estimate the nonradiative decay rates expected for each film. These are presented in Fig. 3b for singlets and triplets. As these rates are expected to better reproduce the experimental results, they are used in all KMC simulations henceforth.

Having tuned the non-radiative rates for the four TADF/emitter pairs, we turn to KMC simulations run under conditions of electroluminescence. In this case, from the total number of excitons used in the simulations, 75% correspond to triplets and 25% to singlets, as expected from the spin statistics of charge recombination. Considering that triplet excitons can undergo conversion into singlets either by means of rISC or TTS, it is fundamental to quantify the relative contribution (η_t) of each of these two triplet conversion mechanisms to the overall efficiency of triplet harvesting observed in each TADF/emitter pair. The breakdowns of the individual contributions to triplet harvesting are shown in Fig. 4a for each of the TADF/emitter pairs. It can be seen that the relative contributions of rISC and TTS vary significantly between pairs. For the Tri-PXZ-TRZ/DBP film, rISC is responsible for 85% of triplet conversions. This is due to the combination of two factors: the fact that both the rISC rates for Tri-PXZ-TRZ and the average intermolecular distance in the corresponding film are the highest among all pairs, as seen in Table 3 and Table S11 (ESI†). Large intermolecular separations significantly decrease the efficiency of the Förster mechanism as its rate decays with the inverse sixth power of the distance; thus, the rISC mechanism dominates. The opposite behavior is seen for the ACRXTN/TTPA film, for which 90% of triplet conversions happen through TTS. It results from the inverse combination of low rISC rates and low average intermolecular distances. For the two remaining films, both triplet conversion mechanisms are seen to contribute roughly equally, indicating similar rates for the two phenomena. The observation that the TTS mechanism may be responsible for a significant portion of triplet conversion events prompts the question of how much such transfers affect the luminescence efficiency for the different films. Fig. 4b shows a comparison between the luminescence quantum yields calculated for simulations that differ only by the deactivation or not of the TTS mechanism. As expected, the deactivation of TTS does not change the quantum yield for simulations of the Tri-PXZ-TRZ/DBP film but cuts by roughly half the yield for the ACRXTN/TTPA pair. More interestingly, for the cases in which TTS and rISC shared the burden of triplet harvesting, the effects on quantum yield differ significantly. While the ACRSA/TBPe film experiences a decrease from 78% to 53% in yield, the PXZ-TRZ/TBRb film sees only a change from 84% to 73%. It can be explained by the difference in nonradiative decay rates, which results in higher yields in the latter film, although the estimated rISC rate for PXZ-TRZ is lower than that of ACRSA.

Fig. 4 (a) Relative contribution of the two triplet conversion mechanisms for each of the four TADF/emitter pairs analyzed here. (b) Comparison between luminescence quantum yields obtained from simulations in which the TTS mechanism was active and inactive.

It is possible to better appreciate the effect of including TTS transfers in the calculations by looking into the time-resolved luminescence plots for simulations run with the 3 : 1 triplet to singlet ratio. These are shown in Fig. 5 for the four TADF/emitter pairs. Comparison between the curves obtained with and without the inclusion of TTS transfers allows us to draw one main conclusion: the addition of TTS transfers results in faster luminescence decay even in the cases in which the overall luminescence quantum yield is not changed despite significant TTS contribution to triplet harvesting. This is the case of the PXZ-TRZ/TBRb film, which shows decay curves that start from similar intensities but decay at different rates. For ACRSA and particularly ACRXTN, luminescence curves from simulations with TTS transfers start with higher intensities in accordance with their higher quantum yields and also present a faster decay rate. Interestingly, such reduction in exciton lifetimes is also expected to alleviate the efficiency roll-off due to the suppression of bimolecular loss processes. It is also worth noting that as the TTS mechanism is not relevant for the Tri-PXZ-TRZ/DBP film, both time-resolved luminescence curves show equal behavior with decay times on the order of tens of microseconds.

Fig. 5 Time-resolved luminescence curves for simulations run with and without the inclusion of TTS transfers for the four TADF/emitter pairs.

The results presented here suggest the importance of accounting for TTS transfers when investigating TADF effects in the solid state. The neglect of this effect may result in the overestimation of rISC rates and may constitute one reason for which theoretical estimates of rISC rates are often underestimated in comparison to experimental reports. To highlight the differences in efficiency for the two triplet recycling processes, Table S8 in the ESI† file shows two sets of ratios: first, the ratios between rISC and TTS (TADF to TADF and TADF to emitter) quantum yields, that shows which triplet-to-singlet conversion mechanism is more efficient for each TADF/emitter pair. These results mirror those shown in Fig. 4a, indicating that when the appropriate combination of intermolecular distance and overlap between phosphorescence and absorption spectra comes in place, it allows TTS rates to increase enough to be dominant. This (ESI†) is even more so when TTS from TADF to emitters is considered, as can be also seen in Table S8 (ESI†). Going one step further, the second set of ratios is calculated between the quantum yields for TTS and those of rISC followed by a FRET transfer to a nearby molecule. This second set incorporates not only the triplet conversion aspect of both mechanisms, but also accounts for the fact that TTS simultaneously consists of a conversion and an exciton transfer process. When this is accounted for, we get the same results from comparing exclusively the triplet conversion mechanisms, except in the case of ACRSA, in which the TTS advantage becomes further evident. This is due to the fact that singlet-to-singlet FRET among ACRSA molecules is not particularly efficient.

Finally, it is also important to address how the differentiation between the two triplet harvesting mechanisms can be achieved experimentally. In principle, an approach that takes advantage of the different dependencies displayed by phosphorescence and rISC rates on the singlet–triplet energy gap (as evidenced by eqn (S4) and (S9) in the ESI†) could be devised. However, methods based on varying intermolecular distances should be more straightforward. As exciton transfer rates are very sensitive to changes in intermolecular distances, the TTS effect is expected to disappear in solution if the concentration of TADF molecules is low enough. However, the comparison between measurements in solution and solid state suffers from the difficulty in accounting for both the variations in hypsochromic shift and nonradiative decay rates. Whereas the first effect is bound to affect the efficiency of Förster transfers due to changes in molecular spectra, the latter can obfuscate the results by overpowering triplet harvesting rates. A better approach towards experimental differentiation of the two mechanisms could come from electroluminescence measurements performed in films doped only with TADF molecules at different concentrations. Increases in concentration should reduce the average distances between TADF molecules, allowing the TTS mechanism to become active. Barring the issues concerning varying efficiency of charge recombination and other bimolecular effects, this approach could quantify the relative contributions of both mechanisms by analyzing changes in the decay rates of time-resolved luminescence curves.

4 Conclusions

In summary, we have analyzed four TADF/fluorescent emitter dopant pairs used in OLED devices. Employing first-principles calculations, we have estimated the relevant photophysical rates for these pairs. Results from the rate calculations showed potential in all TADF/emitter pairs not only for singlet Förster transfers but also for efficient TTS Förster transfers both from TADF to emitter molecules and between TADF molecules. This observation pointed at the existence of a second triplet harvesting mechanism that could act in concert with rISC and improve device efficiency.

The use of KMC calculations with nonradiative decay rates tuned to experimental results showed that the relative contribution from each triplet harvesting mechanism differed notably for each TADF/emitter pair, with situations ranging from practically pure rISC to pure TTS contributions. When simultaneous action of rISC and TTS is present, the intensity of nonradiative decay rates ultimately determines whether this synergy translates itself into higher quantum yields or just faster luminescence decay times.

From an experimental perspective, these results suggest the necessity of taking into account the possibility of TTS transfers when attempting to estimate rISC rates from measurements made in the solid state, as neglect of the TTS mechanism may result in overestimation of the efficiency of rISC. More importantly, our results point at a new dimension for the optimization of molecular design applied to TADF or hyperfluorescent devices, one that could benefit from the synergistic effects of combining two triplet harvesting mechanisms instead of focusing solely on the maximization of rISC rates, whose exclusive optimization may be severely constrained.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support by a research grant (00028053) from VILLUM FONDEN. P. H. O. N. gratefully acknowledges the financial support from Brazilian Research Councils CNPq, CAPES, and FAPDF.

References

1. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Highly efficient organic light-emitting diodes from delayed fluorescence, Nature, 2012, 492, 234–238.
2. K. Goushi, K. Yoshida, K. Sato and C. Adachi, Organic light-emitting diodes employing efficient reverse intersystem crossing for triplet-to-singlet state conversion, Nat. Photonics, 2012, 6, 253–258.
3. M. Pope, H. Kallmann and P. Magnante, Electroluminescence in organic crystals, J. Chem. Phys., 1963, 38, 2042–2043.
4. T. Penfold, F. Dias and A. P. Monkman, The theory of thermally activated delayed fluorescence for organic light emitting diodes, Chem. Commun., 2018, 54, 3926–3935.
5. X.-K. Chen, D. Kim and J.-L. Brédas, Thermally activated delayed fluorescence, (tadf) path toward efficient electroluminescence in purely organic materials: molecular level insight, Acc. Chem. Res., 2018, 51, 2215–2224.
6. P. de Silva, C. A. Kim, T. Zhu and T. Van Voorhis, Extracting design principles for efficient thermally activated delayed fluorescence, (tadf) from a simple four-state model, Chem. Mater., 2019, 31, 6995–7006.
7. H. Sun, Z. Hu, C. Zhong, X. Chen, Z. Sun and J.-L. Brédas, Impact of dielectric constant on the singlet-triplet gap in thermally activated delayed fluorescence materials, J. Phys. Chem. Lett., 2017, 8, 2393–2398.
8. H. Nakanotani, T. Higuchi, T. Furukawa, K. Masui, K. Morimoto, M. Numata, H. Tanaka, Y. Sagara, T. Yasuda and C. Adachi, High-efficiency organic light-emitting diodes with fluorescent emitters, Nat. Commun., 2014, 5, 1–7.
9. C.-Y. Chan, M. Tanaka, Y.-T. Lee, Y.-W. Wong, H. Nakanotani, T. Hatakeyama and C. Adachi, Stable pure-blue hyperfluorescence organic light-emitting diodes with high-efficiency and narrow emission, Nat. Photonics, 2021, 15, 203–207.
10. S. Nam, J. W. Kim, H. J. Bae, Y. M. Maruyama, D. Jeong, J. Kim, J. S. Kim, W.-J. Son, H. Jeong and J. Lee, et al., Improved efficiency and lifetime of deep-blue hyperfluorescent organic light-emitting diode using pt, (ii) complex as phosphorescent sensitizer, Adv. Sci., 2021, 2100586.
11. W. Song and K. S. Yook, Hyperfluorescence-based full fluorescent white organic light-emitting diodes, J. Ind. Eng. Chem., 2018, 61, 445–448.
12. F. Khan, E. Urbonas, D. Volyniuk, J. V. Grazulevicius, S. M. Mobin and R. Misra, White hyperelectrofluorescence from solution-processable oleds based on phenothiazine substituted tetraphenylethylene derivatives, J. Mater. Chem. C, 2020, 8, 13375–13388.
13. T. Förster, Zwischenmolekulare energiewanderung und fluoreszenz, Ann. Phys., 1948, 437, 55–75.
14. J. S. Jang, S. H. Han, H. W. Choi, K. S. Yook and J. Y. Lee, Molecular design of sensitizer to suppress efficiency loss mechanism in hyper-fluorescent organic light-emitting diodes, Org. Electron., 2018, 59, 236–242.
15. J. S. Jang, S. H. Han and J. Lee, Design rule of assistant dopant for high external quantum efficiency in hyperfluorescence organic light-emitting diodes, Adv. Photonics Res., 2021, 2, 2000109.
16. Y. Giret, J. Eng, T. Pope and T. Penfold, A quantum dynamics study of the hyperfluorescence mechanism, J. Mater. Chem. C, 2021, 9, 1362–1369.
17. H. Abroshan, V. Coropceanu and J.-L. Brédas, Hyperfluorescence-based emission in purely organic materials: Suppression of energy-loss mechanisms via alignment of triplet excited states, ACS Mater. Lett., 2020, 2, 1412–1418.
18. M. Jakoby, B. S. Richards, U. Lemmer and I. A. Howard, Investigations of singlet and triplet diffusion in thermally activated delayed-fluorescence emitters: Implications for hyperfluorescence, Phys. Rev. B, 2019, 100, 045303.
19. V. L. Ermolaev and E. B. Sveshnikova, Inductive resonance energy transfer from aromatic molecules in the triplet state, Doklady Akademii Nauk, Russian Academy of Sciences, 1963, vol. 149, pp. 1295–1298.
20. A. Cravcenco, M. Hertzog, C. Ye, M. N. Iqbal, U. Mueller, L. Eriksson and K. Börjesson, Multiplicity conversion based on intramolecular triplet-to-singlet energy transfer, Sci. Adv., 2019, 5, 5978.
21. M. Baldo, M. E. Thompson and S. Forrest, High-efficiency fluorescent organic light-emitting devices using a phosphorescent sensitizer, Nature, 2000, 403, 750–753.
22. S. Kuila and S. J. George, Phosphorescence energy transfer: ambient afterglow fluorescence from water-processable and purely organic dyes via delayed sensitization, Angew. Chem., 2020, 132, 9479–9483.
23. H. Gui, Z. Huang, Z. Yuan and X. Ma, Ambient white-light afterglow emission based on triplet-to-singlet förster resonance energy transfer, CCS Chem., 2021, 481–489.
24. A. Kirch, M. Gmelch and S. Reineke, Simultaneous singlet-singlet and triplet-singlet förster resonance energy transfer from a single donor material, J. Phys. Chem. Lett., 2019, 10, 310–315.
25. T. Förster, 10th spiers memorial lecture. transfer mechanisms of electronic excitation, Discuss. Faraday Soc., 1959, 27, 7–17.
26. C. Nguyen, G. Ingram and Z.-H. Lu, Quantifying interdopant exciton processes in organic light emitting diodes, J. Phys. Chem. C, 2017, 121, 3304–3309.
27. N. Haase, A. Danos, C. Pflumm, P. Stachelek, W. Brütting and A. P. Monkman, Are the rates of dexter transfer in tadf hyperfluorescence systems optically accessible?, Mater. Horiz., 2021, 8, 1805–1815.
28. L. E. de Sousa and P. de Silva, Unified framework for photophysical rate calculations in tadf molecules, J. Chem. Theory Comput., 2021, 17, 5816–5824.
29. L. E. de Sousa, F. T. Bueno, G. M. e Silva, D. A. da Silva Filho and P. H. de Oliveira Neto, Fast predictions of exciton diffusion length in organic materials, J. Mater. Chem. C, 2019, 7, 4066–4071.
30. L. E. de Sousa, D. A. da Silva Filho, P. de Silva, L. Ribeiro and P. H. de Oliveira Neto, A genetic algorithm approach to design principles for organic photovoltaic materials, Adv. Theory Simul., 2020, 3, 2000042.
31. S. Gottardi, M. Barbry, R. Coehoorn and H. Van Eersel, Efficiency loss processes in hyperfluorescent oleds: A kinetic monte carlo study, Appl. Phys. Lett., 2019, 114, 073301.
32. L. Benatto, J. Govatski, C. de Moraes, C. Gouvêa, H. Avila, C. F. Marchiori, C. Oliveira, M. Cremona, M. Koehler and L. Roman, Understanding the effect of solvent additive in polymeric thin film: turning a bilayer into a bulk heterojunction-like photovoltaic device, J. Phys. D: Appl. Phys., 2020, 53, 365101.
33. L. E. de Sousa, F. T. Bueno, L. Ribeiro, L. A. Ribeiro Junior, D. A. da Silva Filho and P. H. de Oliveira Neto, Role of exciton density in organic materials: Diffusion length, lifetime, and quantum efficiency, Chem. Mater., 2019, 31, 6818–6823.
34. R. Coehoorn, H. Van Eersel, P. Bobbert and R. Janssen, Kinetic monte carlo study of the sensitivity of oled efficiency and lifetime to materials parameters, Adv. Funct. Mater., 2015, 25, 2024–2037.
35. K. Nasu, T. Nakagawa, H. Nomura, C.-J. Lin, C.-H. Cheng, M.-R. Tseng, T. Yasuda and C. Adachi, A highly luminescent spiro-anthracenone-based organic light-emitting diode exhibiting thermally activated delayed fluorescence, Chem. Commun., 2013, 49, 10385–10387.
36. H. Tanaka, K. Shizu, H. Miyazaki and C. Adachi, Efficient green thermally activated delayed fluorescence, (tadf) from a phenoxazine-triphenyltriazine, (pxz-trz) derivative, Chem. Commun., 2012, 48, 11392–11394.
37. H. Tanaka, K. Shizu, H. Nakanotani and C. Adachi, Twisted intramolecular charge transfer state for long-wavelength thermally activated delayed fluorescence, Chem. Mater., 2013, 25, 3766–3771.
38. T. Stein, L. Kronik and R. Baer, Reliable prediction of charge transfer excitations in molecular complexes using time-dependent density functional theory, J. Am. Chem. Soc., 2009, 131, 2818–2820.
39. R. Crespo-Otero and M. Barbatti, Spectrum simulation and decomposition with nuclear ensemble: formal derivation and application to benzene, furan and 2-phenylfuran, Marco Antonio Chaer Nascimento, Springer, 2014, pp. 89–102.
40. L. E. de Sousa, L. A. Ribeiro, A. L. d. A. Fonseca and D. A. da Silva Filho, Modeling the emission spectra of organic molecules: A competition between Franck-Condon and nuclear ensemble methods, J. Phys. Chem. A, 2016, 120, 5380–5388.
41. S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the tamm-dancoff approximation, Chem. Phys. Lett., 1999, 314, 291–299.
42. M. J. Peach, M. J. Williamson and D. J. Tozer, Influence of triplet instabilities in tddft, J. Chem. Theory Comput., 2011, 7, 3578–3585.
43. A. Chantzis, A. D. Laurent, C. Adamo and D. Jacquemin, Is the tamm-dancoff approximation reliable for the calculation of absorption and fluorescence band shapes?, J. Chem. Theory Comput., 2013, 9, 4517–4525.
44. G. Scalmani and M. J. Frisch, Continuous surface charge polarizable continuum models of solvation. i. general formalism, J. Chem. Phys., 2010, 132, 114110.
45. L. Kronik and S. Kümmel, Dielectric screening meets optimally tuned density functionals, Adv. Mater., 2018, 30, 1706560.
46. Nemo - photophysics with the nuclear ensemble method, https://github.com/LeonardoESousa/NEMO.
47. Q. Peng, D. Fan, R. Duan, Y. Yi, Y. Niu, D. Wang and Z. Shuai, Theoretical study of conversion and decay processes of excited triplet and singlet states in a thermally activated delayed fluorescence molecule, J. Phys. Chem. C, 2017, 121, 13448–13456.
48. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al., Advances in molecular quantum chemistry contained in the q-chem 4 program package, Mol. Phys., 2015, 113, 184–215.
49. Xcharge: A kinetic monte carlo model for exciton and charge dynamics, https://github.com/LeonardoESousa/xcharge.
50. E. Cho, M. Hong, V. Coropceanu and J.-L. Brédas, The role of intermolecular interactions on the performance of organic thermally activated delayed fluorescence, (tadf) materials, Adv. Opt. Mater., 2021, 2002135.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc05596h

---