Experimental determination of the bulk moduli of hollow nanogels†
Andrea
Scotti
 *a,
Urs
Gasser
b,
Alexander V.
Petrunin
*a,
Urs
Gasser
b,
Alexander V.
Petrunin
 a,
Lisa
Fruhner
a,
Lisa
Fruhner
 c,
Walter
Richtering
c,
Walter
Richtering
 a and
Judith E.
Houston
a and
Judith E.
Houston
 d
d
aInstitute of Physical Chemistry, RWTH Aachen University, 52056 Aachen, Germany. E-mail: andrea.scotti@rwth-aachen.de
bLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, 5232 Villigen, Switzerland
cForschungszentrum Jülich GmbH Jülich Centre for Neutron Science (JCNS-1) and Institute for Biological Information processing (IBI-8), 52425 Jülich, Germany
dEuropean Spallation Source ERIC, Box 176, SE-221 00 Lund, Sweden
First published on 28th July 2022
Abstract
The softness of an object can be quantified by one of the fundamental elastic moduli. The bulk modulus of the particle is most appropriate in the presence of isotropic compressions. Here, we use small-angle neutron scattering with contrast variation to directly access the bulk modulus of polymeric nanocapsules – pNIPAM-based hollow nanogels. We show that the size of the cavity is the most important quantity that determines the softness of hollow nanogels. During initial compression, the polymer collapses into the cavity and leads to a large change in the particle volume, resulting in a very small initial bulk modulus. Once the cavity is partially occupied by the polymer, the hollow nanogels become significantly stiffer since now the highly crosslinked network has to be compressed. Furthermore, we show that the larger the cavity, the softer the nanogel.
1 Introduction
One of the most interesting phenomena in soft matter is the self-assembly of macromolecules or colloidal particles in structures with high hierarchical order. Such self-assembly might lead to both phase transition between different phases, e.g. from a liquid to a solid,1,2 or may result in larger supra-molecular complexes, such as liposomes,3 block copolymer micelles4 and virus5,6 or virus-like particles.7,8 Most of these ordered supra-molecular complexes are characterized by a solvent-filled cavity and, at first glance, can be approximated as hollow spheres. Since the presence of a cavity makes these particles appealing for the targeted delivery of drugs,8–10 it is pivotal to unravel their basic chemical and physical properties, such as their mechanical properties.6 We note that the building blocks of supra-molecular complexes can be both biological materials8,11,12 and synthetic polymers.9,10,13–16Hollow nanogels represent an ideal simplified model system that allows us to investigate the role of the cavity on the compression of the particle. Hollow nanogels are polymeric crosslinked networks which are swollen in a good solvent.17,18 They are characterized by a solvent-filled cavity in their centre.19 When the polymer used for the synthesis possesses a lower critical temperature, such as pNIPAM,20 the resulting hollow nanogels are thermoresponsive: below the volume phase transition temperature (VPTT) of pNIPAM in water the nanogels are swollen. While above the VPTT, they collapse but, as shown by scattering studies and AFM measurements, the particles maintain their cavity.19,21 These hollow nanogels are appealing for both application22 and fundamental studies.23,24
For instance, the presence of the solvent-filled cavity makes hollow nanogels appealing as nanocapsules for drug delivery,9,15,25,26 or as membranes for water purification.27 Furthermore, the phase behavior of hollow nanogels is different from the one observed for hard-sphere and hard or ultra-soft nanogels which show a liquid-to-crystal phase transition independently to their softness.1,28,29 Indeed, crystallisation is suppressed in bulk solutions of hollow nanogels.23 Also their 2D-phase behavior, once confined at oil–water interfaces, differs from the one observed for nanogel monolayers. The absence of a core enables the hollow nanogels to deform more in the direction orthogonal to the interface with respect to crosslinked nanogels.24 As a consequence, a continuous compression of the particle is observed and the system does not show a solid-to-solid transition typical of a monolayer of nanogels.30 It has been shown that the hollow nanogels deswell much more than regular nanogels once they are embedded in a matrix of regular ones.31,32 The cavity also affects how much the nanogels spread once adsorbed at an interface, leading to a particular pancake-like architecture of the adsorbed particle.21,24,33 These examples show how the cavity affects the compressibility and deformability of the nanogels and ultimately the particle softness.34 To quantify this aspect, one of the main elastic moduli of the nanogels has to be determined experimentally. The bulk modulus is the natural candidate to quantify the changes in compressibility of soft compressible colloids for isotropic compressions.
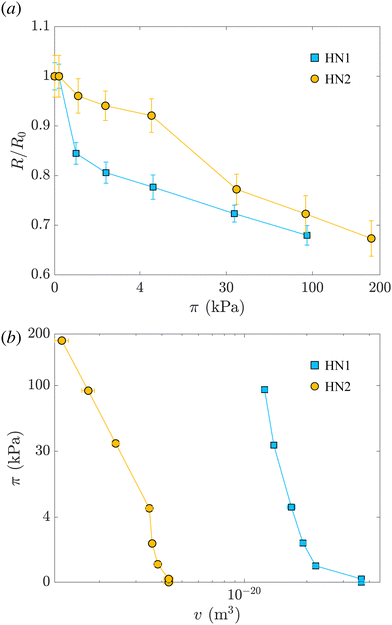
Given the sizes of the nanogels of interest – some hundreds of nanometres in radius – microscopy techniques and capillary micromechanics and microfluidics are not suitable.35 Sierra-Martin et al.36 have shown that scattering techniques, in combination with osmotic stress polymers, can be used to probe the bulk modulus of nanogels. In their approach, the nanogels were mixed with increasing concentration of a high molecular weight polymer, dextran, which was large enough to not penetrate the nanogel networks. As the dextran concentration increases, the nanogels experience increasing osmotic pressures, π, which can be measured by means of a membrane osmometer.28,37 Then, multi-angle dynamic light scattering (DLS) measurements of dextran solutions and dextran-nanogel solutions allowed them to decouple the nanogel and dextran contribution to the scattering signal. In this way, the nanogel hydrodynamic radius and thus the nanogel volume, v, can be determined at different π. From the slope of the π vs. v curve, the bulk modulus can be extracted considering its definition:
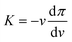 | (1) |
Recently, we used small-angle neutron scattering (SANS) with contrast variation to quantify the bulk modulus of regular and ultra-low crosslinked nanogels.38 Here, we apply our method to quantify the compressibility of hollow nanogels. A partially-deuterated, high molecular weight polymer is used to exert osmotic stress on the nanogels. The scattering length density of the deuterated polymer is matched by heavy water.38 Consequently, the polymer does not contribute to the coherent scattering signal and the nanogels can be probed at unprecedentedly high π. In addition to the advantage of using contrast variation, the use of SANS allows us to probe the form factor of the hollow nanogels. Therefore, not only the total radius but also the characteristic lengths of the particle, such as the radius of the internal cavity, can be determined.
The bulk modulus of hollow 5 mol% crosslinked pNIPAM-based nanogels is probed between 0 and ≈190 kPa, which is one order of magnitude higher then the π applied before.36 We study two different hollow nanogels with different cavity sizes to explore the interplay between internal architecture and compressibility of the nanogels. Our findings show that the cavity leads to a strong decrease of the nanogel volume for moderate applied osmotic stress. This results in a very small value of the initial bulk modulus of the hollow nanogels. The larger the cavity, the stronger is the initial compression. Even if the polymeric network of the studied nanogels has been synthesized using 5 mol% crosslinker agent, the values of K are comparable with the bulk moduli of ultra-soft nanogels.35,36,38,39 We rationalise these results with the fact that the empty cavity allows the pNIPAM to rearrange in its empty volume leading to a pronounced particle deswelling. Our study shows that the bare knowledge on the amount of crosslinks incorporated in the network is not enough to predict the particle compressibility, and that a key role is played by the internal architecture.34
2 Experimental
2.1 Synthesis
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of ethylene oxide-d4 and hydrogenous ethylene oxide at 50 °C for three days. The final product had number average molecular weight, Mn, of 265
2 mixture of ethylene oxide-d4 and hydrogenous ethylene oxide at 50 °C for three days. The final product had number average molecular weight, Mn, of 265![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and molecular weight distribution, Mw/Mn, of 1.02. In our previous work, we showed that the very same deuterated PEG used for this study has a D/H composition of 83% as obtained by 1H-NMR spectroscopy. Such a composition results in a neutron scattering length density of 6.335 × 10−6 Å−2, which is the same expected for pure D2O. Furthermore, SANS measurements show that, d83%PEG is virtually completely contrast matched in pure D2O, see the discussion in the ESI† of Houston et al.38
000 g mol−1 and molecular weight distribution, Mw/Mn, of 1.02. In our previous work, we showed that the very same deuterated PEG used for this study has a D/H composition of 83% as obtained by 1H-NMR spectroscopy. Such a composition results in a neutron scattering length density of 6.335 × 10−6 Å−2, which is the same expected for pure D2O. Furthermore, SANS measurements show that, d83%PEG is virtually completely contrast matched in pure D2O, see the discussion in the ESI† of Houston et al.38
| Name | Sacrificial core | Core | pNIPAM | BIS | SDS | KPS | T (°C) | V (mL) | Core–shell |
|---|---|---|---|---|---|---|---|---|---|
| HN1 | (105 ± 1) nm | (7.50 ± 0.04) × 10−3 | (5.48 ± 0.03) × 10−3 | (3.94 ± 0.02) × 10−4 | (3.24 ± 0.02) × 10−4 | (4.30 ± 0.02) × 10−4 | 70 | 200 | (2.49 ± 0.02) × 10−2 |
| HN2 | (57 ± 1) nm | (6.44 ± 0.03) × 10−3 | (4.53 ± 0.02) × 10−3 | (3.24 ± 0.01) × 10−4 | (5.77 ± 0.02) × 10−4 | (5.80 ± 0.03) × 10−4 | 60 | 245 | (2.20 ± 0.04) × 10−2 |
The functionalised silica cores were redispersed in 5 mL of ethanol. To prevent silica aggregates during the shell polymerisation, the suspensions of silica core in ethanol were first ultrasonicated and then transferred to the flask containing the water, NIPAM, SDS, and BIS. Then the initiator solution was rapidly transferred into the monomer solution to start the polymerisation. After 4 hours under constant nitrogen flow and stirring at T ≥ 60 °C, the reaction was cooled down to room temperature and stopped. Threefold ultra-centrifugation at 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm and redispersion in fresh water was used to purify the silica-core pNIPAM-shell nanoparticles. Lyophilisation was performed for storage.
000 rpm and redispersion in fresh water was used to purify the silica-core pNIPAM-shell nanoparticles. Lyophilisation was performed for storage.
To generate hollow nanogels, the amount of core–shell nanoparticles reported in Table 1 were redispersed in 50 mL of water. After complete dispersion, 50 mL of a 0.1 M NaOH solution was added and allowed to react for 4 days. Dialysis was applied to remove the remaining silica and neutralise the suspension. Finally, the resulting hollow nanogels were centrifuged at 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm to reduce the total volume and lyophilisation was carried out for storage.
000 rpm to reduce the total volume and lyophilisation was carried out for storage.
2.2 Small-angle neutron scattering
Small-angle scattering allows us to characterise the shape and characteristic lengths of colloids with dimensions below a few hundreds of nanometres. For diluted suspensions of colloids in a solvent, the intensity measured, I(q), as a function of the scattering vector q is proportional to the particle form factor P(q). This quantity contains all the information on the shape and characteristic lengths of the colloids.42 It can be written I(q) = nΔρ2v2P(q), where n is the particle density, v the particle volume, and Δρ the difference in scattering length density between the solvent and the sample. When concentration rises, the particles starts to interact with each other. This contributes to I(q) with the structure factor S(q) which contains information on the arrangements and interaction between the suspended colloids.43 In these conditions, it is hard to decouple in the measured intensity, I(q) = nΔρ2v2P(q)S(q), which features are due to the individual particle's shape and structure, and which are due to the particle arrangement.44 Neutrons and light interact with the sample nuclei and with the electron clouds of the atoms composing the sample, respectively. Therefore, the contrast Δρ is different depending on the chosen probe. Importantly, neutrons have different contrast when interacting with hydrogen and deuterium atoms.45 This allows us to change the contrast between the solvent and the sample by selective deuteration, and choosing the appropriate mixture of hydrogenated and deuterated solvent. With this approach, it is possible to access information on individual nanogels in concentrated samples, for instance mixing few hydrogenated particles with a majority of deuterated nanogels that are contrast matched by a mixture of water and heavy water.23,29,32,44,46–49Here, the partially-deuterated d83%PEG, which is contrast matched in pure D2O, is used instead of the deuterated nanogels. In this way, we overcome the problem of using DLS since the d83%PEG does not contribute to the coherent neutron scattering signal. As a consequence, we can reach high π and still get the information on the volume of the nanogel. Furthermore, performing a static scattering experiment allows us to probe P(q) and, therefore, get information on both the total radius and the internal architecture of the nanogel.
| A(q) = ΔρshVshΦsh(q, Rout, σout) + (Δρcore − Δρsh)VcoreΦcore(q, Rin, σin) | (2) |
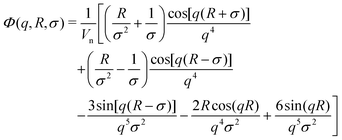 | (3) |
3 Results
Samples were prepared by weighing the d83%PEG, the pNIPAM, and the D2O to reach the desired concentrations. The concentration of nanogels is kept below 0.3 wt% for all the samples, allowing only the form factor of the nanogel to be measured, i.e. S(q) = 1. The concentration of d83%PEG is between 0 and 7.4 wt%. The osmotic pressure exerted by the d83%PEG is computed using an empirical function of its concentrations,38cd83%, determined by measuring π as a function of cd83% with a membrane osmometer: π = 217cd83% + 3.24 × 10−6cd83%2 + 451cd83%3. The osmotic pressure exerted lies between 0 and 184.6 ± 0.2 kPa. The highest π is one order of magnitude larger than the highest π measured by Sierra-Martin et al.36 All samples were prepared in pure D2O and measured at 20 °C.Fig. 1(a) shows the SANS data of the hollow nanogels (squares) resulting from the dissolution of the 105 nm silica core of the core–shell particle, HN1. The circles in panel 1(b) are the intensities measured for the hollow nanogels obtained from the core–shell particles with sacrificial 60 nm silica core, HN2. In both cases, the bottom curves are samples where the nanogels were mixed with D2O only, i.e. π = 0 and the particles are in the swollen state. Then, from bottom to top π increases. The maximum values of π measured are (93.9 ± 0.1) kPa, top curve in Fig. 1(a), and (184.6 ± 0.2) kPa for the top curve in Fig. 1(b).
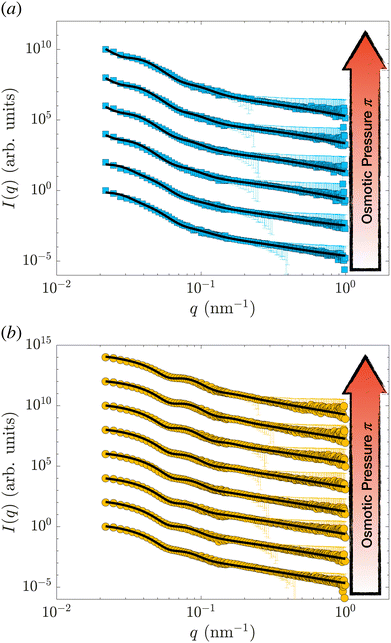 | ||
| Fig. 1 SANS intensity, I(q), as a function of the scattering vector, q, for the hollow nanogels HN1 (squares), obtained from the core–shell particles with sacrificial 105 nm silica core (a) and for the hollow nanogels HN2 (circles), obtained from the core–shell particles with sacrificial 60 nm silica core (b). The osmotic pressure exerted by the d83%PEG are from bottom to top in (a) 0, (0.0222 ± 0.0004), (0.1649 ± 0.0009), (1.040 ± 0.002), (5.99 ± 0.01), (34.33 ± 0.05), and (93.9 ± 0.1) and in (b) 0, (0.0220 ± 0.0004), (0.194 ± 0.001), (1.012 ± 0.002), (5.730 ± 0.009), (35.61 ± 0.05), (92.4 ± 0.1), and (184.6 ± 0.2) kPa. The solid lines are fits of the data with the model in eqn (2) and (3) introduced by Berndt et al.50. Data are shifted in the y-direction for clarity. | ||
The solid lines in Fig. 1 are the fits performed with the model in eqn (2) and (3). The fitting is performed using the function fmincon of Matlab, which finds a constrained minimum of a function of several variables by minimising the χ2. The errors on the fitting parameters are determined from the standard deviation of the parameters estimated from the Jacobian matrix.
In Fig. S1 (ESI†), we show the values of the χ2 and the course of the residuals of the fits shown in Fig. 1. In some cases, we note that the oscillations of the residuals might indicate some overfitting of the data, which might lead to an underestimation of the errors on the fitting parameters. Nevertheless, the variation of the course of the measured intensities indicates that the nanogels are significantly changing architecture once π increases.
As can be seen by the solid line in Fig. 1, the model we used reproduces well the scattering data of hollow nanogels. To further verify that our model is not over-interpreting the data, we also perform a fit of the form factors with a model that does not assume any pre-defined architecture.54 The results of the two models, as well as the fit qualities in terms of χ2, are identical. Furthermore, the differences between the final radii and the characteristic lengths of the particles as obtained from the two models are comparable – within the experimental error, see Section S1 of the ESI.† We can therefore conclude that both the values of the parameters and the associated errors obtained fitting the data with the model in eqn (2) and (3) are consistent.
The main characteristic lengths determined from the fit are reported in Table 2. For both the nanogels studied, a decrease of the total size, R, is observed with increasing π. In the swollen state, the hollow nanogels present a cavity with a radius of (81 ± 2) nm (HN1) and (22 ± 1) nm (HN2). For both the nanogels Rcav is smaller than the radius of the sacrificial silica core since the polymeric network expands into the empty volume after the core dissolution.19,31,41,51 At the same time, the cavity also reduces its size, Rcav, with increasing applied osmotic stress. While our model allows for changing all the characteristic lengths of the nanogel, including the size and the pNIPAM volume fraction in the solvent-filled cavity, the shape of the nanogel is assumed to be spherical. Recent computer simulations, microscopy, osmotic pressure and scattering measurements show that regular and hollow nanogels can facet in crowded environments.23,37,55–58 Furthermore, the combination of SANS data with computer simulations showed that an increase of the fitting parameter related to the size polydispersity is an indication of faceting.59 Indeed, this parameter is the only one which can be adjusted to compensate for the potential non-spherical shape of the particle due to compression.23,29,46,59,60
| Name | Sacrificial core (nm) | π (kPa) | R (nm) | R cav (nm) | p (%) | ξ (nm) |
|---|---|---|---|---|---|---|
| HN1 | 105 ± 1 | 0 | 206 ± 4 | 81 ± 2 | 21 ± 3 | 6.8 ± 0.7 |
| 105 ± 1 | 0.0222 ± 0.0004 | 206 ± 3 | 81 ± 1 | 20 ± 2 | 7.2 ± 0.8 | |
| 105 ± 1 | 0.1649 ± 0.0009 | 174 ± 3 | 50 ± 2 | 23 ± 2 | 5.9 ± 0.9 | |
| 105 ± 1 | 1.040 ± 0.002 | 166 ± 3 | 43 ± 1 | 21 ± 2 | 5.5 ± 0.7 | |
| 105 ± 1 | 5.99 ± 0.01 | 160 ± 4 | 43 ± 2 | 23 ± 2 | 4.9 ± 0.6 | |
| 105 ± 1 | 34.33 ± 0.05 | 149 ± 2 | 35 ± 1 | 21 ± 3 | 5.1 ± 0.8 | |
| 105 ± 1 | 93.9 ± 0.1 | 140 ± 3 | 38 ± 2 | 21 ± 2 | 4.7 ± 0.4 | |
| HN2 | 57 ± 1 | 0 | 101 ± 3 | 22 ± 1 | 16 ± 2 | 12 ± 1 |
| 57 ± 1 | 0.0220 ± 0.0004 | 101 ± 3 | 22 ± 1 | 16 ± 1 | 12 ± 2 | |
| 57 ± 1 | 0.194 ± 0.001 | 97 ± 2 | 17.7 ± 0.9 | 15 ± 2 | 12 ± 1 | |
| 57 ± 1 | 1.012 ± 0.002 | 95 ± 1 | 18.2 ± 0.8 | 15 ± 2 | 12 ± 1 | |
| 57 ± 1 | 5.730 ± 0.009 | 93 ± 2 | 15 ± 1 | 15 ± 1 | 12 ± 2 | |
| 57 ± 1 | 35.61 ± 0.05 | 78 ± 2 | 10 ± 1 | 15 ± 2 | 7 ± 1 | |
| 57 ± 1 | 92.4 ± 0.1 | 73 ± 3 | 8 ± 2 | 15 ± 1 | 9 ± 1 | |
| 57 ± 1 | 184.6 ± 0.2 | 68 ± 3 | 9 ± 2 | 17 ± 2 | 10 ± 2 | |
For instance, for ultra-soft and hollow nanogels in crowded environments of the same nanogels, a respective increase of p from 9 to 16%29,46 and from 15 to 22% has been observed.23 As can be seen in Table 2, this is not the case for our fits for which the size polydispersities for both the nanogels remain constant – within the experimental errors. Therefore, within the experimental error and the SANS resolution, we can neglect faceting for the further analysis and treat our nanogels as hollow spheres.
Fig. 2(a) shows the variation of the radius measured at different π normalized by the radius measured at π = 0 for HN1 and HN2, squares and circles, respectively. We note that the hollow nanogels with the larger initial cavity, HN1, present a significant decrease in size already at very low π. In contrast, π ≳ 4 kPa is needed to have a pronounced deswelling of the nanogels with a cavity with an initial radius of 22 nm.
In the last column of Table 2, the values of the mesh size reported are determined from the Lorentzian term added to our model, and are consistent with the values reported in the literature.42 The qualitative behavior of ξ for the two nanogels is similar to the one of their radii. The mash size of HN1 has an abrupt initial decrease and then it keeps decreasing. In contrast, ξ for HN2 remains constant at the beginning and then it decrease for π ≳ 30 kPa. A more quantitative analysis and comparison between the course of R and ξ is not possible due to the high uncertainty on the values of ξ. This is due to both the high incoherent background at high q-values and the possibility that the fits are trapped in local minima as shown by Lietor-Santos et al.61 and further discussed in Section S2 of the ESI.†
The values of the total radius of the nanogels are used to compute the particle volumes at different compressions. Fig. 2(b) shows the data of π vs. v for the HN1 (squares) and HN2 (circles). We choose to show the data in this way since it is the most suitable representation to determine the particle bulk modulus. With reference at eqn (1), the local slope between two points, let's say i and i + 1, multiplied by −vi allow us to determine the value of K at the compression of the nanogel from the volume vi to the volume vi+1 with vi > vi+1. The values of the bulk moduli obtained from the local slopes of the curves in Fig. 2 are plotted in Fig. 3(a). The squares represents the data relative to HN1 while the circles are relative to HN2. The errors on the values of K are affected by the relative error on the volumes and the error on the pressures and are shown by the bars in the figure. The x-axes shows the value of 1 − v/v0, where v is the volume at a given compression and v0 is the volume of the nanogel in the swollen state. This variable represents the compression with respect to the swollen state, 0 means that the nanogel is not compressed and 1 represents the non-physical condition in which the volume of the nanogel at a given π goes to 0.
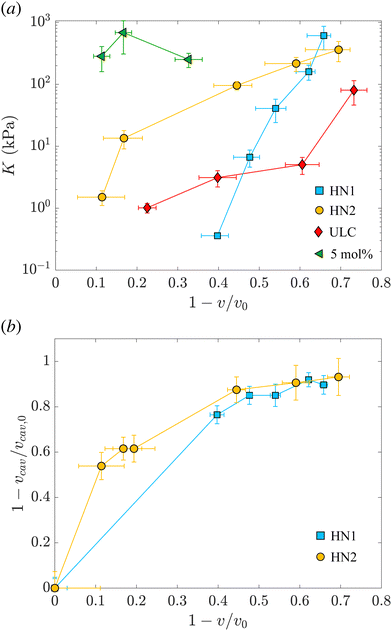 | ||
| Fig. 3 (a) Evolution of the nanogel bulk modulus as a function of compression expressed by the ratio between the volume and the volume of the nanogel in the swollen state. Light blue squares represent data relative to the hollow nanogels HN1 with a sacrificial silica core of 105 nm, orange circles correspond to hollow nanogels HN2 with a sacrificial silica core of 60 nm. Red diamonds and green triangles correspond to the values of the bulk modulus for ultra-low crosslinked and 5 mol% crosslinked nanogels, respectively, as determined in our previous study.38 (b) Relative variation of the volume of the cavity with respect to the volume of the cavity in the swollen state, vcav/vcav,0vs. the relative variation of the total volume of the nanogel, v, with respect to the volume of the nanogel in the swollen state, v0. Same symbols as in (a). | ||
The first trend common to both sets of data is that the bulk modulus does not remain constant with increasing the compression. Even if the increase of K with particle compression is well accepted in the literature58 and considered to be one of the key aspects of the glass-to-jamming transition,62,63 and of the rheological properties of suspensions soft compressible colloids,57,60 before our previous work38 and this contribution it was never determined experimentally for nanogels. Indeed without the use of SANS with contrast variation, it was not possible to probe such a wide π-range and resolve the individual nanogels to extract their volume.
Even if the two hollow nanogels have been synthesised with the addition of 5 mol% BIS during the synthesis of the core-shell particles, the values of their initial bulk moduli are two orders of magnitude smaller compared to the bulk modulus for nanogels synthesised with the same amount of BIS and shown by the green triangles in Fig. 3(a). For HN1 and HN2, we obtain KHN1 = (0.36 ± 0.03) kPa (squares) and KHN2 = (1.5 ± 0.4) kPa (circles) while the value for the 5 mol% crosslinked nanogel is K5mol% = (252 ± 65) kPa. In contrast, the initial values obtained for K of the hollow nanogels are of the same order of magnitude of the K determined for ultra-soft nanogels synthesised without the addition of any crosslinker, known as ultra-low crosslinked (ULC) nanogels.41 These nanogels have an initial KULC = (1.0 ± 0.2) kPa as shown by the red diamonds in Fig. 3(a).
Upon increasing the external osmotic pressure, the bulk modulus of the hollow nanogels increases and, at the highest applied π we obtain KHN1 = (612 ± 252) kPa (squares) and KHN2 = (362 ± 130) kPa (circles). These values are consistent with the value found for the 5 mol% crosslinked nanogels, K5mol% = (252 ± 65), see green triangles. In contrast, the ULC nanogels, red diamonds, even at the highest compression reach a value for K of (80 ± 34) kPa. The large errors on the values of K for the higher compressions result from the fact that once the nanogels collapse, large changes in π lead to small changes from vi to vi+1. In contrast, the error on the difference between the volumes, that is the denominator in eqn (1), is the sum of the absolute errors on the two volumes and therefore, for small volume variations, it becomes comparable to the values of vi − vi+1, leading to the large errors on the values of K.
The picture that emerges from our data is that, even if the polymeric network contains a number of crosslinks comparable to normal nanogels synthesised with 5 mol% BIS, the hollow nanogels show an initial bulk modulus two orders of magnitude smaller. Their bulk modulus – and so their compressibility – is instead comparable to the one of ultra-soft nanogels. However, once they are compressed, the bulk modulus of the hollow nanogels becomes of the same order of magnitude of the nanogel synthesised with comparable amount of BIS. To understand this behavior, we consider now the evolution of the cavity during the compression.
As mentioned, the values of Rcav in Table 2 show that, with increasing π the cavity becomes smaller and smaller. In Fig. 3(b), we show the evolution of the compression of the cavity, expressed as 1 − vcav/vcav,0 with vcav and vcav,0 the volume of the cavity at a given π and at π = 0, respectively. The volumes are computed as 4πRcav3/3. The data are plotted vs. the total compression of the hollow nanogel, 1 − v/v0. The first value of the bulk moduli for the hollow nanogels is computed from the change in volumes between the values of π (0.0222 ± 0.0004) kPa and (0.1649 ± 0.0009) kPa for HN1 and between (0.0220 ± 0.0004) kPa and (0.194 ± 0.001) kPa for HN2. The passage from low to high π produces a compression in the volume of the nanogels of 40 and 10% for HN1 (squares) and HN2 (circles), respectively. These changes in total volume are accompanied by a more pronounced change in the volume of the cavity that is compressed by 76 and 54% for HN1 and HN2, respectively. This is shown by the squares for HN1 and circles for HN2 in Fig. 3(b). This means that the first significant compression of the nanogels corresponding to a small change in π, and, therefore to a small initial value of K (see eqn (1)), is due to the collapse of polymer into the volume of the cavity that is not occupied by pNIPAM in the dilute state. When larger pressures are applied, the cavity keeps decreasing in volume, but not so dramatically as in the first compression. As expected, the data in Fig. 3(b) indicate that at a large compression of the hollow nanogel, the volume occupied by the cavity is ≈90% smaller than its original value. In these condition, the inner volume of the nanogel is virtually inaccessible by the pNIPAM and, therefore, the polymeric network must be compressed. Since the amount of crosslinked points in the networks of the hollow nanogels is, at least, comparable to the number of crosslinks in the network of the normal 5 mol% crosslinked nanogel, the values of the bulk modulus of the hollow nanogels are now comparable to K5mol%.
However, a closer look at the course of the data in Fig. 3 reveals that for the nanogels with the larger cavity – HN1 (squares) – the initial bulk modulus is smaller than for the HN2 – circles in panel 3(a). This is a consequence of a larger change in volume already at the lowest applied π for the nanogel with the larger cavity, panel 3(b). We note that the ratio between the core radius and the total radius is ≈40% for HN1 and ≈20% for HN2. This difference leads the HN1 to collapse already to ≈84% of their original size when π equals (0.1649 ± 0.0009) kPa. At the same exerted stress, HN2 decreases its size only to ≈96% of its initial value. Also, the nanogel with the smaller cavity has a more smooth variation of their size and of the cavity volume with increasing π, as shown by the circles in Fig. 3(b). Such a strong influence on the particle collapse, especially at the first compression stages, suggests that a key parameter to control the compressibility of hollow nanogels is the control of the cavity size. Nanogels with a larger cavity might results even softer than ULC nanogels. It might also be possible that, for very large cavity, or in other words very thin shells, buckling might become more significant than isotropic deswelling or faceting as observed for microgels and hydrogels produced by microfluidics devices and with dimensions of hundreds of micrometres.64
4 Conclusions
In this study, we used small-angle neutron scattering with contrast matching to determine the bulk modulus of hollow nanogels. A partially-deuterated PEG has been used as an osmotic stress polymer to progressively compress the nanogels in solution. The scattering length density of the solvent – heavy water – matches that of the deuterated PEG and, therefore, does not contribute to the coherent neutron scattering. This means that the nanogel radius can be measured, even at the high concentrations of d83%PEG required to reach osmotic pressures one order of magnitude larger than those previously achieved by a similar method that used dynamic light scattering.36 From the local slope of the π vs. v curve, the local bulk modulus of the nanogels and its evolution with compression can be obtained.Our data shows that the hollow nanogels strongly collapse at lower osmotic stress with respect to nanogels synthesized with a comparable amount of crosslinker. The fact that hollow nanogels have a very small initial bulk modulus, i.e. a very large compressibility, is consistent with their behaviour once mixed with regular nanogels. We have observed that when few hollow nanogels are mixed with a majority of regular nanogels, synthesized with the same amount of BIS, the hollow nanogels show greater deswelling.31,41 Also their increased compressibility has been reported to be responsible for the absence of crystals in bulk solutions.23 Additionally, our data are consistent with the higher deformability observed once hollow nanogels are adsorbed at interfaces.24 The same deformability seems to be the origin of the absence of the solid-to-solid transition for a monolayer of hollow nanogels at oil–water interfaces.24
More in general, our study shows how the particle compressibility – or particle softness – is affected by multiple factors.34,38 For the case of hollow nanogels for instance, even if the polymeric network is relatively highly crosslinked, the presence of the solvent-filled cavity defines the first steps of the particle compression leading to very low values of K. As soon as the cavity is occupied by the pNIPAM, the amount of crosslinks in the network determines the further compressibility of the hollow nanogels which become as stiff as regular nanogels synthesised with a comparable amount of BIS.
Further study can be performed to explore more these aspects, for instance by varying systematically the ratio between cavity and total radius, that is the shell thickness. We expect that at a critical shell thickness, buckling will become the dominant mechanism for hollow nanogels experiencing external osmotic stress. Such a response has already been reported for larger microgels – with dimensions of some hundreds of micrometres,64 and might be interesting for application of these hollow nanogels as synthetic platelets for which an high deformability is a fundamental prerequisite.65
Our methodology can be further applied to probe the mechanical properties of other synthetic nanocapsules and biologically-relevant compounds.4–8 Probing the mechanical response to osmotic stress of nanocarriers is pivotal to further advance the production of synthetic virus-like particles able to mimic the behavior of viruses. For instance, the capsid of a virus has to be resistant to significant mechanical stresses exerted by the genetic material contained inside.6 Our methodology can be used to quantify the bulk moduli of their synthetic counterpart9,10,13–16 and verify how their stiffness relates to the one of the natural systems. Furthermore, the osmotic stresses we can apply are of the same order of magnitude needed to stop the ejection of genetic material at different infection stages.6,66 Therefore, our method can be used to investigate the arrangement of genetic material within both viruses and virus-like particles. This might allow us to determine the internal architecture of these nanocarriers and their content, i.e. determining its phase, on length scales of the order of few nanometres in situ and during the infection cycle.
Note
All the data used for this paper have been deposited in the RADAR4Chem database under https://doi.org/10.22000/681.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the financial support of the Deutsche Forschungsgemeinschaft within SFB 985 – Functional Microgels and Microgel Systems (Project no. 191948804), the ERS – OPEN Seed Fund Call 2021 (project no. OPSF630).Notes and references
- P. N. Pusey and W. Van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- D. Paloli, P. S. Mohanty, J. J. Crassous, E. Zaccarelli and P. Schurtenberger, Soft Matter, 2013, 9, 3000–3004 RSC.
- M. Antonietti and S. Förster, Adv. Mater., 2003, 15, 1323–1333 CrossRef CAS.
- R. K. O'Reilly, C. J. Hawker and K. L. Wooley, Chem. Soc. Rev., 2006, 35, 1068–1083 RSC.
- J. J. McManus, P. Charbonneau, E. Zaccarelli and N. Asherie, Curr. Opin. Colloid Interface Sci., 2016, 22, 73–79 CrossRef CAS.
- P. Buzón, S. Maity and W. H. Roos, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2020, 12, e1613 Search PubMed.
- Z. Liao, L. Tu, X. Li, X.-J. Liang and S. Huo, Nanoscale, 2021, 13, 18912–18924 RSC.
- E. J. Hartzell, R. M. Lieser, M. O. Sullivan and W. Chen, ACS Nano, 2020, 14, 12642–12651 CrossRef CAS PubMed.
- S. Hajebi, A. Abdollahi, H. Roghani-Mamaqani and M. Salami-Kalajahi, Langmuir, 2020, 36, 2683–2694 CrossRef CAS PubMed.
- L. Zhao, X. Song, X. Ouyang, J. Zhou, J. Li and D. Deng, ACS Appl. Mater. Interfaces, 2021, 13, 49631–49641 CrossRef CAS PubMed.
- R. F. Garmann, R. Sportsman, C. Beren, V. N. Manoharan, C. M. Knobler and W. M. Gelbart, J. Am. Chem. Soc., 2015, 137, 7584–7587 CrossRef CAS PubMed.
- X. Gao, S. Li, F. Ding, X. Liu, Y. Wu, J. Li, J. Feng, X. Zhu and C. Zhang, Adv. Mater., 2021, 33, 2006116 CrossRef CAS PubMed.
- D. Hua, J. Jiang, L. Kuang, J. Jiang, W. Zheng and H. Liang, Macromolecules, 2011, 44, 1298–1302 CrossRef CAS.
- N. Pippa, A. Meristoudi, S. Pispas and C. Demetzos, Int. J. Pharm., 2015, 485, 374–382 CrossRef CAS PubMed.
- S. Hajebi, A. Abdollahi, H. Roghani-Mamaqani and M. Salami-Kalajahi, Polymer, 2019, 180, 121716 CrossRef CAS.
- M. Brugnoni, F. Fink, A. Scotti and W. Richtering, Colloid Polym. Sci., 2020, 298, 1179–1185 CrossRef CAS.
- L. Zha, Y. Zhang, W. Yang and S. Fu, Adv. Mater., 2002, 14, 1090–1092 CrossRef CAS.
- S. Nayak, D. Gan, M. J. Serpe and L. A. Lyon, Small, 2005, 1, 416–421 CrossRef CAS PubMed.
- J. Dubbert, T. Honold, J. S. Pedersen, A. Radulescu, M. Drechsler, M. Karg and W. Richtering, Macromolecules, 2014, 47, 8700–8708 CrossRef CAS.
- N. Singh and L. A. Lyon, Chem. Mater., 2007, 19, 719–726 CrossRef CAS.
- M. F. Schulte, A. Scotti, A. P. Gelissen, W. Richtering and A. Mourran, Langmuir, 2018, 34, 4150–4158 CrossRef CAS PubMed.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- A. Scotti, A. Denton, M. Brugnoni, R. Schweins and W. Richtering, Phys. Rev. E, 2021, 103, 022612 CrossRef CAS PubMed.
- J. Vialetto, F. Camerin, F. Grillo, S. N. Ramakrishna, L. Rovigatti, E. Zaccarelli and L. Isa, ACS Nano, 2021, 15, 13105–13117 CrossRef CAS PubMed.
- H. Masoud and A. Alexeev, ACS Nano, 2012, 6, 212–219 CrossRef CAS PubMed.
- G. Liu, C. Zhu, J. Xu, Y. Xin, T. Yang, J. Li, L. Shi, Z. Guo and W. Liu, Colloids Surf., B, 2013, 111, 7–14 CrossRef CAS PubMed.
- B. P. Tripathi, N. C. Dubey and M. Stamm, ACS Appl. Mater. Interfaces, 2014, 6, 17702–17712 CrossRef CAS PubMed.
- M. Pelaez-Fernandez, A. Souslov, L. Lyon, P. M. Goldbart and A. Fernandez-Nieves, Phys. Rev. Lett., 2015, 114, 098303 CrossRef CAS PubMed.
- A. Scotti, J. Houston, M. Brugnoni, M. Schmidt, M. Schulte, S. Bochenek, R. Schweins, A. Feoktystov, A. Radulescu and W. Richtering, Phys. Rev. E, 2020, 102, 052602 CrossRef CAS.
- M. Rey, M. Á. Fernández-Rodrguez, M. Steinacher, L. Scheidegger, K. Geisel, W. Richtering, T. M. Squires and L. Isa, Soft Matter, 2016, 12, 3545–3557 RSC.
- A. Scotti, M. Brugnoni, A. Rudov, J. Houston, I. Potemkin and W. Richtering, J. Chem. Phys., 2018, 148, 174903 CrossRef CAS PubMed.
- A. Scotti, A. R. Denton, M. Brugnoni, J. E. Houston, R. Schweins, I. I. Potemkin and W. Richtering, Macromolecules, 2019, 52, 3995–4007 CrossRef CAS.
- K. Geisel, A. A. Rudov, I. I. Potemkin and W. Richtering, Langmuir, 2015, 31, 13145–13154 CrossRef CAS PubMed.
- A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700 CrossRef CAS PubMed.
- P. Voudouris, D. Florea, P. van der Schoot and H. M. Wyss, Soft Matter, 2013, 9, 7158–7166 RSC.
- B. Sierra-Martin, J. A. Frederick, Y. Laporte, G. Markou, J. J. Lietor-Santos and A. Fernandez-Nieves, Colloid Polym. Sci., 2011, 289, 721–728 CrossRef CAS.
- A. Scotti, M. Pelaez-Fernandez, U. Gasser and A. Fernandez-Nieves, Phys. Rev. E, 2021, 103, 012609 CrossRef CAS PubMed.
- J. E. Houston, L. Fruhner, A. de la Cotte, J. Rojo González, A. V. Petrunin, U. Gasser, R. Schweins, J. Allgaier, W. Richtering and A. Fernandez-Nieves, et al. , Sci. Adv., 2022, 8, eabn6129 CrossRef PubMed.
- M. R. Islam, R. Nguyen and L. A. Lyon, Macromol. Rapid Commun., 2021, 42, 2100372 CrossRef CAS PubMed.
- W. Stöber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62–69 CrossRef.
- A. Scotti, S. Bochenek, M. Brugnoni, M.-A. Fernandez-Rodriguez, M. F. Schulte, J. Houston, A. P. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Nat. Commun., 2019, 10, 1–8 CrossRef CAS PubMed.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- T. Hellweg, C. Dewhurst, E. Brückner, K. Kratz and W. Eimer, Colloid Polym. Sci., 2000, 278, 972–978 CrossRef CAS.
- S. Nöjd, P. Holmqvist, N. Boon, M. Obiols-Rabasa, P. S. Mohanty, R. Schweins and P. Schurtenberger, Soft Matter, 2018, 14, 4150–4159 RSC.
- F. S. Varley, Neutron News, 1992, 3, 29–37 Search PubMed.
- A. Scotti, Soft Matter, 2021, 17, 5548–5559 RSC.
- P. S. Mohanty, S. Nöjd, K. van Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa, R. Schweins, A. Stradner and P. Schurtenberger, Sci. Rep., 2017, 7, 1–12 CrossRef CAS PubMed.
- U. Gasser, J. Hyatt, J.-J. Lietor-Santos, E. Herman, L. A. Lyon and A. Fernandez-Nieves, J. Chem. Phys., 2014, 141, 034901 CrossRef CAS PubMed.
- A. Scotti, U. Gasser, E. S. Herman, M. Pelaez-Fernandez, J. Han, A. Menzel, L. A. Lyon and A. Fernández-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5576–5581 CrossRef CAS PubMed.
- I. Berndt, J. S. Pedersen and W. Richtering, Angew. Chem., 2006, 118, 1769–1773 CrossRef.
- M. Brugnoni, A. Scotti, A. A. Rudov, A. P. H. Gelissen, T. Caumanns, A. Radulescu, T. Eckert, A. Pich, I. I. Potemkin and W. Richtering, Macromolecules, 2018, 51, 2662–2671 CrossRef CAS.
- A. Fernandez-Barbero, A. Fernández-Nieves, I. Grillo and E. López-Cabarcos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051803 CrossRef CAS PubMed.
- J. S. Pedersen, D. Posselt and K. Mortensen, J. Appl. Crystallogr., 1990, 23, 321–333 CrossRef.
- O. Virtanen, A. Mourran, P. Pinard and W. Richtering, Soft Matter, 2016, 12, 3919–3928 RSC.
- S. V. Nikolov, A. Fernandez-Nieves and A. Alexeev, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27096–27103 CrossRef CAS PubMed.
- G. M. Conley, P. Aebischer, S. Nöjd, P. Schurtenberger and F. Scheffold, Sci. Adv., 2017, 3, e1700969 CrossRef PubMed.
- G. M. Conley, C. Zhang, P. Aebischer, J. L. Harden and F. Scheffold, Nat. Commun., 2019, 10, 2436 CrossRef PubMed.
- I. B. De Aguiar, T. Van de Laar, M. Meireles, A. Bouchoux, J. Sprakel and K. Schroën, Sci. Rep., 2017, 7, 1–11 CrossRef PubMed.
- T. Höfken, C. Strauch, S. Schneider and A. Scotti, Nano Lett., 2022, 22, 2412–2418 CrossRef PubMed.
- F. Scheffold, P. Daz-Leyva, M. Reufer, N. B. Braham, I. Lynch and J. L. Harden, Phys. Rev. Lett., 2010, 104, 128304 CrossRef PubMed.
- J. Lietor-Santos, U. Gasser, R. Vavrin, Z. Hu and A. Fernandez-Nieves, J. Chem. Phys., 2010, 133, 034901 CrossRef CAS PubMed.
- J. Mattsson, H. M. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. Hu, D. R. Reichman and D. A. Weitz, Nature, 2009, 462, 83–86 CrossRef CAS PubMed.
- P. Van Der Scheer, T. Van De Laar, J. Van Der Gucht, D. Vlassopoulos and J. Sprakel, ACS Nano, 2017, 11, 6755–6763 CrossRef CAS PubMed.
- J. G. Werner, S. Nawar, A. A. Solovev and D. A. Weitz, Macromolecules, 2018, 51, 5798–5805 CrossRef CAS.
- A. C. Brown, S. E. Stabenfeldt, B. Ahn, R. T. Hannan, K. S. Dhada, E. S. Herman, V. Stefanelli, N. Guzzetta, A. Alexeev and W. A. Lam, et al. , Nat. Mater., 2014, 13, 1108–1114 CrossRef CAS PubMed.
- M. G. van Rosmalen, C. Li, A. Zlotnick, G. J. Wuite and W. H. Roos, Biophys. J., 2018, 115, 1656–1665 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00680d |
| This journal is © The Royal Society of Chemistry 2022 |