Mechanical stress affects dynamics and rheology of the human genome†
Christina M.
Caragine
,
Nikitas
Kanellakopoulos
and
Alexandra
Zidovska
 *
*
Center for Soft Matter Research, Department of Physics, New York University, New York, NY 10003, USA. E-mail: alexandra.zidovska@nyu.edu
First published on 7th December 2021
Abstract
Material properties of the genome are critical for proper cellular function – they directly affect timescales and length scales of DNA transactions such as transcription, replication and DNA repair, which in turn impact all cellular processes via the central dogma of molecular biology. Hence, elucidating the genome's rheology in vivo may help reveal physical principles underlying the genome's organization and function. Here, we present a novel noninvasive approach to study the genome's rheology and its response to mechanical stress in form of nuclear injection in live human cells. Specifically, we use Displacement Correlation Spectroscopy to map nucleus-wide genomic motions pre/post injection, during which we deposit rheological probes inside the cell nucleus. While the genomic motions inform on the bulk rheology of the genome pre/post injection, the probe's motion informs on the local rheology of its surroundings. Our results reveal that mechanical stress of injection leads to local as well as nucleus-wide changes in the genome's compaction, dynamics and rheology. We find that the genome pre-injection exhibits subdiffusive motions, which are coherent over several micrometers. In contrast, genomic motions post-injection become faster and uncorrelated, moreover, the genome becomes less compact and more viscous across the entire nucleus. In addition, we use the injected particles as rheological probes and find the genome to condense locally around them, mounting a local elastic response. Taken together, our results show that mechanical stress alters both dynamics and material properties of the genome. These changes are consistent with those observed upon DNA damage, suggesting that the genome experiences similar effects during the injection process.
Introduction
The nucleus is the control center of the cell – it houses the genome in the form of DNA that contains genetic information essential for life as well as subnuclear bodies (e.g., nucleoli) responsible for other vital cellular functions.1 Material properties of the nucleus and its constituents directly impact the timescales and length scales of nuclear processes, which in turn affect all cellular processes via the central dogma of biology.2,3 For example, viscosity of the nucleoplasm affects rates of molecular transport inside the nucleus, while the persistence length of the chromatin fiber – the functional form of DNA inside the cell – affects local organization and dynamics of the genome.4 Hence, elucidating material properties of the nucleus and its components is crucial for understanding biophysical origins of nuclear organization and function.5Rheological properties of the nucleus as a whole have been investigated using micropipette aspiration and micromanipulation techniques, revealing its complex viscoelastic behavior.6–10 The former uncovered a largely elastic contribution of the nuclear envelope and a viscous contribution from chromatin in live cells.8 The latter found chromatin to resist small deformations in isolated nuclei and contribute to the overall nuclear stiffness.9–11 The complex rheological behavior of the cell nucleus highlights the importance of understanding the mechanical contributions of individual nuclear components such as the genome.
To interrogate the rheology of the nuclear interior in live cells, passive and active microrheology approaches have been employed, both relying on rheological probes injected inside the nucleus.12–15 These probes, ranging in size from 100 nm to 1 μm, were either passively moving or actively manipulated by magnetic forces inside the nucleus, their motion reporting on the rheology of their local environment. These measurements yielded nucleoplasmic viscosity of 25–1000 Pa s and elastic modulus of 0.5–850 Pa.12–15 The large range of measured values may stem from the difference in the probe size, exploring different length scales of the system, but also from the heterogeneity of the nuclear interior, as the probes report only on rheology of their immediate environment.5 In addition, injection of particles inside the nucleus is an invasive process, which only few cells survive, causing the cell to mount a stress response.16 Indeed, mechanical stress on the nucleus, for example during cellular migration through tight constrictions, was found to cause DNA damage, affect the genome organization as well as the overall cell phenotype.17–22 Hence, nuclear injection as a form of mechanical stress might alter effective material properties of the nucleus and its components.
To extract rheology of the nuclear interior in a noninvasive way, an approach using naturally occurring nuclear probes and their intrinsic dynamics was recently developed.23,24 Namely, the nucleolus, a natural liquid droplet present in the nucleus, was found to undergo subtle surface fluctuations enabling measurement of surface tension of the nucleolus-nucleoplasm interface ∼10−6 N m−1. In addition, nucleolar coalescence allowed for measurement of the nucleoplasmic viscosity ∼103 Pa s.23 Another technique used artificial droplets, whose components were genetically encoded in the cell and assembled into droplets upon light activation.25,26 The droplet motion as well as their coalescence kinetics revealed an elastic modulus of the nucleoplasm of 0.1–1 Pa.25 It is important to note, that these approaches use equilibrium assumptions for inferring material properties, hence the observed values are likely effective quantities. Furthermore, these approaches employ microscopic probes, informing on the rheology of their surroundings, and thus leaving large parts of the nucleus unexplored. Moreover, the rheological properties of individual nuclear constituents such as the genome remain largely unknown.
In this work, we present a noninvasive technique that allows to measure rheological behavior of the genome locally as well as across the whole nucleus in live cells. We employ Displacement Correlation Spectroscopy (DCS) to map intrinsic dynamics of the chromatin fiber across the nucleus,27 which directly reflects on the physical properties of the genome allowing us to extract the genome's rheology.28 Using this approach we investigate the impact of mechanical stress on the genome's dynamics and rheology. To this end, we inject particles inside the nucleus and assess the effect after 24 hours, when the nucleus has healed from the injection. We find that while some nuclei recover their physiological state, 60% of injected nuclei exhibit changes in the genome's compaction, dynamics and rheology. Specifically, local chromatin displacements increase, while the coherent chromatin motions, which occur in uninjected nuclei, are eliminated. Moreover, chromatin becomes less compact and more viscous across the entire nucleus. In addition, we use the injected particles as rheological probes and find chromatin to condense around these probes, mounting a local elastic response. Taken together, our results show that mechanical stress alters both dynamics and material properties of the genome. Moreover, the observed changes are consistent with induction of DNA damage via mechanical stress.
Materials and methods
Cell culture
The stable human HeLa H2B-GFP cell line (CCL-2) was cultured according to ATCC recommendations. Cells were cultured in a humidified, 5% CO2 (vol/vol) atmosphere in Gibco Dulbecco's modified Eagle's medium (DMEM) supplemented with 10% FBS (vol/vol), 100 units per mL penicillin, 100 μg mL−1 streptomycin (Invitrogen) and 4.5 μg mL−1 Plasmocin Prophylactic (Invivogen). Cells were mycoplasma free, as determined by the PlasmoTest (Invivogen). Cells were plated onto Nunc Lab-Tek II Chambered Coverglass dishes (Thermo Scientific) 48 h prior to injection and imaged during injection as well as 24 h after injection. Prior to live cell imaging, the media was changed to Gibco CO2-independent media (Invitrogen) supplemented with L-glutamine (Invitrogen). Samples were mounted on the microscope stage in a custom-built environmental chamber maintained at 37 °C. For fixation experiments, cells were fixed with 3.7% formaldehyde in PBS (Gibco) at room temperature for 40 min and then washed three times with PBS every 5 min.Nuclear injection
Cell nuclei were injected with 100 nm fluorescent beads (580 nm/605 nm) with carboxylated (negatively charged) surface (Fluospheres, Molecular Probes) using the Femtojet injection system (Eppendorf), and Femtotip needles (Eppendorf) with an inner diameter of 0.5 μm and outer diameter of 1 μm. Beads were diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 in PBS. The injection solution was filtered through centrifuge tube filters with a 0.44 μm pore size (Corning). The nuclei were injected with an injection volume of 100 μm3 (contains ∼1 particle), injection speed of 900 μm3 s−1 and injection time of 0.1 s. Cells were imaged during injection and their position was recorded. After injection, the cell medium in samples was changed to DMEM supplemented with 10% FBS (vol/vol), 100 units per mL penicillin, 100 μg mL−1 streptomycin (Invitrogen) and 4.5 μg mL−1 Plasmocin Prophylactic (Invivogen), followed by 24 h incubation time prior to further imaging. 31 independent nuclear injection experiments were performed, with a total of 106 injected nuclei.
1000 in PBS. The injection solution was filtered through centrifuge tube filters with a 0.44 μm pore size (Corning). The nuclei were injected with an injection volume of 100 μm3 (contains ∼1 particle), injection speed of 900 μm3 s−1 and injection time of 0.1 s. Cells were imaged during injection and their position was recorded. After injection, the cell medium in samples was changed to DMEM supplemented with 10% FBS (vol/vol), 100 units per mL penicillin, 100 μg mL−1 streptomycin (Invitrogen) and 4.5 μg mL−1 Plasmocin Prophylactic (Invivogen), followed by 24 h incubation time prior to further imaging. 31 independent nuclear injection experiments were performed, with a total of 106 injected nuclei.
Microscopy and image acquisition
Cells were imaged with a Yokogawa CSU-X1 spinning disc confocal head with an internal motorized high-speed emission filter wheel, Spectral Applied Research Borealis modification for increased light throughput and illumination homogeneity on a Nikon Ti-E inverted microscope equipped with an oil-immersion 100× Plan Apo NA 1.4 objective lens and the Perfect Focus system. The microscope was mounted on a vibration-isolation air table. To image H2B-GFP and the red fluorescent beads at the same time, we illuminated the sample simultaneously with both excitation wavelengths, 488 and 561 nm. The emission was separated by the W-View Gemini Image Splitter (Hamamatsu) using a dichroic mirror (Chroma Technology), followed by an ET525/30m and an ET630/75m emission filter (Chroma Technology). The two fluorescent signals were allocated to the two halves of the image sensor, producing two distinct images. Images were obtained with a Hamamatsu ORCA-R2 cooled CCD camera controlled with MetaMorph 7 (Molecular Devices). The pixel size for the 100× objective was 0.065 μm. The exposure time for each frame for both signals was 250 ms. The streams of 16-bit images were saved as multi-tiff stacks.Image processing and data analysis
Images were converted to single-tiff images and analyzed with MatLab (The MathWorks). The nuclear contours were determined from the H2B-GFP signal using previously published procedures.29 To find the position of the fluorescent beads, we used a previously published feature-finding algorithm.30 The particle location was found using a MatLab built-in local-maxima function and tracked in time using previously published algorithms.30 The mean squared displacement MSD of particles was computed as MSD(Δt) = 〈(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t + Δt) −
(t + Δt) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t))2〉. Particle motion was corrected for potential nuclear motion by subtracting the nuclear centroid motion. To obtain the noise floor for the particle tracking measurements, we imaged and tracked 100 nm fluorescent beads immobilized on a glass slide.
(t))2〉. Particle motion was corrected for potential nuclear motion by subtracting the nuclear centroid motion. To obtain the noise floor for the particle tracking measurements, we imaged and tracked 100 nm fluorescent beads immobilized on a glass slide.
Displacement correlation spectroscopy
Displacement Correlation Spectroscopy (DCS) maps were calculated for time lags Δt = 0.25–15 s following previously published procedures.27 From the displacement fields![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt), we calculate the mean square network displacement MSND(Δt) = 〈|
,Δt), we calculate the mean square network displacement MSND(Δt) = 〈|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt)|2〉 for displacements across the entire nucleus. The average spatial displacement autocorrelation function is computed as Cdx = 〈dx(
,Δt)|2〉 for displacements across the entire nucleus. The average spatial displacement autocorrelation function is computed as Cdx = 〈dx(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt),dx(
,Δt),dx(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) + Δ
+ Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt)〉 for the x-component of the displacement field. All nuclei were screened for nuclear drift, with no significant nuclear motion detected over 25 s observation time.
,Δt)〉 for the x-component of the displacement field. All nuclei were screened for nuclear drift, with no significant nuclear motion detected over 25 s observation time.
Microrheology calculations
To compute the complex viscoelastic modulus from the MSND, we use the generalized Stokes–Einstein relation (GSER) following procedures described earlier.28,31–34 Specifically, we apply a power-law approximation of the Laplace transform using previously published algorithms.33Statistical analysis
Statistical significance of results was evaluated by computing p-values using a χ2-test for comparing MSND(Δt), MSD(Δt), G′(ω) and G′′(ω) and t-test for comparing intensity distributions (I − Imin)/〈I〉.Results
Mechanical stress alters chromatin dynamics in vivo
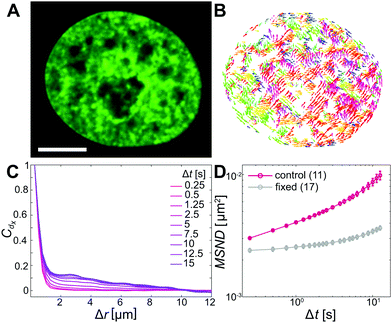
To assess changes in chromatin dynamics upon application of mechanical stress, we observe chromatin motions in live human cells before and after nuclear injection. We visualize chromatin using histone H2B-GFP, a reliable marker of chromatin position,35 and use spinning disc confocal microscopy to record streams of H2B-GFP signal with a temporal resolution of 250 ms over 25 s before and after nuclear injection. We then evaluate chromatin motions in both uninjected and injected nuclei using displacement correlation spectroscopy (DCS),27 mapping chromatin dynamics across the entire nucleus in real time.To establish a benchmark, we first measure chromatin dynamics in nuclei under physiological conditions (Fig. 1A). Using DCS we obtain chromatin displacement fields ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt) for Δt =0.25–15 s. Fig. 1B shows a DCS map for Δt = 10 s, with chromatin displacements color-coded by their direction. Patches with vectors of the same colors are readily visible, indicating that chromatin within large patches moves coherently in the same direction. Such coherent motions have been observed before and found to be a hallmark of the genome's physiological dynamics.27,36–38 To quantify the extent of these coherent motions we compute the spatial displacement autocorrelation function, Cdx = 〈dx(
,Δt) for Δt =0.25–15 s. Fig. 1B shows a DCS map for Δt = 10 s, with chromatin displacements color-coded by their direction. Patches with vectors of the same colors are readily visible, indicating that chromatin within large patches moves coherently in the same direction. Such coherent motions have been observed before and found to be a hallmark of the genome's physiological dynamics.27,36–38 To quantify the extent of these coherent motions we compute the spatial displacement autocorrelation function, Cdx = 〈dx(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt),dx(
,Δt),dx(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) + Δ
+ Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt)〉 where dx(
,Δt)〉 where dx(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt) are the x-components of displacement vectors d(
,Δt) are the x-components of displacement vectors d(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt) (Fig. 1C). Consistent with earlier observations, we find Cdx to increase with increasing Δt.27 In addition, we compute the mean square network displacement, MSND(Δt) = 〈|
,Δt) (Fig. 1C). Consistent with earlier observations, we find Cdx to increase with increasing Δt.27 In addition, we compute the mean square network displacement, MSND(Δt) = 〈|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Δt)|2〉 over all chromatin displacements within a nucleus.27Fig. 1D shows MSND(Δt) averaged over 11 nuclei under physiological conditions (red line). Data for individual nuclei are shown in Fig. S1A (ESI†). As a negative control, we perform the same measurements in formaldehyde-fixed cells, confirming that our measurements are well above the noise floor (Fig. 1D, grey).
,Δt)|2〉 over all chromatin displacements within a nucleus.27Fig. 1D shows MSND(Δt) averaged over 11 nuclei under physiological conditions (red line). Data for individual nuclei are shown in Fig. S1A (ESI†). As a negative control, we perform the same measurements in formaldehyde-fixed cells, confirming that our measurements are well above the noise floor (Fig. 1D, grey).
To evaluate the type of motion that chromatin undergoes, we fit the average MSND(Δt) to f(Δt) =A + BΔtα, where A accounts for dynamics below our temporal resolution (Fig. S1D, ESI†).27,30 Our fit yields Acontrol = 0.0028 ± 0.0001 μm2, Bcontrol = 0.0012 ± 0.0001 μm2 s−α and αcontrol = 0.68 ± 0.02, which suggests that chromatin undergoes a subdiffusive motion and is in excellent agreement with earlier studies.27
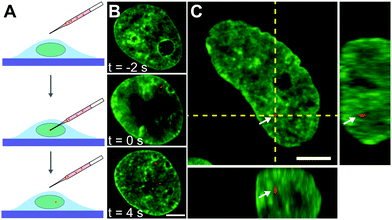
Next, we inject nuclei with a solution of fluorescent beads 100 nm in diameter at a concentration of ∼1 particle per injection volume (Fig. 2A, see Materials and methods). The beads have a negatively charged carboxylate-modified surface, chosen to prevent their interactions with chromatin. Fig. 2B shows a nucleus prior (t = −2 s), during (t = 0 s), and directly after injection (t = 4 s), with fluorescently labelled chromatin (H2B-GFP, green) and injected particle (red). During injection, which lasts ∼0.1 s, the nucleus transiently swells (∼20%), then immediately relaxes to it's original size upon the removal of the needle (Fig. 2B, middle and bottom panels). The outer diameter of the injection needle is 1 μm, and so an opening of that size is left in the nuclear envelope. To allow the cell to repair the hole in the nuclear envelope as well as possible perturbations to the genome by the injection, we wait for 24 h, before we continue the experiment. We injected a total of 106 nuclei, 23 of which survived past 24 h, with 10 nuclei still containing the injected particles. Out of those, 8 nuclei contained a single particle and 2 nuclei contained 2 particles. We then collect concurrent 25 s streams imaging fluorescent signals of both chromatin and injected particles. In addition, we obtain z-stacks of images in both signals to verify that the injected particle is indeed inside the nucleus. We confirm this by reviewing the orthogonal views in xz and yz planes in the overlay of the two signals (Fig. 2C). For further analysis, we keep only cells, which contain an injected particle.
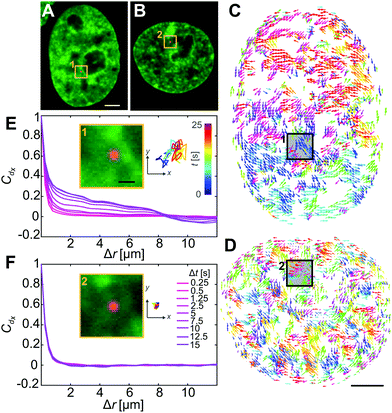
Once we confirm that nuclei were successfully injected (Fig. 3A and B), we analyze chromatin dynamics of 10 injected nuclei in the same way as before by performing DCS. Fig. 3C and D show the DCS maps for the injected nuclei from Fig. 3A and B, respectively. Boxes 1 & 2 highlight the localization of the particles in micrographs (Fig. 3A and B, yellow boxes) and in the corresponding DCS maps (Fig. 3C and D, black boxes). We then compute the spatial displacement autocorrelation function Cdx to check for the presence of large-scale coherence of chromatin motions (Fig. 3E and F). Strikingly, we find that in some cases, these coherent motions are present, as shown by an increase of Cdx with increasing Δt (Fig. 3E), while in other cases the coherent motions cease to exist, with Cdx remaining unchanged at all Δt (Fig. 3F). To better assess this difference, we measure for all injected nuclei the correlation length ξ(Δt), which we define as the distance, when Cdx = 0.1 for each Δt (Fig. 3E and F). We then categorize chromatin motions as coherent for nuclei, where (ξ(25s) − ξ(0.25s))/ξ(0.25s) > 0.5, and not coherent otherwise. We find that from the 10 injected nuclei, only 4 nuclei displayed coherent chromatin motions, while the remaining 6 exhibited uncorrelated chromatin motions at all time scales. The first group exhibits coherent chromatin motions with average maximum 〈ξmax〉 ∼ 3 μm, which agrees with coherence measured for uninjected nuclei (〈ξmax〉 ∼ 3 μm), while the second group lacking chromatin coherence shows 〈ξmax〉 ∼ 0.8 μm (Fig. S2, ESI†). This suggests that the mechanical stress from the injection can significantly alter the physiological chromatin dynamics and eliminate coherent chromatin motions.
During the injection we deposit fluorescent beads inside the nucleus, motion of which directly reports on the rheology of the surrounding chromatin (Fig. 3A and B, yellow boxes). We track motion of these particles (Fig. 3E and F, insets) and observe that their motion varies across the injected nuclei. As illustrated by the particle trajectories over 25 s, particles in nuclei with coherent chromatin motion are more mobile (Fig. 3E, inset) than those in nuclei, whose chromatin lacks such motion (Fig. 3F, inset). This observation suggests that these trace particles probe environments of different rheological properties in nuclei that exhibit coherent chromatin motions versus in those which do not. In the following, we will analyze in detail both the dynamical and rheological changes that chromatin undergoes upon the mechanical stress of an injection.
Dynamical signatures of chromatin upon mechanical stress
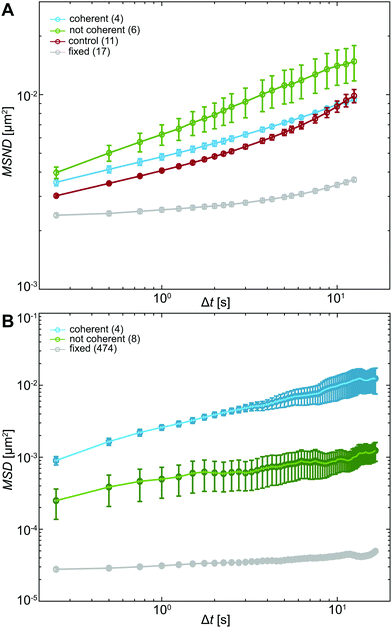
To evaluate the differences in chromatin dynamics before and after nuclear injection, we compute the mean square network displacement MSND(Δt) for all nuclei as described earlier (Fig. S1, ESI†). Specifically, we compare the average MSND(Δt) of three separate groups of nuclei: nuclei before injection (control, Fig. 4A, red), injected nuclei with coherent chromatin motions (coherent, Fig. 4A, blue) and injected nuclei that lack chromatin coherence (not coherent, Fig. 4A, green). We find that MSND(Δt) of control nuclei and injected nuclei with chromatin coherency show similar behavior (Fig. 4A, red & blue), while the injected nuclei without chromatin coherence display visibly larger chromatin displacements, with their MSND(Δt) reaching values ∼50% higher than the control (Fig. 4A, green, p-value <10−7). Strikingly, the extent of the observed MSND(Δt) changes upon injection for nuclei lacking chromatin coherency is comparable to that of functional perturbations of the genome (e.g. inhibition of transcription).27Next, we assess the type of motion that chromatin undergoes in the injected nuclei by fitting the average MSNDs of the two groups (coherent, not coherent) to the model introduced earlier f(Δt) =A + BΔtα (Fig. S1D, ESI†). We obtain the following fitting parameters for the injected nuclei with coherent chromatin motion and without it, denoted by indices c and nc, respectively. For the former we find Ac = 0.0019 ± 0.0001 μm2, Bc = 0.0028 ± 0.0001 μm2 s−α and αc = 0.39 ± 0.01, for the latter, Anc = 10−7 ± 0.001 μm2, Bnc = 0.006 ± 0.001 μm2 s−α and αnc = 0.33 ± 0.04. Interestingly, in both cases, αc/nc is strongly reduced compared to αcontrol ∼ 0.68 in uninjected nuclei (Table S1, ESI†). And although αc and αnc are similar, the short time dynamics captured by A is strongly reduced, when chromatin coherence is eliminated. This suggests that upon mechanical stress chromatin dynamics undergo dramatic changes at both short length scales (as per A) and large length scales (as per possible elimination of coherent motion). Moreover, the change in α upon injection may hint at possible changes in chromatin rheology.
To this end, motion of the tracer particles that we injected inside the nuclei is very informative as it directly reports on the rheology of the particle's surroundings. We track these particles and compute mean square displacement MSD(Δt) = 〈(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t + Δt) −
(t + Δt) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t))2〉 for each particle. We then sort these particles by their location in an injected nucleus with or without coherent chromatin motions (Fig. S3, ESI†). Fig. 4B shows average MSDs for particles inside injected nuclei with coherent chromatin motion (blue, N = 4) and inside nuclei lacking chromatin coherency (green, N = 8). All of these measurements are well above the noise floor (Fig. 4B, grey line, see Materials and methods).
(t))2〉 for each particle. We then sort these particles by their location in an injected nucleus with or without coherent chromatin motions (Fig. S3, ESI†). Fig. 4B shows average MSDs for particles inside injected nuclei with coherent chromatin motion (blue, N = 4) and inside nuclei lacking chromatin coherency (green, N = 8). All of these measurements are well above the noise floor (Fig. 4B, grey line, see Materials and methods).
Clearly, particles in injected nuclei with chromatin coherency are more mobile than those in injected nuclei where chromatin coherency ceased (Fig. 4B, p-value <10−12). We fit the average MSD(Δt) of the two particle groups to MSD(Δt) = BΔtα and obtain B and α for particles in nuclei with and without coherent chromatin motions, denoted by indices c and nc, respectively. For the former we find Bc = 0.0025 ± 0.0001 μm2 s−α and αc = 0.59 ± 0.01, for the latter, Bnc = 0.00048 ± 0.00002 μm2 s−α and αnc = 0.30 ± 0.02 (Table S1, ESI†). The different dynamics of injected particles suggest distinct local chromatin rheology in coherent/uncoherent nuclei. Moreover, our results show that chromatin rheology might sensitively depend on chromatin dynamics. Next, we will explore this connection.
Chromatin rheology changes upon mechanical stress
The measured chromatin dynamics directly reflects its rheology. We assess the frequency-dependent rheological behavior of chromatin analyzing the intrinsic chromatin dynamics using the framework of passive microrheology.28,32–34,39 It is important to note that passive microrheology assumes that the observed particle motion is thermally driven and thus obeys the fluctuation dissipation theorem.32–34,39 In contrast, chromatin motions are active, driven by ATP-consuming nuclear processes.27,36 To account for this activity, we use an effective temperature, which is frequency-independent. This assumption is based on earlier observations that short wavelength chromatin fluctuations are thermal-like and active chromatin dynamics can be modeled by isotropic noise.36,40–42Specifically, we compute the complex viscoelastic modulus Ĝ(s) using the generalized Stokes–Einstein relation:28,32–34,39
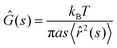 | (1) |
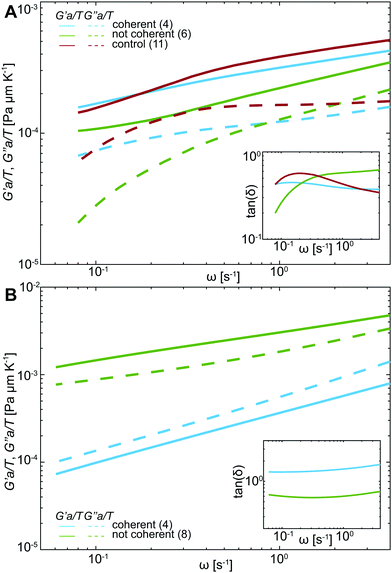
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2(s)〉 is the Laplace transform of the MSND(Δt). For each complex frequency s = iω, we obtain Ĝ(ω) = G′(ω) + iG′′(ω), where G′(ω) is the storage modulus and G′′(ω) is the loss modulus, informing on the frequency-dependent elastic and viscous responses of chromatin, respectively. Since T and a are unknown, we compute G′(ω)a/T and G′′(ω)a/T, which are shown in Fig. 5A. For clarity, plots containing error bars are shown in Fig. S4 (ESI†).
2(s)〉 is the Laplace transform of the MSND(Δt). For each complex frequency s = iω, we obtain Ĝ(ω) = G′(ω) + iG′′(ω), where G′(ω) is the storage modulus and G′′(ω) is the loss modulus, informing on the frequency-dependent elastic and viscous responses of chromatin, respectively. Since T and a are unknown, we compute G′(ω)a/T and G′′(ω)a/T, which are shown in Fig. 5A. For clarity, plots containing error bars are shown in Fig. S4 (ESI†).
Upon initial visual inspection of G′(ω) and G′′(ω), we find that while control nuclei and injected nuclei with coherent motions exhibit rather similar values, injected nuclei lacking coherency are strikingly different (p-value <10−7). We find that the viscoleastic response of uninjected (control) nuclei (Fig. 5A, red) is dominated by the storage modulus at all frequencies. Moreover, the storage modulus increases with increasing frequency, while the loss modulus remains largely unchanged. Similarly, the elastic response dominates in all injected nuclei independent of the presence of chromatin coherent motions, showing an increase with frequency (Fig. 5A, green & blue solid lines). In contrast, the loss modulus for nuclei with coherent motions remains unchanged with increasing frequency (similarly to control), while it monotonically increases for nuclei lacking the coherent motions (Fig. 5A, green & blue dashed lines).
To evaluate the relative contribution of the storage and loss moduli, we calculate the loss tangent, tan(δ) = G′′(ω)/G′(ω) (Fig. 5A, inset). Indeed, the tan(δ) < 1 across all frequencies for all injected as well as control nuclei. We can estimate absolute values of the measured G′ and G′′ by using an effective temperature of 300 °C, found earlier for the nucleus in live human cells,29 and particles sizes ranging from a single nucleosome (∼10 nm) to larger chromatin regions (∼100–1000 nm). This yields G′ ≈ 0.1–30 Pa and G′′ ≈ 0.04–10 Pa (Table S2, ESI†).
Similarly, the motion of injected tracer particles reports on the rheology of the surrounding chromatin. We apply the same procedure as above using the generalized Stokes–Einstein relation (eqn (1)) to extract the complex viscoelastic modulus of chromatin from the MSD(Δt) measured for the injected particles (Fig. 4B). Fig. 5B shows G′(ω)a/T and G′′(ω)a/T obtained for particles in injected nuclei with coherent chromatin motion (blue) and without it (green), showing clearly distinct behavior (p-value <10−6). For clarity, the error bars are shown in Fig. S5 (ESI†). We find that in nuclei with coherent chromatin motions the viscous modulus dominates the rheological response of chromatin at all frequencies (Fig. 5B, blue). In contrast, rheology of nuclei lacking chromatin coherency is dominated by the storage modulus at all frequencies (Fig. 5B, green). This is further illustrated by the loss tangent tan(δ) < 1 at all frequencies (Fig. 5A, inset, green). Using the size of the injected particles a = 100 nm and an effective temperature of T = 300 °C, which was obtained for the human nucleus earlier,29 we can estimate the absolute values of G′ and G′′: for the measured frequency range, we find G′ = 0.4–0.6 Pa and G′′ = 0.6–8.0 Pa for injected nuclei with coherent chromatin motions, and G′ = 6.9–28 Pa and G′′ = 4.4–19.4 Pa for injected nuclei without coherency (Table S2, ESI†). The rheological behavior observed in nuclei without coherency resembles earlier observations, which measured chromatin rheology shortly after injection.12,15
Overall, our data suggest that chromatin rheology can change in response to mechanical stress of injection. Remarkably, the presence of chromatin coherency serves as an indicator of these changes. Specifically, if coherent chromatin motions are preserved, the rheology remains similar to the physiological state prior to injection. However, if the chromatin coherency ceases, chromatin becomes overall more viscous (less elastic). In addition, our tracer particles report on the state of chromatin in their immediate vicinity, providing further insight into rheology of mechanically stressed injected nuclei. Strikingly, the local particle surroundings in injected nuclei with coherent motions are largely viscous, while in injected nuclei lacking coherency particle surroundings are predominantly elastic. This suggests that these particles either preferentially localize in particular types of intranuclear environment, or hint at a local response of the surrounding chromatin to the particle deposition. Next, we will explore this hypothesis.
Mechanical stress induces changes in chromatin compaction
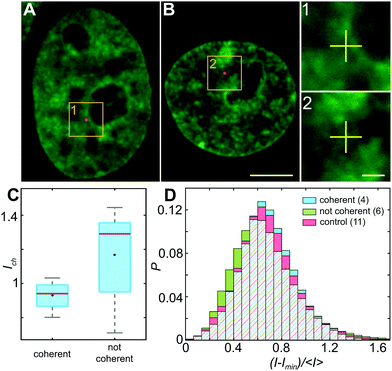
To investigate the impact of the particle presence on the surrounding chromatin, we assess the chromatin compaction at the particle location. To do so, we measure the local intensity of the H2B-GFP signal, which is a direct proxy of chromatin density.27,35 We define the chromatin compaction Ich as the H2B-GFP intensity at the site of the particle normalized by the average H2B-GFP intensity over the nucleus. Fig. 6A and B show injected nuclei with yellow boxes highlighting the position of the injected particles. As shown in the enlarged view of the insets 1–2 in Fig. 6A and B, chromatin is heterogeneously distributed around the injected particle, localization of which is marked by a yellow cross. Strikingly, when we obtain Ich for all particles, we find that chromatin compaction at their respective sites is much lower if they are in nuclei with coherent chromatin motion, 〈Ich〉c = 0.93, as opposed to nuclei not showing chromatin coherency, 〈Ich〉nc = 1.17 (Fig. 6C). Indeed, the former is consistent with liquid-like behavior of particle's surroundings in injected nuclei with chromatin coherency, while the latter agrees with elastic behavior of particle's surroundings in injected nuclei lacking chromatin coherency (Fig. 5B).In addition, we measure distribution of chromatin compaction across the nuclei by evaluating H2B-GFP intensity over all pixels. One way to compare H2B-GFP intensities across nuclei with different expression levels is to compute the normalized pixel intensities (I − Imin)/〈I〉, where Imin is the minimum and 〈I〉 the average H2B-GFP intensity in a given nucleus. The lower and higher H2B-GFP intensity values indicate lower and higher chromatin compaction, respectively. Fig. 6D shows probability distributions of these normalized pixel intensities for population of nuclei prior to injection (red), injected nuclei exhibiting coherent chromatin motions (blue) and injected without chromatin coherency (green). We find the following values of mean ± standard deviation: 0.685 ± 0.250 for control nuclei, 0.686 ± 0.233 for injected nuclei with coherent motions and 0.665 ± 0.278 for injected nuclei lacking coherency. The intensity distributions for control and injected nuclei with coherent motions are quite similar (p-value of 0.17), while injected nuclei lacking coherency are significantly different from both of these (p-values <10−11). Interestingly, the intensity distribution of injected nuclei lacking coherency is slightly shifted to lower values, when compared to control. This suggests that in injected nuclei, which did not recover coherent motions, mechanical stress of the injection leads to chromatin decondensation across the nucleus. This is consistent with the observed increase in their viscous response (Fig. 5A, green).
Discussion
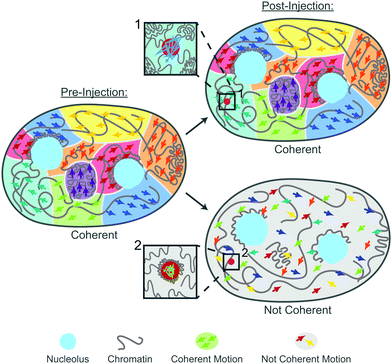
Cells and their constituents often exhibit nontrivial properties when exposed to mechanical stress.43,44 This is rooted both in their non-equilibrium nature as well as mounting a response against the mechanical stress to protect their biological function. In this work, we studied the impact of mechanical stress on the human genome. Specifically, we used microinjection as a mechanical perturbation of the genome inside the cell nucleus. Using our recently developed noninvasive DCS-based microrheology approach,28 we have evaluated nucleus-wide genomic motions before and after the injection, assessing global genomic response. Moreover, during the injection we deposited small probes (100 nm) inside the nucleus, allowing us to assess also local genomic response at the site of the probe.Remarkably, our results reveal that the genome responds to the mechanical stress of injection both locally (around the injected probe) and globally (nucleus-wide). During injection, a needle pierces a 1 μm hole in the nuclear envelope in a nucleus of ∼10 μm in diameter. Moreover, the typical volume of fluid injected into the nucleus is ∼100 μm3, corresponding to ∼20% of the nuclear volume. This leads to a transient nuclear swelling (∼0.1 s) that recedes immediately after the injection, with nucleus relaxing back to its original size. Hence, microinjection experiments are rather invasive, frequently leading to cell apoptosis.45 To this end, we evaluate changes in the genome dynamics and rheology only in the cells that are viable 24 hours after injection, indicating their successful recovery. Our data reveal that only about 40% cells regain physiological dynamics and rheology of their genome, the remaining 60% have altered both genomic motions as well as rheology. Our findings are summarized by the cartoon in Fig. 7: Pre-injection the genome exhibits coherent motions and heterogeneous chromatin distribution across the nucleus. In contrast, there are two types of the genomes behavior post-injection: (i) coherent, where the genome maintains the coherent motions as well as pre-injection chromatin distribution. In this case, the injected particle is mobile, with no chromatin condensation around it (inset 1). (ii) Not coherent, the genome loses coherent motions and undergoes an overall decondensation. Here, the chromatin condenses around the injected particle leading to its reduced mobility (inset 2).
Interestingly, physiological chromatin dynamics is characterized by its hallmark large-scale coherent motions, where 3–5 μm patches of chromatin move together coherently over several seconds (Fig. 7, pre-injection).27,36,37 Local genomic motions are largely subdiffusive to diffusive with occasional directed movement,46–52 with nucleus-wide average being a subdiffusive motion with α∼ 0.7.27 Strikingly, we find that upon mechanical stress of injection only about 40% of the cells recover these dynamical features (Fig. 7, post-injection, coherent). The remaining 60% exhibit increased local genomic displacements with a reduced subdiffusive exponent of α ∼ 0.33 (Fig. 7, post-injection, not coherent). Moreover, these displacements are uncorrelated, lacking large-scale coherency.
These changes in global dynamics directly reflect changes in chromatin bulk rheology in the nucleus. We find that chromatin in unperturbed nuclei is elastically dominated across the studied frequencies, with viscous response being largely constant. In contrast, in the nuclei exhibiting perturbed dynamics upon mechanical stress, the viscous response shows a strong reduction at low frequencies, suggesting chromatin stiffening. The loss modulus monotonically increases across the measured frequencies, hinting at increasing fluidity of the genome. This is consistent with our measurement of the decrease in nucleus-wide chromatin compaction, indicating nucleus-wide chromatin decondensation in response to mechanical stress (Fig. 7).
In addition to these nucleus-wide changes in dynamics and rheology, we studied also mobility of the deposited local probe, from which we extracted rheology of its immediate environment. We find that these probes show almost an order of magnitude reduced mobility (as per MSD) in injected nuclei, which did not recover physiological chromatin dynamics and rheology, when compared to those that recovered its native state. Indeed, the local rheology of the probes in perturbed nuclei is strongly elastically dominated, while in injected nuclei with physiological chromatin dynamics, the local chromatin exhibits viscous dominated behavior. This is further consistent with our measurements of chromatin condensation found around these probes in the perturbed nuclei, whereas no condensation is found in nuclei with physiological behavior. Our results demonstrate a local response of chromatin at the site of an injected probe, which comes in form of changing compaction, dynamics and rheology.
Overall, our data reveal that mechanical stress leads to both global and local changes in chromatin dynamics, compaction and rheology. Surprisingly, the observed changes closely resemble genome's response to DNA damage events in the nucleus. Specifically, chromatin was found to condense at sites of double-stranded DNA breaks at a similar fashion as we found at the sites of deposited probes.30 Furthermore, it was shown that upon DNA damage, as part of the DNA repair, the nucleus-wide chromatin displacements increase, while becoming uncorrelated, eliminating the large-scale coherency.27 In addition, an overall nucleus-wide decondensation of chromatin was observed in response to DNA damage.27,53–55 Strikingly, we observe the same phenomenology upon mechanical stress, suggesting that injection did induce DNA damage in the nucleus. This is further corroborated by earlier observations that mechanical stress of cell migration through tight constrictions, micropipette aspiration and cell compression lead to DNA damage and structural changes in the genome.17–22
In summary, our work unveils rheology of the human genome under physiological conditions in live cells, without exposure to a mechanical trauma of an injection. We use a novel noninvasive approach employing intrinsic chromatin dynamics to extract its rheology, enabling us to compare chromatin rheology pre/post injection, which was not possible with earlier methods that use injected probes to extract chromatin rheology.12–15 Our results reveal that mechanical stress of injection leads to local as well as nucleus-wide changes in chromatin compaction, dynamics and rheology. These changes are consistent with those observed upon DNA damage, suggesting that the genome experiences similar effects during the injection process.
Conclusions
Material properties of the genome and its nuclear environment are critical for understanding physical principles underlying the genome's organization and function. These properties directly control the timescales and length scales of nuclear processes such as transcription, replication and DNA repair, which in turn impact all cellular processes via the central dogma.2–5 Our results show that mechanical stress can affect the genome's material properties, thus affecting timescales and length scales of genomic interactions and the corresponding DNA transactions. Such knowledge is essential for understanding the genome as a living soft matter, providing fundamental insights into the biophysical origins of the genome's dynamical self-organization.Conflicts of interest
Authors declare no conflicts of interest.Acknowledgements
DCS calculations were carried out using New York University (NYU) High Performance Computing cluster. This research was supported by the National Science Foundation Grants CAREER PHY-1554880, CMMI-1762506 and NYU MRSEC DMR-1420073.Notes and references
- B. Alberts, A. Johnson, J. Lewis, D. Morgan, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Science, 2014 Search PubMed.
- F. H. Crick, Symp. Soc. Exp. Biol., 1958, 12, 138–163 CAS.
- F. Crick, Nature, 1970, 227, 561 CrossRef CAS.
- R. Milo and R. Phillips, Cell Biology by the Numbers, Garland Science, 2015 Search PubMed.
- A. Zidovska, Biophys. Rev., 2020, 12, 1093–1106 CrossRef.
- K. N. Dahl, S. M. Kahn, K. L. Wilson and D. E. Discher, J. Cell Sci., 2004, 117, 4779–4786 CrossRef CAS PubMed.
- K. N. Dahl, A. J. Engler, J. D. Pajerowski and D. E. Discher, Biophys. J., 2005, 89, 2855–2864 CrossRef CAS PubMed.
- J. D. Pajerowski, K. N. Dahl, F. L. Zhong, P. J. Sammak and D. E. Discher, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 15619–15624 CrossRef CAS.
- A. D. Stephens, E. J. Banigan, S. A. Adam, R. D. Goldman and J. F. Marko, Mol. Biol. Cell, 2017, 28, 1984–1996 CrossRef CAS PubMed.
- A. D. Stephens, P. Z. Liu, E. J. Banigan, L. M. Almassalha, V. Backman, S. A. Adam, R. D. Goldman and J. F. Marko, Mol. Biol. Cell, 2018, 29, 220–233 CrossRef CAS PubMed.
- M. M. Nava, Y. A. Miroshnikova, L. C. Biggs, D. B. Whitefield, F. Metge, J. Boucas, H. Vihinen, E. Jokitalo, X. Li and J. M. G. Arcos, et al. , Cell, 2020, 181, 800–817 CrossRef CAS PubMed.
- Y. Tseng, J. S. Lee, T. P. Kole, I. Jiang and D. Wirtz, J. Cell Sci., 2004, 117, 2159–2167 CrossRef CAS PubMed.
- A. H. de Vries, B. E. Krenn, R. van Driel, V. Subramaniam and J. S. Kanger, Nano Lett., 2007, 7, 1424–1427 CrossRef CAS.
- A. Celedon, C. M. Hale and D. Wirtz, Biophys. J., 2011, 101, 1880–1886 CrossRef CAS.
- F. M. Hameed, M. Rao and G. Shivashankar, PLoS One, 2012, 7, e45843 CrossRef CAS.
- S. Fulda, A. M. Gorman, O. Hori and A. Samali, Int. J. Cell Biol., 2010, 2010, 214074 Search PubMed.
- C. M. Denais, R. M. Gilbert, P. Isermann, A. L. McGregor, M. Te Lindert, B. Weigelin, P. M. Davidson, P. Friedl, K. Wolf and J. Lammerding, Science, 2016, 352, 353–358 CrossRef CAS.
- F. Aymard, M. Aguirrebengoa, E. Guillou, B. M. Javierre, B. Bugler, C. Arnould, V. Rocher, J. S. Iacovoni, A. Biernacka and M. Skrzypczak, et al. , Nat. Struct. Mol. Biol., 2017, 24, 353–361 CrossRef CAS PubMed.
- J. Irianto, Y. Xia, C. R. Pfeifer, A. Athirasala, J. Ji, C. Alvey, M. Tewari, R. R. Bennett, S. M. Harding and A. J. Liu, et al. , Curr. Biol., 2017, 27, 210–223 CrossRef CAS.
- C. R. Pfeifer, Y. Xia, K. Zhu, D. Liu, J. Irianto, V. M. M. Garca, L. M. S. Millán, B. Niese, S. Harding and D. Deviri, et al. , Mol. Biol. Cell, 2018, 29, 1948–1962 CrossRef CAS.
- P. Shah, C. M. Hobson, S. Cheng, M. Colville, M. Paszek, R. Superfine and J. Lammerding, Curr. Biol., 2021, 31, 1–13 CrossRef.
- R. Golloshi, T. F. Freeman, P. Das, T. I. Raines, R. S. Martin, C. Playter, D. Thurston and R. P. McCord, bioRxiv, 2020, 856583 Search PubMed.
- C. M. Caragine, S. C. Haley and A. Zidovska, Phys. Rev. Lett., 2018, 121, 148101 CrossRef CAS.
- C. M. Caragine, S. C. Haley and A. Zidovska, eLife, 2019, 8, e47533 CrossRef CAS PubMed.
- Y. Shin, Y.-C. Chang, D. S. Lee, J. Berry, D. W. Sanders, P. Ronceray, N. S. Wingreen, M. Haataja and C. P. Brangwynne, Cell, 2018, 175, 1481–1491 CrossRef CAS PubMed.
- D. S. Lee, N. S. Wingreen and C. P. Brangwynne, Nat. Phys., 2021, 17, 531–538 Search PubMed.
- A. Zidovska, D. A. Weitz and T. J. Mitchison, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15555–15560 CrossRef CAS.
- I. Eshghi, J. A. Eaton and A. Zidovska, Phys. Rev. Lett., 2021, 126, 228101 CrossRef CAS PubMed.
- F.-Y. Chu, S. C. Haley and A. Zidovska, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10338–10343 CrossRef CAS PubMed.
- J. A. Eaton and A. Zidovska, Biophys. J., 2020, 118, 2168–2180 CrossRef CAS PubMed.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250 CrossRef CAS PubMed.
- T. G. Mason, K. Ganesan, J. H. Van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282 CrossRef CAS.
- J. C. Crocker, M. T. Valentine, E. R. Weeks, T. Gisler, P. D. Kaplan, A. G. Yodh and D. A. Weitz, Phys. Rev. Lett., 2000, 85, 888 CrossRef CAS PubMed.
- E. M. Furst and T. M. Squires, Microrheology, Oxford University Press, 2017 Search PubMed.
- H. Kimura and P. R. Cook, J. Cell Biol., 2001, 153, 1341–1354 CrossRef CAS PubMed.
- R. Bruinsma, A. Y. Grosberg, Y. Rabin and A. Zidovska, Biophys. J., 2014, 106, 1871–1881 CrossRef CAS PubMed.
- D. Saintillan, M. J. Shelley and A. Zidovska, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 11442–11447 CrossRef CAS PubMed.
- A. Zidovska, Curr. Opin. Genet. Dev., 2020, 61, 83–90 CrossRef CAS PubMed.
- M. Gardel, M. Valentine and D. A. Weitz, Microscale Diagnostic Techniques, Springer, 2005, pp. 1–50 Search PubMed.
- L. Liu, G. Shi, D. Thirumalai and C. Hyeon, PLoS Comput. Biol., 2018, 14, e1006617 CrossRef PubMed.
- G. Shi, L. Liu, C. Hyeon and D. Thirumalai, Nat. Commun., 2018, 9, 1–13 CrossRef CAS PubMed.
- M. Di Pierro, D. A. Potoyan, P. G. Wolynes and J. N. Onuchic, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7753–7758 CrossRef CAS.
- K. A. Barbee, Ann. N. Y. Acad. Sci., 2006, 1066, 67–84 CrossRef PubMed.
- S. Etienne-Manneville, Annu. Rev. Cell Dev. Biol., 2018, 34, 1–28 CrossRef CAS PubMed.
- E. A. Prokhorova, A. V. Zamaraev, G. S. Kopeina, B. Zhivotovsky and I. N. Lavrik, Cell. Mol. Life Sci., 2015, 72, 4593–4612 CrossRef CAS PubMed.
- W. Marshall, A. Straight, J. Marko, J. Swedlow, A. Dernburg, A. Belmont, A. Murray, D. Agard and J. Sedat, Curr. Biol., 1997, 7, 930–939 CrossRef CAS PubMed.
- A. S. Belmont and A. F. Straight, Trends Cell Biol., 1998, 8, 121–124 CrossRef CAS.
- V. Levi, Q. Ruan, M. Plutz, A. S. Belmont and E. Gratton, Biophys. J., 2005, 89, 4275–4285 CrossRef CAS PubMed.
- C.-H. Chuang, A. E. Carpenter, B. Fuchsova, T. Johnson, P. de Lanerolle and A. S. Belmont, Curr. Biol., 2006, 16, 825–831 CrossRef CAS PubMed.
- T. J. Lampo, A. S. Kennard and A. J. Spakowitz, Biophys. J., 2016, 110, 338–347 CrossRef CAS PubMed.
- T. Germier, S. Kocanova, N. Walther, A. Bancaud, H. A. Shaban, H. Sellou, A. Z. Politi, J. Ellenberg, F. Gallardo and K. Bystricky, Biophys. J., 2017, 113, 1383–1394 CrossRef CAS PubMed.
- N. Khanna, Y. Zhang, J. S. Lucas, O. K. Dudko and C. Murre, Nat. Commun., 2019, 10, 1–13 CrossRef CAS PubMed.
- D. Llères, J. James, S. Swift, D. G. Norman and A. I. Lamond, J. Cell Biol., 2009, 187, 481–496 CrossRef PubMed.
- M. J. Kruhlak, A. Celeste, G. Dellaire, O. Fernandez-Capetillo, W. G. Müller, J. G. McNally, D. P. Bazett-Jones and A. Nussenzweig, J. Cell Biol., 2006, 172, 823–834 CrossRef CAS PubMed.
- Y. Ziv, D. Bielopolski, Y. Galanty, C. Lukas, Y. Taya, D. C. Schultz, J. Lukas, S. Bekker-Jensen, J. Bartek and Y. Shiloh, Nat. Cell Biol., 2006, 8, 870–876 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00983d |
| This journal is © The Royal Society of Chemistry 2022 |