Open Access Article
Open Access ArticleUnderstanding chemistry: from “heuristic (soft) explanations and reasoning by analogy” to “quantum chemistry”†
Jeffrey I.
Seeman
 *a and
Dean J.
Tantillo
*a and
Dean J.
Tantillo
 *b
*b
aDepartment of Chemistry, University of Richmond, Richmond, VA 23173, USA. E-mail: jseeman@richmond.edu
bDepartment of Chemistry, University of California – Davis, Davis, CA 95616, USA. E-mail: djtantillo@ucdavis.edu
First published on 28th September 2022
Abstract
“Soft theories,” i.e., “heuristic models based on reasoning by analogy” largely drove chemistry understanding for 150 years or more. But soft theories have their limitations and with the expansion of chemistry in the mid-20th century, more and more inexplicable (by soft theory) experimental results were being obtained. In the past 50 years, quantum chemistry, most often in the guise of applied theoretical chemistry including computational chemistry, has provided (a) the underlying “hard evidence” for many soft theories and (b) the explanations for chemical phenomena that were unavailable by soft theories. In this publication, we define “hard theories” as “theories derived from quantum chemistry.” Both soft and hard theories can be qualitative and quantitative, and the “Houk quadrant” is proposed as a helpful categorization tool. Furthermore, the language of soft theories is often used appropriately to describe quantum chemical results. A valid and useful way of doing science is the appropriate use and application of both soft and hard theories along with the best nomenclature available for successful communication of results and ideas.
1. Introduction
Since World War II, chemistry has grown and morphed tremendously. The complexity of the chemistry achieved has increased almost beyond imagination. The evidence is stunning, including the structures and physical and chemical properties of the compounds being studied, the detailed mechanisms of their reactions being revealed, and the total syntheses of these compounds being accomplished. In addition, the vast number of publications appearing annually, and the speed at which these achievements are being reported has far eclipsed previous generations. It is impossible to read or even scan all the literature in anyone's own research area.Along with this clear progress have been several transformations in the processes used by chemists in their research endeavors. One dramatic change over the past decades has been the increasing power and diversity of instrumentation, driven in part by computer technology that has grown exponentially, as predicted by Moore's Law. Computer technology has also been a driver in the development of expediters of research, such as word processing, on-line literature searching, ChemDraw, bibliographic applications, on-line journal submission and review processes, among other research-process enhancements. The days of typewriters, Leroy Lettering, and paste-on chemical structures are long gone – and largely unknown to most chemists today.
Prior to the application of quantum mechanics to chemistry, chemists had only heuristic models1 to explain their results.
“A heuristic technique is any approach to problem solving or self-discovery that employs a practical method that is not guaranteed to be optimal, perfect, or rational, but is nevertheless sufficient for reaching an immediate, short-term goal or approximation. Where finding an optimal solution is impossible or impractical, heuristic methods can be used to speed up the process of finding a satisfactory solution. Heuristics can be mental shortcuts that ease the cognitive load of making a decision. Examples that employ heuristics include using trial and error, a rule of thumb or an educated guess.”2
In this paper, we shall use the term “soft theories” to mean “heuristic models based on reasoning by analogy.”
A transformation has occurred during the past few decades in the way chemists explain their results, predict future observations, plan the next experiments, and divine physical and chemical properties of hypothetical systems. Today, chemists rely on quantum chemistry, often in the form of density-functional theory (DFT), that goes far beyond what was possible solely in the era of soft theories. This transformation has not led to a complete discard of the old, well-honed intuitive uses of soft theory. Rather, chemists often begin with soft theory, progress to quantum chemistry, which we term “hard theory,” then seize upon the language of soft theory to more clearly describe their findings and conclusions. By “theory” we refer to concepts that connect molecular structure with energy and its broadest applications.
In this paper, we shall use the term “hard theories” to mean “theories derived from quantum chemistry.”
It is also important to understand that both soft and hard theories can be either qualitative or quantitative. That is, a qualitative application does not necessarily belong to a soft theory. And a quantitative application does not necessarily belong to a hard theory. This plurality will be discussed in more detail in Section 6.
The objective of this paper is to distinguish between these different paradigms and highlight the strengths and weaknesses of each. We will focus on why certain experimental observations can be explained only by quantum chemical theory, sometimes with and often without computational assistance. We will also support the continued use of both soft and hard theories – indeed, of all the tools and models1 that enhance scholarship and utility, a further vote in favor of pluralism in chemistry.3–6
2. Soft theories versus hard theories7
Soft theories are based on parametrization and correlation and carry with them inherent approximations. “Ortho- and para-directing substituents” in aromatic chemistry, steric, electronic, and stereoelectronic effects, and the use of curly arrows8 in reaction mechanisms are examples of soft theories. In the history of physical organic chemistry, soft theory was notably used in the nonclassical carbocation debate, as illustrated by Herbert C. Brown's analyses of the nonclassical ion problem and by Paul von R. Schleyer's rebuttals to Brown;9 by Ned Arnett's review of classical and nonclassical “Carbocations”,10 and in William Goodwin's historical analysis of the nonclassical ion problem in 2013.11Soft theories can be manipulated to accommodate almost any set of experimental results.12 Soft theories are typically used to provide qualitative predictions before experiments are performed and to qualitatively explain experimental results after the results have been obtained. Prior to the development of robust, reliable quantum chemical theory and computational software, soft theory was all that could be used to analyze the relationships between structure and the physical and chemical properties of molecules.
Hard theories, if applied without approximations, can predict the exact results of an experiment before the experiment is performed. Hard theories in mechanistic chemistry are directly based on quantum chemistry and thus depend on quantum chemical models that are created outside the phenomena they explain.13,14 Also as described in Section 6, hard theories can be both qualitative and quantitative. Both soft and hard theories can be either qualitative or quantitative. In the course of modern research, there has been mixing of hard and soft theories. Deviation from first principles turns hard theory into soft theory, such as continuum solvation models.15–17
Yexenia Nieves-Quinones and Daniel Singleton have recently divided hard theories into two subcategories: “thick” and “thin” as they relate to reaction mechanisms.18 Thin mechanisms focus exclusively on specific key structures, such as transition states and intermediates. Thick mechanisms “are complete descriptions of the atomic motions that transform reactants to products.”18 Both thick and thin theories are quantitative, with thin theories examining far less of a reaction's potential energy surface (PES).
The transition state (TS) concept has a long and valuable history in chemistry. That history began in the soft theory era and continues vibrantly within the hard theory framework. The slow, i.e., many decades, transition of the transition state from the soft to the hard paradigm will be discussed briefly in Section 5.
To contrast these two modes of analysis, one of us (DJT) jokes with his students that any good organic chemist carries around at least two competing soft explanations for any phenomenon and, once an observation is made and the result is known, proclaims that one of the explanations must be correct. This revelation is immediately followed by comments on how “good quantum chemistry done well” could have predicted the outcome ahead of time. This discourse is intended to provide some levity but also a dose of reality. The other of us (JIS) adds, that had subsequently obtained experimental results demonstrated that the phenomenon observed was actually the opposite of what had been originally thought, the same good organic chemist could easily adopt one of the other competing soft explanations and be equally self-congratulatory and equally well cheered by his peers.
Soft explanations may, in some cases, be shown to originate in quantum chemistry, e.g., note the efforts by some theoretical chemists to provide a theoretical underpinning to arrow pushing (vide infra).19–21 Over 25 years ago, Dennis H. Rouvray discussed the necessity of analogies in the development of science, e.g., “that like structures exhibit like behavior,”22 in mathematical terms.23 Indeed, it would be unreasonable if broadly-successful soft theories – generated over decades of experimental results and deep thinking by the community of chemists – were not ultimately underpinned by quantum chemistry, although such coincidences are possible, e.g., “the right answer for the wrong reason.” It is important to note, however, that the application of hard theories can be hampered by practical factors that induce error bars on predictions that limit their utility (vide infra).
3. Before 1965: soft explanations and reasoning by analogy
To appreciate fully and understand soft theory, examples will be given in a somewhat chronological sequence. We shall begin with structural analysis, then discuss the physical properties of molecules, before moving into the analysis of chemical reactions. In a sense, we shall cross over 100 years of physical organic chemistry in short order.We begin. Benzene was first isolated by Michael Faraday in 1825. A two-hundred-year-old sample from Faraday is on exhibit at the Royal Institution in London. From the 1860s, a number of proposals were made for the structure of benzene, including that of August Kekulé (oscillating 1,3,5-cyclohexatrienes), James Dewar (bicyclo[2.2.0]hexa-1,4-diene), and Albert Ladenburg (“prismane”) (Fig. 1). Using the simple “isomer counting” method, chemists were able to distinguish the Kekulé and Ladenburg structures for benzene from the Dewar structure, in that only one monosubstituted benzene isomer was and is known. Using the same method but for disubstituted benzenes, the Kekulé structure can be distinguished from the Ladenburg structure. The earliest uses of isomer counting of the monosubstituted benzenes is a retrospective justification for Kekulé’s structure, because at the time when this question was open, one did not have access to different mono- or disubstituted benzenes. But this technique continued through the years, even by one of the authors of this paper (JIS) to assign configurational isomers of substituted benzenes using laser jet spectroscopy.24,25
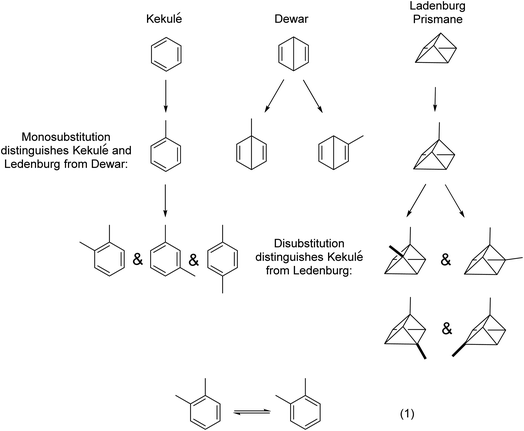 | ||
| Fig. 1 The use of the isomer counting method was key to the 19th century assignment of the Kekulé structure to benzene. Dewar benzene and Ladenburg's prismane structures were abandoned. Isomer counting for aromatic systems was used as late as 1914.26 See text for additional details. The arguments get complicated when considering the isomers shown in the hypothetical eqn (1); exceptionally fast rates of interconversion of these postulated isomers would account for only a single isolated o-xylene. Ultimately, quantum chemistry came to the rescue. The molecular orbital description explored fully by Hückel in the 1930s27–29 and the valence bond description using resonance theory by Pauling and Wheland in 193330 were ultimately demonstrated to be equivalent by Shaik and Hiberty.31–33 Though it was not emphasized at the time, the logic of isomer counting is equivalent to symmetry arguments. See discussion about “unforeseeable knowledge” in Section 7. | ||
Isomer counting, of course, is also based on a theory, the structural theory. But structural theories prior to quantum chemistry were all soft theories. Without the application of quantum chemistry, features such as the instability of cyclobutadiene, or the stability (both kinetic and thermodynamic) of benzene or cyclopentadienyl anion or cyclopropenyl cation are not explicable on any fundamental basis. The argument of the stability of the aromatic sextet is soft theory and a circular argument.14,34–36
The point we are here making is, the scientists involved in the chemistry depicted in Fig. 1 did not rely on fundamental theories of the structure of matter or of molecular bonding to derive the correct structures of the compounds they studied. Chemists used soft theory, which was based on the most sophisticated theoretical understandings of the time. Optimally, experiment and theory ought to develop at the same rate. But typically, experiment precedes theory by a generation or more. This may be changing today.
Parenthetically, we point out that a collection of 217 “basic isomeric topological structures” having the benzene formula C6H6 has been provided by Gopalpur Nagendrapp.37 Surely more advanced analytical and theoretical methodologies would be needed to determine the likelihood of which of these 217 might be a stable or even a metastable molecule.38–40
With a reasonably workable understanding of chemical structure in the late 1800s but with no real knowledge of what a chemical bond is,41,42 chemists began to collect a wide assortment of information about their science: the isolation and structure determination of new compounds; the physical properties of those compounds; and ultimately, the chemical properties – their reactivities and interconversions – of those compounds. Soft theories were used advantageously in these achievements.
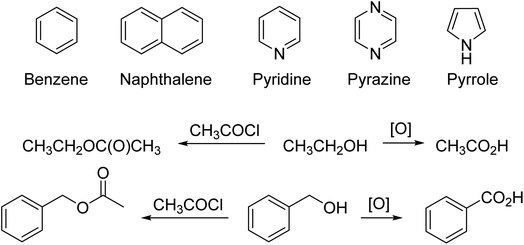
For example, there is structural analogy and reaction analogy. Once chemists knew that benzene had the Kekulé structure, then the structures of pyridine, pyrazine, and ultimately pyrrole and other polyunsaturated compounds were determined one by one (Fig. 2).43 It is standard logic in chemistry to expect that, for example, if one can oxidize any one alcohol to a carbonyl group or prepare an acetate from the alcohol, then one can do the same reactions with other alcohols to get the analogous products (Fig. 2). This logic is based on the recognition and identification of functional groups in organic compounds, a direct intellectual and structural descendant of the 19th century concept of “radicals” which were the stable parts of a compound that retained their identities through a series of reactions. As organic chemistry advanced in the 19th century, several versions of structural “types” were advanced. These eventually led to the concept of functional groups.43–46 Progress in chemistry was made possible by reasoning by analogy and soft theory.
Also in the mid-1860s, even more basic studies of structure determination were under way: the accomplishments of Dmitri Mendeleev and Lothar Meyer.47–50 The periodic system of the elements was based on experimental observations and insightful intuition but not on any fundamental theory. As such, the pre-quantum chemical periodic system is a soft theory.
Another aspect of reasoning by analogy in the fourth quarter of the 19th century was the prediction of the speed of reactions, that is, the effect of substituents on chemical reactivity. For example,51 A. W. Hoffmann and Nikolai Menschutkin observed the role of structure on amine alkylation in the 1870s.52,53 Fifty years later in 1928, Karl Kindler – the Kindler who in 1918 reported the partial synthesis of quinine with Paul Rabe54 – was the first to quantify steric effects by comparing the rates of hydrolysis of substituted benzoates and cinnamates.55 Kindler's steric explanation was surely a soft explanation, given that it was only in 1927 that the strong attractive forces between two atoms had its own quantum chemical explanation.41 Indeed, the entire (early) electronic theory of organic chemistry developed by Robert Robinson56,57 and Christopher Ingold58–60 was a soft theory. Perhaps the most important of the early soft theories was due to Louis P. Hammett who, in the late 1930s, pioneered a linear free energy technique. The Hammett equation compared the electronic effect of substituents on different but related reactions (Fig. 3).61,62 As will be discussed in Section 6, use of the Hammett equation is an example of soft theory used in a quantitative fashion56,57
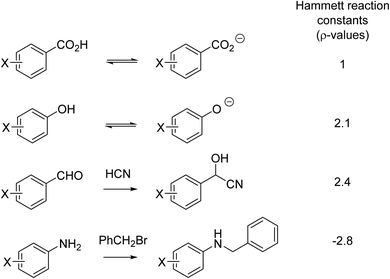 | ||
| Fig. 3 A series of reactions comparing the effect of the same set of substituents (-X) on different reactions. | ||
In the 1950s and 1960s, chemists developed a variety of “principles” that provided soft explanations for the effect of substituents on the rates and product distributions of various reactions. George Hammond's postulate, sometimes referred to as the Hammond–Leffler postulate, related the structure of a transition state to the structure of its reactants and products as a function of the activation energies.63–65 The Curtin–Hammett principle related the product ratio obtained from a compound that exists in multiple conformations to the free energy difference of their respective transition state energies.66–68 In 1963, Ralph G. Pearson proposed a hard and soft acids and bases theory that has been used to explain reaction mechanisms by relating the nature of the charge states and polarizability of the reacting substrates.69 The reactivity–selectivity principle proposed that with increasing reactivity, decreasing selectivity would be observed. It can be readily seen that the above principles are soft, qualitative concepts – even though they can be used with quantitative experimental data. That is, the explanations for the quantitative data are soft. The fact that most of these would not stand the test of time, and chemistry would advance into the realm of hard theory realm did not slow the earlier progress.
Chemists pulled together the “soft theories and reasoning by analogy” as described briefly above to enhance their abilities in structure determination and synthesis. For example, over several centuries, the classical method of structure determination evolved.70,71 The method worked as follows: the unknown compound was treated with reagents that were known to cause partial degradation (or simply heated in the absence of another substance) (Fig. 4). The resultant degradation products were isolated, purified and, if possible, identified by comparison with already known compounds, e.g., 1, or 2 or 3. If a certain degradation product could not be identified, e.g., 1 in the graphic, then it was treated as a new unidentified compound and degraded further, e.g., to 4, 5, and 6, and so on. Thinking backwards, the chemist tried to determine what compound could have been degraded into the subsequently fragmented, then identified compounds. All the logic was based on soft theory and reasoning by analogy. As Roald Hoffmann and Pierre Laszlo said, “Our discipline is a curious mix of empirical observation and abstract reasoning.“72
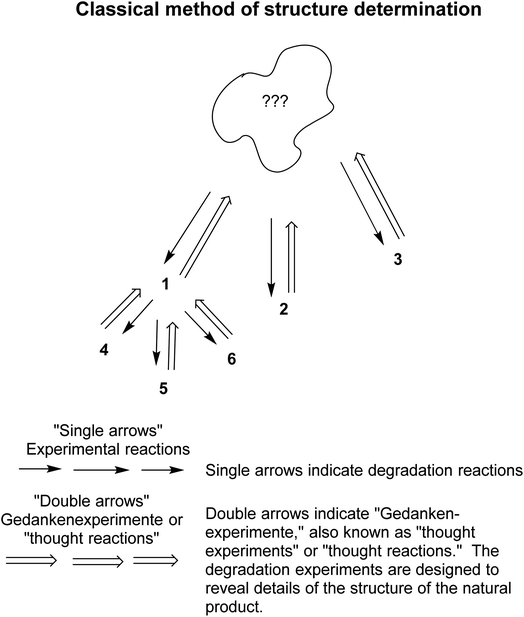 | ||
| Fig. 4 The classical method of structure determination70 involved a series of degradation steps followed by identification steps, and reverse analyses. See the text for further explanation of this method. Modified from a figure in Seeman.71 | ||
As evidence of the success of the classical method of structure determination, the structures of numerous natural products including terpenoids, steroids, and alkaloids were determined prior to 1950; examples are shown in Fig. 5. These structures were also determined using reasoning by analogy, perhaps the most remarkable being the structural assignments made by Emil Fischer's elucidation of 16 stereoisomeric glucoses. True, there were many mistakes made along the way, often by very good chemists,70,73 but overall it is remarkable how well this technique worked. Very important was the parallel growth in synthetic capability, so that many of the structures could be confirmed by total synthesis – another application of soft theory.
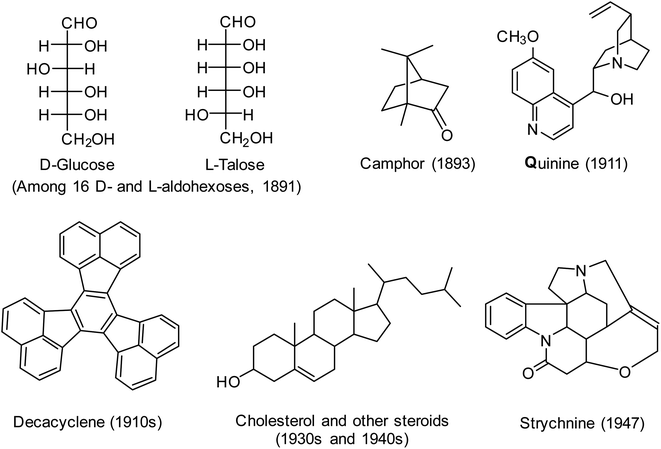 | ||
| Fig. 5 Range of structures determined by organic chemists prior to 1950 using the classical method of structure determination,70 as illustrated in Fig. 4. In most cases shown, absolute and relative configurations were determined in later years. | ||
Here we have an alluring paradox. On the one hand, the explanatory tools available to chemists prior to the 1950s were remarkably simple as they were limited. For example, the eminent organic chemist John D. Roberts said,
“It may seem unbelievable, but in 1938, our best instrument for characterization [of organic compounds] was the thermometer.”74
On the other hand, their achievements were spectacular.
How could chemists have been so successful despite such limited tools? The answer: hard work, brilliance, a dedication to their science to explain the successes, and a zealous commitment to the consistent, logical use of soft theories while using the entire body of chemical knowledge. Chemists of that era were also unaware of the advances and shortcuts that would develop within their own future, and thus they were not prone to prospective depression. Beginning in the mid-1950s, chemists were able to perform structure determination within days, then hours, by X-ray crystallography, rather than the years, if not decades, using the classical method of structure determination (Fig. 4).
What makes chemistry particularly challenging, and thus alluring, is its unpredictability. Soft theories work, most of the time. But the gods of chemistry, smiling from high on Mount Lavoisier, provide many exceptions to “soft theories and reasoning by analogy.” To establish the point, hardly any chemical reaction performed in the laboratory takes place in 100% yield. There are always side products, often described by the performers as “tar” which are removed as quickly as possible in the purification of the desired if not the major product of a reaction. And the desired product is not always formed, even in low yield. If soft theories were perfect, every reaction would proceed exactly as predicted and would proceed without exception in quantitative yield. (As will become evident in the sequel (see Section 11), hard theories are not always perfect either. Indeed, they all incorporate some approximations, given the complexities of the required mathematics.)
Chemists soon enough discovered that even slight structural changes from one molecule to the next could produce unexpected variations in properties. Chemists began to collect the exceptions to the models and develop rules that incorporated, with time and experience, more and more of the exceptions. That is, the exceptions motivated the invention of their own (responsive) soft rules.75 Models were built upon models. Soft upon soft! It was natural for chemists in the years leading up to the 1960s to apply a variety of soft theories. Chemists became adept at applying carefully selected models for specific uses as required in their research trajectories.
For example, nonadditivity of substituent effects has rendered great challenges to soft theories.76–80 As illustrated by the buttressing interactions shown in red in Fig. 6, the effective “steric” size of the substituent R1 can be increased as R2 becomes bulkier, a soft explanation that is impossible to quantify accurately on the basis of intuition. Simple models of steric hindrance were altered to take into consideration nonadditive steric effects. Much research was directed to develop linear free energy models like Hammett's that combined electronic and steric effects, introducing multiparametric relationships with parameters that were often characterized as “unrealistic.”75,81 Such theory manipulation is like adding a soft theory onto a soft theory. Ultimately, quantum chemistry has been used to quantify this type of nonadditive substituent effect.82 This diversity of models may be one of the underlying explanations why several philosophers and historians of chemistry, e.g. Hasok Chang6 and Joachim Schummer,83 say that chemistry is a pluralistic science.
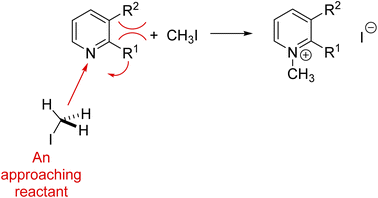 | ||
| Fig. 6 An illustration of the buttressing and thus enhancement of the steric effect on the reactivity of a pyridine nitrogen in a nucleophilic reaction, e.g., the reaction of these pyridines with alkyl halides.84,85 | ||
“Soft theories and reasoning by analogy” share an interesting fate: with time, they either rise to a certain level of sophistication and grow no further in explanative value or they disappear entirely. Many soft theories continue to this day, e.g., every organic chemist uses curly arrows to discuss reaction pathways and mechanisms. And on a much more substantive scale, linear free energy relationships continue to find much utility, even in 2022.86
In contrast, Herbert Mayr has provided strong evidence that both the reactivity-selectivity principle87 and the hard-soft acid-base theory88 have lived far beyond their useful lifetimes. Peter Schreiner et al. showed that certain conformational analyses, once thought to be dominated by destabilizing steric effects, are controlled by attractive electronic effects.89 And Sason Shaik, Philippe Hiberty, et al. showed that the hexagonal shape of benzene is due, not to the aromatic π-bonds but rather the σ-bonds.90 These are examples of “soft theories and reasoning by analogy” being replaced by quantum chemical theories, as discussed below. This transformation in ideas and accepted solutions is an example of competing ideologies in the advancement of science.91
4. What quantum chemistry can do that soft theory and reasoning by analogy cannot do
a. Everything!
As we see it, quantum chemistry serves three functions related to hard and soft theories of structure and reactivity. First, new hard theories can arise directly from quantum chemistry, both from quantum chemical principles and from quantum chemical results. Examples are given in Section 4a–4c. Second, quantum chemistry can be used to validate or invalidate soft theories. Examples are given in Section 4d. Third, quantum chemical results can be used to convert soft models from qualitative to quantitative. Examples are discussed in Section 4e. Section 6 also speaks to these issues, by providing examples of qualitative and quantitative soft and hard theories.In 2022, Gernot Frenking wrote,
“Chemistry is an example of a scientific discipline that can be pursued extremely successfully without understanding its basis – the chemical bond. The formation of the chemical bond can only be understood if the electrons are described by a wave function.”41
Beginning in 1962,92 software for quantum chemical computations was being made available by the Quantum Chemical Program Exchange (QCPE) by the originators of the software. Soon enough, such software became available from commercial enterprises as well. From the mid-1960s, more and more research reporting computational chemistry appeared in the literature. As an early 21st century textbook in computational chemistry reported,
“If one can measure it, one can predict it”93 by computational methods.
We think it is fair to go beyond this statement, to say,
“If one can imagine it, one can calculate it and thus predict its properties.”
In the absence of an experimental observation, to calculate means to predict.
Even the structures of compounds that may not or can never be made can be calculated.94
In the following section, we look at several of the earliest necessary applications of quantum chemistry to solve a problem that otherwise was unsolvable.
b. The application of quantum chemistry to spectroscopy and aromaticity
In the 1930s and 1940s, spectroscopists, who had expertise in theoretical chemistry, applied quantum chemistry to explain their experimental results. Robert S. Mulliken, one of the inventors of molecular orbital theory in 1928,95,96 focused most of his career at explaining the electronic structure of molecules.97–100 The closest Mulliken came to chemical reactions was the study of charge–transfer complexes, mostly between Lewis acids and Lewis bases.101 Mulliken and others certainly applied quantum chemistry to the analysis of the electronic structure of molecules and to the earliest studies of bonding, notably Mulliken's studies of charge–transfer complexes.101,102 It was to others to study chemical reactions and the changes in bonding that occur during those reactions.The successful model of the synergy between molecular spectroscopy and theory did not translate to other fields of chemistry for many reasons, including: the fact that molecular spectroscopy was very specialized with nomenclature and reliance on group theory, symmetry elements and physics-like jargon; the achievements of molecular spectroscopy did not reach across other subdisciplines; spectroscopists were studying individual molecules and their excited states, not reactions; the molecules studied by spectroscopists were simple and chemists studying more complex molecules did not see the transferability or relevance to their research; there was little communication among the subdisciplines.
Using his breakthrough molecular orbital theory, Erich Hückel explained the source of stabilization of benzene and other six-π electron systems in the 1930s and distinguished between 4n and 4n + 2 systems, though he did not propose that mathematical rule.27–29 Hückel's explanations were certainly hard theories. Ironically, even Erich Hückel's brother Walter Hückel, an eminent physical organic chemist, hardly mentioned molecular orbital theory in the 1955 edition of his massive, two-volume textbook Theoretical Principles of Organic Chemistry.43
Quantum chemistry was little used to explain chemical reactivity until the 1950s, when computational and theoretical chemists used Hückel theory and simple LCAO MO (linear combination of atomic orbital molecular orbital)103–106 theory to explain the reactivity of aromatic compounds toward substitution reactions. Their focus was on deriving a wide variety of reactivity indices. The underlying reason for this research strategy is that the compounds being studied were planar. Theory and computing power had not yet reached the stage where calculations could be performed on nonplanar compounds undergoing complex chemical reactions. This all changed with the development of extended Hückel theory (eHT) in William Lipscomb's group at Harvard107,108 followed immediately by applications by one of its key developers, Roald Hoffmann,109 and others110–113 using eHT and related theories.114,115 The first real steps of computational chemistry and reactions in the three-dimensional world were reported by R. B. Woodward and Hoffmann in 1965.116–119
c. The Woodward–Hoffmann rules
In 1962, William von Eggers Doering gave the moniker “no-mechanism” to reactions that were also called valence isomerizations. Doering asserted that
“‘No-mechanism’ is the designation given, half in jest, half in desperation, to ‘thermo-reorganization’ reactions like the Diels–Alder and the Claisen and Cope rearrangements in which modern, mechanistic scrutiny discloses insensitivity to catalysis, little response to changes in medium and no involvement of common intermediates, such as carbanions, free radicals, carbonium ions and carbenes.”120
The first and most dramatic cleavage in complex reaction chemistry from soft theories to quantum chemistry-based theory (hard theory) was the solution to the pericyclic no-mechanism problem (Fig. 7). No amount of linear free energy models, curly arrows, intuitive use of steric effects, and any other of the soft tools used by chemists at that time could solve the no-mechanism problem.
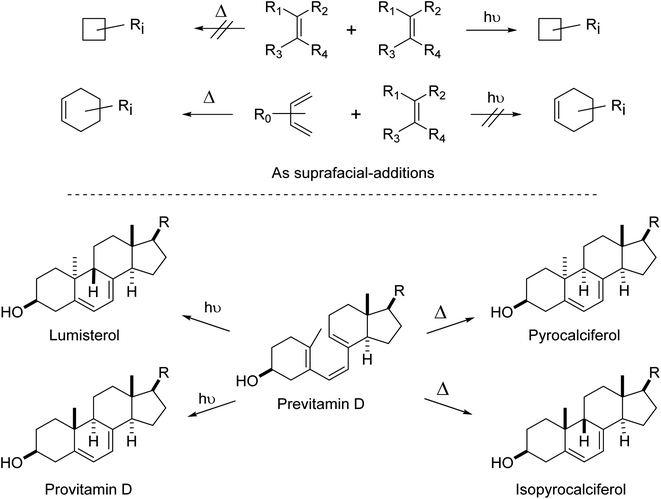 | ||
| Fig. 7 (top) Examples of thermal and photochemical cycloadditions that were or were not reported in the early 1960s and earlier. These reactions depend on geometry, strain, electrostatics and polarization, Pauli repulsion and dispersion effects as well as orbital symmetry factors.121 [2 + 2] cycloadditions are fine thermally – if the appropriate orbital symmetry-required geometries can be achieved and a high energy barrier can be overcome, or if the substituents cause significant asymmetry and the reaction proceeds by a non-Woodward–Hoffmann pathway.122–124 (bottom) Examples of valence isomerizations in vitamin D chemistry.125–127 Importantly, these are examples of alternating stereospecific reactions, alternation in the number of electrons involved and whether the reactions are thermal or photochemical. For more details and leading references, see Woodward and Hoffmann's major treatise of 1969122 or a more recent historical survey.128 | ||
To explain the mechanisms of these reactions and their allowed or forbidden nature as well as their stereochemical outcomes, something new had to be discovered, and it wasn't more experimental data. That something new was the application of quantum chemistry to these chemical reactions. Through a combination of qualitative (frontier molecular orbital consideration, correlation and state diagrams, interaction diagrams, and qualitative perturbation theory) and quantitative quantum chemistry (extended Hückel calculations of very simple potential energy surfaces), the mechanism of all pericyclic reactions was formulated. This solution is known today as the Woodward–Hoffmann rules, as Woodward and Hoffmann produced the explanations and the generalizations for all these reaction types in a series of five communications in 1965116–119,129 and an extensive treatise in 1969.122 Credit also goes to Luitzen Oosterhoff130 and Kenichi Fukui103 who provided orbital symmetry explanations for certain reactions before Woodward and Hoffmann and to H. Christopher Longuet-Higgins,131 Howard E. Zimmerman,132,133 and Michael J. S. Dewar134,135 who provided key insights into the mechanism of pericyclic reactions after Woodward and Hoffmann. The contributions of all these chemists involved quantum chemistry.
From a historical perspective, the solution to the pericyclic no-mechanism problem, i.e., the Woodward–Hoffmann rules, was not particularly distinct from other subsequent explanations that emerged from theory. The fact is, the Woodward–Hoffmann rules were the first and served as very visible and affirmative models for future use of quantum chemistry to explain experimental results in the realm of complex chemical reactions.
d. Providing fundamental explanations for all soft theory conjectures or refuting them
All soft theory conjectures can be examined with quantum chemical tools, though the quantitative aspects of both are subject to uncertainty. This process can lead to validation or invalidation, again subject to the assumptions underlying the theory. The former then associates the model with a physics-based rationale, while the latter can lead to a new physics-based model. A representative example of each is provided here.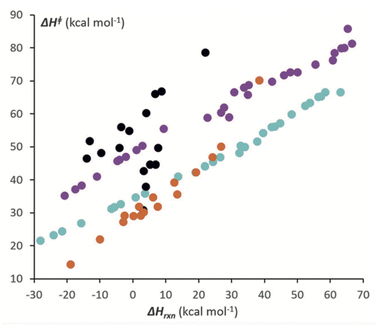 | ||
| Fig. 8 Correlation between the computed activation enthalpies of [4 + 2] cycloaddition reactions and enthalpies of reaction. Black circles refer to heterocycles plus dihydrogen; purple circles refer to PAHs plus dihydrogen; orange circles refer to heterocycles plus ethylene; and teal circles refer to PAHs plus ethylene. From Hayden and Houk.138 Reprinted with permission from A. E. Hayden, K. N. Houk, J. Am. Chem. Soc. 2009, 131, 4084–4089, https//:doi.org/10.1021/ja809142x. Copyright 2009 American Chemical Society. | ||
“The delocalized π-electronic component of benzene is unstable toward a localizing distortion and is at the same time stabilized by resonance relative to a localized reference structure… The duality is not a figment of VB theory or MO theory. It is rather an observable which emerges from all theories including density functional theory (DFT) at almost any level of sophistication.”90
But in this case, for good or bad, the soft model is so entrenched, so comforting, that many choose not to believe the hard evidence.
Note that these examples also highlight that a validation/invalidation dichotomy is too simple. In the first case, soft models were validated, but not universally and not without necessitating refinement of the model. In the second case, the overall model was invalidated, but a key soft principle—delocalization is energetically favorable—was not. As should occur in science, models are refined and only the bathwater is thrown out.
e. Uncovering information that is not visible to practitioners of only soft theory
We have already provided one example: the Woodward–Hoffmann rules (Section 4c). But there are many more.The PES associated with a given chemical formula can be calculated. Of particular interest are the local minima, i.e., the stable or metastable conformations of a compound and its stereoisomers, which are connected by first-order saddle points (transition structures) on the PES. The lowest-energy path connecting two local minima can also be calculated as well as other reaction paths. The deduction of reaction mechanisms is often the target objective of this kind of research. As Frank Jensen said in his review of computational chemistry in 2021,
“Deducing reaction mechanisms by locating transition structures and calculating activation energies has been, and continues to be, a central application of Computational Chemistry methods. The ‘arrow-pushing’ description of the electronic reorganization in a chemical reaction combined with the decades long experience of countless researchers have made the realization of organic reactions hugely successful. Nevertheless, when proposed reaction mechanism are subjected to detailed calculations, it is often found that the computation results indicate modified or alternative reaction pathways. The accuracy of DFT [Density Functional Theory] methods is often sufficient to differentiate between alternative reaction pathways, and their computational efficiency in many cases makes it possible to perform calculations on the exact experimental system without resorting to model reactions.”140
As most compounds exist as a mixture of multiple, quickly interconverting conformational isomers, a measured property of a molecule reflects thermal averaging over the various conformational isomers. And details of calculated reaction dynamics, i.e., changes in structure versus time rather than changes in energy versus structure, as for PESs, can provide enormously telescopic witness to the motion of atoms in a molecule entering or passing the region of an intermediate or a transition state. Trajectories of molecular motion can be determined, essentially following the course of reactions on the femtosecond time scale.141–148
Computational quantum chemistry (hard theory) can also be used to calculate equilibrium constants, reaction thermochemistry, heats of formation and combustion, kinetic isotope effects, complexation energies, acidity and basicity, hydrogen bond strengths, contributions from tunneling, any and all spectroscopic quantities, conductivity, as well as bulk thermodynamic properties such as solvation effects and phase transitions.93 As examples, recent progress has been made in the following areas: the determination of preferred reaction pathways; the identification and characterization of reaction intermediates; the discovery of novel reaction pathways, including those involving unusual post-transition state trajectories;145–148 the distinction between barrier heights and the widths of reaction pathways as controlling factors in reaction selectivity (e.g., entropy effects);149 the prediction of crystal structures, polymorphs and periodic systems; the prediction of morphologies of amorphous materials; reaction and catalyst design; the prediction of ligand-protein binding energies; and materials and device design.150 Two illustrative examples of the sort of information modern hard theory provides follow.
An added explanation may be of value. Many aspects of chemistry remain unsolved, that is, theory has not yet caught up to the experimental challenges. Still, even primitive theoretical and computational approaches of today, as long as they are based on quantum chemistry, remain within the domain of hard theory. That is, the state of the art does not convert a hard theoretical approach to a soft one, though some might consider certain computational results to be more qualitative than quantitative.
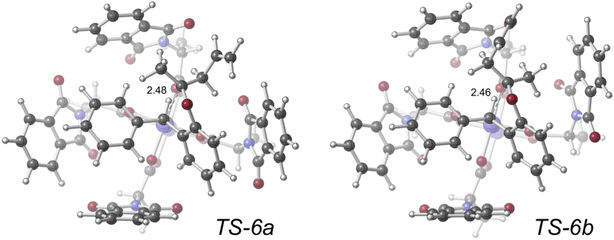 | ||
| Fig. 9 Transition structures (represented in ball-and-stick form; computed with density functional theory at the PCM(CH2Cl2)–B3LYP-D3(BJ)/SDD[6-31+G(d,p)]//PCM(CH2Cl2)–B3LYP-D3(BJ)/LANL2DZ[6-31G(d)] level of theory; key distances labeled in Å) for competing SE2 reactions of dirhodium tetracarboxylate-bound organic zwitterions. Image reproduced from S. N. Dishman, C. J. Laconsay, J. C. Fettinger, D. J. Tantillo, J. T. Shaw, Chem. Sci. 2022, 13, 1030–1036, https//:doi.org/10.1039/D1SC04622E with permission from the Royal Society of Chemistry. | ||
The dynamic matching concept has sparked many subsequent quantum chemistry-based molecular dynamics studies and fueled the development and discovery of other mechanistic features that play important roles in organic reactions. Perhaps the most notable result is the recognition that many organic and biological reactions involve post-transition state bifurcations in downhill paths from transition structures on PESs and that momentum is the key to how molecules navigate past these forks in the road to form one or another product.163–165
f. Distinguishing among various possible quantum chemical-based explanations and establishing a rule or principle
“the intuitively plausible idea of the electronic charge accumulating in the bonding region between two atoms and experiencing attraction to the two nuclei that stabilizes the bound species [but rather] by the lowering of the kinetic energy density of the shared electrons in the bonding region.”42
It should be noted that some still debate the relative importance of the kinetic energy effect.166
5. The transition state within the framework of both soft theory and hard theory
The transition state (TS) model and the PES concept are not, on their own, hard theories. In other words, there is a soft model of potential energy surfaces that relates structure and energy. One does not need quantum mechanics (QM) to think about or use TSs and PESs — even today, chemists do so using molecular mechanics calculated energies. Of course, it is well recognized that one really should get those TS and PES energies and structures from QM.The history of transition state theory is outside the scope of this publication. But we shall give a brief historical discussion. In the 1962 book aptly entitled The Transition State, based on a symposium held at Sheffield on April 3 and 4, 1962, soon to be Nobelist George Porter wrote,
“Transition-state or activated-complex theory is generally associated with the ideas of Wigner, Eyring, Polanyi, and Evans which were put forward in the early 1930s. The idea of representing the reaction in terms of a potential energy surface and calculating the rate of passage over this surface is one which made an immediate appeal, especially one with the equilibrium assumption which made possible the application of familiar statistical thermodynamical concepts to rate processes.”169
In his 1935 breakthrough paper, Henry Eyring acknowledged that bonding is due to the distribution of electrons in a molecule, which must be calculated by quantum chemistry. However, he calculated “the reaction rates by the methods of statistical mechanics (or kinetic theory), if one assumes the aforementioned forces to be known.”170
In their 1935 breakthrough paper, Meredith Evans and Michael Polyani did not discuss quantum mechanics except briefly in their ref. 10 in which they said,
“the substitution of the collision number by the statistical probability of the collided state (Fahrzustand) has been presented by one of the authors (Z. physic., 1920, I, 90) in a paper which applied the transition state method, using the concepts of the old quantum theory. It has been pointed out (Z. Electrochem., 1920, 62, 228) that the method overcomes the difficulty arising when one introduces the Arrhenius equation into the equilibrium constant, since it leads to the exact form of the reaction isochore.”171
A bit further into his Introduction, Porter summarized the state of the art of transition state theory and quantum mechanics as follows:
“Thinking over what has happened in the intervening twenty-five years [from 1935 to 1960], two things are apparent. First, in some ways transition-state theory has not lived up to the promise it then held. At that time there was much interest in calculating potential-energy surfaces and there must have been a feeling that it was only a matter of time before quantitative predictions of such surfaces became a reality. Twenty-five years later we are less optimistic. Indeed, in the matter of the prediction of activation energies of all but the very simplest reactions, not only have we no satisfactory absolute or semi-empirical theory but we have not even a completely empirical theory in which we can place much confidence.”169
Of course, we know today, 60 years further down the road, that high powered quantum chemical calculations are the norm. Even some experimental organic chemists have become computational quantum chemists. Nonetheless, we also understand the slow but steady development that was required to move from the soft ideas of the early 20th century to the sophistication of quantum chemical calculations -- hard theory -- of the 21st century. The models of Eyring170 and Evans and Polanyi171 did not depend on getting energies from quantum chemistry; those models were soft.
During these developmental years, from the 1930s until the 1960s and 1970s when the first quantum chemically-derived TSs and PESs were calculated for complex molecules, chemists mostly used the concepts of transition states and potential energy surfaces qualitatively, knowing little about quantum chemistry and having no quantum chemical data to support their suppositions. It was a time of blended soft and hard theories. And this blend is evident in the derivation of the table that appears in Section 6.
6. Qualitative and quantitative soft and hard theories
In discussions with colleagues and even amongst ourselves, there is a tendency to consider quantitative soft theory as being “hard.” But in our taxonomy, hard theories refer only to approaches that involve doing quantum chemistry. The solution to this confusion is to realize that both soft and hard theories can be either qualitative or quantitative. This is shown in Table 1 which includes examples of all four categories.| Qualitative | Quantitative | |
|---|---|---|
| a Houk's quadrant is named after Kendall N. Houk in honor of his 80th birthday (February 27, 2023) and is modeled after Pasteur's Quadrant.194 Over the course of his career, he has utilized both soft and hard theories, each in qualitative and quantitative ways as the science required. This nomenclature is modelled after “Pasteur's quadrant” that distinguishes the quest for fundamental understanding (yes or no) with applications and considerations of use (yes or no), thereby forming a 2 × 2 matrix.191 b Several of the examples in this table represent borderline situations. For example, the earliest mentions of potential energy surfaces were qualitative yet today, PESs are calculated for both ground and excited states of complex molecules. We posit that the discussion of what category a certain concept is, especially in borderline or ambiguous cases, is itself pedagogical and one of the values of the table, not one of its deficits. | ||
| Soft “heuristic” theories | Electronic effects56,58 | Hammet equation62,67 |
| Steric effects75 | Benson additivity rules for the estimation of thermochemical properties180 | |
| Stereoelectronic effects175–177 | Brønsted–Lowery acid-base theory181–183 | |
| Pearson's hard and soft acid and base theory69 | Curtin–Hammett principle68,184 | |
| Pre-Hückel “aromaticity” including Robinson's and Crocker's sextet36 | Activation barriers based on statistical mechanics (see Eyring170 and Evans and Polanyi171) | |
| Curly arrow pushing178,179 | Molecular mechanics calculations185,186 | |
| Transition state theory based on statistical mechanics162,163 | ||
| Post-transition state bifurcations based on mathematical/symmetry arguments187,188 | ||
| Hard “quantum chemical based” theories | State and correlation diagrams117,131 | Hückel “aromaticity”27–29 |
| Walsh diagrams189 | Fukui's IRC (intrinsic reaction coordinate)191 | |
| Woodward-Hoffmann selection rules122 | Potential energy surfaces based on computational quantum chemistry187 (variational) transition state theory applied using QM154,188 | |
| Hückel/Möbius allowed/forbidden rules132,133 | Post-transition state bifurcations explored with QM and QM-based molecular dynamics155–157 | |
| Perturbation theory based on orbital mixing diagrams190 | Torquoselectivity192,193 | |
Take as a representative case the concept of activation barriers. Activation barriers can, of course, be determined from kinetics experiments, and with high precision. Such kinetics-based data is quantitative and relevant to transition states, but is not, in our taxonomy, hard or based on quantum chemistry. Knowing the Arrhenius-determined energy barrier for a reaction does not provide the structure of a transition state, nor even which step in a reaction is rate-determining. This and other experimental data can be connected to results obtained from quantum chemistry, but it in no way anticipates those results. Kinetics experiments reside in a soft universe, but, when well done, are quantitative and immensely useful. The key point here is that the distinction between soft and hard is not one of data quality; it is one of data origin.
We now examine another much used concept in organic chemistry from the early 1950s, the Curtin–Hammett principle (Scheme 1).68Scheme 1 is the simplest kinetic system representing a compound that exists in multiple conformations, each of which reacts to give a different product. The Curtin–Hammett principle obtains only when the rates of interconversion of the reactant conformations (or isomeric forms) are much faster than the rates of reaction. According to the original derivation and interpretations of the Curtin–Hammett principle, the experimental product ratio is independent of the conformational equilibrium and equal to the difference in free energies between the two reaction transition states (eqn. (2)). Subsequently, it was explained that the product ratio was also equal to the product of the conformational equilibrium distribution times the ratio of reaction rate constants (eqn. (3)).172,173 For either of these two applications, one is using quantitative soft theory.
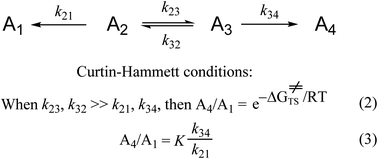 | ||
| Scheme 1 The Curtin–Hammett principle, for a compound that exists in two conformations or two isomers, each of which reacts to form a different product. More complex Curtin–Hammett type systems, e.g., schemes that involve second order reactions,68,174 have more complex mathematical expressions for the product ratio(s). Nonetheless, all these are soft theories regardless of their qualitative–quantitative nature. | ||
We now jump to the era of high-quality computational quantum chemistry. Fig. 10 illustrates the use of hard theory for a chemical reaction also described by the Curtin–Hammett principle. In this latter instance, Houk et al. reported the computed free energy diagram for the reaction of maleic anhydride with the 1,3,5-cycloheptatriene ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) norcaradiene equilibrating system. The quantum calculations provided the energies and structures of the reacting isomers as well as the transition states for three possible reactions and were consistent with the experimental results, i.e., 1,3,5-cycloheptatriene is far more stable than norcaradiene yet the predominant product is the endo adduct of norcaradiene. This is an example of using hard theory to quantify and extend soft theoretical results.
norcaradiene equilibrating system. The quantum calculations provided the energies and structures of the reacting isomers as well as the transition states for three possible reactions and were consistent with the experimental results, i.e., 1,3,5-cycloheptatriene is far more stable than norcaradiene yet the predominant product is the endo adduct of norcaradiene. This is an example of using hard theory to quantify and extend soft theoretical results.
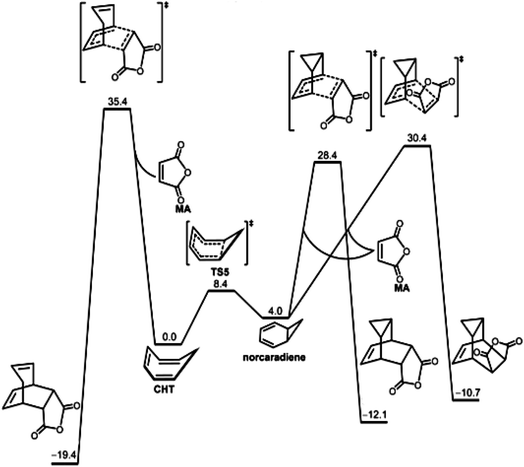 | ||
Fig. 10 The free energy diagram for the reaction of maleic anhydride with the 1,3,5-cycloheptatriene ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) norcaradiene system obtained by high level computational quantum chemistry calculations by Chen, Houk et al.195 While this is a Curtin–Hammett kinetic system,68,174 it was analyzed using hard theory. The results of the calculations were consistent with the experimentally observed product.196,197 Reprinted from P.-P. Chen, J. I. Seeman, K. N. Houk, Angew. Chem. Int. Ed. 2020, 59, 12506–12519, https://doi.org/10.1002/anie.202003279 with permission from John Wiley and Sons. norcaradiene system obtained by high level computational quantum chemistry calculations by Chen, Houk et al.195 While this is a Curtin–Hammett kinetic system,68,174 it was analyzed using hard theory. The results of the calculations were consistent with the experimentally observed product.196,197 Reprinted from P.-P. Chen, J. I. Seeman, K. N. Houk, Angew. Chem. Int. Ed. 2020, 59, 12506–12519, https://doi.org/10.1002/anie.202003279 with permission from John Wiley and Sons. | ||
We acknowledge that the distinction between soft and hard parameters (and even theories) is, at least at first, complicated and for some, confusing. We now add a layer that adds complexity and almost certainly more confusion. How should one classify applications that combine soft theory with hard theory or that have transitioned from soft to hard over time? For example, in what category within the Houk quadrant (Table 1) is molecular mechanics (MM) placed?
Molecular mechanics uses classical mechanics to predict geometries and energies of molecular systems. That being said, certain parts of MM force fields are derived from quantum chemistry. For example, the bond length and angle terms are typically modeled as harmonic potentials which are centered around equilibrium bond-length values. Those bond-length values are often derived from high level quantum chemistry calculations. Does that make MM a hard theory? We think not. In MM calculations, there are no electrons treated explicitly, so the MM model is not doing quantum chemistry. In MM, hard theory is often done to get parameters but soft theory, i.e., molecular mechanics, is done to get geometries and energies.
We suggest that the key is whether a method involves DOING quantum mechanics — that is clearly a hard model — versus USING some quantum chemistry — that would be soft. We acknowledge that MM is a bridged model that is different than not using any quantum chemistry. But MM remains a classical mechanics model. In a sense, MM is a soft theory in which quantum chemistry helped make it quantitative.
We add three comments. First, for the past century, predictions have been based on soft theories and, of course more recently, on hard theories. These predictions typically don't suggest exclusive reactions, just possible reactions. In other words, one generally predicts whether a given reaction is feasible, not what else might happen in a real laboratory experiment.
Second, we note that the nomenclature of both soft and hard theories can be applied to results as well as theories.
Third, as discussed above, over the course of time, some qualitative soft theories have progressed through a sequence as shown in Table 2. This illustrates that some properties or even theories can, in their earliest forms, be rather primitive but can progress, over time, to quantitative quantum chemical-based theories.
| Steric effects | Electronic effects | |
|---|---|---|
| Qualitative soft | From the 1870s observation of steric effects in the alkylation of amines51,52 | Robinson's198,199 and Ingold's58 electronic theories |
| Quantitative soft | Taft's linear free energy relationships76 and force field calculations of steric effects75 | Hammett's equations61,62 |
| Qualitative hard | VSEPR (valence shell electron pair repulsion)200,201 | Through-bond effects by eHT202–204 |
| Quantitative hard | Numerous quantitative evaluations based on quantum chemical calculations that have their beginnings in the 1970s and early 1980s.75,84,205,206 | Various flavors of energy decomposition analysis158,167 |
7. When the language of soft theory is called upon to explain hard theory. “Unforeseeable knowledge”
At some time in the process of performing computational chemistry, one is almost always faced with the question: what does all this data mean?Hoffmann discussed the meaning of “explanation” within the context of the value of “computations” in a very insightful essay published almost 25 years ago.207 Hoffmann discussed the complexity of chemistry, writing:
“Given that complexity, there is a natural tendency on the part of the computational theorist to think that there can be no single, simplified explanation. and to be loath to give such an explanation to experimentalists, especially in their own language, based as it is on vague, time-honored contexts which may bear no relation to what you calculate.”207
Now, 25 years after Hoffmann's words, we take his analyses one step further. We ask another question: in what words do we describe the results?
The literature of today and even in several years past reveals that computational chemists have responded to one important set of consumers for their research – the experimentalists – by providing not only data but also, if not primarily, explanations and understanding. Frequently, those explanations are furnished in the well-used language of their consumers, which originated within soft theory: steric and electronic and stereoelectronic effects; conformational preferences; and so on. These terms are within the vocabularies of the well-known soft theories. But make no mistake: while the quantum chemistry-based data is being summarized in terms of soft theory vocabulary, the knowledge and understanding are still based on hard theory. The computational chemists are adopting a soft teaching strategy but are still, and only, discussing hard theory.
In relation to the categorization of soft and hard theories, it may seem confusing to use the language of soft theories to denote phenomena that hard theories are today explaining. The justification which is implicit in the logic used by current practitioners and which we affirm is as follows: they are actually describing the same phenomena, just today within hard theory applications while in the past, it was within soft theory applications. It would be counterproductive to invent new terms for the same phenomena.208
In contrast, according to Vincezo Politi, the conceptual divide between classical biology and molecular biology has led to scientists using the same terms but for different meanings.209 Politi referred to this multiplicity of language as “semantic incommensurability.”209 Chemists, so far, have retained the general meaning for the same words when using them with both soft and hard theories.
Occasionally, hard theory prompts experimentalists to use hard theory language because a long-standing soft model nomenclature was not previously used. Take, for example, the relatively recent recognition that favorable dispersion interactions can play key roles in structure, reactivity, selectivity and catalysis.160,210 While dispersion was, of course, not unknown to experimental chemists, it was not generally used as one of the go-to soft rationales for observations, i.e., steric effects, stereoelectronic effects, hydrogen-bonding and the like. But now the relevance of favorable dispersion has become appreciated enough that it is invoked in a soft manner! Of course, many concepts from quantum chemical theory are routinely used by experimentalists, including such classical terms as “disrotatory” and “conrotatory” to more modern ideas such as “conical intersection” and “post transition state bifurcation.”154,163,211–213
In some cases, however, the language of hard theory is used by theoreticians and physical chemists to explain experimental results, e.g., in discussions of selectivity in synthetic organic reactions, but is not embraced by the experimental community. Examples include much of the language of the Atoms-in-Molecules (AIM)214 and Molecular Electron Density Theory (MEDT)215 approaches, e.g., “bond critical points,” “gradient vector fields,” “monosynaptic basins,” “pseudoradical centres,” etc. Why has not more of such nomenclature made its way into interdisciplinary language? Perhaps the synthetic chemists are not reading the more theoretical papers; and perhaps the authors of the theoretical papers are not writing them and publishing them such that experimental chemists are attracted to them. Or perhaps the need has not yet developed by the experimental community to discuss those concepts.
Finding the vocabulary of soft theories useful to explain the results of hard theory is related to one of the forms of knowledge, sometimes called “unknown unknowns.”216 According to Drew,
“Unknown unknowns are pieces of knowledge that we do not have and equally are unaware that we don't have it. This is information that may be beyond our comprehension and indeed beyond our wildest dreams. It has never even entered our minds that unknown unknowns are a possibility.”217
We suggest that chemists developing and using soft theories that were later established as valid by quantum chemistry is knowledge more sophisticated than “unknown unknowns.” We believe that they had some anticipation that the future would validate and certify their soft theories. Of course, they could not have anticipated exactly how that would happen. But they had the confidence, as judged by their continuous and even expanded use of their soft theories. These soft theories were correct and useful until the hard theories provided the theoretical underpinning. We propose calling this kind of knowledge “unforeseeable knowledge.”
8. Scientiometric analysis on the chronological transition from soft theory to a blend of soft and hard theories
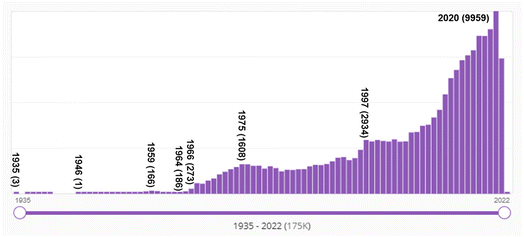
Bibliometric data supports the conclusion that a dramatic transition occurred in the late 1960s in organic chemistry, from a soft theory-base to a quantum chemistry-base for its structural and mechanistic explanations. Fig. 11 shows SciFinder's estimate of the frequency of use of the Hammett equation since 1937. As mentioned above, the Hammett equation is a still-used concept in physical organic chemistry to estimate and predict the role of substitution in various reactions. As a soft theory, the Hammett equation was very popular in physical organic chemistry in the 1960s and 1970s, and its use has tailed off but has not disappeared completely over the succeeding decades. This is evidence of both (a) the transition from “soft theory and reasoning by analogy” to hard theory and quantum chemistry that began in the mid-1960s; and (b) the continued effective use of soft theory by chemists into present times. Keep in mind that these numbers are not normalized to the total number of chemistry publications per year which has also grown substantially over the decades.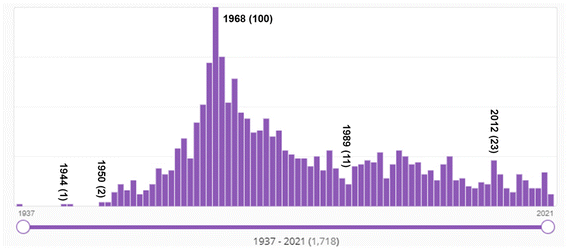 | ||
| Fig. 11 Number of SciFinder “hits” for “Hammett equation” from 1937 (one hit) to 2021. “Hits' refers to the number of publications in which the search term is found at least once in either the publication's title, abstract, or concepts list. The maximum number of hits was 100 in 1968. Although the Hammett equation was first published by Hammett in 1937,61,62 its use continues well into the 2020s. | ||
That a major transition in the practice of chemistry occurred in the mid-1960s can be seen from the SciFinder “hits” shown in Fig. 12. The term “molecular orbital” first appears in the SciFinder search in 1935, with three papers by Robert S. Mulliken,218–220 then papers by John E. Lennard–Jones,221 and Charles Coulson including co-authors H. C. Longuet–Higgins and Dewar,222–233 and a 1938 singly-authored paper by George Wheland.234 Not surprisingly, these are the premier theoretical chemists of the era – two of whom, Longuet–Higgins131 and Dewar134,135,235 made seminal contributions to the concept of orbital symmetry control of pericyclic reactions.
The number of hits prior to 1966 are substantial, even though a quick look at Fig. 12 would suggest otherwise. For example, in 1959, there were 166 abstracts identified with this search term by SciFinder. These pre-1966 hits reflect the papers by theoretical chemists. However, after 1965 – after the Woodward–Hoffmann rules – the increase is due to the publications by (or for) organic chemists.
Organic chemistry has undergone leaps in its use of technology and understanding from the days of isomer counting, Hammett equations, arrow-pushing, and soft theory. That does not mean that soft theories and other qualitative insights have been abandoned. Rather, soft theories and reasoning by analogy were used and continue to be used as talking points and stepping stones to more rigorous and fundamental quantum chemical theory explanations.
Woodward and Hoffmann opened the door for chemists of all levels to apply quantum chemistry in their own research. Chemists from around the world noticed the unique capabilities to answer experimental questions quickly and simply. The door swung widely open, and chemists today perform computational quantum chemistry as an adjunct to their research and ultimately, for some chemists, as their major chemical contributions.
9. Can All Soft Theories Be Made Hard? Should All Hard Theories Be made Quantitative?
Are there cases where soft theories should not or perhaps better, could not be made hard? Hoffmann stated,
“… most concepts in chemistry that have proven productive in the design of new experiments are not reducible to physics. By this I mean that they cannot be redefined adequately using only the language of physics. To be specific, I'm thinking of aromaticity, the acid-base concept, the idea of a functional group, a substituent effect, and that of a chromophore. And let us not forget the chemical bond. Few, if any, new molecules would have been made if we had waited around for rigorous definitions of these productive thought constructions.”236
We take Roald Hoffmann's words as points for future research, not “Do Not Enter” signs. In our opinion, ultimately the basis for every soft theory needs to be found within quantum chemistry; if it isn't, then its utility is questionable and ultimately should disappear. A stronger soft theory or any type of hard theory should be its replacement. Essentially, we ask: should we accept false soft theories because they work? Rather, ought not the theorists be able to provide easy to use theories that have a strong basis in quantum chemistry?
We bring up one of our favorite examples and one of our favorite tools: arrow pushing. When first learning organic chemistry, students are introduced to the practice of “arrow-pushing” or “curly/curved arrow” notation. In short, curly arrows are used to indicate where electrons that change locations during a reaction originated in a reactant (the tail of the arrow) and where they ended up in a product (where the head of the arrow points) (Fig. 13). The development of this practice has a long history.179,237–239 Some theoretical chemists have attached additional meaning to these arrows, related to the path that electrons follow between reactants and products.20,179,240 As of today's knowledge, associating such meaning with the arrows is inappropriate – the arrows are simply a bookkeeping tool.
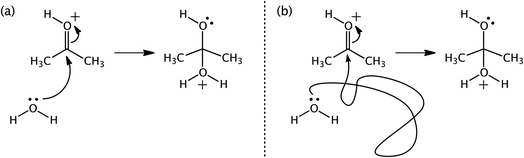 | ||
| Fig. 13 Two arrow-pushing representations (a and b) for a water molecule adding to protonated acetone. | ||
One problem is that using curly arrows requires the user to choose canonical resonance structures of reactants and products, which are not complete quantum chemical representations of molecules with delocalized electrons. How the electron density changes as a molecule transforms from reactant to product is (to us and others)241 worth knowing and computable with quantum chemistry. The issue is just that claiming that characterizing such changes in electron density corresponds to “making curly arrows real” distorts the connection between a soft model and a hard model and could diminish the utility of the soft model by encouraging misinterpretations by consumers (both novices and practicing organic chemists) when those creating such pictures adhere to the limits associated with the original model.241–243
Another example is the simplest use of valence bond (VB) theory – the chemical pictographs we use daily, and which appear in all chemistry journals, the non-quantum chemical version of VB theory. This is clearly a soft model with tremendous utility, utility that might be diminished if only the hard version of VB theory was used. Yet the use of this simple VB model does not prepare most of us for much of organometallic chemistry or for molecules having penta- and hexacoordinate carbon atoms.244–248 Narrow pedagogy, e.g., the focus on tetracoordinate carbon as a law of nature – which, of course, it is not – hampers thinking outside that box. We acknowledge the multitude of complex factors that influence the content of textbooks, but we encourage teachers to consider pointing out that there is more to chemistry than the compartmentalized and simplified world often portrayed in these texts. Flexible thinking, of course, allows for advances in research and again speaks to the value of plurality in chemistry. Pluralism in science3,6,83,249,250 goes hand in hand with flexible thinking and consideration of all the experimental and theoretical data.251
Of course, not all soft theories can be made hard. Some soft theories have been discarded long ago, as they fail to mirror new experimental data, such as in “domino rotations” to explain unimolecular valence isomerizations.252,253 They were wrong to begin with. Some soft theories are ‘right’ for the wrong reasons. That is, they are consistent with the available experimental data but they do so by happy – or unhappy – coincidence.254–256 Examples include the soft theories that “explain” the stability of the hexagonal structure of benzene,90 and the attractive effects of some otherwise steric effects due to favorable dispersion effects.210,257
And are there cases of hard theories that should not be made qualitative? Another long-standing concept that is taught to novices and utilized on a daily basis by practicing organic chemists is the idea of atom hybridization, e.g., the carbonyl carbon in protonated acetone is sp2 hybridized, while the methyl carbons are sp3 hybridized.258,259 This concept is generally introduced to students when initially describing the bonding in organic molecules as consisting of two-electron bonds between adjacent atoms. Often, students are instructed to count how many atoms are connected to a carbon, use that to determine its hybridization, then use an appropriate hybrid orbital on that carbon to pair with one on another atom to make a bond. In this sense, the hybridization concept is circular reasoning,14 in that one must know the answer – the type of bond formed – before one can choose the hybrid orbitals to use. And basis sets for quantum chemical calculations generally do not include hybridized orbitals. For these reasons and others, some have advocated for the removal of the hybridization concept from the organic chemistry curriculum.260,261
Like many soft theories, hybridization has tremendous practical utility. But does its practical utility fade when one tries to make it quantitative? When one generates a wave function, one can check on the contributions of s and p orbitals centered on each atom (although that is often not trivial to accomplish with complex basis sets and complex software) and determine the s- and p-character at any atom.262,263 Doing so results in fractional or non-integer hybridizations.264,265 There are certainly cases where that information is useful,266 but it is difficult to argue that knowing that one molecule has a carbon with sp2.11 hybridization while an analog has a carbon with sp2.09 hybridization is useful. So, context is key. There is no question that qualitative and quantitative models of hybridization are readily available, but one should not assume that the quantitative model is always the one that will push learning forward.
So, after all this, we find ourselves arguing to keep some soft theories soft and some hard theories qualitative. We recognize the value – sometimes – in models that cannot be made hard by their nature. For example, arrow-pushing is not really a structural model; rather it is an immensely useful book-keeping tool that encourages students and researchers to think about other models based on quantum chemistry (e.g., frontier molecular orbital theory). We also recognize that the quantification of some models, e.g., hybridization, while perfectly valid, may not add value and may actually induce confusion or accidentally encourage the overinterpretation of computed data.
10. Quantitative analyses without understanding
Is it possible for hard theory to advance to the point where predictions are routinely made and used without providing an understanding of the origins of the observed phenomena? Or perhaps this is the savior of seeking soft theories, to provide descriptors for hard theories?Some scientists worry about any tool that is used as a “black box.” There is not agreement as to whether black boxes are good or bad. Let us consider the use of sophisticated computational quantum chemistry and its associated software – often provided by others upon whom computational chemists rely but whose names and the derivations of their software may be unknown. On one hand, readily available software – the black box, in this instance – allows the benefits of theory to be distributed widely and often inexpensively. On the other, black box software comes with the danger of misapplication. Black box software also facilitates doing without thinking and learning.
Here is a modern example with which we have been involved: the use of quantum chemistry to compute NMR chemical shifts (and coupling constants).73,154 While current computational chemists and their students, for example, need to know how to run the software used to compute chemical shifts, how to process the results of these calculations, how to deal with the problems of solvation and multiple contributing conformers – a rather daunting collection of scholarly requirements – the black box users need not know the details of the quantum chemistry that is hidden within the confines of the software. Some students (and their professors) do, and some do not, and some do not at the outset but do so in time. Nonetheless, these chemists can use hard theory to learn about molecular structures and, in doing so, empower laboratory experiments (even total syntheses)267–270 and shine light on aspects of chemical history.73,154 Such calculations have proven essential, since soft theories for predicting NMR chemical shifts, which are based on reasoning by analogy (e.g., being a certain distance from a certain functional group is expected to affect a chemical shift by a certain magnitude), are not capable of distinguishing between closely related structures, i.e., often there are many related structures that fit the qualitative predictions.
We would modify Coulson's plea, “Give us insight, not numbers,“271–273 to “Give us insight along with more numbers,” a statement that we have recently learned (quite indirectly, via a footnote in a paper by others) has been used by Frenking as well.273
11. Today's quantum theories are not perfect
If quantum chemical “hard theory” promises unique, solid answers to chemical problems, what does it mean when two quantum chemical explanations for the same phenomenon differ? One issue that stretches the limits of quantum chemistry in constructing models of organic structure and reactivity is the fact that electron density in molecules is delocalized, while organic chemists tend to make arguments based on discrete fragments of molecules (bonds, functional groups) and interactions between them. A quantum chemistry-based approach to this problem is energy decomposition analysis.167 In this approach, a wave function is “decomposed” into parts associated with physical concepts like Pauli repulsion, donor–acceptor orbital interactions, etc. Energies can be associated with each, and these parts can be associated with substructures within molecules such that the difference between the sum of the molecular parts and the whole molecule is used as a measure of interaction. The lack of universal agreement on how wave functions should be decomposed and on how molecular substructures should be defined,158 and the fact that the language used to name each decomposed “part” is often derived from soft theory (see Section 2), does not make the theory soft.158Classic examples include the debate over the relative importance of unfavorable steric repulsion (defined here as 4-electron orbital interactions) and favorable donor–acceptor (2-electron) orbital interactions (hyperconjugation) in controlling the staggered versus eclipsed conformational preference in ethane,257,274–279 and the debate over the origins (e.g., relative importance of electrostatic v, donor–acceptor orbital interactions) of the anomeric effect.280 In these cases, we have the physics, but the delocalized “reality” creates discord with the soft approach of fragment-based models. As described above, experimental organic chemists often crave models described in soft terms and many theoreticians (one of the authors of this paper (DJT) included) try to deliver these. In some cases, though, doing so requires implementing approximations that increase the qualitative nature of a calculation and consequently swing open the doors to disagreement. We each must carry out our own cost–benefit analysis in such situations to decide whether to enter the fray. Confusion in hard theories does not make them soft.
In addition, while rapid and robust methods for fully quantum chemical treatments of explicit solvation, protein structures, photochemical reactions of complex molecules, etc. are still not readily available, the quantum chemical principles for treating them are known. The absence of technology for the implementation of improvements to the use of a methodology does not turn a hard theory into a soft one. It may, however, keep a qualitative theory from becoming a quantitative theory, either within the soft or hard domain.
12. Soft versus hard theory: sources for joy and fulfillment to a scientist
A reviewer asked,
“There is a basic difference between the excitement of an organic chemist and a computational chemist, when the former can hold up crystals while the latter can talk with glowing eyes about the fourth digit in a bond length. Will this be an equivalent source of joy and fulfillment to these chemists?”
We suspect that the reviewer was being intentionally controversial. Surely there are theoretical and computational discoveries that go far beyond the trivial, even if the trivial is real. And this goes for experimental chemistry as well as theoretical chemistry. We believe – indeed, we have observed – real joy, excitement, and fulfillment in the discovery of quantum chemical phenomena. Indeed, we have experienced that ourselves.
For example, DJT remembers vividly the afternoon when he realized how to design a reaction with a post transition state bifurcation. This realization came from his mind combining two different results from quantum chemical studies (both his and others'): (1) many secondary carbocations are not minima on PESs, but are actually transition structures for carbocation rearrangements, and (2) post transition state bifurcations are followed by a second transition state that interconverts the two products. The leap made in DJT's mind (a seemingly simple leap in retrospect) was that a secondary carbocation could serve as this second transition state and be accessed from a higher energy transition state for a well-known process like leaving-group loss or alkene protonation. Joy is indeed the correct word for the feeling accompanying this realization. This design served as the basis for a key section of a subsequent funded grant and was ultimately put to the test through a new collaboration with a synthetic chemist (soon to be published) that DJT hopes will increase the interest of synthetic organic chemists in hard theory.
JIS will never forget his joy when he first fully appreciated that classical explanations were unable to solve the pericyclic no-mechanism problem128 and that there was a theoretical unity in all the quantum chemistry-based mechanistic explanations of orbital symmetry control. JIS also experienced an eye-popping joy in his own personal discovery, during a pedagogical Zoom session with Roald Hoffmann, when he was invited to see the ability to predict the instability of cyclobutadiene by using simple perturbation theory (by bringing 1,3-butadiene's C(1) closer to C(4)).
13. The future
In 1929, Paul A. M. Dirac stated that
“the underlying physical laws necessary for the mathematical theory of … the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble.”281
Time has surely demonstrated that Dirac's prediction has proven to be so wrong, as was IBM's president who said in 1943, “I think there is a world market for maybe five computers,”282 and the founder of Digital Equipment Corporation who said in 1977, “There is no reason anyone would want a computer in their home.”282
But what of the future? Nowadays, quantum chemical calculations are often being replaced by other techniques. Some scientists are developing statistics-based methods, often involving machine learning, to predict NMR chemical shifts283 or chemical reactivities284 or biological properties – as well as host of other important properties of molecules for which quantum chemistry has been the go-to tool.285 Is this a trend toward soft theory and reasoning by analogy? One goal of this trend is super-fast predictions – quantum chemical methods can be slow. The danger is that statistics-based methods are not guaranteed to work when faced with unexpected chemistry, i.e., extrapolations beyond the populations of the databases used to create the statistical models. Developing such methods requires large data sets for “training” and, ironically, these data sets are often generated using quantum chemical calculations. Approximations and insights look to have a future for some time still.
14. Conclusions
We offer the following conclusions:• Soft explanations were sufficient models1 to explain most of experimental chemistry until the 1950s and 1960s when experimental chemistry began to produce an avalanche of complex reactions with exquisite stereochemical properties and previously unknown bonding patterns that required quantum chemical explanations.
• Quantum chemical explanations for molecular spectroscopy began to be published in the 1930s and 1940s, however, that interdisciplinary model did not transfer to other subdisciplines of chemistry.
• Beginning in the early-to-mid-1960s, a confluence of circumstances set off the explosive power of computational quantum chemistry: an abundance of chemical results that were not interpretable by soft theory; improvements in computer technology; advancements in quantum chemical theory; and the model of the Woodward–Hoffmann collaboration and the synergy between theory and experiment.
• Quantum chemistry's explanatory and predictive reach is broad. It is relevant to all known chemistry, and as it goes beyond the universe of experimental chemistry. Quantum chemistry can provide fundamental explanations for all soft theory conjectures or invalidate them. Computational quantum chemistry can uncover information that is hidden from the vision of soft theory.
• Computational quantum chemistry's explanatory and predictive reach is deep and extensive. It can explore potential energy surfaces and molecular dynamics in ground and excited states. Quantum chemistry can explore the chemistry of molecules not yet made and even those that are unmakeable. Quantum chemistry can devise experimental conditions that would be expensive if not impossible to implement.
• Quantum chemistry has thus justified many of the soft theories advanced and used by chemists for decades. That quantum chemistry has provided some measure of justification for the soft theories of the past indicates much credit is deserved by those chemists of the past who had this unforeseeable knowledge.
• Quantum chemistry has revealed new phenomena that go beyond the realm of pre-1960s chemistry. New nomenclature has thus been required, e.g., “conrotatory” and “disrotatory”, “post-transition state bifurcations,” “intrinsic reaction coordinates,” and “conical intersections,” to cite just a few.
• The use of soft theory ideas and nomenclature to describe hard theory results is a pragmatic pedagogical and communicating device. This is especially justified when explaining soft theory phenomena which have been rigorously established by quantum chemistry. We believe in the pluralism of science, that there are many useful models1 and ways to do science and to explain its wonders. The use of soft theories, especially the ideas and nomenclature of soft theory, along with quantum chemistry and computational chemistry adds to the accessibility and understanding of the science that continues to create itself.
We add one final caveat that is well known: quantum chemistry is not a finished science. One of its greatest challenges is to model reactions in normal solvents. Until this and other problems are satisfactorily solved, quantum chemistry cannot be considered a fully developed tool.
15. Coda
There has been some discussion in the recent literature about the danger of “hype” in the chemical literature.286–288 We wonder: is hype less likely to appear in research that deals with soft theory than with hard theory? This is a topic for future research.Author contributions
J. I. S. and D. J. T. performed the research and wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Reinhard W. Hoffmann, Roald Hoffmann, Guillermo Restrepo, Steven M. Weinreb, several readers of advanced drafts of this publication, and especially three very knowledgeable and insightful reviewers for helpful discussions. DJT acknowledges support from NSF (CHE- 1856416). JIS thanks the Boatwright Memorial Library at the University of Richmond for continuing technical assistance.References
- C. J. Suckling, K. E. Suckling and C. W. Suckling, Chemistry Through Models, Cambridge University Press, Cambridge U.K., 1978 Search PubMed.
- Anonymous, Heuristic, https://en.wikipedia.org/wiki/Heuristic, accessed 28 April 2022 Search PubMed.
- K. Ruthenberg and A. Mets, Found. Chem., 2020, 22, 403–419, DOI:10.1007/s10698-020-09378-0.
- A. J. Rocke, Isis, 2018, 109, 577–586, DOI:10.1086/699998.
- M. J. Nye, Isis, 2018, 109, 587–596, DOI:10.1086/699996.
- H. Chang, Is Water H2O? Evidence, Realism and Pluralism in Boston Studies in the Philosophy of Science, Springer, Dordrecht, 2012, vol. 293 Search PubMed.
- We acknowledge that the terms "soft" and "hard" have been used before, e.g., as "soft and hard science." According to Wikipedia, "Hard science and soft science are colloquial terms used to compare scientific fields on the basis of perceived methodological rigor, exactitude, and objectivity. Roughly speaking, the formal sciences & natural sciences are considered "hard", whereas the social sciences are usually described as "soft". Precise definitions vary, but features often cited as characteristic of hard science include producing testable predictions, performing controlled experiments, relying on quantifiable data and mathematical models, a high degree of accuracy and objectivity, higher levels of consensus, faster progression of the field, greater explanatory success, cumulativeness, replicability, and generally applying a purer form of the scientific method, https://en.wikipedia.org/wiki/Hard_and_soft_science, accessed August 27, 2022, We are defining these terms differently in this work.
- H. Rzepa, The oldest reaction mechanism, updated!, http://www.ch.imperial.ac.uk/rzepa/blog/?p=2423, accessed 5 May 2022 Search PubMed.
- H. C. Brown and with comments by P. von R. Schleyer, The Nonclassical Ion Problem, Plenum Press, New York, 1977 Search PubMed.
- E. M. Arnett, T. C. Hofelich and G. W. Schriver, Carbocations in Reactive Intermediates, ed. M. Jones Jr and R. A. Moss, John Wiley & Sons, New York, 1985, vol. 3, ch. 7, pp. 189–226 Search PubMed.
- W. M. Goodwin, Brit. J. Phil. Sci., 2013, 64, 787–816, DOI:10.1093/bjps/axs025.
- H. C. Brown, Chem. Eng. News, 1967, 45, 87–97 CrossRef CAS.
- K. Popper, The Logic of Scientific Discovery, Harper and Row, New York, 1968 Search PubMed.
- R. Hoffmann, Am. Sci., 1988, 76, 182–185 Search PubMed.
- A. Alibakhshi and B. Hartke, Nat. Comm., 2021, 12, 3584, DOI:10.1038/s41467-021-23724-6.
- B. Mennucci, J. Phys. Chem. Lett., 2010, 1, 1666–1674, DOI:10.1021/jz100506s.
- B. Mennucci and R. Cammi, Continuum Solvation Models in Chemical Physics: From Theory to Applications, Wiley, Hoboken, NJ, 2008 Search PubMed.
- Y. Nieves-Quinones and D. A. Singleton, J. Am. Chem. Soc., 2016, 138, 15167–15176, DOI:10.1021/jacs.6b07328.
- J. E. M. N. Klein, G. Knizia and H. S. Rzepa, ChemistryOpen, 2019, 8, 1244–1250, DOI:10.1002/open.201900099.
- G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2015, 54, 5518–5522, DOI:10.1002/anie.201410637.
- A. Q. Cusumano, W. A. Goddard III and B. M. Stoltz, J. Am. Chem. Soc., 2020, 142, 19033–19039, DOI:10.1021/jacs.0c09575.
- D. H. Rouvray, J. Chem. Inf. Comput. Sci., 1994, 34, 446–452 CrossRef CAS.
- D. H. Rouvray, J. Chem. Inf. Comput. Sci., 1992, 32, 580–586 CrossRef CAS.
- P. J. Breen, J. A. Warren, E. R. Bernstein and J. I. Seeman, J. Am. Chem. Soc., 1987, 109, 3453–3455 CrossRef CAS.
- S. Li, E. R. Bernstein and J. I. Seeman, J. Phys. Chem., 1991, 96, 8808–8813 CrossRef.
- A. F. Holleman, J. Am. Chem. Soc., 1914, 36, 2495–2498, DOI:10.1021/ja02189a010.
- E. Hückel, Z. Phys., 1931, 70, 204–286 CrossRef.
- E. Hückel, Z. Phys., 1931, 72, 310–337 CrossRef.
- E. Hückel, Aromatic and Unsaturated Molecules. Contributions to the Problem of their Constitution and Properties, International Conference on Physics. Papers & Discussions. A Joint Conference Organized by the International Union of Pure and Applied Physics and The Physical Society, The Physical Society The Solid State of Matter, 1935, vol. II, pp. 9–35 Search PubMed.
- L. Pauling and G. W. Wheland, J. Chem. Phys., 1933, 1, 362–374, DOI:10.1063/1.1749304.
- R. Hoffmann, S. Shaik and P. C. Hiberty, Acc. Chem. Res., 2003, 36, 750–756 CrossRef CAS PubMed.
- S. Shaik and P. C. Hiberty, Helv. Chim. Acta, 2003, 86, 1063–1084 CrossRef CAS.
- S. Shaik and P. C. Hiberty, Valence Bond Theory, Its History, Fundamentals, and Applications: A Primer in Reviews in Computational Chemistry, ed. K. B. Lipkowitz, R. Larter and T. R. Cundari, Wiley-VCH, Weinheim, Germany, 2004, vol. 20, ch. 1, pp. 1–100 Search PubMed.
- R. Hoffmann and J.-P. Malrieu, Angew. Chem., Int. Ed., 2020, 59, 12590–12610 CrossRef CAS PubMed.
- R. Hoffmann and D. L. V. K. Prasad, Am. Sci., 2020, 109, 144–147, DOI:10.1511/2021.109.3.144.
- A. T. Balaban, P. v. R. Schleyer and H. S. Rzepa, Chem. Rev., 2005, 105, 3436–3447 CrossRef CAS PubMed.
- G. Nagendrapp, Resonance, 2011, 16, 1146–1151 CrossRef (with poster), https://www.ias.ac.in/article/fulltext/reso/006/05/0074-0078, https://www.ias.ac.in/article/fulltext/reso/006/05/0074-0078.
- A. Y. Rogachev, X.-D. Wen and R. Hoffmann, J. Am. Chem. Soc., 2012, 134, 8062–8065, DOI:10.1021/ja302597r.
- R. Hoffmann, Am. Sci., 1987, 619–621 Search PubMed.
- R. Hoffmann and H. Hopf, Angew. Chem., Int. Ed., 2008, 47, 4474–4481 CrossRef CAS PubMed.
- G. Frenking, Isr. J. Chem., 2022, 62, 188, DOI:10.1002/ijch.202100070.
- L. Zhao, W. H. E. Schwarz and G. Frenking, Nature Rev. Chem., 2019, 3, 35–47 CrossRef.
- W. Hückel and F. H. Rathmann (translator), Theoretical Principles of Organic Chemistry, Elsevier, Amsterdam, 1955 Search PubMed.
- A. J. Rocke, Chemical Atomism in the Nineteenth Century, From Dalton to Cannizzaro, Ohio State University Press, Columbus, OH, 1984 Search PubMed.
- L. F. Fieser and M. Fieser, Organic Chemistry, Reinhold Publishing Corporation, New York, 3rd edn, 1956 Search PubMed.
- D. J. Cram and G. S. Hammond, Organic Chemistry, McGraw-Hill, New York, 1959 Search PubMed.
- G. S. Girolami and V. V. Mainz, Bull. Hist. Chem., 2019, 44, 100–108 CAS.
- L. Tambolo and G. Cevolani, Stu. Hist. Phil. Sci. Part A, 2021, 90, 30–38, DOI:10.1016/j.shpsa.2021.09.001.
- M. Fontani, M. V. Orna and M. Costa, Compt. Rend. Chim., 2020, 23, 231–241, DOI:10.5802/crchim.1.
- S. Shaik, E. Cremades and S. Alvarez, Angew. Chem., Int. Ed., 2019, 16, 13194–13206, DOI:10.1002/anie.201904584.
- A. W. Hofmann, Chem. Ber., 1872, 5, 704–719 CrossRef.
- N. Menschutkin, Ann. Chem., 1879, 195, 334–364 CrossRef.
- D. E. Lewis, Chem. - Eur. J., 2021, 27, 15829–15841, DOI:10.1002/chem.202101823.
- P. Rabe and K. Kindler, Ber. Dtsch. Chem. Ges., 1918, 51, 466–467, DOI:10.1002/cber.19180510153.
- K. Kindler, Ann. Chem., 1928, 464, 278–292 CrossRef CAS.
- R. Robinson, J. Soc. Dyers Colour., 1934, 65–76 CAS.
- J. Shorter, Nat. Prod. Rep., 1987, 4, 61–66 RSC.
- C. K. Ingold, Chem. Rev., 1934, 14, 225–274 CrossRef.
- K. Schofield, Ambix, 1994, 41, 87–107 CrossRef CAS.
- C. W. Shoppee, Biogr. Mem. Fellows R. Soc., 1972, 18, 348–411 CrossRef.
- L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103, DOI:10.1021/ja01280a022.
- L. P. Hammett, Physical Organic Chemistry, McGraw-Hill, New York, 1940 Search PubMed.
- J. E. Leffler, Science, 1953, 117, 340–341 CrossRef CAS.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS.
- R. P. Bell, Proc. R. Soc. A, 1936, 154, 414–429 Search PubMed.
- D. Y. Curtin, Rec. Chem. Prog., 1954, 15, 111–128 CAS.
- L. P. Hammett, Physical Organic Chemistry, McGraw-Hill, New York, 1970 Search PubMed.
- J. I. Seeman, Chem. Rev., 1983, 83, 83–134, DOI:10.1021/cr00054a001.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539, DOI:10.1021/ja00905a001.
- R. W. Hoffmann, Classical Methods in Structure Elucidation of Natural Products, Wiley-VHCA, Zürich, Switzerland, 2018 Search PubMed.
- J. I. Seeman, Isr. J. Chem., 2018, 58, 28–44, DOI:10.1002/ijch.201700079.
- R. Hoffmann and P. Laszlo, Angew. Chem., Int. Ed., 1991, 30, 1–16, DOI:10.1002/anie.199100013.
- J. I. Seeman and D. J. Tantillo, Angew. Chem., Int. Ed., 2020, 59, 10702–10721, DOI:10.1002/ange.201916566.
- J. D. Roberts, J. Org. Chem., 2009, 74, 4897–4917 CrossRef CAS PubMed.
- R. Gallo, Treatment of Steric Effects in Progress in Physical Organic Chemistry, ed. R. W. Taft, John Wiley & Sons, 1983, pp. 115–163 Search PubMed.
- R. W. Taft Jr, Separation of Polar, Steric, and Resonance Effects in Steric Effects in Organic Chemistry, ed. M. S. Newman, Wiley, New York, 1956, pp. 556–675 Search PubMed.
- E. Glyde and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1977, 2, 1537–1541 RSC.
- O. Exner, Collect. Czech. Chem. Commun., 1976, 41, 1516–1540, DOI:10.1135/cccc19761516.
- H. C. Brown, Boranes in Organic Chemistry, Cornell University Press, Ithaca, New York, 1972 Search PubMed.
- M. O'Brien and R. A. More O'Ferrall, J. Chem. Soc., Perkin Trans. 2, 1978, 2, 1045 RSC.
- N. B. Chapman and J. Shorter, Advances in Linear Free-Energy Relationships, Plenum Press, London, 1972 Search PubMed.
- V. Gineityte, J. Mol. Struct.: THEOCHEM, 2001, 546, 107–117, DOI:10.1016/S0166-1280(01)00433-X.
- J. Schummer, ed. E. R. Scerri and L. McIntyre, The Methodological Pluralism of Chemistry and Its Philosophical Implications in Philosophy of Chemistry, Boston Studies in the Philosophy and History of Science, Springer, Dordrecht, 2015 Search PubMed.
- J. I. Seeman, R. Galzerano, K. Curtis, J. C. Schug and J. W. Viers, J. Am. Chem. Soc., 1981, 103, 5982–5984 CrossRef CAS.
- J. C. Schug and J. W. Viers, Tetrahedron, 1984, 40, 3971–3978, DOI:10.1016/0040-4020(84)85075-9.
- F. Würthner, J. Org. Chem., 2022, 87, 1602–1615, DOI:10.1021/acs.joc.1c00625.
- H. Mayr and A. R. Ofial, Angew. Chem., Int. Ed., 2006, 45, 1844–1845 CrossRef CAS PubMed.
- H. Mayr, M. Breugst and A. R. Ofial, Angew. Chem., Int. Ed., 2011, 50, 6470–6505 CrossRef CAS PubMed , https://doi.org/10.1002/anie.201007100.
- E. Solel, M. Ruth and P. R. Schreiner, J. Am. Chem. Soc., 2021, 143, 20837–20848, DOI:10.1021/jacs.1c09222.
- S. Shaik, A. Shurki, D. Danovich and P. C. Hiberty, Chem. Rev., 2001, 101, 1501–1539 CrossRef CAS PubMed.
- F. Brandmayr, Soc. Epistem., 2018, 32, 175–195, DOI:10.1080/02691728.2018.1440023.
- D. B. Donald, Quantum Chemistry Program Exchange, Facilitator of Theoretical and Computational Chemistry in Pioneers of Quantum Chemistry, ed. E. T. Strom and A. K. Wilson, American Chemical Society, 2013, vol. 1122, ch. 8 pp. 221–273 Search PubMed.
- C. J. Cramer, Computational Chemistry, Theories and Models, John Wiley & Sons, Chichester, England, 2004 Search PubMed.
- E. G. Lewis, Modeling Marvels. Computational Anticipation of Novel Molecules, Springer, Cham, Switzerland, 2008 Search PubMed.
- R. S. Mulliken, Phys. Rev., 1928, 32, 186–222, DOI:10.1103/PhysRev.32.186.
- R. S. Mulliken, Pure Appl. Chem., 1970, 24, 203–216 CrossRef CAS.
- R. S. Mulliken, Chem. Rev., 1929, 6, 503, DOI:10.1021/cr60024a005.
- R. S. Mulliken, Nobel Lecture: Spectroscopy, Molecular Orbitals, and Chemical Bonding, http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1966/mulliken-lecture.html, accessed 20 March 2022 Search PubMed.
- R. S. Mulliken, Chem. Eng. News, 1983, 61, 36–39 CrossRef CAS.
- R. S. Mulliken, Science, 1967, 157(3784), 13–24 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1951, 19, 514–515 CrossRef CAS.
- R. S. Mulliken, J. Am. Chem. Soc., 1950, 72, 600–608 CrossRef CAS.
- K. Fukui and R. S. Mulliken, A Simple Quantum-Theoretical Interpretation of the Chemical Reactivity of Organic Compounds in Molecular Orbitals, in Chemistry, Physics, and Biology. A Tribute to R. S. Mulliken, ed. P.-O. Löwdin and B. Pullman, Academic Press, New York, 1964, pp. 513–537 Search PubMed.
- K. Fukui, Letter to R. Hoffmann, Kyoto, 1964, February 29.
- A. Streitwieser Jr., Molecular Orbital Theory for Organic Chemists, John Wiley & Sons, New York, 1961 Search PubMed.
- M. J. S. Dewar, Rev. Mod. Phys., 1963, 35, 586–598 CrossRef CAS.
- R. Hoffmann, Current Contents, 1989, p.20 Search PubMed.
- W. N. Lipscomb, Boron Hydrides, ed. W. A. Benjamin, New York/Amsterdam, 1963 Search PubMed.
- R. Hoffmann, J. Chem. Phys., 1963, 39, 1397–1412, DOI:10.1063/1.1734456.
- F. P. Boer, M. D. Newton and W. N. Lipscomb, Proc. Natl. Acad. Sci., 1964, 52, 890–893, DOI:10.1073/pnas.52.4.890.
- J. H. Enemark and R. H. Holm, Inorg. Chem., 1964, 3, 1516–1521, DOI:10.1021/ic50021a009.
- H. Kato, T. Yonezawa, K. Morokuma and K. Fukui, Bull. Chem. Soc. Jpn., 1964, 37, 1710–1713, DOI:10.1246/bcsj.37.1710.
- B. R. McGarvey, J. Chem. Phys., 1964, 41, 3743–3758, DOI:10.1063/1.1725808.
- A. Viste and H. B. Gray, Inorg. Chem., 1964, 3, 1113–1123, DOI:10.1021/ic50018a011.
- C. J. Ballhausen and H. B. Gray, Molecular Orbital Theory, W. A. Benjamin, New York and Amsterdam, 1965 Search PubMed.
- R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395–397, DOI:10.1021/ja01080a054.
- R. Hoffmann and R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 2046–2048, DOI:10.1021/ja01087a034.
- R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 2511–2513, DOI:10.1021/ja01089a050.
- R. Hoffmann and R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388–4389, DOI:10.1021/ja00947a033.
- W. von E. Doering and W. R. Roth, Tetrahedron, 1962, 18, 67–74, DOI:10.1016/0040-4020(62)80025-8.
- A. Sengupta, B. Li, D. Svatunek, F. Liu and K. N. Houk, Acc. Chem. Res., 2022 DOI:10.1021/acs.accounts.2c00343.
- R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed., 1969, 8, 781–853, DOI:10.1002/anie.196907811.
- G. A. Kukier, A. Turlik, X.-S. Xue and K. N. Houk, J. Am. Chem. Soc., 2021, 143, 21694–21704, DOI:10.1021/jacs.1c11058.
- G. K. Bruin, S. Qingyang, J. I. Seeman and K. N. Houk, to be published.
- H. J. C. Jacobs and E. Havinga, Adv. Photochem., 1979, 11, 305–373, DOI:10.1002/9780470133415.ch4.
- E. Havinga, Enjoying Organic Chemistry 1927–1987 in Profiles, Pathways and Dreams, ed. J. I. Seeman, American Chemical Society, Washington, DC, 1990 Search PubMed.
- E. Tapavicza, A. M. Meyer and F. Furche, Phys. Chem. Chem. Phys., 2011, 13, 20986–20998 RSC.
- J. I. Seeman, Chem. Rec., 2022, 22, 1–22, DOI:10.1002/tcr.202100212.
- R. Hoffmann and R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 4389–4390, DOI:10.1021/ja00947a034.
- E. Havinga and J. L. M. A. Schlatmann, Tetrahedron, 1961, 16, 146–152, DOI:10.1016/0040-4020(61)80065-3.
- H. C. Longuet-Higgins and E. W. Abrahamson, J. Am. Chem. Soc., 1965, 87, 2045–2046, DOI:10.1021/ja01087a033.
- H. E. Zimmerman, J. Am. Chem. Soc., 1966, 88, 1564–1565 CrossRef CAS.
- H. E. Zimmerman, J. Am. Chem. Soc., 1966, 88, 1566–1567 CrossRef CAS.
- M. J. S. Dewar, Tetrahedron, 1966,(Suppl 8, Part I), 75–92 CrossRef CAS.
- M. J. S. Dewar, Angew. Chem., Int. Ed., 1971, 10, 761–776 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333–1360, 10.1039/TF9363201333.
- T. Hansen, J. C. Roozee, F. M. Bickelhaupt and T. A. Hamlin, J. Org. Chem., 2022, 87, 1805–1813, DOI:10.1021/acs.joc.1c02354.
- A. E. Hayden and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 4084–4089, DOI:10.1021/ja809142x.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- F. Jensen, Isr. J. Chem., 2022, 62, 1–14, DOI:10.1002/ijch.202100027.
- Z. C. Kramer, B. K. Carpenter, G. S. Ezra and S. Wiggins, J. Phys. Chem. A, 2015, 119, 6611–6630, DOI:10.1021/acs.jpca.5b02834.
- K. N. Houk, F. Liu, Z. Yang and J. I. Seeman, Angew. Chem., Int. Ed., 2021, 60, 12660–12681, DOI:10.1002/anie.202001654.
- Y.-F. Yang, P. Yu and K. N. Houk, J. Am. Chem. Soc., 2017, 139, 18213–18221, DOI:10.1021/jacs.7b08325.
- K. Black, P. Liu, L. Xu, C. Doubleday and K. N. Houk, Proc. Natl. Acad. Sci., 2012, 109, 12860–12865, DOI:10.1073/pnas.1209316109.
- B. K. Carpenter, Angew. Chem., Int. Ed., 1998, 37, 33402–33501, DOI:10.1002/(SICI)1521-3773(19981231)37:24<3340::AID-ANIE3340>3.0.CO.
- B. K. Carpenter, J. N. Harvey and A. J. Orr-Ewing, J. Am. Chem. Soc., 2016, 138, 4695–4705, DOI:10.1021/jacs.6b01761.
- X. Ma and W. L. Hase, Phil. Trans. R. Soc. A. Math. Phys. Eng. Sci., 2017, 375, 20160204, DOI:10.1098/rsta.2016.0204.
- U. Lourderaj, K. Park and W. L. Hase, Int. Rev. Phys. Chem., 2008, 27, 361–403, DOI:10.1080/01442350802045446.
- M. Bai, Z. Feng, J. Li and D. J. Tantillo, Chem. Sci., 2020, 11, 9937–9944, 10.1039/D0SC04036C.
- K. N. Houk and F. Liu, Acc. Chem. Res., 2017, 50, 539–543, DOI:10.1021/acs.accounts.6b00532.
- R. B. Woodward, Synthesis in Perspectives in Organic Chemistry, ed. A. R. Todd, Interscience, New York, 1956, pp. 155–185 Search PubMed.
- R. B. Woodward, Art and Science in the Synthesis of Organic Compounds in Pointers and Pathways in Research: Six Lectures in the Fields of Organic Chemistry and Medicine, ed. M. O'Connor, CIBA of India Limited, Bombay, India, 1963, pp. 23–41 Search PubMed.
- R. B. Woodward, Recent Advances in the Chemistry of Natural Products, Nobel Prize Lecture, Sweden, December 1965, 11, https://www.nobelprize.org/uploads/2018/06/woodward-lecture.pdf, accessed September 14, 2022 Search PubMed.
- D. J. Tantillo and J. I. Seeman, Chem. - Eur. J., 2021, 27, 7000–7016, DOI:10.1002/chem.202002924.
- Y. Guan, V. M. Ingman, B. J. Rooks and S. E. Wheeler, J. Chem. Theory Comput., 2018, 14, 5249–5261, DOI:10.1021/acs.jctc.8b00578.
- A. K. Vitek, T. M. E. Jugovic and P. M. Zimmerman, ACS Catal., 2020, 10, 7136–7145, DOI:10.1021/acscatal.0c00618.
- X. Qi, D. G. Kohler, K. L. Hull and P. Liu, J. Am. Chem. Soc., 2019, 141, 11892–11904, DOI:10.1021/jacs.9b02893.
- J. Andrés, P. W. Ayers, R. A. Boto, R. Carbó-Dorca, H. Chermette, J. Cioslowski, J. Contreras-García, D. L. Cooper, G. Frenking, C. Gatti, F. Heidar-Zadeh, L. Joubert, Á. M. Pendás, E. Matito, I. Mayer, A. J. Misquitta, Y. Mo, J. Pilmé, P. L. A. Popelier, M. Rahm, E. Ramos-Cordoba, P. Salvador, W. H. E. Schwarz, S. Shahbazian, B. Silvi, M. Solà, K. Szalewicz, V. Tognetti, F. Weinhold and É.-L. Zins, J. Comput. Chem., 2019, 40, 2248–2283, DOI:10.1002/jcc.26003.
- T. Lu, R. Zhu, Y. An and S. E. Wheeler, J. Am. Chem. Soc., 2012, 134, 3095–3102, DOI:10.1021/ja209241n.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296, DOI:10.1002/anie.201503476.
- D. J. Tantillo, Adv. Phys. Org. Chem., 2021, 55, 1–16 CrossRef CAS.
- J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596, 10.1039/C7CS00602K.
- D. H. Ess, S. E. Wheeler, R. G. Iafe, L. Xu, N. Çelebi-Ölçüm and K. N. Houk, Angew. Chem., Int. Ed., 2008, 47, 7592–7601, DOI:10.1002/anie.200800918.
- J. Rehbein and B. K. Carpenter, Phys. Chem. Chem. Phys., 2011, 13, 20906–20922, 10.1039/C1CP22565K.
- S. R. Hare and D. J. Tantillo, Pure Appl. Chem., 2017, 89, 679–698 CrossRef CAS.
- D. S. Levine and M. Head-Gordon, Nat. Comm., 2020, 11, 1–8, DOI:10.1038/s41467-020-18670-8.
- P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649–667, DOI:10.1038/s41596-019-0265-0.
- M. J. S. Dewar, J. Am. Chem. Soc., 1984, 106, 669–682, DOI:10.1021/ja00315a036.
- R. Porter, Introduction in The Transition State, A Symposium Held at Sheffield on 3rd and 4th April 1962 (Special Publication No. 16), The Chemical Society, London, England, 1962, pp. 1–2 Search PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115, DOI:10.1063/1.1749604.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894, 10.1039/TF9353100875.
- J. I. Seeman and W. A. Farone, J. Org. Chem., 1978, 43, 1854–1864 CrossRef CAS.
- J. I. Seeman, H. V. Secor, H. Hartung and R. Galzerano, J. Am. Chem. Soc., 1980, 102, 7741–7747 CrossRef CAS.
- J. I. Seeman, E. B. Sanders and W. A. Farone, Tetrahedron, 1980, 36, 1173–1177 CrossRef CAS.
- E. J. Corey, Experientia, 1953, 9, 329–333, DOI:10.1007/BF02155831.
- E. J. Corey and R. A. Sneen, J. Am. Chem. Soc., 1955, 77, 2505–2509 CrossRef CAS.
- P. Deslongchamps, Stereoelectronic Effects in Organic Chemistry, Pergamon, Oxford, England, 1983 Search PubMed.
- W. O. Kermack and R. Robinson, J. Chem. Soc., Trans., 1922, 427–440, 10.1039/CT9222100427.
- R. V. Williams and A. A. Shaffer, Can. J. Chem., 2016, 95, 334–339 CrossRef.
- S. W. Benson, F. R. Cruickshank, D. M. Golden, G. R. Haugen, H. E. O'Neal, A. S. Rodgers, R. Shaw and R. Walsh, Chem. Rev., 1969, 69, 279–324, DOI:10.1021/cr60259a002.
- E. C. Meister, M. Willeke, W. Angst, A. Togni and P. Walde, Helv. Chim. Acta, 2014, 97, 1–31, DOI:10.1002/hlca.201300321.
- G. B. Kauffman, J. Chem. Educ., 1988, 65, 28, DOI:10.1021/ed065p28.
- J. L. Adcock, J. Chem. Educ., 2001, 78, 1495, DOI:10.1021/ed078p1495.
- P. I. Pollak and D. V. Curtin, J. Am. Chem. Soc., 1950, 72, 961–965, DOI:10.1021/ja01158a082.
- U. Burkert and N. L. Allinger, Molecular Mechanics, American Chemical Society, Washington, D.C., 1982 Search PubMed.
- D. B. Boyd and K. B. Lipkowitz, J. Chem. Educ., 1982, 269–274 CrossRef CAS.
- H. Metiu, J. Ross, R. Silbey and T. F. George, J. Chem. Phys., 1974, 61, 3200–3209, DOI:10.1063/1.1682477.
- P. Valtazanos and K. Ruedenberg, Theor. Chim. Acta, 1986, 69, 281–307, DOI:10.1007/BF00527705.
- C. S. Miller and M. Ellison, J. Chem. Educ., 2015, 92, 1040–1043, DOI:10.1021/ed500813d.
- R. Hoffmann, Acc. Chem. Res., 1971, 4, 1–9 CrossRef CAS.
- K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS.
- W. Kirmse, N. G. Rondan and K. N. Houk, J. Am. Chem. Soc., 1984, 106, 7989–7991, DOI:10.1021/ja00337a067.
- A. B. Buda, Y. Wang and K. N. Houk, J. Org. Chem., 1989, 54, 2264–2266, DOI:10.1021/jo00271a003.
- D. E. Stokes, Pasteur's Quadrant. Basic Science and Technological Innovation, Brookings Institution Press, Washington, D.C., 1997 Search PubMed.
- P.-P. Chen, J. I. Seeman and K. N. Houk, Angew. Chem., Int. Ed., 2020, 59, 12506–12519, DOI:10.1002/anie.202003279.
- R. Huisgen, The Adventure Playground of Mechanisms and Novel Reactions in Profiles, Pathways, and Dreams, ed. J. I. Seeman, American Chemical Society, Washington, D.C., 1994 Search PubMed.
- R. Huisgen, F. Mietzsch, G. Boche and H. Seidl, Organic Reaction Mechanisms, The Lectures Delivered and Synopses of Papers Read at an International Symposium Held at Cork, Ireland on 20th-25th July, 1964. Special Publication No. 19, ed. F. L. Scott, The Chemical Society, London, 1965, pp. 3–20 Search PubMed.
- R. Robinson, Outline of an Electrochemical (Electronic) Theory of the Course of Organic Reactions, Institute of Chemistry of Great Britain and Ireland, 1932 Search PubMed.
- J. Allen, A. E. Oxford, R. Robinson and J. C. Smith, J. Chem. Sci., 1926, 401–411 Search PubMed.
- R. J. Gillespie, J. Chem. Educ., 2004, 81, 298–304, DOI:10.1021/ed081p298.
- R. J. Gillespie, Coord. Chem. Rev., 2008, 252, 1315–1327, DOI:10.1016/j.ccr.2007.07.007.
- R. Hoffmann, A. Imamura and W. J. Hehre, J. Am. Chem. Soc., 1968, 90, 1499–1509 CrossRef CAS.
- R. Hoffmann, G. D. Zeiss and G. W. Van Dine, J. Am. Chem. Soc., 1968, 90, 1485–1499 CrossRef CAS.
- W. D. Stohrer and R. Hoffmann, J. Am. Chem. Soc., 1972, 94, 779–786, DOI:10.1021/ja00758a017.
- W. T. Wipke and P. Gund, J. Am. Chem. Soc., 1974, 96, 299–301, DOI:10.1021/ja00808a073.
- B. C. B. Symons, D. J. Williamson, C. M. Brooks, A. L. Wilson and P. L. A. Popelier, ChemistryOpen, 2019, 8, 560–570, DOI:10.1002/open.201800275.
- R. Hoffmann, J. Mol. Struct., 1998, 424, 1–6 CrossRef CAS.
- C. G. Swain, Meeting Report from the Tenth Conference on Reaction Mechanisms, Oregon State University at Corvallis, Oregon, June 24–27, Oregon State University, MIT, Cambridge, MA, 1964 Search PubMed.
- V. Politi, Synthese, 2018, 195, 2267–2293, DOI:10.1007/s11229-017-1339-6.
- K. L. Mears and P. P. Power, Acc. Chem. Res., 2022, 55, 1337–1348, DOI:10.1021/acs.accounts.2c00116.
- E. G. Champenois, D. M. Sanchez, J. Yang, J. P. F. Nunes, A. Attar, M. Centurion, R. Forbes, M. Gühr, K. Hegazy, F. Ji, S. K. Saha, M.-F. Lin, D. Luo, B. Moore, X. Shen, M. R. Ware, X. J. Wang, T. J. Martinez and T. J. A. Wolf, Science, 2021, 374, 178–182 CrossRef CAS PubMed.
- J. A. Chamizo, Found. Chem., 2019, 21, 11–29 CrossRef CAS.
- T. Šolomek, P. Ravat, Z. Mou, M. Kertesz and M. Juríček, J. Org. Chem., 2018, 83, 4769–4774, DOI:10.1021/acs.joc.8b00656.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15, DOI:10.1021/ar00109a003.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2016, 21, 748 CrossRef PubMed.
- S. F. Martin, Acc. Chem. Res., 2022 DOI:10.1021/acs.accounts.1c00773.
- C. Drew, The 14 types of knowledge, https://helpfulprofessor.com/types-of-knowledge/, accessed 27 April 2022 Search PubMed.
- R. S. Mulliken, J. Chem. Phys., 1935, 3, 586–591, DOI:10.1063/1.1749732.
- R. S. Mulliken, J. Chem. Phys., 1935, 3, 573–585, DOI:10.1063/1.1749731.
- R. S. Mulliken, J. Chem. Phys., 1935, 3, 375–378, DOI:10.1063/1.1749683.
- J. E. Lennard-Jones, Proc. R. Soc. London, Ser. A, 1937, 158, 280–296, DOI:10.1098/rspa.1937.0020.
- C. A. Coulson, Trans. Faraday Soc., 1937, 33, 388–398, 10.1039/tf9373300388.
- C. A. Coulson and J. E. Lennard-Jones, Trans. Faraday Soc., 1937, 33, 1479–1492, 10.1039/TF9373301479.
- C. A. Coulson, Proc. R. Soc. London, Ser. A, 1939, 169, 413–428, DOI:10.1098/rspa.1939.0006.
- J. E. Lennard-Jones and C. A. Coulson, Trans. Faraday Soc., 1939, 35, 811–823 RSC.
- C. A. Coulson and G. S. Rushbrooke, Math. Proc. Cambridge Philos. Soc., 1940, 36, 193–200 CrossRef CAS.
- C. A. Coulson and G. S. Rushbrooke, Proc. Cambridge Philos. Soc., 1940, 36, 193–200 CrossRef CAS.
- H. C. Longuet-Higgins and C. A. Coulson, Trans. Faraday Soc., 1946, 42, 756–764, 10.1039/tf9464200756.
- C. A. Coulson, Q. Rev., 1947, 1, 144–178 RSC.
- C. A. Coulson and M. J. S. Dewar, Discuss. Faraday Soc., 1947,(2), 54–62, 10.1039/df9470200054.
- C. A. Coulson and H. C. Longuet-Higgins, Proc. R. Soc. London, Ser. A, 1947, 191, 39–60 CAS.
- C. A. Coulson and H. C. Longuet-Higgins, Proc. R. Soc. London, Ser. A, 1947, 192, 16–32, DOI:10.1098/rspa.1947.0136.
- H. C. Longuet-Higgins and C. A. Coulson, Trans. Faraday Soc., 1947, 43, 87–94, 10.1039/tf9474300087.
- G. W. Wheland, Proc. R. Soc. London, Ser. A, 1938, 164, 397–408 CAS.
- M. J. S. Dewar, Comments on Two Early Papers on the Theory of Pericyclic Reactions in Orbital Symmetry Papers: Comprising Articles from Accounts Chemical Research, Journal of the American Chemical Society, and Other Journals, ed. H. E. Simmons and J. F. Bunnett, American Chemical Society, Washington, DC, 1974, pp. 16–19 Search PubMed.
- R. Hoffmann, Synthese, 2007, 155, 321–336 CrossRef.
- H. Rzepa, The first ever curly arrows, https://www.ch.imperial.ac.uk/rzepa/blog/?p=7234, accessed 30 January 2022 Search PubMed.
- H. Rzepa, A curly-arrow pushing manual, https://www.ch.imperial.ac.uk/rzepa/blog/?p=11741, accessed 30 January 2022 Search PubMed.
- A. R. Straumanis and S. M. Ruder, J. Chem. Educ., 2009, 86, 1389–1391 CrossRef CAS.
- Y. Liu, P. Kilby, T. J. Frankcombe and T. W. Schmidt, Nat. Commun., 2018, 9, 1–6, DOI:10.1038/s41467-018-03860-2.
- N. P. Grove, M. M. Cooper and K. M. Rush, J. Chem. Educ., 2012, 89, 844–849, DOI:10.1021/ed2003934.
- G. Bhattacharyya and G. M. Bodner, J. Chem. Educ., 2005, 82, 1402–1407, DOI:10.1021/ed082p1402.
- S. K. Houchlei, R. R. Bloch and M. M. Cooper, J. Chem. Educ., 2021, 98, 2751–2764, DOI:10.1021/acs.jchemed.1c00099.
- P. von R. Schleyer, V. M. Vera and E. T. Strom, From the Ivy League to the Honey Pot in The Foundations of Physical Organic Chemistry: Fifty Years of the James Flack Norris Award, ed. E. T. Strom and V. V. Mainz, American Chemical Society, Washington, DC, 2015, vol. 1209, ch. 7, pp. 139–168 Search PubMed.
- Y. Wang, Y. Li and Z. Chen, Acc. Chem. Res., 2020, 53, 887–895, DOI:10.1021/acs.accounts.0c00025.
- J.-C. Guo, Y.-X. Cheng and X.-F. Wu, Comput. Theor. Chem., 2020, 1180, 112824, DOI:10.1016/j.comptc.2020.112824.
- V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 0114, DOI:10.1038/s41570-018-0114.
- R. Sun, B. Jin, B. Huo, C. Yuan, H.-J. Zhai and Y.-B. Wu, Chem. Commun. 10.1039/d1cc07313c10.1039/d1cc07313c.
- I. Y. Pavlinov, Philosophies, 2020, 5, 137–232 CrossRef.
- S. Ruphy, Scientific Pluralism Reconsidered. A New Approach to the (Dis)Unity of Science, University of Pittsburgh Press, Pittsburg, PA, 2016 Search PubMed.
- D. J. Tantillo and J. I. Seeman, 2022, submitted for publication.
- J. I. Seeman, Chem. Rec., 2022, 22, 1–67, DOI:10.1002/tcr.202200065.
- H. E. Zimmerman, Science, 1966, 153, 837–844 CrossRef CAS.
- P. Hughes, J. Chem. Educ., 2006, 83, 1152, DOI:10.1021/ed083p1152.
- Y.-L. Ding, J.-R. Mu, C.-H. Wang and Z.-Z. Yang, Int. J. Quantum Chem., 2011, 111, 2778–2787, DOI:10.1002/qua.22619.
- M. Gonzalez-Perez, Int. J. Sci. Adv. Tech., 2015, 5, 1–6 Search PubMed.
- P. R. Schreiner, Angew. Chem., Int. Ed., 2002, 41, 3579–3582, DOI:10.1002/1521-3773(20021004)41:19<3579::AID-ANIE3579>3.0.CO;2-S.
- W. Moffitt and E. K. Rideal, Proc. R. Soc. London, Ser. A, 1950, 202, 548–564, DOI:10.1098/rspa.1950.0119.
- I. V. Alabugin, S. Bresch and G. dos Passos Gomes, J. Phys. Org. Chem., 2015, 28, 147–162, DOI:10.1002/poc.3382.
- A. Grushow, J. Chem. Educ., 2011, 88, 860–862, DOI:10.1021/ed100155c.
- N. J. Tro, J. Chem. Educ., 2012, 89, 567–568, DOI:10.1021/ed2006289.
- E. D. Glendening and F. Weinhold, Molecules, 2021, 26, 14110–14115, DOI:10.3390/molecules26144110.
- A. D. Clauss, S. F. Nelsen, M. Ayoub, J. W. Moore, C. R. Landis and F. Weinhold, Chem. Educ. Res. Pract., 2014, 15, 417–434, 10.1039/C4RP00057A.
- M. D. Mosher and S. Ojha, J. Chem. Educ., 1998, 75, 888–890, DOI:10.1021/ed075p888.
- R. C. Hadden, Science, 1993, 261, 1545–1550 CrossRef.
- I. V. Alabugin, S. Bresch and M. Manoharan, J. Phys. Chem. A, 2014, 118, 3663–3677, DOI:10.1021/jp502472u.
- M. W. Lodewyk, C. Soldi, P. B. Jones, M. M. Olmstead, J. Rita, J. T. Shaw and D. J. Tantillo, J. Am. Chem. Soc., 2012, 134, 18550–18553, DOI:10.1021/ja3089394.
- J. M. Saya, K. Vos, R. A. Kleinnijenhuis, J. H. van Maarseveen, S. Ingemann and H. Hiemstra, Org. Lett., 2015, 17, 3892–3894, DOI:10.1021/acs.orglett.5b01888.
- B. Wang, Y. Xie, Q. Yang, G. Zhang and Z. Gu, Org. Lett., 2016, 18, 5388–5391, DOI:10.1021/acs.orglett.6b02767.
- K.-i. Takao, H. Kai, A. Yamada, Y. Fukushima, D. Komatsu, A. Ogura and K. Yoshida, Angew. Chem., Int. Ed., 2019, 58, 9851–9855, DOI:10.1002/anie.201904404.
- C. A. Coulson, Rev. Mod. Phys., 1960, 32, 170–177, DOI:10.1103/RevModPhys.32.170.
- W. Thiel, Angew. Chem., Int. Ed., 2011, 50, 9216–9217, DOI:10.1002/anie.201105305.
- F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814–2824, DOI:10.1021/jacs.8b13313.
- V. Pophristic and L. Goodman, Nature, 2001, 411, 565–568, DOI:10.1038/35079036.
- Y. Mo and J. Gao, Acc. Chem. Res., 2007, 40, 113–119, DOI:10.1021/ar068073w.
- F. M. Bickelhaupt and E. J. Baerends, Angew. Chem., Int. Ed., 2003, 42, 4183–4188, DOI:10.1002/anie.200350947.
- F. Weinhold, Angew. Chem., Int. Ed., 2003, 42, 4188–4194, DOI:10.1002/anie.200351777.
- Y. Mo, W. Wu, L. Song, M. Lin, Q. Zhang and J. Gao, Angew. Chem., Int. Ed., 2004, 43, 1986–1990, DOI:10.1002/anie.200352931.
- M. Baranac-Stojanović, Struct. Chem., 2015, 26, 989–996, DOI:10.1007/s11224-014-0557-5.
- C. M. Filloux, Angew. Chem., Int. Ed., 2015, 54, 8880–8894, DOI:10.1002/anie.201411185.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733 CAS.
- R. Strohmeyer, The 7 Worst Tech Predictions of All Time, https://www.pcworld.com/article/532605/worst_tech_predictions.html#%7Etext=Foolish%20Tech%20Prediction%201%26text=After%20all%2C%20when%20IBM's%20Thomas,the%20size%<?pdb_no 20of?>20of<?pdb END?>%20their%20desk, accessed July 25, 2022 Search PubMed.
- Y. Guan, S. V. Shree Sowndarya, L. C. Gallegos, P. C. St. John and R. S. Paton, Chem. Sci., 2021, 12, 12012–12026, 10.1039/D1SC03343C.
- B. Mahjour, Y. Shen, W. Liu and T. Cernak, Nature, 2020, 580, 71–75, DOI:10.1038/s41586-020-2142-y.
- W. L. Williams, L. Zeng, T. Gensch, M. S. Sigman, A. G. Doyle and E. V. Anslyn, ACS Cent. Sci., 2021, 7, 1622–1637, DOI:10.1021/acscentsci.1c00535.
- H. Hopf, S. A. Matlin, G. Mehta and A. Krief, Angew. Chem., Int. Ed., 2020, 59, 2150–2154 CrossRef CAS PubMed.
- R. Carlson and T. Hudlicky, Helv. Chim. Acta, 2012, 95, 2052–2062 CrossRef CAS.
- P. Laszlo, Ambix, 2010, 57, 202–215 CrossRef CAS PubMed.
Footnote |
| † Dedicated to Dudley Herschbach in celebration of his 90th year who, when asked whether he was a theoretician or an experimentalist, responded, “The molecules don't know and don't care.” |
| This journal is © The Royal Society of Chemistry 2022 |