Bare and ligand protected planar hexacoordinate silicon in SiSb₃M₃⁺ (M = Ca, Sr, Ba) clusters

Abstract

The occurrence of planar hexacoordination is very rare in main group elements. We report here a class of clusters containing a planar hexacoordinate silicon (phSi) atom with the formula SiSb₃M₃⁺ (M = Ca, Sr, Ba), which have D_3h (¹A₁′) symmetry in their global minimum structure. The unique ability of heavier alkaline-earth atoms to use their vacant d atomic orbitals in bonding effectively stabilizes the peripheral ring and is responsible for covalent interaction with the Si center. Although the interaction between Si and Sb is significantly stronger than the Si–M one, sizable stabilization energies (−27.4 to −35.4 kcal mol⁻¹) also originated from the combined electrostatic and covalent attraction between Si and M centers. The lighter homologues, SiE₃M₃⁺ (E = N, P, As; M = Ca, Sr, Ba) clusters, also possess similar D_3h symmetric structures as the global minima. However, the repulsive electrostatic interaction between Si and M dominates over covalent attraction making the Si–M contacts repulsive in nature. Most interestingly, the planarity of the phSi core and the attractive nature of all the six contacts of phSi are maintained in N-heterocyclic carbene (NHC) and benzene (Bz) bound SiSb₃M₃(NHC)₆⁺ and SiSb₃M₃(Bz)₆⁺ (M = Ca, Sr, Ba) complexes. Therefore, bare and ligand-protected SiSb₃M₃⁺ clusters are suitable candidates for gas-phase detection and large-scale synthesis, respectively.

---

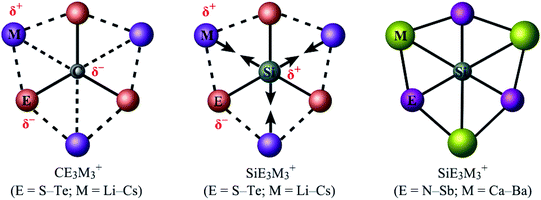
Exploring the bonding capacity of main-group elements (such as carbon or silicon) beyond the traditional tetrahedral concept has been a fascinating subject in chemistry for five decades. The 1970 pioneering work of Hoffmann and coworkers¹ initiated the field of planar tetracoordinate carbons (ptCs), or more generally, planar hypercoordinate carbons. The past 50 years have witnessed the design and characterization of an array of ptC and planar pentacoordinate carbon (ppC) species.^2–14 However, it turned out to be rather challenging to go beyond ptC and ppC systems. The celebrated CB₆²⁻ cluster and relevant species^15,16 were merely model systems because C avoids planar hypercoordination in such systems.^17,18 In 2012, the first genuine global minimum D_3h CO₃Li₃⁺ cluster was reported to have six interactions with carbon in planar form, although electrostatic repulsion between positively charged phC and Li centers and the absence of any significant orbital interaction between them make this hexacoordinate assignment questionable.¹⁹ It was only very recently that a series of planar hexacoordinate carbon (phC) species, CE₃M₃⁺ (E = S–Te; M = Li–Cs), were designed computationally by the groups of Tiznado and Merino (Fig. 1; left panel),²⁰ in which there exist pure electrostatic interactions between the negative C^δ− center and positive M^δ+ ligands. These phC clusters were achieved following the so-called “proper polarization of ligand” strategy.

Fig. 1 The pictorial depiction of previously reported phC CE₃M₃⁺ (E = S–Te; M = Li–Cs) clusters and the present SiE₃M₃⁺ (E = S–Te and N–Sb; M = Li–Cs and Ca–Ba) clusters. Herein the solid and dashed lines represent covalent and ionic bonding, respectively. The opposite double arrows illustrate electrostatic repulsion.

The concept of planar hypercoordinate carbons has been naturally extended to their next heavier congener, silicon-based systems. Although the steric repulsion between ligands decreases due to the larger size, the strength of π- and σ-bonding between the central atom and peripheral ligands dramatically decreases, which is crucial for stability. Planar tetracoordinate silicon (ptSi) was first experimentally observed in a pentaatomic C_2v SiAl₄⁻ cluster by Wang and coworkers in 2000.²¹ Very recently, this topic got a huge boost by the room-temperature, large-scale syntheses of complexes containing a ptSi unit.²² A recent computational study also predicted the global minimum of SiMg₄Y⁻ (Y = In, Tl) and SiMg₃In₂ to have unprecendented planar pentacoordinate Si (ppSi) units.²³ Planar hexacoordinate Si (phSi) systems seem to be even more difficult to stabilize. Previously, a C_2v symmetric Cu₆H₆Si cluster was predicted as the true minimum,²⁴ albeit its potential energy surface was not fully explored. A kinetically viable phSi SiAl₃Mg₃H₂⁺ cluster cation was also predicted.²⁵ However, these phSi systems^24,25 are only local minima and not likely to be observed experimentally. In 2018, the group of Chen identified the Ca₄Si₂²⁻ building block containing a ppSi center and constructed an infinite CaSi monolayer, which is essentially a two-dimensional lattice of the Ca₄Si₂ motif.²⁶ Thus, it is still an open question to achieve a phSi atom to date.

Herein we have tried to find the correct combination towards a phSi system as the most stable isomer. Gratifyingly, we found a series of clusters, SiE₃M₃⁺ (E = N, P, As, Sb; M = Ca, Sr, Ba), having planar D_3h symmetry with Si at the center of the six membered ring, as true global minimum forms. Si–E bonds are very strong in all the clusters, and alkaline-earth metals interact with the Si center by employing their d orbitals. However, electrostatic repulsion originated from the positively charged Si and M centers for E = N, P, and As dominates over attractive covalent interaction, making individual Si–M contacts repulsive in nature. This makes the assignment of SiE₃M₃⁺ (E = N, P, As; M = Ca, Sr, Ba) as genuine phSi somewhat skeptical. SiSb₃M₃⁺ (M = Ca, Sr, Ba) clusters are the sole candidates which possess genuine phSi centers as both electrostatic and covalent interactions in Si–M bonds are attractive. The d orbitals of M ligands play a crucial role in stabilizing the ligand framework and forming covalent bonds with phSi. Such planar hypercoordinate atoms are, in general, susceptible to external perturbations. However, the present title clusters maintain the planarity and the attractive nature of the bonds even after multiple ligand binding at M centers in SiSb₃M₃(NHC)₆⁺ and SiSb₃M₃(Bz)₆⁺. This would open the door for large-scale synthesis of phSi as well.

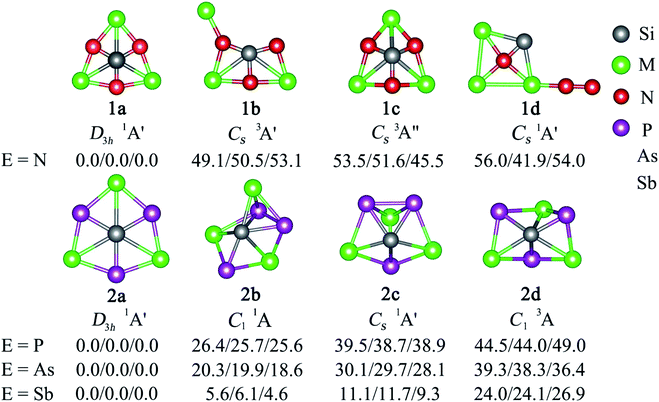
Two major computational efforts were made before reaching our title phSi clusters. The first one is to examine SiE₃M₃⁺ (E = S–Po; M = Li–Cs) clusters, which adopt D_3h or C_3v structures as true minima (see Table S1 in ESI†), being isoelectronic to the previous phC CE₃M₃⁺ (E = S–Po; M = Li–Cs) clusters. In the SiE₃M₃⁺ (E = S–Po; M = Li–Cs) clusters, the Si center always carries a positive charge ranging from 0.01 to +1.03|e|, in contrast to the corresponding phC species (see Fig. 1). Thus, electrostatic interactions between the Si^δ+ and M^δ+ centers would be repulsive (Fig. 1). Given that the possibility of covalent interaction with an alkali metal is minimal, it would be a matter of debate whether they could be called true coordination. A second effort is to tune the electronegativity difference between Si and M centers so that the covalent contribution in Si–M bonding becomes substantial. Along this line, we consider the combinations of SiE₃M₃⁺ (E = N, P, As, Sb; M = Be, Mg, Ca, Sr, Ba). The results in Fig. S1† show that for E = Be and Mg, the phSi geometry has a large out-of-plane imaginary frequency mode, which indicates a size mismatch between the Si center and peripheral E₃M₃ (E = N–Bi; M = Be, Mg) ring. On the other hand, the use of larger M = Ca, Sr, Ba atoms effectively expands the size of the cavity and eventually leads to perfect planar geometry with Si atoms at the center as minima. In the case of SiBi₃M₃⁺, the planar isomer possesses a small imaginary frequency for M = Ca. Although planar SiBi₃Sr₃⁺ and SiBi₃Ba₃⁺ are true minima, they are 2.2 and 2.5 kcal mol⁻¹ higher in energy than the lowest energy isomer, respectively (Fig. S2†). Fig. 2 displays some selected low-lying isomers of SiE₃M₃⁺ (E = N, P, As, Sb; M = Ca, Sr, Ba) clusters (see Fig. S3–S6† for additional isomers). The global minimum structure is a D_3h symmetric phSi with an ¹A₁′ electronic state for all the twelve cases. The second lowest energy isomer, a ppSi, is located more than 49 kcal mol⁻¹ above phSi for E = N. This relative energy between the most stable and nearest energy isomer gradually decreases upon moving from N to Sb. In the case of SiSb₃M₃⁺ clusters, the second-lowest energy isomer is 4.6–6.1 kcal mol⁻¹ higher in energy than phSi. The nearest triplet state isomer is very high in energy (by 36–53 kcal mol⁻¹, Fig. S3–S6†) with respect to the global minimum.

Fig. 2 The structures of low-lying isomers of SiE₃M₃⁺ (E = N, P, As, Sb; M = Ca, Sr, Ba) clusters. Relative energies (in kcal mol⁻¹) are shown at the single-point CCSD(T)/def2-TZVP//PBE0/def2-TZVP level, followed by a zero-energy correction at PBE0. The values from left to right refer to Ca, Sr, and Ba in sequence. The group symmetries and electronic states are also given.

Born–Oppenheimer molecular dynamics (BOMD) simulations at room temperature (298 K), taking SiE₃Ca₃⁺ clusters as case studies, were also performed. The results are displayed in Fig. S7.† All trajectories show no isomerization or other structural alterations during the simulation time, as indicated by the small root mean square deviation (RMSD) values. The BOMD data suggest that the global minimum also has reasonable kinetic stability against isomerization and decomposition.

The bond distances, natural atomic charges, and bond indices for SiE₃Ca₃⁺ clusters are given in Table 1 (see also Tables S2–S5† for M = Sr, Ba). The Si–E bond distances are shorter than the typical Si–E single bond distance computed using the self-consistent covalent radii proposed by Pyykkö.²⁷ In contrast, the Si–M bond distance is almost equal to the single bond distance. This gives the first hint of the presence of covalent bonding therein. However, the Wiberg bond indices (WBIs) for the Si–M links are surprisingly low (0.02–0.04). We then checked the Mayer bond order (MBO), which can be seen as a generalization of WBIs and is more acceptable since the approach of WBI calculations assumes orthonormal conditions of basis functions while the MBO considers an overlap matrix. The MBO values for the Si–M links are now sizable (0.13–0.18). These values are reasonable considering the large difference in electronegativity between Si and M, and, therefore, only a very polar bond is expected between them. In fact, the calculations of WBIs after orthogonalization of basis functions by the Löwdin method gives significantly large bond orders (0.48–0.55), which is known to overestimate the bond orders somewhat. The above results indicate that the presence of covalent bonding cannot be ruled out only by looking at WBI values.

Table 1 Bond distances (r, in Å), different bond orders (WBIs) {MBOs} [WBI in orthogonalized basis], and natural atomic charges (q, in |e|) of SiE₃Ca₃⁺ (E = N, P, As, Sb) clusters at the PBE0/def2-TZVP level

	r Si–E	r Si–Ca	r E–Ca	q Si	q E	q Ca
E = N	1.669	2.555	2.246	1.57	−1.93	1.74
	(1.14) {1.23} [1.84]	(0.02) {0.13} [0.51]	(0.22) {0.67} [0.84]
E = P	2.180	2.935	2.640	0.25	−1.42	1.67
	(1.34) {1.11} [1.52]	(0.03) {0.14} [0.54]	(0.27) {0.74} [1.05]
E = As	2.301	3.004	2.721	0.07	−1.34	1.65
	(1.33) {1.10} [1.45]	(0.03) {0.15} [0.55]	(0.29) {0.71} [1.12]
E = Sb	2.538	3.155	2.896	−0.39	−1.16	1.62
	(1.29) {1.01} [1.33]	(0.04) {0.18} [0.48]	(0.30) {0.78} [1.14]

---

Our following argument regarding the presence of covalent Si–M bonding is based on energy decomposition analysis (EDA) in combination with natural orbital for chemical valence (NOCV) theory. We first performed EDA by taking Ca and SiE₃Ca₂ in different charge and electronic states as interacting fragments to get the optimum fragmentation scheme that suits the best to describe the bonding situation (see Tables S6–S9†). The size of orbital interaction (ΔE_orb) is used as a probe.²⁸ For all cases, Ca⁺ (D, 4s¹) and SiE₃Ca₂ (D) in their doublet spin states turn out to be the best schemes, which give the lowest ΔE_orb value. Table 2 shows the numerical results of EDA-NOCV calculations. The relative contribution of electrostatic and orbital terms shows that the interaction between Ca⁺ and SiE₃Ca₂ is a bit more covalent in nature than electrostatic. The intrinsic interaction energy (ΔE_int) between the two fragments gradually diminishes upon moving from E = N to its heavier homologues. Both decreased electrostatic and orbital interactions are responsible for such a reduction in ΔE_int.

Table 2 The EDA-NOCV results of the SiE₃Ca₃⁺ cluster using Ca⁺ (D, 4s¹) + SiE₃Ca₂ (D) as interacting fragments at the PBE0/TZ2P-ZORA//PBE0/def2-TZVP level. All energy values are in kcal mol⁻¹

Energy term	Interaction	Ca^+ (D, 4s^1) + SiN3Ca2 (D)	Ca^+ (D, 4s^1) + SiP3Ca2 (D)	Ca^+ (D, 4s^1) + SiAs3Ca2 (D)	Ca^+ (D, 4s^1) + SiSb3Ca2 (D)
a The values in parentheses are the percentage contributions to total attractive interactions (ΔEelstat + ΔEorb). b The values in parentheses are the percentage contributions to the total orbital interaction ΔEorb.
ΔEint		−192.9	−153.0	−144.9	−129.9
ΔEPauli		139.8	115.2	115.7	110.9
ΔEelstat^a		−162.0 (48.7%)	−116.4 (43.4%)	−113.0 (43.4%)	−100.9 (41.9%)
ΔEorb^a		−170.7 (51.3%)	−151.8 (56.6%)	−147.6 (56.6%)	−140.0 (58.1%)
ΔEorb(1)^b	SiE3Ca2–Ca^+(s) electron-sharing σ-bond	−89.2 (52.3%)	−79.4 (52.3%)	−74.3 (50.3%)	−66.9 (47.8%)
ΔEorb(2)^b	SiE3Ca2 → Ca^+(d) π‖-donation	−32.9 (19.3%)	−32.0 (21.1%)	−31.8 (21.5%)	−30.8 (22.0%)
ΔEorb(3)^b	SiE3Ca2 → Ca^+(d) σ-donation	−13.1 (7.7%)	−11.9 (7.8%)	−12.0 (8.1%)	−11.9 (8.5%)
ΔEorb(4)^b	SiE3Ca2 → Ca^+(d) π⊥-donation	−12.3 (7.2%)	−12.2 (8.0%)	−12.5 (8.5%)	−12.5 (8.9%)
ΔEorb(5)^b	SiE3Ca2 → Ca^+(d) δ-donation	−8.1 (4.7%)	−9.9 (6.5%)	−10.9 (7.4%)	−11.8 (8.4%)
ΔEorb(rest)^b		−15.1 (8.8%)	−6.4 (4.2%)	−6.1 (4.1%)	−6.1 (4.4%)

---

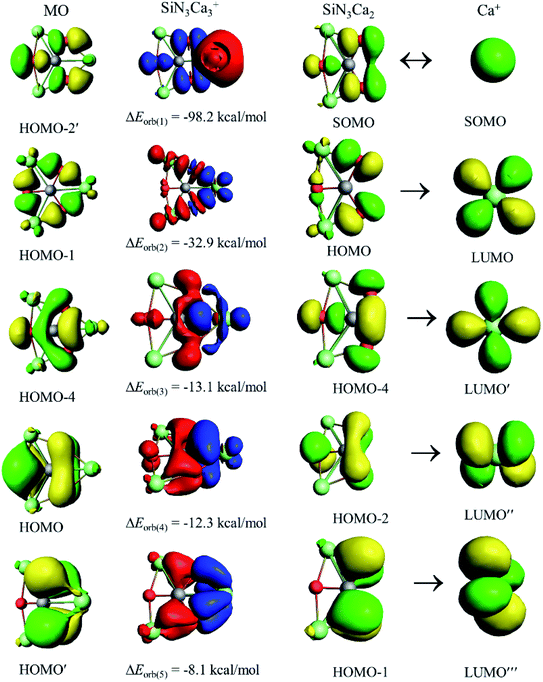
The decomposition of ΔE_orb into pair-wise orbital interaction ΔE_orb(n) in Table 2 and the corresponding deformation densities Δρ_(n) provide us with the most important information about bonding. The strongest orbital contribution, ΔE_orb(1), which accounts for 48–52% of the total covalent interaction, originates from the coupling of unpaired electrons of Ca⁺ and SiE₃Ca₂. The remaining orbital terms, ΔE_orb(2)–(5), mainly come from the donation of electron density from SiE₃Ca₂ to vacant atomic orbitals (AOs) of Ca⁺. The inspection of the shape of Δρ_(n) and the related orbitals of the fragments (Fig. 3) helps us to identify the Si–Ca covalent bond and the orbitals involved in the pairwise interactions. The s orbital of Ca⁺ takes part in the electron-sharing σ-bond formation with SiE₃Ca₂, whereas vacant d AOs of Ca⁺ act as acceptor orbitals in the dative interactions, ΔE_orb(2)–(5). Therefore, d AOs of Ca⁺ are responsible for 39–48% of the total orbital interaction. The present results further strengthen the proposal^29–33 that heavier alkaline-earth elements (Ca, Sr, and Ba) should be classified as transition metals rather than main-group elements. Furthermore, a careful look at the Δρ_(n) plots shows that in ΔE_orb(1) and ΔE_orb(2) only peripheral atoms are involved, but in ΔE_orb(3)–(5) there is direct covalent interaction between Si and Ca centers. To correlate with the molecular orbitals (MOs) of the SiE₃Ca₃⁺ cluster, the related MOs for 24 valence electrons are given in Fig. S8.† Δρ_(3)–(5) can be correlated with HOMO-4, the HOMO and the HOMO′, respectively. Therefore, although the MO coefficient of Ca centers is small, they should not be neglected as the energy stabilization coming from them is significant. Si and M centers are only connected through delocalized bonds which is the reason for not having any gradient path between them as is indicated in the electron density analysis. Instead, there is a ring critical point at the center of the SiE₂M ring (see Fig. S9†). The results of adaptive natural density partitioning (AdNDP) analysis also corroborate this, where M centers are connected with the Si center through 7c–2e π-bonds (see Fig. S10†).

Fig. 3 Plot of the deformation densities, Δρ_(1)–(5) corresponding to ΔE_orb(1)–(5) and the related interacting orbitals of the fragments in the SiN₃Ca₃⁺ cluster at the PBE0/TZ2P-ZORA//PBE0/def2-TZVP level. The orbital energy values are in kcal mol⁻¹. The charge flow of the deformation densities is from red to blue. The isovalue for Δρ₍₁₎ is 0.001 au and for the rest is 0.0005 au.

Another aspect is to check the nature of electrostatic interaction between Si and M. The natural charges in Table 1 shows significant electron transfer from M to E centers that imposes a positive partial charge of 1.7|e|. The E centers possess large negative charges (ranging from −1.2 to −1.9|e|), which decrease with the reduction in electronegativity of E. For a given M, with the variation of E, a drastic change in partial charge on Si is noted. For E = N, the Si center carries a high positive charge (1.6|e|), which is greatly reduced upon moving to E = P (0.3|e|). For E = As, the Si center becomes almost neutral, and eventually, it possesses a negative charge for E = Sb. Therefore, the electrostatic repulsion between Si and M should be largely reduced from N to As, and finally for SiSb₃M₃⁺, the electrostatic interaction between Si and M should be attractive. Note that the energy partitioning scheme in EDA-NOCV taking Ca⁺ + SiE₃Ca₂ provides combined energy contributions for one M–Si contact and two M–E contacts. This argument based on point charges is further verified by the energy components obtained in interacting quantum atom (IQA) analysis, which shows that the covalent (V_Coval) part of the Si–Ca interaction is attractive (ranging between −4.6 and −11.6 kcal mol⁻¹) in all cases. However, the electrostatic (ionic, V_Ionic) part is highly repulsive for E = N, P, As, making the overall interaction repulsive. Such electrostatic repulsion is sharply reduced in moving from N to As, and finally, for E = Sb, it becomes attractive (see Tables S10–S12†). Thus, the SiSb₃M₃⁺ cluster presents a case in which covalent bonding is robust and ionic interaction between Si and M centers is attractive in nature. If we look at the inter-atomic interaction energies (V_Total) for Si–M bonds and M–E bonds, it can be understood that the repulsive energy in Si–M bonds is largely overcompensated by two M–E bonds, even for E = N. This is the reason why electrostatic repulsion between Si and M centers does not result in a very large Si–M bond distance. Nevertheless, repulsive Si–M contacts in SiE₃M₃⁺ (E = N, P, As) make hexacoordination assignment skeptical. SiSb₃M₃⁺ clusters should be considered to possess phSi convincingly. Note that the IUPAC definition of coordination number only demands “the number of other atoms directly linked to that specified atom”,³⁴ but does not say about the overall nature of interaction between them. In SiSb₃M₃⁺, phSi is linked to three Sb atoms through strong covalent bonds and is bound to three M atoms through ionic interaction in combination with a weaker covalent interaction. These clusters are only weakly aromatic because of such polar electronic distribution (see Fig. S11†).

The next challenge is to protect the reactive centers of phSi clusters with bulky ligands, which is required for large scale synthesis. This is not an easy task since slight external perturbation of most of the planar hypercoordinate atom species could result in a loss in planarity. Few years ago, the groups of Ding and Merino³⁵ reported CAl₄MX₂ (M = Zr, Hf; X = F–I, C₅H₅) where ppC is sandwiched and protected by a metallocene framework. Therefore, the presence of X groups is mandatory to provide the electronic stabilization in ppC. In the present cases, surprisingly, SiSb₃M₃⁺ clusters are found to maintain the planarity around hexagons even after the coordination of M centers with six N-heterocyclic carbene (NHC) and benzene (Bz) ligands forming SiSb₃M₃(NHC)₆⁺ and SiSb₃M₃(Bz)₆⁺ (M = Ca, Sr, Ba) complexes, respectively (see Fig. 4). These complexes are highly stable against ligand dissociation as reflected by the high bond dissociation energy (D_e = 236.1 (Ca), 203.9 (Sr) and 171.3 (Ba) kcal mol⁻¹) for SiSb₃M₃(NHC)₆⁺ → SiSb₃M₃⁺ + 6NHC and D_e = 153.8 (Ca), 128.0 (Sr) and 114.0 (Ba) kcal mol⁻¹ for SiSb₃M₃(Bz)₆⁺ → SiSb₃M₃⁺ + 6Bz. The Si–M bond distances are slightly elongated because of coordination with the ligands. But the results of IQA given in Table S13† show that Si–M bonds have attractive interaction energies ranging between −20.0 and −32.4 kcal mol⁻¹. Therefore, the planarity of the phSi core and the attractive nature of all the six contacts of phSi are maintained in ligand-bound SiSb₃M₃(NHC)₆⁺ and SiSb₃M₃(Bz)₆⁺ (M = Ca, Sr, Ba) complexes.

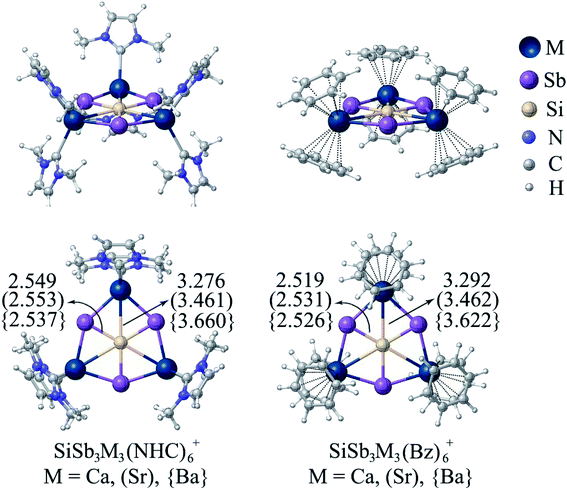Fig. 4 The minimum energy geometries of SiSb₃M₃(NHC)₆⁺ and SiSb₃M₃(Bz)₆⁺ (M = Ca, Sr, Ba) complexes at the PBE0-D3(BJ)/def2-TZVP level.

In summary, we have theoretically achieved the first series of planar hexacoordinate silicon (phSi) clusters, SiSb₃M₃⁺ (M = Ca, Sr, Ba), by exploring their potential energy surfaces. These phSi systems are both thermodynamically and kinetically stable. The global minimum structures of SiE₃M₃⁺ (E = N, P, As, Sb) clusters have a D_3h symmetry with the ¹A₁′ electronic state. The ability of the heavier alkaline-earth metals (Ca–Ba) to utilize their d orbitals in chemical bonding is a key factor that underlies the stability of these systems. The Ca–Ba ligands form weak covalent bonding with Si centers through their d orbitals, mimicking transition metals. The electronic charge distribution and IQA analysis show that electrostatic interaction in the Si–Ca links is essentially repulsive in SiN₃M₃⁺, but it sharply reduces with the decrease in electronegativity of E. Eventually, a sizable electrostatic attractive interaction exists between Si and M centers in SiSb₃M₃⁺, leading to a truly unprecedented phSi bonding motif that is held together by both covalent bonding and attractive ionic interaction. For SiE₃M₃⁺ (E = N, P, As) clusters, the electrostatic repulsion between Si and M dominates over covalent interaction, making Si–M contacts repulsive in nature. Most interestingly, the planarity of the phSi core and the attractive nature of all the six contacts of phSi are maintained in N-heterocyclic carbene (NHC) and benzene (Bz) bound SiSb₃M₃(NHC)₆⁺ and SiSb₃M₃(Bz)₆⁺ (M = Ca, Sr, Ba) complexes. Therefore, such clusters protected by bulky ligands would be suitable candidates for large scale synthesis in the presence of bulky counter-ions. Recent experimental reports on ptSi systems have already stimulated much curiosity within the community, and the present results would undoubtedly act as a stimulus to it.

Data availability

Computational details, extra data and the Cartesian coordinates for all compounds are provided in the ESI† accompanying this paper.

Author contributions

JCG, H-JZ, Z-hC, SP, and GM designed the works and concepts, analyzed the data, wrote the draft, and finalized it. CC and M-hW performed the global minima searching. L-YF and L-QZ performed NBO and IQA. SP performed EDA-NOCV. All authors took part in the discussions and approved the final version.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was funded by the National Natural Science Foundation of China (No. 11922405, 11874178, and 91961204). H. J. Z. acknowledges support from the National Natural Science Foundation of China (22173053 and 21873058). Part of the calculations in this work were supported by the High-Performance Computing Center of Jilin University, China.

References

1. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993.
2. J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427.
3. P. v. R. Schleyer and A. I. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 21, 1536–1538.
4. X. Li, L. S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038.
5. L. S. Wang, A. I. Boldyrev, X. Li and J. Simons, J. Am. Chem. Soc., 2000, 122, 7681–7687.
6. X. Li, H. F. Zhang, L. S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed., 2000, 39, 3630–3632.
7. J. Xu, X. Zhang, S. Yu, Y. H. Ding, K. H. Bowen and J. Phys, Chem. Lett., 2017, 8, 2263–2267.
8. W. Siebert and A. Gunale, Chem. Soc. Rev., 1999, 28, 367–371.
9. R. Keese, Chem. Rev., 2006, 106, 4787–4808.
10. G. Merino, M. A. Mendez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372.
11. L. M. Yang, E. Ganz, Z. Chen, Z. X. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468–9501.
12. Y. Pei, W. An, K. Ito, P. v. R. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394–10400.
13. V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 1–10.
14. J. C. Guo, L. Y. Feng, J. Barroso, G. Merino and H. J. Zhai, Chem. Commun., 2020, 56, 8305–8308.
15. K. Exner and P. v. R. Schleyer, Science, 2000, 290, 1937–1940.
16. (a) K. Ito, Z. Chen, C. Corminboeuf, C. S. Wannere, X. H. Zhang, Q. S. Li and P. v. R. Schleyer, J. Am. Chem. Soc., 2007, 129, 1510–1511; (b) R. Islas, T. Heine, K. Ito, P. v. R. Schleyer and G. Merino, J. Am. Chem. Soc., 2007, 129, 14767–14774.
17. L. M. Wang, W. Huang, B. B. Averkiev, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2007, 46, 4550–4553.
18. B. B. Averkiev, D. Y. Zubarev, L. M. Wang, W. Huang, L. S. Wang and A. I. Boldyrev, J. Am. Chem. Soc., 2008, 130, 9248–9250.
19. Y. B. Wu, Y. Duan, G. Lu, H. G. Lu, P. Yang, P. V. R. Schleyer, G. Merino, R. Islas and Z. X. Wang, Phys. Chem. Chem. Phys., 2012, 14, 14760–14763.
20. L. Leyva-Parra, L. Diego, O. Yanez, D. Inostroza, J. Barroso, A. Vasquez-Espinal, G. Merino and W. Tiznado, Angew. Chem., Int. Ed., 2021, 60, 8700–8704.
21. A. I. Boldyrev, X. Li and L. S. Wang, Angew. Chem., Int. Ed., 2000, 39, 3307–3310.
22. (a) P. Ghana, J. Rump, G. Schnakenburg, M. I. Arz and A. C. Filippou, J. Am. Chem. Soc., 2021, 143, 420–432; (b) F. Ebner and L. Greb, Chem, 2021, 7, 2151–2159.
23. M. H. Wang, X. Dong, Z. H. Cui, M. Orozco-Ic, Y. H. Ding, J. Barroso and G. Merino, Chem. Commun., 2020, 56, 13772–13775.
24. S. D. Li, G. M. Ren and C. Q. Miao, Inorg. Chem., 2004, 43, 6331–6333.
25. A. J. Kalita, S. S. Rohman, C. Kashyap, S. S. Ullah, I. Baruah, L. J. Mazumder and A. K. Guha, Int. J. Quantum Chem., 2021, 121, e2664.
26. Y. Wang, M. Qiao, Y. Li and Z. Chen, Nanoscale Horiz., 2018, 3, 327–334.
27. P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337.
28. F. A. Bickelhaupt, C. Fonseca Guerra, M. P. Mitoraj, F. Sagan, A. Michalak, S. Pan and G. Frenking, Phys. Chem. Chem. Phys., 2022 10.1039/D2CP02153F.
29. X. Wu, L. L. Zhao, J. Y. Jin, S. Pan, W. Li, X. Y. Jin, G. J. Wang, M. F. Zhou and G. Frenking, Science, 2018, 361, 912–916.
30. Q. Wang, S. Pan, Y. B. Wu, G. H. Deng, J. H. Bian, G. J. Wang, L. L. Zhao, M. F. Zhou and G. Frenking, Angew. Chem., Int. Ed., 2019, 58, 17365–17374.
31. Q. Wang, S. Pan, S. J. Lei, J. Y. Jin, G. H. Deng, G. J. Wang, L. L. Zhao, M. F. Zhou and G. Frenking, Nat. Commun., 2019, 10, 3375.
32. (a) I. Fernandez, N. Holzmann and G. Frenking, Chem.–Eur. J., 2020, 26, 14194–14210; (b) T. Bettens, S. Pan, F. De Proft, G. Frenking and P. Geerlings, Chem.–Eur. J., 2020, 26, 12785–12793; (c) G. Frenking, I. Fernández, N. Holzmann, S. Pan, I. Krossing and M. Zhou, JACS Au, 2021, 1, 623–645; (d) P. Stegner, C. Färber, J. Oetzel, U. Siemeling, M. Wiesinger, J. Langer, S. Pan, N. Holzmann, G. Frenking, U. Albold, B. Sarkar and S. Harder, Angew. Chem., Int. Ed., 2020, 59, 14615–14620; (e) Y. Zhou, S. Pan, X. Dong, L. Wang, M. Zhou and G. Frenking, J. Am. Chem. Soc., 2022, 144, 8355–8361.
33. M. F. Zhou and G. Frenking, Acc. Chem. Res., 2021, 54, 3071–3082.
34. P. Muller, Pure Appl. Chem., 1994, 66, 1077–1184.
35. Z.-H. Cui, V. Vassilev-Galindo, J. L. Cabellos, E. Osorio, M. Orozco, S. Pan, Y.-H. Ding and G. Merino, Chem. Commun., 2017, 53, 138–141.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc01761j

---