Entropic control of nanoparticle self-assembly through confinement

Abstract

Entropy can be the sole driving force for the construction and regulation of ordered structures of soft matter systems. Specifically, under confinement, the entropic penalty could induce enhanced entropic effects which potentially generate visually ordered structures. Therefore, spatial confinement or a crowding environment offers an important approach to control entropy effects in these systems. Here, we review how spatial confinement-mediated entropic effects accurately and even dynamically control the self-assembly of nanoscale objects into ordered structures, focusing on our efforts towards computer simulations and theoretical analysis. First, we introduce the basic principle of entropic ordering through confinement. We then introduce the applications of this concept to various systems containing nanoparticles, including polymer nanocomposites, biological macromolecular systems and macromolecular colloids. Finally, the future directions and challenges for tailoring nanoparticle organization through spatial confinement-mediated entropic effects are detailed. We expect that this review could stimulate further efforts in the fundamental research on the relationship between confinement and entropy and in the applications of this concept for designer nanomaterials.

---

Cuiling Hou

Assoc. Prof. Cuiling Hou obtained her PhD in Materials Science from Northwestern Polytechnical University in 2013. She currently teaches at Jiujiang University and is a visiting scholar under the guidance of Prof. Li-Tang Yan at Tsinghua University in China. Her research focuses on the simulation and theoretical analysis of the self-assembly and structural regulation of nanoparticles.

Lijuan Gao

Lijuan Gao received her BS in Chemical Engineering from Tsinghua University in 2020. She is currently a graduate student under the guidance of Prof. Li-Tang Yan at Tsinghua University in China. Her research focuses on the self-assembly of colloidal particles.

Yuming Wang

Yuming Wang received his BS in Chemical Engineering from Tsinghua University in 2021. He is currently a graduate student under the guidance of Prof. Li-Tang Yan at Tsinghua University in China. His research focuses on the crystallization of hard spheres.

Li-Tang Yan

Prof. Li-Tang Yan obtained his PhD in Polymer Physics and Chemistry at Tsinghua University in 2007. Then he went to Bayreuth University in Germany as a Humboldt Research Fellowship. In 2010, he joined Prof. Anna Balazs’ group at the University of Pittsburgh in USA as a Postdoctoral Research Fellowship. He returned to Tsinghua University as a faculty in the Department of Chemical Engineering from May 2011. In 2020, he received the “NSFC Award” for Outstanding Young Scholar. His research interests focus on the computational and theoretical aspects of soft matter systems, including nanoparticle cellular interactions and nano-engineered materials that are self-assembling and self-regulating.

---

1 Introduction

Entropy, with its change indicating the irreversibility of a thermodynamic process, plays a central role in statistical mechanics and the second law of thermodynamics. The understanding of entropy has undergone some revolutions since Clausius proposed the concept of entropy through building its association with lost heat.¹ One of the most important advancements regarding this topic is entropic ordering, which was enlightened from the discovery by Onsager² in the late 1940s of the isotropic–nematic transition of thin, hard rods and then by Wood and Alder^3,4 in the late 1950s of the freezing of hard spheres. In these seminal cases, the systems have an ordered phase with higher entropy than that of the disordered phase at the same density, seeming paradoxical to the second law. Generally, in each case, one type of entropy decreases and another kind of entropy increases such that the total entropy becomes larger, that is, entropic ordering is not a violation of the second law.^5,6

Up to now, entropy-driven ordering transitions have been found in many systems, underscoring that it is not exception but the rule.^7–17 For example, simulations on hard, convex polyhedral particles have shown that entropy can drive the formation of an unexpectedly large number of possible structurally ordered phases, including crystals, liquid crystals, and even quasicrystals.^8,18–21 The entropy variation associated with conformational changes has recently been demonstrated to drive polymer-tethered nanoparticles into spatially ordered structures.^22–29 The rapid progress in the understanding of entropic ordering leads to one essential question: can we develop a new strategy for the structural control of particle self-assembly through the conscious control of entropic effects to achieve the desired structural organization? Here, we term this concept as “entropy-controlled strategy”.

The key to realize the entropy-controlled strategy is developing approaches to precisely control entropy.³⁰ One particular aspect that can be of great relevance is the generation of confinement environments where building blocks are subjected to geometrical or topological constraints, such as packing, curved surfaces, fields, or the anisotropic shapes of the particles themselves.^{14,24,26,31–34} What is interesting is the richness of ordered structures that emerge when we combine particles with simple confinement. For instance, hard particles with no interactions other than an excluded volume can transform from a disordered fluid into an ordered crystal structure, or from one crystal to another, in response to the spatial confinement; these ordered crystals can be surprisingly complex and remarkably structurally diverse.^20,35–37 In contrast to the crystal symmetries in bulk systems, packings in confinement possess inherent local and global orders, which significantly depend on the geometries of confinement. For example, icosahedral symmetry has been widely observed within the spherical confinement both in a cavity^9,38,39 and on a surface.^40,41 Additional symmetries, such as face-centered cubic (FCC) order,⁹ decahedral order,⁴² bipolar orientational order,⁴³ and a wide variety of point groups drawn from particle shapes,⁴⁴ have also been discovered in the spherical confinement. Such an equilibrium crystallization of hard particles belongs to the entropically driven ordering of the particle configuration where, although entropy is the sole contribution to the free energy of the hard particles, the confinement is an essential factor that mediates the entropic effects. Nonetheless, the general principles behind the interplay between confinement and entropy remain elusive. A definite elucidation of the relationship between these two themes will certainly facilitate our understanding on how entropy and confinement govern the structural organization of various particles and lead to new approaches of the entropy-controlled strategy.

In this review, our discussion will thereby focus on how various confinement environments can be harnessed to control entropy effects which govern the structural organization of soft matter systems containing nanoparticles, with an emphasis on our own efforts on this topic. The general principles, entropy types explored and confinements in various systems, such as macromolecular colloids, polymer nanocomposites and life macromolecules, are introduced regarding the applications of confinements to realize the entropy-controlled strategy. We hope that this review will shed light on the development of rationally structured designer materials through well controlled entropic effects by confinements.

2 General principles of entropic control by confinement

The entropic effects can be magnified by tuning the confinement of nanoparticles in geometrical or topological constraints. In this section, we delineate the general principles concerning the relationship between entropy and confinement.^6,13

According to the microscopic interpretation, entropy, S, can be captured by the equation S = k_Bln W, where W represents the number of states accessible to the system and k_B is the Boltzmann's constant.⁴⁵ Following the second law of thermodynamics, irreversible changes in physical systems only occur when entropy increases.¹ In classical statistical mechanics, the number of states can be estimated through considering the volume accessible to the particles. Thus, the unidirectional nature of the entropic increase implies the maximization of the free volume favored by each molecule or particle, which induces the potential competition among these particles for the accessible volume.¹³ When the volume is large enough, the competition is not extreme, and the entropic effect is not eminent. However, for a system within a confined space or a crowded environment, the volume accessed by each particle is evidently reduced and even penalized, intensifying the competition for the free volume among the particles. Thus, the entropic effects can be significantly enhanced and even overwhelm the enthalpic interactions. The associated entropic penalty could drive and even dominate the directional reorganization of the systems towards the maximization of entropy. This, to a large extent, can generate visually ordered microstructures, because the maximum entropy of particles within a certain volume can be reached only when each particle has the same free volume.¹³

The influence of confinement on entropic effects can also be understood based on the physical characters of an entropic force, a force that is generated by entropy.^13,45–48 An entropic force can be defined as an effective macroscopic force that originates in a thermodynamic system by its tendency to increase entropy. The typical entropic force includes osmosis, elasticity of polymer chains, depletion, diffusion and so on. The entropic force is recognized by the facts that it points in the direction of increasing entropy, and, particularly, that it is associated with the deviation from the equilibrium state with maximum entropy. When a system leaves its maximum entropy state, an entropic force appears, and a larger deviation from the maximum entropy state will induce a stronger entropic force. There is no entropic force when the system is in its state with maximum entropy. For example, when a polymer chain is immersed into a heat bath, it presents a large number of randomly coiled conformations since these are entropically favored. However, the conformation number is significantly reduced when it is stretched into an extended configuration. The statistical tendency to return to a maximal entropy state translates into a macroscopic force, in this case the elastic force. Similarly, under confinement environments, such as in a confined geometry, undergoing packing, and within a crowded environment, the limited volume is available for the components of a system which deviates from the state with maximum entropy and thereby the entropic force emerges and directs the structural organization. Through altering the confinement degree, the entropic force can be tuned, allowing approaches to realize the entropy-controlled strategy. Besides the confinement concerned in the present work, there are also other approaches to realize this strategy.^48,55–57

Multiscale simulation methods are widely used to study soft matter systems, for example, molecular dynamics (MD), dissipative particle dynamics (DPD), Brownian dynamics (BD), and so on. Because of the low-enthalpy characteristic of soft matter systems, various novel entropy-driven ordered structures have been revealed by simulations.^22–27 To better obtain the new ordered structure and explain the entropy effects in the equilibrium state, the Monte Carlo method is often favored for simulations.^8,9 Self-consistent field theory (SCFT) is also used to identify the changes of entropy and enthalpy.²⁵

For a clearer description, we provide the definitions of some key parameters referred in the present review, for example, shape entropy, spherical confinement, high performance materials, etc. Specifically, in soft matter systems, the entropy corresponding to shape is shape entropy.⁸ Shape entropy plays the role of a shape-oriented entropic force, which maximizes the entropy of the whole system by coordinating the orientation and arrangement of particles. Spherical confinement means that the confinement environment of particles or molecules expands from the traditional densest packing space to spherical geometry, resulting in richer micro-ordered structures, such as quasicrystals.⁹ High-performance materials usually belong to a class of materials with excellent physical and chemical properties, such as polymer composites suitable for medicine, optoelectronic devices and biosensors.^22,23

3 Applications of the entropy-controlled strategy by confinement

In this section, we elaborate the advancement in the application of the entropy-controlled strategy where various confinement environments are generated to tune entropic effects and thereby control the structural organization of some representative systems containing particles, focusing on the approaches of tailored computer simulations as well as theoretical analysis. In particular, in view of the sequence from a simple system to a more complex one, we discuss in turn macromolecular colloidal systems, polymer composites and biological macromolecular systems. The necessity and control approaches of the entropy-controlled strategy as well as the general principles and entropy types within the confinement are analyzed for these systems.

3.1 Macromolecular colloidal systems

The scale of colloidal particles, which are made mainly from macromolecular materials, generally ranges from 10 to 100 nm, which can not only be observed conveniently but also undergo a thermal motion like small molecules. Hence, the thermodynamic states of colloidal systems may be affected by entropic effects to a great extent. Typically, the entropy types influencing the organization of macromolecular colloidal systems include translational entropy and vibrational entropy for homogeneous particles; for colloidal particles with anisotropic surface or shape, the shape entropy, orientational entropy, and rotational entropy become nontrivial.^39,49–57

Under spatial confinement, novel ordered structures of colloidal particles can emerge, which are usually driven by entropy. As an example, the supraparticles with long-range three-dimensional (3D) icosahedral symmetry have been obtained by placing hard spherical colloidal particles in the spherical confinement, where the structure was proved to be completely driven by entropic effects.⁹ Through spherical confinement, the vibrational entropy of particles is enhanced in the system, resulting in entropic force that governs particles to organize into the unique ordered structure. The fact that spherical confinements can stabilize structures incommensurate with a long-range positional order puts forward a new way to design large-scale crystals with unusual symmetry, which may be beneficial to optical or other applications (Fig. 1).⁹

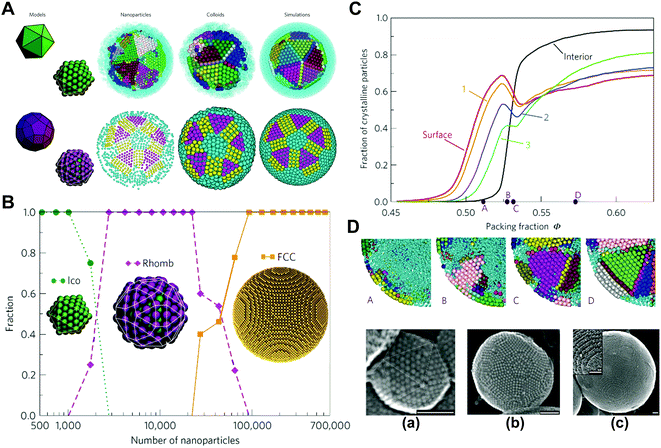Fig. 1 Self-assembly of colloidal particles within spherical confinement. (A) Core and surface ordered structures of the icosahedral clusters. (B) Size dependence of the cluster structure. (C) Crystallization process of the icosahedral clusters. (D) Secondary electron scanning transmission electron microscopy (SE-STEM) images of typical supraparticles containing cobalt iron oxide nanoparticles. (a) Supraparticle with a diameter of 105 nm with Mackay icosahedral symmetry. (b) 216 nm Supraparticle with an anti-Mackay rhombicosidodecahedral structure. (c) 734 nm Supraparticle consisting of a single FCC crystal domain. Inset: a magnified view of the step edges of the FCC supraparticle. All scale bars are 50 nm. Reproduced from ref. 9; Copyright 2015 Macmillan Publishers Limited.

In order to further evaluate the influence of spatial confinement on the structural organization of colloidal systems, we investigated the self-assembly of spherical colloids within cylindrical confinement.^58,59 The densest packing of identical hard spherical colloidal particles in a thin cylinder usually causes the chiral helical order,^60,61 while, for non-densest packing with different volume fractions in wide cylinders, the entropy effect can dominate the self-assembled structure and invalidate Pauling's packing rules, resulting in the emergence of new achiral ordered phases, such as partitioned, circled, and layered structures.⁵⁸ These unconventional ordered phases are stabilized by the confinement-mediated entropic effect. This provides new insight into the confinement physics of colloidal particles and inspires nonintuitive design rules for the fabrication of novel ordered phases through confinement (Fig. 2).⁵⁸

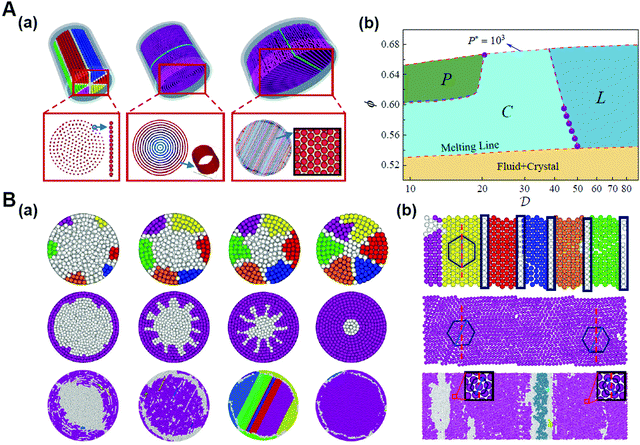Fig. 2 Crystallization of hard spheres within the cylindrical confinement. (A) (a) Illustrations (top) and snapshots (bottom) of partitioned (P), circled (C) and layered (L) structures, respectively. (b) Phase diagram. (B) Arrangements of spheres on a plane unfolded from the outermost layer corresponding to (A). (a) Snapshot sequence of crystal growth. (b) The arrangements of SCNs on a plane unfolded from the outermost layer of P, C and L structures. Reproduced from ref. 58; Copyright 2021 American Physical Society.

It was proposed that shape entropy drives the phase behavior of particles with an anisotropic shape through the directional entropic force.⁸ The directional entropic force has density dependent behavior and therefore emergence, which is not the intrinsic property of a single particle, but the statistical behavior based on the cooperation of the whole particles in the system. The hard shape induces particles to take the optimal arrangement and orientation to maximize the entropy of the system. The mechanism of the directional entropic force is the result of maximizing the shape entropy and promoting particles to adopt a local dense packing structure. This finding provides guideline for the control of the shape-entropy effects in experiments (Fig. 3).⁸

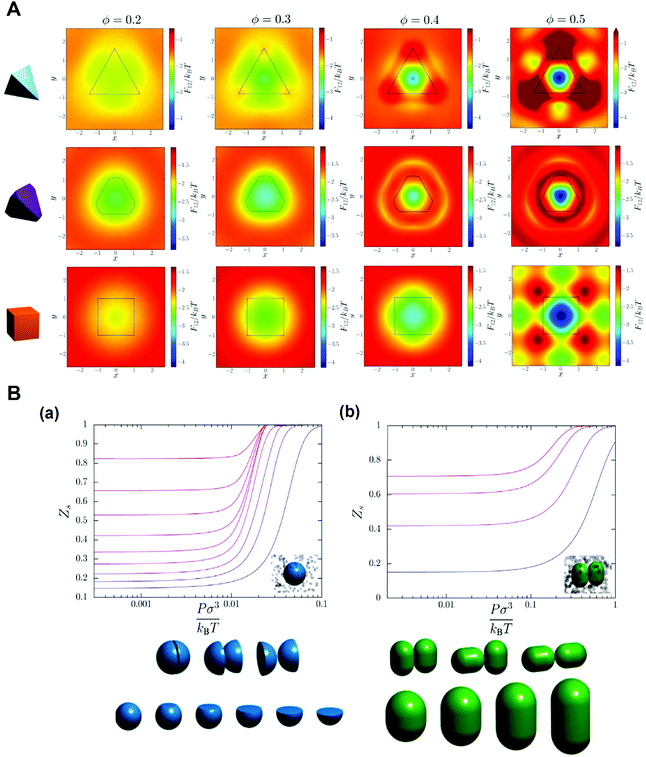Fig. 3 Understanding the shape entropy through local dense packing. (A) Directional entropic force of polyhedral colloidal particles with different shapes characterized by a mean moment potential. ϕ: packing fractions. (B) The probability of specific binding, Zs, for (a) particles with a single facet and (b) capsules in a bath of depletants as a function of depletant pressure. Reproduced from ref. 8; Copyright 2014 National Academy of Sciences.

Janus particles tend to self-assemble into various structures due to their asymmetry in surface or shape. In the case of non-dense packing, unstable small cluster structures can be formed at low concentrations and can evolve into a tetrahedral mode at high concentrations. In the case of dense packing, the plastic crystal structures with a periodic arrangement but a random orientation can be formed, and then the crystal structure with orientation perpendicular to the shear direction can be formed when applying a shear force.⁶² Although the result of thermodynamic stability mainly depends on enthalpy, the rotational and vibrational entropy of Janus particles also greatly affects the dynamic process. We demonstrated a new phase transition occurring in the dense suspension of Janus spheres under shear, that is, from the initial plastic crystal to the oriented crystal with a layered structure along the shear direction.⁶³ That is, the transformation from the plastic crystal to the oriented crystal of densely packed Janus particles can be realized by the shear field. This finding provides a unique approach for the control of the orientation order of anisotropic particles in an non-equilibrium state, and allows a new idea and effective theoretical guidance for the development of reconfigurable stimulus-responsive materials (Fig. 4).⁶⁴

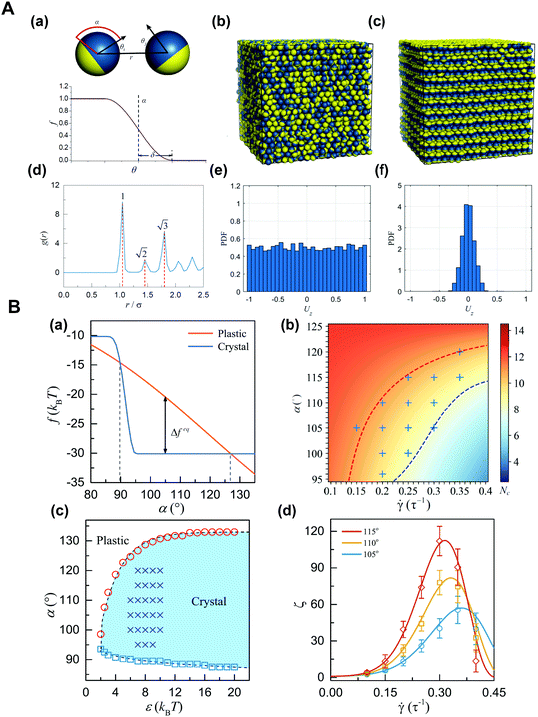Fig. 4 (A) Plastic crystal-to-crystal transition of Janus colloidal particles. (a) Schematic diagrams of the Janus-particle model (top) and the angular dependence, w(θ) (bottom). (b) Representative snapshot of the initial state. (c) Snapshot of the shear-induced orientational crystal. (d) Radial distribution function for particle locations in (c). (e and f) Probability distributions of U_z = sig n(x, y)||n × e_z|| for phases in (b) and (c), respectively. Where n = (x, y, z) is the orientation vector, and e_z = (0, 0, 1). (B) Theoretical analysis of the transition from the plastic to crystalline phases. (a) Modified Helmholtz free energy, f. (b) Heatmap of the threshold, N_c. (c) Phase diagram. (d) The shear-rate dependence of the rescaled nucleation rate, ζ. Reproduced from ref. 64; Copyright 2019, American Physical Society.

3.2 Polymer nanocomposites

Polymer nanocomposites play a very important role in the preparation of new high-performance materials which demonstrate distinct physicochemical properties that are closely related to the spatial distribution of microstructures regulated by the interaction between nanoparticles and polymers. Particularly, more and more evidences demonstrate that the conformational entropy of polymer chains greatly influences the dispersion state and spatial organization of nanoparticles in the polymer matrix.^22,65–67 Essentially, as mentioned in the previous section, when nanoparticles are wrapped by their affiliative polymer chains to reduce the enthalpy of a system, the conformation of the chains will however become constrained, resulting in the increase of the free contributed by entropy. If the change degree of the free energy contributed by entropy overwhelms that by enthalpy, it will induce a strong entropic effect, so that the microstructure of the system may present counterintuitive behaviors. Such an entropic effect can thereby be tuned by tailoring the size, concentration, shape, surface properties of nanoparticles and the flexibility of polymer chains, or by exerting external pressure and spatial confinement.^{23,27,68–71}

For the purpose of in-depth understanding of the interplay between conformational entropy and enthalpy on the self-assembly in polymer nanocomposites, we have investigated the self-assembly structures for tethered Janus nanoparticles at a flat interface or a spherical surface, and the dynamic transition of hierarchical nanostructures in block copolymers.^{24–26,33,72}

Generally, the effective control of entropic effects facilitates the design of self-assembly systems with desired structures. For example, entropic templating is such a strategy where the entropic repulsion due to the conformational entropy of the tethered chains can be controlled through applied lateral pressures.⁶⁶ Using molecular dynamics simulations, we demonstrated that the mixing state of tethered Janus particles at the fluid–fluid interface has a strong dependence on the stiffness of tethered chains, in which semiflexible chains are more likely to exhibit a perfect intercalation structure at the single-molecule level. The entropic templating regulated by the stiffness of tethered chains gives rise to different entropic repulsion states, which can be explored to design mechanically responsive nanocomposites at the interface of the binary fluid mixture (Fig. 5).²⁷ In this case, the interface structure undergoes a reversible transition between the random state and the long-range intercalation state in response to various structural parameters of tethered Janus nanoparticles and lateral pressures. The difference between the tethered chains plays a critical role in the mechanical response of the system. The transfer and recovery of the interface nanopatterns point to a precise and mechanomutable response behavior (Fig. 6).²⁴

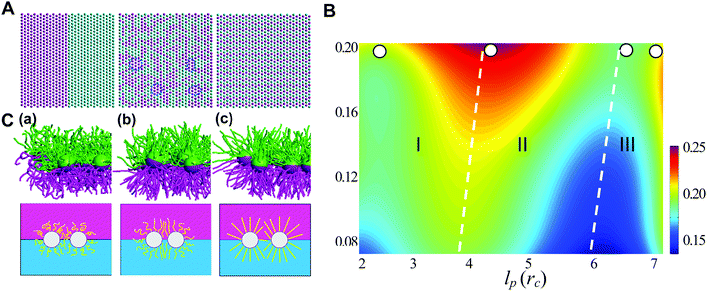Fig. 5 Chain stiffness regulates entropy-templated perfect mixing at the single-nanoparticle level. (A) Representative patterns of three different nanoparticle-mixing states: phase-separated, Monte Carlo-generated randomly dispersed state and perfect mixing at the single-nanoparticle level. (B) Dependence of the mixing parameter, φ, on the persistence length of the long tethers, l_p, and the compression ratio, δ. (C) Conformational transition of the tethered chains in systems of pure long-tether nanoparticles in response to a lateral compression of δ ≈ 0.1, where l_p = 0.50r_c (a), l_p = 3.28r_c (b), l_p = 5.90r_c (c), and r_c is the truncate distance. Reproduced from ref. 27; Copyright 2016 Royal Society of Chemistry.

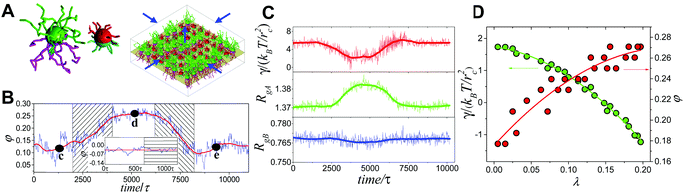Fig. 6 Mechanomutable nanocomposites consisting of binary mixtures of tethered Janus nanoparticles at the fluid–fluid interface. (A) Janus nanoparticles and initial configuration at the interface. (B) Plot of mixing parameter, φ, against time in a successive compressing-stretching process. (C and D) Time dependence of the surface tension, γ, and radii of gyration of the long and short tethers, R_gA and R_gB, respectively. Reproduced from ref. 24; Copyright 2014 American Physical Society.

Furthermore, the entropic templating can be regulated through tuning the competition between the polymerization rate and nanoparticle diffusion kinetics in the polymerization-induced self-assembly of grafted Janus nanoparticles.⁷³ The transition of the mixing parameter exhibits an increase at a slow reaction rate, similar to that of the first-order transformation. However, increasing the reaction rate will reduce the increase until the transition becomes continuous, behaving like a second-order transformation. This is because the polymerization of Janus nanoparticles with a surface grafting initiator initiates a transformation of the interface structures from a randomly mixed phase to an intercalation phase. With the growing of the chains, significant spatial repulsion between neighboring chains results in the stretching of the chains and the decrease of the conformational entropy. The interpenetration of nonreactive nanoparticles increases the chain spacing and thereby conformational entropy, leading to the intercalation structure. The findings might provide further opportunities for the manipulation of entropic effects through the dynamic control based on reactions (Fig. 7).⁷²

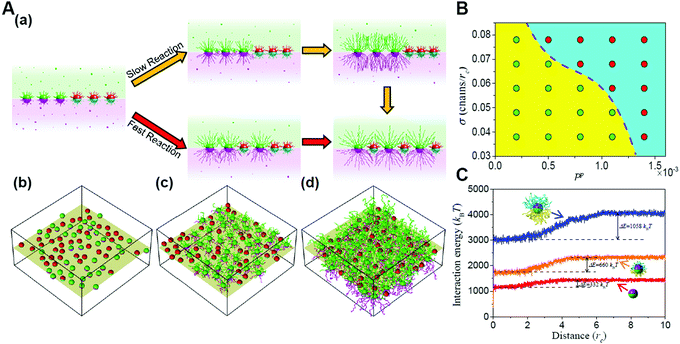Fig. 7 Reaction-induced interfacial assembly of grafted Janus nanoparticles. (A) Phase behaviors of interfacial nanostructures. (a) Schematic representations of the transition from the randomly mixed phase to the intercalated phase in the mixtures of grafted Janus nanoparticles. (b–d) Typical interfacial nanoparticle organizations obtained at different stages of the reaction. (B) State diagram of the phase transition. (C) Interaction energy of grafted nanoparticles with solvent beads vs. the distance from the interface. Reproduced from ref. 72; Copyright 2018 American Chemical Society.

Another form of confinement for the nanoparticle self-assembly is a curved space which subjects nanoparticles to geometrical or topological constraints. For instance, through systematically changing the length asymmetry of tethered chains and the Janus balance of nanoparticles, tethered Janus nanoparticles self-assemble into various novel structures, as mapped on a phase diagram in Fig. 8.³³ Through examining the detailed kinetic pathways as well as free energy, the dynamical mechanism for the formation of these structure states is analyzed, indicating the defect-enhanced entropy effect on a curved surface. By modifying the free volume of tethered chains and thereby the conformational entropy, the analytical model that rationalizes the regimes of these structure states is developed, which is found to fit simulations reasonably well and result in a mechanistic interpretation based on the order through entropy. These results shed light on curvature engineering as a versatile strategy to tailor the superstructures formed by anisotropic building blocks toward advantageous properties.³³

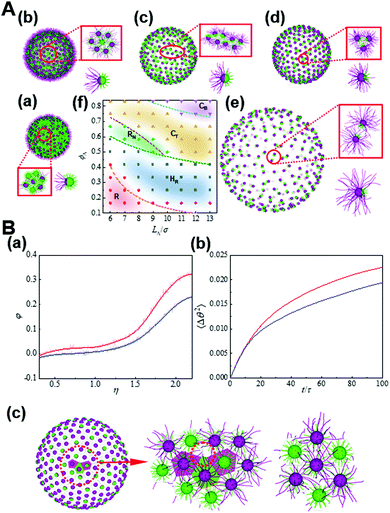Fig. 8 Entropy-driven self-assembly of tethered Janus nanoparticles on a sphere. (A) Typical states formed by the self-assembly of tethered Janus nanoparticles with various anisotropy on spherical surfaces: (a) Random state (R), (b) hexagon with centered reverse (H_R), (c) nanoribbon (R_N), (d) trinary nanocluster (C_T), and (e) binary nanocluster (C_B). (f) Phase diagram. (B) Defect-enhanced entropy effects. (a) φ as a function of η for the nanoparticles on the defects (red) and hexagons (blue). (b) The mean-square angular displacement (MSAD) for the nanoparticles on the defects (red) and hexagons (blue). (c) Voronoi tessellation of the Janus nanoparticles on a spherical surface where the topological defects are marked. Reproduced from ref. 33; Copyright 2021 Elsevier.

The external compression is one important approach to realize the spatial confinement. Under mechanical pressure, the novel entropy mediated-mechanical response behavior of nanoparticles in diblock copolymer scaffolds was demonstrated.²⁵ It is found that external stress can significantly change the hierarchical self-assembly of nanoparticles in block copolymer scaffolds. That is, nanoparticles transform continuously and inversely among various distribution states in their preferred domains. Large nanoparticles are driven by block chains from the domain center to the interface, which is in sharp contrast to the entropy effect in the equilibrium state.²² With the increase of the compression ratio, the minimum of the free energy in the phase domain gradually transfers from the middle to the interface. Theoretical analysis reveals that the compression-induced transition of the nanoparticle distribution can be fundamentally attributed to unique entropic effects originated from the compacted block chains. In addition, through the study of thermal conductivity, we also found that the hierarchical structure of nanoparticles with different distribution states determines well the thermal conductivity of the whole system, resulting in mechanomutable thermal transport properties (Fig. 9).²⁵

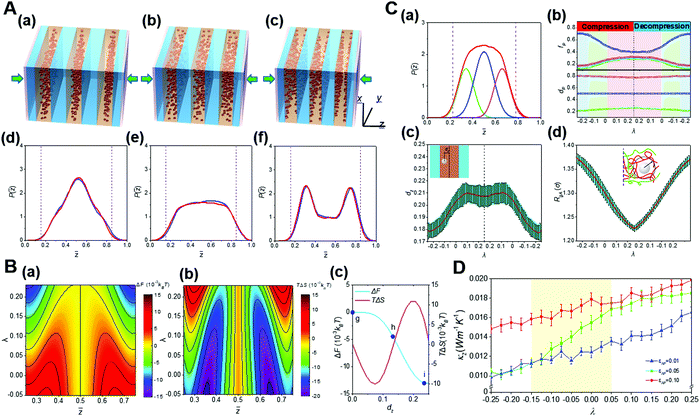Fig. 9 Mechanoresponsive behaviors of the hierarchical nanostructures of block copolymer-based nanocomposites. (A) Structural transition for the hierarchical self-assembly of block copolymer-based nanocomposites under external pressure. (a–c) Diagrams showing the mechanoresponsive spatial transition of nanoparticles inside their preferential domain. (d–f) Distribution of nanoparticles inside their preferential domain upon various compression ratios, λ. (B) Key thermodynamic quantities calculated from the self-consistent field theory (SCFT). (a and b) The contour maps give (a) the free energy change, ΔF, and (b) entropic change, TΔS. (c) ΔF and TΔS as a function of the normalized distance between the centers of the nanoparticle and its preferential domain, d_z. (C) Kinetics of the mechanoresponsive spatial transition of nanoparticles inside their preferential domain. (a) The peak separation of the probability density function of nanoparticles P(z̄) leads to a central peak and two interfacial peaks, corresponding respectively to the local energy minima in the free energy landscape, where P(z̄) is the probability density to find a nanoparticle at the normalized distance in the z-direction. (b) The peak areas, f_p, and peak locations, d_p, obtained from the peak separation as a function of the strain λ. (c) The ensemble-averaged d_zversus λ. (d) The λ dependence of the radius of the gyration of block A, R_gA, for the block segments interacting with nanoparticles, as schemed by the insetting diagram. (D) Dependence of the thermal conductivity, κ_z, for the block copolymer nanocomposites on λ. Reproduced from ref. 25; Copyright 2019 American Chemical Society.

In addition, through organic–inorganic hybridization, molecular construction or self-assembly can perform on the basis of specific interactions at the nano or molecular level to achieve the multiscale combination of organic and inorganic components for giving full play to the characteristics of each component.^63,74 In collaboration with experimental studies, we conducted coarse-grained molecular simulations to demonstrate that the self-assembly of co-clusters can form various superstructures at the fluid interface, which mainly depends on the shape of building blocks. For the Janus co-cluster containing one polyoxometalate (POM) and four polyhedral oligomeric silsesquioxanes (POSS), the building blocks first self-assemble into triangular clusters, and further into hexagonal clusters, and finally into the mesoscale 2D monolayer superlattice with graphene-like honeycomb symmetry. The structure obtained by this hierarchical self-assembly is directly related to the shape of the building blocks, where the shape entropy plays an essential role. In high-density systems, the shape entropy can cause shape-mediated directional entropic forces to maximize the state number of crowded particles. There is no doubt that the shape entropy offers a way to tailor the interface self-assembly of nanoparticles with an anisotropic shape, towards various interfacial nanostructures (Fig. 10).⁷⁵

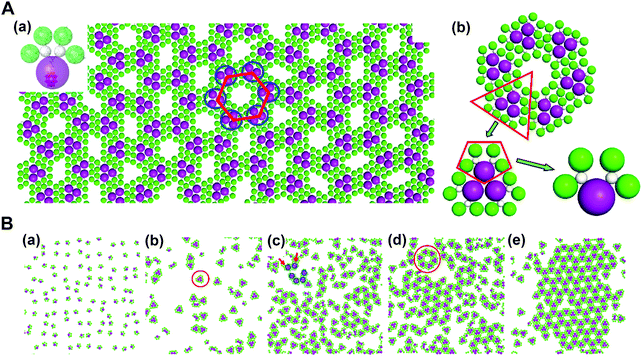Fig. 10 Mesoscale graphene-like honeycomb constructed via the self-assembly of co-clusters. (A) (a) Typical snapshot of the honeycomb superstructure. (b) Hierarchical structure of a honeycomb cell. (B) (a–e) Evolution dynamics of the self-assembly. Reproduced from ref. 75; Copyright 2018 American Chemical Society.

3.2 Biological macromolecular systems

As biological macromolecules are not only the basic structural and functional unit of cells but also the material basis for the research of life phenomena, the research on biological macromolecular systems can significantly prompt our understanding of the life process. Particularly, many functions of biological macromolecular systems are difficult to realize without the contribution of entropy effects, such as the shape entropy in the structural organization of many protein macromolecules with shape anisotropy, the conformational entropy on which the realization of the function of an intrinsically disordered protein depends, and entropy in thermodynamics of the liquid–liquid phase separation of living macromolecular systems.^76–79 It has been recognized that the chain stiffness or flexibility of active macromolecules can be harnessed to tune the entropy–enthalpy balance, which is also identified in biological macromolecular systems. For example, recent research has shown that, with the increase of the DNA chain length, the conformational entropy of chains plays a more important role in the structural organization, and can even determine the type of superlattice structures.⁸⁰ Therefore, we developed and simulated the DNA-functionalized Janus nanoparticles, that is, Janus nanoparticles grafted with long and short DNA chains on their two surface moieties, respectively. The results demonstrate that in addition to the primary nanoparticle crystallization into FCC structure, sequence-specific DNA hybridization events further direct the rotational orientation of Janus nanoparticles functionalized with two types of DNA chains (DNA-JNPs) to diverse secondary crystalline phases (Fig. 11).⁸¹ The crystallization dynamics of such hierarchical crystals is featured by two consequent processes: entropy-dominated translational order for the primary crystalline structure and enthalpy-dominated rotational order for the secondary crystalline structure. These findings might prompt new classes of nanoparticle crystals with designed structures and properties at multiple levels and in a predictable manner.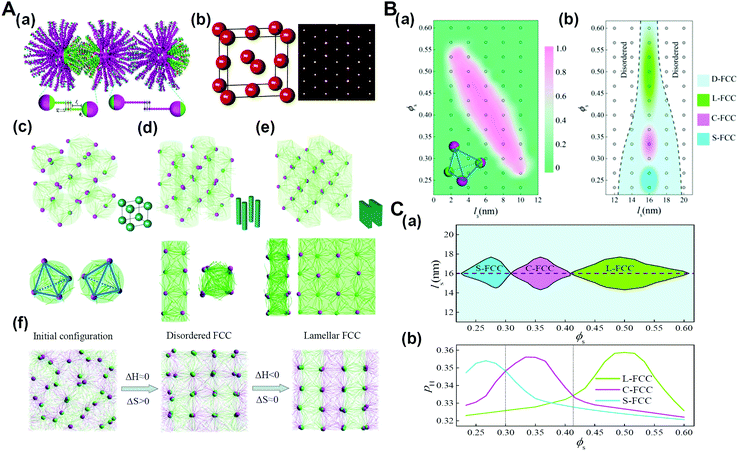

Fig. 11 Hierarchical crystals formed from DNA-functionalized Janus nanoparticles. (A) Hierarchical self-assembly structures. (a) Schematic illustration of the coarse-grained model for DNA-functionalized Janus nanoparticles and their hybridization. (b) Primary crystal structure of DNA-JNPs. (c–e) Secondary crystalline structures at different surface fractions of A-DNA chains, ϕ_s. (f) Representative structures during the formation of L-FCC at different stages. (B) Phase diagrams as a function of the length of the space-bead portion, l_s, and ϕ_s. (a) The fraction of tetrahedral nanoclusters of DNA-JNPs, as depicted by the insetting image, f_T depending on l_s and ϕ_s, where l_s 12 nm. (b) Phase diagram of the hierarchical crystalline structures, where l_s >12 nm. (C) Phase diagram constructed by the complementary contact model. (a) The regions of different secondary crystal structures are determined as a function of l_s and ϕ_s. (b) Two-dimensional “slice” through the plot at l_s = 16 nm in (a). Reproduced from ref. 81; Copyright 2018 American Chemical Society.

4 Conclusions and outlook

Structural organization of particles under confinement is ubiquitous in nature and technology.⁸² What is interesting is that the richness of the phenomena emerging when simple constraints are induced into these systems. The advantage of the general principles of entropic ordering through confinement may lie at that: when the dominant degrees of freedom are constrained, the other degrees of freedom come to the fore, boosting the state numbers and stabilizing new structures. In this review, we introduce how such a relationship between confinement and entropy is controlled to tailor the structural organization of various systems containing particles, including the conformational entropy-mediated self-assembly of Janus nanoparticles at the interface, biological macromolecules, and anisotropic nanoparticles within spherical or cylindrical confinements, where the confinement-mediated entropic effects drive the systems to self-assemble into various unique structures.

Despite the fascinating progress in the past few years, there remain challenges that require interdisciplinary efforts from the fields of experiment, theory, and computer simulations.^83–85 Research on this promising topic is expected to evolve in several directions. For instance, it is necessary to consider various topologies of confinement spaces, such as the confinement-mediated entropic effects in curved spaces where defects of structural organization are inevitable and may exhibit new forms distinguished from those in the plat space.^14,86,87 Although it has been demonstrated that, under confinement due to packing, the shape entropy can drive anisotropic particles to form a variety of crystals, liquid crystals, and even quasicrystals, the rules behind such shape entropy effects and the transition from one crystal structure to another require a more definite elucidation, facilitating engineering entropy for the inverse design of ordered structures from colloidal particles. The other intrinsic physical properties of building blocks, such as the particle size and chain flexibility, may also give rise to new entropic effects under confinement, which need to be further examined. All in all, we expect that the relationship between the confinement and entropy could be engineered as a versatile strategy in the development of designer materials towards advantageous applications.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We thank Xiaobin Dai, Xuanyu Zhang, Duo Xu, Haixiao Wan, Lijun Dai and Xueqing Jin for helpful discussions. We acknowledge financial support from the National Natural Science Foundation of China (Grants No. 22025302 and No. 21873053). L.-T. Y. acknowledges financial support from the Ministry of Science and Technology of China (Grant No. 2016YFA0202500).

References

1. R. Clausius, Ann. Phys., 1865, 125, 353–400.
2. L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659.
3. B. J. Alder and T. E. Wainwright, J. Chem. Phys., 1957, 27, 1208–1209.
4. W. W. Wood and J. D. Jacobson, J. Chem. Phys., 1957, 27, 1207–1208.
5. D. Frenkel, Nat. Mater., 2015, 14, 9–12.
6. G. Zhu, Z. Huang, Z. Xu and L.-T. Yan, Acc. Chem. Res., 2018, 51, 900–909.
7. D. Frenkel, Physica A, 1999, 263, 26–38.
8. G. van Anders, D. Klotsa, N. K. Ahmed, M. Engel and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E4812–E4821.
9. B. de Nijs, S. Dussi, F. Smallenburg, J. D. Meeldijk, D. J. Groenendijk, L. Filion, A. Imhof, A. van Blaaderen and M. Dijkstra, Nat. Mater., 2015, 14, 56–60.
10. D. Wang, T. Dasgupta, E. B. van der Wee, D. Zanaga, T. Altantzis, Y. Wu, G. M. Coli, C. B. Murray, S. Bals, M. Dijkstra and A. van Blaaderen, Nat. Phys., 2021, 17, 128–134.
11. P. F. Damasceno, M. Engel and S. C. Glotzer, ACS Nano, 2012, 6, 609–614.
12. X. Mao, Q. Chen and S. Granick, Nat. Mater., 2013, 12, 217–222.
13. G. Zhu, Z. Xu and L.-T. Yan, Nano Lett., 2020, 20, 5616–5624.
14. V. N. Manoharan, Science, 2015, 349, 1253751.
15. K. K. Frederick, M. S. Marlow, K. G. Valentine and A. J. Wand, Nature, 2007, 448, 325–329.
16. U. Agarwal and F. A. Escobedo, Nat. Mater., 2011, 10, 230–235.
17. C. X. Du, G. van Anders, R. S. Newman and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3892–E3899.
18. C. X. Du, G. van Anders, J. Dshemuchadse, P. M. Modd and S. C. Glotzer, Mol. Simul., 2020, 46, 1037–1044.
19. F. Lu, T. Vo, Y. Zhang, A. Frenkel, K. G. Yager, S. Kumar and O. Gang, Sci. Adv., 2019, 5, eaaw2399.
20. P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457.
21. B. C. Rocha, S. Paul and H. Vashisth, Entropy, 2020, 22, 877.
22. R. B. Thompson, V. V. Ginzburg, M. W. Matsen and A. C. Balazs, Science, 2001, 292, 2469–2472.
23. B. Dong, Z. Huang, H. Chen and L.-T. Yan, Macromolecules, 2015, 48, 5385–5393.
24. Z. Liu, R. Guo, G. Xu, Z. Huang and L.-T. Yan, Nano Lett., 2014, 14, 6910–6916.
25. X. Dai, P. Chen, G. Zhu, Z. Xu, X. Zhang and L.-T. Yan, J. Phys. Chem. Lett., 2019, 10, 7970–7979.
26. G. Xu, Z. Huang, P. Chen, T. Cui, X. Zhang, B. Miao and L.-T. Yan, Small, 2017, 13, 1603155.
27. Z. Huang, C. Lu, B. Dong, G. Xu, C. Ji, K. Zhao and L.-T. Yan, Nanoscale, 2016, 8, 1024–1032.
28. R. Zhang, B. Lee, C. M. Stafford, J. F. Douglas, A. V. Dobrynin, M. R. Bockstaller and A. Karim, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2462–2467.
29. L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139–4142.
30. Y. Geng, G. van Anders, P. M. Dodd, J. Dshemuchadse and S. C. Glotzer, Sci. Adv., 2019, 5, eaaw0514.
31. E. Barry and Z. Dogic, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 10348–10353.
32. C.-H. Tai, G.-T. Pan and H.-Y. Yu, Langmuir, 2019, 35, 16835–16849.
33. G. Zhu, Y. Wang, L. Gao, Z. Xu, X. Zhang, X. Dai, L. Dai, C. Hou and L.-T. Yan, Fundam. Res., 2021, 1, 641–648.
34. H. Lu, F. Yang, B. Liu, K. Zhang, Y. Cao, W. Dai, W. Li and H. Dong, Nanoscale Horiz., 2019, 4, 472–479.
35. A. V. Petukhov, R. Tuinier and G. J. Vroege, Curr. Opin. Colloid Interface Sci., 2017, 30, 54–61.
36. E. S. Harper, G. van Anders and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 16703–16710.
37. S. Belli, A. Patti, M. Dijkstra and R. van Roij, Phys. Rev. Lett., 2011, 107, 148303.
38. V. N. Manoharan, M. T. Elsesser and D. J. Pine, Science, 2003, 301, 483–487.
39. D. Wang, M. Hermes, R. Kotni, Y. Wu, N. Tasios, Y. Liu, B. de Nijs, E. B. van Der Wee, C. B. Murray, M. Dijkstra and A. van Blaaderen, Nat. Commun., 2018, 9, 1–10.
40. R. E. Guerra, C. P. Kelleher, A. D. Hollingsworth and P. M. Chaikin, Nature, 2018, 554, 346–350.
41. M. J. Bowick and L. Giomi, Adv. Phys., 2009, 58, 449–563.
42. J. Lacava, P. Born and T. Kraus, Nano Lett., 2012, 12, 3279–3282.
43. A. Nikoubashman, D. A. Vega, K. Binder and A. Milchev, Phys. Rev. Lett., 2017, 118, 217803.
44. E. G. Teich, G. van Anders, D. Klotsa, J. Dshemuchadse and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E669–E678.
45. X. Dai, X. Zhang, L. Gao and L.-T. Yan, Acta Polym. Sin., 2021, 52, 1076–1099.
46. S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256.
47. H. N. W. Lekkerkerker and R. Tuinier, Colloids and the Depletion Interaction. Dordrecht: Springer, 2011.
48. K. Miyazaki, K. S. Schweizer, D. Thirumalai, R. Tuinier and E. Zaccarelli, J. Chem. Phys., 2022, 156, 080401.
49. R. K. Cersonsky, G. van Anders, P. M. Dodd and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1439–1444.
50. A. Santos, J. A. Millan and S. C. Glotzer, Nanoscale, 2012, 4, 2640–2650.
51. J. Wang, C. F. Mbah, T. Przybilla, B. A. Zubiri, E. Spiecker, M. Engel and N. Vogel, Nat. Commun., 2018, 9, 5259.
52. P. Tan, N. Xu and L. Xu, Nat. Phys., 2014, 10, 73–79.
53. W. T. M. Irvine, M. J. Bowick and P. M. Chaikin, Nat. Mater., 2012, 11, 948–951.
54. W. Poon, Science, 2004, 304, 830–831.
55. G. van Anders, N. K. Ahmed, R. Smith, M. Engel and S. C. Glotzer, ACS Nano, 2014, 8, 931–940.
56. A. V. Petukhov, R. Tuinier and G. J. Vroege, Curr. Opin. Colloid Interface Sci., 2017, 30, 54–61.
57. C. Avendaño and F. A. Escobedo, Curr. Opin. Colloid Interface Sci., 2017, 30, 62–69.
58. G. Zhu, L. Gao, Z. Xu, X. Dai, X. Zhang and L.-T. Yan, Nano Lett., 2021, 21, 8439–8446.
59. C. Hou, G. Zhu, X. Dai, Z. Xu, P. Chen, X. Zhang, L. Gao and L.-T. Yan, Chem. J. Chin. Univ., 2020, 41, 44–48.
60. G. T. Pickett, M. Gross and H. Okuyama, Phys. Rev. Lett., 2000, 85, 3652.
61. L. Fu, W. Steinhardt, H. Zhao, J. E. S. Socolar and P. Charbonneau, Soft Matter, 2016, 12, 2505–2514.
62. H. Rezvantalab, D. J. Beltran-Villegas and R. G. Larson, Phys. Rev. Lett., 2016, 117, 128001.
63. X. Zeng, G. Ungar, Y. Liu, V. Percec, A. E. Dulcey and J. K. Hobbs, Nature, 2004, 428, 157–160.
64. Z. Huang, G. Zhu, P. Chen, C. Hou and L.-T. Yan, Phys. Rev. Lett., 2019, 122, 198002.
65. A. C. Balazs, T. Emrick and T. P. Russell, Science, 2006, 314, 1107–1110.
66. S. S. Sheiko, J. Zhou, J. Arnold, D. Neugebauer, K. Matyjaszewski, C. Tsitsilianis and M. Rubinstein, Nat. Mater., 2013, 12, 735–740.
67. B. J. Kim, J. J. Chiu, G. R. Yi, D. J. Pine and E. J. Kramer, Adv. Mater, 2005, 17, 2618–2622.
68. X. Dai, C. Hou, Z. Xu, Y. Yang, G. Zhu, P. Chen, Z. Huang and L.-T. Yan, Entropy, 2019, 21, 186.
69. J. J. Burgos-Mármol and A. Patti, Polymers, 2021, 13, 1524.
70. H. Gao, S. Bettscheider, T. raus and M. H. Müser, Nano Lett., 2019, 19, 6993–6999.
71. Z. Su, M. Huang and S. Z. D. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 19618–19620.
72. Y. Yang, P. Chen, Y. Cao, Z. Huang, G. Zhu, Z. Xu, X. Dai, S. Chen, B. Miao and L.-T. Yan, Langmuir, 2018, 34, 9477–9488.
73. P. Chen, Y. Yang, B. Dong, Z. Huang, G. Zhu, Y. Cao and L.-T. Yan, Macromolecules, 2017, 50, 2078–2091.
74. R. Liang, J. Xu, R. Deng, K. Wang, S. Liu, J. Li and J. Zhu, ACS Macro Lett., 2014, 3, 486–490.
75. X.-S. Hou, G.-L. Zhu, L.-J. Ren, Z.-H. Huang, R.-B. Zhang, G. Ungar, L.-T. Yan and W. Wang, J. Am. Chem. Soc., 2018, 140, 1805–1811.
76. M. R. Jones, R. J. Macfarlane, B. Lee, J. Zhang, K. L. Young, A. J. Senesi and C. A. Mirkin, Nat. Mater., 2010, 9, 913–917.
77. J. M. Robert, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Science, 2011, 334, 204–208.
78. I. N. Ting, G. Li, R. Sknepnek and M. O. de la Cruz, J. Am. Chem. Soc., 2013, 135, 8535–8541.
79. Y. Du, H. Wang, L. Chen, Q. Fang, B. Zhang, L. Jiang, Z. Wu, Y. Yang, Y. Zhou, B. Chen, J. Lyu and Z. Wang, Mol. Biosci., 2021, 8, 614443.
80. R. V. Thaner, Y. Kim, T. I. N. G. Li, R. J. Macfarlane, S. T. Nguyen, M. O. de la Cruz and C. A. Mirkin, Nano Lett., 2015, 15, 5545–5551.
81. G. Zhu, Z. Xu, Y. Yang, X. Dai and L.-T. Yan, ACS Nano, 2018, 12, 9467–9475.
82. M. J. Solomon, Langmuir, 2018, 34, 11205–11219.
83. A. A. Klishin and G. van Anders, Soft Matter, 2020, 16, 6523–6531.
84. P. S. Mohanty, P. Bagheri, S. Nöjd, A. Yethiraj and P. Schurtenberger, Phys. Rev. X, 2015, 5, 011030.
85. S. D. Allen, S. Bobbala, N. B. Karabin and E. A. Scott, Nanoscale Horiz., 2019, 4, 258–272.
86. W. T. M. Irvine, V. Vitelli and P. M. Chaikin, Nature, 2010, 468, 947–951.
87. G. Meng, J. Paulose, D. R. Nelson and V. N. Manoharan, Science, 2014, 343, 634–637.

---

Footnote

† These authors contributed equally.

---