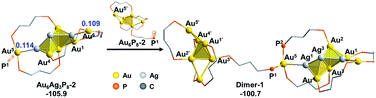Mechanistic insights into Ag⁺ induced size-growth from [Au₆(DPPP)₄]²⁺ to [Au₇(DPPP)₄]²⁺ clusters

Abstract

The size conversion of atomically precise metal nanoclusters lays the foundation to elucidate the inherent structure–activity correlations on the nanometer scale. Herein, the mechanism of the Ag⁺-induced size growth from [Au₆(dppp)₄]²⁺ to [Au₇(dppp)₄]³⁺ (dppp is short for 1,3-bis(diphenylphosphino)propane) is studied via density functional theory (DFT) calculations. In the absence of extra Au sources, the one “Au⁺” addition was found to be regulated by the Ag⁺ doping induced Au-activation, i.e., the formation of formal Au(I) blocks via the Ag⁺ alloying processes. The Au(I) blocks could be extruded from the core structure in the formed Au–Ag alloy clusters, triggering a facile Au⁺ migration to the Au₆ precursor to form the Au₇ product. This study sheds light on the structural and stability changes of gold nanoclusters upon the addition of Ag⁺ and will hopefully benefit the development of more metal ion-induced size-conversion of metal nanoclusters.

---

Introduction

The stimuli response upon exposure to extra metal ions represents an attractive characteristic of metal nanoclusters.^1–8 The structural response may be reflected in the complexation of the metal ion(s) with the surface ligands,^9–11 the doping/exchange/addition of the metal ion(s) into the metallic framework of the cluster,^12–15 the slightly changed structure with a different charge state¹⁶ or the re-arrangement of the entire cluster structure.^17–20 Moreover, enhanced physicochemical properties (such as thermostability) and novel applications^21–23 could be achieved due to the synergistic effect.

Associated with the experimental outcomes, the atomic precision, spectroscopic characterization, and theoretical simulations have greatly improved our mechanistic understanding on these reactions. For example, the [M⁺] − Cl (M = Ag/Cu) interactions of the M⁺ with the vertex AuCl moiety of the rod-shaped Au₂₄(SR)₅(PR₃)₁₀Cl₂ were found to be a dominating effect to initiate the single atom addition, and thus, the formation of the rod-shaped Au₂₄M(SR)₅(PR₃)₁₀Cl₂ clusters.²⁴ The Cs–S/O and cation–π interactions are pivotal to the Cs⁺ induced one-dimensional linear assembly of Ag₂₉(SSR)₁₂(PPh₃)₄.²⁵ In addition, the anti-galvanic mechanism was proposed to account for the cation-stimulated alloying.^26–28 Nevertheless, the reported mechanistic study mainly focuses on the metal ion-induced alloying/assembly, while the mechanistic details on the ion “catalyzed” size conversion of nanoclusters (Ag⁺ induced [Au₆(dppp)₄]²⁺ to [Au₇(dppp)₄]³⁺ and Cu²⁺ induced Au₂₅(PET)₁₈ → Au₄₄(PET)₁₈)^18,23 have been largely unknown.

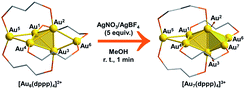
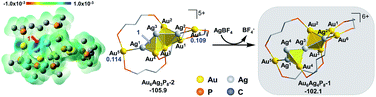
Intrigued by the fantastic foreign metal effect,^29–31 we sought to perform a detailed mechanistic study on the Ag⁺ induced reaction of [Au₆(dppp)₄]²⁺ → [Au₇(dppp)₄]³⁺ with density functional theory (DFT) calculations. According to Konishi's experiments,¹⁸ [Au₆(dppp)₄]²⁺ transformed into [Au₇(dppp)₄]³⁺ within one minute after 5 molars equivalent AgBF₄ was added. According to single-crystal structure analysis, [Au₆(dppp)₄]²⁺ comprises a bi-capped tetrahedral skeleton. The tetrahedral Au atoms (Au^1–4) are each protected by one P hand of the dppp ligand, while the two-terminal Au atoms (Au^5,6) are each protected by two P hands from two dppp ligands. The framework of [Au₇(dppp)₄]³⁺ is similar to that of [Au₆(dppp)₄]²⁺, except for the addition of one formal Au⁺, and the re-arrangement of one dppp ligand (one P coordination on the Au⁶ atom migrates to coordinate to Au⁷).

According to the DFT calculation results, the addition of Ag⁺ on clusters favorably generates the alloy structure with higher nucleation (i.e. with more tetrahedral and triangular blocks in the core structure). The incorporated Ag⁺ induced activation of the exterior Au atoms in the metal framework, resulting in an easy structural tautomerization therein. This proposal correlates with the heavily doping-induced size-rearrangement of metal nanoclusters in recent studies^27,32 and will be hopefully applicable to other alloying systems (Scheme 1).¹⁸

Scheme 1 The Ag⁺ induced size-conversion of [Au₆(dppp)₄]²⁺ to [Au₇(dppp)₄]³⁺. The phenyl groups on the P atoms of dppp and the counter anion were omitted in both clusters. Color legends: Au, gold; P, orange; C, gray; H, omitted.

Results and discussion

Throughout this study, the experimentally used dppp ligands (i.e. bis(diphenylphosphino)propane) were simplified with dmpp (i.e. bis(dimethylphosphino)propane ligands) to reduce computational costs. Similar structural simplification has also been used in recent studies.^33,34

The doping of Ag⁺ in Au₆P₈ clusters

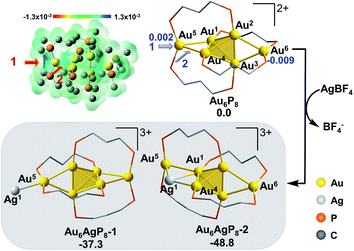
The formula of Au₆P₈ is differentiated from Au₇P₈ by only one Au⁺, which is unlikely to be released directly from the Au₆P₈ precursor. To this end, the dissociation of Au⁺ is anticipated to be induced by the Ag⁺ doping of Au₆P₈. Given the high activity of the mono-nuclear, cationic Au⁺ species, the generation of Au⁺ from the gold cluster precursors is designated as the activation of the Au atom. Of note, the Ag⁺ alloying-induced activation of the “Au” site(s) correlates with the general concept of anti-galvanic reduction.²⁶ Using Ag⁺ as a dopant, we considered the possible configurations and energy demands for successive doping procedures.

Considering the structural symmetry and the Fukui function analysis (f⁻, Fig. 1)³⁵ of the Au₆P₈ precursor, the terminal Au^5/6 atom, Au^1/4-Au⁵ bond, and Au^2/3-Au⁶ bond are the most labile sites for the electrophilic attack of the first Ag⁺. In this study, the isodesmic reaction of NCⁿ⁺ + AgBF₄ → [NCAg]⁽ⁿ⁺¹⁾⁺ + BF₄⁻] (NC denotes the reaction precursor for the Ag⁺ addition steps) was used to determine the reaction energy of the Ag⁺ addition steps. As shown in Fig. 1, the addition of the first Ag⁺ could possibly generate Au₆AgP₈-1 and Au₆AgP₈-2, and the suffix of −1/−2 denotes the isomeric products via adding Ag⁺ on different sites. Both two doping processes are thermodynamically highly feasible. Nevertheless, adding an exterior Ag⁺ makes little perturbation on the Au⁶ skeleton in the former case, but results in a stretched core structure in the latter case (Fig. 1 and S1†). From Fig. 1, the Au⁴–Au⁵ bond insertion is significantly more feasible than the Au⁵-binding mode (−48.8 vs. −37.3 kcal mol⁻¹). Alternatively, Ag⁺ is more likely to be reduced by Au₆; that is, Ag⁺ is incorporated into the core sites to form a highly coordinated structure (the coordination number³⁶ of Ag¹ in Au₆AgP₈-1 and Au₆AgP₈-2 is 1 and 3; please see ESI† for more details), and thus Au₆AgP₈-2 is preferentially formed.

Fig. 1 The isosurface of the f⁻ for Au₆P₈, using the width of Gaussian function of 0.01 au, and the energy (in kcal mol⁻¹) and structural change for the doping of first Ag⁺ into Au₆P₈. The Hirshfeld charge of Au^5/6 in the starting structure is given in blue and bold.

According to the Hirshfeld charge analysis, the charge state of the terminal Au^5/6 in Au₆P₈ (0.002/−0.009, Table S1†) is slightly higher than that of the tetrahedral Au (avg. −0.030). By contrast, the charge of Au⁵ in Au₆AgP₈-1 and Au₆AgP₈-2 (0.055 and 0.057) is significantly more positive than that of tetrahedral Au atoms (avg. −0.012) and becomes closer to the charge of Au in the Au₂(dppp)₂Cl₂³⁷ complex (0.082). The results unambiguously demonstrate the improved positive charge of the Au⁵ atom after Ag⁺ incorporation, and thus the higher reactivity for bond dissociation (due to the increased electrostatic repulsion between the cationic metal centers). In other words, the incorporation of Ag⁺ activates the core Au atoms, particularly in the corner sites.³⁸ Of note, compared to the aforementioned Ag⁺-addition processes, the metal exchange of Ag with Au in Au₆P₈ is thermodynamically much more disfavored (Scheme S1†). Therefore, the metal exchange pathways were not examined in the following section.

According to the Fukui function analysis, the most nucleophilic sites of Au₆AgP₈-2 are located in the region nearby Au⁵ and Au⁶ atoms (Fig. 2). Accordingly, we examined four possible binding modes of the second Ag⁺.

Fig. 2 The isosurface of the f⁻ for Au₆AgP₈-2, using the width of Gaussian function of 0.01 au and the energy (in kcal mol⁻¹) and structural changes for the doping of second Ag⁺ into Au₆AgP₈-2. The Hirshfeld charge of Au^5/6 in the starting structure is given in blue and bold.

As shown in Fig. 2, the activation of the terminal Au⁵ could occur via the addition of Ag⁺ on the site 1 of Au⁵ or site 2 of attacking the Au²–Ag¹ bond to form the isomeric Au₆Ag₂P₈-1 and Au₆Ag₂P₈-2, respectively. Similarly, the corner Au⁶ could be possibly activated via Ag⁺ insertion into the space behind (site 3) or in front (site 4) of the butterfly-like Au^1/4-Au²-Au³-Au⁶ structure to form Au₆Ag₂P₈-3 or Au₆Ag₂P₈-4.

The results indicate that the binding of second Ag⁺ (i.e. Ag²) directly on Au⁵ makes little perturbation on the framework, correlating with the results of Au₆P₈ + AgBF₄ → Au₆AgP₈-1 + BF₄⁻ (Fig. 1). Nevertheless, the reaction energy is remarkably higher (−5.4 kcal mol⁻¹ in Au₆AgP₈-2 + AgBF₄ → Au₆Ag₂P₈-1vs. −37.3 kcal mol⁻¹ in Au₆P₈ + AgBF₄ → Au₆AgP₈-1 + BF₄⁻), implying that the structure of the precursor is pivotal to the facilitation of alloying. Moreover, the attack of Ag² to Ag¹ resembles a synergistic bi-molecular electrophilic reaction mechanism as the Au¹ atom migrates from cis-to trans-configuration (refer to Au⁴) around the Au²–Au³ bond spontaneously during the geometry optimization (see Fig. S2† for the details). The formation of Au₆Ag₂P₈-2 from Au₆AgP₈-2 is exothermic by 30.7 kcal mol⁻¹. Besides, the approaching of Ag² to either Au¹–Au²–Au³–Au⁶ or Au⁴–Au²–Au³–Au⁶ results in a core-structure re-organization, predominantly via incorporating Ag¹ into the tetrahedral blocks and forming the face-sharing tri-tetrahedral structure. Due to the meta-orientation of the two Ag⁺ and the symmetry of the tri-tetrahedral core structure, the relative energy and the M-P framework of the formed Au₆Ag₂P₈-3 are almost the same as those of Au₆Ag₂P₈-4. Both steps are highly exothermic (−44.8 and −45.1 kcal mol⁻¹). Through the structural re-organization, the reduced coordination number of Au⁵ and Au⁶ (compared to the related one in the precursor) is overwhelmed by the extra stability associated with the formation of a larger metallic core structure. Therefore, the formation of Au₆Ag₂P₈-3/4 is favored over that of Au₆Ag₂P₈-1/2.

Comparing the optimized geometries of Au₆AgP₈-2 and Au₆Ag₂P₈-3/4, we found that the bond distance between the Au⁵/Au⁶ and the core metal atoms is significantly lengthened after incorporating the second Ag⁺. Moreover, the charge on Au⁵/Au⁶ atoms becomes more positive (Au₆AgP₈-2: 0.057/0.035 → Au₆Ag₂P₈-2: 0.086/0.083, Table S1†), and is comparable to that of the aforementioned Au(I) complex (0.082). The results indicate the formation of a formal Au(I) center on the cluster, and thus, the enhanced activity for the nucleophilic coordination and Au–Au dissociation (the charge of the other Au atoms also becomes more positive, Table S1†). Nevertheless, the alloying with Ag⁺ remains thermodynamically feasible, and therefore, we examined the energetics for further doping of Ag⁺ in the target system.

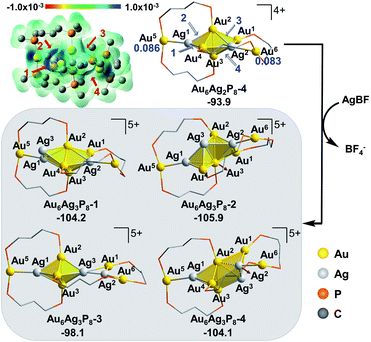
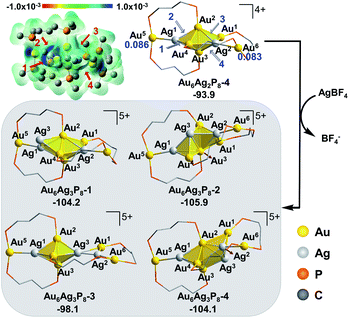
In view of the preferential core expansion via Ag⁺ doping (over the Ag addition steps), we mainly examined the core-expansion pathways from Au₆Ag₂P₈-4. As shown in Fig. 3, the third Ag-doping process leads to four possible Au₆Ag₃P₈ isomers. The third Ag⁺ (i.e. Ag³) could possibly attack site 1 of the Ag¹–Au⁴ bond, site 2 of the Au²–Ag¹ bond, site 3 of the Au²–Ag² bond, and site 4 of the Ag²–Au³ bond, forming Au₆Ag₃P₈-1, Au₆Ag₃P₈-2, Au₆Ag₃P₈-3, and Au₆Ag₃P₈-4, respectively. The approaching of Ag³ into the Ag¹–Au⁴ bond internalizes Ag³ into the left tetrahedral Ag¹Au^2,3,4 block, forming a square pyramid (Ag^1,3Au^2,3,4) therein. Moreover, the approaching of Ag³ to the Au²–Ag¹ bond results in the enlargement of the Au²–Au³–Ag¹/Au⁴ bond angle, and the incorporation of Ag³ to form two vertex-sharing tetrahedral blocks (see Fig. S3† for the partial optimization energy profile). The approaching of Ag³ to the Au²–Ag² bond leads to the extrusion of the Au¹–Au² bond from the metallic core structure, resulting in the formation of a face-sharing bi-tetrahedral block with a vertex-sharing triangular Au¹Ag^2,3 unit (Au₆Ag₃P₈-3). The attack of Ag³ on the Ag²-Au³ bond results in the formation of a distorted square-pyramid Au^2,3Ag^2,3,4 block, and the cleavage of the Au¹/Ag²–Au³ bonds. In the formed Au₆Ag₃P₈-4, the new-formed square-pyramid shares one facet with the original left tetrahedron. According to the calculation results, the four types of Ag⁺ insertion steps are exothermic by 10.3, 12.0, 4.2, and 10.2 kcal mol⁻¹, respectively.

Fig. 3 The f⁻ isosurface of Au₆Ag₂P₈-4, using the width of Gaussian function of 0.01 au, and the energy (in kcal mol⁻¹) and structure change after doping of the third Ag⁺ into Au₆Ag₂P₈-4. The Hirshfeld charge of Au^5/6 in the starting structure is given in blue and bold.

The slightly higher energy of Au₆Ag₃P₈-3 than the other isomers is predominantly caused by the lower cohesive degree of the whole metal skeleton³⁹ (the average coordination number of the metal atoms is 3.4/3.4/3.1/3.3 for Au₆Ag₃P₈-1/2/3/4, see details in Table S2†).³⁶ In addition, the comparable energies of Au₆Ag₃P₈-1, Au₆Ag₃P₈-2, and Au₆Ag₃P₈-4 indicate the competitive Ag⁺ doping sites. For clarity reasons, the following analysis and discussions mainly refer to the most stable intermediate Au₆Ag₃P₈-2.

According to Hirshfeld charge analysis, the doping with the third Ag⁺ further enhances the electron deficiency of the Au⁵/Au⁶ atoms (with the charge of 0.114/0.109, compared to the charge of 0.086/0.083 in Au₆Ag₂P₈-4, Table S1†). Moreover, the average charge of the Au₄Ag_n (Au₄ denotes the tetrahedral Au₄ block in the Au₆ reactant, and n = 1–4) blocks also significantly increases with the doping with the third Ag⁺ (Au₆P₈: −0.030 → Au₆AgP₈-2: −0.012 → Au₆Ag₂P₈-4: 0.019 → Au₆Ag₃P₈-4: 0.070), resulting in critically increased electrostatic repulsion within the metal skeleton and the reduced stability. This is also the reason why the Ag⁺ doping becomes less feasible after each doping process (the first, second, and third Ag⁺ doping steps are exothermic by −48.8, −45.1, and −12.0 kcal mol⁻¹).

Starting from Au₆Ag₃P₈-2, the fourth Ag⁺ (i.e. Ag⁴) could be capped on the Ag^1,3Au⁴ facet as the maximum of f⁻ appears above the Ag^1,3Au⁴ facet, and then the four-Ag⁺-doped product Au₆Ag₄P₈-1 was formed.

The incorporation of Ag⁴ also resembles a synergistic bi-molecular electrophilic reaction mechanism, similar to the reaction of Au₆AgP₈-2 + AgBF₄ → Au₆Ag₂P₈-2. When the Ag⁴ atom is capped on the bare Ag^1,3Au⁴ facet, the Au³ atom leaves the back capping site (on the Ag^1,3Au⁴ facet) with the right part of the face-sharing bi-tetrahedron remaining. Distinct from the aforementioned exothermic doping processes in the 1–3 Ag⁺ incorporation steps, adding the fourth Ag⁺via this pathway was endothermic by 3.8 kcal mol⁻¹ (Fig. 4). In other words, the incorporation of the fourth Ag⁺ is thermodynamically disfavored. The reason is mainly ascribed to the significantly enhanced electrostatic repulsion among the metal atoms (the average Hirshfeld charge of the metal atoms in the Au₄Ag_n core is 0.112 for Au₆Ag₄P₈-1). Throughout the Ag-doping pathway, Ag⁺ favors the core site of Au₆Ag_n and leads to the oxidation of Au atoms (i.e. Au^5,6). As shown in Scheme S2,† the contribution of Ag⁺ to the HOMO of Au₆Ag_n (n = 0, 1, 2, and 3) increased remarkably with the increased doping number of Ag⁺ (Au₆: 0.00%, Au₆Ag: 21.74%, Au₆Ag₂: 41.27%, and Au₆Ag₃: 43.05%). In combination with the Fukui function analysis (Fig. 1–4), the Au sites adjacent to Ag atoms are the active sites for the electrophilic attack of the incoming-Ag⁺.

Fig. 4 The isosurface of the f⁻ for Au₆Ag₃P₈-2, using the width of Gaussian function of 0.01 au, and the energy (in kcal mol⁻¹) and structure changes after doping of the fourth Ag⁺ into Au₆Ag₃P₈-2. The Hirshfeld charge of Au^5/6 in the starting structure is given in blue and bold.

Size-growth by the dimerization of Au₆Ag₃P₈-2

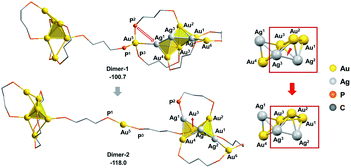
According to the aforementioned results and discussion, the successive addition of Ag⁺ on Au₆P₈ favorably generates the alloy structure with a higher degree of nucleation (i.e. with more tetrahedral and triangular blocks in the core structure).⁴⁰ Meanwhile, the most plausible doping number of Ag⁺ is 3 (Au₆P₈ + 3 AgBF₄ → Au₆Ag₃P₈-2 + 3 BF₄⁻), wherein the metallic core has been largely activated due to the strong electrostatic repulsion therein (most Au atoms show Au(I) character, Table S1†). In this context, the terminal Au⁵ and Au⁶ atoms are the most labile sites for the subsequent reactions because of the relatively lower steric hindrance and the higher electron deficiency (compared to all other metal sites). For this reason, the Au⁵ (or Au⁶) in Au₆Ag₃P₈-2 is used as the [Au]⁺ source to react with the Au₆P₈ cluster precursor to form Au₇P₈.

Of note, the direct approaching of Au₆Ag₃P₈-2 to Au₆P₈ is precluded due to the high inter-cluster steric hindrance (see Fig. S4;† note: the steric hindrance would be much higher for the experimental dppp protected system). In this context, a prior Au⁵–P dissociation on Au₆P₈ (Au₆P₈ → Au₆P₈-2, see Fig. S5†) might occur first to release the steric hindrance.³⁴ After that, the nucleophilic attack of P¹ to Au⁵ occurs with the formation of Dimer-1 (Fig. 5), and this step is slightly endothermic by 5.2 kcal mol⁻¹. By contrast, the coordination of P¹ to the Au⁶ atom is thermodynamically slightly less disfavored (6.7 kcal mol⁻¹, Scheme S3†); thus, its subsequent transformations were omitted for clarity reasons. The P–Au bonding makes no obvious influence on the framework of both cluster precursors. To this end, the endothermicity might be caused by the high steric hindrance around the over-protected Au⁵ (coordination number: 4, with three P-coordination).

Fig. 5 The energy (in kcal mol⁻¹) and structural changes after the reaction of Au₆P₈-2 with Au₆Ag₃P₈-2. The labels Auⁿ and Auⁿ’ denote the same Au sites from the two Au₆P₈ reactants. The Hirshfeld charge of terminal Au is given in blue and bold.

Given the high steric hindrance around Au⁵, the adjacent bare Ag¹ in Dimer-1, and the easiness for 1,2 P migration in cluster systems,^41–43 we examined the possibility of a 1,2-P² migration from Au⁵ to Ag¹. The kinetic analysis by partial optimization (via gradually shortening the P²–Ag¹ bond distance; see Fig. S6† for details) demonstrates the gradual bond cleavage of Au⁵–Ag¹ and Au³–Ag² bonds. As a result, the triangular bi-pyramidal block of Au^1,2,3Ag^2,3 (Fig. 6, inset) tautomerizes into a twisted square pyramid. The energy curve indicates a low energy barrier (12.4 kcal mol⁻¹, Fig. S6†), which could be easily overcome under the experimental condition (i.e. room temperature).¹⁸ Meanwhile, due to the released steric hindrance around the Au⁵ atom, the concerned P²-migration from Dimer-1 to Dimer-2 is exothermic by 17.3 kcal mol⁻¹.

Fig. 6 The energy (in kcal mol⁻¹) and structural changes after the P²-migration of Dimer-1, and the details of the tautomerized core structure.

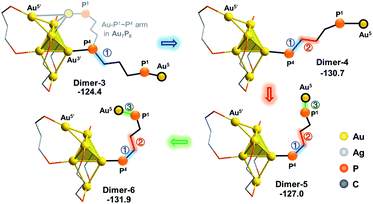
As the square pyramid block has been found to be less stable than the triangular bipyramid block (Au₆Ag₃P₈-1vs.Au₆Ag₃P₈-2, Fig. 3), we further examined an isomerization of Dimer-2via changing the square pyramidal block into a triangular bi-pyramidal one (Dimer-3 in Fig. 7).⁴⁰ This isomerization was found to occur easily via lengthening the Au¹–Au³ bond distance, with a barrier of 8.0 kcal mol⁻¹ (Fig. S7†). The relative energy of Dimer-3 is lower than that of Dimer-2 by 6.4 kcal mol⁻¹, demonstrating the thermodynamic facility of this step.

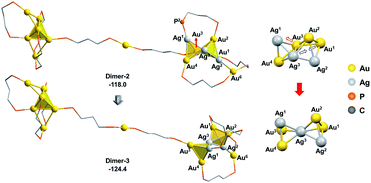Fig. 7 The isomerization of the alloy core in Dimer-2. The relative energies are given in kcal mol⁻¹. The methyl groups on the dmpp ligands and all H atoms are omitted for clarity reasons.

From Dimer-3, the approaching of the Au⁵ atom to the Au₆ block is requisite to forming the target Au₇ structure, which could be regulated by a series of single bond rotation processes of the related dmpp ligand (Dimer-3 → Dimer-6 in Scheme 2; see Fig. S8† for the details). Throughout the transformations, the structure of the alloy moiety is preserved, and the system energy is decreased by 7.5 kcal mol⁻¹.

Scheme 2 Illustrative diagram for the structural tautomerization of the transformation of Dimer-3 to Dimer-6 (the relative energies are given in kcal mol⁻¹). The alloy block away from Au⁵ was omitted for clarity reasons.

From Dimer-6, the target Au₇ block of Au₇P₈ could be formed via the binding of Au⁵ to the Au^{1’,4’,5’} facet of the Au₆ block, and the dissociation of the Au⁵–P³ bond (Fig. 8). According to the calculation results, the binding of Au⁵ is exothermic by 3.2 kcal mol⁻¹ and occurs with a very low barrier of <5 kcal mol⁻¹ (Fig. S9†). From Dimer-7, the Au⁵–P³ cleavage occurs to generate Au₇P₈ and a by-product Au₅Ag₃P₈. In contrast, the progress of moving an Ag⁺ from Au₆Ag₃P₈-3 to Au₆P₈ to generate Au₆AgP₈ is thermodynamically less feasible (−18.7 kcal mol⁻¹, see exothermic by only 2.3 kcal mol⁻¹. The total reaction energy of Au₆P₈ + Au₆Ag₃P₈-3 → Au₇P₈ + Au₅Ag₃P₈ is −31.4 kcal mol⁻¹. See Scheme S3† for more details), demonstrating that the alloy cluster after Ag⁺ doping is a good [Au]⁺ donor, but not a good [Ag]⁺ donor.

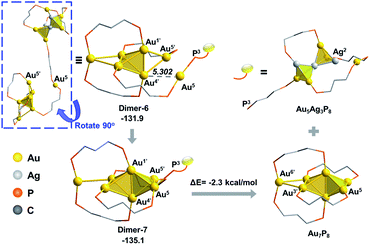Fig. 8 The formation of the Au₇ skeleton from Dimer-6 to Dimer-7 and the subsequent Au⁵–P³ cleavage step. The relative energies are given in kcal mol⁻¹.

Due to the lack of experimental evidence and the complexity of the reaction system, we are not able to confirm the final state of Ag at this stage. However, in view of the bare Ag² atom and the dangling P³ atom, we assumed that Au₅Ag₃P₈ could possibly undergo the P³–Ag² coordination to generate a more stable intermediate. The calculation results (Au₅Ag₃P₈ → Au₅Ag₃P₈-2, Scheme S4†) indicate this step to be highly feasible (exothermic by 26.8 kcal mol⁻¹). In particular, after the Au–P coordination, the Au₆ atom was further extruded from the metallic core and could possibly act as the second “[Au]⁺” source to regulate the second Au₆P₈ → Au₇P₈ conversion. The formed Au₄Ag₃P₈ could undergo further Ag–P coordination (Scheme S4†) or comprehensive nucleation/decomposition processes. Due to the complexity of the target reaction system, the details for the conversion of Au₅Ag₃P₈ are still ambiguous and deserve more studies.

Experimentally, AgBF₄ was not largely excessive, and thus, the transformation from Au₆P₈ to Au₇P₈ might deviate from a pseudo-first-order reaction. Hence, the reaction pathways using Au₆AgP₈-2 and Au₆Ag₂P₈-4 as [Au⁺] sources were also examined. As shown in Scheme S5,† the Au⁺ migration from Au₆AgP₈-2 or Au₆Ag₂P₈-3 to the Au₆ skeleton was as feasible as that from Au₆Ag₃P₈-3 (energy demands are all lower than 15 kcal mol⁻¹). According to the aforementioned results and discussion, the Ag⁺ induced size conversion from Au₆P₈ to Au₇P₈ could occur via a series of competitive pathways. For clarity, the most feasible pathway deduced in this study is shown in Scheme 3 (the relative energies are given with the reference states of Au₆P₈ and AgBF₄).

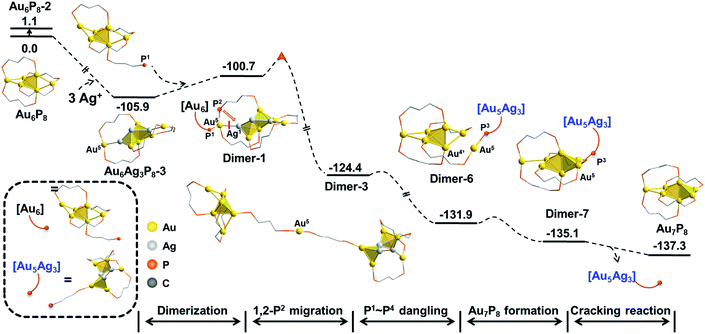Scheme 3 The total energy profile of Ag⁺ catalyzed size-growth of Au₆P₈ to Au₇P₈. The relative energies are given in kcal mol⁻¹.

In this mechanism, the continuous doping of Au₆P₈ clusters with Ag⁺ (dominant doping product: Au₆Ag₃P₈-2) activates the terminal Au atoms and generates the [Au]⁺ source for subsequent size conversion. After that, Au–P coordination between the dangling phosphine ligand of the Au₆ precursor and the formal [Au⁺] occurs, followed by the intramolecular migration of [Au⁺] through a series of isomerization steps (on the diphosphine ligand). Finally, the Au₇P₈ product is formed via the Au–P dissociation and the release of the alloy cluster block. Albeit the comprehensive calculations, the experimental evidence for the proposed mechanism is still lacking, predominantly due to the rapid reaction rate and the lability of the formed [Au₇(dppp)₄](BF₄)₃ to convert to [Au₈(dppp)₄Cl₂].^33,34 Moreover, some other mechanistic possibilities, such as the formation of the target Au₇ products via the reaction of one alloy intermediate with another one, could not be excluded.

Computational details

The modeling clusters were constructed by simplifying the dppp ligands with dmpp ligands. Geometry optimization of all species was performed with Dmol³ software⁴⁴ with the generalized gradient approximation^45–47 Perdew–Burke–Ernzerhof functional.^48–50 Effective core potentials and double numerical orbital basis group + orbital polarization function (DNP) base groups (Basic 4.4) were chosen with the values of 2 × 10⁻⁵ Ha for total energy, 0.004 Ha Å⁻¹ for force, 0.05 Å for displacement, and 1 × 10⁻⁵ Ha for the self-consistent field (SCF) computation criterion. Following the recent studies,^51–54 the constrained structural optimization strategy is used in evaluating the barrier of the elementary steps. Based on the optimized structures, the solution-phase single point energy calculations were conducted with the COSMO^55,56 model, using methanol as the solvent (corresponding to Konishi's experimental conditions¹⁸). Unless otherwise specified, the solution-phase binding energy (in kcal mol⁻¹) was used to determine the energy changes of all steps. The Fukui function of the f⁻ evaluated using finite difference approximations and the orbital composition analysis of the metal skeleton was calculated with Multiwfn version 3.8.^35,57,58

Conclusions

Herein, a plausible mechanism for the Ag⁺ induced conversion from [Au₆(dppp)₄]²⁺ to [Au₇(dppp)₄]³⁺ was proposed with DFT calculations. The size growth starts with the successive doping of Ag⁺ (preferentially adopts high nucleation), associated with the gradual formation of formal Au(I) on terminal sites and the weakened metal–metal bonding interactions. In this context, the release of the terminal Au atom (i.e. the activated Au(I) atom) to the Au₆ precursor occurs easily to generate the Au₇ cluster product, while the alloy cluster could further function as a “Au(I)” donor to regulate another group of the Au₆P₈ → Au₇P₈ conversion. Due to the complexity of the target reaction system, the full details on the overall size growth remain to be established. Nevertheless, the mechanism insights, such as the preferential doping site of Ag⁺ on the cluster precursor (on the most nucleophilic site, and favorably forms structures with a higher degree of nucleation), the activation of exterior Au atom(s) via the gradual incorporation of Ag⁺ (i.e. formation of formal Au(I) and its subsequent dissociation, re-assembly, etc.), and the easy structure tautomerization in the metallic core and the diphosphine ligands, will be helpful for understanding the inherent correlation between different nanoclusters and their alloying reactivity in future studies.

Author contributions

H. Y. conceived and supervised the project. Y. L. carried out the experimental planning, simulations, and data analysis. X. W. and S. H. provided constructive suggestions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support from National Science Foundation of Anhui Province (2108085J08), The University Synergy Innovation Program of Anhui Province (GXXT-2021-023), 2021 university scientific research projects of Anhui Province (YJS20210031), and the technical support of high-performance computing platform of Anhui University. Supercomputing facilities were provided by the Hefei Advanced Computing Center.

Notes and references

1. A. George, A. Sundar, A. S. Nair, M. P. Maman, B. Pathak, N. Ramanan and S. Mandal, J. Phys. Chem. Lett., 2019, 10, 4571–4576.
2. S. Li, Z. Y. Wang, G. G. Gao, B. Li, P. Luo, Y. J. Kong, H. Liu and S. Q. Zang, Angew. Chem., Int. Ed., 2018, 57, 12775–12779.
3. Z. J. Guan, F. Hu, J. J. Li, Z. R. Wen, Y. M. Lin and Q. M. Wang, Isomerization in Alkynyl-Protected Gold Nanoclusters, J. Am. Chem. Soc., 2020, 142, 2995–3001.
4. L. L. Yan, L. Y. Yao, M. Ng and V. W. Yam, J. Am. Chem. Soc., 2021, 143, 19008–19017.
5. J. M. Lopez-de-Luzuriaga, M. Monge, M. E. Olmos, J. Quintana and M. Rodriguez-Castillo, Inorg. Chem., 2019, 58, 1501–1512.
6. Y. Zhao, M. Yu, C. Liu, S. Li, Z. Li, F. Jiang, L. Chen and M. Hong, J. Mater. Chem. C, 2021, 9, 2890–2897.
7. Y. Yuan, K. Sheng, S. Zeng, X. Han, L. Sun, I. Loncaric, W. Zhan and D. Sun, Inorg. Chem., 2020, 59, 5456–5462.
8. N. Yan, L. Liao, J. Yuan, Y.-j. Lin, L.-h. Weng, J. Yang and Z. Wu, Chem. Mater., 2016, 28, 8240–8247.
9. N. Yan, N. Xia and Z. Wu, Small, 2021, 17, 2000609.
10. Z. Liu, X. Jing, S. Zhang and Y. Tian, Anal. Chem., 2019, 91, 2488–2497.
11. Q. Zhou, Y. Lin, M. Xu, Z. Gao, H. Yang and D. Tang, Anal. Chem., 2016, 88, 8886–8892.
12. J. Lin, Q. Zhang, L. Wang, X. Liu, W. Yan, T. Wu, X. Bu and P. Feng, J. Am. Chem. Soc., 2014, 136, 4769–4779.
13. C. Yao, J. Chen, M. B. Li, L. Liu, J. Yang and Z. Wu, Nano Lett., 2015, 15, 1281–1287.
14. M. Kim, K. L. D. M. Weerawardene, W. Choi, S. M. Han, J. Paik, Y. Kim, M.-G. Choi, C. M. Aikens and D. Lee, Chem. Mater., 2020, 32, 10216–10226.
15. R. P. B. Silalahi, Q. Wang, J. H. Liao, T. H. Chiu, Y. Y. Wu, X. Wang, S. Kahlal, J. Y. Saillard and C. W. Liu, Angew. Chem., Int. Ed., 2022, 61, e202113266.
16. M. Zhu, G. Chan, H. Qian and R. Jin, Nanoscale, 2011, 3, 1703–1707.
17. P. K. Liao, C. S. Fang, A. J. Edwards, S. Kahlal, J. Y. Saillard and C. W. Liu, Inorg. Chem., 2012, 51, 6577–6591.
18. Y. Shichibu, M. Zhang, Y. Kamei and K. Konishi, J. Am. Chem. Soc., 2014, 136, 12892–12895.
19. C. Yao, Y. J. Lin, J. Yuan, L. Liao, M. Zhu, L. H. Weng, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 15350–15353.
20. S. Lee, M. S. Bootharaju, G. Deng, S. Malola, H. Hakkinen, N. Zheng and T. Hyeon, J. Am. Chem. Soc., 2021, 143, 12100–12107.
21. R. Jiang, Y. Zhang, Q. Zhang, L. Li and L. Yang, ACS Appl. Nano Mater., 2021, 4, 9760–9767.
22. L. Liao, S. Zhou, Y. Dai, L. Liu, C. Yao, C. Fu, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 9511–9514.
23. M. B. Li, S. K. Tian, Z. Wu and R. Jin, Chem. Commun., 2015, 51, 4433–4436.
24. S. Wang, H. Abroshan, C. Liu, T.-Y. Luo, M. Zhou, H. J. Kim, N. L. Rosi and R. Jin, Shuttling single metal atom into and out of a metal nanoparticle, Nat. Commun., 2017, 8, 848.
25. X. Wei, X. Kang, Q. Yuan, C. Qin, S. Jin, S. Wang and M. Zhu, Chem. Mater., 2019, 31, 4945–4952.
26. Z. Wu, Anti-Galvanic Reduction of Thiolate-protected Gold and Silver Nanoparticles, Angew. Chem., Int. Ed., 2012, 51, 2934–2938.
27. M. Zhu, P. Wang, N. Yan, X. Chai, L. He, Y. Zhao, N. Xia, C. Yao, J. Li, H. Deng, Y. Zhu, Y. Pei and Z. Wu, Angew. Chem., Int. Ed., 2018, 57, 4500–4504.
28. X. Liu, J. Yuan, J. Chen, J. Yang and Z. Wu, Part. Part. Syst. Charact., 2019, 36, 1900003.
29. X. Lin, W. Ma, K. Sun, B. Sun, X. Fu, X. Ren, C. Liu and J. Huang, J. Phys. Chem. Lett., 2021, 12, 552–557.
30. F. Tian and R. Chen, J. Am. Chem. Soc., 2019, 141, 7107–7114.
31. A. K. Das, S. Mukherjee, S. R. Sreehari, A. S. Nair, S. Bhandary, D. Chopra, D. Sanyal, B. Pathak and S. Mandal, ACS Nano, 2020, 14, 16681–16688.
32. Y. Negishi, T. Iwai and M. Ide, Chem. Commun., 2010, 46, 4713–4715.
33. Y. Kamei, Y. Shichibu and K. Konishi, Angew. Chem., Int. Ed., 2011, 50, 7442–7445.
34. Y. Lv, R. Zhao, S. Weng and H. Yu, Chem. – Eur. J., 2020, 26, 12382–12387.
35. P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874.
36. C. Liu, Y. Pei, H. Sun and J. Ma, J. Am. Chem. Soc., 2015, 137, 15809–15816.
37. W. Kaim, A. Dogan, A. Klein and S. Záliš, Z. Anorg. Allg. Chem., 2005, 631, 1355–1358.
38. J. H. Stenlid and T. Brinck, J. Am. Chem. Soc., 2017, 139, 11012–11015.
39. M. G. Taylor and G. Mpourmpakis, Nat. Commun., 2017, 8, 15988–15995.
40. W. W. Xu, B. Zhu, X. C. Zeng and Y. Gao, Nat. Commun., 2016, 7, 13574–13581.
41. D. S. Matteson, Chem. Rev., 1989, 89, 1535–1551.
42. J. Q. Wang, Z. J. Guan, W. D. Liu, Y. Yang and Q. M. Wang, J. Am. Chem. Soc., 2019, 141, 2384–2390.
43. X. Wu, Y. Lv, Y. Bai, H. Yu and M. Zhu, Dalton Trans., 2021, 50, 10113–10118.
44. B. Delley, J. Chem. Phys., 1990, 92, 508–517.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
47. K. Weerawardene, P. Pandeya, M. Zhou, Y. Chen, R. Jin and C. M. Aikens, J. Am. Chem. Soc., 2019, 141, 18715–18726.
48. Q. Li, M. A. Mosquera, L. O. Jones, A. Parakh, J. Chai, R. Jin, G. C. Schatz and X. W. Gu, ACS Nano, 2020, 14, 11888–11896.
49. J. V. Rival, P. Mymoona, R. Vinoth, A. M. V. Mohan and E. S. Shibu, ACS Appl. Mater. Interfaces, 2021, 13, 10583–10593.
50. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans., 1993, 2, 799–805.
51. M. F. Matus, S. Malola, E. Kinder Bonilla, B. M. Barngrover, C. M. Aikens and H. Hakkinen, Chem. Commun., 2020, 56, 8087–8090.
52. S. Malola and H. Hakkinen, J. Am. Chem. Soc., 2019, 141, 6006–6012.
53. A. Fernando and C. M. Aikens, J. Phys. Chem. C, 2015, 119, 20179–20187.
54. C. L. Heinecke, T. W. Ni, S. Malola, V. Makinen, O. A. Wong, H. Hakkinen and C. J. Ackerson, J. Am. Chem. Soc., 2012, 134, 13316–13322.
55. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
56. A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981.
57. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
58. T. Lu and F. Chen, Acta Chim. Sin., 2011, 69, 2393–2406.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00301e

---