Open Access Article
Open Access ArticleCell deformability heterogeneity recognition by unsupervised machine learning from in-flow motion parameters†
Maria Isabella
Maremonti
 ,
David
Dannhauser
,
David
Dannhauser
 *,
Valeria
Panzetta
*,
Valeria
Panzetta
 ,
Paolo Antonio
Netti
and
Filippo
Causa
,
Paolo Antonio
Netti
and
Filippo
Causa
 *
*
Interdisciplinary Research Centre on Biomaterials (CRIB) and Dipartimento di Ingegneria Chimica, dei Materiali e della Produzione Industriale, Università degli Studi di Napoli “Federico II”, Piazzale Tecchio 80, 80125 Naples, Italy. E-mail: david.dannhauser@unina.it; causa@unina.it
First published on 7th November 2022
Abstract
Cell deformability is a well-established marker of cell states for diagnostic purposes. However, the measurement of a wide range of different deformability levels is still challenging, especially in cancer, where a large heterogeneity of rheological/mechanical properties is present. Therefore, a simple, versatile and cost-effective recognition method for variable rheological/mechanical properties of cells is needed. Here, we introduce a new set of in-flow motion parameters capable of identifying heterogeneity among cell deformability, properly modified by the administration of drugs for cytoskeleton destabilization. Firstly, we measured cell deformability by identification of in-flow motions, rolling (R), tumbling (T), swinging (S) and tank-treading (TT), distinctively associated with cell rheological/mechanical properties. Secondly, from a pool of motion and structural cell parameters, an unsupervised machine learning approach based on principal component analysis (PCA) revealed dominant features: the local cell velocity (VCell/VAvg), the equilibrium position (YEq) and the orientation angle variation (Δφ). These motion parameters clearly defined cell clusters in terms of motion regimes corresponding to specific deformability. Such correlation is verified in a wide range of rheological/mechanical properties from the elastic cells moving like R until the almost viscous cells moving as TT. Thus, our approach shows how simple motion parameters allow cell deformability heterogeneity recognition, directly measuring rheological/mechanical properties.
Introduction
Single cell deformability represents a straightforward indicator of changes in many cellular activities, such as signal transduction, gene expression or apoptosis.1–3 These functions are strictly related to the cell state, as healthy or pathological. In particular, a high cellular heterogeneity has been associated to deformability and rheological and mechanical properties of cancer diseases, representing a distinctive marker for the detection of different degrees of cancer invasiveness.4 In fact, such morphological alterations and cytoskeletal changes are indicative of malignant transformations of cancer cells usually marked by high replication and motility.2,5–8 However, the recognition of such highly variable deformability levels is a daunting challenge.9During the last years, numerous techniques identified heterogeneous rheological/mechanical properties existing both within and between different cell lines.2,5,10 For example, single-cell optical stretcher studies on three different breast cancer cell lines showed that MDA-MB-231 cells and MDA-MB-436 cells, which are both highly-invasive epithelial breast cancer cell lines, are mechanically more different from each other than from non-malignant epithelial MCF-10A cells.10 Instead, by means of the atomic force microscopy technique, a local cell deformability was measured examining the role of the cytoskeletal actin disassembly in the softening process of highly invasive cancer cells, such as MDA-MB-231.11 Moreover, results of micropipette aspiration experiments confirmed that alterations in cell viscoelastic properties induced by cancer are highly correlated with changes in the actin cortex and microtubule content and arrangement.12 However, all of these techniques face some obstacles such as low cell throughput, mechanical contact of the used probe leading to possible adhesion and active cellular responses or special preparation procedures. Moreover, none of the presented techniques allow variable deformability levels to be recognized and measured among different cell types in a sample.
Trying to overcome the aforementioned drawbacks, a variety of microfluidic systems enabled alignment, deformation and/or separation of particles and/or cells, at high-throughput rates and coupled with high-speed bright field imaging techniques.13–21 Particularly, alignment and deformation can be achieved thanks to a tight control of the imposed hydrodynamic forces ordering particles/cells on different equilibrium positions and trajectories depending on the channel geometry, the fluid properties, the dimensions and the deformability of the particle/cell itself.13,22,23 To date, viscoelastic fluids have been employed for such purposes to work in the absence of inertia (Re ≪ 1), over a wide range of flow rates. Even though at lower throughput than the inertial conditions (Re ≫ 1), viscoelastic fluids allow to better govern particles and cells of variable dimensions and deformability for the in-flow observation of multiple motion dynamics in simple straight channels.17,24–26 In a viscoelastic Poiseuille flow, it has been demonstrated that suspended deformable particles, red blood cells (RBCs) and rigid spherical particles tend to differently align towards the channel centre line thanks to the action of a viscoelastic lift force in a microfluidic rectangular cross-section.27 In particular, RBCs and non-spherical deformable particles align at positions closer to the centre line of the channel compared to the rigid spherical particles. Thus, the interplay of size, shape and deformability plays a fundamental role in the definition of cell equilibrium positions and local cell velocities for alignment and separation purposes.27–33
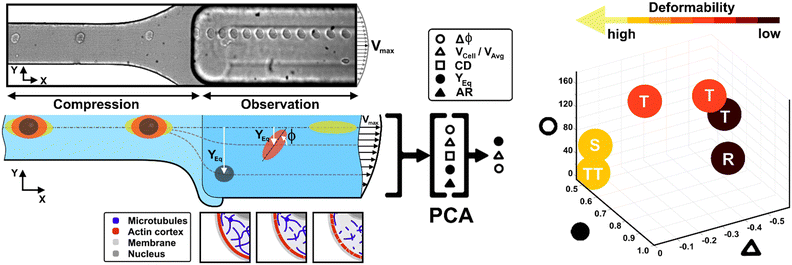
Recently, a straightforward viscoelastic-based microfluidic approach was used to in-flow compress cells in a controlled and precise manner and to analyse compressed cells by coupling the classical descriptors of morphological and shape alterations with in-flow orientation angles.34 Inspired by the motion dynamics laws known for RBCs,35–40 we already demonstrated that suspended cancer and healthy breast cells with variable cell deformations (CDs) and aspect ratios (ARs) followed multiple in-flow trajectories defined as rolling (R), tumbling (T) and tank-treading (TT).34 However, the possibility to measure a wide range of deformability as a function of morphological and motion dynamic properties remains little explored and difficult to obtain.
Here, we present a combination of motion dynamics features useful for a completely label-free measurement of a wide range of deformability levels for different cell types with distinct rheological and mechanical characteristics. To measure these properties, we decided to change the deformability of cells with two treatments to destabilize the cytoskeletal structures mainly involved in the rheological/mechanical response of suspended cells. In particular, we refer to cytochalasin-D (CytD) and nocodazole (Noco) to destabilize the actin cortex and microtubule network, respectively, for the used breast cell lines (MCF-10A and MDA-MB-231) (Fig. 1). What we expect is randomly distributed or poorly interconnected proteins with a more irregular and compliant state of cells. To measure the resulting different levels of deformability, we imposed a viscoelastic-based compression force on cells into the so-called compression region (Fig. 1, S1 and Table S1†).34 The microfluidic channel was designed to be small enough to guarantee alignment and deformation of cells in a contactless manner (∼20 μN, ESI† Table S1). After compression release, cells exit the section at the channel centre line, with the major axis aligned to the gradient-axis (z-axis, Fig. 1) arriving at an enlarged observation region, properly conceived to allow the in-flow motion investigation (Fig. 1 and S1†).34 By tracking the centroid position of the deformed cells, we further defined the in-flow cell lateral equilibrium position (YEq, ranging from 0.5 to 1, identified by the channel centre line and wall respectively, Fig. 1) and the local cell velocity, evaluated with respect to the average fluid velocity (VCell/VAvg). This allows us to improve the cell classification, so far dependent on the cell orientation angle (φ, Fig. 1) with its own variation (Δφ) and the morphological parameters –CD and AR– occurring along the observation region (Fig. 1). In particular, both VCell/VAvg and YEq were chosen since they are standard references of deformability, being well-established that highly deformable cells move faster towards the centre line than less deformable cells. However, only the combination of such dynamic and morphological parameters reveals the possibility to coherently classify different cell classes and to mechanically characterize them. In general, to reduce parameters sets, unsupervised machine learning approaches are widely used in literature for cell classification.41 Among them, we assessed principal component analysis (PCA) as a machine learning approach, to verify whether it is suitable for the distinction of cell clusters grouped depending on a specific combination of parameters associated to different rheological and mechanical cell responses (Fig. 1). As a result, a new master curve for inner cell viscosity measurement is proposed, representing such a viscosity change as a function of the described motion regime and perceived deformation.
Materials and methods
Viscoelastic alignment and compression forces
To induce deformation of single cells under viscoelastic flow conditions, we use a highly biocompatible polyethylene oxide (PEO, 4MDa, Sigma Aldrich). Fluid rheological properties were previously investigated and properly characterized.34 We decided to work with the so-called PEO 0.5 concentration, which corresponds to a polymer concentration of 0.53 wt%. We calibrated the initial pressure and velocity conditions in the microfluidic device, as well as the channel geometry to align and deform cells in a contactless way. We computed viscoelastic compressive force (FEMax) values coming from the channel walls (see ESI† Table S1), supposing that the cell is already at its own equilibrium position where the competing viscoelastic and drag forces are balanced.34Experimental setup for the in-flow measurement
The setup includes a pressure pump (P-pump, Dolomite Microfluidics), round shaped flexible fused silica capillary tubing (Molex), an ad hoc designed microfluidic chip, a fluid connector (N-333, IDEX) and an inverted microscope (X81, Olympus) with a CMOS camera (ORCA FLASH 4.0, Hamamatsu Photonics K.K.). Briefly, a pressure pump pushes the sample volume through the capillary in the microfluidic device inlet, while at the end of the chip a reservoir collects the cells (ESI† Fig. S1). The chip is made of two separate parts made with polymethyl methacrylate, which are placed together by magnetic forces. The main part was machined using a standard CNC based micromilling technique (Minitech Machinery) to develop microfluidic duct sections of different height, width, and length, while the cover part was simply used to close the chip (ESI† Fig. S1).34 In particular, the third section has the smallest height (W × H: 100 × 25 μm) implying that a well-defined viscoelastic compression over a certain time period on each passing cell is applied, enabling precise cell deformation in flow. Then, a subsequent enlarged section (W × H: 200 × 90 μm) is conceived for the observation and analysis of the compressed cells (ESI† Fig. S1).Cell culture
We have investigated MCF-10A and MDA-MB-231 cells. MCF-10A cells were donated by S. Piccolo (Istituto FIRC di oncologia molecolare, IFOM, Milan, Italy) and cultured in a mammary epithelial basal medium (MEBM) supplemented with a mammary epithelial growth media (MEGM) bullet kit (Lonza). MDA-MB-231 cell lines were kindly donated by Daidone's group and Dr P. F. Cammarata (Institute of Molecular Bioimaging and Physiology, IBFM-CNR, Cefalù (PA), Italy), respectively. MDA-MB-231 cells are cultured in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Dulbecco's modified essential medium (DMEM, Euroclone) and Ham's F-12 medium (Microtech) supplemented with 10% FBS, 1% non-essential amino acid mixture and 100 U ml−1 penicillin/streptomycin.
1 mixture of Dulbecco's modified essential medium (DMEM, Euroclone) and Ham's F-12 medium (Microtech) supplemented with 10% FBS, 1% non-essential amino acid mixture and 100 U ml−1 penicillin/streptomycin.
Finally, each investigated cell type is diluted in 500 μl of viscoelastic medium to reach a final cell concentration of circa 50 cells per μl. No evidence of mycoplasma infection is present.
Additionally, target-specific drugs are employed to induce cytoskeletal perturbations and cell deformability changes. We decided to test CytD from Sigma-Aldrich at 37 °C for 30 minutes, at a final concentration of 30 μM in serum free medium to inhibit actin polymerization and disrupt main actin filaments. For microtubules, cells were treated with Noco to destabilize the microtubules, which consequently promotes their depolymerization. Noco (Sigma-Aldrich, M1404) was dissolved in 1 ml of dimethyl sulfoxide and 100 μg of the dissolved drug was further dissolved in 5 ml of culture medium. From this, the necessary volume was added to the cells to obtain the needed concentrations, while cells were adherent. The treatment duration was 30 minutes.
For immunostaining, cells were fixed with 4% paraformaldehyde (Sigma-Aldrich) for 15 min at room temperature, then rinsed twice with PBS. Permeabilization –with 0.1% Triton X-100 (Sigma-Aldrich) for 5 min– was performed. Thus, the actin cortex was stained at the level of F-actin components with Alexa 488 phalloidin (Invitrogen) at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 dilution for 1 h. The microtubule network, instead, was stained with Beta III Tubulin monoclonal antibody overnight at 4 °C with Alexa543 anti-mouse secondary antibody. For the image acquisition of the actin cortex and microtubule network, we used a 63× oil immersion objective (NA 1.4) of a confocal laser scanning microscope (LSM 710, Zeiss) equipped with argon and HeNe laser lines at wavelengths of 488 and 543 nm, respectively. Image resolution was fixed at 512 × 512 square pixels with a 4× zoom factor.
200 dilution for 1 h. The microtubule network, instead, was stained with Beta III Tubulin monoclonal antibody overnight at 4 °C with Alexa543 anti-mouse secondary antibody. For the image acquisition of the actin cortex and microtubule network, we used a 63× oil immersion objective (NA 1.4) of a confocal laser scanning microscope (LSM 710, Zeiss) equipped with argon and HeNe laser lines at wavelengths of 488 and 543 nm, respectively. Image resolution was fixed at 512 × 512 square pixels with a 4× zoom factor.
Measurement procedure
Before each measurement, the capillary tubing and microfluidic chip are flushed with a 50% ethanol–H2O mixture for 10 minutes and subsequently with a PBS solution for 15 minutes. In addition, for each in-flow investigated cell class, new capillary tubing is used. A three-fold higher flow rate compared to the measurement condition is used to fill the microfluidic system with the viscoelastic medium. Afterwards, the cell sample is placed in the pressure pump and pushed with the measurement flow rate through the microfluidic chip. Measurements are initiated 5 min after the filling procedure started to allow the chip to equilibrate. In a typical experiment duration of 20 seconds, circa 0.74 μl of cell suspension is pushed through the chip and investigated using the imaging system (∼50 cell per μl). Such performance results in a total amount of around 35 cells per measurement, ensuring a cell-to-cell distance of more than 200 μm in the compression section. Of note, the experiment duration was limited to ensure a constant acquisition rate of 1000 frames per second. The cells which passed through the chip during the filling process are discarded. However, to enable a versatile tracing of morphometric and dynamic cell details under flow conditions, we use a 10× objective and a field of view of 2048 × 200 square pixels (0.65 μm per pixel), which covers a final cell tracing length –as the region of interest (ROI)– of 1.33 mm in the beginning of the observation channel. Of note –for all experiments– we performed cell investigations with constant cell velocities in the compression region.Experimental data analysis
In-flow cell analysis was performed over the full cell tracing length (∼0.3 s of measurement in the tracing region). The lateral equilibrium positions (YEq) of individual particles/cells were determined by measuring the cell centroid coordinates and comparing them with the observation channel coordinates. We fixed 0 and 1 as the two wall extremes, placing the channel centre line at 0.5 along the channel width (y-axis direction-ESI† Fig. S4). Then, we estimated VCell as the difference between the local cell velocity and the local fluid velocity from velocity COMSOL simulation (ESI† Fig. S4), at the same y-coordinate. Such velocity values were then divided by the average fluid velocity (VAvg).42VCell gives a measure of how much the cell lags the fluid during the alignment process, and it tends to go to zero as long as the cell reaches the channel centre line and the alignment is reached at the equilibrium positions.43We measured the dynamic in-flow cell parameters, such as the major axis (d1), minor axis (d2), area (A), perimeter (P) and orientation angles (φ) in the range of [−90° to 90°] (ESI† Fig. S2 and S3), at each 0.03 s.
Out of such parameters, the cell deformation (CD), cell aspect ratio (AR) and angle variation (Δφ, at the beginning and the end of the tracing region) are calculated as follows:
| AR = d1/d2 | (1) |
| CD = 1 − c = 1 − 4πA/P2 | (2) |
| |Δφ| = |φe − φb| | (3) |
In the specific case of tumbling motion of oblate cells, we computed the variation of the cell orientation angle as follows:45
Trev = 2π(AR + AR−1)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1 −1 | (4) |
| tan(φ(t)) = AR·tan(2πt/Trev) | (5) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate. Of note, in the limit of
is the shear rate. Of note, in the limit of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ~ 15 s−1, the symmetry remains allowing to re-write eqn (5) also with a minus sign since φ ∼ −φ.
~ 15 s−1, the symmetry remains allowing to re-write eqn (5) also with a minus sign since φ ∼ −φ.
φ(t) can be re-written as a function of μ′/μ, as follows:40
| tan(φ(t)) = (A + B/(A2 − B2)1/2)·tan(2πt/Trev) | (6) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and B = f(
and B = f(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , AR, μ′/μ). From the known oscillation (φ(t)) of the cell in tumbling motion, we can retrieve the B parameter and then the value of μ′/μ.40
, AR, μ′/μ). From the known oscillation (φ(t)) of the cell in tumbling motion, we can retrieve the B parameter and then the value of μ′/μ.40
In particular, for a tank-treading cell motion, eqn (6) can be expressed as a stationary angle, only dependent on the fixed ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and AR:40
and AR:40
| φstationary = 1/2 arccos (−A/B) | (7) |
PCA and statistical analysis
For the unsupervised machine learning based on PCA, we used Matlab R2020a (Mathworks Inc.). In particular, the analysis returns the PC scores and variances. We chose the PCs whose variance combination reproduces the highest possible number of data. In our case, the two chosen PCs cover around 80% of the cumulative variance of data. Moreover, the scree plot suggests that three main features are necessary for the data clustering (elbow rule), since only components with eigenvalues equal to or higher than 1 are usually of interest (ESI† Fig. S6).For the statistical analysis, significance was indicated by p values (nsp > 0.05; *p < 0.05, **p < 0.01, ***p < 0.001) computed by the application of a Kruskal–Wallis statistical test with Microsoft Excel 2019.
Results and discussion
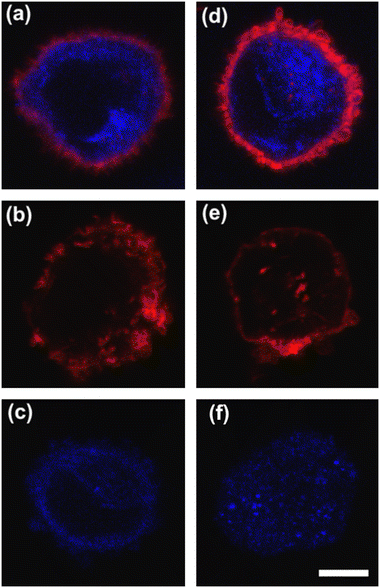
To deform cells, we defined an applied compression force of ∼20 μN (ESI† Table S1) since no alterations of cell viability and vitality that would occur at higher compression are present.46 Moreover, we already verified that only at a force compression in the order of ∼101 μN, it is possible to read multiple motion regimes.34 In fact, only covering a certain range of CDs enables the known motion regimes of R (CD ∼ (0; 0.15)), T (CD ∼ (0.10; 0.21)) and TT (CD ∼ (0.15; 0.45)) to be read.34 For this reason, we decided to work at a compression of about 20 μN, in order to be sure to have all of the prescribed regimes.From a structural point of view, it is well-known that suspended cells develop a defined spherical shape, free of visible stress fibers with the actin cytoskeleton forming a cortex-like structure immediately under the plasma-membrane (Fig. 2a and d).47,48 Instead, the microtubule network shows a random distribution at the cell interior with pronounced bundles at the cell periphery, being usually recognized as the main characters in cell response to compression (Fig. 2a and d).49 Moreover, for heterogeneity in deformability, it has been already demonstrated the importance of actin cortex and microtubule organization in deformability determination. In particular, abnormal expression levels of microtubules have been identified in highly invasive breast cancer cells, such as MDA-MB-231, while higher actin cortex intensity has been found in normal cells (MCF-10A) compared to cancer cells.12,50 Instead, reductions of actin cortex thickness have been observed in breast cancer cells compared to normal cells.12 In our case, in order to modify cell deformability and in-flow response of MCF-10A and MDA-MB-231, we administered CytD and Noco leading to destabilization of actin and microtubule contents, respectively (Fig. 2b and f). Thus, a wide range of deformability levels was reached. Both in the case of no treatment (no drug) and treatment administration, we verified that MCF-10A versus MDA-MB-231 react differently to compression forces, causing distinct in-flow responses, since both resulting cell deformation and orientation are strictly correlated to both rheological and mechanical cell properties such as cell viscoelasticity.47 Recently, we showed that deformed cells move following the multiple motion dynamics of R, T and TT depending on their own initial position at the beginning of the observation channel and the level of CD and AR.34 Here, we demonstrate that not only treated and no drug cells are different depending on the motion dynamics, but also that from such motions it is possible to retrieve viscoelastic properties of all cells of interest in a wide range of rheological/mechanical heterogeneity. Under both no drug and treated conditions, MCF-10A and MDA-MB-231 have been analysed depending on the CD, AR and Δφ (eqn (1)–(3)).34 With treatments, new exciting scenarios of deformation levels and motion dynamics have been observed, according to the deformability heterogeneity of interest. In particular, CytD on MCF-10A led to a significant actin cortex deconstruction and then to a higher and never reached deformation level of CD ∼ (0.15; 0.35) corresponding to a Δφ ≤ 50° with a TT motion (Fig. 2a, b and 3c). Instead, MDA-MB-231 expresses a comparable level of CD at CytD and no drug measurements, resulting in a dominant T motion (Fig. 3d). Not by chance, no relevant structural differences have been observed in the uncompressed cells stained after CytD treatment under the no drug and the treated conditions (Fig. 2d and e). In particular, with eqn (5), we precisely fitted the experimental data of φ(t) and AR measured at each instance of time along the tracing length (Fig. 3d, S2 and S3†).
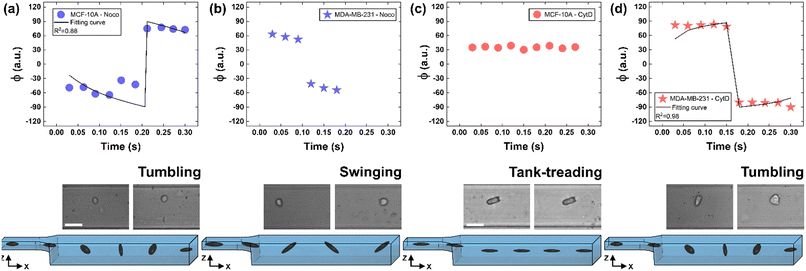 | ||
| Fig. 3 Noco and CytD effects on cell motion dynamics. (a) With Noco treatment, φ(t) variation with respect to each instance of time during the acquisition time of 0.3 s for MCF-10A. Each reported experimental φ is a mean value (N = 4, mean and standard deviation in ESI† Table S2). As expected for a T motion, φ changes are present during the measurement time between −90° and 90°. On the bottom, a flowing MCF-10A is presented moving along the enlarged section changing its own orientation from one side to the other. Scale bar 20 μm. (b) φ(t) variation with respect to each instant of time during the acquisition time of 0.3 s for MDA-MB-231 treated with Noco. Each reported experimental φ is a mean value (N = 3, mean and standard deviation in ESI† Table S2). The recognized angle variation has been addressed as S motion, with a higher frequency in the orientation change. (c) φ(t) variation with respect to each instant of time during the acquisition time of 0.3 s for MCF-10A treated with CytD. Each reported experimental φ is a mean value (N = 6, mean and standard deviation in ESI† Table S3). As expected for a TT motion, no φ changes are present during the measurement time. On the bottom, a flowing MCF-10A is presented moving along the enlarged section without changing its own orientation. Scale bar 30 μm. (d) With CytD, φ(t) variation with respect to each instant of time during the acquisition time of 0.3 s for MDA-MB-231. Each reported experimental φ is a mean value (N = 4, mean and standard deviation in ESI† Table S3). As expected for a T motion, φ changes are present during the measurement time between −90° and 90°. On the bottom, a flowing MDA-MB-231 is presented moving along the enlarged section changing its own orientation from one side to the other. | ||
On the other hand, the Noco effect revealed different and novel dynamic behaviours. In the case of MCF-10A, no relevant differences have been noticed in terms of CD, AR and Δφ between the no drug and treated conditions, as well as at the structure level (Fig. 2a and c). However, among different cell subclasses moving both as R and T motions, we were able to detect the ∼65% of MFC-10A moving as T after Noco, in good agreement with Jeffery's orbit fitting curve (Fig. 3a). Instead, MDA-MB-231 moved with a new kind of motion dynamics, what we re-called ‘swinging’ (S), like an intermittent transition between T and TT as usually defined for RBCs.38,51 In particular, S has been described by high CD associated with 50° ≤ Δφ ≤ 180° defining a transition motion condition between T and TT. What we observed is that cells oscillate in φ(t) values ranging between −60° and 60°, in half of the rotation time. A lower excursion of φ(t) has been correlated to the highest reached velocity, approximating VMax, which translates into a lower period of rotation (∼0.15 s). Fitting with Jeffery's orbit was not possible, since not one of the required conditions in terms of φ(t) variation and travelling time was satisfied (Fig. 3b, S2 and S3†).
All things considered, compared to no drug conditions,34 cells express higher CD and AR at CytD and Noco. In particular, MCF-10A is more sensitive to the actin cortex destabilization, with two-times higher CD entities compared to the no drug condition. Instead, MDA-MB-231 increases in deformability (CD ∼0.334) at microtubule destabilization, probably being the most effective response of MDA-MB-231 (Fig. 2d and f). On the other hand, comparable values of CD in the CytD and no drug cases have been found. At this point, we retrieved the cell classes characterized by the motion regimes and specific rheological/mechanical properties. Hereby, we noticed that cell groups are not distinguished, using only CD, AR and Δφ. This is reasonable, since the same CD and Δφ values could be associated to multiple in-flow motion types without distinction (Fig. 4a). For this reason, we decided to optimize the cell classification and heterogeneity recognition finding new relevant parameters from the in-flow behaviour of deformed cells. Thus, we further investigated the cells depending on their in-flow channel position, YEq, along the cross-section width (Fig. 4b, from 1 to 0.5) estimating VCell/VAvg (Fig. 4b).
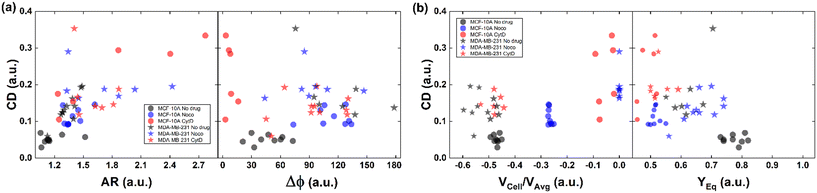 | ||
| Fig. 4 CD variation with respect to AR, Δφ, VCell/VAvg, and YEq for MCF-10A and MDA-MB-231 under no drug and treated conditions for each analysed cell. (a) CD variation with respect to AR and Δφ is plotted for each cell. Increasing CD and AR are present for the treated cells. MCF-10A deforms more at CytD expressing lower values of Δφ (≤50°) related to a high CD range of (0.15–0.35) while MDA-MB-231 still shows 50° ≤ Δφ ≤ 180° after CytD treatment, in the same range of no drug. MCF-10A deforms less at Noco expressing slightly equal values of Δφ, AR and CD typical of a T motion. (b) CD variation with respect to VCell/VAvg and YEq is shown for each cell. It is verified that an increase of the CD values corresponds to a decrease of the VCell/VAvg since cells tend to move at the same velocity of the fluid, without lagging it anymore. According to the VCell/VAvg changes, the YEq values decrease as cells move faster towards the centre line (YEq ∼0.5) as the CD increases. The total number of analysed cells NTot = 49. The Kruskal–Wallis test performed on the experimental data is reported in Table S4.† | ||
As expected, we found a strict relationship between the ability of cells to align at the centre line and the measured CD. In fact, more deformed cells immediately place at the centre line (YEq ∼0.5) compared to more rigid cells, for the same extent of blockage ratio (βW = d1/W, ESI† Fig. S5). Then, the cells with higher CD have a VCell/VAvg value almost equal to zero, since no more difference exists with respect to the fluid. Already at ∼2 mm after compression release, MDA-MB-231 cells are already at the channel centre line, with velocities V ∼ VMax, where VMax is the maximum fluid velocity. Such an outcome confirms that increasing CD translates into lower or zero values of VCell/VAvg, since more centered positions (YEq ∼0.5) are observed as well as lower values of Δφ ≤ 50° (Fig. 4b).
However, understanding which of the computed in-flow parameters are dominant in the rheological/mechanical description of cells was necessary. Thus, we decided to extract such relevant parameters to identify different cell clusters. For this, we implemented an unsupervised machine learning by using PCA to test the ability of the parameter selection for cell motion and deformability recognition. As shown, the cells described by the aforementioned morphological and dynamic parameters form distinct clusters of data. In particular, the loading plot (Fig. 5, on the top and S6†) shows the principal component subspace of the original feature space spanned by the peaks of the VCell/VAvg, CD, AR, Δφ and YEq. The biplot of cell population shows six cell clusters that can be separated from each other by forming well-defined clusters (Fig. 5, on the bottom). Both for the loading and biplot representation, the two PCs, which returned a variance capable of covering almost 80% of the cumulative variance, are presented. The comparison of the loading and biplot lets us consider the dominant parameters VCell/VAvg, YEq and Δφ in precisely dividing cells. In fact, these are the only features characterized by eigenvector coefficients greater than 0.4 and useful for the identification of the principal components.
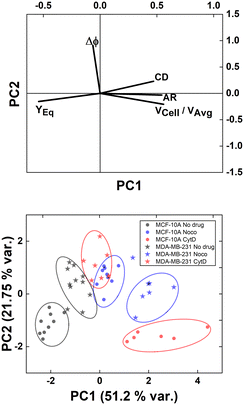 | ||
| Fig. 5 PCA results on cell populations with respect to the parameter set. On the top, the loading plot representing the eigenvector scores, from the velocity through the morphological parameters until the orientation angle and the equilibrium position. On the bottom, the biplot with the data scores represented with respect to the highlighted eigenvectors. The most discriminant features are VCell/VAvg, YEq and Δφ. Such PCA reveals a precise cluster distinction among cell classes, confirmed by the performed computation of the separation degree among clusters (ESI† Table S5). | ||
Of note, these clusters are separated depending on the dynamic motion behaviour ranging from R and T until S and TT. In particular, by comparing the diameter of each cluster with the distance among couples of clusters, the most separated clusters are the R-cases with respect to the T, S, and TT as well as T and S with respect to TT. Of note, the T-cases represented by the no drug MDA-MB-231, the CytD MDA-MB-231 and the Noco MCF-10A are not separated from each other, indicating comparable rheological/mechanical properties among the lines moving in the same way (ESI† Table S5). Less separated are the clusters S and TT. This is reasonable if we think about that the S behaviour is an intermediate among T and TT, where highly deformed cells ‘swing’ moving fast towards the centre line but with still high angle variation (50° ≤ Δφ ≤ 180°, ESI† Table S5).
Thus, the reduction of parameters, set to a combination of only three, helped in re-plotting cell populations in a three-dimensional representation. This shows relevant differences among clusters only related to motion regimes, each of which is associated to a scaling deformability level as low or high (Fig. 6– on the right). In fact, deformability properties span from rigid cells (low deformability) moving as R, going through cells flowing as T dynamics, until highly soft cells (high deformability) travelling with S and TT motions (Fig. 6).
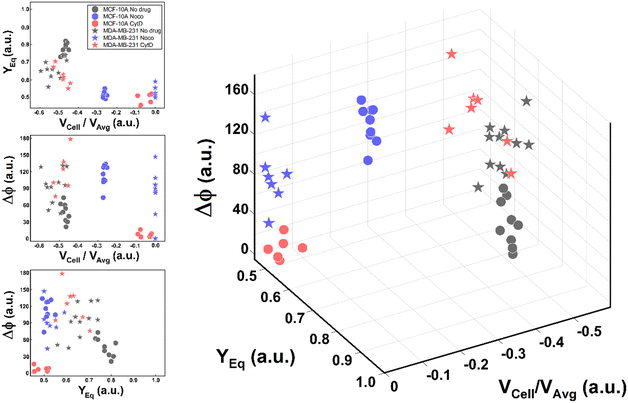 | ||
| Fig. 6 Three-dimensional representation of cell classes depending on VCell/VAvg, YEq and Δφ. Cell classes are distinguished depending on the motion dynamics which range from R to TT according to deformability characteristics indicated by the applied treatments and cell state as healthy or pathological. On the left, the combination of the different parameters on two-dimensional plots is presented for each analysed cell. Only these motion dynamics parameters satisfy the necessity of a cell classification. The total number of analysed cells NTot = 49. The Kruskal–Wallis test performed on the experimental data is reported in Table S4.† | ||
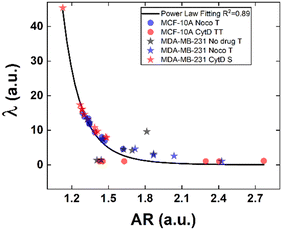
Structural modifications at the actin cortex and microtubule network level revealed modified MCF-10A in-flow behaviour ascribed to altered cell state conditions instead; for the S case, we performed a non-linear extrapolation procedure to collect λ data from the known AR (Fig. 7). From our outcome, we were able to definitely consider suspended cells as a viscoelastic medium with the viscosities as the expression of a resistance opposed by cells to the imposed fluid-flow condition, as it would be for pathological cells like cancer cells. In fact, modified MCF-10A resembles motion dynamics characteristics typical of MDA-MB-231 cells. Such evidence further supports the possibility to correlate a heterogeneous deformability to the identified cell classes, creating a completely new way to read and measure rheological and mechanical properties of suspended cells simply relying on in-flow motion features.
Since the inner content of suspended cells can be modelled as a viscoelastic fluid, with the intracellular concentrations of protein filaments dissolved in a water-like liquid,52,53 only below a certain length time-scale the resulting behaviour is ascribable to purely viscous effects. In particular, at stimuli frequencies less than 0.5 s−1 as the ones we used during compression, such viscous behaviour is dominant.54 Taking advantage of this, we used the previously presented cell classification to extract an estimation of the inner cell viscosities from the computation of (λ = μ′/μ) using the T, S and the TT data (eqn (6) and (7)). The R case has been not considered in this computation, the reason is that this motion, which permits the cells to avoid energetically costly shape changes, is a sign of cell elasticity.47 Then, the combination of morphological parameters such the AR with Δφ leads to the identification of a master-curve describing the deformability property of cells in terms of inner viscosity. Very low values of λ correspond to low values of Δφ, inversely correlated with high AR values, in agreement with previously demonstrated data showing λ ≤ 0.5 typical for cells going towards the channel centre easily.55
Whereas, 0.5 ≤ λ ≤10 classically describes an intermediate condition, for which it is known that cells move more slowly to the centre.55 Both the mentioned ranges well match our outcome, precisely correlating for the first time the motion regimes with rheological and mechanical properties of cells. In fact, TT defines λ ≤ 0.5 while S and T describe 0.5 ≤ λ ≤10 for pathological cells of heterogeneous deformability.
Conclusions
The proposed microfluidic approach based on viscoelastic compression forces has successfully enabled the recognition of heterogeneous cell deformability properties in a completely label-free manner. Our approach aimed to compress cells at forces at least greater than 101 μN to cover a certain CD range (CD ∼ [0–0.45]), capable of returning all of the motion regimes of interest. Thus, the approach appears to be highly versatile and generalizable for other cell samples, despite different cell diameter dimensions. In fact, scaling the compression force with respect to the cell diameter, a change in PEO concentration and/or applied pressure drop would be necessary to still obtain a value of ∼101 μN for compression and the desired CD range.Overall, we demonstrated a simple and easy-to-use way to compress and analyse cells by unsupervised machine learning. We introduce a set of motion parameters namely VCell/VAvg, YEq and Δφ capable of recognizing different levels of cell deformability in a wide range of measurable rheological/mechanical properties. As a benchmark in terms of deformability measurement, we used the VCell/VAvg estimation coupled with the YEq, since it is well-established that less deformable cells move slower than more deformable cells towards the centre line. By the CytD and Noco administration, we noticed that no relevant differences are present in terms of structure organization, CD and AR between MCF-10A at no drug and after Noco treatment, as well as for MDA-MB-231 between no drug and CytD treatment. Of note, motion dynamics succeeded in distinguishing such cell samples, by identifying more rigid no drug MCF-10A as R, while modified Noco MCF-10A as T which is then more deformable. On the other hand, the T regime was confirmed for no drug MDA-MB-231 and modified CytD MDA-MB-231, supporting the fact that no relevant contribution comes from the actin compartment in compression. As a result, we demonstrate how the approach allows to detect the intrinsic heterogeneity of cells depending on the deformability characteristics. In particular, by the application of an unsupervised machine learning with the PCA approach, distinct cell clusters are identified varying the motion features. These describe the regimes spanning from R, T, S until TT corresponding to gradual levels of deformability from the lowest (R) to the highest (TT). Thus, the combination of VCell/VAvg, YEq and Δφ gives the complete description of the rheological and mechanical properties of cells since this is not allowed with only classical descriptors such as CD and AR. Such an approach also opens the possibility to quantify such properties as inner cell viscosity. The future development of our approach has a great potential application in rapid, label-free, cost-effective and non-invasive disease diagnostics towards a personalized healthcare management.
Author contributions
FC and DD contributed to the conceptualization of the research project. MIM, DD and VP developed the methodology. MIM implemented the measurement and performed the FEM computation and the data analysis. MIM wrote the paper, and the review-editing was carried out by FC, MIM, VP, DD and PAN. The project supervision was done by FC.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Sabrina Napoletano for valuable discussions.Notes and references
- S. Suresh, Biomechanics and biophysics of cancer cells, Acta Biomater., 2007, 3, 413–438 CrossRef PubMed.
- S. Suresh, J. Spatz, J. P. Mills, A. Micoulet, M. Dao, C. T. Lim, M. Beil and T. Seufferlein, Connections between single-cell biomechanics and human disease states: gastrointestinal cancer and malaria, Acta Biomater., 2005, 1, 15–30 CrossRef CAS PubMed.
- D. Di Carlo, A mechanical biomarker of cell state in medicine, J. Lab. Autom., 2012, 17, 32–42 CrossRef CAS PubMed.
- F. Lüönd, S. Tiede and G. Christofori, Breast cancer as an example of tumour heterogeneity and tumour cell plasticity during malignant progression, Br. J. Cancer, 2021, 125, 164–175 CrossRef PubMed.
- J. Guck, S. Schinkinger, B. Lincoln, F. Wottawah, S. Ebert, M. Romeyke, D. Lenz, H. M. Erickson, R. Ananthakrishnan, D. Mitchell, J. Käs, S. Ulvick and C. Bilby, Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence, Biophys. J., 2005, 88, 3689–3698 CrossRef CAS PubMed.
- A. Moustakas and C. Stournaras, Regulation of actin organisation by TGF-beta in H-ras-transformed fibroblasts, J. Cell Sci., 1999, 112, 1169–1179 CrossRef CAS PubMed.
- B. Lincoln, H. M. Erickson, S. Schinkinger, F. Wottawah, D. Mitchell, S. Ulvick, C. Bilby and J. Guck, Deformability-based flow cytometry, Cytometry, Part A, 2004, 59, 203–209 CrossRef PubMed.
- W. Xu, R. Mezencev, B. Kim, L. Wang, J. McDonald and T. Sulchek, Cell stiffness is a biomarker of the metastatic potential of ovarian cancer cells, PLoS One, 2012, 7, 1–12 CrossRef.
- J. Lv, Y. Liu, F. Cheng, J. Li, Y. Zhou, T. Zhang, N. Zhou, C. Li, Z. Wang, L. Ma, M. Liu, Q. Zhu, X. Liu, K. Tang, J. Ma, H. Zhang, J. Xie, Y. Fang, H. Zhang, N. Wang, Y. Liu and B. Huang, Cell softness regulates tumorigenicity and stemness of cancer cells, EMBO J., 2021, 40, 106123 Search PubMed.
- Y. Shen, B. Schmidt, H. Kubitschke, E. W. Morawetz, B. Wolf, J. A. Käs and W. Loser, Detecting heterogeneity in and between breast cancer cell lines, Cancer Converg., 2020, 4, 1–11 CrossRef PubMed.
- R. Omidvar, M. Tafazzoli-shadpour, M. A. Shokrgozar and M. Rostami, Atomic force microscope-based single cell force spectroscopy of breast cancer cell lines: An approach for evaluating cellular invasion, J. Biomech., 2014, 47, 3373–3379 CrossRef PubMed.
- M. Tabatabaei, M. Tafazzoli-Shadpour and M. M. Khani, Altered mechanical properties of actin fibers due to breast cancer invasion: parameter identification based on micropipette aspiration and multiscale tensegrity modeling, Med. Biol. Eng. Comput., 2021, 59, 547–560 CrossRef PubMed.
- Y. Zheng, J. Nguyen, Y. Wei and Y. Sun, Recent advances in microfluidic techniques for single-cell biophysical characterization, Lab Chip, 2013, 13, 2464–2483 RSC.
- M. Piergiovanni, V. Galli, G. Holzner, S. Stavrakis, A. DeMello and G. Dubini, Deformation of leukaemia cell lines in hyperbolic microchannels: investigating the role of shear and extensional components, Lab Chip, 2020, 20, 2539–2548 RSC.
- D. R. Gossett, W. M. Weaver, A. J. Mach, S. C. Hur, H. T. K. Tse, W. Lee, H. Amini and D. Di Carlo, Label-free cell separation and sorting in microfluidic systems, Anal. Bioanal. Chem., 2010, 397, 3249–3267 CrossRef CAS PubMed.
- K. D. Nyberg, K. H. Hu, S. H. Kleinman, D. B. Khismatullin, M. J. Butte and A. C. Rowat, Quantitative deformability cytometry: rapid, calibrated measurements of cell mechanical properties, Biophys. J., 2017, 113, 1574–1584 CrossRef CAS PubMed.
- X. Lu, C. Liu, G. Hu and X. Xuan, Particle manipulations in non-newtonian microfluidics: A review, J. Colloid Interface Sci., 2017, 500, 182–201 CrossRef CAS PubMed.
- M. Urbanska, H. E. Muñoz and J. Shaw Bagnall, et al., A comparison of microfluidic methods for high-throughput cell deformability measurements, Nat. Methods, 2020, 17, 587–593 CrossRef CAS PubMed.
- O. Otto, P. Rosendahl and A. Mietke, et al., Real-time deformability cytometry: on-the-fly cell mechanical phenotyping, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- M. H. Panhwar, F. Czerwinski and V. A. S. Dabbiru, et al., High-throughput cell and spheroid mechanics in virtual fluidic channels, Nat. Commun., 2020, 11, 2190 CrossRef CAS PubMed.
- B. Fregin, F. Czerwinski and D. Biedenweg, et al., High-throughput single-cell rheology in complex samples by dynamic real-time deformability cytometry, Nat. Commun., 2019, 10, 415 CrossRef CAS PubMed.
- J. Zhou and I. Papautsky, Viscoelastic microfluidics: Progress and challenges, Microsyst. Nanoeng., 2020, 6, 1–24 CrossRef PubMed.
- Z. Zhou, Y. Chen, S. Zhu, L. Liu, Z. Ni and N. Xiang, Inertial microfluidics for high-throughput cell analysis and detection, Analyst, 2021, 146, 6064–6083 RSC.
- G. Romeo, G. D'Avino, F. Greco, P. A. Netti and P. L. Maffettone, Viscoelastic flow-focusing in microchannels: scaling properties of the particle radial distributions, Lab Chip, 2013, 13, 2802–2807 RSC.
- X. Lu and X. Xuan, Elasto-inertial pinched flow fractionation for continuous shape-based particle separation, Anal. Chem., 2015, 87, 11523–11530 CrossRef CAS PubMed.
- T. Zhang, H. Liu, K. Okano, T. Tang, K. Inoue, Y. Yamazaki, H. Kamikubo, A. K. Cain, Y. Tanaka, D. W. Inglis, Y. Hosokawa, Y. Yaxiaer and M. Li, Shape-based separation of drug-treated escherichia coli using viscoelastic microfluidics, Lab Chip, 2022, 22, 2801–2809 RSC.
- T. Go, H. Byeon and S. J. Lee, Focusing and alignment of erythrocytes in a viscoelastic medium, Sci. Rep., 2017, 7, 1–10 CrossRef PubMed.
- S. Yang, S. S. Lee, S. W. Ahn, K. Kang, W. Shim, G. Lee, K. Hyun and J. M. Kim, Deformability-selective particle entrainment and separation in a rectangular microchannel using medium viscoelasticity, Soft Matter, 2012, 8, 5011–5019 RSC.
- M. Abkarian and A. Viallat, Dynamics of vesicles in a wall-bounded shear flow, Biophys. J., 2005, 89, 1055–1066 CrossRef CAS PubMed.
- M. Trofa, M. M. Villone, G. D'Avino, M. A. Hulsen, P. A. Netti and P. L. Maffettone, Numerical simulations of the separation of elastic particles in a t-shaped bifurcation, J. Non-Newtonian Fluid Mech., 2016, 233, 75–84 CrossRef CAS.
- D. Yuan, S. Yan, J. Zhang, R. M. Guijt, Q. Zhao and W. Li, Sheathless separation of cyanobacterial anabaena by shape using viscoelastic microfluidics, Anal. Chem., 2021, 93, 12648–12654 CrossRef CAS PubMed.
- P. Liu, H. Liu, L. Semenec, D. Yuan, S. Yan, A. K. Cain and M. Li, Length-based separation of bacillus subtilis bacterial populations by viscoelastic microfluidics, Microsyst. Nanoeng., 2022, 8, 1–11 CrossRef PubMed.
- C. W. Tai and V. Narsimhan, Experimental and theoretical studies of cross-stream migration of non-spherical particles in a quadratic flow of viscoelastic fluid, Soft Matter, 2022, 18, 4613–4624 RSC.
- D. Dannhauser, M. I. Maremonti, V. Panzetta, D. Rossi, P. A. Netti and F. Causa, Mechanical phenotyping of breast cell lines by in-flow deformation-dependent dynamics under tuneable compressive forces, Lab Chip, 2020, 20, 4611–4622 RSC.
- X. Lu, L. Zhu, R. M. Hua and X. Xuan, Continuous sheath-free separation of particles by shape in viscoelastic fluids, Appl. Phys. Lett., 2015, 107, 264102 CrossRef.
- G. D'Avino, M. A. Hulsen, F. Greco and P. L. Maffettone, Numerical simulations on the dynamics of a spheroid in a viscoelastic liquid in a wide-slit microchannel, J. Non-Newton. Fluid Mech., 2019, 263, 33–41 CrossRef.
- J. M. Skotheim and T. W. Secomb, Red blood cells and other nonspherical capsules in shear flow: Oscillatory dynamics and the tank-treading-to-tumbling transition, Phys. Rev. Lett., 2007, 98, 078301 CrossRef CAS PubMed.
- M. Abkarian, M. Faivre and A. Viallat, Swinging of red blood cells under shear flow, Phys. Rev. Lett., 2007, 98, 188302 CrossRef PubMed.
- C. Dupont, F. Delahaye, D. Barthès-Biesel and A. V. Salsac, Stable equilibrium configurations of an oblate capsule in simple shear flow, J. Fluid Mech., 2016, 791, 738–757 CrossRef CAS.
- S. R. Keller and R. Skalak, Motion of a tank-treading ellipsoidal particle in a shear flow, J. Fluid Mech., 1982, 120, 27–47 CrossRef.
- B. Desgraupes, Clustering indices, University of Paris Ouest-Lab Modal' X, 2013, 1: 34 and Aggarwal, Charu C., et al. Data mining: the textbook, Springer, New York, 2015 Search PubMed.
- K. Kang, S. S. Lee, K. Hyun, S. J. Lee and J. M. Kim, Dna-based highly tunable particle focuser, Nat. Commun., 2013, 4, 1–8 Search PubMed.
- G. Li, G. H. McKinley and A. M. Ardekani, Dynamics of particle migration in channel flow of viscoelastic fluids, J. Fluid Mech., 2015, 785, 486–505 CrossRef CAS.
- M. Urbanska, P. Rosendahl, M. Kräter and J. Guck, High-throughput single-cell mechanical phenotyping with real-time deformability cytometry, Microfluidics in Cell Biology Part B: Microfluidics in Single Cells, of Methods in Cell Biology, Academic Press, 2018, ch. 10, vol. 147, pp. 175–198 Search PubMed.
- G. B. Jeffery, The motion of ellipsoidal particles immersed in a viscous fluid, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 Search PubMed.
- M. I. Maremonti, V. Panzetta, D. Dannhauser, P. A. Netti and F. Causa, Wide range viscoelastic compression forces in microfluidics to probe cell-dependent nuclear structural and mechanobiological responses, J. R. Soc., Interface, 2022, 19, 20210880 CrossRef CAS PubMed.
- J. Dupire, M. Socol and A. Viallat, Full dynamics of a red blood cell in shear flow, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20808–20813 CrossRef CAS PubMed.
- Y. Nematbakhsh, K. T. Pang and C. T. Lim, Correlating the viscoelasticity of breast cancer cells with their malignancy, Convergent Sci. Phys. Oncol., 2017, 3, 034003 CrossRef.
- H. Kubitschke, J. Schnauss, K. D. Nnetu, E. Warmt, R. Stange and J. Kaes, Actin and microtubule networks contribute differently to cell response for small and large strains, New J. Phys., 2017, 19, 093003 CrossRef.
- M. A. H. Albahde, B. Abdrakhimov, G. Q. Li, X. Zhou, D. Zhou, H. Xu, H. Qian and W. Wang, The role of microtubules in pancreatic cancer: Therapeutic progress, Front. Oncol., 2021, 11, 1236 Search PubMed.
- S. Atwell, C. Badens, A. Charrier, E. Helfer and A. Viallat, Dynamics of individual red blood cells under shear flow: A way to discriminate deformability alterations, Front. Physiol., 2022, 12, 2406 Search PubMed.
- T. Kalwarczyk, N. Ziebacz, A. Bielejewska, E. Zaboklicka, K. Koynov, J. Szymanski, A. Wilk, A. Patkowski, J. Gapinski, H. J. Butt and R. Hołyst, Comparative analysis of viscosity of complex liquids and cytoplasm of mammalian cells at the nanoscale, Nano Lett., 2011, 11, 2157–2163 CrossRef CAS PubMed.
- R. Vaippully, V. Ramanujan, S. Bajpai and B. Roy, Measurement of viscoelastic properties of the cellular cytoplasm using optically trapped brownian probes, J. Phys.: Condens. Matter, 2020, 32, 235101 CrossRef CAS PubMed.
- F. Wottawah, S. Schinkinger, B. Lincoln, R. Ananthakrishnan, M. Romeyke, J. Guck and J. Käs, Optical rheology of biological cells, Phys. Rev. Lett., 2005, 94, 98103 CrossRef PubMed.
- S. C. Hur, N. K. Henderson-MacLennan, E. R. B. McCabe and D. Di Carlo, Deformability-based cell classification and enrichment using inertial microfluidics, Lab Chip, 2011, 11, 912–920 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00902a |
| This journal is © The Royal Society of Chemistry 2022 |