Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum chemical calculation of the vapor pressure of volatile and semi volatile organic compounds†
Marcel
Stahn
 a,
Stefan
Grimme
a,
Stefan
Grimme
 a,
Tunga
Salthammer
a,
Tunga
Salthammer
 *b,
Uwe
Hohm
*b,
Uwe
Hohm
 c and
Wolf-Ulrich
Palm
c and
Wolf-Ulrich
Palm
 d
d
aMulliken Center for Theoretical Chemistry, Institute for Physical and Theoretical Chemistry, University of Bonn, 53115 Bonn, Germany
bDepartment of Material Analysis and Indoor Chemistry, Fraunhofer WKI, 38108 Braunschweig, Germany. E-mail: tunga.salthammer@wki.fraunhofer.de
cInstitute of Physical and Theoretical Chemistry, University of Braunschweig – Institute of Technology, 38106 Braunschweig, Germany
dInstitute of Sustainable and Environmental Chemistry, Leuphana University Lüneburg, 21335 Lüneburg, Germany
First published on 3rd October 2022
Abstract
The vapor pressure is a specific and temperature-dependent parameter that describes the volatility of a substance and thus its driving force for evaporation or sublimation into the gas phase. Depending on the magnitude of the vapor pressure, there are different methods for experimental determination. However, these are usually associated with a corresponding amount of effort and become less accurate as the vapor pressure decreases. For purposes of vapor pressure prediction, algorithms were developed that are usually based on quantitative structure–activity relationships (QSAR). The quantum mechanical (QM) approach followed here applies an alternative, much less empirical strategy, where the change in Gibbs free energy for the transition from the condensed to the gas phase is obtained from conformer ensembles computed for each phase separately. The results of this automatic, so-called CRENSO workflow are compared with experimentally determined vapor pressures for a large set of environmentally relevant compounds. In addition, comparisons are made with the single structure-based COSMO-RS QM approach, linear-free-energy relationships (LFER) as well as results from the SPARC program. We show that our CRENSO workflow is superior to conventional prediction models and provides reliable vapor pressures for liquids and sub-cooled liquids over a wide pressure range.
Environmental significanceThe vapor pressure of a liquid or a sub-cooled liquid is a fundamental molecular property for describing the partitioning and the dynamics of organic pollutants in environmental compartments. For volatile compounds, the vapor pressure can usually be measured accurately. However, as the volatility decreases, the available experimental techniques provide increasingly inaccurate values. Even the classic prediction algorithms based on QSAR are then only applicable to a limited extent. The quantum mechanical approach presented here is based on the solvation properties of individual molecules, taking into account conformer ensembles. The method is superior to previously published calculation tools and allows the prediction of vapor pressures with an accuracy of <0.5 log units. |
1. Introduction
The increasing production of new chemicals makes it hard for producers to accurately determine or predict their physical properties before being released into the life cycle. The vapor pressure at a given temperature is of central importance in describing the behavior of a substance in the environment. The phase transitions from liquid to gaseous and solid to gaseous can be characterized, the saturation concentration in the gaseous phase can be calculated, the vapor pressure is linked to Henry’s constant,1 and finally, the adsorption tendency of substances on particle surfaces can be estimated.2Even if a pure substance is solid at room temperature, the vapor pressure of its sub-cooled melt can still be of physical importance. This is the case, for example, when the substance is dissolved in a liquid medium. Therefore, the vapor pressure of the sub-cooled liquid is always used to describe partitioning processes.3 In a phase diagram, the sub-cooled liquid state is the extension of the liquid phase vapor pressure line below the triple point temperature, as shown in Fig. 1.
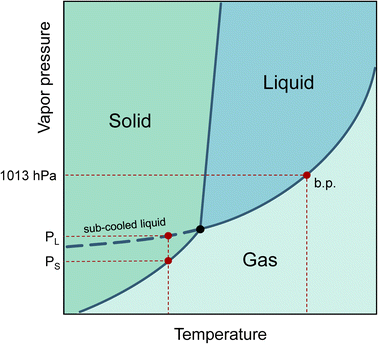 | ||
| Fig. 1 Phase diagram with boiling point (b.p.) and vapor pressures for solid (PS) and sub-cooled liquid (PL) (see dashed curve). | ||
For many compounds, the vapor pressure can be measured very accurately.4 However, the determination is methodologically complex. Unless it is a chromatographic method,5 highly purified substances are needed. Even small amounts of contamination can severely disrupt the measurement. Moreover, several measurements at different temperatures are usually required. In general, the lower the vapor pressure, the more sophisticated and error-prone the measurement becomes. Experiments are therefore often carried out at higher temperatures and the result is then extrapolated to the desired temperature using the Antoine equation.6 This is a convenient procedure as long as there is no phase transition between the measuring range and the extrapolated temperature.
Because of these experimental difficulties and uncertainties, there is a need to estimate vapor pressure using other, more readily available procedures. The simplest theoretical models are based on the Pictet–Trouton rule, which states that the vaporization entropy reaches a constant value at the boiling point. From the calculated enthalpy of vaporization at the boiling point and with the help of correction factors introduced by Fishtine,7 the vapor pressure of a compound can then be linked to the boiling point.8–10
An alternative approach is chemical structure-based and calculates the excess Gibbs free energy of a compound in a liquid from the contributions of its characteristic groups.11,12 Another possibility is to use empirical linear free energy relationships (LFER) to calculate the vapor pressure of a compound (see below for a more detailed discussion). The algorithm implemented in SPARC (Sparc Performs Automated Reasoning in Chemistry)13 is widely used to predict vapor pressures. However, it was repeatedly found that the values calculated with SPARC for substances with low vapor pressures (approximately <10−2 Pa) are too small.14,15 This may be attributed to missing data points in the calibration for low pressures or that the involved more significant intermolecular interactions cannot be fathomed with pure empiricism.
Quantum mechanical (QM) methods enable the calculation of fundamental thermodynamic properties of molecules and compute vapor pressures from the difference in Gibbs free energy between the condensed and gaseous states of a molecule. The three-dimensional structure of a molecule is explicitly considered. For several organic compounds, vapor pressures have been estimated using density functional theory (DFT) based quantum mechanics,16–20 primarily using the COSMO-RS (conductor-like screening model for realistic solvation) method, developed by Klamt and co-workers.21
While this is straightforward for small, usually quite rigid molecules, open questions arise for larger, often conformationally rather flexible systems. Most important seems to be the dependence of vapor pressure on the available conformational space, which to the best of our knowledge, has not been studied systematically so far. The composition of conformational ensembles and the three-dimensional structures of individual conformers are highly dependent on the environment and can differ widely between solution and gas phase, e.g., the shortest n-alkane with a nonlinear global conformer minimum changes when solvent and temperature (entropy) effects are considered.22 Neglecting conformational changes from the condensed to the gas-phase state in theoretical procedures could potentially lead to significant errors in the computed Gibbs free energy difference.
In a previous publication, we proposed a general multilevel QM workflow to determine liquid phase partition coefficients for molecules and tested it on compounds with environmental relevance.23 Key aspects of this workflow are an automated, comprehensive exploration of the conformational space by artificially changing the potential energy surfaces of the compounds in the CREST24 program to find many energetically low-lying conformers in solution, followed by re-ranking of the resulting conformer ensembles at higher DFT levels of theory using an energetic sorting and optimization algorithm (ENSO).25 The combination of these ensemble generation and post-processing methods was dubbed CRENSO. We showed that depending on the flexibility and complexity of a system, the conformer space can have a significant impact on the thermally averaged observables. For example, the computed Kow (octanol/water) values improved by up to 1.8 log units when conformational averaging was considered. For more conformer-sensitive properties, like optical rotation,26 the effects can be even more drastic and completely change the computed property value.
In this work, we will therefore mostly focus on flexible organic compounds with low vapor pressures for which both the theoretical methodology and the data are currently insufficient. After setting a baseline by comparing our computationally obtained values to reliable reference data from the literature, we also investigate newly emerging, environmentally relevant compounds like plasticizers, biocides and pharmaceuticals, for which no reliable vapor pressure data are available.
2. Methods
2.1 CRENSO
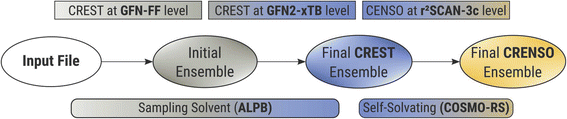
To accurately describe conformational effects in our workflow, we need to be able to sample the target compound independently in the condensed and gas phase to calculate the Gibbs free energy change. This is necessary because different three-dimensional molecular structures can be stabilized by enhanced or damped interactions in one of the two phases. While the idea of sampling the conformational space to obtain various solvation-dependent properties is not new,27 widespread approaches such as COSMOconf still show large errors for flexible compounds with RMSE’s (root mean square errors) of about 2.16 kcal mol−1,28 which can probably be attributed to the heuristic approach of conformer sampling and low-level DFT reranking,29 making it easy to miss an important conformer. In addition, it can be hard to find the correct settings and conformer distributions, leading to errors of up to 4.69 log units for highly flexible systems,30 if used without any customization. This makes sampling the chemical space of a compound a tedious work, and the CRENSO25 workflow proved a valuable tool for automatizing such exploration without the need to adjust default settings manually.Fig. 2 shows a short schematic overview of the applied workflow, with slight changes applied here to the solvation treatment (see below). For a more detailed description, we refer to our previous work on partition coefficients.23
In short, we utilize very fast force-field (GFN-FF)31 and semi-empirical QM (GFN2-xTB)32 methods to extensively explore the chemical space and create an initial ensemble with conformer candidates. Then, by using carefully selected higher-level DFT methods (B97-d,33 def2-SV(P)34 and r2SCAN-3c35), this initial ensemble is energetically screened, and higher lying conformers are sorted out before the next higher level of theory is employed. In all steps, we use appropriate solvation models (ALPB,36,37 and COSMO-RS21,38), which are selected based on the respective accuracy and computational effort of the underlying method. Thermostatistical contributions are included using the single-point Hessian approach.39
The free energy of a molecule in each phase can then be determined by a Boltzmann weighted average over the free energies of the conformers in the ensemble giving 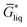 for the liquid and
for the liquid and 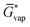 for the vapor state, both determined at the standard conditions of 1 mol l−1.40 Following Ben-Naim40 from these quantities, the vapor pressure P can be obtained from the equilibrium between the liquid and vapor state viaeqn (1),
for the vapor state, both determined at the standard conditions of 1 mol l−1.40 Following Ben-Naim40 from these quantities, the vapor pressure P can be obtained from the equilibrium between the liquid and vapor state viaeqn (1),
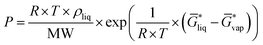 | (1) |
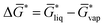 of not more than 0.1 kcal mol−1, which is smaller than the expected standard deviation of our workflow which can be estimated from typical errors of COSMO-RS for solvation free energies of about 0.8 kcal mol−1.43
of not more than 0.1 kcal mol−1, which is smaller than the expected standard deviation of our workflow which can be estimated from typical errors of COSMO-RS for solvation free energies of about 0.8 kcal mol−1.43
The analytical linearized Poisson Boltzmann (ALPB)36,37 implicit solvation model used for the initial generation of conformer ensembles in our procedure (CREST step) is only parameterized for a fixed set of common solvents, and a self-solvation treatment is not feasible. However, neglecting the influence of the solvent entirely when creating the conformer ensemble can lead to significant errors. Therefore, in the first steps of the calculations, we used solvents, that were parameterized for the ALPB solvation model and have a similar dielectric constant as the target compound. These so-called sampling solvents for each compound can be found in the ESI.†
With this approximation, we are still able to create differing conformer ensembles for the condensed and gas phase in the early stages of the workflow without the need to explicitly parameterize the ALPB solvation model for each new compound. The final solvation contributions are always computed at the COSMO-RS level and hence are specific for each target compound.
2.2 COSMO-RS
As a post-processing method, COSMO-RS uses input files created by density functional theory (DFT) calculations. These calculations were once performed as single point calculations on optimized random conformers (R) obtained from the PubChem database44 and once on the optimized structure from the lowest lying-conformer (L) obtained after our workflow in the self-solvated phase as described above with the r2SCAN-3c35 composite method. If there was no 3D conformer available from the PubChem database, the corresponding 2D conformer was converted to a 3D structure for the random conformer using the 3D structure converter implemented in the xTB program.45 The COSMO-RS calculations on these single structures for comparison with the complete CRENSO treatment were also performed using COSMO-RS version ‘16’ with fine parametrization. Vapor pressures were obtained using the intrinsic vapor pressure routine implemented in COSMOtherm. These calculations mainly serve to illustrate the effect of including extended conformer ensembles for the property calculation.Note that we use the term “COSMO-RS” throughout our work to calculate the COSMO-RS solvation free energy for a given molecular structure or a complete conformer ensemble after the CRENSO workflow. This approach should not be confused with the result of the recommended procedure in the COSMOconf/COSMOtherm commercial software.
2.3 LFER and SPARC
Poly-parameter linear free energy relationships (pp-LFER) describe a set of tools to predict physical and thermodynamic properties and partition coefficients of organic compounds. The general method is based on the determination of the following compound descriptors: the molar volume (Vi), the excess molar refraction (Ei), the logarithmic hexadecane/air partitioning coefficient (Li), the H-donor, or electron acceptor property (Ai), the H-acceptor or electron donor property (Bi) and a dipolarity/polarizability parameter (Si).46 Some of the parameters are accessible experimentally, Vi is usually determined using the McGowan increment method.47 Schwarzenbach et al.3 applied a data set of 199 apolar, monopolar, and bipolar organic compounds with known, experimentally determined vapor pressures to obtain an LFER for predicting the vapor pressure of a sub-cooled liquid with Li, Si, Ai, and Bi. The experimental vapor pressure range covered more than 12 orders of magnitude (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL (Pa) ≈ −6 → +6). Using multiple regression analysis, eqn (2) was obtained (R2 = 0.99; SD = 0.30).
PL (Pa) ≈ −6 → +6). Using multiple regression analysis, eqn (2) was obtained (R2 = 0.99; SD = 0.30).log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL,i(298 K) = −0.89 × Li − 0.44 × Si2 − 5.43 × Ai × Bi + 6.51 PL,i(298 K) = −0.89 × Li − 0.44 × Si2 − 5.43 × Ai × Bi + 6.51 | (2) |
Eqn (2) was used to calculate the vapor pressures (in Pa) of the compounds discussed in this work. The required LFER coefficients L, S, A and B are listed in the ESI.† All experimentally determined coefficients were taken from the UFZ-LSER database.48 If experimental data were not available, these were calculated based on SMILES (simplified molecular input line entry specification) structure codes using a QSAR tool implemented in the UFZ-LSER database.
The SPARC algorithm uses a summation over interaction forces between molecules (dispersion, induction, dipole and H-bonding). The energies are expressed in terms of molecular-level descriptors (volume, polarizability, dipole moment and donor/acceptor properties). These are calculated from the molecular structure. The computational approach combines LFER, structure–activity relationships and molecular orbital theory.13 SPARC needs the melting point to calculate the vapor pressure. If this was not available, or if the substance was solid at 298 K (see ESI†), “assume not solid” was selected in the SPARC menu. The SPARC vapor pressure algorithm was trained with 747 experimental data for 298 K in a vapor pressure range between approximately 5 × 10−7 atm and 50 atm.49
Both LFER and SPARC use the SMILES notation to calculate descriptors and parameters. Please note that SMILES only describes the basic structure of molecules, but not specific conformers.
2.4 Compounds
Reliable vapor pressure measurements are available for a large number of organic compounds. The recommended measurement method depends on the corresponding volatility. An OECD publication lists eight methods for the range between 10−10 Pa and 105 Pa.4 All methods are experimentally complex and require highly purified substances. In comparison, the gas chromatographic method, as described by Hinckley et al.,5 needs only small amounts of substance and is much simpler.For testing and validation of the CRENSO method, a total of 41 volatile and semi volatile organic compounds, so-called VOCs and SVOCs,50 were selected, for which experimentally determined vapor pressures are available. Of these, 40 data were rated as reliable, only the experimental vapor pressure for dihexyl phthalate (DHP) was doubtful. A vapor pressure range of 10−6 Pa to 102 Pa was covered at 298 K. The molecular flexibility of the substances varies widely, as do properties such as polarity, water solubility and partition coefficients. All compounds have no or only weak donor/acceptor properties. These substances (named “reference compounds” in the following) are compiled in Table 1. The vapor pressures relate to the liquid phase or the sub-cooled melt. If necessary, the units were converted to Pascal (Pa). In the ESI,† the melting point, boiling point and enthalpy of vaporization are also provided.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PrefL (Pa) of the reference compounds. All data for 298 K, SL = sub-cooled liquid
PrefL (Pa) of the reference compounds. All data for 298 K, SL = sub-cooled liquid
| Compound | Abbr. | CAS | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PrefL PrefL |
Ref. |
|---|---|---|---|---|
| a Literature value doubtful. | ||||
| n-Decane | C10 | 124-18-5 | 2.26 | 54 |
| n-Hexadecane | C16 | 544-76-3 | −0.72 | 55 |
| n-Tridecylbenzene | TDB | 123-02-4 | −2.15 | 56 and 57 |
| 3-Cresol | 3CR | 108-39-4 | 1.26 | 58 |
| Naphthalene (SL) | NAP | 91-20-3 | 1.57 | 59 |
| Anthracene (SL) | ANT | 120-12-7 | −1.14 | 59 |
| Fluoranthene (SL) | FLU | 206-44-0 | −2.22 | 59 |
| 2-Butoxy ethanol | EGBE | 111-76-2 | 2.06 | 60 and 61 |
| 1-Undecanol | UDC | 112-42-5 | −0.36 | 62 |
| Oleyl alcohol | OA | 143-28-2 | −3.43 | 63 |
| Glycerol | GLY | 56-81-5 | −1.60 | 64 |
| Benzophenone (SL) | BP | 119-61-9 | −0.80 | 65 |
| Benzophenone-3 (SL) | BP-3 | 131-57-7 | −2.32 | 66 |
| Homosalate | HS | 118-56-9 | −1.96 | 66 |
| Dimethyl phthalate | DMP | 131-11-3 | −0.52 | 67 |
| Diethyl phthalate | DEP | 84-66-2 | −1.00 | 68 |
| Di-n-butyl phthalate | DnBP | 84-74-2 | −2.37 | 69 |
| Butyl benzyl phthalate | BBzP | 85-68-7 | −3.70 | 69 |
| Dihexyl phthalatea | DHP | 84-75-3 | (−2.96) | 70 |
| Di-(2-ethylhexyl) phthalate | DEHP | 117-81-7 | −4.80 | 15 and 69 |
| Di-(2-ethylhexyl) terephthalate | DEHTP | 6422-86-2 | −5.27 | 69 |
| Methyl palmitoleate | MP | 1120-25-8 | −2.29 | 71 |
| Glutaric acid (SL) | GA | 110-94-1 | −3.00 | 72 |
| Pimelic acid (SL) | PA | 111-16-0 | −3.66 | 72 |
| Tris-(2-ethylhexyl) phosphate | TEHP | 78-42-2 | −4.52 | 66 |
| Tris-(2-butoxyethyl) phosphate | TBOEP | 78-51-3 | −4.17 | 66 and 73 |
| 2,4,4′-Trichlorobiphenyl (SL) | PCB-28 | 7012-37-5 | −1.57 | 74 |
| 2,2′,4,5,5′-Pentachlorobiphenyl (SL) | PCB-101 | 37680-73-2 | −2.60 | 74 |
| 2,4,5,2′,4′,5′-Hexachlorobiphenyl (SL) | PCB-153 | 35065-27-1 | −3.21 | 74 |
| 2,2′,3,4,4′,5,5′-Heptachlorobiphenyl (SL) | PCB-180 | 35065-29-3 | −3.96 | 74 |
| 1,10-Dichlorodecane | C10Cl2 | 2162-98-3 | −0.30 | 75 |
| 1,2,11,12-Tetrachlorododecane (SL) | C12Cl4 | 210115-98-3 | −2.46 | 75 |
| 2,2′,4,4′-Tetrabromodiphenyl ether (SL) | BDE-47 | 5436-43-1 | −3.49 | 76 |
| 2,2′,4,4′,5-Pentabromodiphenyl ether (SL) | BDE-99 | 60348-60-9 | −4.17 | 76 |
| 1,2,3,4,5-Pentabromo-6-ethyl benzene (SL) | PBEB | 85-22-3 | −2.54 | 66 |
| Dodecamethylcyclohexasiloxane | D6 | 540-97-6 | 0.35 | 77 |
| Hexadecamethylheptasiloxane | L7 | 541-01-5 | −1.13 | 77 |
| Octadecamethyloctasiloxane | L8 | 556-69-4 | −2.03 | 77 |
| pp′-DDT (SL) | DDT | 50-29-3 | −3.32 | 66 and 78 |
| Diazinon | DZN | 333-41-5 | −2.23 | 79 and 80 |
| Fipronil (SL) | FIP | 120068-37-3 | −5.72 | 79 |
For further, unbiased comparison with LFER and QSAR methods, 21 relevant compounds from the groups of plasticizers, biocides and pharmaceuticals were selected, whose vapor pressures are not sufficiently known. With some certainty, these compounds have so far not been used for the calibration of vapor pressure prediction methods. The plasticizers are compounds currently used in products that have completely or partially replaced classic additives.51 Many of the selected pharmaceuticals were identified as emerging contaminants in wastewater.52 The biocides are included in the list of biocidal products that may be made available on the market and used, e.g. in Germany due to an ongoing decision-making process.53
3. Results
All vapor pressure calculations for the 41 reference compounds from Table 1 are summarized in Table 2. The decimal logarithm of the vapor pressure PL (Pa) is given in each case. If the respective substance is solid at 298 K, the value represents the vapor pressure of the sub-cooled liquid.| Compound | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL CRENSO (COSMO-RS) PL CRENSO (COSMO-RS) |
SD log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL CRENSO (COSMO-RS) PL CRENSO (COSMO-RS) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL LFER PL LFER |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL SPARC PL SPARC |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL COSMO-RS (R) PL COSMO-RS (R) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL COSMO-RS (L) PL COSMO-RS (L) |
|---|---|---|---|---|---|---|
| C10 | 2.28 | 0.12 | 2.34 | 2.28 | 1.93 | 1.87 |
| C16 | −1.14 | 0.05 | −0.41 | −0.82 | −1.40 | −1.48 |
| TDB | −2.97 | 0.23 | −1.93 | −2.53 | −3.39 | −3.44 |
| 3CR | 1.01 | 0.07 | 1.28 | 1.62 | 0.78 | 0.81 |
| NAP | 1.48 | 0.00 | 1.54 | 1.52 | 1.14 | 1.14 |
| ANT | −0.81 | 0.07 | −1.02 | −1.31 | −1.21 | −1.22 |
| FLU | −1.75 | 0.08 | −2.40 | −2.07 | −2.11 | −2.13 |
| EGBE | 2.52 | 0.15 | 1.66 | 1.70 | 0.57 | 1.58 |
| UDC | −0.76 | 0.01 | 0.01 | −0.64 | −1.21 | −1.22 |
| OA | −3.51 | 0.33 | −3.50 | −4.15 | −3.85 | −3.56 |
| GLY | −0.69 | 0.03 | −0.72 | −1.26 | −4.00 | −4.33 |
| BP | −0.87 | 0.02 | −0.58 | −0.74 | −1.72 | −1.30 |
| BP-3 | −2.40 | 0.02 | −2.53 | −3.79 | −6.56 | −2.71 |
| HS | −2.12 | 0.02 | −1.72 | −2.44 | −5.23 | −2.36 |
| DMP | −0.92 | 0.05 | 0.26 | −1.25 | −1.62 | −1.23 |
| DEP | −1.09 | 0.31 | −0.40 | −1.82 | −2.38 | −1.72 |
| DnBP | −2.47 | 0.22 | −2.18 | −3.47 | −3.14 | −3.13 |
| BBzP | −4.49 | 0.09 | −4.12 | −5.47 | −6.26 | −4.89 |
| DHP | −4.49 | 0.35 | −4.11 | −5.40 | −4.70 | −4.64 |
| DEHP | −4.73 | 0.20 | −5.48 | −6.85 | −9.40 | −7.08 |
| DEHTP | −5.40 | 0.30 | −4.96 | −6.44 | −9.40 | −6.80 |
| MP | −1.68 | 0.74 | −1.59 | −1.95 | −1.92 | −1.98 |
| GA | −2.47 | 0.09 | −2.23 | −4.03 | −4.40 | −3.25 |
| PA | −3.28 | 0.43 | −3.90 | −5.10 | −4.92 | −4.29 |
| TEHP | −4.54 | 0.43 | −4.39 | −6.13 | −6.56 | −5.81 |
| TBOEP | −3.85 | 0.75 | −3.76 | −4.80 | −9.08 | −6.63 |
| PCB-28 | −1.07 | 0.06 | −1.30 | −2.05 | −1.51 | −1.83 |
| PCB-101 | −1.80 | 0.01 | −2.52 | −3.59 | −2.41 | −2.60 |
| PCB-153 | −2.56 | 0.01 | −3.35 | −4.61 | −2.97 | −3.04 |
| PCB-180 | −2.90 | 0.04 | −4.30 | −5.71 | −3.61 | −3.69 |
| C10Cl2 | −0.61 | 0.06 | 0.42 | −0.24 | −0.77 | −1.11 |
| C12Cl4 | −2.77 | 0.05 | −1.77 | −2.59 | −4.06 | −3.40 |
| BDE-47 | −4.18 | 0.01 | −3.90 | −5.18 | −4.96 | −4.95 |
| BDE-99 | −5.16 | 0.00 | −4.92 | −6.87 | −6.08 | −5.91 |
| PBEB | −2.72 | 0.00 | −3.07 | −4.23 | −3.21 | −3.16 |
| D6 | −0.89 | 0.19 | 1.09 | −0.23 | −1.45 | −1.80 |
| L7 | −1.79 | 0.01 | −0.48 | −0.27 | −3.38 | −2.44 |
| L8 | −2.75 | 0.16 | −1.33 | −1.08 | −3.15 | −3.57 |
| DDT | −3.11 | 0.00 | −3.77 | −4.19 | −3.58 | −3.58 |
| DZN | −2.74 | 0.39 | −1.28 | −3.10 | −3.03 | −3.10 |
| FIP | −5.13 | 0.08 | −8.35 | −4.60 | −9.16 | −6.42 |
Fig. 3A shows the direct comparison of the experimental values from Table 1 with the values from Table 2 calculated using CRENSO (COSMO-RS). Because our workflow contains stochastic elements, the average from three independent runs is provided. The corresponding standard deviation is usually smaller than the inherent error of the underlying QM methods. DHP was not taken into account because the experimental value appeared implausible. The data scatter around the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line, systematic deviations are not recognizable. This is also supported by the residual analysis (difference between experimental and calculated value) shown in Fig. 3B. The data are normally distributed at the 5% level, and the Grubbs outlier test was negative. The arithmetic mean is AM = 0.03 and the standard deviation SD = 0.54.
1 line, systematic deviations are not recognizable. This is also supported by the residual analysis (difference between experimental and calculated value) shown in Fig. 3B. The data are normally distributed at the 5% level, and the Grubbs outlier test was negative. The arithmetic mean is AM = 0.03 and the standard deviation SD = 0.54.
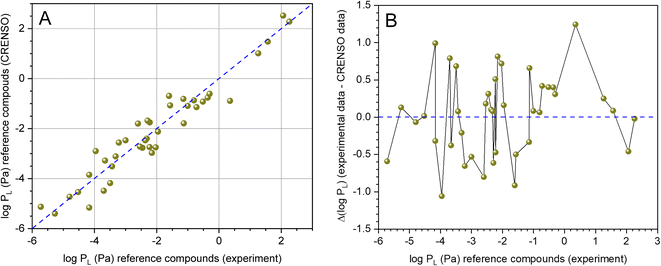 | ||
Fig. 3 (A) Correlation between experimental (see Table 1) and calculated data (CRENSO, see Table 2) for 40 reference compounds (DHP was not considered), (- - -) is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line. (B) Residual analysis of experimental data versus calculated CRENSO data. The residues are normally distributed (Shapiro–Wilk test, 5% level) with AM = 0.03 and SD = 0.54. 1 line. (B) Residual analysis of experimental data versus calculated CRENSO data. The residues are normally distributed (Shapiro–Wilk test, 5% level) with AM = 0.03 and SD = 0.54. | ||
It is also important which results our CRENSO method delivers in comparison to other calculation tools. In Fig. 4A this is shown for COSMO-RS, based on both, the random conformer (R) and the lowest-lying conformer (L). A clear deviation from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line is obvious, which increases with lower vapor pressures. A similar behavior can be seen for the comparison with SPARC, as shown in Fig. 4B. Here, too, large deviations from the 1
1 line is obvious, which increases with lower vapor pressures. A similar behavior can be seen for the comparison with SPARC, as shown in Fig. 4B. Here, too, large deviations from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line can be observed in the area of low vapor pressures. In contrast, the correlation with the LFER method is comparatively good. However, a clear exception is the substance fipronil (FIP).
1 line can be observed in the area of low vapor pressures. In contrast, the correlation with the LFER method is comparatively good. However, a clear exception is the substance fipronil (FIP).
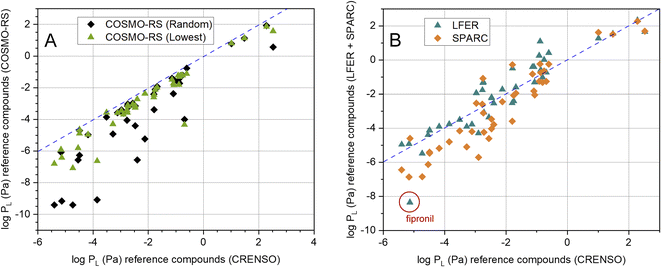 | ||
Fig. 4 (A) Correlation between calculated CRENSO data and COSMO-RS data (see Table 2) for 41 reference compounds, (- - -) is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line. (B) Correlation between calculated CRENSO data, calculated LFER and SPARC data (see Table 2) for 41 reference compounds, (- - -) is the 1 1 line. (B) Correlation between calculated CRENSO data, calculated LFER and SPARC data (see Table 2) for 41 reference compounds, (- - -) is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line. 1 line. | ||
Table 3 lists 21 relevant substances from the categories of plasticizers, biocides and pharmacologically active ingredients for which, to the best of our knowledge, no reliable vapor pressure data are available. For these substances, the vapor pressures or the vapor pressures of the sub-cooled liquid were calculated using CRENSO, LFER and SPARC. The results are also shown in Table 3. Substances were deliberately chosen for which a low vapor pressure (<1 Pa) was to be expected.
| Compound | Abbr. | CAS | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL CRENSO (COSMO-RS) PL CRENSO (COSMO-RS) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL LFERa PL LFERa |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL SPARCb PL SPARCb |
|---|---|---|---|---|---|
| a Vapor pressure for the sub-cooled liquid. Calculation: Schwarzenbach et al. (2017).3 b It was assumed that the substance is not solid at room temperature. c SMILES is for the isomer bis(7-methyloctyl) phthalate. d SMILES is for the isomer bis(7-methyloctyl) 1,2-cyclohexanedicarboxylate. e SMILES is for the isomer bis(7-methyloctyl) adipate. | |||||
| Plasticizers | |||||
| Di-2-propylheptyl phthalate | DPHP | 53306-54-0 | −5.40 | −6.71 | −8.87 |
| Di-isononyl phthalatec | DINP | 28553-12-0 | −5.09 | −6.65 | −8.04 |
| 1,2-Cyclohexane dicarboxylic acid diisononyl esterd | DINCH | 166412-78-8 | −4.50 | −6.22 | −6.88 |
| Tri-(2-ethylhexyl) trimellitate | TOTM | 3319-31-1 | −8.22 | −9.15 | −12.11 |
| Di-iso-butyl adipate | DIBA | 141-04-8 | −1.13 | −0.61 | −1.35 |
| Di-n-butyl adipate | DnBA | 105-99-7 | −0.75 | −1.25 | −1.54 |
| Di-2-ethylhexyl adipate | DEHA | 103-23-1 | −3.51 | −3.92 | −5.08 |
| Di-isononyl adipatee | DINA | 33703-08-1 | −4.51 | −5.16 | −7.12 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Biocides | |||||
| Acetamiprid (SL) | ACP | 135410-20-7 | −5.36 | −1.59 | −2.15 |
| Icaridin (SL) | ICD | 119515-38-7 | −0.71 | −2.26 | −3.08 |
| Cyromazine (SL) | CMZ | 66215-27-8 | −5.73 | −4.76 | −5.19 |
| Diflubenzuron (SL) | DFB | 35367-38-5 | −5.17 | −3.66 | −6.14 |
| Cyphenothrin | CPT | 39515-40-7 | −5.88 | −7.07 | −6.96 |
| Methoprene (SL) | MTP | 40596-69-8 | −3.00 | −1.67 | −3.54 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Pharmaceuticals | |||||
| Bisoprolol (SL) | BPL | 66722-44-9 | −4.04 | −8.02 | −6.47 |
| Diclofenac (SL) | DIC | 15307-86-5 | −4.23 | −7.11 | −6.68 |
| Dapagliflozin (SL) | DLF | 461432-26-8 | −9.61 | −19.56 | −17.85 |
| Ibuprofen (SL) | IBU | 15687-27-1 | −1.91 | −2.50 | −2.3 |
| Metoprolol (SL) | MPL | 51384-51-1 | −2.67 | −2.22 | −4.58 |
| Naproxen (SL) | NPX | 22204-53-1 | −4.05 | −5.66 | −4.65 |
| Torasemide (SL) | TS | 56211-40-6 | −8.26 | −13.44 | −9.66 |
The graphical comparison of the CRENSO versus LFER and SPARC data is displayed in Fig. 5. For SPARC, the correlation is similar to that of the reference compounds shown in Fig. 4B: larger deviations with decreasing vapor pressure. However, it is immediately apparent that for these 21 compounds of emerging interest, the correlation between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL using CRENSO and LFER is also significantly lower than for the reference compounds.
PL using CRENSO and LFER is also significantly lower than for the reference compounds.
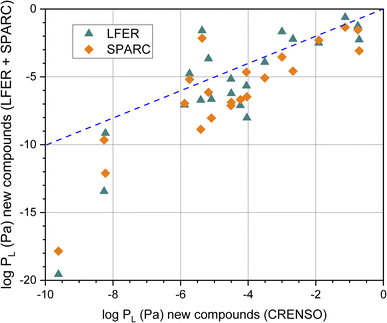 | ||
Fig. 5 Correlation of the calculated logarithmic vapor (in Pa) pressure using the LFER and SPARC method with the CRENSO data (see Table 3) for the 21 compounds of emerging interest, (- - -) is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line. 1 line. | ||
4. Discussion
4.1 Comparison of CRENSO calculations with experimental data
For substances that are liquid at room temperature and have sufficient volatility, the vapor pressure and enthalpy of vaporization can be determined experimentally with high accuracy. As can be seen from Fig. 3B, the deviations between experimental and CRENSO data have a standard deviation of approximately 0.5 log units. This means that the vapor pressure can be calculated approximately to a factor of 3. It is therefore clear that the CRENSO calculations for volatile substances deliver results, which can be regarded as reasonable trends. A typical example is 2-butoxyethanol (EGBE). Koga60 has accurately determined temperature-dependent values for this substance. At 298 K the experimental vapor pressure is 105 Pa, while CRENSO gives 331 Pa. This difference is of practical importance since vapor pressures are used to calculate saturation concentrations for inhalation exposure tests.81 Nevertheless, the deviation is within the predicted error of the CRENSO method.A completely different situation arises for substances with low volatility, especially at vapor pressures <10−2 Pa. The Knudsen and Langmuir methods are particularly suitable in this range, but require highly purified substances and temperature-dependent measurements and are only useful if no phase transition occurs in the temperature interval of interest. Therefore, the vapor pressure of the sub-cooled liquid PL often has to be extrapolated from measurements of the melt using the Antoine equation.6 Here, however, the problem can arise that organic compounds, such as fipronil, decompose at higher temperatures. This leaves only a small temperature window for the measurements, which further reduces the accuracy. Alternatively, indirect methods can be applied to determine PL, for example via gas chromatography.66 The vapor pressure of a sub-cooled liquid plays a role in atmospheric chemistry. On the basis of previous work, Pankow2 states that this parameter is more important for determining a gas/particle equilibrium than the vapor pressure of the subliming solid. Below a vapor pressure of approximately 10−2 Pa, direct measurements are usually associated with a great deal of effort and become increasingly inaccurate. For the substance DEHP alone, Mackay et al.82 list more than 20 values for vapor pressures at room temperature, some of which differ by orders of magnitude. Attempts were made to develop alternative measurement methods for compounds of low volatility.15 However, these are also associated with larger experimental inaccuracies. In comparison with the experimental data, we are convinced that in the range between 10−2 Pa and 10−5 Pa, the CRENSO method does not lead to worse results than direct vapor pressure measurements. Furthermore, we believe that at vapor pressures <10−5 Pa, our theoretical method is even more reliable.
4.2 Comparison of CRENSO calculations with LFER and SPARC data
Not particularly surprising is the fundamentally good agreement between the CRENSO and LFER data. Many of the approximately 200 compounds used for the multiple regression of eqn (2) are also listed in Table 1. Among others, these include alkanes, PCBs, PAHs, phthalates and brominated diphenyl ethers, the descriptors of which are well known.3 The CRENSO calculations and the LFER results were at least partially evaluated using the same reference data, so the comparison is biased. It is important to note at this point, that while COSMO-RS in itself contains empirical parameters, nothing has been specially adapted here or adjusted for the calculation of vapor pressures.However, the differences between the methods are already clear from Fig. 3B and exemplified in the case of fipronil (FIP). Here, the LFER descriptors had to be calculated using QSAR. At the same time, it is known that fluorinated compounds cannot be represented by the descriptors of hydrocarbon-based compounds.83 The differences for the compounds of emerging interest listed in Table 3 are even more striking (see Fig. 4B). Again, most of the descriptors had to be calculated from the SMILES using QSAR. Overall, as expected, the correlation between CRENSO and LFER for these compounds is unsatisfactory. For this reason, we also refrained from comparing the reported statistical errors and standard deviations. We can assume that with the CRENSO method, there is an uncertainty of 0.5 log units for all substances. In the case of the LFER method, a standard deviation of 0.3 log units, the standard deviation of eqn (2), can only be assumed if the target compound is structurally related to the calibration compound.
With regard to SPARC the results are clear and no extensive discussion is required. It was found earlier that SPARC gives unsatisfactory results in the range of low vapor pressures.14 Here too, both the reference compounds (see Fig. 4B) and the compounds of emerging interest (see Fig. 5) clearly show that SPARC fails at vapor pressures <1 Pa. The reason for this may be methodological. The SPARC algorithm was trained with 747 substances, but none of them had a vapor pressure <5 × 10−7 atm (<0.05 Pa).49
4.3 Conformational flexibility and comparison with COSMO-RS
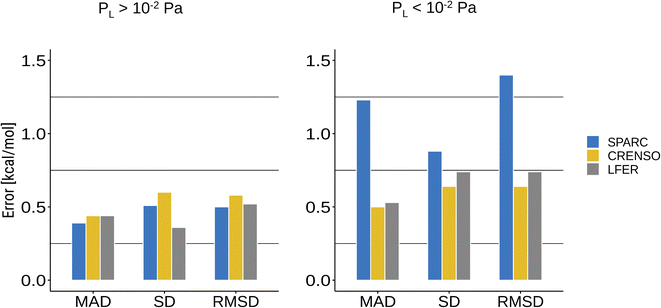
Common programs that can predict vapor pressures are often based on qualitative structure–activity relationship methods (QSAR).13 They mostly use group contributions methods based on a single molecular structure. In addition, empirical methods are highly dependent on the available experimental data that was used to train the respective methods. This makes these methods prone to errors for molecules that were not in the scope of the trained data or cannot be described by the same structure in both phases. This is especially true for compounds with small vapor pressure since the condensed phase will be dominated by strong interactions between the molecules, whereas these are not present in the gas phase and, in part, are replaced by intramolecular non-covalent interactions.For this reason, the SPARC program may yield very reasonable results for compounds with higher vapor pressure while failing for compounds with lower vapor pressure, which can be seen in Fig. 4B and 5. Fig. 6 shows a statistical analysis of the errors made by LFER, SPARC and CRENSO for lower and higher vapor pressure. The CRENSO workflow and LFER show very similar statistics for the complete set of molecules, with a mean absolute deviation (MAD) between 0.44 and 0.50 log units depending on the vapor pressure of the compounds. On the other hand, SPARC significantly undershoots for compounds with small vapor pressures, reaching a MAD between 0.39 log units for higher vapor pressures and 1.23 log units for lower ones. For the entire data set, SPARC reaches a MAD of 0.87 log units, a standard deviation (SD) of 0.91 log units and a root mean square deviation (RMSD) of 1.10 log units.
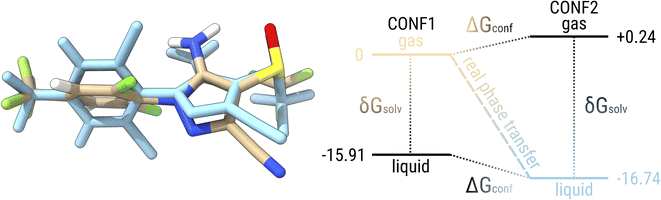
Before going into a detailed analysis of the errors that would arise in quantum chemical approaches due to the neglect of conformational flexibility, let us use fipronil (FIP) as an example to explain the difference in conformational energy contributions between two phases. Fig. 7 shows the lowest conformer of fipronil found in the condensed phase by our workflow and the lowest conformer in the gas phase. For simplicity, we consider only one structure for each phase instead of a complete ensemble of conformers. The free energy diagram on the right side of the figure shows the calculated levels for the two conformers with respect to the lowest conformer in the gas phase. These energy levels are given once in the gas phase and once with the additional solvation contribution modeling the condensed phase. Considering only the lowest conformers in each phase, the “real” phase transition would correspond to the process from CONF1 in the gas phase (beige) to CONF2 in the condensed phase (blue) with an associated free energy change of −16.74 kcal mol−1, which is equivalent to a saturation pressure of about −5.87 log units. On the other hand, if only the solvation contribution is added to CONF1, the energy contribution of the conformational rearrangement is absent and an artificial condensed state would be obtained (black, bottom). The energy change that can be attributed to this “frozen” phase change is −15.91 kcal mol−1 and thus would lead to a saturation pressure of −5.26 log units. If we consider the lowest conformer in the condensed phase and remove the contribution from solvation, this would correspond to an energy change of −16.98 kcal mol−1 and a saturation pressure of −6.05 log units. Thus, by neglecting conformational flexibility, we would introduce an error of about 0.24–0.83 kcal mol−1 or 0.18–0.61 log units, depending on which structure we assume.
To check the influence of conformations more generally, we applied the COSMO-RS method to a random and the lowest-lying conformer in the liquid, as described in section COSMO-RS, thus neglecting the conformational ensembles and their change in both phases. The results can be found in Table 2. As expected, completely neglecting the conformational flexibility by using a random conformer leads to the worst results with a MAD of 1.87 and a SD of 1.49 log units. This shows the significant effect of a molecule's actual three dimensional molecular structure (shape) for the self-solvation free energy, which is difficult to account for by empirical QSAR or LFER models because linear combinations of intramolecular and intermolecular interactions are involved. Still significant is the error of the lowest-lying conformer-only approach with a MAD of 0.91 and a SD of 0.78, which is in the range of the errors made by the SPARC program, and larger than the best performing complete ensemble method with a MAD of only 0.47 and a SD of 0.62. We attribute the considerable improvement of about 0.4–0.5 log units mainly to the proper account of the conformational ensemble change in the gas phase. Although we have shown in our previous work23 that there are significant variations in the conformational ensembles for flexible molecules in different solvents, they appear to be much smaller than the structural changes between the gas and condensed phases reported here.
5. Conclusion
The quantum mechanical workflow presented here has a decisive advantage over the usual QSAR tools: the calculated vapor pressure does not depend on structure–activity relationships, but is calculated individually for each molecule mostly based on fundamental QM and thus less susceptible to systematic errors. Our basic ansatz is non-empirical and can be systematically improved in the future by application of better procedures for the involved steps conformational search (xTB and CREST), structures and free energy ranking of conformers (DFT) and solvation free energy (COSMO-RS). The necessity of an enhanced conformer sampling workflow for predicting vapor pressures is shown by comparison to a single conformer COSMO-RS approach.From the comparison of LFER, SPARC with CRENSO (which is based on COSMO-RS), we conclude that CRENSO is currently the most reliable approach for predicting the vapor pressures of liquids and the sub-cooled liquids of solids. At high vapor pressures (>10−2 Pa), our method is suitable for realistic estimates but cannot compete with the accuracy of measurements. However, when looking at the variability of data in the range between 10−2 Pa and 10−5 Pa, for example for phthalates, PCBs, BDEs and many other substances,80,82,84,85 the quality of the CRENSO data is definitely comparable to that of experiments. Furthermore, at vapor pressures <10−5 Pa, which are difficult to determine experimentally, our method also opens up very reliable predictions, so that measurements might no longer be necessary in some circumstances.
With further developed solvation models and/or by inclusion of explicit molecules in the self-solvation treatment in an automated cluster generation approach,86 even higher accuracy of the predictions over the entire pressure range probably down to an MAD of 0.1–0.3 log units may be achieved.
Author contributions
MS: data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review and editing; SG: methodology, supervision, writing – review and editing; TS: conceptualization, formal analysis, investigation, validation, visualization, writing – original draft, writing – review and editing; UH: investigation, methodology, validation, writing – review and editing; WUP: investigation, methodology, validation, writing – review and editing.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
TS is grateful to Ms. Manuela Lingnau, Fraunhofer WKI, for the final design of Fig. 1.References
- R. Sander, Compilation of Henry's law constants (version 4.0) for water as solvent, Atmos. Chem. Phys., 2015, 15, 4399–4981, DOI:10.5194/acp-15-4399-2015.
- J. F. Pankow, Review and comparative analysis of the theories on partitioning between the gas and aerosol particulate phases in the atmosphere, Atmos. Environ., 1987, 21, 2275–2283, DOI:10.1016/0004-6981(87)90363-5.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental Organic Chemistry, John Wiley & Sons, Hoboken, NJ, 3rd edn, 2017 Search PubMed.
- OECD, Guidelines for the Testing of Chemicals, Section 1, Test No. 104: Vapour Pressure, OECD Publishing, Paris, 2006 Search PubMed.
- D. A. Hinckley, T. F. Bidleman, W. T. Foreman and J. R. Tuschall, Determination of vapor pressures for nonpolar and semipolar organic compounds from gas chromatographic retention data, J. Chem. Eng. Data, 1990, 35, 232–237, DOI:10.1021/je00061a003.
- C. L. Yaws, The Yaws Handbook of Vapor Pressure - Antoine Coefficients, Gulf Professional Publishing, Oxford, UK, 2015 Search PubMed.
- S. H. Fishtine, Reliable latent heats of vaporization, Ind. Eng. Chem., 1963, 55, 20–28, DOI:10.1021/ie50640a003.
- C. F. Grain, Vapor Pressure, in Handbook of Chemical Property Estimation Methods, eds. W. J. Lyman, W. F. Reehl and D. H. Rosenblatt, American Chemical Society, Washington D.C., 1990, Ch. 14, pp. 14/11–14/20 Search PubMed.
- E. J. Baum, Chemical Property Estimation, Lewis Pubishers, Boca Raton, 1998 Search PubMed.
- M. L. Sage and G. W. Sage, Vapor Pressure, in Handbook of Property Estimation Methods, eds. R. S. Boethling and D. Mackay, Lewis Publishers, Boca Raton, FL, 2000, Ch. 3, pp. 53–65 Search PubMed.
- W. E. Asher and J. F. Pankow, Vapor pressure prediction for alkenoic and aromatic organic compounds by a UNIFAC-based group contribution method, Atmos. Environ., 2006, 40, 3588–3600, DOI:10.1016/j.atmosenv.2005.12.004.
- W. E. Asher, J. F. Pankow, G. B. Erdakos and J. H. Seinfeld, Estimating the vapor pressures of multi-functional oxygen-containing organic compounds using group contribution methods, Atmos. Environ., 2002, 36, 1483–1498, DOI:10.1016/S1352-2310(01)00564-7.
- S. H. Hilal, S. W. Karickhoff and L. A. Carreira, Prediction of the vapor pressure boiling point, heat of vaporization and diffusion coefficient of organic compounds, QSAR Comb. Sci., 2003, 22, 565–574, DOI:10.1002/qsar.200330812.
- P. Schossler, T. Schripp, T. Salthammer and M. Bahadir, Beyond phthalates: Gas phase concentrations and modeled gas/particle distribution of modern plasticizers, Sci. Total Environ., 2011, 409, 4031–4038, DOI:10.1016/j.scitotenv.2011.06.012.
- Y. Wu, C. M. A. Eichler, S. Chen and J. C. Little, Simple method to measure the vapor pressure of phthalates and their alternatives, Environ. Sci. Technol., 2016, 50, 10082–10088, DOI:10.1021/acs.est.6b02643.
- T. Dupeux, T. Gaudin, C. Marteau-Roussy, J. M. Aubry and V. Nardello-Rataj, COSMO-RS as an effective tool for predicting the physicochemical properties of fragrance raw materials, Flavour Fragrance J., 2022, 37, 106–120, DOI:10.1002/ffj.3690.
- J. Hammer, H. Matsukami, H. Kuramochi and S. Endo, Direct measurements and modeling of congener group specific vapor pressure for chlorinated paraffins, Chemosphere, 2021, 281, 130909, DOI:10.1016/j.chemosphere.2021.130909.
- S. T. Lin, J. Chang, S. Wang, W. A. Goddard III and S. I. Sandler, Prediction of vapor pressures and enthalpies of vaporization using a COSMO solvation model, J. Phys. Chem. A, 2004, 108, 7429–7439, DOI:10.1021/jp048813n.
- K. Yui, T. Motoki, H. Kato, H. Kuramochi, T. Tsuji, S.-i. Sakai and F. Wania, Measurement of vapor pressures and melting properties of five polybrominated aromatic flame retardants, J. Chem. Eng. Data, 2018, 63, 2578–2585, DOI:10.1021/acs.jced.7b01040.
- L. Jiřiště and M. Klajmon, Predicting the thermodynamics of ionic liquids: what to expect from PC-SAFT and COSMO-RS?, J. Phys. Chem. B, 2022, 126, 3717–3736, DOI:10.1021/acs.jpcb.2c00685.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, Refinement and parametrization of COSMO-RS, J. Phys. Chem. A, 1998, 102, 5074–5085, DOI:10.1021/jp980017s.
- J. M. Goodman, What is the longest unbranched alkane with a linear global minimum conformation?, J. Chem. Inf. Comp. Sci., 1997, 37, 876–878, DOI:10.1021/ci9704219.
- T. Salthammer, S. Grimme, M. Stahn, U. Hohm and W.-U. Palm, Quantum chemical calculation and evaluation of partition coefficients for classical and emerging environmentally relevant organic compounds, Environ. Sci. Technol., 2022, 56, 379–391, DOI:10.1021/acs.est.1c06935.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192, 10.1039/C9CP06869D.
- S. Grimme, F. Bohle, A. Hansen, P. Pracht, S. Spicher and M. Stahn, Efficient quantum chemical calculation of structure ensembles and free energies for nonrigid molecules, J. Phys. Chem. A, 2021, 125, 4039–4054, DOI:10.1021/acs.jpca.1c00971.
- F. Bohle, J. Seibert and S. Grimme, Automated quantum chemistry-based calculation of optical rotation for large flexible molecules, J. Org. Chem., 2021, 86, 15522–15531, DOI:10.1021/acs.joc.1c02008.
- S. Jakobtorweihen, T. Ingram and I. Smirnova, Combination of COSMOmic and molecular dynamics simulations for the calculation of membrane–water partition coefficients, J. Comp. Chem., 2013, 34, 1332–1340, DOI:10.1002/jcc.23262.
- M. Kolář, J. Fanfrlík, M. Lepšík, F. Forti, F. J. Luque and P. Hobza, Assessing the accuracy and performance of implicit solvent models for drug molecules: conformational ensemble approaches, J. Phys. Chem. B, 2013, 117, 5950–5962, DOI:10.1021/jp402117c.
- A. Klamt, F. Eckert and M. Diedenhofen, Prediction of the free energy of hydration of a challenging set of pesticide-like compounds, J. Phys. Chem. B, 2009, 113, 4508–4510, DOI:10.1021/jp805853y.
- P. Yamin, R. Isele-Holder and K. Leonhard, Predicting octanol/water partition coefficients of alcohol ethoxylate surfactants using a combination of molecular dynamics and the conductor-like screening model for realistic solvents, Ind. Eng. Chem. Res., 2016, 55, 4782–4789, DOI:10.1021/acs.iecr.5b04955.
- S. Spicher and S. Grimme, Robust atomistic modeling of materials, organometallic, and biochemical systems, Angew. Chem., Int. Ed., 2020, 59, 15665–15673, DOI:10.1002/anie.202004239.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB - an accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671, DOI:10.1021/acs.jctc.8b01176.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799, DOI:10.1002/jcc.20495.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305, 10.1039/B508541A.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, r2SCAN-3c: A “Swiss army knife” composite electronic-structure method, J. Chem. Phys., 2021, 154, 064103, DOI:10.1063/5.0040021.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, Robust and efficient implicit solvation model for fast semiempirical methods, J. Chem. Theory Comput., 2021, 17, 4250–4261, DOI:10.1021/acs.jctc.1c00471.
- G. Sigalov, A. Fenley and A. Onufriev, Analytical electrostatics for biomolecules: Beyond the generalized Born approximation, J. Chem. Phys., 2006, 124, 124902, DOI:10.1063/1.2177251.
- A. Klamt, Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena, J. Phys. Chem., 1995, 99, 2224–2235, DOI:10.1021/j100007a062.
- S. Spicher and S. Grimme, Single-point Hessian calculations for improved vibrational frequencies and rigid-rotor-harmonic-oscillator thermodynamics, J. Chem. Theory Comput., 2021, 17, 1701–1714, DOI:10.1021/acs.jctc.0c01306.
- A. Ben-Naim and Y. Marcus, Solvation thermodynamics of nonionic solutes, J. Chem. Phys., 1984, 81, 2016–2027, DOI:10.1063/1.447824.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396, DOI:10.1021/jp810292n.
- A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805, 10.1039/P29930000799.
- J. Reinisch, M. Diedenhofen, R. Wilcken, A. Udvarhelyi and A. Glöβ, Benchmarking different QM levels for usage with COSMO-RS, J. Chem. Inf. Model., 2019, 59, 4806–4813, DOI:10.1021/acs.jcim.9b00659.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, PubChem in 2021: new data content and improved web interfaces, Nucleic Acids Res., 2021, 49, D1388–D1395, DOI:10.1093/nar/gkaa971.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended tight-binding quantum chemistry methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e01493, DOI:10.1002/wcms.1493.
- K.-U. Goss, Predicting the equilibrium partitioning of organic compounds using just one linear solvation energy relationship (LSER), Fluid Phase Equilib, 2005, 233, 19–22, DOI:10.1016/j.fluid.2005.04.006.
- M. H. Abraham and J. C. McGowan, The use of characteristic volumes to measure cavity terms in reversed phase liquid chromatography, Chromatographia, 1987, 23, 243–246, DOI:10.1007/BF02311772.
- N. Ulrich, S. Endo, T. N. Brown, N. Watanabe, G. Bronner, M. H. Abraham and K.-U. Goss, UFZ-LSER Database V 3.2.1 [Internet], Helmholtz Centre for Environmental Research, Leipzig, 2017 Search PubMed.
- S. H. Hilal, S. W. Karickhoff and L. A. Carreira, Verification and Validation of the SPARC Model, U.S. EPA, EPA/600/R-03/033, Athens, GA, 2003 Search PubMed.
- T. Salthammer, TVOC - revisited, Environ. Int., 2022, 167, 107440, DOI:10.1016/j.envint.2022.107440.
- T. Salthammer, Emerging indoor pollutants, Int. J. Hyg. Environ. Health, 2020, 224, 113423, DOI:10.1016/j.ijheh.2019.113423.
- B. Petrie, R. Barden and B. Kasprzyk-Hordern, A review on emerging contaminants in wastewaters and the environment: Current knowledge, understudied areas and recommendations for future monitoring, Water Res., 2015, 72, 3–27, DOI:10.1016/j.watres.2014.08.053.
- Bundesanstalt für Arbeitsschutz und Arbeitsmedizin (BAUA), Liste der Biozidprodukte, die in Deutschland aufgrund eines laufenden Entscheidungsverfahrens auf dem Markt bereitgestellt und verwendet werden dürfen, Dortmund, 2022, assessed: 20 February 2022 Search PubMed.
- K. Růžička and V. Majer, Simultaneous treatment of vapor pressures and related thermal data between the triple and normal boiling temperatures for n-alkanes C5–C20, J. Phys. Chem. Ref. Data, 1994, 23, 1–39, DOI:10.1063/1.555942.
- J. S. Chickos and W. Hanshaw, vapor pressures and vaporization enthalpies of the n-alkanes from C21 to C30 at T = 298.15 K by correlation gas chromatography, J. Chem. Eng. Data, 2004, 49, 77–85, DOI:10.1021/je0301747.
- P. M. Sherblom, P. M. Gschwend and R. P. Eganhouse, Aqueous solubilities, vapor pressures, and 1-octanol-water partition coefficients for C9-C14 linear alkylbenzenes, J. Chem. Eng. Data, 1992, 37, 394–399, DOI:10.1021/je00008a005.
- W. V. Wilding, T. A. Knotts, N. F. Giles and R. L. Rowley, DIPPR Data Compilation of Pure Chemical Properties, Design Institute for Physical Properties - AIChE, New York, NY, 2020 Search PubMed.
- D. P. Biddiscombe and J. F. Martin, Vapour pressures of phenol and the cresols, Trans. Faraday Soc., 1958, 54, 1316–1322, 10.1039/TF9585401316.
- Y. D. Lei, R. Chankalal, A. Chan and F. Wania, Supercooled liquid vapor pressures of the polycyclic aromatic hydrocarbons, J. Chem. Eng. Data, 2002, 47, 801–806, DOI:10.1021/je0155148.
- Y. Koga, Vapor pressures of aqueous 2-butoxyethanol solutions at 25.degree.C: transitions in mixing scheme, J. Phys. Chem., 1991, 95, 4119–4126, DOI:10.1021/j100163a041.
- W. Acree and J. S. Chickos, Phase transition enthalpy measurements of organic and organometallic compounds. sublimation, vaporization and fusion enthalpies from 1880 to 2015. Part 1. C1 − C10, J. Phys. Chem. Ref. Data, 2016, 45, 033101, DOI:10.1063/1.4948363.
- J. N'Guimbi, H. Kasehgari, I. Mokbel and J. Jose, Tensions de vapeur d'alcools primaires dans le domaine 0.3 Pa à 1.5 kPa, Thermochim. Acta, 1992, 196, 367–377, DOI:10.1016/0040-6031(92)80100-B.
- B. Koutek, M. Hoskovec, P. Vrkočová, K. Konečný and L. Feltl, Gas chromatographic determination of vapour pressures of pheromone-like compounds II. Alcohols, J. Chromatogr. A, 1994, 679, 307–317, DOI:10.1016/0021-9673(94)80573-3.
- H. K. Cammenga, F. W. Schulze and W. Theuerl, Vapor pressure and evaporation coefficient of glycerol, J. Chem. Eng. Data, 1977, 22, 131–134, DOI:10.1021/je60073a004.
- V. Štejfa, M. Fulem, K. Růžička and P. Morávek, New static apparatus for vapor pressure measurements: Reconciled thermophysical data for benzophenone, J. Chem. Eng. Data, 2016, 61, 3627–3639, DOI:10.1021/acs.jced.6b00523.
- J. O. Okeme, T. F. M. Rodgers, J. M. Parnis, M. L. Diamond, T. F. Bidleman and L. M. Jantunen, Gas chromatographic estimation of vapor pressures and octanol–air partition coefficients of semivolatile organic compounds of emerging concern, J. Chem. Eng. Data, 2020, 65, 2467–2475, DOI:10.1021/acs.jced.9b01126.
- V. Roháč, J. E. Musgrove, K. Ružička, V. Ružička, M. Zábranský and K. Aim, Thermodynamic properties of dimethyl phthalate along the (vapour + liquid) saturation curve, J. Chem. Thermodyn., 1999, 31, 971–986, DOI:10.1006/jcht.1999.0494.
- V. Roháč, K. Růžička, V. Růžička, D. H. Zaitsau, G. J. Kabo, V. Diky and K. Aim, Vapour pressure of diethyl phthalate, J. Chem. Thermodyn., 2004, 36, 929–937, DOI:10.1016/j.jct.2004.07.025.
- C. Gobble, J. Chickos and S. P. Verevkin, Vapor pressures and vaporization enthalpies of a series of dialkyl phthalates by correlation gas chromatography, J. Chem. Eng. Data, 2014, 59, 1353–1365, DOI:10.1021/je500110d.
- V. A. Tsendrovskaya, Determination of vapor pressure and volatility of some diesters of phthalic acid, Gigiena i Sanitarija, 1972, 37, 101–103 Search PubMed.
- D. Lipkind, Y. Kapustin, P. Umnahanant and J. S. Chickos, The vaporization enthalpies and vapor pressures of a series of unsaturated fatty acid methyl esters by correlation gas chromatography, Thermochim. Acta, 2007, 456, 94–101, DOI:10.1016/j.tca.2007.02.008.
- M. Bilde, K. Barsanti, M. Booth, C. D. Cappa, N. M. Donahue, E. U. Emanuelsson, G. McFiggans, U. K. Krieger, C. Marcolli, D. Topping, P. Ziemann, M. Barley, S. Clegg, B. Dennis-Smither, M. Hallquist, Å. M. Hallquist, A. Khlystov, M. Kulmala, D. Mogensen, C. J. Percival, F. Pope, J. P. Reid, M. A. V. Ribeiro da Silva, T. Rosenoern, K. Salo, V. P. Soonsin, T. Yli-Juuti, N. L. Prisle, J. Pagels, J. Rarey, A. A. Zardini and I. Riipinen, Saturation vapor pressures and transition enthalpies of low-volatility organic molecules of atmospheric relevance: from dicarboxylic acids to complex mixtures, Chem. Rev., 2015, 115, 4115–4156, DOI:10.1021/cr5005502.
- S. Brommer, L. M. Jantunen, T. F. Bidleman, S. Harrad and M. L. Diamond, Determination of vapor pressures for organophosphate esters, J. Chem. Eng. Data, 2014, 59, 1441–1447, DOI:10.1021/je401026a.
- N. Li, F. Wania, Y. D. Lei and G. L. Daly, A comprehensive and critical compilation, evaluation, and selection of physical–chemical property data for selected polychlorinated biphenyls, J. Phys. Chem. Ref. Data, 2003, 32, 1545–1590, DOI:10.1063/1.1562632.
- K. G. Drouillard, G. T. Tomy, D. C. G. Muir and K. J. Friesen, Volatility of chlorinated n-alkanes (C10–C12): Vapor pressures and Henry's law constants, Environ. Toxicol. Chem., 1998, 17, 1252–1260, DOI:10.1002/etc.5620170709.
- A. Wong, Y. D. Lei, M. Alaee and F. Wania, vapor pressures of the polybrominated diphenyl ethers, J. Chem. Eng. Data, 2001, 46, 239–242, DOI:10.1021/je0002181.
- Y. D. Lei, F. Wania and D. Mathers, Temperature-Dependent Vapor Pressure of Selected Cyclic and Linear Polydimethylsiloxane Oligomers, J. Chem. Eng. Data, 2010, 55, 5868–5873, DOI:10.1021/je100835n.
- L. Shen and F. Wania, Compilation, evaluation, and selection of physical−chemical property data for organochlorine pesticides, J. Chem. Eng. Data, 2005, 50, 742–768, DOI:10.1021/je049693f.
- A. Goel, L. L. McConnell and A. Torrents, Determination of vapor pressure-temperature relationships of current–use pesticides and transformation products, J. Environ. Sci. Health, Part B, 2007, 42, 343–349, DOI:10.1080/03601230701309494.
- D. Mackay, W. Y. Shiu, K.-C. Ma and S. C. Lee, Handbook of Physical-Chemical Properties and Environmental Fate for Organic Chemicals. Volume IV: Nitrogen and Sulphur Containing Compounds and Pesticides, CRC Press, Boca Raton, 2nd edn, 2006 Search PubMed.
- OECD, Guidelines for the Testing of Chemicals, Section 4, Test No. 403: Acute Inhalation Toxicity, OECD Publishing, Paris, 2009 Search PubMed.
- D. Mackay, W. Y. Shiu, K.-C. Ma and S. C. Lee, Handbook of Physical-Chemical Properties and Environmental Fate for Organic Chemicals. Volume III: Oxygen Containing Compounds, CRC Press, Boca Raton, 2nd edn, 2006 Search PubMed.
- S. Endo and K.-U. Goss, Predicting partition coefficients of polyfluorinated and organosilicon compounds using polyparameter linear free energy relationships (PP-LFERs), Environ. Sci. Technol., 2014, 48, 2776–2784, DOI:10.1021/es405091h.
- D. Mackay, W. Y. Shiu, K.-C. Ma and S. C. Lee, Handbook of Physical-Chemical Properties and Environmental Fate for Organic Chemicals. Volume I: Introduction and Hydrocarbons, CRC Press, Boca Raton, 2nd edn, 2006 Search PubMed.
- D. Mackay, W. Y. Shiu, K.-C. Ma and S. C. Lee, Handbook of Physical-Chemical Properties and Environmental Fate for Organic Chemicals. Volume II: Halogenated Hydrocarbons, CRC Press, Boca Raton, 2nd edn, 2006 Search PubMed.
- S. Spicher, C. Plett, P. Pracht, A. Hansen and S. Grimme, Automated molecular cluster growing for explicit solvation by efficient force field and tight binding methods, J. Chem. Theory Comput., 2022, 18, 3174–3189, DOI:10.1021/acs.jctc.2c00239.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2em00271j |
| This journal is © The Royal Society of Chemistry 2022 |