Open Access Article
Open Access ArticleThe carbon chain growth during the onset of CVD graphene formation on γ-Al2O3 is promoted by unsaturated CH2 ends†
Qi
Zhao
 a,
Masanori
Yamamoto
a,
Masanori
Yamamoto
 b,
Kaoru
Yamazaki‡
b,
Kaoru
Yamazaki‡
 c,
Hirotomo
Nishihara
c,
Hirotomo
Nishihara
 b,
Rachel
Crespo-Otero
b,
Rachel
Crespo-Otero
 *a and
Devis
Di Tommaso
*a
*a and
Devis
Di Tommaso
*a
aDepartment of Chemistry, Queen Mary University of London, Mile End Road, London E1 4NS, UK. E-mail: r.crespo-otero@qmul.ac.uk; d.ditommaso@qmul.ac.uk
bAdvanced Institute for Materials Research (WPI-AIMR)/Institute of Multidisciplinary Research for Advanced Materials, Tohoku University, 2-1-1 Katahira, Aoba, Sendai 980-8577, Japan
cInstitute for Materials Research, Tohoku University, 2-1-1 Katahira, Aoba, Sendai 980-8577, Japan
First published on 12th September 2022
Abstract
Chemical vapor deposition of methane onto a template of alumina (Al2O3) nanoparticles is a prominent synthetic strategy of graphene meso-sponge, a new class of nano porous carbon materials consisting of single-layer graphene walls. However, the elementary steps controlling the early stages of graphene growth on Al2O3 surfaces are still not well understood. In this study, density functional theory calculations provide insights into the initial stages of graphene growth. We have modelled the mechanism of CH4 dissociation on the (111), (110), (100), and (001) γ-Al2O3 surfaces. Subsequently, we have considered the reaction pathway leading to the formation of a C6 ring. The γ-Al2O3(110) and γ-Al2O3(100) are both active for CH4 dissociation, but the (100) surface has higher catalytic activity towards the carbon growth reaction. The overall mechanism involves the formation of the reactive intermediate CH2* that then can couple to form CnH2n* (n = 2–6) intermediates with unsaturated CH2 ends. The formation of these species, which are not bound to the surface-active sites, promotes the sustained carbon growth in a nearly barrierless process. Also, the short distance between terminal carbon atoms leads to strong interactions, which might lead to the high activity between unsaturated CH2* of the hydrocarbon chain. Analysis of the electron localization and geometries of the carbon chains reveals the formation of C–Al–σ bonds with the chain growing towards the vacuum rather than C–Al–π bonds covering the γ-Al2O3(100) surface. This growth behaviour prevents catalyst poisoning during the initial stage of graphene nucleation.
1. Introduction
Graphene, an atomic thick layer of carbon, has been called a ‘wonder material’ due to its superior properties such as its high charge carrier mobility, high optical transmissivity, high tensile strength, and excellent thermal conductivity.1–4 Geim and Novoselov first produced graphene by using a mechanical exfoliation technique using Scotch® tape, which provides monolayer and defect-free graphene.1 However, this method is only applicable to small-area production. A variety of methods have then been developed to produce large-area and high-quality graphene including chemical exfoliation,1 electrochemical exfoliation,5,6 chemical synthesis,7,8 and chemical vapor deposition (CVD).9,10 Among these techniques, CVD is one of the most promising synthesis methods because it can produce monolayer graphene over a large area.7,8,11–14Various hydrocarbon feedstocks have been successfully used as carbon sources, ranging from gases such as methane (CH4)3,15,16 and ethylene,17 liquids such as benzene,18 to solids such as polymethylmethacrylate (PMMA)19 and amorphous carbon thin films.20,21 Since it can generate single-layered graphene (SLG), the most popular combination of carbon feedstock and substrates for graphene production is CH4 on Cu.22 In addition to Cu, different metal substrates, including Ni,14,23–26 Ru,27–29 Ir,30–32 Co,33,34 Fe,35 Au,36 Rh,37 Pt,38,39 and their alloys,40,41 have been used for CVD synthesis of graphene films. Also, graphene layers can directly grow on insulating substrates such as SiC,41,42 sapphire,43 SiO2,44,45 and h-BN.46,47 Previously, Li et al.48,49 provided an atomic picture of the step-by-step nucleation process of graphene growth on the metal Cu (111) surface. This work demonstrated that at the early stages of the CVD process, linear chains form on the Cu surface, followed by Y-type (furcate) carbon species when new carbon atoms absorb on the side of the linear chains. Finally, ring-containing carbon species and graphene islands form spontaneously stepwise.
Recently, oxides of earth abundant catalysts without noble metal supporting like MgO,50 CaO,51 and Al2O352 have been reported as substrates in the synthesis of novel graphene meso-sponge (GMS), a new class of mesoporous carbon materials consisting mainly of single-layer graphene walls with a unique set of properties compared to traditional graphene materials: higher surface area, more developed mesopores, higher oxidation resistance,53,54 higher softness and elasticity, lower bulk modulus, and force-driven reversible liquid–gas phase transition.55 But until now, there is a lack of an atomistic description of the steps controlling the early stages of graphene nucleation on metal oxides. Hence, a better understanding of the reaction mechanisms is required to modify the catalytic sites and make them more active in the processes involved. These processes include the activation of adsorbed methane (CH4*), formation of carbon–hydrogen nuclei, and the subsequent edge growth of graphene islands. By combining experiments and density functional theory (DFT), we previously found that oxygen vacancies on the metal oxide surface of γ-Al2O3,56,57 play an influential role in the CH4* activation. Park et al. reported calculations of the graphene nucleation mechanism on γ-Al2O3.57 In this work, the hypothesis was that growth occurs from adsorbed carbon (C*) atoms. Page et al.58 also reported graphene nucleation on γ-Al2O3 using a simplified surface model that did not consider hydroxylated surfaces, which we recently demonstrated to be important in experimental conditions.56
In this work, we focus on the mechanism of carbon chain growth during the initial stages of graphene formation on hydroxylated models of γ-Al2O3 using DFT calculations. CH4* activation and the early stages of graphene nucleation occur preferentially on the γ-Al2O3 (100) surface. In the complete dehydrogenation process from CH4* to C*, methylene (CH2*) is the most stable species on the γ-Al2O3 surface whilst C* is highly unstable. The CH2* radical is involved in the CH4 conversion into various CnH2n* (n = 2–6) intermediates to form carbon chains on γ-Al2O3 (100) during the initial CVD of graphene.
2. Computational details
The “Vienna ab initio simulation package” (VASP.5.4.1) was used to conduct spin polarized DFT calculations. The Perdew–Burke–Ernzerhof (PBE) generalized-gradient approximation (GGA) was adopted to describe the exchange and correlation terms,59 together with the Grimme's-D3 dispersion correction60 to provide a more accurate description of the ionic induce dipole interaction than standard DFT–GGA methods.61 A plane-wave basis set was employed within the framework of the projector augmented wave method.62 The transition states (TSs) for the elementary reactions were located using the climbing image nudged elastic band (CI-NEB) method,63 setting the convergence criteria at 0.05 eV Å−1 during the TS searching.1 A Monkhorst–Pack k-point grid of (3 × 3 × 1) and a plane-wave cut-off of 450 eV were used throughout calculations. All atoms were relaxed during the structural optimization of γ-Al2O3 and reaction intermediates.Our previous IR experiments showed that isolated hydroxyl (OH) groups (around 3701 cm−1) at the γ-Al2O3 surfaces are present even after annealing at 900 °C for 30 min.56 Therefore, the surface of γ-Al2O3 was modelled using a supercell approach with periodic boundary conditions. The coordinates of γ-Al2O3 (the P21/m space group)64 were used as the starting geometry to optimise the internal coordinates and cell parameters of the bulk structure of γ-Al2O3.65 The values of the optimized lattice parameters of γ-Al2O3 were a = 5.538 Å, b = 8.347 Å, c = 8.024 Å, β = 90.60° and α = β = 90.00° (Fig. S1, ESI†). The partially hydroxylated slabs of γ-Al2O3 (100), γ-Al2O3 (110), γ-Al2O3 (001), and γ-Al2O3 (111) surface containing four atomic layers of the oxide and 15 Å vacuum were constructed starting from the optimised bulk structure. All atoms were relaxed during the optimization. The structures of the surfaces are provided in Section S2 of the ESI.† The mechanisms of CH4 activation and the early stages of graphene nucleation were investigated using the OH-covered γ-Al2O3 (111), γ-Al2O3 (110) and γ-Al2O3 (001) surfaces. These models are shown in Fig. S2 (ESI†). The adsorption energies of CH4 on the γ-Al2O3 surfaces were computed using the following expression:
| Eads = E(adsorbate⋯CH4) − E(CH4) − E(slab) | (1) |
| ΔG = ΔEDFT + ΔEZPE − TΔS | (2) |
3. Results and discussion
3.1 Methane activation on γ-Al2O3
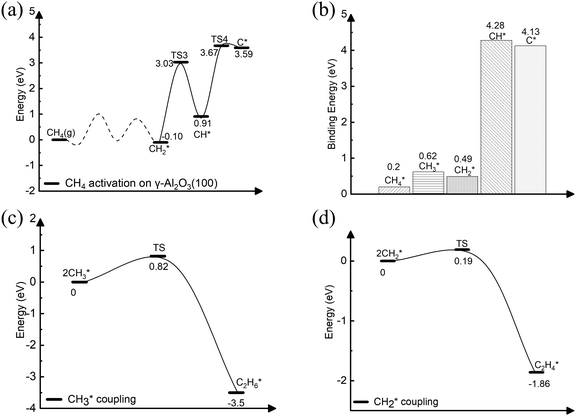
We report the calculations of the intermediates and transition states of the first two steps of the CH4* dehydrogenation, CH4* → CH3* + H* and CH3* → CH2* + H*. The profiles in Fig. 1 show the ability to activate CH4* depending on the surface of γ-Al2O3: (100), (110), (111), and (001). The structures of the intermediates and transitions states on the γ-Al2O3 (100) surface are reported in Fig. 2. For the other surfaces, these structures are shown in Fig. S3 of the ESI.†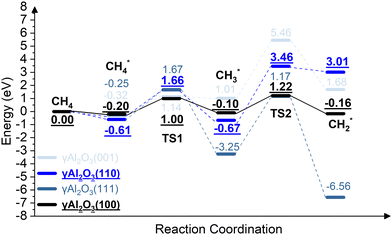 | ||
| Fig. 1 The energy profiles of the first two steps of the CH4* dehydrogenation, CH4* → CH3* + H* and CH3* → CH2* + H*, on the γ-Al2O3 (001), γ-Al2O3 (111), γ-Al2O3 (110), and γ-Al2O3 (100) surfaces. | ||
On γ-Al2O3 (100), after the exothermic adsorption of CH4* (Eads = −0.20 eV), the breakage of the first C–H bond has a barrier of 1.20 eV and a reaction energy of 0.10 eV. The subsequent dehydrogenation of CH3* has a barrier of 1.32 eV and reaction energy of −0.06 eV. The barriers for the dissociation step CH4* → CH3* + H* on the (111), (001), and (110)57,66 are 1.92 eV, 1.46 eV, and 2.20 eV, respectively (Fig. 1). The subsequent step, CH3* → CH2* + H*, on these surfaces requires even higher barriers. Consequently, the first two CH4* dehydrogenation steps are kinetically favorable on the γ-Al2O3 (100) surface. Martínez et al. reported that CH2* leads to spontaneous C–C chain growth.67 Hence, the ability to promote the CH3* dehydrogenation step to generate a stable CH2* species will also denote the catalytic activity towards carbon growth. However, CH2* will be a trapped species on the (111) surface due to highly exothermic conversion energies depicted in Fig. 1. We have considered the γ-Al2O3 (100) surface to investigate the subsequent steps of CH2* coupling that initiates the graphene growth due to its favorable CH4 dissociation properties (Fig. 1). Note also that the (111) surface is more unstable than the (100) and (110) surfaces.68 In addition, the C–H bond activation barrier on the three-coordinated Al site of the γ-Al2O3 (110) surface obtained in this work (1.9 eV) is slightly higher than the one reported by Wischert et al. (1.6 eV).69 Such a difference might be mainly related to differences in the surface model and methods adopted, including the OH coverage, surface unit size, the distance between OH and active sites as well as exchange–correlation functional, pseudopotentials used in the calculations. However, the barriers of the CH4* → CH3* + H* and CH3* → CH2* + H* steps on the (100) surface are 1.0 eV and 1.2 eV, respectively. These barriers are still lower than the value of 1.6 eV reported by Wischert et al. for the (110) surface. In this work the conclusion that the first two CH4* dehydrogenation steps are kinetically favourable on (100) is still significant.
Park et al.57,66 and Cholewinski et al.57,66 reported that γ-Al2O3 (110) can have different levels of hydroxyl coverages that in turn could affect the strength of CH4* interaction with the surface. The work by Digne et al. on the stability of the γ-Al2O3 (110) surface as a function of temperature for different hydroxyl coverage68 showed that at T = 1000 K, the approximate temperature necessary to grow porous nanographene on γ-alumina nanoparticles,56,57 the low OH coverage model (2OH/θ = 2.4 nm−2) is the most stable surface. Moreover, in our previously reported experimental work of the CH4-CVD, air and moisture were excluded by supplying Ar and CH4 gases,54 which decreases the concentration of hydroxyl groups as the reaction proceeds. These previous reports justify the use of a low OH coverage model for the γ-Al2O3(110) surface.
3.2 Contribution of the (100) and (110) surfaces to CH2 generation
CH2 generation on the γ-Al2O3 surface is a pseudo-first order reaction on the methane partial pressure.56 If the entropy contribution is negligible, the activation rate constant k can be approximated with an Eyring-like equation as a function of reaction temperature T,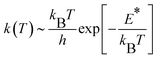 | (3) |
3.3 Onset of graphene formation: methylene coupling and carbon chain growth
The complete dehydrogenation of CH4 on γ-Al2O3 would lead to the formation of an adsorbed carbon atom (C*). We have computed the energy profile of CH4 dehydrogenation on γ-Al2O3 (100) as a representative surface leading to C*. Fig. 3(a) shows that while the first two dehydrogenation steps CH4* → CH3* + H* and CH3* + H* → CH2* + 2H* are both favourable, the subsequent steps CH2* + 2H* → CH* + 3H* and CH* + 3H* → C* + 4H* are endothermic with high activation barriers. But since the pyrolytic carbon deposition of CH4 occurs at temperatures higher than 800 °C,56 CH4 could still dissociate into CH3*, CH2*, CH* and C* species on the catalyst surface. To verify the relative stability of these species, we have compared in Fig. 3(b) the binding energies (Eb) of CHn (n = 0–4) on γ-Al2O3 (100). For CH4*, CH3*, and CH2*, the values of Eb are 0.2, 0.6, and 0.5 eV, respectively, but for CH* and C* they are above 4 eV. According to the Sabatier principle, the strong binding of CH* and C* on γ-Al2O3 (100) may poison the active centres. Therefore, we propose that the initial CVD growth of graphene on alumina does not involve CH* and C* species. The next steps in the formation of C–C bonds on the γ-Al2O3 (100) surface are the coupling reactions 2CH3* → C2H6* (Fig. 3(c)) and 2CH2* → C2H4* (Fig. 3(d)). The pathway leading to C2H4* in Fig. 3(d) has a lower activation barrier (0.2 eV) compared to C3H6* (0.8 eV) in Fig. 3(c). Moreover, the subsequent coupling of CH3* with the C2H6* intermediate is unlikely to occur as the CH3 ends of the molecule are saturated (the C atom has reached the four coordination), inhibiting further growth as shown in Fig. S4 of the ESI.† We have also calculated the dehydrogenation of C2H6* into C2H4* but this process is both kinetically hindered (overall Ea = 4.01 eV) and thermodynamically unfavourable (overall ΔE = 2.05 eV) as shown in Fig. S5 (ESI†). Based on the above results, we conclude that CH2* is the key intermediate for the subsequent carbon growth steps on the γ-Al2O3 (100) surface.Starting from C2H4*, we have considered the methylene coupling processes to form linear CnH2n* (n = 3–6) species and the C6H12 ring unit, the minimal unit of graphene on γ-Al2O3 (100). The energy profile of the chain growth reactions and the corresponding snapshots are shown in Fig. 4 and 5, respectively. Like the CH2* to C2H4* coupling reaction, Fig. 4 shows that the subsequent methylene coupling processes are thermodynamically favourable with each adsorption step, CnH2n + CH2(g) → CnH2n + CH2*, having negative reaction energies of approximately −2 eV. The formation of the linear species C2H4*, C3H6*, C5H10*, and C6H12* and of the C6 ring have low activation barriers, all well below 1 eV. The exception is the step CH2* + C3H6* →C4H8* with an activation energy of 1.87 eV (see Section 3.4 for explanation).
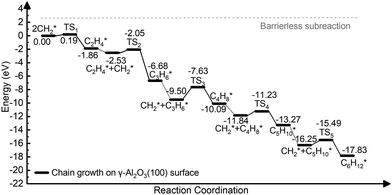 | ||
| Fig. 4 Energy profile of the formation of CnH2n* (n = 2–6) species via CH2* coupling on the γ-Al2O3 (100) surface. | ||
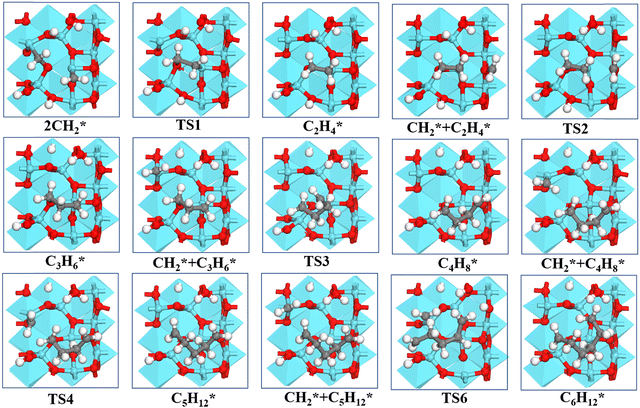 | ||
| Fig. 5 Structures of the formation of CnH2n* (n = 2–6) species via CH2* coupling on the γ-Al2O3 (100) surface. | ||
The formation of CH2* from CH4 is favourable in entropy but unfavourable in enthalpy on most facets. However, chain growth and cyclization are favourable in enthalpy and unfavourable in entropy. Both factors impact the reaction kinetics and, consequently, how fast the graphene layer grows. To address the role of entropy, we have performed frequency calculations of the reaction intermediates in Fig. 4 involved in CnH2n* (n = 2–6) species formation via CH2* coupling on the γ-Al2O3 (100) surface. The Gibbs free energy diagram confirms that the chain growth is overall a thermodynamically favourable process as well. In the calculation of the reaction barriers, the ZPEs for some systems are non-negligible,71,72 while in some surface catalytic reactions, adsorption removes many of the degrees of freedom associated with the reaction vacuum, and the ZPE contribution would be negligible relative to the calculated electronic energy.73 Since our case is similar to the latter, we have neglected ZPE corrections in reaction barrier calculations. These results confirm that the role of unsaturated CH2* ends for carbon chain growth during the graphene nucleation stage, which makes the initial growth process highly favourable.
3.4 The role of unsaturated CH2 end in promoting graphene growth
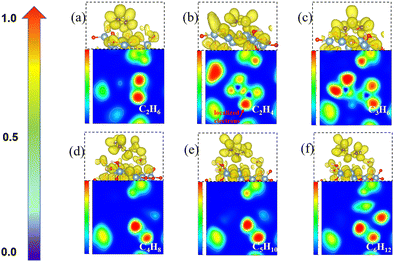
To understand the process of CH2* coupling leading to the carbon chain growth on the γ-Al2O3 (100) surface, we have computed the electron localization function (ELF) of the linear CnH2n (n = 2–6) intermediates. The ELF maps in Fig. 6 represent the electron cloud localized and delocalized around atoms. Using this information, we can determine critical points, chemical bonds, and regions relevant for reactivity (red and orange).The ELF map for the C2H4* structure in Fig. 6(b) shows a localized electron around one end of CH2* (red area) and a lower electronic charge density distribution around the other end. This weakly saturated CH2* end allows coupling with free CH2* on the γ-Al2O3 (100) surface making the formation of C2H4* highly favorable (Fig. 4). When the longer carbon chains C4H8*, C5H10* and C6H12* are formed, the sole CH2* in one position of CnH2n* is located on the γ-Al2O3 (100) surface as shown in Fig. 6(d)–(f). Consequently, the initial growth direction of carbon occurs in the vacuum, away from the surface, and the long carbon species form a C–Al–σ bond with the γ-Al2O3 (100) surface rather than grow along the catalytic surface to form a C–Al–π bond. This protects the CVD graphene nucleation reaction sites on γ-Al2O3 (100). Otherwise, the accumulation of CnH2n* species on the surface would poison the catalyst in the early stage by covering these heavy carbon species on the surface. This ‘loop’ away surface carbon growth mechanism was previously proposed by Zhu et al.74 in the case of Ni clusters.
The ELF analysis can be used to rationalize the high activation energy (1.87 eV) of the CH2* + C3H6* coupling step shown in Fig. 4. The ELF map of C3H6* (Fig. 6(c)) shows the high localization of the electron density on both ends of CH2* ends in C3H6* on the catalyst surface. The high barrier is because the two ends of C3H6* are bound to the surface-active sites forming highly hindered carbon ends. This is not beneficial for the coupling with the next CH2*. Therefore, we propose that the carbon chain growth mechanism mostly involves the free CH2* ends. The work by Lidia Martínez et al.67 also demonstrated that the presence of CH2 leads to efficient C–C chain growth producing micron-length fibres under metal-catalyst-free gas-phase synthesis. This situation leads to a high barrier for the CH2* + C3H6*→ C4H8* step (Fig. 4) as both the CH2* ends have been bonded with surface hindering further reaction. Therefore, unsaturated CH2* species play a crucial role in promoting the nucleation reaction on γ-Al2O3.
The detachment after the carbon chain growth on γ-Al2O3(100) can be rationalized because the length between the CnH2n ends and the active sites on the catalyst surface increases with the chain growth (Fig. S7, ESI†). This is beneficial for the release of the carbon chain as reported by Martínez et al.67 In long carbon chains, the unsaturated CH2* end would drive sustainable chain growth. There is also a termination pathway that involves the coupling of such open ends with CH3* species (1.83 eV barrier and −1.79 exothermic reaction energy, as shown in Fig. S8, ESI† depicted). This path would suppress the chain growth as the saturated hydrocarbon will desorb, especially if it occurs at the early stage. Thus, not all reactions will lead to the formation of graphene as there are parallel reactions that form other heavier hydrocarbons which also compete for methane.56
The length of the C–C bonds in the CnH2n species binding on γ-Al2O3(100) expands with the chain length (Fig. 7), which could support the carbon units growing away from the γ-Al2O3 (100) surface with the formation of C–Al–σ bonds rather than C–Al–π bonds covering the surface.67 In addition, the C–C length between carbon atoms close to the solid surface is longer than the C–C length of the carbon atoms away from the surface. For instance, the structure of C6H12* in Fig. 7(g) shows that for the C atoms in the middle positions, C1, C2, C3 and C4, the distances are d(C1–C2) = 1.54 Å, d(C1–C3) = 1.54 Å, d(C2–C4) = 1.54 Å. In comparison, for the terminal C atoms, C5 and C6, d(C4–C6) = 1.49 Å and d(C3–C5) = 1.49 Å. A similar situation can be found in C4H8* and C5H10*. Short bond lengths between terminal carbons correspond to strong interatomic interaction, which might contribute to the high activity among the unsaturated CH2* of the hydrocarbon chain.
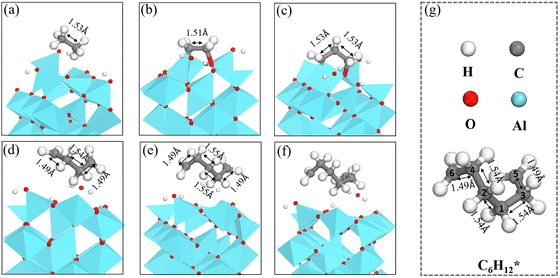 | ||
| Fig. 7 The structures of (a) C2H6*, (b) C2H4*, (c) C3H6*, (d) C4H8*, (e) C5H10*, (f) and C6H12* on γ-Al2O3(100). (g) Bond lengths in C6H12*. | ||
3.5 Dehydrogenation of CnH2n species and ring condensation
Methylene coupling reaction on γ-Al2O3 leading to CnH2n species is favorable compared to the complete CH4* dehydrogenation (Fig. 3(a) and 4). Consequently, according to our simulations the species involved in the early stage of graphene growth will contain hydrogen atoms. Previous experimental works showed that metal oxides such as alumina75 and zirconia76 can effectively catalyze the dehydrogenation of small alkanes such as propane at high temperatures.Given the high temperature used in the CVD process, we have computed the dehydrogenation of the intermediates C3H6* and C6H12* with unsaturated CH2 ends: C3H6* to C3H4* and C6H12* to C6H10*. In a related computational study, Dixit and co-workers investigated the propane dehydrogenation on γ-Al2O3 according to two possible surface mechanisms: the concerted and stepwise pathways.77,78 In the former the olefin formation occurs in a single step, whereas the latter occurs sequential abstraction of hydrogen atoms from the reactant. For the propane molecule, Dixit and co-workers concluded that the concerted pathway was preferred over the stepwise mechanism. As the CnH2n* intermediates considered in this study (Fig. 5) are not alkanes, as in the work by Dixit and co-workers,78 but hydrocarbon chains with unsaturated CH2* ends they will behave differently.
The energy profiles of C3H6* and C6H12* dehydrogenation according to the concerted mechanism are reported in Fig. S9 of the ESI.† In the concerted pathway, the initial step (C–H activation) involves a six-membered transition state, and the dehydrogenation of CnH2n* generates two surface-bound hydrogens on the acid–base pair. In the second step (H2 production), the two surface-bound hydrogen atoms recombine to form molecular hydrogen. For both C3H6* and C6H12* unsaturated intermediates, the dehydrogenation and H2 formation steps have much higher reaction energies and activation barriers than those reported by Dixit et al. for propane on γ-Al2O3 (100).78 The energy profiles of C3H6* and C6H12* dehydrogenation, computed according to the stepwise mechanism, are reported in Fig. S10 of the ESI.† In the stepwise pathway, the initial step (C–H activation) occurs by the abstraction of a proton by a surface oxygen atom followed by a H2 formation through β-hydrogen elimination78 elimination. Notwithstanding, the stepwise pathway (Fig. S10, ESI†) is favoured compared to the concerted one (Fig. S9, ESI†), and the stepwise dehydrogenation reactions have much higher activation barriers than the CH2* coupling reaction in Fig. 4.
The carbon coupling reaction forming a C6 ring was also explored since it represents the early stage of graphene nucleation.79 As shown in Fig. 8, the ring formation from C6H12* is energetically favourable (−3.09 eV) and has a low activation barrier (0.34 eV). The calculations suggest that even at the high temperatures at which CVD occurs, the dehydrogenation of the C2H2n intermediates during initial stage is unlikely because the process is kinetically and thermodynamically unfavourable compared to the ring formation. In addition, as depicted in Fig. S10 (ESI†), the activation barriers of the two elementary dehydrogenation steps of C3H6* (4.15 eV and 3.85 eV) are much higher than those of C6H12* (1.58 eV and 1.96 eV). This could indicate that the dehydrogenation of longer carbon chains could be easier than that of short ones. Thus, in the initial nucleation stage, small-size carbon species may not be stable without hydrogen until they grow to a specific size.
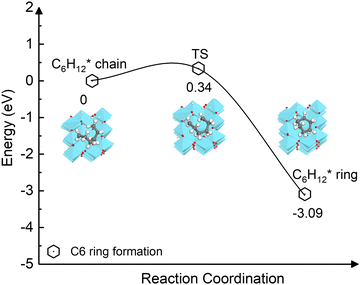 | ||
| Fig. 8 Energy profile of the ring formation from the carbon chain C6H12* species on the γ-Al2O3 (100) surface. | ||
These results indicate that the initial steps of graphene growth involve carbon species that contain hydrogen atoms and confirm that the process does not occur through the formation of single carbon. These hydrogen atoms could also hinder the formation of a binding carbon island covering the catalyst surface. Based on these results, an interesting question is when hydrogen-free graphene flake would nucleate. A possible mechanism is that small carbon-containing species are not stable without hydrogen until they grow to a defined size. However, in the early nucleation stage, hydrogen transfer among carbon atoms is much easier than hydrogen desorption from carbon (Fig. S11, ESI†). In perspective, we look forward to answering this question with our future work and understanding the link between hydrogen-free graphene nucleation and hydrocarbon sub-intermediates.
4. Conclusions
This work has reported a systematic investigation of the mechanism of CH4* dissociation and formation of CnH2n (n = 2–6) species on γ-Al2O3. We found γ-Al2O3 (100) to be the most active for the CH4* dissociation compared with other low-index surfaces of γ-Al2O3. On the (100) surface, methylene coupled to C2H4* is kinetically and thermodynamically favoured over the complete CH4* dehydrogenation to C. Starting from C2H4*, we have modelled the formation of linear CnH2n* (n = 3–6) species and the C6H12 ring unit, which is the fundamental graphene unit. We found that this early carbon chain formation stage before graphene nucleation is nearly barrierless. Electron localization function and structural analyses of carbon chains reveal that the early stages of nucleation involve the formation of C–Al–σ bonds with chains “looping” away from the catalyst surface and the unsaturated CH2* end remaining active. This is favorable for the initial steps of graphene growth. Our calculations show that hydrogenated carbon species are involved in the early stages of graphene nucleation. These protective bonded hydrogen atoms could weaken the direct C–Al interaction and protect the active sites from carbon covering the γ-Al2O3 (100) surface. In summary, our calculations illustrate the first steps of graphene nucleation on γ-Al2O3 surfaces and provide insight into the role of active species during the catalytic process.Author contributions
Qi Zhao, Rachel Crespo-Otero and Devis Di Tommaso conceived and designed the project, and summarized all the ideas provided by co-authors. Qi Zhao conducted the quantum chemistry calculations and wrote the original draft. Hirotomo Nishihara, Masanori Yamamoto, and Kaoru Yamazaki provided valuable comments and suggestions for the original draft. All authors contributed to review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Cooperative Research Program for CORE lab of “Five-star Alliance”, JST SICORP Grant no. JPMJSC2112, Ensemble Grant for Early Career Researchers at Tohoku University, and the UK's Royal Society International Exchanges Cost Share (IEC\R3\193106). Q. Z. thanks the China Scholarship Council for financial support. K. Y. is grateful for the financial support from the Building of Consortia for the Development of Human Resources in Science and Technology funded by MEXT and the Core Research for Evolutional Science and Technology of the Japan Science and Technology Agency (JST CREST, Grant No. JPMJCR16P3). D. D. T. acknowledges the ACT program (Accelerating CCS Technologies, Horizon2020 Project No. 294766), which funded the FUNMIN project. Financial contributions were made from Department for Business, Energy & Industrial Strategy (BEIS) together with extra funding from NERC and EPSRC research councils, United Kingdom, ADEME (FR), MINECO-AEI (ES). We are grateful to the UK Materials and Molecular Model-ling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (https://www.archer.ac.uk). This research utilized Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT. https://doi.org/10.5281/zenodo.438045.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- A. Balandin, Nat. Mater., 2011, 10, 569–581 CrossRef CAS PubMed.
- A. A. Balandin, Nat. Nanotechnol., 2010, 5, 574–578 CrossRef PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- P. Yu, S. E. Lowe, G. P. Simon and Y. L. Zhong, Curr. Opin. Colloid Interface Sci., 2015, 20, 329–338 CrossRef CAS.
- J. Liu, Graphene-based composites for electrochemical energy storage, Springer, Singapore, 2017 Search PubMed.
- S. Eigler, M. Enzelberger-Heim, S. Grimm, P. Hofmann, W. Kroener, A. Geworski, C. Dotzer, M. Röckert, J. Xiao and C. Papp, Adv. Mater., 2013, 25, 3583–3587 CrossRef CAS PubMed.
- S. Stankovich, D. A. Dikin, R. D. Piner, K. A. Kohlhaas, A. Kleinhammes, Y. Jia, Y. Wu, S. T. Nguyen and R. S. Ruoff, Carbon, 2007, 45, 1558–1565 CrossRef CAS.
- A. Reina, S. Thiele, X. Jia, S. Bhaviripudi, M. S. Dresselhaus, J. A. Schaefer and J. Kong, Nano Res., 2009, 2, 509–516 CrossRef CAS.
- X. Li, W. Cai, L. Colombo and R. S. Ruoff, ACS Nano Lett., 2009, 9, 4268–4272 CrossRef CAS.
- K. Parvez, S. Yang, X. Feng and K. Müllen, Synth. Met., 2015, 210, 123–132 CrossRef CAS.
- Y. Zhang, L. Zhang and C. Zhou, Acc. Chem. Res., 2013, 46, 2329–2339 CrossRef CAS PubMed.
- M. A. Azam, N. N. Zulkapli, N. Dorah, R. N. A. R. Seman, M. H. Ani, M. S. Sirat, E. Ismail, F. B. Fauzi, M. A. Mohamed and B. Y. Majlis, ECS J. Solid State Sci. Technol., 2017, 6, M3035–M3048 CrossRef CAS.
- A. Reina, X. Jia, J. Ho, D. Nezich, H. Son, V. Bulovic, M. S. Dresselhaus and J. Kong, ACS Nano Lett., 2009, 9, 30–35 CrossRef CAS PubMed.
- X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung and E. Tutuc, Science, 2009, 324, 1312–1314 CrossRef CAS.
- J. K. Wassei, M. Mecklenburg, J. A. Torres, J. D. Fowler, B. Regan, R. B. Kaner and B. Weiller, Small, 2012, 8, 1415–1422 CrossRef CAS PubMed.
- L. Gao, J. R. Guest and N. P. Guisinger, ACS Nano Lett., 2010, 10, 3512–3516 CrossRef CAS.
- Z. Li, P. Wu, C. Wang, X. Fan, W. Zhang, X. Zhai, C. Zeng, Z. Li, J. Yang and J. Hou, ACS Nano, 2011, 5, 3385–3390 CrossRef CAS PubMed.
- Z. Sun, Z. Yan, J. Yao, E. Beitler, Y. Zhu and J. M. Tour, Nature, 2010, 468, 549–552 CrossRef CAS PubMed.
- T. Liang, Y. Kong, H. Chen and M. Xu, Chin. J. Chem., 2016, 34, 32–40 CrossRef CAS.
- H. Ji, Y. Hao, Y. Ren, M. Charlton, W. H. Lee, Q. Wu, H. Li, Y. Zhu, Y. Wu and R. Piner, ACS Nano, 2011, 5, 7656–7661 CrossRef CAS PubMed.
- P. Wu, W. Zhang, Z. Li and J. Yang, Small, 2014, 10, 2136–2150 CrossRef CAS PubMed.
- M. Xu, D. Fujita, K. Sagisaka, E. Watanabe and N. Hanagata, ACS Nano, 2011, 5, 1522–1528 CrossRef CAS PubMed.
- Q. Yu, J. Lian, S. Siriponglert, H. Li, Y. P. Chen and S. S. Pei, Appl. Phys. Lett., 2008, 93, 113103 CrossRef.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J. H. Ahn, P. Kim, J. Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710 CrossRef CAS PubMed.
- J. Lahiri, T. Miller, L. Adamska, I. I. Oleynik and M. Batzill, ACS Nano Lett., 2011, 11, 518–522 CrossRef CAS PubMed.
- P. W. Sutter, J. I. Flege and E. A. Sutter, Nat. Mater., 2008, 7, 406–411 CrossRef CAS PubMed.
- E. Loginova, N. C. Bartelt, P. J. Feibelman and K. F. McCarty, New J. Phys., 2008, 10, 093026 CrossRef.
- E. Loginova, N. Bartelt, P. Feibelman and K. McCarty, New J. Phys., 2009, 11, 063046 CrossRef.
- E. Loginova, S. Nie, K. Thürmer, N. C. Bartelt and K. F. McCarty, Phys. Rev. B, 2009, 80, 085430 CrossRef.
- J. Coraux, M. Engler, C. Busse, D. Wall, N. Buckanie, F. J. M. Zu Heringdorf, R. Van Gastel, B. Poelsema and T. Michely, New J. Phys., 2009, 11, 023006 CrossRef.
- P. Lacovig, M. Pozzo, D. Alfe, P. Vilmercati, A. Baraldi and S. Lizzit, Phys. Rev. Lett., 2009, 103, 166101 CrossRef.
- O. Rader, A. Varykhalov, J. Sánchez-Barriga, D. Marchenko, A. Rybkin and A. Shikin, Phys. Rev. Lett., 2009, 102, 057602 CrossRef CAS PubMed.
- D. Eom, D. Prezzi, K. T. Rim, H. Zhou, M. Lefenfeld, S. Xiao, C. Nuckolls, M. S. Hybertsen, T. F. Heinz and G. W. Flynn, Nano Lett., 2009, 9, 2844–2848 CrossRef CAS.
- N. A. Vinogradov, A. A. Zakharov, V. Kocevski, J. Rusz, K. A. Simonov, O. Eriksson, A. Mikkelsen, E. Lundgren, A. S. Vinogradov, N. Mårtensson and A. B. Preobrajenski, Phys. Rev. Lett., 2012, 109, 026101 CrossRef CAS PubMed.
- S. Nie, N. C. Bartelt, J. M. Wofford, O. D. Dubon, K. F. McCarty and K. Thürmer, Phys. Rev. B, 2012, 85, 205406 CrossRef.
- E. N. Voloshina, Y. S. Dedkov, S. Torbrügge, A. Thissen and M. Fonin, Appl. Phys. Lett., 2012, 100, 241606 CrossRef.
- P. Sutter, J. T. Sadowski and E. Sutter, Phys. Rev. B, 2009, 80, 245411 CrossRef.
- X. Feng, J. Wu, A. T. Bell and M. Salmeron, J. Phys. Chem. C, 2015, 119, 7124–7129 CrossRef CAS.
- X. Liu, L. Fu, N. Liu, T. Gao, Y. Zhang, L. Liao and Z. Liu, J. Phys. Chem. C, 2011, 115, 11976–11982 CrossRef CAS.
- T. Wu, X. Zhang, Q. Yuan, J. Xue, G. Lu, Z. Liu, H. Wang, H. Wang, F. Ding, Q. Yu, X. Xie and M. Jiang, Nat. Mater., 2016, 15, 43–47 CrossRef CAS PubMed.
- C. Riedl, C. Coletti, T. Iwasaki, A. A. Zakharov and U. Starke, Phys. Rev. Lett., 2009, 103, 246804 CrossRef CAS PubMed.
- M. K. Jeonghyun Hwang, D. Campbell, H. A. Alsalman, J. Young Kwak, S. Shivaraman, A. R. Woll, A. K. Singh, R. G. Hennig, S. Gorantla, M. H. Rümmeli and M. G. Spencer, ACS Nano, 2013, 7, 385–395 CrossRef PubMed.
- J. Chen, Y. Wen, Y. Guo, B. Wu, L. Huang, Y. Xue, D. Geng, D. Wang, G. Yu and Y. Liu, J. Am. Chem. Soc., 2011, 133, 17548–17551 CrossRef CAS PubMed.
- H. Bi, S. Sun, F. Huang, X. Xie and M. Jiang, J. Mater. Chem., 2012, 22, 411–416 RSC.
- J. Xue, J. Sanchez Yamagishi, D. Bulmash, P. Jacquod, A. Deshpande, K. Watanabe, T. Taniguchi, P. Jarillo Herrero and B. J. LeRoy, Nat. Mater., 2011, 10, 282–285 CrossRef CAS PubMed.
- W. Yang, G. Chen, Z. Shi, C.-C. Liu, L. Zhang, G. Xie, M. Cheng, D. Wang, R. Yang, D. Shi, K. Watanabe, T. Taniguchi, Y. Yao, Y. Zhang and G. Zhang, Nat. Mater., 2013, 12, 792–797 CrossRef CAS.
- Y. Li, M. Li, T. Wang, F. Bai and Y. X. Yu, Phys. Chem. Chem. Phys., 2014, 16, 5213–5220 RSC.
- Y. Li, M. Li, T. Gu, F. Bai, Y. Yu, M. Trevor and Y. Yu, Appl. Surf. Sci., 2013, 284, 207–213 CrossRef CAS.
- S. Sunahiro, K. Nomura, S. Goto, K. Kanamaru, R. Tang, M. Yamamoto, T. Yoshii, J. N. Kondo, Q. Zhao, A. Ghulam Nabi, R. Crespo-Otero, D. Di Tommaso, T. Kyotani and H. Nishihara, J. Mater. Chem. A, 2021, 9, 14296–14308 RSC.
- C. Tang, B. Q. Li, Q. Zhang, L. Zhu, H. F. Wang, J. L. Shi and F. Wei, Adv. Funct. Mater., 2016, 26, 577–585 CrossRef CAS.
- H. Nishihara, T. Simura, S. Kobayashi, K. Nomura, R. Berenguer, M. Ito, M. Uchimura, H. Iden, K. Arihara, A. Ohma, Y. Hayasaka and T. Kyotani, Adv. Funct. Mater., 2016, 26, 6418–6427 CrossRef CAS.
- M. Yamamoto, S. Goto, R. Tang, K. Nomura, Y. Hayasaka, Y. Yoshioka, M. Ito, M. Morooka, H. Nishihara and T. Kyotani, ACS Appl. Mater. Interfaces, 2021, 13, 38613–38622 CrossRef CAS PubMed.
- K. Nomura, H. Nishihara, N. Kobayashi, T. Asada and T. Kyotani, Energy Environ. Sci., 2019, 12, 1542–1549 RSC.
- K. Nomura, H. Nishihara, M. Yamamoto, A. Gabe, M. Ito, M. Uchimura, Y. Nishina, H. Tanaka, M. T. Miyahara and T. Kyotani, Nat. Commun., 2019, 10, 2559 CrossRef.
- M. Yamamoto, Q. Zhao, S. Goto, Y. Gu, T. Toriyama, T. Yamamoto, H. Nishihara, A. Aziz, R. Crespo Otero and D. Di Tommaso, Chem. Sci., 2022, 13, 3140–3146 RSC.
- J. Park, J. Lee, J. H. Choi, D. K. Hwang and Y. W. Song, Sci. Rep., 2015, 5, 11839 CrossRef PubMed.
- A. J. Page, S. Saha, H. B. Li, S. Irle and K. Morokuma, J. Am. Chem. Soc., 2015, 137, 9281–9288 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102 CrossRef PubMed.
- J. Gu, J. Wang and J. Leszczynski, ACS Omega, 2018, 3, 1881–1888 CrossRef CAS PubMed.
- G. Paglia, C. E. Buckley, A. L. Rohl, R. D. Hart, K. Winter, A. J. Studer, B. A. Hunter and J. V. Hanna, Chem. Mater., 2004, 16, 220–236 CrossRef CAS.
- M. C. Cholewinski, M. Dixit and G. Mpourmpakis, ACS Omega, 2018, 3, 18242–18250 CrossRef CAS PubMed.
- L. Martínez, P. Merino, G. Santoro, J. I. Martínez, S. Katsanoulis, J. Ault, Á. Mayoral, L. Vázquez, M. Accolla, A. Dazzi, J. Mathurin, F. Borondics, E. Blázquez Blázquez, N. Shauloff, R. Lebrón Aguilar, J. E. Quintanilla López, R. Jelinek, J. Cernicharo, H. A. Stone, V. A. de la Peña O’Shea, P. L. de Andres, G. Haller, G. J. Ellis and J. A. Martín Gago, Nat. Commun., 2021, 12, 5937 CrossRef.
- M. Digne, J. Catal., 2004, 226, 54–68 CrossRef CAS.
- R. Wischert, P. Laurent, C. Copéret, F. Delbecq and P. Sautet, J. Am. Chem. Soc., 2012, 134, 14430–14449 CrossRef CAS.
- W. Grünert, Angew. Chem., 2012, 51, 5289 CrossRef.
- Y. X. Yu, J. Phys. Chem. C, 2019, 123, 205–213 CrossRef CAS.
- R. Gholizadeh and Y. X. Yu, Appl. Surf. Sci., 2015, 357, 1187–1195 CrossRef CAS.
- M. D. Higham, M. G. Quesne and C. R. A. Catlow, Dalton Trans., 2020, 49, 8478–8497 RSC.
- W. Zhu, A. Börjesson and K. Bolton, Carbon, 2010, 48, 470–478 CrossRef CAS.
- P. Wang, Z. Xu, T. Wang, Y. Yue, X. Bao and H. Zhu, Catal. Sci. Technol., 2020, 10, 3537–3541 RSC.
- Y. Zhang, Y. Zhao, T. Otroshchenko, H. Lund, M.-M. Pohl, U. Rodemerck, D. Linke, H. Jiao, G. Jiang and E. V. Kondratenko, Nat. Commun., 2018, 9, 1–10 CrossRef PubMed.
- J. Joubert, F. Delbecq and P. Sautet, J. Catal., 2007, 251, 507–513 CrossRef CAS.
- M. Dixit, P. Kostetskyy and G. Mpourmpakis, ACS Catal., 2018, 8, 11570–11578 CrossRef CAS.
- W. Zhang, P. Wu, Z. Li and J. Yang, J. Phys. Chem. C, 2011, 115, 17782–17787 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: See the supplementary material for the bulk cell of γ-Al2O3 (Fig. S1); structural models for CH4 adsorption on γ-Al2O3(111), γ-Al2O3(110), γ-Al2O3(100), and γ-Al2O3(001) catalyst surfaces (Fig. S2); the energy diagram of the first two CH4 dehydrogenation steps on γ-Al2O3 different main exposed surfaces (Fig. S3); energy diagram and intermediate structures for C2H6 interacting with surface flexible carbon species (Fig. S4); energy diagram and structures of the C2H6 dehydrogenation (Fig. S5); Gibbs energy profile of (a) complete CH4* dehydrogenation and (b) the formation of CnH2n* (n = 2–6) species via CH2* coupling on the γ-Al2O3 (100) surface at an experimental temperature of 1000 K (Fig. S6); structures and bond lengths between carbon end near surface and center sites of (a) C2H4*, (b) C3H6*, (c) C4H8*, (d) C5H10*, and (e) C6H12* on the γ-Al2O3(100) surface (Fig. S7); the energy profiles and structures for C6H12* chain ends with CH3* on the γ-Al2O3(100) surface (Fig. S8); the energy profiles and structures for the concerted mechanism and stepwise mechanism dehydrogenation of C3H6* and C6H12* on γ-Al2O3 (100) (Fig. S9 and S10); energy diagram and structures for further H behaviour after carbon ring formation (Fig. S11). See DOI: https://doi.org/10.1039/d2cp01554d |
| ‡ Present address: RIKEN Center for Advanced Photonics, RIKEN, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan. |
| This journal is © the Owner Societies 2022 |