Solid-solution (alloying) strategies in crystalline molecular conductors
Marc
Fourmigué

Univ Rennes, CNRS, ISCR (Institut des Sciences Chimiques de Rennes), UMR 6226, Campus de Beaulieu, 35000 Rennes, France. E-mail: marc.fourmigue@univ-rennes1.fr
First published on 18th June 2021
Abstract
In this review, we describe solid solution strategies employed in molecular conductors, where the control of their transport and magnetic properties (metallic or superconducting behavior, metal–insulator transitions, etc.) is the main goal. We first describe the main features of molecular conductors in order to identify which molecular entities are prone to be substituted by others in solid solutions, to which extent and for what purpose. We then describe the different crystal growth techniques used toward solid solution preparation and the nature of the molecular species, whether electroactive or not, which have been used, in cation or anion radical salts, in charge transfer salts and in single component conductors, in more than sixty reported examples. Topics such as preferential insertion and miscibility, the nature of disorder and the different analytical tools used for characterizing these alloys are presented. The consequences of alloying on conductivity and on phase transitions (superconductivity, anion ordering, Peierls transition, spin-Peierls transition), and the concepts of chemical pressure effects, band filling manipulation, and π–d interactions with magnetic anions are also discussed.
1 Introduction
Engineering crystal properties through solid solutions offers an opportunity to fine-tune the structural and physico-chemical properties of molecular materials, with, in some cases, the appearance of novel, unexpected behaviors. As stated by Lusi,1 a plethora of terms has been used over the years to define what we called indiscriminately solid solutions or alloys. They can be defined as multi-component phases for which the component ratios can be varied in continuum. They differ in that respect from salts or co-crystals where the stoichiometry defines the exact composition expressed by integer ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, etc.).2 Solid solutions therefore have high potential for tuning molecular properties in a smooth and controlled way, over a broad range of compositions. Working with molecular solid solutions also induces notable differences in well-known inorganic alloys such as steel (Fe + C), brass (Zn + Cu), and binary (SixGe1−x) and ternary (InxGa1−xAs) semiconductors built out of atomic constituents which are held by strong covalent bonds.3 Interactions between molecules in molecular solids are usually much weaker and the molecular entities maintain their integrity in the solid. Note, however, that in organic conductors, metallic bonding can play an important role in controlling the overall solid-state arrangement. In the following, we will restrict ourselves to crystalline, single-phase materials and will not consider molecular amorphous blends as used, for example, in molecular semiconductors,3 or crystals grown on crystals through stepwise 3D epitaxial growth.4
1, etc.).2 Solid solutions therefore have high potential for tuning molecular properties in a smooth and controlled way, over a broad range of compositions. Working with molecular solid solutions also induces notable differences in well-known inorganic alloys such as steel (Fe + C), brass (Zn + Cu), and binary (SixGe1−x) and ternary (InxGa1−xAs) semiconductors built out of atomic constituents which are held by strong covalent bonds.3 Interactions between molecules in molecular solids are usually much weaker and the molecular entities maintain their integrity in the solid. Note, however, that in organic conductors, metallic bonding can play an important role in controlling the overall solid-state arrangement. In the following, we will restrict ourselves to crystalline, single-phase materials and will not consider molecular amorphous blends as used, for example, in molecular semiconductors,3 or crystals grown on crystals through stepwise 3D epitaxial growth.4
The more general question of the effect of disorder in molecular alloys has been addressed from a thermodynamic point of view in relation with the effect of an increased entropy.5 Several entropic effects can be considered in molecular crystals: configurational entropy, vibrational entropy and rotational entropy. Configurational entropy can be found because of molecular disorder (one molecule or a part of a molecule disordered at two or more sites), eventually associated with temperature-dependent molecular motions and thermal expansion behaviors.6 In solid solutions of molecular compounds, the nature of disorder (vs. clustering or spinodal decomposition) can play an important role, as shown recently in CH3NH3PbI3/CH3NH3PbBr3 alloys of hybrid halide perovskite semiconductors used for photovoltaic applications.7 Furthermore, in addition to static substitutional disorder that arises from molecular substitution, orientational disorder at a given site can also play a role, with two isomorphous molecules or ions adopting different orientations.8 Another difficulty one can encounter is the situation where co-crystallization of similar molecules does not, as previously believed, necessarily result in the formation of macroscopic crystals with the same homogeneous distribution of components.9 This effect, observed in [MxM′1−x(bipy)3](PF6)2 (M, M′ = Ni2+, Fe2+, Ru2+; bipy: 2,2′-bipyridine) solid solutions, gives rise to crystals from the same batch with the composition varying notably (by as much as 15%) from the averaged composition. This effect described as supramolecular selectivity is explained by molecular recognition processes that lead to the partially selective aggregation of like molecules. These illustrate how difficult the full characterization of molecular solid solutions can be. For most reported examples detailed below, many of these questions about the nature of the disorder, the exact composition and structure of the crystals, and their homogeneity, were never addressed, limiting to some extent the conclusions that many authors draw on the correlation between alloy composition and physical properties.
In molecular materials, solid solution strategies are used extensively to control their different properties, such as magnetic, luminescence, and catalytic properties. The molecular magnetism community makes extensive use of alloying strategies. This is particularly true in coordination complexes exhibiting spin crossover (SCO) behavior. Substitution of counterions (for example, PF6−vs. AsF6−) or ligands or dilution of the magnetic center with other cations can have very important consequences on the cooperativity of the SCO and the eventual presence of structural phase transitions.10–12 Another striking example involves the modulation of the Single Molecule Magnet (SMM) properties of pentadecanuclear cyanide-bridged clusters formulated as {Fe9−xCox[W(CN)8]6(MeOH)24}, where different Co/Fe metal ratios favor either HSFeIIWV ↔ HSFeIIIWIV charge transfer transition or slow magnetic relaxation effects.13 Luminescent species, particularly those based on rare-earth complexes, offer another playing field for alloying strategies. For example, lanthanide complexes of the 5-methoxyisophthalate (mip2−) ligand, formulated as [Ln2(mip)3(H2O)8·4H2O], are prepared with a mixture of up to six different lanthanide ions (Nd3+, Sm3+, Eu3+, Gd3+, Tb3+, Dy3+). At a unique irradiation wavelength (λexc = 325 nm), these compounds exhibit almost 20 emission peaks in both the visible and NIR regions at RT, an unprecedented richness of the emission spectrum of great interest as far as luminescent barcodes are concerned.14 The chemistry of metal organic frameworks (MOFs) also provides several examples of successful alloying strategies as those reported (i) to tune catalytic properties through the In3+/Ga3+ metal ion ratio,15 or (ii) to manipulate the mechanical and dynamical properties of formate-based perovskites in the [NH3NH2]1−x[NH3OH]xZn(HCOO)3 series.16
In this review, we will focus on solid solution strategies employed in molecular conductors, where the control of the transport properties (metallic or superconducting behavior, metal–insulator transitions with associated magnetic properties) is the main goal. To do so, it is important to first describe the main features of molecular conductors in order to identify which molecular entities are prone to be substituted by others in solid solutions and for what purpose.
The term “molecular conductors” encompasses, in this review, a broad range of crystalline materials built out of molecular entities, be they of organic or of coordination chemistry origin, able to generate charge carriers. Intermolecular interactions in the solid state, most often of 1D or 2D nature, favor the formation of bands, with a limited gap in semiconducting systems (≈10−4 S cm−1 < σRT < ≈1 S cm−1), and a limited bandwidth in gapless metallic systems (σRT > ≈1 S cm−1). These characteristics are the consequences of strong electronic correlations between charge carriers,17 and offer a wide variety of ground states and phase transitions, referred to as charge density waves (CDWs), spin density waves (SDWs), Peierls transition, spin-Peierls (SP) transition, dimer-Mott (DM) insulating phase, Mott-insulator states, charge-order (CO), superconductivity, etc.18 From a composition point of view, we can distinguish three main different classes of compounds, each of them amenable to different solid solution strategies.
Charge-transfer salts are based on the association of two different electroactive molecules: one is referred to as the electron donor (D) and the other is referred to as the electron acceptor (A). Upon co-crystallization from solution or co-sublimation, a D·A co-crystal is formed and its electronic nature varies with the E1/2 redox potentials of both D and A molecules.19 In solution, electron transfer can normally occur if Ered(A) > Eox(D). Since the formation of a crystalline solid favors ionic phases, electron transfer in D·A co-crystals can be observed already if Ered(A) − Eox(D) > −(0.25–035) V. A partial degree of charge transfer, 0 < ρ < 1, is found in segregated structures with DDD and AAA stacks, as in TTF+ρ·TCNQ−ρ (Scheme 1),20 where the Fermi level crosses both the HOMO band of D and the LUMO band of A, at the origin of the metallic character. Solid solutions can be considered within such charge-transfer salts by replacing either D or A with an isomorphous molecule, i.e. (DxD′1−x)·A or D·(AxA′1−x).
Ion-radical salts are based on one single electroactive molecule (either D or A), respectively, oxidized or reduced in the radical cation D+˙ or radical anion A−˙ form. Partial charge transfer is also possible, for example with the recurrent 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry in (D)2·X (ρ = 0.5 if X is a monovalent anion). More complex situations are found in systems like (D)3·X2 or with non-stoichiometric band filling,21 as in TTF halides (TTF)Xx (x = 0.77–0.80 with Cl−, x = 0.71–076 with Br− and x = 0.70–0.72 for I−).22 The Fabre salts (2
1 stoichiometry in (D)2·X (ρ = 0.5 if X is a monovalent anion). More complex situations are found in systems like (D)3·X2 or with non-stoichiometric band filling,21 as in TTF halides (TTF)Xx (x = 0.77–0.80 with Cl−, x = 0.71–076 with Br− and x = 0.70–0.72 for I−).22 The Fabre salts (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts built out of TMTTF molecules), the Bechgaard salts (2
1 salts built out of TMTTF molecules), the Bechgaard salts (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts built out of TMTSF molecules),18 and the large family of BEDT-TTF salts23 (and BETS and BET analogs)24,25 belong to this class of molecular conductors. Solid solutions here can take on different aspects, by replacing the electroactive molecule with an isomorphous one as in charge-transfer salts, i.e. (DxD′1−x)nX, or by replacing the counter-ion with an isomorphous one, i.e. Dn(XxY1−x). If X and Y differ in charge, band filling will also be impacted, a difficult but sought-after goal, as we will see in the following.
1 salts built out of TMTSF molecules),18 and the large family of BEDT-TTF salts23 (and BETS and BET analogs)24,25 belong to this class of molecular conductors. Solid solutions here can take on different aspects, by replacing the electroactive molecule with an isomorphous one as in charge-transfer salts, i.e. (DxD′1−x)nX, or by replacing the counter-ion with an isomorphous one, i.e. Dn(XxY1−x). If X and Y differ in charge, band filling will also be impacted, a difficult but sought-after goal, as we will see in the following.
Single component conductors are built from one single molecular species, be it radical in nature or not. Among the organic radical species, we can mention spiro-bis(phenalenyl)boron radicals,26 dithiadiazolyl27 or dithiazolyl radicals,28 and hydrogen-bonded TTF dimers.29,30 Among the coordination complexes, the most famous series is based on neutral tetrathiafulvalene dithiolate complexes such as [M(tmdt)2],31 while neutral radical gold complexes such as [Au(R-thiazdt)2]˙ have emerged as an attractive family.32 In-between we can find neutral nickel bis(dithiolene) complexes whose semiconducting behavior can be changed into a metallic one under application of high pressures.33 Among all these single-component conductors, alloying strategies have been considered up to now only upon metal substitution, in spiro-bis(phenalenyl)boron radicals (B vs. Be) and in TTF–dithiolate complexes (M = Ni, Pd, Pt vs. Cu, Au).
Reported solid solutions of molecular conductors analyzed in this Review are gathered in Tables 1 and 2, distinguishing those involving alloys based on electroactive molecules (Table 1) and those involving alloys based on counter-ions (Table 2).
| Compound | Pairs of alloyed molecules or ions | Composition | Ref. |
|---|---|---|---|
| Charge-transfer salts | |||
| (TSF)x(TTF)1−x(TCNQ) | TTF, TSF | 0 ≤ x ≤ 1 | 34–36 |
| (HMTSF)1−x(HMTTF)xTCNQ | HMTTF, HMTSF | 0.05 | 37 |
| (NMP)x(Phen)1−xTCNQ | NMP, Phen | 0.5 ≤ x ≤ 1 | 38 and 39 |
| Cation-radical salts | |||
| [(TMTSF)1−x(TMTTF)x]2ClO4 | TMTTF, TMTSF | 0 ≤ x ≤ 0.30 | 40 |
| [(TMTSF)1−x(TMTTF)x]2ReO4 | TMTTF, TMTSF | 0 ≤ x ≤ 1 | 41 and 42 |
| [(TMTSF)1−x(TMTTF)x]2PF6 | TMTTF, TMTSF | x < 0.25, 0.85 | 43 |
| κ-[(ET)1−x(BEDT-STF)x]2, Cu[N(CN)2]Br | BEDT-TTF, BEDT-STF | 0 ≤ x ≤ 1 | 44 |
| κ-[(ET)1−x(BEDSeT-TTF)x]2, Cu[N(CN)2]Br | BEDT-TTF, BEDSeT-TTF | 0 ≤ x ≤ 0.26 | 45 |
| [(EDO-TTF)1−x(MeEDO-TTF)x]2PF6 | EDO-TTF, MeEDO-TTF | x < 0.6, 0.9 < x | 46 |
| (Perylene)2[Au1−xPtx(mnt)2] | Au3+, Pt2+ | 0 ≤ x ≤ 0.50 | 47–49 |
| Single component conductors | |||
| [NiOC4]1−x[AuOC4]x | Ni2+, Au3+ | 0 ≤ x ≤ 1 | 50 |
| [Ni1−xAux(tmdt)2] | Ni2+, Au3+ | 0 ≤ x ≤ 1 | 51 |
| [Ni1−xCux(tmdt)2] | Ni2+, Cu2+ | x ≤ 0.27 | 52 |
| [PLY(O,O)]2B1−xBex | B3+, Be2+ | 0 ≤ x ≤ 0.2 | 53 |
| [MePLY(O,O)]2B1−xBex | B3+, Be2+ | 0 ≤ x ≤ 0.59 | 54 |
| Anion-radical salts | |||
| [Cl-BzPy][NixPt1−x(mnt)2] | Ni2+, Pt2+ | 0 ≤ x ≤ 1 | 55 |
| [NO2-BzPy][NixAu1−x(mnt)2] | Ni2+, Au2+ | 0 ≤ x ≤ 1 | 56 |
| (Me4N)[NixPd1−x(dmit)2]2 | Ni2+, Pd2+ | 57 | |
| [(Me2DCNQI)1−x(Me2DCNQI-d8)x]2Cu | Me2DCNQI, Me2DCNQI-d8 | 0 ≤ x ≤ 1 | 58 and 61 |
| [(Me2)1−x(MeBr)xDCNQI]2Cu | Me2DCNQI, MeBrDCNQI | 0 ≤ x ≤ 1 | 59–61 |
| [(Me2)1−x(MeCl)xDCNQI]2Cu | Me2DCNQI, MeClDCNQI | 0.75 | 62 |
| [(Me2)1−x(MeI)xDCNQI]2Cu | Me2DCNQI, MeIDCNQI | 0.70 | 61 and 62 |
| [(MeCl)1−x(MeBr)xDCNQI]2Cu | MeClDCNQI, MeBrDCNQI | 0.60 | 62 |
| [(MeBr)1−x(MeI)xDCNQI]2Cu | MeBrDCNQI, MeIDCNQI | 0 ≤ x ≤ 1 | 61 and 62 |
| [(MeCl)1−x(MeI)xDCNQI]2Cu | MeClDCNQI, MeIDCNQI | 0.25 | 62 |
| K3(C60)1−x(C70)x | C60, C70 | x ≤ 0.5 | 63 |
| TDAE·(C60)1−x(C70)x | C60, C70 | 0 ≤ x ≤ 0.5 | 64 |
| Compound | Mixed counter-ions | Composition | Ref. |
|---|---|---|---|
| Anion radical salts | |||
| (Me2DCNQI)2Li1−xCux | Li+, Cu+,2+ | 0 ≤ x ≤ 1 | 65 and 66 |
| (Me4Sb)1−x(EtMe3Sb)x[Pd(dmit)2]2 | Me4Sb+, EtMe3Sb+ | 0 ≤ x ≤ 1 | 67 |
| (Et2Me2Sb)1−x(EtMe3Sb)x[Pd(dmit)2]2 | Et2Me2Sb+, EtMe3Sb+ | 0 ≤ x ≤ 1 | 67 |
| Cation-radical salts | |||
| (o-DMTTF)2BrxCl1−x | Br−, Cl− | 0 ≤ x ≤ 1 | 68 |
| (o-DMTTF)2BrxI1−x | Br−, I− | 0 ≤ x ≤ 1 | 68 |
| (TMTSF)2(ClO4)1−x(ReO4)x | ClO4−, ReO4− | x < 0.17 | 69–72 |
| (TMTSF)2(AsF6)1−x(FeCl4)x | AsF6−, FeCl4− | 10−3 | 73 |
| (TMTTF)2(SbF6)1−x(AsF6)x | AsF6−, SbF6− | 0 ≤ x ≤ 1 | 74 and 75 |
| (TMTSF)2(TaF6)1−x(PF6)x | TaF6−, PF6− | 0 ≤ x ≤ 1 | 76 |
| δm-(ET)2(TaF6)1−x(PF6)x | TaF6−, PF6− | 0.06 | 76 |
| δo-(ET)2(TaF6)1−x(PF6)x | TaF6−, PF6− | 0.57 | 76 |
| β-(ET)2(I3)1−x(IBr2)x | IBr2−, I3− | 0 ≤ x ≤ 1 | 77 and 78 |
| β-(ET)2(IBr2)1−x(I2Br)x | IBr2−, I2Br− | 0 ≤ x ≤ 1 | 77 and 78 |
| β-(ET)2(I2Br)1−x(I3)x | I2Br−, I3− | 0 ≤ x ≤ 1 | 77 and 78 |
| β-(ET)2(I3)1−x(AuI2)x | AuI2−, I3− | 0.1, 0.26, 0.9 | 79 and 80 |
| θ-(ET)2(I3)1−x(AuI2)x | AuI2−, I3− | <0.02 | 81 |
| (ET)4[Ni(CN)4]x[Pt(CN)4]1−x | [Ni(CN)4]2−, Pt(CN)4]2− | ≈0.5, 0.14 | 82 |
| κ-(ET)2Cu[N(CN)2]BrxCl1−x | Cl−, Br− | 0 ≤ x ≤ 1 | 83–85 |
| θ-(ET)2(Rb1−xCsx)Zn(SCN)4 | Rb+, Cs+ | 0 ≤ x ≤ 1 | 86 |
| λ-(ET)2(GaCl4)1−x(CoCl4)x | GaCl4−, CoCl42− | 0 ≤ x ≤ 0.06 | 87 |
| δ′-(ET)2(GaCl4)1−x(CoCl4)x | GaCl4−, CoCl42− | 0.05, 0.14 | 87 |
| α-(ET)3(CoCl4)1−x(GaCl4)x(TCE) | GaCl4−, CoCl42− | 0.54, 0.57, 0.62 | 87 |
| β′-(ET)3(CoCl4)1−x(GaCl4)x | GaCl4−, CoCl42− | 0.88, 0.66 | 87 |
| β′′-(ET)2(SF5RSO3)1−x(SF5R′SO3)x | R,R′ = CH2CF2, CHF | 0 ≤ x ≤ 1 | 88 |
| β′′-(ET)2(SF5RSO3)1−x(SF5R′SO3)x | R,R′ = CH2–CF2, CHFCF | 0 ≤ x ≤ 1 | 88 |
| λ-(BETS)2GaBrxCl4−x | (GaBrxCl4−x)− (x = 1–4) | 89 and 90 | |
| λ-(BETS)2GaFxCl4−x | (GaFxCl4−x)− (x = 1–4) | 91 | |
| λ-(BETS)2FexGa1−xCl4 | FeCl4−, GaCl4− | 0.43, 0.55 | 92–94 |
| (DIETSe)2GaBrxCl4−x | (GaBrxCl4−x)− (x = 1–4) | 95 | |
| (DIETSe)2FeBrxCl4−x | (FeBrxCl4−x)− (x = 1–4) | 95 | |
| (TTM-TTP)FeBrxCl4−x | (FeBrxCl4−x)− (x = 1–4) | 96 | |
| (TTM-TTP)GaBrxCl4−x | (GaBrxCl4−x)− (x = 1–4) | 97 | |
| (TTM-TTP)Fe1−xGaxCl4 | FeCl4−, GaCl4− | 0.1 | 97 |
| (TTM-TTP)Fe1−xCoxCl4 | FeCl4−, CoCl42− | 0.05, 0.40 | 98 |
| (TTM-TTP)Ga1−xCoxCl4 | GaCl4−, CoCl42− | 0.30 | 98 |
| (TTM-TTP)Mn1−xCoxCl4 | MnCl42−, CoCl42− | 0.90 | 98 |
| β-(EDT-TTF-I2)2[Pb2/3+xAg1/3−2x□xI2]3 | Pb2+, Ag+ | 0.05 | 99 |
2. Chemical properties of solid solutions in molecular conductors
In the following, we will describe the different methods used for the preparation of solid solutions of molecular conductors, together with the analytical methods used to particularly characterize their composition. We will also address important issues about the nature of the mixed species (volume, shape, charge, spin, etc.).2.1 Crystal growth methods
Crystalline molecular conductors are essentially obtained through two different methods both involving an electron transfer, either crystallization from solution using an oxidant or a reducing agent (eventually inserted itself in the structure), or electrocrystallization where the electron transfer performed at the electrode is followed by the precipitation (crystallization) of the conducting salts on the electrode itself.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 HMTTF/HMTSF ratio in solution, an indication of the probably much lower solubility of the selenated phase.37
75 HMTTF/HMTSF ratio in solution, an indication of the probably much lower solubility of the selenated phase.37
Reducing agents such as TDAE [tetrakis(dimethylamino)ethylene] are used for the preparation of TDAE·(C60)1−x(C70)x alloys, which precipitate rapidly from solutions of C60 and C70 in a benzene/toluene mixture.64 TDAE was also used a reducing agent without insertion into the crystal in the single-component conductor derived by the reduction of the spiro-bis(9-oxidophenalenone)boron cation denoted [PLY(O,O)]2B+.53 Co-crystallization of solutions of this cation with selected amounts of the neutral beryllium analog [PLY(O,O)]2Be in the presence of TDAE leads to the formation of a series of solid-state solutions with the composition [PLY-(O,O)]2B1−xBex. The crystallization process is driven by the insolubility of the radical [PLY(O,O)]2B, which apparently induces the co-crystallization of [PLY(O,O)]2Be with x values not exceeding 0.2. Higher Be concentrations are reached in the methyl-substituted analogs with x values up to 0.59.54
Reduction processes are also involved in the preparation of solid solutions of the DCNQI acceptor and analogs. As reported by Hünig et al., mixing two (or even three) different DCNQIs in the presence of CuBr2 and copper wire afforded crystallization of 26 binary alloys such as [(Me2)1−x(MeBr)xDCNQI]2Cu, and even one ternary alloy.61 Under these conditions, the different reduction potentials of two DCNQIs do not affect the composition of the salt and the most reducible acceptor was not inserted preferentially. Solid solutions involving Me2DCNQI and for example its deuterated analog Me2DCNQI-d8 were also prepared upon reaction of the acceptor molecules with Bu4NI as a reductant in the presence of a copper salt, namely (Et4N)2CuBr4.58 These DCNQI salts can also be prepared by electrocrystallization (see below).59,60
Chemical oxidation processes have also been used in the crystallization of solid solutions of [Pd(dmit)2] dithiolene complexes, such as (Me4Sb)1−x(EtMe3Sb)x[Pd(dmit)2]2 and (Et2Me2Sb)1−x(EtMe3Sb)x[Pd(dmit)2]2.67 They are prepared indeed through the slow air oxidation of [Pd(dmit)2]2− ions in the presence of the corresponding cations (Me4Sb+vs. EtMe3Sb+ and Et2Me2Sb+vs. EtMe3Sb+) and acetic acid. This method proved to be very suitable for the preparation of large and high-quality alloyed crystals.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts with ClO4−,40 ReO4−,41 and PF6−.43 Indeed both TMTTF and TMTSF salts exhibit closely related structures and can be described using a unique (p,T) phase diagram.18 Considering that both molecules do not oxidize at the same potential, the PF6− alloy [(TMTSF)1−x(TMTTF)x]2PF6 was originally prepared in a potentiostatic mode at 0.25–0.30 V, i.e. below the oxidation potential of both donor molecules (TMTTF: +0.26 V; TMTSF: +0.43 V).43 A slightly different strategy was used for the ClO4− alloy prepared at a higher intermediate potential value (0.4 V).40 The lower solubility of the TMTSF salts limited, however, the insertion of TMTTF to a maximum value of x = 0.30 in [(TMTSF)1−x(TMTTF)x]2ClO4, and of x = 0.25 in [(TMTSF)1−x(TMTTF)x]2PF6. These problems were not found for the ReO4− salt, i.e. [(TMTSF)1−x(TMTTF)x]2ReO4,41 where galvanostatic methods associated with smaller current densities and hence a slower crystallization process afforded three alloys with x ≈ 0.2, 0.55 and 0.8. The well-known κ-(ET)2Cu[N(CN)2]Br kappa-Br phase has also been the subject of alloying strategies involving as second donor molecules BEDT-STF or BEDSe-TTF.44,45 Finally, dithiolene complexes offer another series where solid solutions can be easily prepared by electrocrystallization of two different complexes differing only by the nature of the central metal, as in the isoelectronic series based on Ni/Pd/Pt complexes. Besides, solid solutions mixing group 10 (Ni, Pd, Pt) and group 11 (Cu, Au) metal complexes lead to a modification of the overall electron count and hence of the band filling.47–57
1 salts with ClO4−,40 ReO4−,41 and PF6−.43 Indeed both TMTTF and TMTSF salts exhibit closely related structures and can be described using a unique (p,T) phase diagram.18 Considering that both molecules do not oxidize at the same potential, the PF6− alloy [(TMTSF)1−x(TMTTF)x]2PF6 was originally prepared in a potentiostatic mode at 0.25–0.30 V, i.e. below the oxidation potential of both donor molecules (TMTTF: +0.26 V; TMTSF: +0.43 V).43 A slightly different strategy was used for the ClO4− alloy prepared at a higher intermediate potential value (0.4 V).40 The lower solubility of the TMTSF salts limited, however, the insertion of TMTTF to a maximum value of x = 0.30 in [(TMTSF)1−x(TMTTF)x]2ClO4, and of x = 0.25 in [(TMTSF)1−x(TMTTF)x]2PF6. These problems were not found for the ReO4− salt, i.e. [(TMTSF)1−x(TMTTF)x]2ReO4,41 where galvanostatic methods associated with smaller current densities and hence a slower crystallization process afforded three alloys with x ≈ 0.2, 0.55 and 0.8. The well-known κ-(ET)2Cu[N(CN)2]Br kappa-Br phase has also been the subject of alloying strategies involving as second donor molecules BEDT-STF or BEDSe-TTF.44,45 Finally, dithiolene complexes offer another series where solid solutions can be easily prepared by electrocrystallization of two different complexes differing only by the nature of the central metal, as in the isoelectronic series based on Ni/Pd/Pt complexes. Besides, solid solutions mixing group 10 (Ni, Pd, Pt) and group 11 (Cu, Au) metal complexes lead to a modification of the overall electron count and hence of the band filling.47–57
Electrocrystallization is the synthetic method of choice for the elaboration of solid solutions involving two different counter-ions with analogous symmetry, shape and charge: for example, ClO4−vs. ReO4−. Numerous examples have been reported and some are collected in Table 2. In most cases, the whole composition range can be explored. Also, because the electrolytes are used in large excess compared to the electroactive species, very small x values can be investigated when doping effects are considered rather than exploration of the whole 0 ≤ x ≤ 1 range. Electrocrystallization conditions might require a difficult optimization in order to be able to isolate solid solutions with a broad composition range. For example, in the series of β-(ET)2(X1)1−x(X2)x alloys (X1, X2 = I3−, I2Br−, IBr2−),78 mixed crystals having a wide composition range of anions were obtained from only nitrobenzene for X1 = IBr2− and X2 = I3−, from only chlorobenzene for X = I2Br− and X2 = I3−, and from only THF for X1 = I2Br− and X2 = IBr2−, and crystals having such a wide composition range of anions were not obtained from other organic solvents. Note that the electrocrystallization itself can generate two different anions, as reported upon crystal growth of β-(BEDT-TTF)2AuI2 in the presence of solely Bu4NAuI2. When performed at high potentials, it afforded the solid solution β-(BEDT-TTF)2[(AuI2)0.26(I3)0.74], a probable consequence of the oxidation and decomposition of the AuII2− anion.80
2.2 Nature of the components of a molecular alloy
Engineering molecular solid solutions is not always a straightforward task.101 It is essentially based on the assumption that the similarity of size and shape is sufficient, although the intermolecular interactions between molecules in the crystal also play an important role.102 In that respect, the examples reported in Tables 1 and 2 are not so numerous and often limited to very similar systems.Perhaps the most identical, yet different molecules to be alloyed are those with different isotopes (H vs. D, 13C, 34S, 77Se). In the field of molecular conductors, isotope introduction has been originally performed in order to observe any change in Tc, i.e. the “isotope effect” in superconducting salts.103 Besides, solid state NMR is an important tool for investigating the magnetic and conducting properties of such systems in order to estimate the density of states from the Knight-shift and the spin–lattice relaxation rate. It requires a 13C enrichment of the molecules, most often on the two central carbon atoms of the TMTTF,104 TMTSF or BEDT-TTF molecules.105 With this enrichment, spectral splitting occurs because of the resulting coupled spin system and induces a so-called Pake doublet.106 To avoid this problem, 13C-enriched TMTTF and ET molecules were prepared from a mixture of labelled and unlabelled dithiole precursors, affording a mixture with 10% 13C-TMTTF in unlabelled TMTTF,104 and that containing less than 7% 13C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 13C double side-enriched ET in a major 13C-single side-enriched ET molecule respectively.105 These mixtures were electro-crystallized to yield solid solutions composed of double side-enriched, single side-enriched and non-enriched donor molecules.
13C double side-enriched ET in a major 13C-single side-enriched ET molecule respectively.105 These mixtures were electro-crystallized to yield solid solutions composed of double side-enriched, single side-enriched and non-enriched donor molecules.
Another series where isotopic substitution proved to be particularly fruitfull is based on the Me2DCNQI acceptor, also known as its fully deuterated analog, Me2DCNQI-d8.58 Indeed, the slightly smaller size of deuterium compared to hydrogen makes deuteration of molecules a very useful tool for tentatively paralleling the effect of an external pressure, as also explored in this area with BEDT-TTF-d8.107
As shown in Scheme 2a, the donor molecules used in alloys of cation radical salts are essentially based on a S/Se substitution, on the central TTF core as well as on side substituents. One single example involves the introduction of an extra methyl group in [(EDO-TTF)1−x(MeEDO-TTF)x]2PF6 alloys but the whole composition range could not be prepared except for x < 0.6 and x > 0.9.46 A much broader choice was offered in the (DCNQI)2Cu salts where many acceptors with different substituents in the 2 and 5 positions could be mixed (Scheme 2b).
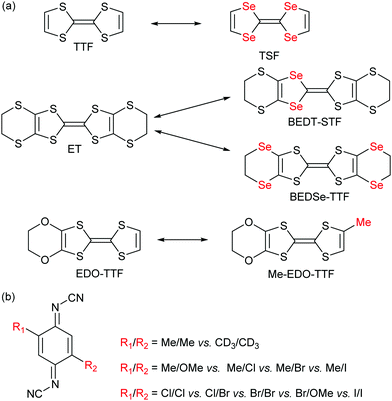 | ||
| Scheme 2 (a) Examples of pairs of donor molecules investigated in alloys. (b) The different DCNQI acceptor molecules used in alloys. | ||
Most common solid solutions involve two different counter-ions with analogous symmetry, shape and charge: for example, Cl−vs. Br−vs. I−, ClO4−vs. ReO4−, PF6−vs. AsF6−vs. SbF6−, FeCl4−vs. GaCl4−, and I3−vs. I2Br−vs. IBr2−, or in radical anion salts, Li+vs. Cu+, all collected in Table 2. In most cases, the whole composition range can be explored.
Organic counter-ions offer an increased degree of complexity as reported in the alloys involving Me4Sb+vs. EtMe3Sb+,67 and SF5CH2CF2SO3−vs. SF5CHFSO3−.88 In these salts, to the positional disorder of the two species at a given crystallographic site for the counter-ion is added substitutional disorder even more difficult to characterize (see Section 2.4). A specific warning should be made here for reported solid solutions involving the GaCl4−/GaBr4− and FeCl4−/FeBr4− pairs. Indeed, several interesting phases with the BETS donor molecule have been reported, such as the organic superconductor λ-(BETS)2GaCl4 and the isostructural λ-(BETS)2FeCl4 which exhibits a sharp MI transition around 8 K. On the other hand, κ-type salts with various anions such as GaC14−, GaBr4−, FeCl4−, FeBr4−, and InC14− exhibit metallic behavior down to 4 K.24 Solid solutions of the λ-phases were investigated with, for example, GaCl4− and GaBr4− in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio written as “GaBrCl3−”.89,90 It has been reported, however, that the halogen ions of mixed halide gallium anions tend to be easily substituted by other halogen ions in solution.108 This scrambling in solution implies that the description “GaBrC13−” does not represent just one species GaBrC13−, but rather a complex mixture of GaC14−, GaBrCl3−, GaBr2C12−, GaBr3Cl−, and GaBr4−. In the present example, the distribution was approximatively 5
3 ratio written as “GaBrCl3−”.89,90 It has been reported, however, that the halogen ions of mixed halide gallium anions tend to be easily substituted by other halogen ions in solution.108 This scrambling in solution implies that the description “GaBrC13−” does not represent just one species GaBrC13−, but rather a complex mixture of GaC14−, GaBrCl3−, GaBr2C12−, GaBr3Cl−, and GaBr4−. In the present example, the distribution was approximatively 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and the Br/Cl distribution was different on the four crystallographically different halide sites. Similar scrambling reactions and added complexity are also reported in solid solution involving DIETS or TTM-TTP donor molecules with mixtures of FeCl4− and FeBr4− iron complexes.95,96
0 and the Br/Cl distribution was different on the four crystallographically different halide sites. Similar scrambling reactions and added complexity are also reported in solid solution involving DIETS or TTM-TTP donor molecules with mixtures of FeCl4− and FeBr4− iron complexes.95,96
2.3 Miscibility: doping, preferential insertion
In several situations where the two extreme structures differ too much from each other, a full miscibility of the two partners cannot be reached and the resulting salts are much better described as doped materials. These compositions are also of interest for highly sensitive properties such as superconductivity (see Section 3.4), upon insertion of disorder or of magnetic defects. For example, insertion of the tetrahedral and magnetic (S = 5/2) FeCl4− anion into (TMTSF)2(AsF6) was limited to an x value of 10−3 in the alloy formulated as (TMTSF)2(AsF6)1−x(FeCl4)x, despite the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of AsF6−
2 ratio of AsF6−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FeCl4− in the electrolyte.73 Such doped systems are also prepared on purpose for EPR investigations of paramagnetic dithiolene complexes diluted in diamagnetic matrices: for example, [Ni(dt)2]− in diamagnetic [Au(dt)2]−109 and [Cu(dt)2]2− in diamagnetic [Ni(dt)2]2−.110
FeCl4− in the electrolyte.73 Such doped systems are also prepared on purpose for EPR investigations of paramagnetic dithiolene complexes diluted in diamagnetic matrices: for example, [Ni(dt)2]− in diamagnetic [Au(dt)2]−109 and [Cu(dt)2]2− in diamagnetic [Ni(dt)2]2−.110
In most situations, however, the full range of compositions can be obtained but often with an x value in the crystal which differs from the nominal concentration in solution. Concerning the S/Se exchange in donor molecules, (TSF)x(TTF)1−x(TCNQ) is the only example where a slight enrichment in TTF is observed over that of the initial solution composition.34 Other examples go in the opposite direction, i.e. a systematic preferential insertion of the selenated molecule associated with a decreased solubility of the corresponding salt, as in [(TMTSF)1−x(TMTTF)x]2ClO4,40a [(TMTSF)1−x(TMTTF)x]2PF6,43 (HMTTF)0.05(HMTSF)0.95TCNQ,37 and κ-[(ET)1−x(BEDSeT-TTF)x]2Cu[N(CN)2]Br.45 Similar strong effects are observed in radical-anion salts as the DCNQI alloys [(Me2)1−x(MeBr)xDCNQI]2Cu, where a 0.2 molar fraction of (MeBr)DCNQI in solution results in an x = 0.7 fraction in the solid.59,60 Systematic studies related to these preferential insertion effects are scarce but give invaluable information about the relative stability/solubility of two different compounds differing only by the counterion. In that respect we can mention, for example, the mixed-valence 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 salts of the electroactive [Pd(dmit)2] with Me4Sb+, EtMe3Sb+ or Et2Me2Sb+ cations.67 As shown in Fig. 1, the molar fraction of the bulkier/disordered EtMe3Sb+ cation in crystalline solid solutions with Me4Sb+ is systematically smaller than that in the electro-crystallized solution, showing a more “favorable” crystal growth with the more compact Me4Sb+ cation. On the other hand, introduction of the even bulkier Et2Me2Sb+ cation in competition with EtMe3Sb+ (Fig. 1b) shows no sign of discrimination, a consequence of the similar steric constraints brought by the two ethyl-containing cations. Indeed, in the pristine EtMe3Sb+ salt, the EtMe3Sb+ cation is located on a two-fold axis and exhibits disorder with two possible orientations, giving an overlapped image with an apparent Et2Me2Sb+ cation with 50% occupancy of the ethyl groups.
2 salts of the electroactive [Pd(dmit)2] with Me4Sb+, EtMe3Sb+ or Et2Me2Sb+ cations.67 As shown in Fig. 1, the molar fraction of the bulkier/disordered EtMe3Sb+ cation in crystalline solid solutions with Me4Sb+ is systematically smaller than that in the electro-crystallized solution, showing a more “favorable” crystal growth with the more compact Me4Sb+ cation. On the other hand, introduction of the even bulkier Et2Me2Sb+ cation in competition with EtMe3Sb+ (Fig. 1b) shows no sign of discrimination, a consequence of the similar steric constraints brought by the two ethyl-containing cations. Indeed, in the pristine EtMe3Sb+ salt, the EtMe3Sb+ cation is located on a two-fold axis and exhibits disorder with two possible orientations, giving an overlapped image with an apparent Et2Me2Sb+ cation with 50% occupancy of the ethyl groups.
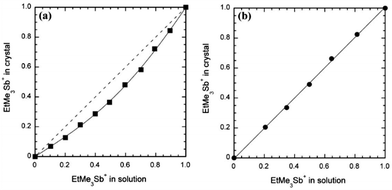 | ||
| Fig. 1 Mole fraction of EtMe3Sb+ in the crystal (x) as a function of that in solution for (a) (Me4Sb)1−x(EtMe3Sb)x[Pd(dmit)2]2 and (b) (Et2Me2Sb)1−x(EtMe3Sb)x[Pd(dmit)2]2. Reproduced from ref. 67 with permission from Wiley-VCH. | ||
A very different situation is observed in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cation radical salts of o-Me2TTF with Cl−, Br− and I− anions.68 In this original quadratic structure, the halide is embedded in a set of weak C–H⋯X− hydrogen bonds. Solid solutions were reported involving either Cl−/Br− or Br−/I− pairs. As shown in Fig. 2, preferential insertion is observed here with the Br− anion, in solid solutions with either Cl− or I−, demonstrating that the most “stable” structure, or the best compromise between size and all intermolecular interactions, is reached with the intermediate-size Br− anion. Note that the authors reported that this bromide phase actually gives the largest crystals during the electrocrystallization experiments.
1 cation radical salts of o-Me2TTF with Cl−, Br− and I− anions.68 In this original quadratic structure, the halide is embedded in a set of weak C–H⋯X− hydrogen bonds. Solid solutions were reported involving either Cl−/Br− or Br−/I− pairs. As shown in Fig. 2, preferential insertion is observed here with the Br− anion, in solid solutions with either Cl− or I−, demonstrating that the most “stable” structure, or the best compromise between size and all intermolecular interactions, is reached with the intermediate-size Br− anion. Note that the authors reported that this bromide phase actually gives the largest crystals during the electrocrystallization experiments.
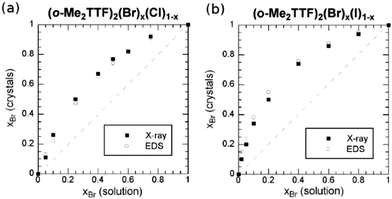 | ||
| Fig. 2 Mole fraction (x) of the Br− anion in the crystals, as a function of that in solution for (a) (o-Me2TTF)2(Br)x(Cl)1−x and (b) (o-Me2TTF)2(Br)x(I)1−x. Reproduced from ref. 68 with permission from Wiley-VCH. | ||
More complex anions can also have similar effects, as reported in θ-(BEDT-TTF)2(Rb1−xCsx)Zn(SCN)4 with preferential insertion of Cs+ over Rb+,86 or in κ-(BEDT-TTF)2Cu[N(CN)2]BrxCl1−x salts with preferential insertion of the Br− ion.83
2.4 Disorder evaluation
In essentially all reported examples, the statistical mixing of two partners in solid solutions is taken for granted. This was investigated in one single example by X-ray diffraction at low temperatures (T < 30 K) where the diffuse scattering due to thermal vibrations is negligible, in comparison with the effects of intrinsic substitutional disorder. In TMTSF2(ReO4)1−x(ClO4)x solid solutions,71 the intense diffuse scattering observed near the origin of the reciprocal space was shown to decrease with increasing Bragg (θ) angle. This θ dependence follows, at all concentrations, the monotonic Laue scattering associated with random disorder which can be written as:| I(θ) = Cx(1 − x)[fA(θ) − fB(θ)]2 |
The question of substitutional vs. positional disorder was elegantly addressed in the β′′-(BEDT-TTF)2(SF5-R-SO3) series known to exhibit superconducting (R = CH2CF2), metallic (R = CHF), or metal–insulator (R = CHFCF2) character.88 With the latter chiral SF5CHFCF2SO3− anion, positional disorder of the two enantiomers is observed in the pure phase and two characteristic, low-energy electronic excitations (centered at ≈5200 and 9600 cm−1) were tentatively attributed to either correlation-driven or disorder-related localization. To test this assumption, solid solutions were prepared. When combining the superconducting (R = CH2CF2) and metallic (R = CHF) systems, only positional disorder is expected. The strongest charge-transfer excitations are observed for x = 0.5 where positional disorder is indeed maximum. On the other hand, when combining the superconducting (R = CH2CF2) with the metal–insulator (R = CHFCF2) chiral anion, it appears that local orientational disorder effects (chiral anion) are much stronger than positional effects (alloying) as the strongest charge-transfer excitations are observed for x = 1. This demonstrates that the anion pocket disorder results in large-amplitude modulations of the electrostatic potential, which are very effective in localizing charge on the BEDT-TTF stack, revealed by these low-energy electronic excitations.
A specific situation needs to be mentioned where order emerges from disorder for the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 composition, for example in [(TMTSF)1−x(TMTTF)x]2ReO4 for x ≈ 0.50.41 Independently of the q1 = (½, ½, ½) superstructure associated with well-known anion ordering (AO) transition observed at low temperatures in both pure compounds and the alloys, another q2 = (0, ½, ½) superstructure found already at room temperature has been attributed to an alternate order of the TMTTF and TMTSF molecules along the stacks, with a spatial coherence of ≈300 Å.
50 composition, for example in [(TMTSF)1−x(TMTTF)x]2ReO4 for x ≈ 0.50.41 Independently of the q1 = (½, ½, ½) superstructure associated with well-known anion ordering (AO) transition observed at low temperatures in both pure compounds and the alloys, another q2 = (0, ½, ½) superstructure found already at room temperature has been attributed to an alternate order of the TMTTF and TMTSF molecules along the stacks, with a spatial coherence of ≈300 Å.
2.5 Tools for analyzing solid solutions’ compositions
The evaluation of the exact composition and nature of solid solutions is a complex challenge. Several points are indeed of interest for any analytical method aimed at determining the alloy composition, such as its precision (important for low x values), its spatial extension, its reproducibility also in relation to the homogeneity of the samples themselves, and its eventual destructive character.Energy-dispersive X-ray spectroscopy (EDS, EDX, EDXS or XEDS), sometimes called energy dispersive X-ray analysis (EDXA or EDAX) or energy dispersive X-ray microanalysis (EDXMA), has been the analytical technique of choice to analyze most solid solutions. Different elements can be probed simultaneously: for example, S vs. Se in (TSF)x(TTF)1−x(TCNQ),34 [(TMTSF)1−x(TMTTF)x]2PF6,43 and κ-[(ET)1−x(BEDSeT-TTF)x]2Cu[N(CN)2]Br.45
X-Ray diffraction on single crystals is a useful tool when the two mixed species differ notably by their electron count and hence their diffracting power. Typical examples involve refinement of Cl−vs. Br− in (o-Me2TTF)2Cl1−xBrx,68 Br vs. CH3 in [(Me2)1−x(MeBr)xDCNQI]2Cu,60 Ni vs. Pd in [(CH3)4N][NixPd1−x(dmit)2]2,57 and Pt vs. Au in (Perylene)2[Au1−xPtx(mnt)2].49 The method, however, requires that a complete data set is collected and refined for each composition, while EDS methods (see above) provide comparable precision in a much faster way. On the other hand, the method gives a precise indication of the evolution of the structure (unit cell, molecular orientations) with x.
Inductively coupled plasma atomic emission spectroscopy (ICP-AES) has been used only rarely and is mentioned to evaluate the beryllium amount in the [PLY-(O,O)]2B1−xBex solid solutions of spiro-bis(9-oxidophenalenone)boron [PLY(O,O)]2B with the neutral beryllium analog [PLY(O,O)]2Be.53,54
Neutron activation analysis (NAA) has been reported by two groups to analyze solid solutions, in mixed crystals of (BEDT-TTF)-trihalides such as β-(ET)2(I3)1−x(IBr2)x, β-(ET)2(IBr2)1−x(I2Br)x and β-(ET)2(I2Br)1−x(I3)x to determine the atomic ratio of bromine to iodine,77,78 and in the extensive series of (DCNQI)2Cu salts to analyze Br and Cu.61
Elemental analysis can be used but its precision is relatively low; it requires large amounts of materials, most often not available when obtained by electrocrystallization. The method has therefore been limited to materials obtained in larger quantities by chemical routes, as in the series of (DCNQI)2Cu salts,61 or in magnetic salts such as [NO2BzPy][AuxNi1−x(mnt)2], where [NO2BzPy]+ stands for 1-(4′-nitrobenzyl)pyridinium and [M(mnt)2]− for bis(maleonitriledithiolato)metallate.55,56
Mass spectrometry (EI-MS) has been used to discriminate between closely related molecular species, as between EDO-TTF and MeEDO-TTF in [(EDO-TTF)1−x(MeEDO-TTF)x]2PF6 where the two molecules only differ by a methyl group.46 Experimental deviations of the x value were ≈0.01–0.02. It should be noted that the estimation of x values by this method bear some systematic error since the efficiencies of EDO-TTF and MeEDO-TTF molecules to produce molecular ions are different from each other. The same method was used for the mixed-valence [Pd(dmit)2] salts with mixtures of Me4Sb+, EtMe3Sb+ and Et2Me2Sb+ cations.67
Solution NMR has been reported in one recent example for (TMTSF)2(TaF6)1−x(PF6)x solid solutions involving TaF6− and AsF6− anions thanks to 19F NMR measurements of solutions prepared by dissolving small amounts of all materials in DMSO-d6.76 The integration of the signal of PF6−, appearing as a doublet at −70 ppm with respect to the signals of fluorine atoms connected to Ta(V), provided the TaF6−/PF6− ratio in the bulk material. Satisfyingly, the ratios estimated by this method were in good agreement with those obtained by the refinement of the single crystal diffraction data.
3. Manipulation of physical properties in solid solutions
Investigations of solid solutions in molecular conductors are associated with a variety of objectives, which concern the analogy with external pressure (chemical pressure) effects, the influence of disorder and/or doping on conductivity and eventually superconductivity, the manipulation of band filling, the insertion of magnetic defects, and the evolution of structural and/or electronic phase transitions characteristic of the pure compounds. These effects proved to be very complex to analyze and they will be illustrated in the following by only some representative examples.3.1 Chemical pressure effects
Once the actual composition of the solid solution (x value in crystal) has been determined (cf. Section 2.5), it is possible to follow the evolution of the unit cell parameters with x. In the only situations where both pure compounds have the same crystal structure, a linear evolution of these parameters between the x = 0 and x = 1 situations is often observed, referred to as Vegard's law. Typical examples are reported, for example, in (TMTSF)2(ClO4)1−x(ReO4)x,71 θ-(BEDT-TTF)2(Rb1−xCsx)Zn(SCN)4,86 (o-DMTTF)2BrxCl1−x,68 and β-(BEDT-TTF)2(I3)1−x(IBr2)x.77,78 These linear evolutions are often described, in a misuse of language, as chemical pressure effects, as in most cases the actual evolutions of the pure systems under pressure are not known. In other words, the compressibility (and its anisotropy) of a pure system might be notably different from its evolution in a solid solution upon insertion of a smaller species. An illustration is provided by the β-(ET)2(I3)1−x(IBr2)x alloy where the smooth evolution of the unit cell parameters (contraction with increasing amount of the smaller IBr2− anion) parallels that observed in the pure β-(ET)2I3 phase (x = 0) under pressure between 0 and 4 kbar. The pure IBr2− phase (x = 1) is indeed crystallographically comparable to the x = 0 I3− phase at 4 kbar.77 The situation is more delicate in the κ-(BEDT-TTF)2Cu[N(CN)2]BrxCl1−x system,83,85 where increasing amounts of Br− anions do have the same effect as that of the physical pressure on the pure chloride salts (x = 0), while the unit cell volume is actually increasing (negative chemical pressure) with x.Deviations from Vegard's law are common and can be indicative of the evolution of the molecular orientations such as the tilt angle of the stacks in (TSeF)x(TTF)1−x·TCNQ.34 Such displacements are characteristic of molecular alloys and can have important consequences on the physical properties up to the point where a continuous change in composition can have non-linear effects on the structural and hence electronic properties. This is beautifully illustrated in the behavior of solid solutions of the (DCNQI)2Cu salts. Indeed, two groups emerge from this family: those with a stable metallic state down to low temperatures as found with Me2DCNQI and I2DCNQI, and those with a sharp metal–insulator transition as found with Me2DCNDI-d8, MeBrDCNQI and MeClDCNQI.58–61 The first group is sensitive to pressure and undergoes a metal–insulator transition at a very low pressure (≈50 bar) in (Me2DCNQI)2Cu but a notably higher one (15.3 kbar) in the I2DCNQI salt, indicating a very stable metallic state in the latter. Solid solutions combining two acceptors from group I, or two acceptors from group II, led to the expected group I or group II behavior respectively.61,62 On the other hand, combining two acceptor molecules, one from each group, into solid solutions was reported for example in [(Me2)1−x(MeBr)xDCNQI]2Cu, where a small doping range (x < 0.1) was already sufficient to favor the occurrence of the M–I transition, with re-appearance of the metallic phase at lower temperatures. This behavior was already known for the pristine (Me2DCNQI)2Cu under pressure.59 The main origin of these evolutions is, however, to be found in the evolution of the structure itself, with the α angle characterizing the tetrahedral coordination around the Cu ion which exhibits a notable increase with MeBrDCNQI concentration (Fig. 3).59 This sensitivity varies with the nature of the acceptors. In the [(MeIDCNQI)1−x(MeBrDCNQI)x]2Cu alloy, the group I behavior of (MeIDCNQI)2Cu was for example maintained up to x = 0.60.61 These examples illustrate how prudent one should be when referring to chemical pressure effects.
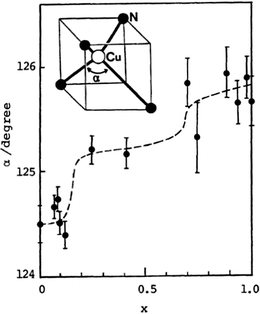 | ||
| Fig. 3 Evolution of the α angle with x in the coordination sphere of Cu in the [(Me2)1−x(MeBr)xDCNQI]2Cu alloys. Taken from ref. 59. © 1989 The Chemical Society of Japan. | ||
Another convincing illustration is provided by [(Me2DCNQI)1−x(Me2DCNQI-d8)x]2Cu alloys involving the deuterated Me2DCNQI-d8 belonging to group II. This system clearly reproduced the low-pressure region (1–500 bar) of the exotic pressure–temperature phase diagram of [Me2DCNQI]2Cu including the reentrant M–I–M transition at ambient pressure.58 The sharp transitions observed in the resistivity measurements indicated that the system is homogeneous and that the disorder effect brought by deuteration was reduced here to a minimum, which cannot be realized in other alloyed (DCNQI)2Cu salts. In this case, the very high sensitivity of the [Me2DCNQI]2Cu system to pressure and the chemical pressure control using the deuteration were the key elements for reproducing with alloying the pressure–temperature diagram of the pure hydrogenated system.
3.2 Anion ordering transitions
Since TMTTF/TMTSF (Fabre/Bechgaard) salts crystallize in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group with the counter ion located at the inversion center, non-centrosymmetric anions such as ReO4− and ClO4− are disordered at room temperature. At low temperatures, they order in such a way that neighboring anions align or alternate their orientation. In (TMTSF)2ReO4, the anions alternate in the three crystallographic directions below TAO = 176 K, an ordering characterized by a reduced wave vector q1 = (½, ½, ½). In (TMTSF)2ClO4, the AO is found at q2 = (0, ½, 0) with a much lower TAO value (24 K), indicating an average decrease of the electron–anion coupling, with the ClO4− anions having weaker interactions with the TMTSF stacks than the ReO4− ones.70 In (TMTSF)2(ReO4)1−x(ClO4)x solid solutions,71 it was shown that the q1 long range order (LRO) of the ReO4− phase (x = 0) was maintained for x < 0.5, while the q2 LRO of the ClO4− phase (x = 1) was destroyed for x < 0.97. For the intermediate 0.5 < x < 0.97 compositions, the complex coexistence of short range orders (SRO) at q1 and q2 is observed. The phase diagram of this solid solution was analyzed within the framework of an Ising model, with an Ising variable ηi = ±1 depending on the anion orientation.
space group with the counter ion located at the inversion center, non-centrosymmetric anions such as ReO4− and ClO4− are disordered at room temperature. At low temperatures, they order in such a way that neighboring anions align or alternate their orientation. In (TMTSF)2ReO4, the anions alternate in the three crystallographic directions below TAO = 176 K, an ordering characterized by a reduced wave vector q1 = (½, ½, ½). In (TMTSF)2ClO4, the AO is found at q2 = (0, ½, 0) with a much lower TAO value (24 K), indicating an average decrease of the electron–anion coupling, with the ClO4− anions having weaker interactions with the TMTSF stacks than the ReO4− ones.70 In (TMTSF)2(ReO4)1−x(ClO4)x solid solutions,71 it was shown that the q1 long range order (LRO) of the ReO4− phase (x = 0) was maintained for x < 0.5, while the q2 LRO of the ClO4− phase (x = 1) was destroyed for x < 0.97. For the intermediate 0.5 < x < 0.97 compositions, the complex coexistence of short range orders (SRO) at q1 and q2 is observed. The phase diagram of this solid solution was analyzed within the framework of an Ising model, with an Ising variable ηi = ±1 depending on the anion orientation.
3.3 Alloying effects on conductivity
The conductivity of solid solutions is almost systematically investigated but its evolution with alloy composition and with temperature can be extremely complex to analyze as it depends on many different factors. We need for example to distinguish here two situations, those related to weak doping with x values close to 0 or 1, and those related to systems where x continuously covers the whole spectrum between 0 and 1. We will concentrate here on the second situation, and illustrate it first with the prototypical TTF·TCNQ system and its solid solution with TSF. As shown in Fig. 4, the RT conductivity is decreased in the solid solution by comparison with the pure salts, a consequence of disordering the donor stack. This effect of disorder due to alloy formation also manifests itself in a smaller increase in conductivity with decreasing temperature. The conductivity increases indeed for the solid solutions by 7–10 times in going from room temperature to the temperature TMI at which it peaks (Peierls transition), compared to values for TTF·TCNQ and TSF·TCNQ (12–20 times). Furthermore, the dominance of the TCNQ stacks and the unimportance of fulvalene disorder in producing the metal–insulator transition are confirmed for 0 < x < 0.9,36 as only 3% incorporation of TSF into TTF–TCNQ completely obscures the 38 K transition associated with the TTF fstacks in TTF–TCNQ, while the 53 K transition remains relatively sharp.34 These evolutions are compared with those observed in an analogous salt isolated with the (Z,E-DTDSF)·TCNQ (see Fig. 4). The notably higher RT conductivity of (Z,E-DTDSF)·TCNQ than that of the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 solid solution indicates that the donor stack conductivity is much less affected by disorder due to the random arrangement of Z- and E-DTDSF molecules than that of the TSF and TTF molecules. This is because both Z- and E-DTDSF molecules are electronically very close, at variance with TSF and TTF whose oxidation potential differs by 0.17 V.36
50 solid solution indicates that the donor stack conductivity is much less affected by disorder due to the random arrangement of Z- and E-DTDSF molecules than that of the TSF and TTF molecules. This is because both Z- and E-DTDSF molecules are electronically very close, at variance with TSF and TTF whose oxidation potential differs by 0.17 V.36
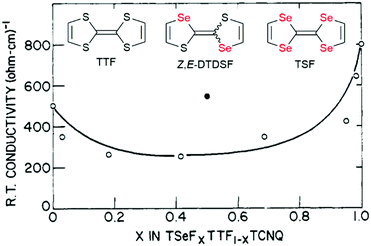 | ||
| Fig. 4 Room temperature conductivity of (TSF)x(TTF)1−x(TCNQ) (open circles). The closed black circle refers to [(Z,E)-DTDSF]TCNQ (see text). Adapted from ref. 34. © 1977 American Chemical Society. | ||
Another example of the effect of disorder on the phase diagram is provided by (TMTTF)2(SbF6)1−x(AsF6)x solid solutions. At low temperatures, a non-magnetic (spin-Peierls) ground state is reported for (TMTTF)2AsF6, while an antiferromagnetic ground state characterizes the pure SbF6− salt. The (TMTTF)2(SbF6)1−x(AsF6)x alloys behave as pure salts for x < 0.2 and x > 0.8, while in the middle range, higher disorder prevents the condensation of any ordered phase.74
3.4 Alloying effects on superconductivity
The well-known sensitivity of superconductivity to disorder or defects was investigated soon after it was discovered at ambient pressure in (TMTSF)2ClO4. It was indeed shown that introduction of only 5% TMTTF in [(TMTSF)1−x(TMTTF)x]2ClO4 was sufficient to suppress the superconductivity.40 On the other hand, when replacing the ClO4− anion with a nominal concentration of ReO4− up to x = 0.06 in (TMTSF)2(ClO4)1−x(ReO4)x, the superconducting transition temperature is decreased by a factor of about two.72a,bβ-(BEDT-TTF)2I3 is the first superconductor in the I3− salts of BEDT-TTF and was intensively studied at an early stage.23 The coexistence of high-Tc and low-Tc states was a puzzle that is related to an incommensurate lattice modulation below 200 K. In order to clarify this problem, an alloy system with the superconducting β-(BEDT-TTF)2AuI2 salt, β-(ET)2(I3)1−x(AuI2)x (x = 0.1, 0.9), was examined by low-temperature X-ray diffraction and transport measurements.79,81 It was suggested that two types of disorder, namely the conformational disorder of the terminal ethylene groups and the distortions in the anion sites, can affect the superconducting state. The superconductivity was destroyed in the x = 0.1 and x = 0.6 alloys, while in the AuI2− rich phase (x = 0.9), stepwise resistivity drops were observed at 4.5 and 2.1 K. The high-temperature anomaly at 4.5 K has been attributed to the high-Tc anomaly of β-(BEDT-TTF)2I3 and the superconducting transition at 2.1 K will correspond to the low-Tc transition.
In β-(BEDT-TTF)2(I3)1−x(IBr2)x alloys, the superconductivity of the pure I3− phase was destroyed already for x = 0.05 and above, while on the other side of the alloy, the superconducting state of the pure IBr2− phase was maintained for x ≥ 0.75.77 In that respect, the superconductivity of the so-called κ-Br phase of BEDT-TTF, i.e. κ-(BEDT-TTF)2Cu[N(CN)2]Br, appears to be particularly robust as substitution of the donor molecule with the diselenated BEDT-SFT analog (see Scheme 2) allowed maintaining the superconductivity for x values up to 0.20 in κ-[(BEDT-TTF)1−x(BEDT-STF)x]2Cu[N(CN)2]Br.44
Similar disorder/size effects on superconductivity have been reported in the superconducting K3C60. The superconducting temperature of the pure compound K3C60 at 19 K was progressively reduced upon alloying it with C70 in K3(C60)1−x(C70)x and the SC state disappeared for x > 0.25.63
3.5 Band filling manipulation
At variance with inorganic (super)conductors where band filling can be easily modified, for example through oxygen doping in high-Tc superconductors, molecular conductors with their fixed stoichiometry are most often not amenable to such strategies. Attempts have been reported, however, (i) in cation-radical salts upon replacement of a monovalent anion with a divalent one (GaCl4−/FeCl4−vs. MnCl42−/CoCl42−),87,98,111 (ii) in anion radical salts upon replacement of Cu+/Cu2+ with Li+ and (iii) in single component conductors where neutral metallic complexes are mixed with analogous neutral complexes having different electron counts.Modification of band filling in cation radical salts proved to be very difficult as most often the structure resists the insertion of a divalent anion in place of a monovalent one. This strategy was successfully investigated, for example, in BEDT-TTF salts such as λ-(ET)2(GaCl4)1−x(CoCl4)x with x < 0.06 and in δ′-(ET)2(GaCl4)1−x(CoCl4)x with x < 0.14. In both systems, at maximum doping, the RT conductivity was found to decrease by one order of magnitude relative to the pure GaCl4− salts.87 The most successful examples were reported from TTM-TTP salts, which are known to crystallize not only with monovalent anions (FeCl4−, GaCl4−) to give 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 phases, i.e. with a ρ = 1 charge transfer and associated ½ band filling and a metallic character at RT, but also with divalent anions (MnCl42−, CoCl42−) with the same 1
1 phases, i.e. with a ρ = 1 charge transfer and associated ½ band filling and a metallic character at RT, but also with divalent anions (MnCl42−, CoCl42−) with the same 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry and regular stacking but now with ρ = 2, zero band-filling and semiconducting character.98 Three alloys prepared by combining CoCl42− with either FeCl4− or GaCl4− in (TTM-TTP)Fe1−xCoxCl4 (x = 0.05, 0.40) and (TTM-TTP)Ga1−xCoxCl4 (x = 0.30) were reported. The decreased band filling associated with increasing x values was correlated with a regular increase of the room-temperature resistivity and thermoelectric power.
1 stoichiometry and regular stacking but now with ρ = 2, zero band-filling and semiconducting character.98 Three alloys prepared by combining CoCl42− with either FeCl4− or GaCl4− in (TTM-TTP)Fe1−xCoxCl4 (x = 0.05, 0.40) and (TTM-TTP)Ga1−xCoxCl4 (x = 0.30) were reported. The decreased band filling associated with increasing x values was correlated with a regular increase of the room-temperature resistivity and thermoelectric power.
In radical anion salts, the Cu(DCNQI)2 system is also a beautiful example of variable doping in the solid solutions where the copper is substituted with Li+. Indeed, in the pure Cu(DCNQI)2 salt, the valence of the copper is intermediate (+1.3) between those of Cu+ and Cu2+. Replacing progressively copper with Li+ hence modifies continuously the band filling and turns the metallic Cu(DCNQI)2 system into a semiconductor in the whole temperature range (Fig. 5).65,66
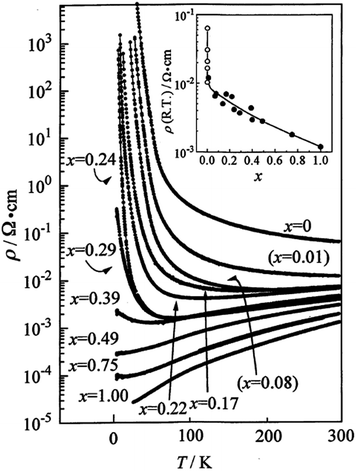 | ||
| Fig. 5 Temperature dependence of the resistivity of (DMDCNQI)2Li1−xCux. The inset shows the dependence of resistivity at RT with the white circles for the x = 0 compound with various impurity levels. Reproduced from ref. 66. © 1999 The Physical Society of Japan. | ||
Single-component conductors offer another possibility for modifying the band filling, as illustrated below in several examples where neutral complexes with different electron counts can be mixed. For example, [Ni(tmdt)2] (see Scheme 1) is a 3D metal stable down to 4 K, while [Au(tmdt)2], bearing one extra electron, is reported to undergo an antiferromagnetic transition around 110 K (TNéel) without loss of its high conductivity. The temperature dependence of the resistivities of the compressed pellet samples of [Ni1−xAux(tmdt)2] alloys51 (0 < x < 1) showed the systems to be essentially metallic down to low temperature, while TNéel was moved to lower temperatures with decreasing x value, essentially disappearing for x ≤ 0.6. Moving to solid solutions involving the isoelectronic copper analog [Cu(tmdt)2] rather than the gold one gives a fully different picture,52 as the extra electron in [Cu(tmdt)2] is now localized in an antibonding metal–ligand orbital with dx2−y2 symmetry. The magnetic behavior of [Ni1−xCux(tmdt)2] for x = 0.098, 0.13 and 0.18 was described as a molecular Kondo system, while, at a higher copper concentration (x = 0.27), the magnetic moments begin to interact antiferromagnetically with each other through the so-called π–d interaction.
The situation is also rather complex in phenalenyl-based single-component conductors such as [PLY(O,O)]2B (see Scheme 1).53,54 The radical complex can be substituted with the diamagnetic beryllium analog lacking this extra electron. At low doping levels (x ≤ 0.15), substitutional doping is effective and increases the conductivity while lowering the activation energy of both compounds. Higher doping proved to be more difficult as the beryllium analog is not isostructural with its boron congeners, a striking consequence of this different electron count. It has been argued that this effect on the conductivity cannot be described as a classical semiconductor hole doping as the energy levels of the beryllium dopant are not located in the semiconducting gap of the boron complex. The increase in conductivity would rather be a consequence of decreased antiferromagnetic interactions between pairs of boron radicals.
3.6 Alloying effects on magnetic properties
Because of the strong electronic correlations present in these conducting systems (especially in Mott insulators), specific magnetic properties are closely related to these conducting properties and their evolution within solid solutions provides another extremely rich tool for exploring phase diagrams. One first example is provided by the TMTTF salts with either AsF6− or SbF6−.74,75 While the AsF6− salt exhibits a non-magnetic (spin-Peierls) ground state below 14 K, the SbF6− salt gives rise to an antiferromagnetic ground state below TNéel = 8 K. At higher temperatures, the resistivity of (TMTTF)2SbF6 shows clear evidence of an anomaly around Tρ = 154 K, below which dρ/dT becomes negative, where ρ is the resistivity. This semiconducting charge-ordered phase (below Tρ) gradually weakens by alloying it with AsF6−,74b but proved to be present in all compositions.75 First experiments on (TMTTF)2[(AsF6)x(SbF6)1−x] solid solutions using electron spin resonance (ESR) and magnetic susceptibility have detected the antiferromagnetic phase transition and the spin-gap transition near the pure AsF6− and SbF6− salts, respectively, that is for x > 0.8 and x < 0.2, while the absence of any ordered ground state was postulated in the intermediate (x ≈ 0.5) region.74c13C NMR studies of the ground states and critical behavior in this alloy system for x = 0.3, 0.5 and 0.67 suggested, however, that the antiferromagnetic phase and spin-gap phase are in contact at low temperatures. The x = 0.5 alloy is situated on the edge of the spin-gap phase, showing a gradual phase transition and significant critical fluctuations at low temperatures, which can be attributed to the quantum critical effect.Another example is the alloyed quantum spin liquid system based on salts of Pd(dmit)2.112 Indeed, the anion radical salt EtMe3Sb[Pd(dmit)2]2 is a Mott insulator with a triangular lattice where the spin frustration plays an important role. By changing the cation, the degree of frustration can be tuned without serious changes in the crystal structure. The magnetic ground state of this Mott system depends on the degree of frustration, characterized by the t′/t ratio of interdimer transfer integrals t and t′ (see Fig. 6). With the smaller Me4Sb+ cation, the salt shows an antiferromagnetic long-range order (AFLO), while with the larger Et2Me2Sb+ cation, the salt exhibits a non-magnetic charge-order state (CO). The alloying of the EtMe3Sb+ salt with either Me4Sb+ or Et2Me2Sb+ cations changes lattice constants67 and the degree of frustration continuously. This alloyed system conformed to a phase diagram where the quantum spin liquid exists as a “phase” (not a critical “point”) located between the antiferromagnetic phase and the charge order phase as shown in Fig. 6.
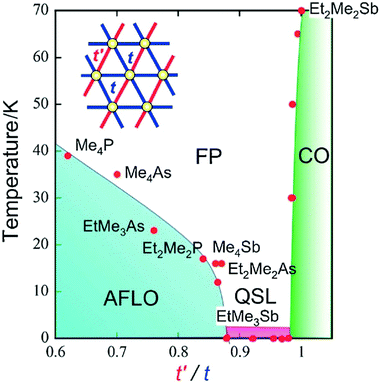 | ||
| Fig. 6 Phase diagram for the series of β′-X[Pd(dmit)2]2 salts. Points referring to the (Me4Sb)1−x(EtMe3Sb)x[Pd(dmit)2]2 and (Et2Me2Sb)1−x(EtMe3Sb)x[Pd(dmit)2]2 solid solutions are those located between t′/t = 0.87 (for pure Me4Sb+ salt) and t′/t = 1 (for pure Et2Me2Sb+ salt), with the pure EtMe3Sb+ salt at t′/t = 0.92. Abbreviations: FP, frustrated paramagnetic (state); AFLO, antiferromagnetically long-range ordered (state); CO, charge-ordered (state); QSL, quantum spin liquid (state). Reproduced from ref. 112. © 2014 The Chemical Society of Japan. | ||
3.7 Magnetic doping
Another sought-after strategy for the preparation of solid solutions of molecular conductors is the sequential introduction of localized magnetic ions in the neighborhood of a conducting stack. Perhaps one of the first experimental demonstrations was reported in the perylene salts (Per)2[PtxAu1−x(mnt)2], where the anionic chains of [M(mnt)2]− complexes are either diamagnetic (M = Au) or paramagnetic (M = Pt).47,48 Both pure compounds, in their α-phase, present a metal-to-insulator transition at 8 K and 12 K, respectively, which has been ascribed to the Peierls distortion (tetramerisation) of the perylene chains. The Pt compound presents, in addition to the Peierls transition involving the conducting perylene chains, a spin-Peierls transition at the same critical temperature that corresponds to the dimerization of the spin-carrying units [Pt(mnt)2]−.113 This metallic α-phase was still observed in the alloys for x < 0.50 and x > 0.95, while in the intermediate range 0.50 ≤ x ≤ 0.95, the salt adopts another structural β-type associated with a semiconducting behavior in the whole temperature range.49One of the most investigated systems along these lines is λ-(BETS)2MCl4 where the diamagnetic GaCl4− anion can be substituted with the high-spin FeIII FeCl4− anion (S = 5/2).92,93 Indeed, λ-(BETS)2GaCl4 undergoes a superconducting transition at ≈6 K, and the superconductivity is destroyed under a magnetic field of 13 T parallel to the conduction plane. On the other hand, its isostructural analogue λ-(BETS)2FeCl4 exhibits a coupled metal–insulator and antiferromagnetic transition at 8.5 K, suggesting the important role of the interaction between the π electrons of BETS and the d electrons of the high-spin Fe3+ ion. The insulating phase for λ-(BETS)2FeCl4 is destabilized by the magnetic field above ≈10 T, where the paramagnetic state of the Fe moments is recovered. A complete phase diagram is shown in Fig. 7.
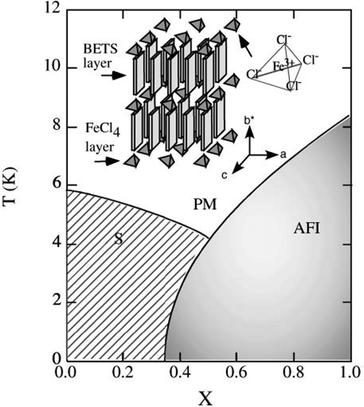 | ||
| Fig. 7 Phase diagram of the organic alloys λ-(BETS)2FexGa1−xCl4 in the absence of an external magnetic field. PM, AFI and S denote paramagnetic metal, antiferromagnetic insulator and superconductor, respectively. Reproduced from ref. 94. © 2003 The Physical Society of Japan. | ||
The field-induced superconductivity for λ-(BETS)2FeCl4 has been understood in terms of the Jaccarino–Peter effect,114 in which the internal magnetic field due to the exchange interaction with localized Fe moments is crucial. In (BETS)2FexGa1−xCl4 alloys,94 superconductivity is observed only under very high magnetic fields parallel to the conducting layer for x ≥ 0.47 (Fig. 8). As x decreases, the field induced superconducting phase shifts towards lower fields and a striking field-induced insulator to superconductor transition is observed below 4 T for x = 0.45.
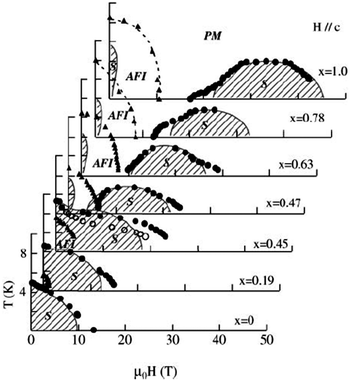 | ||
| Fig. 8 Global magnetic phase diagram of λ-(BETS)2FexGa1−xCl4 under fields applied parallel to the c axis. The PM–S transition fields are defined as the midpoints of the resistive transitions (closed circles), and the AFI–PM or AFI–S transition fields are given by the onset of a sharp change in resistance (triangles). For x = 0.45, the onset of the steep change in the PM–S transition is also plotted with open circles for comparison. The phase boundaries shown by circles and triangles are second and first order transitions, respectively. The shaded areas show the superconducting phases. Reproduced from ref. 94. © [2003] The Physical Society of Japan. | ||
4. Conclusions
Solid solution strategies in molecular conductors have been considered since the very beginning of this active research area as an invaluable tool for modulating, in a continuous way, the structural and electronic properties of these materials. Such crystalline molecular conductors are characterized by specific properties such as (i) fixed stoichiometry, (ii) low dimensionality, (iii) limited band dispersions, (iv) strong electron correlations and (v) high compressibility. As a consequence, their electronic structure is generally highly sensitive to not only minute modifications of the solid-state organization, with strong effects of external pressure, but also composition modifications such as those brought by solid solutions. Both cation and anion radical salts, and single-component conductors, have been modified upon alloying and often in the whole composition range, even if novel crystal growth conditions are sometimes needed.Topics such as preferential insertion and miscibility, the nature of disorder and the different analytical tools used for characterizing these alloys have been presented, showing the often-overlooked complexity of these systems. The consequences of alloying on conductivity and on phase transitions (superconductivity, anion ordering, Peierls transition, spin-Peierls transition, antiferromagnetic ground state), and the concepts of chemical pressure effects, band filling manipulation, and π–d interactions with magnetic anions have been discussed. In many instances, however, it proved to be difficult to sort out which peculiarity of the solid solutions is at the origin of the physical properties’ evolution. This complexity makes use of solid solutions a difficult but extremely rich strategy to also investigate the electronic properties of pure compounds, even if we feel that the structural properties of solid solutions themselves require in most cases deeper investigations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank past and current colleagues for discussions on this topic, P. Batail (Orsay, Nantes, Angers), C. Lenoir (Orsay), K. Boubekeur (Orsay, Nantes), R. Clérac (Bordeaux), C. Mézière (Nantes, Angers), O. Jeannin (Rennes) and S. Bertaina (Marseille). Financial support was granted by ANR (France) under contract number ANR-20-CE29-0011-02.Notes and references
- M. Lusi, Cryst. Growth Des., 2018, 18, 3704–3712 CrossRef CAS.
- S. Aitipamula, R. Banerjee, A. K. Bansal, K. Biradha, M. L. Cheney, A. Roy Choudhury, G. R. Desiraju, A. G. Dikundwar, R. Dubey, N. Duggirala, P. P. Ghogale, S. Ghosh, P. Kumar Goswami, N. Rajesh Goud, R. R. K. R. Jetti, P. Karpinski, P. Kaushik, D. Kumar, V. Kumar, B. Moulton, A. Mukherjee, G. Mukherjee, A. S. Myerson, V. Puri, A. Ramanan, T. Rajamannar, C. Malla Reddy, N. Rodriguez-Hornedo, R. D. Rogers, T. N. Malla Row, P. Sanphui, N. Shan, G. Shete, A. Singh, C. C. Sun, J. A. Swift, R. Thaimattam, T. S. Thakur, R. Kumar Thaper, S. P. Thomas, S. Tothadi, V. R. Vangala, N. Variankaval, P. Vishweshwar, D. R. Weyna and M. J. Zaworotko, Cryst. Growth Des., 2012, 12, 2147–2152 CrossRef CAS.
- X. Huang, X. Liu, K. Ding and S. R. Forrest, Mater. Horiz., 2020, 7, 244–251 RSC.
- C. R. Adolf, S. Ferlay and M. W. Hosseini, CrystEngComm, 2018, 20, 2233–2236 RSC.
- K. T. Butler, A. Walsch, A. K. Cheetham and G. Kieslich, Chem. Sci., 2016, 7, 6316–6324 RSC.
- X. Ding, D. K. Unruh, R. H. Groeneman and K. M. Hutchins, Chem. Sci., 2020, 11, 7701–7707 RSC.
- F. Brivio, C. Caetano and A. Walsch, J. Phys. Chem. Lett., 2016, 7, 1083–1087 CrossRef CAS.
- M. Habgood, R. Grau-Crespo and S. L. Price, Phys. Chem. Chem. Phys., 2011, 13, 9590–9600 RSC.
- J. Bouzaid, M. Schultz, Z. Lao, J. Bartley, T. Bostrom and J. McMurtrie, Cryst. Growth Des., 2012, 12, 3906–3916 CrossRef CAS.
- (a) M. Sorai, J. Ensling and P. Gütlich, Chem. Phys., 1976, 18, 199–209 CrossRef CAS; (b) P. Gütlich, R. Link and H. G. Steinhauser, Inorg. Chem., 1978, 17, 2509–2514 CrossRef; (c) P. Gütlich, R. Link, H. Klippen and H.-G. Steinhauser, J. Chem. Phys., 1979, 70, 3977–3983 CrossRef; (d) O. Kahn and C. J. Martinez, Science, 1998, 279, 44–48 CrossRef CAS.
- T. Tayagaki, A. Galet, G. Molnár, M. C. Muñoz, A. Zwick, K. Tanaka, J.-A. Real and A. Bousseksou, J. Phys. Chem. B, 2005, 109, 14859–14867 CrossRef CAS.
- For recent examples, see: (a) F. J. Valverde-Munoz, M. Seredyuk, M. Meneses-Sanchez, M. C. Munoz, C. Bartual-Murguia and J. A. Real, Chem. Sci., 2019, 10, 3807–3816 RSC; (b) N. Paradis, F. Le Gac, P. Guionneau, A. Largeteau, D. S. Yufit, P. Rosa, J.-F. Létard and G. Chastanet, Magnetochemistry, 2016, 2, 15 CrossRef; (c) M. S. Sylla, C. Baldé, N. Daro, C. Desplanches, M. Marchivie and G. Chastanet, Eur. J. Inorg. Chem., 2018, 297–304 CrossRef CAS; (d) C. Bartual-Murgui, C. Pérez-Padilla, S. J. Teat, O. Roubeau and G. Aromí, Inorg. Chem., 2020, 59, 12132–12142 CrossRef CAS.
- S. Chorazy, J. J. Stanek, W. Nogaś, A. M. Majcher, M. Rams, M. Kozieł, E. Juszyńska-Gałązka, K. Nakabayashi, S.-I. Ohkoshi, B. Sieklucka and R. Podgajny, J. Am. Chem. Soc., 2016, 138, 1635–1646 CrossRef CAS.
- J. Wang, Y. Suffren, C. Daiguebonne, S. Freslon, K. Bernot, G. Calvez, L. Le Pollès, C. Roiland and O. Guillou, Inorg. Chem., 2019, 58, 2659–2668 CrossRef PubMed.
- L. M. Aguirre-Díaz, F. Gándara, M. Iglesias, N. Snejko, E. Gutiérrez-Puebla and M. A. Monge, J. Am. Chem. Soc., 2015, 137, 6132–6135 CrossRef PubMed.
- G. Kieslich, S. Kumagai, A. C. Forse, S. Sun, S. Henke, M. Yamashita, C. P. Grey and T. Cheetham, Chem. Sci., 2016, 7, 5108–5116 RSC.
- (a) H. Seo, C. Hotta and H. Fukuyama, Chem. Rev., 2004, 104, 5005–5036 CrossRef CAS; (b) T. Giamarchi, Chem. Rev., 2004, 104, 5037–5055 CrossRef CAS.
- D. Jérôme, Chem. Rev., 2004, 104, 5565–5591 CrossRef PubMed.
- H. Jiang, P. Hu, J. Ye, K. K. Zhang, Y. Long, W. Hu and C. Kloc, J. Mater. Chem. C, 2018, 6, 1884–1902 RSC and references therein.
- (a) F. Wudl, G. Smith and E. Hufnagel, J. Chem. Soc., Chem. Commun., 1970, 1453–1454 RSC; (b) J. Ferraris, D. O. Cowan, W. Walatka and J. Perlstein, J. Am. Chem. Soc., 1973, 95, 948–949 CrossRef CAS.
- T. Mori, Chem. Rev., 2004, 104, 4947–4969 CrossRef CAS.
- B. A. Scott, S. J. La Placa, J. B. Torrance, B. D. Silverman and B. Welber, J. Am. Chem. Soc., 1977, 99, 6631–6639 CrossRef CAS.
- R. P. Shibaeva and E. B. Yagubskii, Chem. Rev., 2004, 104, 5347–5378 CrossRef CAS.
- H. Kobayashi, H. B. Cui and A. Kobayashi, Chem. Rev., 2004, 104, 5265–5288 CrossRef CAS PubMed.
- C. Rovira, Chem. Rev., 2004, 104, 5289–5318 CrossRef CAS.
- (a) S. K. Pal, M. E. Itkis, F. S. Tham, R. W. Reed, R. T. Oakley and R. C. Haddon, Science, 2005, 309, 281–284 CrossRef CAS PubMed; (b) S. Mandal, S. Samanta, M. E. Itkis, D. W. Jensen, R. W. Reed, R. T. Oakley, F. S. Tham, B. Donnadieu and R. C. Haddon, J. Am. Chem. Soc., 2006, 128, 1982–1994 CrossRef CAS PubMed.
- (a) M. P. Andrews, A. W. Cordes, D. C. Douglass, R. M. Fleming, S. H. Glarum, R. C. Haddon, P. Marsh, R. T. Oakley, T. T. M. Palstra, L. F. Schneemeyer, G. W. Trucks, R. W. Tycko, J. V. Waszczak, K. M. Young and N. M. Zimmerm, J. Am. Chem. Soc., 1991, 113, 3559–3568 CrossRef CAS; (b) A. W. Cordes, R. C. Haddon, R. G. Hicks, R. T. Oakley, T. T. M. Palstra, L. F. Schneemeyer and J. V. Waszczak, J. Am. Chem. Soc., 1992, 114, 1729–1732 CrossRef CAS.
- (a) A. A. Leitch, R. W. Reed, C. M. Robertson, J. F. Britten, X. Yu, R. A. Secco and R. T. Oakley, J. Am. Chem. Soc., 2007, 129, 7903–7914 CrossRef CAS; (b) D. Tian, S. M. Winter, A. Mailman, J. W. L. Wong, W. Yong, H. Yamaguchi, Y. Jia, J. S. Tse, S. Desgreniers, R. A. Secco, S. R. Julian, C. Jin, M. Mito, Y. Ohishi and R. T. Oakley, J. Am. Chem. Soc., 2015, 137, 14136–14148 CrossRef CAS PubMed.
- (a) T. Isono, H. Kamo, A. Ueda, K. Takahashi, A. Nakao, R. Kumai, H. Nakao, K. Kobayashi, Y. Murakami and H. Mori, Nat. Commun., 2013, 4, 1344–1349 CrossRef; (b) A. Ueda, S. Yamada, T. Isono, H. Kamo, A. Nakao, R. Kumai, H. Nakao, Y. Murakami, K. Yamamoto, Y. Nishio and H. Mori, J. Am. Chem. Soc., 2014, 136, 12184–12192 CrossRef CAS.
- Y. Kobayashi, T. Terauchi, S. Sumi and Y. Matsushita, Nat. Mater., 2017, 16, 109–114 CrossRef CAS PubMed.
- (a) H. Tanaka, Y. Okano, H. Kobayashi, W. Suzuki and A. Kobayashi, Science, 2001, 291, 285–287 CrossRef CAS PubMed; (b) A. Kobayashi, E. Fujiwara and H. Kobayashi, Chem. Rev., 2004, 104, 5243–5264 CrossRef CAS PubMed; (c) H. B. Cui, H. Kobayashi, S. Ishibashi, M. Sasa, F. Iwase, R. Kato and A. Kobayashi, J. Am. Chem. Soc., 2014, 136, 7619–7622 CrossRef CAS.
- (a) N. Tenn, N. Bellec, O. Jeannin, L. Piekara-Sady, P. Auban-Senzier, J. Iniguez, E. Canadell and D. Lorcy, J. Am. Chem. Soc., 2009, 131, 16961–16967 CrossRef CAS; (b) Y. Le Gal, T. Roisnel, P. Auban-Senzier, N. Bellec, J. Iniguez, E. Canadell and D. Lorcy, J. Am. Chem. Soc., 2018, 140, 6998–7004 CrossRef CAS PubMed.
- (a) H. B. Cui, T. Tsumuraya, T. Miyazaki, Y. Okano and R. Kato, Eur. J. Inorg. Chem., 2014, 3837–3840 CrossRef CAS; (b) H. Hachem, H. B. Cui, T. Tsumuraya, R. Kato, O. Jeannin, M. Fourmigué and D. Lorcy, J. Mater. Chem. C, 2020, 8, 11581–11592 RSC.
- E. M. Engler, B. A. Scott, S. Etemad, T. Penney and V. V. Patel, J. Am. Chem. Soc., 1977, 99, 5909–5916 CrossRef CAS.
- (a) Y. Tomkiewicz, E. M. Engler and T. D. Shultz, Phys. Rev. Lett., 1975, 35, 456–459 CrossRef CAS; (b) P. M. Chaikin, J. F. Kwak, R. L. Greene, S. Etemadt and E. M. Engler, Solid State Commun., 1976, 19, 1201–1204 CrossRef CAS.
- S. Etemad, E. M. Engler, T. D. Schultz, T. Penney and B. A. Scott, Phys. Rev. B, 1978, 17, 513–528 CrossRef CAS.
- S. Ravy, J. P. Pouget and R. Comes, J. Phys. I France, 1992, 2, l173–l190 CrossRef.
- P. Alemany, E. Canadell and J.-P. Pouget, Europhys. Lett., 2016, 113, 27006 CrossRef.
- (a) A. J. Epstein, J. S. Miller, J.-P. Pouget and R. Comès, Phys. Rev. Lett., 1981, 47, 741–744 CrossRef CAS; (b) J.-P. Pouget, R. Comès, A. J. Epstein and J. S. Miller, Mol. Cryst. Liq. Cryst., 1982, 85, 203–213 CrossRef; (c) A. J. Epstein, J. W. Kaufer, H. Rommelmann, I. A. Howard, E. M. Conwell, J. S. Miller, J.-P. Pouget and R. Comès, Phys. Rev. Lett., 1982, 49, 1037–1041 CrossRef CAS.
- (a) C. Coulon, P. Delhaes, J. Amiell, J. P. Manteau, J. M. Fabre and I. Giral, J. Phys., 1982, 43, 1721–1729 CrossRef CAS; (b) J. P. Pouget, R. Moret, R. Comes, G. Shirane, K. Bechgaard and J. M. Fabre, J. Phys. (Paris) Colloq. C3, 1983, 44, 969–975 Search PubMed.
- V. Ilakovac, S. Ravy, J. P. Pouget, C. Lenoir, K. Boubekeur, P. Batail, S. Dolanski Babic, N. Biskup, B. Korin-Hamzic, S. Tomic and C. Bourbonnais, Phys. Rev. B, 1994, 50, 7136–7139 CrossRef CAS PubMed.
- P. Auban-Senzier, C. Lenoir, P. Batail, D. Jérome and S. Tomic, Eur. Phys. J. B, 1999, 7, 529–532 CrossRef CAS.
- K. Mortensen and E. M. Engler, Phys. Rev. B, 1984, 29, 842–850 CrossRef CAS.
- (a) T. Naito, A. Miyamoti, H. Kobayashi, R. Kato and A. Kobayashi, Chem. Lett., 1992, 119–122 CrossRef; (b) T. Naito, K. Bun, A. Miyamoto, H. Kobayashi, H. Sawa, R. Kato and A. Kobayashi, Synth. Met., 1993, 56, 2234–2240 CrossRef CAS.
- J. Sasaki, A. Kawamoto and K. Kumagai, Synth. Met., 2003, 137, 1249–1250 CrossRef CAS.
- T. Murata, X.-F. Shao, Y. Nakano, H. Yamochi, M. Uruichi, K. Yakushi, G. Saito and K. Tanaka, Chem. Mater., 2010, 22, 3121–3132 CrossRef CAS.
- M. J. Matos, V. Gama, G. Bonfait and R. T. Henriques, Synth. Met., 1993, 55-57, 1858–1863 CrossRef.
- M. J. Matos, M. Almeida, L. Alcacer and R. T. Henriques, Synth. Met., 1997, 86, 2089–2090 CrossRef CAS.
- M. Matos, G. Bonfait, I. C. Santos, M. L. Afonso, R. T. Henriques and M. Almeida, Magnetochemistry, 2017, 3(22), 1–13 Search PubMed.
- K. Mebrouk, W. Kaddour, P. Auban-Senzier, C. Pasquier, O. Jeannin, F. Camerel and M. Fourmigué, Inorg. Chem., 2015, 54, 7454–7460 CrossRef CAS PubMed.
- B. Zhou, M. Shimamura, E. Fujiwara, A. Kobayashi, T. Higashi, E. Nishibori, M. Sakata, H. B. Cui, K. Takahashi and H. Kobayashi, J. Am. Chem. Soc., 2006, 128, 3872–3873 CrossRef CAS PubMed.
- Y. Idobata, B. Zhou, A. Kobayashi and H. Kobayashi, J. Am. Chem. Soc., 2012, 134, 871–874 CrossRef CAS PubMed.
- S. K. Pal, P. Bag, M. E. Itkis, F. S. Tham and R. C. Haddon, J. Am. Chem. Soc., 2014, 136, 14738–14741 CrossRef CAS.
- P. Bag, M. E. Itkis, D. Stekovic, S. K. Pal, F. S. Tham and R. C. Haddon, J. Am. Chem. Soc., 2015, 137, 10000–10008 CrossRef CAS.
- G.-J. Yuan, H. Yang, S.-X. Liu, J.-L. Liua and X. M. Ren, Dalton Trans., 2014, 43, 11908–11914 RSC.
- X. M. Ren, T. Akutagawa, S. Noro, S. Nishihara, T. Nakamura, Y. Yoshida and K. Inoue, J. Phys. Chem. B, 2006, 110, 7671–7677 CrossRef CAS PubMed.
- A. Fukaya and R. Kato, J. Phys. Soc. Jpn., 2008, 77, 094710 CrossRef.
- R. Kato, H. Sawa, S. Aonuma, M. Tamura, M. Kinoshita and H. Kobayashi, Solid State Commun., 1993, 85, 831–835 CrossRef CAS.
- A. Kobayashi, R. Kato and H. Kobayashi, Chem. Lett., 1989, 1843–1846 CrossRef CAS.
- Y. Nishio, K. Kajita, W. Sasaki, R. Kato, A. Kobayashi and H. Kobayashi, Solid State Commun., 1992, 81, 473–476 CrossRef CAS.
- S. Hünig, M. Kemmer, H. Meixner, K. Sinzger, H. Wenner, T. Bauer, E. Tillmanns, F. R. Lux, M. Hollstein, H.-G. Groß, U. Langohr, H.-P. Werner, J. U. von Schütz and H. C. Wolf, Eur. J. Inorg. Chem., 1999, 899–916 CrossRef.
- P. Erk, S. Hünig, H. Meixner, H.-J. Gross, U. Langohr, H.-P. Werner, J. U. von Schütz and H. C. Wolf, Angew. Chem., Int. Ed. Engl., 1989, 1245–1246 CrossRef.
- (a) A. A. Zakhidov, K. Yakushi, K. Imaeda, H. Inokuchi, K. Kikuchi, S. Suzuki, I. Ikemoto and Y. Achiba, Mol. Cryst. Liq. Cryst., 1992, 218, 299–306 CrossRef CAS; (b) A. A. Zakhidov, K. Imaeda, A. Ugawa, K. Yakushi, H. Inokuchi, Z. Iqbal, R. H. Baughman, B. L. Ramakrishna and Y. Achiba, Phys. C, 1991, 185–189, 411–412 CrossRef CAS.
- (a) K. Tanaka, K. Yoshizawa, T. Sato, T. Yamabe, K. Okahara and A. A. Zakhidov, Solid State Commun., 1993, 87, 1055–1059 CrossRef CAS; (b) K. Tanaka, T. Sato, T. Yamabe, K. Yoshizawa, K. Okahara and A. A. Zakhidov, Phys. Rev. B, 1995, 51, 990–995 CrossRef CAS.
- K. Hiraki and K. Kanoda, Synth. Met., 1997, 86, 2111–2112 CrossRef CAS.
- T. Yamamoto, H. Tajima, J. Yamaura, S. Aonuma and R. Kato, J. Phys. Soc. Jpn., 1999, 68, 1384–1391 CrossRef CAS.
- R. Kato, T. Fukunaga, H. M. Yamamoto, K. Ueda and H. B. Cui, Phys. Status Solidi B, 2012, 249, 999–1003 CrossRef CAS.
- E. W. Reinheimer, A. Assaf, O. Jeannin, A. Benallouche, P.-T. Nguyen, C. Coulon and M. Fourmigué, Phys. Status Solidi B, 2012, 249, 943–946 CrossRef CAS.
- S. Tomic, D. Jérome, D. Mailly, M. Ribault and K. Bechgaard, J. Phys. Colloq. France C3, 1983, 44, 1075–1079 Search PubMed.
- S. Ravy, R. Moret, J.-P. Pouget and R. Comes, Phys. B+C, 1986, 143, 542–546 CrossRef CAS.
- V. Ilakovac, S. Ravy, K. Boubekeur, C. Lenoir, P. Batail and J. P. Pouget, Phys. Rev. B, 1997, 56, 13878–13887 CrossRef CAS.
- (a) N. Joo, P. Auban-Senzier, C. R. Pasquier, P. Monod, D. Jérome and K. Bechgaard, Eur. Phys. J. B, 2004, 40, 43–48 CrossRef CAS; (b) N. Joo, P. Auban-Senzier, C. R. Pasquier, D. Jérome and K. Bechgaard, Europhys. Lett., 2005, 72, 645–651 CrossRef CAS.
- T. Yamaguchi, Synth. Met., 2001, 120, 1005–1006 CrossRef CAS.
- (a) R. Laversanne, J. Amiell, C. Coulon, C. Garrigou-Lagrange and P. Delhaes, Mol. Cryst. Liq. Cryst., 1985, 119, 317–320 CrossRef CAS; (b) R. Laversanne, C. Coulon, B. Gallois, J. P. Pouget and R. Moret, J. Phys. France Lett., 1984, 45, L393–L399 CrossRef; (c) R. Laversanne, J. Amiell and C. Coulon, Mol. Cryst. Liq. Cryst., 1986, 137, 169–178 CrossRef CAS.
- F. Iwase, K. Sugiura, K. Furukawa and T. Nakamura, Phys. Rev. B, 2010, 81, 245126 CrossRef.
- M. Allain, C. Mézière, P. Auban-Senzier and N. Avarvari, Crystals, 2021, 11, 386 CrossRef CAS.
- M. Tokumoto, H. Anzai, K. Murata, K. Kajimura and T. Ishiguro, Synth. Met., 1988, 27, A251–A256 CrossRef CAS.
- H. Anzai, M. Tokumoto, K. Takahashi and T. Ishiguro, J. Cryst. Growth, 1988, 91, 225–228 CrossRef CAS.
- H. Kobayashi, R. Kato, A. Kobayashi, T. Mori and H. Inokuchi, Solid State Commun., 1986, 60, 473–480 CrossRef CAS.
- E. Amberger, H. Fuchs and K. Polborn, Synth. Met., 1987, 19, 605–610 CrossRef CAS.
- H. Kobayashi, R. Kato, A. Kobayashi, Y. Nishio, K. Kajita and W. Sasaki, Chem. Lett., 1986, 789–792 CrossRef CAS.
- M. Fettouhi, L. Ouahab, D. Grandjean, L. Ducasse, J. Amiell, R. Canet and P. Delhaes, Chem. Mater., 1995, 7, 461–471 CrossRef CAS.
- (a) V. A. Bondarenko, Yu. V. Sushko, V. I. Barchuk, V. S. Yefanov, V. V. Dyakin, M. A. Tanatar, N. D. Kushch and E. B. Yagubskii, Synth. Met., 1993, 56, 2386–2390 CrossRef CAS; (b) Yu. V. Sushko, K. Andres, N. D. Kusch and E. B. Yagubskii, Solid State Commun., 1993, 87, 589–592 CrossRef CAS; (c) H. Posselt, H. Müller, K. Andres, Yu. V. Sushko and G. Saito, Synth. Met., 1995, 70, 917–918 CrossRef CAS.
- D. Faltermeier, J. Barz, M. Dumm, M. Dressel, N. Drichko, B. Petrov, V. Semkin, R. Vlasova, C. Mézière and P. Batail, Phys. Rev. B, 2007, 76, 165113 CrossRef.
- S. Yasin, M. Dumm, B. Salameh, P. Batail, C. Mézière and M. Dressel, Eur. Phys. J. B, 2011, 79, 383–390 CrossRef CAS.
- H. Mori, T. Okano, S. Tanaka, M. Tamura, Y. Nishio, K. Kajita and T. Mori, J. Phys. Soc. Jpn., 2000, 69, 1751–1756 CrossRef CAS.
- H. Mori, M. Kamiya, M. Haemori, H. Suzuki, S. Tanaka, Y. Nishio, K. Kajita and H. Moriyama, J. Am. Chem. Soc., 2002, 124, 1251–1260 CrossRef CAS PubMed.
- A. D. Garlach, J. L. Musfeldt, J. M. Pigos, B. R. Jones, I. Olejniczak, A. Graja, M.-H. Whangbo, J. A. Schlueter, U. Geiser, R. W. Winter and G. L. Gard, Chem. Mater., 2002, 14, 2969–2976 CrossRef CAS.
- H. Tanaka, A. Kobayashi, T. Saito, K. Kawano, T. Naito and H. Kobayashi, Adv. Mater., 1996, 8, 812–815 CrossRef CAS.
- H. Akutsu, K. Kato, E. Ojima, H. Kobayashi, H. Tanaka, A. Kobayashi and P. Cassoux, Phys. Rev. B, 1998, 58, 9294–9302 CrossRef CAS.
- H. Kobayashi, H. Akutsu, E. Arai, H. Tanaka and A. Kobayashi, Phys. Rev. B, 1997, 56, R8526 CrossRef CAS.
- H. Kobayashi, A. Sato, E. Arai, H. Akutsu, A. Kobayashi and P. Cassoux, J. Am. Chem. Soc., 1997, 119, 12392–12393 CrossRef CAS.
- S. Uji, C. Terakura, T. Terashima, T. Yakabe, Y. Terai, M. Tokumoto, A. Kobayashi, F. Sakai, H. Tanaka and H. Kobayashi, Phys. Rev. B, 2002, 65, 113101 CrossRef.
- S. Uji, T. Terashima, C. Terakura, T. Yakabe, Y. Terai, S. Yasuzuka, Y. Imanaka, M. Tokumoto, A. Kobayashi, F. Sakai, H. Tanaka, H. Kobayashi, L. Balicas and J. S. Brooks, J. Phys. Chem. Jpn., 2003, 72, 369–373 CrossRef CAS.
- G. Kawaguchi, M. Maesato, T. Komatsu, T. Imakubo, A. Kiswandhi, D. Graf and H. Kitagawa, Chem. Mater., 2016, 28, 7276–7286 CrossRef CAS.
- M. Katsuhara, M. Aragaki, T. Mori, Y. Misaki and K. Tanaka, Chem. Mater., 2000, 12, 3186–3191 CrossRef CAS.
- M. Katsuhara, M. Aragaki, S. Kimura, T. Mori, Y. Misaki and K. Tanaka, J. Mater. Chem., 2001, 11, 2125–2130 RSC.
- M. Katsuhara, S. Kimura, T. Mori, Y. Misaki and K. Tanaka, Chem. Mater., 2002, 14, 458–462 CrossRef CAS.
- T. Devic, M. Evain, Y. Moëlo, E. Canadell, P. Auban-Senzier, M. Fourmigué and P. Batail, J. Am. Chem. Soc., 2003, 125, 3295–3301 CrossRef CAS PubMed.
- P. Batail, K. Boubekeur, M. Fourmigué and J.-C. P. Gabriel, Chem. Mater., 1998, 10, 3005–3015 CrossRef CAS.
- A. Kitaigorodskii, Mixed crystals, Springer Verlag, Berlin, 1984 Search PubMed.
- K. Sarsuns, A. Berzins and T. Rekis, Cryst. Growth Des., 2020, 20, 7997–8004 CrossRef CAS.
- J. E. Eldridge, C. C. Homes, J. M. Williams, A. M. Kini and H. H. Wang, Spectrochim. Acta, Part A, 1995, 51, 947–960 CrossRef.
- E. Barthel, G. Quirion, P. Wzietek, D. Jérome, J. B. Christensen, M. Jørgensen and K. Bechgaard, Europhys. Lett., 1993, 21, 87–92 CrossRef CAS.
- M. Yamashita, A. Kawamoto and K. Kumagai, Synth. Met., 2003, 133–134, 125–127 CrossRef CAS.
- G. E. Pake, J. Chem. Phys., 1948, 16, 327–336 CrossRef CAS.
- A. Kawamoto, K. Miyagawa and K. Kanoda, Phys. Rev. B, 1997, 55, 14140–14143 CrossRef CAS.
- B. R. McGarvey, M. J. Taylor and D. G. Tuck, Inorg. Chem., 1981, 20, 2010–2013 CrossRef CAS.
- R. Kirmse, J. Stach, W. Dietzsch, G. Steimecke and E. Hoyer, Inorg. Chem., 1980, 19, 2679–2685 CrossRef CAS.
- J. Stach, R. Kirmse, W. Dietzsch, R. M. Olk and E. Hoyer, Inorg. Chem., 1984, 23, 4779–4780 CrossRef CAS.
- R. Kumai, A. Asamitsu and Y. Tokura, J. Am. Chem. Soc., 1998, 120, 8263–8264 CrossRef CAS.
- R. Kato, Bull. Chem. Soc. Jpn., 2014, 87, 355–374 CrossRef CAS.
- J.-P. Pouget, P. Foury-Leylekian and M. Almeida, Magnetochemistry, 2017, 3, 13 CrossRef.
- V. Jaccarino and M. Peter, Phys. Rev. Lett., 1962, 9, 290–292 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |