Open Access Article
Open Access ArticleReal-time monitoring of crystallization from solution by using an interdigitated array electrode sensor†
Jincheng
Tong
 *,
Amadou
Doumbia
*,
Amadou
Doumbia
 ,
Michael L.
Turner
,
Michael L.
Turner
 and
Cinzia
Casiraghi
and
Cinzia
Casiraghi
 *
*
Department of Chemistry, University of Manchester, Manchester, M13 9PL, UK. E-mail: tongjincheng@outlook.com; cinzia.casiraghi@manchester.ac.uk
First published on 21st April 2021
Abstract
Monitoring crystallization events in real-time is challenging but crucial for understanding the molecular dynamics associated with nucleation and crystal growth, some of nature's most ubiquitous phenomena. Recent observations have suggested that the traditional nucleation model, which describes the nucleus having already the final crystal structure, may not be valid. It appears that the molecular assembly can range during nucleation from crystalline to partially ordered to totally amorphous phases, and can change its structure during the crystallization process. Therefore, it is of critical importance to develop methods that are able to provide real-time monitoring of the molecular interactions with high temporal resolution. Here, we demonstrate that a simple and scalable approach based on interdigitated electrode array sensors (IESs) is able to provide insights on the dynamics of the crystallization process with a temporal resolution of 15 ms.
New conceptsAn interdigitated electrode sensor (IES) is used for real-time monitoring of the crystallization dynamics of small organic molecules, such as glycine, L-alanine, and D-mannitol in water, reaching a temporal resolution of 15 ms. Real-time monitoring of crystallization is usually made by using very specialized techniques, such as liquid-phase transmission electron microscopy, cryo-TEM or environmental atomic force microscopy, which have temporal resolution of seconds. On the other hand, electrical readouts allow ultrafast time response, making them very attractive for monitoring of the dynamics of complex ensemble processes. We demonstrate that a simple and scalable technology based on a IES can be used to monitor in real-time the crystallization process. In particular, the induction time and the supersaturation ratio can be easily and precisely extracted from the measurements. We observe characteristic fluctuations in the current after the induction time, which could be ascribed to the molecular assembly dynamics. Getting insights on the nucleus dynamics will enable a better control on the polymorph outcome, which is one of the most challenging problems to solve in crystal engineering. |
Introduction
Crystallization from solutions is one of nature's ubiquitous phenomena, describing ice formation,1 biomineralization2 and rock formation,3 to give a few examples. This process also plays a crucial role in many industries and scientific fields.4 Despite this, a full understanding on the molecular mechanisms involved in nucleation and crystal growth from solution is still lacking, mostly due to current limitation in spatial and temporal resolutions of the most widely used experimental techniques.4 In particular, the classic nucleation theory,5,6 which describes the nucleus as having already the final crystal structure, has been challenged by recent observations, indicating that the nuclei can range from crystalline to partially ordered to totally amorphous phases.7 These observations have been obtained by using very specialized techniques, such as liquid-phase transmission electron microscopy (TEM) and cryo-TEM.7 Environmental atomic force microscopy (AFM) has also been widely used to study nucleation of porous materials.8,9 However, the temporal resolution involved in these microscopic studies is still limited to seconds. Other experimental techniques, such as optical microscopy, light scattering, and X-ray approaches are suitable only for studying crystallization process based on statistically analysis of a large number of independent nucleation and crystal growth events due to their limited spatial resolution. In general, many of these techniques do consider averages taken over the whole crystallization process, or individual measurements, taken only at fixed times.10–12Developing methods, based on simple techniques, to unravel the dynamic of crystallization in real-time is therefore of crucial importance: this would give fundamentals insights to the nucleation process, potentially helping in achieving crystals with the desired final structure (i.e. polymorph). In this framework, electrical devices allow ultrafast time response (down to nanoseconds), making them very attractive for monitoring of the dynamics of complex ensemble processes. Only very few attempts have been previously attempted, ranging from the use of nanopipette electrodes for tracking crystallization events in confinement,13 to nanopore electrodes for DNA sequencing.14 Very recently, a graphene field effect transistor (FET) was used to monitor in real-time the dynamics of self-assembly of molecules on a surface,15 demonstrating that electrical readout can indeed be applied for monitoring processes of a large ensemble of interacting molecules. However, monitoring of crystallization from solution is more challenging than self-assembly because nucleation is a stochastic event: in self-assembly experiments, polymerization is achieved by UV illumination, hence the time at which the molecules should start changing their interactions is known. Furthermore, in self-assembly experiments, the molecules interact with the surface by producing a monolayer, while in nucleation, the interactions between molecules and the surface may happen in random points on the surface and this interaction is expected to change dramatically over the time, e.g. the nucleus may be formed at the surface, then it can detach and then re-adsorb on the surface, maybe with a different crystal structure. Furthermore, the solvent is evaporating, so additional effects coming from this process need also to be taken into account when reading the electrical readout.
In this work, we demonstrate real-time monitoring of nucleation and crystal growth from an evaporative droplet by using a IES. This technology is fast, precise, selective, sensitive, and already largely used for the analysis of environmental samples and it can be performed on a small samples volume. Specifically, the monitoring is performed by using the sensor in the non-Faradaic mode by measuring the changes of the electron double layer (EDL) capacitance between the interdigitated electrodes over time.16 This achieves a very high sensitivity to species close to the electrode since the EDL usually has a thickness from sub to a few nanometers.17 Hence, changes in the nanoscale range at the solid–liquid interface can be monitored by using an IES. By measuring the temporal evolution of the current, we demonstrate that it is possible to monitor the process of crystallization in real-time, within 15 ms intervals, over the whole process, starting from the solvent evaporation to the heterogeneous nucleation and the crystal growth. The ultra-high surface sensitivity of the IES allows the induction time of crystallization to be determined at different molecular concentrations. From these measurements, a critical supersaturation ratio of 1.08 for glycine was determined. We also observed that the dynamics of interaction of the molecular ensemble is completely different from that observed for self-assembly, confirming indeed that crystallization from solution is a completely different process. Further experiments based on D-mannitol and L-alanine prove the universality of our monitoring approach.
The IES does not require any advanced material or special processing, as in the case of a graphene FET,18–21 hence our results show that this approach can be easily adopted to get new insights into molecular interactions and the interaction of molecules with surfaces, which are at play in many fundamental processes, ranging from interface chemistry, crystallization, materials chemistry, and drugs manufacturing.
Results and discussion
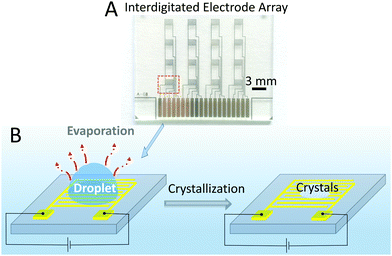
An array of interdigitated electrodes22 (Fig. 1A and Fig. S1, ESI†) was fabricated using the procedure detailed in the Experimental Section. The array combines 16 devices, divided into 4 columns (Fig. 1A). In principle, 4 droplets can be monitored by the devices in different columns at the same time, which would minimize the error between different experiments and also would help fast screening. In this study, as a proof of concept, measurements for in situ monitoring of crystallization were performed by using one device at a time.Glycine was used as reference molecule, being widely used in crystallization studies.23–25 A droplet (2 μL) of water or glycine solution was drop cast onto the patterned electrode area, as shown schematically in Fig. 1B. Then, a potential of 0.7 V was applied between the two electrodes and the current was recorded during the evaporation process. The time interval between two recorded current points was 15 ms. To optically visualize this process, an optical microscope was also used to observe the changes of the droplet and to measure the induction time of the crystals, which is defined as the time at which the crystals first appear.
Fig. 2A shows a sequence of pictures extracted from Movie S1 (ESI†) showing the droplet evolution at different times. Time equal 0 s corresponds to the initial drop casting, while time of 643 s corresponds to complete crystallization. This figure shows that the size of the droplet strongly decreases upon solvent evaporation until 533 s; then, in a very short time (at 533–534 s), the crystals appear and start to grow from the edge of the droplet towards the center, covering the whole surface and leading to a change in the color of the droplet. Only small changes in the droplet color were observed until 643 s, after which the color does not change any further, indicating complete (or almost complete) evaporation of water.
Fig. 2B shows the current recorded over the crystallization experiment by the IES. Despite the noise, one can see an overall decrease of the current (shown by the red line), caused by the evaporation of the solvent: as the droplet decreases in size, the active area decreases, lowering the current. However, there is an unexpected change in the current exactly at 533 s (see dashed arrow, inset Fig. 2B), which corresponds to the time at which the crystals become visible (Fig. 2A), i.e. to the induction time. After this, the current shows again a slow decrease over time until 643 s, and then it goes quickly to zero, reaching the off state of the device, due to complete solvent evaporation.
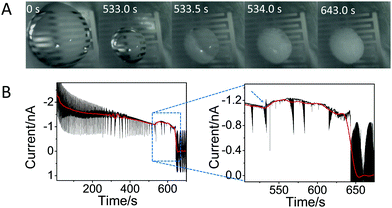 | ||
| Fig. 2 In situ monitoring of glycine crystallization by IES and optical microscopy. (A) Images of the droplet over the time covering the whole process of crystallization of 1 M glycine from solution taken from ESI† Movie S1. To give an idea of the size of the droplet, one can note that the separation and length of the electrodes are 60 μm and 1600 μm, respectively. (B) The corresponding temporal evolution of the current at a fixed voltage of 0.7 V; the red line, obtained by applying fast Fourier transform (FFT) filtering of the curve, is a guide for the eyes. The large noise is due to the measurements being performed without any Faraday cage to allow optical inspections of the crystals. Inset: Enlarged view showing the change in current at ∼533 s and afterwards. The blue and dashed arrow shows the sudden change of the current, associated to the induction time. | ||
Note that the experiments were repeated twice using two devices, demonstrating that the results are reproducible (Fig. S2, ESI†). Furthermore, a control experiment, made using only pure water was also performed: in this case, the sudden change and fluctuations in current were not observed (Fig. S3, ESI†), hence the current change at ~533 s can be ascribed to the presence of the glycine molecules, and ultimately, to a change in their interactions, driven by the crystallization.
Considering the importance of detecting small changes in the current, the same experiments were performed by applying a Faraday cage21 that decreases the ambient electrical noise. Note that this change in the setup does not allow the use of the optical microscope. Fig. S4 and S5 (ESI†) show that when a constant voltage is applied to the water or glycine droplets, the current first decreases quickly until it reaches a relatively steady state in ∼20 s. After that, in the case of the water droplet, the current decreases roughly linearly over time, as a result of the reduction of the contact area of the droplet with the electrodes. In the very last few seconds, before evaporation is complete, a sharp increase in the current is observed (Fig. S4, ESI†), which may be associated to nanoconfinement of the water molecules under the electrical field26 or to an effect caused by the local potential generated by the droplet movement between the electrodes.27 Further investigations of this effect are beyond the scope of this work.
In the case of glycine solutions, an obvious increase of the current is visible well before evaporation is complete (Fig. 3A, see arrows). An enlargement of the plot (Fig. 3B) shows that the increase is also accompanied by strong fluctuations of the current, in contrast to what was observed with water. These current fluctuations have been observed in all glycine solutions tested, i.e. with starting concentrations of 2.5 M, 2 M, 1.5 M, 1 M, 0.7 M, and 0.4 M (Fig. 3B and Fig. S6, ESI†), suggesting that these fluctuations are fingerprint of the process of interaction between molecules driven by crystallization. Indeed, the time at which the fluctuation starts strongly depends on the concentration of glycine. The larger time observed at the lower concentration is due to the fact that it takes longer time to reach oversaturation upon evaporation of the solvent. Note that the duration of the current fluctuation is also dependent on the glycine concentration (Fig. 3A): under the same conditions, crystallization takes a longer time if the number of molecules is higher. After the fluctuations, the current decreases slowly over time and reaches the off state.
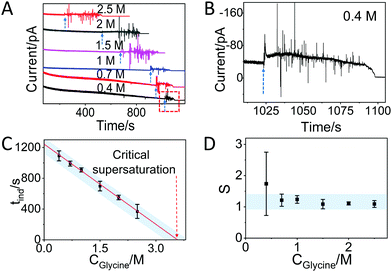 | ||
| Fig. 3 Glycine crystallization dynamics monitored and revealed by IES. (A) The recorded current curves over time measured during the evaporation of glycine droplets solutions with concentrations of 0.4 M, 0.7 M, 1 M, 1.5 M, 2 M and 2.5 M. The blue dashed arrows indicate the sudden change in current. (B) Enlarged range (highlighted red square in panel A) of the curve corresponding to the crystallization for a 0.4 M glycine droplet. The blue dashed arrow is showing the beginning of the current fluctuation. (C) The induction time (tind) for different concentrations of glycine obtained from the recorded curves in Fig. S6 and summarized in Table S1 (ESI†). The red dashed arrow indicates the glycine concentration at the critical supersaturation. The blue shadow is a guide for the eyes. (D) The corresponding supersaturation ratio (S) for different concentration of glycine solutions. The blue shadow is a guide for the eyes. | ||
Note that in self-assembly experiments, the current was observed to increase with coverage and reaches saturation for monolayer formation.15 Here, in contrast, the current does not show any exponential behavior and saturation is never reached, indicating a continuous change in the molecular assembly. This observation is reasonable because self-assembly and crystallization are very different processes from a thermodynamic point of view, despite both being based on molecular interactions. In crystallization, the nucleus is expected to change in size or structure before crystal growth, and this is possibly reflected in the fluctuations observed in the current. Section S4 (ESI†) reports a tentative molecular model that can explain the fluctuations observed in the current after the induction time.
Assuming that the induction time (calculated as the average on 4 replicates) could be assigned to the time when the fluctuation of current began, then we found the following induction times: 369 ± 91 s, 551 ± 30, 699 ± 63 s, 909 ± 27 s, 991 ± 32 s and 1092 ± 65 s for the 2.5 M, 2 M, 1.5 M, 1 M, 0.7 M and 0.4 M solutions, respectively (Fig. S6 and summary in Table S1, ESI†). Note that the induction time for 1 M glycine solution is larger than 533 s, which is the time found without a Faraday cage (Fig. 2), as a consequence of the difference between open and closed environments on the evaporation rate. Fig. 3C plots the induction time as a function of the initial glycine concentration, showing that the induction time decreases almost linearly with the concentration, indicating that the evaporation rate of the solutions at different glycine concentrations was the same in all experiments.28
By using a linear extrapolation, a critical concentration of 3.59 M is extracted from Fig. 3C: this is the concentration at which the solution will crystallize immediately, without any water evaporation. The corresponding critical supersaturation ratio (S*) is 1.08 as the saturation concentration (Csat) for glycine in aqueous solution at 25 °C is 3.33 M.29 This value is in good agreement with the one determined by a previous study based on microdroplet crystallization experiments (1.12 at 21 °C).28
Fig. S4 (ESI†) shows that water takes 1203 ± 53 s (average on 3 replicates) to completely evaporate after it is drop cast on the array – this value is in good agreement with Fig. 3C by extrapolating the data to glycine concentration (Cgly) equal to 0. Moreover, one can also observe that glycine solutions follow a similar trend to those of pure water before the point at which fluctuations are observed (Fig. S4 and S5, ESI†), showing that the evaporation rate of water (vw) and glycine (vgly) solutions are roughly the same in the range of glycine concentrations used.
The critical concentration of glycine reached at the time corresponding to the induction time (Cgly*) can be calculated as:
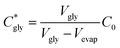 | (1) |
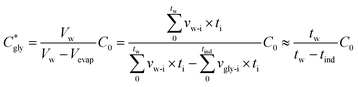 | (2) |
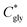 can thus be derived. The obtained
can thus be derived. The obtained 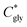 can be further used to calculate the supersaturation ratio (S), as
can be further used to calculate the supersaturation ratio (S), as 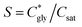 . Fig. 3d shows that S is in the range of 1–1.3, which is comparable with S*. Under these conditions, glycine aqueous solutions are expected to mainly crystallize into the α-polymorph, as confirmed by Raman spectroscopy measurements (Fig. S9, ESI†).30,31
. Fig. 3d shows that S is in the range of 1–1.3, which is comparable with S*. Under these conditions, glycine aqueous solutions are expected to mainly crystallize into the α-polymorph, as confirmed by Raman spectroscopy measurements (Fig. S9, ESI†).30,31
In order to demonstrate that the method can also be applied to other molecules, we have used the IES to monitor the crystallization of L-alanine and D-mannitol in aqueous solution. Fig. 4A and C show similar changes in the current as observed for glycine. By testing different concentrations of L-alanine (0.2 M, 0.4 M, 0.8 M, 1.2 M and 1.6 M) and D-mannitol (0.1 M, 0.2 M, 0.4 M, 0.6 M, 0.8 M and 1 M) solutions by IES (Fig. S7, S8 and summary in Tables S2, S3, ESI†) and by using the same approach described for glycine, a linear relationship between the induction time and concentration is observed. By taking the saturation concentration of L-alanine (1.88 M) and D-mannitol (1.17 M) in aqueous solution at 25 °C and the critical concentration (2.69 M for L-alanine and 1.25 M for D-mannitol) determined by extrapolation of our data, critical supersaturation ratios of 1.43 and 1.07 for L-alanine and D-mannitol, respectively, are found. Fig. 4C and F show that the corresponding supersaturation ratios at different concentrations derived from the IES measurements for both molecules are in the range of the critical supersaturation ratio, in agreement with what was observed for crystallization of glycine (Fig. 3D).
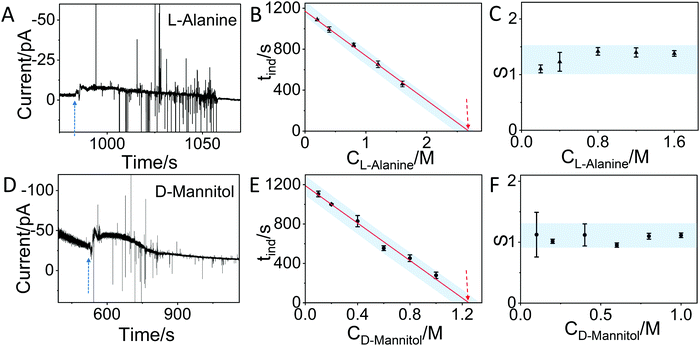 | ||
| Fig. 4 In situ monitoring of the crystallization of L-alanine and D-mannitol by IES. (A) The recorded current over time during the evaporation of a 0.4 M L-alanine solution. The blue dashed arrow indicates the sudden change in current. (B) The induction time (tind) for different concentrations of L-alanine solutions obtained from the curves in Fig. S7 and summarized in Table S2 (ESI†). The dashed arrow indicates the concentration at the critical supersaturation. (C) The corresponding supersaturation ratio (S) for different concentrations of L-alanine solutions. (D) The recorded current curve over time measured during the evaporation of a 0.6 M D-Mannitol solution. (E) The tind for different concentrations of D-mannitol solutions obtained from the recorded curves in Fig. S8 and summarized in Table S3 (ESI†). (F) The corresponding supersaturation ratio (S) for different concentration of D-mannitol solutions. The blue shadows in panels B, C, E and F are guides for the eyes. | ||
Conclusion
Herein, we demonstrate the ability to monitor in real-time the crystallization of small molecules, such as glycine, L-alanine, and D-mannitol, in water by using an interdigitated array electrode sensor. This type of electrical readout allows us to accurately determine the induction time and the critical supersaturation ratios as well as to monitor the whole crystallization process with a temporal resolution of 15 ms. It is observed that after reaching supersaturation, a short period (of the order of few seconds) of fluctuations in the current is observed and ascribed to a change in molecular interactions driven by nucleation and crystallization.In conclusion, our work shows that a simple and scalable technology can provide a highly sensitive strategy for real-time monitoring of complex dynamic processes involving molecular interactions, such as the crystallization of organic molecules.
Methods
Materials
Glycine (Reagent Plus®, ≥99%), L-alanine (99%, solubility in water is 1.88 M at 25 °C) and D-mannitol (ACS Reagent, ≥99%, solubility in water is 1.17 M at 25 °C) were purchased from Sigma-Aldrich and pure water was purchased from Fisher Scientific.Fabrication of the interdigitated electrode array
The interdigitated electrode array22 is made by gold contacts (width of 1600 μm and separation of 60 μm), and is fabricated via a combination of direct laser photoresist (s1805) lithography, metal evaporation and lift-off techniques. The substrate is polyethylenenaphthalate (PEN) stacked on glass. The substrate is sonicated in isopropanol for 5 minutes, blown dry by nitrogen and coated with S1805 (7000 rpm, 1000 rpm s−1, 60 s). Then it is heated at 110 °C for 5 min to remove residual solvents and a pattern is written by a 405 nm laser beam using a direct laser writer (mr-DWL, micro resist technology GmbH, Germany). After exposure to the laser, the substrate was immersed in MF319 solution and water in sequence for 60 s. The process was followed by coating the substrate with 5 nm of chromium and 40 nm of gold by physical vapor deposition. Finally, the substrate was sonicated in acetone for a few minutes to lift-off the gold and produce the interdigitated electrode array.In situ detection of crystallization by electrical measurement
Electrical measurements are obtained by using an Agilent B1500A semiconductor parameter analyzer in conjunction with a probe station. All measurements are done in the ambient environment at room temperature. For the real-time monitoring of the crystal growth, the patterned array was used for recording the electric signal change after a droplet (2 μL) of water or glycine solutions at different concentrations (0.4 M, 0.7 M, 1 M, 1.5 M, 2 M and 2.5 M) or L-alanine solutions (0.2 M, 0.4 M, 0.8 M, 1.2 M and 1.6 M) or D-mannitol solutions (0.1 M, 0.2 M, 0.4 M, 0.6 M, 0.8 M and 1 M) was drop-casted on the top. To operate the device in the non-Faradaic mode and to obtain a relative large current, a constant bias of 0.7 V was applied between the positive and negative electrodes during the whole process and the current was recorded. It is noticed that the use of a Faraday cage is important to achieve a lower noise in the recorded signal. Measurements taken by recording the video simultaneously by optical microscope alongside the IES resulted in much bigger noise and also faster evaporation rate of the droplets.Raman spectroscopy
Raman spectroscopy was conducted with a Renishaw inVia Raman spectrometer equipped with a 514.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm excitation wavelength laser. The measurements were performed with a 100× objective, 2400 l mm−1 grating, while the laser power was kept well-below 1.5 mW.
nm excitation wavelength laser. The measurements were performed with a 100× objective, 2400 l mm−1 grating, while the laser power was kept well-below 1.5 mW.
Author contributions
J. T. and C. C. conceived the study. A. D. prepared the interdigitated electrodes. J. T. performed in situ crystallization measurements and Raman characterization. J. T. and C. C. wrote and revised the manuscript with input from all authors.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work is partially supported by the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme under grants agreement no. 648417. J. T. acknowledges University of Manchester for the President Doctoral Scholarship Award (PDSA). A. D. and M. L. T. thank Cambridge Display Technology for financial support.References
- H. Machguth, M. MacFerrin, D. van As, J. E. Box, C. Charalampidis, W. Colgan, R. S. Fausto, H. A. J. Meijer, E. Mosley-Thompson and R. S. W. van de Wal, Nat. Clim. Change, 2016, 6, 390–393 CrossRef.
- S. Weiner and L. Addadi, Annu. Rev. Mater. Res., 2011, 41, 21–40 CrossRef CAS.
- W. E. Halter, A. E. Williams-Jones and D. J. Kontak, Chem. Geol., 1998, 150, 1–17 CrossRef CAS.
- G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen and A. Michaelides, Chem. Rev., 2016, 116, 7078–7116 CrossRef CAS PubMed.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS PubMed.
- D. W. Oxtoby, Philos. Trans. R. Soc., A, 2003, 361, 419–427 CrossRef CAS PubMed.
- J. J. De Yoreo, P. U. Gilbert, N. A. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Colfen and P. M. Dove, Science, 2015, 349, aaa6760 CrossRef PubMed.
- M. Sleutel, J. Lutsko, A. E. Van Driessche, M. A. Durán-Olivencia and D. Maes, Nat. Commun., 2014, 5, 5598 CrossRef CAS PubMed.
- R. Wagia, I. Strashnov, M. W. Anderson and M. P. Attfield, Angew. Chem., Int. Ed., 2016, 55, 9075–9079 CrossRef CAS PubMed.
- G. Giri, R. P. Li, D. M. Smilgies, E. Q. Li, Y. Diao, K. M. Lenn, M. Chiu, D. W. Lin, R. Allen, J. Reinspach, S. C. B. Mannsfeld, S. T. Thoroddsen, P. Clancy, Z. A. Bao and A. Amassian, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- J. A. Sellberg, C. Huang, T. A. McQueen, N. D. Loh, H. Laksmono, D. Schlesinger, R. G. Sierra, D. Nordlund, C. Y. Hampton, D. Starodub, D. P. DePonte, M. Beye, C. Chen, A. V. Martin, A. Barty, K. T. Wikfeldt, T. M. Weiss, C. Caronna, J. Feldkamp, L. B. Skinner, M. M. Seibert, M. Messerschmidt, G. J. Williams, S. Boutet, L. G. M. Pettersson, M. J. Bogan and A. Nilsson, Nature, 2014, 510, 381–384 CrossRef CAS PubMed.
- M. J. Van Vleet, T. T. Weng, X. Y. Li and J. R. Schmidt, Chem. Rev., 2018, 118, 3681–3721 CrossRef CAS PubMed.
- F. M. Maddar, D. Perry and P. R. Unwin, Cryst. Growth Des., 2017, 17, 6565–6571 CrossRef CAS.
- J. Clarke, H. C. Wu, L. Jayasinghe, A. Patel, S. Reid and H. Bayley, Nat. Nanotechnol., 2009, 4, 265–270 CrossRef CAS PubMed.
- M. Gobbi, A. Galanti, M. A. Stoeckel, B. Zyska, S. Bonacchi, S. Hecht and P. Samori, Nat. Commun., 2020, 11, 1–8 Search PubMed.
- N. S. Mazlan, M. M. Ramli, M. M. A. B. Abdullah, D. S. C. Halin, S. S. M. Isa, L. F. A. Talip, N. S. Danial and S. A. Z. Murad, AIP Conf. Proc., 2017, 1885 Search PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- A. Qureshi, J. H. Niazi, S. Kallempudi and Y. Gurbuz, Biosens. Bioelectron., 2010, 25, 2318–2323 CrossRef CAS PubMed.
- A. Rivadeneyra, J. Fernandez-Salmeron, J. Banqueri, J. A. Lopez-Villanueva, L. F. Capitan-Vallvey and A. J. Palma, Sens. Actuators, B, 2014, 204, 552–560 CrossRef CAS.
- L. Wang, M. Veselinovic, L. Yang, B. J. Geiss, D. S. Dandy and T. Chen, Biosens. Bioelectron., 2017, 87, 646–653 CrossRef CAS PubMed.
- D. L. Li, C. Batchelor-McAuley, L. F. Chen and R. G. Compton, ACS Sens., 2019, 4, 2250–2266 CrossRef CAS PubMed.
- A. Doumbia, M. Webb, M. L. Turner, J. M. Behrendt and R. Wilson, Organic Sensors and Bioelectronics X, International Society for Optics and Photonics, 2017, vol. 10364, p. 103640N Search PubMed.
- E. V. Boldyreva, V. A. Drebushchak, T. N. Drebushchak, I. E. Paukov, Y. A. Kovalevskaya and E. S. Shutova, J. Therm. Anal. Calorim., 2003, 73, 419–428 CrossRef CAS.
- M. Boyes, A. Alieva, J. C. Tong, V. Nagyte, M. Melle-Franco, T. Vetter and C. Casiraghi, ACS Nano, 2020, 14, 10394–10401 CrossRef CAS PubMed.
- A. Alieva, M. Boyes, T. Vetter and C. Casiraghi, CrystEngComm, 2020, 22, 7075–7081 RSC.
- H. Daiguji, Chem. Soc. Rev., 2010, 39, 901–911 RSC.
- J. Yin, X. Li, J. Yu, Z. Zhang, J. Zhou and W. Guo, Nat. Nanotechnol., 2014, 9, 378–383 CrossRef CAS PubMed.
- G. W. He, V. Bhamidi, R. B. H. Tan, P. J. A. Kenis and C. F. Zukoski, Cryst. Growth Des., 2006, 6, 1175–1180 CrossRef CAS.
- Y. G. Bushuev, S. V. Davletbaeva and O. I. Koifman, CrystEngComm, 2017, 19, 7197–7206 RSC.
- Y. Liu, M. H. van den Berg and A. J. Alexander, Phys. Chem. Chem. Phys., 2017, 19, 19386–19392 RSC.
- N. Javid, T. Kendall, I. S. Burns and J. Sefcik, Cryst. Growth Des., 2016, 16, 4196–4202 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nh00685h |
| This journal is © The Royal Society of Chemistry 2021 |