From polygons to polyhedra through intermediate structures. A shape measures study of six-atom inorganic rings and clusters

Abstract

Among the wealth of well-established molecular structures, inorganic rings and clusters present an overwhelming variety of geometries that chemists try to describe with a limited assortment of regular polygons and polyhedra. In the case of six-atom structures we usually employ the hexagon, the pentagonal pyramid, the trigonal prism and the octahedron. More often than not, however, real world structures deviate from those ideal geometries, and we try to cope with non-ideality by adding adjectives such as distorted, twisted, puckered or flattened, additionally nuanced by adverbs such as slightly, significantly or severely. This contribution presents a systematic structural perspective of six-atom groups in molecules by means of a continuous shape measures (CShM) analysis. The shape of a group of N points is defined by all the sets of 3 N Cartesian coordinates that can be generated by rigid translation, rotation, or isotropic scale change. Among all possible arrangements of N points in space, we select as reference shapes the corresponding regular N-vertex polygons and polyhedra, together with univocally defined combinations thereof (e.g., two coplanar or perpendicular edge-sharing squares). The present CShM study allows us to classify most of the structures not only by their closeness to a particular regular shape, but also by quantifying their position along minimal distortion interconversion pathways between two regular shapes.

---

“The time is short, and much remains to be done before you are fit to proclaim the Gospel of Three Dimensions to your blind benighted countrymen of Flatland”.

Edwin A. Abbott, Flatland, a Romance of Three Dimensions, 1884.

Introduction

Chemists are often deceived by the representations of three-dimensional molecules in a plane,¹ yet, the way in which planar molecules can evolve away from Flatland and into the 3D world is a thought experiment from which much can be learnt about stereochemistry, chemical bonding, isomerism, and even chemical reaction paths. We have earlier shown how, in the realm of organic chemistry, the non planarity of six member rings in their chair conformation is nicely described by the minimal distortion path from the planar hexagon to the Platonic octahedron, whereas the rings with a boat conformation are found along the path between the hexagon and the regular trigonal prism.² Similarly, cyclobutane rings have shapes that are intermediate between the planar square and the regular tetrahedron, represented by tetrahedrane, and the cyclic eight-carbon molecules cover several portions of the path from the octagon to the cube.

The continuous shape measures^3,4 have demonstrated to constitute a remarkable toolset for the stereochemical analysis of molecular skeletons, based on their comparison with regular or semiregular polygons and polyhedra, or as distortions therefrom.^5,6 Some previous studies on eight,⁷ nine,⁸ eleven,⁹ and twelve-atom¹⁰ transition metal clusters explored some specific distortion pathways, although in a non-comprehensive way. A logical sequel of such studies consists in applying similar concepts and methods to the stereochemical analysis of the wealth of inorganic rings and clusters that present a variety of compositions and shapes.^11–16 A recently reported study of systems formed by four atoms of main group elements¹⁷ has shown the relationship between shape, conformation and electron count, allowing for a differentiation of butterfly-shaped, square, rectangular, rhombic, and tetrahedral compounds. In the present work, a similar study is extended to six-member main group rings and clusters, to explore in more depth the connections between the corresponding polygonal and polyhedral structures and to discover new paths and new relationships between apparently unrelated molecules.

Continuous shape measures concepts

For a detailed description of the continuous shape measures methodology and the minimal interconversion paths, the reader is addressed to previous works,^2–6 and only a brief summary of the main concepts that will be used throughout this work will be presented in this section.

The shape measure of a set of atoms with respect to a reference shape (e.g., the octahedron, abbreviated OC-6 by the IUPAC) calibrates the overall distance of those atoms to the vertices of the reference shape, in the same position and with the same size and orientation. Thus, a zero shape measure for a set of atoms indicates that it has exactly the reference shape, expressed as S(OC-6) = 0.00 for the case of an ideal octahedron. For increasingly distorted octahedra we will obtain increasing values of the shape measure. Commonly, values of a few tenths indicate minor distortions, while values of more than one unit reveal more severe deviations from the reference shape.

Since a shape measure tells us the magnitude but not the type of deviation from the reference shape, it is useful to compare a given structure with two different ideal shapes. From those two shape measures we can determine a path deviation function that gauges the separation of our problem structure from the minimal distortion pathway between the two references. A path deviation of 0% corresponds to structures that are exactly along that pathway, but values of up to 5–10% or a little higher are usually acceptable for describing the stereochemistry of our molecule as being in-between the two reference shapes. Moreover, we can calculate the degree of distortion of our structure from one shape toward the other as a generalized distortion coordinate, that may adopt values between 0 and 100%.

Notice that throughout this paper the reference shapes are those that are univocally defined by regular polygons or polyhedra, whereas structures aligned with a portion of a minimal distortion interconversion pathway between two reference shapes are referred to as conformations. For instance, the chair and boat conformations of six-member rings are two families of shapes that can be found along the hexagon-to-octahedron and hexagon-to-trigonal-prism paths, respectively. In other words, each conformation corresponds to a family of geometries in the same region of the shape hypersphere.¹⁸

To name the reference shapes, the standard upper case abbreviations proposed by IUPAC¹⁹ are adopted for the regular coordination spheres, that include the number of atoms of the fragment under consideration. We thus use TBPY-5 for trigonal bipyramidal, TPR-6 for trigonal prismatic, OC-6 for octahedral, etc. For other reference shapes, the standard abbreviations are modified with lower case prefixes. A vacancy in a regular figure, let's say a square, is therefore referred to as vSP-3 (a right triangle), while dvCU-6 refers to a cube with two vacant positions. Similarly, two edge-sharing figures will be indicated by the prefix “es”, esTP-4 referring to two equilateral triangles sharing an edge. A list of all abbreviations used in this work is provided at the end of the paper.

Methodological aspects

Structural database searches were carried out in the CSD,²⁰ version 5.42. Disordered structures were disregarded only when the disorder affects the atoms of the ring or cluster under consideration. For hexawater clusters the searches were restricted to structures with a crystallographic agreement factor R ≤ 7.5%, non disordered, and with only six water molecules connected in independent clusters not containing coordinated water, since the latter often present strongly distorted geometries. Shape measures were obtained with the Shape code, version 2.2.²¹ In this work, non-standard reference shapes have been defined with all edges of the same length, at difference with our previous work in the field of coordination chemistry, in which reference shapes are defined as having all distances from the centre to the vertices identical. Note that in several cases the two definitions are coincident, as in the square, the hexagon, the tetrahedron, the octahedron and the trigonal prism.

Regular six-vertex shapes and their interconversion paths

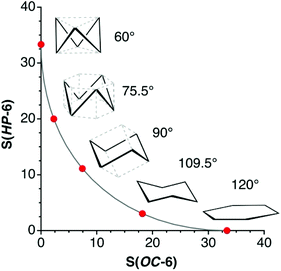
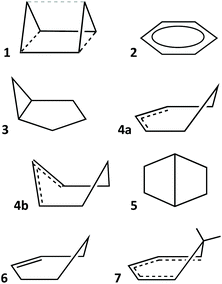
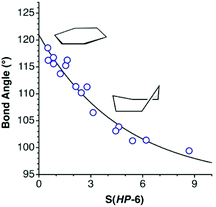
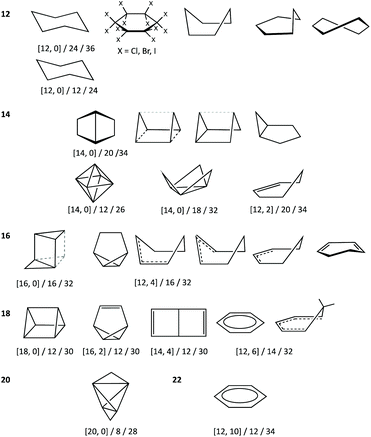
In earlier work devoted to polyhedral organic molecules,² we noticed in passing that the chair conformation of cyclohexane can be considered as intermediate between a hexagon and an octahedron while its boat conformation is a hexagon distorted toward the trigonal prism, and the structurally characterized cyclohexyl groups could be classified according to their conformations from their deviations to the corresponding minimal distortion pathways. Interestingly, the distribution of the chair rings, for instance, is seen to concentrate around an octahedrality of 26%, but cover a variety of geometries from the planar hexagon (0% octahedral) to puckered roughly halfway (54%) towards the octahedron. In this section, other distortions of the hexagon will be described to address the study of the envelope (called also half-boat or sofa), twist-boat (also known as skew-boat) and half-chair conformations.^22,23 In subsequent sections the structures of a host of inorganic six-member groups will be discussed with the help of the corresponding shape analysis.

Comparing six-member puckered rings such as cyclohexane with a Platonic octahedron may seem odd. However, we will see in what follows that there are a variety of rings that get rather close to, e.g., the octahedron or the trigonal prism, as well as fully octahedral or trigonal prismatic molecules of main group elements. Therefore, the use of those pathways provides us with a wide perspective for structural comparison. The hexagon to octahedron pathway implies the puckering of a ring, changing its bond angles from 120 to 60°. Notice that such a distortion retains the symmetry operations of the D_3d symmetry point group. During this work two additional six-atom shapes with that symmetry, derived from regular polyhedra, were identified as intermediate milestones along that path. One of them results from removal of two opposing vertices of a cube, a divacant cube (dvCU-6), and corresponds to a chair conformation that lays precisely along the hexagon–octahedron minimal distortion path (Fig. 1), with a degree of conversion of 55% and bond angles of 90°. In addition, occupation of alternating vertices of a hexagonal prism, in a hexa-vacant hexagonal prism (hvHPR-6), yields a shape still closer to the octahedron, a 75% along the way, with bond angles of 75.5°. A six-member ring with tetrahedral bond angles, such as cyclohexane,²⁴ appears much closer to the planar hexagon, with a 28.5% of octahedricity.

Fig. 1 Shape map relative to the octahedron and the planar hexagon, showing the position of several intermediate univocally defined shapes and their bond angles, from left to right: the octahedron, half hexagonal prism, trans-divacant cube, cyclohexane with tetrahedral bond angles, and the planar hexagon.

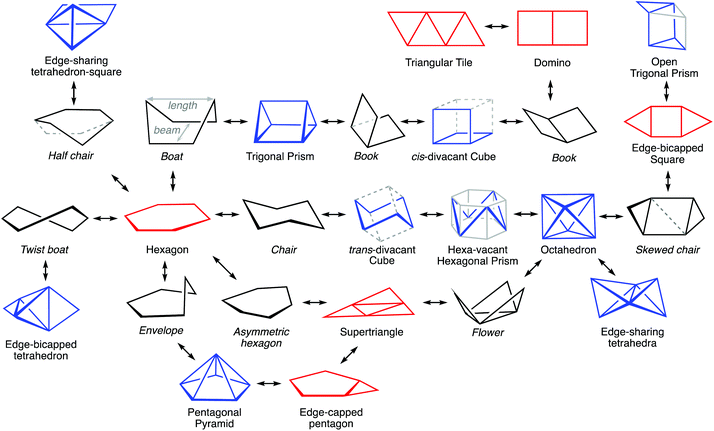
The interconversion of the hexagon and the trigonal prism proceeds through a C_2v symmetry pathway and has no regular intermediate shape (Fig. 2, third row, left). Thus, it gives raise only to a variety of boats that differ from each other in length and beam (Fig. 2, second row, left). Another regular planar shape, a domino formed by two edge-sharing squares (esSP-6, Fig. 2, top), can be bent around the shared edge, passing through a whole range of book conformations, including a cis-divacant cube (cdvCU-6), ultimately reaching the trigonal prism (Fig. 2, second row. The domino may alternatively undergo a shear distortion within the plane to yield a regular tile of four triangles. Yet another regular planar shape, an edge-bicapped square (ebcSP-6) can be defined. Alternatively, shifting the two extreme vertices of the triangular tile above and below the plane, respectively, generates the skewed chair conformation, that may end up in a regular octahedron (Fig. 2, third row, right).

Fig. 2 Regular six-vertex shapes and pathways that convert the planar geometries (red) into 3D ideal shapes (blue). Geometries along minimal distortion interconversion paths, including conformations of puckered rings, are also shown (black, names in italics).

The so-called twist boat conformation can be roughly approximated to intermediate structures along the hexagon to edge bicapped tetrahedron (ebcT-6) path (Fig. 2, fourth row, left). Note that an ebcT-6 shape was introduced in an earlier work to describe the distortion of octahedral transition metal complexes induced by two pincer tridentate ligands such as terpyridine.²⁵ However, in that case the reference shape was defined with six identical metal–ligand distances, whereas in the present work the criterion for ideality is that all the edges of polygons and polyhedra must have the same distances, in other words, the triangles formed by the capping atoms and the capped edges are defined as equilateral.

An out of plane displacement of one of the vertices of the regular hexagon may result – with some reorganization of the remaining vertices to form a pentagon – in a pentagonal pyramid (PPYR-6, Fig. 2, fifth row), passing through the intermediate envelope conformation. Notice that the ideal shape used here is not a Johnson (or edge-regular) pentagonal pyramid,²⁶ but one in which the distances of all vertices to the centre of the plane are identical. The pentagonal pyramid can also be related to another regular planar shape formed by a tetrahedron and a planar square group sharing an edge (esTSP-6, first row, Fig. 2 left). Along this path we find the half-chair conformation. Finally, a planar distortion of the hexagon that retains its trigonal symmetry axis generates asymmetric hexagons characteristic of rings of A₃B₃ composition, as will be seen below. As three alternating vertices approach the centre of the hexagon, at some point they will become aligned with the edges of the larger triangle, resulting in a super triangle (sT-6, Fig. 2, fourth row, centre) formed by one central and three peripheral triangles. If the three outer triangles are bent around the edges of the central one to the same side of the plane, a sort of three-petal flower is generated. Continuing that motion, the flower becomes finally a bud with the shape of an octahedron.

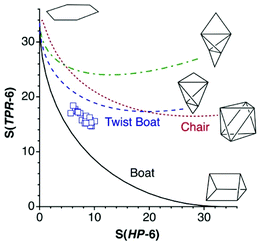
To illustrate how different interconversion paths between the hexagon and 3D shapes cover different regions of the 6-points shape space, Fig. 3 plots the position of structures along three minimal distortion pathways projected onto the hexagon–trigonal prism space. Notice that two ideal ebcT-6 shapes can be defined, a spherical version in which all distances from the vertices to the centre are identical, and a regular version in which the two caping atoms form equilateral triangles.

Fig. 3 Shape map relative to the regular hexagon (HP-6) and the trigonal prism (TPR-6) showing the minimal distortion path between those two shapes (continuous line), as well as structures of six-vertex shapes that fall along the paths from the hexagon to the octahedron (dotted line) and the hexagon to a spherical (dashed line) or to a regular (dot-dashed line) tetrahedra. The structures shown correspond to the end points of the paths shown.

Before analysing the stereochemical behaviour of a variety of families of six-atom cores by comparing their structures with those of the paths just discussed, let us give a couple of examples of molecular structures that correspond to some of the shapes presented in Fig. 2. Those structures were located from subsets of the CSD structures containing six-atom fragments of specific groups of elements, subject to a scanning of their shape measures relative to the desired distortion paths. Thus, the edge-sharing tetrahedron-square composite can be chemically represented by the coordination spheres of the two metal atoms in a bis(oxo-bridged mixed valence Cr^IV(high spin)–Cr^II(high spin) compound (Fig. 4a),²⁷ that has a small shape measure relative to the esTSP-6 (0.80). A pentagonal pyramidal shape, on the other hand, nicely corresponds to the geometry of the C₆ core of the Hogeveen dication^28,29 (MeC-Cp*)²⁺ (Fig. 4b), with a shape measure S(PPYR-6) of 0.02. The structures of several analogous isoelectronic pyramids are known, in which the apical carbon atom is replaced by Ga, In, Tl, Si, Ge, Sn, Pb, P or As. The difference with the all-carbon pyramid is that in all other cases the molecular shape deviates from the regular pentagonal pyramid because the larger size of the apical atom results in elongated pyramids. In fact, the pentagonal pyramidal shape measures present an excellent correlation with the E–Cp distance. An example of a severely elongated TlCp pentagonal pyramid is shown in Fig. 4c for comparison with the regular pyramid of the Hogeveen dication.

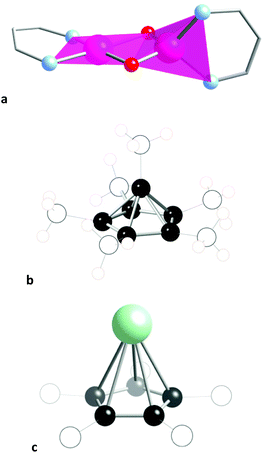Fig. 4 (a) The edge-sharing tetrahedron-square planar shape is represented by the coordination spheres of the two chromium atoms in this binuclear compound.²⁷ Only the skeletons of the bidentate nacnac ligands are shown for clarity. (b) The pentagonal pyramidal shapes of the Hogeveen dication (MeC-Cp*)²⁺ and (c) Tl(CCH₂Ph)₅.³⁰

Inorganic E₆ groups

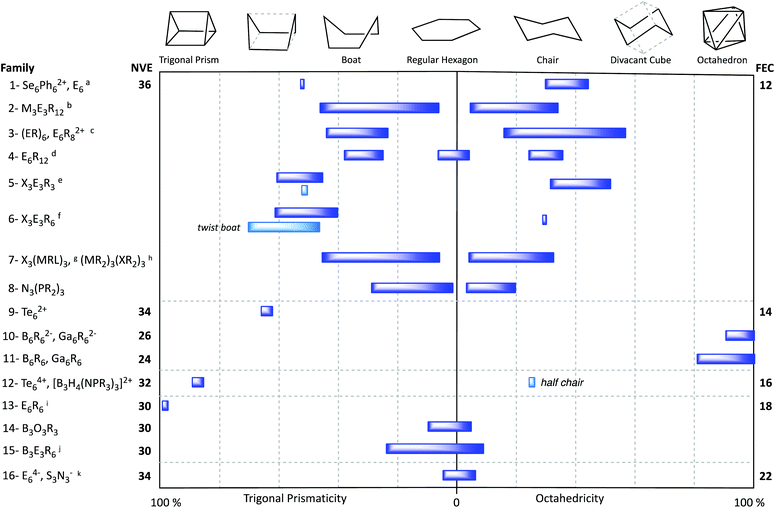
In this section the shapes of a few families of six-atom rings and clusters of main group elements are analysed after having searched for the geometrical path that best describes their structures. Since the number of combinations of six main group elements is enormous, the results presented are by no means comprehensive, even if a large number of structures classified in a variety of families should provide a wide panoramic view. Let us start this analysis with the rather simple and well-known molecule S₆, present in one of the allotropes of sulphur, and in its selenium analogue (Fig. 7a), both presenting chair conformations at 30–44% along the path from the hexagon to the octahedron (Fig. 5, first row). Each of these molecules has a total of 36 valence electrons, 12 of which correspond to the six bonds, and the remaining 24 are hosted by two sp³ lone pair orbitals at each sulphur atom that point to the periphery of the ring. The sp³ hybridization at the sulphur (or selenium) atoms is consistent with the conformation of the molecule, as in cyclohexane, another 36-electron molecule in which the 24 peripheral electrons correspond to the twelve C–H bonds. Similarly, a Se₆ ring coordinated to two silver ions is also a chair, although it appears disordered in its X-ray structure.³¹ The isoelectronic Se₆Ph₂²⁺ cation³² appears instead in a boat conformation with a 56% of trigonal prismacity. With one more electron, the S₆⁻ radical anion appears in a boat conformation, at a 44% of distortion toward the octahedron.³³

Fig. 5 Number of valence electrons (NVE) and ranges of generalized coordinates covered by different families of six-member groups (or polyhedra) along minimal distortion paths from the hexagon to the octahedron (right) and to the trigonal prism (left), that comprise as intermediate geometries the chair and boat conformations, respectively. Families are ordered according to their number of framework electrons (FEC). Notes: (a) E = S, Se; (b) M = B–Tl, E = N–Bi; (c) E = N–Sb; (d) E = Si–Sn; (e) X = S–Te, E = P–Sb; (f) Y = S–Te, E = Si–Pb; (g) M = Ga–In, X = S–Se; (h) M = B–Tl, X = N–Bi; (i) E = Si–Sn; (j) E = N–P; (k) E = P, As.

One or several atoms of the S₆ ring can be replaced by other six-electron atoms of groups such as X (X = S–Te), (BR₂)⁻, (NR₂)⁺, (PR₂)⁺, ER₂ (E = Si–Sn), ER (E = N–Sb) and MRL (M = Ga, In). In that way one we come out with a variety of molecules or ions with also 36 valence electrons. The ranges of boat and chair conformations found for this and several other families of rings formed by atoms from periodic groups 13 to 16 are shown in Fig. 5. In all of them we can find both chairs and boats with varying degrees of puckering along the corresponding paths. An exception to that conformational behaviour is found for the dodecahalohexasilylanes, which appear in most cases as planar Si₆ rings (Fig. 5, row 4).

The molecules of the (ER)₆ family (E = N–Sb) appear most commonly with the chair conformation, while the boat conformation is found only for the symmetric N₃E₃R₆ subclass. The degree of puckering of the chair conformers varies between 16 and 57% (Fig. 5, row 3) and increases roughly with the number of heavy atoms of the ring: N₃P₃ ≈ N₄P₂ ≈ N₂P₄ < P₆ < As₆ ≈ Sb₆. The isoelectronic dication of formula P₆Me₄Ph₄²⁺ also adopts a chair conformation, whereas the analogous P₆Ph₈²⁺ presents a twisted boat conformation, a 70% in the way to an edge-bicapped tetrahedron. We can include in this family the hexagonal structures of As, Sb and Bi,³⁴ in which the six R groups can be formally substituted by a neighbouring atom in their extended layered structures. All these elemental chair conformation rings appear at around 48% of the path toward the octahedron.

A group of X₃E₃R₆ 36-electron rings (X = S–Te, E = P–Sb) appear mostly in a chair conformation, with only a few cases in the boat conformation (Fig. 5, row 6). These rings show a significant degree of puckering toward the octahedron (32–53%) and the trigonal prism (44–60%), respectively. With only one exception, the boats have an Sb₃S₃ composition and are closer to the trigonal prism than to the planar hexagon.

Mixed group 13-group 16 rings of general formula X₃(MRL)₃, where X is S or Se, and M is Ga or In, are also 36-electron species. Only one of those molecules, [GaCl(Me₂py)]₃S₃, presents the boat conformation, while all others appear in chair conformations (Fig. 5, row 7), including a THF solvate of the same Ga compound.³⁶ Although the boat and chair conformations seem to be by far the most common ones among 36-electron inorganic rings, eventually structures with some of the alternative conformations discussed above can be found. This is especially evident in the X₃E₃R₆ family (X = S–Te; E = Si–Pb), for which the most common conformation is the twist-boat one (Fig. 2), which can be easily identified by its proximity to the hexagon to edge-bicapped tetrahedron path, with deviations of less than 14%.

Notice that the 36 valence electrons of all the six-member rings discussed so far correspond to six atoms with sp³ hybridization that form two bonds to the nearest neighbours and have two outward-pointing electron pairs, be them lone pairs or electron pairs of E–R or E–L bonds. One must therefore be cautious when counting electrons for signs of the presence of sp²-hybridized atoms that may hold only one peripheral electron pair. As an example, consider the structures of three Pb-containing rings (Fig. 6).^35,37 In these compounds we can count 34 valence electrons but, since the sum of the bond angles around the N atoms are within 0.1° of a planar coordination, the total number of electrons available for bonding within the ring is 16, consistent with Lewis structures with four π electrons shared by the N–Pb–N trio.

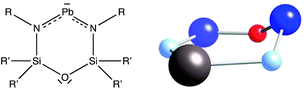Fig. 6 Lewis and molecular structure of a lead-containing ring³⁵ with an envelope conformation, at 34% along the pathway from the hexagon to the pentagonal pyramid. Colour code: Dark blue, Si; light blue, N; red, O, and grey, Pb.

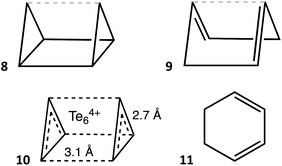
Species with two less valence electrons (34) are the Te₆²⁺ cation^38,39 (Fig. 5, row 10) and the E₆⁴⁻ (E = P, As) and S₃N₃⁻ anions⁴⁰ (Fig. 5, row 16). The former has a strongly puckered boat conformation 1 that is the structure closest to the trigonal prism (77%) for a monocyclic six member molecule (Fig. 7b). In contrast, the E₆⁴⁻ anions (E = P, As) are all planar, corresponding to aromatic 10 π-electron systems (Fig. 7c) which have been reported as K, Rb and Cs salts,^41–43 or π-coordinated to transition metals in a variety of complexes,^44–49 that can be described as in 2. The same situation is found for the S₃N₃⁻ isoelectronic anion⁴⁰ and the E₆¹⁰⁻ Zintl anions (E = Si, Ge).⁵⁰

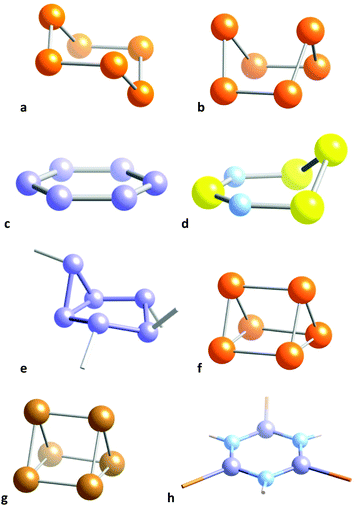Fig. 7 Conformations of (a) the 36 electron Se₆ molecule in its chair conformation,⁵¹ (b) the 34 electron Te₆²⁺ cation with a nearly trigonal prismatic geometry,³⁹ (c) the 34 electron P₆⁴⁻ anion with a hexagonal shape,⁴³ (d) the envelope conformation of the 34 electron S₄N₂,⁵² (e) the 34 electron asymmetric chair of a P₆R₄ molecule,⁵³ (f) the 32 electron Te₆⁴⁺ cation with an elongated trigonal prismatic structure,⁵⁴ (g) the core of the 30 electron compound Ge₆(PhⁱPr₂)₆ with a regular trigonal prismatic structure,⁵⁵ and (h) the hexagonal 30 electron B₃N₃ core of (BBr)₃(NH)₃.⁵⁶

Other 34-electron molecules analogous to bicyclo(3.1.0)hexane (3) contain P, As, Sb or Bi, with other elements appearing less frequently. Prototypical examples of this family are (PR₂)₄(ER)₂ molecules (E = P, Sb, Bi),^53,57 whose shapes can be described as asymmetric chairs with the back narrower and much more bent than the footrest (Fig. 7d). With also 34 valence electrons, the S₄N₂ molecule⁵² is severely distorted away from the hexagon toward the pentagonal pyramid (33.7%, Fig. 7e) in an envelope conformation. As in the lead-containing ring discussed in the previous section (Fig. 4), the 16 skeletal electrons in this case result in an allylic N–S–N group 4a with S–N distances of 1.56 Å, compared to 1.68 Å of the other two N–S bonds. Similarly, in the family of 34-electron alazanes with Al₃N₃ rings and general formula (LAlR)₂(AlR)(NR)₃ we find the envelope^58,59 and boat⁶⁰ (4b) conformations, with RN–Al(R)–NR allylic groups in both cases and distortions along the respective paths of 19–20%.

Several bicyclic compounds of type 5 have been reported with a variety of p-block elements in the corners: B, Ga, Si, Ge, Sn, N, Bi and O. If we think on the planar geometry as an open book, then the pathway that takes to the trigonal prism can be imagined as the action of closing a book, i.e., going from a domino to a trigonal prism. The bicyclic compounds analysed appear scattered close to that path (Fig. 8a), with shapes of more or less open books. In some of them the covers are not strictly square and somewhat twisted, as if they were paperback books, and therefore deviate significantly from the minimal distortion track. The most closed book (lowest circle in Fig. 8a) is represented by the metallic frame of the Bi₂(Ge(C₆F₅)₂)₄ molecule,⁶¹ in which the Bi–Bi bond is the spine and two Bi₂Ge₂ squares the covers of the book (Fig. 8b), with a 74% conversion to the trigonal prism. Among the most open books –smallest S(esSP-6) values–, the one closest to the minimal distortion path (i.e., a hardback book) is the Sn₆ core of Sn₆(2,6-C₆Et₂H₅)₉(ⁿBu),⁶² shown in Fig. 6c.

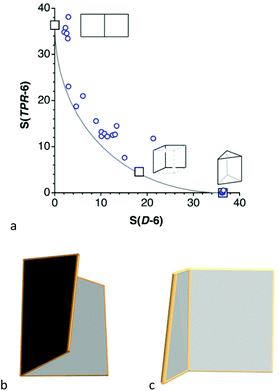Fig. 8 Shape map of bicyclic six-member rings relative to the domino and the trigonal prism. Open book shapes of (b) the Bi₂Ge₄ core in Bi₂(Ge(C₆F₅)₂)₄,⁶¹ and (c) the Sn₆ group of Sn₆(2,6-C₆Et₂H₅)₉(ⁿBu).⁶² The position in the map of three reference shapes are indicated by squares, including the two extremes and an intermediate cis-divacant cube.

Some of the six-member rings with one double bond retrieved in a structural database search contain an hypervalent phosphorus atom and are therefore out of the scope of this study. Other structures found correspond to the E₆⁴⁻ anions (E = P, As) commented above, that should be considered as 10 π–electron aromatic rings. Another structure found in that search should instead be considered to have two double bonds and will be discussed with the 32 electron systems. However, Ph₃PN–S₃N₃, found in a search for rings with two double bonds, both in the original report⁶³ and in the CSD, has a S₃N₃ core with one short (1.52 Å) and five longer (1.59–1.69 Å) S–N bonds, and the sulphur atom participating in one of the purported double bonds has a clear sp³ hybridization. That structure is therefore consistent with only one double bond and 34 valence electrons as in the envelope structure 6. In summary, 34-electron groups can be found in the six different conformations 1–6.

Systems with two less (32) valence electrons can present special versions of the envelope, boat, and chair conformations. The former is found in a small family of compounds with the general formulae (BR₂)B₂N₃ and (RBR₂)BN₄, in which there are six π electrons delocalized through five practically coplanar sp² atoms, while a saturated BR₂ group is out of that plane and occupies the tip of the envelope (7), including (BF₂)(NPh)₂N(NR)(BR), where R is the anthracene-9-yl group,⁶⁴ which was retrieved as having only one double bond. An extreme boat conformation appears for the cationic species Te₆⁴⁺,^54,65,66 that has an elongated trigonal prismatic shape (Fig. 7f) with short (≈2.7 Å) Te–Te bonds within the triangular bases and longer distances (≈3.1 Å) between them, reaching a 96% of a regular trigonal prism. Its bond length distribution indicates a high degree of electron delocalization that can be represented by Lewis structures a of types 8 and 9, or by a single structural formula 10 in which the black dashed lines represent four delocalized bonding electrons (the grey dashed lines in 8, 9 and elsewhere are given only to facilitate the visualization of a close ideal shape). With the same electron count, the cation [(BH)₂(BH₂)(NPEt₃)₃]²⁺ has a cyclohexadiene-like structure 11 with a half-chair conformation.⁶⁷

The peculiar chair conformation of 32 valence electron systems depicted in 12 as a tricyclic molecule appears in electron-precise compounds of formulae R₂Si(P₂Si₂R₂)SiR₂, R₂Si(Si₄R₄)SiR₂, RP(P₄)PR, or R₂Si(R₂Ge₂Si₂R₂)SiR₂, as well as Li(py)₂(NMe₂)₂(NSiMe₃)₂. These rings have 16 skeletal electrons that account for eight single bonds. Their shapes have a higher degree of regularity than the common chairs, allowing for their description as a square sharing opposite edges with two equilateral triangles. More precisely, in the ideal reference shape adopted here the two triangles are perpendicular to the square, and it will be named open trigonal prism (oTPR-6), since it can be thought of as a trigonal prism with one of its triangular faces open. The molecule that is closest to this ideal shape is that containing an all-phosphorus ring, RP(P₄)PR,⁶⁸ as calibrated by its coordinate along the hexagon to oTPR-6 path of 97% (12 in Fig. 9). Similar rings with a different substitution pattern^69,70 present the completely different basket shape 13 (Fig. 9), with also eight skeletal bonding electron pairs.

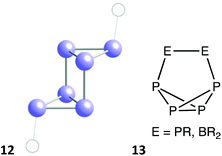Fig. 9 Structure of the P₆ core in RP(P₄)PR (12),⁶⁸ and skeletal bonding in analogous compounds with a 1,2 substitution pattern (13).

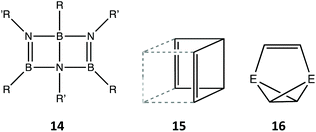
With two less electrons we find the 30-electron E₆R₆ molecules (E = Si, Ge, Sn), with the same 100% regular trigonal prismatic shape (Fig. 5, row 13, and Fig. 7g) as the organic prismanes, C₆R₆. In contrast, two families with the same electron count have essentially a planar hexagonal shape, that indicates aromaticity, as in the isoelectronic benzene molecule. One such family has the general formula B₃X₃R₆ (E = group 13, X = group 15 element) and includes borazines (X = N) and triphosphatriborinanes (X = P). Most of them are close to the hexagon, with shape measures in the 0.00–0.40 range, a good example being 2,4,6-tribromo-borazine,⁵⁶ (BrB-NH)₃, shown in Fig. 7h. Larger deviations from the hexagon, calibrated by the S(HP-6) shape measures, are nicely correlated with the decrease in the bond angle around the most pyramidalized atom (Fig. 10), and appear only in the presence of bulky substituents, such as ⁱPr, ^tBu, ferrocenyl, SiMe_3−nCl_n or NⁱPr₂. The most common values of the chair and boat distortions in this family of compounds are summarized in Fig. 5 (row 15). Two of the most puckered members of this family, [HP-B(NR₂)]₃, appear in two different conformations, a 38% trigonal prismatic boat for R = ⁱPr,⁷¹ and a 29% octahedral chair for R = SiMe₃.⁷² The resulting loss of aromaticity in the former has provided an explanation for the long B–P bond lengths compared to those in similar rings. An isoelectronic compound intimately related to this family, a diazatetraborinin with a para-B₄N₂ core, is a nearly perfectly planar hexagonal six π electron aromatic molecule 2.⁷³

Fig. 10 Relationship between the hexagonal planar shape measure of E₃X₃ rings (E = group 13, X = group 15 element) and the bond angle subtended by the most pyramidalized atom in puckered rings (only molecules with S(HP-6) > 0.5 included) of the group 15 atom in the prow position of a boat or the back of a chair as the ring deviates from planarity.

Another family of 30 valence electron aromatic hexagonal rings can be generated by formal substitution of the N–R or P–R groups by oxygen atoms in the B₃X₃R₆, compounds, responding to a general formula (BR)₃O₃. In this family, the rings deviate from planarity at most a 5% along the chair distortion path, and less than 10% along the boat coordinate (Fig. 5, row 14).

Yet another option for 30-electron species is to form a bicyclo(2.2.0)cyclohexa-2,5-diene (or Dewar benzene) type structure built up by three boron and three nitrogen atoms (14).^74,75 These molecules adopt a shape close to that of a cis-divacant cube (15 and Fig. 11). The two such compounds structurally characterized deviate slightly from the minimal distortion path between the hexagon and a cis-divacant cube (13%) and both are rather close to the latter reference shape (75%), similar to the values found for organic analogues (12–24 and 79–85%, respectively). Finally, a couple of compounds^76,77 with 30 valence electrons present a basket shape 16 (E = P, SiR), analogous to those with two more electrons and a single bond for the handle (13), and whose purely organic analogue has gone so far unreported.

Fig. 11 Tridimensional structure of the B₃N₃ ring in 14 with R = ⁱPr, R′ = ^tBu.

With two less electrons (28), and related to the 30-electron prismatic E₆R₆ molecules (E = Si–Sn) just discussed, we find the silicon and germanium E₆R₄ analogues,^78,79 that form an additional E–E bond across the diagonal of a square face, producing a severe loss of the trigonal prismatic shape. In fact, the shapes of those molecules are best described as octahedra distorted toward the edge-bicapped tetrahedron (Fig. 12), up to a 47% for E = Si.⁷⁸

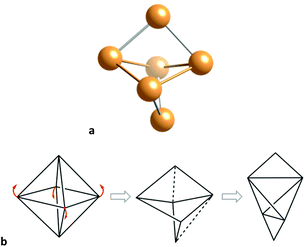Fig. 12 (a) Structure of the skeleton of a Ge₆R₄ cluster⁷⁹ with an octahedral geometry distorted toward the edge-bicapped tetrahedron. Two opposed edges of a planarized tetrahedron formed by the four intermediate atoms, are capped by the upper and lower atoms, along the distortion pathway b.

Moving to groups with two less valence electrons, 26, we find a large set of closo-hexaborates, B₆R₆²⁻, and a few closo-gallanates, Ga₆R₆²⁻. All of them appear as 90 to 100% octahedral (Fig. 5, row 10), i.e., the closo geometry expected from the Wade–Mingos–Lauher rules for a 6-atom cluster with 7 skeletal electron pairs. Interestingly, three examples of analogous neutral species, with two less valence electrons, have been also characterized as octahedral molecules (Fig. 5, row 11): B₆I₅F is a practically perfect octahedron,⁸⁰ whereas the other two cases,^81,82 Ga₆(Si{SiMe₃}₂Me)₆ and B₆(NMe₂)₆ are 80 and 88% along the hexagon to octahedron path, respectively.

Rings that incorporate alkaline or alkaline-earth atoms appear with a variety of electron counts. In some cases, the alkaline atoms are electron precise and the stereochemical behaviour of the rings is similar to those families of the p block discussed above. For instance, a family of compounds with 36-electron Be₃O₃ rings, such as (BeL₂)₃(OH)₃, includes three members with a chair conformation (6–15% octahedral) and seven with the boat one (12–25% trigonal prismatic). In many instances, however, the alkaline atoms are coordinatively unsaturated and the number of valence electrons of the ring can be rather small, but still accounting for six two-electron bonds. The family of M₃E₃ (M = Li, Na; E = OR, NR₂) compounds is a good example. They have 24 valence electrons and roughly half of them can be found along either the chair (2–15% octahedral) or boat (2–25% trigonal prismatic) pathways, as found for the electron-precise 36-electron systems discussed above. Similarly, the related (BNMe₂)₃ molecule^83,84 appears in a chair conformation with 26% of octahedrality. However, the other half of compounds deviate more than 10% from those paths, a fact that can be associated to a size mismatch of the two types of atoms that gives raise to asymmetric hexagons.

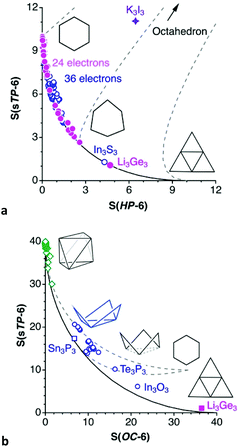
Compounds with a supertriangle as reference shape

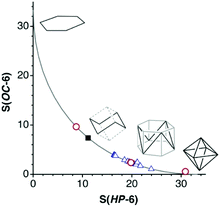
At this point it is worth exploring the planar asymmetrisation path that leads to a supertriangle, presented in the previous section (Fig. 2, rows 3 and 4). In a shape map (Fig. 13a) we can see that a good number of 24-electron rings have shapes along that path, and one of them, Li₃(Ge{SiMe₃}₃)₃,⁸⁵ gets very close to a supertriangle. It can also be seen how some nearly planar 36-electron groups behave similarly, with also one example of a supertriangle, found in (In^tBu)₃(S-Me₂pyrimidine)₃.⁸⁶ We must not forget, however, that a large part of molecules of those families do not follow such a planar distortion pathway, and they are omitted from Fig. 13a since they have substantially puckered conformations, e.g., chairs and boats. To widen our perspective, the plot also shows with dashed lines the positions that occupy the intermediate geometries along paths to the octahedron from the planar regular hexagon (Fig. 13b left), an asymmetric planar hexagon (Fig. 13b, middle) and a supertriangle (Fig. 13b, right). The octahedron is characterized in this shape map by the coordinates S(HP-6) = 33.33 and S(sT-6) = 40.00. These values tell us that the hexagon to supertriangle pathway is much shorter than those from these planar shapes to the octahedron.

Fig. 13 (a) Shape map for the conversion of a hexagon to a supertriangle. The symbols correspond to main group E₆ rings that deviate less than 10% from the corresponding path: empty circles for 36-electron rings, filled circles for 24-electron cores, and a star for K₃I₃. The dashed lines refer to minimal distorted structures from planar undistorted (left), planar asymmetric (centre) hexagons, and from a supertriangle (right) toward the octahedron. (b) Shape map for the octahedron-supertriangle interconversion. Symbols as in a and rhombuses for 26-electron borates and gallanates. The dashed lines represent the structures along the paths from the hexagon to the octahedron (upper line) and to the middle of the flower path.

Let us consider just an example of the many structures that present simultaneously asymmetrisation and puckering distortions, an interesting member of the 24-electron family, an outstanding molecular form of potassium iodide, K₃I₃, which appears coordinated to three tungsten atoms.⁸⁷ In the more common KI monomer the potassium atom is surrounded by a crown ether or an N-donor macrocyclic ligand and linked to an iodine atom that may or may not be coordinated to a metal atom. The K–I bond distance in the cyclic trimer, 3.52(10) Å, is similar to those in the monomers (average 3.54(10) Å) and in the ionic cubic crystals with the NaCl structure⁸⁸ (3.52 Å). The K₃I₃ ring presents a boat conformation, 42% along the trigonal prismatic path, combined with the bond angle asymmetry, and appears in the present shape map as a point nearby the path from a 50% asymmetrised planar hexagon to the octahedron (Fig. 13a).

The supertriangle is geometrically related also to the octahedron through a minimal distortion path, an issue that is addressed now from the chemical point of view by means of the corresponding shape map (Fig. 13b). A special case is that of the 32-electron species Sn₃(PCy)₃²⁻,⁸⁹ an electron deficient compound that forms a delocalized bond between the three tin atoms, and is the closest structure to the supertriangular shape. In contrast, the only 24-electron compound that deviates at most 10% from the path between the octahedron to the supertriangle is the already mentioned Li₃Ge₃ core⁸⁵ (Fig. 13b). This compound seems to be closer to such an ideal shape in this map than in the supertriangle to regular hexagon path (Fig. 13a) because that distance is magnified in the latter case due to the shorter path length. It is among the 36-electron molecules that we find structures within a 10% of the minimal distortion pathway, corresponding to intermediate geometries, i.e., flower conformations. However, the flower and chair paths are rather close to each other, so it is not easy to tell one conformation from another, unless one of the shape measures is very small, as is Sn₃(PCy)₃²⁻,⁸⁹ or for structures more than halfway along the path to the supertriangle, where the two paths strongly diverge, as is the case of Te₃(P{CPh₃}₃)₃ and (InR₂)₃(OH)₃ (Fig. 14d).^90,91

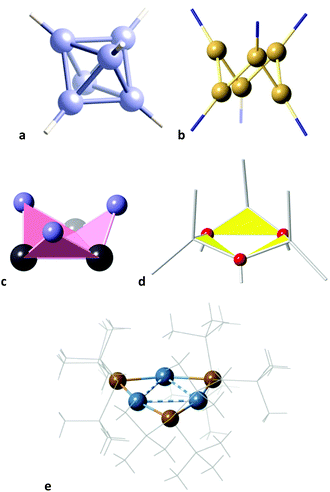Fig. 14 Some structures that represent snapshots along the octahedron to supertriangle pathway: (a) (B₆H₆)²⁻, (b) Ga₆R₆, R = Si(SiMe₃)₂Me, (c) Sn₃(PCy)₃²⁻, (d) (InR₂)₃(OH)₃, and (e) Li₃(Ge{SiMe₃}₃)₃.

Altogether, several molecules that are well aligned with the octahedron to supertriangle path provide us with a visual description of the geometric changes along the way (Fig. 2), from the 26-electron octahedral boranes and gallanes which can be considered as buds at the beginning of the path, represented by the hexaborate dianion (B₆H₆)²⁻,⁹² and the slightly open 24-electron Ga₆R₆, R = Si(SiMe₃)₂Me, on to the 36-electron flowers in full blossom Sn₃(PCy)₃²⁻,⁸⁹ and (InR₂)₃(OH)₃,⁹¹ and finally reaching the supertriangular shape in the 24-electron Li₃(Ge{SiMe₃}₃)₃.⁸⁵

To offer a systematic view of the stereochemistry of groups of six atoms from the p and s blocks of the periodic table, they have been discussed in this section in decreasing order of number of valence electrons (v). Their shapes, however, depend essentially on the number of electrons available for bonding within the cluster or ring (c), disregarding the electrons used for bonding with peripheral atoms (p) and the outwards-pointing lone pairs (l). Moreover, we have seen that the electrons not involved in peripheral bonding can be either used in σ- or π-bonding (c = σ + π), and the distribution of the valence electrons in the cluster is expressed by eqn (1).

v = σ + π + p + l (1)

c = σ + π = v − p − l. (2)

It is easy to figure out that the wide choice of atoms that can form the cluster, as well as its charge (chemical formula and v), the number and nature of peripheral groups (p value), and the possibility of having electron-precise, electron-deficient or expanded-octet atoms (l value) within the cluster offers an astronomic number of possible combinations that could be classified according to the number of cluster bonding electrons c, easily deduced from eqn (2). Moreover, there is still the possibility of having different combinations of the number of electrons employed in cluster σ and π bonding, giving raise to different isomers. An attempt to summarize all that amount of information is presented in Fig. 15, where the different shapes found are organized according to the value of c, and some of the combinations of σ, π, p and l found are annotated. It is interesting to see there how similar shapes may result from different combinations of these electronic parameters, while very differet shapes are compatible with a given number of cluster electrons.

Fig. 15 Summary of the shapes found for compounds with different number of cluster bonding electrons (in boldface). The numbers given for each group of structures indicate the number of σ and π framework electrons (in square brackets), the number of peripheral electrons (lone pairs and electron pairs involved in bonding to peripheral groups), and total number of valence electrons: [σ, π]/p + l/v.

Hexawater rings in Ice and crystallization water

“Our question is, why snowflakes in their first falling, before they are entangled in larger plumes, always fall with six corners and with six rods, tufted like feathers”.

Johannes Kepler, De nive sexangula, 1611 (transl. Colin Hardie).

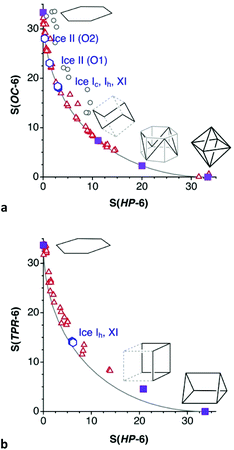
The water molecules that appear in hydrated crystal structures often form clusters linked by hydrogen bonds. This section presents a statistical analysis of the geometries of hexawater clusters in a host of crystal structures of organic and metallo-organic compounds. A similar study of tetrawater clusters has been reported recetnly.¹⁷ The specific cases of the same clusters present in some ice structures^93–95 or as calculated on a Cu(111) surface⁹⁶ will be also commented upon. Since the hydrogen atoms are often disordered, the focus is placed on the positions of the oxygen atoms only. The structures of the (H₂O)₆ groups in the mentioned systems are represented in the shape maps for either the chair or the boat distortion pathway of the hexagon from which it appears to be closer, by comparison of the corresponding path deviation values (Fig. 16). It must be noted, however, that for small deviations from the regular hexagon one cannot tell one path from the other and the representation of very little distorted structures in one or the other map is arbitrary. Among the “independent” clusters, a handful of them present asymmetric structures with significant differences between short and long O⋯O distances, that deviate markedly from the minimal distortion path. Those asymmetries are usually associated to the presence of further hydrogen bonding to other nearby groups (e.g., chloride or thiocyanate).

Fig. 16 Shape maps for independent (H₂O)₆ hydration clusters in CSD crystal structures (triangles) and in ice structures (hexagons) along (a) the chair pathway and (b) the boat pathway. The ideal shapes schematized in the maps are indicated by filled squares: the hexagon, the trans-divacant cube, a hexa-vacant hexagonal prism and the octahedron in a, and the hexagon, the cis-divacant cube and the trigonal prism in b. The geometries of asymmetric clusters with sizeable differences in O⋯O distances are shown as small empty circles.

From that shape map we can pinpoint the structures of hexawater clusters that best represent three rather different geometries along the minimal distortion path between the hexagon and the octahedron. First we see a regular hexagonal planar O₆ ring⁹⁷ (Fig. 17a) which, interestingly, seems to be supported not by O⋯H but by Cl⋯H hydrogen bonds with two chloride anions sitting above and below the ring. Notice that the connections shown between the oxygen atoms do not intend to indicate chemical bonds but only to show the geometrical arrangement of the O₆ cluster. The second selected structure⁹⁸ is halfway between the hexagon and the octahedron, with the shape of a divacant cube (Fig. 17b), and seen to be held by well oriented O–H⋯O hydrogen bonds. Finally, an outstanding O₆ octahedron is formed by hydration water molecules,⁹⁸ apparently held by six hydrogen bonds (O⋯O = 2.84 Å) along the six edges that join two opposed trigonal faces (in which the O⋯O distances are 2.92 Å) of the octahedron (Fig. 17c).

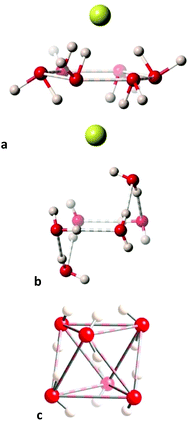Fig. 17 Structures of hexawater clusters that represent snapshots along the hexagon to octahedron pathway: (a) Planar hexagon (the spheres above and below the O₆ plane represent chloride ions.⁹⁷ (b) A chair conformation with a divacant-cube shape,⁹⁸ and (c) an octahedron.⁹⁸

We can choose as representative of independent water clusters with boat conformations the one found in a dysprosium complex⁹⁹ (Fig. 18a) that is bent away from the planar hexagon, 20% along the path toward the trigonal prism. By independent it is meant that there are six and only six water molecules connected via hydrogen bonds, but naturally the cluster always forms further hydrogen bonds with the organic or metallo-organic molecules in the crystal structure. More often than chair rings, most hexawater boats tend to be fused together and/or linked to extra water molecules or organic groups. One example appears in the crystal structure of D,L-histidyl-L,D-histidine penta-hydrate,¹⁰⁰ whose hydration water molecules form fused rings with boat conformation in a chain supported by hydrogen bonding to an extra water molecule hydrogen-bonded also to a carboxylate group (Fig. 18b). Another example is provided by the crystal structure of the zwitterionic 2-[(2-ammonioethyl)amino]acetate dihydrate,¹⁰¹ in which the hydration molecules form layers of fused boats, hydrogen-bonded above and below to the carboxylate groups (Fig. 18c).

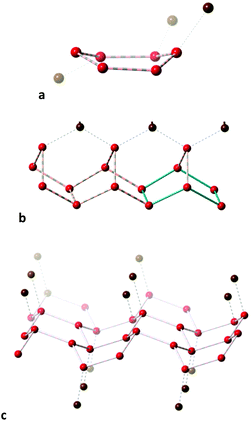Fig. 18 Hexawater groups with boat conformation: (a) independent and connected to an organic molecule by further hydrogen bonding, and fused together forming (b) chains¹⁰⁰ and (c) layers.¹⁰¹ All connecting lines indicate hydrogen bonds; hydrogen atoms are omitted for clarity and non-water oxygen atoms are depicted in brown.

The phase diagram of ice comprises some seventeen different structures.¹⁰² Some ice structures containing hexawater groups are shown in the shape maps for the boat and chair conformations (Fig. 16a). It must be noted that the hexawater rings in the ice structures analysed appear well aligned with the independent hydration clusters discussed so far along the minimal distortion pathways. In the common form of ice at ambient pressure,^93,103 known as structure I_h, both boat (40% trigonal prismatic) and chair (29% octahedral) rings coexist fused together and extending in the three directions of space (Fig. 19a). The same topology and similar degree of puckering is found in the ice XI structure,⁹³ whereas ice Ic has the diamond structure⁹⁴ with only one type of chair rings and a similar degree of puckering (Fig. 19b). In ice II,⁹⁵ two types of chairs formed each by one of the crystallographically independent oxygen atoms, with different degrees of puckering (9 and 19%) are connected forming columns in one direction (Fig. 19c).

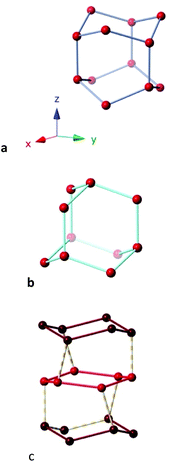Fig. 19 Fragments of the crystal structure of (a) ice 1 h,^93,103 constituted by boats in the x, and y directions and chairs in the z direction (b) ice Ic with a diamond structure, and (c) ice II,⁹⁵ showing the chairs formed by each of the two crystallographically independent oxygen atoms, connected vertically forming irregular rings in the perpendicular direction.

Remarkably, the hexawater rings present in some ice structures fit perfectly into the general stereochemical picture of independent clusters found in molecular crystals as solvation molecules or adsorbed on a Cu(111) surface. It is also noteworthy that layers formed by such hydration water molecules seem to have some relationship to the ice structures, suggesting the possible formation of ice microlayers during the nucleation process of those hydrated compounds.

Li₆ clusters

The lithium atoms in many compounds, though formally present as cations, have a marked tendency to group together forming clusters of varying sizes. A recent study¹⁰⁴ analysed the role of Lewis bases coordinated to lithium in favouring the proximity of lithium ions in the case of dilithium groups. It is therefore timely to look for stereochemical trends among lithium clusters, as presented in this section for Li₆ cores. They are found in a variety of compounds, and all of them have structures along the planar hexagon to octahedron pathway, mostly in the region between the regular octahedron and the trans divacant octahedron, as seen in a shape map (Fig. 20). The structures of three of them provide us with snapshots along the distortion path (Fig. 21). At one extreme of the path we can see a highly bent chair geometry (Fig. 21a),¹⁰⁵ close to a divacant cube shape and roughly midway (49% octahedral) between the planar hexagon and the octahedron, as nicely illustrated by the Li₆ group in Li₆(N^tBu)₆(SiMe)₂. Then we have a structure closer to the octahedron (75%),¹⁰⁶ that of Li₆(μ₃-ⁱPrNHMeO)₆ with the shape of a non planar hexagon occupying half of the vertices of a hexagonal prism (Fig. 21b). The third snapshot corresponds to the nearly perfect (96%) octahedron¹⁰⁷ of Li₆(μ₃-C-ⁿPr)₂(μ₂-[(Me₂HSi)N(SiHⁱPr₂)])₂ (Fig. 21c).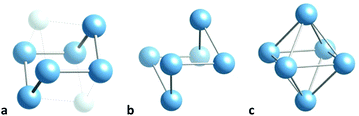

Fig. 20 Shape map showing the position of the structures of Li₆ groups (triangles) along the distortion path from the regular hexagon, S(HP-6) = 0, to the octahedron, S(OC-6) = 0. The three structures marked with circles are shown in figure; the solid square indicates the position of the trans-divacant cube (dvCU-6).

Fig. 21 Structure of a Li₆ groups with (a) a chair conformation and a divacant cube shape,¹⁰⁵ (b) an open octahedron,¹⁰⁶ and (c) an octahedron.¹⁰⁷ The light blue spheres represent two Si atoms that occupy the two vacant positions of a cube.

Dominoes

The Ga₆R₈²⁻ anion (R = SiMePh₂),¹⁰⁸ presents an uncommon planar structure (Fig. 22), intermediate between those of two fused squares (the domino) and four fused equilateral triangles (Fig. 2, row 1, right), 74% along the path from which it deviates only a 3.7%. Let us recall that the related Ga₆R₆²⁻ anions adopt instead the regular octahedral shape.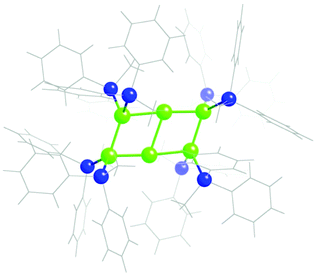

Fig. 22 Structure of the core of the Ga₆R₈²⁻ anion¹⁰⁸ with a shape intermediate between a domino and a tile of four fused equilateral triangles (Fig. 1).

Planar hexagonal coordination spheres

In transition metal chemistry, the most common number of ligands coordinated to a metal atom is 6. However, the shapes of their coordination spheres is overwhelmingly the 3D octahedron,⁴ with a smaller, non negligible presence of the trigonal prism¹⁰⁹ or distortions from these two regular polyhedra. Only two of the very little number of existing planar hexagonal complexes were known for years. They had the general formula [Ni(cyclo-{E^tBu}₆)] (E = P,¹¹⁰ As¹¹¹), whose distortion coordinates from the hexagon to the octahedron (1 and 4%, respectively) qualify them as nearly perfect hexagons (Fig. 23a).

Fig. 23 Hexagonal coordination spheres in (a) the [Ni(cyclo-{P^tBu}₆)] complex with a planar cyclic hexadentate P₆ ring,¹¹⁰ (b) a PdH₃Mg₃ compound,¹¹² (c) a Co₂⁺ ion within a metalloorganic framework¹¹⁵ (d) the [Ag(cyclo-{OSiMe₂}₆)]⁻ anion, (e) a VO₆ group in the [VMo₁₂V₂O₄₄]⁴⁻ anion,¹¹⁶ and (f) an AgO₆ core within a polyoxotungstate.¹¹⁷

No wonder the recent report of two compounds in which a palladium atom is surrounded by a planar Mg₃H₃ coordination sphere (Fig. 23b) has been qualified as unusual.¹¹² Given the different Pd–Mg and Pd–H bond distances (∼2.56 and 1.60 Å, respectively), these coordination spheres are highly irregular planar hexagons, with S(HP-6) values of 3.14 and 5.44. In fact these structures are in the path from the hexagon to the supertriangle, 55 and 73% along the way, respectively. If we concentrate on the orientation of the metal–ligand bonds by using normalized bond distances,¹¹³ the hexagonal shape measures (0.14 and 0.38) are small enough as to describe it as a quasi regular hexagon. In other words, if we disregard the differences in bond distances, the directions of the six bonds to Pd correspond to a very good approximation to those from the centre to the vertices of a regular hexagon. It is to be noted that the design of these compounds was based on the molecular orbital analysis of the hexagonal NiP₆ compound made by Hoffmann and coworkers.¹¹⁴

A last known example of a hexagonal planar coordination sphere appears in a Gd–Co coordination polymer¹¹⁵ in which six bridging chelidamato ligands are coordinated through their phenolic oxygen atoms to a cobalt with a perfect hexagonal planar coordination geometry (Fig. 23c), as indicated by a shape measure relative to the hexagon of 0.00. This compound is obtained from a hydrated pink precursor in which the Co₂⁺ ion is presumably coordinated by water molecules.

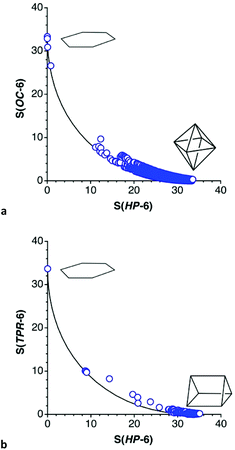
To find out if there might be some other complexes that are close to the hexagon or intermediate between that polygon and the two regular polyhedra, a CSD search for six-coordinated transition metals with only single metal–ligand bonds was carried out, and 183 517 ML₆ crystallographically independent fragments from 123 521 crystal structures were found. Filtering out those that deviate more than 10% from the chair and boat pathways, 75 326 and 351 independent structural data sets, respectively, were retained. The position of these coordination spheres along the hexagon–octahedron and hexagon–trigonal prism paths can be seen in the corresponding shape maps (Fig. 24). The hexagons just discussed correspond to the uppermost points in those plots, in which the practically undistorted hexagonal CoO₆ and NiP₆ cores are departing points for both chair and boat distortions and are therefore plotted in both maps, whereas the NiAs₆ group is unequivocally on the chair path, although with a very small (4%) puckering, and it is plotted only in Fig. 24a.

Fig. 24 Coordination spheres of six-coordinated transition metal complexes represented in the shape maps for the hexagon–octahedron (a) and hexagon–trigonal prism (b) minimal distortion pathways. Only structures that deviate less than 10% from the corresponding paths are shown.

The next closest structure to the planar hexagon seen on the path to the octahedron, with a 15% puckering, is the coordination sphere of a Ag(I) ion coordinated by the hexadentate ligand cyclodimethylsiloxane (Fig. 23d),¹¹⁸ whose structure has been commented upon in more detail recently.¹ A few other structures that appear in that region of the shape maps have been disregarded because either the position of the metal and/or donor atoms are disordered or because there are one or more extra atoms semi coordinated to the metal, so there seems not to be well characterized complexes as far as a 55% of the path to the octahedron (S(HP-6) ≈ 9.0), where we find a vanadium ion encapsulated within a polyoxomolybdate (Fig. 23e).¹¹⁶ In contrast, silver ions in polyoxotungstates appear practically halfway along the path to the trigonal prism (Fig. 23f).¹¹⁷ The rest of the structures are far away from the hexagon, but many of them are distant enough from the octahedron or the trigonal prism as to describe a wide range of intermediate shapes. The much higher preference for the chair geometries compared to the boat ones can be also appreciated by comparison of the two shape maps.

M₆ transition metal clusters

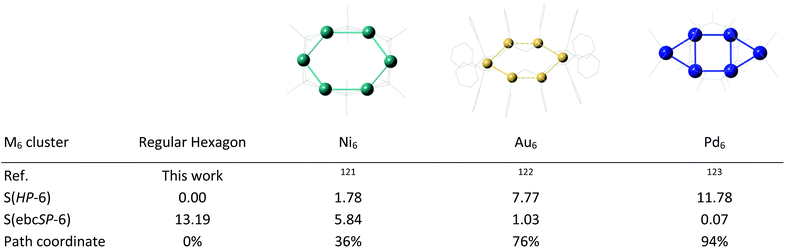
The synthesis and structural characterization of transition metal clusters, characterized by having metal–metal bonds, have been widely explored in the last few decades,^16,119 and no attempt will be made here to cover the rich structural chemistry of cluster compounds. This section will rather focus on the existence of examples of the wide palette of ideal geometries and of intermediate shapes along their minimal distortion interconversion pathways presented in Fig. 2 and 5, some of which are not found with main group elements.

Let us start by looking at the pathway for the interconversion of a pair of edge-sharing tetrahedra and the octahedron (17). A search for all molecules with six transition metal atoms in the CSD and subsequent filtering for deviations of less than 20% from that path, yielded 1,466 crystallographically independent fragments. Most of them are octahedral or nearly octahedral, although some of them are slightly distorted along the path. However, a handful of structures appear as fused tetrahedra or with intermediate shapes in the way to the octahedron (between 24 and 70% octahedral). Three structures^130–132 from different spots of the path are shown in Fig. 25, together with their shape coordinates and some geometrical parameters for comparison. Notice that the presently discussed path implies a decrease in the b/a ratio (17) from 1.414 to 1.000, an increase in the separation of the two atoms occupying the shared edge, and a decrease in the angle between two edges β, from 90° to 60°.

Fig. 25 Shape coordinates and geometrical parameters (see 17) for the ideal edge-sharing tetrahedra (esTT-6) and three examples of clusters with shapes along the pathway from esTT-6 to the octahedron.

The conversion of a hexagon to a bicapped square follows a simple geometrical path. A number of structures can be found at its two ends, the regular hexagon being rather commonly found, as in a Ag@Au₆ “jeweler's ring”.¹²⁰ and a small number of examples appear to be around the central portion of the path. Some examples of metal clusters found to follow such a distortion mode are given in Fig. 26, together with their shape coordinates. Two of them are elongated hexagons with Ni₆¹²¹ and Au₆¹²² cores, and the third one is a Pd₆ cluster nicely sandwiched between aromatic cyclo-octatetraene and cyclononatetraenyl anions.¹²³

Fig. 26 Structures and shape coordinates for the regular hexagon and for examples of molecules that are found along the path from the hexagon to the edge bicapped square (ebcSP-6). The Ni₆ ring is held by bridging ligands, with no Ni–Ni bonds.

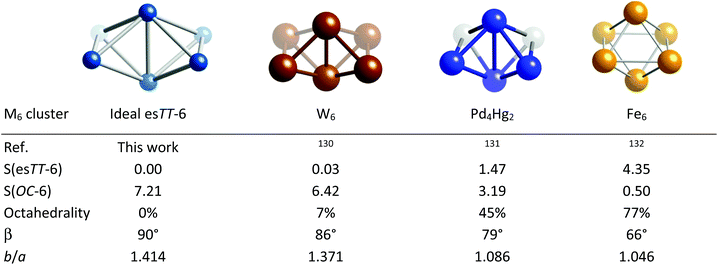
The third path explored here for hexametallic clusters connects the octahedron and the linear ribbon formed by fusing together four triangles (Fig. 27), the latter represented by an Ag₆ cluster.¹²⁴ By bending the ribbon around the vertical edges it starts winding up, as illustrated by Au₄Ag₂,¹²⁵ Ru₆,¹²⁶ and Cu₆¹²⁷ groups, approaching the octahedron in a Cu₆ cluster¹²⁸ and closes the three upper and the three lower vertices to form the two missing faces of the octahedron in an Fe₆ example.¹²⁹

Fig. 27 Structures and shape coordinates of transition metal clusters that illustrate the winding up of a triangular tile into an octahedron. The ligands in those clusters are omitted for clarity.

Concluding remarks

A reasonable coverage of the structures and geometries of six atom cores in molecular chemistry can be obtained by means of six planar and ten three-dimensional reference shapes, together with some of their interconversion pathways that correspond to ten families of conformations. Besides those commonly used in organic chemistry (chair, boat, half-chair, or envelope) other useful conformations found can be referred to as flower, book, or asymmetric hexagon.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from MINECO, project PGC2018-093863-B-C21, the Spanish Structures of Excellence María de Maeztu program through grant MDM-2017-0767, and AGAUR through grant 2017-SGR-1289 is gratefully acknowledged.

References

1. S. Alvarez, C. R. Chim., 2019, 22, 437.
2. S. Alvarez and J. Echeverría, J. Phys. Org. Chem., 2010, 23, 1080.
3. M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575.
4. S. Alvarez, D. Avnir and M. Llunell, New J. Chem., 2002, 26, 996.
5. S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693.
6. S. Alvarez and E. Ruiz, in Supramolecular Chemistry, From Molecules to Nanomaterials, ed. J. W. Steed and P. A. Gale, Chichester, UK, 2012.
7. D. Casanova, M. Llunell, P. Alemany and S. Alvarez, Chem. – Eur. J., 2005, 11, 1479.
8. A. Ruiz-Martínez, D. Casanova and S. Alvarez, Dalton Trans., 2008, 2583.
9. S. Alvarez, J. Coord. Chem., 2018, 71, 590.
10. S. Alvarez, Inorg. Chim. Acta, 2010, 363, 4392.
11. R. J. Gillespie, Chem. Soc. Rev., 1979, 8, 315.
12. R. Steudel and M. Kustos, in Encyclopedia of Inorganic Chemistry, ed. R. B. King, Chichester, 1994.
13. R. Steudel, The Chemistry of Inorganic Ring Systems, Elsevier, Amsterdam, 1992.
14. M. Driess and H. Nöth, Molecular Clusters of the Main Group Elements, Wiley-VCH, Weinheim, 2004.
15. D. Mallick and E. D. Jemmis, Main Group Metal Clusters, Elsevier, Amsterdam, 2nd edn, 2013, vol. 9.
16. P. Braunstein, L. A. Oro and P. R. Raithby, Metal Clusters in Chemistry, Wiley-VCH, Weinheim, 1999.
17. S. Alvarez, An. Quím., 2021, 117, 219.
18. D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755.
19. N. G. Connelly, T. Damhus, R. M. Harisborn and A. J. Hutton, Nomenclature of inorganic Chemistry. IUPAC Recommendations 2005, RSC Publishing, Cambridge, 2005.
20. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171.
21. M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE. Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Associated Tools (2.2), Universitat de Barcelona, Barcelona, 2013.
22. D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354.
23. J. C. A. Boeyens, J. Cryst. Mol. Struct., 1978, 8, 317.
24. N. B. Wilding, J. Drain, P. D. Hatton and G. Bushnell-Wye, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 320.
25. S. Alvarez, Chem. Rev., 2015, 115, 13447.
26. S. Alvarez, Dalton Trans., 2005, 2209.
27. F. Dai, P. A. Yap and K. H. Theopold, J. Am. Chem. Soc., 2017, 135, 16774.
28. H. Hogeveen and P. W. Kwant, Acc. Chem. Res., 1975, 8, 413.
29. M. Malischewski and K. Seppelt, Angew. Chem., Int. Ed., 2017, 56, 368.
30. H. Schumann, C. Janiak, J. Pickardt and U. Borner, Angew. Chem., Int. Ed. Engl., 1987, 26, 789.
31. D. Aris, J. Beck, A. Decken, I. Dionne, J. S. auf der Gunne, W. Hoffbauer, T. Kochner, I. Krossing, J. Passmore, E. Rivard, F. Steden and X. Wang, Dalton Trans., 2011, 40, 5865.
32. R. Faggiani, R. J. Gillespie and J. W. Kolis, J. Chem. Soc., Chem. Commun., 1987, 592.
33. B. Neumuller, F. Schmock, R. Kirmse, A. Voigt, A. Diefenbach, F. M. Bickelhaupt and K. Dehnicke, Angew. Chem., Int. Ed., 2000, 39, 4580.
34. A. F. Wells, Structural Inorganic Chemistry, Oxford University Press, Oxford, 5th edn., 1984.
35. R. J. Schwamm, M. Lein, M. P. Coles and C. M. Fitchett, J. Am. Chem. Soc., 2017, 139, 16490.
36. S. D. Nogai and H. Schmidbaur, Dalton Trans., 2003, 2488.
37. R. J. Schwamm, J. R. Harmer, M. Lein, C. M. Fitchett, S. Granville and M. P. Coles, Angew. Chem., Int. Ed., 2015, 54, 10630.
38. J. Beck, Chem. Ber., 1995, 128, 23.
39. J. Beck and G. Bock, Z. Anorg. Allg. Chem., 1996, 622, 823.
40. R. Jones, P. F. Kelly, D. J. Williams and J. D. Woollins, Polyhedron, 1987, 6, 1541.
41. H.-P. Abicht, W. Hönle and H.-G. v. Schnering, Z. Anorg. Allg. Chem., 1984, 519, 7.
42. W. Schmettow, A. Lipka and H.-G. v. Schnering, Angew. Chem., Int. Ed. Engl., 1974, 13, 345.
43. H.-G. v. Schnering, W. Hönle, W. Bauhofer, G. Kliche, T. Meyer, W. Schmettow and U. Hinze, Z. Anorg. Allg. Chem., 1987, 553, 261.
44. M. Fleischmann, F. Dielmann, L. J. Gregoreiades, E. V. Peresypkina, A. V. Virovets, S. Huber, A. Y. Timoshkin, G. Balazs and M. Scheer, Angew. Chem., Int. Ed., 2015, 54, 13110.
45. O. J. Scherer, J. Schwalb, H. Swarowsky, G. Wolmenshauser, W. Kaim and R. Gross, Chem. Ber., 1988, 121, 443.
46. M. Fleischmann, F. Dielmann, G. Balazs and M. Scheer, Chem. – Eur. J., 2016, 22, 15248.
47. M. Piesch, S. Reichl, M. Seidl, G. Balazs and M. Scheer, Angew. Chem., Int. Ed., 2019, 58, 16563.
48. A. C. Reddy, E. D. Jemmis, O. J. Scherer, R. Winter, G. Heckmann and G. Wolmershäuser, Organometallics, 1992, 11, 3894.
49. O. J. Scherer, H. Sitzmann and G. Wolmershauser, Angew. Chem., Int. Ed. Engl., 1989, 28, 212.
50. H.-G. v. Schnering, R. Bolle, J. Curda, K. Peters, W. Carrillo-Cabrera, M. Somer, M. Schultheiss and U. Wedig, Angew. Chem., Int. Ed. Engl., 1996, 35, 984.
51. J. Dietz, U. Müller, V. Müller and K. Dehnicke, Z. Naturforsch., B: J. Chem. Sci., 1991, 46, 1293.
52. S. C. Abrahams, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 790.
53. P. Jutzi, R. Kroos, A. Müller, H. Bögge and M. Penk, Chem. Ber., 1991, 124, 75.
54. C. Schulz, J. Daniels, T. Bredow and J. Beck, Angew. Chem., Int. Ed., 2016, 55, 1173.
55. A. Sekiguchi, T. Yatabe, C. Kabuto and H. Sakurai, J. Am. Chem. Soc., 1993, 115, 5853.
56. A. Y. Timoshkin, I. V. Kazakov, A. S. Lisovenko, M. Bodensteiner and M. Scheer, Inorg. Chem., 2011, 50, 9039.
57. K.-F. Tebbe and T. Heinlein, Z. Kristallogr., 1982, 160, 285.
58. K. Maheswari, N. M. Rajendran, J. Meyer and N. D. Reddy, Organometallics, 2010, 29, 3799.
59. J. Lobi, A. Y. Timoshkin, T. Cong, M. Necas, H. W. Roesky and J. Pinkas, Inorg. Chem., 2007, 46, 5678.
60. D. A. Doinikov, I. Dollhammerova, J. Löbl, M. Necas, A. Y. Timoshkin and J. Pinkas, J. Organomet. Chem., 2016, 809, 38.
61. L. V. Pankratov, L. N. Zakharov, R. I. Bochkova, G. K. Fukin and Y. T. Struchkov, Russ. Chem. Bull., 1994, 43, 867.
62. L. R. Sita and R. D. Bickerstaff, J. Am. Chem. Soc., 1989, 111, 3769.
63. E. M. Holt and S. L. Holt, J. Chem. Soc., Dalton Trans., 1974, 1990.
64. D. Prieschl, G. Belanger-Chablot, X. Duo, M. Dietz, M. Muller, L. Krummenacher, Z. Lin and H. Braunschweig, J. Am. Chem. Soc., 2020, 142, 1065.
65. J. Beck and M. Zink, Z. Anorg. Allg. Chem., 2009, 635, 692.
66. R. C. Burns, R. J. Gillespie, W.-C. Luk and D. R. Slim, Inorg. Chem., 1979, 3086.
67. K. Mayer, J. V. Dums, W. Klein and T. F. Fässler, Angew. Chem., Int. Ed., 2017, 56, 15159.
68. J. Bresien, A. Schulz and A. Villinger, Chem. – Eur. J., 2015, 21, 18543.
69. P. Jutzi, R. Kroos, A. Müller and M. Perk, Angew. Chem., Int. Ed. Engl., 1989, 28, 600.
70. W. Lu, K. Xu, Y. Li, H. Hirao and R. Kinjo, Angew. Chem., Int. Ed., 2018, 57, 15691.
71. D. Dou, G. W. Linti, T. Chen, E. N. Duesler, R. T. Paine and H. Nöth, Inorg. Chem., 1995, 35, 3626.
72. D. Dou, M. Westerhausen, G. L. Wood, E. N. Duesler, R. T. Paine, G. Linti and H. Nöth, Chem. Ber., 1993, 126, 379.
73. K. Ota and R. Kinjo, Angew. Chem., Int. Ed., 2020, 59, 6572.
74. P. Paetzold, C. von Plotho, G. Schmid and R. Boese, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1984, 39, 1069.
75. P. Paetzold, J. Kiesgen, K. Krahe, H.-U. Meier and R. Boese, Z. Naturforsch., B: J. Chem. Sci., 1991, 46, 853.
76. W. Ando, T. Shiba, T. Hidaka, K. Morihashi and O. Kikuchi, J. Am. Chem. Soc., 1997, 119, 3629.
77. A. Mack, S. Danner, U. Bergsträsser, H. H. Heydt and M. Regitz, J. Organomet. Chem., 2002, 643, 409.
78. J. Keuter, C. Schwemann, A. Hepp, K. Bergander, J. Droste, M. R. Hansen, N. L. Doltsinis, C. Mück-Lichtenfeld and F. Lips, Chem. Sci., 2020, 11, 5895.
79. J. Helmer, A. Hepp and F. Lips, Dalton Trans., 2020, 49, 11843.
80. H. Thomsen and W. Preetz, Z. Naturforsch., B: J. Chem. Sci., 1998, 53, 829.
81. G. Linti, S. Coban and D. Dutta, Z. Anorg. Allg. Chem., 2004, 630, 319.
82. W. Mesbah, M. Soleimani, E. Klanfar, G. Geiseler, W. Massa, M. Hofmann and A. Berndt, Eur. J. Inorg. Chem., 2009, 5577.
83. H. Nöth and H. Pommerening, Angew. Chem., Int. Ed. Engl., 1980, 19, 482.
84. Y. Nie, H. Pritzkow and W. Siebert, Z. Naturforsch., B: J. Chem. Sci., 2005, 60, 1016.
85. M. Nanjo, E. Nanjo and K. Mochida, Eur. J. Inorg. Chem., 2004, 2961.
86. B. Yearwood, S. U. Ghazi, M. J. Heeg, N. Richardson and J. P. Oliver, Organometallics, 2000, 19, 865.
87. D. F. Schafer, P. T. Wolczanski and E. B. Lobkovsky, Organometallics, 2011, 30, 6539.
88. M. Ahtee, Ann. Acad. Sci. Fenn., Ser. A, 1969, 313, 1.
89. P. Alvarez-Bercedo, A. D. Bond, R. Haigh, A. D. Hopkins, G. T. Lawson, M. M. McPartlin, D. Moncrieff, M. E. G. Mosquere, J. M. Rawson, A. D. Woods and D. S. Wright, Chem. Commun., 2003, 1288.
90. A. Nordheiner, T. Chivers, O. Schön, K. Karaghiosoff, K. S. A. Arachchige, A. M. Z. Slawin and J. D. Woollins, Chem. – Eur. J., 2014, 20, 704.
91. A. Walz, M. Niemeyer and J. Weidlein, Z. Anorg. Allg. Chem., 1999, 625, 547.
92. R. Schaeffer, Q. Johnson and G. S. Smith, Inorg. Chem., 1965, 4, 917.
93. A. J. Leadbetter and R. C. Ward, J. Chem. Phys., 1985, 82, 424.
94. G. P. Arnold, E. D. Finch, S. W. Rabideau and R. G. Wenzel, J. Chem. Phys., 1968, 49, 4365.
95. B. Kamb, J. Chem. Phys., 1971, 55, 1934.
96. S. Duan, I. Y. Zhang, Z. Xie and X. Xu, J. Am. Chem. Soc., 2020, 142, 6902.
97. H. Martínez-García, D. Morales, J. Pérez, M. Puerto and I. del Río, Chem. – Eur. J., 2014, 20, 5821.
98. P. Seller and J. Dunitz, Helv. Chim. Acta, 1989, 72, 1125.
99. A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Angew. Chem., Int. Ed., 2019, 58, 14146.
100. J. A. Krause, P. W. Baures and D. S. Eggleston, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 506.
101. T. Wiklund, C. J. McKenzie and A. Lennartson, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2010, 66, 0410.
102. L. del Rosso, F. Grazzi, M. Celli, D. Colognesi, V. Garcia-Sakai and L. Ulivi, J. Phys. Chem. C, 2016, 120, 26955.
103. K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 644.
104. J. D. Velasquez, J. Echeverría and S. Alvarez, Inorg. Chem., 2021, 60, 345.
105. M. Veith, A. Spaniol, J. Pohlman, F. Gross and V. Huch, Chem. Ber., 1993, 126, 2625.
106. X. Tian, M. Woski, C. Lustig, T. Pape, R. Frohlich, D. Le Van and K. Bergander, Organometallics, 2005, 24, 82.
107. J. Schneider, E. Popowski and H. Reinke, Z. Anorg. Allg. Chem., 2002, 628, 719.
108. A. Donchev, A. Schnepf, E. Baum, G. Stösser and H. Schnöckel, Z. Anorg. Allg. Chem., 2002, 628, 157.
109. E. Cremades, J. Echeverría and S. Alvarez, Eur. J. Inorg. Chem., 2010, 16, 10389.
110. R. Ahlrichs, D. Fenske, H. Oesen and U. Schneider, Angew. Chem., Int. Ed. Engl., 1992, 31, 323.
111. E. Hey-Hawkins, M. Pink, H. Oesen and D. Fenske, Z. Anorg. Allg. Chem., 1996, 622, 689.
112. M. Garçon, C. Bakewell, G. A. Sackman, A. J. P. White, R. I. Cooper, A. J. Edwards and M. R. Crimmin, Nature, 2019, 574, 390.
113. S. Alvarez, B. Menjón, A. Falceto, D. Casanova and P. Alemany, Inorg. Chem., 2014, 53, 12151.
114. H. Tang, D. M. Hoffman, T. A. Albright, H. Deng and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1993, 32, 1616.
115. Z. Niu, J.-G. Ma, W. Shi and P. Cheng, Chem. Commun., 2014, 50, 1839.
116. S. Cevik, Z. Alkan, M. Poyraz, M. Sari and O. Buyukgungor, Cryst. Res. Technol., 2007, 42, 955.
117. C. Zhan, J. M. Cameron, J. Gao, J. W. Purcell, D.-L. Long and L. Cronin, Angew. Chem., Int. Ed., 2014, 53, 10362.
118. T. S. Cameron, A. Decken, I. Krossing, J. Passmore, J. M. Rautiainen, X. Wang and X. Zeng, Inorg. Chem., 2013, 52, 3113.
119. M. N. Sokolov, N. G. Naumov, P. P. Samoylov and V. P. Fedin, Clusters and Cluster Assemblies, Elsevier, Amsterdam, 2nd edn, 2013, vol. 2.
120. E. Cerrada, M. Contel, A. D. Valencia, M. Laguna, T. Gelbrich and M. B. Hursthouse, Angew. Chem., Int. Ed., 2000, 39, 2353.
121. T. A. Wark and D. W. Stephan, Organometallics, 1989, 8, 2836.
122. Y. Takemura, H. Takenaka, T. Nakajima and T. Tanase, Angew. Chem., Int. Ed., 2009, 48, 2157.
123. T. Ishikawa, A. Kawamura, T. Sugawa, R. Moridaira, K. Yamamoto and T. Murahasi, Angew. Chem., Int. Ed., 2019, 48, 15318.
124. D. A. Padron and K. K. Klausmeyer, Eur. J. Inorg. Chem., 2013, 299.
125. C. R. Wade, A. A. Yakovenko and F. P. Gabbai, New J. Chem., 2010, 34, 1646.
126. M. I. Bruce, P. A. Humphrey, B. W. Skelton and A. H. White, J. Chem. Soc., Dalton Trans., 1997, 1485.
127. J. He, Y.-G. Yin, T. Wu, D. Li and X.-C. Huang, Chem. Commun., 2006, 2845.
128. N. Narasimhamurthy, A. G. Samuelson and H. Manohar, J. Chem. Soc., Chem. Commun., 1989, 1803.
129. C. A. Goddard, J. R. Long and R. H. Holm, Inorg. Chem., 1996, 35, 4347.
130. S. S. Yarovoy, A. I. Smolentsev, S. G. Kozlova, N. B. Kompankov, Y. M. Gayfulin, I. P. Asanov, V. V. Yanshole and Y. V. Mironov, Chem. Commun., 2018, 54, 13837.
131. E. G. Mednikov, V. V. Bashilov, V. I. Sokolov, Y. L. Slovokhotov and Y. T. Struchkov, Polyhedron, 1983, 2, 141.
132. R. H. Sánchez and T. A. Betley, J. Am. Chem. Soc., 2015, 137, 13949.

---