Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
[(VIVO)2MII5] (M = Ni, Co) Anderson wheels†
Hector W. L.
Fraser‡
 a,
Emily H.
Payne‡
a,
Emily H.
Payne‡
 a,
Arup
Sarkar
a,
Arup
Sarkar
 b,
Lucinda R. B.
Wilson
a,
Dmitri
Mitcov
c,
Gary S.
Nichol
b,
Lucinda R. B.
Wilson
a,
Dmitri
Mitcov
c,
Gary S.
Nichol
 a,
Gopalan
Rajaraman
a,
Gopalan
Rajaraman
 *b,
Stergios
Piligkos
*b,
Stergios
Piligkos
 *c and
Euan K.
Brechin
*c and
Euan K.
Brechin
 *a
*a
aEaStCHEM School of Chemistry, The University of Edinburgh, David Brewster Road, Edinburgh, EH9 3FJ Scotland, UK. E-mail: E.Brechin@ed.ac.uk
bDepartment of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India. E-mail: rajaraman@chem.iitb.ac.in
cDepartment of Chemistry, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen, Denmark. E-mail: piligkos@chem.ku.dk
First published on 2nd July 2021
Abstract
Heterometallic Anderson wheels of formula [(VIVO)2MII5(hmp)10Cl2](ClO4)2·2MeOH (M = Ni, 1; Co, 2) have been synthesised from the solvothermal reaction of M(ClO4)2·6H2O and VCl3 with hmpH (2-(hydroxymethyl)pyridine). The metallic skeleton describes a centred hexagon, with the two vanadyl ions sitting on opposing sides of the outer ring. Magnetic susceptibility and magnetisation measurements indicate the presence of both ferromagnetic and antiferromagnetic exchange interactions. Theoretical calculations based on density functional methods reproduce both the sign and strength of the exchange interactions found experimentally, and rationalise the parameters extracted.
Introduction
Alongside its prominent role in polyoxometalate chemistry,1 vanadium has had significant impact in the field of molecule-based magnetism. For example, orthogonal magnetic orbitals were exploited to produce ferromagnetic exchange in a [(VIVO)–CuII] dimer,2 the Prussian blue V[Cr(CN)6]0.86 was one of the initial examples of a coordination compound exhibiting room temperature magnetic order,3 single-molecule magnet behaviour was observed in a [VIII4] butterfly,4 [V30] and [V15] have been widely studied to examine the influence of geometrical spin-frustration and antisymmetric exchange,5 and most recently monometalic VIV compounds such as (Bu4N)2[V(C8S8)3] and [VOPc] have been touted as excellent candidates for electron-spin based qubits.6Heterometallic 3d cages containing vanadium are however rather rare, and indeed those containing nickel or cobalt are relatively scarce. A search of the Cambridge Structural Database reveals only eight (Ni) and sixteen (Co) unique structure types with a nuclearity of four or more. When the nuclearity is increased to seven or more metal ions this number reduces to just four (Ni) and five (Co) examples.7 Restricting the search to complexes of any nuclearity containing the VIV–O–MII (M = Ni, Co) moiety, and excluding polyoxometalates,8 surprisingly affords only two different structure types: [(VO)M] dimers,9 and a single [(VO)6M] wheel.10 The latter complex has the formula [MVIV6O6{(OCH2CH2)2N(CH2CH2OH)}6]X (X = halide) in which the six vanadyl moieties form a wheel that ‘encapsulates’ a variety of s- and 3d metal ions (M).10 Given the paucity of such species we have begun a program of research aimed at synthesising a variety of heterometallic VIVO-3d cluster compounds. The recent success we have had in employing the ligand 2-(hydroxymethyl)pyridine (hmpH) in the construction of heterometallic Anderson wheels of general formula [MIII2MII5(hmp)12]4+ (where MIII = Cr, Al and MII = Mn, Fe, Co, Ni, Cu, Zn),11 hinted that this might be a viable route to isolating similar MIV–MII cages.
Experimental
Experimental procedures
All chemicals were procured from commercial suppliers and used as received (reagent grade). Caution: although no issues were encountered here care should be taken when handling potentially explosive perchlorate salts.Synthesis of [(VO)2Ni5(hmp)10Cl2](ClO4)2·2MeOH (1)
Ni(ClO4)2·6H2O (0.366 g, 1 mmol) and VCl3 (0.079 g, 0.5 mmol) were dissolved in MeOH (24 ml) with NaOMe (0.162 g, 3 mmol) to give a green solution. Upon full dissolution, hmpH (0.285 ml, 3 mmol) was added dropwise resulting in a darkening of the solution colour. The reaction was left overnight with continuous stirring. 10 ml samples of the resulting dark green solution were heated in Teflon-lined autoclaves at 140 °C for 24 hours. After slowly cooling to room temperature the reaction vessels were allowed to sit undisturbed for 24 hours yielding dark green, triangular prism-shaped crystals suitable for X-ray diffraction. Yield 0.126 g (34.2% by Ni weight). Anal. Calcd (%) for C62H68Cl4N10Ni5O22V2: C 40.42, H 3.72, N 7.60, Ni 15.93, V 5.53; found: C 40.24, H 3.42, N 7.34, Ni 16.00, V 5.75.Synthesis of [(VO)2Co5(hmp)10Cl2](ClO4)2·2MeOH (2)
Co(ClO4)2·6H2O (0.366 g, 1 mmol) and VCl3 (0.079 g, 0.5 mmol) were dissolved in MeOH (24 ml) with NaOMe (0.162 g, 3 mmol) to give a red/orange solution. Upon full dissolution, hmpH (0.285 ml, 3 mmol) was added dropwise resulting in a darkening of the solution colour. The reaction was left overnight with continuous stirring. 12 ml samples of the resulting solution were heated in Teflon-lined autoclaves at 100 °C for 12 hours. After slowly cooling to room temperature the reaction vessels were allowed to sit undisturbed for 24 hours yielding red, plate-shaped single crystals suitable for X-ray diffraction. Yield 0.130 g (35.3% by Co weight). Anal. Calcd (%) for C62H68Cl4N10Co5O22V2: C 40.39, H 3.72, N 7.58, Co 15.98, V 5.53; found: C 40.02, H 3.51, N 7.56, Co 16.11, V 5.76.Crystallographic details
Diffraction data for compound 1–2 were collected using a Rigaku Oxford Diffraction SuperNova diffractometer with MoKα radiation (Table 1). An Oxford Cryosystems Cryostream 700+ low temperature device was used to maintain a crystal temperature of 120 K. The structures were solved using ShelXT and refined with ShelXL interfaced through Olex2.12,13 All non-hydrogen atoms were refined using anisotropic displacement parameters. H atoms were placed in calculated positions geometrically and refined using the riding model. CCDC: 1847956 and 1847957.† Powder XRD measurements were performed using a Bruker D2 PHASER spectrometer, and are shown in Fig. S1.†| Compound | 1 | 2 |
|---|---|---|
| Formula | C62H68Cl4N10Ni5O22V2 | C62H68Cl4Co5N10O22V2 |
| D calc./g cm−3 | 1.721 | 1.712 |
| μ/mm−1 | 1.779 | 1.613 |
| Formula weight | 1842.49 | 1843.59 |
| Colour | Dark green | Pale brown |
| Shape | Block | Plate |
| Size/mm3 | 0.52 × 0.29 × 0.16 | 0.50 × 0.14 × 0.06 |
| T/K | 120.0 | 120.0 |
| Crystal system | Monoclinic | Monoclinic |
| Space group | P21/n | P21/n |
| a/Å | 15.7800(3) | 15.7439(9) |
| b/Å | 12.4392(2) | 12.4867(5) |
| c/Å | 19.0165(4) | 18.9773(12) |
| α/° | 90 | 90 |
| β/° | 107.745(2) | 106.591(6) |
| γ/° | 90 | 90 |
| V/Å3 | 3555.16(12) | 3575.4(4) |
| Z (Z′) | 2 (0.5) | 2 (0.5) |
| Wavelength/Å | 0.71073 | 0.71073 |
| Radiation type | MoKα | MoKα |
| Θ min/°–Θmax/° | 3.072–32.985 | 3.079–28.897 |
| Measured refl. | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 810 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370 |
| Independent refl. | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 777 777 |
8344 |
| Reflections used | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 678 678 |
5589 |
| R int | 0.0447 | 0.0715 |
| Parameters | 516 | 479 |
| Restraints | 155 | 1 |
| Largest peak | 0.678 | 1.013 |
| Deepest hole | −0.475 | −0.678 |
| GooF | 1.042 | 1.041 |
| wR2 (all data) (wR2) | 0.0770 (0.0719) | 0.1612 (0.1465) |
| R 1 (all data) (R1) | 0.0461 (0.0341) | 0.1147 (0.0704) |
Magnetisation data collection
Magnetic susceptibility and magnetisation measurements in the temperature range T = 2–290 K were performed on a Quantum Design MPMS XL SQUID magnetometer equipped with a 5 T dc magnet in the field range, B = 0.1–5.0 T. Samples were mounted in gelatine capsules and restrained by addition of a small quantity of hexadecane. The observed paramagnetic susceptibilities were corrected for diamagnetic contributions using Pascal's constants.Computational details
Density functional theory (DFT) calculations were carried out using Gaussian 09 (Rev D.01).14 The unrestricted hybrid B3LYP functional along with the all-electron triple-ζ valence (TZV) basis set was used to evaluate the spin state energies for all atomic centres, performed on crystal structures. SCF convergence criteria were set to tight using the quadratic convergence method, followed by a stability test as implemented in G09. Overlap integral calculations were carried out to reveal the extent of magnetic exchange occurring between neighbouring metal centres. Local magnetic anisotropies on the CoII ions were computed using ab initio methods in ORCA 4.0.1.15 During these local zero-field splitting (zfs) calculations, paramagnetic metal ions were substituted by diamagnetic ZnII ions. Since the estimation of zfs and other spin-Hamiltonian (SH) parameters requires an accurate description of electronic excited states, the multi-configurational CASSCF-NEVPT2 method was applied. The scalar relativistic DKH Hamiltonian and DKH contracted version of basis sets (DKH-def2-TZVP for Co; DKH-def2-TZVP(-f) for Zn, N, O; DKH-def2-SVP for C, H) were used throughout the calculations. Spin–orbit coupling (SOC) and subsequent spin-Hamiltonian parameters were determined using the QDPT-EHA approach.16 For Co(II), CAS(7,5) with ten quartets and forty doublets were allowed to mix in the SOC step.Results and discussion
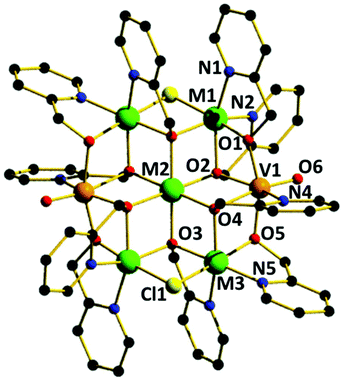
The reaction of M(ClO4)2·6H2O with VCl3 and hmpH in a basic MeOH solution under solvothermal conditions produces crystals of [(VO)2M5(hmp)10Cl2](ClO4)2·2MeOH (M = Ni, 1; Co, 2) in approximately 35% yield. Complexes 1–2 crystallise in the monoclinic space group P21/n (Table 1) with half the cationic cage, one perchlorate counter ion and one molecule of methanol in the asymmetric unit. The metallic skeleton (Fig. 1) describes a centred [(VIVO)2MII5] wheel in which the vanadyl moieties (V1 and symmetry equivalent, s.e.) oppose each other on the outer [VIV2MII4] rim, i.e. they occupy positions 1, 4 (Fig. 4). The central MII ion (M2, position 7, Fig. 4) is bridged to the six outer ring metals by six μ3-OR groups from six deprotonated hmp ligands. The four remaining hmp ligands each provide a μ-OR bridge on the exterior of the ring between one VIV ion and one MII ion. The two opposing Cl ions also μ-bridge in the external wheel, between M1 and M3 (positions 2 and 6, respectively, Fig. 4) and s.e. All seven metal ions display distorted octahedral coordination geometries, with the vanadyl moiety having a V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length of ∼1.6 Å (Tables S1 and 2†).
O bond length of ∼1.6 Å (Tables S1 and 2†).
The perchlorate anions and MeOH molecules of crystallisation H-bond to each other (O⋯O, ∼2.8 Å), sitting in-between the planes of the cationic cages (Fig. S2†). The closest intermolecular contacts between cations exist between aromatic rings on neighbouring molecules with C(Ar)⋯H(Ar) separations in the range ∼2.3–2.8 Å, and between the aromatic rings and the Cl ions, (Ar)⋯Cl at ∼2.9 Å.
In the extended structure the cations pack in columns down the b axis, with the columns arranged into rows with each neighbouring column composed of molecules which are eclipsed with respect to the adjacent column (Fig. S3†).
Complexes 1–2 are structurally related to the [MIII2MII5(hmp)12]4+ (MIII = Cr, Al and MII = Mn, Fe, Co, Ni, Cu, Zn) family of Anderson wheels,11 the species [MVIV6O6{(OCH2CH2)2N(CH2CH2OH)}6]n+ (M = Li, Na, Mg, Mn, Fe, Co, Ni) reported by Khan,10 and the complex [MII6Cr(HLzw)6(HL)6]3+ (M = Ni, Co; HL = 2-hydroxy-4-methyl-6-phenyl-pyridine-3-amidoxime) published by Murrie and Milios.17 This highlights the apparent stability of the Anderson wheel structure, and the modular nature of the molecule whereby different metals in different oxidation states can be combined with the same (or similar) ligand sets to afford analogous species.18 Note that in the [MIII2MII5(hmp)12]4+ family, the MIII ion is positionally disordered around the external wheel. In [MIV2MII5(hmp)10]2+ (1–2) the MIV is not positionally disordered.
Magnetic properties
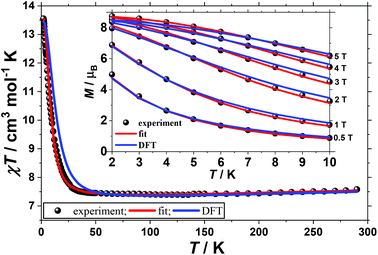
The direct-current molar magnetic susceptibility, χ, of polycrystalline samples of complexes 1 and 2 were measured in an applied magnetic field, B, of 0.1 T, over the 2–290 K temperature, T, range. The experimental results are shown in Fig. 2 and 3 as the χT product versus T, where χ = M/B and M is the magnetisation.At room temperature the χT product of 1 is 7.5 cm3 K mol−1, from where a g-value of gNi = 2.32 can be inferred based on the sum of Curie constants of five uncorrelated NiII ions (SNi = 1) and two uncorrelated VIV ions (SV = 1/2), with gV = 2.00. Upon cooling the value of the χT product of 1 first slowly drops to reach 7.4 cm3 K mol−1 at 100 K, then it slowly increases to reach 7.6 cm3 K mol−1 at 30 K and finally rapidly increases below 30 K to reach 13.6 cm3 K mol−1 at 2 K. This behaviour is indicative of competing antiferromagnetic and ferromagnetic interactions. To better define the low-temperature magnetic properties of 1, variable-temperature-variable-field (VTVB) magnetisation measurements were performed in the temperature and field ranges 2 to 10 K and 0.5 to 5 T, respectively (inset of Fig. 2). The VTVB magnetisation of 1 at 2 K and 5 T reaches a maximum of 8.7μB (μB is the Bohr magneton). Notably, when the VTVB magnetisation data of 1 are plotted against the reduced quantity μBB/kT (k is the Boltzmann constant) no nesting of the VTVB curves is observed (Fig. S4†), indicative of negligible magnetic anisotropy.
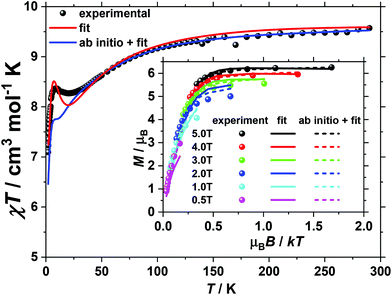
For 2, magnetisation measurements were performed on wet polycrystalline samples (of known mass, solvent content) because measurements performed on dry, powdered samples evidenced deterioration over time, consistent with PXRD data (Fig. S1†). This is likely due to lattice solvent loss, exacerbated by the reduced pressure conditions experienced by the sample during the SQUID measurements. The room temperature value of the χT product of 2 (Fig. 3) is 9.6 cm3 K mol−1, somewhat lower than the value of 10.125 cm3 K mol−1 expected for five uncorrelated CoII ions and two uncorrelated VIV ions, assuming (vide infra) both that g = 2 for all centres (to avoid over-parameterisation) and that a low symmetry ligand field quenches the orbital angular momentum of the octahedral CoII ions (i.e. spin-only SCo = 3/2). Upon cooling the χT product of 2 drops continuously reaching a plateau value of 8.3 cm3 K mol−1 at 20 K, whereupon it slightly increases to a local maximum of 8.5 cm3 K mol−1 at 9 K, after which it drops to reach 7.1 cm3 K mol−1 at 2 K. In contrast to 1, when the VTVB magnetisation data of 2 are plotted against the reduced quantity μBB/kT, significant nesting of the VTVB curves is observed (inset of Fig. 3), indicative of significant anisotropy.
The quantitative interpretation of the magnetic properties of 1 and 2 were performed by numerically fitting the experimental data to the full spin-Hamiltonian matrix, of dimension 972 for 1 and 4096 for 2, by use of the simplex algorithm19 and spin-Hamiltonian (1):
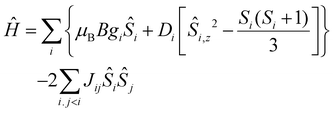 | (1) |
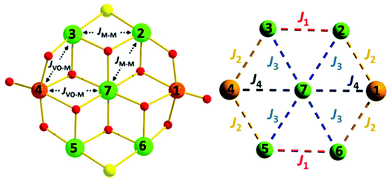 | ||
| Fig. 4 (Left) Representation of the isotropic exchange interactions included in spin-Hamiltonian (1) used in the experimental fit of the susceptibility and magnetisation data for complexes 1 and 2. (Right) The exchange interaction scheme used in the theoretical modelling of the magnetic data. Colour code as Fig. 1. | ||
For 2, the temperature dependence of the χT product was fitted to the full spin-Hamiltonian (1) resulting in the best fit parameters: JCo–Co = −0.45 cm−1, JCo–VO = −4.85 cm−1 and |DCo| = 6.65 cm−1. However, these parameters do not accurately reproduce the VTVB data (Fig. S6†). In order to obtain a better estimate of DCo, the VTVB data of 2 were therefore fitted to spin-Hamiltonian (1) by fixing the values of the isotropic exchange and letting DCo vary. This resulted in the best-fit parameter |DCo| = 21.40 cm−1, with the resulting VTVB curves shown in the inset of Fig. 3. The persistent deviation of the calculated curves from the experimental data, originating from the simplicity of the model employed and assumptions made, therefore only allows us at this stage to estimate that |DCo| likely lies in the range 5 to 25 cm−1.
The sign and magnitude of the exchange interactions in 1 and 2 are consistent with previous examples reported in the literature for both dialkoxo- and alkoxo/chloro-bridged MII2 units, and alkoxo-bridged (VO)–MII moieties with similar bridging angles.9,20–22
Theoretical calculations
In order to further probe the magnitude and origin of the exchange interactions, and anisotropy of the CoII ions, we now turn to theoretical methods. For this purpose we no longer assume that all magnetic exchange interactions between MII–MII ions (JM–M) and VIV–MII (JVO–M) ions are equivalent, but assign individual pairwise exchange interactions between the constitutive centres in 1 and 2 (Fig. 4, right). Pairwise exchange interactions between neighbouring paramagnetic centres have been computed using the broken symmetry approach (Scheme S1,† eqn (S1)).23 Four different isotropic exchange pathways (J1–J4) have been considered: J1 = J23 = J56 (MII(ring)–(Cl)(O)–MII(ring)); J2 = J12 = J34 = J45 = J16 (MII(ring)–(O)(O)–VIV(ring)); J3 = J27 = J37 = J57 = J67 (MII(ring)–(O)(O)–MII(centre)); J4 = J17 = J47 (MII(centre)–(O)(O)–VIV(ring)).For 1, the computed J values are shown in Table 2, together with the values obtained from numerical fitting of the experimental data for comparison. Calculation of the temperature dependence of the χT product and of the VTVB data using the DFT computed J values and neglecting the uniaxial anisotropy parameter for all metal centres results in good agreement with the experimental data (Fig. 2), with deviations mainly arising for the lower temperatures as a consequence of the isotropic model. The DFT computed J values suggest that the J2 (MII(ring)–(O)(O)–VIV(ring)) interaction is relatively strongly antiferromagnetic, with all other interactions being weakly ferromagnetic in nature. This results in an S = 4 ground state, with the spin of the two V ions being antiparallel to the spins of the five Ni ions (Fig. S5†). The computed spin densities for the high spin state, as well as four broken symmetry (bs) solutions, provide values in the range of 1.66–1.74 for the NiII centres, and a spin polarized value of 1.12(1) for the VO centres (Fig. 5, S7, Table S3†). These are in good agreement with previously reported six coordinate NiII and VIV species.24 The reduced spin density values on the Ni ions indicate strong spin delocalisation onto the coordinating O, N and Cl ligand orbitals. The increased spin density value on the VO moiety reflects strong spin polarisation.
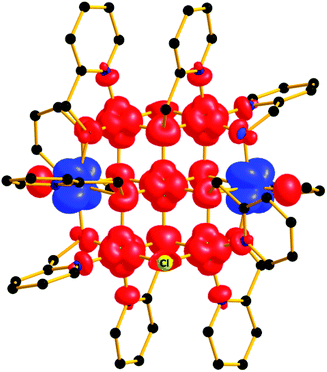 | ||
| Fig. 5 Spin density plot of the ground state of complex 1 at an iso-surface value of 0.0065 e bohr−3. | ||
| Complex | Method | J 1/cm−1 | J 2/cm−1 | J 3/cm−1 | J 4/cm−1 |
|---|---|---|---|---|---|
| 1 | Fit | 1.30 | −3.49 | 1.30 | −3.49 |
| 1 | DFT | 0.11 | −9.89 | 3.18 | 0.23 |
| 2 | Fit | −0.45 | −4.85 | −0.45 | −4.85 |
| 2 | NEVPT2-QDPT-EHA + fit | −1.48 | −8.19 | 3.72 | 6.13 |
The computed isotropic exchange interactions for complex 1 can be rationalised by analysing the overlap of magnetic orbitals between interacting pairs of metal centres (Table S4 and Fig. S8†), together with their corresponding bridging angles (Table S1†). In the case of J1 (MII(ring)–(Cl)(O)–MII(ring)), the Ni–Cl–Ni and Ni–O–Ni angles (84.2° and 103.2°, respectively) would be expected to result in a weak ferromagnetic interaction. For J2 (MII(ring)–(O)(O)–VIV(ring)) the alkoxide bridging angles (Ni–O–V) are 104.27° (102.11°) and 96.81° (95.93°) and lead to significant antiferromagnetic coupling. Computation reveals significant overlap (SNi–V = 0.07) between the dxy orbital of VIV and the dx2−y2/dxz orbitals of NiII – the lower symmetry and strong spin polarisation of the bridging oxygen atom maximises the V(dxy)–Ni(dx2−y2/dxz) orbital overlap. J3 (MII(ring)–(O)(O)–MII(centre)) is weakly ferromagnetic in nature, due to the presence of small Ni–O–Ni angles (96°–100°).25,26J4 is also weakly ferromagnetic because of minimal overlap between magnetic orbitals.
For 2 the magnetic anisotropy parameters of the Co(II) centres were estimated by ab initio calculations. In this case the zfs parameters (DCo) were found to be much larger than the exchange parameters as Co(II) ions in distorted octahedral environments possess sizeable magnetic anisotropy.27–31 The local anisotropy parameters, computed from the NEVPT2-QDPT-EHA level of theory, were found to be DCo(ring) = ±87 cm−1, E/D = 0.27 and DCo(central) = +82 cm−1, E/D = 0.19 (Tables S5 and S6†), about a factor of four larger than the best fit DCo parameter obtained by numerically fitting the experimental data to spin-Hamiltonian (1). Due to the very strong anisotropy, single determinant DFT calculations are unable to yield reasonable exchange values (J1 = −18.7 cm−1, J2 = 54.42 cm−1, J3 = −0.66 cm−1 and J4 = 84.71 cm−1). Thus, attempts to simulate the experimental susceptibility and magnetisation data of 2 using the DFT computed J values along with the highly anisotropic D values were unsuccessful. Therefore, for the quantitative interpretation of the experimental data, we fix the anisotropy parameters of the Co(II) centres to those calculated as described above and fit the four exchange parameters in spin-Hamiltonian (1). This resulted in the best fit parameters: J1 = −1.48 cm−1, J2 = −8.19 cm−1, J3 = 3.72 cm−1 and J4 = 6.13 cm−1 (solid blue line and dashed lines in Fig. 3).
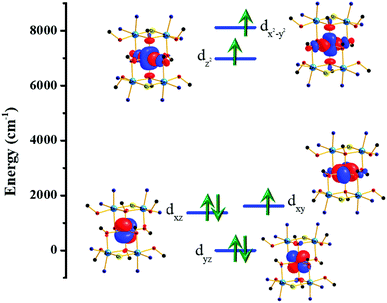
In order to further investigate the origin of the magnetic anisotropy of the CoII ions, we have plotted the ligand-field d-orbital splitting diagram of the central Co ion (M2 in Fig. 1) of complex 2 (Fig. 6). 58% of the ground state electronic configuration consists of (dyz)2(dxz)2(dxy)1(dz2)1(dx2−y2)1. The major contribution towards the very large D value arises from the first two excited states (Table S5†) which lie 619 cm−1 and 1294 cm−1 above the ground state and contribute 38 cm−1 and 24 cm−1, respectively, towards the overall D value. These two excited states arise from the dxz/dyz → dxy spin allowed electronic transitions. The multi-determinant nature of the wavefunction also suggests that a single electronic configuration is not sufficient to describe the true electronic structure of the CoII centres. The anisotropy axes (Dzz axes) of the five CoII ions are oriented in a ‘random’ fashion (Fig. S9†).
Conclusions
A structurally unique Anderson-type wheel of formula [(VO)2M5(hmp)10Cl2](ClO4)2·2MeOH (M = Ni, Co), in which the VIV ions oppose each other in the outer wheel has been synthesised via solvothermal methods using the pro-ligand hmpH. Complexes 1–2 are rare examples of heterometallic VIV–NiII/CoII cluster compounds. Magnetic susceptibility and magnetisation studies reveal competing ferro- and antiferromagnetic exchange interactions; the strongest interaction in each case being the antiferromagnetic exchange between MII(ring)–(O)(O)–VIV(ring) – consistent between experiment and theory. The observation of structurally analogous homo- and heterometallic, and homo- and heterovalent [M7] Anderson wheels containing d- (and s-) block metals in the II+, III+ and IV+ oxidation states points toward the exceptional stability of the structure type. It further suggests that an enormous number of similar [M7] complexes containing a combination of different metal ions in different oxidation states and displaying different magnetic behaviours have yet to be isolated. Given the prevalence of “brucite-like” molecular 2D sheets based on shared [M3] triangular building blocks in 3d polymetallic coordination chemistry,11 we also speculate that similar species to 1 and 2 but with larger nuclearities in sheet-like “2D” frameworks can be formed.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the EPSRC for funding grants EP/P025986/1 and EP/N01331X/1. EKB, GR and AS thank the British Council, UKIERI grant 2017-18-04. S. P. thanks the VILLUM FONDEN for research grant 13376. AS thanks IIT Bombay for funding. GR would like to thank DST and SERB (CRG/2018/000430; DST/SJF/CSA-03/2018-10; SB/SJF/2019-20/12), UGC-UKIERI (184-1/2018(IC)) and SUPRA (SPR/2019/001145) for funding.Notes and references
- M. T. Pope and A. Müller, Angew. Chem., Int. Ed. Engl., 1991, 30, 34 CrossRef
.
- O. Kahn, J. Galy, Y. Journaux, J. Jaud and I. Morgenstern-Badarau, J. Am. Chem. Soc., 1982, 104, 2165 CrossRef CAS
.
- S. Ferlay, T. Mallah, R. Ouahès, P. Veillet and M. Verdaguer, Nature, 1995, 378, 701 CrossRef CAS
.
- S. L. Castro, Z. M. Sun, C. M. Grant, J. C. Bollinger, D. N. Hendrickson and G. Christou, J. Am. Chem. Soc., 1998, 120, 2365 CrossRef CAS
.
- See for example:
(a) J. Schnack, M. Luban and R. Modler, Europhys. Lett., 2001, 56, 863 CrossRef CAS
; (b) G. Chaboussant, S. T. Ochsenbein, A. Sieber, H.-U. Güdel, H. Mutka, A. Müller and B. Barbara, Europhys. Lett., 2004, 66, 423 CrossRef CAS
; (c) V. V. Maslyuk, I. Mertig, O. V. Farberovich, A. Tarantul and B. Tsukerblat, Eur. J. Inorg. Chem., 2013, 1897 CrossRef CAS
.
-
(a) J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 15841 CrossRef CAS PubMed
; (b) M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154 CrossRef CAS PubMed
.
- See for example:
(a) R. H. Laye, F. K. Larsen, J. Overgaard, C. A. Muryn, E. J. L. McInnes, E. Rentschler, V. Sanchez, S. J. Teat, H. U. Güdel, O. Waldmann, G. A. Timco and R. E. P. Winpenny, Chem. Commun., 2005, 1125 RSC
; (b) T. Kurata, A. Uehara, Y. Hayashi and K. Isobe, Inorg. Chem., 2005, 44, 2524 CrossRef CAS PubMed
.
- See for example:
(a) E. Antonova, C. Näther, P. Kögerler and W. Bensch, Inorg. Chem., 2012, 51, 2311 CrossRef CAS PubMed
; (b) M. Rasmussen, C. Näther, J. van Leusen, P. Kögerler, L. Zhechkov, T. Heine and W. Bensch, Inorg. Chem., 2017, 56, 7120 CrossRef CAS PubMed
; (c) F. Lia, L. Xua, Y. Weib, X. Wanga, W. Wanga and E. Wang, J. Mol. Struct., 2005, 753, 61 CrossRef
; (d) Z. Shi, J. Peng, C. J. Gómez-García, S. Benmansour and X. Gua, J. Solid State Chem., 2006, 179, 253 CrossRef CAS
.
-
(a) K. K. Nanda, S. Mohanta, S. Ghosh, M. Mukherjee, M. Helliwell and K. Nag, Inorg. Chem., 1995, 34, 2861 CrossRef
; (b) S.-Z. Du, J. Feng, L. An and X.-M. Lu, Z. Anorg. Allg. Chem., 2012, 638, 411 CrossRef CAS
; (c) M. D. Glick, R. L. Lintvedt, D. P. Gavel and B. Tomlonovic, Inorg. Chem., 1976, 15, 1654 CrossRef CAS
; (d) D. Mandal, P. B. Chatterjee, R. Ganguly, E. R. T. Tienik, R. Clérac and M. Chaudhury, Inorg. Chem., 2008, 47, 584 CrossRef CAS PubMed
; (e) B.-S. Kang, X.-J. Wang, C.-Y. Su and H.-Q. Liu, Transition Met. Chem., 1999, 24, 712 CrossRef CAS
.
- M. I. Khan, S. Tabussum, R. J. Doedens, V. O. Golub and C. J. O'Connor, Inorg. Chem., 2004, 43, 5850 CrossRef CAS PubMed
.
-
(a) H. W. L. Fraser, G. S. Nichol, D. Uhrín, U. G. Nielsen, M. Evangelisti, J. Schnack and E. K. Brechin, Dalton Trans., 2018, 47, 11834 RSC
; (b) H. W. L. Fraser, G. S. Nichol and E. K. Brechin, Dalton Trans., 2018, 47, 15530 RSC
.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3 CrossRef PubMed
.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed
.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977 CrossRef CAS PubMed
.
- F. E. Kakaroni, A. Collet, E. Sakellari, D. I. Tzimopoulos, M. Siczek, T. Lis, M. Murrie and C. J. Milios, Dalton Trans., 2018, 47, 58 RSC
.
- O. Cador, D. Gatteschi, R. Sessoli, F. K. Larsen, J. Overgaard, A.-L. Barra, S. J. Teat, G. A. Timco and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2004, 43, 5196 CrossRef CAS PubMed
.
-
H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, Cambridge, 2nd edn, 1992 Search PubMed
.
- L. N. Zheng, S. Y. Zhang, K. Li, W. Q. Chen, Y. M. Chen, B. Xu, B. Hu, Y. H. Li and W. Li, J. Mol. Struct., 2010, 984, 153 CrossRef CAS
.
- M. K. Hänninen, J. Välivaara, J. Cano, R. Sillanpää and E. Colacio, Eur. J. Inorg. Chem., 2016, 1192 CrossRef
.
- S. S. Massoud, M. Spell, C. C. Ledet, T. Junk, R. Herchel, R. C. Fischer, Z. Trávníček and F. A. Mautner, Dalton Trans., 2015, 44, 2110 RSC
.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737 CrossRef CAS
.
- G. Rajaraman, K. E. Christensen, F. K. Larsen, G. A. Timco and R. E. P. Winpenny, Chem. Commun., 2005, 3053 RSC
.
- M. A. Halcrow, J.-S. Sun, J. C. Huffman and G. Christou, Inorg. Chem., 1995, 34, 4167 CrossRef CAS
.
- R. Sen, A. M. L. Lopes, Z. Lin, P. Brandão and J. P. Araújo, Eur. J. Inorg. Chem., 2019, 3840 CrossRef CAS
.
- F. El-Khatib, B. Cahier, F. Shao, M. López-Jordà, R. Guillot, E. Rivière, H. Hafez, Z. Saad, J. J. Girerd, N. Guihéry and T. Mallah, Inorg. Chem., 2017, 56, 4601–4608 CrossRef PubMed
.
- S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300 CrossRef PubMed
.
- F. Shao, B. Cahier, E. Rivière, R. Guillot, N. Guihéry, V. E. Campbell and T. Mallah, Inorg. Chem., 2017, 56, 1104 CrossRef CAS PubMed
.
- J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, J. Am. Chem. Soc., 2012, 134, 15704 CrossRef CAS PubMed
.
- V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M.-E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional crystallographic, magnetic and theoretical data. CCDC 1847956 and 1847957. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1dt01710a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |