Structure determination of small molecule compounds by an electron diffractometer for 3D ED/MicroED

Abstract

3D electron diffraction (3D ED)/Micro electron diffraction (MicroED) has extended the limits of crystallography by enabling the determination of three dimensional molecular structures from sub-μm microcrystals. However, 3D ED/microED measurements using current state-of-the-art electron microscopes require experts in both electron microscopy and crystallography making the method rather difficult for researchers who simply need structures. Here, we present a diffractometer specifically designed for 3D ED/microED and show how it works for determining crystal structures. The newly developed electron diffractometer will provide many researchers with an easy path to structure determination of crystals that are less than 1 μm in size.

---

Introduction

X-ray crystallography has long been used as a powerful technique to determine the three dimensional molecular structure of small molecule compounds and biological macromolecules at atomic resolution. We have developed a series of X-ray diffractometers, which enables researchers to provide structures of crystals of a few microns in size. Although X-ray crystallography is a very powerful technique, it requires crystals that are at least 1 μm in size. Crystallization involves a lot of trial and error to determine the best conditions. Furthermore, crystallization is not always successful. Much effort has been expended to accelerate the determination of crystal structures, including the construction of synchrotron radiation facilities and the development of the crystalline sponge method.^1,2 Structure determination using powder XRD has also been carried out using Rietveld methods, real-space methods, and maximum entropy methods.^31–34 However, there are numerous crystal structures of many important compounds that have yet to be determined due to this obstacle.

3D electron diffraction (3D ED)/Micro electron diffraction (MicroED) has already been around for more than 20 years and originated from Dorset et al.^3,4 and Hovmöller et al.^5,6 who independently showed that it was possible to acquire diffraction data using a transmission electron microscope (TEM). A well-organized review of the development of 3D ED/MicroED to date has been published by Gemmi et al.⁷ In recent years, 3D ED/microED, has rapidly come into use^8–16 because the interaction between electrons and materials is much stronger than that of X-rays, therefore, the difficulty of crystallization can be mitigated; 3D ED/microED can determine the molecular structure of crystals smaller than 1 μm, which are difficult to measure routinely even with synchrotron undulator beamlines. For instance, the structure of lomaiviticin,¹⁷ which could not be determined by X-ray diffraction for twenty years, was determined by 3D ED/microED. Although 3D ED/microED is becoming more widely known and used, the technique still requires two experts, one in electron microscopy and the other in crystallography. Furthermore, to the best of our knowledge, almost all 3D ED/microED datasets are collected using cryo-EM optimized to perform single particle analysis of macromolecules, and not dedicated to 3D ED/microED experiments. Therefore, the current problem is that it is not easy to perform 3D ED/microED experiments. We have developed an instrument specifically for 3D ED/microED measurements to streamline 3D ED/microED measurements. The electron diffractometer has been thoroughly tested in the course of development and has successfully produced crystal structures of a variety of compounds. In this paper, we report the configuration of the electron diffractometer coupled with CrysAlis^Pro for ED software, giving a seamless workflow from data collection, structure determination, and the results of structural analysis.

Experimental section

Configuration of the electron diffractometer

The configuration of the newly developed electron diffractometer is briefly described below. The most important components are the lens system (Fig. 1), the HyPix-ED, a direct electron detector, and CrysAlis^Pro for ED, the software controlling these components. Fig. 1b shows the major difference in the lens system between this study and the conventional TEM. A diffractometer dedicated to electron diffraction does not require the ability to acquire high-resolution TEM images. The diffraction experiment requires a parallel beam and minimal changes in lens values when switching between image and diffraction. In order to achieve this goal, the electron optics in this instrument does not incorporate a condenser minilens into the lens system (Fig. 1b). In addition, compared to a conventional TEM, weak objective lenses are implemented. These changes made the beam more parallel and minimized the change in lens values when switching between image and diffraction modes. This allows us to switch between image and diffraction modes by clicking a button. This lens system allows the instrument to use a fixed setting for the electron diffraction lens, which reduces the amount of work for the measurer, such as manual adjustment of each lens value. When searching the target area, the image of the specimen is obtained on the HyPix-ED by changing the current of the intermediate lens 1. 2. HyPix-ED; direct electron detection of diffraction spots by HPC detectors such as HyPix-ED allows for very precise measurements. The detector is also very robust and can make measurements even when the primary beam is directly incident on the detector. In fact, all the measurements in this study were performed without the use of a direct beam stop. In addition, due to the high dynamic range of the detector (up to 31 bits), saturated diffraction spots rarely occur even in measurements that require long exposure time due to poor crystallinity of the crystals. 3. CrysAlis^Pro for ED; the most important component of electron diffractometer is CrysAlis^Pro for ED, the integrated control and processing software. This software performs stage control, diffraction experiments, data integration, and reduction. In the 3D ED/microED experiment, it is necessary to switch between image and diffraction modes to confirm the position and crystallinity of the crystals. With the electron diffractometer, this switching can be performed with a single mouse click, which greatly reduces the burden on researchers. The data merging of crystals belonging to the space groups with low symmetry is easy with CrysAlis^Pro for ED, and some of the samples in this study were merged using this function.

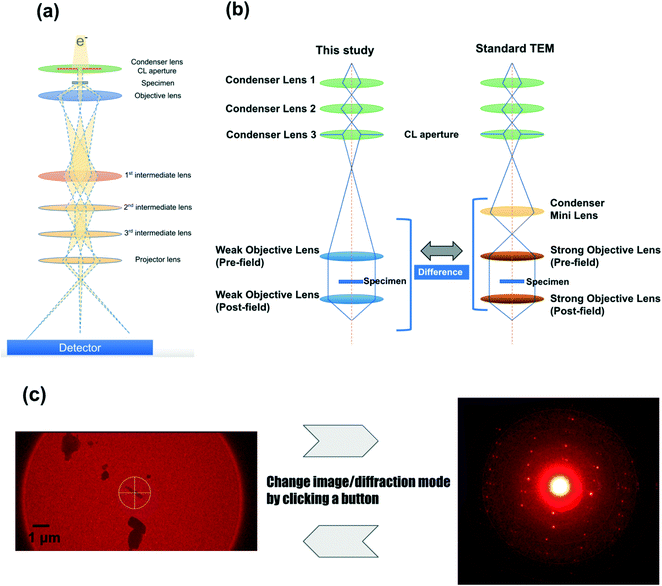Fig. 1 Electron diffractometer specifically designed for 3D ED/microED experiments (a) overall view of the lens system of the electron diffractometer used in this study. Although simplified in this figure, there are three condenser lenses and two objective lenses installed as shown in (b). (b) Differences in lens systems between this study and a standard TEM (c) CrysAlis^Pro for ED allows easy switching between the image mode and the diffraction mode. Finding the eucentric is performed in image mode, and then the crystal is irradiated with an electron beam in diffraction mode to confirm the crystallinity of the crystal. If diffraction is observed, data collection commences. Diffraction mode of CrysAlis^Pro for ED: The diffraction pattern of L-tyrosine is shown as an example. The diffraction spots were observed to 0.84 Å resolution (see also Table 1). Since the beam stop was not used in this study, a very intense white spot was observed in the center of the figure (primary beam).

Sample preparation and diffraction experiment

All compounds used in this study were purchased from Tokyo Chemical Industry Co., Ltd, FUJIFILM Wako Pure Chemical Corporation, or Nacalai Tesque. Table 1 summarizes compounds subjected to the structure determinations in this study. For all compounds except gefitinib, iron(II) phthalocyanine bis(pyridine) complex, diosgenin, and florasulam, purchased samples were used as received. Gefitinib and iron(II) phthalocyanine bis(pyridine) complex were measured from re-crystallized samples. Diosgenin and florasulam were crystallized directly on the grid (Fig. 2b). Specifically, 1 mg of the compound was dissolved in 500 μL of ethanol. Then, 1.5 μL of the solutions were added to each grid and left for 10 min to dry, producing microcrystals of the compounds. Equal amounts of TiO₂ rutile and anatase were mixed and deposited on a grid to determine if crystal polymorphs could be detected. The measurement process can be briefly described as follows (see also Fig. 2a): 1. Spread the microcrystals of the compound on a grid. A pair of microscope glass slides was used to crush the samples to reduce the grain size when the average crystal size was larger than 1 μm. Importantly, the thickness of the crystal is more important than its size. Even if the crystal size itself is large, it can be measured if the thickness (the distance through which the electron beam penetrates the crystal) is less than 1 μm. It is important to note that the optimal sample thickness depends on the type of compound; for organic molecules, less than 1 μm, for organometallic complexes, less than 500 nm, and for inorganic materials, less than 100 nm. However, any sample can be screened if the sample thickness is less than 1 μm. 2. Install the grid into the electron diffractometer. 3. Locate the crystals in imaging mode and find the eucentric position (a step known to X-ray crystallographers as centering). 4. Irradiate the crystal with an electron beam and measure the diffraction intensity by the rotation method.³⁵

Table 1 Data collection and refinement statistics

Compound	Gefitinib	D-Glucose	L-Tyrosine	1,3,5-Triphenylbenzene
Merged crystals	5	1	1	1
Resolution	12.87–0.98 (1.01–0.98)^a	15.27–0.90 (0.94–0.90)	21.59–0.837 (0.87–0.84)	20.24–1.00 (1.04–1.00)
Reflections	7301 (756)	1536 (170)	2546 (270)	3427 (374)
Unique reflections	2129 (208)	557 (65)	855 (87)	932 (96)
Unit cell	9.146(4), 9.990(5), 13.028(5)	5.177(2), 10.691(5), 15.272(7)	5.96(9), 7.09(14), 21.59(15)	7.8(5), 20.2(2), 11.5(2)
	93.78(4), 97.00(4), 101.72(4)
Space group	P1̄	P212121	P212121	Pna21
Completeness	83.0 (79.7)	73.5 (78.3)	85.2 (84.5)	80.9 (82.1)
I/sig(I)	19.30 (1.81)	13.12 (2.13)	27.57 (7.74)	6.86 (1.50)
Redundancy	3.4 (3.6)	2.8 (2.6)	3.0 (3.1)	3.7 (3.9)
R int	9.5 (59.0)	11.1 (41.4)	10.7 (31.8)	19.1 (59.0)
R pim	6.3 (35.2)	8.4 (33.5)	7.9 (21.2)	11.7 (34.1)
CC1/2	0.996 (0.660)	0.991 (0.368)	0.985 (0.730)	0.986 (0.546)
R 1	15.45	11.94	13.63	10.67
wR2	36.97	34.69	32.35	30.98
GooF	2.167	1.156	1.116	1.031

---

Compound	Finasteride	K 2 PtCl 4	Florasulam	Acetaminophen
Merged crystals	1	1	10	7
Resolution	26.77–0.95 (0.99–0.95)	7.07–0.84 (0.89–0.85)	9.59–0.95 (0.98–0.95)	11.99–0.90 (0.93–0.90)
Reflections	5375 (602)	423 (83)	12 142 (1341)	5392 (528)
Unique reflections	1418 (146)	113 (17)	1506 (152)	1303 (129)
Unit cell	6.66(19), 13.2(3), 26.77(12)	7.07(11), 4.16(16)	8.302(3), 10.025(6), 10.638(6)	7.344(5), 9.645(6), 12.087(7)
			115.25(6), 91.67(5), 95.51(4)	97.37(5)
Space group	P212121	P4/mmm	P1̄	P21/n
Completeness	82.8 (84.4)	84.3 (100.0)	77.5 (77.6)	99.4 (97.7)
I/sig(I)	14.42 (2.42)	43.95 (20.42)	14.48 (3.43)	22.38 (4.09)
Redundancy	3.8 (4.1)	3.7 (4.9)	8.1 (8.8)	4.1 (4.1)
R int	14.9 (59.0)	6.5 (12.0)	19.5 (64.1)	8.8 (37.8)
R pim	9.0 (31.5)	4.5 (6.1)	7.2 (21.8)	5.9 (21.0)
CC1/2	0.989 (0.450)	0.976 (0.970)	0.992 (0.570)	0.992(0.859)
R 1	13.51	16.52	16.02	12.02
wR2	30.83	44.66	37.69	33.94
GooF	1.086	3.167	2.269	1.074

---

Compound	Iron(II) phthalocyanine bis(pyridine) complex	2,4,6-Tri(4-pyridyl)-1,3,5-triazine	Cytidine
Merged crystals	4	3	1
Resolution	19.99–0.90 (0.93–0.90)	10.46–0.90 (0.93–0.90)	14.60–0.95 (0.98–0.95)
Reflections	14 611 (1541)	3614 (286)	2411 (270)
Unique reflections	2435 (251)	996 (95)	699 (72)
Unit cell	9.25(12), 19.99(19), 9.66(10)	13.507(10), 11.432(7), 11.114(9)	5.1(5), 13.8(3), 14.6(3)
	111.6(6)	109.81(7)
Space group	P21/c	C2/c	P212121
Completeness	98.0 (99.2)	81.0 (77.2)	87.7 (83.7)
I/sig(I)	8.37 (3.61)	29.16 (5.45)	5.11 (2.12)
Redundancy	6.0 (6.2)	3.6 (3.0)	3.4 (3.8)
R int	18.1 (42.5)	8.9 (32.2)	15.4 (48.9)
R pim	7.6 (17.3)	5.4 (23.6)	9.9 (28.9)
CC1/2	0.991 (0.881)	0.996 (0.878)	0.983 (0.655)
R 1	16.59	19.00	9.88
wR2	36.04	43.28	26.34
GooF	1.276	2.477	1.044

---

Compound	ZIF-8	Rubrene	Diosgenine (not deposited)
a Values in parentheses are for the highest resolution shell.
Merged crystals	1	1	3
Resolution	12.37–1.00 (1.05–1.00)	14.16–0.90 (14.16–0.90)	34.06–1.10 (1.14–1.10)
Reflections	2256 (290)	4535 (497)	20 271 (246)
Unique reflections	308 (38)	954 (101)	2004 (211)
Unit cell	17.497(5)	26.34(10), 7.03(10), 14.16(16)	7.6, 20.35, 34.06
Space group	I4̄3m	Cmce	P212121
Completeness	97.2 (100.0)	86.0 (84.9)	81.8 (85.8)
I/sig(I)	11.39 (1.41)	5.96 (2.57)	14.26 (3.79)
Redundancy	7.3 (7.6)	4.8 (4.9)	10.1 (11.0)
R int	20.8 (78.1)	18.6 (46.3)	20.9 (65.5)
R pim	8.7 (30.1)	9.4 (23.5)	7.3 (19.7)
CC1/2	0.993 (0.611)	0.983 (0.793)	0.989 (0.655)
R 1	11.37	9.20	21.2
wR2	31.36	24.52	52.43
GooF	1.089	1.111	1.862

---

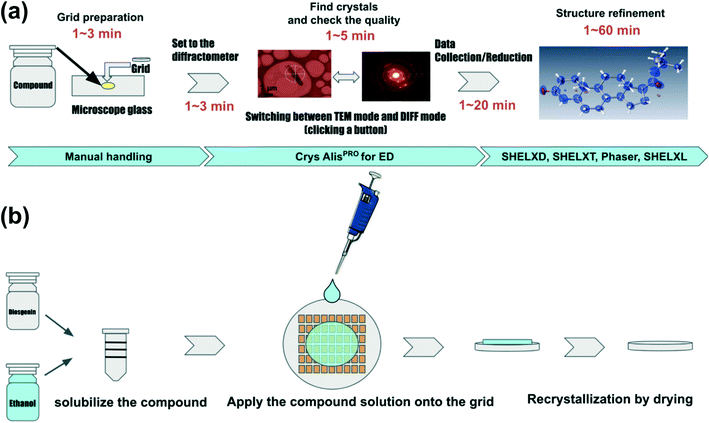Fig. 2 Flow of structural analysis by 3D ED/microED (a) flow from sample preparation to structural analysis. For samples with high crystallinity, the crystals are loaded directly into the grid. The amount of sample required is less than 1 mg, and the crystals are scattered on the grid by simply placing the grid on the crystals placed on a microscope glass. Instrument control, data acquisition, and data reduction are all performed by CrysAlis^Pro for ED. Phasing and refinement are performed in the conventional way used in X-ray crystallography. (b) Improvement of crystallinity by on-grid re-crystallization for samples with poor crystallinity, re-crystallization on-grid may improve the crystallinity. Dissolve the compound in some solution, load a few μL of the solution onto the grid, and dry the solution.

Diffraction experiment and structure analysis

A total of 14 compounds were measured using the electron diffractometer. The measured samples are listed in Table 1. Although all the measurements were performed at room temperature, the diffractometer was designed so that commercial Cryo-Transfer Holders could also be used. Therefore, low temperature measurements using liquid nitrogen and hydrates are also possible. For the electron beam, the accelerating voltage was set to 200 kV (corresponding to a wavelength of 0.0251 Å). Mechanically, the rotation range is −80 to +80 degrees. The rotation range required for the measurement depends on the symmetry of the crystal (crystallographic point group). Also, if the crystal to be measured is located near the grid frame, the rotation range may be reduced because the incident electron beam is blocked by the frame. In such a case, the dataset obtained from multiple crystals must be merged to improve the data completeness. The rotation range used for a typical measurement is −45° to +45°, 90° in total. The exposure time was set between 1 and 10 s so that the corresponding frame rate ranged between 0.1 Hz and 1.0 Hz.

To reduce the radiation damage to the crystals, the dose rate was set to ca. 0.01 e⁻ Å⁻² s⁻¹. For the rutile and anatase of TiO₂, only the determination of the unit cell (i.e., indexing) was performed. Intensity integration, scaling, and merging were performed by CrysAlis^Pro for ED. In the case of crystals with low symmetry, such as triclinic, multiple datasets were merged so that the data completeness exceeded 70%. Apart from diosgenin, the initial phases for each compound were determined by SHELXD or SHELXT.^18,19 For the determination of the initial phases of diosgenin, the molecular replacement program in Phaser was used with CCDC 1522829 as a search model. The structure refinement was performed by the full matrix least-squares method of SHELXL.²⁰ The SFAC instructions were used to input atomic scattering factors for electrons²¹ to replace those for X-rays.

Results and discussion

Crystal structures determined with the electron diffractometer

The results of structural analysis are shown in Table 1 and Fig. 3. All datasets were collected at least to 1.2 Å resolution. The resolution of 1.2 Å is derived from Sheldrick's rule^22,23 and is a threshold at which the initial phase determination by direct methods/intrinsic phasing method is likely to be successful. The statistics of all datasets were appropriate for 3D ED/microED data measurements. Multiple datasets were merged for gefitinib, iron(II) phthalocyanine bis(pyridine) complex, 2,4,6-tri(4-pyridyl)-1,3,5-triazine, 1,3,5-triphenylbenzene, acetaminophen, florasulam, and diosgenin to improve data completeness. The R_int and R_pim values did not deteriorate severely after data merging, suggesting not only high isomorphism of the crystals but also the high accuracy of the measurements from the diffractometer. The crystal with the lowest symmetry among the crystals measured in this study was the P1̄ of gefitinib. Five datasets were merged to increase the completeness of the data. After merging, the data completeness reached 86%, which appears to be sufficient to determine the initial phases for P1̄ crystals. On the other hand, for crystals such as D-glucose and L-tyrosine, which crystallize in the space group of P2₁2₁2₁ and K₂PtCl₄, tetragonal crystal, it was possible to collect datasets with completeness above 80% from one crystal. The results show that crystals belonging to a crystal system with higher symmetry than the orthogonal system can obtain sufficient completeness from one crystal. In addition, the anisotropic displacement parameter remained positive definite for all structures, which indicates that the data collection and refinement were performed successfully. The shortest time taken to load a sample on the grid and finish data collection was about 5 minutes, and even the most time-consuming compound took about 30 minutes. The sample holder used in this measurement can take only one grid at a time, therefore, the measurement can be further accelerated by using a sample holder that can store multiple grids at once. Importantly, two different unit cells were observed in the TiO₂ sample (Fig. 4), indicating that rapid measurement using 3D ED/microED is also effective in detecting polymorphism and quantitative analysis.

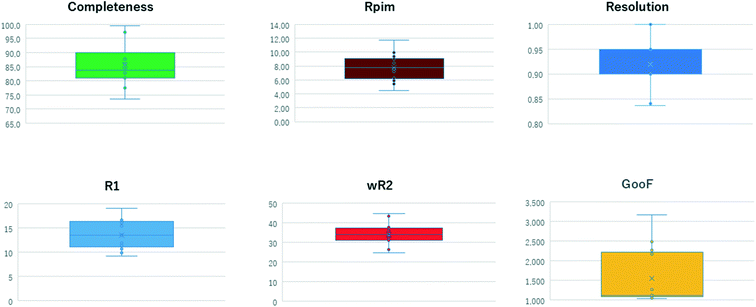Fig. 3 Distribution of statistical values of measured data.

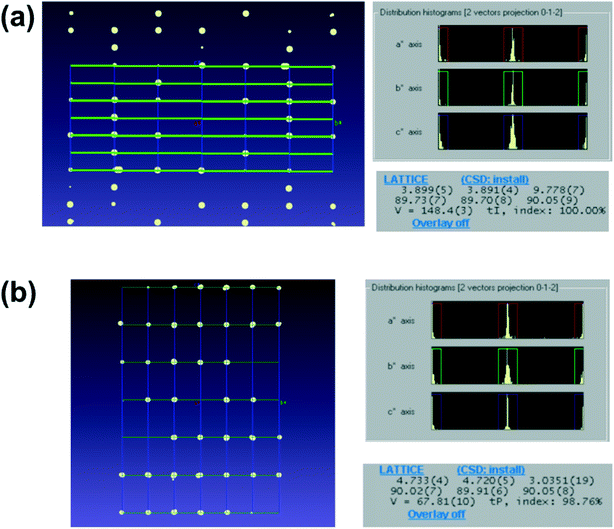Fig. 4 Detection of polymorphism in TiO₂ by comparing the unit cells it was confirmed that anatase and rutile microcrystals can be distinguished by 3D ED/microED. Distribution of reciprocal lattice points (a axis projection) and unit cell for (a) anatase and (b) rutile. In both (a) and (b), the diffraction spots are at the intersections of the unit cells represented by the grid points in the figures (left figures), therefore the indexings were probably correct. In addition, the unit cell of the two crystals was determined with very high index rates (100.0% and 97.86% respectively).

Small molecules structure determination with molecular replacement

Of the samples measured in this study, diosgenin was the only sample for which initial phases could not be determined by direct methods. About 80% of the macromolecular structures deposited in PDB have been determined by molecular replacement and several 3D ED/microED structures were determined by molecular replacement.²⁴ As a test of feasibility, we also investigated whether initial phases for diosgenin could be determined by the molecular replacement method. As a result, initial phases for diosgenin were determined successfully. As mentioned above, it is very difficult to determine the initial phases for datasets with a resolution lower than 1.2 Å by direct methods. On the other hand, datasets with moderate resolution, between 2.0 and 1.2 Å, are often observed. For small crystals of this quality, the molecular replacement method can be a very effective tool. Furthermore, single atom molecular replacement²⁵ may also be useful for initial phase determination when no crystal structure is available as a search model. For compounds whose structure has not been determined, even just obtaining the three dimensional structures of non-hydrogen atoms can be important information, so the molecular replacement method may come into use to determine the structure of small molecule compounds in the future.

Conclusions

In this paper, we demonstrated the usefulness of a newly developed, 3D ED/microED diffractometer by performing crystal structure analysis of several compounds. The ability to routinely measure diffraction data on crystals smaller than 1 μm is expected to accelerate structure determination for compounds that have not been determined by X-ray crystallography. As indicated by the two types of the unit cells of TiO₂ in this study, the crystal polymorphs can be easily detected by 3D ED/microED. This shows that 3D ED/microED will enable not only simple structure determination, but also analysis that is not possible with conventional powder X-ray diffraction. Quantitative analysis, such as identification of the trace amount of impurity, will also be widely performed with 3D ED/microED.¹³ In order to perform these experiments using 3D ED/microED routinely, it is essential to use a diffractometer such as the one we have developed in this study to perform the experiments. While 3D ED/microED has been shown to be a very powerful tool for structure determination, there are still some challenges to be overcome. The first point is the multiple scattering (also known as a dynamical effect) and reduction of intensity of the primary beam because electrons interact much stronger with materials than X-rays.²⁶ In fact, the crystal structures obtained in this study displayed poorer statistics compared to the general statistics obtained with X-rays. Even in the case of X-ray analysis, the dynamical effect becomes critical for highly ordered crystals. However, the primary and secondary extinction in X-ray diffraction is within the range correctable by assuming the extinction length, in particular using the EXTI instruction in SHELXL. The EXTI instruction was used for all the compounds in this study. However, since the dynamical effect in electron diffraction is quite large, the introduction of extinction length is insufficient to model dynamical diffraction. Palatinus et al. described a complex relationship between crystal orientation and thickness on the reflection intensity to correct for multiple scattering.²⁷ Furthermore, they introduced some special parameters and showed that multiple scattering can be successfully corrected. This method was implemented in PETS, DynGo, and Jana2006.^28,29 However, in the near future, we are planned to link CrysAlis^Pro ED and Jana2006. The second issue is the determination of absolute structure. In crystallography, absolute structures are determined by utilizing the violation of the Friedel rule, i.e., I(hkl) ≠ I(–h–k–l), which occurs in both X-ray and electron diffraction. However, in X-ray diffraction, this effect is caused by anomalous dispersion, whereas in electron diffraction, it is caused by multiple scattering. Therefore, to determine the absolute structure by electron diffraction, the effect of multiple scattering has to be accurately estimated in the structure refinement. In fact, Palatinus et al. and Brázda et al. showed that the absolute structure can be determined by comparing the R₁ values for the inverted and original structures resulting from the refinement that takes multiple scattering into account.^27,30 Although 3D ED/microED currently has these problems, this method will be widely used as a new option in addition to X-ray, NMR, MS, and other structure determination methods. In the near future, it will be routine for researchers to use X-ray crystallography for crystals above 1 μm, and 3D ED/microED for those below 1 μm, using these two techniques in a complementary manner for structural studies (Fig. 5).

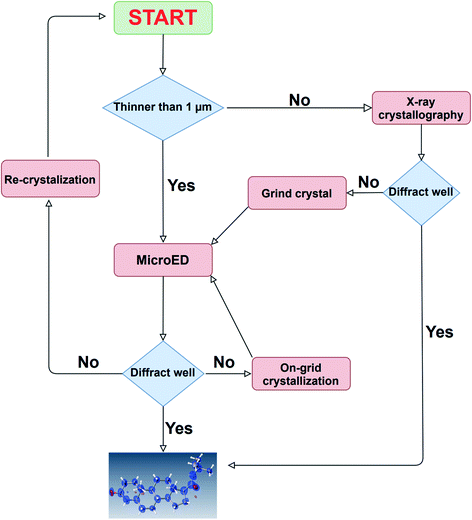Fig. 5 A comprehensive strategy for structure determination. In case the crystal size is large, structure determination is first attempted using the conventional method of X-ray crystallography. If the crystal size is too small, or if high resolution diffraction points cannot be obtained by X-ray diffraction, then 3D ED/microED is used to determine the structure. These two methods are used in a complementary manner to determine crystal structures.

Author contributions

S. I., F. J. W., E. O., Y. A., A. Y., H. S., J. D. F., M. J., and M. M. conceptualized the study. E. O. and Y. A. designed the electron diffractometer. M. J. and M. M. developed the software. S. I. and H. S. prepared the sample. S. I., F. J. W., A. Y., and H. S. determined the crystal structures. S. I. wrote the original draft. S. I. and M. M. supervised the study. S. I., F. J. W., E. O., Y. A., A. Y., H. S., J. D. F., M. J., and M. M. wrote, reviewed, and edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Drs. N. Muroyama, T. Matsumoto, T. Kikuchi, N. Wakui, and K. Yoshida for valuable comments and helpful discussions.

References

1. M. Hoshino, A. Khutia, H. Xing, Y. Inokuma and M. Fujita, The Crystalline Sponge Method Updated, IUCrJ, 2016, 3 DOI:10.1107/S2052252515024379.
2. Y. Inokuma, S. Yoshioka, J. Ariyoshi, T. Arai, Y. Hitora, K. Takada, S. Matsunaga, K. Rissanen and M. Fujita, X-Ray Analysis on the Nanogram to Microgram Scale Using Porous Complexes, Nature, 2013, 495(7442) DOI:10.1038/nature11990.
3. D. L. Dorset and H. A. Hauptman, Direct Phase Determination for Quasi-Kinematical Electron Diffraction Intensity Data from Organic Microcrystals, Ultramicroscopy, 1976, 1(3–4) DOI:10.1016/0304-3991(76)90034-6.
4. D. L. Dorset, Electron Crystallography, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52(5) DOI:10.1107/S0108768196005599.
5. T. E. Weirich, R. Ramlau, A. Simon, S. Hovmöller and X. Zou, A Crystal Structure Determined with 0.02 Å Accuracy by Electron Microscopy, Nature, 1996, 382(6587) DOI:10.1038/382144a0.
6. T. E. Weirich, X. Zou, R. Ramlau, A. Simon, G. L. Cascarano, C. Giacovazzo and S. Hovmöller, Structures of Nanometre-Size Crystals Determined from Selected-Area Electron Diffraction Data, Acta Crystallogr., Sect. A: Found. Crystallogr., 2000, 56(1) DOI:10.1107/S0108767399009605.
7. M. Gemmi, E. Mugnaioli, T. E. Gorelik, U. Kolb, L. Palatinus, P. Boullay, S. Hovmöller and J. P. Abrahams, 3D Electron Diffraction: The Nanocrystallography Revolution, ACS Cent. Sci., 2019, 5(8) DOI:10.1021/acscentsci.9b00394.
8. U. Kolb, T. Gorelik, C. Kübel, M. T. Otten and D. Hubert, Towards Automated Diffraction Tomography: Part I—Data Acquisition, Ultramicroscopy, 2007, 107(6–7) DOI:10.1016/j.ultramic.2006.10.007.
9. U. Kolb, T. Gorelik and M. T. Otten, Towards Automated Diffraction Tomography. Part II—Cell Parameter Determination, Ultramicroscopy, 2008, 108(8) DOI:10.1016/j.ultramic.2007.12.002.
10. U. Kolb, E. Mugnaioli and T. E. Gorelik, Automated Electron Diffraction Tomography - a New Tool for Nano Crystal Structure Analysis, Cryst. Res. Technol., 2011, 46(6) DOI:10.1002/crat.201100036.
11. D. Shi, B. L. Nannenga, M. G. Iadanza and T. Gonen, Three-Dimensional Electron Crystallography of Protein Microcrystals, Elife, 2013, 2 DOI:10.7554/elife.01345.
12. M. R. Sawaya, J. Rodriguez, D. Cascio, M. J. Collazo, D. Shi, F. E. Reyes, J. Hattne, T. Gonen and D. S. Eisenberg, Ab Initio Structure Determination from Prion Nanocrystals at Atomic Resolution by MicroED, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(40) DOI:10.1073/pnas.1606287113.
13. C. G. Jones, M. W. Martynowycz, J. Hattne, T. J. Fulton, B. M. Stoltz, J. A. Rodriguez, H. M. Nelson and T. Gonen, The CryoEM Method MicroED as a Powerful Tool for Small Molecule Structure Determination, ACS Cent. Sci., 2018, 4(11) DOI:10.1021/acscentsci.8b00760.
14. J. Hattne, F. E. Reyes, B. L. Nannenga, D. Shi, M. J. De La Cruz, A. G. W. Leslie and T. Gonen, MicroED Data Collection and Processing, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71 DOI:10.1107/S2053273315010669.
15. B. L. Nannenga, MicroED Methodology and Development, Struct. Dyn., 2020, 7(1) DOI:10.1063/1.5128226.
16. D. Shi, B. L. Nannenga, M. J. De La Cruz, J. Liu, S. Sawtelle, G. Calero, F. E. Reyes, J. Hattne and T. Gonen, The Collection of MicroED Data for Macromolecular Crystallography, Nat. Protoc., 2016, 11(5) DOI:10.1038/nprot.2016.046.
17. L. J. Kim, M. Xue, X. Li, Z. Xu, E. Paulson, B. Mercado, H. M. Nelson and S. B. Herzon, Structure Revision of the Lomaiviticins, J. Am. Chem. Soc., 2021, 143(17) DOI:10.1021/jacs.1c01729.
18. T. R. Schneider and G. M Sheldrick, Substructure Solution with SHELXD, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2002, 58(10 I) DOI:10.1107/S0907444902011678.
19. G. M. Sheldrick, SHELXT - Integrated Space-Group and Crystal-Structure Determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71(1) DOI:10.1107/S2053273314026370.
20. G. M. Sheldrick, Crystal Structure Refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71 DOI:10.1107/S2053229614024218.
21. L. M. Peng, Electron Atomic Scattering Factors and Scattering Potentials of Crystals, Micron., 1999 DOI:10.1016/S0968-4328(99)00033-5.
22. G. M. Sheldrick, Phase Annealing in SHELX-90: Direct Methods for Larger Structures, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46(6) DOI:10.1107/S0108767390000277.
23. R. J. Morris and G. Bricogne, Sheldrick's 1.2 Å Rule and Beyond, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2003, 59(3) DOI:10.1107/S090744490300163X.
24. A. J. McCoy, R. W. Grosse-Kunstleve, P. D. Adams, M. D. Winn, L. C. Storoni and R. J. Read, Phaser Crystallographic Software, J. Appl. Crystallogr., 2007, 40(4) DOI:10.1107/S0021889807021206.
25. A. J. McCoy, R. D. Oeffner, A. G. Wrobel, J. R. M. Ojala, K. Tryggvason, B. Lohkamp and R. J. Read, Ab Initio Solution of Macromolecular Crystal Structures without Direct Methods, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(14) DOI:10.1073/pnas.1701640114.
26. R. Uyeda, Dynamical Effects in High-voltage Electron Diffraction, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1968, 24(1) DOI:10.1107/S0567739468000240.
27. L. Palatinus, V. Petříček and C. A. Correâ, Structure Refinement Using Precession Electron Diffraction Tomography and Dynamical Diffraction: Theory and Implementation, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71 DOI:10.1107/S2053273315001266.
28. V. Petrícek, M. Dušek and L. Palatinus, Crystallographic Computing System JANA2006: General Features, Z. Kristallogr., 2014 DOI:10.1515/zkri-2014-1737.
29. L. Palatinus, PETS-Program for Analysis of Electron Diffraction Data, Inst. Phys. AS CRPrague, Czechia, 2011.
30. P. Brázda, L. Palatinus and M. Babor, Electron Diffraction Determines Molecular Absolute Configuration in a Pharmaceutical Nanocrystal, Science, 2019, 364(6441) DOI:10.1126/science.aaw2560.
31. K. D. M. Harris and M. Tremayne, Crystal Structure Determination from Powder Diffraction Data, Chem. Mater., 1996 DOI:10.1021/cm960218d.
32. W. I. F. David, Extending the Power of Powder Diffraction for Structure Determination, Nature, 1990, 346(6286) DOI:10.1038/346731a0.
33. H. M. Rietveld, A Profile Refinement Method for Nuclear and Magnetic Structures, J. Appl. Crystallogr., 1969, 2(2) DOI:10.1107/s0021889869006558.
34. C. J. Gilmore, K. Shankland and G. Bricogne, Applications of the Maximum Entropy Method to Powder Diffraction and Electron Crystallography, Proc. R. Soc. London, Ser. A, 1993, 442(1914) DOI:10.1098/rspa.1993.0093.
35. W. Kabsch, The Rotation Method in Crystallography Edited by U. W. Arndt and A. J. Wonacott, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34(3) DOI:10.1107/s0567740878004896.

---

Footnote

† CCDC 2097594–2097606. For crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ce01172c

---