Molecular understanding for large deformations of soft bottlebrush polymer networks†
Li-Heng
Cai

Department of Materials Science and Engineering, Department of Chemical Engineering, Department of Biomedical Engineering, School of Engineering and Applied Science, University of Virginia, Wilsdorf Hall 228, 395 McCormick Road, Charlottesville, VA 22904, USA. E-mail: liheng.cai@virginia.edu; Fax: +1-434-982-5660; Tel: +1-434-924-2512
First published on 9th June 2020
Abstract
Networks formed by crosslinking bottlebrush polymers are a class of soft materials with stiffnesses matching that of ‘watery’ hydrogels and biological tissues but contain no solvents. Because of their extreme softness, bottlebrush polymer networks are often subject to large deformations. However, it is poorly understood how molecular architecture determines the extensibility of the networks. Using a combination of experimental and theoretical approaches, we discover that the yield strain γy of the network equals the ratio of the contour length Lmax to the end-to-end distance R of the bottlebrush between two neighboring crosslinks: γy = Lmax/R − 1. This relation suggests two regimes: (1) for stiff bottlebrush polymers, γy is inversely proportional to the network shear modulus G, γy ∼ G−1, which represents a previously unrecognized regime; (2) for flexible bottlebrush polymers, γy ∼ G−1/2, which recovers the behavior of conventional polymer networks. Our findings provide a new molecular understanding of the nonlinear mechanics for soft bottlebrush polymer networks.
In a bottlebrush polymer, a long linear backbone is densely grafted by many relatively short linear side chains.1 Analogous to “sausage versus spaghetti”, a bottlebrush polymer is essentially a type of ‘fat’ linear polymer, but with an entanglement molecular weight (MW) much higher than that of linear polymers. Compared to conventional elastomers formed by crosslinking linear polymers, networks formed by crosslinking bottlebrush polymers are often free of entanglements.2,3 Thus, the stiffness of bottlebrush elastomers is solely determined by the concentration of crosslinks. Because the MW of a bottlebrush polymer can be very large, the concentration of crosslinks can be very low; this results in networks with stiffnesses orders of magnitude lower than that of conventional elastomers. As such, in addition to the most commonly seen hydrogels,4–6 bottlebrush elastomers present a new class of soft materials with stiffnesses matching that of most ‘watery’ biological tissues and cells.7 Unlike hydrogels that contain a large number of water molecules that can leach out and thus deteriorate materials properties, bottlebrush elastomers are ‘solvent-free’.3,9 Moreover, the extreme softness allows bottlebrush elastomers to be easily deformed to a large extent under small mechanical stresses. The exceptional combination of softness and deformability enables potential applications of soft bottlebrush elastomers in ultrasensitive sensors,10 dielectric elastomer actuators,11,12 stretchable electronics,8,13 and soft robotics.14 Yet, these applications would require materials with mechanical properties tailor-designed for specific needs, which often involve large deformations. It is therefore critical to be able to predict how the molecular architecture of bottlebrush polymer networks determines their macroscopic mechanical properties at large deformations.
Two key parameters, stiffness and extensibility, can be used to describe the mechanical properties of soft bottlebrush polymer networks. The equilibrium shear modulus presents the linear mechanical properties of soft bottlebrush elastomers. It is well-described by the classic phantom network model that the modulus is kBT per volume of an elastically effective network strand.2 By contrast, the extensibility describes the nonlinear mechanical behavior, which is dependent on both the rate and the extent of deformation. In most experiments, however, these two parameters are inevitably coupled, which poses challenges in the development of molecular understanding for nonlinear mechanics. Consequently, it remains to be elucidated the molecular origin for the behavior of soft bottlebrush elastomers under large deformations.
Here, we use a combination of experimental and theoretical approaches to study the behavior of soft bottlebrush elastomers at large deformations. Exploiting recently developed poly(dimethyl siloxane) (PDMS) bottlebrush elastomers as a model system,2 we use large amplitude oscillatory shear (LAOS)15 to quantify the quasi-equilibrium shear yield strain for networks with stiffnesses ranging two orders of magnitude from 1 to 100 kPa. Experimentally, we discover a new regime in which the yield strain γy is inversely proportional to the stiffness G: γy ∼ G−1. This is qualitatively different from what has been reported: for conventional networks formed by crosslinking linear polymers, γy ∼ G−1/2; for networks formed by end-crosslinking loosely grafted comb-like polymers, γy ∼ G−1/3; for networks formed by end-crosslinking densely grafted bottlebrush polymer, γy ∼ G1/4.16,17 Remarkably, our experimental observation can be quantitatively explained by a molecular theory: the yield strain equals the ratio of the contour length, Lmax, to the end-to-end distance, R, of the bottlebrush between two neighboring crosslinks: γy = Lmax/R − 1. This theory predicts two regimes: for stiff bottlebrush polymers, γy ∼ G−1, which captures our experimental observation; whereas for flexible bottlebrush polymers, γy ∼ G−1/2, which recovers the behavior of conventional networks. Our findings reveal a new molecular understanding in mechanics of soft bottlebrush elastomers under large deformations, and therefore, provide insights in the design of soft bottlebrush elastomers with prescribed nonlinear mechanical properties.
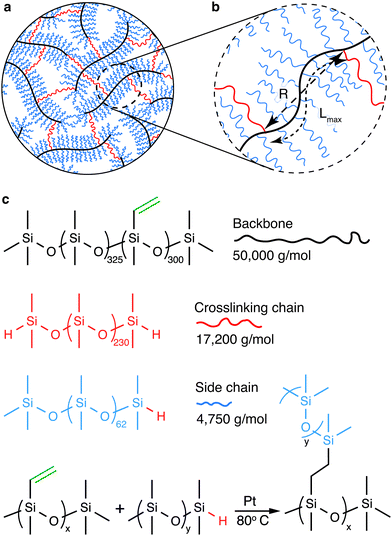
The mechanical properties of polymer networks and gels are known to be sensitive to their preparation condition.18–20 To this end, we explore a model system in which the bottlebrush elastomers are prepared without chemical solvents. In our study, the bottlebrush PDMS elastomers are formed by chemically crosslinking three types of precursor linear PDMS polymers: backbone, side chain, and crosslinking chain (Fig. 1a, b and ESI,† Materials and Methods). The backbone is a long linear PDMS of a MW 50 000 g mol−1 and carries about 300 vinyl groups, the side chain is a short linear PDMS with a MW 4750 g mol−1 and carries a hydride group at one of its two ends, and the crosslinking chain is a relatively long linear PDMS with a MW 17 200 g mol−1 and carries a hydride group at both ends (Fig. 1c and Fig. S1, ESI†). The reaction between vinyl and hydride groups allows the formation of the bottlebrush elastomers (Fig. 1c). Importantly, the MW of the crosslinking chain is about 4 times of the side chain, such that its end-to-end distance is about twice of the side chain in a melt. This ensures that the crosslinking chain is long enough to bridge two neighboring backbone molecules without being pre-stretched. Moreover, the short linear PDMS act as an effective solvent to facilitate the reaction. However, once reacted, they are chemically attached to the backbone, becoming part of the network and do not have to be removed. Therefore, the formation of the bottlebrush PDMS elastomers is a one-step, solvent-free process, such that all polymers are in a melt, where linear chains adopt the same ideal chain conformation before and after network formation. This contrasts with bottlebrush elastomers that must be crosslinked in the presence of small solvent molecules and the subsequent removal of the solvents, which would result in the change of polymer chain conformation compared to the preparation state. Thus, the bottlebrush PDMS elastomers provide an ideal model system for investigating the deterministic relation between molecular architecture and macroscopic mechanical properties.
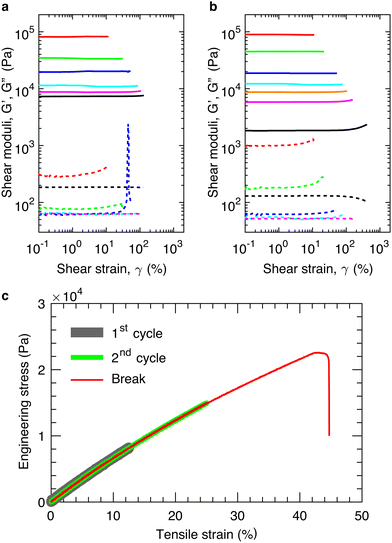
We cure in situ the mixture of precursor linear chains at 80 °C for >40 hours to ensure the complete crosslinking of the bottlebrush PDMS elastomers (see ESI,† Materials and Methods). We perform LAOS measurements at an oscillatory shear frequency of 1 rad s−1 to determine the shear yield strain, γy, at above which the loss modulus, G′′, becomes larger than the storage modulus, G′, as denoted by the arrow in Fig. 2a. Below γy, the elastomers deform elastically without strain stiffening, as evidenced by the nearly constant shear storage moduli (solid lines in Fig. 2a). Above γy, the elastomers fracture rather than being further elongated, as evidenced by the vanished shear moduli (lines in Fig. 2a). These indicate that the elastomers are brittle. Indeed, cyclic tensile tests reveal that the materials are elastic, non-dissipative; the loading and unloading stress–strain curves nearly perfect overlap, and this overlap applies not only to strain rates ranging from 1.67 × 10−3 to 1.67 × 10−1 s−1 (Fig. S2, ESI†) but also to different extents of strain (thick and medium lines in Fig. 2c). Moreover, for elastomers of similar stiffness, the strain at break measured by the tensile test is nearly the same as the shear yield strain measured by the LAOS (red, thin line in Fig. 2c). Therefore, for the elastic, non-dissipative bottlebrush networks, in addition to the elongation at break measured by tensile test, the shear yield strain provides an alternative describing the extensibility of elastomers.
Importantly, in the LAOS measurements, the samples are cured in situ, enabling a seamless contact between the samples and the geometry of the rheometer, and thereby avoiding possible error due to sample preparation and loading. Moreover, the shear frequency is relatively low of 1 rad s−1, corresponding to a time scale of 6 s; and each data point at certain strain is collected over the period of 30 s. These time scales are longer than the relaxation time of the polymers in the bottlebrush elastomers.2 Such measurements prevent strain-rate dependent mechanical behavior common to polymer networks,21,22 enabling us to focus on the behavior of the elastomers under a quasi-equilibrium, large amplitude shear.
To explore the relation between the network modulus and the yield strain, we tune the modulus by varying the number fraction of crosslinking chains while keeping constant the molar ratio between vinyl and hydride groups at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 using a previously reported procedure.2 Doing so keeps a constant the grafting density of the bottlebrush polymers, preventing the decrease of bottlebrush flexibility due to the increased grafting density. By decreasing the equilibrium shear modulus, G, of the network from nearly 100 kPa to 10 kPa, we find that the yield strain increases from 0.1 to 1.3, as shown in Fig. 2a. To further test this finding, we use another set of precursor polymers to lower the modulus by one order of magnitude to ∼1 kPa, at which the yield strain increases to 4, as shown in Fig. 2b. Both measurements are consistent with the classical understanding that the extensibility of an elastic, non-dissipative network increases with network strand size, which decreases with the modulus.
1 using a previously reported procedure.2 Doing so keeps a constant the grafting density of the bottlebrush polymers, preventing the decrease of bottlebrush flexibility due to the increased grafting density. By decreasing the equilibrium shear modulus, G, of the network from nearly 100 kPa to 10 kPa, we find that the yield strain increases from 0.1 to 1.3, as shown in Fig. 2a. To further test this finding, we use another set of precursor polymers to lower the modulus by one order of magnitude to ∼1 kPa, at which the yield strain increases to 4, as shown in Fig. 2b. Both measurements are consistent with the classical understanding that the extensibility of an elastic, non-dissipative network increases with network strand size, which decreases with the modulus.
The data sets from the two independent experiments agree well with each other, as shown by the circles and squares in Fig. 3. Surprisingly, the yield strain appears to be inversely proportional to the shear modulus, G ∼ γy−1, as shown by the dashed line in Fig. 3. This is qualitatively different from recently reported experimental studies, which suggest that for conventional networks formed by crosslinking linear polymers G ∼ γy−2 and for bottlebrush elastomers G ∼ γy−3.16
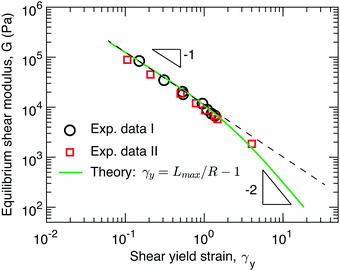 | ||
| Fig. 3 Dependence of stiffness on yield strain. The symbols are experimental data points extracted from Fig. 2a (circles) and Fig. 2b (squares). Solid line: theoretical prediction for the dependence of network stiffness G on the shear yield strain γy calculated based on γy = Lmax/R − 1 (eqn (1)), where both Lmax and R are determined by the G (eqn (2), (3), (9), and (11)). | ||
To understand these controversial findings, we propose a theory that the elastomers yield when the bottlebrush polymer between two neighboring crosslinks is stretched to its contour length, Lmax:
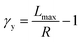 | (1) |
| Lmax = nscl | (2) |
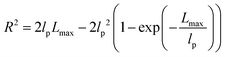 | (3) |
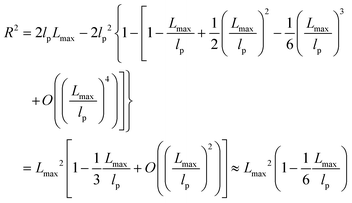 | (4) |
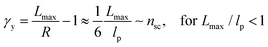 | (5) |
| R2 ≈ 2lpLmax − 2lp2 ≈ 2lpLmax | (6) |
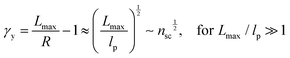 | (7) |
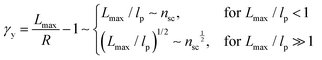 | (8) |
The shear yield strain (eqn (8)) describes the maximum extent to which the backbone of a network strand can be stretched. This physical picture is also described as the locking strain of a polymer chain under tension, which is a term introduced by Arruda and Boyce in a continuum mechanics model for large deformations of elastomers.23 Yet, in bottlebrush elastomers, the network strand is not a simple linear chain but a more complex bottlebrush polymer, in which the dangling side chains cannot sustain stress and are not elastically effective; and only the backbone of the bottlebrush is elastically effective. Importantly, here Lmax is not the contour length of a whole bottlebrush, but the contour length of a section of the bottlebrush between two neighboring crosslinks, as schematically shown by the section between the two red lines in Fig. 1b.
For the regime Lmax/lp ≫ 1, the section of the bottlebrush molecule becomes a ‘fat’ yet flexible linear polymer. For the regime Lmax/lp < 1, it indicates that the section has a contour length smaller than the size of the side chain while maintaining a bottlebrush molecular architecture. This would not be possible if the section is not part of a large bottlebrush polymer, at which the side chains tend to occupy the space near the two ends of the polymer backbone, resulting in a star-like molecular architecture.24,25 Therefore, the approximations for eqn (8) are physically meaningful and are applicable to the soft bottlebrush elastomers.
The value of nsc is directly related to the network modulus. Because the network is unentangled, its shear modulus is kBT per volume, V, of the bottlebrush section between two neighboring crosslinks: G = kBT/V. Here it is neglected the correction to stiffness from the fluctuation of network junctions, which is inversely proportional to the crosslinking functionality and is much smaller than one.2 The contribution to the MW of the bottlebrush polymer is predominately from long side chains, and therefore: V = M0nscNsc/(ρNAv), where M0 is the molar mass of a Kuhn monomer, Nsc is the number of Kuhn monomers per side chain, ρ is the density of the polymer, and NAv is the Avogadro number. As a result, the number of side chains per bottlebrush polymer is related to the network shear modulus by:
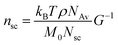 | (9) |
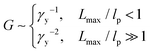 | (10) |
The yield strain (eqn (1)) can be precisely calculated provided with Lmax and R: Lmax can be determined from the measured network modulus (eqn (2) and (9)), and R can be calculated provided the persistence length (eqn (3)). The persistence length of a densely grafted bottlebrush is determined by its molecular architecture. Consider a bottlebrush formed by nsc side chains of Nsc Kuhn monomers each. The side chains are densely grafted to a backbone polymer, occupying a cylindrical space surrounding the backbone. The cross-section size of the cylindrical space is about the size Rsc of a side chain. Within such a cylindrical space, a side chain occupies a volume, Rsc2l, that is the product of the cross-section area Rsc2 and the distance between two neighboring grafting sites l. This volume is equal to the volume of a side chain itself, Nscv0, in which v0 is the volume of a Kuhn monomer and Nsc is the number of Kuhn monomers per side chain. Therefore, the cross-section size of the bottlebrush is Rsc ≈ (Nscv0/l)1/2. The persistence length of the bottlebrush polymer is about its cross-section size,
| lp = β(Nscv0/l)1/2 | (11) |
In summary, we use a combination of experimental and theoretical approaches to study the behavior of soft bottlebrush networks under large deformations. We experimentally discover a previously unrecognized regime in which the yield strain is inversely proportional to the network stiffness. This relation is qualitatively different from that recently reported by experimental and computer simulation studies.17,21 Moreover, the extensibility of the bottlebrush elastomers is quantitatively explained by a molecular theory that the yield strain, γy, is equal to the ratio of the contour length, Lmax, to the end-to-end distance, R, of the bottlebrush between two neighboring crosslinks: γy = Lmax/R − 1. The ratio Lmax/R is correlated to the macroscopic network shear modulus G: for stiff bottlebrush polymers, γy ∼ G−1; whereas for flexible bottlebrush polymers, γy ∼ G−1/2. Our studies provide a new molecular understanding for the large deformations of soft bottlebrush polymers networks, which will enable the development of soft, stretchable, and solvent-free materials with nonlinear mechanical properties tailor-designed for specific applications.8,10–14
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation through DMR-1944625. The authors are indebted to stimulating discussions with Dr. Jian Qin at Stanford University, and thank Dr. Shifeng Nian, Zihao Gong, and Zhijian He for proof-reading the manuscript.Notes and references
- J. Paturej, S. S. Sheiko, S. Panyukov and M. Rubinstein, Sci. Adv., 2016, 2, 1601478 CrossRef PubMed.
- L. H. Cai, T. E. Kodger, R. E. Guerra, A. F. Pegoraro, M. Rubinstein and D. A. Weitz, Adv. Mater., 2015, 27, 5132–5140 CrossRef CAS PubMed.
- W. F. M. M. Daniel, J. Burdyńska, M. Vatankhah-Varnoosfaderani, K. Matyjaszewski, J. Paturej, M. Rubinstein, A. V. Dobrynin and S. S. Sheiko, Nat. Mater., 2016, 15, 183–189 CrossRef CAS PubMed.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155 CrossRef CAS.
- J.-Y. J.-Y. Y. Sun, X. H. Zhao, W. R. K. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. G. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- C. Creton, Macromolecules, 2017, 50, 8297–8316 CrossRef CAS.
- I. Levental, P. C. Georges and P. A. Janmey, Soft Matter, 2007, 3, 1–9 RSC.
- S. Wang, J. Xu, W. Wang, G.-J. N. J. N. Wang, R. Rastak, F. Molina-Lopez, J. W. Chung, S. Niu, V. R. Feig, J. Lopez, T. Lei, S.-K. K. Kwon, Y. Kim, A. M. Foudeh, A. Ehrlich, A. Gasperini, Y. Yun, B. Murmann, J. B.-H. B. H. Tok and Z. Bao, Nature, 2018, 555, 83–88 CrossRef CAS PubMed.
- S. Nian, H. Lian, Z. Gong, M. Zhernenkov, J. Qin and L.-H. Cai, ACS Macro Lett., 2019, 8, 1528–1534 CrossRef CAS.
- V. G. Reynolds, S. Mukherjee, R. Xie, A. E. Levi, A. Atassi, T. Uchiyama, H. Wang, M. L. Chabinyc and C. M. Bates, Mater. Horiz., 2020, 7, 181–187 RSC.
- R. Pelrine, R. Kornbluh, Q. Pei and J. Joseph, Science, 2000, 287, 836–839 CrossRef CAS PubMed.
- X. Zhao and Z. Suo, J. Appl. Phys., 2008, 104, 123530 CrossRef.
- J. A. Rogers, T. Someya and Y. Huang, Science, 2010, 327, 1603–1607 CrossRef CAS PubMed.
- D. Rus and M. T. Tolley, Nature, 2015, 521, 467–475 CrossRef CAS PubMed.
- K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697–1753 CrossRef CAS.
- M. Vatankhah-Varnosfaderani, W. F. M. Daniel, M. H. Everhart, A. A. Pandya, H. Liang, K. Matyjaszewski, A. V. Dobrynin and S. S. Sheiko, Nature, 2017, 549, 497–501 CrossRef PubMed.
- H. Liang, S. S. Sheiko and A. V. Dobrynin, Macromolecules, 2018, 51, 638–645 CrossRef CAS.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, UK, 2003 Search PubMed.
- Y. Li and T. Tanaka, Annu. Rev. Mater. Sci., 1992, 22, 243–277 CrossRef CAS.
- T. Van Vliet and P. Walstra, Faraday Discuss., 1995, 101, 359–370 RSC.
- J. Wu, L. H. Cai and D. A. Weitz, Adv. Mater., 2017, 29, 1702616 CrossRef PubMed.
- E. M. Arruda and M. C. Boyce, J. Mech. Phys. Solids, 1993, 41, 389–412 CrossRef CAS.
- G. Polymeropoulos, G. Zapsas, K. Ntetsikas, P. Bilalis, Y. Gnanou and N. Hadjichristidis, Macromolecules, 2017, 50, 1253–1290 CrossRef CAS.
- K. Inoue, Prog. Polym. Sci., 2000, 25, 453–571 CrossRef CAS.
- C. A. Helfer and W. L. Mattice, in Physical Properties of Polymers Handbook, ed. J. E. Mark, Springer, New York, NY, 2nd edn, 2007, pp. 43–57 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00759e |
| This journal is © The Royal Society of Chemistry 2020 |