Open Access Article
Open Access ArticleThe effect of structural heterogeneity upon the microviscosity of ionic liquids†
Ryan
Clark
 a,
Mohd A.
Nawawi
a,
Ana
Dobre
a,
David
Pugh
ab,
Qingshan
Liu
ac,
Aleksandar P.
Ivanov
a,
Mohd A.
Nawawi
a,
Ana
Dobre
a,
David
Pugh
ab,
Qingshan
Liu
ac,
Aleksandar P.
Ivanov
 a,
Andrew J. P.
White
a,
Andrew J. P.
White
 a,
Joshua B.
Edel
a,
Joshua B.
Edel
 a,
Marina K.
Kuimova
a,
Marina K.
Kuimova
 a,
Alastair J. S.
McIntosh
a,
Alastair J. S.
McIntosh
 a and
Tom
Welton
a and
Tom
Welton
 *a
*a
aDepartment of Chemistry, Molecular Science Research Hub, Imperial College London, 80 Wood Lane, London, W12 0BZ, UK. E-mail: t.welton@imperial.ac.uk
bDepartment of Chemistry, Kings College London, Britannia House, 7 Trinity Street, London, SE1 1DB, UK
cSchool of Science, Shenyang Agricultural University, Shenyang 110866, P. R. China
First published on 27th May 2020
Abstract
The behaviour of two molecular rotors, one charged – 3,3′-diethylthiacarbocyanine iodide (Cy3) and one neutral – 8-[4-decyloxyphenyl]-4,4-difluoro-4-bora-3a,4a-diaza-s-indacene (BODIPY-C10), have been studied in various ionic liquids. The fluorescent decay lifetime has been used to elucidate the structure of the immediate region around the rotor. The neutral BODIPY-C10 was found to prefer the non-polar alkyl chain environment, leading to two trends in the lifetime of the dye: one when it was fully partitioned into the non-polar domain, and one when it also sampled polar moieties. The positively charged Cy3 dye showed a complex relationship between the bulk viscosity of the ionic liquid and lifetime of the molecular rotor. This was attributed to a combination of polarity related spectral changes, changes in anion cages around the dye, and temperature dependent fluorescent lifetimes alongside the dependence of the rotor upon the viscosity.
1 Introduction
Ionic liquids are a family of salts that are liquid at room temperature.1,2 Most of these being non-flammable, having very low volatility, relatively high conductivity and wide electrochemical windows has made ionic liquids suitable candidates as solvents for synthesis,2 and as electrolytes in a wide range of electrochemical devices and processes, such as energy generation and storage,3,4 metal deposition5 and electrochemical sensors.6 While ionic liquids have many attractive properties, in many of these applications their high viscosities pose a problem; this has led to many studies of the viscosities of ionic liquids.7Molecular rotors are a group of fluorescent compounds with a bond around which rotation in the excited state can lead to non-radiative decay. This occurs because twisting around the coordinate brings the energies of the excited and ground states closer together (Fig. 1). This allows fast relaxation to the ground state to occur without the emission of a photon of visible light, and thus reduces the lifetime of the dye in the excited state. The ability of the rotor to twist around this coordinate is dictated by the viscosity of the immediate solvent environment (cybotactic region), which leads to the fluorescence lifetime of these dyes being sensitive to the viscosity of the medium in which they are studied.8,9
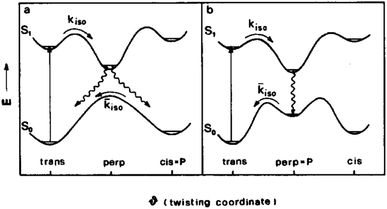 | ||
| Fig. 1 Model potential energy diagram showing the two possible modes of decay of a molecular rotor by twisting around a coordinate. (a) Corresponds to the more common scenario of a spontaneous isomerisation after relaxation, (b) corresponds to the rare scenario where the ground state has a metastable perpendicular isomer. Figure reprinted from F. Momicchioli, I. Baraldi and G. Berthier, Chem. Phys., 1988, 123, 103–112 (ref. 10) with permission, copyright Elsevier. | ||
With suitable calibration, molecular rotors can be used to measure the local viscosity of the cybotactic region – its microviscosity. The standard for calibrations of molecular rotors is to measure the lifetime of the rotor in solutions with a range of different viscosities. These are usually made up of sugars in a solvent, where the concentration of the sugar is used to modify the viscosity of the solution. The lifetime data obtained in this way is then usually fitted to the Förster–Hoffmann equation9,11
log10(τ) = C + m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(η) log10(η) | (1) |
A number of molecular rotors have been applied to the measurement of the microviscosities of ionic liquids.13–16 When the microviscosities, determined by reference to calibrations conducted in molecular solutions, were compared to the bulk viscosities of the ionic liquids determined by rheometry, complex relationships were observed.
Measurements of the photoluminescence quantum yields of the molecular rotor 1,1-dimethyl-2,3,4,5-tetraphenylsilole in [C4C1im][BF4], [C4C1im][PF6] or [C8C1im][BF4] predicted lower viscosities than directly measured by viscometry using common calibrations.13 For Thioflavin-T in [C2C1im][FAP] or [(HO)2C2C1im][FAP] (FAP = tris(pentafluoroethyl)trifluorophosphate)14 and for 9-(dicyanovinyl)julolidine in [C2C1im][NTf2], [C4C1im][NTf2], [(OH)2C2C1im][NTf2], [C2C1im][EtSO4], [C4C1im][BF4] or [(OH)2C2C1im][BF4] the fluorescence measurements predicted higher viscosities than rheometric measurements (although in this study this was reversed for [C2C1im][PF6]).15 Other reports also describe the relationship between fluorescence spectra of molecular rotors and the viscosity measured by rheometry as complex.16 This behaviour is generally ascribed to the effects of microheterogeneity and/or to the existence of free volume around the rotor, perhaps with some contribution from direct solvent–solute interactions.
Microheterogeneity in ionic liquids is a well-studied phenomenon, both theoretically and experimentally.17 It is known that ionic liquids have two domains, a polar domain containing the charged and polar moieties of both the ions, and a non-polar domain containing uncharged non-polar moieties.
For [CnC1im][NTf2] it has been shown that for n < 6 the alkyl chains aggregate to isolated non-polar domains within a continuous ionic phase. As the length of the alkyl chain increases, these non-polar domains increase in size, contain more alkyl chains and become more oblate; by [C6C1im][NTf2] these mostly join to form extended non-polar aggregates and for n ≥ 7 a continuous non-polar domain is a constant feature of the structure.18–20
Phosphonium-based ionic liquids are less well studied, but it is generally understood that they also contain interpenetrating polar and non-polar domains that become more segregated as the alkyl chain length increases.21
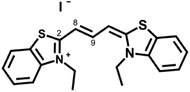
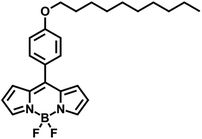
It has also been shown that the non-polar domains present a more fluid environment than the polar domains.22 Hence, one might expect the microviscosity measured by a probe that mainly experiences the non-polar domain to be lower than that measured by a probe that largely resides in the polar domain. In order to investigate this systematically, we chose to compare the behaviour of two dyes, one charged – 3,3′-diethylthiacarbocyanine iodide (Cy3, Fig. 2) and one neutral – 8-[4-decyloxyphenyl]-4,4-difluoro-4-bora-3a,4a-diaza-s-indacene (BODIPY-C10, Fig. 3) in a range of ionic liquids. These probes were chosen due to their proven high sensitivity to the ranges of viscosities in which the chosen ionic liquid bulk viscosities lie.12,23
The ionic liquids were chosen to probe the effect of varying both the cation and anion separately, as well as the effect of different degrees of structural heterogeneity – 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([CnC1im][NTf2] (n = 2, 3, 4, 6, 8 or 12)), tributylhexylphosphonium bis(trifluoromethylsulfonyl)imide ([P4446][NTf2]), 1-butyl-3-methylimidazolium triflate ([C4C1im][OTf]), 1-butyl-3-methylimidazolium tetrafluoroborate ([C4C1im][BF4]) and 1-butyl-3-methylimidazolium hexafluorophosphate ([C4C1im][PF6]). These were complemented with variable temperature measurements with one ionic liquid, [C4C1im][NTf2] to further probe the effect of changes to the viscosity.
2 Experimental
2.1 Materials
All chemicals were purchased from Sigma-Aldrich and used without any further purification unless otherwise stated. All solvents were purchased from Fisher Scientific and were of ultrapure grade (>99.5%) and extra dry (Acros Organics AcroSeal™) and were used without any further purification. The charcoal was Norit® acid washed and steam activated charcoal, and sterile 0.2 μm PTFE syringe filters were purchased from Cole-Parmer.Cy3 iodide was purchased from Alfa Aesar (96% purity) and used without purification.
BODIPY-C10 was synthesised as described in previous literature.23
2.2 Syntheses of low fluorescence background ionic liquids
Production of high quality ionic liquids was essential for this project to ensure as low background signal as possible, and only ionic liquids with a background fluorescence of <5000 counts per second were used.‡ In order to ensure this, reactions were carried out at low temperatures for longer, all glassware was cleaned thoroughly, and all the starting materials were rigorously purified before use.Glassware was washed with a 5% (v/v) Decon® 90 solution in distilled water then rinsed with piranha solution (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 30% hydrogen peroxide: 95–98% sulphuric acid). This was followed by distilled water and a final rinse with ethanol. The glassware was then dried in a clean oven operating at 120 °C. To minimise the introduction of contaminants during synthesis, thick-walled PTFE sleeves were used instead of grease.
3, 30% hydrogen peroxide: 95–98% sulphuric acid). This was followed by distilled water and a final rinse with ethanol. The glassware was then dried in a clean oven operating at 120 °C. To minimise the introduction of contaminants during synthesis, thick-walled PTFE sleeves were used instead of grease.
The ionic liquids precursors, i.e. chloride and bromide salts of the cations, were synthesised by alkylation of 1-methylimidazole (or tributylphosphine in the case of the [P4446]+ cation) with the relevant haloalkane. The haloalkanes were purified by repeated washing with concentrated sulphuric acid until the acid layer remained colourless. Then the organic layer was neutralised with sodium hydrogen carbonate and washed with distilled water until the aqueous washings gave a consistent pH of 6. After drying over magnesium sulphate, and then phosphorus pentoxide overnight, they were distilled. 1-Methylimidazole was dried and distilled from potassium hydroxide before treating with freshly cut sodium (1 g per 500 ml) in a nitrogen atmosphere overnight and then redistilled. Tri-n-butylphosphine was purified by distillation.
All of the bis(trifluoromethylsulfonyl)imide ionic liquids were synthesised via a metathesis route. Equal molar amounts of the chloride or bromide salt and lithium bis(trifluoromethylsulfonyl)imide were stirred in solvent overnight. The bis(trifluoromethylsulfonyl)imide ionic liquid was isolated and washed with water until the washings gave a negative response to the silver nitrate test. Excess solvent was removed on a rotary evaporator and the crude ionic liquid was washed with n-hexane then treated with charcoal for 24 h before being passed through filter paper and then a sterile 0.2 μm PTFE filter. The ionic liquid was further dried under vacuum at a maximum of 50 °C for at least 24 h before use.
Full synthetic procedures, characterisation and yields are presented in the ESI Section S1.†
2.3 Cy3 metathesis
Experiments were carried out in air unless otherwise stated. Cy3 iodide was purchased from TCI and used as received. The metal salts LiNTf2, AgOTf, KPF6, NaBF4 and AgBF4 were purchased from Sigma Aldrich and used as received. NaCHTf2 was synthesized according to the procedure of Waller et al.24 MeOH, Et2O (both HPLC grade) and CH2Cl2 were purchased from VWR and used as received.For the metathesis of Cy3 anions, Cy3 iodide was dissolved in a suitable solvent. Solid metal salt was added and the reaction stirred at RT for 2–4 days. After this time the reaction was filtered and volatiles were removed in vacuo, affording solid [Cy3][X] (X = NTf2, OTf, PF6, BF4, or CHTf2), which was recrystallised from a suitable solvent.
Full synthetic procedures, characterisation and yields are presented in the ESI Section S2.†
2.4 Absorption spectra
The absorption spectra were recorded on a PerkinElmer Lambda 25 spectrophotometer using 10 mm path length quartz cuvettes. For the variable temperature measurements, an ethylene glycol-water bath was connected to a temperature controllable cuvette holder. The temperature of every sample was checked using an Omega OS-MINIUSB temperature probe before measuring.2.5 Emission spectra
The emission spectra of the dyes in various ionic liquids were recorded on a Fluoromax-4 spectrofluorometer (Jobin-Yvon; Horiba). The excitation wavelength used was 520 nm for Cy3 and 445 nm for BODIPY-C10. The temperature was controlled using a Peltier thermostat cuvette holder (F3004) with temperature control accurate to ±0.5 °C.The emission spectra of the dyes in [C4C1im][NTf2] at various temperatures were measured on a Delta Flex system (Horiba Scientific) using an excitation wavelength of 467 nm.
2.6 Fluorescence lifetime measurement of dyes in variable-ion ionic liquids
The lifetimes of the neat ionic liquids and the samples of dyes in different ionic liquids were measured on a custom built confocal microscope using a sub-micrometre precision stage to position the sample in the laser beam. The sample was excited using a 466 nm pulsed diode laser (PicoQuant GmbH, PDL 800-B) operating at a frequency of 20 MHz (50 ns pulse separation) and an average power of 1.35 mW. Beam steering mirrors along with a dichroic mirror was used to direct the laser beam into the objective. An infinity corrected, high numerical aperture (NA) microscope objective (Olympus 60×/1.2, water immersion) focuses the laser into a diffraction limited spot within the sample. Fluorescence from the sample was collected by the same microscope objective, directed to the same dichroic mirror, then passed through an emission filter (z488lp, Chroma Technology Corp.) to remove residual excitation photons. A plano-convex lens (+50.2 F, Newport Ltd.) focused the filtered light onto a 75 μm pinhole positioned on the confocal plane of the microscope objective. Another dichroic mirror (630dcxr, Chroma Technology Corp.) was then used to split the beam towards two avalanche photodiodes (AQR-141, EG&G, PerkinElmer). The light was further filtered by another emission filter (hq 540/80 m, Chroma Technology Corp.) and focused by a plano-convex lens (f = 30.0, i.d. 25.4 mm, Thorlabs) onto the first avalanche photodiode (green detector, photons in the range 500–580 nm). The second avalanche photodiode (red detector) was not used in these experiments. The signal from the green detector was coupled to a multifunction DAQ device for data logging (PCI 6602, National Instruments), as well as to a time-correlated single-photon counting card (SPC-130 EM, Becker & Hickl GmbH) running on a separate PC.The data was collected at 298 K, and the raw data was deconvoluted using the instrument response function (IRF), which was measured using a 15 μM solution of auramine O in distilled water. Auramine O has a lifetime of a few ps, and is much shorter than the IRF which has a FWHM of ≈0.9 ns.
2.7 Fluorescence lifetime measurement of dyes in variable-temperature ionic liquid
The lifetimes of the dyes in [C4C1im][NTf2] at various temperatures were measured using a Delta Flex system (Horiba Scientific) using an excitation wavelength of 467 nm. Each measurement was repeated three times, and the data presented is the average and error of the fitted lifetimes.2.8 Data analysis
The data were analysed using a modified version of the JLife program written at Imperial College London, with amplitudes and lifetimes loosely constrained to give positive, non-zero values. Goodness of fit was judged based upon χ2 values, and all presented data are from fittings with χ2 values of less than 1.2.The fluorescence decay was treated as an n component exponential decay of the form shown in eqn (2), and the IRF was fitted to the measured data using the sequential quadratic programming method with an error tolerance of 10−6.
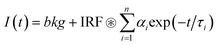 | (2) |
3 Results and discussion
3.1 Fluorescence lifetimes of neat [NTf2]− based ionic liquids
In order to distinguish ionic liquid autofluorescence from dye fluorescence, we measured the time resolved fluorescence decays of samples of all ionic liquids used in this study, without any dye. The observed decays can be fitted to three components, which we have assigned the labels τ1, τ2 and τ3 (Table 1, ESI Fig. S7A–G†).| Ionic liquid | τ 1 [ns] | Contribution [%] | τ 2 [ns] | Contribution [%] | τ 3 [ns] | Contribution [%] |
|---|---|---|---|---|---|---|
| [C2C1im][NTf2] | 6.17 ± 0.53 | 33.1 ± 3.0 | 1.52 ± 0.22 | 21.0 ± 1.9 | 0.107 ± 0.012 | 45.9 ± 1.9 |
| [C3C1im][NTf2] | 6.12 ± 0.21 | 36.9 ± 1.6 | 1.40 ± 0.09 | 22.9 ± 1.3 | 0.115 ± 0.004 | 40.2 ± 0.4 |
| [C4C1im][NTf2] | 6.27 ± 0.25 | 38.3 ± 1.6 | 1.42 ± 0.15 | 23.9 ± 1.3 | 0.123 ± 0.019 | 37.8 ± 1.0 |
| [C6C1im][NTf2] | 6.34 ± 0.31 | 38.9 ± 0.5 | 1.32 ± 0.09 | 25.7 ± 0.8 | 0.137 ± 0.010 | 35.4 ± 0.9 |
| [C8C1im][NTf2] | 6.24 ± 0.29 | 41.2 ± 2.1 | 1.57 ± 0.16 | 26.5 ± 1.6 | 0.125 ± 0.010 | 32.3 ± 1.1 |
| [C12C1im][NTf2] | 6.98 ± 0.20 | 42.4 ± 0.6 | 1.61 ± 0.09 | 31.0 ± 1.5 | 0.158 ± 0.013 | 26.5 ± 1.0 |
| [P4446][NTf2] | 6.85 ± 0.18 | 43.7 ± 1.6 | 1.52 ± 0.07 | 20.7 ± 0.7 | 0.096 ± 0.006 | 35.6 ± 1.3 |
| [C4C1im][OTf] | 6.39 ± 1.38 | 21.5 ± 1.4 | 1.27 ± 0.15 | 32.5 ± 4.0 | 0.065 ± 0.007 | 46.1 ± 3.1 |
| [C4C1im][BF4] | 6.41 ± 0.15 | 22.1 ± 0.7 | 0.95 ± 0.04 | 54.6 ± 1.1 | 0.097 ± 0.018 | 23.4 ± 1.4 |
| [C4C1im][PF6] | 6.07 ± 1.11 | 14.2 ± 2.1 | 1.60 ± 0.50 | 20.0 ± 6.0 | 0.070 ± 0.010 | 70.5 ± 1.3 |
Previous studies of the fluorescence decays of [C4C1im][X] (X = BF4 or PF6) and [C2C1im][BF4] have also shown that the decays of neat ionic liquids can be fitted by three separate components. Two of these were attributed to ‘associated structures’ including cation–anion and cation–cation interactions in the ionic liquid, while the third is a high contribution fast decay component, which was attributed to an internal fluorescence of the imidazolium ring.25–27
We also observe a fast decay component, τ3, with a large amplitude (27–70%) for all ionic liquids including [P4446][NTf2], which does not have an imidazolium ring in its structure. In our measurements this short component is near the limit of the detection capability of our spectrometer, 0.1 ns. Hence, at present we are unable to resolve whether this signal arises due to a genuine fluorescence from the ionic liquids, or whether it arises from some other process, such as scattering.
3.2 Fluorescence lifetimes of BODIPY-C10 in ionic liquids
3.2.1.1 Components present for BODIPY-C10 in ionic liquids. The time resolved fluorescence decay of BODIPY-C10 was measured in [C4C1im][NTf2] at temperatures of 277–329 K, leading to viscosities of 17–148 cP,28 and the results are shown in Table 2 (decays shown in ESI Fig. S11A–N†).
| Temperature [K] | τ BDPY [ns] | Temperature [K] | τ BDPY [ns] |
|---|---|---|---|
| 277 | 2.193 ± 0.001 | 298 | 1.082 ± 0.001 |
| 279 | 2.015 ± 0.003 | 302 | 0.951 ± 0.001 |
| 282 | 1.797 ± 0.001 | 311 | 0.757 ± 0.001 |
| 286 | 1.597 ± 0.001 | 320 | 0.611 ± 0.001 |
| 290 | 1.398 ± 0.002 | 329 | 0.504 ± 0.002 |
| 294 | 1.234 ± 0.001 |
For all the variable temperature samples for BODIPY-C10 in [C4C1im][NTf2], the time resolved fluorescence decays can be fitted to 1 component which can be attributed to the rotor (τBDPY). No contribution to the decays from the ionic liquids were observed.
To study the fluorescence of BODIPY-C10 in ionic liquids with different ion combinations, the time resolved fluorescence decay was measured in the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4, 6, 8 or 12), [P4446][NTf2], [C4C1im][OTf], [C4C1im][BF4] and [C4C1im][PF6] (decays shown in ESI Fig. S10A–J,† results in Table 3).
| Ionic liquid | τ BDPY [ns] | τ A [ns] | τ B [ns] |
|---|---|---|---|
| [C2C1im][NTf2] | 0.865 ± 0.011 | 0.181 ± 0.019 | — |
| [C3C1im][NTf2] | 1.138 ± 0.022 | 0.203 ± 0.019 | — |
| [C4C1im][NTf2] | 1.282 ± 0.019 | 0.221 ± 0.015 | — |
| [C6C1im][NTf2] | 1.655 ± 0.014 | 0.282 ± 0.015 | — |
| [C8C1im][NTf2] | 1.941 ± 0.018 | 0.422 ± 0.039 | — |
| [C12C1im][NTf2] | 2.331 ± 0.015 | 0.674 ± 0.063 | — |
| [P4446][NTf2] | 2.648 ± 0.014 | 0.532 ± 0.031 | — |
| [C4C1im][OTf] | 1.649 ± 0.031 | 0.247 ± 0.022 | 6.57 ± 0.53 |
| [C4C1im][BF4] | 1.868 ± 0.104 | 0.487 ± 0.041 | — |
| [C4C1im][PF6] | 2.780 ± 0.010 | 0.693 ± 0.064 | — |
For all these samples, except for [C4C1im][OTf], the time resolved fluorescence decays were fitted to 2 components. The short lifetime component, τA, which has a low contribution to the overall decay (<10%) and a lifetime similar to τ3 in the neat samples, was assigned to the ionic liquid. As with τ3 in Table 1, τA is below the detection limit for this spectrometer meaning it cannot be assigned with certainty to any process within the ionic liquid and will not be included in this discussion. The second component with a lifetime around 1–2 ns which is present in all samples was attributed to the lifetime of the BODIPY-C10 rotor (τBDPY) as it was found to contribute over >90% of photons to all of the decays. In order to adequately fit the time resolved fluorescence decay in [C4C1im][OTf] the same two components were required, as well as an additional third component, (τB). As the lifetime of τB is similar to that of τ1 in the neat ionic liquids, the contribution is very low (2%), and the lifetime is far too large to be associated with BODIPY-C10, it is also attributed to the ionic liquid and will not be included in our discussion of the rotor.
3.2.1.2 Viscosity dependence of τBDPY in ionic liquids. When considering the variable temperature measurements of BODIPY-C10 in [C4C1im][NTf2], τBDPY was plotted against the viscosity of the ionic liquid at different temperatures, with the viscosity being that measured by Tariq et al.28
Fig. 4 shows that when changing the temperature of this sample, the lifetime of the rotor clearly increases with viscosity, and that this trend is different to that of BODIPY-C10 in methanol/glycerol mixtures.12 The log–log plot shows that the rotor lifetime varies with viscosity as would be expected from the Förster–Hoffmann equation (eqn (1)). This data can be fitted to the Förster–Hoffmann equation of the form:
log10(τBDPY) = 0.684![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(η) − 1.138, R2 = 0.9992 log10(η) − 1.138, R2 = 0.9992 | (3) |
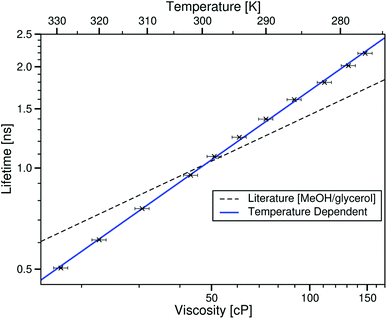 | ||
| Fig. 4 log–log plot of the temperature dependent fluorescence lifetime of BODIPY-C10 in the ionic liquid [C4C1im][NTf2] against the viscosity at the corresponding temperature, taken from ref. 28. The blue line is the best fit to this data (eqn (3)). The dashed black line is the fit to values derived from the literature methanol/glycerol calibration.12 | ||
Considering the ionic liquids with the same cation and various anions, τBDPY was plotted against the viscosity measured by Tokuda et al.29 and a curve fitted to this data (Fig. 5). This trend was also compared to the calibration of the lifetime of BODIPY-C10 in methanol/glycerol mixtures.12
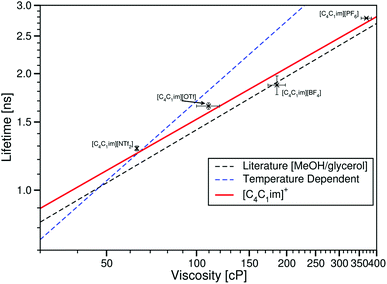 | ||
| Fig. 5 Fluorescence lifetime of BODIPY-C10 in the ionic liquids [C4C1im][NTf2], [C4C1im][OTf], [C4C1im][BF4] and [C4C1im][PF6] plotted against the ionic liquid viscosities from ref. 29. The red line is the best fit to this data (eqn (4)). The dashed black line is the fit to values derived from the literature methanol/glycerol calibration.12 The dashed blue line is the best fit to the temperature dependent data in [C4C1im][NTf2]. | ||
In all of these samples, the lifetime of the rotor clearly increases with viscosity as would be expected. When comparing the ionic liquid and molecular solvent data, a molecular solvent with the same bulk viscosity as an ionic liquid presents a slightly lower lifetime of BODIPY-C10. This indicates that the microviscosity of the BODIPY-C10 cybotactic region is slightly greater in an ionic liquid than in a molecular solvent of the same bulk viscosity. This is not the case for [C4C1im][BF4]; however, it should be noted that this data point has large error bars for both its viscosity and lifetime.
Our data for these ionic liquids can be fitted to the Förster–Hoffmann equation (eqn (1)) as
log10(τBDPY) = 0.440![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(η) − 0.697, R2 = 0.9897 log10(η) − 0.697, R2 = 0.9897 | (4) |
Considering the ionic liquids with the same anion and various cations, τBDPY is plotted against the ionic liquid viscosities taken from Tariq et al.28 in Fig. 6.
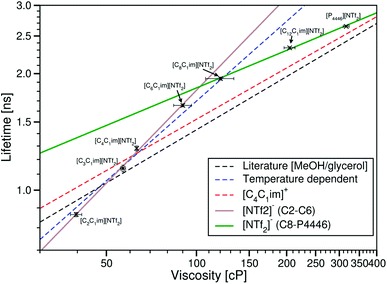 | ||
| Fig. 6 Fluorescence lifetime of BODIPY-C10 in the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4, 6, 8 or 12) and [P4446][NTf2] plotted against the ionic liquid viscosities on a log–log plot. The brown line is the Förster–Hoffmann equation fitted to the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4 or 6) (eqn (5)). The green line is the Förster–Hoffmann equation fitted to the ionic liquids [CnC1im][NTf2] (n = 8 or 12) and [P4446][NTf2] (eqn (6)). The dashed black line is the fit to values derived from the literature methanol/glycerol calibration.12 The dashed blue line is the best fit to the temperature dependent data in [C4C1im][NTf2]. The dashed red line is the best fit to the variable anion data. | ||
As before, the lifetime of the rotor clearly increases with viscosity, and the microviscosity of the BODIPY-C10 cybotactic region is greater in an ionic liquid than a molecular solvent of the same bulk viscosity, with the exception of [C2C1im][NTf2].
When trying to find a fit, it is obvious that the whole of this data set cannot be fitted to a single Förster–Hoffmann equation. Careful observation of the graph shows that instead, there are two regions in the log–log plot, each of which can be fitted to a separate Förster–Hoffmann equation.
The trend of τBDPY to η for the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4 or 6) can be fitted to the Förster–Hoffmann equation as
log10(τBDPY) = 0.797![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(η) − 1.336, R2 = 0.9968 log10(η) − 1.336, R2 = 0.9968 | (5) |
log10(τBDPY) = 0.322![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(η) − 0.380, R2 = 0.9980 log10(η) − 0.380, R2 = 0.9980 | (6) |
When considering the cybotactic region of solutes in ionic liquids, these are often studied by looking at the differences in the diffusivities of charged and uncharged species, which are well-established.30–32 As BODIPY-C10 is a neutral molecule comprised of a mixture of aliphatic and aromatic moieties (Fig. 3), it is expected to partition into ‘soft’ non-polar domains generated by the alkyl chains of the ionic liquid cations.33 However, due to the large size of the molecule compared to the ionic liquid ions, it may have to stretch between the domains as the completeness of this partitioning is dependent on the relative sizes of these domains and the solute. What is clear from the literature is that the frictional force to translation for a neutral molecule will always be lower than that for a similarly sized ion.34 The same effects have also been observed on the rotational dynamics of charged and uncharged solutes.35
The non-radiative quenching pathways of BODIPY dyes have been investigated computationally by Kee et al. and Polita et al.36,37 It was discovered that in the most stable conformation in the ground state, the boraindacene ring and the phenyl ring are twisted at an angle of approximately 50° from each other.36,37 Kee et al. used X-ray crystallography to confirm this for a structurally similar dye, and X-ray crystallography of our BODIPY-C10 dye agrees with this as BODIPY-C10 crystallises in two forms with twist angles of 50.94° and 52.11°.
From the computational studies the radiative decay pathway was found to be a S0 → S1 excitation and emission with the BODIPY-C10 remaining in its twisted conformer.
The non-radiative decay pathway can be accessed by twisting of the phenyl group into the plane of the boraindacene ring. In this conformer, the energy of the ground and excited state were brought closer together, allowing relaxation back to the ground state by emission of a low energy infrared photon. A small energy barrier was present in this process at a twist angle of 25°, which could be attributed to a ‘buckling’ of the molecule around the rotor bond. This was required to avoid a steric clash of protons, and pushed the BF2 group of the boraindacene ring up and out of the plane of the phenyl group.36,37
Therefore in order for the BODIPY-C10 to undergo non-radiative decay, the rotor must be able to both rotate the phenyl group 50° and push its boraindacene ring out of the plane of the phenyl group.
When measuring the lifetime of the BODIPY-C10 rotor in [C4C1im][NTf2] and modifying the viscosity by changing the temperature, the log of the rotor lifetime is proportional to the log of the viscosity. It is known that temperature variations do not have a direct effect on the photophysics of BODIPY-C10, and that changes in polarity do not have an effect in polar systems i.e. the lifetimes of this dye respond to viscosity only, and the radiative and non-radiative decay pathways are unaffected by changes to the polarity or temperature.38 Therefore this trend in lifetime measurements can be attributed to the change in viscosity.
Comparing these measurements to the molecular solvent calibration, the ionic liquid fit has a larger gradient indicating a greater dependence of the lifetime of BODIPY-C10 on the viscosity in the ionic liquid. However interestingly, the rotor lifetime in high temperature ionic liquid samples (low viscosity) is lower than molecular liquids of the same viscosity.
When keeping the cation constant and varying the anion to modify viscosity, the log of lifetime of the BODIPY-C10 rotor is also directly proportional to the log of the viscosity.
The variable temperature and variable anion measurements show that having a constant cation for measurements of BODIPY-C10 in ionic liquids leads to a change in the rotor lifetime that can be predicted by the Förster–Hoffmann equation. This means that the rotor lifetime is changing in a predictable way with viscosity, and there are no significant changes in the cybotactic region.
However, the difference between the variable temperature measurements and the variable anion measurements highlight that the environment in which the rotor resides is very important. BODIPY-C10 appears to be more sensitive to changes in the bulk viscosity caused by temperature than changes caused by changing the anion. It is known that this molecular rotor is sensitive to the polarity only when the overall environment is low polarity.37,39 Therefore it is likely that the difference between these two trends is due to the changing specific interactions with the different anions of the ionic liquids.40
When keeping the anion constant and varying the cation to change the viscosity, the lifetime of the BODIPY-C10 rotor shows a more complex trend with the viscosity. While slight changes to the polarity occur between these ionic liquids, these are as close as possible to each other while allowing for variation of the viscosity.40
The relationship between τBDPY and the ionic liquid viscosity follows two different and distinct trends, one in the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4 or 6) and another in the ionic liquids [CnC1im][NTf2] (n = 8 or 12) and [P4446][NTf2]. The crossover for these trends occurs at a viscosity of 104 cP, which corresponds to the viscosity of [C7C1im][NTf2].28 This crossover point, as well as the ionic liquids associated with each trend suggests that the two trends are related to the microheterogeneity of the ionic liquids.
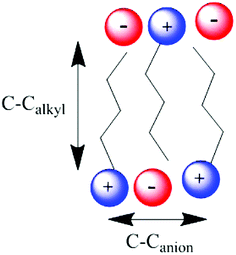
It has been shown that for the ionic liquids [CnC1im][NTf2] (n = 6, 7, 8, 9 or 10) the distance between the centres of two imidazolium rings separated by alkyl chains, which is indicative of the size of the non-polar domains (C–CAlkyl, Fig. 7), follows the relationship C–CAlkyl (Å) = 1.96 × nCH2 + 3.12.41
The crystal structure of BODIPY-C10 shows that it adopts a fully extended alkyl chain configuration. We would expect this to remain the case in ionic liquids in order to maximise the dispersion interactions between its alkyl chain and those of the ionic liquids. This gives BODIPY-C10 a length of approximately 21 Å.
When considering the ionic liquids in the first trend ([CnC1im][NTf2] (n = 2, 3, 4 or 6)), these liquids have a continuous polar domain with dispersed non-polar regions within this domain.18–20 In these ionic liquids, the maximum C–CAlkyl distance occurs in [C6C1im][NTf2] and is approximately 15 Å. This confirms that BODIPY-C10 is too large to fit entirely in the region between two cations, and must therefore be experiencing an averaged structure of the ionic liquids, with a cybotactic region containing both polar and non-polar moieties.
The consistent trend indicates that in these ionic liquids, the partitioning of the dye does not change and BODIPY-C10 cannot fit entirely into the non-polar region, so changing the length of the alkyl chain within these limits changes only the viscosity. This means that this trend is a representation of the viscosity dependent lifetime of BODIPY-C10 when surrounded by both polar and non-polar moieties in ionic liquids.
Considering the ionic liquids in the second trend, τBDPY in both [CnC1im][NTf2] (n = 8 or 12) is lower than would be expected if the first trend had been maintained for these ionic liquids. That is, while intramolecular rotation is more restricted in these more viscous ionic liquids, this restriction is not as great as expected from the previous trend. For these ionic liquids, continuous and persistent non-polar domains are present within the liquid19 along with an increase in the C–CAlkyl distance.
Comparing the C–CAlkyl distances of approximately 19 Å and 26 Å for [C8C1im][NTf2] and [C12C1im][NTf2], respectively, one can see that these are much closer to the 21 Å length of BODIPY-C10. In addition, the tendency of BODIPY-C10 to partition into these non-polar domains could be enhanced by its decyl chain acting as a template, as has been seen for dodecanol in ionic liquids.42 Both of these increase the ability of the non-polar domain to encapsulate the relatively large BODIPY-C10 molecule and to displace polar moieties from its solvation shell. Further to this, the fluorescence lifetimes of BODIPY-C10 in these ionic liquids are similar to those that have been measured in lipid phases,43 supporting the conclusion that BODIPY-C10 is mainly experiencing the more lipid-like environment generated by the aggregation of these longer alkyl chains of the cation. Hence, BODIPY-C10 is likely to be almost entirely solvated by the alkyl chains of these ionic liquids.
This leaves the remaining ionic liquid, [P4446][NTf2], to be considered. The phosphonium ionic liquids are less well studied than imidazolium ionic liquids and no structural investigations of [P4446][NTf2] itself have been reported in other literature. The closest structures that are available are for [P4444]Cl and [P4448]Cl.21 Both are described as having interpenetrating polar and non-polar networks, with [P4448]Cl having a greater separation of ionic domains.
τ BDPY in [P4446][NTf2] is below that predicted by the trend for [CnC1im][NTf2] (n = 2, 3, 4 or 6); suggesting the presence of significant non-polar domains. This lifetime along with the lifetimes of BODIPY-C10 in [C8C1im][NTf2] and [C12C1im][NTf2] can all be fitted by the same Förster–Hoffmann equation, which would indicate that [P4446][NTf2] has similar segregation of its polar and non-polar domains as [C8C1im][NTf2] and [C12C1im][NTf2]. All of this data combined led us to suspect that [P4446][NTf2] has a large enough non-polar domain to fully encapsulate BODIPY-C10. Thus the rotor sits entirely within the non-polar region and the microviscosity it experiences is dominated by the alkyl chains.
A simulation of [P4446][NTf2] was carried out to investigate this for this work; the simulation protocol is described in the ESI (Section S3).† It was discovered that [P4446][NTf2] has one continuous polar domain, and one continuous non-polar domain, and that these are a permanent feature of this ionic liquid. The non-polar domain constitutes approximately 55% of the liquid by volume, with the polar domain accounting for the rest. From comparing these results to those of the imidazolium ionic liquids (see ESI†) it can be deduced that the non-polar domain is large enough to fully encapsulate the dye, thus BODIPY-C10 can be fully segregated into the non-polar domain.
3.3 Fluorescence lifetimes of Cy3 in ionic liquids
3.3.1.1 Components present for Cy3 in ionic liquids. To study the fluorescence of Cy3 in an ionic liquid when varying the temperature to change the viscosity, the time resolved fluorescence decay was measured in [C4C1im][NTf2] in temperatures of 276–320 K, corresponding to viscosities of 23–157 cP (decays shown in ESI Fig. S9A–K,† results in Table 4).
| Temperature [K] | τ Cy3 [ns] | Temperature [K] | τ Cy3 [ns] |
|---|---|---|---|
| 276 | 1.323 ± 0.002 | 294 | 0.839 ± 0.002 |
| 279 | 1.244 ± 0.001 | 302 | 0.660 ± 0.001 |
| 282 | 1.159 ± 0.001 | 311 | 0.519 ± 0.001 |
| 286 | 1.050 ± 0.001 | 320 | 0.409 ± 0.002 |
| 290 | 0.942 ± 0.002 |
The time resolved decay of Cy3 in these measurements can all be fitted to one component which can be attributed to the lifetime of Cy3 in the solution. As with the BODIPY-C10 variable temperature measurements, no contribution to the decays from the ionic liquids were observed.
To study how the fluorescence of Cy3 changes in ionic liquids with different ion combinations, the time resolved fluorescence decay was measured in the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4, 6, 8 or 12), [P4446][NTf2], [C4C1im][OTf], [C4C1im][BF4] and [C4C1im][PF6] (decays shown in ESI Fig. S8A–J,† results in Table 5).
| Ionic liquid | τ Cy3 [ns] | τ C [ns] | τ D [ns] |
|---|---|---|---|
| [C2C1im][NTf2] | 0.727 ± 0.003 | 0.023 ± 0.003 | — |
| [C3C1im][NTf2] | 0.865 ± 0.009 | 0.027 ± 0.004 | — |
| [C4C1im][NTf2] | 0.908 ± 0.003 | 0.020 ± 0.005 | — |
| [C6C1im][NTf2] | 1.090 ± 0.005 | 0.017 ± 0.006 | — |
| [C8C1im][NTf2] | 1.227 ± 0.004 | 0.058 ± 0.005 | 3.75 ± 0.10 |
| [C12C1im][NTf2] | 1.352 ± 0.005 | 0.045 ± 0.004 | 4.01 ± 0.22 |
| [P4446][NTf2] | 1.385 ± 0.005 | 0.039 ± 0.004 | 3.79 ± 0.23 |
| [C4C1im][OTf] | 1.189 ± 0.001 | 0.024 ± 0.002 | 6.76 ± 0.32 |
| [C4C1im][BF4] | 1.161 ± 0.005 | 0.026 ± 0.004 | 4.32 ± 0.14 |
| [C4C1im][PF6] | 1.304 ± 0.007 | 0.062 ± 0.004 | — |
The time resolved decay of Cy3 in the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4 or 6) and [C4C1im][PF6] can be fitted with two components. Using the same logic as with BODIPY-C10 it can be deduced that the short lifetime component, τC, is similar to τ3 in Table 1 seen for the neat ionic liquid sample, and therefore it is assigned to a signal from the ionic liquid of unknown source and not included in our discussion. The longer component around 0.7–1.4 ns has a much higher contribution to all decays (>90% of photons in each decay), so we assign this component to the Cy3 rotor (τCy3). For the time resolved decay of Cy3 in [C8C1im][NTf2], [C12C1im][NTf2], [P4446][NTf2] [C4C1im][OTf] and [C4C1im][BF4] a third component, τD, is required for an accurate fit. As with τB for BODIPY-C10 samples, this is similar to the longer lifetime components that arise from the pure ionic liquids. This similarity along with its minor contribution (<2% of each decay it is present) leads us to believe it also arises from the ionic liquid and therefore will not be included in our discussion of the rotor lifetime.
3.3.1.2 Viscosity dependence of τCy3 in ionic liquids. When considering the sample of Cy3 in [C4C1im][NTf2], τCy3 was plotted against the viscosity of [C4C1im][NTf2] at different temperatures. Viscosities are those measured by Tariq et al.28
It can be seen from Fig. 8 that the lifetime of Cy3 increases with increasing viscosity of the ionic liquid, as would be expected. An interesting trend when comparing these data to a literature calibration is that for any given viscosity τCy3 is lower in the ionic liquid than the sucrose/water mixtures, and this difference decreases with increasing viscosity.
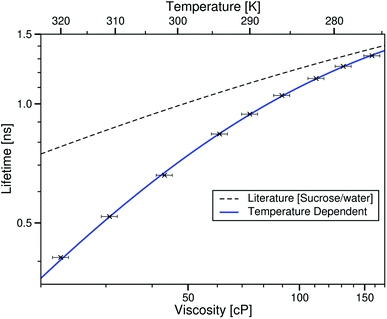 | ||
| Fig. 8 log–log plot of the temperature dependent fluorescence lifetime of Cy3 in the ionic liquid [C4C1im][NTf2] plotted against the ionic liquid viscosity at the corresponding temperature, taken from ref. 28. The blue line is the best fit to this data (eqn (7)). The dashed black line is the fit to values derived from the literature sucrose/water calibration.12 | ||
This data set cannot be fitted to a Förster–Hoffmann equation, which has been seen for this rotor before.12 Hosny et al. found that Cy3 data could be fitted to a Hill type function, and we can use the same function to fit our temperature dependent Cy3 data to the equation
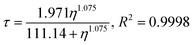 | (7) |
Considering τCy3 in ionic liquids with the same anion, these are plotted against the ionic liquid viscosities measured by Tariq et al.28 in Fig. 9.
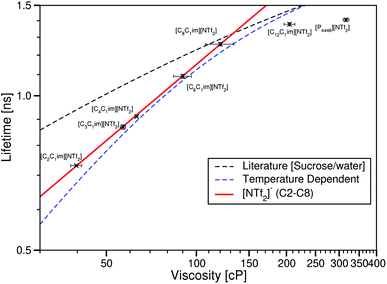 | ||
| Fig. 9 log–log plot of the fluorescence lifetime of Cy3 in the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4, 6, 8 or 12), [P4446][NTf2] plotted against the ionic liquid viscosities taken from ref. 28. The red line is the Förster–Hoffmann equation fitted to the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4, 6 or 8, eqn (8)). The dashed black line is the fit to values derived from the literature sucrose/water calibration.12 The dashed blue line is the best fit to the temperature dependent data in [C4C1im][NTf2]. | ||
As for the temperature dependent measurements, the lifetime of Cy3 in these ionic liquids increases with viscosity for all ionic liquids. When drawing the comparison between these data and the literature calibration again for any given viscosity τCy3 is lower in the ionic liquid than the sucrose/water mixtures, and this difference mostly decreases with increasing viscosity, with the exception of [C12C1im][NTf2] and [P4446][NTf2].
When considering the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4, 6 or 8) a clear trend can be seen for τCy3 against η. This can be fitted to the Förster–Hoffmann equation as
log10(τCy3) = 0.493![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(η) − 0.925, R2 = 0.9998 log10(η) − 0.925, R2 = 0.9998 | (8) |
The ionic liquids [C12C1im][NTf2] and [P4446][NTf2] do not fit this trend, and we do not have enough ionic liquids in this region to attempt to fit these data to a curve.
Considering the ionic liquids with a constant cation and various anions, Fig. 10 shows a plot of τCy3 against the viscosity taken from Tokuda et al.29
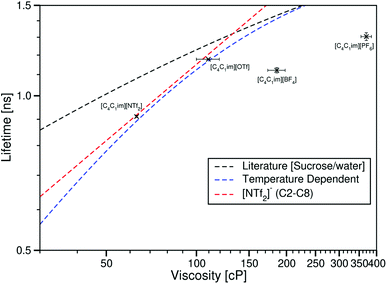 | ||
| Fig. 10 log–log plot of the fluorescence lifetime of Cy3 in the ionic liquids [C4C1im][NTf2] [C4C1im][OTf], [C4C1im][BF4] and [C4C1im][PF6] plotted against the ionic liquid viscosities taken from ref. 29. The dashed black line is the fit to values derived from the literature sucrose/water calibration.12 The dashed blue line is the best fit to the temperature dependent data in [C4C1im][NTf2]. The dashed red line is the fit to the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4, 6 or 8). | ||
As with our previous Cy3 measurements, for any given viscosity, ηCy3 is lower in the ionic liquid than the sucrose/water mixture.
However, here the lifetime of Cy3 is no longer dominated by viscosity, unlike with our BODIPY-C10 data and the temperature and cation variation data sets for Cy3. τCy3 in [C4C1im][OTf] is greater than τCy3 in [C4C1im][BF4], despite the viscosity of [C4C1im][OTf] being lower than that of [C4C1im][BF4]. Along with this, when comparing these data to the constant anion data, [C4C1im][PF6] has a higher viscosity than all the [NTf2]− ionic liquids, yet shows a lower τCy3 value than both [C12C1im][NTf2] and [P4446][NTf2].
These results suggest that there is a difference in the interaction between Cy3 and different anions which affects its lifetime. The different anions of the ionic liquid will each interact differently with both the excited and ground states of Cy3. This leads to an anion-specific interaction effect that appears to supersede a simple viscosity effect. While no measurements of polarity-based spectral effects on Cy3 are currently available, calculations by Vladimirova et al. show a lower twist of the benzothiazole rings in polar solvents in the excited state than non-polar solvents, with both being lower twists than gas phase calculations by Baraldi et al.44,45
To understand how the anion interactions affect the ground state of Cy3, we have analysed crystal structures of Cy3 with these and other anions (ESI Section 4 for details†). All of the bridging bonds were found to be mid-way between a classical C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond (≈1.33 Å) and a C–C single bond (≈1.54 Å), consistent with the notion that there is complete delocalisation across both benzothiazole rings and the C3 linker. These bonds were also all found to be the same length, within experimental error. Hence the interactions between anion and Cy3 do not appear to influence the bonding in the Cy3 cation.
C double bond (≈1.33 Å) and a C–C single bond (≈1.54 Å), consistent with the notion that there is complete delocalisation across both benzothiazole rings and the C3 linker. These bonds were also all found to be the same length, within experimental error. Hence the interactions between anion and Cy3 do not appear to influence the bonding in the Cy3 cation.
However, notable differences were found in the twist angle between the benzothiazole rings (θ in Table 6). These vary from 3.3° to 26.8° which indicate a large degree of flexibility in the Cy3 cation despite the formal complete delocalisation of the pi-symmetry orbitals. This is especially notable within [Cy3][NTf2] and [Cy3][CHTf2] where each structure contains two symmetry-independent cations with hugely different twist angles in the same structure. This is shown for [Cy3][NTf2] in Fig. 11. The combined evidence of the Cy3-anion distances indicating only weak interactions, the similarity of the intramolecular bonds across the different structures and yet the significantly different twists around the bonds of the linking conjugated chain in Cy3 indicate the extreme flexibility and ease of distortion of the Cy3 cation.
| Cy3 anion | θ | NC2C8C9 | SC2C8C9 | C2C8C9C8′ | C8C9C8′C2′ | C9C8′C2′N′ | C9C8′C2′S′ |
|---|---|---|---|---|---|---|---|
| a Cation with larger overall twist. b Cation with smaller overall twist. c Related by symmetry to C2C8C9C8′. d Related by symmetry to NC2C8C9. e Related by symmetry to SC2C8C9. | |||||||
| BF4(MeCN) | 10.4 | 175.4 (4.6) | −4.4 (4.4) | −180.0 (0) | 177.2 (2.8) | 175.8 (4.2) | −5.6 (5.6) |
| NTf2a | 26.8 | −170.9 (9.1) | 10.7 (10.7) | −174.5 (5.5) | |||
| NTf2b | 10.4 | 174.7 (5.3) | −5.2 (5.2) | 178.8 (1.2) | |||
| CHTf2a | 21.8 | −169.4 (10.6) | 11.1 (11.1) | −176.6 (3.4) | −175.1 (4.9) | −174.0 (6.0) | 6.4 (6.4) |
| CHTf2b | 8.31 | −173.2 (6.8) | 5.7 (5.7) | −179.9 (0.1) | −178.3 (1.7) | 0.177.0 (3.0) | 3.5 (3.5) |
| OTf | 15.07 | 179.8 (0.2) | −0.4 (0.4) | 178.1 (1.9) | 178.2 (1.8) | 168.4 (11.6) | −12.7 (12.7) |
| BF4/I | 9.02 | 176.0 (4.0) | −4.2 (4.2) | −179.0 (1.0) | 176.6 (3.4) | 176.5 (3.5) | −5.0 (5.0) |
| PF6 | 5.12 | 178.2 (1.8) | −3.1 (3.1) | 177.7 (2.3) | −179.3 (0.7) | 176.6 (3.4) | −3.4 (3.4) |
| I | 3.28 | 179.8 (0.2) | 1.5 (1.5) | −178.3 (1.7) | 178.2 (1.8) | −177.8 (2.2) | 1.0 (1.0) |
Further evidence of this flexibility comes from examination of the 3-bond torsion angles across the conjugated C3 linker (Table 6). For an ideal planar molecule, all of these torsion angles should either be 0° or 180°. In most cases the deviation from planarity is small, being 5° or less. This indicates that the overall twist angle between the benzothiazole rings is comprised of lots of small twists, which sum to a larger twist across the entire delocalised C3 linker. However, the cations with the biggest overall twists ([Cy3][OTf], [Cy3][CHTf2] and [Cy3][NTf2]) have torsion angles which deviate by 11° or more. These relatively large torsion angles all occur across the C2–C8 bond (or C8′–C2′) with only small torsion angles noted across the C8–C9 (or C9–C8′) bond, implying that the C2–C8 bond is the most flexible across the entire conjugated linker.
The study of the diffusion and rotational dynamics of charged solutes in various ionic liquids shows that charged solutes will partition into the ‘stiff’ polar domain generated by the charge carrying moieties in the cation and anion.30–35 The partitioning into the polar domain is very strong for solutes that are significantly smaller than the ionic liquid ions, while solutes that are larger in comparison to the ionic liquid will partition less strongly.34
As Cy3 is a relatively large molecular ion with a single positive charge distributed across its symmetrical structure (Fig. 2), it is expected that it will be solvated directly by the anions of the ionic liquid in an ion-cage like structure.
Although the mechanism for non-radiative decay in cyanine molecules is not fully understood, there have been some studies on the structures of the ground and excited states of Cy3. In molecular solvents the ground state has been taken to be a planar conformation, with the linking carbon chain being in an all-trans/(E)- isomer (as shown in Fig. 2), confirmed by both 1H NMR and computational analysis.10,46 Initially, it was thought that upon absorption of a photon, the Cy3 cation underwent a full cis/trans isomerisation about the C8–C9 bond.10 However 1H NMR analysis of coupling constants in the excited state found that the protons were not in a fully cis or trans isomer.46 Instead, in combination with computational analysis on a model system, it was determined that the benzothiazole ring of the photoisomer was twisted by 90° around the C2–C8 bond in comparison to the ground state.47 This confirmed previous studies by O'Brien et al. and Cooper et al. suggesting photoisomerisation around the C2–C8 bond.48,49 It was assumed that a full (E)- to (Z)-isomerisation was needed to non-radiatively quench based upon the calculations on a model system.10 Vladimirova et al. calculated the ground and excited state conformers of the entire cation in the gas phase and found that the minimum energy conformer in the excited state involves a twist of the benzothiazole ring around the C2–C8 bond leading to a perpendicular, twisted conformation. However on inclusion of an implicit dielectric solvent model they found that the optimum structure of the dye in the excited state had an angle of 76° between the benzothiazole rings, therefore not requiring a completely perpendicular orientation. They also found that because of this, it was possible for quenching to occur via a (E)-isomer → 76° → (E)-isomer pathway, eliminating the need for a full (E)- to (Z)-isomerisation.44
Returning to our results, the crystal structures show that different anions do not affect the bond lengths, instead they affect the twist of the molecule in the crystal phase. This is best seen when comparing the angles between the planes of the benzothiazole rings, which vary between 3.3° and 26.8°. In addition, the twist occurs over multiple dihedrals in the linker chain. This indicates that the twist angles generated by photoexcitation of the Cy3 cation calculated through computation may be misleading, as the calculations all involve a fixed linker chain with rotation around a single bond.44,46 These crystal structures show that allowing the whole linker to twist is a more realistic model of Cy3 twisting.
While the C2–C8 bond has the largest single twist angle in every structure, this apparent ease of twisting Cy3 highlights the high degree of flexibility of the Cy3 cation while in its ground state. In the liquid phase, this flexibility could also lead to greater accessibility to the secondary decay pathway.
All of our results show that Cy3 has a shorter lifetime in ionic liquids than in molecular solvents of the same bulk viscosity. That is, the microviscosity reported by a dye which we expect to be mostly partitioned into the ‘stiff’ polar region of the ionic liquid is lower than the microviscosity of the same dye recorded in an aqueous sucrose solution, opposite to what would be expected.
Ions in ionic liquids are solvated by oppositely-charged counterions which form a ‘cage’ structure within which the original ion is contained. For diffusion to occur, the ion must ‘jump’ from this cage to a neighbouring cage.50–52 It is this jump that provides a high activation barrier to translation, thus leading to slow diffusion of ions in ionic liquids. In their study of the size, shape, and charge of a solute rotating in [C4C1im][BF4] Rumble et al. demonstrated that such diffusive jumps were much more common and of greater amplitude for the smaller probes, where they significantly contributed to rotational diffusion coefficients, but rarer in the case of larger probes.35 Hence, one would expect Cy3 to experience a large friction to its diffusive motion. However, within the same study, Rumble et al. also showed other faster, spatially restricted motions of all of their solutes, regardless of size. These consisted of oscillations within a slowly relaxing environment which, along with other similar motions, are often described as ‘rattling’ inside the cage.35,53–55
This gives rise to the likely explanation for the lower than expected lifetime reported by Cy3, when compared to aqueous sucrose solutions with the same bulk viscosity. Rather than requiring a jump or movement between cages, it appears that sufficient molecular rotation of the dye can occur within its ion cage to allow non-radiative decay to take place.
Returning to our results, when considering the temperature dependent measurements, the ion cage flexibility is affected by both the bulk viscosity of the liquid, and short range inter-ionic interactions. Both of these factors change with temperature, therefore the lifetime of the rotor changes as such.
While the photophysical properties of Cy3 were found to be temperature independent upon binding to DNA,56 the direct effect of temperature on the viscosity dependent properties has not been previously investigated. Therefore we cannot exclude the effect of temperature on the trend observed in Fig. 8. Higher temperature may cause the non-radiative decay pathway to be more easily accessible, leading to an additional decrease in Cy3 lifetime, beyond the effect on viscosity of the solution, and one may expect to see lower lifetimes at high temperature if this was the case.
The changing fluorescence lifetimes of Cy3 in the different ionic liquids likely more closely reflects the changing flexibility of the anion cages in these liquids and hence the ease of rotation of Cy3 within these cages, and not the resistance of the cage to diffusive motion. This is most influenced by a change in the anion of the ionic liquid, however changes to the cation also affect the flexibility of the anion cage around the dye.
In these ionic liquids, the effect of the polarity of the ionic liquids upon the dye also requires consideration. The photophysical properties of Cy3 in different polarity environments have not been rigorously studied previously, therefore it is possible that there is some polarity related contribution to this effect i.e. polarity could effect the radiative and non-radiative decay pathways. As this dye is cationic, the polarity of the anions is the important quantity. This information is reflected in the β values of the ionic liquids, which is the Kamlet–Taft polarity scale measure of the ability of a solvent to donate electron density. The ionic liquids [C4C1im][X] where X = OTf, PF6, BF4 or NTf2 have very different β values.40 Therefore, the lack of a correlation between lifetimes and viscosities is likely due to a complex interplay between bulk viscosity, ion cage strength and flexibility, and polarity.
When using different cations to modify the viscosity and keeping the anion constant, this removes the issue of different polarities and ion cage structures. As mentioned previously, these ionic liquids have as little as possible difference in their polarities while still having variation in their viscosities. Therefore the interactions between the liquid and the dye should remain approximately constant and polarity related spectral changes will not be seen.
For the ionic liquids [CnC1im][NTf2] (n = 2, 3, 4, 6 or 8) a linear trend in the log–log plot is observed and the viscosity dependence of the lifetime can be fitted to the Förster–Hoffmann equation. The lifetimes of Cy3 in [C12C1im][NTf2] and [P4446][NTf2] are lower than would be predicted by this line.
Following the reasoning above, this suggests that the anion cages surrounding Cy3 in the latter two ionic liquids are more flexible than would be predicted from bulk viscosity changes alone. This further suggests that the presence of a continuous non-polar domain is enabling this greater flexibility. This implies that increasing the size of the non-polar domain is indirectly (i.e. via cation motion) affecting the flexibility of the anion cage. Confirmation of this will require further study.
4 Conclusions
In summary, by measuring the fluorescent lifetime decay of Cy3 and BODIPY-C10 in various ionic liquids, we have been able to infer the composition of the cybotactic regions of the dyes and how these change when systematically changing the ionic liquid.The neutral dye BODIPY-C10 appears to partition into the non-polar region of the ionic liquids. When there is not a large enough non-polar domain to fully encapsulate it, the BODIPY-C10 samples both polar and non-polar moieties, therefore there is a strong dependence of the rotor lifetime upon the bulk viscosity of the ionic liquid.
In ionic liquids with a large enough non-polar region to fully encapsulate the dye ([C8C1im][NTf2], [C12C1im][NTf2] and [P4446][NTf2]), BODIPY-C10 can fully partition into the non-polar domain, possibly templating the non-polar domain around itself. This leads to the dye reporting the microviscosity of only one domain, and therefore the lifetime of BODIPY-C10 has a lesser dependence upon the bulk viscosity of the ionic liquid.
The cationic Cy3 data indicates that this dye partitions into the polar domain, where it will be surrounded primarily by anions. The variable anion measurements show a complex trend, with no direct correlation between lifetime and viscosity. This most likely arises because the Cy3 fluorescence lifetime is affected by the interplay of the effects of the viscosity of its environment and specific cation–anion interactions.
When varying temperature, the lifetime and viscosity are correlated; however, the lifetime of the dye does not change in the way predicted by the Förster–Hoffmann equation. This has been attributed to a combination of temperature-dependent viscosity, temperature-dependent ion cage properties, and possible temperature-dependent fluorescence of the dye.
When keeping the anion and temperature constant, there is a clearer trend. In the absence of polarity and temperature effects, a simpler correlation with the bulk viscosity of the ionic liquids is observed.
Taken together, these results indicate that a simple picture of the rotor directly reporting the bulk viscosity is not applicable in ionic liquids. The viscosity reported depends greatly upon the nature of the probe. For example, the different charges on Cy3 and BODIPY-C10 lead to these sampling different domains, and therefore reporting a different fluorescence lifetime dependencies when changes are made to the ionic liquids. Not just this, but the suitability of the rotor to the measurement can be seen to make a large difference e.g. the possible polarity and temperature dependence of Cy3 means it is unsuitable for measuring variable anion ionic liquids.
Also the extent of partitioning into the non-polar domain by a neutral probe will depend upon the relative sizes of the probe itself and the non-polar domains. As the non-polar domain becomes large enough to completely encapsulate the probe it will report the fluidity of this domain alone. While less sensitive to these effects, charged probes are affected directly by cation–anion interactions which change with the ions of which the ionic liquids are composed, as well as viscosity effects.
Finally, we come to the question of suitable comparisons and calibration. Since there is no simple relationship between the fluorescent lifetimes of the dyes and the bulk viscosity of the ionic liquids, there is also no direct relationship between the fluorescence lifetime of any given dye in the ionic liquid and the bulk viscosity of any molecular system typically used to calibrate molecular rotors. Instead, when used with ionic liquids, careful consideration of which structural properties are being investigated is required to determine which rotor should be used, and how to relate the rotor lifetime to the microviscosity.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
RC would like to thank the EPSRC for a studentship via the Imperial College DTP allocation. QL acknowledges funding from the China Scholarship Council.Notes and references
- M. Galiński, A. Lewandowski and I. Stȩpniak, Electrochim. Acta, 2006, 51, 5567–5580 CrossRef.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- J. F. Wishart, Energy Environ. Sci., 2009, 2, 956 RSC.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS PubMed.
- A. P. Abbott and K. J. McKenzie, Phys. Chem. Chem. Phys., 2006, 8, 4265 RSC.
- D. Wei and A. Ivaska, Anal. Chim. Acta, 2008, 607, 126–135 CrossRef CAS PubMed.
- S. Jiang, Y. Hu, Y. Wang and X. Wang, J. Phys. Chem. Ref. Data, 2019, 48, 033101 CrossRef.
- M. A. Haidekker and E. A. Theodorakis, Org. Biomol. Chem., 2007, 5, 1669–1678 RSC.
- M. K. Kuimova, Phys. Chem. Chem. Phys., 2012, 14, 12671 RSC.
- F. Momicchioli, I. Baraldi and G. Berthier, Chem. Phys., 1988, 123, 103–112 CrossRef CAS.
- M. A. Haidekker and E. A. Theodorakis, J. Biol. Eng., 2010, 4, 11 CrossRef PubMed.
- N. A. Hosny, C. Fitzgerald, A. Vyšniauskas, A. Athanasiadis, T. Berkemeier, N. Uygur, U. Pöschl, M. Shiraiwa, M. Kalberer, F. D. Pope and M. K. Kuimova, Chem. Sci., 2016, 7, 1357–1367 RSC.
- R. E. Scalise, P. A. Caradonna, H. J. Tracy, J. L. Mullin and A. E. Keirstead, J. Inorg. Organomet. Polym. Mater., 2014, 24, 431–441 CrossRef CAS.
- P. K. Singh, A. K. Mora and S. Nath, Chem. Phys. Lett., 2016, 644, 296–301 CrossRef CAS.
- A. Paul and A. Samanta, J. Phys. Chem. B, 2008, 112, 16626–16632 CrossRef CAS PubMed.
- J. D. Kimball, S. Raut, L. P. Jameson, N. W. Smith, Z. Gryczynski and S. V. Dzyuba, RSC Adv., 2015, 5, 19508–19511 RSC.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- J. N. Canongia Lopes and A. A. Pádua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef CAS PubMed.
- K. Shimizu, C. E. Bernardes and J. N. Canongia Lopes, J. Phys. Chem. B, 2014, 118, 567–576 CrossRef CAS PubMed.
- D. Pontoni, J. Haddad, M. Di Michiel and M. Deutsch, Soft Matter, 2017, 13, 6947–6955 RSC.
- Y.-L. Wang, B. Li, S. Sarman and A. Laaksonen, J. Chem. Phys., 2017, 147, 224502 CrossRef PubMed.
- J. C. Araque, S. K. Yadav, M. Shadeck, M. Maroncelli and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 7015–7029 CrossRef CAS PubMed.
- J. A. Levitt, M. K. Kuimova, G. Yahioglu, P.-H. Chung, K. Suhling and D. Phillips, J. Phys. Chem. C, 2009, 113, 11634–11642 CrossRef CAS.
- F. J. Waller, A. G. Barrett, D. C. Braddock, D. Ramprasad, R. M. McKinnell, A. J. White, D. J. Williams and R. Ducray, J. Org. Chem., 1999, 64, 2910–2913 CrossRef CAS.
- A. Paul, P. K. Mandal and A. Samanta, Chem. Phys. Lett., 2005, 402, 375–379 CrossRef CAS.
- A. Paul, P. K. Mandal and A. Samanta, J. Phys. Chem. B, 2005, 109, 9148–9153 CrossRef CAS PubMed.
- A. Paul and A. Samanta, J. Chem. Sci., 2006, 118, 335–340 CrossRef CAS.
- M. Tariq, P. J. Carvalho, J. A. Coutinho, I. M. Marrucho, J. N. C. Lopes and L. P. Rebelo, Fluid Phase Equilib., 2011, 301, 22–32 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593–16600 CrossRef CAS.
- A. Skrzypczak and P. Neta, J. Phys. Chem. A, 2003, 7800–7803 CrossRef CAS.
- Y. Nishiyama, M. Terazima and Y. Kimura, J. Phys. Chem. B, 2009, 113, 5188–5193 CrossRef CAS PubMed.
- R. G. Evans, O. V. Klymenko, P. D. Price, S. G. Davies, C. Hardacre and R. G. Compton, ChemPhysChem, 2005, 6, 526–533 CrossRef CAS PubMed.
- R. P. Daly, J. C. Araque and C. J. Margulis, J. Chem. Phys., 2017, 147, 061102 CrossRef PubMed.
- A. Kaintz, G. Baker, A. Benesi and M. Maroncelli, J. Phys. Chem. B, 2013, 117, 11697–11708 CrossRef CAS PubMed.
- C. A. Rumble, C. Uitvlugt, B. Conway and M. Maroncelli, J. Phys. Chem. B, 2017, 121, 5094–5109 CrossRef CAS PubMed.
- H. L. Kee, C. Kirmaier, L. Yu, P. Thamyongkit, W. J. Youngblood, M. E. Calder, L. Ramos, B. C. Noll, D. F. Bocian, W. R. Scheidt, R. R. Birge, J. S. Lindsey and D. Holten, J. Phys. Chem. B, 2005, 109, 20433–20443 CrossRef CAS PubMed.
- A. Polita, S. Toliautas, R. Žvirblis and A. Vyšniauskas, Phys. Chem. Chem. Phys., 2020, 15–18 Search PubMed.
- A. Vyšniauskas, M. Qurashi, N. Gallop, M. Balaz, H. L. Anderson and M. K. Kuimova, Chem. Sci., 2015, 6, 5773–5778 RSC.
- A. Vyšniauskas, I. López-Duarte, N. Duchemin, T.-T. Vu, Y. Wu, E. M. Budynina, Y. A. Volkova, E. Peña Cabrera, D. E. Ramírez-Ornelas and M. K. Kuimova, Phys. Chem. Chem. Phys., 2017, 19, 25252–25259 RSC.
- M. A. Ab Rani, A. Brant, L. Crowhurst, A. Dolan, M. Lui, N. H. Hassan, J. P. Hallett, P. A. Hunt, H. Niedermeyer, J. M. Perez-Arlandis, M. Schrems, T. Welton and R. Wilding, Phys. Chem. Chem. Phys., 2011, 13, 16831 RSC.
- O. Russina, A. Triolo, L. Gontrani, R. Caminiti, D. Xiao, L. G. Hines, R. A. Bartsch, E. L. Quitevis, N. Plechkova and K. R. Seddon, J. Phys.: Condens. Matter, 2009, 21, 424121 CrossRef.
- R. Elfgen, O. Hollóczki and B. Kirchner, Acc. Chem. Res., 2017, 50, 2949–2957 CrossRef CAS PubMed.
- Y. Wu, M. Štefl, A. Olzyńska, M. Hof, G. Yahioglu, P. Yip, D. R. Casey, O. Ces, J. Humpolíčková and M. K. Kuimova, Phys. Chem. Chem. Phys., 2013, 15, 14986 RSC.
- K. G. Vladimirova, A. Y. Freidzon, A. A. Bagatur'yants, G. V. Zakharova, A. K. Chibisov and M. V. Alfimov, High Energy Chem., 2008, 42, 275–282 CrossRef CAS.
- I. Baraldi, A. Carnevali, F. Momicchioli and G. Ponterini, Spectrochim. Acta, Part A, 1993, 49, 471–495 CrossRef.
- S. Ghelli and G. Ponterini, J. Mol. Struct., 1995, 355, 193–200 CrossRef CAS.
- F. Dietz and S. K. Rentsch, Chem. Phys., 1985, 96, 145–151 CrossRef CAS.
- D. O'Brien, T. Kelly and L. Costa, Photogr. Sci. Eng., 1974, 18, 76–84 Search PubMed.
- W. Cooper, S. Lovell and W. West, Photogr. Sci. Eng., 1970, 14, 184–191 CAS.
- M. G. Del Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 1744–1752 CrossRef.
- S. Zahn, J. Thar and B. Kirchner, J. Chem. Phys., 2010, 132, 124506 CrossRef PubMed.
- G. Feng, M. Chen, S. Bi, Z. A. H. Goodwin, E. B. Postnikov, N. Brilliantov, M. Urbakh and A. A. Kornyshev, Phys. Rev. X, 2019, 9, 021024 CAS.
- T. Burankova, R. Hempelmann, A. Wildes and J. P. Embs, J. Phys. Chem. B, 2014, 118, 14452–14460 CrossRef CAS.
- F. Ferdeghini, Q. Berrod, J.-M. Zanotti, P. Judeinstein, V. G. Sakai, O. Czakkel, P. Fouquet and D. Constantin, Nanoscale, 2017, 9, 1901–1908 RSC.
- M. Casalegno, G. Raos, G. B. Appetecchi, S. Passerini, F. Castiglione and A. Mele, J. Phys. Chem. Lett., 2017, 8, 5196–5202 CrossRef CAS PubMed.
- M. E. Sanborn, B. K. Connolly, K. Gurunathan and M. Levitus, J. Phys. Chem. B, 2007, 111, 11064–11074 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Full synthetic procedures, crystallographic and simulation procedures and data, absorption and emission data for dyes in ionic liquids, full lifetime traces for the dyes in the ionic liquids and at various temperatures. CCDC 1995025 and 1995224–1995229. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc02009e |
‡ For comparison, distilled water gives a count of ≈1000 counts per second. Regular ionic liquids can have a fluorescence of >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 counts per second, even when pure by standard analytical techniques. 000 counts per second, even when pure by standard analytical techniques. |
| This journal is © The Royal Society of Chemistry 2020 |