Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New scaling relations to compute atom-in-material polarizabilities and dispersion coefficients: part 1. Theory and accuracy†
Thomas A. Manz *a,
Taoyi Chen
*a,
Taoyi Chen a,
Daniel J. Cole
a,
Daniel J. Cole b,
Nidia Gabaldon Limasa and
Benjamin Fiszbeina
b,
Nidia Gabaldon Limasa and
Benjamin Fiszbeina
aDepartment of Chemical & Materials Engineering, New Mexico State University, Las Cruces, New Mexico 88003-8001, USA. E-mail: tmanz@nmsu.edu
bSchool of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
First published on 19th June 2019
Abstract
Polarizabilities and London dispersion forces are important to many chemical processes. Force fields for classical atomistic simulations can be constructed using atom-in-material polarizabilities and Cn (n = 6, 8, 9, 10…) dispersion coefficients. This article addresses the key question of how to efficiently assign these parameters to constituent atoms in a material so that properties of the whole material are better reproduced. We develop a new set of scaling laws and computational algorithms (called MCLF) to do this in an accurate and computationally efficient manner across diverse material types. We introduce a conduction limit upper bound and m-scaling to describe the different behaviors of surface and buried atoms. We validate MCLF by comparing results to high-level benchmarks for isolated neutral and charged atoms, diverse diatomic molecules, various polyatomic molecules (e.g., polyacenes, fullerenes, and small organic and inorganic molecules), and dense solids (including metallic, covalent, and ionic). We also present results for the HIV reverse transcriptase enzyme complexed with an inhibitor molecule. MCLF provides the non-directionally screened polarizabilities required to construct force fields, the directionally-screened static polarizability tensor components and eigenvalues, and environmentally screened C6 coefficients. Overall, MCLF has improved accuracy compared to the TS-SCS method. For TS-SCS, we compared charge partitioning methods and show DDEC6 partitioning yields more accurate results than Hirshfeld partitioning. MCLF also gives approximations for C8, C9, and C10 dispersion coefficients and quantum Drude oscillator parameters. This method should find widespread applications to parameterize classical force fields and density functional theory (DFT) + dispersion methods.
1. Introduction
When combined with large-scale density functional theory (DFT) calculations, the DDEC method has been shown to be suitable for assigning atom-centered point charges for flexible molecular mechanics force-field design.1–8 The assignment of C6 coefficients and atomic polarizabilities is another active area of research in force field design.3,9–12 Polarization effects are especially important for simulating materials containing ions.13–20 When considered alongside the importance of accurate theoretical methods to study van der Waals interactions at the nanoscale,21 it is clear that a crucial feature of new methods to compute these important quantities is the ability to scale to large system sizes in reasonable computational time.In this article, we develop new scaling laws and an associated method to compute polarizabilities and dispersion coefficients for atoms-in-materials (AIMs). These new scaling laws and computational method give good results for isolated atoms, diatomic molecules, polyatomic molecules, nanostructured materials, solids, and other materials. This new method is abbreviated MCLF according to the authors' last name initials (where the C is both for Chen and Cole). We performed tests on isolated neutral and charged atoms, small molecules, fullerenes, polyatomic molecules, solids, and a large biomolecule with MCLF. The results were compared with experimental data, high level CCSD calculations, time-dependent DFT (TD-DFT) calculations, or published force-field parameters.
As discussed in several recent reviews and perspectives, the dispersion interaction is a long-range, non-local interaction caused by fluctuating multipoles between atoms in materials.22–26 It is especially important in (i) condensed phases including liquids, supercritical fluids, solids, and colloids, (ii) nanostructure binding such as the graphene layers forming graphite, and (iii) the formation of noble gas dimers. The dispersion interaction is closely related to AIM polarizabilities. The dispersion energy can be described by an expansion series. The leading term is inversely proportional to R6, where R is the distance between two atoms. The coefficient of this term is called the C6 dispersion coefficient, and this term quantifies fluctuating dipole–dipole interactions between two atoms. The intermolecular C6 coefficient is given by the sum of all interatomic contributions
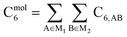 | (1) |
Methods for computing polarizabilities and dispersion coefficients can be divided into two broad classes: (A) quantum chemistry methods that explicitly compute the system response to an electric field (e.g., TD-DFT, CCSD perturbation response theory, etc.) and (B) AIM models. Class A methods can be highly accurate for computing polarizabilities and dispersion coefficients of a whole molecule, but they do not provide AIM properties. Therefore, class A methods cannot be regarded as more accurate versions of class B methods. Parameterizing a molecular mechanics force-field from quantum mechanics requires an AIM (i.e., class B) model. Our goal here is not merely to develop a computationally cheaper method than TD-DFT or CCSD perturbation response theory to compute accurate system polarizabilities and dispersion coefficients, but rather to exceed the capabilities of both of those methods by providing accurate AIM properties for force-field parameterization.
One must distinguish the polarizability due to electron cloud distortion from the polarization due to molecular orientation (and other geometry changes) such as occurs in ferroelectric materials. Herein, we are solely interested in the polarizability that occurs due to electron cloud distortions. Electric polarization due to molecular orientation and other geometric changes can be described by a geometric quantum phase.28–30
There are several existing frameworks for calculating AIM polarizabilities and/or dispersion coefficients. Applequist et al. 31 introduced a formalism that represents the molecular polarizability tensor in terms of AIM polarizabilities via the dipole interaction tensor. Thole32 refined this formalism by replacing atomic point dipoles with shape functions to avoid infinite interaction energies between adjacent atoms. Applequist's and Thole's methods use empirical atomic polarizability fitting to reproduce observed polarizability tensors of small molecules.31,32 Mayer et al. added charge–charge and dipole–charge interaction terms to calculate more accurate polarizabilities of conducting materials.33,34 Grimme et al. presented the D3 geometry-based method to calculate C6, C8, and C9 dispersion coefficients and dispersion energies, but this method does not yield polarizability tensors.11 The recently formulated D4 models are geometry-based methods that extend the D3 formalism by including atomic-charge dependence.35–37 The exchange-dipole model (XDM) is an orbital-dependent approach that yields AIM dipole, quadrupole, and octupole polarizabilities and C6, C8, and C10 dispersion coefficients.38–42 Several density-dependent XDM variants have been formulated.43,44 In 2009, Tkatchenko and Scheffler introduced the TS method for isotropic AIM polarizabilities and C6 coefficients.12 Both the XDM and TS methods yielded isotropic AIM polarizabilities rather than molecular polarizability tensors.12,38–44 In both the XDM and TS methods, the AIM unscreened polarizability is given by
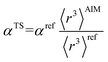 | (2) |
In 2012, Tkatchenko et al. introduced self-consistent screening (TS-SCS) via the dipole interaction tensor to yield the molecular polarizability tensor and screened C6 coefficients.46 The TS-SCS dipole interaction tensor uses a quantum harmonic oscillator (QHO) model similar to that used by Mayer but extended over imaginary frequencies and omitting charge–dipole and charge–charge terms.33,34,46 That same article also used a multibody dispersion (MBD46,47) energy model based on a coupled fluctuating dipole model (CFDM47,48). The TS-SCS screened static polarizability and characteristic frequency for each atom are fed into the CFDM model to obtain the MBD energy.46 The TS-SCS approach has advantages of yielding a molecular polarizability tensor and AIM screened polarizabilities and AIM screened C6 coefficients using only the system's electron density distribution as input.46
The TS-SCS method has several key limitations. Two key assumptions of the TS-SCS method are: (i) for a specific chemical element, the unscreened atomic polarizability is proportional to the atom's 〈r3〉 moment, and (ii) for a specific chemical element, the unscreened C6 coefficient is proportional to the atom's polarizability squared.12,46 However, in their work these hypotheses were not directly tested.12,46 Later, Gould tested these two assumptions and found them inaccurate for describing isolated neutral atoms placed in a confinement potential.49 Hirshfeld partitioning was used in the TS-SCS method12,46 to compute the 〈r3〉AIM. Because Hirshfeld partitioning uses isolated neutral atoms as references,45 the Hirshfeld method typically severely underestimates net atomic charge magnitudes.50–53 The TS-SCS method assumes a constant unscreened polarizability-to-〈r3〉 ratio and constant characteristic frequency (wp) for all charge states of a chemical element,46 but these assumptions are not realistic. Due to these assumptions, the TS and TS-SCS methods are inaccurate for systems with charged atoms.54–57 Bucko et al. showed the TS and TS-SCS methods severely overestimate polarizabilities for dense solids.57 The TS-SCS method has also not been optimized to work with conducting materials, and we show in Section 5.2 below the TS and TS-SCS methods sometimes predict erroneous polarizabilities even greater than for a perfect conductor. As discussed in Sections 4 and 5 below, the TS-SCS method overestimates directional alignment of fluctuating dipoles at large interatomic distances. We also show the TS-SCS method sometimes gives asymmetric AIM polarizability tensors and unphysical negative AIM polarizabilities.
Several research groups developed improvements to the TS-SCS method. Ambrosetti et al. introduced range separation to avoid double counting the long-range interactions in TS-SCS followed by MBD (aka MBD@rsSCS).58 MBD@rsSCS improves the accuracy of describing directional alignments of fluctuating dipoles at large interatomic distances.58 Bucko et al. used Iterative Hirshfeld (IH51) partitioning in place of Hirshfeld partitioning to compute 〈r3〉AIM.55,57 While this was an improvement, it did not address several problems mentioned above. For example, the TS-SCS/IH method still unrealistically assumed the unscreened polarizability-to-〈r3〉 ratio is the same for various charge states of a chemical element.55,57 This assumption was removed in the subsequent Fractionally Ionic (FI) method.54 However, the FI approach requires separate reference polarizabilities and C6 dispersion coefficients for all charge states of a chemical element.54 This is extremely problematic, because some anions that exist in condensed materials (e.g., O−2) have unbound electrons in isolation.59 Although methods to compute charge-compensated reference ion densities have been developed,53,55,59–64 those methods do not presently extend to computing charge-compensated polarizabilities and C6 coefficients of ions. Thus, several problems with the TS-SCS approach have not been satisfactorily resolved in the prior literature.
In Gould et al.'s FI method, reference free atom polarizabilities were computed for various whole numbers of electrons and interpolated to find fractionally charged free atom reference polarizabilities.54 This yields different polarizability-to-〈r3〉 ratios for different charge states of the same chemical element.54 Due to the instability of highly charged anions, the −1 states of halogens were the only anions Gould et al. computed self-consistently.54,65 For other anions, Gould and Bucko resorted to using DFT orbitals from the neutral atoms to build non-self-consistent anions for polarizability and C6 calculations,65 but this severely underestimates the diffuseness of anions (i.e., underestimates their polarizabilities and C6 coefficients). Unfortunately, this problem cannot be easily resolved by performing self-consistent calculations for all charged states, because some highly charged anions (e.g., O2−)59 contain unbound electrons. This makes the FI method problematic for materials containing highly charged anions. Because FI was not included in VASP version 6b that we currently have access to, we did not perform FI calculations for comparison in this work.
In this article, we develop a new approach that resolves these issues. Our method uses DDEC6 (ref. 61 and 66–68) partitioning to provide accurate net atomic charges (NACs), atomic volumes, and radial moments as inputs. Our method has new scaling laws for the unscreened atomic polarizabilities, characteristic frequency (wp), and C6 dispersion coefficients. The different scaling behaviors of surface and buried atoms are included via m-scaling. Our approach accurately handles the variability in polarizability-to-〈r3〉 moment ratio for charged surface atoms while only requiring reference atomic polarizabilities, reference C6 coefficients, and reference radial moments for isolated neutral atoms. It uses a new self-consistent screening procedure to compute screened polarizability tensors and C6 coefficients. Our approach separates non-directional screening from directional screening of the dipole interaction tensor. This allows a conduction limit upper bound to be applied between non-directional and directional screening to ensure buried atoms do not have a screened polarizability above the conduction limit. Our method yields three different types of dipole polarizabilities: (a) induced static polarizabilities corresponding to a uniform applied external electric field, (b) isotropic screened polarizabilities suitable as input into polarizable force-fields, and (c) fluctuating polarizabilities that are used to compute C6 dispersion coefficients via the Casimir–Polder integral. When computing C6 dispersion coefficients, we use multi-body screening to taper off the dipole directional alignment at large interatomic distances. The self-consistent screening is applied incrementally. Richardson extrapolation provides high numeric precision. Through quantum Drude oscillator (QDO) parameterization, our method also yields higher-order polarizabilities (e.g., quadrupolar, octupolar, etc.) and higher-order dispersion coefficients (e.g., C8, C9, C10, etc.) for AIMs. Other important improvements include: improved damping radii, proportional partitioning of shared polarizability components to avoid negative AIM polarizabilities, iterative update of the spherical Gaussian dipole width, and AIM polarizabilities are symmetric tensors.
Our method was designed to satisfy the following criteria:
(1) The method should require only the system's electron and spin density distributions as input;
(2) The method should work for materials with 0, 1, 2, or 3 periodic boundary conditions;
(3) The method should give accurate results for charged atoms in materials while only requiring reference polarizabilities and reference C6 coefficients for neutral free atoms; (In this context, reference polarizabilities and reference C6 coefficients refer to those polarizabilities and C6 coefficients stored within the software program that are used during application of the method.)
(4) The method should give accurate results for diverse materials types: isolated atoms; small and large molecules; nanostructured materials; ionic, covalent, and metallic solids, etc.;
(5) The method should give accurate results for both surface and buried atoms;
(6) The method should yield both static polarizability tensors and polarizabilities suitable for constructing molecular mechanics force-fields;
(7) The method should accurately describe both short- and long-range ordering of dipole polarizabilities and C6 coefficients;
(8) The method should have less than approximately 10% average unsigned error on C6 coefficients and dipole polarizabilities for the benchmark sets studied here;
(9) The method should include estimates for higher-order AIM polarizabilities (e.g., quadrupolar, octupolar, etc.) and dispersion coefficients (e.g., C8, C9, C10, etc.);
(10) The method should have low computational cost for both small and large systems.
There are two main applications for this MCLF method. First, the polarizabilities and dispersion coefficients can be used to partially parameterize molecular mechanics force-fields. In addition to polarizabilities and C6 dispersion coefficients, those force-fields would also need to include net atomic charges (NACs), flexibility parameters (e.g., bond, angle, and torsion terms), exchange–repulsion parameters, (optionally) charge penetration parameters, and optionally other parameters. Second, the dispersion coefficients can be used to partially parameterize DFT + dispersion methods.23 In addition to the C6 dispersion coefficients, an accurate DFT + dispersion method should also include higher-order dispersion (e.g., C8, C9, and/or C10 terms) or multi-body dispersion (MBD) combined with an accurate damping function.22,23 (Partially analogous to the MBD@rsSCS method,58 range separation would be required to avoid double counting dispersion interactions when combining a MCLF variant with a MBD Hamiltonian.) Because DFT and molecular mechanics are widely used in computational chemistry, our new method can have widespread applications.
The remainder of this article is organized as follows. Section 2 contains the background information. Section 3 contains the new isolated atom scaling laws developed for MCLF. Section 4 describes the theory of the MCLF method. Section 5 contains calculation results of C6 coefficients and polarizabilities and comparisons to benchmark data. Section 6 is the conclusions.
2. Background information
2.1 Benchmarking methods
Experimental data and high-level quantum chemistry calculations were used as references in this work. Section 3.1 below describes reference polarizabilities and dispersion coefficients (C6, C8, and C10) for the isolated atoms. For diatomic molecules in Section 5.1, we computed static polarizability tensors using CCSD calculations combined with the “polar” keyword in Gaussian09 (ref. 69). As explained in Section 5.2 below, we set the reference static polarizability for dense solids to the lesser of the Clausius–Mossotti relation value and the conduction limit upper bound based on the experimental crystal structure geometry and dielectric constant.For the small molecules in Section 5.3, reference static polarizabilities were obtained from published experiments. Experimental isotropic polarizabilities were extracted from dielectric constant or refractive index measurements having approximately 0.5% or less error.70 Refractive index can be measured by passing a light ray through a gas-phase sample.71 The polarizability α(ν) of the sample at frequency ν can then be calculated using
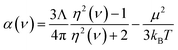 | (3) |
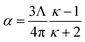 | (4) |
Reference C6 coefficients for the atom/molecule pairs (Section 5.4) were taken from the experimentally extracted dipole oscillator strength distribution (DOSD) data of Meath and co-workers74,75 as tabulated by Bucko et al.55
Time-dependent DFT (TD-DFT) and time-dependent Hartree–Fock (TD-HF) can be used to compute benchmark polarizabilities and dispersion coefficients. The Casimir–Polder integral is used to calculate C6 coefficients from polarizabilities at imaginary frequencies (imfreqs).76 For polyacenes (Section 5.5), reference C6 coefficients and isotropic static polarizabilities are from the TD-DFT calculations of Marques et al.77 For selected polyacenes, static polarizability tensor components were available as reference from Jiemchooroj et al.'s TD-DFT calculations.78 Jiemchooroj et al. found their TD-DFT results were similar to TD-HF, experimental (where available), and CCSD (where available) results. For fullerenes (Section 5.5), the reference C6 coefficients and isotropic static polarizabilities are from the TD-HF calculations of Kauczor et al.116 Kauczor et al. also obtained similar results using TD-DFT.116
2.2 Notation
A system may have either 0, 1, 2, or 3 periodic boundary conditions. In periodic materials, the term ‘image’ refers to a translated image of the reference unit cell. Each image is designated by translation integers (L1, L2, L3) that quantify the unit cell translation along the lattice vectors. The reference unit cell is the image designated by (L1, L2, L3) = (0, 0, 0). −∞ ≤ Li ≤ ∞ along a periodic direction. Li = 0 along a non-periodic direction. Similar to the notation previously used in the bond order article,67 a capital letter (A, B,…) designates an atom in the reference unit cell and a lowercase letter (a, b,…) designates an image atom. For example, b = (B, L1, L2, L3) denotes a translated image of atom B.Let ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) B represent the nuclear position of atom B in the reference unit cell. Then, the nuclear position of a translated image is
B represent the nuclear position of atom B in the reference unit cell. Then, the nuclear position of a translated image is
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) b = b = ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) B + L1 B + L1![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (1) + L2 (1) + L2![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (2) + L3 (2) + L3![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (3) (3)
| (5) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (1),
(1), ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (2), and
(2), and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (3) are the lattice vectors. The distance between the nuclear position of atom A and the translated image of atom B is
(3) are the lattice vectors. The distance between the nuclear position of atom A and the translated image of atom B is
dAb = rAB,L = ‖![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) b − b − ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) A‖ A‖
| (6) |
rAB,Ls = ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) b − b − ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) A A
| (7) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A is the vector from the image of atom A's nuclear position to the spatial position
A is the vector from the image of atom A's nuclear position to the spatial position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) :
:
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A = A = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) − L1 − L1![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (1) − L2 (1) − L2![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (2) − L3 (2) − L3![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (3) − (3) − ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) A A
| (8) |
rA = ‖![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A‖ A‖
| (9) |
A stockholder partitioning method assigns a set of atomic electron densities {ρA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A)} in proportion to atomic weighting factors {wA(rA)}
A)} in proportion to atomic weighting factors {wA(rA)}
ρA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A) = ρ( A) = ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )wA(rA)/W( )wA(rA)/W(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) )
| (10) |
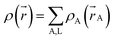 | (11) |
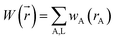 | (12) |
NA = ∮ρA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A)d3 A)d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A = ΘA − qA A = ΘA − qA
| (13) |
〈(rA)ϕ〉 = ∮(rA)ϕρA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A)d3 A)d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A A
| (14) |
Since a particular dispersion-polarization model can be combined with different charge partitioning methods, we indicate the combination by the dispersion-polarization model followed by ‘/’ followed by the charge partitioning method. For example, TS-SCS/IH indicates the TS-SCS dispersion-polarization model using IH charge partitioning. Where our computed data are simply labeled ‘TS-SCS’, the DDEC6 charge partitioning method was used. Since all of the MCLF results reported in this paper used DDEC6 charge partitioning, we used the less precise but shorter term ‘MCLF’ in place of the full ‘MCLF/DDEC6’ designation. More generally, the MCLF dispersion-polarization model could potentially be combined with other charge partitioning methods (e.g., MCLF/IH), but that is beyond the scope of the present study.
Calculating dispersion coefficients involves integrating polarizabilities over imfreqs. This is inconvenient in two respects. First, it is easier to deal with real-valued variables rather than imaginary-valued ones. Second, numeric integration from zero to infinite imaginary frequency is inconvenient, because infinity cannot be readily divided into finite intervals for numeric integration. Letting ω represent an imaginary frequency magnitude, we used the following variable transformation to solve these two problems:
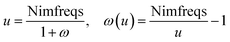 | (15) |
2.3 Details of the TS-SCS methodology
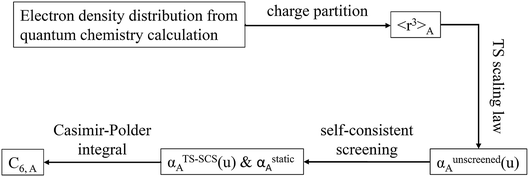
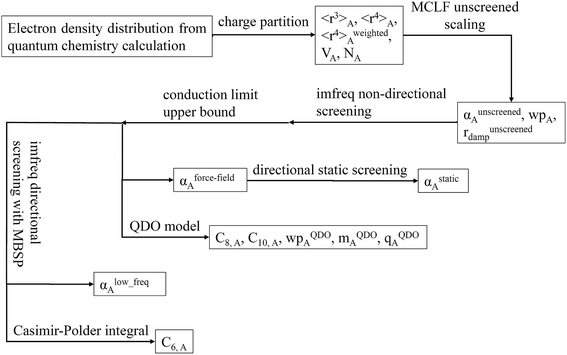
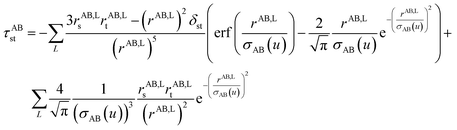
Fig. 1 is a flow diagram of the TS-SCS method. Bucko et al.56 gave the step-by-step calculation of the self-consistent screening process. Here, we follow the presentation of Bucko et al., except using the variable substitution of eqn (15). For atoms A and B, they define a many-body polarizability matrix P, with its inverse Q having the form
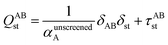 | (16) |
 | (17) |
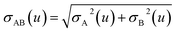 | (18) |
The spherical Gaussian dipole width is obtained from
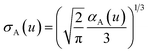 | (19) |
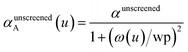 | (20) |
In the TS and TS-SCS methods,
| αunscreened = αTS | (21) |
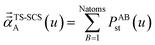 | (22) |
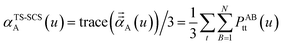 | (23) |
These are fed into the Casimir–Polder integral expressed in terms of u (see companion article for derivation79)
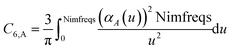 | (24) |
2.4 Electron density partitioning methods
In Hirshfeld partitioning introduced in 1977, atoms are partitioned to resemble the neutral reference atom.45 This makes the atoms tend to have lower charge than they should have.50 The iterative Hirshfeld partition (IH) keeps updating the reference with the charge state of the atom.51 However, this approach leads to the runaway charge problem in some cases.61 As shown in ref. 57 and Section 5.2 below, using TS or TS-SCS with Hirshfeld or IH partitioning overestimates polarizabilities for dense solids.Manz and Sholl presented DDEC1 and 2 atomic population analysis methods in 2010.60 By simultaneously optimizing the AIM density distributions to be close to spherically symmetric and to resemble charge-compensated reference ion densities, this method can give chemically meaningful NACs and accurate electrostatic potential for some materials, but was later found to give runaway charges in other materials. In 2012, Manz and Sholl presented the DDEC3 method that partially fixes the runaway charge problem by increasing the optimization landscape curvature via conditioned reference densities and imposing an exponential decay constraint on each atom's electron density tail.53
Manz and Limas presented DDEC6 partitioning in 2016.61,66 This method fixes the runaway charge problem. Also, new constraints are added to the decay rate of the buried atom tails. The weighted spherical average improves the effect of spherical averaging during charge partitioning. Along with guaranteed convergence in seven steps, this method is very accurate, cost efficient, and produces chemically meaningful NACs.61,66,68 In 2017, Manz published a new method for computing bond orders, which is based on DDEC6.67
3. New isolated atom scaling laws
3.1 Reference data
The reference polarizabilities (αCCSD) used in this work are our calculated polarizabilities using the CCSD method with def2QZVPPDD basis set (the def2QZVPPDD basis set is defined in the ESI†). We tested two different methods: (a) using Gaussian09 (ref. 69) keyword ‘polar’ to compute the molecular static polarizability tensor using perturbation response theory and (b) using Gaussian09 keyword ‘field’ to manually apply a small constant external electric field![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) in order to calculate the molecular static polarizability tensor as
in order to calculate the molecular static polarizability tensor as 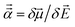 where μ→ is the molecular dipole moment. However, many of the manual (i.e., keyword = ‘field’) calculations did not converge and the converged results were not as consistent with Gould and Bucko's data65 as the perturbation response calculations. So we decided to use the perturbation response calculations (i.e., keyword = ‘polar’) for all elements except Y. For Y, the keyword = ‘field’ polarizability was used, because the perturbation response calculation gave an unreasonably low polarizability of 88.98 compared to αGould = 163 while the manually applied field polarizability of 158.81 was close to Gould and Bucko's value and followed the trend of neighboring elements: αSr,CCSD = 204.51 αZr,CCSD = 143.47.
where μ→ is the molecular dipole moment. However, many of the manual (i.e., keyword = ‘field’) calculations did not converge and the converged results were not as consistent with Gould and Bucko's data65 as the perturbation response calculations. So we decided to use the perturbation response calculations (i.e., keyword = ‘polar’) for all elements except Y. For Y, the keyword = ‘field’ polarizability was used, because the perturbation response calculation gave an unreasonably low polarizability of 88.98 compared to αGould = 163 while the manually applied field polarizability of 158.81 was close to Gould and Bucko's value and followed the trend of neighboring elements: αSr,CCSD = 204.51 αZr,CCSD = 143.47.
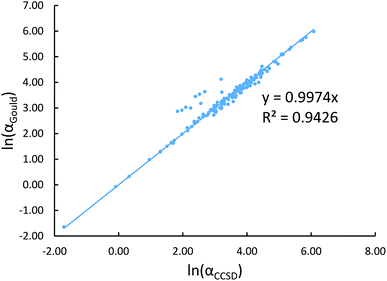
Fig. 2 shows that our calculated polarizabilities are mostly consistent with Gould and Bucko's values. We used αCCSD rather than αGould as the reference free atom polarizability, because our radial moments come from the same CCSD calculations as used to compute αCCSD. For elements using a relativistic effective core potential (RECP) in the def2-QZVPPDD basis set, the radial moments of core electrons replaced by the RECP are added back in using a reference core density library; thus yielding effective all-electron radial moments. Since Gould and Bucko used the aufbau principle for electron configurations of transition metal atoms, their calculations do not necessarily correspond to the ground state spin multiplicity for transition metal atoms.65 Recently, Schwerdtfeger and Nagle published a set of recommended polarizabilities for chemical elements 1 to 120 (except livermorium), but those were not used in our study because they do not have a corresponding set of C6 values.80
CCSD in Gaussian09 does not have the capability of calculating C6 coefficients. Therefore, to maximize consistency between the free atom reference radial moments, polarizabilities, and C6 coefficients, our reference C6 coefficients were calculated as
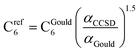 | (25) |
The reference α, C6, wp, r moments, and damping radii are listed in the ESI.† This dataset contains neutral elements 1–86 except the f-block elements (58–71). The reason for excluding the f-block and heavier elements is the def2QZVPPDD basis set we are using does not include these elements. The dataset also includes +1 cations of elements 3–7, 11–17, 19–57 and 72–86 and −1 anions of F, Cl, Br, I, and At. These ions were also self-consistently calculated by Gould and Bucko.65 Gould and Bucko included additional anions which were not computed self-consistently, and we omit these because self-consistent polarizabilities are unavailable.65 The reference wp were calculated from the CCSD polarizability and the Cref6 using81
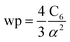 | (26) |
The reference C8 and C10 are from several sources compiled by Porsev and Derevianko82 and Tao et al.83 and are listed in the ESI.† This dataset contains H, Li, Na, K, Rb, Cs, He, Ne, Ar, Kr, Xe, Be, Mg and Ca. Most of these reference values are based on correlated quantum chemistry calculations.
3.2 Deriving the new scaling laws
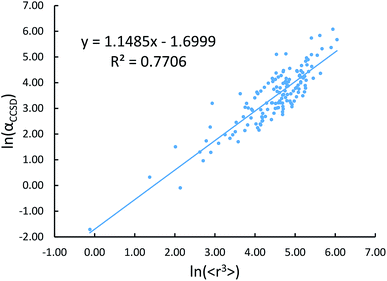
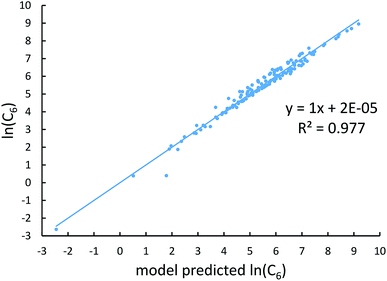
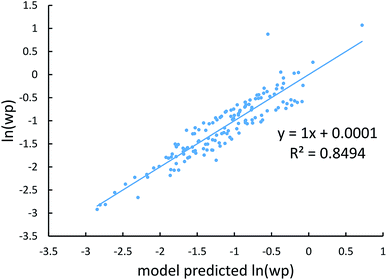
Johnson and Becke assumed that for a given chemical element, the polarizability of atoms in a material should be proportional to the 〈r3〉 moment of the atom-in-material.42 This assumption was subsequently adopted by Tkatchenko and Scheffler when formulating the TS method.12 Of course, this is not the same as assuming polarizabilities of isolated atoms across different chemical elements should be proportional to their 〈r3〉 moments. As pointed out by Gould, the isolated atom polarizabilities are not proportional to their 〈r3〉 moments.49 Fig. 3 is a plot of ln(polarizability) versus ln(〈r3〉) for the isolated atoms. This plot shows a weak correlation (R2 = 0.7706). This motivated us to develop a new polarizability scaling law that applies both to isolated atoms and to atoms-in-materials across different chemical elements.We tested seven models containing electron number and different combinations of the r moments as the independent variables and α, C6, and wp as the dependent functions. Table 1 lists the R2 values of the 7 models. The coefficients were obtained by least squares fitting of a linear combination of the log values of r moments and electron numbers to α, C6, or wp using a Matlab program we wrote. For example, the entry in row 2 and column 2 in Table 1 is the R2 value of 0.6626 obtained by fitting log(〈r〉) and log of electron number to log(αCCSD). The results show that using only one r moment does not yield high R2 value. Combinations of two or more r moments give higher R2 values, with the 〈r3〉 & 〈r4〉 model giving the best average performance.
| Model | αCCSD | C6 | wp |
|---|---|---|---|
| N & 〈r〉 | 0.6626 | 0.7619 | 0.3922 |
| N & 〈r2〉 | 0.8021 | 0.8809 | 0.5489 |
| N & 〈r3〉 | 0.8831 | 0.9414 | 0.6615 |
| N & 〈r4〉 | 0.9242 | 0.9672 | 0.7317 |
| N, 〈r2〉 & 〈r3〉 | 0.9457 | 0.973 | 0.8222 |
| N, 〈r2〉 & 〈r4〉 | 0.9545 | 0.9772 | 0.8452 |
| N, 〈r3〉 & 〈r4〉 | 0.9549 | 0.977 | 0.8494 |
Table 2 lists parameters for the 〈r3〉 & 〈r4〉 model. The proposed relations between α, wp, and C6 and the parameters have the following form, where all quantities are expressed in atomic units:
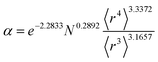 | (27) |
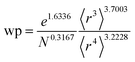 | (28) |
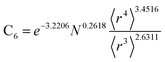 | (29) |
| α | C6 | wp | |||
|---|---|---|---|---|---|
| Component | Coefficient | Component | Coefficient | Component | Coefficient |
| Constant | −2.2833 | Constant | −3.2206 | Constant | 1.6336 |
| N | 0.2892 | N | 0.2618 | N | −0.3167 |
| 〈r3〉 | −3.1657 | 〈r3〉 | −2.6311 | 〈r3〉 | 3.7003 |
| 〈r4〉 | 3.3372 | 〈r4〉 | 3.4516 | 〈r4〉 | −3.2228 |
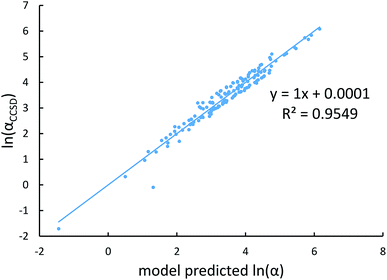
Fig. 4, 5, and 6 show strong correlation between the model predicted α, C6, and wp and the reference data with R2 values of 0.9549, 0.977, and 0.8494, respectively.
To test the robustness and transferability of the different models, the following tests were performed as shown in Table 3. The “PW91 refitted” column are the R2 values obtained by refitting the model parameters with r moments from PW91. Manz and Limas performed these PW91 calculations in Gaussian09 using an all-electron fourth-order Douglas–Kroll–Hess relativistic Hamiltonian with spin–orbit coupling (DKHSO) and the MUGBS basis set near the complete basis set limit employing a finite-size Gaussian nuclear model.60,61 The “PW91 predicted” column are the R2 values calculated using CCSD model parameters from Table 1 but with PW91 r moments instead of CCSD r moments. Table 3 shows that the 〈r3〉 & 〈r4〉 model has the highest R2 in both tests; therefore, this model is the most robust and transferable.
| Model | PW91 refitted | PW91 predicted | ||||
|---|---|---|---|---|---|---|
| αCCSD | C6 | wp | αCCSD | C6 | wp | |
| N, 〈r2〉 & 〈r3〉 | 0.8785 | 0.9130 | 0.7571 | 0.8127 | 0.8658 | 0.6181 |
| N, 〈r2〉 & 〈r4〉 | 0.8904 | 0.9176 | 0.7942 | 0.8276 | 0.8706 | 0.6780 |
| N, 〈r3〉 & 〈r4〉 | 0.8942 | 0.9181 | 0.8159 | 0.8345 | 0.8726 | 0.7104 |
Hence, the new polarizability scaling law for an isolated atom is
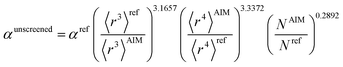 | (30) |
 | (31) |
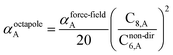
3.3 Higher-order dispersion coefficients and quantum Drude oscillator parameters
In this section, we consider higher-order dispersion coefficients C8, C9, and C10 and their mixing rules. The contribution of the three-body C9 term to the dispersion energy is typically less than 10%.11 Nevertheless, McDaniel and Schmidt84 showed that in order to obtain accurate results from force-field simulations for condensed phases, the three-body term (EABC) should be included. Tang and Toennies showed that the attractive potential at well depth for two free atoms is mainly composed of C6, C8, and C10 with contributions of roughly 65%, 25%, and 7% respectively.85 The rest comes from higher-order terms. Because the C8, C9, and C10 terms have modest contributions, we decided to include them in our model.The C8,A coefficient describes the fluctuating-dipole-fluctuating-quadrupole two-body dispersion interaction between atoms of the same type. We defined two groups (with all quantities expressed in atomic units) for least-squares fitting to obtain a model for C8,A:
 | (32) |
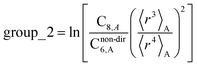 | (33) |
The reason for using 〈r3〉 and 〈r4〉 is that these are the same r moments used in models discussed above. Since C8,A describes the fluctuating dipole–quadrupole coupling while C6,A describes the fluctuating dipole–dipole coupling, there is no reason to believe directional effects on C8,A follow those on C6,A. Therefore, our correlations for higher-order dispersion coefficients (i.e., C8, C9, and C10) do not include directional coupling. Cnon-dir6,A is obtained using the imfreq-dependent non-directionally screened atomic polarizability αnon-dirA(u) in the Casimir–Polder integral. Linear fitting was performed to obtain the slope and intercept for group 2 as a function of group 1. The results were 0.8305 for the slope and 1.7327 for the intercept yielding:
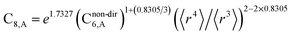 | (34) |
The Quantum Drude Oscillator (QDO) model provides a natural framework for describing multibody polarizability and dispersion interactions beyond the dipole approximation, including quadrupolar, octupolar, and high-order interactions.9,86,87 A QDO consists of a negative pseudoparticle coupled via a harmonic potential to a pseudonucleus.9,86,87 This harmonic coupling produces a Gaussian charge distribution.9,86 In our model, one QDO is centered on each atom in the material. Each QDO is completely described by three parameters: (a) an effective mass (mQDO), (b) an effective charge (qQDO), and (c) an effective frequency (wpQDO).9,86 Using literature relations9 applied to our non-directionally screened quantities yields
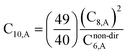 | (35) |
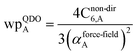 | (36) |
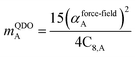 | (37) |
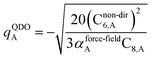 | (38) |
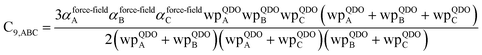 | (39) |
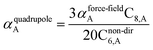 | (40) |
 | (41) |
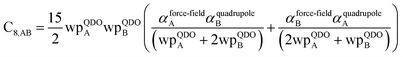 | (42) |
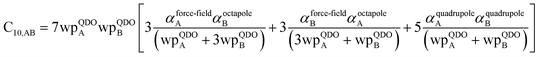 | (43) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(∠a)cos(∠b)cos(∠c))/(RABRACRBC)3 where ∠a, ∠b, and ∠c are the angles of the ABC triangle.81,164–166 The top right panel of Fig. 7 shows strong correlation between the model predicted C10,A and the reference data82,83 for selected isolated atoms with MARE of 18.6%.
cos(∠a)cos(∠b)cos(∠c))/(RABRACRBC)3 where ∠a, ∠b, and ∠c are the angles of the ABC triangle.81,164–166 The top right panel of Fig. 7 shows strong correlation between the model predicted C10,A and the reference data82,83 for selected isolated atoms with MARE of 18.6%.
When constructing a force-field using the MCLF dispersion coefficients, care should be taken not to double-count the three-body dipole–dipole–dipole interactions. Specifically, the MCLF directional screening (i.e., Cscreened6) already includes the three-body dipole–dipole–dipole interactions for the calculated system. (These were included via the directional dipole interaction tensor which was used in turn to compute Cscreened6.) For example, if Cscreened6 is computed using the MCLF method for a single benzene molecule, then the intramolecular dipole–dipole–dipole interactions are already included via the Cscreened6 coefficient term, but the intermolecular dipole–dipole–dipole interactions are not already included and should be added in the force-field using the C9 coefficient term. In this case, the force-field's C9 three-body term should be constructed to include atom triplets from two or three molecules, but not from a single molecule.
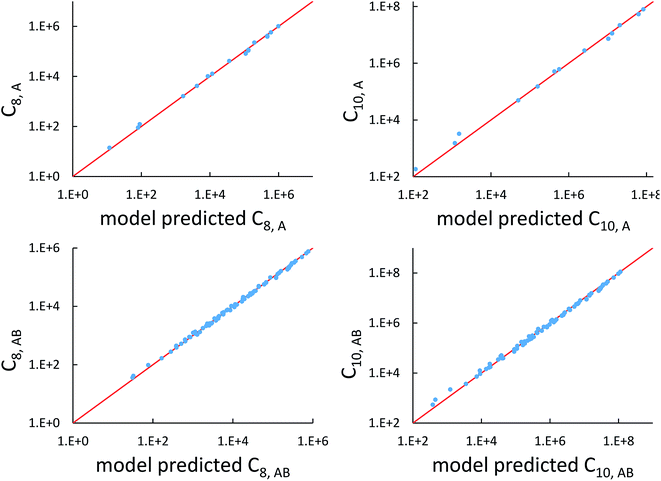
Fig. 7 compares model predicted to reference C8 and C10 dispersion coefficients. Reference values are from Porsev and Derevianko82 and Tao et al.83 and sources cited therein. Chemical elements included in Fig. 7 are: (a) the alkali metals Li, Na, K, Rb, Cs, (b) the noble gases He, Ne, Ar, Kr, Xe, (c) hydrogen H, and (d) the alkaline earths Be, Mg, Ca. Plotted C8,AB and C10,AB included 73 different heteroatomic pairs (see ESI† for details) formed from a subset of these elements.
3.4 Extension to element 109
The CCSD reference data are missing for elements 58–71 and 87–109 because Def2QZVPPDD basis set is not available for those elements. In order for the method to be more applicable, we used eqn (26)–(28) to estimate the reference polarizability, wp, and C6 for these elements. This is a reasonable approach since Table 3 already showed that CCSD model with PW91 r moments yields reasonable results. For these elements, the PW91 〈r3〉 and 〈r4〉 moments required as inputs were taken from all-electron fourth-order DKHSO calculations with MUGBS basis set near the complete basis set limit employing a finite-size Gaussian nuclear model.60,61 Furthermore, data for La (element 57, an f block element) is available for both CCSD and PW91. Comparing its PW91 α and wp with CCSD ones, the change is 5.4% and 2.7% respectively. The reference data for elements 58–71 and 87–109 are listed in ESI.†4. Theory of MCLF method
4.1 New polarizability component partition
During tests, we noticed TS-SCS sometimes gives negative atomic polarizabilities. For example, in the ZrO molecule, the polarizability of oxygen is −0.607 from TS-SCS. This causes subsequent methods depending on the TS-SCS method to fail: (a) the C6 coefficient from the Casimir–Polder integral will be unphysical, (b) corresponding vdW radii in the TS-SCS method will be complex (since they depend on the cubed root of the polarizability),12 and (c) MBD, MBD@rsSCS, and related methods require non-negative AIM polarizabilities as input.46,54,58 In TS-SCS, the partial contraction of P follows the assumed form of Applequist et al.:31
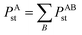 | (44) |
In our new method, atoms with larger pre-screened polarizability get a proportionally larger piece of the screening mixed polarizability contribution:
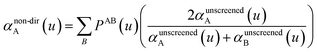 | (45) |
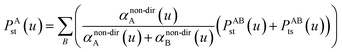 | (46) |
 | (47) |
The symmetric AIM polarizability tensor can be visualized by plotting the ellipsoid88,89
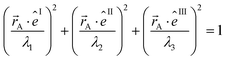 | (48) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) is quantified by the projection
is quantified by the projection 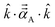 . Choosing
. Choosing ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) parallel to the inter-nuclear direction gives the bond polarizability of two bonded atoms:
parallel to the inter-nuclear direction gives the bond polarizability of two bonded atoms: 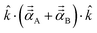 .88,89 Of interest, Raman spectrum peak intensities are proportional to the change in projected polarizability as vibration occurs.90–92
.88,89 Of interest, Raman spectrum peak intensities are proportional to the change in projected polarizability as vibration occurs.90–92
4.2 Polarizability upper bound
Consider a perfectly conducting plate with thickness d in an external electric field Eext applied perpendicular to its surface. From Gauss' Law, the two faces perpendicular to Eext develop surface charge densities σ′ = ±ε0Eext and form a dipole moment μ = σ′d × area = ε0Eextd × area. The local polarizability must be computed based on the electric field (Eloc) felt by each local volume element within the material. In this geometry, Eloc = Eext/2 is the average of the field before (Eext) and after (Efinal = 0 inside the conductor) polarization. Its local polarizability is p = μ/Eloc = 2ε0d × area, which in atomic units (4πε0 = 1 in atomic units) gives α = p/(4πε0) = d × area/(2π), also referred to as the polarizability volume since it carries volume units. Thus, the local polarizability-to-volume ratio of the perfectly conducting plate is 1/(2π) in atomic units. For this geometry, the overall polarizability-to-volume ratio (p = μ/Eext) is 1/(4π).As a second example, consider a sphere of radius R and dielectric constant κ placed in a constant externally applied electric field Eext along the z-direction. This sphere will develop a dipole moment of93
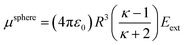 | (49) |
In theory, the polarizability caused by distortion of the electron cloud for fixed nuclear positions should be less than or equal to that of a perfect conductor. Comparing the above results for the conducting plate and conducting sphere shows the overall polarizability-to-volume ratio of a perfect conductor is shape-dependent; this is due to directional interactions within the material. To address this issue, we apply a conduction limit upper bound during non-directional screening, before any directional screening occurs. Applying the conduction limit upper bound before directional screening allows it to be based on the local polarizablity-to-volume ratio instead of the overall polarizability-to-volume ratio. The local polarizability-to-volume ratio should be approximately independent of the material's shape. Therefore, the local polarizability-to-volume ratio of the conducting plate is operational for the non-directional screening. So we defined the polarizability upper bound of atom A as
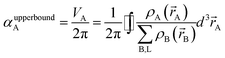 | (50) |
During MCLF calculation, if the calculated non-directionally screened polarizability is higher than this upper bound, the result will be replaced by the upper bound polarizability. This procedure is carried out by a smooth minimum function
| αA = smooth_min(αestA, αupperboundA) | (51) |
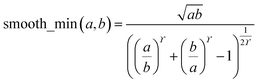 | (52) |
4.3 M scaling to describe both surface and buried atoms
Section 3.2 above shows the polarizability of an isolated atom scales approximately proportional to its effective radius to the 4th power. Brinck et al. showed the polarizability of a polyatomic molecule is approximately proportional to its volume divided by an effective electron removal energy.94 As shown in Section 4.2, the polarizability of a conducting plate or sphere is proportional to its volume. For non-conducting fluids, the Clausius–Mossotti relationship describes a polarizability-to-volume ratio that is a weak function of the dielectric constant.73 This implies the polarizability-to-volume ratio of a buried atom is approximately proportional to its volume. This means the atom-in-material polarizability transitions from approximately 4th power to 3rd power dependence on the atom's effective radius as the atom goes from isolated to buried.We define m to quantify how exposed an atom is:
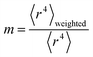 | (53) |
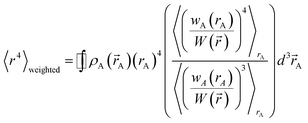 | (54) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A) is the electron density of atom A, wA(rA)/W(
A) is the electron density of atom A, wA(rA)/W(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the fraction of the total electron density ρ(
) is the fraction of the total electron density ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) at position
) at position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) that is assigned to atom A, and 〈
that is assigned to atom A, and 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉rA means the spherical average. m equals 1 for an isolated atom and goes towards zero when an atom gets more and more buried.
〉rA means the spherical average. m equals 1 for an isolated atom and goes towards zero when an atom gets more and more buried.
The modified unscreened scaling law for α now has the form
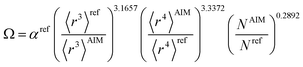 | (55) |
| αunscreened = (C〈r3〉)(1−m)Ωm | (56) |
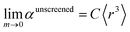 | (57) |
There are two primary justifications for eqn (57). First, the Clausius–Mossotti relation and conduction limit upper bound show the polarizability of a condensed phase (e.g., liquid or solid) is approximately proportional to its volume. Here, 〈r3〉 is a proxy for the volume of an atom, so the sum of 〈r3〉 moments for atoms in a material is a proxy for the material's volume. The Clausius–Mossotti relation and conduction limit upper bound show the polarizability-to-volume ratio of a material is not strongly element-dependent and has modest dependence on the material's dielectric constant (see eqn (75) and (76)). Second, in condensed phases electrons undergo chemical potential equilibration that transfers some electron density from the least electronegative elements to the most electronegative elements. Accordingly, the chemical potential of the equilibrated condensed phase is not as extreme as either the most electropositive elements nor the most electronegative elements. For atoms in condensed materials, the polarizability to 〈r3〉 moment ratios will typically be lower than an isolated neutral alkali metal atom (extremely electropositive) on the one hand and higher than an isolated neutral fluorine atom (extremely electronegative) on the other hand. The polarizability to 〈r3〉 moment ratios of atoms in condensed materials thus exhibit a narrower range of values than for isolated atoms. Group 14 elements have approximately equal tendency to gain or lose electrons, thereby readily forming both positive and negative oxidation states. The isolated atom polarizability to 〈r3〉 moment ratios of Group 14 elements are approximately independent of the periodic row: C (0.34), Si (0.37), Ge (0.34), Sn (0.32), and Pb (0.31). Accordingly, we expect the same constant C in eqn (57) will work for both light and heavy elements.
Tests on the polarizabilities of 28 solids were performed to optimize C. The criteria are that without any upper bound imposed, the MRE should be 0–10% and after the upper bound is imposed, the MARE should be ≤∼10%. These criteria make sure the scaling law is as accurate as possible without the upper bound and the upper bound will not decrease the accuracy. Table 4 shows that C = 0.4 is optimal. This value is slightly higher than the polarizability to 〈r3〉 moment ratios of isolated Group 14 atoms.
| C = 0.35 | C = 0.4 | C = 0.45 | C = 0.35 | C = 0.4 | |
|---|---|---|---|---|---|
| NU | NU | NU | U | U | |
| MRE | 1.14% | 6.87% | 11.91% | −12.22% | −9.14% |
| MARE | 26.75% | 27.26% | 29.09% | 13.59% | 11.89% |
The characteristic frequency wp also has different expressions for isolated and buried atoms. For an isolated atom (i.e., m = 1), wp should be proportional to α−1/2 which has been captured by the isolated atom scaling law. For a buried atom (i.e., m ≪ 1), the polarizability becomes nearly proportional to 〈r3〉AIM and C6 remains proportional to the atom's effective radius to the sixth power; therefore, wp is less sensitive to changes in α when the atom is buried. So the scaling for wp has been modified to:
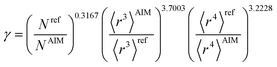 | (58) |
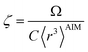 | (59) |
| wp = ζ(1−m2)/4γwpref | (60) |
4.4 Iterative polarizability screening
The non-directional, fluctuating, and induced dipole interaction tensors are defined in eqn (61)–(63):
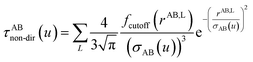 | (61) |
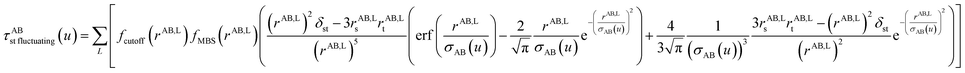 | (62) |
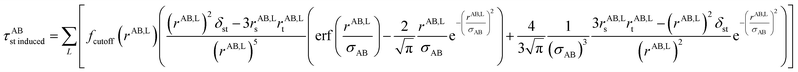 | (63) |
fcutoff(dAb) is a smooth cutoff function that smoothly turns off dipole–dipole interactions between atoms as the distance between them increases:
 | (64) |
Imagine a parameter 0 ≤ λ ≤ 1 that continuously turns on a particular screening type (e.g., non-directional, fluctuating, or static). When λ = 0, the corresponding screening type is fully off. When λ = 1, the corresponding screening type is fully on. Thus, the corresponding screening process can be envisioned as transitioning continuously from λ = 0 to λ = 1. We expect the partially screened system (i.e. 0 < λ < 1) to have a polarizability intermediate between that for λ = 0 and λ = 1. Since the Gaussian width σAB(u) depends on the polarizability (eqn (19)), the MCLF method continuously updates σAB(u) during the screening process. In contrast, the TS-SCS method uses σAB(u) corresponding to λ = 0 for the entire screening process, which does not allow the Gaussian width to update during the screening process.
The screening of each tensor is now an iterative process. In each iteration, we compute
| Qj+1 = Dj + Δjτj | (65) |
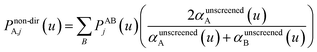 | (66) |
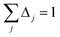 | (67) |
Because the polarizability upper bound is calculated for uniform applied electric field and does not include any directional interactions between dipoles, it is applied at the end of non-directional screening and before directional screening. For each u value, the polarizability upper bound was applied to the raw non-directionally screened polarizability (i.e., αraw_non-dirA(u)) via the following equation to generate
 | (68) |
| αforce-fieldA = αnon-dirA(u = Nimfreqs) | (69) |
| αlow_freqA = αscreenedA(u = Nimfreqs) | (70) |
4.5 Anisotropic polarizability correction
We found that both the TS-SCS and MCLF screening processes often overestimate anisotropy of the static polarizability tensor. Physically, this occurs because the TS-SCS and MCLF methods use spherical Gaussian dipoles in their screening models. In reality, the effective screening width should be larger along the direction of increased polarizability and smaller along the direction of decreased polarizability. Consequently, using a spherical Gaussian dipole model under-screens along the direction of increased polarizability and over-screens along the direction of decreased polarizability. This inflates the polarizability tensor anisotropy.This can be approximately corrected by mixing the pre-corrected AIM static polarizability tensor,  , with the isotropic AIM static polarizability, αstaticA:
, with the isotropic AIM static polarizability, αstaticA:
 | (71) |
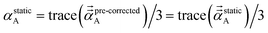 | (72) |
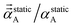 onto any direction exceeds C.F.
onto any direction exceeds C.F.
To find a reasonable value for C.F., polarizability anisotropy ratios for four polyacenes were compared in Table 5. The reference ratios were calculated from Jiemchooroj et al.’s TD-DFT results.78 As shown in Table 5, C.F. = 0.2 gave the lowest mean relative error (MRE) and mean absolute relative error (MARE) for these materials. This value performed better than C.F. = 0 and better than the TS-SCS method. Therefore, we used C.F. = 0.2 as the regular value for the MCLF method. Except where otherwise specified, all reported MCLF results used this C.F. value.
| Reference | TS-SCS | C.F. = 0 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| αxx/α | αyy/α | αzz/α | αxx/α | αyy/α | αzz/α | αxx/α | αyy/α | αzz/α | |
| C6H6 | 1.18 | 1.18 | 0.64 | 1.27 | 1.27 | 0.47 | 1.29 | 1.28 | 0.43 |
| C10H8 | 1.42 | 1.04 | 0.54 | 1.49 | 1.10 | 0.41 | 1.52 | 1.10 | 0.38 |
| C14H10 | 1.61 | 0.92 | 0.47 | 1.66 | 0.97 | 0.37 | 1.69 | 0.97 | 0.34 |
| C18H12 | 1.76 | 0.83 | 0.41 | 1.78 | 0.88 | 0.34 | 1.82 | 0.87 | 0.31 |
| MRE | −4.12% | −5.48% | |||||||
| MARE | 11.0% | 13.8% | |||||||
| C.F. = 0.1 | MCLF C.F. = 0.2 | C.F. = 0.3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| αxx/α | αyy/α | αzz/α | αxx/α | αyy/α | αzz/α | αxx/α | αyy/α | αzz/α | |
| C6H6 | 1.26 | 1.26 | 0.49 | 1.23 | 1.23 | 0.54 | 1.20 | 1.20 | 0.60 |
| C10H8 | 1.47 | 1.09 | 0.44 | 1.42 | 1.08 | 0.50 | 1.37 | 1.07 | 0.56 |
| C14H10 | 1.62 | 0.97 | 0.40 | 1.55 | 0.98 | 0.47 | 1.48 | 0.98 | 0.54 |
| C18H12 | 1.74 | 0.89 | 0.38 | 1.65 | 0.90 | 0.45 | 1.57 | 0.91 | 0.52 |
| MRE | −2.57 | 0.35% | 3.26 | ||||||
| MARE | 8.31 | 5.66% | 7.95 | ||||||
As a second example, we chose a linear C6H2 molecule. This molecule's structure was optimized using B3LYP functional and def2QZVPPDD basis set in Gaussian09. Optimized bond lengths from one end to another were 1.06 (H–C), 1.21 (C–C), 1.35 (C–C), 1.21 (C–C), 1.35 (C–C), 1.21 (C–C), 1.06 (C–H) Å. The calculated molecular polarizability along the bonds is 181.15 au and perpendicular to the bonds is 41.83 au giving an isotropic polarizability of ⅔(41.83) + ⅓(181.15) = 88.27 au. The reference polarizability anisotropy ratios are 41.83/88.27 = 0.47 and 181.15/88.27 = 2.05 compared to 0.41 and 2.19 with C.F. = 0.2, and 0.26 and 2.48 with C.F. = 0.
Additional examples were provided by two test sets described in the following sections. For a test set containing 57 diatomic molecules (see Section 5.1), the MRE and MARE for eigenvalues are −6.90% and 11.77% with C.F. = 0.2, and −7.96% and 13.67% with C.F. = 0. For a test set containing small molecules (see Section 5.3), the MRE and MARE for eigenvalues are 5.45% and 8.10% with C.F. = 0.2, and 4.85% and 9.40% with C.F. = 0.
4.6 Multibody screening parameter (MBSP)
When a uniform external electric field is applied, the atomic dipoles induced by the field will align and atoms will interact with not only their neighbors but also atoms far away. The dispersion force, however, is caused by fluctuating dipoles. The fluctuating dipoles of the atoms will align with their neighbors but out of sync with atoms far away. The MBSP controls the length scale over which directional alignment persists:
 | (73) |
| MBSP→ | 2.0 | 2.25 | 2.5 | 2.75 | |
|---|---|---|---|---|---|
| MRE | Polyacenes | −7.37% | −4.73% | −2.38% | −0.28% |
| Fullerenes | 5.16% | 6.09% | 6.84% | 7.45% | |
| MARE | Polyacenes | 10.76% | 9.14% | 7.77% | 7.01% |
| Fullerenes | 5.16% | 6.09% | 6.84% | 7.45% | |
4.7 Flow diagram and explanation for three polarizability types
Fig. 9 is the flow diagram for MCLF method. This method yields three kinds of polarizabilities: αforce-field, αstatic and αlow_freq. αforce-field is the polarizability with no directional ordering of the electric field and intended for use in force-field simulations. αstatic is the static polarizability in a constant applied electric field. αlow_freq reflects the short-range order and long-range disorder of the fluctuating dipoles present in the dispersion interaction.Because polarizability is a multibody effect, the polarizability of a molecule is not the sum of polarizabilities of isolated atoms. (In contrast to an atom in a material, the term isolated atom means an atom sitting alone in vacuum.) Directional interactions between atoms create components to the molecular polarizability that do not exist for the isolated atoms.31,32 Directional dipole–dipole interactions31,32 are considered during classical atomistic (e.g., molecular dynamics or Monte Carlo) simulations that utilize polarizable force fields.16,95 To avoid double counting these directional dipole–dipole interactions, the force field's atomic polarizability parameters must be the non-directionally screened values.96–99 Many authors proposed direct additive partitioning of the quantum-mechanically computed molecular polarizability tensor into constituent atoms.10,100–105 Because those values already incorporate directional dipole–dipole interactions, their use in force fields would result in double counting the directional dipole–dipole interactions; therefore, we do not recommend their use as force field parameters. Our method provides both the non-directionally screened and directionally screened AIM polarizabilities, and the non-directionally screened values should be used as polarizable force-field parameters. The directional screening then arises during the course of the classical atomistic simulation.
Although the mixed C6,AB dispersion coefficients could in principle be computed directly from the Casimir–Polder integral using the AIM polarizabilities at imfreqs, this would involve many integrations for materials containing thousands of atoms in the unit cell. Therefore, we used the following mixing formula which is consistent with both Padé approximation81 and QDO9 models:
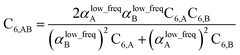 | (74) |
5. Results and discussion
Unless otherwise labeled, the following results are calculated using DDEC6 partitioning. The DDEC6 results were calculated using the Chargemol program.61,66–68 The MCLF results computed in this article avoided large matrix inversions. Details of the MCLF computational algorithm and computational parameters (i.e., dipole interaction cutoff length, Rhomberg integration order, and Richardson extrapolation of the screening increments) are presented in the companion article.79 TS-SCS results in the present article were computed using matrix inversion via Gaussian elimination with partial pivoting (GEPP). The dipole interaction cutoff length for both MCLF and TS-SCS calculations was 50 bohr. Our MCLF calculations used a smooth cutoff function (eqn (64)). Our TS-SCS calculations used a hard cutoff (as consistent with prior literature106). As explained in the companion article, Rhomberg integration for both MCLF and TS-SCS used 16 imfreq points.79 For MCLF, Richardson extrapolation of the screening increments used the number of steps recommended in the companion article.795.1 Diatomic molecules
We first tested our model's sensitivity to the choice of exchange-correlation functional and basis set used to compute the system's electron and spin density distributions. A set of 57 diatomic molecules with elements across the periodic table were chosen as the test set. Three sets of electron density distributions of the test set were generated using Gaussian09 with CCSD/def2QZVPPDD, Gaussian09 with B3LYP/def2QZVPPDD, and VASP with PBE/planewave. The Chargemol program was then used to DDEC6 partition the electron density followed by MCLF analysis to obtain the static polarizabilities and C6 coefficients. Fig. 10 shows polarizability and C6 computed using CCSD/def2QZVPPDD densities versus polarizability and C6 computed using the PBE/planewave and B3LYP/def2QZVPPDD densities. This figure shows our model did not show strong dependence on the choice of exchange-correlation functional or basis set. Hence, MCLF gives similar results using electron density distributions from different proficient quantum chemistry levels of theory.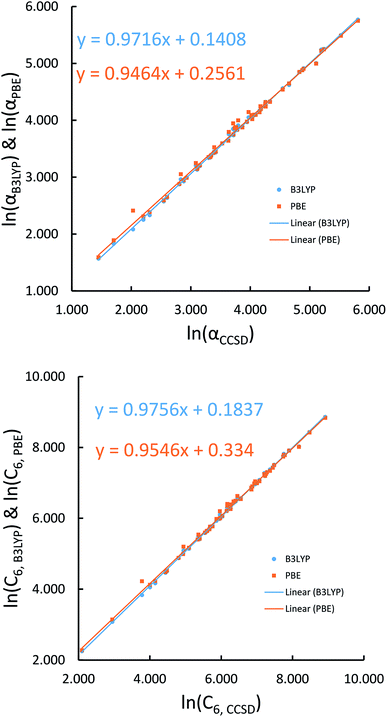 | ||
| Fig. 10 Comparison of MCLF α and C6 of 57 diatomic molecules computed using electron and spin density distributions from CCSD, PBE, and B3LYP calculations with large basis sets. | ||
For the same 57 diatomic molecules, the isotropic static polarizability and the three eigenvalues of the static polarizability tensor from TS-SCS and MCLF were compared to the reference data. The reference is CCSD calculations with def2QZVPPDD basis set. System-specific polarizabilities for CCSD reference, TS-SCS, and MCLF are listed in the ESI.† Table 7 summarizes the error statistics. The TS-SCS method gave large errors independent of the charge partitioning method used (Hirshfeld or DDEC6). On average, MCLF was four times more accurate than TS-SCS for these materials.
| TS-SCS/H | TS-SCS/DDEC6 | MCLF | ||||
|---|---|---|---|---|---|---|
| Isotropic | Eigenvalues | Isotropic | Eigenvalues | Isotropic | Eigenvalues | |
| MRE | 34.4% | 36.1% | 27.8% | 29.4% | −7.78% | −6.9% |
| MARE | 41.1% | 44.9% | 36.6% | 40.2% | 10.4% | 11.8% |
| Range | −21–437% | −35–484% | −24–440% | −35–491% | −34–17% | −40–49% |
Fig. 11 is the absolute percentage error of isotropic polarizability from TS-SCS versus DDEC6 NAC magnitude for these diatomic molecules. From the plot, we can see TS-SCS gives large errors when the NAC magnitude is high. This confirms the TS-SCS model is less accurate for charged atoms and MCLF fixed this problem.
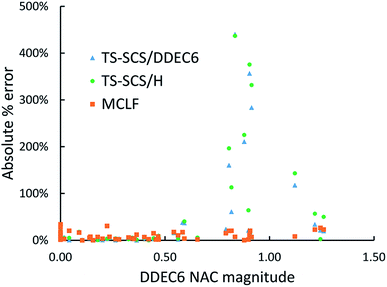 | ||
| Fig. 11 The absolute % error of isotropic static polarizabilities from TS-SCS/H, TS-SCS/DDEC6, and MCLF versus DDEC6 NAC magnitude of 57 diatomic molecules. | ||
5.2 Dense periodic solids
Static polarizabilities were computed for 28 dense periodic solids including electric insulators, semi-conductors, and conductors. The geometries are from Inorganic Crystal Structure Database (ICSD).107,110 We generated electron densities in VASP108 using the PBE109 functional. See Gabaldon-Limas and Manz68 for a description of the VASP computational settings used.Since the polarizability should not exceed the conduction limit, the reference static polarizability was set equal to the smaller value of the Clausius–Mosotti relation (eqn (75)) and conduction limit (eqn (76)):
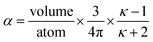 | (75) |
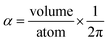 | (76) |
Table 8 summarizes the error statistics. Comparing the MRE and MARE of the screened and unscreened polarizabilities with the same partitioning method (e.g., TS/H vs. TS-SCS/H), screening increases the accuracy for each partitioning method. Because all of the unscreened methods gave >100% error for some materials, screening is an essential step in polarizability calculations. Comparing TS-SCS with different partitioning methods: IH is more accurate than H, and DDEC6 is more accurate than IH. The tendency of TS-SCS/H and TS-SCS/IH to overestimate polarizabilities for solids was previously reported by Bucko et al.57 with improved results reported using the fractionally ionic approach of Gould et al.54 (Those studies included some of the same materials as here.54,57) Using DDEC6 partitioning, MCLF gives more accurate results than TS-SCS with MARE of 12% and 24%, respectively.
| Unscreened methods | ||||
|---|---|---|---|---|
| TS/H | TS/IH | TS/DDEC6 | Unscreened MCLF | |
| MRE | 297% | 141% | 86% | 36% |
| MARE | 297% | 152% | 93% | 55% |
| Range | 11–714% | −53–537% | −28–379% | −36–180% |
| Screened methods | ||||
|---|---|---|---|---|
| TS-SCS/H | TS-SCS/IH | TS-SCS/DDEC6 | MCLF | |
| MRE | 46% | 16% | 15% | −9% |
| MARE | 47% | 30% | 24% | 12% |
| Range | −10–76% | −53–50% | −31–50% | −37–14% |
5.3 Polarizabilities of small molecules
A set of 22 molecules were selected from Thole32 and Applequist et al.31 that have experimentally measured isotropic static polarizability. Six of these also have experimentally measured polarizability tensor eigenvalues.31,32 The geometries are from geometry optimization we performed in Gaussian09 with B3LYP functional and def2QZVPPDD basis set. Tables 9 and 10 show that both TS-SCS/DDEC6 and MCLF performed well for this test set.| Reference | TS-SCS/DDEC6 | MCLF | Reference | TS-SCS/DDEC6 | MCLF | ||
|---|---|---|---|---|---|---|---|
| C2H2 | 22.472 | 23.540 | 27.855 | CH3CN | 30.233 | 33.818 | 34.111 |
| C2H4 | 28.694 | 28.886 | 29.127 | (CH3)2CO | 43.122 | 47.864 | 43.785 |
| H2O | 9.785 | 9.168 | 9.845 | CH3OCH3 | 35.361 | 38.102 | 36.270 |
| C6H6 | 69.868 | 70.437 | 75.646 | CH2ClCN | 41.165 | 46.973 | 49.071 |
| CF4 | 19.705 | 21.928 | 23.071 | CH2OCH2 | 29.900 | 32.003 | 30.739 |
| CFCl3 | 63.907 | 57.929 | 61.873 | C2H5OH | 34.282 | 37.546 | 35.429 |
| NH3 | 16.129 | 13.862 | 14.368 | H2CO | 16.533 | 17.979 | 18.624 |
| CO2 | 19.644 | 17.884 | 19.532 | HCONH2 | 27.938 | 28.328 | 30.208 |
| CS2 | 59.385 | 51.175 | 53.566 | CH2Br2 | 60.735 | 57.041 | 57.983 |
| C3H8 | 42.829 | 47.435 | 42.233 | SF6 | 44.134 | 35.627 | 37.522 |
| C2H6 | 30.233 | 32.626 | 29.131 | SO2 | 26.993 | 25.164 | 26.650 |
| MRE | 1.04% | 2.92% | |||||
| MARE | 8.74% | 7.49% |
| Reference | TS-SCS/DDEC6 | MCLF | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Eigen 1 | Eigen 2 | Eigen 3 | Eigen 1 | Eigen 2 | Eigen 3 | Eigen 1 | Eigen 2 | Eigen 3 | |
| C2H5OH | 30.368 | 33.607 | 38.870 | 30.219 | 34.512 | 47.909 | 31.648 | 33.579 | 41.061 |
| CF4 | 19.705 | 19.705 | 19.705 | 21.928 | 21.928 | 21.928 | 23.071 | 23.071 | 23.071 |
| C2H6 | 27.668 | 27.668 | 35.361 | 28.210 | 28.210 | 41.457 | 27.822 | 27.823 | 31.749 |
| CH3CN | 25.981 | 25.981 | 38.735 | 23.995 | 23.996 | 53.463 | 25.01 | 25.01 | 52.312 |
| (CH3)2CO | 31.380 | 48.959 | 49.027 | 35.472 | 49.630 | 58.489 | 35.706 | 47.354 | 48.294 |
| CH3OCH3 | 29.625 | 33.337 | 43.054 | 31.823 | 31.989 | 50.495 | 32.853 | 32.989 | 42.968 |
| MRE | 8.75% | 5.45% | |||||||
| MARE | 10.95% | 8.10% | |||||||
5.4 C6 coefficients of atom/molecule pairs
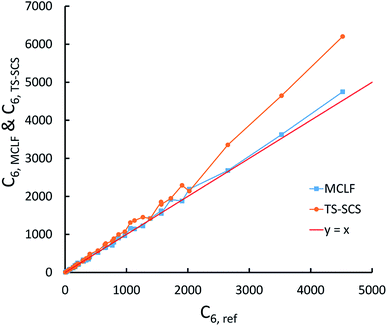
This test involves C6 coefficients for pairs of atoms and molecules studied by Tkatchenko and Scheffler.12 Our geometries are from geometry optimization we performed in Gaussian09 with B3LYP functional and def2QZVPPDD basis set.Fig. 12 compares the TS-SCS/DDEC6 and MCLF C6 coefficients to the reference values derived from the dipole oscillator strength distribution (DOSD) data of Meath and co-workers74,75 as tabulated by Bucko et al.55 As shown in Fig. 12, TS-SCS predicts too large C6 values for the larger molecules, while MCLF is consistently accurate for different sized molecules. For these 49 atoms/molecules, MCLF gave 1.15% MRE and 5.79% MARE while TS-SCS/DDEC6 gave 8.09% MRE and 10.29% MARE.
The same reference data source was also used for the 1225 pairs formed from these 49 atoms/molecules. Fig. 13 plots MCLF versus reference C6 values for these pairs. These MCLF C6,AB values were computed from the C6,A values using eqn (74). Then, the molecular C6 were computed from these C6,AB using eqn (1). MCLF yielded highly accurate results with 0.80% MRE and 4.45% MARE. Results for individual materials in this data set are listed in the ESI.†
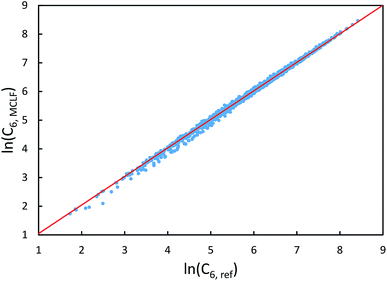 | ||
| Fig. 13 MCLF predicted C6 coefficients in atomic units for 1225 pairs formed from 49 atoms/molecules compared to the experimentally-derived reference C6 coefficients. | ||
Compared to the dense solids discussed in Section 5.2 above, this test set is much less sensitive to the choice of charge partitioning method. For these same 1225 pairs, prior studies reported excellent results from the TS/H (MARE = 5.5%12 or 5.3%55), TS-SCS/H (MARE = 6.3%46), TS-SCS/IH (MARE = 8.6%55), D3 (MARE = 4.7%112), and D4 (MARE = 3.8%37) methods. The minimal basis iterative stockholder (MBIS) method at the TS/MBIS level gave a 6.9% root mean squared percent error for this test set (minus the Xe-containing dimers).113 Other studies also investigated this test set.
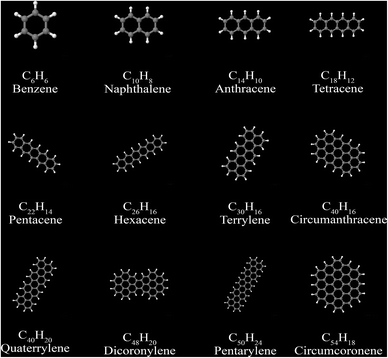
5.5 Polyacenes and fullerenes
Polycyclic aromatic compounds, such as polyacenes, and fullerenes, have strong directional alignment of induced and fluctuating dipoles in the ring planes. A set of 12 polyacenes and a set of 6 fullerenes were selected as test sets. We generated electron densities in VASP108 using the PBE109 functional. See Gabaldon-Limas and Manz68 for a description of the VASP computational settings used.The polyacene geometries are from our VASP geometry optimization using the PBE functional. Polyacene reference static polarizabilities and C6 coefficients are from Marques et al.77 The polyacene structures are shown in Fig. 14. Computed results are summarized in Table 11. The MRE and MARE show MCLF was significantly more accurate than TS-SCS for describing both the static polarizabilities and the C6 coefficients of these materials.
| Static polarizability, α | C6 dispersion coefficient | |||||
|---|---|---|---|---|---|---|
| Reference | TS-SCS | MCLF | Reference | TS-SCS | MCLF | |
| C6H6 | 70.5 | 71.864 | 79.100 | 1730 | 2018.50 | 1999.34 |
| C10H8 | 123 | 122.500 | 133.052 | 4790 | 5641.58 | 5298.26 |
| C14H10 | 189 | 181.475 | 197.738 | 9920 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866.54 866.54 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477.15 477.15 |
| C18H12 | 264 | 247.574 | 271.016 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191.56 191.56 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595.20 595.20 |
| C22H14 | 353 | 319.109 | 350.487 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936.60 936.60 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638.47 638.47 |
| C26H16 | 454 | 395.191 | 434.779 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407.20 407.20 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626.79 626.79 |
| C30H16 | 484 | 402.755 | 441.127 | 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318.93 318.93 |
46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503.57 503.57 |
| C40H16 | 612 | 523.270 | 590.151 | 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014.04 014.04 |
81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 069.67 069.67 |
| C40H20 | 799 | 570.497 | 626.426 | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 993.06 993.06 |
83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472.16 472.16 |
| C48H20 | 770 | 665.562 | 745.500 | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407.13 407.13 |
118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431.09 431.09 |
| C50H24 | 1196 | 748.553 | 822.271 | 168![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
175![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992.78 992.78 |
131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300.24 300.24 |
| C54H18 | 840 | 707.953 | 806.519 | 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
173![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 114.17 114.17 |
147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130.26 130.26 |
| MRE | −13.15% | −4.14% | 16.40% | −2.38% | ||
| MARE | 13.47% | 8.75% | 16.40% | 7.77% | ||
Table 12 summarizes calculation results for fullerenes. The fullerene geometries are from Saidi and Norman.114 Tao et al. studied this set of fullerenes in 2016 and obtained excellent results using a hollow sphere model with modified single frequency approximation.115 The reference static polarizabilities and C6 coefficients are from Kauczor et al.’s TD-DFT calculations.116 For this test set, TS-SCS systematically underestimates the polarizabilities by 18.7% and C6 coefficients by 10.4%.
| Static polarizability, α | C6 dispersion coefficient | |||||
|---|---|---|---|---|---|---|
| Reference | TS-SCS | MCLF | Reference | TS-SCS | MCLF | |
| C60 | 536.6 | 446.9 | 512.6 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 860 |
106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 808 |
| C70 | 659.1 | 534.4 | 616.6 | 141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502 |
150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 150 |
| C78 | 748.3 | 605.6 | 701.3 | 178![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
159![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842 842 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0785 0785 |
| C80 | 798.8 | 626.6 | 727.1 | 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229 229 |
201![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 557 557 |
| C82 | 779.7 | 642.9 | 746.1 | 196![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
179![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 254 254 |
213![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111 111 |
| C84 | 806.1 | 659.3 | 765.4 | 207![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
188![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430 430 |
224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
| MRE | −18.7% | −5.92% | −10.4% | 6.84% | ||
| MARE | 18.7% | 5.92% | 10.4% | 6.84% | ||
In these two test sets, MCLF has better overall performance than TS-SCS with all four MCLF MAREs under 10% compared to all four TS-SCS MAREs over 10%. In contrast to TS-SCS, MCLF uses (i) an iterative update of the Gaussian dipole width and (ii) a multi-body screening function (eqn (73)) to describe decay of the fluctuating dipole directional order. These allow MCLF to describe induced and fluctuating dipole directional alignment effects more accurately than TS-SCS.
5.6 Large biomolecule
Non-reactive molecular mechanics force fields are model potentials containing several different parameter types: dispersion–repulsion parameters (e.g., Lennard-Jones, Buckingham, or other forms), point charges or model atomic charge distributions (e.g., Gaussian, Slater), flexibility parameters, and (optionally) polarizabilities.117,118 These molecular mechanics force fields enable classical atomistic simulations, such as molecular dynamics or Monte Carlo, to be performed over larger distance and time scales than would be practical using quantum chemistry methods such as DFT.118–120 These atomistic simulations are useful to estimate thermodynamic ensemble properties (e.g., density, vapor pressure, adsorption isotherms, etc.), transport properties (e.g., diffusion coefficients, viscosity, etc.), and structures (e.g., protein folding and other conformational changes).118,119,121–124An approach often used is to classify atoms into types, where similar atoms share the same atom type and same force-field parameters.125,126 We will refer to these as Typed Force Fields (TFF). TFFs have been successively improved over the past few decades by refining their atom type definitions and parameter values to make them more accurate and robust.127–129 Today, several TFFs perform reasonably well on various organic molecules and some small inorganic molecules.122,123,130–133
There are still areas for further improving force fields, especially for systems containing high chemical bonding diversity and charged ions. Metal-containing systems are especially prone to high chemical bonding diversity. For example, metal–organic frameworks (MOFs) can contain dozens of different metal elements in a plethora of different bonding motifs.134–136 While some efforts have been made to define new atom types for MOFs,137 the high chemical diversity makes it difficult to completely parameterize force fields for all MOFs using atom types. Quantum-mechanically derived force-fields (QMDFFs) are ideal for modeling these systems, because QMDFFs do not require pre-defined atom types.138,139 Machine learning is a recent approach in which force-field parameterization is trained to a machine learning model using QM-derived parameters.4,140,141 Advantages of the machine learning approach include high automation, fast computation, and the ability to handle large chemical diversity without having to manually define atom types.4,140,141
Non-polarizable force fields often model charged ions with reduced effective charges, but this places artificial constraints on the simulation.142 To make the parameters more transferable between different chemical systems and compositions, the reduced effective charge model should be replaced with a polarizable force-field.16,19,143–145 Kiss and Baranyai concluded for water that “It is impossible to describe the vapor–liquid coexistence properties consistently with nonpolarizable models, even if their critical temperature is correct.”15 Hence, an automated method like MCLF to assign atom-in-material polarizabilities is extremely important for modeling materials containing ions.
Useful insights can be gained by comparing TFF parameters for an atom type to QM-derived ones. Where the TFF parameters and the QM-derived ones are in good agreement, this validates the parameterization. Conversely, where the TFF parameters and the QM-derived ones differ substantially, this indicates areas for further study to potentially refine the atom type definitions and/or parameter values. A multimodal distribution or wide range of QM-derived parameter values suggests when to divide atoms into multiple atom types. A narrow distribution of QM-derived parameter values that is substantially offset from the TFF parameter value can indicate a need to update the TFF parameter value. In such a way, these comparisons can produce force-field improvements.
In this section, we compare MCLF C6 atom-in-material dispersion coefficients and polarizabilities to OPLS and AMOEBA force-field parameters, respectively, for the Human Immunodeficiency Virus reverse-transcriptase (HIV-RT) enzyme complexed with an inhibitor molecule. HIV is a retrovirus with RNA genome.146 Retroviruses replicate in a host cell by using a reverse-transcriptase enzyme to transcribe the virus's RNA genome into the host cell's DNA that is subsequently replicated by the host.146 Therefore, inhibition of the reverse-transcriptase enzyme is a potential way to slow virus replication, which is extremely important for controlling disease caused by the virus.146
Bollini et al. and Cole et al. previously studied several oxazole derivatives as HIV-RT inhibitors.147–149 As an example of the MCLF method applied to macromolecules, we study one of these HIV-RT inhibitors, C20H16ClF2N3O (CAS # 1422256-80-1), shown in Fig. 15 together with a significant portion (2768 atoms) of its complex with wild-type HIV-RT. We computed the electron density distribution for this complex in ONETEP150,151 using the PBE109 exchange-correlation functional. Preparation of the input structure is described elsewhere.147,148 It was constructed from the 1S9E PDB file152 using the MCPRO153 and BOMB154 software. The 178 amino acids closest to the ligand were retained. The complex was solvated in a 25 Å water cap and equilibrated at room temperature for 40 million Monte Carlo steps using the MCPRO software. Water molecules were stripped from the final configuration, and the resulting structure (Fig. 15) was used as input for the ONETEP calculations.
Interactions between electrons and nuclei were described by Opium norm-conserving pseudopotentials.155 NGWFs were initialized as orbitals obtained from solving the Kohn–Sham equation for isolated atoms.156 The NGWFs were expanded as a psinc basis set157 with an equivalent plane-wave cutoff energy of approximately 1000 eV and the electron density was stored on a Cartesian grid of spacing 0.23 Bohr. The localization radii of the NGWFs were 10.0 Bohr. Calculations were performed using an implicit solvent model with a dielectric constant of 78.54 to mimic the water environment.158 Electron density partitioning was performed using the DDEC6 method implemented in the Chargemol program.61,66–68
Table 13 compares the computed C6 coefficients in the HIV-RT complex for a number of frequently-occurring OPLS atom types,122 including both backbone and side chain atoms. The C6 coefficients computed using MCLF generally show a much smaller range than the corresponding TS-SCS/DDEC6 data. Also, the OPLS force field C6 coefficients are usually closer to the MCLF results than to the TS-SCS results. While one should not draw too many conclusions from this, the OPLS parameters have been carefully fit over a number of decades to accurately reproduce experimental observables, such as organic liquid properties122 and protein NMR measurements.159 It is also noteworthy that the OPLS C6 coefficient is slightly higher than the MCLF result. This is expected since the C6 term in the OPLS force-field must effectively compensate for higher-order dispersion (C8, C10,…) terms that are not explicitly included in the OPLS force-field.160 The high value of C6 on the backbone carbonyl carbon (C (bb)) has been noted previously,3 and should be revisited in future force fields.
| Atom type | MCLF | TS-SCS | OPLS | ||
|---|---|---|---|---|---|
| Range | Mean (MUD) | Range | Mean (MUD) | ||
| N (bb) | 31.7–47.2 | 39.0 (1.9) | 33.7–71.9 | 48.2 (5.2) | 58.2 |
| H (bb) | 0.7–1.2 | 0.9 (0.1) | 0.2–1.4 | 0.6 (0.2) | 0.0 |
| C (bb) | 20.1–28.9 | 24.4 (1.0) | 19.3–54.8 | 34.7 (4.1) | 84.8 |
| O (bb) | 25.3–39.9 | 31.8 (2.8) | 18.4–31.5 | 24.1 (1.8) | 41.0 |
| CT (bb) | 27.8–32.7 | 30.3 (0.9) | 50.7–81.2 | 64.8 (5.0) | 35.2 |
| CT (CH3) | 30.2–34.7 | 32.2 (0.8) | 45.0–76.0 | 55.1 (4.2) | 35.2 |
| CT (CH) | 24.7–37.0 | 30.5 (2.2) | 35.7–98.8 | 53.8 (8.0) | 35.2 |
| HC | 1.1–2.6 | 1.6 (0.2) | 0.4–2.1 | 0.7 (0.2) | 2.1 |
| CA | 32.6–43.1 | 36.9 (1.9) | 36.0–65.2 | 45.7 (4.1) | 40.7 |
| HA | 1.1–2.2 | 1.6 (0.2) | 0.6–2.5 | 1.3 (0.3) | 1.8 |
Table 14 compares the three kinds of MCLF polarizabilities (i.e., force-field, static, and low_freq) to parameters used in the AMOEBA16,144 polarizable force field. For the H atoms, the AMOEBA polarizabilities are larger than the MCLF polarizabilities, though both are small compared to the polarizabilities of C, N, and O atoms. For the N (bb) atom, the AMOEBA polarizability is similar to the MCLF force-field polarizability. For the O (bb) atom, the AMOEBA polarizability (5.6) is smaller than the MCLF polarizability (6.9). Since the polarizability of an isolated neutral oxygen atom is ∼5.2,65,80 these polarizabilities are in line with O (bb) being slightly negatively charged and more diffuse than an isolated neutral oxygen atom. For the C atoms, the AMOEBA polarizabilities are substantially larger than the MCLF force-field polarizabilities and close to the MCLF static polarizabilities; this suggests the AMOEBA C atom polarizabilities include some directional screening effects. The AMOEBA polarizabilities use Thole32 model atomic charge distributions16 c1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−c2(rA)3) while the MCLF polarizabilities use Gaussian model charge distributions, so the optimized atomic polarizabilities can be different in these two methods and still approximately reproduce the molecular polarizability. Importantly, computed results presented earlier in this article show the MCLF force-field polarizabilities input into the dipole interaction tensor and solved yield good accuracy molecular static polarizabilities. Therefore, the MCLF force-field polarizabilities are appropriate for use in polarizable force-fields.
exp(−c2(rA)3) while the MCLF polarizabilities use Gaussian model charge distributions, so the optimized atomic polarizabilities can be different in these two methods and still approximately reproduce the molecular polarizability. Importantly, computed results presented earlier in this article show the MCLF force-field polarizabilities input into the dipole interaction tensor and solved yield good accuracy molecular static polarizabilities. Therefore, the MCLF force-field polarizabilities are appropriate for use in polarizable force-fields.
| Atom type | MCLF (force-field) | MCLF (static) | MCLF (low freq) | AMOEBA | |||
|---|---|---|---|---|---|---|---|
| Range | Mean (MUD) | Range | Mean (MUD) | Range | Mean (MUD) | ||
| N (bb) | 6.4–7.8 | 7.4 (0.2) | 8.8–15.0 | 11.4 (0.9) | 8.1–11.1 | 9.6 (0.4) | 7.2 |
| H (bb) | 1.4–2.0 | 1.6 (0.1) | 1.5–2.0 | 1.7 (0.1) | 1.5–2.0 | 1.7 (0.1) | 3.3 |
| C (bb) | 5.6–6.4 | 6.1 (0.1) | 7.3–11.5 | 9.0 (0.5) | 7.0–8.6 | 7.8 (0.2) | 9.0 |
| O (bb) | 6.2–7.7 | 6.9 (0.3) | 6.3–11.4 | 8.4 (0.9) | 6.5–9.4 | 7.8 (0.5) | 5.6 |
| CT (bb) | 6.7–7.3 | 7.0 (0.1) | 8.8–11.3 | 9.9 (0.4) | 8.1–9.0 | 8.5 (0.2) | 9.0 |
| CT (CH3) | 7.0–8.0 | 7.6 (0.2) | 8.3–10.1 | 9.0 (0.3) | 8.0–8.9 | 8.4 (0.2) | 9.0 |
| CT (CH) | 6.6–8.1 | 7.4 (0.3) | 7.8–12.8 | 9.5 (0.7) | 7.5–9.7 | 8.5 (0.4) | 9.0 |
| HC | 1.6–2.9 | 2.1 (0.1) | 1.7–3.1 | 2.2 (0.1) | 1.6–3.0 | 2.1 (0.1) | 3.3 |
| CA | 7.2–8.3 | 7.7 (0.2) | 9.6–13.1 | 10.9 (0.6) | 8.9–10.5 | 9.6 (0.3) | 11.8 |
| HA | 1.8–2.4 | 2.0 (0.1) | 1.9–2.9 | 2.3 (0.2) | 1.9–2.6 | 2.2 (0.1) | 4.7 |
OPLS atom types122 were assigned using MCPRO software153 and have the following descriptions. Sidechain atom types included: CT(CH3): alkane carbon bonded to three hydrogen atoms; CT(CH): alkane carbon atom bonded to one hydrogen atom; HC: alkane hydrogen atom; CA: carbon atom in an aromatic ring; HA: hydrogen bonded to an aromatic ring. Backbone atoms were classified according to: N: amide nitrogen; H: hydrogen bonded to amide nitrogen; C: amide carbon; O: amide oxygen; CT: alpha carbon atom. Only the most common atom types were analyzed to ensure adequate statistics. The substantial ranges of QM-derived parameter values in Tables 13 and 14 suggest there is room to further improve the atom type definitions. An alternative approach defines atom types as the set of unique local environment subgraphs that extend up to one or two bonds, and this approach has been successfully used with DDEC NACs.4,68,161 We recommend the atom type definitions be explored further in future work.
6. Conclusions
In summary, we introduced a new method (MCLF) to compute polarizabilities and dispersion force coefficients. This method can be applied to large and complex materials for which ab initio methods such as time-dependent DFT or CCSD perturbation response theory are too computationally expensive. Like TS-SCS, this method: (i) only requires the electron and spin density distributions as inputs, (ii) is capable of computing polarizability tensors and C6 coefficients for atoms-in-materials as well as for the whole molecule or unit cell, and (iii) works for materials containing 0, 1, 2, or 3 periodic boundary conditions. For TS-SCS, we showed that using DDEC6 partitioning increases accuracy compared to Hirshfeld and IH partitioning. The MCLF method achieves a long list of important improvements compared to existing methods:(1) MCLF has new polarizability and C6 scaling relations for isolated atoms to set the reference values. These cover the charged atom states using a fundamentally different approach than the Fractional Ionic (FI) and TS-SCS methods. Unlike FI, this new approach does not require quantum mechanically computed reference polarizabilities and C6 values for isolated charged atoms; this is a huge advantage, because some isolated charged atoms are unstable. Unlike the TS method, this new approach describes changes in the polarizability-to-volume ratio with atomic charge state.
(2) MCLF uses a new polarizability partition and iterative polarizability screening to improve accuracy and avoid negative polarizabilities for highly charged atoms (e.g., ZrO molecule) by partitioning the mixed pair contribution proportional to the polarizability of each atom in the pair. In contrast, the TS-SCS method sometimes assigns negative polarizabilities to atoms-in-materials, which may prohibit some subsequent calculations (e.g., MBD or van der Waals radius) that require non-negative AIM polarizabilities as inputs. (A proof that αforce-field, αnon-dir(u), αlow_freq, and αscreened(u) are ≥0 is provided in the companion article.79)
(3) M scaling provides a unified scaling law describing the different behaviors of isolated atoms and buried atoms. This allows MCLF to accurately describe both surface and buried atoms. The TS-SCS method (which does not use m scaling) could not accurately describe static polarizabilities for polar diatomic molecules irrespective of the partitioning method.
(4) MCLF separates non-directional from directional screening of the dipole interaction tensor. The non-directionally screened polarizability is constrained to be less than or equal to the conduction limit upper bound, and this provides improved accuracy for buried atoms. In contrast, the TS-SCS method often produces atomic polarizabilities that are unphysically higher than the conduction limit.
(5) MCLF uses a multibody screening function to capture the fluctuating dipole alignment at short distances and disorder at long distances. This leads to more accurate C6 coefficients.
(6) MCLF computes three different types of screened dipole polarizabilities: (a) the non-directionally screened polarizabilities that are used as force-field and QDO input parameters, (b) the imfreq fluctuating polarizabilities that describe the local directional alignment contributing to C6 coefficients, and (c) the static polarizability containing long-range directional alignment of dipoles due to a constant externally applied electric field. MCLF computes the full polarizability tensors including diagonal and off-diagonal components.
(7) MCLF parameterizes a quantum Drude oscillator (QDO) model to yield higher-order (e.g., quadrupolar and octupolar) AIM polarizabilities and higher-order AIM dispersion coefficients (e.g., C8, C9, C10) and associated mixing rules.
(8) The MCLF atom-in-material polarizability tensors are always symmetric, while the TS-SCS atom-in-material polarizability tensors are sometimes asymmetric. Symmetric polarizability tensors are more convenient, because they can be displayed as ellipsoids.
(9) As explained in the companion article, the computational cost of MCLF scales linearly with increasing number of atoms in the unit cell for large systems.79 This is achieved using a dipole interaction cutoff function combined with computational routines that avoid both large matrix inversions and large dense matrix multiplications.79
Tests were performed on diverse material types: isolated atoms, diatomic molecules, periodic solids, small organic and inorganic molecules, fullerenes, polyacenes, and an HIV reverse transcriptase biomolecule. For each test set in this study, MCLF gave ≤12% MARE on the static polarizabilities, C6 coefficients, and static polarizability eigenvalues. This substantially improves over the TS-SCS method. For the static polarizabilities of solids: (a) TS-SCS with H, IH, and DDEC6 partitioning gave MARE of 47%, 30%, and 24%, respectively, (b) MCLF gave MARE of 12%, and (c) all of the unscreened methods gave much larger errors than the screened methods. For the static polarizabilities of diatomic molecules: (a) TS-SCS/H gave 41% MARE with a largest error of 437%, (b) TS-SCS/DDEC6 gave 37% MARE with a largest error of 440%, and (c) MCLF gave 10% MARE with a largest error of 34%. We anticipate MCLF should be useful for parameterizing polarizable force fields and DFT + dispersion methods.
There are several key differences between the MCLF and D3 and D4 approaches. The MCLF and D4 (ref. 35 and 37) approaches incorporate atomic charge information, while the D3 (ref. 11) method does not. The D3 and D4 approaches are based on the molecular geometry without requiring a quantum-mechanically computed electron density distribution,11,35,37 while MCLF uses a quantum-mechanically computed electron density distribution. (The atomic charges used in D4 method variants can be computed from a quantum-mechanically computed electron density distribution, but this is not required.35,37) The MCLF method explicitly considers dipole–dipole tensor interactions, while the D4 method only does so when a damped MBD Hamiltonian is included. (Without the MBD Hamiltonian, some dipole–dipole tensor interactions may be implicitly included in the D3 and D4 methods via coordination number effects, but only to the extent those dipole–dipole interactions correlate to the atom's coordination number and resemble dipole–dipole interactions in the reference compounds.) When using classical electronegativity equilibration NACs, the D4 method facilitates computing analytic forces during DFT + dispersion calculations37 MCLF yields AIM and system polarizability tensors, while D4 yields isotropic AIM and system polarizabilities. MCLF yields three types of polarizabilities: (a) non-directionally screened polarizabilities suitable for use in polarizable force-fields, (b) fluctuating polarizabilities that describe London dispersion interactions, and (c) static induced polarizabilities that include directional dipole–dipole interactions under a constant externally applied electric field.
As summarized in Table 15, we believe it is most useful to regard the MCLF method as a set of guiding principles and their empirical implementations. Some of the guiding principles are non-empirical (i.e., derived from first-principles) while their implementation involves some empirical aspects (i.e., fitting functional forms to observational data). Both the non-empirical and the empirical aspects of the MCLF method are highly innovative and important. Therefore, we do not believe it is reasonable to categorize the entire MCLF method as being exclusively empirical or exclusively non-empirical. If one had to choose a single word to categorize it, “semiempirical” is the appropriate choice. The Merriam-Webster dictionary defines semiempirical as “partly empirical”.162
| Guiding principle | Empirical implementation |
|---|---|
| a The physical basis for this is that some isolated anions have unbound electrons and therefore could not be used as reference states. | |
| Method should require reference polarizabilities and C6 coefficients for neutral free atoms only (not charged free atoms) and still properly describe scaling laws for charged atomsa | Isolated atom scaling laws (eqn (30) and (31)) |
| Conduction limit upper bound for a material's non-directional polarizability at fixed geometry and fixed orientation | Conduction limit upper bound function (eqn (52)) applied to non-directional polarizabilities as a function of frequency (eqn (68)) using AIM volume (eqn (50)) |
| Polarizability interaction not necessarily distributed equally between a pair of atoms | Proportional polarizability component partition (eqn (45)–(47)) |
| Different polarizability scaling behaviors for surface and buried atoms | m-Scaling (eqn (53)–(60)) |
| Fluctuating dipoles have a different effective range of directional alignment than static induced dipoles | Multi-body screening function (eqn (73)) used to compute αscreenedA(u) |
| Higher-order AIM polarizabilities and higher-order dispersion coefficients can be approximately described by a QDO model | QDO parameters computed from MCLF C8,A (eqn (34)), Cnon-dir6,A, and αforce-fieldA |
| αforce-fieldA and αscreenedA(u) should be mathematically guaranteed to be non-negative | Iterative polarizability screening (see ref. 79 for proof) |
| Directional dipole–dipole interactions should not be double counted when using a polarizable force-field | αforce-fieldA based on non-directionally screened dipole–dipole interactions |
| Use spherical Gaussian dipole model for computational simplicity followed by an anisotropic correction | Anisotropic polarizability correction (eqn (71)) |
| For computational efficiency, there should be a simple mixing rule to compute C6,AB from the individual AIM properties | Padé approximation (eqn (74)) |
| Computational time and memory should scale linearly with increasing number of atoms in the unit cell for large systems | Dipole interaction cutoff function (eqn (64)), see ref. 79 for proof of linear scaling |
Notably, one could generate alternative empirical implementations of the same guiding principles. For example, the isolated atom scaling laws could be reconstructed using the 〈r2〉 and 〈r4〉 moments in place of the 〈r3〉 and 〈r4〉 moments, as shown in Table 1. This implementation change would usually produce minor differences in results, because both models are trained to the same underlying dataset of isolated atom polarizabilities and C6 coefficients. As another example, using a different but similar smooth minimum function to impose the conduction limit upper bound could usually produce similar results, because both functions are ultimately controlled by the same physical limit of the non-directional polarizability of an ideal conductor at fixed geometry and fixed orientation. Furthermore, the MCLF method must be applied using some chosen partitioning method (e.g., DDEC6). Clearly, some partitioning methods are poor choices (e.g., Hirshfeld as shown in Table 8), while others (e.g., DDEC6) are good choices. The DDEC6 method is also a set of guiding principles (which contain some non-empirical aspects) and their empirical implementations that comprise a semiempirical method.61,68
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was funded by National Science Foundation (NSF) CAREER Award DMR-1555376. Supercomputing resources were provided by the Extreme Science and Engineering Discovery Environment (XSEDE).163 XSEDE is funded by NSF grant ACI-1548562. XSEDE project grant TG-CTS100027 provided allocations on the Comet clusters at the San Diego Supercomputing Center (SDSC) and the Stampede cluster at the TACC. The authors sincerely thank the technical support staff of XSEDE, Texas Advanced Computing Center (TACC), and SDSC. Calculations on the HIV-RT complex were performed on the Rocket High Performance Computing Service at Newcastle University.References
- L. P. Lee, N. G. Limas, D. J. Cole, M. C. Payne, C. K. Skylaris and T. A. Manz, J. Chem. Theory Comput., 2014, 10, 5377–5390 CrossRef CAS PubMed.
- L. P. Lee, D. J. Cole, C.-K. Skylaris, W. L. Jorgensen and M. C. Payne, J. Chem. Theory Comput., 2013, 9, 2981–2991 CrossRef CAS PubMed.
- D. J. Cole, J. Z. Vilseck, J. Tirado-Rives, M. C. Payne and W. L. Jorgensen, J. Chem. Theory Comput., 2016, 12, 2312–2323 CrossRef CAS PubMed.
- P. Bleiziffer, K. Schaller and S. Riniker, J. Chem. Inf. Model., 2018, 58, 579–590 CrossRef CAS PubMed.
- A. Mondal and S. Balasubramanian, J. Phys. Chem. B, 2015, 119, 11041–11051 CrossRef CAS PubMed.
- A. Mondal and S. Balasubramanian, J. Phys. Chem. B, 2014, 118, 3409–3422 CrossRef CAS PubMed.
- D. J. Cole, I. C. de Vaca and W. L. Jorgensen, Computation of protein–ligand binding free energies using quantum mechanical bespoke force fields, MedChemComm, 2019 10.1039/C9MD00017H.
- X. J. Wu, J. Huang, W. Q. Cai and M. Jaroniec, RSC Adv., 2014, 4, 16503–16511 RSC.
- A. P. Jones, J. Crain, V. P. Sokhan, T. W. Whitfield and G. J. Martyna, Phys. Rev. B, 2013, 87, 144103 CrossRef.
- A. J. Misquitta and A. J. Stone, Theor. Chem. Acc., 2018, 137, 153 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- K. Bica, M. Deetlefs, C. Schroder and K. R. Seddon, Phys. Chem. Chem. Phys., 2013, 15, 2703–2711 RSC.
- P. T. Kiss and A. Baranyai, J. Chem. Phys., 2013, 138, 204507 CrossRef PubMed.
- P. Kiss and A. Baranyai, J. Chem. Phys., 2012, 137, 194103 CrossRef PubMed.
- J. W. Ponder, C. J. Wu, P. Y. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- W. L. Jorgensen, K. P. Jensen and A. N. Alexandrova, J. Chem. Theory Comput., 2007, 3, 1987–1992 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chem. Theory Comput., 2007, 3, 1877 CrossRef CAS PubMed.
- T. A. Halgren and W. Damm, Curr. Opin. Struct. Biol., 2001, 11, 236–242 CrossRef CAS.
- A. Warshel, M. Kato and A. V. Pisliakov, J. Chem. Theory Comput., 2007, 3, 2034–2045 CrossRef CAS PubMed.
- A. Ambrosetti, N. Ferri, R. A. DiStasio and A. Tkatchenko, Science, 2016, 351, 1171–1176 CrossRef CAS PubMed.
- J. Hermann, R. DiStasio and A. Tkatchenko, Chem. Rev., 2017, 117, 4714–4758 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- E. R. Johnson, I. D. Mackie and G. A. DiLabio, J. Phys. Org. Chem., 2009, 22, 1127–1135 CrossRef CAS.
- J. Klimes and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- R. DiStasio, V. Gobre and A. Tkatchenko, J. Phys.: Condens. Matter, 2014, 26, 213202 CrossRef PubMed.
- G. Starkschall and R. G. Gordon, J. Chem. Phys., 1972, 56, 2801–2806 CrossRef CAS.
- R. Resta, Europhys. Lett., 1993, 22, 133–138 CrossRef CAS.
- R. Resta, Rev. Mod. Phys., 1994, 66, 899–915 CrossRef CAS.
- R. Resta and D. Vanderbilt, in Physics of Ferroelectrics: A Modern Perspective, ed. K. M. Rabe, C. H. Ahn and J.-M. Triscone, 2007, ch. 2, pp. 31–68 Search PubMed.
- J. Applequist, J. R. Carl and K. K. Fung, J. Am. Chem. Soc., 1972, 94, 2952–2960 CrossRef CAS.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- A. Mayer and P. O. Astrand, J. Phys. Chem. A, 2008, 112, 1277–1285 CrossRef CAS PubMed.
- A. Mayer, Phys. Rev. B, 2007, 75, 045407 CrossRef.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- S. Grimme, C. Bannwarth, E. Caldeweyher, J. Pisarek and A. Hansen, J. Chem. Phys., 2017, 147, 161708 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 122, 154104 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 014104 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104 CrossRef PubMed.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Phys., 2011, 134, 044117 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- J. Cao and B. J. Berne, J. Chem. Phys., 1992, 97, 8628–8636 CrossRef CAS.
- A. G. Donchev, J. Chem. Phys., 2006, 125, 074713 CrossRef CAS PubMed.
- T. Gould, J. Chem. Phys., 2016, 145, 084308 CrossRef PubMed.
- E. R. Davidson and S. Chakravorty, Theor. Chim. Acta, 1992, 83, 319–330 CrossRef CAS.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbo-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541 CrossRef CAS PubMed.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2012, 8, 2844–2867 CrossRef CAS PubMed.
- T. Gould, S. Lebegue, J. G. Angyan and T. Bucko, J. Chem. Theory Comput., 2016, 12, 5920–5930 CrossRef CAS PubMed.
- T. Bucko, S. Lebegue, J. Hafner and J. G. Angyan, J. Chem. Theory Comput., 2013, 9, 4293–4299 CrossRef CAS PubMed.
- T. Bucko, S. Lebegue, J. Hafner and J. G. Angyan, Phys. Rev. B, 2013, 87, 064110 CrossRef.
- T. Bucko, S. Lebegue, J. G. Angyan and J. Hafner, J. Chem. Phys., 2014, 141, 034114 CrossRef PubMed.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- R. E. Watson, Phys. Rev., 1958, 111, 1108–1110 CrossRef CAS.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468 CrossRef CAS PubMed.
- T. A. Manz and N. Gabaldon Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- T. A. Manz, J. Comput. Chem., 2013, 34, 418–421 CrossRef CAS PubMed.
- D. E. P. Vanpoucke, P. Bultinck and I. Van Driessche, J. Comput. Chem., 2013, 34, 405–417 CrossRef CAS PubMed.
- D. E. P. Vanpoucke, I. Van Driessche and P. Bultinck, J. Comput. Chem., 2013, 34, 422–427 CrossRef CAS PubMed.
- T. Gould and T. Bucko, J. Chem. Theory Comput., 2016, 12, 3603–3613 CrossRef CAS PubMed.
- N. Gabaldon Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747 RSC.
- T. A. Manz, RSC Adv., 2017, 7, 45552–45581 RSC.
- N. Gabaldon Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, 2010 Search PubMed.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, FL, 2016-2017, pp. 10.188–10.203 Search PubMed.
- Y. P. Kathuria, J. Opt., 1991, 22, 149–151 CrossRef.
- J. N. Wilson, Chem. Rev., 1939, 25, 377–406 CrossRef CAS.
- E. Talebian and M. Talebian, Optik, 2013, 124, 2324–2326 CrossRef CAS.
- D. J. Margoliash and W. J. Meath, J. Chem. Phys., 1978, 68, 1426–1431 CrossRef CAS.
- G. D. Zeiss and W. J. Meath, Mol. Phys., 1977, 33, 1155–1176 CrossRef CAS.
- H. B. G. Casimir and D. Polder, Phys. Rev., 1948, 73, 360–372 CrossRef CAS.
- M. A. L. Marques, A. Castro, G. Malloci, G. Mulas and S. Botti, J. Chem. Phys., 2007, 127, 014107 CrossRef PubMed.
- A. Jiemchooroj, P. Norman and B. E. Sernelius, J. Chem. Phys., 2005, 123, 124312 CrossRef PubMed.
- T. A. Manz and T. Chen, New scaling relations to compute atom-in-material polarizabilities and dispersion coefficients: part 2. Linear-scaling computational algorithms and parallelization, RSC Adv., 2019 Search PubMed , in press.
- P. Schwerdtfeger and J. K. Nagle, Mol. Phys., 2019, 117, 1200–1225 CrossRef CAS.
- K. T. Tang, Phys. Rev., 1969, 177, 108–114 CrossRef CAS.
- S. G. Porsev and A. Derevianko, J. Chem. Phys., 2003, 119, 844–850 CrossRef CAS.
- J. M. Tao, J. P. Perdew and A. Ruzsinszky, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18–21 CrossRef CAS PubMed.
- J. G. McDaniel and J. R. Schmidt, J. Phys. Chem. B, 2014, 118, 8042–8053 CrossRef CAS PubMed.
- K. T. Tang and J. P. Toennies, J. Chem. Phys., 1984, 80, 3726–3741 CrossRef CAS.
- M. Sadhukhan and F. R. Manby, Phys. Rev. B, 2016, 94, 115106 CrossRef.
- T. W. Whitfield and G. J. Martyna, J. Chem. Phys., 2007, 126, 074104 CrossRef PubMed.
- A. Krawczuk-Pantula, D. Pérez, K. Stadnicka and P. Macchi, Trans. Am. Crystallogr. Assoc., 2012, 42, 1–25 Search PubMed.
- A. Krawczuk, D. Perez and P. Macchi, J. Appl. Crystallogr., 2014, 47, 1452–1458 CrossRef CAS.
- J. Applequist, Acc. Chem. Res., 1977, 10, 79–85 CrossRef CAS.
- P. Rostron, S. Gaber and D. Gaber, Int. J. Eng. Tech. Res., 2016, 6, 50–64 Search PubMed.
- R. S. Tobias, J. Chem. Educ., 1967, 44, 2–8 CrossRef CAS.
- W. K. H. Panofsky and M. Phillips, Classical Electricity and Magnetism, Addison-Wesley Publishing Company, Reading, MA, 2nd edn, 1962, pp. 84–86 Search PubMed.
- T. Brinck, J. S. Murray and P. Politzer, J. Chem. Phys., 1993, 98, 4305–4306 CrossRef CAS.
- P. Y. Ren and J. W. Ponder, J. Comput. Chem., 2002, 23, 1497–1506 CrossRef CAS PubMed.
- J. M. Wang, P. Cieplak, J. Li, T. J. Hou, R. Luo and Y. Duan, J. Phys. Chem. B, 2011, 115, 3091–3099 CrossRef CAS PubMed.
- J. M. Wang, P. Cieplak, J. Li, J. Wang, Q. Cai, M. J. Hsieh, H. X. Lei, R. Luo and Y. Duan, J. Phys. Chem. B, 2011, 115, 3100–3111 CrossRef CAS PubMed.
- D. Elking, T. Darden and R. J. Woods, J. Comput. Chem., 2007, 28, 1261–1274 CrossRef CAS PubMed.
- P. T. van Duijnen and M. Swart, J. Phys. Chem. A, 1998, 102, 2399–2407 CrossRef CAS.
- J. G. Angyan, G. Jansen, M. Loos, C. Hattig and B. A. Hess, Chem. Phys. Lett., 1994, 219, 267–273 CrossRef CAS.
- A. Krishtal, P. Senet, M. Yang and C. Van Alsenoy, J. Chem. Phys., 2006, 125, 034312 CrossRef CAS PubMed.
- E. Heid, A. Szabadi and C. Schroder, Phys. Chem. Chem. Phys., 2018, 20, 10992–10996 RSC.
- R. F. W. Bader, T. A. Keith, K. M. Gough and K. E. Laidig, Mol. Phys., 1992, 75, 1167–1189 CrossRef CAS.
- A. J. Stone, Mol. Phys., 1985, 56, 1065–1082 CrossRef CAS.
- B. A. Bauer, T. R. Lucas, A. Krishtal, C. Van Alsenoy and S. Patel, J. Phys. Chem. A, 2010, 114, 8984–8992 CrossRef CAS PubMed.
- T. Bucko, S. Lebegue, T. Gould and J. G. Angyan, J. Phys.: Condens. Matter, 2016, 28, 045201 CrossRef PubMed.
- M. Hellenbrandt, Crystallogr. Rev., 2004, 10, 17–22 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 364–369 CrossRef PubMed.
- K. F. Young and H. P. R. Frederikse, J. Phys. Chem. Ref. Data, 1973, 2, 313–410 CrossRef.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- T. Verstraelen, S. Vandenbrande, F. Heidar-Zadeh, L. Vanduyfhuys, V. Van Speybroeck, M. Waroquier and P. W. Ayers, J. Chem. Theory Comput., 2016, 12, 3894–3912 CrossRef CAS PubMed.
- W. A. Saidi and P. Norman, J. Chem. Phys., 2016, 145, 024311 CrossRef PubMed.
- J. M. Tao, Y. X. Mo, G. C. Tian and A. Ruzsinszky, Phys. Rev. B, 2016, 94, 085126 CrossRef.
- J. Kauczor, P. Norman and W. A. Saidi, J. Chem. Phys., 2013, 138, 114107 CrossRef PubMed.
- I. G. Kaplan, Intermolecular Interactions: Physical Picture, Computational Methods and Model Potentials, John Wiley & Sons, West Sussex, England, 2006, pp. 183–254 Search PubMed.
- Q. Yang, D. Liu, C. Zhong and J.-R. Li, Chem. Rev., 2013, 113, 8261–8323 CrossRef CAS PubMed.
- R. O. Dror, R. M. Dirks, J. P. Grossman, H. F. Xu, D. E. Shaw and D. C. Rees, Annu. Rev. Biophys., 2012, 41, 429–452 CrossRef CAS PubMed.
- D. Dubbeldam, A. Torres-Knoop and K. S. Walton, Mol. Simul., 2013, 39, 1253–1292 CrossRef CAS.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- B. Chen and J. I. Siepmann, J. Phys. Chem. B, 1999, 103, 5370–5379 CrossRef CAS.
- Y. Zhang, A. Otani and E. J. Maginn, J. Chem. Theory Comput., 2015, 11, 3537–3546 CrossRef CAS PubMed.
- K. Vanommeslaeghe and A. D. MacKerell, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- B. L. Bush and R. P. Sheridan, J. Chem. Inf. Comput. Sci., 1993, 33, 756–762 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- C. J. Dickson, B. D. Madej, A. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879 CrossRef CAS PubMed.
- P. Hobza, M. Kabelac, J. Sponer, P. Mejzlik and J. Vondrasek, J. Comput. Chem., 1997, 18, 1136–1150 CrossRef CAS.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- S. L. James, Chem. Soc. Rev., 2003, 32, 276–288 RSC.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- Y. J. Cui, Y. F. Yue, G. D. Qian and B. L. Chen, Chem. Rev., 2012, 112, 1126–1162 CrossRef CAS PubMed.
- Q. Xu and C. L. Zhong, J. Phys. Chem. C, 2010, 114, 5035–5042 CrossRef CAS.
- S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, Phys. Status Solidi B, 2013, 250, 1128–1141 CrossRef CAS.
- L. Vanduyfhuys, S. Vandenbrande, T. Verstraelen, R. Schmid, M. Waroquier and V. Van Speybroeck, J. Comput. Chem., 2015, 36, 1015–1027 CrossRef CAS PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schutt and K. R. Muller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- V. Botu, R. Batra, J. Chapman and R. Ramprasad, J. Phys. Chem. C, 2017, 121, 511–522 CrossRef CAS.
- I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626 RSC.
- J. A. Lemkul, J. Huang, B. Roux and A. D. MacKerell, Chem. Rev., 2016, 116, 4983–5013 CrossRef CAS PubMed.
- Y. Shi, Z. Xia, J. J. Zhang, R. Best, C. J. Wu, J. W. Ponder and P. Y. Ren, J. Chem. Theory Comput., 2013, 9, 4046–4063 CrossRef CAS PubMed.
- O. Borodin, J. Phys. Chem. B, 2009, 113, 11463–11478 CrossRef CAS PubMed.
- Retroviruses: Molecular Biology, Genomics and Pathogenesis, ed. R. Kurth and N. Bannert, Caister Academic Press, Norfolk, UK, 2010 Search PubMed.
- M. Bollini, R. Gallardo-Macias, K. A. Spasov, J. Tirado-Rives, K. S. Anderson and W. L. Jorgensen, Bioorg. Med. Chem. Lett., 2013, 23, 1110–1113 CrossRef CAS PubMed.
- D. J. Cole, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2014, 10, 565–571 CrossRef CAS PubMed.
- D. J. Cole, J. Tirado-Rives and W. L. Jorgensen, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 966–971 CrossRef CAS PubMed.
- C. K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 084119 CrossRef PubMed.
- N. D. M. Hine, P. D. Haynes, A. A. Mostofi, C. K. Skylaris and M. C. Payne, Comput. Phys. Commun., 2009, 180, 1041–1053 CrossRef CAS.
- K. Das, A. D. Clark, P. J. Lewi, J. Heeres, M. R. de Jonge, L. M. H. Koymans, H. M. Vinkers, F. Daeyaert, D. W. Ludovici, M. J. Kukla, B. De Corte, R. W. Kavash, C. Y. Ho, H. Ye, M. A. Lichtenstein, K. Andries, R. Pauwels, M. P. de Bethune, P. L. Boyer, P. Clark, S. H. Hughes, P. A. J. Janssen and E. Arnold, J. Med. Chem., 2004, 47, 2550–2560 CrossRef CAS PubMed.
- W. L. Jorgensen and J. Tirado-Rives, J. Comput. Chem., 2005, 26, 1689–1700 CrossRef CAS PubMed.
- W. L. Jorgensen, Acc. Chem. Res., 2009, 42, 724–733 CrossRef CAS PubMed.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- A. Ruiz-Serrano, N. D. M. Hine and C. K. Skylaris, J. Chem. Phys., 2012, 136, 234101 CrossRef PubMed.
- A. A. Mostofi, P. D. Haynes, C. K. Skylaris and M. C. Payne, J. Chem. Phys., 2003, 119, 8842–8848 CrossRef CAS.
- J. C. Womack, L. Anton, J. Dziedzic, P. J. Hasnip, M. I. J. Probert and C. K. Skylaris, J. Chem. Theory Comput., 2018, 14, 1412–1432 CrossRef CAS PubMed.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509 CrossRef CAS PubMed.
- E. T. Walters, M. Mohebifar, E. R. Johnson and C. N. Rowley, J. Phys. Chem. B, 2018, 122, 6690–6701 CrossRef CAS PubMed.
- K. M. Visscher and D. P. Geerke, J. Chem. Theory Comput., 2019, 15, 1875–1883 CrossRef CAS PubMed.
- Semiempirical, in Merriam-Webster’s online dictionary, https://www.merriam-webster.com/dictionary/semiempirical, accessed May 2019.
- J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka, G. D. Peterson, R. Roskies, J. R. Scott and N. Wilkins-Diehr, Comput. Sci. Eng., 2014, 16, 62–74 Search PubMed.
- B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299–300 CrossRef CAS.
- K. T. Tang, J. M. Norbeck and P. R. Certain, J. Chem. Phys., 1976, 64, 3063–3074 CrossRef CAS.
- J. M. Standard and P. R. Certain, J. Chem. Phys., 1985, 83, 3002–3008 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A pdf file containing: damping radii definition (S1); def2QZVPPDD basis set definition (S2); m scaling formula for wp (S3); and plot of the smooth cutoff function (S4). A 7-zip format archive containing: isolated atoms reference data and regression results and their extrapolation up to element 109; def2QZVPPDD.gbs and def2QZVPPDD.pseudo files containing the full basis set and RECP parameter tabulations, respectively; HIV reverse transcriptase complex geometry, ONETEP input files, and tabulated MCLF and TS-SCS results for every atom in the material; MCLF and TS-SCS input and output files for the CH2Br2 example showing symmetric (MCLF) and asymmetric (TS-SCS) atom-in-material polarizability tensors; C8,A and C10,A models for isolated atoms; and detailed MCLF and TS-SCS results for each material in the following test sets: diatomic molecules, small molecules and molecule pairs, solids, polyacenes and fullerenes. See DOI: 10.1039/c9ra03003d |
| This journal is © The Royal Society of Chemistry 2019 |