Insights into defective TiO₂ in electrocatalytic N₂ reduction: combining theoretical and experimental studies

Abstract

Artificial N₂ fixation via the Haber–Bosch process requires high temperature and high pressure at the expense of CO₂ release. Electrochemical NH₃ synthesis is emerging as an environmentally friendly alternative that operates under ambient conditions, calling for electrocatalysts with efficient N₂ reduction reaction (NRR) performance. In this paper, we experimentally and theoretically prove that defective TiO₂ on Ti mesh (d-TiO₂/TM) acts as an electrocatalyst for the NRR. In 0.1 M HCl, d-TiO₂/TM achieves a much higher NH₃ yield of 1.24 × 10⁻¹⁰ mol s⁻¹ cm⁻² and FE of 9.17% at −0.15 V (versus reversible hydrogen electrode) than pristine TiO₂ (NH₃ yield: 0.17 × 10⁻¹⁰ mol s⁻¹ cm⁻²; FE: 0.95%). Notably, d-TiO₂/TM also shows great electrochemical stability and durability. Theoretical investigation further reveals the possible catalytic mechanism involved.

---

Introduction

As one of the most important chemicals for human beings, NH₃ is a basis for fertilizers and a promising hydrogen storage material.^1–3 The synthesis of NH₃ from atmospherically abundant N₂ causes a profound effect on modern agricultural development.⁴ However, it remains a challenge to convert N₂ into NH₃ for N₂ is non-polar and chemically inert.⁵ The century-old Haber–Bosch process is still a leader in NH₃ manufacture and production, in which N₂ and H₂ react over iron-based catalysts at high temperatures and pressures.^6,7 Handicapped by the massive scale of energy consumption and CO₂ emission for H₂ production, an energy-efficient and ecologically friendly substitute for sustainable NH₃ synthesis under ambient conditions is highly desirable.

Powered by renewable energy sources, electrocatalytic reduction offers a feasible and green process for N₂ fixation under ambient conditions.^8,9 Efforts focus mainly on screening electrocatalysts which can activate dinitrogen with alleviated activation barriers for an efficient N₂ reduction reaction (NRR).^10,11 Previously reported noble metal (Au,^12,13 Ag,¹⁴ Ru,¹⁵ and Rh^15,16)-based catalysts show high NRR activity, but the relatively high manufacturing cost hinders their widespread use. Much attention has thus centered on non-noble-metal catalysts (Fe₂O₃-CNT,¹⁰ Fe₃O₄/Ti,¹⁷ PEBCD/C,¹⁸ MoS₂/CC,¹⁹ (110)-oriented Mo nanofilm,²⁰ VN,²¹ and doped carbon^22,23) for efficient NRR electrocatalysis. However, most of these catalysts suffer from unsatisfactory faradaic efficiency (FE) for NH₃ formation (Fe₂O₃–CNT: 0.15%; Fe₃O₄/Ti: 2.6%; MoS₂/CC: 0.096%; (110)-oriented Mo nanofilm: 0.72%; MoO₃: 1.9%; MoN: 1.15%; VN: 2.25%; N-doped carbon: 1.42%). Drawing inspiration from amorphization which induces new defective sites to promote catalytic activity, Yu and co-workers recently reported a hybrid nanofiber of amorphous Bi₄V₂O₁₁ and CeO₂ for N₂ reduction electrocatalysis with a high FE of 10.16%.²⁴

It is well established that oxygen vacancies (V_os) make great contribution in manipulating the electronic properties of metal oxides in different electrochemical energy conversion and storage systems.^25–28 As V_os can trap electrons in the metastable state, electrons may be injected into an antibonding orbital of adsorbed N₂, which thereby weakens the N≡N triple bond for subsequent activation.^29,30 This thus provides an intriguing picture for constructing a V_os-catalyst for N₂ adsorption under aqueous conditions, which has been scarcely reported before.²⁴

Our recent study shows that TiO₂-reduced graphene oxide nanohybrids manifest an efficient NRR performance with a FE of 3.3% in 0.1 M Na₂SO₄.³¹ Our another study demonstrates that TiO₂ nanosheet arrays also operate efficiently with a FE of 2.50% at neutral pH, and the V_osin situ generated during the electrochemical test favours enhanced adsorption and activation of N₂.³² However, both the NRR application of the TiO₂ catalyst in acidic electrolytes and the catalytic mechanism involved still remain unexplored. Herein, we report that defective TiO₂ on Ti mesh (d-TiO₂/TM) acts as a NRR electrocatalyst for ambient N₂-to-NH₃ fixation under acidic conditions, in conjunction with experimental studies and density functional theory (DFT) calculations. After the introduction of defects in pristine TiO₂ (p-TiO₂), the NH₃ yield significantly increases from 0.17 × 10⁻¹⁰ mol s⁻¹ cm⁻² to 1.24 × 10⁻¹⁰ mol s⁻¹ cm⁻² with an enhanced FE from 0.95% to 9.17% at −0.15 V (versus reversible hydrogen electrode) in 0.1 M HCl. Notably, p-TiO₂ also shows great electrochemical stability and durability. These findings provide new insights into the rational design of highly active catalysts with defects toward efficient, stable, and sustainable N₂ fixation under ambient conditions.

Results and discussion

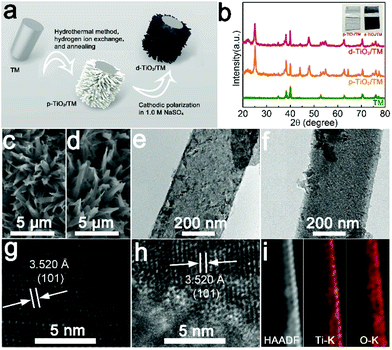
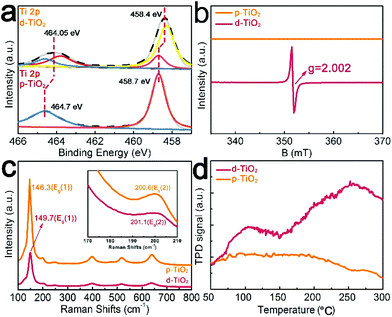
d-TiO₂/TM was derived from the cathodic electrochemical polarization of p-TiO₂/TM at −1.8 V (vs. Ag/AgCl), and Fig. 1a illustrates the fabrication of d-TiO₂/TM. Fig. 1b shows the X-ray diffraction (XRD) patterns of bare TM, p-TiO₂/TM and d-TiO₂/TM. Except for the peaks of TM (JCPDF No. 44-1294), all other peaks of p-TiO₂/TM and d-TiO₂/TM can be indexed to anatase TiO₂ (JCPDF No. 21-1272).³³ And the decrease of the intensity of the XRD pattern for d-TiO₂/TM in Fig. 1b may reflect the decrease of crystallinity. Interestingly, the colour grade changed gradually from white (p-TiO₂) to blue-black (d-TiO₂) (inset of Fig. 1b). The scanning electron microscopy (SEM) image in Fig. 1c displays that the p-TiO₂ array is directly grown on TM with a single nanobelt diameter of ∼300 nm (Fig. 1e). Following cathodic polarization, the resulting d-TiO₂ still maintains its initial morphology (Fig. 1d and f). The clear lattice with an interplanar distance of 3.520 Å on the high-resolution transmission electron microscopy (HRTEM) image (Fig. 1g) corresponds to the (101) plane. However, the lattice becomes blurred after polarization (Fig. 1h), indicating a distortion in the atomic lattice structures of d-TiO₂. The energy-dispersive X-ray (EDX) spectrum (Fig. S1†), the high-angle annular dark-field scanning TEM (HAADF-STEM) image and the corresponding energy dispersive X-ray (EDX) elemental mapping images for d-TiO₂ (Fig. 1i) clearly confirm the existence and homogeneous distribution of Ti and O elements.

Fig. 1 (a) Illustration of the fabrication of d-TiO₂/TM. (b) XRD patterns of TM, p-TiO₂/TM, and d-TiO₂/TM. SEM images of (c) p-TiO₂/TM and (d) d-TiO₂/TM. TEM and HRTEM images of (e, g) p-TiO₂ and (f, h) d-TiO₂. (i) HAADF-STEM and corresponding EDX elemental mapping images of Ti and O for the d-TiO₂.

X-ray photoelectron spectroscopy (XPS) is a surface sensitive characterization method. In Fig. 2a, the XPS spectrum in the Ti 2p region for p-TiO₂ shows two peaks at binding energies (BEs) of 458.7 and 464.7 eV, assignable to 2p_3/2 and 2p_1/2 of Ti⁴⁺, respectively.³⁴ In comparison, Ti 2p for d-TiO₂ shows an evident shift towards lower energy, suggesting that electrons are obtained from deficient oxygen atoms.³⁵ And two extra peaks at BEs of 458.2 eV and 463.5 eV for Ti 2p_3/2 and Ti 2p_1/2 are observed in d-TiO₂, respectively, indicating the presence of Ti³⁺.³⁵ The existence of Ti³⁺ in d-TiO₂ indicates that the V_os are generated to maintain electrostatic balance.³⁶

Fig. 2 (a) X-ray photoelectron spectroscopy (XPS) spectrum in the Ti 2p region for p-TiO₂. (b) Room-temperature ESR spectra of p-TiO₂ and d-TiO₂. (c) Raman spectra of p-TiO₂ and d-TiO₂. (d) Ti 2p core-level XPS spectra of p-TiO₂ and d-TiO₂. (d) N₂-TPD profiles of p-TiO₂ and d-TiO₂.

Based on the ultraviolet–visible (UV-Vis) absorption spectra of p-TiO₂ and d-TiO₂ (Fig. S2a†), we plot the transformed Kubelka–Munk function against the light energy for both samples (Fig. S2b†). The band gap of p-TiO₂ is determined as 3.22 eV by extrapolating the linear fitting, consistent with the reported value of 3.20 eV.^37,38 The extrapolated edge of the visible light absorption of d-TiO₂ is 2.45 eV, which is actually controlled by the formation of Ti³⁺ defects from the charge imbalance bandgap.³⁹ In the room-temperature electron spin resonance (ESR) spectrum of d-TiO₂ after cathodic polarization (Fig. 2b) a definite V_O signal (g = 2.002, ν = 9.8547 GHz) emerges in the wake of Ti³⁺ centers.⁴⁰ A faint blueshift and broadening of Eg(1) and Eg(2) Raman vibrational modes⁴¹ of the d-TiO₂ sample (Fig. 2c) further indicate increased surface disorder ascribed to the introduced V_os.⁴² Temperature-programmed desorption (TPD) measurements were performed to comprehend N₂ adsorption on the p-TiO₂ or d-TiO₂ surface (Fig. 2d). d-TiO₂ shows two strong peaks at around 100 °C assigned to the physical adsorption and 250 °C corresponding to the chemisorption of N₂. However, no chemisorption of N₂ is observed on p-TiO₂, suggesting the enhanced absorption of N₂ for this defect-engineered catalyst.

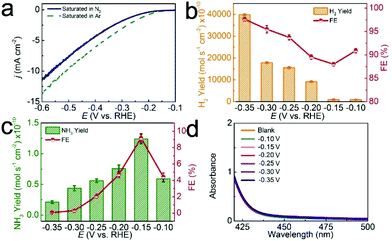
The NRR process involves the charge transfer of electrons for one N₂ molecule and the reaction of protons with N₂.⁴³ In the electrocatalytic process, N₂ gas was continually supplied in a feed stream to the cathode chamber, where N₂ reacts with protons (H⁺ ions from pH = 1 HCl aqueous solution) on the surface of the d-TiO₂/TM cathode to form NH₃. All of the potentials are reported on a RHE scale except those specifically explained. The produced H₂ is determined by the gas chromatographic method. The produced NH₃ and N₂H₄ are measured according to previous reports.^44,45 Fig. S3 and S4† show the corresponding calibration curves. In this study, we firstly measure the linear sweep voltammetry (LSV) of d-TiO₂/TM in Ar- or N₂-saturated 0.1 M HCl aqueous solution to probe the electrocatalytic performance (Fig. 3a). When the potential is more negative than −0.10 V, the current density of d-TiO₂/TM under Ar increases obviously compared with that under N₂, indicating the possibility of suppression of the hydrogen evolution reaction (HER) in the N₂-saturated electrolyte. In order to prove this, we calculated the H₂ yields and FEs in Ar- or N₂-saturated 0.1 M HCl. Constant potential electrolysis was conducted by applying potentials in the range of −0.10 V to −0.35 V, as demonstrated by the chronoamperometric data in Fig. S5.† The corresponding UV–vis absorption spectra are shown in Fig. S6.†

Fig. 3 (a) LSV curves of d-TiO₂/TM in Ar- and N₂-saturated 0.1 M HCl at a scan rate of 5 mV s⁻¹, respectively. (b) H₂ yields and FEs at each given potential in N₂-saturated 0.1 M HCl. (c) NH₃ yields and FEs at each given potential in N₂-saturated 0.1 M HCl. (d) UV-Vis absorption spectra of the electrolytes stained with the p-C₉H₁₁NO indicator after NRR electrolysis at a series of potentials. Error bar associated with each value is also provided.

Compared with H₂ yields and FEs in Ar-saturated electrolytes (Fig. S7†), both of the H₂ yields and FEs obviously decrease under N₂ at each given potential (Fig. 3b), indicating the suppression of the HER in N₂-saturated electrolytes. As shown in Fig. 3c, the highest NH₃ yield of 1.24 × 10⁻¹⁰ mol s⁻¹ cm⁻² and FE of 9.17% are achieved at −0.15 V. Beyond the potential of −0.15 V, both the NH₃ yields and FEs decline gradually, attributed to the enhancement of FEs for the HER (Fig. 3b). We also used ion chromatography, a well-established technique for ion analysis, to determine the NH₃ contents. Fig. S8† shows the corresponding data, suggesting that the NH₃ yields determined by both techniques are comparable. N₂H₄ was not detected in this study, demonstrating the good selectivity of this catalyst for NH₃ formation (Fig. 3d). Note that d-TiO₂/TM also shows higher NH₃ yields and FEs than most reported catalysts under ambient conditions (Table S1†).

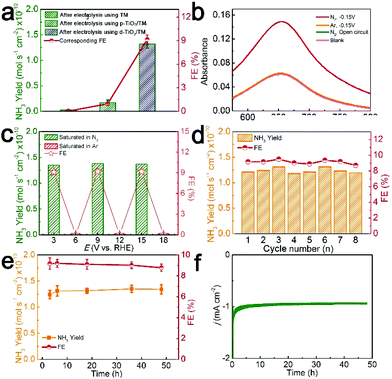
In control experiments, bare TM almost shows no activity for the NRR, and p-TiO₂/TM exhibits inferior activity (NH₃ yield: 0.17 × 10⁻¹⁰ mol s⁻¹ cm⁻²; FE: 0.95%) (Fig. 4a), indicating the significant importance of V_os in d-TiO₂/TM in promoting the NRR process. Moreover, the UV-Vis adsorption spectra of the electrolyte after electrolysis in Ar at −0.15 V or in N₂ at open circuit potential show that no NH₃ was examined (Fig. 4b). After electrolysis with alternating 3 h cycles between N₂- and Ar-saturated 0.1 M HCl for a total of 18 h at −0.15 V (Fig. S9†), NH₃ was only obtained in the periods of the N₂-saturated electrolyte (Fig. 4c). The ¹⁵N isotopic labeling experiment was further conducted to certify the origin of N in the generated NH₃. As shown in Fig. S10,† no response signal was detected after electrolysis under an Ar atmosphere, a doublet coupling in the 1H nuclear magnetic resonance (1H NMR) spectrum was observed in the system after electrolysis in ¹⁵N₂. Only ¹⁵NH₄⁺ was observed in the electrolyte after electrolysis in the ¹⁵N₂ bubbled cathode chamber only.⁴⁶ All the above results confirm that no contaminant N appears in our standard experiments and the N source of the produced NH₃ in the electrolyte originates from N₂. As shown in Fig. 4d, the NH₃ yield and FE are almost constant in the cycling tests, confirming that the detection of NH₃ is repeatable.

Fig. 4 (a) NH₃ yields and FEs for TM, p-TiO₂/TM, and d-TiO₂/TM after NRR electrolysis. (b) UV-Vis absorption spectra of the electrolytes under different conditions. (c) NH₃ yields and FEs of d-TiO₂ with alternating 3 h cycles between N₂- and Ar-saturated electrolytes for a total of 18 h at −0.15 V. (d) Cycling stability test of d-TiO₂/TM. (e) NH₃ yields and FEs after different time electrolysis using the d-TiO₂/TM catalyst. (f) Chronoamperometric data for d-TiO₂/TM at a potential of −0.15 V in N₂-saturated electrolytes. Error bar associated with each value is also provided.

Additionally, it is noticeable that another crucial factor to evaluate NRR performance is the durability under long-term electrolysis. The electrocatalysis time dependence of NH₃ yields and FEs is stable with increased electrolysis time (Fig. S11,†Fig. 4e). The d-TiO₂/TM also maintains its electrolysis activity at −0.15 V for at least 48 h (Fig. 4f). Note that such d-TiO₂/TM still retains its nanoarray feature after the stability test with the increased surface disorder of TiO₂ (Fig. S12†). It is worth mentioning that p-TiO₂/TM is also active for the NRR (Fig. S13†) and constant potential electrolysis was conducted by applying potentials in the range of −0.10 V to −0.35 V (Fig S13a and b†). When the potentials were more negative, at −0.25 V, the highest NH₃ yield of 0.53 × 10⁻¹¹ mol s⁻¹ cm⁻² and FE of 0.6% are achieved (Fig. S13c and d†).

We also prepared different d-TiO₂/TM derived from cathodic polarization under other potentials: −1.2 V, −1.4 V, −1.6 V, and −2.0 V (vs. Ag/AgCl), as shown in Fig. S14–S17.† The electrocatalytic NRR performance of these catalysts was evaluated at −0.15 V (Fig. S18†). As observed, the optimum cathodic polarization potential is determined as −1.8 V (vs. Ag/AgCl) considering the highest NH₃ yields and FEs (Fig. S18a†), which may be assigned to the competition between the NRR and HER (Fig. S18b†).

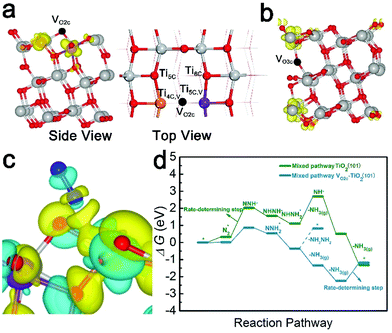
The (101) surface has the lowest energy and is the most frequently exposed surface of anatase TiO₂.^47,48 Thus, for a deeper understanding of the NRR reaction mechanism on the d-TiO₂ surface at an atomic scale, we carried out extensive DFT calculations on the active sites, the corresponding electronic properties and the free energy changes on the d-TiO₂(101) surface. The adsorption sites and energies of N₂ on TiO₂(101) with both topmost surface (V_O2c–TiO₂(101)) and subsurface (V_O3c–TiO₂(101)) oxygen vacancies are investigated (Fig. 5a and b). The calculated adsorption energies of N₂ adsorption in the two positions are −0.576 and −0.352 eV, respectively. We can see that the N₂ adsorption and activation, which is written as N₂(g) → N₂* with the asterisk * representing an adsorption site, should be energetically preferred on the V_O2c–TiO₂(101) surface. The adsorption of N₂ on TiO₂(101) with V_O on the topmost surface (V_O2c–TiO₂(101)) is located in between the four- and five-coordinated Ti atoms (denoted as Ti_4C,VO2c and Ti_5C,VO2c, respectively) adjacent to the vacancy site but tilted to the Ti_4C,VO2c site with a N–Ti bond length of 2.33 Å (Fig. 5a). The calculated electron density difference in Fig. 5c also shows the strong electron accumulations between N₂ and the Ti_4C,VO2c atom, indicating that the Ti_4C,VO2c site most likely serves as the active site for the following NRR process. Hydrogenation of N₂ is then carried out by adding H atoms one by one to the adsorbed species with a distal or alternating mechanism (see Fig. S19† for details). It was found that the NRR process on the V_O2c–TiO₂(101) surface is highly possible to be carried out through a mixed pathway, as shown in Fig. 5d.

Fig. 5 Triplet states of V_O2c (a) and V_O3c (b) defects on the anatase TiO₂(101) surface, respectively (the isosurface level is 0.005 e Å⁻³). (c) Electron density difference upon adsorption of an N₂ atom on the V_O2c–TiO₂(101) surface (Δρ = ρ_N2/TiO2(101) − ρ_N2 − ρ_TiO2(101)). The topological construction represents electron accumulation (yellow) and depletion (blue), respectively, and the isosurface level is 0.005 e Å⁻³. (d) Free energy diagram for the NRR on V_O2c–TiO₂(101) and TiO₂(101). For TiO₂(101), the rate-determining step is N₂ dissociation (reductive adsorption N₂* to form NNH*); for V_O2c–TiO₂(101), the rate-determining step is the second NH₃ desorption (reductive adsorption NH₂* to form NH_3(g)).

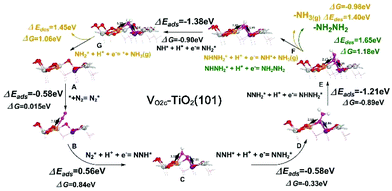
Fig. 6 shows the corresponding atomic configurations of the mixed pathway. Strikingly, we can see that the free energy of N₂ (ΔG(N₂*)) on the V_O2c–TiO₂(101) surface is only 0.015 eV, implying a high NRR reactivity. The hydrogenation of NNH₂* forms NHNH₂* with a negative ΔG of −0.89 eV and the first release of NH₃(g) comes from the hydrogenation of NHNH₂* with a further decrease of ΔG by −0.98 eV. Indeed, the NH₂NH₂ molecule is difficult to produce at room temperature in experiments due to the big positive ΔG of NHNH₂* → NH₂NH₂ (1.18 eV). The NRR rate determining step comes from the desorption of the second NH₃ gas which may occur more easily at higher temperatures. The NRR process on the p-TiO₂(101) surface (TiO₂(101)) also prefers a mixed pathway as shown in the green lines in Fig. 5d and atom configurations in Fig. S19.† We can see that the value of ΔG(N₂*) is 20 times higher than that on the V_O2c–TiO₂(101) surface, indicating the low catalytic activity of the TiO₂(101) surface. The hydrogenation of the first N atom needs a large ΔG(NNH*) of 1.71 eV, a value that is almost twice the corresponding value on V_O2c–TiO₂(101), decreasing greatly the NRR rate. The desorption of the first NH₃ gas also requires a higher positive ΔG of 1.58 eV (see Fig. S20† for details).

Fig. 6 The mixed pathway atom configurations for the NRR on V_O2c–TiO₂(101). ΔE_ads, ΔE_des and ΔG refer to the adsorption energy, desorption energy, and reaction free energy, respectively. The elementary steps depicted include the adsorption of N₂ (A to B), hydrogenation of N₂ one by one to the adsorbed species (B to A) and desorption of NH₃ (E to F and G to A).

The HER on the V_O2c–TiO₂(101) surface is considered because the NRR and HER are competitive reactions under reduction conditions. A large number of research studies have indicated that a single H atom adsorbs preferentially on the top of the bridging 2-fold coordinated oxygen atom (O_2c) on TiO₂(101).⁴⁹ The relevant active-site ΔG_H* results are displayed in Fig. 7a and the insets depict the H adsorption configurations. The comparative examination reveals that the Ti_4C,VO2c active site has a very small ΔG(H*) of 0.011 eV, indicating a good HER performance compared with the Ti_5C,VO2c site on V_O2c–TiO₂(101) and the O_2c site on the perfect TiO₂(101) surface. However, the very close values of ΔG(H*) and ΔG(N₂*) on the Ti_4C,VO2c active site may cause the competition between the HER and NRR processes. Overall, DFT calculations show that the perfect TiO₂(101) exhibits low NRR performance, in good agreement with our experiment. However, the very close free energy values of ΔG(H*) and ΔG(N₂*) on the Ti_4C,VO2c active site (0.011 eV vs. 0.015 eV) may cause the competition between the HER and NRR processes.

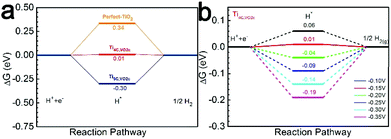Fig. 7 (a) Free energy diagrams for the HER process on V_O2c–TiO₂(101) and TiO₂(101). (b) Free energy diagrams for the HER process on Ti_4C,VO2c at various U values.

We have also further discussed why the highest yield of NH₃ is at U = −0.15 V. The calculation results showed that when the U electrode potential is less than −0.15 V the ΔG(H*) is always a negative value, as shown in Fig. 7b, indicating that the active site (Ti_4C,VO2c) prefers to adsorb the H atom with a negative ΔG(H*) rather than the N₂ molecule with a positive ΔG(N₂*). As U = –0.15 V, the ΔG(H*) should shift to a positive value of 0.01 eV on the Ti_4C,VO2c site (Fig. 7a), implying that the adsorption of the H* intermediate is suppressed. The U electrode potential with −0.10 V is too low so that the hydrogenation of N₂* is weakened. Therefore, we suggested that the NRR efficiency is maximum at U = −0.15 V.

Experimental

Materials

Hydrazine hydrate (N₂H₄·H₂O), hydrochloric acid (HCl), ethyl alcohol (C₂H₅OH), and sodium hydroxide (NaOH) were purchased from Chengdu Kelong Chemical Regent Co. Ltd (China). Sodium salicylate (C₇H₅O₃Na), ammonium chloride (NH₄Cl), p-dimethylaminobenzaldehyde (p-C₉H₁₁NO), sodium nitroferricyanide dihydrate (C₅FeN₆Na₂O·2H₂O) and sodium hypochlorite solution (NaClO) were purchased from Beijing Chemical Corp. (China). TM was purchased from a Hangxu filter flagship store, treated with concentrated HCl, and then cleaned by sonication sequentially in acetone, H₂O and C₂H₅OH several times to remove the surface impurities. The water used throughout all experiments was purified using a Millipore system.

Preparation of p-TiO₂/TM and d-TiO₂/TM

p-TiO₂ was grown on a TM substrate using a hydrothermal method. Typically, a piece of clean TM (2 cm × 3 cm) was steeped into a 40 mL aqueous solution including 5 M NaOH in a 50 mL Teflon-lined stainless steel autoclave. The autoclave was enclosed and transferred into the oven for 24 h at 200 °C. The resulting precursor was then immersed in a dilute HCl solution (0.5 M) for 1 h to replace Na⁺ with H⁺ since the autoclave was chilled to room temperature. Subsequently, the product was repetitively cleaned with deionized water and then annealed for 3 h at 350 °C to form crystallized p-TiO₂/TM. Finally, the resulting p-TiO₂/TM was then adopted as a working electrode in a three-electrode setup and cathodically polarized (−1.8 V vs. Ag/AgCl, 5 min) in 1.0 M Na₂SO₄ at room temperature to obtain d-TiO₂/TM.

Characterization studies

XRD patterns were obtained with a Shimadzu XRD-6100 diffractometer accompanied by Cu Kα radiation (40 kV, 30 mA) with a wavelength of 0.154 nm (Japan). SEM images were acquired with a tungsten lamp-equipped SU3500 scanning electron microscope at an accelerating voltage of 20 kV (HITACHI, Japan). TEM images, HRTEM images, STEM images and the corresponding EDX elemental mapping images were obtained with a Zeiss Libra 200FE transmission electron microscope operated at 200 kV. XPS measurements were performed on an ESCALABMK II X-ray photoelectron spectrometer in which the Mg element was used as the exciting source. The absorbance data were measured with a Shimadzu UV-1800 UV-Vis spectrophotometer. A JASCO V-550 UV-Vis diffuse reflectance spectrophotometer was used to record the optical absorption spectra of the samples in the region of 300–800 nm. Raman spectroscopy (DXR Raman microscope with a 532 nm excitation laser, ThermoFisher Scientific, Waltham, MA, USA) was employed for chemical state analysis. GC analysis was conducted on a GC-2014C system (Shimadzu Co.) with a thermal conductivity detector. Pressure data were obtained by using a CEM DT-8890 Differential Air Pressure Gauge Manometer Data Logger Meter Tester. The ion chromatography method was conducted by using a ThermoFisher ICS 5000 plus ion chromatograph, containing a dual temperature heater, injection valve, conductivity detector, and AERS 500 anion suppressor.

Electrocatalytic N₂ reduction measurements

Before the NRR test, a protonated Nafion membrane was obtained from the order of 1 h in boiling water, 1 h in H₂O₂, 2 h in water, 3 h in 0.5 M H₂SO₄, and 6 h in water, which were maintained at 80 °C.⁵⁰ Electrochemical testing of the working electrode was performed with a CHI 660E electrochemical analyzer (CH Instruments, Inc., Shanghai) using a standard three-electrode system (with a reference saturated Ag/AgCl (saturated KCl electrolyte) electrode and a counter graphite rod electrode) at room temperature (∼25 °C). Before data collection, the working electrode was stabilized with a steady-state electrochemical experiment. The electrolyte was ventilated by using N₂ for 0.5 h before N₂ reduction experiments. Constant potential electrolysis was performed with a two-compartment cell (each cell contains 35 mL HCl solution corresponding to pH = 1, separated by a Nafion membrane). Pure N₂ gas was injected into the cathodic compartment around the clock.

Determination of NH₃

The produced NH₃ concentration was confirmed by the indophenol blue method with a spectrophotometer in 0.1 M HCl. As for the calibration curve, 2 mL standard NH₄Cl solutions in 0.1 M HCl of various concentrations (0.0, 0.1, 0.3, 0.5, 1.0, 2.0, 3.5 and 5.0 μg mL⁻¹) were considered, and then 2 mL oxidizing solution (1.0 M NaOH solution containing C₇H₆O₃ and 5 wt% C₆H₅Na₃O₇·2H₂O), 1 mL oxidizing solution (0.05 M NaClO) and 0.2 mL catalyst solution (1 wt% Na₂[Fe(NO)(CN)₅]·2H₂O) were mixed in order. The mixtures were tested with a UV-Vis spectrophotometer at 655 nm and then the standard curve was obtained after 2 h at room temperature. The calibration curve (Y = 0.160X + 0.067, R² = 0.9999) showed a good linear relationship between the absorbance value and NH₄Cl concentration by independent calibrations three times.

Determination of N₂H₄

The N₂H₄ content in 0.1 M HCl after electrolysis was detected by the Watt and Chrisp method. p-C₉H₁₁NO (5.99 g), HCI (concentrated, 30 mL) and C₂H₅OH (300 mL) were mixed to obtain a color reagent. As for the calibration curve, 5 mL standard N₂H₄ solutions with various concentrations (0.0, 0.2, 0.4, 0.8, 1.2, 1.6 and 2.0 μg mL⁻¹) were considered, and then mixed with 5 mL of the above prepared color reagent. Subsequently, the mixtures were tested with a UV-Vis spectrophotometer at 455 nm after 10 min at room temperature and then the standard curve of N₂H₄ was obtained. After three time independent calibrations, the calibration curve shows a good linear relationship (Y = 0.419X + 0.055, R² = 0.9995).

Calculations of H₂ formation and faradaic efficiency

The produced gas was confirmed by gas chromatography (GC) analysis and clearly quantified with a calibrated pressure sensor. The FE was calculated by comparing the amount of the measured H₂ generated by potentiostatic electrolysis with calculated H₂ (assuming 100% FE).

Calculations of the NH₃ formation rate and faradaic efficiency

The yield and FE of NH₃ were calculated as follows:

NH₃ yield = ([NH₄Cl]/53.5) × V × 10⁻⁶/(t × A) (1)

FE = 3 × F × ([NH₄Cl]/53.5) × V/Q (2)

where [NH₄Cl]/53.5 is the measured NH₃ concentration; V is the volume of the cathodic reaction electrolyte; t is the electrolysis time and A is the geometric area of the cathode (0.5 × 0.5 cm²); and F and Q are the Faraday constant and the quantity of applied electricity, respectively.

Calculation details

Spin-polarized density functional theory (DFT) calculations were performed by using the plane wave-based Vienna ab initio simulation package (VASP).^51,52 The generalized gradient approximation method with the Perdew–Burke–Ernzerhof (PBE) functional was used to describe the exchange–correlation interaction among electrons.^53,54 An on-site Hubbard-U of 4.2 eV was added for Ti-3d to correct the Coulomb repulsion between localized Ti-3d orbitals.^55,56 The van der Waals (vdW) correction with the Grimme approach (DFT-D3) was included in the interaction between single molecule/atoms and substrates.⁵⁷ The energy cutoff for the plane wave-basis expansion was set to 500 eV and the atomic relaxation was continued until the forces acting on atoms were smaller than 0.01 eV Å⁻¹. The Brillouin zone was sampled with 3 × 3 × 1 gamma-center k-point mesh, and the electronic states were smeared using the Fermi scheme with a broadening width of 0.1 eV. The anatase TiO₂(101) surface was modeled with a 1 × 2 slab in the lateral plane separated by 15 Å of vacuum in between to avoid the interaction between the slab and its period images.

The free energies of the reaction intermediates were obtained by ΔG = ΔE_ads + ΔZPE − TΔS + ΔG(U) + ΔG(pH), where ΔE_ads is the adsorption energy, ZPE is the zero point energy and S is the entropy at 298 K. The effect of a bias was included in calculating the free energy change of elementary reactions involving transfer of electrons by adding ΔG(U) = n eV, where n is the number of electrons transferred and U is the electrode potential.^58–60 In our calculations, we used U = −0.15 V (vs. RHE). ΔG(pH) = k_BT ln 10 × pH, where k_B is the Boltzmann constant, and pH = 1 for 0.1 M HCl electrolyte. In this study, the entropies of molecules in the gas phase are obtained from the literature.⁶¹

Conclusions

In summary, d-TiO₂/TM is proven as a NRR electrocatalyst in acid media under ambient conditions, in conjunction with experimental studies and DFT calculations. At an applied potential of −0.15 V, this catalyst shows much superior electrocatalytic NRR activity (NH₃ yield: 1.24 × 10⁻¹⁰ mol s⁻¹ cm⁻²; FE: 9.17%) to p-TiO₂ (NH₃ yield: 0.17 × 10⁻¹⁰ mol s⁻¹ cm⁻²; FE: 0.95%). Notably, d-TiO₂/TM also shows great electrochemical stability and durability. These findings not only provide insight into the rational design of highly active catalysts with defects in N₂-fixing electrochemistry, but would also open up a new avenue to explore defective materials as catalysts for N₂ fixation and other applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 21575071 and 21575137). We also appreciate Hui Wang from the Analytical & Testing Center of Sichuan University for her help with SEM characterization.

Notes and references

1. R. Schlögl, Angew. Chem., Int. Ed., 2003, 42, 2004–2008.
2. V. Rosca, M. Duca, M. T. de Groot and M. T. Koper, Chem. Rev., 2009, 109, 2209–2244.
3. T. Vegge, R. Z. Sørensen, A. Klerke, J. S. Hummelshøj, T. Johannessen, J. K. Nørskov and C. H. Christensen, Solid-State Hydrogen Storage, 2008, 533–568.
4. B. M. Hoffman, D. Lukoyanov, Z. Yang, D. R. Dean and L. C. Seefeldt, Chem. Rev., 2014, 114, 4041–4062.
5. E. Shilov, Russ. Chem. Bull., 2003, 52, 2555–2562.
6. Catalytic Ammonia Synthesis—Fundamentals and Practice, ed. J. R. Jennings, Springer Science+Business Media, New York, 1991.
7. R. Schlögl, Ammonia Synthesis, in Handbook of Homogeneous Catalysis, ed. G. Ertl, H. Knözinger, F. Schüth and J. Weitkamp, Wiley, 2008.
8. M. A. Shipman and M. D. Symes, Catal. Today, 2017, 286, 57–68.
9. V. Kyriakou, I. Garagounis, E. Vasileiou, A. Vourros and M. Stoukides, Catal. Today, 2017, 286, 2–13.
10. S. Chen, S. Perathoner, C. Ampelli, C. Mebrahtu, D. Su and G. Centi, Angew. Chem., Int. Ed., 2017, 56, 2699–2703.
11. W. Qiu, X. Xie, J. Qiu, W. Fang, R. Liang, X. Ren, X. Ji, G. Cui, A. M. Asiri, G. Cui, B. Tang and X. Sun, Nat. Commun., 2018, 9, 3485.
12. S. Li, D. Bao, M. Shi, B. Wulan, J. Yan and Q. Jiang, Adv. Mater., 2017, 29, 1700001.
13. M. Nazemi, S. R. Panikkanvalappil and M. A. El-Sayed, Nano Energy, 2018, 49, 316–323.
14. H. Huang, L. Xia, X. Shi, A. M. Asiri and X. Sun, Chem. Commun., 2018, 54, 11427–11430.
15. K. Kugler, M. Luhn, J. A. Schramm, K. Rahimi and M. Wessling, Phys. Chem. Chem. Phys., 2015, 17, 3768–3782.
16. H. Liu, S. Han, Y. Zhao, Y. Zhu, X. Tian, J. Zeng, J. Jiang, B. Xia and Y. Chen, J. Mater. Chem. A, 2018, 6, 3211–3217.
17. Q. Liu, X. Zhang, B. Zhang, Y. Luo, G. Cui, F. Xie and X. Sun, Nanoscale, 2018, 10, 14386–14389.
18. G. Chen, X. Cao, S. Wu, X. Zeng, L. Ding, M. Zhu and H. Wang, J. Am. Chem. Soc., 2017, 139, 9771–9774.
19. L. Zhang, X. Ji, X. Ren, Y. Ma, X. Shi, Z. Tian, A. M. Asiri, L. Cheng, B. Tang and X. Sun, Adv. Mater., 2018, 30, 1800191.
20. D. Yang, T. Chen and Z. Wang, J. Mater. Chem. A, 2017, 5, 18967–18971.
21. R. Zhang, Y. Zhang, X. Ren, G. Cui, A. M. Asiri, B. Zheng and X. Sun, ACS Sustainable Chem. Eng., 2018, 6, 9545–9549.
22. L. Xia, X. Wu, Y. Wang, Z. Niu, Q. Liu, T. Li, X. Shi, A. M. Asiri and X. Sun, Small Methods, 2018 DOI:10.1002/smtd.201800251.
23. Y. Liu, Y. Su, X. Quan, X. Fan, S. Chen, H. Yu, H. Zhao, Y. Zhang and J. Zhao, ACS Catal., 2018, 8, 1186–1191.
24. C. Lv, C. Yan, G. Chen, Y. Ding, J. Sun, Y. Zhou and G. Yu, Angew. Chem., Int. Ed., 2018, 57, 6073–6076.
25. J. Y. Shin, J. H. Joo, D. Samuelis and J. Maier, Chem. Mater., 2012, 24, 543–551.
26. R. Schaub, P. Thostrup, N. Lopez, E. Lægsgaard, I. Stensgaard, J. K. Nørskov and F. Besenbacher, Phys. Rev. Lett., 2001, 87, 266104.
27. D. Yan, Y. Li, J. Huo, R. Chen, L. Dai and S. Wang, Adv. Mater., 2017, 29, 1606459.
28. H. J. la O’, S. J. Ahn, E. Crumlin, Y. Orikasa, M. D. Biegalski, H. M. Christen and Y. Shao-Horn, Angew. Chem., Int. Ed., 2010, 49, 5344–5347.
29. H. Li, J. Shang, Z. Ai and L. Zhang, J. Am. Chem. Soc., 2015, 137, 6393–6399.
30. Y. Zhao, Y. Zhao, G. I. N. Waterhouse, L. Zheng, X. Cao, F. Teng, L. Wu, C. H. Tung, D. O'Hare and T. Zhang, Adv. Mater., 2017, 39, 1703828.
31. X. Zhang, Q. Liu, X. Shi, A. M. Asiri, Y. Luo, T. Li and X. Sun, J. Mater. Chem. A, 2018, 6, 17303–17306.
32. R. Zhang, X. Ren, X. Shi, F. Xie, B. Zheng, X. Guo and X. Sun, ACS Appl. Mater. Interfaces, 2018, 10, 28251–28255.
33. X. Meng and D. Deng, ACS Appl. Mater. Interfaces, 2015, 7, 6867–6874.
34. G. Wang, H. Wang, Y. Ling, Y. Tang, X. Yang, C. R. Fitzmorris, C. Wang, J. Zhang and L. Yat, Nano Lett., 2011, 11, 3026–3033.
35. P. Yan, G. Liu, C. Ding, H. Han, J. Shi, Y. Gan and C. Li, ACS Appl. Mater. Interfaces, 2015, 7, 3791–3796.
36. X. Jiang, Y. Zhang, J. Jiang, Y. Rong, Y. Wang, Y. Wu and C. Pan, J. Phys. Chem. C, 2012, 116, 22619–22624.
37. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798–801.
38. Z. Yu, Q. Sun, W. Pan, N. Li and B. Tang, ACS Nano, 2015, 9, 11064–11074.
39. H. Irie, Y. Watanabe and K. Hashimoto, J. Phys. Chem. B, 2003, 107, 5483–5486.
40. N. Liu, C. Schneider, D. Freitag, M. Hartmann, U. Venkatesan, J. Müller, E. Spiecker and P. Schmuki, Nano Lett., 2014, 14, 3309–3313.
41. T. Ohsaka, F. Izumi and Y. Fujiki, J. Raman Spectrosc., 1978, 7, 321–324.
42. A. Naldoni, M. Allieta, S. Santangelo, M. Marelli, F. Fabbri, S. Cappelli, C. L. Bianchi, R. Psaro and V. Dal Santo, J. Am. Chem. Soc., 2012, 134, 7600–7603.
43. J. Deng, J. A. Iñiguez and C. Liu, Joule, 2018, 2, 846–856.
44. J. Han, Z. Liu, Y. Ma, G. Cui, F. Xie, F. Wang, Y. Wu, S. Gao, Y. Xu and X. Sun, Nano Energy, 2018, 52, 264–270.
45. L. Zhang, X. Ren, Y. Luo, X. Shi, A. M. Asiri, T. Li and X. Sun, Chem. Commun., 2018, 54, 12966–12969.
46. L. Zhang, X. Ji, X. Ren, Y. Luo, X. Shi, A. M. Asiri, B. Zheng and X. Sun, ACS Sustainable Chem. Eng., 2018, 6, 9550–9554.
47. H. Cheng and A. Selloni, J. Chem. Phys., 2009, 131, 054703.
48. Y. Li, U. Aschauer, J. Chen and A. Selloni, Acc. Chem. Res., 2014, 47, 3361–3368.
49. M. M. Islam, M. Calatayud and G. Pacchioni, J. Phys. Chem. C, 2011, 115, 6809–6814.
50. S. Suarez and D. Paterno, J. Power Sources, 2016, 331, 544–552.
51. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
52. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396–1396.
55. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
56. B. J. Morgan and G. W. Watson, J. Phys. Chem. C, 2010, 114, 2321–2328.
57. S. Grimme, J. Antony, S. Ehrlich and H. J. Krieg, Chem. Phys., 2010, 132, 154104.
58. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
59. L. Yu, X. Pan, X. Cao, P. Hu and X. Bao, J. Catal., 2011, 282, 183–190.
60. E. Finazzi, C. Di Valentin, G. Pacchioni and A. Selloni, J. Chem. Phys., 2008, 129, 154113.
61. P. W. Atkins, Physical Chemistry, Oxford University Press, 1998.

---

Footnotes

† Electronic supplementary information (ESI) available: EDX, UV-Vis and XPS spectra; ion chromatograms; calibration, chronoamperometric, and NRR data; 1H NMR spectra; SEM images; optical photograph; DFT calculations; Table S1. See DOI: 10.1039/c8nr09564g

‡ These authors contributed equally to this work.

---