Open Access Article
Open Access ArticleSingle shot laser ablation MC-ICP-MS for depth profile analysis of U isotopes in UO2 single crystals
M.
Krachler
 *a,
A.
Bulgheroni
a,
A. I.
Martinez Ferri
a,
Y.
Ma†
b,
A.
Miard
b and
Ph.
Garcia
b
*a,
A.
Bulgheroni
a,
A. I.
Martinez Ferri
a,
Y.
Ma†
b,
A.
Miard
b and
Ph.
Garcia
b
aEuropean Commission – Joint Research Centre Karlsruhe, P.O. Box 2340, D-76125 Karlsruhe, Germany. E-mail: michael.krachler@ec.europa.eu
bCEA, DEN, DEC, Centre de Cadarache, 13108 Saint-Paul-lez-Durance, France
First published on 11th September 2019
Abstract
An analytical procedure for determining the n(235U)/n(238U) amount ratio in consecutive layers of UO2 single crystals was developed and validated. A 25 μm circular shaped laser beam with a fluence of only 0.24 J cm−2 was employed for depth profiling 235U and 238U in UO2 single crystals with U isotopes being detected via MC-ICP-MS. The time-resolved 235U and 238U MC-ICP-MS signals obtained from individual laser shots were processed automatically using software specifically developed for this purpose. Downhole fractionation of the n(235U)/n(238U) amount ratio was excluded by shooting 80 laser pulses on a reference UO2 single crystal of known composition, revealing no measurable change in its U isotopic ratio during depth profiling. A linear relationship between the number of laser shots and the average depth of the laser ablation craters was established using confocal laser scanning profilometry. The ns-laser ablation system produced conical craters whose diameters were shown to increase with the number of laser pulses. The shape and roughness of the craters were studied as a function of both the number of pulses and focusing conditions. Using a dual beam focused ion beam (FIB), high resolution scanning electron microscopy (SEM) micrographs revealed the formation of rectangular “tiles” on the reference UO2 single crystal after as little as five laser shots. The ordered, rectangular structure disappeared progressively with increasing number of laser pulses, while simultaneously a sub-micrometric porosity developed. The depth profiling capabilities of the laser ablation system were applied to two UO2 single crystals produced under different experimental conditions involving solid state isotopic mixing of 235U and 238U in order to characterise U self-diffusion in UO2+x. Both UO2 single crystals featured a n(235U)/n(238U) ratio gradient, containing enriched U at the surface and depleted U in the bulk.
Introduction
The study of uranium dioxide (UO2) single crystals is often a necessary starting point for determining nuclear oxide fuel bulk properties, as they constitute a yardstick against which actual nuclear fuels, used on an industrial scale, may be assessed.1 Because single crystal samples are deemed homogeneous and to have a well-defined crystal structure on a macroscopic scale, they enable materials scientists to study underlying physical mechanisms. This allows them in certain cases to apply their findings to more complex structures such as polycrystalline sintered UO2 pellets prior to, during or following in-reactor irradiation.1It is essential to study uranium self-diffusion as it is thought to control many key engineering properties such as creep, sintering, and fission product behaviour that are all very important to several stages of the nuclear fuel cycle. Further a systematic study of this property provides an insight into the characteristics of uranium point defects which is difficult to do any other way as these defects are present in the material only in very small quantities.1
Nowadays, the accurate and precise determination of the elemental and/or isotopic composition of advanced crystalline materials is of utmost importance to guarantee their properties and to identify potential contaminants.2–12 Classical analytical approaches employing dissolution of a fragment of such materials followed by subsequent chemical analysis are not effective because their features are captured either in thin (nm to μm thick) layers or within local hot spots. Therefore, solid sampling techniques such as Electro-Thermal Vaporisation (ETV) or Laser Ablation (LA) are employed frequently for this purpose.7 LA-based techniques additionally offer easy access to spatially resolved information on the elemental/isotopic composition of the investigated material.
While the use of other surface analytical techniques such as secondary ion mass spectrometry (SIMS), glow discharge-mass spectrometry (GD-MS), X-ray photoelectron spectroscopy (XPS) or transmission electron microscopy (TEM) may also be advantageous within this context, LA combined with ICP-MS has found widespread use during the last decade.7 The benefits of LA-ICP-MS include easy manipulation of samples under atmospheric pressure as well as providing both high spatial resolution and high sensitivity because specimens are analysed directly.7 The lateral resolution of a few μm enables identifying potential inhomogeneity within a sample, with extended line scan analysis providing results reflecting bulk analysis.11,12 In addition, depth profiling capabilities of LA provide sub-μm depth resolution.4,6–8
Despite all of its advantages, LA-ICP-MS suffers from some important limitations such as non-uniform ablation processes and matrix-dependent melting events.6,8 These drawbacks are known to be less prominent for fs-LA units compared to their ns-counterparts.3 Employing laser beam homogenisers, thereby converting the Gaussian beam profiles into flat-top beam profiles, further improvements of the analytical performance have been achieved.8,13
Depth profiling may suffer from so-called downhole fractionation (DHF), mainly caused by differences in the volatility and chemical properties of the measured elements.14,15 For a given number of laser pulses, this phenomenon occurs earlier in small-diameter laser spots (greater depth/width ratio) compared to large-diameter spots.
Even though the use of a two-volume LA cell largely accelerates washout of the generated particle plume,4,6,14 the lowest repetition rate of the LA system and/or the minimum selectable acquisition time of the ICP-MS instrument might hinder the independent acquisition of analytical signals generated by subsequent laser pulses. If these technical restrictions are overlooked, mixing of neighbouring material layers may occur thereby deteriorating the depth resolution. To circumvent this issue, measurement protocols recording single shot events have been applied successfully.16
Combining a ns-LA unit and MC-ICP-MS, this study aims to develop an analytical procedure for depth profiling UO2 single crystals with respect to their n(235U)/n(238U) ratio. The complementary use of confocal laser scanning profilometry and high resolution scanning electron microscopy (SEM) micrographs, obtained by using a dual beam focused ion beam (FIB), contributed largely to the understanding of the laser/material interaction.
Experimental
Instrumentation
The Faraday detectors of a double-focusing multi-collector inductively coupled plasma mass spectrometer (MC-ICP-MS, Nu Plasma™, NU Instruments, Wrexham, Wales, U.K.) measured the abundance of 235U and 238U in the ablated particle cloud. Before switching to LA, the MC-ICP-MS was tuned for sensitivity and stability of U signals in solution mode employing an aqueous 30 ng L−1 U calibration solution having natural U isotopic composition. The key parameters of the entire LA-MC-ICP-MS set-up are summarised in Table 1. Additional information can be found elsewhere.10–12 A minimum of five sets of LA-MC-ICP-MS experiments were conducted for each parameter reported in this study. The signal intensities of 235U and 238U were recorded with the time-resolved-analysis option of MC-ICP-MS software.
| LA parameters | |
| Wavelength | 213 nm |
| Fluence | 0.24 J cm−2 |
| Spot diameter, circular | 25 μm |
| Ablation frequency | 1 Hz, single shots |
| Carrier gas | He, 170 mL min−1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Acquisition parameters | |
| Isotopes measured | 235U and 238U; both on Faraday detectors |
| Background | 60 s |
| Integration time | 200 ms per data point |
| Time between laser shots | 10 s |
| Number of replicates | 5 |
Employing the highest magnification objective (150×), a field of view of 95 μm × 70 μm was acquired within a few seconds with a theoretical z-resolution of 0.5 nm, a repeatability of 7 nm and a lateral resolution of 120 nm. Several slightly overlapping images were stitched together to obtain a larger field of view.
The advantage of having the ion gun is evident when the sample underneath the crater position has to be studied; in fact, a trench can be milled inside the crater to reveal a cross-sectional view of the sample just below the ablated level. Ion currents as high as 3 nA were used for coarse trench milling, while distinctly lower currents (down to 30 pA) were applied for fine-polishing of the cross-section.
Investigated uranium samples
Macroscopic UO2 single crystals were retrieved from experimental activities carried out in 1987 at the JRC-Ispra FARO (Furnace And Release Oven) experimental facility in which severe reactor accidents were simulated by out-of-pile experiments.17 The UO2 single crystal used in this study was taken from a larger piece with an irregular shape and an original mass of ∼25 g from which several 2 mm thick slices were prepared. The 〈100〉 crystal direction was established using an X-ray Laue camera. Prior to LA-MC-ICP-MS analysis, the sample surface of the UO2 single crystal was fine-polished using mono-dispersed diamond suspensions with a decreasing grain diameter down to 1 μm.
LA-MC-ICP-MS measurement protocol
To automate single laser shot analysis and to reduce operator intervention as much as possible,15 the following measurement protocol was developed and used throughout all time-resolved experiments:• At the start of each analysis the background signal of both 235U and 238U was recorded for 60 s.
• Prior to each ablation, the laser was allowed to warm up for 8 s, firing at 1 Hz, before the shutter was opened for one second.
• After a single laser shot the shutter was subsequently closed with the laser warming up again for 8 s before releasing the next laser shot. This way, an automated procedure was set-up that produced a single laser shot about every 10 s.
• The generated 235U and 238U ion currents were recorded with the time-resolved software of the MC-ICP-MS.
• The raw data thus obtained were imported into home-made data evaluation software that automatically searched for the generated 235U and 238U signals and further processed the data as described in detail below.
Single shot analysis data evaluation software
The software of the MC-ICP-MS acquired the time-resolved 235U and 238U signals employing an integration time of 200 ms per data point. Because both U isotopes were measured simultaneously, the assignment of a unique timestamp to each measurement point was possible.Ad-hoc software developed in-house enabled us to analyse the time-resolved MC-ICP-MS signals generated by each individual laser shot. After having subtracted the baseline, calculated as the average of the signals obtained throughout the first 60 s, an automated peak search procedure was performed on the 238U data stream, employing a minimum signal threshold of 200 mV. For each peak, the following information was identified:
• 238Umax: maximum peak height
• tmax: timestamp corresponding to 238Umax
• t−, t+: timestamps corresponding to the lower and upper limit of the identified peak. For this analysis Δt = t+ − t− = 10 s.
Subsequently, the software calculated the n(235U)/n(238U) amount ratio using the integral Ri, as given in eqn (1).
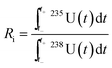 | (1) |
Being a multi-collection system, the timescale was identical for 235U and 238U MC-ICP-MS signals. However, all specific timestamps (t−, t+ and tmax) were defined considering the 238U signal only. Additionally, a merit index was applied to each laser pulse to identify 238U signals that exceeded the maximum input range (11 V) of the digitizer, or where the 235U signals were too close to the noise level of the Faraday detectors (<5 mV).
The software produces a reduced dataset, containing only the laser pulse index, tmax and Ri. Using these data, a depth calibration could be established based upon the pulse index and the laser ablation rate.
Quality control
For the main purpose of this study, no mass bias correction was applied to any of the raw data. However, the certified reference material CRM U-020 (∼2 wt% enriched in 235U) was measured repeatedly to obtain an evaluation of potential inaccuracy of the measured U isotope ratio. The experimental n(235U)/n(238U) amount ratio of 0.02069 ± 0.00014 (N = 206) agreed well with the corresponding certified value of 0.02081 ± 0.00020. Similarly, repeated measurements (N = 241) of the n(235U)/n(238U) amount ratio of 0.002228 ± 0.000032 for the reference UO2 single crystal matched reasonably well with the corresponding amount ratio of 0.0021494 ± 0.0000057 measured via isotope dilution mass spectrometry. Consequently, both LA-MC-ICP-MS and isotope dilution mass spectrometry results indicated that the reference UO2 single crystal contains ∼0.22 wt% of 235U.Results and discussion
Influence of laser ablation parameters on the generated MC-ICP-MS signal
The bulk of the three investigated UO2 single crystals consisted of depleted (either ∼0.2 wt% or ∼0.4 wt% 235U) U. The principal goal of this study – to obtain highly resolved depth profiles of the n(235U)/n(238U) amount ratio – created some striking boundary conditions for potential parameters for the LA set-up. First, a MC-ICP-MS maximum signal was required to remain within the linear region of the Faraday detector response signal. To this end, 238U signals were kept below 11 V. Second, low 235U signals had to simultaneously remain detectable using a Faraday detector. This was challenging at times because of the depleted nature of the UO2 materials. By selecting laser parameters appropriately, the above-mentioned difficulty was well controlled. Enlarging the laser spot size, for example, increased the MC-ICP-MS signals if 235U signals were too low to be measured reliably. Adjusting the MC-ICP-MS signal to 4–8 V for the more abundant U isotope also allowed the reliable measurement of the less abundant U isotope using a Faraday detector. Generating a shorter but higher “intensity pulse” of the MC-ICP-MS by increasing the He gas flow of the LA unit, for instance, was not aimed at because this approach frequently led to high ion currents that exceeded the linear range of the Faraday detector. Only time-resolved 235U signals with a maximum of at least 5 mV were considered in the evaluation of the n(235U)/n(238U) amount ratio for all experiments.Faraday detectors were selected to measure both 235U and 238U because this type of detector provides much higher precision compared to secondary electron multipliers (SEM). However, Faraday detectors require relatively high signals to overcome their internal electrical noise. Small signals may be preferably measured using an SEM, but its required dead time correction and non-linear behaviour limit the obtainable overall measurement precision. Employing a Faraday detector to measure one U isotope while using a SEM for the other low abundant U isotope suffers from the fact that the relative gain between both detectors varies randomly and therefore limits the achievable measurement precision.
The selected diameter of the laser beam at a given laser fluence determined the intensity of the MC-ICP-MS signal, providing an increasing response with larger spot diameters. The laser fluence, in turn, dictated the UO2 sputtering rate of the laser beam into the investigated UO2 materials. The lower the fluence, the less material was removed from the solid samples with a single laser shot. The selected fluence has been considered the most critical parameter for any spatially resolved LA analysis.3 One of the main challenges in the determination of U isotopic abundance profiles lies in achieving a high spatial resolution. As a result and considering the intensity restrictions mentioned above, a circular laser beam was selected for all experiments with a 25 μm diameter and a laser fluence of ∼0.24 J cm−2 (0.4% of the nominal maximum laser power). At such low fluences, fluctuations may be expected that are liable to have an essential impact on the laser ablation rate.8
Compared to our previous work,10–12 the carrier gas of the LA unit was changed from Ar to He in this study. The use of He instead of Ar is known to change the aerosol expansion and to improve the transport efficiency.3 Employing He as the carrier gas, the ICP-MS signal arrived within ∼1 s at the detector (as compared to ∼15 s with Ar) after the laser shot and returned to the background after about 2 s (∼10–15 s with Ar). This fast response and wash-out of the MC-ICP-MS signal was an important feature to avoid mixing of information obtained from subsequent laser shots, i.e., different sample layers. Consequently, the use of He was also conducive to a greater depth resolution.
In the same vein, laser repetition rates had to be sufficiently low to prevent mixing of U signals originating from different laser shots. High laser repetition rates of up to 100 Hz in combination with ultra-fast wash-out LA chambers have been successfully utilised for fast and highly spatially resolved LA-ICP-SFMS analysis for imaging of elemental distributions in single cells and rat retina tissue.18,19 This experimental approach, however, requires a high ICP-MS acquisition rate. Such fast acquisition rates of 2 ms per isotope were obtained for ICP-sector field MS,18 however, ICP-time-of-flight MS might be preferable for multiple isotope analysis.18,20 Even though the TV2 laser ablation cell employed in this study provided a fast washout, the electronics of the MC-ICP-MS limited the lowest acquisition rate to 200 ms per data point.
As a consequence, even though signals of 235U and 238U were acquired simultaneously in this study, the lowest possible laser repetition rate of 1 Hz was not sufficiently low to completely separate two consecutive U signals when the laser was operated continuously at this low repetition rate. Therefore, a single shot approach was favoured over continuous laser operation. Together with the TV2 laser ablation cell, guaranteeing a fast wash-out of the particle plume from the LA, well separated MC-ICP-MS signals from individual laser shots were obtained. Applying this single laser shot approach, different Faraday detector response times that can potentially lead to bias in the measured U isotope ratio of transient signals during LA, did not need to be considered.21–23 In other words, integrating the entire signal for both 235U and 238U from the before-shot baseline to the after-shot baseline will not result in a systematic offset of the measured n(235U)/n(238U) amount ratios.16
Evaluating downhole fractionation
The measured n(235U)/n(238U) amount ratio associated with a given depth profile can suffer from so-called matrix-dependent downhole fractionation (DHF).13,14 Generally speaking, for a given ablation time, when using small laser spot sizes, DHF can become an issue even for shallow craters. As the laser spot size increases, DHF will only become an issue at larger crater depths. To guarantee that the data generated throughout this study were not influenced by this phenomenon, 80 laser pulses (fluence 0.24 J cm−2) with a beam diameter of 25 μm were shot on the reference UO2 single crystal and the n(235U)/n(238U) amount ratio was measured in all 80 sub-samples.This experiment, repeated on five different laser spots, revealed no measurable fractionation. To this end, the n(235U)/n(238U) amount ratio was plotted vs. pulse number for all five measurement series. Each of the plots was fitted with a straight line yielding an average slope of 5 × 10−8 per pulse. In other words, assuming that the linear regression is valid, one would expect a variation of the n(235U)/n(238U) amount ratio of as little as 1‰ only after 20 thousand laser pulses. As only up to 40 laser pulses were required to reach the bulk isotope ratios for actual sample analyses (SC2 and SC3), DHF can be excluded in this study.
Laser ablation rate and crater bottom roughness
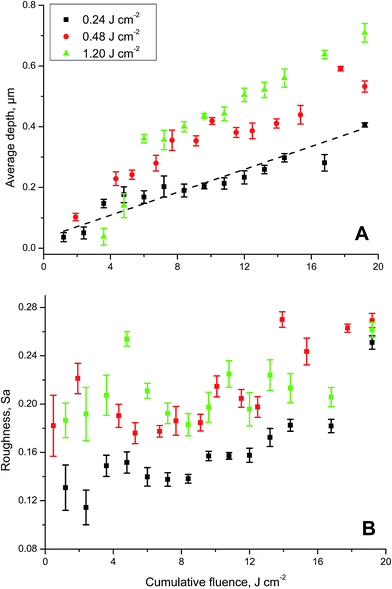
To determine crater depths using laser scanning profilometry, groups of five craters were ablated with an increasing number of laser pulses on the reference UO2 single crystal SC1. This experiment was conducted at three different fluence-per-shot settings, i.e., with 0.24 J cm−2, 0.48 J cm−2, and 1.2 J cm−2, respectively. The average depth (±standard errors) of each group of craters was plotted as a function of the cumulative fluence in Fig. 1A. To arrive at a cumulative fluence of ∼20 J cm−2, the corresponding maximum number of laser shots needed varied from 16 for a fluence of 1.2 J cm−2 to 80 for a fluence of 0.24 J cm−2.For all three series of different fluence settings, a linear relationship between the average depth and cumulative fluence was searched for (Fig. 1A). While all data points were considered for fluence settings of 0.24 J cm−2 and 0.48 J cm−2, for the highest fluence setting of 1.20 J cm−1 linearity did not start before 7 J cm−2 (Fig. 1A). The aim of fitting the experimental values was to highlight the potential linear behaviour of depth (Fig. 1A) and surface roughness (Fig. 1B) of the laser ablation craters with increasing fluence. Generally, the slope of the linear regression curves increased with increasing single shot fluence, as summarised in Table 2. This somewhat counterintuitive behaviour can be explained by taking into account the non-linearity of the LA process.6 Compared to the slope obtained with a fluence of 0.24 J cm−2, this parameter was ∼45% greater for experiments carried out with fluence settings of 0.48 J cm−2 or 1.20 J cm−2 (Table 2).
| Fluence, J cm−2 | Min. | Max. | Intercept | Std. error | Slope | Std. error |
|---|---|---|---|---|---|---|
| 0.24 | 0 | 20 | 0.0330 | 0.0146 | 0.0189 | 0.0011 |
| 0.48 | 0 | 20 | 0.0835 | 0.0269 | 0.0277 | 0.0021 |
| 1.20 | 7 | 20 | 0.1645 | 0.0251 | 0.0280 | 0.0023 |
Increased roughness of the crater bottom is expected as the number of laser pulse increases.6 However, this parameter remained relatively constant for the reference UO2 single crystal (Fig. 1B). There appears to be a slight tendency for the surface roughness Sa to increase with cumulative fluence for experiments conducted with a single shot fluence of 0.24 J cm−2. At higher fluences (0.48 J cm−2 or 1.2 J cm−2), the surface roughness is somewhat greater, but no clear trend with increasing cumulative fluence is evident (Fig. 1B).
The confocal laser scanning profilometer employed here offers a clear advantage versus contact stylus-based systems6 because no part of the instrument is physically touching and thereby possibly altering the sample surface and thus no artefacts are expected due to the stylus head size. While an Atomic Force Microscope (AFM) will provide superior vertical resolution, the acquisition speed for a large surface is definitively in favour of the laser system employed in this study. Moreover, compared to other optical based techniques (triangulation and white light interferometry), the results of the confocal laser system are not affected by the reflectivity of the sample surface.
Microscopic analysis of the laser interaction with the UO2 single crystal
Focused ion beam (FIB) investigations help better understand the 3-dimensional microstructure of solid materials.24 For a deeper insight into the way the laser beam interacts with UO2 single crystals, several high resolution SEM micrographs of the reference UO2 single crystal SC1 were acquired along with cross-sectional images taken after FIB milling of lateral trenches (Fig. 2).After fives laser pulses each with a fluence of 0.24 J cm−2, the sample surface was characterised by the formation of large rectangular “tiles” (Fig. 2). The size of these tiles was larger in the centre of the crater than at its periphery. Some tiles were detached completely from the UO2 single crystal, while others were bent and about to be released from the sample surface with the next laser pulse. In the vicinity of the ablation craters, several tiles of medium (1 × 1 μm) and large (3 × 3 μm) size were identified, possibly because not all of these tiles were removed efficiently by the helium gas flow passing through the LA chamber. The ordered, rectangular structure progressively disappeared with increasing number of laser pulses as is evident from the micrographs recorded after 40 laser pulses (Fig. 2).
Another noticeable effect of the laser/UO2 single crystal interaction was the formation of sub-micrometric porosity, present at particularly high concentrations in the periphery of the laser crater. This porosity was unquestionably generated by the laser/sample interaction because it was not visible in the pristine material, neither on the surface nor in the bulk of the reference UO2 single crystal as revealed by the FIB cross-sections in Fig. 2. A similar behaviour was also observed during SIMS ion sputtering and generally speaking, during corrosion experiments (data not shown), possibly caused by the presence of local defects in the crystal structure.
From cross-sectional images (Fig. 2, right column), it was evident that cavities were formed below the tiles, even below the ones that still appeared to be attached firmly to the substrate. This effect, along with the bending of the large tiles that were about to be removed with the subsequent laser pulse, is the reason why the first data points displayed in Fig. 1A had a large deviation from linearity, in particular at high single shot fluence.
Depth assessment of LA craters
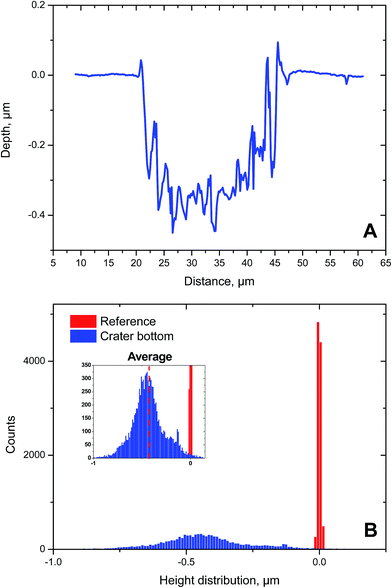
A confocal laser scanning profilometer was used to measure the physical dimensions of the laser ablation craters. A representative example of such a circular laser ablation crater with a 25 μm nominal diameter after 40 laser shots on the reference UO2 single crystal is shown in Fig. 3A. While the scale of both axes in Fig. 3A is given in μm, one has to consider the aspect ratio in this figure. A small change in the depth of the ablation crater is reflected by a comparatively large distance on the y-axis and vice versa for the distance plotted on the x-axis. The conical shape of the crater, typical for ns-laser ablation systems,3,6 leads to partial mixing of consecutively ablated layers of the crater and thereby limits the obtainable depth resolution. The use of a state-of-the-art fs-laser ablation system improves substantially both the crater shape and depth resolution.3,8,13As the laser is not removing matter from the UO2 single crystal layer by layer, the crater bottom is not flat, but largely uneven (Fig. 3A). Consequently, this leads to a measurable difference between the maximum depth (0.47 μm) and the average depth (0.43 μm) of the LA crater (Fig. 3A). And the variability in the assessment of the crater depth, in turn, will impact the calculation of the laser ablation rate, for example. To circumvent the above-mentioned issue, the concept of average step depth is employed frequently in this context. The average step depth, or more generally, the average step height, is a methodology to calculate the height difference between two surfaces. This approach is particularly effective when, due to the high level of roughness, it is not possible to define a mathematical plane representing the two surfaces.
To this end, two regions within the sample were selected, the first one (hereafter named “reference”) representing the zero level, while a second one represented the “crater bottom”. An absolute height value was assigned to all pixels of the generated computer image of the surfaces of these two areas, obtaining two height distributions. Since only the height difference of the two levels is of interest, the absolute height scale was shifted by a constant factor bringing the average of the reference height distribution to a value distributed around zero. In Fig. 3B the height distributions of both the reference area (red) and one of the deepest craters (blue) ablated on the reference UO2 single crystal SC1 are shown. The red histogram is very narrow because the corresponding pristine surface of the single crystal was mirror-polished prior to LA-MC-ICP-MS analysis. By contrast, the blue distribution, representing the crater bottom, was broad in comparison, ranging from almost −1 μm to even slightly positive values. This broadening is indeed the direct consequence of the ablation-induced roughness. Despite this broad height distribution, the calculation of the average of the distribution allowed the assignment of an individual depth value to each LA crater in the most unbiased way. All depths reported here are expressed as average step depth.
Laser ablation crater diameter
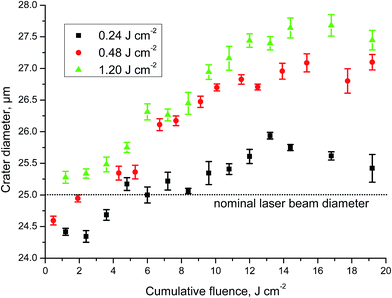
The confocal laser profilometer also served for the characterisation of surface features such as the diameter of the generated LA craters of the reference UO2 single crystal SC1. To this end, a circle defining the LA crater needed to be established. To minimise operator bias when defining a circle corresponding to the crater being measured, the analysis software offers the so-called multi-point approach which enables the operator to select a redundant number (8) of points lying on the laser footprint. The software then automatically defines the circle which passes closest to the selected points.In this way, the diameters of all LA craters of the reference UO2 single crystal SC1, generated with an increasing number of laser shots, were measured. This experiment, repeated on five individual spots, revealed expanding crater diameters with increasing number of laser pulses indicated as cumulative fluence in Fig. 4. This suggests a crater edge effect in the case of the presence of a concentration gradient. While this relative trend towards larger crater diameters is obvious, also their absolute values were striking. Note that the nominal diameter of the laser beam was set to 25 μm, while the measured diameters ranged from ∼24.3 μm to 27.8 μm (Fig. 4). Additionally, a higher fluence of individual laser shots resulted in larger crater diameters, even though the cumulative fluence was the same for all three experiments, i.e., using pulses of 0.24 J cm−2, 0.48 J cm−2, and 1.20 J cm−2.
Please note that for low laser power, i.e., 0.24 J cm−2 and 0.48 J cm−2, crater diameters were lower than the nominal laser beam diameter at low cumulative fluence. As the minimum selectable power (0.1% and 0.2% of the maximum nominal power) was considered here, the interaction of the laser beam with the UO2 single crystal at the first few laser shots was not sufficiently intense to generate craters that have the dimensions of the laser beam at least. The small standard deviations on the average of five replicate measurements, however, reveal the highly reproducible behaviour of this laser/matter interaction (Fig. 4).
While the pattern of increasing crater diameters was very similar for laser fluence settings of 0.48 J cm−2 and 1.20 J cm−2, the lowest laser fluence adjustment of 0.24 J cm−2 yielded a somewhat different pattern with lower crater diameters (Fig. 4). Starting from a cumulative fluence of ∼11 J cm−2, crater diameters tended to remain constant and did not further increase with increasing cumulative fluence. Taken together, this experiment highlighted the impact of the way the energy of individual laser pulses is delivered towards the sample surface, even though the total amount of energy, i.e., cumulative fluence was identical for all three experimental settings. In other words, delivering the same amount of energy to the sample surface, but in various individual laser energy packages produced different crater diameters.
To ascertain the accuracy of the absolute values of the crater diameters, the x- and y-calibration of the profilometer was regularly checked and confirmed with two calibrated references.
Influence of laser focus on ablation crater geometry
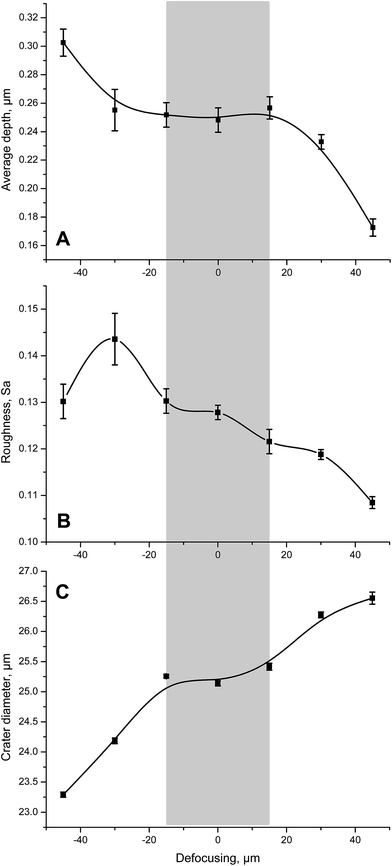
Accurately focusing the laser beam on the sample surface is not always straightforward, especially if the specimen is black and mirror-polished, such as the UO2 single crystals in this study. Therefore, the potential influence of the beam being out of focus upon the laser-UO2 surface interaction was investigated in more detail. Initially the laser beam was focussed as accurately as possible onto the surface of the reference UO2 single crystal SC1, which was then followed by shooting 40 laser pulses of 0.24 J cm−2 each. Subsequently, the average depth and diameter of ablation craters were assessed together with the corresponding surface roughness of the bottom of the crater. This experiment was repeated five times and served as a reference point for data obtained when the laser beam was out of focus. Following this, the laser beam was stepwise defocussed by 15 μm, 30 μm, 45 μm, −15 μm, −30 μm, and −45 μm and the above procedure was repeated.The outcome of this investigation is graphically summarised in Fig. 5. In general, a defocussing of the laser beam by ± 15 μm had almost no impact on any of the three investigated parameters as indicated by the grey area in Fig. 5. Changing the focus of the laser beam from +45 μm to −45 μm, however, increased the laser ablation rate and surface roughness by as much as ∼75% (Fig. 5A) and ∼20% (Fig. 5B), respectively. Concurrently, the crater diameter decreased by about ∼13% (Fig. 5C). Taken together, small inaccuracies (±15 μm) of the laser focus will not systematically bias the laser ablation rate, surface roughness and crater diameter, while larger defocussing certainly will have an impact.
Depth profile of UO2 single crystals having different 235U gradients
To establish U self-diffusion coefficients in UO2 single crystals, depth profiling with secondary ion mass spectrometry (SIMS) has been applied in the past.25 Similarly, laser ablation microprobe (LAMP)-ICP-MS was employed to study the diffusion of U in solid cement monoliths.26For an appropriate investigation of U self-diffusion in UO2 single crystals, the depth profiling capabilities of the laser ablation system were applied to the two UO2 single crystals SC2 and SC3, both featuring a uranium isotopic concentration gradient (235U enriched on the surface and depleted in the bulk). Several repetitions of the LA experiment (8 for SC2 and 10 for SC3) were performed applying the same laser parameters (diameter, fluence, repetition rate and wash out delay) as used for the analysis of the reference UO2 single crystal SC1. The acquired data stream from the LA-MC-ICP-MS measurements was evaluated using home-made single-shot data evaluation software.
The surface layers of both investigated UO2 single crystals consisted of enriched U (∼21 wt% to 26 wt% 235U) that diffused into the depleted body of the specimens (Fig. 6). The relative standard deviation of the average of five consecutive measurements ranged from ∼3 to ∼6% for the first 13 data points of the depth profiles of both UO2 single crystals where the largest and most relevant changes in the n(235U)/n(238U) amount ratio were seen (Fig. 6), increasing to about 12% for replicate measurements of depleted U, i.e., the base material. It is important to note that this precision was fit-for-purpose for this study. The limiting factor for the overall analytical performance was the reproducibility of the removal of the sample material with the laser ablation rather than the measurement precision.
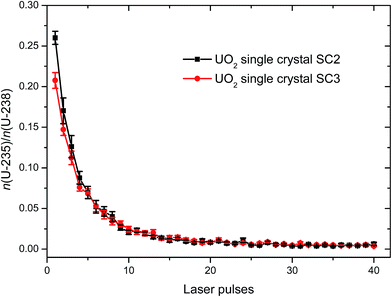 | ||
| Fig. 6 In-depth n(235U)/n(238U) amount ratios (n = 5) measured for the two UO2 single crystals SC2 and SC3 revealing penetration of 235U into the bulk material. | ||
The experimental conditions (reaction temperature, O2 partial pressure, etc.) applied during the preparation of the test samples revealed only a small impact on the diffusion of 235U into the two UO2 single crystals. While a discussion of more technical details is beyond the scope of this study, the developed analytical procedures will be employed to study the diffusion behaviour of U into UO2 with the goal of setting up diffusion coefficients for this material.1 Due to the presence of a brittle thin top layer left from sample preparation, it was not possible to derive a unique laser ablation rate for the two UO2 single crystals SC2 and SC3. The variability of the thickness of this layer was strongly affecting the laser ablation rate. Consequently, a serious quantification of this parameter was not possible for these two specific samples. For this reason the n(235U)/n(238U) amount ratio in Fig. 6 is presented as a function of the laser pulse number. The use of an uncalibrated depth axis (x-axis) in Fig. 6, however, may reduce the potential difference in diffusivity between the two samples.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the U isotopic analysis of a fragment of the investigated reference UO2 single crystal using TIMS by the Analytical Service of JRC Karlsruhe.References
- Y. Ma, A study of point defects in UO2+x and their impact upon fuel properties, Materials Science [cond-mat.mtrl-sci], Université d'Aix-Marseille, 2017, English. <tel-01714468v2>.
- J. Pisonero, J. Koch, M. Wäle, W. Hartung, N. D. Spencer and D. Günther, Anal. Chem., 2007, 79, 2325–2333 CrossRef CAS.
- J. Pisonero and D. Günther, Mass Spectrom. Rev., 2008, 27, 609–623 CrossRef CAS.
- B. Hattendorf, J. Pisonero, D. Günther and N. Bordel, Anal. Chem., 2012, 84, 8771–8776 CrossRef CAS PubMed.
- V. Grimaudo, P. Moreno-García, A. Riedo, M. B. Neuland, M. Tulej, P. Broekmann and P. Wurz, Anal. Chem., 2015, 87, 2037–2041 CrossRef CAS.
- A. Gutiérrez-González, C. Gonzáles-Gago, J. Pisonero, N. Tibbetts, A. Menéndez, M. Vélez and N. Bordel, J. Anal. At. Spectrom., 2015, 30, 191–197 RSC.
- A. Limbeck, M. Bonta and W. Nischkauer, J. Anal. At. Spectrom., 2017, 32, 212–232 RSC.
- D. Käser, L. Hendriks, J. Koch and D. Günther, Spectrochim. Acta, Part B, 2018, 149, 176–183 CrossRef.
- X. Cheng, W. Li, W. Hang and B. Huang, Spectrochim. Acta, Part B, 2015, 111, 52–56 CrossRef CAS.
- Z. Varga, M. Krachler, A. Nicholl, M. Ernstberger, T. Wiss, M. Wallenius and K. Mayer, J. Anal. At. Spectrom., 2018, 33, 1076–1080 RSC.
- M. Krachler, Z. Varga, A. Nicholl, M. Wallenius and K. Mayer, Microchem. J., 2018, 140, 24–30 CrossRef CAS.
- M. Krachler, Z. Varga, A. Nicholl and K. Mayer, Analytica Chimica Acta: X, 2019, 2, 100018 CrossRef.
- J.-I. Kimura, Q. Chang, N. Kanazawa, S. Sasaki and B. S. Vaglarov, J. Anal. At. Spectrom., 2016, 31, 790–800 RSC.
- T. J. Ver Hoeve, J. S. Scoates, C. J. Wall, D. Weis and M. Amini, Chem. Geol., 2018, 483, 201–217 CrossRef CAS.
- P. K. Mukherjee, A. K. Souders and P. J. Sylvester, J. Anal. At. Spectrom., 2019, 34, 180–192 RSC.
- J. M. Cottle, M. S. A. Horstwood and R. R. Parrish, J. Anal. At. Spectrom., 2009, 24, 1355–1363 RSC.
- D. Magallon, H. Schins, R. Zeyen and R. Hohmann, The FARO experimental programme: quick look on UO2 melting and BLOKKER I results, European Commission, Joint Research Centre, Ispra, 1989 Search PubMed.
- J. Pisonero, D. Bouzas-Ramos, H. Traub, B. Cappella, C. Alvarez-Llamas, S. Richter, J. C. Mayo, J. M. Costa-Fernandez, N. Bordell and N. Jakubowski, J. Anal. At. Spectrom., 2019, 34, 655–663 RSC.
- A. J. Managh and P. Reid, J. Anal. At. Spectrom., 2019, 34, 1369–1373 RSC.
- O. B. Bauer, O. Hachmöller, O. Borovinskaya, M. Sperling, H.-J. Schureck, G. Ciarimboli and U. Karst, J. Anal. At. Spectrom., 2019, 34, 694–701 RSC.
- T. Pettke, F. Oberli, A. Audétat, U. Wiechert, C. R. Harris and C. A. Heinrich, J. Anal. At. Spectrom., 2011, 26, 475–492 RSC.
- M. Klaver, R. J. Smeets, J. M. Koornneef, G. R. Davies and P. Z. Vroon, J. Anal. At. Spectrom., 2016, 31, 171–178 RSC.
- F. Claverie, A. Hubert, S. Berail, A. Donard, F. Pointurier and C. Pécheyran, Anal. Chem., 2016, 88, 4375–4382 CrossRef CAS.
- S. R. Lewis, A. Simonetti, L. Corcoran, T. L. Spana, B. W. Chung, N. E. Teslich and P. C. Burns, J. Radioanal. Nucl. Chem., 2018, 318, 1389–1400 CrossRef CAS.
- A. C. S. Sabioni, W. B. Ferraz and F. Millot, J. Nucl. Mater., 1998, 257, 180–184 CrossRef CAS.
- D. Sugiyama, T. Chida and M. Cowper, Radiochim. Acta, 2008, 96, 747–752 CAS.
Footnote |
| † Current address: Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-Sen University, Zhuhai 519082, P. R. China. |
| This journal is © The Royal Society of Chemistry 2019 |