Open Access Article
Open Access ArticleA quantitative nanoparticle extraction method for microsecond time resolved single-particle ICP-MS data in the presence of a high background†‡
Darya
Mozhayeva
 a and
Carsten
Engelhard
a and
Carsten
Engelhard
 *ab
*ab
aUniversity of Siegen, Department of Chemistry and Biology, Adolf-Reichwein-Str. 2, D-57076 Siegen, Germany. E-mail: engelhard@chemie.uni-siegen.de; Fax: +49 2717402041
bCenter of Micro- and Nanochemistry and Engineering, University of Siegen, Adolf-Reichwein-Str. 2, D-57076 Siegen, Germany
First published on 30th May 2019
Abstract
The detection of nanoparticles (NPs) in the presence of a high background (BG) is challenging in single particle inductively coupled plasma mass spectrometry (SP-ICP-MS) and leads to inaccurate quantification. In this study, we report a data processing procedure for the deconvolution of SP-ICP-MS data and its application to quantification of both the Ag NP size distribution (20 to 100 nm Ag NPs) and the concentration of dissolved silver ions (Ag+ up to 7.5 μg L−1) in mixtures using Poisson statistics to determine thresholds to identify the beginning and end of NP signal events. SP-ICP-MS with a microsecond time resolution data acquisition system (μsDAQ) and conventional pneumatic nebulization was used for the detection of Ag NPs in the presence of a significant concentration of ionic BG (107Ag+ up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps). In contrast to conventional three times standard deviation of the BG (3 × SDBG) decision criterion (normal distribution), our NP ion cloud extraction mechanism from the μsDAQ is based on setting thresholds to determine the beginning and the end of an ion cloud using Poisson statistics, which is suitable for the low count data. The algorithm was applied here for the flagging and detection of Ag NPs in the presence of Ag+. Critical level (false positive probability was set to 5%) and detection limit (false positive and false negative probabilities were set to 5%) based on Poisson distributions were implemented to determine the thresholds. A range of different sets of NP ion cloud extraction conditions were tested to verify the calculated thresholds and to obtain optimal extraction conditions at different BGs (Ag+ concentration). The method can be universally applied for the detection of different elements with SP-ICP-MS.
000 cps). In contrast to conventional three times standard deviation of the BG (3 × SDBG) decision criterion (normal distribution), our NP ion cloud extraction mechanism from the μsDAQ is based on setting thresholds to determine the beginning and the end of an ion cloud using Poisson statistics, which is suitable for the low count data. The algorithm was applied here for the flagging and detection of Ag NPs in the presence of Ag+. Critical level (false positive probability was set to 5%) and detection limit (false positive and false negative probabilities were set to 5%) based on Poisson distributions were implemented to determine the thresholds. A range of different sets of NP ion cloud extraction conditions were tested to verify the calculated thresholds and to obtain optimal extraction conditions at different BGs (Ag+ concentration). The method can be universally applied for the detection of different elements with SP-ICP-MS.
Introduction
Manufactured nanomaterials (MNMs) are used increasingly in the modern society.1 In the case of silver (Ag) NPs, the release of ionic silver (Ag+) frequently leads to increased toxicity of this type of NP.2,3 However, even though a significant number of publications report on the mechanism of Ag NP toxicity, they might use NPs with different sizes, surface coatings and exposure media, and in different organisms/cell cultures; thus, it is still not clear to which degree toxicity stems from silver ions and NPs, respectively.4 Advanced analytical methods are required to assess the presence and the quantity of different silver species, especially at environmentally relevant concentrations. Centrifugal ultrafiltration and membrane filtration could be used for the separation of Ag+ from Ag NPs; however, the methods are limited by the membrane pore size, possible Ag+ adsorption, and possible changes in the initial state of NPs.5Techniques based on inductively coupled plasma mass spectrometry (ICP-MS) can be used to separate and directly analyse the NPs and dissolved metals. Liquid chromatography coupled to ICP-MS6–8 and capillary electrophoresis (CE) coupled to ICP-MS9–11 both can be used for this type of separation, yet these methods still require an experienced operator. Single particle (SP)-ICP-MS utilizes short dwell times (DT) (typically in the low to sub-millisecond range) and time-resolved data acquisition to detect single NPs in a sufficiently diluted dispersion with minimal sample pretreatment (dilution) at environmentally relevant concentrations (low nanogram per litre range for NPs). Individual NP sizes can be assessed through mass-related counts detected at a given mass-to-charge (m/z) ratio. These signals can be characterized as individual spikes from NPs, whereas the background (BG) represents the level of dissolved metal in the solution.12 Several reviews summarized the capabilities and limitations of SP-ICP-MS,13–15 emphasizing that there is still room for improvement. Namely, more well-characterized standards are needed for size and particle number concentration (PNC) determination, matrix effects require more detailed investigations and should be accounted for, the linear dynamic range of the pulse counting stage of the secondary electron multiplier (SEM) is limited, etc. Ideally, NPs can be distinguished from the BG as pulses, if the BG is low. Frequently, this is not the case, and BG increase hinders the detection of NPs, because of increased standard deviation (SD) of the BG; therefore, the detection limit (LD) for NP size drastically deteriorates. Laborda et al. could detect Ag NPs of size from 40 to 80 nm (with a DT of 5 ms) in the presence of the Ag+ BG below 1 μg L−1; however, the presence of already 300 ng L−1 of Ag+ resulted in the increase of the calculated particle size LD from 18 nm (in ultrapure water) to 32 nm (with 300 ng L−1 of Ag+).12 TiO2 NPs could be distinguished from the continuous BG, where up to 0.5 μg L−1 of Ti(IV) was added.16 Schwertfeger et al. introduced an approach for NP and dissolved analyte quantification, where three dilutions were implemented for the detection of gold and silver NPs in the presence of the dissolved ions.17 First, the solution without any dilutions was measured to quantify the dissolved metal; afterwards, two dilutions were done for single NP measurements. Without the dilution, it was shown that the presence of already 1 μg L−1 of dissolved silver leads to errors (size overestimation and a lower number of particles detected) in the detection of 30 nm Ag NPs.
In conventional multi-elemental analysis with ICP quadrupole MS (ICP-Q-MS) a signal at a selected m/z is recorded for a certain DT (typically in the low to sub-millisecond range for NP detection and up to 1 s during homogeneous sample analysis). As NPs result in relatively short ion signal events in ICP-Q-MS (e.g. the ion signal duration for one 60 nm Ag NP was approximately 500 μs in our previous study),10 the choice of an appropriate DT is crucial to ensure a correct detection. The use of a DT on the microsecond time scale allows acquiring several data points per NP18–26 and helps to avoid incorrect detection, when e.g. one NP event is split between two DTs (split-particle event). An approach to use a 5 μs DT without a significant dead time (other than the SEM dead time) between consequent dwells was introduced by our group earlier.26 When the prototype data acquisition system with 5 μs time resolution (μsDAQ) is used, the counts that would otherwise be counted in e.g. 3 ms are split into 600 dwells of 5 μs each; then, the counts detected per NP are summed up to get a signal reading per particle. This approach helps to minimize particle coincidence and split-particle events. Meanwhile, the BG is also split, and e.g. 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps of a constant BG signal would theoretically correspond to only 0.5 counts in 5 μs; however, the counts that are recorded are positive integer numbers, so some of the readings would be 0 and others 1. This type of data should be described with a Poisson distribution, and not the Gaussian type. In this way, the low BG allows extending the concentration range of dissolved metals, in the presence of which NPs can still be detected and quantified. The data obtained with the μsDAQ are later processed to extract NPs with an optimized algorithm. In the algorithm, a NP event starts when a count value exceeds a certain threshold, and ends, when a second but lower threshold is reached.26 However, there is a challenge: a high BG (e.g. 100
000 cps of a constant BG signal would theoretically correspond to only 0.5 counts in 5 μs; however, the counts that are recorded are positive integer numbers, so some of the readings would be 0 and others 1. This type of data should be described with a Poisson distribution, and not the Gaussian type. In this way, the low BG allows extending the concentration range of dissolved metals, in the presence of which NPs can still be detected and quantified. The data obtained with the μsDAQ are later processed to extract NPs with an optimized algorithm. In the algorithm, a NP event starts when a count value exceeds a certain threshold, and ends, when a second but lower threshold is reached.26 However, there is a challenge: a high BG (e.g. 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps) can adversely influence the total counts per extracted NP ion cloud because the BG is extracted together with the NPs and the extraction conditions (thresholds) have to be carefully selected. In addition, the ICP-MS user has to decide, which signal should still be counted as a signal from a NP and which signal should be counted as BG fluctuation when working at a low count level (a single 20 nm Ag NP can result in a signal of approximately 30 counts with an optimized ICP-Q-MS). Additionally, a new LD definition is required to tackle this issue based on Poisson and not solely on normal statistics, and we present our approach in detail further below.
000 cps) can adversely influence the total counts per extracted NP ion cloud because the BG is extracted together with the NPs and the extraction conditions (thresholds) have to be carefully selected. In addition, the ICP-MS user has to decide, which signal should still be counted as a signal from a NP and which signal should be counted as BG fluctuation when working at a low count level (a single 20 nm Ag NP can result in a signal of approximately 30 counts with an optimized ICP-Q-MS). Additionally, a new LD definition is required to tackle this issue based on Poisson and not solely on normal statistics, and we present our approach in detail further below.
Typically, researchers use the three times the SD of the BG (3 × SDBG) based on the normal distribution of the data to differentiate NP signal distributions from the BG when ICP-MS data are obtained with millisecond time resolution.14,15,27 Cornelis and Hassellöv reported a deconvolution approach to differentiate the NPs that are not fully separated from the BG by modelling the noise contribution in ICP-Q-MS.28 Recently, Gundlach-Graham et al. used a Monte Carlo simulation approach to obtain the signal distribution of noise and low-count signals in ICP time-of-flight (TOF)-MS data at a mass spectral acquisition rate of 200 Hz. In their study, thresholds for the detection of NPs were determined using Poisson statistics.29 Beginning in 2014, ICP-Q-MS instruments became commercially available that feature DT settings down into the hundred-microsecond regime and up to 25 μs DT. However, a standardized data processing approach for microsecond-time resolved data in ICP-Q-MS is not established so far. Data processing is also limited by the software of current ICP-MS instruments, where only a few million data points can be recorded and/or processed per measurement, causing a limitation in the available total analysis time. Researches are still evaluating different types of data processing techniques and the possibilities that a higher time resolution might provide. For example, with 100 μs microsecond time resolution, the NPs were separated from the BG signal by applying the 3 × SDBG criterion.19,30 M. D. Montaño et al.23 used 25, 50, and 100 μs DTs to distinguish a 28Si+ signal from a high [14N14N]+ BG during silica colloid analysis. In their study, an iterative algorithm with an initial threshold according to the 3 × SDBG criterion, subsequent smoothing, and BG subtraction was used. An algorithm based on outlier detection was presented by J. Tuoriniemi et al. for data with 100 μs time resolution.20 A different approach reported by Donard et al. utilizes the detection of peak maxima.24,25
In the present study, we report a data processing method based on Poisson statistics for simultaneous quantification of NPs and dissolved ions (recorded with a prototype μsDAQ). The method is rapid and can be used to process ICP-MS measurements of any duration. Ag NPs are selected as a model sample because they are widely discussed in the literature on SP-ICP-MS. A general algorithm for the analysis of NPs and dissolved ions is developed that is not limited to silver ions and NPs, but can also be used for ions and NPs with different elemental compositions. Throughout the discussion below, the term “NP size” refers to the calculated NP size, if not stated otherwise.
Experimental section
Sample preparation
Monodisperse spherical Ag NPs with nominal diameters of 20, 40, 60, and 100 nm with a citrate coating and an initial concentration of 0.020 g L−1 were bought from nanoComposix (San Diego, CA, USA). The diameters of the NPs determined by transmission electron microscopy (TEM) by the manufacturer were 18.5 ± 3.4, 39 ± 4, 62 ± 7, and 98 ± 10 nm, respectively. The suspensions were preserved at 4 °C in darkness before analyses and manually shaken for 30 s prior dilution. No data were provided by the manufacturer on the content of silver ions in the suspensions. Dilutions were done with bi-distilled deionized water directly prior the analyses to achieve a PNC of approximately 2.5 × 105 NP mL−1. Ag+ solution (999 ± 5 mg L−1, Inorganic Ventures, Christiansburg, VA, USA) was diluted for external calibration and added to NP suspensions with nine different concentrations from 10 ng L−1 to 7.5 μg L−1 (with experimental dilution uncertainty). NaNO3 (≥99%, analytical reagent grade, Carl Roth GmbH, Karlsruhe, Germany) and HNO3 (70%, analytical reagent grade, Fisher Scientific, Loughborough, UK) were used for the matrix modification of bi-distilled water.Instrumentation
All measurements were done on a model ICAP Qc (Thermo Fisher Scientific, Bremen, Germany) ICP-Q-MS instrument. The instrument was controlled by using Qtegra ISDS software (2.4.1800.192, Thermo Fisher Scientific). The ICP-Q-MS was equipped with a model ESI SC-2 DX autosampler (ESI Elemental Service & Instruments GmbH, Mainz, Germany), a model MicroFlow PFA-50 nebulizer (Thermo Fisher Scientific, Bremen, Germany) with a self-aspiration flow rate of around 65 μL min−1 at 1 L min−1 Ar (manufacturers' data), and a Peltier-cooled cyclonic quartz spray chamber held at 3 °C. A second roughing pump (Sogevac SV40 BI, Leybold Vacuum Cologne, Germany) allowed achieving a lower interface pressure of 1.36 ± 0.02 mbar, and together with a high sensitivity skimmer insert (insert “2.8”, Glass Expansion, Melbourne, Australia), nickel cones helped to increase the sensitivity of the instrument. The main instrumental parameters of the ICP-MS are presented in Table 1.| Parameter | Value |
|---|---|
| RF power | 1450 W |
| Ar cooling gas flow | 14 L min−1 |
| Ar auxiliary gas flow | 0.8 L min−1 |
| Ar nebulizer flow | 0.6 L min−1 |
| Sampling position | 2 mm |
| Skimmer type | Ni (insert version) |
| Insert type | Skimmer cone insert “2.8” |
| Torch injector inner diameter | 1 mm |
| Dwell time for the μsDAQ | 5 μs |
| Dwell time for vendor software | 10 ms |
| Monitored isotope | 107Ag+ |
Data acquisition and data processing
The μsDAQ (5 μs DT) was operated simultaneously with the vendor software (10 ms DT). All NP suspensions were analysed for 3 min in triplicates, and the dissolved ionic standard calibration was performed once per day by measuring each calibration standard for 1 min. After each measurement the probe was washed in 2% HNO3 for 45 s to ensure no carry-over between the samples. To guarantee the continuous detection with the μsDAQ, the detection was performed only in the counting mode of the SEM. The maximum concentration of Ag+ was chosen to be 7.5 μg L−1 resulting in approximately 106 cps, which does not lead to detector saturation. The graphical representation of results was done in Origin 2017 (OriginLab Corporation, Northampton, MA, USA).Millisecond time resolution
The data obtained with the 10 ms DT from the Ag NP suspensions with and without additions of Ag+ and from the calibration standards were binned to obtain signal distribution diagrams. Gaussian fitting was used both for NPs and for the continuous BG fitting. The maximum of the Gaussian distribution was taken as an average count value. Also, the width of the distribution (“W”) parameter that is equal to two SDs was used in the calculations.μsDAQ data processing
With the 5 μs time resolution, 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points are generated per second, and several data points are obtained per NP; therefore, to reduce the number of data points, extract the NP ion cloud events from the BG, and reduce the size of the data file; the ion cloud extraction is needed. As there are only e.g. 5000 NPs distributed more or less homogeneously over a 180 s ICP-MS measurement (3.6 × 107 data points), the majority of the data collected represent the BG. As described earlier,26 the ion cloud extraction was done with a command line tool written in “C”. The basis of the ion cloud extraction mechanism is to set three parameters, namely, “S” (how many data points should be grouped and summed up to judge, if the chosen threshold conditions are reached), “T” (a threshold value; when it is reached, an ion cloud extraction begins), “E” (an end threshold; when it is reached, the ion cloud extraction ends). Only positive integer numbers were used as thresholds, since the output of the detector (acquired data) contains only positive integer numbers. The counts obtained per particle are summed up; and the output contains time stamps of the ion cloud beginning and end, the duration of each ion cloud, and the number of counts per ion cloud, along with the time-resolved profiles of the extracted ion clouds. To reduce the number of variables in the current study, S = 5 was used in all of the tested extraction condition combinations. Specific examples are described below. In order to test different sets of extraction parameters, another command line tool was used to process file batches under different extraction conditions.
000 data points are generated per second, and several data points are obtained per NP; therefore, to reduce the number of data points, extract the NP ion cloud events from the BG, and reduce the size of the data file; the ion cloud extraction is needed. As there are only e.g. 5000 NPs distributed more or less homogeneously over a 180 s ICP-MS measurement (3.6 × 107 data points), the majority of the data collected represent the BG. As described earlier,26 the ion cloud extraction was done with a command line tool written in “C”. The basis of the ion cloud extraction mechanism is to set three parameters, namely, “S” (how many data points should be grouped and summed up to judge, if the chosen threshold conditions are reached), “T” (a threshold value; when it is reached, an ion cloud extraction begins), “E” (an end threshold; when it is reached, the ion cloud extraction ends). Only positive integer numbers were used as thresholds, since the output of the detector (acquired data) contains only positive integer numbers. The counts obtained per particle are summed up; and the output contains time stamps of the ion cloud beginning and end, the duration of each ion cloud, and the number of counts per ion cloud, along with the time-resolved profiles of the extracted ion clouds. To reduce the number of variables in the current study, S = 5 was used in all of the tested extraction condition combinations. Specific examples are described below. In order to test different sets of extraction parameters, another command line tool was used to process file batches under different extraction conditions.
Different ion cloud extraction conditions were tested only on one data set out of the three replicates, because the number of NPs per 3 min run was always higher than 3500 for 40, 60, and 100 nm NPs. The number of detected NPs was considered to be sufficient to construct a size distribution with statistical significance (also because the determination of PNC was not the goal of the study). External size calibration was made daily with 20, 40, 60, and 100 nm Ag NPs without addition of dissolved silver. To have a starting point for the investigation of the influence of the extraction conditions on the calculated NP size external size calibration has been performed under S = 5, T = 5, and E = 1 extraction conditions (when 5 counts (T = 5) were detected in 25 μs (S = 5) an ion cloud starts and when there was only 1 count (E = 1) in 25 μs, the ion cloud ends). These values were calculated using the formulas from Table 2, when the average BG is low (see Table 3 and further sections for details). The BG was subtracted, and the linear fit resulted in R2 = 0.996 ± 0.002 based on the sizes provided by the manufacturer. A high correlation coefficient is the evidence of the stability of the NPs in the suspensions. After size calibration and BG subtraction, the size distribution diagrams were constructed by binning the data into 2 nm bins. Fitting of all obtained size distributions was performed with a Gaussian model. This allows us to easily compare the maxima of the distributions, which is not always straightforward with other fitting models (e.g. Poisson distribution). In this study, different criteria including the BG maximum, mean NP size, width of the size distribution, total number of detected NPs, and size starting from which the NP size distribution can be distinguished obtained from the constructed size distributions were used to compare different extraction conditions (see the ESI and Fig. S1‡).
Results and discussion
Quantification of ionic silver in the presence of NPs with millisecond time resolution
The goal of this study is to develop a method that is capable of determining both the concentration of dissolved metal and the NP size. First, the possibility to quantify ionic silver in the presence of NPs was evaluated. The quantification of Ag+ in solution was performed with ICP-Q-MS and 10 ms DT. LD (3.29 × SDBG) calculated from ionic standard analysis was 16 ± 2 ng L−1, and the limit of quantification (LQ) (10 × SDBG) was 47 ± 6 ng L−1. The data obtained with the μsDAQ could also be used for the quantification of the BG signal; however, the data processing would take a lot of time. Each 3 min measurement results in 3.6 × 107 data points, and this number of data points could not be visualized with the software available to us nowadays (limited to only a few millions of data points). Thus, data with millisecond time resolution were used to determine the BGs throughout this study. The BGs obtained with 10 ms DT in counts per second were recalculated to average BGs in 5 and 25 μs in order to be used in the further data evaluation. Computers with more computational power and software able to handle more input data will make the extraction of the average BG from the microsecond time resolution data much faster in the future.Matrix effects in the plasma
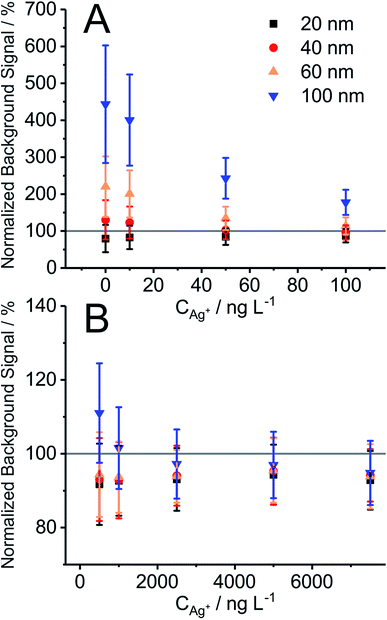
In order to verify that the BG obtained in the presence of NPs corresponds to the concentration of Ag+ in the suspension, the mean BG signal obtained with 10 ms DT for Ag+ in the presence of Ag NPs of different diameters was compared with the mean BG signal obtained from Ag+ calibration solutions at different concentrations (Fig. 1). The mean BG signal was found to be typically higher in the presence of NPs compared to the mean BG signal from a neat Ag+ calibration solution (up to 1 μg L−1) (Fig. 1A). Among the different NPs under investigation, larger particles (60 nm and 100 nm) had a greater effect and resulted in a larger ionic mean BG signal increase, compared to the NPs of smaller diameter (20 nm and 40 nm). One explanation is that the former suspensions already may have contained elevated levels of Ag+ (Fig. 1A at 0 ng L−1 of Ag+). Therefore, the fraction of Ag+ in the Ag NP suspensions is significant and results in an elevated BG, especially when low concentrations of Ag+ (10–500 μg L−1) are added. The mean BG signal slightly decreases (94.6 ± 1.4%) when NPs are present in the samples compared to solutions with only ionic silver (100%, cf.Fig. 1B; noticeable trend started at >1 μg L−1 Ag+). The same effects were observed in the study for polyvinylpirrolidone (PVP)-coated NPs (data not shown here). The depletion of the signal may be a potential indication of matrix effects in the plasma, according to the following studies. As Chan and Hieftje31 have recently demonstrated, droplets in the plasma cause local plasma cooling during evaporation followed by the reheating of the plasma to even higher temperature in a time period of a few milliseconds (the effect is slower than the typical ion cloud duration of a NP, which is on the order of a few hundreds of microseconds). Accordingly, we assume that NPs result in similar local plasma cooling and reheating, which then shortly thereafter may influence the ionization efficiency of ionic species. Another experimental proof for the effects of NPs on fundamental plasma parameters was presented by Murtazin et al.32 In their study, the position of atomization and ionization of calcium in the ICP was delayed relative to the increasing diameter of SiO2 particles (from 0.83 to 1.55 μm), which were added to the aspirated sample. Both studies are certainly relevant for SP-ICP-MS studies and one should be aware of potential matrix effects during the analysis of dissolved species in the presence of nanoparticles (and vice versa) and a potential shift of the ideal sampling position in ICP-MS. In our study, we observed a signal drop for the silver ion BG (>1 μg L−1 of Ag+ added) of approximately 5% (as discussed above) when NPs were present, compared to the solution without NPs. Please note that different NPs (20, 40, 60, and 100 nm) did not significantly change the degree of signal depletion; and according to Fig. 1B, 100% signal is in the range of one SD of the mean BG from triplicate analysis. In addition, it should be noted here that the counting stage of SEM has a limited linear dynamic range. The upper level of the linear dynamic range can be limited due to pulse pile-up at high count rates because of the large number of incoming ions (especially relevant for larger AgNPs). In the current work, an ionic silver concentration and thus the average BG signal were used below the saturation level of the used SEM. A future study on potential NP matrix effects in SP-ICP-MS with microsecond time resolution and a study on how to expand the upper level of the linear dynamic range in SP-ICP-MS are planned to further understand these observations in more detail.BG correction for NP signals recorded with microsecond time resolution (μsDAQ)
As the total signal of an ion cloud is the sum of the extracted counts, it is important to compensate for any BG influence to achieve a more precise sizing. To avoid an artificial NP size increase, we propose a BG subtraction mechanism, where the BG is subtracted mathematically from each extracted ion cloud, taking into the account the specific durations of each ion cloud with the following formula:| Scor,i = Si − Di × BG5 μs | (1) |
After data processing with the BG subtraction (eqn (1)), the BG corrected Ag NP sizes in the presence of ionic silver were found to be in better agreement with Ag NP reference values (sizes obtained from suspensions without an addition of ionic silver). In fact, the NP sizes were gradually decreasing with increasing Ag+ concentration, with around a 4 nm size decrease for 40, 60, and 100 nm Ag NPs after the addition of 7.5 μg L−1 of Ag+. As 107Ag+ is detected in ICP-MS, Ag+ and Ag NPs are not differentiated from each other; therefore, the slight decrease in the calculated NP size may occur due to partial suppression of the BG, when NPs are detected; or due to a lower number of counts detected per NP, when the BG is present. As it was discussed in the previous section, the simultaneous presence of Ag NPs and Ag+ may cause matrix effects in the plasma due to changes in plasma characteristics, it is also confirmed by the fact that the average BG obtained with the vendor software decreased 5.4 ± 1.4% compared to the values obtained for calibration solutions (after adding 1 μg L−1 of Ag+) (Fig. 1B). The NP sizes obtained under different ion cloud extraction conditions were not compensated for the discovered NP size decrease, as the mentioned matrix effects require more investigations (in a future study).
Limits for qualitative NP ion cloud extraction for the μsDAQ
Usually 3 × SDBG is used as LD in SP-ICP-MS.27 Because a time resolution of 5 μs is now feasible in SP-ICP-MS, the concept of LD for NPs should be revisited as well. Early papers on the detection limit were published by Kaiser in 1947 (ref. 33) and Currie in 1968.34 In the paper by Currie, the detection limit formula was derived for the normal distribution and for the Poisson distribution under an assumption of a normal distribution. In the mathematical transformations, errors of both the first kind (α, detecting false positives) and the second kind (β, failing to detect the substance when it is present) were set to 5%. Another parameter that was introduced was the critical level (LC), over which a substance may be considered detected. Here, only a value for α of 5% was used (LC < LD) assuming that risks of 5% are acceptable and random errors are normally distributed.33In contrast to conventional SP-ICP-MS operation, which provides only one count value per particle event at 1–10 ms DT, data from our μsDAQ are comprised of a time-resolved profile of counts, where the sum of counts gives the total NP signal. Therefore, we propose that the LD can represent a value, above which an ion cloud profile can be detected on top of BG fluctuations. As it was not feasible in the current study to get an average BG from 5 μs resolved data due to a high number of data points and limitations in the software, the BG was obtained from data acquired with 10 ms DT and then recalculated (discussed above) to match shorter DTs. After a recalculation to 25 μs (S = 5), the BG is typically only between fractions of a count and 32 counts. In this case, a normal distribution, which was assumed for the conventional LD formula derivation, does not apply anymore, and a Poisson distribution can be used instead.34 Three main criteria determine the Poisson distribution:
– The values are positive integer numbers, which is the case for the μsDAQ.
– If a time interval tends to zero, then also the probability to get a count tends to zero, which is also true for the NP detection, as the detection occurs at discrete time intervals.
– A value xn does not depend on the next value xn+1. In order to achieve this condition, there should be only one data point detected per NP, which is not the case for the μsDAQ. As a NP represents a profile of data points, each data point is not independent.
In order to determine the LD for an ion cloud, the ion cloud extraction process should be considered. To fulfil all three criteria of the Poisson distribution, especially the third criterion, we can consider only the beginning of an ion cloud, namely the T threshold value (an ion cloud starts when the value is reached), so the decision for the detection of an ion cloud would depend only on the rising edge of the ion cloud count profile. Consequently, the LD calculation for a low number of counts in the Poisson distribution has to be found. As in the ion cloud extraction process one of the conditions is that T > E (when T = E, the algorithm would go to a loop), we propose to use LC to determine the end of an ion cloud. Thus, the T parameter should be above LD (α ≤ 5%, β ≤ 5%), and the E parameter should be equal to LC (α ≤ 5%). Cases of a low number of counts are often found in radiochemistry; and Currie34 treated the Poisson distribution under an assumption of a normal distribution, “if the number of counts is sufficiently large”. The LD formulas for the Poisson distribution (with the assumption of a normal distribution) were determined for two cases: paired observations and well-known blank (where the deviations of the BG are neglected).34 Later, the paper was extended35 in order to address the issue of “very low-level counting data” below 5 counts. The initial paper and a more recent summary36 presented a table based on the calculations using a cumulative exact Poisson distribution (without Gaussian approximation), a well-known blank; α ≤ 5% and β ≤ 5% for LD (α ≤ 5% for LC). Formulae and example calculations for the exact Poisson distribution to determine LD and LC are presented in the ESI and Table S1.‡ It should be noted that for the Poisson distribution, LQ should be above 100 counts; therefore, this parameter was not considered in the calculations.
For a user friendly calculation of LD and LC, we propose to use the formulas that are presented in Table 2 (Poisson distribution with the normal distribution approximation). The values obtained from the cumulative exact Poisson distributions were compared (Table 3) with the values obtained for the Poisson distribution with normality approximation, where only an average BG (μB) is sufficient to conduct the calculations (Table 2).34 In the formula of paired observations, the deviation of the BG is taken into account, resulting in higher values compared to the case with “well-known” BG values. After the comparison of the values (Table 3), the formula of paired observations (Table 2) can be used as an approximation for the BG below 5 counts, and the “well-known” blank formula can be used for the BG above 5 counts. According to this approximation, the difference between the values obtained with the cumulative Poisson distribution and the normality approximated values was below 1 count (only two values of LD differed less than 2 counts, with the higher values obtained for the normality approximation). In practice, false positives and false negatives can still be separated from the NP events, since the size distribution diagram is constructed, and the remaining BG can still be distinguished from the NPs by the 3.29 × SDBG criterion.
| L C (limit to identify the end of an ion cloud) | L D (limit to identify the beginning of an ion cloud) | |
|---|---|---|
| a The paired observations case takes into the account the deviation of BG, resulting in higher values compared to the case with “well-known” BG values. The “well-known” BG represents the case, where the deviations of the BG are neglected. | ||
| Paired observations (μB < 5) |
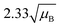
|
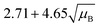
|
| “Well-known” BG (μB > 5) |
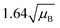
|
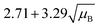
|
| c Ag+/ng L−1 | μ B/counts in 25 μs (S = 5) | SD/counts in 25 μs (S = 5) | Poisson distribution35,36 | Paired observations34 | “Well-known” BG34 | |||
|---|---|---|---|---|---|---|---|---|
| y C | y D | y C | y D | y C | y D | |||
| a The first set of yC and yD was calculated for the exact Poisson distribution with a “well known” BG (Table S1), and further sets were calculated with an assumption of normality for the Poisson distribution according to Table 2. LC and LD are obtained from yC and yD, respectively, by subtraction of μB. | ||||||||
| 0 | 0.09 | 0.02 | 1 | 4.74 | 0.77 | 4.16 | 0.57 | 3.76 |
| 10 | 0.12 | 0.02 | 1 | 4.74 | 0.92 | 4.44 | 0.69 | 3.97 |
| 50 | 0.28 | 0.03 | 1 | 4.74 | 1.51 | 5.45 | 1.15 | 4.73 |
| 100 | 0.48 | 0.04 | 2 | 6.30 | 2.10 | 6.42 | 1.62 | 5.48 |
| 500 | 2.1 | 0.1 | 5 | 10.51 | 5.51 | 11.59 | 4.50 | 9.61 |
| 1000 | 4.2 | 0.2 | 8 | 14.44 | 8.91 | 16.35 | 7.50 | 13.57 |
| 2500 | 9.9 | 0.4 | 15 | 23.10 | 17.24 | 27.26 | 15.07 | 22.98 |
| 5000 | 19.9 | 0.7 | 28 | 38.38 | 30.35 | 43.42 | 27.27 | 37.35 |
| 7500 | 30 | 1 | 39 | 50.94 | 42.37 | 57.72 | 38.61 | 50.31 |
In order to get the ion cloud extraction parameters E and T, μB should be added to the obtained LC and LD to obtain the corresponding gross counts (yC and yD). It should be noted that only positive integer numbers are used in the ion cloud extraction, since only integer counts are detected; thus, the obtained non-integers can be rounded to the closest integer number to obtain the suitable ion cloud extraction conditions. In the next section, the hypothesis of using LC and LD for NP ion cloud extraction will be tested in detail.
Optimization of the ion cloud extraction conditions
Different ion cloud extraction conditions below and above LC and LD were chosen to study their effect on the obtained NP size distributions. It is noted here that 20 nm sized Ag NPs could only be partially separated from the BG in the count histogram. The size LD was at least 16 nm (S = 5, T = 5, and E = 1) (Table S2‡); therefore, 20 nm Ag NPs do not follow the same trends that were observed with 40, 60, and 100 nm sized Ag NPs (discussed below). All other tested NP size distributions could be separated from the BG even in the presence of ionic silver up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps, which is a significant improvement compared to the data obtained with 10 ms DT due to the high time resolution in SP-ICP-MS.
000 cps, which is a significant improvement compared to the data obtained with 10 ms DT due to the high time resolution in SP-ICP-MS.
Fig. 2 and S2‡ show average calculated NP sizes (label B in Fig. S1‡) obtained under different extraction conditions without an addition of dissolved silver (Fig. 2) and with the addition of 7.5 μg L−1 of Ag+ (Fig. S2‡). In general, the main trends are very similar, and the obtained sizes are more or less independent of the T parameter and change dependent on the E parameter. Lower E results in higher sizes, since more counts are added in the end of ion clouds and higher E results in lower sizes. No specific trends were found for the changes in the width of the NP size distributions (label C in Fig. S1‡) under varying extraction conditions. The obtained NP sizes do not change to a large degree under the varied extraction conditions: maximum deviation is up to 4.7 nm for 40 nm, up to 2.1 nm for 60 nm, and up to 1.0 nm for 100 nm Ag NPs (Fig. 2 and S2‡). Considering the trends from Fig. 2 and S2,‡T and E parameters can be chosen from the proposed LC and LD calculations (Table 2).
The number of detected particles (label E in Fig. S1‡) is an important parameter in quantitative SP-ICP-MS applications and was, therefore, used here to identify suitable ion cloud extraction conditions (Fig. S3 and S4‡). It was found that there was a significant difference in the number of detected particles in the case of 20 nm sized Ag NPs with the change of extraction conditions; however, this happens because they could not completely be separated from the BG. The trends are more difficult to follow (Fig. S3 and S4‡), with the number of detected NPs being more dependent on E than on T. In general, it was found that a relatively wide range of extraction conditions can be used for larger sized NPs, specifically for 60 nm and 100 nm Ag NPs, because only minimal differences in the number of detected NPs were obtained. The number of detected 20 nm Ag NPs and 40 nm NPs with Ag+ above 1 μg L−1 was significantly affected by the extraction conditions, with a few hundreds more NPs detected under the extraction conditions below LC and LD (false positives). Clearly, the choice of extraction conditions according to LC and LD assures a more reliable detection of smaller sized NPs.
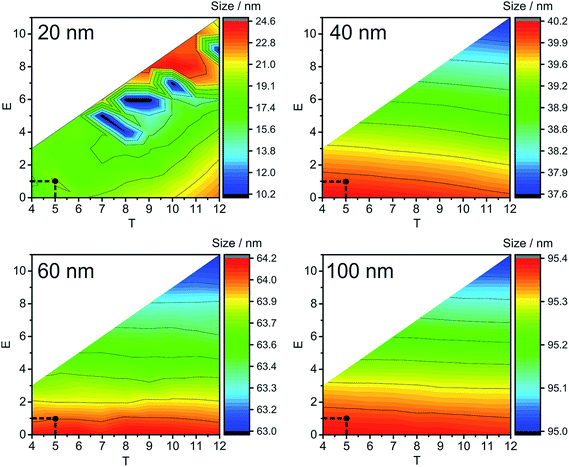
The next parameter to consider is the BG maximum (label A in Fig. S1‡). A high BG results in a high number of false positives, hinders the detection of NPs with sizes close to the BG, and increases the file size, which leads to time-consuming data processing. In our study, the BG was high at low T values, and found to be mostly independent of E values (Fig. 3); therefore, T is the decisive factor in choosing the BG. Similar trends are detected for all NP sizes and all the concentrations of Ag+ that were tested: the BG decreases with increasing T values.
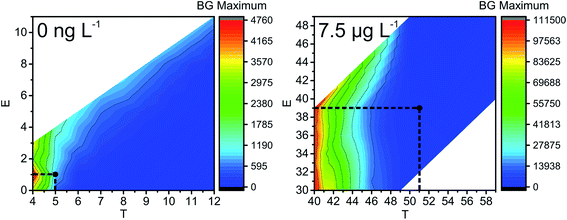 | ||
| Fig. 3 Influence of ion cloud extraction conditions on the maximum of the number of BG events (BG count distribution maximum, see label A in Fig. S1‡) during the analysis of 60 nm Ag NPs (left: without and right: with 7.5 μg L−1 Ag+ added to the NP suspension). Optimal conditions are highlighted with black dots. Note: the step size in size resolution is for illustrative purposes only and a result of data processing. It does not represent the actual size resolution of the SP-ICP-MS method. Also, areas of white colour indicate extraction conditions, which were not tested. | ||
If the Gaussian distribution would be used instead of the Poisson distribution, then the decision threshold would be 3 × SDBG. For example, let us calculate this threshold for 60 nm Ag NPs with 7.5 μg L−1 Ag+ and the Gaussian distribution. With an average BG of 29.033 ± 1.178 counts in 25 μs, LD for the Gaussian distribution is 32.567 counts or 33 counts, if rounded. The optimal conditions obtained with Poisson statistics are higher (T = 51 and E = 39, Fig. 3) than the ones obtained with Gaussian statistics. In Fig. 3 it can be seen that, when T = 40 and E = 33, the BG that was extracted from the raw data was high, around 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 events at BG maximum (file size approximately 14 Mb each). When Gaussian statistics were used, the average NP size (at T = 40 and E = 33) was higher than the NP size detected at T = 51 and E = 39 (Fig. S2‡), the BG maximum was significantly higher (cf.Fig. 3, T = 40 and E = 33), the number of detected NPs was decreasing (cf. Fig. S4,‡T = 40 and E = 33), and the size starting from which NPs could be distinguished from the BG significantly increased by 10 nm (cf.Fig. 3, at T = 40 and E = 33), compared to T = 51 and E = 39 as optimal extraction conditions with Poisson statistics. In conclusion, Gaussian distribution statistics at a low number of counts (average BG below 100 counts) results in underestimation of thresholds in SP-ICP-MS: more BG is extracted together with NPs, and, in turn, the detection and characterization of the NPs are less precise.
000 events at BG maximum (file size approximately 14 Mb each). When Gaussian statistics were used, the average NP size (at T = 40 and E = 33) was higher than the NP size detected at T = 51 and E = 39 (Fig. S2‡), the BG maximum was significantly higher (cf.Fig. 3, T = 40 and E = 33), the number of detected NPs was decreasing (cf. Fig. S4,‡T = 40 and E = 33), and the size starting from which NPs could be distinguished from the BG significantly increased by 10 nm (cf.Fig. 3, at T = 40 and E = 33), compared to T = 51 and E = 39 as optimal extraction conditions with Poisson statistics. In conclusion, Gaussian distribution statistics at a low number of counts (average BG below 100 counts) results in underestimation of thresholds in SP-ICP-MS: more BG is extracted together with NPs, and, in turn, the detection and characterization of the NPs are less precise.
Considering all the parameters discussed in the section, LC and LD can be used for quantitative extraction of NP ion clouds. As an option, the T parameter may be chosen 4–5 counts above the LD value to decrease the BG further, which will not significantly affect the size or the number of extracted NPs.
Workflow after method optimization
The μsDAQ with subsequent data processing allows extracting the NPs in the presence of up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps of the BG signal using Poisson statistics to determine thresholds to identify the beginning and end of NP signal events. Higher BG signals were not tested because of the use of the SEM in the counting mode. The principle of the data processing algorithm can be extended to different types of NPs, to the detection of different elements, or to NPs containing a high natural or instrumental BG. The method allows quantifying NPs in a wider range of the BG signal, compared to conventional SP-ICP-MS with a millisecond DT.
000 cps of the BG signal using Poisson statistics to determine thresholds to identify the beginning and end of NP signal events. Higher BG signals were not tested because of the use of the SEM in the counting mode. The principle of the data processing algorithm can be extended to different types of NPs, to the detection of different elements, or to NPs containing a high natural or instrumental BG. The method allows quantifying NPs in a wider range of the BG signal, compared to conventional SP-ICP-MS with a millisecond DT.
In order to determine the concentration of dissolved metal in the presence of NPs and to assess the NP size distribution the following steps are proposed:
– Perform a calibration with dissolved metal with a millisecond DT (e.g. 10 ms). This is done in order to ascertain the concentration of dissolved metal in the mixture, taking into account possible matrix effects.
– Construct the signal distribution after sample analysis to determine the average BG. It represents the dissolved metal concentration.
– In order to determine the NP size distribution, extract the NP ion clouds from the data obtained with the μsDAQ. This is done by setting thresholds (S, T, and E), and the threshold typically increase with the increasing BG signal. The thresholds can be calculated using the average BG obtained from the vendor software from the cumulative Poisson distribution or with the normality approximation (Table 2). The ion cloud beginning threshold (T) may be increased by 4–5 counts to decrease the BG further.
– Subtract the average BG from each ion cloud to obtain more precise sizing information.
– Construct the size distribution based on the NP size calibration.
Conclusions
A data processing procedure was developed for SP-ICP-MS with microsecond time resolution (μsDAQ) to determine both the concentration of dissolved metal and NP sizes in a mixture using Poisson statistics to determine thresholds to identify the beginning and end of NP signal events. Possible matrix effects were discussed, and a BG subtraction procedure was developed in order to obtain more precise quantitative information on the NPs. Data acquired with a millisecond DT were used to determine the average BG, which is related to the concentration of the dissolved ionic species. Data acquired with the μsDAQ were used for the characterization of NPs. NPs were extracted based on thresholds, which were related to quantitative limits (LC and LD) for the Poisson distribution to get probability theory based NP ion cloud extraction from the raw data. Different extraction condition combinations were tested and used to verify the use of LC and LD for NP ion cloud extraction. The developed method is based on Ag NP detection, but it can be universally used with NPs containing elements detectable by ICP-MS, a high natural BG or high dissolved ion concentration; it can also be used for environmental samples or NP production quality control.Conflicts of interest
There are no conflicts to declare. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. The authors declare no competing financial interest.Acknowledgements
Funding within the project FENOMENO (Grant No. 03XP0005) is acknowledged. FENOMENO is funded in the FP7 ERA-NET on Nanosafety: Safe Implementation of Innovative Nanoscience and Nanotechnology (SIINN) (http://www.siinn.eu/en/). We also acknowledge the House of Young Talents of the University of Siegen for providing funding for Darya Mozhayeva. Ingo Strenge is gratefully acknowledged for his work on the prototype data acquisition system for ICP-MS and the extraction tool. Johannes Schmitt is gratefully acknowledged for the programming support. The machine shop team (especially Markus Rabe for help with the ICP-MS) in the Department of Chemistry and Biology of the University of Siegen is gratefully acknowledged.References
- S. P. Forster, S. Olveira and S. Seeger, Int. J. Nanotechnol., 2011, 8, 592–613 CrossRef.
- D. A. Notter, D. M. Mitrano and B. Nowack, Environ. Toxicol. Chem., 2014, 33, 2733–2739 CrossRef CAS PubMed.
- M. H. Shen, X. X. Zhou, X. Y. Yang, J. B. Chao, R. Liu and J. F. Liu, Sci. Rep., 2015, 5, 9674 CrossRef CAS PubMed.
- D. McShan, P. C. Ray and H. Yu, J. Food Drug Anal., 2014, 22, 116–127 CrossRef CAS PubMed.
- S. K. Misra, A. Dybowska, D. Berhanu, S. N. Luoma and E. Valsami-Jones, Sci. Total Environ., 2012, 438, 225–232 CrossRef CAS.
- A. Helfrich, W. Brüchert and J. Bettmer, J. Anal. At. Spectrom., 2006, 21, 431–434 RSC.
- A. Helfrich and J. Bettmer, Int. J. Mass Spectrom., 2011, 307, 92–98 CrossRef CAS.
- J. Soto-Alvaredo, M. Montes-Bayón and J. Bettmer, Anal. Chem., 2013, 85, 1316–1321 CrossRef CAS.
- B. Franze and C. Engelhard, Anal. Chem., 2014, 86, 5713–5720 CrossRef CAS PubMed.
- D. Mozhayeva, I. Strenge and C. Engelhard, Anal. Chem., 2017, 89, 7152–7159 CrossRef CAS PubMed.
- D. Mozhayeva and C. Engelhard, Anal. Chem., 2017, 89, 9767–9774 CrossRef CAS PubMed.
- F. Laborda, J. Jiménez-Lamana, E. Bolea and J. R. Castillo, J. Anal. At. Spectrom., 2011, 26, 1362–1371 RSC.
- F. Laborda, E. Bolea and J. Jiménez-Lamana, Anal. Chem., 2014, 86, 2270–2278 CrossRef CAS PubMed.
- M. D. Montaño, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Anal. Bioanal. Chem., 2016, 408, 5053–5074 CrossRef.
- B. Meermann and V. Nischwitz, J. Anal. At. Spectrom., 2018, 33, 1432–1468 RSC.
- J. Vidmar, R. Milačič and J. Ščančar, Microchem. J., 2017, 132, 391–400 CrossRef CAS.
- D. M. Schwertfeger, J. R. Velicogna, A. H. Jesmer, R. P. Scroggins and J. I. Princz, Anal. Chem., 2016, 88, 9908–9914 CrossRef CAS.
- A. Hineman and C. Stephan, J. Anal. At. Spectrom., 2014, 29, 1252–1257 RSC.
- M. D. Montaño, H. R. Badiei, S. Bazargan and J. F. Ranville, Environ. Sci.: Nano, 2014, 1, 338–346 RSC.
- J. Tuoriniemi, G. Cornelis and M. Hassellöv, J. Anal. At. Spectrom., 2015, 30, 1723–1729 RSC.
- I. Abad-Alvaro, E. Pena-Vazquez, E. Bolea, P. Bermejo-Barrera, J. R. Castillo and F. Laborda, Anal. Bioanal. Chem., 2016, 408, 5089–5097 CrossRef CAS PubMed.
- A. J. Managh, D. N. Douglas, K. M. Cowen, H. J. Reid and B. L. Sharp, J. Anal. At. Spectrom., 2016, 31, 1688–1692 RSC.
- M. D. Montaño, B. J. Majestic, A. K. Jamting, P. Westerhoff and J. F. Ranville, Anal. Chem., 2016, 88, 4733–4741 CrossRef PubMed.
- K. Newman, C. Metcalfe, J. Martin, H. Hintelmann, P. Shaw and A. Donard, J. Anal. At. Spectrom., 2016, 31, 2069–2077 RSC.
- P. Shaw and A. Donard, J. Anal. At. Spectrom., 2016, 31, 1234–1242 RSC.
- I. Strenge and C. Engelhard, J. Anal. At. Spectrom., 2016, 31, 135–144 RSC.
- F. Laborda, J. Jiménez-Lamana, E. Bolea and J. R. Castillo, J. Anal. At. Spectrom., 2013, 28, 1220–1232 RSC.
- G. Cornelis and M. Hassellöv, J. Anal. At. Spectrom., 2014, 29, 134–144 RSC.
- A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Günther, Anal. Chem., 2018, 90, 11847–11855 CrossRef CAS PubMed.
- S. Bazargan and H. Badiei, Systems and methods for automated analysis of output in single particle inductively coupled plasma mass spectrometry and similar data sets, US Pat., US9754774B2, 2017.
- G. C. Y. Chan and G. M. Hieftje, Spectrochim. Acta, Part B, 2016, 121, 55–66 CrossRef CAS.
- A. Murtazin, S. Groh and K. Niemax, Spectrochim. Acta, Part B, 2012, 67, 3–16 CrossRef CAS.
- H. Kaiser, Spectrochim. Acta, 1947, 3, 40–67 CrossRef CAS.
- L. A. Currie, Anal. Chem., 1968, 40, 586–593 CrossRef CAS.
- L. A. Currie, IEEE Trans. Nucl. Sci., 1972, 19, 119–126 CAS.
- L. A. Currie, J. Radioanal. Nucl. Chem., 2008, 276, 285–297 CrossRef CAS.
Footnotes |
| † Dedicated to Professor Alfredo Sanz-Medel on the occasion of his retirement. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ja00042a |
| This journal is © The Royal Society of Chemistry 2019 |