Open Access Article
Open Access ArticleIt's not just the defects – a curved crystal study of H2O desorption from Ag
Sabine V.
Auras
 *a,
Robert A. B.
van Bree
a,
Dima L.
Bashlakov
*a,
Robert A. B.
van Bree
a,
Dima L.
Bashlakov
 b,
Richard
van Lent
b,
Richard
van Lent
 a and
Ludo B. F.
Juurlink
a and
Ludo B. F.
Juurlink
 a
a
aLeiden Institute of Chemistry, Leiden University, P.O. Box 9502, 2300 RA Leiden, The Netherlands. E-mail: s.v.auras.2@lic.leidenuniv.nl; Tel: +31 71 527 4232
bILTPE, National Academy of Sciences of Ukraine, 47 Nauky Ave., Kharkiv 61103, Ukraine
First published on 3rd July 2019
Abstract
We investigate water desorption from hydrophobic surfaces using two curved Ag single crystals centered at (111) and (001) apices. On these types of crystals the step density gradually increases along the curvature, allowing us to probe large ranges of surface structures in between the (001), (111) and (110) planes. Subtle differences in desorption of submonolayer water coverages point toward structure dependencies in water cluster nucleation. The B-type step on hydrophobic Ag binds water structures more strongly than adjacent (111) planes, leading to preferred desorption from steps. This driving force is smaller for A-type steps on (111) terraces. The A′-type step flanked by (001) terraces shows no indication of preferred desorption from steps. Extrapolation to the (311) surface, not contained within either curved surface, demonstrates that both A- and A′-type steps can be regarded chemically identical for water desorption. The different trends in desorption temperature on the two crystals can thus be attributed to stronger water adsorption at (001) planes than at (111) planes and identical to adsorption at the step. These results show that our approach to studying the structure dependence of water desorption is sensitive to variations in desorption energy smaller than ‘chemical accuracy’, i.e. 1 kcal mol−1.
1 Introduction
Water is ubiquitous on our planet and crucial to many processes both in nature and industry. As such, the study of water sparks interest in many different areas of research, from meteorology and astronomy to physics, chemistry, and engineering. Specifically, the interface of water with metal surfaces, relevant for electrochemistry, corrosion phenomena, and others, is complex and highly structure sensitive. Despite many years of research in this area, the underlying principles that determine water structures on different metals are not yet fully understood.1,2Generally, water on metal surfaces tends to form 2D clusters with distinct structures at sufficiently low temperatures, due to a low diffusion barrier even at those temperatures.2 At sub-monolayer coverages, adsorption is influenced by the competition between water–metal bonding and the internal hydrogen bonding of water networks. As a consequence, three types of adsorption are found: wetting, non-wetting and (partially) dissociative.
The exact structure of adsorbed water is highly surface dependent and can have a strong influence on the resulting adsorption/desorption behaviour. We have previously shown this for water adsorption on Pt(111) surfaces.3–6 There, nucleation of ice preferentially occurs at step edges. The subsequent growth depends not only on the width of the adjacent terrace but differences were also observed for the two different step types found on (111) terraces, A- and B-type steps.3 To understand the principles of water adsorption it is therefore necessary to not only consider high symmetry facets, but also the influence of lower coordinated sites, which can have deviant reactivities, adsorption or desorption properties. However, while there is substantive literature on water on close packed surfaces of various metals, less is known about surfaces with a more open symmetry.
This study focuses on differences in water adsorption on Ag surfaces with different terrace and step geometries. As Ag is a less reactive metal than Pt, the changes in adsorption on different surfaces are expected to be even more subtle. Ag surfaces are known to be non-wetting for the first layer of H2O. Their weak metal–water interactions7 cause the formation of 3D clusters that optimise hydrogen bonding in the water network. On Ag(100) 3D clusters are found even before the first layer is completed.8 Subsequent multilayer water adsorption can result in the formation of amorphous solid water (ASW) or crystalline ice (CI); the transition from ASW to CI on water happens at >145 K.9,10
In an early flash desorption study comparing Ag surfaces on a small spherical crystal it was found that Ag(100) and Ag(111) have the same 0th order desorption feature at 170 K (in agreement with a study on Ag(311)). The resulting desorption energy matched the sublimation energy of ice.11 The authors therefore concluded that ASW on Ag is not substrate dependent and sublimates freely. However, it is known that water on Ag(111) exclusively forms clusters of hexamers up to nonamers at very low coverages, while with increasing coverage larger amorphous clusters start to dominate.12 It is therefore possible that at low coverages water adsorption has surface dependencies that were not observed in the earlier study.
Here we report that despite identical behaviour of multilayers of ASW on the different Ag surfaces, substrate dependence is observable for sub-monolayer adsorption. We use our curved crystal approach to examine these effects that would likely not be observable with a traditional flat single-crystal approach. Two curved Ag single crystals allow for easy variation of surface structure in order to examine small influences of step type and density. The two crystals, one with (111) the other with (001) terraces, linearly increase their step density from 0.01 nm−1 at the apex to >1 nm−1 at the sides.
2 Experimental
Cleaning and structural investigation by electron diffraction of the curved Ag crystals described in this study were performed using a UHV instrument with a base pressure of 1.5 × 10−10 mbar as measured with an uncalibrated cold cathode pressure gauge (Pfeiffer IKR 261). It is equipped with a Balzers QME 200 quadrupole mass spectrometer (QMS) used for residual gas analysis (RGA), a Low Energy Electron Diffraction (LEED) apparatus consisting of an electron gun (LEG 24) and LEED optics (VG, RVL-900), a sputter gun (Prevac IS 40C1), and a hot cathode pressure gauge controlled by a Multi Varian controller. After trying different cleaning procedures, it was found that both crystals could be cleaned over their entire surface areas by 10 min Ar+ sputtering at low sputtering currents (0.5 μA) from low sputtering energies (0.25 kV). We sputtered under a 45° angle from the apex so that ions approached the surface along the step edges. Subsequently, crystals were annealed for 20 minutes at 670 K.Scanning Tunneling Microscopy (STM) images were taken in a commercial vacuum system (OMICRON) consisting of a preparation and analysis chamber, as well as a load lock for transferring samples in and out of vacuum. The preparation and analysis chamber both had a base pressure of 2 × 10−10 mbar measured by two individual Bayard–Alpert type manometers and could be separated by a gate valve. The Omicron STM system has been described in detail before.13
Spatially resolved temperature-programmed desorption (TPD) experiments were carried out in a third UHV chamber with a base pressure of 9 × 10−11 mbar as measured with a uncalibrated cold cathode pressure gauge (Pfeiffer IKR 261). This system has been described previously as well.4,14 Cleaning of samples followed the same procedure that had been confirmed by LEED and STM to deliver clean and well-defined surfaces. Water (Millipore, 18.2 MΩ) was degassed by multiple freeze–pump–thaw cycles prior to dosing. The water flask was part of a homebuilt dosing system based on the design of a capillary array doser and exposed to 1.1 bar He as a carrier gas at a water temperature of 323 K. The gas mixture was subsequently directly dosed onto the crystal at 90 K. The lowest coverages shown in this paper were achieved by determining the lowest dose that still resulted in an observable desorption signal. In the case of c-Ag(111) this was 4 L (He/H2O), in the case of Ag(001) 8 L (He/H2O). A second quadrupole mass spectrometer (Baltzers QMA400) in a differentially pumped stage was separated from the main chamber by a plate with a 0.5 × 5 mm2 rectangular slot. In order to optimize the spatial resolution during TPD experiments, the crystal was brought in close proximity of the slot and aligned parallel to it. TPDs were performed at a temperature rate of 1 K s−1, going from 90 K to 270 K.
To mount either of the two curved Ag samples in the UHV instruments, it was held by a polycrystalline Ag cap onto a Cu baseplate. Two screws firmly attached the cap to the plate. The assembly was attached to a Cu extension of a bath cryostat using two screws at the top of the Cu base plate. Crystal temperatures as low as 88 K could be reached. The Cu base plate was heated radiatively or by electron bombardment with a commercial light bulb filament positioned behind the crystal assembly. The crystal temperature was measured with a type-K thermocouple inserted into a small opening between the crystal and the Ag cap. To obtain temperature control we used a PID controller (Eurotherm 2416).
The curved crystals may be viewed as 31° sections of a cylinder with a 15 mm radius that has its rotational axis along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction. On the c-Ag(111)31° [1
0] direction. On the c-Ag(111)31° [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] crystal, the section is centered at the [111] vector as depicted in Fig. 1(a). The macroscopic curvature is caused by decreasing (111) terraces separated by {001}-oriented steps at one side (blue section in Fig. 1(a)) and {110}-oriented steps at the other side of the crystal (red section). These two different step types are referred to as A- and B-type respectively.15 Their atomic structure in bird's eye view and side view can be found in Fig. 1(a) and (b) respectively. Step densities on this crystal go up to 0.114 Å−1 at the edges, which corresponds to stepped surfaces with 8.77 Å wide terraces. Respectively, the c-Ag(001)31° [1
0] crystal, the section is centered at the [111] vector as depicted in Fig. 1(a). The macroscopic curvature is caused by decreasing (111) terraces separated by {001}-oriented steps at one side (blue section in Fig. 1(a)) and {110}-oriented steps at the other side of the crystal (red section). These two different step types are referred to as A- and B-type respectively.15 Their atomic structure in bird's eye view and side view can be found in Fig. 1(a) and (b) respectively. Step densities on this crystal go up to 0.114 Å−1 at the edges, which corresponds to stepped surfaces with 8.77 Å wide terraces. Respectively, the c-Ag(001)31° [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] crystal is centered at [001]. To both sides of the (001) apex steps with {111}-oriented microfacets cause the curvature. In the absence of restructuring, surfaces range from (001) at the middle of the crystal to a step density of 0.132 Å−1, or 7.58 Å wide terraces, at the outer edges. We suggest the nomenclature of c-Ag(111)31° [1
0] crystal is centered at [001]. To both sides of the (001) apex steps with {111}-oriented microfacets cause the curvature. In the absence of restructuring, surfaces range from (001) at the middle of the crystal to a step density of 0.132 Å−1, or 7.58 Å wide terraces, at the outer edges. We suggest the nomenclature of c-Ag(111)31° [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and c-Ag(001)31° [1
0] and c-Ag(001)31° [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] to fully describe the crystallographic properties of these crystals, however for the sake of brevity we will use the shorter notation of c-Ag(111) and c-Ag(001) to distinguish the two crystals within this paper.
0] to fully describe the crystallographic properties of these crystals, however for the sake of brevity we will use the shorter notation of c-Ag(111) and c-Ag(001) to distinguish the two crystals within this paper.
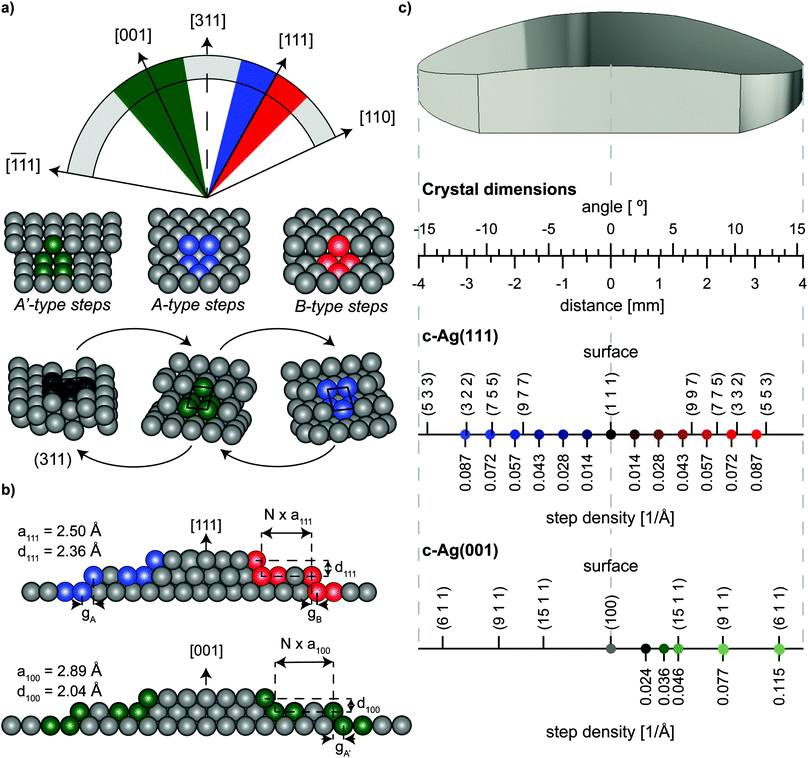 | ||
Fig. 1 Schematic drawings of orientation and surface structures of the two curved crystals employed in this study. (a) Orientation of the c-Ag(001)31° [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] (green) and c-Ag(111)31° [1 0] (green) and c-Ag(111)31° [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] (blue and red) crystals on a cylinder with its rotational axis along [1 0] (blue and red) crystals on a cylinder with its rotational axis along [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]. Below the step types that separate (001)/(111) terraces on the two crystals respectively. Also shown, the (311) surface and its unit cell, and how this surface can be seen as consisting of only A- or only A′-type steps. (b) Schematic microscopic side view of the two crystals, indicating parameters used in eqn (1). In the center, the crystals feature wide terraces. As the crystal curves to the sides, steps are introduced to accommodate the macroscopic curvature. (c) Drawing of the macroscopic shape of the crystals linking macroscopic properties of the crystal (angle of curvature, distance from apex), to microscopic properties found on the surface, i.e. Miller indices of surface structures at specific points of the crystal. Positions of measurements in Fig. 4 are indicated in blue, red, and green with their respective step densities. Step densities for monoatomic steps do not follow the same scale on the two crystals because of different step heights on (001) and (111) terraces, as indicated in (b). 0]. Below the step types that separate (001)/(111) terraces on the two crystals respectively. Also shown, the (311) surface and its unit cell, and how this surface can be seen as consisting of only A- or only A′-type steps. (b) Schematic microscopic side view of the two crystals, indicating parameters used in eqn (1). In the center, the crystals feature wide terraces. As the crystal curves to the sides, steps are introduced to accommodate the macroscopic curvature. (c) Drawing of the macroscopic shape of the crystals linking macroscopic properties of the crystal (angle of curvature, distance from apex), to microscopic properties found on the surface, i.e. Miller indices of surface structures at specific points of the crystal. Positions of measurements in Fig. 4 are indicated in blue, red, and green with their respective step densities. Step densities for monoatomic steps do not follow the same scale on the two crystals because of different step heights on (001) and (111) terraces, as indicated in (b). | ||
As Fig. 1(a) illustrates, the hollow site of steps on the (001) terraces resembles the hollow site of A-type steps on (111) terraces. We consequently note them as A′-type steps. This hollow site, known as a B5 site,16 consists of 5 atoms arranged in a square site adjacent to a triangular site. This site is a {311} microfacet. The crystallographic orientation of (311) relative to the (001) and (111) surfaces is indicated in Fig. 1(a). While we cannot investigate this surface directly, we approach it from two sides on two separate crystals.
Both crystals used here have the same dimensions: 8 mm along the length across a curvature of 31° and a width of 7 mm at the widest part of the crystal. Fig. 1(c) indicates positions across the crystals where our measurements were carried out and the prevailing step density at that position in case of monoatomic height steps. The figure also indicates the Miller indices of some commonly used vicinal surfaces and where they can be found on our curved crystals.
3 Results
Results for the curved Ag(111) crystal have been published before, but were newly analysed from the raw data here for consistent comparison with the curved Ag(001) crystal, leading to new insights.143.1 Surface structure investigation
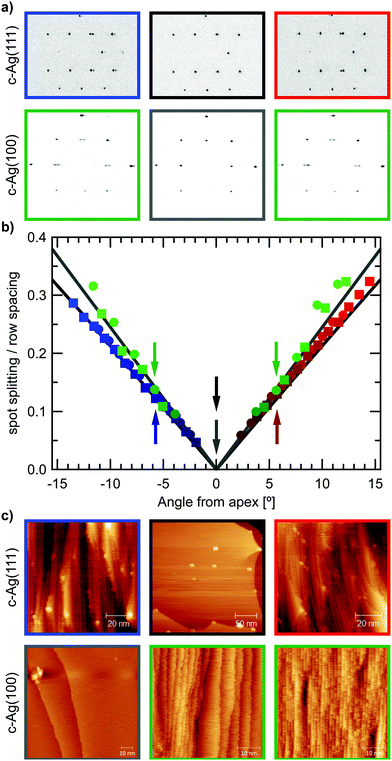
In order to confirm that the crystal surface exhibits the structures we would predict at each position on the crystal, we first investigate the surface structure and cleanliness with LEED and STM.LEED is a useful technique to acquire information on the overall order of a surface. While expected diffraction patterns at the low Miller index surfaces at the center of the crystals are easy to construct, at angles away from the apex, the crystal curvature causes periodic steps on the surface. The offset between successive terraces yields additional diffraction,17 that can be described according to eqn (1):18
Δφ = λ/[(Na + g)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ − dsin φ − dsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ] φ] | (1) |
The low energy electron diffraction pattern was checked over the entire surface areas of the two crystals to ensure cleanliness and the absence of faceting. Additionally, the energy dependence of the (0,0) spot splitting behaviour was examined according to Henzler18 to confirm the presence of mono-atomic steps across the crystals, as has also been previously described for a similar curved Ag crystal.20
After sufficient cleaning, the apices yielded the typical hexagonal and square patterns for the (111) and (001) surfaces respectively. As Fig. 2(a) displays, diffraction spots at the apices are well-defined and symmetrically round. Moving away from the apex results in elongated, oval-shaped spots that eventually split into two spots. Spot splitting then increases linearly with angle away from the apex in both cases. Fig. 2(b) plots the measured spot splitting to row spacing ratios (ss/rs) at different positions on the crystal surface, which follows the predicted values closely.19 The different slope of ss/rs on the c-Ag(111) and c-Ag(001) crystals is a direct result of the difference in step height on (111) and (001) terraces, as indicated in Fig. 1(b). Larger step heights require fewer steps, i.e. a smaller step density, on a flat terrace to achieve the same tilt in surface normal, thus a smaller spot splitting will be observed. The ratio between ss/rs on the stepped Ag(111) surfaces (slope111 = 0.021/1°) and ss/rs on the stepped Ag(001) surfaces (slope100 = 0.0245/1°) is 0.857. The inverse of the ratio between step heights (d111 = 2.36 Å and d100 = 2.04 Å) is 0.864.
STM images (Fig. 2(c)) from the apices of the two crystals and the sides confirm cleanliness as well as the absence of faceting and show large arrays of ordered steps with the predicted orientation. Images show frizzy step edges as commonly found on Ag surfaces.20–22
On the c-Ag(111) crystal, white protrusions appear over <2% of the surface area. As they cannot be removed by extensive cleaning procedures, they appear to be chemically inert and likely remnants of the polishing process. While the mean terrace width expected at each position along the curvature is not affected by these protrusions, they impact the regular ordering of the terrace arrays, by pinning the steps. Checking their occurrence at different positions on the surface gives a uniform density over the entire range of the c-Ag(111) crystal. Therefore they cannot be the cause for structure dependencies in water desorption discussed in this paper. On the c-Ag(001) crystal, while the overall step density is as expected, we find large variations between the widths of terraces as well as within individual terraces. At more highly stepped surfaces, very regular arrays of terraces are found.
3.2 Temperature programmed desorption
In the following we elucidate step for step the observations that allow us to internally calibrate temperature readings from separate sets of data: firstly, Fig. 3(a) shows TPD spectra from Ag(001) at various initial coverages. Only one desorption feature is present with the typical shape of 0th order desorption: all traces follow the same onset, then rapidly drop off at a point determined by the different coverages. This 0th order behaviour is observed for all Ag surfaces, i.e. not only on the c-Ag(001) crystal, but also on the c-Ag(111) crystal.
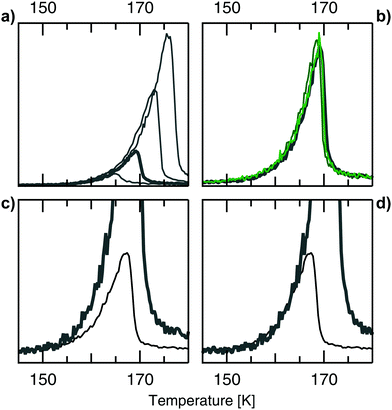 | ||
| Fig. 3 (a) TPD spectra from Ag(001) after various doses of the He/H2O gas mixture. Doses from 40 L, 120 L (bold), 240 L, and 480 L. The spectra follow the same onset, with the position of the peak maximum depending on the dose. This behaviour is typical for 0th order desorption. The same behaviour at varying doses was observed at all measured surfaces on both the c-Ag(001) and c-Ag(111) crystal. Doses refer to the pressure of the He/H2O mixture dosed during experiments. (b) TPD spectra from Ag(001) (grey bold) and stepped surfaces (green) after the same (120 L) dose. The spectra overlap very well, showing consistent dosing within one set of experiments and no surface dependency of the desorption feature. Similarly, dosing the same amount at different surfaces on the c-Ag(111) crystal resulted in overlapping TPD spectra.14 (c) Comparing TPD spectra from Ag(001) (grey bold) and Ag(111) (black) after a dose of 120 L reveals that the onsets don't overlap. (d) Shifting the Ag(001) data in (b) by 2.8 K gives a good overlap of the onset of desorption in both cases. | ||
Next, comparing desorption from different surfaces on the c-Ag(001) crystal after the same dose in Fig. 3(b) demonstrates a good overlap in onset, height and overall shape of the desorption feature. This confirms that there is no temperature gradient across the surface of our crystal. Again, the same is observed when comparing the same dose on various surfaces on the c-Ag(111) crystal. We conclude that high coverages of H2O give the same 0th desorption feature independent of Ag surface structure, in agreement with results obtained by Klaua and Madey.11 However, when comparing data from the (001) and the (111) surface in Fig. 3(c), the onset of desorption differs visibly. This must be due to slight experimental differences in our temperature measurements at the two different crystals. We thus need to adjust the temperature scales of the two sets of data. As we do not know which scale is closer to the actual temperature, we arbitrarily choose to shift surfaces on the c-Ag(001) crystal to match the onset of the c-Ag(111) surfaces. Analysing the onset of desorption from all measured surfaces after 120 L doses gives a difference of 2.8 K between the two crystals. Shifting data from Ag(001) by 2.8 K in Fig. 3(d) results in a matching onset of desorption with Ag(111). When comparing various surfaces on the two crystals we now observe the same good overlap as observed internally on each crystal. This observation allows us to internally calibrate our temperature measurements between the two sets of experiments. In the following all data from the c-Ag(001) crystal is shifted by the same value, regardless of coverage. This temperature shift is crucial as in the following section we are investigating rather subtle surface dependencies in water adsorption, i.e. the influence of terrace and step geometries on the overall weak interactions between water and the Ag surfaces.
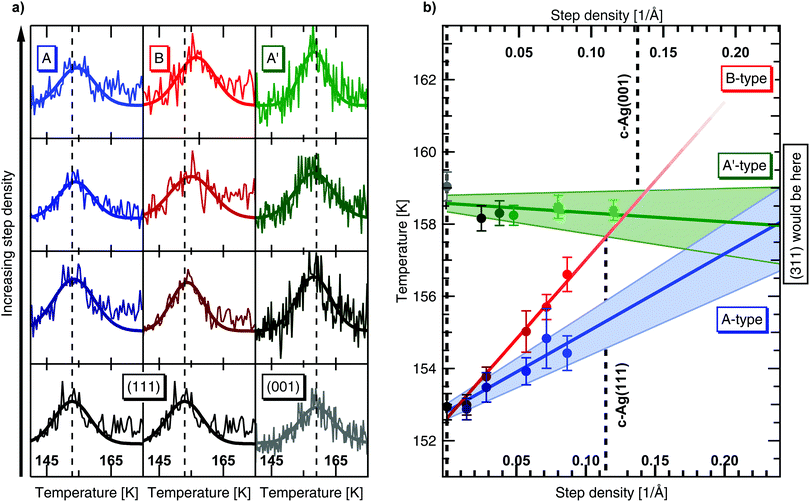
Results from experiments performed with the c-Ag(001) crystal after a 8 L dose of the He/H2O mixture are shown in the right panel of Fig. 4(a). Results after a 4 L dose show the same trends but the water desorption signals are barely distinguishable from the baseline and difficult to fit. In both cases the same flux as in the experiments on c-Ag(111) was used. Additionally, a 16 L dose also shows the same, allowing us to exclude a coverage dependence on desorption. Contrarily to c-Ag(111), the peak desorption temperature at the (001) apex, indicated with the grey dashed line, shows no clear shift as the density of A′-type steps is increased. The peak desorption temperature of (001) even seems marginally higher than at the stepped surfaces.
We analyze our data quantitatively by considering the Gaussian fit parameters. Each fit yields three parameters, i.e. a peak desorption temperature, an amplitude and a width. The peak desorption temperatures as obtained from our fits are plotted against step density in Fig. 4(b). Note that both step density axes (c-Ag(111) at the bottom and c-Ag(001) at the top) are extended considerably beyond the densities present on the curved crystals. The range on the crystals is indicated by vertical dashed lines.
For the c-Ag(111) crystal, the desorption temperature monotonically increases with step density over the entire crystal curvature. A linear fit to the data for the A-type steps (blue), indicates that the desorption temperature increases with 22 K Å. Error bars to the linear fit are represented by the shaded area. On the B side the increase is significantly steeper, 44 K Å. Error bars are of similar size, but not shown for clarity. We have also analyzed the amplitude and width parameters – they show no trend with step density and vary only marginally over the entire step density range that was investigated. This indicates that the area under the curves, i.e. the H2O coverage, does not vary significantly between experiments and thus confirms consistency in the very small doses of water required for these measurements.
In line with our qualitative observation from Fig. 4(a), the desorption temperature for c-Ag(001) crystal in Fig. 4(b) is mostly independent of step density. A linear fit to the data yields a small negative slope of −2.6 K Å. When extrapolating this linear fit, a change in desorption temperature of <0.7 K is implied over the range of (001) to (311), i.e. the smallest possible (001) terrace separated by A′-type steps. The shaded area reflects that this slope is smaller than the uncertainty in the fit.
4 Discussion
Submonolayer desorption from Pt, a metal that more strongly interacts with water, but also shows no thermal dissociation, is reflected in two separate desorption peaks for terraces and steps.6,24 Similarly, for the stepped Ni (11 11 9) surface, a separate desorption peak of molecular water from steps could be identified.25,26 For various stepped Pt(111) surfaces with A-type steps, we have found that the desorption peak attributed to the step occurs at the same temperature regardless of step density.27Considering the similarity of Pt and Ag in not dissociating water, we have previously explained the linear shift in peak desorption temperature for c-Ag(111) as also resulting from two independent contributions from terraces and steps.14 However, the peak temperatures of the individual contributions apparently differ so little that desorption is not deconvoluted in our experiments on Ag and only a single peak is observed. A simple modelling exercise using two individual Gaussian contributions representing step and terrace desorption for a fixed total coverage at different surfaces confirms an apparent linear shift in desorption temperature for the convoluted peaks. Assuming the shift is due to an increasing contribution of desorption from steps indicates stronger binding at the steps than at terraces. This pragmatic, but somewhat risky interpretation of desorption temperature with binding energy, is supported by STM studies on Ag(111) which have also shown that H2O preferentially binds to step edges on Ag(111).28,29
At the apex of our c-Ag(111) surface, the step density is far too low to accommodate the submonolayer coverage of water, and water desorbs predominantly from (111) planes. As steps become more closely spaced moving toward the sides of our c-Ag(111) crystal, a growing fraction of the fixed total coverage desorb from step sites. The steeper slope in Fig. 4(b) indicates a larger difference in peak desorption temperature for the B-type step than the A-type step in comparison to the Ag(111) plane. It is noteworthy that the same step-type effect was observed for Pt.23
In the absence of a general and specific understanding of diffusion rates of monomers and water clusters on low-Miller index surfaces of metals,30 we will here assume similar diffusion rates of water on the (001) terraces as on the (111) terraces and consequently the formation of ice clusters on both terraces and steps. In the following we extend the interpretation of the shift in peak desorption temperature to our results for c-Ag(001). The absence of a detectable shift within our uncertainty implies that if there are two separate contributions, the peak desorption temperatures must be so close that varying step-to-terrace ratios does not yield a clear shift. We conclude that A′-type steps do not bind water molecules more strongly than the (001) terraces. Since there appears to be no preference for desorption from steps or terraces, it may be suggested that water cluster nucleation should occur evenly over the entire surface, regardless of the presence of steps. Similarly, in a previous study using electron energy loss spectroscopy, no separate step and terrace contributions could be observed for water adsorbed on Ag(115), a stepped surface with (001) terraces and A′-type steps.8
Due to the range of surface structures contained on our c-Ag(111) crystal, we can only measure desorption temperatures that are a combination of desorption from (111) terraces and steps. In Fig. 4(b), the data from A-type steps shows a clear linear trend, indicating that the observed desorption peak is indeed a linear combination of the two contributions (of water desorbing from terraces and molecules desorbing from steps). In order to separate the terrace and step contributions we extrapolate the fit to (311), a surface that can be seen as only consisting of A-type steps with no terraces (Fig. 1(a)). Thus, the contribution from terraces in a linear combination would be zero. The temperature we obtain from this extrapolation to (311) corresponds to the step contribution of desorption temperatures we measure on our crystal. At this point we must stress that this extrapolation cannot predict which desorption temperature would actually occur for H2O on Ag(311), as highly corrugated surfaces like this often feature different surface structures than those observed at stepped surfaces with wider terraces.4,31–34 We can not say how far the linear dependence of desorption temperature on step density extends beyond the surface range of our crystals. We therefore solely use this extrapolation to extract the step contribution on the surfaces contained on the curved crystals.
As (311) only consists of square {100} microfacets adjacent to hexagonal {111} microfacets, the steps could also be seen as A′-type steps when approaching the step edge from the other direction, see Fig. 1(a). Strikingly, extrapolating the linear fit of data from the c-Ag(001) crystal towards (311) gives the same value with the same error bars. This indicates that the A- and A′-type steps at surfaces present on our crystals have the same binding energy for water. They can therefore be considered the same step type in regards to both their atomic arrangement and chemical behaviour. As the A- and A′-type steps would give the same desorption temperature, the different trends in desorption temperature between stepped Ag(111) and stepped Ag(001) surfaces must indicate the difference in binding energy of the two terrace types flanking the steps.
The linear dependence of desorption temperature on step density can reasonably be expected to hold true until the terraces become so short that the structures nucleating at the step edges must change in order to accommodate the water clusters on the surface. On Ag(111) terraces, hexamers as the smallest nucleation cluster at very low coverages have previously been observed by STM.12 These hexamers would not fit flat on short terraces even before (311) is reached. Further studies of H2O adsorbed on steps of Ag surfaces with short terrace lengths would be very helpful in order to evaluate for which structures the linear trends in desorption temperature can still hold true.
Applying a Redhead analysis using the extremes of the desorption temperatures from the linear fits in Fig. 4(b) suggests that the binding energy difference for Ag(111) and the A-type step is 1.04 kJ mol−1. The difference in binding energy for Ag(001) and the A′-type step is at most on the order of 0.17 kJ mol−1. Here, we have used the desorption temperatures as extrapolated to Ag(311) for both A- and A′-type steps. These small differences were likely not observable to Klaua and Madey11 in their flash desorption experiments with limited spatial resolution. In contrast, here it proves that in our spatially resolved experiments we can achieve an accuracy well within chemical accuracy.35
5 Conclusions
Due to the design of our experiments, the interactions between water molecules and Ag surfaces can be probed consistently and in great detail. We have shown the influence of both terrace and step type on the adsorption of water on stepped surfaces of a weakly reactive hydrophobic metal.Within the interpretation that desorption reflects binding, on the c-Ag(111) crystal the steps bind water molecules measurably stronger than the (111) terraces, resulting in a desorption temperature shift as the step density increases. We detect changes in binding energy that vary less than <1 kcal mol−1, which is considered ‘chemical accuracy’. The binding energy at the two step types can also be shown to not be the same – the difference between B-type steps and the (111) terrace is twice as large as the difference between the A-type step and the same terrace. On the c-Ag(001) crystal, the A′-type steps bind water approximately equally strong as the (001) terrace. As a result the desorption temperature at very low coverages does not change significantly with step density. We predict that on (001) terraces water cluster nucleation is not dominated by steps.
As the trendlines for water desorption from surfaces with A-type steps and A′-type steps runs towards the same value at the maximally stepped (311) surface, we conclude that the steps themselves have the same binding energy for water and can in fact be seen as the same type of step. However, here we can clearly see the influence of the different terrace types. When extending the (111) facets from (311), we see a decrease in desorption temperature, indicating a weaker binding at the (111) terraces. On the other hand, extending the (001) facets from (311) doesn't result in a change in desorption temperature, indicating that the (001) terraces have a very similar binding energy. The difference indicates the fundamental difference between (111) and (001) terraces and illustrates the influence of terrace type on adsorption at steps. Controlling the combination of terraces and steps in terms of terrace type, step type and step density thus provides an extremely sensitive tuning mechanism for the location of water nucleation.
Conflicts of interest
There are no conflicts to declare.References
- A. Hodgson and S. Haq, Surf. Sci. Rep., 2009, 64, 381–451 CrossRef CAS.
- J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674 CrossRef CAS PubMed.
- M. J. Kolb, F. Calle-Vallejo, L. B. Juurlink and M. T. Koper, J. Chem. Phys., 2014, 140, 134708 CrossRef PubMed.
- C. Badan, M. T. Koper and L. B. Juurlink, J. Phys. Chem. C, 2015, 119, 13551–13560 CrossRef CAS.
- M. J. Kolb, R. G. Farber, J. Derouin, C. Badan, F. Calle-Vallejo, L. B. Juurlink, D. R. Killelea and M. T. Koper, Phys. Rev. Lett., 2016, 116, 1–5 CrossRef PubMed.
- C. Badan, Y. Heyrich, M. T. M. Koper and L. B. F. Juurlink, J. Phys. Chem. Lett., 2016, 7, 1682–1685 CrossRef CAS PubMed.
- V. A. Ranea, A. Michaelides, R. Ramírez, J. A. Vergés, P. L. De Andres and D. A. King, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1–9 CrossRef.
- H. Ibach, Surf. Sci., 2012, 606, 1534–1541 CrossRef CAS.
- M. G. Sceats and S. A. Rice, Water and Aqueous Solutions at Subzero Temperatures, Springer, 1982, pp. 83–214 Search PubMed.
- R. S. Smith, C. Huang, E. K. Wong and B. D. Kay, Surf. Sci., 1996, 367, L13–L18 CrossRef CAS.
- M. Klaua and T. E. Madey, Surf. Sci., 1984, 136, L42–L50 CrossRef CAS.
- A. Michaelides and K. Morgenstern, Nat. Mater., 2007, 6, 597–601 CrossRef CAS PubMed.
- D. L. Bashlakov, L. B. Juurlink, M. T. Koper and A. I. Yanson, Catal. Lett., 2012, 142, 1–6 CrossRef CAS.
- J. Janlamool, D. Bashlakov, O. Berg, P. Praserthdam, B. Jongsomjit and L. B. Juurlink, Molecules, 2014, 19, 10845–10862 CrossRef PubMed.
- H. Ibach, Physics of Surfaces and Interfaces, Springer, 2006, vol. 2006, p. 646 Search PubMed.
- R. van Hardeveld and A. van Montfoort, Surf. Sci., 1966, 4, 396–430 CrossRef CAS.
- W. Ellis and R. Schwoebel, Surf. Sci., 1968, 11, 82–98 CrossRef CAS.
- M. Henzler, Surf. Sci., 1970, 19, 159–171 CrossRef CAS.
- M. A. Van Hove and G. A. Somorjai, Surf. Sci., 1980, 92, 489–518 CrossRef CAS.
- J. E. Ortega, M. Corso, Z. M. Abd-El-Fattah, E. A. Goiri and F. Schiller, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–7 Search PubMed.
- K. Morgenstern, K. F. Braun and K. H. Rieder, Phys. Rev. Lett., 2002, 89, 20–23 Search PubMed.
- J. E. Ortega, G. Vasseur, I. Piquero-Zulaica, S. Matencio, M. A. Valbuena, J. E. Rault, F. Schiller, M. Corso, A. Mugarza and J. Lobo-Checa, New J. Phys., 2018, 20, 073010 CrossRef.
- M. J. Van Der Niet, A. Den Dunnen, L. B. Juurlink and M. T. Koper, J. Chem. Phys., 2010, 132, 174705 CrossRef PubMed.
- A. Picolin, C. Busse, A. Redinger, M. Morgenstern and T. Michely, J. Phys. Chem. C, 2009, 113, 691–697 CrossRef CAS.
- C. Nöbl and C. Benndorf, Surf. Sci., 1987, 182, 499–520 CrossRef.
- C. Mundt and C. Benndorf, Surf. Sci., 1993, 287–288, 119–124 CrossRef CAS.
- A. Den Dunnen, M. J. Van Der Niet, C. Badan, M. T. Koper and L. B. Juurlink, Phys. Chem. Chem. Phys., 2015, 17, 8530–8537 RSC.
- K. Morgenstern, Surf. Sci., 2002, 504, 293–300 CrossRef CAS.
- K. Morgenstern and J. Nieminen, Phys. Rev. Lett., 2002, 88, 1–66102 CrossRef PubMed.
- C. Bertram, W. Fang, P. Pedevilla, A. Michaelides and K. Morgenstern, Nano Lett., 2019, 19, 3049–3056 CrossRef CAS PubMed.
- T. Yamada, S. Tamamori, H. Okuyama and T. Aruga, Phys. Rev. Lett., 2006, 96, 2–5 Search PubMed.
- J. Carrasco, A. Michaelides, M. Forster, S. Haq, R. Raval and A. Hodgson, Nat. Mater., 2009, 8, 427–431 CrossRef CAS PubMed.
- C. Lin, G. Corem, O. Godsi, G. Alexandrowicz, G. R. Darling and A. Hodgson, J. Am. Chem. Soc., 2018, 140, 15804–15811 CrossRef CAS PubMed.
- C. Lin, N. Avidor, G. Corem, O. Godsi, G. Alexandrowicz, G. R. Darling and A. Hodgson, Phys. Rev. Lett., 2018, 120, 76101 CrossRef CAS PubMed.
- C. Díaz, E. Pijper, R. A. Olsen, H. F. Busnengo, D. J. Auerbach and G. J. Kroes, Science, 2009, 326, 832–834 CrossRef PubMed.
| This journal is © the Owner Societies 2019 |