Electron bifurcation: progress and grand challenges
Jonathon L.
Yuly†
 a,
Carolyn E.
Lubner†
a,
Carolyn E.
Lubner†
 *b,
Peng
Zhang
c,
David N.
Beratan
*b,
Peng
Zhang
c,
David N.
Beratan
 *acd and
John W.
Peters
*acd and
John W.
Peters
 *e
*e
aDepartment of Physics, Duke University, Durham, NC 27708, USA. E-mail: dberatan@duke.edu
bBiosciences Center, National Renewable Energy Laboratory, Golden, CO 80401, USA. E-mail: cara.lubner@nrel.gov
cDepartment of Chemistry, Duke University, Durham, NC 27708, USA
dDepartment of Biochemistry, Duke University, Durham, NC 27710, USA
eInstitute of Biological Chemistry, Washington State University, Pullman, WA 99163, USA. E-mail: jw.peters@wsu.edu
First published on 30th August 2019
Abstract
Electron bifurcation moves electrons from a two-electron donor to reduce two spatially separated one-electron acceptors. If one of the electrons reduces a high-potential (lower energy) acceptor, then the other electron may proceed “uphill” to reduce a low-potential (higher energy) acceptor. This mechanism is now considered the third mode of energy transduction in biology, and offers promise for the development of novel bioinspired energy conversion strategies. Nature uses electron bifurcation to realize highly sought-after reactions: reversible CO2 reduction, nitrogen fixation, and hydrogen production. In this review, we summarize the current understanding of electron bifurcation, including both recent progress and outstanding questions in understanding and developing artificial electron bifurcation systems.
 Peng Zhang | Peng Zhang is a research associate professor of Chemistry at Duke University. He is interested in theoretical understanding of the mechanism and kinetics of biological electron transfer. |
Introduction
“Electron bifurcation” (EB) describes more than simply diverting electrons down two independent pathways (Fig. 1). What began in the 1970's as an attempt to explain the bizarre “oxidant-induced reduction”3 observed in mitochondrial inner membranes has, in the last decade, grown into an international effort spanning multiple scientific disciplines. This is not surprising, as electron bifurcation was discovered outside of mitochondrial and photosynthetic membranes, elevating EB reactions to status as a fundamental player in energy transduction in biology.5–7 As such, EB reaches a status in bioenergetics similar to the chemiosmotic mechanism itself. A better understanding of EB seems to promise insight into some of life's deepest mysteries (including the development of primordial life) and reveals a treasure map for truly astonishing bioinspired energy technologies of the future.The term “electron bifurcation” was first used by Peter Mitchell in the 1970s to describe the phenomena associated with the Q-cycle of respiratory complex III (the cytochrome bc1 complex) of the mitochondrial electron transfer chain (ETC).8,9 The net effect of this cycle is the release of protons in the inner membrane space associated with QH2 oxidation, together with the consumption of protons in the matrix associated with Q reduction. This transmembrane proton translocation maintains a proton motive force to the mitochondrial inner membrane. This proton motive force determines the chemiosmotic potential, providing the driving force for ATP synthase; thus, the Q-cycle reaction described above would not be thermodynamically spontaneous. However, Nature makes up the free energy deficit of this endergonic proton translocation via coupling with an exergonic reaction, namely the reduction of cytochrome c (cyt c) at high reduction potential. The coupling of thermodynamically “uphill” reactions (ΔG > 0) with thermodynamically “downhill” (ΔG < 0) reactions is perhaps the leitmotif of bioenergetics.
Electron bifurcation is another example of this type of energetic coupling. Put simply, electron bifurcation moves one electron thermodynamically “downhill”, and this energy is leveraged to move another electron “uphill” without breaking the second law of thermodynamics.12 More precisely, electron bifurcation oxidizes a medium-potential two-electron donor, using its two electrons to reduce a high-potential acceptor with one electron and the second electron to reduce a low potential acceptor (Fig. 1).
For many years, EB was thought to be unique to complex III. About a decade ago, however, flavin-based electron bifurcation (FBEB) was discovered.14–18 FBEB is now understood to support anaerobic metabolism through a variety of reactions that involve the oxidation of NAD(P)H and the reduction of ferredoxin or flavodoxin coupled to various exergonic reductions. Overall, the mechanisms involved in FBEB and EB in complex III seem analogous. Flavins and quinones have similar redox properties: they are effective at mediating both one and two electron transfer reactions and can function by employing inverted reduction potentials (we use the term “inverted” rather than the newer term “crossed” in this review to remind the reader of an older and separate literature on the subject19–23) with highly reducing intermediates.
Electron bifurcation is now understood to drive some of the most valued reactions in all of chemistry. For instance, nature uses the high energy electrons generated by EB to drive CO2 reduction,24 nitrogen fixation,2,25 and hydrogen production26,27 at biological temperatures and pressures, in addition to its role in the Q-cycle where it contributes to the chemiosmotic potential, which in turn drives ATP synthase. Furthermore, it is claimed that many electron bifurcases are reversible,14,16,28–31 many (but perhaps not all14) in vivo. This suggests that it is possible for the energy interconversion associated with these reactions to be accomplished with near 100% efficiency.18 This is not science fiction; these EB reactions occur in nature.
Because of the use of EB in living systems, we believe that astonishing insights for bioinspired energy technologies may lurk within electron bifurcases. The low-potential electron produced by EB could in principle be guided to a targeted acceptor (as long as that acceptor has a reduction potential similar to or higher than the reduction potential of the low potential pathway). So EB might be used to drive many reactions of vital importance to the energy and environmental sciences. Indeed, there seems no reason to doubt that, in principle, any low potential acceptor could be reduced in an EB reaction.
Unfortunately, the simplicity and elegance of biological EB masks the extreme difficulty of deploying EB in artificial systems. If all the redox species to be used in electron bifurcation were added to a mixture and electrons fed from an electrode, they would not perform electron bifurcation. Instead, most electrons would flow to the high-potential acceptors, as this configuration achieves the lowest free energy. Thus, to achieve electron bifurcation, the electrons must be “gated” towards the proper acceptors, despite a large driving force for “short circuit” reactions.12,30 Biology must therefore exert precise microscopic control to realize electron bifurcation. Understanding this control is a major motivation behind the study of biological EB.
The discoveries of EB outside of complex III have been a gold mine for mechanistic studies on the microscopic control wielded by biological EB. These reactions are performed in a variety of chemical and physical contexts, including in hyperthermophiles. For instance, many examples of biological EB do not require membrane-bound proteins and seem to play roles quite different from those of complex III. These EB systems also use a variety of schemes to channel electron flow down the endergonic and exergonic reaction paths. Thus, biology not only achieves astonishing microscopic control to accomplish EB, but also appears to have evolved multiple mechanistic routes to achieve this control. This multiplicity of options for control suggests that EB may constitute some of the most fertile ground for inspiring biomimetic energy technologies.
Structural and mechanistic studies on complex III,32–35 and more recently on FBEB,1,2,15,27,36–41 reveal two basic requirements that are paramount in EB catalysis. The first major requirement is the use of an energetic (highly reducing) species capable of driving the reduction of the endergonic (compared to the mean reduction potential of the two-electron donor) half reaction. This is accomplished in complex III and FBEB through the formation of a metastable SQ intermediate. The presence of a metastable low-potential intermediate is a signature of inverted (or “crossed”) reduction potentials.1,6,9,12 A variety of different multiple electron redox cofactors may exhibit inverted potentials, including metal containing species.20–23 The second requirement is an effective mechanism to gate electron flow, to direct the energetic electron toward the low-potential pathway with high fidelity.
In our view, much understanding of the bifurcating steps in these enzymatic reactions has been gained. Indeed, flavin-based EB has been reviewed many times.7,14–18,24,31,42–45 However, there remain many unanswered questions surrounding the EB mechanisms and the biology of EB. The answers to these questions could enable significant advances in bioenergetics and energy science more broadly. We outline (in the second half of this review) several important conceptual issues that prevent a complete understanding of the molecular mechanisms behind EB, and that prevent the bioinspired inventor from taking further advantage of EB reactions. The opportunities and unresolved issues discussed here reflect the authors’ tastes, and other productive directions for exploration exist as well. To summarize, this feature article elaborates the recent progress in understanding biological electron gating mechanisms used by EB enzymes, in the context of the parameters defined by electron transfer theory, discusses unresolved questions in this field, and explains why we find these questions compelling: a “new era”17 for electron bifurcation truly lies ahead.
Gating electron flow
Gating electron flow in EB is vital, directing electron flow from one donor to two spatially separate acceptors, and preventing both electrons from proceeding to the overall high-potential (lower energy) acceptor. This allows the EB enzyme to minimize the free energy lost through the electron flow. Rates of electron-transfer events are well approximated using the Marcus theory of electron transfer46 and are influenced by distance, thermodynamic driving force, and dielectric environment. For instance, the nonadiabatic (tunneling) electron transfer rate in the small electronic coupling regime is given by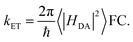 | (1) |
 | (2) |
The factor 〈|HDA|2〉 is the temperature averaged electronic coupling, often falling exponentially with electron donor/acceptor edge-to-edge distance,48λ is the reorganization energy, and ΔG0 is the standard reaction free energy of the electron transfer.
Presumably, during the turnover of an electron bifurcase, electron gating mechanisms may be achieved by modulating parameters that determine electron transfer rates, above. For example, the distance between the bifurcating donor and one of the acceptors might change during EB to allow the bifurcating site to deliver individual electrons to the two spatially separated acceptors in a highly selective manner. Side reactions that would disrupt the equal portioning of electrons into the high and low potential acceptors are known as “short circuits.”30
Conformational electron gating
Electron bifurcation is employed within the Q-cycle, coupling the oxidation of quinol (QH2) to quinone (Q) at the Qo site with reduction of the low-potential heme and the high-potential Rieske-type iron–sulfur (FeS) cluster. The reduction of the low-potential heme generates a driving force for quinone to become reduced again at the Qi site,49 accumulating over two bifurcating cycles (Fig. 2). The proton-coupled oxidation of QH2 and reduction of Q occur against a transmembrane proton motive force. However, this uphill process is coupled to the reduction of the high potential cytochrome c which allows the Q-cycle to occur spontaneously. The net result of the Q-cycle is that half of the electrons that travel through the ETC are briefly detoured through the Q-cycle to generate additional proton motive force.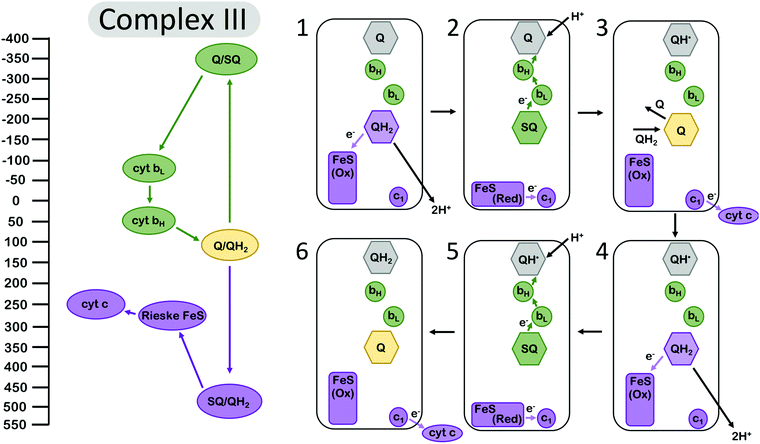 | ||
| Fig. 2 Energy landscape (left) and depiction of electron transfers and conformational changes (right) in the cytochrome bc1 complex (complex III). Cofactors with low (more negative) reduction potentials are shown in green, and the cofactors with high (more positive) potential in purple. Quinone at the Qi site is shown in grey, and the fully oxidized Q at the Qo site is shown in yellow. A first (1–3) and second (4–6) electron bifurcating cycle complete one enzymatic turnover of complex III, resulting in one (net) QH2 oxidation, two reduced cytochrome c (cyt c), and two protons transduced across the membrane. In (1), quinone is oxidized at the Qo site, reducing the high-potential Rieske FeS cluster. Then (2) the complex undergoes a conformational change, so the Rieske center is in position to reduce cyt c1, and the low-potential semiquinone Q˙− is no longer in range to reduce the Rieske center, instead reducing the low potential heme bL. Another QH2 from the Q pool (3) replaces oxidized Q at the Qi site, and (4–6) the process repeats again, allowing Q to be fully reduced to QH2 at the Qi site. Cofactor reduction potentials from Bergdoll et al.4 from measurements of submitochondrial particles from R. sphaereoides in the absence of the membrane potential. The Q/SQ and SQ/QH2 couples were estimated to be roughly as shown in this figure by Zhang et al.10 and later by Crofts et al.11 Cytochrome c redox properties were reviewed by Battistuzzi et al.13 | ||
A first oxidation of QH2 results in the production of a metastable SQ state with low oxidation potential. The oxidation of QH2 to SQ occurs at a potential of almost +500 mV.4 The reduction of the Rieske FeS at a reduction potential of ∼+275 mV, and subsequent reduction of cyt c1 at ∼+250 mV, occur against an electrochemical potential gradient, so they are kinetically limited but feasible at the appropriate equilibrium conditions.49 Since the overall reduction potential of QH2 to Q is about +100 mV and represents the average of the QH2 to SQ and the SQ to Q couples, this translates to a SQ to Q transition at a reduction potential more negative than −300 mV,4,10,11 which is more than ample to drive the reduction of Q in a stepwise manner that is mediated by the cytochrome b (cyt b) hemes bL and bH. The reduction of the Rieske FeS cluster, assuming that it has transferred an electron to cyt c1, is more favored and should occur at a higher rate if the protein conformation and the relative distances of the Rieske FeS cluster and the nearest cyt b site remain unchanged. The complex, however, undergoes a conformational change that increases the distance between the SQ oxidation site and the Rieske center and, as a result, the balance is tipped to kinetically favor reduction at the cyt b site32,34,35 (Fig. 2). This conformational change, however, is not sufficient to suppress the rate constants of all possible short-circuits.29
Mechanistically, complex III has manipulated the energy landscapes of the two half reactions (the exergonic reduction of cyt c by QH2 and the endergonic coupling of the oxidation of QH2 in the inner membrane space to the reduction of Q in the matrix) so that the electron flux through the b hemes to reduce Q occurs against an electrochemical potential gradient. Specifically, the first electron transfer from QH2 to the Rieske cluster is rate limiting, and the downhill flow of electrons from the semiquinone Q˙− to the bH occurs quickly, suppressing semiquinone (Q˙−) population at the Qo site.11 However, it is important to note that this gating mechanism is not sufficient to suppress the rate constants for all “short circuit” reactions in complex III, but perhaps in combination with at least one other gating mechanism.30 The other short-circuits arise as a result of the physiological conditions (near equilibrium) leading to the reversibility of the Q-cycle.29
It has been proposed that the electron bifurcating flavoproteins operate in a manner that invokes conformational changes similar to those found in complex III.38,39 For example, the FixABCX enzyme (Fig. 3), which produces reducing equivalents for nitrogen fixation, couples the oxidation of nicotinamide adenine dinucleotide (NADH) to the reduction of quinone and to the reduction of the low potential electron carriers ferredoxin (Fd) or flavodoxin (Fld).14,16,50 Biochemical studies have revealed that the energy landscapes are likely to be qualitatively similar for the EB flavoproteins and for complex III,2 in the sense that the first electron transfer step from the EB cofactor is endergonic (along the overall exergonic pathway), and that it is the second electron that proceeds through the overall low-potential pathway. The oxidation of NADH is coupled to the reduction of the bifurcating flavin. The oxidation of the hydroquinone form of the flavin (FADH−) is coupled to the reduction of a flavin site along the path toward Q.2 This occurs at a relatively high (positive) reduction potential and produces a metastable flavin ASQ intermediate (FAD−) at the bifurcating site with sufficient driving force to affect the reduction of Fd or Fld with reduction potentials of ∼−500 mV.
 | ||
| Fig. 3 Energy landscape (left) and depiction of proposed electron transfers and conformational changes (right) in the FixABCX complex. Cofactors with low (more negative) reduction potentials are shown in green, and the cofactors with high (more positive) reduction potentials in purple. Fully oxidized FAD is shown in yellow. Analogous to complex III (Fig. 2), the turnover of FixABCX proceeds via two electron bifurcating cycles (1–3) and (4–6). The net result is the two oxidations of NADH to NAD+, two reductions of ferredoxin (or flavodoxin), and one reduction of Q to QH2. The (1) oxidation of FADH− by one electron and transfer to the B flavin triggers (2) a conformational change increasing the distance between B flavin and/or decreasing the distance between the FixX FeS cluster and the bifurcating flavin. This makes the (3) rate of electron transfer from the A flavin along the low potential path to the reduction of Fld via FixX FeS cluster faster than the rate of transfer for the second electron from the A flavin to the B and C flavins. After reduction of the A flavin by NADH, the B flavin (4) returns to its original position within electron transfer range of the bifurcating FAD, and dissociation of reduced Fld initiates the second round of electron bifurcation (4–6). Energy landscape proposed by Ledbetter et al.2 | ||
It was proposed that conformational changes analogous to those in complex III may be invoked for FBEB. Structural and biochemical results on the enzyme butyryl CoA reductase39 and caffeyl-CoA dehydrogenase38 support a model in which the distance between the proximal electron acceptor along the high potential pathway is increased after the first electron transfer, resulting in a decrease in the rate of a second electron transfer down the same (high potential) pathway and favoring the transfer of the second electron down the low potential pathway toward ferredoxin reduction. It is presumed that the homologous FixABCX/Electron transfer flavoprotein (EtfABCX) complexes2,41,50 undergo similar conformational changes in which the relative distances of the nearest acceptors along the low and high potential pathways are modulated in a manner that causes the reduction of the low potential acceptor to be kinetically favored. This conformational change could hypothetically be realized by increasing the distance to the nearest high potential acceptor and/or decreasing the distance to the nearest low potential acceptor. The FixABCX (Fig. 3) enzyme couples the oxidation of FADH− to the reduction of flavodoxin for use in nitrogenase catalysis,2 and the reduction of quinone. EtfABCX couples the reduction of FADH− with the reduction of quinone and ferredoxin.41 Both FixABCX and EtfABCX utilize NADH to initially reduce the bifurcating FAD site.
Gating electron transfer by cofactor placement
The NADH-dependent ferredoxin–NADP+ oxidoreductase (Nfn) is another well studied FBEB enzyme. The enzyme couples the oxidation of NADPH to the exergonic reduction of NAD+ and the endergonic reduction of Fd. In contrast to complex III and bifurcating Fix/Etf enzymes, Nfn is a simple dimeric complex with a large and small subunit1,51 (Fig. 4). The bifurcating flavin is in the large (L) subunit which also harbours two low potential [4Fe–4S] clusters and the site for Fd reduction. The small (S) subunit harbours a single [2Fe–2S] cluster and an additional flavin near the site of NAD+ reduction. The clusters in the dimer are arranged such that the bifurcating flavin is central, near the L and S subunit interface. | ||
| Fig. 4 Energy landscape (left) and depiction of proposed electron transfers and conformational changes (right) in the NADH-dependent ferredoxin NADP+ oxidoreductase (Nfn). Cofactors with low (more negative) reduction potentials are shown in green, and the cofactors with high (more positive) reduction potentials in purple. The oxidized form of the electron bifurcating flavin (FAD) is shown in yellow. The oxidation of FADH2 by one electron (1) results in the formation of FAD− with an extremely negative reduction potential. Since [4Fe–4S] is much closer to the electron bifurcating flavin than [2Fe–2S], this makes the (2) rate of electron transfer along the low potential path to the reduction of Fd via FeS clusters faster than the short circuit transfer from FAD− to [2Fe–2S] in the S subunit. (3) A second reduction of the bifurcating FAD and dissociation of reduced Fd initiates (4–6) the second round of electron transfer steps analogous to (1–3) resulting in the formation of an additional reduced Fd and completing the reduction of NAD+ to NADH. Cofactor reduction potentials shown from Lubner et al.1 | ||
The energy landscape of Nfn based on biochemical and spectroscopic studies is qualitatively similar yet quantitatively inflated compared with the energy landscape of complex III and the Fix/Etf enzymes, encompassing a much larger range of reduction potentials. During catalysis, the bifurcating site is reduced by NADPH and the bifurcating flavin transfers the first electron to a [2Fe–2S] cluster on the path to NAD+ reduction (overall exergonic pathway). In a similar manner as in complex III and Fix, transfer of the first electron occurs at a relatively high (positive) reduction potential, leading to a highly energetic low (negative) potential intermediate. The measured reduction potentials of the [4Fe–4S] clusters along the endergonic pathway to Fd reduction are very low, with the cluster proximal to the bifurcating site estimated at ∼−700 mV. This cluster is within 8 Å of the bifurcating site, and the rate of electron transfer from the bifurcating flavin to this cluster was determined experimentally to be very fast, in the range of 10 ps.1 These parameters imply that the reduction potential of the energetic FAD− is more negative than −900 mV, allowing an estimate of the complete redox energy landscape (Fig. 4). The two electron FAD → FADH− reduction potential of ∼−300 mV, and the one-electron FAD → FAD− couple estimated at −900 mV, places the FAD− → FADH− redox couple at ∼+350 mV, resulting in an energy landscape that spans more than 1 V in electrochemical potential, about 2-fold larger than the span of electrochemical potentials accessed by complex III and the bifurcating ETFs. Also unique to Nfn is the lack of experimental evidence indicating large scale conformational changes that could serve to gate electrons as in complex III and bifurcating ETFs, indicating a need for a different mechanism for electron gating to avoid short circuits (i.e. both electrons flowing down the exergonic path).
The gating mechanism that is likely employed by Nfn arises from the electron acceptor placement near the electron bifurcating L-FAD.12 The first electron proceeds from L-FAD to reduce the [2Fe–2S] cluster, as the alternative reduction of the [4Fe–4S] cluster would be significantly uphill. Once this first electron has transferred, the highly reducing FAD− can reduce the [4Fe–4S] cluster. Why does the second electron not follow the first to reduce [2Fe2S]? It may, but the rate of [4Fe–4S] reduction has been estimated to be orders of magnitude faster,12 as the tunneling distance to [4Fe–4S] is about 7 Å closer to L-FAD than to [2Fe–2S].1
The unique energy landscape in Nfn also invites speculation on another gating mechanism that does not involve conformational changes. The large difference between the FAD one-electron reduction potential estimated at −900 mV and the reduction potential of the unproductive acceptor ([2Fe–2S]) at +100 mV suggests that this electron transfer may be Marcus inverted12 (Fig. 4). At this reduction potential difference of ∼1 V, electron transfer rates decrease as the driving force for electron transfer grows. This manner of gating has been proposed to be relevant in Nfn, although Marcus inversion likely plays a significantly smaller role than the tunnelling distance effect described above.
Grand challenges and opportunities
While recent work has progressed our understanding of the structures and gating mechanisms underpinning EB, there remain significant challenges. These challenges also represent great opportunities, as their resolution may unlock secrets that could enable the creation of artificial EB. The next section summarizes several confounding issues that prevent a clearer understanding of EB at the molecular scale.EB kinetics: what is missing?
The redox potentials of the electron bifurcating flavin (L-FAD) in Nfn are striking: they are inverted by almost 1 Volt!1 This immediately begs the troubling question of how electrons at the FAD−/FADH− potential can reduce NAD+ at a reasonable turnover rate, as they must proceed ≈ 600 meV uphill thermodynamically to do so (Fig. 4). If the FAD−/FADH− potential were several hundred mV lower, it would seem more reasonable (based on thermodynamic grounds) for electrons in the S subunit to reduce NAD+.14,18 However, in our view this alone would not resolve the enigmas surrounding the kinetics of the Nfn enzyme for three main reasons, which suggest opportunities for fundamental discoveries.First, we contend that the only roadblock for electrons to reduce NAD+ from L-FAD is not the L-FAD reduction potentials, but the back-ET rate from S-FAD to [2Fe–2S]. Invoking detailed balance (kforward = kreversee−ΔG/kT) requires that the reverse rate constant from S-FAD back to [2Fe–2S] is ∼106 times faster than the forward rate. This suggests that electrons in the S subunit will fall into the “sink” at the [2Fe–2S] cluster and have difficulty proceeding further. This difficulty is present regardless of the values of the L-FAD reduction potentials.
Second, as with many enzymes, the catalytic cycle of Nfn is observed to be reversible: simply adding excess reduced Fd to the solution will put the reaction in reverse28 (“electron confurcation”31,52). In the electron confurcating regime, NADH and reduced Fd are oxidized to produce NADPH. Here, there seems to be no issue with electrons flowing through the S subunit, as reverse flow through the S subunit is thermodynamically downhill. However, one now has the difficulty of explaining how electrons flow through the L subunit, where, in the bifurcating regime, there were no issues! Specifically, backward flow between the [4Fe–4S] clusters must proceed uphill by ≈200 mV. So what exactly determines the rate of Nfn turnover? It seems unlikely that all the reduction potentials in Fig. 4 will be updated.
There are additional complexities which may be relevant for the kinetics of Nfn from the energy landscape in Fig. 4. For instance, almost every electron transfer in Nfn is (or could be) proton coupled (even [4Fe–4S] cluster redox chemistry may involve protons, such as for the H cluster in [FeFe]-hydrogenases26,53) opening the possibility that proton motion may significantly influence the electron transfer dynamics. Indeed, the astute reader may notice that a proton is unaccounted for in the scheme of Fig. 4 (two protons are removed during NADPH oxidation, but only one is used to reduce NAD+ to NADH), suggesting that solvated protons may serve as a fourth substrate, and another possible source of driving force and kinetic influence. Furthermore, it has been suggested that the kinetics of Nfn proceed through two bifurcating cycles14,54 (Fig. 4), and that the electron from the first cycle waits in the S subunit for the second electron to join it in reducing NAD+. This first electron may affect the reduction potentials that the second electron experiences during the second cycle. If nothing else, evaluation of the effects of changing oxidation states in the S subunit between bifurcating cycles may be warranted.
Third, even when lingering issues surrounding the kinetics and chemistry of the Nfn enzyme itself are resolved, an enigma surrounding EB generally remains. A steep energy landscape in the high and low potential branches seems to be conserved for all EB enzymes, regardless of whether conformational gating is involved (Fig. 2–4). Steep energy landscapes are generally undesirable in reversible catalysis, as they hinder fast turnover. Why does biology seem to be slowing itself down? To suppress short circuits?11,29 If so, what exactly is the tradeoff between turnover speed and short circuiting in EB? Does this tradeoff specify a physical limit on the turnover rate for efficient EB?
In short, attempting to build a simple kinetics model of Nfn based on the thermodynamics of its cofactors seems challenging, as electrons apparently proceed significantly uphill thermodynamically in both branches, depending on whether the reaction runs in the forward (bifurcating) regime or the reverse (confurcating) regime. Furthermore, the unusually reducing L-FAD is almost certainly not the root of the enigmas surrounding the Nfn enzyme. Indeed, similar phenomena seem to occur for the other energy landscapes in Fig. 2 and 3. Perhaps Nature hides a fundamental discovery?
Inverted reduction potentials
All known electron bifurcating cofactors employ inverted reduction potentials. This means that the free energy required to remove a first electron from these cofactors is greater than to remove a second. More precisely, the reduction potentials of a two-electron species are “inverted”19–22,44 (some authors use “crossed”1,6,12,16,55) if the first reduction occurs at a lower reduction potential than the second.The importance of inverted reduction potentials for EB was first noted by Nitschke and Russell almost a decade ago, where it was proposed to be a thermodynamic requirement for EB.6 Later, several hypothetical scenarios were derived that showed electron bifurcation (i.e. one electron proceeding to a low-potential acceptor and another to a different high-potential acceptor) was possible without inverted potentials, as long as the electrons were properly gated to each acceptor.12 However, some argued that these alternate scenarios would not be biologically useful, as they would require low-potential (high energy) electrons to refill electron bifurcating donors to reinitiate EB.44 Indeed, if inverted potentials were useless to biology, why do all known EB systems employ them?
The debate surrounding inverted potentials and EB is not resolved. For instance, it is not clear how inverted reduction potentials may enhance the electron refilling process. If electrons are refilled one-at-a-time, the hole left behind by the low potential electron must be refilled by a donor with a reduction potential as or more negative, regardless of whether the bifurcating donor's reduction potentials are inverted or not. Thus, if the refilling process is sequential (one electron at a time), a low potential “refilling” donor is always required.
Instead of two single electron steps, it is possible that the refilling process may be concerted (i.e. there is no metastable intermediate with only one electron transferred). Although possibly hinted at in previous studies of FBEB,6,44 a concerted refill mechanism has not been clearly shown, as no previous literature on FBEB (to our knowledge) has defined or even used the term “concerted”. Concerted transfer has been considered as a possible electron gating mechanism for EB in complex III29,30 (with controversy11) but not, to our knowledge, for the quinone refilling step at the Qi site. Indeed, the refilling process at the Qi site appears to proceed unhindered, despite not exhibiting inverted potentials.56 In any case, a concerted mechanism would have many implications for the kinetics and dynamics of the refilling process (for example kinetic isotope effects57,58), and no evidence for a concerted mechanism has been proposed. Furthermore, these issues seem deeply rooted in kinetics, not thermodynamics (reduction potentials are thermodynamic quantities). What would prevent concerted refilling without inverted potentials? If concerted refilling is possible without inverted potentials, of what use are inverted potentials? In our view, the precise mechanistic role that inverted potentials play in EB remains poorly understood.
In addition to their biological utility, the precise chemical and physical causes of inverted reduction potentials are also vague or missing from the literature. Several studies on inverted reduction potentials exist,19,20 and they play an important role in the activation of certain Pt(IV) tumor pro-drugs.22 However, to our knowledge no comprehensive and systematic approach to understanding and engineering the order of reduction potentials has been proposed. Importantly, none of the cited studies examine inverted reduction potentials for proton-coupled redox chemistry, and all known EB reactions are proton-coupled. Even more fascinating, the ordering of both quinone's and flavin's first and second reduction potentials is known to be different, depending on the electrochemical and protein environment. For instance, the electron-bifurcating quinone in complex III has inverted reduction potentials at the Qo site, but not at the Qi site.56 Flavin's reduction potentials are highly inverted when it performs EB in Nfn,1 but not when it serves as a one electron carrier in flavodoxins.59 In our view, a quantitative perspective on the chemical and physical origins of inverted reduction potentials is needed, to calculate and predict how the ordering of first and second reduction potentials may be switched by the environment of a two-electron donor. This would not only provide insights into the structure–function relationship of these enzymes but could also be useful for guiding the development of novel electrochemical technologies. For example, it may be possible to build a molecular electrochemical switch that functions by dynamically switching the order of a molecule's reduction potentials.
Quinone vs. flavin EB
Clearly, some of the appeal of flavin-based EB lies in its analogy with the EB reaction in complex III. But how far exactly does this analogy extend? A precise answer to this question has important implications: every aspect of flavin-based EB that carries over to quinone-based EB could (in principle) be used as a mechanistic proxy to study the quinone systems (such as complex III). On the other hand, every aspect of flavin-based EB that does not carry over from complex III provides not only fundamental new insight into bioenergetics, but also gives the bioinspired chemist multiple tools to accomplish EB and related reactions. How many such tools exist? Are any of them easier to mimic in an artificial system?Furthermore, differences between complex III and flavin-based EB may reflect differences in the problems solved by these systems deep in their evolutionary past. Indeed, the discovery of flavin-based electron bifurcation prompted a suggestion that EB played an important role in energy transduction for early life forms.6,44 Recent genomic analysis suggested that contemporary FBEB enzymes may have emerged from non-bifurcating analogs after the last universal common ancestor and spread through lateral gene transfer.45,60 Of course, genetics data reveals little concerning the primordial presence of EB, as life presumably needed to perform energy transduction before the emergence of the genetic code, and EB has apparently evolved more than once (as quinone- and flavin-based EB) as a rediscovered solution to the common challenge of efficient free energy transduction. However, the new genomics evidence suggests that flavin-based EB may not be the best proxy for the study of truly ancient EB (older than quinone- and flavin-based). For instance, alternate forms of EB involving transition metals have been hypothesized as the truly ancient forms.44 However, others have hypothesized that native metal chemistry might have enabled primordial life to accomplish difficult chemical reactions without EB at all.61
Reversibility and efficiency
As mentioned previously, catalysis performed by the Nfn enzyme is easily reversed, at least in vitro.28 This is enigmatic given the redox landscape of Nfn (see “Nfn kinetics: what is missing?”). This is not the only reason that reversibility may become a central theme in future studies on EB. Here we associate reversibility with small heat dissipation for the forward and reverse reactions, even at a high turnover rate (equivalently, high turnover at low bias, or high turnover near equilibrium).For example, there is evidence that complex III operates in a nearly reversible regime.29 Enforcing reversibility at the Qo site was predicted to allow for several new “short circuit” reactions that may not pose a threat in a non-reversible regime.30 Indeed, it was shown that at least two electron gating mechanisms are required to suppress the rate constants of these wasteful reactions and allow both reversible and robust EB in complex III.30 Possible additional short circuits arising from reversibility have not previously been considered in studies on flavin-based EB, so it is unknown if any of these mechanisms carry over to flavin-based EB enzymes.
Role of protons
Both the quinone- and flavin-based bifurcating systems use hydride transfer to reduce the bifurcating site during the refill process, albeit through different mechanisms for proton delivery.1,62 The resulting fully reduced hydroquinone species (either QH2 in complex III or FADH− in Nfn and ETF) then bifurcates these electrons down two separate pathways with different energies. Oxidation of the hydroquinone by one electron results, in both systems, in the generation of a transient, and thermodynamically unstable SQ species.1,63 This first electron-transfer step is essentially the rate-determining step for the electron bifurcating step (not necessarily the rate-determining step for Nfn turnover), as it represents a thermodynamically uphill step.1,12 Because this rate-determining process involves the proton transfer that is required for the formation of FAD−, this suggests that proton-coupled electron transfer could provide other forms of electron gating relevant to electron bifurcating enzymes. PCET likely plays an important role for EB, as all known electron bifurcating reactions in nature are proton-coupled. But what exactly does PCET bring to the table?The phenomena of PCET is the subject of intense study.58 PCET can facilitate large scale conformational changes by altering pKa's in H-bonding networks through amino acids that connect cofactor sites to bulk solvent.64 Furthermore, these processes can control overall reaction kinetics by affecting the binding affinities of cofactors. It has been postulated that the proton transfer step is unfavorable in the oxidation of QH2 in complex III and explains the peculiarly slow first electron-transfer step.64 A similar process may occur in flavin-based systems and may be important for coordinating the two electron transfer events of bifurcation. But this connection has yet to be experimentally established. Once PCET occurs, the FAD− species is formed and drives electron transfer down the alternate pathway from the first electron transfer event.12
The precise role of PCET for EB is poorly understood and cannot be determined based solely on structural data. However, structural information can provide clues for how proton availability and access can impact specific cofactors or routes between cofactors, or how conformational gating mechanisms may be initiated. Investigations of how different types of PCET processes may contribute to electron bifurcation, in particular the multiple-site concerted proton–electron transfer65 where the proton and electron transfer to two different acceptor species, may be good hunting grounds to uncover additional electron control mechanisms.
Summary
Electron bifurcation requires a redox site that can perform two-electron redox reactions and gating mechanisms to ensure that the electrons are directed to spatially and energetically distinct acceptors. With respect to two-electron chemistry, we know that quinone and flavin cofactors can act as electron bifurcating sites, but we should anticipate that other organic and inorganic redox species can bifurcate electrons. Achieving effective electron gating mechanisms to ensure that one electron reduces the low potential acceptor and one reduces the high potential acceptor is the challenging aspect of EB that, intriguingly, nature has solved.In the FBEB systems that have been studied to date, it seems reasonable that electron gating could occur through protein conformational changes that modulate the distance between the bifurcating site and the acceptors, or through strategic placement of the cofactors. Driving force electron gating through Marcus inversion could also play a role. We look forward to the discovery of other potential electron gating mechanisms in FBEB enzymes.
Despite much progress in characterizing the structure and basic properties of EB systems, there remain many grand challenges to resolve in order to complete our understanding of EB function and to accomplish artificial EB. These challenges include understanding the biophysical logic that underpins inverted reduction potentials, solving the energy landscape/kinetics enigma apparent in many EB enzymes, enumerating the differences between quinone- and flavin-based EB, uncovering the tools behind EB reversibility, and unraveling the mechanistic/electron-gating role of PCET in EB. Addressing any of these fascinating issues may provide the crucial clues needed to design EB reactions that accomplish difficult chemical transformations with high thermodynamic efficiency.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported as part of the Biological and Electron Transfer and Catalysis (BETCy) EFRC, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science (DE-SC0012518). This work was authored in part by Alliance for Sustainable Energy, LLC, the manager and operator of the National Renewable Energy Laboratory for the U.S. Department of Energy (DOE) under contract DEAC36-08GO28308. Funding was provided by the U.S. Department of Energy Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences. The U.S. Government and the publisher, by accepting the article for publication, acknowledge that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.Notes and references
- C. E. Lubner, D. P. Jennings, D. W. Mulder, G. J. Schut, O. A. Zadvornyy, J. P. Hoben, M. Tokmina-Lukaszewska, L. Berry, D. M. Nguyen, G. L. Lipscomb, B. Bothner, A. K. Jones, A. F. Miller, P. W. King, M. W. W. Adams and J. W. Peters, Nat. Chem. Biol., 2017, 13, 655–659 CrossRef CAS PubMed.
- R. N. Ledbetter, A. M. G. Costas, C. E. Lubner, D. W. Mulder, M. Tokmina-Lukaszewska, J. H. Artz, A. Patterson, T. S. Magnuson, Z. J. Jay, H. D. Duan, J. Miller, M. H. Plunkett, J. P. Hoben, B. M. Barney, R. P. Carlson, A. F. Miller, B. Bothner, P. W. King, J. W. Peters and L. C. Seefeldt, Biochemistry, 2017, 56, 4177–4190 CrossRef CAS PubMed.
- M. K. Wikström and J. A. Berden, Biochim. Biophys. Acta, Bioenerg., 1972, 283, 403–420 CrossRef.
- L. Bergdoll, F. Ten Brink, W. Nitschke, D. Picot and F. Baymann, Biochim. Biophys. Acta, 2016, 1857, 1569–1579 CrossRef CAS PubMed.
- R. K. Thauer, Annu. Rev. Microbiol., 2015, 69, 1–30 CrossRef CAS.
- W. Nitschke and M. J. Russell, BioEssays, 2012, 34, 106–109 CrossRef CAS.
- J. W. Peters, A.-F. Miller, A. K. Jones, P. W. King and M. W. Adams, Curr. Opin. Chem. Biol., 2016, 31, 146–152 CrossRef CAS.
- P. Mitchell, FEBS Lett., 1975, 59, 137–139 CrossRef CAS.
- P. Mitchell, J. Theor. Biol., 1976, 62, 327–367 CrossRef CAS PubMed.
- H. Zhang, A. Osyczka, P. L. Dutton and C. C. Moser, Biochim. Biophys. Acta, 2007, 1767, 883–887 CrossRef CAS PubMed.
- A. R. Crofts, S. Hong, C. Wilson, R. Burton, D. Victoria, C. Harrison and K. Schulten, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1362–1377 CrossRef CAS PubMed.
- P. Zhang, J. L. Yuly, C. E. Lubner, D. W. Mulder, P. W. King, J. W. Peters and D. N. Beratan, Acc. Chem. Res., 2017, 50, 2410–2417 CrossRef CAS PubMed.
- G. Battistuzzi, M. Borsari and M. Sola, Antioxid. Redox Signaling, 2001, 3, 279–291 CrossRef CAS PubMed.
- W. Buckel and R. K. Thauer, Chem. Rev., 2018, 118, 3862–3886 CrossRef CAS PubMed.
- G. Herrmann, E. Jayamani, G. Mai and W. Buckel, J. Bacteriol., 2008, 190, 784–791 CrossRef CAS PubMed.
- V. Muller, N. P. Chowdhury and M. Basen, Annu. Rev. Microbiol., 2018, 72(72), 331–353 CrossRef PubMed.
- J. W. Peters, D. N. Beratan, B. Bothner, R. B. Dyer, C. S. Harwood, Z. M. Heiden, R. Hille, A. K. Jones, P. W. King, Y. Lu, C. E. Lubner, S. D. Minteer, D. W. Mulder, S. Raugei, G. J. Schut, L. C. Seefeldt, M. Tokmina-Lukaszewska, O. A. Zadvornyy, P. Zhang and M. W. W. Adams, Curr. Opin. Chem. Biol., 2018, 47, 32–38 CrossRef CAS PubMed.
- W. Buckel and R. K. Thauer, Front. Microbiol., 2018, 9, 401 CrossRef PubMed.
- D. H. Evans and K. Hu, J. Chem. Soc., Faraday Trans., 1996, 92, 3983–3990 RSC.
- D. H. Evans, Chem. Rev., 2008, 108, 2113–2144 CrossRef CAS PubMed.
- R. L. Lord, C. K. Schauer, F. A. Schultz and M.-H. Baik, J. Am. Chem. Soc., 2011, 133, 18234–18242 CrossRef CAS PubMed.
- M. C. McCormick, K. Keijzer, A. Polavarapu, F. A. Schultz and M.-H. Baik, J. Am. Chem. Soc., 2014, 136, 8992–9000 CrossRef CAS PubMed.
- D. H. Evans and M. W. Lehmann, Acta Chem. Scand., 1999, 53, 765–774 CrossRef CAS.
- C. E. Lubner and J. W. Peters, ChemBioChem, 2017, 18, 2295–2297 CrossRef CAS PubMed.
- R. N. Ledbetter, A. M. Garcia Costas, C. E. Lubner, D. W. Mulder, M. Tokmina-Lukaszewska, J. H. Artz, A. Patterson, T. S. Magnuson, Z. J. Jay and H. D. Duan, Biochemistry, 2017, 56, 4177–4190 CrossRef CAS PubMed.
- C. Sommer, A. Adamska-Venkatesh, K. Pawlak, J. A. Birrell, O. Rüdiger, E. J. Reijerse and W. Lubitz, J. Am. Chem. Soc., 2017, 139, 1440–1443 CrossRef CAS PubMed.
- G. J. Schut and M. W. W. Adams, J. Bacteriol., 2009, 191, 4451–4457 CrossRef CAS PubMed.
- G. Schut, Personal communication.
- A. Osyczka, C. C. Moser, F. Daldal and P. L. Dutton, Nature, 2004, 427, 607–612 CrossRef CAS PubMed.
- A. Osyczka, C. C. Moser and P. L. Dutton, Trends Biochem. Sci., 2005, 30, 176–182 CrossRef CAS PubMed.
- Z. Yan and J. G. Ferry, Front. Microbiol., 2018, 9, 1322 CrossRef.
- A. R. Crofts, Photosynth. Res., 2004, 80, 223–243 CrossRef CAS PubMed.
- A. R. Crofts and E. A. Berry, Curr. Opin. Struct. Biol., 1998, 8, 501–509 CrossRef CAS PubMed.
- A. R. Crofts, S. W. Rose, R. L. Burton, A. V. Desai, P. J. A. Kenis and S. A. Dikanov, J. Phys. Chem. B, 2017, 121, 3701–3717 CrossRef CAS PubMed.
- A. Osyczka, C. C. Moser, F. Daldal and P. L. Dutton, Nature, 2004, 427, 607–612 CrossRef CAS PubMed.
- J. Bertsch, A. Parthasarathy, W. Buckel and V. Muller, J. Biol. Chem., 2013, 288, 11304–11311 CrossRef CAS PubMed.
- N. P. Chowdhury, J. Kahnt and W. Buckel, FEBS J., 2015, 282, 3149–3160 CrossRef CAS.
- J. K. Demmer, J. Bertsch, C. Oppinger, H. Wohlers, K. Kayastha, U. Demmer, U. Ermler and V. Muller, FEBS Lett., 2018, 592, 332–342 CrossRef CAS PubMed.
- J. K. Demmer, N. P. Chowdhury, T. Selmer, U. Ermler and W. Buckel, Nat. Commun., 2017, 8, 1577 CrossRef PubMed.
- A. K. Kaster, J. Moll, K. Parey and R. K. Thauer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 2981–2986 CrossRef CAS PubMed.
- G. J. Schut, N. Mohamed-Raseek, M. Tokmina-Lukaszewska, D. W. Mulder, D. M. N. Nguyen, G. L. Lipscomb, J. P. Hoben, A. Patterson, C. E. Lubner, P. W. King, J. W. Peters, B. Bothner, A. F. Miller and M. W. W. Adams, J. Biol. Chem., 2019, 294, 3271–3283 CrossRef CAS PubMed.
- W. Buckel and R. K. Thauer, Biochim. Biophys. Acta, 2013, 1827, 94–113 CrossRef CAS PubMed.
- J. W. Peters, D. N. Beratan, G. J. Schut and M. W. Adams, Chem. Commun., 2018, 54, 4091–4099 RSC.
- F. Baymann, B. Schoepp-Cothenet, S. Duval, M. Guiral, M. Brugna, C. Baffert, M. J. Russell and W. Nitschke, Front. Microbiol., 2018, 9, 1357 CrossRef PubMed.
- J. Liang, H. Huang and S. Wang, Front. Microbiol., 2019, 10, 373 CrossRef PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966 CrossRef CAS.
- W. Schmickler and W. Vielstich, Electrochim. Acta, 1973, 18, 883–888 CrossRef CAS.
- H. B. Gray and J. R. Winkler, Q. Rev. Biophys., 2003, 36, 341–372 CrossRef CAS PubMed.
- C. C. Moser, T. A. Farid, S. E. Chobot and P. L. Dutton, Biochim. Biophys. Acta, Bioenerg., 2006, 1757, 1096–1109 CrossRef CAS PubMed.
- A. M. G. Costas, S. Poudel, A. F. Miller, G. J. Schut, R. N. Ledbetter, K. R. Fixen, L. C. Seefeldt, M. W. W. Adams, C. S. Harwood, E. S. Boyd and J. W. Peters, J. Bacteriol., 2017, 199, e00440-17 CrossRef PubMed.
- J. K. Demmer, H. Huang, S. N. Wang, U. Demmer, R. K. Thauer and U. Ermler, J. Biol. Chem., 2015, 290, 21985–21995 CrossRef CAS PubMed.
- V. Müller, N. P. Chowdhury and M. Basen, Annu. Rev. Microbiol., 2018, 72, 331–353 CrossRef PubMed.
- D. W. Mulder, M. W. Ratzloff, M. Bruschi, C. Greco, E. Koonce, J. W. Peters and P. W. King, J. Am. Chem. Soc., 2014, 136, 15394–15402 CrossRef CAS PubMed.
- S. Wang, H. Huang, J. Moll and R. K. Thauer, J. Bacteriol., 2010, 192, 5115–5123 CrossRef CAS PubMed.
- J. K. Demmer, N. P. Chowdhury, T. Selmer, U. Ermler and W. Buckel, Nat. Commun., 2017, 8, 1577 CrossRef PubMed.
- H. Zhang, S. E. Chobot, A. Osyczka, C. A. Wraight, P. L. Dutton and C. C. Moser, J. Bioenerg. Biomembr., 2008, 40, 493–499 CrossRef CAS PubMed.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939–6960 CrossRef CAS PubMed.
- A. Migliore, N. F. Polizzi, M. J. Therien and D. N. Beratan, Chem. Rev., 2014, 114, 3381–3465 CrossRef CAS PubMed.
- S. Alagaratnam, G. van Pouderoyen, T. Pijning, B. W. Dijkstra, D. Cavazzini, G. L. Rossi, W. M. Van Dongen, C. P. van Mierlo, W. J. van Berkel and G. W. Canters, Protein Sci., 2005, 14, 2284–2295 CrossRef CAS PubMed.
- S. Poudel, E. C. Dunham, M. R. Lindsay, M. J. Amenabar, E. M. Fones, D. R. Colman and E. S. Boyd, Front. Microbiol., 2018, 9, 1762 CrossRef PubMed.
- F. L. Sousa, M. Preiner and W. F. Martin, Curr. Opin. Microbiol., 2018, 43, 77–83 CrossRef CAS PubMed.
- V. R. I. Kaila, J. R. Soc., Interface, 2018, 15, 141 CrossRef PubMed.
- P. R. Vennam, N. Fisher, M. D. Krzyaniak, D. M. Kramer and M. K. Bowman, ChemBioChem, 2013, 14, 1745–1753 CrossRef CAS PubMed.
- A. R. Crofts, Biochim. Biophys. Acta, Bioenerg., 2004, 1655, 77–92 CrossRef CAS PubMed.
- J. W. Darcy, B. Koronkiewicz, G. A. Parada and J. M. Mayer, Acc. Chem. Res., 2018, 51, 2391–2399 CrossRef CAS PubMed.
Footnote |
| † Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |





