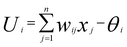Solubility prediction of gases in polymers based on an artificial neural network: a review

Abstract

As an important physical chemistry property, solubility is still a popular research topic. Its theoretical calculation method has developed rapidly. In particular, the artificial neural network (ANN) has attracted the attention of researchers because of its unique nonlinear processing ability. This review provides a brief explanation of the ANN approaches that are most commonly applied to predict gas solubility in polymers, and states the implementation principle, progress, and performance analysis of hybrid ANNs based on the intelligence algorithm. The prospect of solubility prediction based on current research trends is then proposed. This review attempts to analyze the solubility calculation method and provides an insight into and reference for the application of the artificial intelligence method in chemistry and material fields, and can expand in the future because of the increasing number of solubility prediction approaches being introduced.

---

Li Mengshan, Wu Wei, Chen Bingsheng, Wu Yan and Huang Xingyuan

Li Mengshan received his Ph.D. in 2014. He is currently working at the Gannan Normal University (in the College of Physics and Electronic Information). He has coauthored more than 40 publications that include articles in peer-reviewed international journals, communications at national and international conferences. His research interests include polymer materials processing, polymer theoretical calculation and simulation, polymer physical chemistry, artificial intelligence, swarm intelligence algorithm and its application, and quantitative structure–activity relationship. Wu Wei is currently a senior student at Gannan Normal University (in the College of Physics and Electronic Information). She has published about 10 peer reviewed journal articles. Her current research interests include a swarm intelligence algorithm and its application. Chen Bingsheng is currently working as Assistant Professor at Gannan Normal University (in the College of Physics and Electronic Information). His current research interests include polymer theoretical calculation and simulation, artificial intelligence and quantitative structure–activity relationship. He has published over 10 peer reviewed journal articles. Wu Yan is currently working at the Gannan Normal University (in the College of Mathematics and Computer Science). She has published over 20 peer reviewed journal articles. Her current research interests include polymer theoretical calculation and simulation, swarm intelligence algorithm and its application, and quantitative structure–activity relationship. Huang Xingyuan received his Ph.D. in 2007. He is currently working as a Professor at Nanchang University (in the College of Mechanical and Electric Engineering). He has coauthored more than 100 publications that include articles in peer-reviewed international journals and communications at national and international conferences. His research interests include polymer chemistry, polymer modification, polymer materials processing, microcellular plastics, and polymer theoretical calculation and simulation.

1 Introduction

The solubility of gases in polymers is an important physicochemical property, it is widely applied in the fields of material extraction and separation, material modification, and new material preparation and processing.^1–4 Solubility data can be obtained by experimental measurements and computational simulations; given the rapid change in solubility with small changes in temperature and pressure under supercritical high temperature and pressure, experimental research is difficult, and the experiment is laborious and time-consuming. Therefore, a reliable prediction model must be established.

Many solubility factors, such as system temperature, pressure, polarity, and system density, show strong non-linear mapping relationships.⁵ Mutually restricted nonlinear characteristics exist among the influencing factors, especially in the supercritical high temperature and pressure conditions; the traditional thermodynamics research method is relatively difficult, and the simulation precision and efficiency cannot satisfy the demand.^6–8 Artificial neural network (ANN) has many characteristics, such as self-organization and self-learning ability, suitable fault tolerance, and strong non-linear processing power; hence, it exhibits superior performance when calculating solubility problems.⁹ The most commonly employed methods to predict solubility are back propagation ANN (BP ANN) and radial basis function ANN (RBF ANN). Scientists are working to explore computing methods that are more efficient, accurate, and adaptive to obtain a reliable solubility model.^10,11

Therefore, the solubility of gases in different polymers based on many varieties of ANN is taken as an example in this review. The basic principles, research status, advantages, and disadvantages of different types of ANNs in solubility calculation are reviewed. Combined with our previous studies in recent years, this review mainly states the progress of the solubility prediction of ANNs based on the swarm intelligence algorithm. The solubility calculation is then summarized and prospected based on current research trends. This review attempts to analyze the solubility calculation method and provide an insight into and reference for the application of the artificial intelligence method in chemistry and material fields.

2 ANN solubility model

ANN is one of the most commonly employed methods in the nonlinear application field. It has excellent functions, such as nonlinear mapping, classification and recognition, optimization calculation, and data processing. The basic mathematical model can be expressed as follows:¹²

Y_i = f(U_i)

where X₁, X₂, …, and X_n are the model inputs; n is the number of input nodes; w_ij is the weight coefficient of the neuron and input node; θ_i is the threshold value of neuron i; Y_i is the output of neuron i; and f(U_i) is the network excitation function.

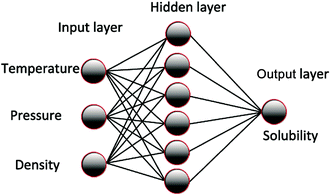
The ANN was trained according to the experimental data and optimized to obtain the parameter matrix in the network model. Thus, a mathematical model that reflects the inherent complex rules between the input and output of the experiment was developed. The basic structure of the model is shown in Fig. 1. The influence of system temperature, pressure, density, and other factors on solubility is generally analyzed according to the solubility of the supercritical carbon dioxide in polymer. The node number in the input layer is determined by the influence factors, such as temperature, pressure, and density. The output layer nodes are generally soluble, and the number of hidden layers and nodes is commonly determined by the empirical formula method or the heuristic method.

Fig. 1 Solubility prediction model based on ANN.

Many scholars have successfully applied ANN to correlate and predict solubility under supercritical conditions. Gharagheizi F. et al.¹³ utilized ANN to predict the solubility of solid complexes in supercritical carbon dioxide. Eslamimanesh A. et al.¹⁴ utilized ANN to predict solubility of supercritical carbon dioxide in ionic liquids, and showed the capability of the presented model. Modarress H. et al.¹⁵ also proposed a solubility prediction model with ANN, and showed that the presented model can predict the gas solubility satisfactorily. Khajeh A. et al.¹⁶ proposed the use of ANN to predict the solubility of carbon dioxide in polymers, and indicated that the presented model is an effective method. Bakhbakhi Y.¹⁷ and Lashkarbolooki M. et al.^18–22 compared the solubility prediction of ANN with several state equations Mehdizadeh B. et al.^23,24 compared the solubility predictions of ANNs and semi-empirical equations. Hussain M. A. et al.²⁵ utilized the Kent–Eisenberg model in conjunction with ANN to predict dissolution. Torrecilla J. S. et al.²⁶ proposed the solubility model based on multilayer ANN and mathematical regression methods. Their results show that the performance of ANN is suitable for correlating and predicting solubility, and showed that the ANN model is a superior technique with high accuracy.

The reliability and accuracy of ANN prediction are better than the traditional thermodynamics method. Researchers also reported that the performance of ANN relies heavily on its training algorithm, and the commonly utilized BP algorithm can easily fall into the local search and other deficiencies. Meanwhile, the center of the base function of the RBF ANN model and expansion constant and the network weights have a more significant impact on the model performance. Khajeh A. et al.²⁷ proposed the use of RBF ANN and the adaptive fuzzy neural system method to predict gas solubility in polymers and determined that the adaptive fuzzy neural system method has superior performance. Khayamian T. et al.²⁸ utilized wavelet ANN to establish the solubility model, which largely improved the performance. The training algorithm of the ANN model is currently attracting significant attention. Thus, many researchers have attempted to train ANN using the intelligent optimization method and have applied different chemicals and materials in different fields.

3 Hybrid ANN model

3.1 Hybrid ANNs based on some optimization algorithm

The ANN method overcomes the difficulties of modeling in traditional prediction, is easy to implement, and has attained remarkable results in terms of accuracy and efficiency. However, ANN still has shortcomings. The rapid development of computer science and the advanced computer technology for solubility studies can generate new ideas to address these limitations. The combination of ANN and optimization algorithms (or hybrid ANN) has been a popular research topic in recent years. Some commonly used hybrid ANNs are collected and shown in Table 1. The more discussions on the hybrid ANNs elaborate on the correlative references.

Table 1 Hybrid ANNs commonly used in recent years

Abbreviation	Hybrid method	Reference
SA-ANN	ANN trained by simulated annealing (SA)	29 and 30
GA-ANN	ANN with genetic algorithms (GA)	31–34
AC-A-RBF ANN	RBF ANN with an adaptive Ant Colony Algorithm (AC-A)	35 and 36
AC-AR-RBF ANN	Adaptive regulation (AR) ant colony algorithm and RBF ANN	37
ANFIS	Adaptive neuro-fuzzy inference system	38
SVM-ANN	Support vector machine algorithm and ANN	39–42
BA-MPL-ANN	ANN with Bees algorithm and multi-layer perceptron (MLP) method	43
MLR, MQR, MLP, RBF ANN	RBF ANN based on Multiple Linear Regression (MLR), Multiple Quadratic Regression (MQR), and Multi Layer Perceptron (MLP)	26
SVR-ANN CI-ANN	ANN based on Support Vector Regression (SVR), and generalized regression ANN based Computational Intelligent (CI)	44
RS–BP ANN	Rough sets and BP ANN	45
KE-ANN	The Kent–Eisenberg (KE) model in combination with ANN	25
BP-NL ANN	Back-propagation (BP) multi-layer (ML) ANN	46
WANN	Wavelet artificial neural network (WNN)	47 and 48
FANN	Fuzzy artificial neural network (FANN)	49–51
HSF-RBF ANN	Hybrid self-organizing fuzzy (HSF) and RBF ANN	52
ICO-VSA RBF ANN	RBF ANN with improved chaos optimization and variable-scale analysis	53

---

3.2 Hybrid ANNs based on particle swarm optimization algorithm

Particle swarm optimization (PSO) algorithm, which has a simple implementation and fewer parameters, is one of the most widely adopted intelligent algorithms.^54,55 The two main types of PSOs combined with ANN are as follows.⁵⁶ One type utilizes the PSO algorithm to optimize the weights of the ANN; the other embeds the ANN PSO optimization process. Lazzus J. A. et al.⁵⁷ utilized PSO to predict the phase equilibrium data of supercritical carbon dioxide and show that the PSO provides a good method to optimize the parameters with high accuracy. Ahmadi M. A. et al.⁵⁸ applied unified PSO to train the feed forward ANN, the results demonstrate the effectiveness of the proposed model. Zhang J. R. et al.⁵⁹ proposed the combination of PSO and BP algorithms, and their results show that their hybrid algorithm performs better than the single algorithm. Hybrid ANNs based on PSO algorithm are collected and shown in Table 2. The more discussions on the hybrid ANNs based on PSO elaborate on the correlative references.

Table 2 Hybrid ANNs based on PSO algorithms

Abbreviation	Hybrid method	Reference
UPSO-FFANN	Feed-forward artificial neural network (FFANN) optimized by unified particle swarm optimization (UPSO)	58
ADPSO-RBF ANN	Linearly decreased inertia weight particle swarm optimization (ADPSO) model for RBF ANN	60
PSO ANN	Artificial neural network trained by particle swarm optimization	61–63
BBPSO-AD RBF ANN	RBF ANN based on bare-bones particle swarm optimization (BBPSO) with an adaptive disturbance factor (AD)	64
GC-PSO ANN	Group Contribution (GC) plus ANN plus PSO	65
ALPSO-RBF ANN	RBF ANN with linearly decreased inertia weight (ALPSO)	60
PSO-FNN	Fuzzy artificial neural networks (FANN) with PSO algorithm	66 and 67
IOFC-PSO RBF ANN	RBF ANN using input–output fuzzy clustering (IOFC) and PSO	68
HPSO-GSA FFANN	FFANN using hybrid particle swarm optimization (HPSO) and gravitational search algorithm (GSA)	69

---

The PSO algorithm has several disadvantages, such as slow local search and premature convergence.⁷⁰ Our research group has discussed and developed some hybrid methods based on the chaos theory, the adaptive PSO algorithm, and the clustering method in recent years. We have also presented several solubility models based on hybrid ANNs. Table 3 shows these solubility models we proposed in the past few years.

Table 3 Solubility model of hybrid ANN based on improved PSO and several cluster methods

Abbreviation	Method description	Instance	Reference
CSAPSO-BP ANN	ANN trained by chaotic self-adaptive particle swarm optimization (CSAPSO) algorithm and back propagation (BP) algorithm	Solubility prediction of carbon dioxide (CO2) in polystyrene (PS), polypropylene (PP) and nitrogen (N2) in PS	71 and 72
CSAPSO-KCM RBF NN	RBF ANN trained by CSAPSO and k-means clustering method (KCM)	Solubility prediction of N2 in polystyrene (PS) and CO2 in PS, PP, poly(butylene succinate) (PBS), and poly(butylene succinate-co-adipate) (PBSA)	73
KCM-PSO FNN	Four-layer fuzzy neural network (FNN) model combining PSO algorithm and KCM	Solubility prediction of CO2 in PS, PP, and N2 in PS	74
CSAPSO-FCM RBF ANN	RBF ANN model based on CSAPSO and fuzzy c-means clustering method (FCM)	Solubility prediction of CO2 in PS, PP, PBS and PBSA	75
CSAPSO-KHM RBF ANN	RBF ANN model combined with CSAPSO algorithm and K-harmonic means clustering method (KHM)	Solubility prediction of supercritical carbon dioxide in 10 different polymers	76
CEAPSO KHM RBF ANN	RBF ANN trained by accelerated particle swarm optimization (APSO) algorithm with chaotic enhanced disturbance factor (CE) and KHM algorithm	Solubility prediction of CO2 in polymers including PP, PS, poly(vinyl acetate) (PVA), carboxylated polyesters (CPEs) and PBSA	77

---

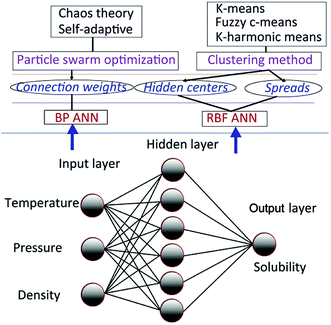
There are mainly two types of solubility prediction models based on PSO and ANN. First, BP ANN solubility prediction models based on PSO and its variant; second, RBF ANN models based on several clustering method, PSO and its variant. The improved PSO algorithm called CSAPSO was developed.

The improved PSO algorithm based on chaos theory and self-adaptive weight strategy was developed, called CSAPSO. And three clustering methods such as k-means clustering method (KCM), fuzzy c-means clustering method (FCM) and K-harmonic means clustering method (KHM) are used to model training. The first type of model called CSAPSO-BP ANN was proposed by training the BP ANN with CSAPSO algorithm. The second type of model, such as CSAPSO-KCM RBF ANN, CSAPSO-FCM RBF ANN and CSAPSO-KHM RBF ANN, were established by optimizing the RBF ANN parameters by combining the improved CSAPSO algorithm with clustering methods. The experimental results show the superiority of each model in predicting dissolution. The overall scheme of the said model is shown in Fig. 2.

Fig. 2 Hybrid ANN solubility model based on PSO.

The detailed model of the process and the detailed performance analysis and discussion of these models can serve as reference in the relevant literature.

4 Performance analysis of the hybrid ANN model

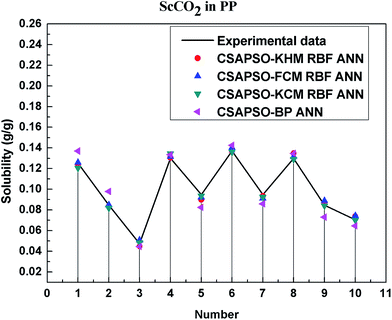
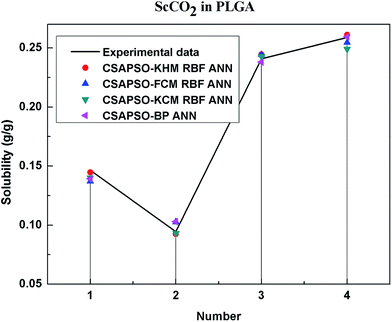
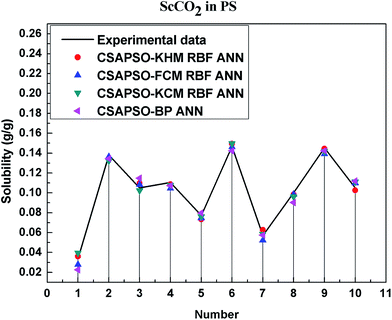
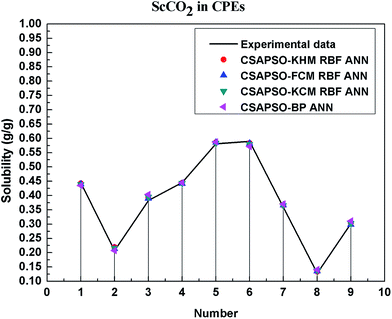
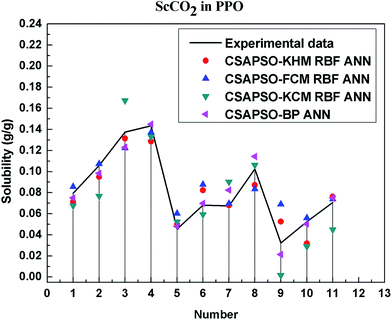
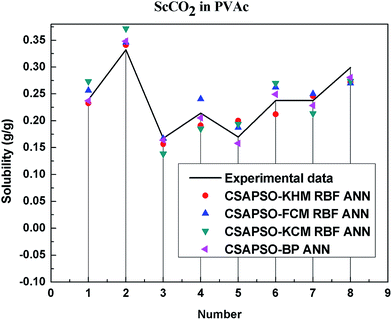
So as to compare and analyze the performance of the hybrid ANN model, four types of solubility prediction models, proposed by the members of our research group recent years, consisted of CSAPSO-BP ANN, CSAPSO-KCM RBF ANN, CSAPSO-FCM RBF ANN, and CSAPSO-KHM RBF ANN, are employed as comparative models. The more discussion on the hybrid ANNs model elaborate on the correlative references.^71–77 CSAPSO-KCM RBF ANN, CSAPSO-FCM RBF ANN and CSAPSO-KHM RBF ANN were referred to as CSAPSO-C RBF ANN. To verify the efficiency and validity, the experimental data commonly divides into two subsets, namely, training subset and non-training subset, according to the different polymers. In this review, the training subset consisted of 4 polymers such as polypropylene (PP), poly(D,L-lactide-co-glycolide) (PLGA), polystyrene (PS) and carboxylated polyesters (CPEs), respectively; and the non-training subset consisted of poly(2,6-dimethyl-1,4-phenylene ether) (PPO) and poly(vinyl acetate) (PVAc). Fig. 3–6 show the correlation between prediction and experimental values of the different comparative models in the training subset, and Fig. 7 and 8 show the correlation in the non-training subset.^71–77

Fig. 3 Prediction of ScCO₂ in PP (training subset).

Fig. 4 Prediction of ScCO₂ in PLGA (training subset).

Fig. 5 Prediction of ScCO₂ in PS (training subset).

Fig. 6 Prediction of ScCO₂ in CPEs (training subset).

Fig. 7 Prediction of ScCO₂ in PPO (non-training subset).

Fig. 8 Prediction of ScCO₂ in PVAc (non-training subset).

From the figures, we can summarize the following characteristics.

(1) The performances of the three models in the CSAPSO-C RBF ANN are the same.

The CSAPSO-KCM RBF ANN, CSAPSO-FCM RBF ANN, and CSAPSO-KHM RBF ANN models based on the CSAPSO and clustering methods are consistent in terms of prediction error and correlation. The accuracy and efficiency of the three models are basically the same. CSAPSO-KHM RBF ANN is slightly superior in terms of stability, and its prediction performance is suitable in most polymer systems. These can be attributed to the global search ability of the CSAPSO training algorithm and optimized model weight. The integration of each clustering method also makes the center of the basis function and expansion constant more reasonable, which eventually leads to the superior prediction performance of the model.

(2) The performance of the CSAPSO-C RBF ANN model is better than that of the training set.

Model training guarantees the performance, as shown in the training data. The model has suitable development and mining abilities. In particular, the model has a suitable prediction effect in the context of the experimental data and can be applied to predict new experimental data under the same experimental conditions.

(3) The CSAPSO-BP ANN model exhibits better stability in untested training experiments.

First, the CSAPSO and BP algorithms have a suitable ability to explore. The two algorithms also promote and complement each other in the exploration of the model and provide a solid theoretical basis. In particular, the exploration and development of this model are better. Here, pioneering performance refers to the absence of any target material under the premise of experimental data through other existing material prediction approaches of target substances.

(4) The predictive model has better performance, higher precision, and better correlation in the training set than in the non-trained set.

The essence of model prediction is the data fitting in mathematics, specifically by mining the inherent data law through known data and then predicting the fitting process of the new data. The data without training essentially have a similar principle (i.e., predicting new items through other similar data). The training set is clearly more theoretical than the unsupervised training set, and its comprehensive performance is better.

5 Model evaluation

The ANN model is generally developed in three steps: training, verification, and testing. The purpose of training is to explore the regularity between the input and output data and save them through network parameters. The purpose of verification is to fine-tune the trained network parameters and enhance the comprehensive performance and fault tolerance. Finally, the model is applied for practice. The main features of the ANN utilized in the solubility prediction are as follows:

(1) ANN avoids the problem of non-steady-state correction in the traditional thermodynamic solubility model.

The supercritical gas in the traditional thermodynamic solubility prediction model is regarded as a compressed gas or expanded liquid. The solubility problem is determined by calculating the mass and volume. Under low temperatures and pressures, the gas can be regarded as an ideal gas, and the results are more accurate. By contrast, high temperatures and pressures in supercritical conditions transform the system into a non-steady state, thus the gas cannot be regarded as an ideal gas.

(2) ANN has suitable prediction reliability under high temperatures and pressures.

ANN predicts solubility by modeling the nonlinear relationship between the model input and output. For the model parameters, the numerical value of the condition data is unrecognized, and the prediction reliability is also suitable even at high temperatures and pressures.

(3) The ANN model has suitable fault-tolerance and strong anti-interference ability.

ANN establishes a non-linear relationship according to the training data, and the accuracy of the training data directly affects the comprehensive effect. Training data are generally real experimental data. However, experimental operation errors and other reasons can make some of the training data false, which are then called invalid data. An error in the experimental record and writing a higher or lower number of data bits can cause individual data to become extremely abnormal, which are then called disturbing data. ANN can train the model with other data when it encounters invalid or disturbing data. This model can then determine this type of abnormal data during training. The ANN model can slowly address such abnormal data by training normal data to minimize their impact on the model and deal with them effectively. Hence, this model has better fault-tolerance and stronger anti-interference ability.

The main deficiencies of the ANN solubility model are as follows:

(1) Lacks a rational explanation of the dissolving machine.

The essence of ANN prediction is data fitting. The model is a function of the black box, which can obtain the output as long as the input is received. However, what is the mechanism by which the output is obtained? What is the law between the input and output? What is the relationship between the output and the impact of factors on the model that cannot be reflected? Although the predictive effect of the solubility model has an impeccable function, its solubility mechanism still needs to be comprehensively explained.

(2) The prediction performance depends on the experimental data.

The realization principle of the ANN model is to study and train the experimental data, as well as record the law between the input and output data by network weight. If no experimental data are available, then the model cannot work. Moreover, the model performance and experimental data quantity and accuracy are also highly relevant. The more experimental data available, the better the training model. Hence, the ANN is extremely dependent on the experimental data.

(3) Its prediction performance depends on its training algorithm.

Model training adjusts the model parameters. A suitable training algorithm has a decisive influence on the model performance. However, the training algorithm does not have a unified standard, and the algorithm for suitable performance is not necessarily applicable to all types of ANN training. The selection of a training algorithm, which is often through comparison or the test method, is relatively difficult. Thus, this process is more difficult for non-computer professionals to grasp.

6 Prospects

Computer simulations have replaced experiments in laboratories to a certain extent. The significance of this is undeniable. Approximately 100 types of calculation models exist for two-phase or multi-phase systems. The performance of each prediction model is slightly different. However, none can be properly applied to all engineering analyses of the forecast. The advantages and disadvantages of the prediction model and the calculation accuracy are critical in the actual selection of a forecasting model according to the system and model characteristics.

The combination of hybrid ANN technology and chemical engineering can be further developed and has a broad application prospects. Given the solubility prediction of supercritical carbon dioxide in polymers, the following aspects can be discussed intensively.

(1) Study on the solubility mechanism.

The actual process parameters of the solubility prediction model can be studied by combining with the actual industrial production processes and conditions, such as adsorption, diffusion, and interface renewal theory. The model can determine the law and mechanism of solubility in industrial production and provide theoretical guidance for the selection of process parameters.

(2) Explore the solubility of new ideas.

The most considered factors in current solubility studies are system temperature and pressure, and the solubility model of many influencing factors can reflect the real implementation rules better, which can improve model adaptability. Solubility prediction based on hybrid ANN technology, such as combining with diffusion theory and synergy theory, must also be studied further. Hybrid ANN methods can be adopted to solve different nonlinear problems in chemistry, material science, biology, and medicine.

(3) Study the solubility method of multi-scale calculation.

Multi-scale studies from different times and spatial scales can be referenced to study the physical and chemical properties of materials. Multi-scale solubility studies can also be utilized to analyze the solubility problems of different substances at the microscopic, mesoscopic, and macroscopic levels. For example, the ANN model can provide scientific and theoretical guidance for the selection of process parameters at the multi-scale level in the field of materials processing. It also has suitable application prospects in polymer self-assembly, phase rheological properties, and kinetic analysis. The multi-scale computation method has important interdisciplinary, cross-level, and time-span research values. The multi-scale calculation method will be discussed in future studies and applied to chemical, material, and other related computing fields.

Nomenclature

ANN	Artificial neural network
BP	Back propagation
RBF	Radial basis function
PSO	Particle swarm optimization
CSAPSO	Chaotic self-adaptive particle swarm optimization
SA	Simulated annealing
GA	Genetic algorithms
ACO	Ant colony optimization
BA	Bees algorithm
SVM	Support vector machine
KCM	k-Means clustering method
FCM	Fuzzy c-means clustering method
KHM	K-Harmonic means clustering method
PBS	Poly(butylene succinate)
PBSA	Poly(butylene succinate-co-adipate)
PP	Polypropylene
PS	Polystyrene
PLLA	Poly(L-lactide)
PLGA	Poly(D,L-lactide-co-glycolide)
HDPE	High-density polyethylene
PVAc	Poly(vinyl acetate)
PPO	Poly(2,6-dimethyl-1,4-phenylene ether)
CPEs	Carboxylated polyesters
ANFIS	Adaptive neuro-fuzzy inference system

Acknowledgements

The authors gratefully acknowledge the support from the National Natural Science Foundation of China (Grant Numbers: 51663001, 51463015, 51377025) and the science and technology research project of the education department of Jiangxi province (Grant Numbers: GJJ151012, GJJ150983).

Notes and references

1. S. Lee, H. Jeon, M. Jang, K. Y. Baek and H. Yang, ACS Appl. Mater. Interfaces, 2015, 7, 1290–1297.
2. E. Girard, T. Tassaing, C. Ladaviere, J. D. Marty and M. Destarac, Macromolecules, 2012, 45, 9674–9681.
3. D. Karandur, K. Y. Wong and B. M. Pettitt, J. Phys. Chem. B, 2014, 118, 9565–9572.
4. Y. S. Zhao, J. B. Gao, Y. Huang, R. M. Afzal, X. P. Zhang and S. J. Zhang, RSC Adv., 2016, 6, 70405–70413.
5. M. Minelli and F. Doghieri, Fluid Phase Equilib., 2014, 381, 1–11.
6. E. B. de Melo, J. P. A. Martins, E. H. Miranda and M. M. C. Ferreira, J. Hazard. Mater., 2016, 304, 233–241.
7. P. P. Sun, X. Y. Liu, L. Sun, S. Zhang, Q. Wei, Y. Yin, Q. Yang and S. P. Chen, Acta Phys.-Chim. Sin., 2015, 31, 211–220.
8. C. Loschen and A. Klamt, Ind. Eng. Chem. Res., 2014, 53, 11478–11487.
9. Y. A. Nizhegorodova, N. A. Belov, V. G. Berezkin and Y. P. Yampol'skii, Russ. J. Phys. Chem. A, 2015, 89, 502–509.
10. B. Vaferi, M. Karimi, M. Azizi and H. Esmaeili, J. Supercrit. Fluids, 2013, 77, 44–51.
11. M. Safamirzaei and H. Modarress, Thermochim. Acta, 2012, 545, 125–130.
12. F. Valdez, P. Melin and O. Castillo, Inf. Sci., 2014, 270, 143–153.
13. F. Gharagheizi, A. Eslamimanesh, A. H. Mohammadi and D. Richon, Ind. Eng. Chem. Res., 2011, 50, 221–226.
14. A. Eslamimanesh, F. Gharagheizi, A. H. Mohammadi and D. Richon, Chem. Eng. Sci., 2011, 66, 3039–3044.
15. H. Modarress, M. Mohsen-Nia and M. Safamirzaei, Iran. Polym. J., 2008, 17, 483–491.
16. A. Khajeh, H. Modarress and B. Rezaee, Expert Syst. Appl., 2009, 36, 5728–5732.
17. Y. Bakhbakhi, Expert Syst. Appl., 2011, 38, 11355–11362.
18. M. Lashkarbolooki, B. Vaferi and M. R. Rahimpour, Fluid Phase Equilib., 2011, 308, 35–43.
19. M. Lashkarbolooki, A. Z. Hezave and S. Ayatollahi, Fluid Phase Equilib., 2012, 324, 102–107.
20. A. Z. Hezave, M. Lashkarbolooki and S. Raeissi, Fluid Phase Equilib., 2012, 314, 128–133.
21. A. Z. Hezave, S. Raeissi and M. Lashkarbolooki, Ind. Eng. Chem. Res., 2012, 51, 9886–9893.
22. M. A. Sabegh, H. Rajaei, F. Esmaeilzadeh and M. Lashkarbolooki, J. Supercrit. Fluids, 2012, 72, 191–197.
23. B. Mehdizadeh and K. Movagharnejad, Fluid Phase Equilib., 2011, 303, 40–44.
24. B. Mehdizadeh and K. Movagharnejad, Chem. Eng. Res. Des., 2011, 89, 2420–2427.
25. M. A. Hussain, M. K. Aroua, C. Y. Yin, R. A. Rahman and N. A. Ramli, Korean J. Chem. Eng., 2010, 27, 1864–1867.
26. J. S. Torrecilla, J. Palomar, J. Garcia, E. Rojo and F. Rodriguez, Chemom. Intell. Lab. Syst., 2008, 93, 149–159.
27. A. Khajeh and H. Modarress, Expert Syst. Appl., 2010, 37, 3070–3074.
28. T. Khayamian and M. Esteki, J. Supercrit. Fluids, 2004, 32, 73–78.
29. B. Abbasi and H. Mahlooji, Expert Syst. Appl., 2012, 39, 3461–3468.
30. W. Shao and Y. J. Zuo, Comput. Stat. Data Anal., 2012, 56, 4026–4036.
31. B. Kim, D. Kim, S. W. Baik, S. B. Lee and D. H. Kim, Mater. Manuf. Processes, 2011, 26, 382–387.
32. C. C. Huang and T. T. Tang, J. Appl. Polym. Sci., 2006, 100, 2532–2541.
33. S. Oreski, D. Oreski and G. Oreski, Expert Syst. Appl., 2012, 39, 12605–12617.
34. M. Vadood, D. Semnani and M. Morshed, J. Appl. Polym. Sci., 2011, 120, 735–744.
35. J. B. Li and X. G. Liu, J. Appl. Polym. Sci., 2011, 119, 3093–3100.
36. J. B. Li, X. G. Liu, H. Q. Jiang and Y. D. Xiao, J. Appl. Polym. Sci., 2012, 125, 943–951.
37. B. A. I. Jizhong, S. H. I. Biao, F. Minquan, Z. Likun and L. I. Xiaolong, Journal of Hydroelectric Engineering, 2011, 30, 50–56.
38. H. Fazilat, M. Ghatarband, S. Mazinani, Z. A. Asadi, M. E. Shiri and M. R. Kalaee, Comput. Mater. Sci., 2012, 58, 31–37.
39. H. Ziaee, S. M. Hosseini, A. Sharafpoor, M. Fazavi, M. M. Ghiasi and A. Bahadori, J. Taiwan Inst. Chem. Eng., 2015, 46, 205–213.
40. S. Kang and S. Cho, Expert Syst. Appl., 2014, 41, 4989–4995.
41. H.-Y. Fu, H.-L. Wu, H.-Y. Zou, L.-J. Tang, L. Xu, C.-B. Cai, J.-F. Nie and R.-Q. Yu, Anal. Methods, 2010, 2, 282–288.
42. Danishuddin and A. U. Khan, Drug Discovery Today, 2016, 21, 1291–1302.
43. A. E. Shrme, Expert Syst. Appl., 2011, 38, 6000–6006.
44. A. Majid, A. Khan, G. Javed and A. M. Mirza, Comput. Mater. Sci., 2010, 50, 363–372.
45. T. Yun and L. U. O. Junsong, Computer Simulation, 2011, 28, 219–222.
46. Y. Bakhbakhi, Math. Comput. Model., 2012, 55, 1932–1941.
47. R. Tabaraki, T. Khayamian and A. A. Ensafi, Dyes Pigm., 2007, 73, 230–238.
48. R. Tabaraki, T. Khayamian and A. A. Ensafi, J. Mol. Graphics Modell., 2006, 25, 46–54.
49. B. Subathra and T. K. Radhakrishnan, Instrum. Sci. Technol., 2012, 40, 29–50.
50. S. Aydin, Expert Syst. Appl., 2010, 37, 7819–7824.
51. V. Arcotumapathy, A. Siahvashi and A. A. Adesina, AIChE J., 2012, 58, 2412–2427.
52. L. Jeen and L. Ruey-Jing, Int. J. Innov. Comput. I., 2011, 7, 3359–3378.
53. M. Huang, X. Liu and J. Li, J. Appl. Polym. Sci., 2012, 126, 519–526.
54. H. Wang, H. Sun, C. H. Li, S. Rahnamayan and J. S. Pan, Inf. Sci., 2013, 223, 119–135.
55. Y. Wang, J. J. Huang, N. Zhou, D. S. Cao, J. Dong and H. X. Li, J. Chemom., 2015, 29, 627–636.
56. J. J. Xing, R. M. Luo, H. L. Guo, Y. Q. Li, H. Y. Fu, T. M. Yang and Y. P. Zhou, Chemom. Intell. Lab. Syst., 2014, 130, 37–44.
57. J. A. Lazzus, A. Ponce and L. Chilla, Fluid Phase Equilib., 2012, 317, 132–139.
58. M. A. Ahmadi, Fluid Phase Equilib., 2012, 314, 46–51.
59. J. R. Zhang, J. Zhang, T. M. Lok and M. R. Lyu, Appl. Math. Comput., 2007, 185, 1026–1037.
60. S. Leung, Y. Tang and W. K. Wong, Expert Syst. Appl., 2012, 39, 395–405.
61. G. Das, P. K. Pattnaik and S. K. Padhy, Expert Syst. Appl., 2014, 41, 3491–3496.
62. J. A. Lazzus, Thermochim. Acta, 2011, 512, 150–156.
63. J. A. Lazzus, Math. Comput. Model., 2013, 57, 2408–2418.
64. R. Xia, X. Huang and M. Li, J. Appl. Polym. Sci., 2016, 133, APP.44252.
65. J. A. Lazzus, Ind. Eng. Chem. Res., 2009, 48, 8760–8766.
66. X. G. Liu and C. Y. Zhao, AIChE J., 2012, 58, 1194–1202.
67. J. A. Lazzus, Int. J. Thermophys., 2011, 32, 957–973.
68. G. E. Tsekouras and J. Tsimikas, Fuzzy Set. Syst., 2013, 221, 65–89.
69. S. Mirjalili, S. Z. M. Hashim and H. M. Sardroudi, Appl. Math. Comput., 2012, 218, 11125–11137.
70. A. Alexandridis, E. Chondrodima and H. Sarimveis, IEEE Trans. Neural Netw. Learn. Syst., 2013, 24, 219–230.
71. M. S. Li, X. Y. Huang, H. S. Liu, B. X. Liu, Y. Wu, A. H. Xiong and T. W. Dong, Fluid Phase Equilib., 2013, 356, 11–17.
72. M. S. Li, X. Y. Huang, H. S. Liu, B. X. Liu, Y. Wu and F. R. Ai, Acta Chim. Sin., 2013, 71, 1053–1058.
73. M. S. Li, X. Y. Huang, H. S. Liu, B. X. Liu and Y. Wu, J. Appl. Polym. Sci., 2013, 130, 3825–3832.
74. M. S. Li, X. Y. Huang, H. S. Liu, B. X. Liu, Y. Wu and X. Z. Deng, J. Appl. Polym. Sci., 2013, 129, 3297–3303.
75. Y. Wu, B. X. Liu, M. S. Li, K. Z. Tang and Y. B. Wu, Chin. J. Chem., 2013, 31, 1564–1572.
76. M. Li, X. Huang, H. Liu, B. Liu, Y. Wu and L. Wang, RSC Adv., 2015, 5, 45520–45527.
77. X. Ru-Ting and H. Xing-Yuan, RSC Adv., 2015, 5, 76979–76986.

---