Effect of pressure on two polymorphs of tolazamide: why no interconversion?

Abstract

Two polymorphs of tolazamide, N-[(azepan-1-ylamino)carbonyl]-4-methylbenzenesulfonamide, a sulfonylurea anti-diabetic drug, have different densities and molecular packings. Polymorph II converts into polymorph I in the solid state on heating or via recrystallization if solvent-assisted. The effect of pressure on the two forms and the possibility of a transformation to a denser form on compression have been studied. No phase transitions have been observed in either of the forms in a pentane–isopentane mixture (when no recrystallization is possible). Polymorph II recrystallized partly into a denser polymorph I in methanol at 0.1 GPa, but the transformation stopped at an early stage. Solid state DFT calculations of the two forms as well as conformational landscape investigation in the gas phase were used to rationalize this result. The anisotropic pressure-induced strain of the two polymorphs has been compared in relation to changes in the hydrogen bond geometry and the behavior of stacking interactions.

---

Introduction

The same molecules can form different periodic structures – polymorphs – depending on the crystallization conditions. Control of polymorphism is one of the major challenges in crystal engineering.¹ At any given temperature and pressure, only one polymorph is thermodynamically stable. However, it is not always this stable polymorph that is actually formed under certain conditions. Other polymorphs can crystallize as well instead of the stable form, or concomitantly with it due to the kinetic control of nucleation and nuclei growth.² When a crystal of a selected polymorph is cooled, heated or compressed, its structure can be changed as a result of a polymorphic transformation, yielding a more stable polymorph than the original one under the new (P, T) conditions. However, this new form is not necessarily the most thermodynamically stable polymorph under these conditions. Different polymorphs can be formed, depending on the starting structure,^3–7 compression–decompression protocol,^8–12 in particular the rate of pressure increase,^12–15 the presence of nuclei of other phases,¹⁶ or the nature of the pressure-transmitting fluid.^10,17–22 Some polymorphic transformations are purely solid-state, whereas others are solvent-assisted and are related to complete or partial recrystallization.^16,21–25 It is also not uncommon that a polymorph does not undergo any transformations on variation of (P, T) conditions, even if it becomes thermodynamically unstable.^26–28 This is often due to kinetic restrictions on nucleation and/or nuclei growth of a new phase. Whilst researchers today are coming close to predicting the stable structure of a given compound, they still cannot answer why some compounds are polymorphic, or which of the predicted forms can be realized experimentally, and how.²⁹ Studying the effect of pressure on polymorphism is very helpful in order to gain better insight into the various factors that control the formation of organic crystal structures and their transformations. Such information will ultimately allow better prediction of solid-form landscapes and polymorphism.^30–34

Tolazamide, N-[(azepan-1-ylamino)carbonyl]-4-methylbenzenesulfonamide (Fig. 1), is an oral blood glucose lowering drug of the sulfonylurea class. Recently it has been shown to have polymorphs with significantly different molecular packings.³⁵ The crystallization of its polymorphs provides an example of kinetic control, based on the rates of the nucleation and nuclei growth. When crystallized from solution at ambient pressure, the nuclei of the two polymorphs, I and II, seem to be formed almost simultaneously, then the crystals of form II grow much faster than those of form I. However, if the crystals of polymorph II are stored in solution, they eventually recrystallize into polymorph I. The irreversible II to I transformation has also been detected in the solid state by single-crystal and powder X-ray diffraction and thermomicroscopy upon heating. This suggested that polymorph I must be the stable form both at ambient temperature and on heating up to the melting point. However, DSC revealed no thermal effects corresponding to this transition, so the polymorphs have been classified as isoenergetic,‡ using the terminology from ref. 36 and 37. Different intermolecular interactions were investigated to explain the absence of noticeable thermal effects of transition between the two polymorphs with different molecular packings at ambient pressure.³⁵

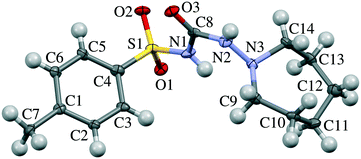Fig. 1 Molecular structure of tolazamide. Atom numbering corresponds to that in Table S7 and Fig. 7, S3–S7.†

The aim of this study was to monitor the effect of increasing pressure on polymorphs I and II experimentally, in order to verify the possibility of polymorphic transformation, and computationally, to rationalize experimental results and reveal trends in the crystal structures of the polymorphs at pressures higher than those achieved in experiments. The choice of pressure-transmitting fluid can have a great influence on a phase transition.^10,17–22 Therefore, in the experiments described in this work the samples of tolazamide were compressed for comparison in two types of hydrostatic fluids: a) one that can dissolve tolazamide, so that a solvent-assisted transformation and recrystallization were possible (methanol), and b) a fluid in which tolazamide is not soluble (an equimolar pentane–isopentane mixture).

We were also interested in comparing the compressibility of the two polymorphs and the anisotropy of their strain. This was done so as to investigate the effect of pressure on intermolecular interactions, in particular, hydrogen bonds and stacking contacts. In-depth analysis of molecular conformations in the two polymorphs and conformational disorder in both structures under pressure has been carried out using both experimental and computational techniques. Molecular modeling included solid state quantum calculations of the energies and enthalpies of the two crystalline forms across a wide pressure range, seeking an answer as to which of the forms can be expected to be the most thermodynamically stable at high pressure. Thus, rationalization of any phase transition was sought.

Experimental

Materials

A commercial sample of tolazamide was purchased from Sigma-Aldrich and contained tolazamide form I (pur. ≥98%). This was confirmed by single-crystal and powder X-ray diffraction. All fluids used in this work for polymorph crystallization and high-pressure experiments (1,4-dioxane, pentane, isopentane, methanol) were used without additional purification or drying.

Crystallization

The crystals of the two tolazamide polymorphs were grown from a hot (65 °C) 1,4-dioxane solution as described in ref. 35. Crystallization conditions differed only in the concentration of solutions which was 20 g L⁻¹ for obtaining form I and 50 g L⁻¹ for form II growth. The crystals were used for high-pressure and low-temperature experiments as well as for recrystallization from a saturated tolazamide solution in methanol.

High-pressure experiments

Hydrostatic pressure was generated using a Boehler-Almax diamond anvil cell (DAC).³⁸ A stainless steel gasket with an initial thickness of 200 μm was pre-indented to 100 μm. A hole of 300 μm in diameter was drilled in the gasket using the spark erosion technique. The ruby fluorescence line was used for pressure calibration with an accuracy of ±0.05 GPa.^39,40 As the choice of pressure-transmitting fluid can affect phase transitions,^10,17–22 two different fluids were used as hydrostatic media: a tolazamide saturated solution in methanol (this medium allows recrystallization of tolazamide and, therefore, solvent-assisted transformation is possible) and an equimolar pentane–isopentane mixture (in this medium tolazamide is not soluble).⁴¹

Single-crystal X-ray diffraction

Diffraction data were collected from ambient pressure up to 6.1 GPa for tolazamide-I and up to 6.8 GPa for tolazamide-II using an Oxford Diffraction Gemini R Ultra X-ray diffractometer with Mo-Kα radiation and a CCD 2D detector. The typical duration of data collection was 36 hours for both polymorphs of tolazamide. Data collection, cell determination and data integration were performed using the CrysAlisPro software.⁴² Sample reflections overlapping with the diamond and gasket reflections were manually excluded. Gaussian absorption correction was performed using Absorb-7 with Absorb-GUI.⁴³

The initial crystal structure models for structure refinement were taken from the ambient pressure data.³⁵ Refinement was carried out with SHELXL2014 (ref. 44) with X-Step 32 as the GUI.⁴⁵ Hydrogen atom parameters were constrained using a riding model with the AFIX 137 instruction for H-atoms in CH₃-groups with U_iso(H) = 1.5U_eq(C), the AFIX 23 instruction for H-atoms involved in CH₂-groups with U_iso(H) = 1.2U_eq(C) and the AFIX 43 instruction for other H-atoms with U_iso(H) = 1.2U_eq(C). Atomic parameters for non-hydrogen atoms were refined anisotropically for all pressure points excluding polymorph II at 6.8 GPa (the last pressure point achieved in experiments), which was refined in isotropic approximation. To make anisotropic refinement reasonable, SIMU, DELU and SADI restraints were also used. Deformations along the strain ellipsoid principal axes were calculated using WinStrain.⁴⁶ Mercury,⁴⁷ Platon^48,49 and enCIFer⁵⁰ were used for structure visualization, analysis and preparation of the CIF for publication. Complete structural data were deposited in the Cambridge Structural Database⁵¹ (CCDC numbers are 1495203–1495210 for polymorph I and 1493069–1493078 for polymorph II).

Optical microscopy

The behavior of the tolazamide form II crystal in methanol under pressure was monitored using a Nikon AZ100 optical microscope. At first the pressure value was set at 0.1 GPa, and then it was increased at ∼1 GPa steps up to 6 GPa. The sample was kept at each pressure point from 6 to 12 hours.

Computational techniques

Gas phase calculations were carried out using the Gaussian 09 program.⁵² The M062X functional with the 6-311++g(d,p) basis set was used for optimizing the geometry of the tolazamide molecule in relation to five dihedral angles (C3–C4–S1–N1, C4–S1–N1–C8, S1–N1–C8–N2, N1–C8–N2–N3 and C8–N2–N3–C9, numeration according to Fig. 1) in a 5 degree step. The molecular geometry of the tolazamide-I structure at ambient pressure was taken as the starting geometry for gas phase optimization. Pair-wise interactions in form I were calculated using the abovementioned level of theory, providing full optimization for both molecules, and taking into account basis set superposition error (BSSE) correction as implemented in Gaussian 09. The starting guess for optimization was taken from X-ray data at the corresponding pressure.

All periodic DFT calculations were performed using the Vienna ab initio simulation package (VASP)^53–56 using the functional of Perdew, Burke and Ernzerhof (PBE),⁵⁷ a plane-wave basis set with a kinetic energy cutoff of 500 eV and projector augmented wave (PAW)^58,59 atomic pseudopotentials. The integrals in reciprocal space were calculated on a k-point Monkhorst-Pack mesh of 6 × 4 × 4.⁶⁰ Alongside the uncorrected functional, different dispersion correction schemes were tested for accuracy, including Grimme's D2,⁶¹ D3 (ref. 62) and D3-Becke–Johnson^63–65 methods, of which the latter yields the best match with the experimental structures and was selected for further treatment (see the “Computational details” section in the ESI†). The unit cell parameters, energies and enthalpies of the tolazamide polymorphs were calculated at multiple pressure points in the range between ambient pressure and 20 GPa. The effect of external pressure was enforced by the stress tensor (PSTRESS keyword) as implemented in the VASP package. The models for all calculations were built on the basis of the experimental single-crystal X-ray diffraction data collected at ambient pressure.³⁵ The CIF2Cell script was used to convert the CIF structure files into VASP input files.⁶⁶ For each considered model (forms I and II at various external pressure values) geometry optimization was performed. Optimization included relaxation of both atomic positions and unit cell parameters (ISIF = 3). Optimization was followed by calculation of harmonic frequencies using the finite difference method, facilitating determination of the vibrational zero point energy (ZPE) term.

Experimentally and computationally obtained pressure dependencies of unit cell volumes of the polymorphs were fitted by the EoSFit7-GUI program.^67,68 Standard deviations of the volumes and pressures were taken into account.

Results and discussion

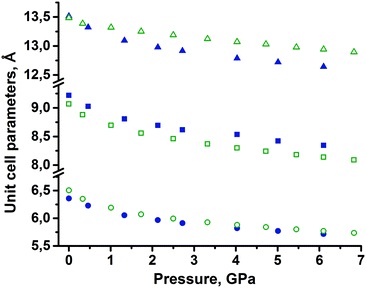
None of the two polymorphs of tolazamide showed any evidence of polymorphic transformations on compression in the pentane–isopentane mixture, in which tolazamide is not soluble. Crystal data, data collection and refinement for the two polymorphs at different pressures are summarized in the ESI† (Tables S1 and S2). Across the entire studied pressure range, the X-ray measured density of polymorph I remained slightly higher than that of polymorph II. The changes in unit cell parameters a, b, c and volume with pressure were monotonic (Fig. 2, deposited CIFs, and Tables S1 and S2 in the ESI†).

Fig. 2 Experimental unit cell parameters of tolazamide polymorphs at different pressures (a – circles, b – squares, c – triangles). Full blue symbols correspond to form I and green open ones to form II. Standard deviations are less than the symbol size.

The pressure dependencies of the unit cell volumes of both polymorphs were fitted by the third-order Tait equation of state with different V_o, a, b, c coefficients:⁶⁹

V = V_o{1 − a [1 − (1 − bP)^−c]},

where V_o is the unit cell volume at P = 0, the parameters a, b, c are related to the bulk modulus K_0,T = −V(∂P/∂V)_T and its derivatives at ambient pressure as shown in ref. 70. The fitted parameters are summarized in Table S3 in the ESI.† The bulk modulus at 293 K was defined for both polymorphs: it is equal to 6.4(3) GPa for form I and 5.8(2) GPa for form II.

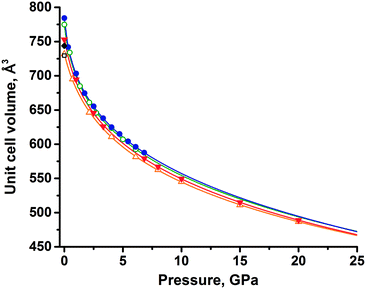
An extrapolation of experimental data using the equation of state showed that the unit cell volumes of the two forms (assuming that these forms still exist at pressures above 6 GPa) remain close up to 25 GPa (Fig. 3), with the difference between thezm decreasing with increasing pressure (Table S4†). Eventually, the functions describing the volume change under pressure have an intersection at 23 GPa, where polymorph II would become denser, if no phase transitions and amorphization occur at pressures higher than those achieved in experiments. Analyzing the equations of state for both polymorphs, one could find that the volume of polymorph II decreases faster than that of polymorph I on compression, considering the available experimental data. This agrees well with the lower value of the bulk modulus of form II than that of form I.

Fig. 3 Unit cell volumes of tolazamide polymorphs at different pressures: green open circles (form I) and full blue circles (form II) – data obtained experimentally; orange open triangles (form I) and full red triangles (form II) – data obtained computationally at T = 0 K, assuming that the same phases still exist at these extremely low temperature and pressures above 7 GPa; gray open square (form I) and full gray diamond (form II) – results of extrapolating the V(T) functions to 0 K at ambient pressure.

Convergence and intersection of the V(P) curves with increasing pressure (predicted by extrapolating the experimental data) were also well reproduced by the periodic DFT calculations (Table S4†). The unit cell volumes of both polymorphs were calculated at several pressure points. The data were fitted by the aforementioned Tait equations of state and extrapolated up to 25 GPa, similar to what has been done for the experimental data. Extrapolation of both experimental and calculated volumes shows an intersection near the upper pressure limit (20–25 GPa), but the decrease of volume difference between phases is very slow (Fig. 3), hence the estimate of the intersection is tentative. In terms of the extrapolated V(P) curves derived from the equation of state, the agreement between the experiment and calculations is good, suggesting that only at pressures beyond 20 GPa may polymorph II become favorable. However, rather than relying on thermodynamic quantities, this assumption relies solely on the density criterion.

Despite the good agreement between experimental and calculated data, the information derived from the equation of state should be considered with care, due to the limitations of experimental data and computational techniques, which cannot predict phase transitions or amorphization of materials.⁷¹ Nevertheless, both experimental and computational approaches showed the same trends for the behavior of polymorphs, proving form I to be denser at all pressures discussed in this work.

Not only did the crystals of polymorph I not transform into polymorph II with increasing pressure, but the crystals of polymorph II also did not transform into the denser polymorph I when immersed in a non-dissolving fluid, i.e. in the solid state. A similar behavior when pressure does not induce the solid-state transition into a denser polymorph was observed for imidazole,⁷² benzene,^73,74 and 4,4′-bipyridine hydrobromide monohydrate.^75,76 Two possible reasons could explain why these solid-state phase transitions do not occur:

1) the polymorphs remain approximately equal in free energies across the entire studied pressure range, such that there is no thermodynamic driving force for a polymorphic transformation in either direction;

2) one of the polymorphs (for tolazamide it is presumably polymorph II, which recrystallizes into polymorph I when stored in solution at ambient pressure) is less thermodynamically stable, but a solid-state transformation is kinetically hindered. In this case the more stable phase cannot form due to a high nucleation barrier or slow nuclei growth.

Such examples, when a stable high-pressure phase cannot be obtained on compression via a solid-state transformation, but is formed via recrystallization, often on decompression from a higher pressure, have been documented for other compounds: paracetamol,^8,26,77 β-alanine,¹⁰ imidazole,⁷² 4,4′-bipyridine hydrobromide monohydrate,⁷⁵ 3-hydroxy-4,5-dimethyl-1-phenylpyridazin-6-one,²⁷ and bromochlorofluoroacetic acid.⁷⁸ In the latter case, in particular, the preference for dimeric over catemeric polymorphs was impossible to detect without completely dissolving or melting the compound. Also for 3-hydroxy-4,5-dimethyl-1-phenylpyridazin-6-one, though high pressure destabilizes the high Z′ polymorph, recrystallization is needed for obtaining a low Z′, denser polymorph.²⁷

To verify the first hypothesis, DFT calculations were performed for the two polymorphs across a range of pressures from the ambient pressure point up to 20 GPa. Polymorph I was found to have lower values of internal crystal energy and enthalpy at all simulated pressures, with an estimate of the enthalpy difference between the two phases of 6.1 kJ mol⁻¹ at ambient pressure and 96.8 kJ mol⁻¹ at 20 GPa (Fig. S1 and Table S5†). Interestingly, both internal energy and PV term differences increase with pressure, and the difference in the internal energy increases with pressure at an about two to three times higher rate than the PV term. Thus, the internal energy contribution appears to be dominant in the computed enthalpy difference between polymorphs. The internal energy of form II is higher at ambient pressure and continues to increase faster than the internal energy of form I with pressure (Fig. S1b and Table S5†). Thus, multiplication of the quickly growing pressure and slowly decreasing volume difference gives a positive PV term difference for the entire pressure range from ambient to 20 GPa (Fig. S1c and Table S5†). Noteworthily, the zero-point energy (ZPE) contribution to the difference between the enthalpies of the polymorphs does not exceed 4 kJ mol⁻¹ and does not affect the result.

The calculated enthalpy difference between the polymorphs is larger than could be expected from the DSC experiment, in which no thermal event could be observed corresponding to the polymorphic II to I phase transition (i.e. the heat effect of the transformation was below the detection limit of a DSC instrument).³⁵ On the one hand, this discrepancy between the experiment and the calculations can reflect the general problem with calculations in ranking the energies of molecular organic polymorphs,⁷⁹ especially if entropic terms are neglected.^80–82 On the other hand, we cannot fully exclude the possibility that no phase transition took place when a powder sample was put into a calorimeter in the experiments described in ref. 35, even though the transition has been reliably detected both in powder samples and in single crystals by X-ray powder diffraction and thermomicroscopy. Examples when phase transitions have been observed in single crystals, but not in powders have been documented,⁸³ as well as examples when phase transitions in powder samples strongly depended on how long a sample is kept at a certain temperature or whether it was heated in a sealed or open capillary, etc.⁸⁴ In all of these examples, the DSC and X-ray powder diffraction experiments could give different results. An additional experiment with simultaneous DSC and X-ray powder diffraction measurements is needed to shed more light on the problem. Finally, tolazamide polymorph I could be truly energetically more favorable than form II, which can be proved by II → I recrystallization in solution.³⁵ It is also important to understand that DSC measurements of phase transition were performed at high temperatures, where the enthalpy difference can be noticeably less than that at ambient temperature or at 0 K.

Regardless of the above discussed possible limitations of the employed theoretical model, in the context of this work it is important that the calculations confirm that polymorph I remains the more stable form across the entire studied pressure range. This means that no transformation of polymorph I into polymorph II should be expected, but that form II could in fact transform into form I, if the transformation was not kinetically hindered. To facilitate this potential transformation, we have studied the effect of pressure on a tolazamide-II single crystal loaded into a DAC with a saturated solution of tolazamide in methanol as a pressure-transmitting fluid. In this case, polymorph II recrystallized partly into a denser polymorph I at 0.1 GPa, but the transformation stopped at an early stage (Fig. 4). At ambient pressure polymorph II recrystallized from the tolazamide saturated solution in methanol into polymorph I completely. One can see that the solubility of tolazamide in methanol decreases with pressure since crystal edges became sharper (see Fig. 4), and therefore the completeness of the transformation is still limited by the low solubility of tolazamide in this medium at high pressure.

Fig. 4 Crystal of tolazamide form II loaded into a DAC with a saturated solution of tolazamide in methanol. The growth of new rectangular-shaped crystals (form I) at 0.1 GPa is clearly seen. The absence of any significant changes in the DAC between 0.1 and 6.1 GPa is also observed.

A similar behavior where recrystallization facilitates the transition into a more stable form under pressure was previously monitored for other organic compounds: bromochlorofluoroacetic acid,⁷⁸ 3-hydroxy-4,5-dimethyl-1-phenylpyridazin-6-one,²⁷ imidazole,⁷² and 4,4′-bipyridine hydrobromide monohydrate.⁷⁵ In the latter two cases, high-pressure phases could be obtained only through recrystallization by heating and further slow cooling at definite pressure points. These phases did not form on isothermal compression and transformed spontaneously into other forms on releasing pressure, so they were called hidden polymorphs.^72,75

The fact that the two polymorphs of tolazamide do not transform into each other with increasing pressure made it possible to compare the pressure-induced strain across a wide pressure range in relation to different molecular packings. Despite the close similarity of V(P) functions for the two polymorphs, the anisotropy of pressure-induced structural strain in them differed significantly. The values of strain along the directions of the principal axes of the strain ellipsoid in the range from ambient pressure to 7 GPa are plotted in Fig. 5. The angles that these axes form with the crystallographic axes are given in Table S6 in the ESI† (also see the orientation of the principal axes with respect to structure-forming motifs in Fig. 6). The largest strain was observed at the highest pressure points achieved in the experiments (6.1 GPa for form I and 6.8 GPa for form II). For both polymorphs, linear strain in any direction did not exceed 15%. For comparison, in the simplest analogue of tolazamide containing a urea core – the urea – a very high (48%) linear strain was observed in one of the directions ([010]) at a relatively low pressure of 0.48 GPa.^85,86 At this pressure the phase transition between polymorphs I and III of urea occurs easily despite this giant strain.⁸⁶ The major difference in strain reflects different intermolecular interactions resulting from different molecular sizes, shapes and packings.

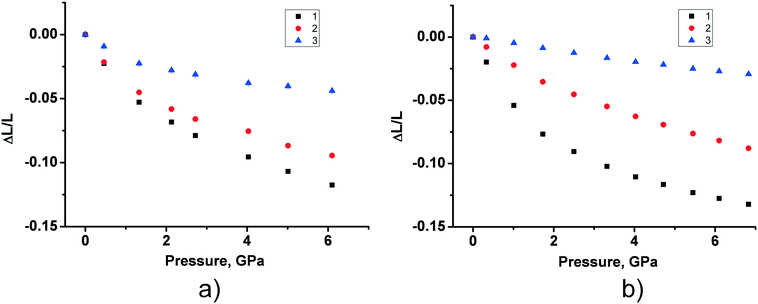Fig. 5 The experimental values of strain along the directions of the principal axes of the strain ellipsoid for form I (a) and form II (b) in the range from ambient pressure to 7 GPa. The angles of the principal axes with the crystallographic axes are given in Table S6 in the ESI;† see also Fig. 6.

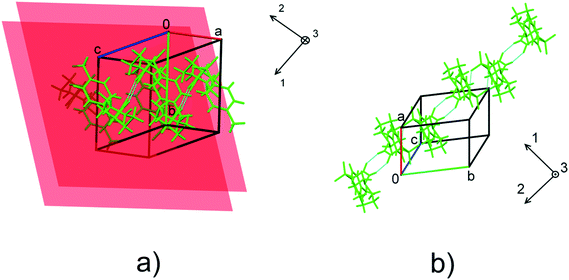Fig. 6 The orientation of the principal axes of strain ellipsoids with respect to structure-forming motifs in form I (a) and form II (b). The planes in a) show the orientation of the stacked benzene rings in form I. For the values of the angles formed by the principal axes of the strain ellipsoid and unit cell directions, see Table S6.†

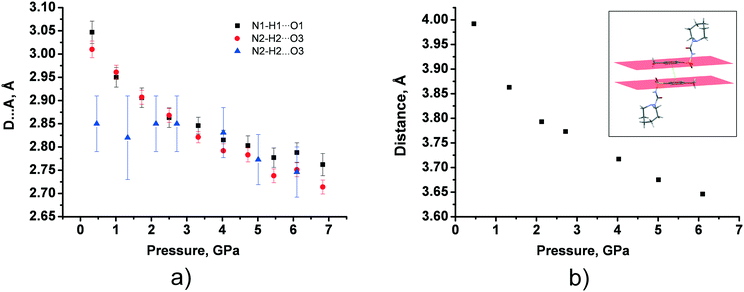
In tolazamide polymorphs, intermolecular interactions change significantly under pressure. The only H-bond in polymorph I does not undergo any significant changes, shrinking by about 0.1 Å across the studied pressure range, whereas the D⋯A distances of the two types of H-bonds in form II decrease with pressure to a much greater extent, by about 0.3 Å, reaching a value close to that observed in the ambient pressure structure of polymorph I (Fig. 7a and Table S7†). The same trends were observed for the calculated structures, additionally showing a decrease in H-bond compressibility at pressures above 7 GPa. At the same time, the distance between benzene fragments in polymorph I shortens from 3.95 to 3.65 Å as pressure increases (Fig. 7b and Table S7†). These observations are in agreement with our calculations. Calculations also show that moderate shortening of the distance by 0.54 Å (from 3.98 Å at ambient pressure to 3.44 Å at 15 GPa) provides additional structure stabilization up to 15 GPa; however, maximum stabilization is achieved at 2.1 GPa (Table S8 in the ESI†).

Fig. 7 Experimental pressure dependencies of the donor–acceptor distances for hydrogen bonds in forms I and II (a) and distances between two stacked benzene rings in form I (b). Blue color in a) corresponds to the H-bond N2–H2⋯O3 (−x, 1 − y, 1 − z) in form I, black color to the H-bond N1–H1⋯O1 (−x + 1, −y + 2, −z + 1) in form II and the red one to the H-bond N2–H2⋯O3 (−x, −y + 1, −z + 1) in form II.

The difference in the intermolecular interactions of tolazamide polymorphs at ambient and higher pressure makes a contribution to the energy cost of the II to I transformation. The total barrier that must be overcome to let the polymorphic transition occur includes changing the molecular conformation, besides breaking and forming intermolecular bonds. Conformers in the tolazamide forms have close energies, the difference being 4.2 kJ mol⁻¹ between them, which is common for polymorphs.⁸⁷ Not only the energy gap between the conformers, but also the energy barrier between the two forms should be addressed, to rationalize the possible phase transition. The barrier related to molecular motions at high pressure can be expected to be even more difficult to overcome than the energy separating conformations of an individual molecule. Often, the increase in temperature may diminish this barrier and the transition may occur (like sluggish transitions in pyridine and benzene).⁷⁴ However, everything is defined by the strength of intermolecular interactions and their stabilization with pressure. It was shown for guanidinium nitrate that its high-pressure phase IV has a denser packing and can be formed from phase II.⁸⁸ In contrast to this, phase III does not transform into phase IV on compression, even when additionally heated, in order to assist overcoming a kinetic barrier of structural reconstruction. A similar study on tolazamide polymorphs could contribute to understanding the role of intermolecular interactions in stabilizing different crystal structures with increasing pressure.

The direction of the significant strain in polymorph II coincides with that of H-bonded molecular chains. This fact accounts for the anisotropy of compression. No obvious correlation between the lattice strain and orientation of molecular dimers in form I can be found. Stabilization of stacking interactions with increasing pressure gradually diminishes at pressures higher than 2.1 GPa as confirmed by pair-wise DFT calculations (Table S8 in the ESI†). This can explain why the compressibility of polymorph I is lower than that of polymorph II.

Under ambient conditions, molecular disorder was found to be present in polymorph II. It was related to the conformations of the azepane ring and decreased gradually on compression, disappearing completely at 3.3 GPa (Fig. S2 in the ESI†). In this respect, tolazamide resembles methyl-2-(carbazol-9-yl)benzoate,⁸⁹ or 3-hydroxy-4,5-dimethyl-1-phenyl-pyridazin-6-one,²⁷ which becomes more ordered at high pressures, but differs radically from chlorpropamide or tolbutamide, in which the number of molecules with different conformations increases after the polymorphic transitions induced by increasing pressure,²² or on varying the temperature.^90–92 Disorder in structure I was not observed at any of the elevated pressures studied in this work. It is important to note that disorder was taken into account for the aforementioned energy and enthalpy calculations (see “Computational details” in the ESI†), because calculations based on only one disordered form for any polymorph can lead to misleading energy calculations (e.g. the change of relative energies is up to 10 kJ mol⁻¹ in this work). It is also worth mentioning that the less abundant disordered structure of form I was found to be more stable than form II computationally and experimentally.

Not only the packing motifs, but also the molecular conformations in the two polymorphs differ under ambient conditions. The main conformational difference is related to the value of one torsional angle, namely C4–S1–C1–C8 (numeration according to Fig. 1), whereas other geometrical parameters are similar. Despite the potential conformational flexibility of the tolazamide molecule (the orientation of the tolyl and azepane fragments and the displacement of atoms in the azepane ring), only minor conformational changes related to the ordering of molecules on compression were observed. Overall, molecular conformations did not change significantly with increasing pressure in either of the polymorphs. The root-mean-square deviation (RMSD) of atomic positions (as implemented in Mercury 3.8)⁴⁷ is equal to 0.133 Å between the molecules in the structures of form I at ambient pressure and 6.1 GPa; the corresponding value for the molecules in the structures of form II at ambient pressure and 6.8 GPa is equal to 0.258 Å (Table S9†). To estimate the minimum energy paths and the energy barriers corresponding to transitions between conformers (mainly related to the changes in the C4–S1–C1–C8 angle), the conformational landscape of the tolazamide molecule was investigated. For this reason, we used the approximation of an isolated molecule, not taking crystal effects into account. Rotational barriers around five dihedral angles were estimated independently (this procedure is described in detail in ref. 87), showing that a 28 kJ mol⁻¹ energy barrier corresponds to the transformation of one conformer into another (Fig. S3–S7 in the ESI†). These calculations agree well with previously reported data³⁵ based on geometrical parameters analysis – tolazamide polymorphs I and II are conformational polymorphs.^35,87 Following the energy profiles with denoted real structure dihedral angles (Fig. S3–S7†), one can see that, despite a significant energy barrier, the absolute energy difference between conformers in both structures is very small. The resulting enthalpy difference between I and II is likely due to the intermolecular interactions. The rate limiting energy barrier between molecular conformers clearly corresponds to a change of the C4–S1–C1–C8 dihedral angle. Such a barrier can be rapidly crossed in solutions under ambient conditions. Experimental data confirm these calculations, showing easy recrystallization of form II crystals into form I in dioxane and methanol. In contrast to that, due to a large body of intermolecular interactions the barrier required to change the molecular conformation in the solid state can be significantly higher, even if the final state is stabilized by new intermolecular interactions. This can offer a potential explanation as to why a solid-state transformation even into the more stable phase is kinetically hindered and is not observed.

Conclusions

Kinetic factors often need to be taken into account, both when aiming to preserve a metastable form at high pressures, or conversely, when the aim is to obtain a new polymorph. The effect of pressure on the two polymorphs of tolazamide provides one more example of kinetic control of high-pressure polymorphism of molecular solids.

Polymorph II does not transform into polymorph I with increasing pressure if no recrystallization is possible, even though this transformation would reduce the molar volume and give a slightly more stable polymorph I. This is in sharp contrast to the ease at which polymorph II transforms into polymorph I in solution, in the presence of solvent on grinding, or in the solid state on heating.³⁵ Apparently, nucleation of phase I is hindered at ambient temperature, and the packing of molecules in polymorph II does not change even at 6 GPa. This was rationalized using computational techniques, where enthalpies of both forms under pressure were calculated and supplemented with molecule energy landscape investigation. If nucleation is facilitated through dissolution and recrystallization in another hydrostatic fluid, the completeness of the transformation is still limited by the low solubility of tolazamide in this medium. The transformation of polymorph II into polymorph I at ambient pressure is facilitated by increasing temperature. A separate study of the effect of pressure on the temperature of this transition (if any) could shed more light on the nature and the values of energy barriers related to the transformation in the solid state.

Acknowledgements

This work was supported by RSF (Russian Science Foundation, http://rscf.ru/en/) (project 14-13-00834), and Slovenian Research Agency (program group P1-0012). The Siberian Branch of the Russian Academy of Sciences (SB RAS) Siberian Supercomputer Center is gratefully acknowledged for providing supercomputer facilities (http://www2.sscc.ru/). The authors acknowledge Dr. A. Chupakhin for very fruitful discussions and advice and Mr. A. Michalchuk for language polishing.

References

1. J. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, New York, 2002.
2. E. V. Boldyreva, Cryst. Growth Des., 2007, 7, 1662.
3. E. V. Boldyreva, S. N. Ivashevskaya, H. Sowa, H. Ahsbahs and H.-P. Weber, Z. Kristallogr., 2005, 220, 50.
4. S. V. Goryainov, E. N. Kolesnik and E. V. Boldyreva, Phys. B, 2005, 357, 340.
5. N. A. Tumanov, E. V. Boldyreva and H. Ahsbahs, Powder Diffr., 2008, 23, 307.
6. E. V. Boldyreva, S. N. Ivashevskaya, H. Sowa, H. Ahsbahs and H.-P. Weber, Dokl. Phys. Chem., 2004, 396, 358.
7. S. V. Goryainov, E. V. Boldyreva and E. N. Kolesnik, Chem. Phys. Lett., 2006, 419, 496.
8. E. V. Boldyreva, T. P. Shakhtshneider, H. Ahsbahs, H. Sowa and H. Uchtmann, J. Therm. Anal. Calorim., 2001, 68, 437.
9. N. A. Tumanov, E. V. Boldyreva, B. A. Kolesov, A. V. Kurnosov and R. Q. Cabrera, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 458.
10. B. A. Zakharov, N. A. Tumanov and E. V. Boldyreva, CrystEngComm, 2015, 17, 2074.
11. J. Ridout, L. S. Price, J. A. K. Howard and M. R. Probert, Cryst. Growth Des., 2014, 14, 3384.
12. M. Fisch, A. Lanza, E. Boldyreva, P. Macchi and N. Casati, J. Phys. Chem. C, 2015, 119, 18611.
13. E. N. Kolesnik, S. V. Goryainov and E. V. Boldyreva, Dokl. Phys. Chem., 2005, 404, 169.
14. S. A. Moggach, D. R. Allan, C. A. Morrison, S. Parsons and L. Sawyer, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 58.
15. E. V. Boldyreva, H. Sowa, Y. V. Seryotkin, T. N. Drebushchak, H. Ahsbahs, V. Chernyshev and V. Dmitriev, Chem. Phys. Lett., 2006, 429, 474.
16. B. A. Zakharov, S. V. Goryainov and E. V. Boldyreva, CrystEngComm, 2016, 18, 5423.
17. E. V. Boldyreva, H. Ahsbahs, H. Utchmann and N. E. Kashcheeva, High Pressure Res., 2000, 17, 79.
18. B. A. Zakharov, Y. V. Seryotkin, N. A. Tumanov, D. Paliwoda, M. Hanfland, A. V. Kurnosov and E. V. Boldyreva, RSC Adv., 2016, 6, 92629.
19. E. Eikeland, M. K. Thomsen, S. R. Madsen, J. Overgaard, M. A. Spackman and B. B. Iversen, Chem. – Eur. J., 2016, 22, 4061.
20. F. P. A. Fabbiani, D. R. Allan, W. I. F. David, A. J. Davidson, A. R. Lennie, S. Parsons, C. R. Pulham and J. E. Warren, Cryst. Growth Des., 2007, 7, 1115.
21. E. V. Boldyreva, V. Dmitriev and B. C. Hancock, Int. J. Pharm., 2006, 327, 51.
22. Y. V. Seryotkin, T. N. Drebushchak and E. V. Boldyreva, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 77.
23. E. V. Boldyreva, Z. Kristallogr., 2014, 229, 236.
24. F. P. A. Fabbiani, D. R. Allan, W. I. F. David, S. A. Moggach, S. Parsons and C. R. Pulham, CrystEngComm, 2004, 6, 504.
25. J. Schöll, D. Bonalumi, L. Vicum, M. Mazzotti and M. Müller, Cryst. Growth Des., 2006, 6, 881.
26. E. V. Boldyreva, T. P. Shakhtshneider, M. A. Vasilchenko, H. Ahsbahs and H. Uchtmann, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 299.
27. K. Roszak, A. Katrusiak and A. Katrusiak, Cryst. Growth Des., 2016, 16, 3947.
28. F. P. A. Fabbiani, D. R. Allan, W. G. Marshall, S. Parsons, C. R. Pulham and R. I. Smith, J. Cryst. Growth, 2005, 275, 185.
29. A. J. Cruz-Cabeza, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 437.
30. E. V. Boldyreva, Cryst. Eng., 2004, 6, 235.
31. E. V. Boldyreva, H. Ahsbahs, V. V. Chernyshev, S. N. Ivashevskaya and A. R. Oganov, Z. Kristallogr., 2006, 221, 178.
32. E. V. Boldyreva, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 218.
33. E. V. Boldyreva, Phase Transitions, 2009, 82, 303.
34. D. A. Rychkov, S. Hunter, V. Y. Kovalskii, A. A. Lomzov, C. R. Pulham and E. V. Boldyreva, Comput. Theor. Chem., 2016, 1088, 52.
35. E. V. Boldyreva, S. G. Arkhipov, T. N. Drebushchak, V. A. Drebushchak, E. A. Losev, A. A. Matvienko, V. S. Minkov, D. A. Rychkov, Y. V. Seryotkin, J. Stare and B. A. Zakharov, Chem. – Eur. J., 2015, 21, 15395.
36. A. Bauer-Brandl, E. Marti, A. Geoffroy, A. Poso, J. Suurkuusk, E. Wappler and K. H. Bauer, J. Therm. Anal. Calorim., 1999, 57, 7.
37. J. T. Carstensen and M. K. Franchini, Drug Dev. Ind. Pharm., 1995, 21, 523.
38. R. Boehler, Rev. Sci. Instrum., 2006, 77, 115103.
39. R. A. Forman, G. J. Piermarini, J. D. Barnett and S. Block, Science, 1972, 176, 284.
40. G. J. Piermarini, S. Block, J. D. Barnett and R. A. Forman, J. Appl. Phys., 1975, 46, 2774.
41. G. J. Piermarini, J. Appl. Phys., 1973, 44, 5377.
42. CrysAlisPro Software system, Agilent Technologies UK Ltd, Yarnton, Oxfordshire, UK, 2013.
43. R. J. Angel, J. Appl. Crystallogr., 2004, 37, 486.
44. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3.
45. X-Area and X-RED32 Software, Stoe & Cie GmbH, Darmstadt, Germany, 2006.
46. R. J. Angel, Win_Strain, 2011 (http://www.rossangel.com).
47. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466.
48. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7.
49. A. L. Spek, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 9.
50. F. H. Allen, O. Johnson, G. P. Shields, B. R. Smith and M. Towler, J. Appl. Crystallogr., 2004, 37, 335.
51. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380.
52. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Peterssonet al., GAUSSIAN 09 (Revision A.1), Gaussian Inc., Wallingford, CT, 2009.
53. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
54. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
55. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
56. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
57. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
58. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
59. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
60. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
61. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
62. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
63. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 122, 154101.
64. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101.
65. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104.
66. T. Björkman, Comput. Phys. Commun., 2011, 182, 1183.
67. J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. J. Angel, J. Appl. Crystallogr., 2016, 49, 1377.
68. R. J. Angel, J. Gonzalez-Platas and M. Alvaro, Z. Kristallogr., 2014, 229, 405.
69. Y. K. Huang and C. Y. Chow, J. Phys. D: Appl. Phys., 1974, 7, 2021.
70. J. Freund and R. Ingalls, J. Phys. Chem. Solids, 1989, 50, 263.
71. D. A. Rychkov, J. Stare and E. V. Boldyreva, Phys. Chem. Chem. Phys., 2017, 19, 6671.
72. D. Paliwoda, K. F. Dziubek and A. Katrusiak, Cryst. Growth Des., 2012, 12, 4302.
73. A. Katrusiak, M. Podsiadło and A. Budzianowski, Cryst. Growth Des., 2010, 10, 3461.
74. M. Podsiadło, K. Jakóbek and A. Katrusiak, CrystEngComm, 2010, 12, 2561.
75. M. Anioła and A. Katrusiak, CrystEngComm, 2016, 18, 3223.
76. M. Anioła and A. Katrusiak, Cryst. Growth Des., 2015, 15, 764.
77. I. D. H. Oswald, I. Chataigner, S. Elphick, F. P. A. Fabbiani, A. R. Lennie, J. Maddaluno, W. G. Marshall, T. J. Prior, C. R. Pulham and R. I. Smith, CrystEngComm, 2009, 11, 359.
78. R. Gajda, A. Katrusiak and J. Crassous, CrystEngComm, 2009, 11, 2668.
79. A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell and R. Car, et al. , Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439.
80. J. Nyman, O. S. Pundyke and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 15828.
81. J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154.
82. E. O. Pyzer-Knapp, H. P. G. Thompson and G. M. Day, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 477.
83. V. S. Minkov, V. A. Drebushchak, A. G. Ogienko and E. V. Boldyreva, CrystEngComm, 2011, 13, 4417.
84. K. R. Morris, U. J. Griesser, C. J. Eckhardt and J. G. Stowell, Adv. Drug Delivery Rev., 2001, 48, 91.
85. A. Olejniczak, K. Ostrowska and A. Katrusiak, J. Phys. Chem. C, 2009, 113, 15761.
86. K. Roszak and A. Katrusiak, J. Phys. Chem. C, 2017, 121, 778.
87. A. J. Cruz-Cabeza and J. Bernstein, Chem. Rev., 2013, 114, 2170.
88. A. Katrusiak, M. Szafrański and M. Podsiadło, Chem. Commun., 2011, 47, 2107.
89. R. D. L. Johnstone, M. Ieva, A. R. Lennie, H. McNab, E. Pidcock, J. E. Warren and S. Parsons, CrystEngComm, 2010, 12, 2520.
90. T. N. Drebushchak, V. A. Drebushchak and E. V. Boldyreva, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 163.
91. T. N. Drebushchak, V. A. Drebushchak, N. A. Pankrushina and E. V. Boldyreva, CrystEngComm, 2016, 18, 5736.
92. T. N. Drebushchak, Yu. A. Chesalov and E. V. Boldyreva, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 770.

---

Footnotes

† Electronic supplementary information (ESI) available: Information on tolazamide crystallization in methanol, low-temperature experiments, details of computational techniques and other data for tolazamide polymorphs: summary of the structural data at multiple pressures and temperatures; data on H-bonds and stacking interactions under pressure, parameters of the equations of state, and information on the strain ellipsoids; figures presenting the tolazamide molecule conformational landscape, conformational disorder in form II and pressure dependencies of tolazamide polymorphs' enthalpies. CCDC 1495203–1495210 and 1493069–1493078. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ce02527g

‡ That is, having practically the same energies, though it would be more correct to term them isoenthalpic.

---