The nature and effects of rhodium and antimony dopants on the electronic structure of TiO₂: towards design of Z-scheme photocatalysts

Abstract

The nature and effects of rhodium and antimony doping in TiO₂ have been investigated using X-ray diffraction (XRD), X-ray Photoelectron Spectroscopy (XPS), Extended X-ray Absorption Fine Structure (EXAFS) analysis, X-ray Absorption Near Edge Structure (XANES) analysis and diffuse reflectance spectroscopy. Together these techniques build up a comprehensive picture of the dopant chemistry in this system. A range of Sb/Rh ratios have been analysed, and it is shown that the Fermi level can be tuned within the band gap through control of dopant stoichiometry, offering the possibility of designing Z-scheme components with specific band offsets. Spontaneous spatial segregation of dopants is measured using TiO₂ (110) single crystals. This is shown to have a direct impact on the electronic structure in the region of the semiconductor surface, creating band bending that is expected to be critical for photocatalytic activity of these materials.

---

Introduction

Photocatalysis has applications in many different important processes such as water splitting, water cleaning, and microbial deactivation.^1–3 TiO₂ is an abundant, naturally-occurring mineral that has been widely studied since its photocatalytic properties were discovered;⁴ as a result a large amount of research has been devoted specifically to understanding and improving the photocatalytic processes that can occur at its surface.^5–8

Photocatalysis can only take place for a given reaction when the conduction band edge of the catalyst material lies at a more negative potential than the reduction potential of the reaction and the valence band edge at a more positive potential than the oxidation potential of the reaction.⁹ TiO₂ fulfils this criterion for water photolysis and can therefore successfully split water into hydrogen and oxygen. However, since the two common forms of TiO₂, rutile and anatase, have bands gaps of 3.00 eV and 3.20 eV respectively,¹⁰ they are active under Ultra Violet (UV) radiation only. Since UV light accounts for just 4–5% of solar radiation that reaches the Earth's surface,¹¹ much research has focused on modifying TiO₂ based photocatalysts to enable their activation under visible light and improve the overall efficiency of these catalysts. Since the conduction band edge is positioned appropriately to enable H⁺ reduction, modification is usually focussed on changes to the valence band. Addition of dopants can act by mixing of the dopant and basis material valence band orbitals (as in N- and S-doping^12–14) or by introduction of discrete energy levels above the basis material valence band (as in C- and B-doping).^15–19 Noble metal doping in titanate semiconductor materials has been an area of interest for a number of years, with much research indicating that these materials produce a visible light response.^20–25

However, despite intensive research for decades, to date there is no stable single phase material, based on TiO₂ or otherwise, capable of efficiently (i.e. >10% quantum yield) carrying out overall (i.e. non-sacrificial) water splitting using sunlight. It may be that more complex doping regimes are necessary in order to achieve efficient visible light photocatalysis, and recently TiO₂ and other materials co-doped with two or more dopants together have been studied. The greater complexity afforded by using multiple dopants offers opportunities for fine tuning of electronic, optical and chemical properties that may lead to the desired visible light active catalysts. However, greater complexity requires more detailed understanding of the physical and chemical effects of the dopants on the host material. An alternative to single phase catalysts is to couple photocatalysts together. By forming a heterojunction, photoexcited electrons and holes can be separated by migrating across the junction according to the relative energies of the valence and conduction bands of the two catalysts. A notable type of heterojunction currently receiving much attention is the Z-scheme.²⁶ This mechanism mimics biological photosynthesis, which is based on two photosystems. Z-schemes have a number of advantages, chiefly that two narrow band gap semiconductors can be used to produce the same redox power as a single wide band gap semiconductor.

When selecting materials to combine to form a water splitting Z-scheme it is necessary to consider how the band edges of the two materials align with each other and the redox potentials of water. This can be achieved by comparing the band edges relative to the Fermi level (E_F) for each material. To date, materials that naturally exhibit band edges at appropriate offsets have been used to construct Z-schemes, for example, Ta₃N₅/TaON.²⁷

Overall, the trend in photocatalysis research is for greater complexity, either in codoped systems or through combination of two or more phases to create heterojunctions and Z-schemes. In both these approaches, there is a need for a good understanding of the catalysts themselves to allow rational design of effective materials. Here we seek to better understand the effects of a complex doping regime on the properties of TiO₂. Rh/Sb codoped TiO₂ and related materials, such as Y₂Ti₂O₇, SrTiO₃ and BaTiO₃, have been recently developed as effective photocatalysts, both as single phase materials and as part of a Z-scheme.^28–31 Domen et al. produced a Z-scheme combining Ta₃N₅ and Rh doped SrTiO₃, achieving visible light water splitting, with H₂ evolution at rates of up to 12 μmol h⁻¹, when loaded with an Ir co-catalyst. Rosseinsky and co-workers have achieved >7 μmol⁻¹ O₂ evolution using visible light over a Rh-doped Y₂Ti₂O₇ catalyst.²⁵ Kudo and co-workers³² reported visible light photoactivity of Rh and Sb codoped TiO₂ (where Sb/Rh = 0, 0.5, 1, 2 and 3 were investigated) and showed that, with Sb/Rh ≥ 2, O₂ evolution exceeds 10 μmol h⁻¹. Their Sb/Rh doped SrTiO₃ system has also achieved sacrificial O₂ and H₂ evolution under visible light.²⁹

It has been shown that doping TiO₂ with Rh introduces 4d t_2g states into the band gap.^33,34 The occupancy of these Rh 4d states naturally depends on the oxidation state of the Rh dopant. It has been found that upon doping of TiO₂ with Rh onto the Ti⁴⁺ site, Rh⁴⁺ is the most stable oxidation state, presumably in order to maintain overall charge neutrality. However, Rh⁴⁺ possesses a partially filled 4d t⁵_2g energy level, the inclusion of which causes the Fermi level to be positioned at a lower energy than that of pristine TiO₂. The addition of electrons by introducing Sb(V), allows t⁶_2g Rh(III) to exist in the system and the n-type character of the material to be retained.^32,34

Here we report a comprehensive study of the dopant chemistry of Rh/Sb doped TiO₂. By using both ceramic powder samples and single crystals we are able to gain greater understanding of the effects of Rh/Sb codoping regimes in TiO₂, which can allow us to tune the electronic properties, making possible the design and optimisation of the individual Z-scheme components. We demonstrate the use of these co-dopants to tune the Fermi level position to yield materials with the required band offsets to form a Z-scheme.

Where previous investigations have focussed on equimolar doping regimes, here a range of dopant ratios have been incorporated into the TiO₂ lattice and comparisons between TiO₂:Rh and TiO₂:RhSb have been made. A comprehensive characterisation of the materials has been completed using XPS, XRD, UV-vis, EXAFS and XANES to provide information about the electronic structures of the materials in addition to the oxidation states, chemical environments and concentration of dopant ions. In order to profile the dopant concentration penetrating into the materials, a TiO₂ single crystal was doped by high temperature diffusion, depth profiling used to determine the spatial distribution of dopants, and revealing that the spontaneous spatial arrangement of dopants leads to a built in electric field that may be highly beneficial for charge carrier separation in photocatalysis.

Experimental section

Rhodium doped TiO₂ samples were synthesised by solid-state reaction of TiO₂ powder (Aldrich 99.99%) with the appropriate amount of Rh₂O₃. The powders were ground using an agate pestle and mortar, calcined at 1100 °C for 10 hours, then re-ground and calcined at 1100 °C for a further 10 hours.

Antimony co-doped TiO₂ samples were produced by grinding Rh doped powders with the appropriate amount of Sb₂O₃, calcination at 900 °C for 10 hours, re-grinding and calcination at 900 °C for a further 10 hours.

For comparison an antimony doped sample was synthesised, again by solid stated reaction. TiO₂ was ground with the appropriate amount of Sb₂O₃, calcined at 900 °C for 10 hours, then re-ground and calcined at 900 °C for a further 10 hours. Table 1 outlines the samples and their synthesis conditions.

Table 1 Synthesis conditions for all powder samples

Sample	Calcination temperature (°C)	Total calcination time (h)
TiO2:Rh[1%]	1100	20
TiO2:Rh[3%]	1100	20
TiO2:Rh[5%]	1100	20
TiO2:Rh[7%]	1100	20
TiO2:Rh[9%]	1100	20
TiO2:Rh[5%]Sb[1%]	1100 then 900	20
TiO2:Rh[5%]Sb[3%]	1100 then 900	20
TiO2:Rh[5%]Sb[5%]	1100 then 900	20
TiO2:Rh[5%]Sb[7%]	1100 then 900	20
TiO2:Rh[5%]Sb[9%]	1100 then 900	20
TiO2:Sb[5%]	900	20

---

A TiO₂ single crystal was doped with Rh and Sb by solid state diffusion of dopants from the prepared doped powder into a TiO₂ (110) single crystal, purchased from Alineason.

The phase composition of the resultant powders was confirmed by X-ray diffraction (XRD) on a Bruker D4 powder diffractometer, using Cu-Kα radiation (λ = 1.54 Å). The surface compositions of the powders were measured by X-ray photoelectron spectroscopy (XPS) using a Thermo K-alpha instrument utilising a 72 W monochromated Al Kα X-ray source (with photon energy of 1486.6 eV). A dual beam flood gun was used to compensate for sample charging, instrument specific relative sensitivity factors were used to normalise the data and the binding energy scale was referenced by setting the C 1s peak from adventitious carbon to 285.0 eV.

Sb and Rh K-edge X-ray Absorption Spectra (XAS) were taken at beamline (B18), Diamond Light Source, UK. The beamline is equipped with Si (111) double crystal monochromator, ion chambers for measuring incident and transmitted beam intensity and operates at 3 GeV and 300 mA. All measurements were carried out in absorption mode and typically 12 scans were averaged to produce the data. Spectra were processed using Athena software.

Results

X-ray diffraction

X-ray diffraction patterns of all doped TiO₂ samples confirm single phase samples, with no detectable Rh₂O₃ or Sb₂O₃ phases present. Patterns were indexed in the rutile structure (tetragonal P42/mnm) and lattice parameters were determined by least squares refinement. Both the a and c lattice parameters of all TiO₂:Rh powders increase upon incorporation of Rh into the lattice up to 5% doping (ESI Fig. S1a and b†). The cell volume of TiO₂:Rh[5%] is 62.5775 ų compared with 62.1216 ų for pristine TiO₂. Above 5% Rh doping lattice parameters increase slightly. Given the modest increase in cell volume upon doping, it is expected that the Rh dopant substitutes onto the Ti site rather than interstitially, a conclusion supported by XAS data presented below. However, the ionic radius of six coordinate Rh⁴⁺ is very similar to that of Ti⁴⁺ (0.60 Å and 0.605 Å, respectively³⁵) and therefore the observed lattice parameter increase cannot be explained in terms of the size of the dopant ion. It may indicate the presence of some Rh³⁺, which has an ionic radius of 0.665 Å,³⁵ in these samples.

Incorporation of Sb affects both lattice parameters; again an increase in both a and c parameters is observed as nominal Sb doping increases. However, above 5% Sb doping the lattice parameters decrease slightly. Since the presence of Sb⁵⁺ is expected to encourage the formation of Rh³⁺, the initial lattice parameter increase could be caused by an increased proportion of Rh³⁺ ions. The presence of bulk Sb³⁺, which has an ionic radius of 0.76 Å (ref. 35) and could also account for increases in these lattice parameters, is eliminated by XAS data presented below. With excess Sb doping, the lattice parameters decrease. In this regime, excess Sb⁵⁺ may be compensated for by titanium vacancies, leading to a reduction in unit cell size.

X-ray absorption spectroscopy

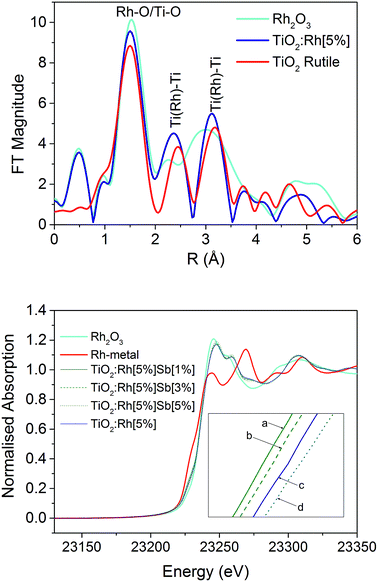
Fig. 1 shows the EXAFS Fourier transform of TiO₂:Rh[5%] measured at the Rh K-edge which is compared with TiO₂ (measured at the Ti K-edge) and Rh₂O₃ (Rh K-edge) standard powders. Labelled peaks show the distances between nearest neighbours (at around 1.5 Å) and second nearest neighbours (2.3–3.5 Å); note these distances appears short, since they are not corrected for the phase shift. A detailed analysis of the Rh K-edge EXAFS data shows the nearest neighbour distances TiO₂:Rh (Fig. 1b) suggest the Rh–O distance in the TiO₂:Rh system is ca. 2.0 Å which is similar to Rh–O distances in Rh₂O₃; this may be due to the presence of Rh₂O₃ phase or substituted Rh³⁺ in TiO₂ lattice with increase in distance due to its higher ionic radii. More convincing evidence for Rh substitution in TiO₂ lattice comes from the analysis of higher neighbours. Ti–Ti distances in TiO₂ are 2.96, 3.4 and 3.6 Å whereas in Rh₂O₃ Rh–Rh distances are at ca. 2.72, 2.99, 3.3 and 3.52 Å. Thus by comparing these FTs, it appears that Rh–Ti distances are similar to those observed for TiO₂ structure rather than Rh₂O₃. Therefore, we conclude that Rh ions are substituted in TiO₂ structure than present as RhO_x secondary phase.

Fig. 1 Fourier transform of the Rh K-edge EXAFS of TiO₂:Rh[5%] by comparison with TiO₂ (Ti K-edge EXAFS) and Rh₂O₃ (Rh K-edge EXAFS) standard powders (top), and Rh K-edge XANES of Rh₂O₃, Rh-metal, TiO₂Rh[5%], TiO₂Rh[5%]Sb[1%], TiO₂Rh[5%]Sb[3%] and TiO₂Rh[5%]Sb[5%] (bottom); note that the Fourier transform presented here are not phase shift corrected and therefore the distances appear shorter than expected values. Actual distances reported here are based on the full analysis of the EXAFS data which includes phase shift correction.

Rh K-edge X-ray absorption near edge structure (XANES) data for Rh₂O₃, Rh-metal, and doped samples TiO₂:Rh[5%], TiO₂:Rh[5%]Sb[1%], TiO₂:Rh[5%]Sb[3%] and TiO₂:Rh[5%]Sb[5%] are also shown in Fig. 1 (bottom). It is clear that the XANES of all doped samples is closely comparable Rh₂O₃, and that there is minimal similarity with the absorption spectrum of Rh-metal. Between 23 215 eV and 23 235 eV some distinction can be seen between doped samples (Fig. 1b inset), suggesting variance in Rh oxidation state across the series.

The Ti/Sb-edge EXAFS Fourier transform data for TiO₂, Sb₂O₃, Sb₂O₅ and doped samples TiO₂:Rh[5%]Sb[1%], TiO₂:Rh[5%]Sb[3%] and TiO₂:Rh[5%]Sb[5%] (ESI, Fig. S2a†) demonstrates the lack of distinct position of Sb ions in the doped samples. It is unclear if Sb ions reside on the Ti⁴⁺ site, though second nearest neighbour distances suggest that as more Sb is incorporated into the material, the Sb environment is more Sb₂O₅-like. However, what is more clear is that X-ray absorption of the Sb K-edge (ESI Fig. S2b†) shows that all Sb atoms are likely Sb(V), as opposed to Sb(III).

X-ray photoelectron spectroscopy

Surface composition. XPS was used to quantify the surface composition of the samples. In most TiO₂ samples studied, the surface dopant composition (of both Rh and Sb) was found to be above the nominal doping value, i.e. both Rh and Sb dopants were found to be surface segregated. Fig. 2a shows surface enrichment of Rh in TiO₂:Rh[X%} samples at lower nominal doping (X ≤ 5%). At higher Rh concentrations, this trend is reversed; observed dopant levels are lower than the nominal amount. By comparison, the Rh surface enrichment increases dramatically in the presence of Sb in the codoped samples; Sb is also significantly surface segregated (Fig. 2b and c). Note that codoped samples were produced by first doping TiO₂ with Rh, then reacting with Sb₂O₃ in air in a second step. Thus the change in surface enrichment of Rh upon Sb doping represents a bulk to surface migration of the Rh ions that occurs during the Sb doping step.

Fig. 2 (a–d) Dopant percentage amount as determined from XPS; (a) Rh in TiO₂:Rh, (b) Rh in TiO₂:RhSb and (c) Sb in TiO₂:RhSb, (d) depth profile showing atomic% of Rh and Sb as determined by XPS spectra taken after intervals of etching with an Ar⁺ ion gun.

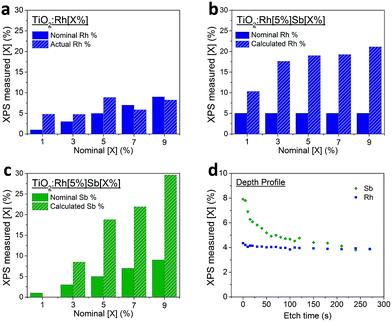
In the highest levels of doping studied here, TiO₂:Rh[5%]Sb[9%], the Rh and Sb cations represent over half of the surface cations detected by XPS. Such a large change in surface composition will inevitably have effects on surface photochemical processes. It has been reported previously that Sb dopants surface segregate in Sb doped TiO₂, although this has been speculated to be due to the presence of Sb³⁺ lone pair cations preferring surface sites where they may adopt a less symmetric coordination. The attraction of Rh dopants to Sb at the surface identified here is best explained by a defect clustering model where Sb⁵⁺ and Rh³⁺ dopants preferentially reside on neighbouring or closely spaced cation sites in order to maintain local charge neutrality. The preference of Sb dopants at surface sites is therefore seen to ‘pull’ Rh ions out of the bulk to the surface. This is evidence not only for electronic interaction between the dopants (i.e. reduction of Rh⁴⁺ to Rh³⁺ through Sb doping), but also significant interdependence of the spatial distribution of dopants within the TiO₂ matrix.

To investigate further, a single crystal diffusion study was undertaken. The random orientation and small size of particulates in powder samples is not conducive to meaningful compositional depth profiling using XPS or similar techniques. Instead, by using a doped TiO₂ single crystal as a model system, the relationship between bulk and surface dopants can be revealed more clearly. A TiO₂ (110) polished single crystal was heated under a TiO₂:Rh[5%]Sb[9%] powder at 1100 °C for 10 h to induce diffusion of the dopants into the crystal. Depth profiles were then recorded in XPS using Ar ion sputtering. Fig. 2d shows the amount of dopant determined by XPS at intervals between Ar⁺ ion etchings.

As with doped TiO₂ powders, Sb in this doped TiO₂ single crystal is much more highly concentrated at the surface than in the bulk. The depth profile reveals that relative Sb percentage diminishes further into the material. By comparison, Rh is evenly distributed throughout the depth studied. It is evident that Rh diffuses into the TiO₂ (110) surface to a much greater degree than Sb under the conditions used. This could be due to either a higher diffusion coefficient of Rh – i.e. the Rh ions (of whatever oxidation state) can move through the TiO₂ lattice more easily than Sb ions can, or alternatively, the Sb ions are thermodynamically more stable at the surface and do not diffuse extensively to the bulk. Surface enrichment of Rh in this material is less pronounced than in powder samples, though a small amount of enrichment is observed in the first few layers of the profile. This interesting contrast with the powder samples may indicate that the (110) TiO₂ surface is atypical in not showing significant surface enrichment of Rh in the presence of Sb dopants.

Valence band spectra. The valence band (VB) spectrum of undoped TiO₂ powder showed the two-peaked shape typical of rutile TiO₂. The area under the VB curve for pristine TiO₂ was fitted with two Gaussian–Lorentzian components. This model was then used to represent the TiO₂ contribution to all doped VB spectra. In the case of Rh doped samples, there was an additional feature at the low binding energy side of the VB spectrum compared with the pristine TiO₂ model. This feature, centred at a binding energy of ∼1.6 eV, is highlighted in blue in the spectra shown in Fig. 3, and represents filled states within the TiO₂ bandgap.

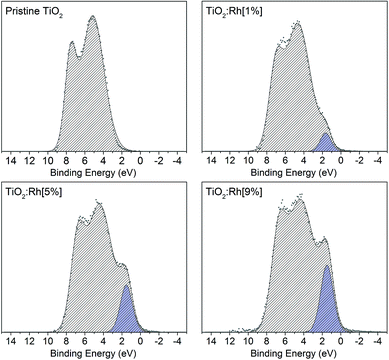Fig. 3 Valence band spectra of pristine TiO₂ and 1, 5 and 9% Rh doped TiO₂. As the nominal amount of Rh increases, the prominence of an in-gap feature due to Rh 4d t_2g electrons also increases.

The area of this component is proportional to the Rh content, and is assigned to the presence of filled Rh 4d t_2g states. In samples codoped with Sb, this band gap feature becomes more prominent with increased Sb doping. While EXAFS results indicated that bulk Sb dopant ions are Sb⁵⁺, it is still possible that surface Sb³⁺ is present,^34,35 which would be expected to contribute filled Sb 5s states to the valence band region. Such features were not identified here, which may suggest the amount of Sb³⁺ is small, or that an Sb 5s feature is masked by the more intense Rh 4d peak. Since codoped samples were synthesised with nominal 5% Rh, this increased prominence of the Rh valence band feature correlated with the increased surface segregation of Rh cause by the presence of Sb as a codopant.

High resolution core level X-ray photoemission spectra. A difficulty with interpretation of binding energies of the XPS core lines in the present case is the combined effect of both chemical shift and changing Fermi level. A change in the oxidation state of Rh from +4 to +3 is expected to result in a shift of the Rh core level XPS peaks to lower binding energy. However, this same Rh oxidation state change is also expected to increase the Fermi level energy due to population of the Rh 4d mid band gap states; this would result in an increase in the measured binding energy of the Rh peaks. These competing effects make simple interpretation of the absolute binding energy of the Rh peaks problematic. To overcome this we take binding energy differences between core lines. In this analysis we assume that there is no chemical shift to the oxide O 1s peak upon doping. O 1s peaks from oxide anions in metal oxides, of whatever structure and composition, fall within a very narrow range of binding energies.^36–38 Since the environment of the oxide anions in the present samples is changed upon doping by replacement of up to 12% of the Ti ions with Sb or Rh, with otherwise no change in crystal structure or oxidation state of the anion, it is a reasonable to assume that the chemical shift to the oxide O 1s peak upon doping is small. This assumption lets us proceed in two ways.

Firstly, we can determine the extent of Fermi level shift by using O 1s peak position as a reference point. Since the E_F of a material is calibrated as 0 eV in XPS, any shift of E_F will be observed as a shift of all other core line peaks. Assuming as we do that O²⁻ is not chemically changed by the doping process, the absolute position of the main O 1s peak and any shift that is observed by comparison to that of O 1s in pristine TiO₂ can be assumed to be caused by movement of the Fermi level.

Secondly, the energy difference between the O 1s peak and a second core line will change only due to chemical shift of the second core line. This can be used to eliminate the effect of Fermi level shift from the Rh corelines and allow accurate assessment of any chemical shift.

The presence of antimony presents the complication that the Sb 3d_5/2 core line lies under the O 1s core line and is masked by it completely. For quantification of dopants the Sb 3d_3/2 peak, which lies 9.4 eV higher than Sb 3d_5/2,³⁹ was utilised along with the appropriate relative sensitivity factor determined from the spectrometer. However, for determination of the binding energy of the O 1s peak, a Sb 3d_5/2 peak was fitted by constraining its area (2 : 3 ratio with Sb 3d_3/2), full-width half-maximum (equal to Sb 3d_3/2) and doublet separation (9.4 eV lower than Sb 3d_3/2) to that of the Sb 3d_3/2. Additional components to represent the oxide anions and another to account for surface hydroxyl groups, which manifest as a shoulder to the high binding energy side of the O 1s, were added. An example spectrum is shown in Fig. S3 of the ESI;† the O 1s positions quoted in Fig. 4 and Table 2 are those of the oxide anion generated from these fits.

Fig. 4 Oxide O 1s absolute binding energy vs. nominal amount of Sb dopant. As O²⁻ is assumed chemically unchanged in the doped systems by comparison with pristine TiO₂, the observed variation in oxide O 1s binding energy can be attributed to movement of the Fermi level, which provides the 0 eV binding energy reference in XPS.

Table 2 Absolute binding energy of O1s peak to illustrate Fermi level movement, core-line separation between O1s and Rh 3d 5/2 peaks to demonstrate relative Rh oxidation state and Kubelka-Munk derived band gap energy for all codoped samples (singly doped TiO₂:[Sb5%] and TiO₂:[Rh5%] included for reference)

Sample	O 1s position (eV)	Core line separation (O 1s–Rh 3d5/2) (eV)	Band gap energy (eV)
a Band edge obscured by Rh d–d transition.
TiO2:Sb[5%]	530.1	—	3.1
TiO2:Rh[5%]	529.0	220.2
TiO2:Rh[5%]Sb[1%]	528.4	220.2
TiO2:Rh[5%]Sb[3%]	529.5	220.0
TiO2:Rh[5%]Sb[5%]	529.6	220.2	2.25
TiO2:Rh[5%]Sb[7%]	530.0	220.6	2.24
TiO2:Rh[5%]Sb[9%]	530.2	220.8	2.23

---

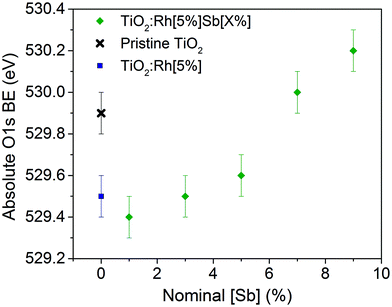
TiO₂:Rh[5%] exhibits an oxide O 1s shift of −0.4 eV by comparison to pristine TiO₂. As can be seen in Fig. 4, codoping with Sb causes the oxide O 1s peak position to shift to higher binding energies as more Sb is doped into the sample. Undoped TiO₂ is an n-type semiconductor, where the Fermi level is pinned close to the conduction band minimum by the presence of a small concentration of Ti³⁺ defects. The oxide O 1s core line shifts observed here are interpreted as follows. Upon Rh doping of TiO₂, the Fermi level shifts downwards, towards the valence band, by 0.4 eV. This is due to the introduction of partially filled Rh 4d states within the band gap. When Sb is codoped into the structure in increasing amounts, the Fermi level (E_F) rises. This is assigned to filling of the Rh states within the band gap through introduction of Sb⁵⁺, an electron dopant and reduction of Rh⁴⁺ to Rh³⁺, which has a filled t⁶_2g configuration in the low spin state. Since E_F is the reference point for the binding energy scale in XPS, a rising E_F leads to an apparent increase in binding energy for all core lines. Since the chemical shift of the oxide O 1s peak is assumed to be small, the shift in oxide O 1s shown in Fig. 4 is directly representative of the variation in E_F induced by the cooping regime. Thus, there is a direct link between the Rh/Sb ratio of dopants in TiO₂ and the E_F position: more Rh rich materials will have more p-type character, whilst more Sb rich materials will be more n-type in character. Interestingly, at nominal equimolar Sb/Rh doping, the Fermi level is still significantly lower than in pristine TiO₂, showing that not all of the Rh⁴⁺ has been reduced to Rh³⁺. It is not until Sb/Rh ≥ 1.4 that the Fermi level is situated at a higher energy even than that of pristine TiO₂. This is in agreement with reported Electron Spin Resonance (ESR) measurements, which indicate that Sb/Rh must be greater than 1 to eliminate all Rh³⁺,³² and perhaps suggests that some Sb is present in the +3 charge state, or that some Sb is lost from the samples on annealing, making the nominal Sb doing values higher than the true value. The total variation seen in the O 1s peak across all samples is 0.8 eV. Thus variable levels Sb doping can be used to tune the Fermi level of these materials within a good proportion of the band gap, and this may be a useful method for designing photocatalytic materials with specific band edge relationships, for example, when constructing a Z-scheme.

The interpretation of Rh oxidation state from the Rh core line XPS peaks is also complicated by competing chemical shifts and Fermi level movement. Once again utilising the well-defined and chemically unaltered oxide O 1s core line as a reference point, the effect of Fermi level shift on the Rh core line can be removed, allowing determination of any chemical shift in the Rh 3d coreline.

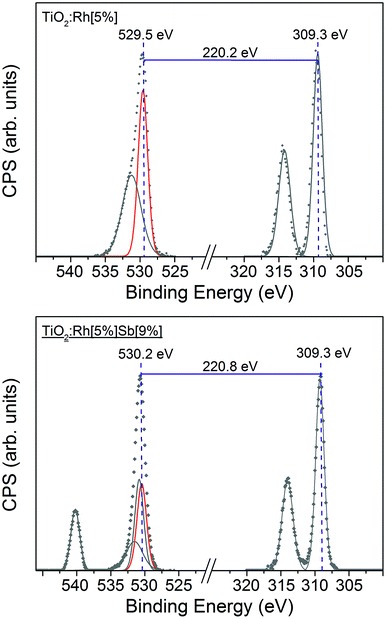
As shown in Fig. 5, the absolute binding energy of Rh 3d_5/2 electrons in TiO₂:Rh[5%] and TiO₂:Rh[5%]Sb[9%] is 309.3 eV for both samples. Ordinarily, absent Fermi level shifts, this would indicate that Rh in these samples is in the same oxidation state. Fig. 5 shows comparison between two samples with the same nominal Rh amount but different nominal Sb amounts, TiO₂:Rh[5%] and TiO₂:Rh[5%]Sb[9%]. The O 1s–Rh 3d_5/2 core line separation is considerably larger (220.8 eV) in TiO₂:Rh[5%]Sb[9%] than in TiO₂:Rh[5%] (220.2 eV). Again, assuming that the oxide O 1s peak is unmoved by chemical shift, any increase in core line separation will be due to change in the chemical shift of the Rh 3d line. An increase in separation represents a movement of the Rh 3d coreline to lower binding energy, indicating that Rh in TiO₂:Rh[5%]Sb[9%] is in a lower oxidation state than in TiO₂:Rh[5%]. This correlates with the expected oxidation states of Rh in TiO₂:Rh[5%] (+4) and TiO₂:Rh[5%]Sb[9%] (+3). The O 1s–Rh 3d_5/2 core line separation values for all codoped samples are shown in Table 2. By comparison all singly Rh doped samples exhibited a core line separation value of between 220.0 eV and 220.3 eV, indicating that only in samples where Sb/Rh ≥ 1.4 does it appear that all Rh is found in the +3 state.

Fig. 5 Binding energy separation between O 1s and Rh 3d peaks in TiO₂:Rh[5%] (top) and TiO₂:Rh[5%]Sb[9%] (bottom). The energy difference between the corelines increases with Sb doping. Assuming a static oxide O 1s peak with no chemical shift, the increasing energy difference upon Sb doping is attributed to a decrease in the binding energy of the Rh 3d coreline, corresponding to a less positive oxidation state for Rh.

UV-vis analysis

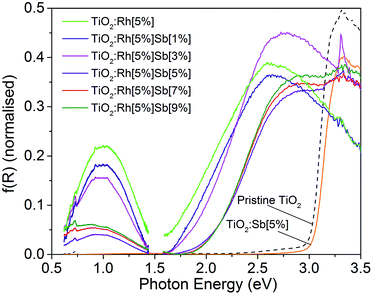
Diffuse reflectance spectra transformed using the Kubelka–Munk function⁴⁰ are shown in Fig. 6 in the range 0.6–3.5 eV for all samples. Two changes in the optical absorption spectra of TiO₂ are seen upon Rh doping. Firstly, a broad absorption peak appears centred at 1.0 eV. Secondly, the band edge, which in TiO₂ is around 3 eV, shifts to lower energy, corresponding to a band gap, calculated using the Tauc method, of 1.8 eV, although as discussed below, this is thought not to be a true interband transition but rather a d–d transition. Upon Rh/Sb doping, both these new features are modified. On increasing levels of Sb doping, the feature at 1.0 eV decreases in intensity, reaching a minimum at TiO₂:Rh[5%]Sb[5%]. The band edge moves to higher energies, resulting in a band gap of 2.2 eV. These features can be interpreted in terms of the electronic configuration of the dopants. Rh⁴⁺ has a 4d⁵ configuration, and doping into oxide matrices has been reported to cause absorption band in the near infrared, as is observed here.^41,42

Fig. 6 Absorption spectra for all TiO₂:Rh[5%]Sb[X%] powders. A decrease in photon energy required for photoexcitation is exhibited by all Rh doped samples by comparison to pristine TiO₂. An additional absorption around 1.0 eV, which can be attributed to a valence band to Rh⁴⁺ t_2g transition, is prominent in samples containing Rh⁴⁺. The reduction in intensity of this feature is evidence of the suppression of Rh⁴⁺ in samples of higher Sb⁵⁺ concentration.

This has been assigned to a O 2p → Rh t_2g transition, i.e. a transition from the TiO₂ VB to the partially filled interband gap Rh 4d state. The VB spectra in Fig. 3 shows that the Rh 4d states are situated approximately 1 eV above the TiO₂ VB, which correlates with the optical transition observed here. Upon addition of Sb, the Rh⁴⁺ is reduced to Rh³⁺ which has 4d⁶ configuration. In a low spin state, the Rh t_2g orbitals are filled, so the O 2p → Rh t_2g transition does not occur. This correlates with the decrease in intensity of the 1.0 eV absorption feature with increasing Sb. Previously, the 1.0 eV transition in similar oxide systems has been assigned to Rh d–d transitions.⁴³ However, in the few reported electronic spectra of Rh⁴⁺ compounds, the Rh⁴⁺ d orbital splitting is known to be significantly larger than 1.0 eV.⁴⁴ The shift in band gap to lower energies upon Rh doping can be assigned to Rh 4d → conduction band (CB) transitions; similar transitions are seen in Rh doped oxides. Given this assignment, it is unexpected that the band gap should increase upon Sb doping: reduction of Rh should lead to raising of the Rh 4d energy levels toward the CB, which would result in a smaller band gap.

Another possibility is that in the Rh⁴⁺ doped samples, a Rh d–d transition occurs in the visible region. There are few reports of the electronic spectra of low spin Rh⁴⁺ compounds. [RhF₆]²⁻ displays its lowest energy d–d transition at 2.54 eV. Naturally for an oxide coordinated Rh ion the d orbital splitting will vary. Low spin Rh³⁺ d⁶ ions have no spin allowed d–d transitions. Therefore it is possible that he feature resembling a band edge at 1.8 eV may be a Rh⁴⁺ d–d transition, which is attenuated as the Rh is reduced upon addition of Sb codopant.

Discussion

It has been established by the results reported above that the electronic structure, specifically the Fermi level, of Rh/Sb co-doped TiO₂ is strongly dependent upon the Rh/Sb ratio. In a semiconductor, the occupation of inter band states strongly affects the Fermi level. Here, E_F depends upon the filling of Rh 4d orbitals that are positioned between the TiO₂ VB and CB. The total E_F shift possible in the range of dopant ratios studied here is 0.8 eV, between TiO₂:Rh[1%]Sb[1%] and TiO₂:Rh[5%]Sb[9%]. This suggests that combination of these two materials in a Z-scheme would be viable.

It has also been shown that the spatial distribution of Sb and Rh cations within the TiO₂ matrix is quite complex. In Rh doped TiO₂, with no Sb co-dopant, there is modest surface segregation of the Rh. However, upon introduction of Sb, surface segregation of Rh is significantly enhanced – Rh is pulled from the bulk of TiO₂ to the surface, presumably by favourable defect clustering. The single crystal study presented in Fig. 2d illustrates that Sb is strongly surface segregated in TiO₂ (110) crystals, which serves as a model for the polycrystalline powders used in photocatalysis. In contrast, Rh is present throughout the single crystal in approximately even proportions. Due to this spontaneous spatial arrangement of the dopants, the Rh/Sb ratio changes with depth (Fig. 2d). As already stated, the Rh/Sb ratio strongly affects the Fermi level in this system. Therefore, it can be concluded that the Fermi level, relative to the band edges also changes with depth in the Rh/Sb doped single crystal studied here. The surface is more Sb rich, so will be more n-type, whilst the bulk is more Rh rich, so will be more p-type. Thus by the spatial arrangement of the dopants, a material with a built in electric field is produced – such a field will certainly affect the charge carrier migration necessary for photocatalysis, and the direction of the field is expected to enhance electron migration towards the surface whilst hindering hole movement in the same direction.

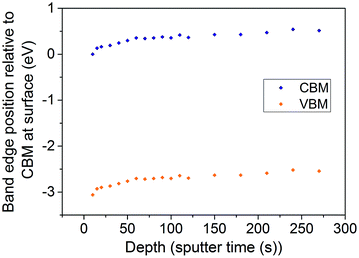
The Rh/Sb ratio can be calculated at each point along the depth profile of the co-doped TiO₂ (110) crystal shown in Fig. 2d. The position of the Fermi level relative to the band edges can then be estimated at each point by matching the Rh/Sb ratio with a curve drawn through the experimental points shown in Fig. 4. Using this method, and assuming that the Fermi level is constant in the material (and so it is the band edges that change energy with depth), we have calculated the conduction band minimum (CBM) and valence band maximum (VBM) positions as a function of depth in our TiO₂ (110) single crystal sample. This is shown in Fig. 7. It is clear that significant band bending, of around 0.5 eV, occurs due to the influence of the dopants spatial arrangement. It should be emphasised that only the effects of the dopants are shown in Fig. 7 – there will be other contributions to surface band bending, such as the presence of surface states, as occurs with all semiconductors.

Fig. 7 VBM and CBM variation with depth in a Sb/Rh codoped TiO₂ (110) crystal. The CBM at the surface is placed at 0 eV and the band gap is assumed to be 3.06 eV as in bulk rutile TiO₂. The Sb/Rh dopant ratio was measured by XPS depth profiling. This was correlated with the Fermi level shifts as described in the text.

The band bending postulated for TiO₂ (110) crystals may also apply to powders, and is likely to strongly affect charge carrier migration. The spatial confinement of dopants to affect (and effect) charge carrier migration is of fundamental importance in the field of silicon electronics. However, despite this the approach has not so far been intentionally taken in designing photocatalysts or photoelectrocatalysts. Our results indicate for the first time that a photocatalyst system exhibits spontaneous dopant segregation which is expected to cause significant band bending. This may contribute to the high photoactivity reported in this system; as previously stated Kudo and co-workers³² reported photoactivity of Rh and Sb codoped TiO₂ (where Sb/Rh = 0, 0.5, 1, 2 and 3 were investigated) and showed that, with Sb/Rh ≥ 2, O₂ evolution exceeds 10 μmol h⁻¹. This increased knowledge of the electronic properties of these materials may serve as a starting point for design of more highly effective photocatalysts. It is important to note that the materials we have synthesised are model systems; the use of solid state synthesis results in low surface area powders due to the high temperatures used. This renders the samples unsuitable for photocatalysis, but provides a quick, simple and highly reproducible route to production of the materials, allowing a high throughput of varying doping ratios. As such we were not able to measure water splitting from these samples, but work is ongoing to translate the design principles derived here to high surface area nanomaterials.

Conclusions

This study investigates the effect of dopant ratio on the structural and electronic properties of Rh/Sb codoped materials. Issues with XPS chemical shift referencing were overcome by using the position of the well-defined and chemically unchanged oxide O 1s peak as a reference from which movement of E_F (at 0 eV) and other core lines can be observed. The absolute position of oxide O 1s peaks across all codoped samples provided information about the position of E_F within the bandgap, which is dependent of Rh oxidation state. It was observed that the O 1s peak appears to decrease in binding energy, which is indicative of a lowering of the Fermi level energy, when doped with rhodium. However, the O 1s binding energy is restored and even increased from that of pristine TiO₂, with increasing levels of Sb codoping. It was determined that the Sb/Rh ratio must be atleast 1 to allow the Fermi level to revert to the position of pristine TiO₂. These materials could provide the basis for Z-scheme photocatalysts, with highly tunable band alignments.

Charge separation of O 1s and Rh 3d core lines provided further support that a reduction in oxidation state occurs when TiO₂:Rh is codoped with Sb. A larger core-line separation for codoped powders indicates that Rh 3d electrons are held at a lower binding energy than Rh 3d electrons singly doped TiO₂:Rh powders. This indicates, Rh³⁺ dominates in codoped powders whereas Rh⁴⁺ dominates in singly doped powders. This suppression of Rh⁴⁺ by Sb codoping was further corroborated by diffuse reflectance spectra, which show an additional absorption due to VB → Rh⁴⁺ 4d t_2g transitions.

All samples showed evidence of surface enrichment of the dopant ions, a phenomenon that has previously been observed for Sb in TiO₂ and SnO₂.^45,46 Sb incorporation was seen to cause migration of Rh from bulk to surface in all codoped powders, likely due to defect clustering of the Sb⁵⁺ and Rh³⁺ ions. A single crystal depth profile confirmed surface segregation of Sb in TiO₂:RhSb. This spontaneous spatial arrangement of the co dopants is expected to cause a built in electric field in the region of the semiconductor surface, which may strongly affect the photogenerated charge carrier migration and hence photocatalytic and photoelectrocatalytic efficiency.

Detailed characterisation of these materials has revealed that they exhibit interesting structural and electrical properties in the context of photocatalytic water splitting. Ability to control the position of the Fermi level by dopant ratio, and surface segregation of dopants and its electronic effects, provide two interesting possibilities for optimising photocatalytic materials.

Acknowledgements

RGP acknowledges EPSRC grant EP/K014099/1. ENKG thanks the Department of Chemistry, UCL for funding a studentship. Dr Matthew S. Dyer is thanked for helpful discussions. The authors acknowledge Diamond B18 beamtime allocation number SP10306. Diego Gianolio is thanked for assistance with XAS measurements.

Notes and references

1. I. P. Parkin and R. G. Palgrave, J. Mater. Chem., 2005, 15, 1689–1695.
2. K. Page, R. G. Palgrave, I. P. Parkin, M. Wilson, S. L. P. Savin and A. V. Chadwick, J. Mater. Chem., 2007, 17, 95–104.
3. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
4. K. H. A. Fujishima, Nature, 1972, 238, 1.
5. M. A. Henderson, Surf. Sci., 1996, 355, 151–166.
6. J. Tang, J. R. Durrant and D. R. Klug, J. Am. Chem. Soc., 2008, 130, 13885–13891.
7. A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515–582.
8. M. Ni, M. K. H. Leung, D. Y. C. Leung and K. Sumathy, Renewable Sustainable Energy Rev., 2007, 11, 401–425.
9. A. L. Linsebigler, G. Lu and J. T. Yates, Chem. Rev., 1995, 95, 735–758.
10. U. Diebold, J. Lehman, T. Mahmoud, M. Kuhn, G. Leonardelli, W. Hebenstreit, M. Schmid and P. Varga, Surf. Sci., 1998, 411, 137–153.
11. M. Pelaz, N. T. Nolan, S. C. Pillai, M. K. Seery, P. Falaras, A. G. Kontos, P. S. M. Dunlop, J. W. J. Hamilton, J. A. Byrne, K. O'Shea, M. H. Entezari and D. D. Dionysiou, Appl. Catal., B, 2012, 125, 19.
12. M. J. Powell, C. W. Dunnill and I. P. Parkin, J. Photochem. Photobiol., A, 2014, 281, 27–34.
13. C. W. Dunnill, Z. A. Aiken, A. Kafizas, J. Pratten, M. Wilson, D. J. Morgan and I. P. Parkin, J. Mater. Chem., 2009, 19, 8747–8754.
14. M. V. Dozzi and E. Selli, J. Photochem. Photobiol., C, 2013, 14, 13–28.
15. J. H. Park, S. Kim and A. J. Bard, Nano Lett., 2006, 6, 24–28.
16. H. Irie, Y. Watanabe and K. Hashimoto, Chem. Lett., 2003, 32, 772–773.
17. W. Ren, Z. Ai, F. Jia, L. Zhang, X. Fan and Z. Zou, Appl. Catal., B, 2007, 69, 138–144.
18. S. In, A. Orlov, R. Berg, F. García, S. Pedrosa-Jimenez, M. S. Tikhov, D. S. Wright and R. M. Lambert, J. Am. Chem. Soc., 2007, 129, 13790–13791.
19. N. Lu, X. Quan, J. Li, S. Chen, H. Yu and G. Chen, J. Phys. Chem. C, 2007, 111, 11836–11842.
20. Y. Matsumoto, T. Shimuzu and E. Sato, Electrochim. Acta, 1982, 27, 419–424.
21. I. Watanabe, Y. Matsumoto and E.-I. Sato, J. Electroanal. Chem. Interfacial Electrochem., 1982, 133, 359–366.
22. A. Kudo, R. Niishiro, A. Iwase and H. Kato, Chem. Phys., 2007, 339, 104–110.
23. Z. Zhang, A. Kladi and X. E. Verykios, J. Phys. Chem., 1994, 98, 6804–6811.
24. K. Maeda, D. Lu, K. Teramura and K. Domen, Energy Environ. Sci., 2010, 3, 470–477.
25. B. Kiss, C. Didier, T. Johnson, T. D. Manning, M. S. Dyer, A. J. Cowan, J. B. Claridge, J. R. Darwent and M. J. Rosseinsky, Angew. Chem., 2014, 126, 14708–14712.
26. H. J. Yun, H. Lee, N. D. Kim, D. M. Lee, S. Yu and J. Yi, ACS Nano, 2011, 5, 4084–4090.
27. W.-J. Chun, A. Ishikawa, H. Fujisawa, T. Takata, J. N. Kondo, M. Hara, M. Kawai, Y. Matsumoto and K. Domen, J. Phys. Chem. B, 2003, 107, 1798–1803.
28. Q. Wang, T. Hisatomi, S. S. K. Ma, Y. Li and K. Domen, Chem. Mater., 2014, 26, 4144–4150.
29. R. Niishiro, S. Tanaka and A. Kudo, Appl. Catal., B, 2014, 150, 187–196.
30. K. Furuhashi, Q. Jia, A. Kudo and H. Onishi, J. Phys. Chem. C, 2013, 117, 19101–19106.
31. R. Asai, H. Nemoto, Q. Jia, K. Saito, A. Iwase and A. Kudo, Chem. Commun., 2014, 50, 2543–2546.
32. R. Niishiro, R. Konta, H. Kato, W.-J. Chun, K. Asakura and A. Kudo, J. Phys. Chem. C, 2007, 111, 17420–17426.
33. S. Kitano, N. Murakami, T. Ohno, Y. Mitani, Y. Nosaka, H. Asakura, K. Teramura, T. Tanaka, H. Tada, K. Hashimoto and H. Kominami, J. Phys. Chem. C, 2013, 117, 11008–11016.
34. F. E. Oropeza and R. G. Egdell, Chem. Phys. Lett., 2011, 515, 249–253.
35. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
36. J. E. Castle, J. Adhes., 2008, 84, 368–388.
37. B. Erdem, R. A. Hunsicker, G. W. Simmons, E. D. Sudol, V. L. Dimonie and M. S. El-Aasser, Langmuir, 2001, 17, 2664–2669.
38. M. C. Biesinger, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2010, 257, 887–898.
39. M. V. Pessa, A. Vuoristo, M. Vulli, S. Aksela, J. Väyrynen, T. Rantala and H. Aksela, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20(8), 3115–3123.
40. V. Dzimbeg-Malcic, Z. Barbaric-Mikocevic and K. Itric, Tech. Gaz.–Univ. Osijek, 2011, 18, 7.
41. M. Kučera, J. Kuneš and R. Gerber, J. Appl. Phys., 1999, 85, 5986–5988.
42. K. Shinagawa, E. Tobita, K. Ando, T. Saito and T. Tsushima, J. Appl. Phys., 1997, 81, 1368–1371.
43. R. Konta, T. Ishii, H. Kato and A. Kudo, J. Phys. Chem. B, 2004, 108, 8992–8995.
44. G. C. Allen, G. A. M. El-Sharkawy and K. D. Warren, Inorg. Chem., 1973, 12, 2231–2237.
45. P. A. Cox, R. G. Egdell, C. Harding, W. R. Patterson and P. J. Tavener, Surf. Sci., 1982, 123, 179–203.
46. A. Gulino, G. G. Condorelli, I. Fragalà and R. G. Egdell, Appl. Surf. Sci., 1995, 90, 289–295.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ta00293e

---