Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optical properties of metal–organic networks from distributed atomic polarizabilities†
Michelle
Ernst
,
Leonardo H. R.
Dos Santos‡
and
Piero
Macchi
 *
*
Department of Chemistry and Biochemistry, University of Bern, Freiestrasse 3, Bern, CH3012, Switzerland. E-mail: piero.macchi@dcb.unibe.ch
First published on 13th June 2016
Abstract
Metal–organic networks have become very popular materials in view of various chemical and physico-chemical applications. Much attention is normally focused on porous compounds (metal–organic frameworks), although densely packed polymers may also find applications. In this paper, we propose a rather simplified method to estimate the dielectric constants and the optical indicatrices of metal–organic networks, which could be useful for rapid selection of materials with specific optical properties. The method adopts the distributed atomic polarizabilities calculated for secondary building units of metal–organic networks. With the atomic quantities, one can evaluate the crystal susceptibility, assuming an oriented gas model corrected for the polarization induced by the crystal medium. A simple oriented gas model enables a rapid evaluation of the anisotropy of the optical indicatrix of a crystal, as confirmed by calculations under periodic boundary conditions. The correction for polarization induced by the crystalline environment provides, in addition, more accurate estimation of the refractive indices, at least in the regime of low frequencies. The computational costs are smaller than those for fully periodic calculations and could be significantly smaller if a set of precomputed, transferable atomic polarizabilities would be used.
Introduction
In order to make materials science predictive, it is vital to address the molecular or sub-molecular key features that impart a specific property to the bulk.1 State of the art studies require a rather sophisticated and robust level of prediction. Therefore, empirical or heuristic approaches are nowadays not sufficiently accurate for engineering functional materials and selecting the most appropriate building blocks. First principles calculations of ideal crystals using periodic boundary conditions (PBC) may successfully predict materials properties, but the selection of the atoms, groups or molecules that trigger a given functionality is still empirical.2 In fact, a periodic wavefunction does not address directly which subpart of the system (crystal) contributes most to a specific property. Moreover, it suffers from significant computational costs, from an approximate description of the electron correlation effects (limited to density functional theory, DFT) and restrictions in the atomic one-electron basis sets.For materials based on molecular fragments, a suitable alternative is to calculate the specific contribution of each building block to the desired property, using molecular (instead of PBC) quantum mechanics. Once such a connection is established, the selection of a material from first principle calculations becomes more efficient, because only convenient combinations of suitable building blocks are to be tested.3
For this reason, engineering functional materials necessarily requires accurate evaluation of the connections between electronic features of atoms and groups and the bulk properties.4 This implies, first of all, a definition of atoms within molecules and within aggregations of molecules, as it occurs in crystals. The second step is the identification and quantification of the contribution of each atom or functional group to the crystalline properties. Finally, it is necessary to investigate how the atomic or group properties change due to intermolecular interactions.5 Once these criteria are fulfilled, a good predictive tool is one that minimizes the computational costs and the inaccuracy of the calculation, in order to provide a rapid, though reliable, estimation of the material properties.6
In view of developing a tool for engineering materials from their building blocks, we focus here on one family of materials, namely, metal–bioorganic networks (MBioF), and one kind of property, namely, light refraction. In particular, following a preliminary study on pure amino acids,6 we now aim at testing whether networks based on metal connectors and amino acid linkers could provide high refractive indices, at least along some directions of their crystal structures. High refractive index polymers are an important class of materials for technological applications, in particular for anti-reflecting coatings and wave-guides,7 and requirements of transparency and low conduction usually foster the research toward organic based polymers, often poly-aromatic chains.2,7 In this work, we aim at testing whether non-porous, densely packed coordination polymers may be suitable materials for high refractivity. Despite the inherent smaller transparency of transition metals in the visible range, they can increase the polarizabilities of the ligands and therefore that of the crystal, thus producing higher refractivity.
In our procedure, we adopt the Quantum Theory of Atoms in Molecules (QTAIM) to compute atomic or group polarizabilities in a crystal.8 QTAIM is one of the most popular methods for space partitioning into atomic domains and for estimating the exact subsystem contributions to a given electronic property. The adjective “exact” means that the total property of a system is the exact sum of the atomic components. The calculated value may, of course, suffer from imprecision and accuracy issues. The former may arise if numerical integration steps are necessary to estimate the atomic counterparts. Inaccuracies depend instead on the level of theory employed for the calculation of the wavefunction describing the system.
Other partition schemes are also able to provide exact atomic values, like Voronoi polyhedra, Hirshfeld atoms etc., whereas methods based on projection or fitting, like the multipolar expansion fitting of the electron density or the electrostatic potential, can only provide approximate quantities.
In previous works,6,9 we could demonstrate that functional group polarizabilities calculated with the QTAIM partitioning are quite transportable, meaning that the atomic and group tensors representing these quantities are sufficiently similar in different molecules and supramolecular aggregates. This enabled us to ascertain that some groups contribute more to the total crystal refractivity than others do. Thus, the three criteria enunciated above can be fulfilled. However, the ability to reconstruct the properties of a system from their parameterized building blocks needs further evaluation, especially for polymeric materials. The perturbation due to intermolecular interactions was already investigated in some hydrogen bonded species,10 whereas the combination of coordinative bonds and intermolecular interactions has not been investigated in detail yet.
Our analysis is structured as follows: first, we investigate the polarizabilities of secondary building units, i.e. the molecular subunits that assemble to produce coordination networks based on two reference amino acids (alanine and tryptophan) and a series of metals. Then, we estimate the crystal polarizabilities and dielectric susceptibilities based on different approaches. Finally, we compare these results with periodic DFT calculations of the electric susceptibilities.
Theoretical background and computational details
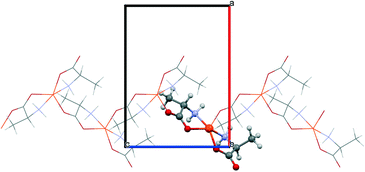
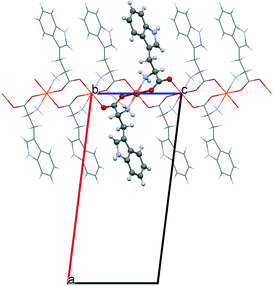
The starting geometries of the two network types investigated in this work are known as crystal structures, retrieved from the Cambridge Crystallographic Database,11 namely, Cu(L-Ala)2 (1, Fig. 1; Ala = C3H6NO2, CCDC refcode: CIYQAC12a) and M(D,L-Try)2 (2; Fig. 2; M = Mn,12c,e Fe,12d Co,12b Ni,12e Zn;12f Try = C11H11N2O2, CCDC refcodes: VENCOH01, SITPUH, POHRIO, TIPFAA, and HUHCOD01).1 -Cu crystallizes in a chiral space group (P212121), whereas all crystals of species 2 are isomorphic, with the racemic space group P21/c. In both kinds of structures, the stoichiometric ratio implies one metal cation to two amino acid anions; therefore, the crystal structures feature amino acids with a neutral amino group and an anionic carboxylate group (see Scheme 1). The protonation state is confirmed for 1 by neutron diffraction data.12a In 1, the asymmetric unit contains one metal cation and two amino acid anions, whereas in 2, the metal sits on an inversion center, and therefore, the asymmetric unit contains only one amino acid. In 1, the metal is overall coordinated to three anions, forming a distorted square-pyramidal environment (see Fig. 1), whereas in 2, four amino acids coordinate the metal, which sits in the center of a distorted octahedron, as shown in Fig. 2. In both structures, two amino acids chelate the metal with strong coordination bonds (N → and O → donor) forming a square-like plane (the base of the pyramid for 1, the equatorial plane of the distorted octahedron for 2). The apical sites in 1 and 2 are occupied, respectively, by one or two O → M coordinative bonds with other amino acids (see the ESI† for details on the geometries), which then bridge neighboring metals and form a one-dimensional chain (1) or a two-dimensional layer (2) (see Fig. 1 and 2). The apical bonds are weaker for all structures but 1-Zn. The coordination mode of 1 leaves one unsaturated electron donor oxygen, which is instead involved in weaker N–H⋯O bonds interconnecting different chains. In 2, the layers interact only through van der Waals forces.
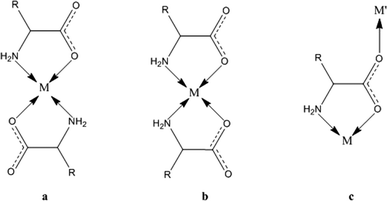 | ||
| Scheme 1 The coordination modes of an amino acid skeleton to a metal: the antiparallel and parallel coordination of two ligands (a and b) through glycinate chelation and the bridging mode (c). | ||
Although 1 is known only with Cu, isomorphic crystal structures (not yet known experimentally) were simulated, replacing Cu with other first row transition metals, ranging from Mn to Zn, all in the oxidation state +2. Despite only one crystal is known, this network type is representative of coordination modes, which are rather frequent also for the other metals (in MBioF as well). In fact, Ni and Zn show similar penta-coordination in other MBioFs with other amino acid linkers.
Periodic DFT calculations
We simulated the network structure types 1 and 2 applying periodic boundary condition calculations using the program CRYSTAL14.13For all calculations, we adopted the B3LYP density functional. We used basis sets specifically optimized for periodic calculations for the metal ions, namely, the functions proposed by Jaffe et al.14 (21s,13p,6d, contracted to 6s,5p,3d), and Pople-basis 6-31G(d,p) for C, N, O and H. For an unbiased comparison with the gas phase simulations (see below), a cc-pVDZ basis set was also tested, but serious wavefunction convergence problems occurred for all structures.
For the network type 1, only the Cu2+ structure is known, which is clearly affected by pseudo Jahn–Teller distortion. Therefore, for all other metals, crystal structures were fully optimized, using a dispersion correction, as proposed by Grimme.15 For the sake of consistency, also the experimentally known Cu structure was optimized.
For the structures of 2, which are all known from X-ray diffraction analysis, the experimental geometries of species containing Fe to Zn were used, after normalizing the positions of H atoms to satisfy averaged distances from neutron diffraction data. In order to investigate the role of the metal atomic size, we simulated structure 2 also with Cd ions, after geometry optimization. Because the same basis set of Jaffe et al.14 is not suitable for second row metals, we used instead effective core potentials.16 For a fair comparison, the structure of 2-Zn was also recalculated with the same potential.
Coupled perturbed Kohn–Sham calculations were used to compute analytically the crystal polarizability αcryst, and therefore the linear electric susceptibility χ, the dielectric constants ε and the refractive indices n, based on the optimized geometries.
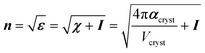 | (1) |
Noteworthy, αcryst, χ, ε and n are second order tensors and I is an identity matrix.
Gas phase DFT calculations on building blocks
If a crystal can be partitioned into constituent building blocks, the crystal polarizability αcryst may be approximated as: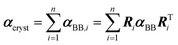 | (2) |
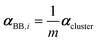 | (3) |
In this work, we adopted a modified cluster approach, based on secondary building units (SBU) of coordination networks. Noteworthy, the SBU may not be commensurate to the crystal asymmetric unit, as it occurs for species 1 and 2. From atomic partitioning, one can retrieve the appropriate asymmetric unit of the crystal and use these polarizabilities for calculation of the crystal properties. Therefore,
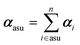 | (4) |
For the Cu structure of species 1 (1-Cu), we tested the effect of augmenting the SBU, modelling a chain of two or three metal centres and saturating the hydrogen bond sites with appropriate molecules (using NH3 and H2O). A full list of these results is given in the ESI.† For all the other structures, we tested only minimal SBUs calculated with or without a PCM environment.
The starting geometries of the building units came from the optimized crystal structures of species 1 or the known experimental structures of species 2 (see the previous section).
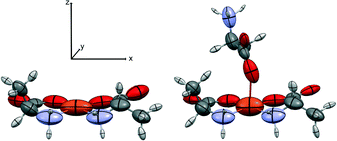
The distributed atomic polarizabilities of the fragment (Fig. 3 and 4) were calculated by numerical derivation according to Krawczuk et al.18 Gaussian 09 (ref. 19) was used to calculate the wavefunctions of the selected fragments with and without the application of an electric field (0.001 a.u.) along each one of the positive and negative x, y and z directions of an orthonormal coordinate system.18 The calculations were performed at the B3LYP/cc-pVDZ and B3LYP/aug-cc-pVDZ levels of theory.
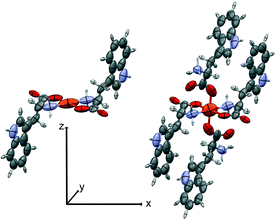 | ||
| Fig. 4 The SBUs used for the oriented gas model of 2-Fe. Left, the pseudo-square planar; right, the pseudo-octahedral complex. Symmetrized ellipsoids represent the atomic polarizability tensors, rescaled for the sake of clarity (see discussion in ref. 17). The local coordinate system is shown. | ||
The electron density distributions computed with and without the electric field were partitioned into individual atomic contributions according to the QTAIM scheme using AIMAll.20 Within the finite field approach, the atomic polarizabilities are the numerical derivatives of the dipole moment with respect to the electric field and were calculated using the program PolaBer.18 The polarizabilities of the atoms constituting the asymmetric unit yield the polarizability of the entire system and the dielectric properties, according to eqn (1)–(4).
Spin polarization
Some of the metal ions considered in our simulations are, of course, paramagnetic. For metal ions with uneven number of d electrons (Mn, Co and Cu), a spin polarized solution was calculated for both gas and crystalline phases, with the appropriate spin states and assuming ferromagnetic coupling. For the Zn structures, closed-shell solutions only were computed. For structures with Ni, we tested both the atomic spin S = 0 and S = 1 states, but the latter gave convergence problems under periodic boundary conditions, so full characterization was possible only for the gas phase calculations. Noteworthy, the presence of magnetic moments and the types of magnetic coupling occurring in the networks do not affect significantly the electric polarizabilities. In the ESI† (Table S4), we report the refractive indices calculated for 1-Ni assuming the metal in different spin states, showing small differences in the individual components of the optical indicatrix that do not change qualitatively the rationalization presented in the next section.Results and discussion
As discussed in the introduction, the strategy for selecting suitable building blocks for a high refraction material includes starting from the analysis of the building block polarizabilities in isolation. Our previous study6 demonstrated that amino acids containing phenyl groups in the lateral chains feature a larger polarizability density (i.e. polarizability per unit of volume). According to eqn (1), this should impart a higher refractivity to the structures, especially along the directions parallel to the aromatic ring. From calculations on atomic ground states,21 transition metals are known to exhibit a rather large polarizability, especially those centrally located in the transition series. This does not hold for cations in isolation, which are very poorly polarizable. However, in coordination complexes, the effective valence electrons of metals overwhelm the formal oxidation state and this leads to rather large polarizabilities, especially along the direction(s) of the coordination bonds. For example, Cu2+ in isolation has a polarizability of 2.5 Bohr3, compared to 42.6 Bohr3 for neutral Cu (from B3LYP/aug-cc-pVDZ calculations, in agreement with multi-reference complete active space calculations21). In Cu(L-Ala)2, the isotropic polarizability αCu = 14.4 Bohr3, with largest components along the Cu–O and Cu–N bonds (19.1 and 17.7 Bohr3, respectively). In addition, the highly polarizing power of metals enhances the ligand polarizabilities. For example, α of alanine increases by ca. 20% from the isolated anion to the QTAIM partitioned ligand in the Cu(L-Ala)2 square planar complex.On extending the complex into a polymer, the enhanced polarizabilities along Cu–ligand directions add up, due to the periodic and homogeneous arrangement of building blocks, eventually demonstrating significant optical anisotropy.
Secondary building units
The polymeric networks of species 1 and 2 contain penta- or hexa-coordinated metal cations. The amino acids may act as simple ligands in metal complexes or as linkers in metal networks,22 taking advantage of their rather flexible binding groups (see Scheme 1). All amino acids in anionic configurations possess at least three donor atoms: the two oxygens of the carboxylic group and the amino nitrogen. One of the classical coordination modes is the five-membered glycinate chelate ring (O,N-chelating mode, see Scheme 1), which leaves the other carboxylic oxygen available for coordination to another metal or for accepting a hydrogen bond.Both the model structures we analysed contain a double glycinate chelation (see Scheme 1), forming a strong “square planar” coordination, with the amino acids being parallel (1) or antiparallel (2). 1 is homochiral and has an asymmetric apical site around the metal, whereas 2 is racemic and the metal sits on an inversion centre, therefore producing symmetry related coordinations at the apical sites. As a result, the metal in 1 forms a square pyramid (with a long M–O apical bond), whereas in 2 it forms an elongated octahedron. The asymmetric coordination at the metal centre in 1 generates metal–amino acid chains interconnected through medium-weak N–H⋯O hydrogen bonds, whereas the symmetric coordination in 2 produces layers connected through weak van der Waals interactions (see Fig. 1 and 2).
We first computed the refractive indices of the structures using an oriented gas model and tested two kinds of secondary building units: a) the pseudo-square planar complex and b) the complexes including the axial coordination(s) as well (Fig. 3 and 4). Noteworthy, the square planar building unit corresponds to the asymmetric unit of crystal species 1 and twice the asymmetric unit of 2. In both cases, the secondary building unit with apical coordination exceeds the asymmetric unit. Using the atomic partitioning and eqn (4), one can extract the polarizabilities of the atoms within the asymmetric unit, thus allowing the calculation of the crystal dielectric constant and the refractivity. If at least one apical ligand is included, the axial component (direction z in Fig. 3 and 4) of the metal polarizability increases by ca. 15% at the expense of components x and y in the plane. Nevertheless, the metal polarizability (and that of the SBU) remains larger along the direction connecting the two linkers in the plane (direction x in Fig. 3 and 4). For example, in the experimental geometry of 1-Cu, αxx = 20.5 Bohr3, whereas αyy = 6.5 Bohr3 and αzz = 9.3 Bohr3. This is certainly a key feature of these networks, and therefore, one can anticipate a larger refractivity along this direction. Because of the 222 crystal symmetry of 1 (see Fig. 1), the x direction of the various SBUs are oriented along the ac diagonal, producing a zig-zag kind of packing, with the chain propagating along c (see Fig. 1). As a result, the oriented gas models predict that the c direction has the largest refractivity. Direction b is poorly polarizable, whereas a is intermediate. This analysis clearly shows that this packing motif is not efficient for maximizing the refractivity. In fact, a parallel, instead of a zig-zag, arrangement of the x directions of the SBUs would produce the largest refractivity. Calculations based on square planar SBUs give qualitatively similar results but larger anisotropy (see Table S3†).
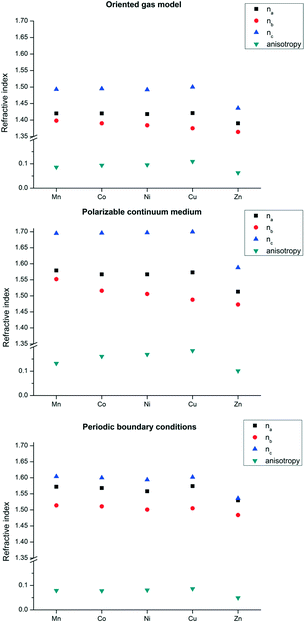
Fig. 5 reports the results of the oriented gas models with different metals for network 1. The global refractivity does not change much on changing the metal atom, apart from the Zn homologue that features a significant reduction though preserving the anisotropy. This is not unexpected because Zn behaves as a post transition metal, therefore with an inherently smaller atomic polarizability as it has no possibility to rearrange the electrons in the 3d shell. On the other hand, central transition metals are the most polarizable ones and a trend is clearly visible, albeit small.
For the structures of species 2, instead, the trans coordination mode in the equatorial plane makes the main direction of the polarizability not so evenly oriented. As a matter of fact, the metal polarizability tensors have the largest component preferentially along the N⋯N direction, therefore approximately along xy in Fig. 4. In addition, the lateral chain of tryptophan contains an indole fragment, which is, as all aromatic groups, highly polarizable in the plane.6 In tryptophan, this is almost perpendicular to the equatorial plane of the metal coordination sphere.
The combination of these two effects makes crystal direction a more polarizable (see Fig. 2). More precisely, the direction of highest polarizability forms an angle of ca. 25° with the unit cell direction a. The refractivity is therefore quite anisotropic (see Fig. 6). In species 2, the role of the metal seems to be less relevant, as the refractivity is almost independent from the number of d electrons and the spin state. Even the Zn structure has very similar refractive indices. The reason is that the organic part in this case is larger and the contribution of the metal is smaller, in relative terms.
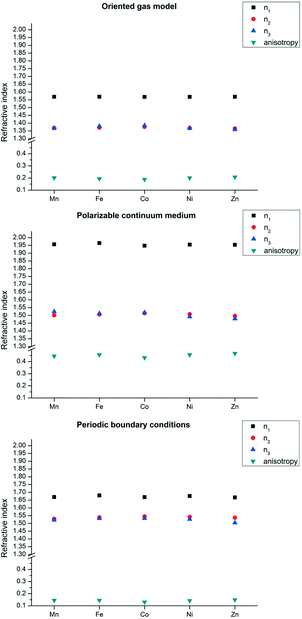 | ||
| Fig. 6 Refractive indices for structure 2 from oriented gas model polarizabilities, calculated using the pseudo-octahedral SBU (top), the same SBU in a PCM based on the average dielectric function of the crystal (centre) and with periodic boundary conditions (bottom). Symbols as in Fig. 5. Because of the crystal symmetry, n2 coincides with nb, whereas n1 and n3 do not coincide with na and nc. | ||
Secondary building units in polarizable medium
The results reported in the previous paragraph are rather straightforward. As we recently demonstrated,6 transferable atomic polarizabilities for each functional group and for the metal would lead to similar results. This model is optimal for a rapid prediction of the directions of highest refractivity in crystals, but it underestimates the effective refractivity, because it neglects the mutual polarization produced by packing the SBUs. The semi-classical approach of Lorentz–Lorenz correction,23a using the Lorentz dipole-tensor,23b can correct for this limitation. The induced electric field is calculated at some points of the building unit (e.g. the nuclear sites) and then assumed homogeneous, using the polarizability of the unit to calculate the induced dipole.24This approach can be improved using the distributed atomic polarizabilities, which means that the induction is evaluated from the field at each atomic site and the atomic polarizability.6 The results of Lorentz–Lorenz correction are reported in the ESI† (Fig. S2 and S3). Here, instead, we illustrate another procedure that does not depend on the evaluation of the field at specific sites, but it includes the effect in the Kohn–Sham molecular orbital calculations. Using the approximate dielectric constant obtained from the oriented gas model, one can perform a calculation in a polarizable continuum medium (PCM). The pitfall of this method is that the anisotropy of the permanent field is not taken into account, whereas the accuracy of the calculation is higher because the field induced polarization is inherently calculated at all points of the building unit and automatically included in the new polarizability. With PCM calculations, new atomic and SBU polarizabilities are obtained. The PCM generally increases the polarizability tensors by ca. 50%, resulting in refractive indices n about 0.15–0.3 larger, without modifying substantially the shape of the optical indicatrix calculated without PCM. In fact, the intramolecular chemical bonds are the ones that mainly determine the direction of highest polarizability. In the ESI,† the results obtained correcting the SBU oriented gas models with the Lorentz tensor are compared against PCM calculations, showing that these two approaches are quite comparable.
Noteworthy, the PCM procedure is computationally as expensive as the simple SBU oriented gas model described in the previous section or the SBU corrected by the Lorentz tensor. It actually requires an estimated dielectric constant of the material. A preliminary guess easily comes from the oriented gas model or even from transferable atomic polarizabilities, at very low computational costs. The procedure would instead be more time consuming if one is seeking a fine convergence of the dielectric constant, because this would require several iterations.
Periodic boundary conditions
As discussed in the introduction, the most accurate simulation of an ideal crystal is, in principle, a wavefunction calculation with periodic boundary conditions (PBC). Here, the crystal field is fully included in the self-consistent procedure at variance from the various cluster approaches presented above. There are however some inherent limitations:a) At variance from SBU simulations, PBC calculations cannot go beyond single determinant wavefunctions; therefore, the electron correlation is approximated at the density functional theory level.
b) In crystal orbital calculations (the method we adopted), the atomic basis sets are limited, because diffuse primitive functions produce divergence of the self-consistent field calculations.
c) Calculation with plane waves, instead, does not accurately describe the core electron densities, simulated only with pseudo-potentials.
The PBC calculated refractive indices of structure types 1 and 2 are reported in Fig. 5 and 6. These results confirm the type of anisotropy of the refractivity predicted by the oriented gas model, although, as expected, the overall refractivity is larger because interactions between the secondary building units are explicitly accounted for. For the two directions of lower refractivity, the PBC indices are quite close to those obtained for SBUs in a polarizable continuum medium. For the direction of largest refractivity, especially n1 of species 2, the PCM calculations predict significantly larger values for all metals. This discrepancy fosters experimental confirmations, which are presently not available. The difference between PBC and SBU + PCM could be due to the limited basis set used for the PBC calculations. The derived crystal polarizabilities may be inaccurate along the direction of the van der Waals connections between layers, which almost coincides with the direction of largest refractivity (as explained above). Directions with interruption of the covalent skeleton clearly depend more on the basis set incompleteness of crystal orbital calculations.
In order to investigate the effect of metal size, we carried out PBC calculations of 2-Cd. This structure is not known, and therefore, it was optimized (see the experimental section for details). Because this required an effective core potential basis set, the 2-Zn homologue was also calculated with the same functions for a fair comparison. The two optical indicatrices are very similar with differences within 0.01 for each direction. The angle between the two optical axes is however quite smaller for Cd than for Zn (49° vs. 66°). In general, one cannot expect severe changes to occur through the transition series, because the contribution of the metal polarizability is not so large.
Conclusions
In this work, we used distributed atomic polarizabilities to investigate the light refractivity of metal–organic coordination networks. The purpose of this work was twofold: a) testing a new portable method for rapid identification of directions of large refractivity in crystals and b) checking if non-porous metal–organic polymers could act as high refractive index materials.The distributed atomic polarizabilities offer a useful partitioning of SBUs and address the key features necessary for enhancing the refractivity. In particular, calculations of SBUs in a polarizable continuum medium lead to sufficiently reliable refractivities, offering the following advantages: a) computational costs are smaller than PBC by ca. one order of magnitude; b) the partition into atomic polarizabilities addresses the individual contribution of each building block; c) post-Hartree–Fock calculations are doable; d) there is no basis set limitation.
All simulations shown in this work assumed a static field, therefore ideally an infinite wavelength. Of course, practical applications requires knowing the refractivity at a specific wavelength, for example in the visible region. The atomic partitioning based on QTAIM requires a static electron density; therefore, it is not applicable to systems perturbed by an oscillating electric field. However, as recently proposed by Champagne and co-workers,25 an appropriate scaling of the QTAIM atomic polarizabilities would enable an estimation of the wavelength dispersion. The scale factor for the atomic polarizabilities would correspond to the ratio between cluster (or SBU) polarizabilities computed with double energy derivatives at infinite and finite wavelengths.
For the networks analysed in this paper, we conclude that the stereochemistry at the metal centre plays a central role for the crystal refractivity. In fact, the directions of largest refraction occur along the coordinative bonds. This is not only due to the M–O or M–N bonds themselves but also due to the specific conformation that the metal coordination imposes to the organic linkers. The side chain of the amino acid is then useful to tune the polarizability of the linker, using suitable functional groups and the packing may amplify or quench the features of a secondary building unit. The metal polarizability itself is, instead, much less important, given that only minor trends are visible along a transition series and even a post-transition metal does not affect too much the refractivity, especially if the organic linker is large. On changing the transition series, the differences are also quite smaller.
The choice of the metal is, of course, more important when the transmittance in the visible range is considered. Only the Zn polymers would be ideal in this respect.
In conclusion, we have shown that the combination of transferable polarizabilities and automation in the calculation of SBU polarizabilities from parametrized atomic polarizabilities will enable a more rapid screening of the suitable species in the future.
Acknowledgements
We thank the Swiss National Science Foundation for financial support (project 160157).Notes and references
- Supramolecular Materials for Opto-Electronics, RSC Smart Materials series, ed. N. Koch, The Royal Society of Chemistry, Cambridge, 2015 Search PubMed.
- H. Ma, A. K.-Y. Jen and L. R. Dalton, Adv. Mater., 2002, 14, 1339–1365 CrossRef CAS.
- M. Spackman, Charge Densities and Crystal Engineering, in Modern Charge-Density Analysis, ed. C. Gatti and P. Macchi, Springer, Heidelberg, 2012, ch. 16, pp. 553–573 Search PubMed.
- P. Macchi, Chimia, 2014, 68, 31–37 CrossRef CAS PubMed.
- B. Champagne and D. M. Bishop, Adv. Chem. Phys., 2003, 126, 41–92 CAS.
- L. H. R. Dos Santos, A. Krawczuk and P. Macchi, J. Phys. Chem. A, 2015, 119, 3285–3298 CrossRef CAS PubMed.
- T. Higashihara and M. Ueda, Macromolecules, 2015, 48, 1915–1929 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules – A Quantum Theory, Oxford University Press/Clarendon Press, Oxford, 1994 Search PubMed.
- A. Krawczuk-Pantula, D. Pérez, K. Stadnicka and P. Macchi, Trans. Am. Crystallogr. Assoc., 2012, 41, 1–25 Search PubMed.
- L. H. R. Dos Santos and P. Macchi, Crystals, 2016, 6, 43 CrossRef.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- (a) S. M. Moussa, R. R. Fenton, B. J. Kennedy and R. O. Piltz, Inorg. Chim. Acta, 1999, 288, 29–34 CrossRef CAS; (b) J. Wang, X. Xu, W. Ma, X. Hu, P. Shi, M. Wang, L. Lu, X. Yang and X. Wang, Chin. J. Inorg. Chem., 2008, 24, 1514–1518 CAS; (c) W. Jian, Ph. D. Thesis, Nanjing University of Science and Technology, China, 2009 Search PubMed; (d) J. Wang, X. Xu, W. Ma, R. Xu, Y. Tong, L. Lu, X. Yang and D. Wang, Chin. J. Struct. Chem., 2008, 27, 153–158 Search PubMed; (e) J. Wang, X. Xu, W. Ma, L. Lu and X. Yang, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, m2867–m2868 CAS; (f) S. Shen and L. Zhao, Z. Anorg. Allg. Chem., 2011, 637, 2099–2101 CrossRef CAS.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà and Y. Noël, CRYSTAL14 User's Manual., University of Torino, Torino Search PubMed.
- J. E. Jaffe and A. C. Hess, Phys. Rev. B, 1993, 48, 7903–7909 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299 CrossRef CAS; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS.
- K. Wu, J. G. Snijders and C. Lin, J. Phys. Chem. B, 2002, 106, 8954–8958 CrossRef CAS.
- A. Krawczuk, D. Pérez and P. Macchi, J. Appl. Crystallogr., 2014, 47, 1452–1458 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- Todd A. Keith, AIMAll (Version 16.01.09), TK Gristmill Software, Overland Park, KS, USA, 2016 (aim.tkgrisstmill.com) Search PubMed.
- J. Klos, J. Chem. Phys., 2005, 123, 024308 CrossRef CAS PubMed.
- I. Imaz, M. Rubio-Martínez, J. An, I. Solé-Font, N. L. Rosi and D. Maspoch, Chem. Commun., 2011, 47, 7287–7302 RSC.
- (a) R. W. Munn, Mol. Phys., 1988, 64, 1–20 CrossRef; (b) G. Cummins, D. A. Dunmur, R. W. Munn and R. J. Newham, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 847–853 CrossRef.
- M. A. Spackman, P. Munshi and D. Jayatilaka, Chem. Phys. Lett., 2007, 443, 87–91 CrossRef CAS.
- T. Seidler, A. Krawczuk, B. Champagne and K. Stadnicka, J. Phys. Chem. C, 2016, 120, 4481–4494 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Optimized crystal geometries, results of calculations with Lorentz correction and with larger secondary building units. See DOI: 10.1039/c6ce00918b |
| ‡ Current address: Department of Chemistry, The University of Toledo, 2801 W. Bancroft St., OH 43606, Toledo, USA. |
| This journal is © The Royal Society of Chemistry 2016 |