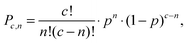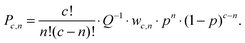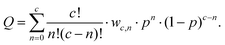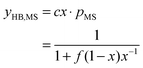Hydrogen bonding in a mixture of protic ionic liquids: a molecular dynamics simulation study
Received
21st November 2014
, Accepted 20th January 2015
First published on 21st January 2015
Abstract
We report results of molecular dynamics (MD) simulations characterising the hydrogen bonding in mixtures of two different protic ionic liquids sharing the same cation: triethylammonium-methylsulfonate (TEAMS) and triethylammonium-triflate (TEATF). The triethylammonium-cation acts as a hydrogen-bond donor, being able to donate a single hydrogen-bond. Both, the methylsulfonate- and the triflate-anions can act as hydrogen-bond acceptors, which can accept multiple hydrogen bonds via their respective SO3-groups. In addition, replacing a methyl-group in the methylsulfonate by a trifluoromethyl-group in the triflate significantly weakens the strength of a hydrogen bond from an adjacent triethylammonium cation to the oxygen-site in the SO3-group of the anion. Our MD simulations show that these subtle differences in hydrogen bond strength significantly affect the formation of differently-sized hydrogen-bonded aggregates in these mixtures as a function of the mixture-composition. Moreover, the reported hydrogen-bonded cluster sizes can be predicted and explained by a simple combinatorial lattice model, based on the approximate coordination number of the ions, and using statistical weights that mostly account for the fact that each anion can only accept three hydrogen bonds.
1 Introduction
During the past 15 years ionic liquids (ILs) have received great attention from the scientific community.1–4 More recently, also the ability to design targeted liquid properties by forming binary and ternary mixtures has become a focus of interest.5,6 In particular, it has been recognized that the balance between different competing interactions, such as Coulomb interactions, van der Waals interactions, and hydrogen bonds is of great importance. In a situation, where strong (Coulombic) forces compete with each other and partly cancel each other out, also weaker interactions, such as hydrogen-bonds, might be able to significantly affect the properties of the fluid.7,8 This is particularly important for mixtures of ionic liquids, where different constituents (ions) might compete with each other for specific interactions. The mixing behavior of several ionic liquids has been discussed recently with a focus on their thermodynamic and transport properties.5,6,9–13 However, mostly the behavior of aprotic ionic liquids has been considered so far. We would like to point out that physical properties reported in these studies, such as the density and the viscosity, were mostly exhibiting ideal-like mixing behavior in the sense that the properties vary almost linearly with the mixture composition. In addition, also the molar mixing-enthalpies and -entropies indicated only a small deviation from the ideal mixture-behavior.10,11 Recently, Welton and co-workers have commented on the tendency for ideal-mixture behavior in mixtures of ionic liquids and reviewed IL mixtures with a focus on property design an opportunities for applications.5,9
The situation seems to be different for protic ionic liquids, where strongly directional hydrogen-bonds (can) exist.14,15 We could show very recently, that for a mixture of triethylammonium-methylsulfonate (TEAMS) and triethylammonium-triflate (TEATF), which are both sharing the same cation, the two different anions compete with each other for a hydrogen bond to the triethylammonium-cation (TEA).16 Using far-infrared spectroscopy, we could assign signatures distinguishing between hydrogen-bonded aggregates of TEA to each of the two anions within the mixture.16 A population analysis as a function of mixture-composition is suggesting a favorable interaction of TEA with the methylsulfonate-ion. In addition, also the experimentally determined viscosity is showing a strongly non-linear mixture dependence, pointing at the changing size of aggregates in the liquid as a function of the mixture-composition.16 With the present study we would like to complement our earlier endeavour with an in-depth analysis of a detailed molecular model of the same binary TEATMS–TEATF mixture, focusing on the local solvation-structure of the ions, and, in particular, on the hydrogen-bonding. In addition, we will show that the size of the hydrogen-bonded aggregates can be predicted and explained by a simple combinatorial lattice model, which is based on an approximate coordination number of the ions, and is using statistical weights that mostly account for the fact that each anion can only accept up to three hydrogen bonds.
Finally, we would like to point out that Rogers and co-workers have argued recently that ions in a mixture of ILs do not seem to retain their individual nature and proposed to consider them as double salt ionic liquids.6 Double salts are salts containing more than one cation or anion, obtained by combination of two different salts which were crystallized in the same regular ionic lattice. Although this definition is not strictly applicable to the case of an amorphous state such as a liquid, we can provide evidence for double-salt-like behavior of the TEAMS–TEATF mixture.
2 Methods
2.1 Molecular dynamics simulations
We employ molecular dynamics (MD) simulations in the isobaric isothermal (NPT) ensemble using the Nosé–Hoover thermostat17,18 and the Rahman–Parrinello barostat19,20 with coupling-times τT = 0.5 ps and τp = 2 ps (assuming the isothermal compressibility to be χT = 5 × 10−5 bar−1), respectively. The electrostatic interactions are treated in the “full potential” approach by the smooth particle mesh Ewald summation21 with a real space cutoff of 1.0 nm and a mesh spacing of approximately 0.12 nm and 4th order interpolation. The Ewald convergence factor α was set to 3.38 nm−1 (corresponding to a relative accuracy of the Ewald sum of 10−5). A 2.0 fs timestep was used for all simulations and the constraints were solved using the SETTLE procedure.22 During the simulations all bond-length were kept fixed. All simulations reported here were carried out using the GROMACS 4.6 program.23,24 Statistical errors in the analysis were computed using the method of Flyvbjerg and Petersen.25 For all reported mixtures and temperatures initial equilibration runs of 1 ns length were performed using the Berendsen weak coupling scheme for pressure and temperature control τT = τp = 0.5 ps.26 A total of 16 different compositions were investigated with compositions of x = xCH3SO3 = {0.0, 0.125, 0.25, 0.3125, 0.40625, 0.5, 0.5625, 0.625, 0.6875, 0.75, 0.8125, 0.84375, 0.875, 0.90625, 0.9375, 1.0} at T = 300 K, 300 K, and 400 K. In each case the simulated system consisted of 256 ion pairs in a cubic box with periodic boundary conditions. As shown in Fig. 1, the density of the model-system follows rather well the experimental density, both as a function of temperature and composition. Production runs of 120 ns (300 K), 48 ns (350 K), and 24 ns (400 K) simulation-length were finally recorded and analyzed.
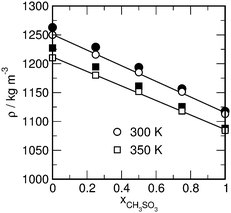 |
| | Fig. 1 Densities of selected TEATF–TEAMS mixtures as a function of their composition as obtained from the molecular dynamics simulations at 300 K and 350 K, respectively. The closed symbols refer to experimental densities obtained at 298 K and 343 K.16 | |
2.2 The molecular model
For the description of the potential model, a classical forcefield approach has been used, similar to the OPLS-model of Jorgensen et al.27 All employed partial charges are atom-centered and were determined from ab initio calculations of the individual ions by applying many body perturbation theory (MP2) and using the 6-311++G** basis set. All reported ab initio calculations were performed with the Gaussian 09 program.28 The charges were fitted to the electrostatic potential surrounded by the atoms using the ESP29 and RESP30 methods. Due to the rather small size of the ions no significant changes were found between the ESP and RESP charges. CH3- and CH2-groups treated as united atoms and represented by a single interaction site. Nonbonded Lennard-Jones parameters for the triflate-ions were taken from the [NTF2] forcefield-model of Köddermann et al.,31 while the starting point for the nonbonded parameters for the triethylammonium were parameters reported by Krienke et al.32 for the ammonium group, in addition to the TraPPE-parameters of Martin and Siepmann33 for the united-atom CH3- and CH2-groups. The σ-parameter for the nitrogen atom needed to be resized to 3.25 Å in order to match the H⋯O distance of the hydrogen bonded ion pair in the gas-phase with the distance obtained for the energy minimized structure using ab initio calculations. Constant pressure simulations of the model describes the density of triethylammonium-triflate quite satisfactorily. For the methylsulfonate-ion, the Lennard-Jones parameters of Köddermann were also used for the SO3-group. The starting point for the Lennard-Jones parameters for the methyl-group was again the forcefield of Martin and Siepmann.33 In this case, the Lennard-Jones σ of the methyl-group needed to be resized to match the density of the liquid phase of neat triethylammonium-methylsulfonate. Due to a significantly stronger bond-polarization of the S–O bond within the methylsulfonate-ion, compared to the triflate-ion, larger partial charges on the oxygens were obtained for the methylsulfonate, leading to stronger hydrogen-bonding with the triethylammonium ion. In order to represent molecular configurations of the ions properly, the equilibrium bond distances and angles were adjusted in such a way that they lead to minimum energy configurations close to the structures obtained from the ab initio calculations. All nonbonded Lennard-Jones parameters and partial charges are summarized in Table 1. The bond-length and bond-bending parameters can be found in Tables 2 and 3. Dihedral potentials for intramolecular torsions around the N–C2-bond in the triethylammonium ion and the S–C-bond in the triflate ions were fitted to ab initio calculations to represent the molecular conformations accurately. The values are summarized in Table 4. The full torsion potential also include nonbonded 1–4-interactions. Here both, the nonbonded Lennard-Jones and Coulomb 1–4-interactions are scaled by a factor of 0.5.
Table 1 Non-bonding Lennard-Jones interaction parameters with Vij = 4εij[(σij/rij)12 − (σij/rij)6] and partial charges used in the MD Simulations of the PIL-mixtures. Lorentz–Berthelot mixing-rules with σij = (σii + σjj)/2 and εij = (εii·εjj)1/2 were applied for determining the cross-parameters
| Atom i |
σ
ii
/Å |
ε
ii
·kB−1/K |
q
i
/|e| |
| Triflate |
| S |
4.08 |
37.3 |
1.40 |
| O |
3.46 |
31.7 |
−0.73 |
| C |
3.15 |
10.0 |
0.48 |
| F |
2.66 |
8.0 |
−0.23 |
|
|
| Methylsulfonate |
| S |
4.08 |
37.3 |
1.620 |
| O |
3.46 |
31.7 |
−0.825 |
| C3 |
2.90 |
98.0 |
−0.145 |
|
|
| Triethylammonium |
| H |
0.0 |
0.0 |
0.37 |
| N |
3.25 |
75.0 |
−0.39 |
| C2 |
3.95 |
46.0 |
0.28 |
| C3 |
3.75 |
98.0 |
0.06 |
Table 2 Harmonic bond-stretching parameters employed in the forcefield model using Vbij = (kbij/2)·(rij − r0ij)2
| Bond i–j |
r
0
ij
/Å |
k
b
ij
/kJ mol−1 Å−2 |
| Triflate |
| C–F |
1.347 |
3700.0 |
| C–S |
1.860 |
1850.0 |
| O–S |
1.469 |
5850.0 |
|
|
| Methylsulfonate |
| C3–S |
1.8040 |
1850.0 |
| O–S |
1.4816 |
5850.0 |
|
|
| Triethylammonium |
| H–N |
1.020 |
2500.0 |
| C2–N |
1.500 |
2500.0 |
| C2–C3 |
1.540 |
2500.0 |
Table 3 Harmonic bond-bending parameters employed in the forcefield model using Vaijk = (kaijk/2)·(θijk − θ0ijk)2
| Angle i–j–k |
θ
0
ijk
/degrees |
k
a
ijk
/kJ mol−1 rad−2 |
| Triflate |
| F–C–F |
108.4 |
650.0 |
| F–C–S |
110.5 |
420.0 |
| C–S–O |
102.6 |
620.0 |
| O–S–O |
119.5 |
850.0 |
|
|
| Methylsulfonate |
| C3–S–O |
104.26 |
620.0 |
| O–S–O |
114.14 |
850.0 |
|
|
| Triethylammonium |
| H–N–C2 |
108.4 |
460.0 |
| C2–N–C2 |
108.4 |
460.0 |
| C3–C2–N |
108.4 |
460.0 |
Table 4 Dihedral-potential for the rotation around the N–C2 bond in the triethylammonium-ion and for the C–S bond in the triflate-ion according to 
|
m(i–j–k–l) |
n
m
|
k
dm/kJ mol−1 |
| Triflate F–C–S–O |
| 1 |
3.0 |
0.8619 |
|
|
| Triethylammonium H–N–C2–C3 |
| 1 |
1.0 |
8.734 |
| 2 |
2.0 |
3.224 |
| 3 |
3.0 |
5.514 |
| 4 |
4.0 |
−0.465 |
| 5 |
5.0 |
−0.481 |
| 6 |
6.0 |
0.756 |
3 Discussion
3.1 Structure of the ionic liquid mixture
To provide an impression of the structure of the discussed ionic liquid mixture, a snapshot of the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of TEATF–TEMS at T = 300 K is given in Fig. 2. Indicated are the positions of the centers of mass of the ions, which can be identified via their respective colors. From visual inspection it is evident that the charge of the ions impose a long-range ion-alternating order, which is leading to a significant structural homogeneity of the ionic liquid. This behavior is typical for ionic liquids and has been pointed out earlier by Maroncelli and co-workers.34 The ion-alternating order is a consequence of the fact that the ions are predominantly surrounded by a solvation shell of ions with opposite charge. This defining structural feature is well represented by the location of the first peak of the center-of-mass pair distribution functions of the ions: in Fig. 3a and b the center-of-mass pair distribution functions for all ion-pair combinations are shown for a 50
50 mixture of TEATF–TEMS at T = 300 K is given in Fig. 2. Indicated are the positions of the centers of mass of the ions, which can be identified via their respective colors. From visual inspection it is evident that the charge of the ions impose a long-range ion-alternating order, which is leading to a significant structural homogeneity of the ionic liquid. This behavior is typical for ionic liquids and has been pointed out earlier by Maroncelli and co-workers.34 The ion-alternating order is a consequence of the fact that the ions are predominantly surrounded by a solvation shell of ions with opposite charge. This defining structural feature is well represented by the location of the first peak of the center-of-mass pair distribution functions of the ions: in Fig. 3a and b the center-of-mass pair distribution functions for all ion-pair combinations are shown for a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture obtained at 300 K. From Fig. 3a we can conclude that the first peak of the anion–cation pair correlation function is shifted to significantly lower values, with the dominant first peak of the TEA–MS-pair found at 0.41 nm, and the peak of the TEA–TF-pair at 0.54 nm. The first TEA–TEA-peak is found at a much larger distance of 0.70 nm. The anion–anion pair correlation functions are shown in Fig. 3b: here, we would like to point out that, besides the dominant main first peak around 0.8 nm, there also exists pre-peak at a distance of about 0.55 nm, which is most strongly pronounced for the correlation between the two methylsulfonate ions, and is only weakly pronounced in the pair-correlation of the triflate-ions. In addition, Fig. 3b also shows that this structural feature of the first peak is completely absent for the TEA–TEA correlations. The pre-peak in the anion–anion pair correlation function is indicating the existence of direct anion–anion contacts, whereas direct cation–cation contacts are apparently avoided. Moreover, also the snapshot in Fig. 2 reveals the presence of anion–anion-pairs in close proximity on many occasions.
50 mixture obtained at 300 K. From Fig. 3a we can conclude that the first peak of the anion–cation pair correlation function is shifted to significantly lower values, with the dominant first peak of the TEA–MS-pair found at 0.41 nm, and the peak of the TEA–TF-pair at 0.54 nm. The first TEA–TEA-peak is found at a much larger distance of 0.70 nm. The anion–anion pair correlation functions are shown in Fig. 3b: here, we would like to point out that, besides the dominant main first peak around 0.8 nm, there also exists pre-peak at a distance of about 0.55 nm, which is most strongly pronounced for the correlation between the two methylsulfonate ions, and is only weakly pronounced in the pair-correlation of the triflate-ions. In addition, Fig. 3b also shows that this structural feature of the first peak is completely absent for the TEA–TEA correlations. The pre-peak in the anion–anion pair correlation function is indicating the existence of direct anion–anion contacts, whereas direct cation–cation contacts are apparently avoided. Moreover, also the snapshot in Fig. 2 reveals the presence of anion–anion-pairs in close proximity on many occasions.
 |
| | Fig. 2 Snapshot of a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of TEATF–TEAMS at T = 300 K. The spheres represent the centers of gravity of the ions. The TEA-positions are indicated by blue spheres. The triflate- and methylsulfonate-positons are color-coded in white and yellow, respectively. 50 mixture of TEATF–TEAMS at T = 300 K. The spheres represent the centers of gravity of the ions. The TEA-positions are indicated by blue spheres. The triflate- and methylsulfonate-positons are color-coded in white and yellow, respectively. | |
 |
| | Fig. 3 Complete set of ion–ion center of mass pair distribution functions g(r) obtained for the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of TEATF–TEMS at T = 300 K. 50 mixture of TEATF–TEMS at T = 300 K. | |
The coordination number of the ion-solvation is deduced from the anion–cation pair correlation functions, shown in Fig. 4a and b for both pure ionic liquids. First, we would like to point at the characteristic three-sub-peak nature of peak of the first solvation-shell, which is present in both ionic liquids, although significantly more “structured” in the case of TEAMS. The integral over the pair correlation function reveals the number of neighbors as function of their distance
| | 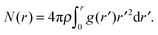 | (1) |
Here
ρ represents the number density of the selected ion-species. The data for
N(
r) are also given in
Fig. 4. Integrating over the entire first peak leads to a consistent number of nearest neighbors of about 6.8 to 6.9 counter-ions for both ionic liquids. Here, the first sub-peak corresponds in both cases to about one neighbor, strongly suggesting that this is indicative of a hydrogen-bonded ion-pair configuration. The second and third sub-peaks are contributing about three additional neighbors each. Both are apparently related to configurations with different orientational order. As shown in
Fig. 5, the average first-shell counter-ion coordination number of about 6.8 to 6.9 remains constant over the entire mixture range.
 |
| | Fig. 4 Anion–cation center of mass pair distribution functions g(r) obtained for (a) pure TEAMS and (b) pure TEATF at T = 300 K. The position of the first minimum is used as a cut-off distance for the nearest neighbor computation (TEA–MS: 0.78 nm, TEA–TF: 0.81 nm). | |
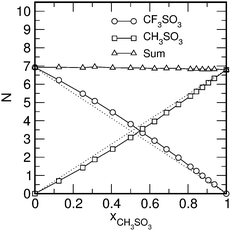 |
| | Fig. 5 Average number of both anion species N, as well as their sum, found in the first solvation shell of a TEA-cation as a function of mixture composition at T = 300 K. | |
At this point we would like to discuss apparent deviations from an ideal mixture-behavior in these ionic liquids: a significant structural difference between the pure liquids and the mixture is observed for first sub-peak of the anion–cation pair distribution functions for the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 TEATF–TEAMS mixture, shown in Fig. 3a, compared to the pure liquids shown in Fig. 4. From Fig. 4 it is evident that the first sub-peak has about the same height for both pure ionic liquids. In the 50
50 TEATF–TEAMS mixture, shown in Fig. 3a, compared to the pure liquids shown in Fig. 4. From Fig. 4 it is evident that the first sub-peak has about the same height for both pure ionic liquids. In the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture (Fig. 3a), however, the first peak is very strongly pronounced for the TEA–MS pair, and is almost completely absent for the TEA–TF pair, which is suggesting a preference for the formation of TEA–MS hydrogen bonded conformations. This preference is also evident from Fig. 2, where many of the supposedly hydrogen-bonded TEA–MS-pairs can be identified as dumbbell-like configurations, formed by a pair of blue and yellow spheres. This imbalance of the hydrogen-bond strengths has also a surprising consequence for the structure of solvation-shells of the ions in the mixture. In Fig. 5 the average coordination-number of the anions surrounding a central cation is depicted as a function of the mixture-composition. While the total number of anions varies only slightly between 6.8 and 6.9 as a function of mixture composition, the build-up of the individual solvation shells changes more strongly: as shown in Fig. 5, in a 50
50 mixture (Fig. 3a), however, the first peak is very strongly pronounced for the TEA–MS pair, and is almost completely absent for the TEA–TF pair, which is suggesting a preference for the formation of TEA–MS hydrogen bonded conformations. This preference is also evident from Fig. 2, where many of the supposedly hydrogen-bonded TEA–MS-pairs can be identified as dumbbell-like configurations, formed by a pair of blue and yellow spheres. This imbalance of the hydrogen-bond strengths has also a surprising consequence for the structure of solvation-shells of the ions in the mixture. In Fig. 5 the average coordination-number of the anions surrounding a central cation is depicted as a function of the mixture-composition. While the total number of anions varies only slightly between 6.8 and 6.9 as a function of mixture composition, the build-up of the individual solvation shells changes more strongly: as shown in Fig. 5, in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
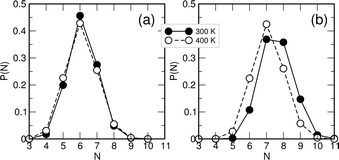
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture the average number of TF-anions (NTF = 3.82) in the first solvation shell of a TEA-cation is significantly larger than the number of MS-anions (NMS = 3.08). This imbalance is also represented in the solvation shell of the anions: Fig. 6 shows the distribution of the number of the TEA-cations in the first solvation shell around each anion. For the pure ionic liquids (given in Fig. 6a), the distribution functions are almost identical with a maximum at 7 neighbors. In the 50–50 mixture, however, the distribution for methylsulfonate is shifted to lower values, with a maximum at 6, whereas the distribution for triflate is shifted to larger values. Apparently, the triflate-ion is able to “steal away” cations from the methylsulfonate in the mixture. This effect might be just due to the larger size of triflate-ion compared to the methylsulfonate. However, the reduced number of TEA-cations in the solvation shell of methylsulfonate leaves the methylsulfonate-ion prone to direct anion–anion contacts in the mixture as observed in Fig. 3. The number of TEA-cations attracted by the triflate- and methylsulfonate-ions is related with an average free energy of association, which has, of course, both entropic and an enthalpic contributions. The temperature dependence of the distribution functions shown in Fig. 7 indicates that the “binding” of TEA to the triflate-ion is significantly more temperature-sensitive than that of TEA to the methylsulfonate-ion and, hence, can be considered more weakly.
50 mixture the average number of TF-anions (NTF = 3.82) in the first solvation shell of a TEA-cation is significantly larger than the number of MS-anions (NMS = 3.08). This imbalance is also represented in the solvation shell of the anions: Fig. 6 shows the distribution of the number of the TEA-cations in the first solvation shell around each anion. For the pure ionic liquids (given in Fig. 6a), the distribution functions are almost identical with a maximum at 7 neighbors. In the 50–50 mixture, however, the distribution for methylsulfonate is shifted to lower values, with a maximum at 6, whereas the distribution for triflate is shifted to larger values. Apparently, the triflate-ion is able to “steal away” cations from the methylsulfonate in the mixture. This effect might be just due to the larger size of triflate-ion compared to the methylsulfonate. However, the reduced number of TEA-cations in the solvation shell of methylsulfonate leaves the methylsulfonate-ion prone to direct anion–anion contacts in the mixture as observed in Fig. 3. The number of TEA-cations attracted by the triflate- and methylsulfonate-ions is related with an average free energy of association, which has, of course, both entropic and an enthalpic contributions. The temperature dependence of the distribution functions shown in Fig. 7 indicates that the “binding” of TEA to the triflate-ion is significantly more temperature-sensitive than that of TEA to the methylsulfonate-ion and, hence, can be considered more weakly.
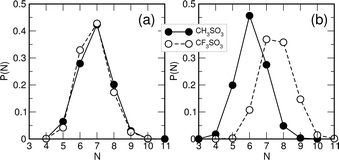 |
| | Fig. 6 Distribution of the number N of TEA-cations in the first solvation shell of the triflate- and methylsulfonate-anions at T = 300 K. (a) Pure ionic liquids (b) 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of TEATF–TEAMS. 50 mixture of TEATF–TEAMS. | |
 |
| | Fig. 7 Distribution of the number N of TEA-cations in the first solvation shell of the triflate- and methylsulfonate-anions in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of TEATF–TEAMS obtained for T = 300 K and T = 400 K. (a) Methylsulfonate–TEA (b) triflate–TEA. 50 mixture of TEATF–TEAMS obtained for T = 300 K and T = 400 K. (a) Methylsulfonate–TEA (b) triflate–TEA. | |
3.2 Hydrogen bonding
Numerous geometrical procedures for the determination of hydrogen bonds have been proposed35 in the past. Mostly, they rely on distance criteria in addition to some angular constraints.35,36 We will see that for the case of protic ionic liquids discussed here, the use of angular constraints can even be omitted, since the distance distribution between the ammonium–hydrogen and the sulfonate–oxygen itself does very well discriminate between hydrogen bonded and non-hydrogen bonded states. As shown in Fig. 8, the pair correlation function between an ammonium–hydrogen and the sulfonate–oxygen exhibits a very sharp narrow first peak which goes almost down to zero for both, the pure ionic liquids, as well as for the mixtures. The number of nearest oxygen-neighbors around a hydrogen atom as a function of distance has a very well defined step-like form with a plateau at 1 for the pure liquids, which indicates that an N–H-group in both ionic liquids stays practically always involved in a hydrogen-bond. Here we use a distance criterion of rH–O ≤ 0.24 nm to define a hydrogen bond for both, the triflate- and the methylsulfonate-ions. When applying this cutoff-distance of 0.24 nm, the sum of the computed number of oxygen-neighbors N for both anion-species add up to one with δN < |±0.01| for all investigated mixtures and temperatures. To further substantiate that the intermolecular H–O distance is a proper criterion for a hydrogen-bonded configuration, we have computed a probability density map of the distance rH–O and the cosine of the angle αN–H/S–O between the N–H bond on the TEA and the respective S–O-bond on the methylsulfonate anion, depicted in Fig. 9. The density-plot in Fig. 9 shows that distances rH–O < 0.24 nm correspond to an anti-parallel alignment, essentially confined to angles between 120 and 180 degrees. A second basin located at larger distances is well separated from the hydrogen-bonded basin by a free energy barrier at about rH–O ≈ 0.24 nm. The minimum of the second basin is located at a 60 degree angle, which is certainly incompatible with hydrogen bonded configurations. In fact, these configurations correspond to correlations with oxygen-sites adjacent to the oxygen involved in a hydrogen bond. An alternative representation is given in Fig. 10a, showing those angle-distributions for selected rH–O-distance intervals. Distances with rH–O > 0.44 nm show almost no orientational bias with respect to the N–H and S–O bonds involved. For comparison, Fig. 10b shows the distribution of the cosine of the angle between the intermolecular N–O-vector and the N–H-bond αN–H/N–O, which has been used previously to identify linearly hydrogen-bonded configurations.36 An angular cutoff of 30 degrees is suitable for hydrogen-bonds in liquid water.35,36 In the ionic liquid systems discussed here, the computed αN–H/N–O fall well below this threshold. In fact, the computed αN–H/N–O complies with a much narrower threshold-value of about 18 degrees, suggesting an even better defined linear hydrogen-bond configuration as in liquid water. We conclude that the O–H distance is a suitable measure to identify hydrogen bonds for the discussed systems. This has to be attributed to the peculiarities of the investigated IL, where we only have a single hydrogen-bond donor located on the cation, which is partially shielded by the ethyl-groups, in combination with an abundance of rather strong hydrogen-bond acceptor sites on the anions.
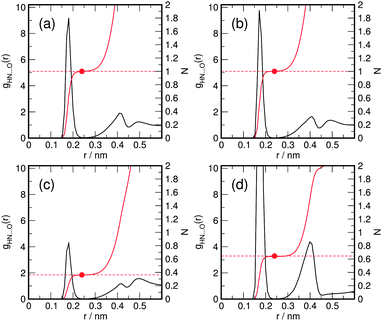 |
| | Fig. 8 H–O intermolecular site–site radial pair distribution functions g(r) obtained for pure TEATF and TEAMS ionic liquids and their 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture at 300 K. Also shown are the number of nearest neighbors as a function of distance N(r). (a) pure TEATF (b) pure TEAMS (c) H–O correlation between TEA and TF in the xMS = 0.25 mixture (d) H–O correlation between TEA and MS in the xMS = 0.25 mixture. 50 mixture at 300 K. Also shown are the number of nearest neighbors as a function of distance N(r). (a) pure TEATF (b) pure TEAMS (c) H–O correlation between TEA and TF in the xMS = 0.25 mixture (d) H–O correlation between TEA and MS in the xMS = 0.25 mixture. | |
 |
| | Fig. 9 Logarithmic representation of the probability-density of finding an intermolecular H–O distance rH–O and the cosine angle between the respective N–H and S–O vectors cos(αN–H/S–O) obtained for the TEA–methylsulfonate pairs in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 TEAMS–TEATF-mixture at 300 K. The pairs were preselected with respect to their intermolecular N–O distance using rN–O < 0.8 nm. 50 TEAMS–TEATF-mixture at 300 K. The pairs were preselected with respect to their intermolecular N–O distance using rN–O < 0.8 nm. | |
 |
| | Fig. 10 Distribution of the cosine angles between two vectors for selected rH–O-distance ranges. (a) Cosine angle between the N–H-vector in TEA and S–O vector in methylsulfonate cos(αN–H/S–O) (b) cosine angle between N–H-vector in TEA and intermolecular N–O vectors cos(αN–H/N–O). Data is shown for TEA–methylsulfonate pairs in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 TEAMS–TEATF-mixture at 300 K. The pairs were preselected with respect to their intermolecular N–O distance using rN–O < 0.8 nm. 50 TEAMS–TEATF-mixture at 300 K. The pairs were preselected with respect to their intermolecular N–O distance using rN–O < 0.8 nm. | |
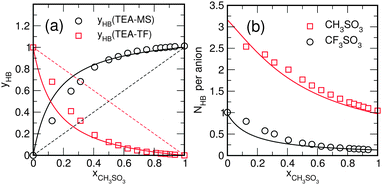
In the previous section we have seen that hydrogen bonding also affects the center-of-mass pair correlation functions and is assumed to be responsible for the splitted first peak of the anion–cation pair correlation function (shown in Fig. 4). As shown in Fig. 8c and d, the hydrogen-bond donated by the cation in the mixture is not shared by both anions according to their abundance in the mixture (xMS = 0.25). In fact, the hydrogen bond to the methylsulfonate-ion appears to be formed in the majority of cases, shifting the equilibrium towards the formation of hydrogen bonds with the methylsulfonate-ion. This effect is not unexpected, given the larger negative partial charges on the methylsulfonate-oxygen sites. To quantify the shift, we have computed the percentage of TEA-cations involved in a hydrogen bond with respect to either anion (see Fig. 11). The data shown in Fig. 11 demonstrates the shift in equilibrium, and also indicates only a weak temperature dependence. Moreover, from the equimolar mixture we can directly estimate the difference in strength of the hydrogen-bond of a TEA-ion to either anion as a free-energy difference at 300 K according to 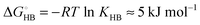 with KHB = yHB,TF/yHB,MS ≈ 0.13.
with KHB = yHB,TF/yHB,MS ≈ 0.13.
 |
| | Fig. 11 Percentage of TEA-cations connected via a hydrogen bond to either a triflate- or a methylsulfonate-ion as a function of the mixture-composition at 300 K and 400 K, respectively. | |
The fact that both anions can accept up to three hydrogen bonds and that these hydrogen bonds are differently strong leads to a formation of hydrogen-bonded aggregates of varying size as a function of the composition of the mixture. First, we discuss the total number of hydrogen bonds accepted by each of the anions as a function of the mixture-composition shown in Fig. 12. In the pure liquids, each anion accepts on average one single hydrogen bond. Since each sulfonate group can accept up to three hydrogen-bonds, the strong TEA–MS hydrogen bonds causes the methylsulfonate-ion to accepting about up to ≈2.8 hydrogen bonds in the diluted solution (xMS → 0). By increasing the methylsulfonate-concentration, this number drops monotonously, since the methylsulfonate-ions start to compete with each other for TEA hydrogen-bonds. The triflate-ion in the dilute triflate-solution (xMS → 1) only receives about ≈0.1 hydrogen-bonds on average, and is hence almost completely stripped of hydrogen bonds.
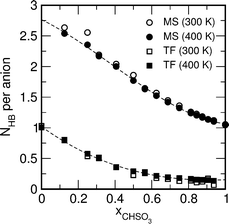 |
| | Fig. 12 Average number of hydrogen bonds accepted by the triflate- and methylsulfonate-ions at 300 K and 400 K, respectively. | |
The distribution of the hydrogen-bonded aggregates are finally shown in Fig. 13. Indicated are the percentages of each of the anions connected to either no, one, two or three TEA-cations via hydrogen-bonding. Note that for both pure ionic liquids, the distribution of aggregate sizes is almost identical: single hydrogen-bonded (n = 1) aggregates contribute about ≈50%, whereas the configurations with no (n = 0) and two hydrogen bonds (n = 1) are both near at about ≈24%. Configurations with three hydrogen bonds (n = 3) are rare and contribute only to ≈2–3%. With increasing methylsulfonate-concentration, the population of triflate-ions with no hydrogen-bonds (“free” triflate-ions) is increasing strongly to a plateau value of about 85% to 90% for xMS → 1. At the same time the percentage of configurations with one hydrogen bond drops down to 10% to 15%. Configurations with more than one hydrogen bond are practically non-existent. With increasing triflate-concentration, on the other hand, the methylsulfate-ions attract more and more hydrogen-bonds, leading to an increasing percentage of MS-ions attached to two (n = 2) and three (n = 3) TEA-cations. Here the configurations with two hydrogen-bonds first increase, but are getting increasingly replaced by configurations with three hydrogen-bonds. For xMS → 0, finally, the n = 3-fraction represents the majority of configurations with ≈75%, and n = 2 representing the rest with ≈25%. Configurations with no or one hydrogen-bond have practically vanished.
 |
| | Fig. 13 Percentage of triflate- and methylsulfonate-ions hydrogen-bonded to zero, one, two, and three TEA-cations as a function of the mixture-composition. Open symbols: 300 K. Closed symbols: 400 K (a) methylsulfonate (b) triflate. | |
We summarize that the exact size and distribution of the hydrogen-bonded aggregates is apparently determined by the strengths of the hydrogen-bonds, the number of hydrogen-bonded donors and acceptors on the ions, as well as their respective coordination-numbers. In the following section, we will introduce a “cartoon-like” representation of the ionic liquid, which is based on a minimal set of assumptions extracted from our MD-simulation, and can be used compute the observed cluster-sizes as a function of the mixture-composition in a semi-quantitative fashion.
3.3 A “cartoon-like” model of hydrogen bonding in the IL mixture
For a better understanding of the hydrogen-bonded cluster-sizes in the IL mixtures, we would like to introduce a simplified description of the hydrogen bond equilibrium. For this purpose we construct a simplified model of the ionic liquid as outlined in Fig. 14. Here, the liquid is represented by a cubic lattice, where the anions and cation occupy sites in an alternating fashion, leading to a octahedral coordination of each ion with a coordination number of c = 6. In addition, we assume that each TEA-cation stays always involved in a hydrogen-bond, and is pointing with its N–H-bond towards one of the c surrounding anions. In a pure ionic liquid, the cation–anion hydrogen-bond is, of course, supposed to connect the TEA-cation randomly with one of its c anion neighbors. If each anion would be able to accept c hydrogen-bonds from the surrounding TEA-cations equally well, the probability of finding an anion accepting n hydrogen-bonds simultaneously Pc,n would exactly follow a binomial distribution| | 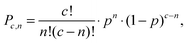 | (2) |
where p represents the probability of a TEA-cation pointing with its N–H bond towards the central anion. Assuming a purely random orientation of the TEA–N–H-bond on the lattice, p corresponds to the inverse coordination number of the TEA-ion (p = 1/c). However, to account for the fact that the triflate and methylsulfonate-anions can each accept only up to three hydrogen-bonds, we have to modify the distribution function by introducing configuration-specific weights-factors wc,n with wc,n = 0 for n > 3.| | 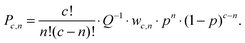 | (3) |
To ensure proper normalisation, the modified weights are counter-balanced by a constant Q, which has to be computed numerically according to| | 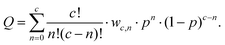 | (4) |
In a first step, we will discuss a situation, where the non-zero statistical weights are all equal (wc,n = 1 for n ≤ 3). In addition, we will assume that the chosen weights do not change as function of the mixture-composition. In the mixture, however, the hydrogen-bond of TEA to each of the two anion-species varies in strength. This will, hence, also modify the hydrogen-bond acceptance probability for each of the anions. In all cases, the TEA cation points to one of the c surrounding neighbors with a site-specific probability pi. Of course, those probabilities do add all up to unity:| |  | (5) |
Since each of the sites i is assumed to be statistically occupied by one of the two anion-species according to their mixture composition x = xMS, the average probability pi of accepting a hydrogen-bond is hence a composition-weighted sum of the individual probabilities of the anions according to| | | pi = x·pMS + (1 − x)·pTF | (6) |
From eqn (5) and (6), the universal anion-specific hydrogen-bond-acceptance probabilities follow as| |  | (7) |
with f = pTF/pMS. From eqn (7) we can directly determine the fraction of times, a N–H bond of a TEA-cation points to either a methylsulfonate- or triflate-ion as| | 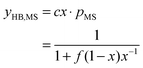 | (8) |
and| |  | (9) |
The ratio f can be determined from MD simulation data by taking the values for the fraction of hydrogen-bonds of one TEA-molecule to each of the two anion-species from the equimolar mixture. Using the data shown in Fig. 11, we determine f = yHB,TF/yHB,MS ≈ 0.13. Assuming that f does not change significantly as a function of the composition x, we can now compute the hydrogen-bonded cluster sizes Pc,n for both, the methylsulfonate and the triflate anions, as well as the average number of hydrogen bonds accepted by each anion according to| |  | (10) |
 |
| | Fig. 14 “Cartoon-like” representation of the ionic liquid: the liquid is represented by a cubic lattice, where the anions and cations occupy sites in an alternating fashion. Each ion is octahedrally coordinated and surrounded by c = 6 counter-ions. Each anion (either triflate or methylsulfonate) can accept up to three hydrogen bonds. The N–H groups of each of the TEA-molecules are involved in a hydrogen-bond to one of their c surrounding neighbors. | |
Fig. 15 shows the prediction of the sizes of the hydrogen-bonded aggregates according the model using equal weights with w6,n = 1 for n ≤ 3 and w6,n = 0 for n > 3. Essential features of the distributions obtained from the MD-simulation, such as the existence of a maximum of MS–TEA aggregates with two hydrogen bonds, are well recovered by just using an approximate coordination number, and taking into account that both anions can accept no more than three hydrogen bonds. Also, the percentage of hydrogen-bonds of TEA to either anion-species, as well as the total number of accepted hydrogen bonds (Fig. 16) are nicely captured. However, the distribution of aggregate-sizes in the pure TEAMS and TEATF liquids are not correctly represented. In particular, the model underestimates the single-bonded configurations and overestimates the configurations with no hydrogen-bond. To better represent the distribution within the pure liquids and to improve the model, we adjust the non-zero weight-factors wc,n for n ≤ 3 to match the MD simulation results (as shown in Fig. 13) for the respective pure ionic liquids with P6,0 = 0.24, P6,1 = 0.51, P6,2 = 0.22, and P6,3 = 0.03. For simplicity, we use the same values for both, TEATF and TAMS. Those probabilities are recovered by using statistical weights of w6,0 = 0.75, w6,1 = 1.3, w6,2 = 1.12, and w6,3 = 0.5 for both anions. The weight-factors indicate that the anions in the pure IL feel most comfortable with just one hydrogen bond pointing towards them. Situations with three hydrogen bonds have a significantly lower statistical weight, most likely due to orientational restraints, introduced by a configuration involving three hydrogen bonds to adjacent ions. Particularly, the situation without any hydrogen-bonds exhibits a significantly reduced statistical weight compared to the random distribution of hydrogen-bonds. The distribution of clusters shown in Fig. 17 demonstrate a significant improvement, leading to a semi-quantitative description of the MD-data. Moreover, the good overall description of the simulation-data by our model is suggesting that the two anion-species are statistically distributed in the liquid. However, also certain weaknesses of the model are evident, particularly for the percentage of hydrogen-bonds of TEA to either anion-species in the range xMS < 0.3. By introducing a composition-dependent factor f(xMS) a better representation of the data shown in Fig. 16a and 18a could be achieved (not shown). Interestingly, this does, in fact, worsen the description of the distribution of cluster-sizes, indicating the need to also account for the changing coordination-numbers, and thus pointing at the limits of the model.
 |
| | Fig. 15 Percentage of methylsulfonate- (a) and triflate-ions (b) hydrogen-bonded to zero, one, two, and three TEA-cations, as a function of the mixture-composition at 400 K. Symbols: MD-simulation. Solid lines: model using equal statistical weights with w6,n = 1 for n ≤ 3 and w6,n = 0 for n > 3. | |
 |
| | Fig. 16 (a) Percentage of TEA-cations connected via a hydrogen bond to either a triflate-ion or a methylsulfonate-ion as a function of the mixture-composition. (b) Average number of hydrogen bonds accepted by the triflate- and methylsulfonate-ions. Open symbols: MD-data obtained at 400 K. Solid lines: model using equal statistical weights with w6,n = 1 for n ≤ 3 and w6,n = 0 for n > 3. | |
 |
| | Fig. 17 Percentage of methylsulfonate- (a) and triflate-ions (b) hydrogen-bonded to zero, one, two, and three TEA-cations, as a function of the mixture-composition at 400 K. Symbols: MD-simulation. Solid lines: model using statistical weights adjusted to the distribution in the pure liquids with w6,0 = 0.75, w6,1 = 1.3, w6,2 = 1.12, w6,3 = 0.5, and w6,n = 0 for n > 3. | |
 |
| | Fig. 18 (a) Percentage of TEA-cations connected via a hydrogen bond to either a triflate-ion or a methylsulfonate-ion as a function of the mixture-composition. (b) Average number of hydrogen bonds accepted by the triflate- and methylsulfonate-ions. Open symbols: MD-data obtained at 400 K. Solid lines: model using statistical weights adjusted to the distribution in the pure liquids with w6,0 = 0.75, w6,1 = 1.3, w6,2 = 1.12, w6,3 = 0.5, and w6,n = 0 for n > 3. | |
4 Conclusions
We have reported results of molecular dynamics simulations characterising the hydrogen bonding in mixtures of two protic ionic liquids sharing the same cation: triethylammonium-methylsulfonate and triethylammonium-triflate. The triethylammonium-cation acts as a hydrogen-bond donor, being able to donate a single hydrogen bond. Both, the methylsulfonate- and the triflate-anions can act as hydrogen-bond acceptors, which can accept multiple hydrogen bonds via their SO3-groups. Replacing a methyl-group in the methylsulfonate by a trifluoromethyl-group in the triflate significantly weakens the strength of a hydrogen bond from an adjacent triethylammonium-cation to the oxygen-site in the SO3-group of the respective anion. Our MD simulations show that these rather subtle differences in hydrogen bond strength significantly affect the formation of differently-sized hydrogen-bonded aggregates in the mixtures as a function of the mixture-composition. A defining structural feature of ionic liquids in general and of the studied protic ionic liquid in particular is the charge-alternating order of the ions, leading to counter-ion coordination numbers between six and eight. This fact is represented in a simple “cartoon-like” lattice model of the liquid, placing ions on a cubic lattice in an alternating fashion with an approximate counter-ion coordination number of six. By introducing statistical weights that mostly account for the fact that each anion can only accept up to three hydrogen bonds, and by adjusting the balance between of the hydrogen bond of TEA to either of the two anions, the simple model is able to qualitatively predict the distribution of differently-sized hydrogen-bonded aggregates as well as the total number of hydrogen bonds accepted by the anions as a function of the mixture-composition. By adjusting the statistical weights for each cluster in such a way that the cluster sizes match the distribution observed in the pure liquids, an even semiquantitative description of the data obtained from MD simulation emerges. Finally, we would like to comment of the issue of the “doublesaltiness” of the studied ionic liquid mixture as pointed out by Rogers et al.6 Their line of reasoning is that in a mixture of ILs, the constituents (ions) do not seem to retain their individual nature. Hence, they proposed to consider them as double-salt ionic liquids. We think that our model-system is a particularly nice demonstration of the concept: although the pure ionic liquids and their mixtures exhibit great similarity with respect to the overall ion-alternating structure, each of the statistically distributed anions experiences a completely different local environment.
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG) Priority Programme SPP 1191 “Ionic Liquids” and the DFG Collaborative Research Center SFB 652 “Strong correlations and collective effects in radiation fields: Coulomb systems, clusters and particles”
References
-
P. Wasserscheid and T. Welton, Ionic Liquids in Synthesis, Wiley-VCH, 2nd edn, 2008 Search PubMed.
- F. Endres and S. Z. El Abedin, Phys. Chem. Chem. Phys., 2006, 8, 2101–2116 RSC.
- H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150 RSC.
- H. Niedermeyer, J. P. Hallett, I. J. Villar-Garcia, P. A. Hunt and T. Welton, Chem. Soc. Rev., 2012, 41, 7780–7802 RSC.
- G. Chatel, J. F. B. Pereira, V. Debbeti, H. Wang and R. D. Rogers, Green Chem., 2014, 16, 2051–2083 RSC.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 8731–8734 CrossRef CAS PubMed.
- K. Fumino and R. Ludwig, J. Mol. Liq., 2014, 192, 94–102 CrossRef CAS PubMed.
- M. Y. Lui, L. Crowhurst, J. P. Hallett, P. A. Hunt, H. Niedermeyer and T. Welton, Chem. Sci., 2011, 2, 1491–1496 RSC.
- P. Navia, J. Troncoso and L. Romani, J. Chem. Eng. Data, 2007, 52, 1369–1374 CrossRef CAS.
- A. Arce, M. J. Earle, S. P. Katdare, H. Rodriguez and K. R. Seddon, Chem. Commun., 2006, 2548–2550 RSC.
- J. N. Canongia Lopes, T. C. Cordeiro, J. M. S. S. Esperanca, H. J. R. Guedes, S. Huq, L. P. N. Rebelo and K. R. Seddon, J. Phys. Chem. B, 2005, 109, 3519–3525 CrossRef PubMed.
- D. Xiao, J. R. Rajian, L. G. Hines, S. Li, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2008, 112, 13316–13325 CrossRef CAS PubMed.
- K. Fumino, V. Fossog, K. Wittler, R. Hempelmann and R. Ludwig, Angew. Chem., Int. Ed., 2013, 52, 2368–2372 CrossRef CAS PubMed.
- P. Stange, K. Fumino and R. Ludwig, Angew. Chem., Int. Ed., 2013, 52, 2990–2994 CrossRef CAS PubMed.
- K. Fumino, A. M. Bonsa, B. Golub, D. Paschek and R. Ludwig, ChemPhysChem, 2015, 16, 299–304 CrossRef CAS PubMed.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys, 1981, 52, 7182–7190 CrossRef CAS PubMed.
- S. Nosé and M. L. Klein, Mol. Phys., 1983, 50, 1055–1076 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. A. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS PubMed.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317 CAS.
-
M. Abraham, E. Apol, R. Apostolov, H. J. Berendsen, A. van Buuren, P. Bjelkmar, R. van Drunen, A. Feenstra, S. Fritsch, G. Groenhof, C. Junghans, J. Hub, P. Kasson, C. Kutzner, B. Lambeth, P. Larsson, J. A. Lemkul, E. Marklund, P. Meulenhoff, T. Murtola, S. Pall, S. Pronk, R. Schulz, M. Shirts, A. Sijbers, P. Tieleman, M. Wolf, B. Hess, D. van der Spoel and E. Lindahl, GROMACS - Groningen Machine for Chemical Simulations User Manual Version 4.6.1, 2013 Search PubMed.
- H. Flyvbjerg and H. G. Petersen, J. Chem. Phys., 1989, 91, 461–466 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS PubMed.
- W. L. Jorgensen and M. Ibrahim, J. Am. Chem. Soc., 1981, 103, 3976–3985 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc, Wallingford, CT, 2009 Search PubMed.
- U. C. Singh and P. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- T. Köddermann, D. Paschek and R. Ludwig, ChemPhysChem, 2007, 8, 2464–2470 CrossRef PubMed.
- H. Krienke, V. Vlachy, G. Ahn-Ercan and I. Bako, J. Phys. Chem. B, 2009, 113, 4360–4371 CrossRef CAS PubMed.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- D. Roy, N. Patel, S. Conte and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 8410–8424 CrossRef CAS PubMed.
- R. Kumar, J. R. Schmidt and J. L. Skinner, J. Chem. Phys., 2007, 126, 204107 CrossRef CAS PubMed.
- A. Luzar and D. Chandler, Nature, 1996, 379, 55–57 CrossRef CAS.
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of TEATF–TEMS at T = 300 K is given in Fig. 2. Indicated are the positions of the centers of mass of the ions, which can be identified via their respective colors. From visual inspection it is evident that the charge of the ions impose a long-range ion-alternating order, which is leading to a significant structural homogeneity of the ionic liquid. This behavior is typical for ionic liquids and has been pointed out earlier by Maroncelli and co-workers.34 The ion-alternating order is a consequence of the fact that the ions are predominantly surrounded by a solvation shell of ions with opposite charge. This defining structural feature is well represented by the location of the first peak of the center-of-mass pair distribution functions of the ions: in Fig. 3a and b the center-of-mass pair distribution functions for all ion-pair combinations are shown for a 50
50 mixture of TEATF–TEMS at T = 300 K is given in Fig. 2. Indicated are the positions of the centers of mass of the ions, which can be identified via their respective colors. From visual inspection it is evident that the charge of the ions impose a long-range ion-alternating order, which is leading to a significant structural homogeneity of the ionic liquid. This behavior is typical for ionic liquids and has been pointed out earlier by Maroncelli and co-workers.34 The ion-alternating order is a consequence of the fact that the ions are predominantly surrounded by a solvation shell of ions with opposite charge. This defining structural feature is well represented by the location of the first peak of the center-of-mass pair distribution functions of the ions: in Fig. 3a and b the center-of-mass pair distribution functions for all ion-pair combinations are shown for a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture obtained at 300 K. From Fig. 3a we can conclude that the first peak of the anion–cation pair correlation function is shifted to significantly lower values, with the dominant first peak of the TEA–MS-pair found at 0.41 nm, and the peak of the TEA–TF-pair at 0.54 nm. The first TEA–TEA-peak is found at a much larger distance of 0.70 nm. The anion–anion pair correlation functions are shown in Fig. 3b: here, we would like to point out that, besides the dominant main first peak around 0.8 nm, there also exists pre-peak at a distance of about 0.55 nm, which is most strongly pronounced for the correlation between the two methylsulfonate ions, and is only weakly pronounced in the pair-correlation of the triflate-ions. In addition, Fig. 3b also shows that this structural feature of the first peak is completely absent for the TEA–TEA correlations. The pre-peak in the anion–anion pair correlation function is indicating the existence of direct anion–anion contacts, whereas direct cation–cation contacts are apparently avoided. Moreover, also the snapshot in Fig. 2 reveals the presence of anion–anion-pairs in close proximity on many occasions.
50 mixture obtained at 300 K. From Fig. 3a we can conclude that the first peak of the anion–cation pair correlation function is shifted to significantly lower values, with the dominant first peak of the TEA–MS-pair found at 0.41 nm, and the peak of the TEA–TF-pair at 0.54 nm. The first TEA–TEA-peak is found at a much larger distance of 0.70 nm. The anion–anion pair correlation functions are shown in Fig. 3b: here, we would like to point out that, besides the dominant main first peak around 0.8 nm, there also exists pre-peak at a distance of about 0.55 nm, which is most strongly pronounced for the correlation between the two methylsulfonate ions, and is only weakly pronounced in the pair-correlation of the triflate-ions. In addition, Fig. 3b also shows that this structural feature of the first peak is completely absent for the TEA–TEA correlations. The pre-peak in the anion–anion pair correlation function is indicating the existence of direct anion–anion contacts, whereas direct cation–cation contacts are apparently avoided. Moreover, also the snapshot in Fig. 2 reveals the presence of anion–anion-pairs in close proximity on many occasions.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of TEATF–TEMS at T = 300 K.
50 mixture of TEATF–TEMS at T = 300 K.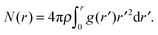

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 TEATF–TEAMS mixture, shown in Fig. 3a, compared to the pure liquids shown in Fig. 4. From Fig. 4 it is evident that the first sub-peak has about the same height for both pure ionic liquids. In the 50
50 TEATF–TEAMS mixture, shown in Fig. 3a, compared to the pure liquids shown in Fig. 4. From Fig. 4 it is evident that the first sub-peak has about the same height for both pure ionic liquids. In the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture (Fig. 3a), however, the first peak is very strongly pronounced for the TEA–MS pair, and is almost completely absent for the TEA–TF pair, which is suggesting a preference for the formation of TEA–MS hydrogen bonded conformations. This preference is also evident from Fig. 2, where many of the supposedly hydrogen-bonded TEA–MS-pairs can be identified as dumbbell-like configurations, formed by a pair of blue and yellow spheres. This imbalance of the hydrogen-bond strengths has also a surprising consequence for the structure of solvation-shells of the ions in the mixture. In Fig. 5 the average coordination-number of the anions surrounding a central cation is depicted as a function of the mixture-composition. While the total number of anions varies only slightly between 6.8 and 6.9 as a function of mixture composition, the build-up of the individual solvation shells changes more strongly: as shown in Fig. 5, in a 50
50 mixture (Fig. 3a), however, the first peak is very strongly pronounced for the TEA–MS pair, and is almost completely absent for the TEA–TF pair, which is suggesting a preference for the formation of TEA–MS hydrogen bonded conformations. This preference is also evident from Fig. 2, where many of the supposedly hydrogen-bonded TEA–MS-pairs can be identified as dumbbell-like configurations, formed by a pair of blue and yellow spheres. This imbalance of the hydrogen-bond strengths has also a surprising consequence for the structure of solvation-shells of the ions in the mixture. In Fig. 5 the average coordination-number of the anions surrounding a central cation is depicted as a function of the mixture-composition. While the total number of anions varies only slightly between 6.8 and 6.9 as a function of mixture composition, the build-up of the individual solvation shells changes more strongly: as shown in Fig. 5, in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture the average number of TF-anions (NTF = 3.82) in the first solvation shell of a TEA-cation is significantly larger than the number of MS-anions (NMS = 3.08). This imbalance is also represented in the solvation shell of the anions: Fig. 6 shows the distribution of the number of the TEA-cations in the first solvation shell around each anion. For the pure ionic liquids (given in Fig. 6a), the distribution functions are almost identical with a maximum at 7 neighbors. In the 50–50 mixture, however, the distribution for methylsulfonate is shifted to lower values, with a maximum at 6, whereas the distribution for triflate is shifted to larger values. Apparently, the triflate-ion is able to “steal away” cations from the methylsulfonate in the mixture. This effect might be just due to the larger size of triflate-ion compared to the methylsulfonate. However, the reduced number of TEA-cations in the solvation shell of methylsulfonate leaves the methylsulfonate-ion prone to direct anion–anion contacts in the mixture as observed in Fig. 3. The number of TEA-cations attracted by the triflate- and methylsulfonate-ions is related with an average free energy of association, which has, of course, both entropic and an enthalpic contributions. The temperature dependence of the distribution functions shown in Fig. 7 indicates that the “binding” of TEA to the triflate-ion is significantly more temperature-sensitive than that of TEA to the methylsulfonate-ion and, hence, can be considered more weakly.
50 mixture the average number of TF-anions (NTF = 3.82) in the first solvation shell of a TEA-cation is significantly larger than the number of MS-anions (NMS = 3.08). This imbalance is also represented in the solvation shell of the anions: Fig. 6 shows the distribution of the number of the TEA-cations in the first solvation shell around each anion. For the pure ionic liquids (given in Fig. 6a), the distribution functions are almost identical with a maximum at 7 neighbors. In the 50–50 mixture, however, the distribution for methylsulfonate is shifted to lower values, with a maximum at 6, whereas the distribution for triflate is shifted to larger values. Apparently, the triflate-ion is able to “steal away” cations from the methylsulfonate in the mixture. This effect might be just due to the larger size of triflate-ion compared to the methylsulfonate. However, the reduced number of TEA-cations in the solvation shell of methylsulfonate leaves the methylsulfonate-ion prone to direct anion–anion contacts in the mixture as observed in Fig. 3. The number of TEA-cations attracted by the triflate- and methylsulfonate-ions is related with an average free energy of association, which has, of course, both entropic and an enthalpic contributions. The temperature dependence of the distribution functions shown in Fig. 7 indicates that the “binding” of TEA to the triflate-ion is significantly more temperature-sensitive than that of TEA to the methylsulfonate-ion and, hence, can be considered more weakly.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of TEATF–TEAMS.
50 mixture of TEATF–TEAMS.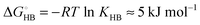 with KHB = yHB,TF/yHB,MS ≈ 0.13.
with KHB = yHB,TF/yHB,MS ≈ 0.13.