Open Access Article
Open Access ArticleSolvent effects of 1-ethyl-3-methylimidazolium acetate: solvation and dynamic behavior of polar and apolar solutes†
Volker
Lesch
a,
Andreas
Heuer
a,
Christian
Holm
b and
Jens
Smiatek
*b
aInstitute of Physical Chemistry, University of Muenster, Muenster, Germany
bInstitute for Computational Physics, University of Stuttgart, Stuttgart, Germany. E-mail: smiatek@icp.uni-stuttgart.de; Fax: +49 711 68563658; Tel: +49 711 68563757
First published on 6th February 2015
Abstract
We study the solvation properties of the ionic liquid 1-ethyl-3-methylimidazolium acetate ([EMIM]+[ACE]−) and the resulting dynamic behavior for differently charged model solutes at room temperature via atomistic molecular dynamics (MD) simulations of 300 ns length and 200 ns equilibration time. The solutes are simple model spheres which are either positively or negatively charged with a valency of one, or uncharged. The numerical findings indicate a distinct solvation behavior with the occurrence of well-pronounced solvation shells whose composition significantly depends on the charge of the solute. All the results of our simulations evidence the existence of a long-range perturbation effect in presence of the solutes. Our findings validate the dominance of electrostatic interactions with regard to unfavorable entropic ordering effects which elucidates the enthalpic character of the solvation process in ionic liquids for charged solutes.
1 Introduction
Ionic liquids (ILs) are promising materials for different technological applications and can be used as electrolytes1–3 or pure solvents.4–7 Their broad usage in technological devices relies on the fact that ILs exhibit high thermal stability, desirable ionic conductivity, negligible vapor pressure and non-flammability.8–14 In addition, a special advantage of room-temperature ionic liquids (RTILs) for electrochemical applications is their entire dissociation into anions and cations such that they can be also regarded as molten salts.15 Notably, there exists a large number of ionic liquids that differ in their anion and cation composition which offers tunable functionalities and a broad applicability.16,17 Specifically the ionic dissociation behavior and the corresponding transport properties of ILs have been studied by computer simulations and experiments in a series of publications.11,12,14,18–30Nowadays, ionic liquids have attracted a broad interest in the usage as solvents due to their desirable, less hazardous properties compared to other media.5,7,31 A series of studies, both experimental as well as numerical investigations have focused on the solvation behavior of small solutes in ionic liquids.21,22,32–42 In addition to the solvation behavior of small molecules in ILs, further effort has been also spent on the investigation of ionic liquid behavior at surfaces43–45 and general solute properties.22,31,36,46–48
In terms of numerical simulations, the number of publications that study non-aqueous solvents and their solvation properties is rather scarce. This can be mostly explained by the overwhelming dominance of water in most biochemical processes as well as the still poorly understood hydrophobic and hydrophilic hydration behavior.49 Indeed, promising approaches towards the full understanding of solvent behavior for macromolecular properties have been recently published.50–52 However, it has to be stated that only a few aspects of solvophilic and solvophobic solvation properties are in general known.53–55 The study of the IL solvent behavior is therefore a challenging task with often unexpected outcomes.
It has been recently revealed56–58 that ionic liquids are able to stabilize proteins. Micaelo et al. found that the stabilization of the enzyme cutinase significantly depends on the ionic liquid content of the solution.56 According to these results and additional experiments, it was assumed that ionic liquid mediated hydrogen bonds prevent the denaturation of proteins and maintain their higher-order structure even above a critical temperature.59,60
An often used approach to study bulk properties of ionic liquids on large length scales, which are also of importance for a full understanding of the solution structure, is given by the development of reliable coarse-grained models.61–68 Although being a promising approach due to the accessible long time and length scales, the usage and the development of valid coarse-grained IL models is a sophisticated challenge. With respect to additional problems, it has been pointed out that even the application of standard atomistic force fields is questionable with regard to often neglected polarization effects.12,17,26,69–74 An overview of well-known force field artefacts and the importance of polarization effects has been published in ref. 71 and 74–76. Nevertheless, atomistic MD simulations remain the method of choice for the study of IL properties with respect to the accessible time scales and the number of considered particles.71,77
With this article, we present the results of all atom MD simulations with respect to the solvation behavior of 1-ethyl-3-methylimidazolium acetate ([EMIM]+[ACE]−) for differently charged model spheres.
In contrast to previous findings which mostly rely on the solvation properties of small molecules,32–35,37,38 the aim of this study is devoted to the investigation of the general accumulation behavior of ionic liquids around spherical particles. In addition, the resulting dynamical behavior is also elucidated. Due to the spherical shape, molecular details of the solutes can be disregarded such that some general conclusions about the solvation behavior can be drawn. Our findings indicate a strong dominance of enthalpic electrostatic contributions for the solvation process which result in a long range ordering effect of the solvent.
The paper is organized as follows. In the next section we present the theoretical background for the study of solvent structures in terms of standard procedures. The simulation details will be presented in the third section. The results are discussed in Section 4. We conclude and summarize in the last section.
2 Theoretical background
The radial distribution function of molecules or atoms β around solutes α is given by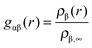 | (1) |
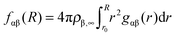 | (2) |
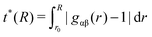 | (3) |
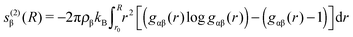 | (4) |
For the investigation of the solvent orientation around a solute, it is valuable to study the angular distribution of solvent molecular configurations.85 A common order parameter is given by
| S1 = 〈cos(ϕ)〉 | (5) |
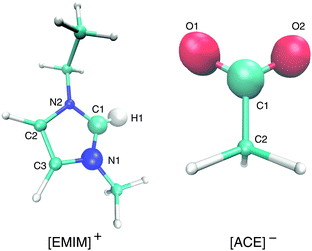 | ||
| Fig. 1 Molecular representation of [EMIM]+ (left) and acetate [ACE]− ions (right). The bigger spheres denote the atoms that are involved in the calculation of the orientation angle (eqn (5)). | ||
In order to study the dynamic properties of the solution, one can calculate the dipolar relaxation time of the ions. The evaluation of this quantity allows us to estimate the persistence in time for specific configurations as it has been originally proposed for glassy liquids and liquid solvents.80,86,87 The autocorrelation time for the dipolar orientation vector ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) can be calculated by
can be calculated by
Cμ(t) ∼ 〈![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) (t) (t)![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) (0)〉 ∼ exp(−t/τ)β. (0)〉 ∼ exp(−t/τ)β. | (6) |
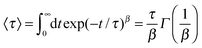 | (7) |
Another important quantity is the rearrangement time of the solvent shells around the solute. Herewith, the relative stability of the solvent shell can be estimated by the binding contact autocorrelation function
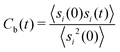 | (8) |
The van Hove correlation function89 is given by
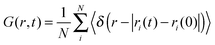 | (9) |
3 Simulation details
All simulations were performed with the MD simulation package GROMACS (version 4.6.5).90–92 The starting structures were produced with PACKMOL.93,94 The force field parameters for the ionic liquid were extracted from the CL&P force field developed by Canongia Lopes and Padua.95–98 A recent review has shown that the study of solvation properties for small solutes with this force field produces valid results that are in good agreement with experimental findings.99 Nevertheless, the dynamic properties may have some artefacts due to the neglect of polarization effects.71,74 We therefore do not explicitly focus on exact numbers for dynamic quantities but merely try to elucidate the general trends and differences between the systems which shall remain valid.The parameters of the solute spheres were inspired by the diadamine model proposed in ref. 100 which was also recently used for aqueous systems.101 The van-der-Waals radius of the spheres is 0.34 nm while the well-depth of the Lennard-Jones interactions is given by 0.28 kcal mol−1. Compared with the work of Markowski et al.,100 we used a smaller ε to weaken the Lennard-Jones interactions. Herewith, the electrostatic interactions are more pronounced. The valency for the charged spheres was either q = ±1e or q = 0 for the uncharged neutral solute. In the following, we denote the 1-ethyl-3-methylimidazolium ions ([EMIM]+) with EMIM if not otherwise mentioned. The synonym [ACE]− will be called acetate ions or ACE. Periodic boundary conditions were applied in each direction of a cubic box and 500 [EMIM]+ ions and 500 [ACE]− ions were inserted. To achieve electroneutrality, an additional acetate or EMIM ion was inserted to compensate the charge of the spheres. We used the Lincs algorithm102 to constrain all bonds with connected hydrogen atoms. The electrostatic interactions were calculated via the smooth Particle-Mesh-Ewald method103,104 with a cutoff range of 1.2 nm and an accuracy of 10−6. For energy minimization, we used the conjugate gradient method with an energy tolerance value of 100 kJ mol−1 nm−1 and a step size of 10−4 nm. The time step in all simulations was 1 fs and the equilibration procedure had five successive steps. We conducted NpT simulations each with 5 ns length at the temperatures 500 K, 450 K, 400 K, 350 K and 298 K by using the Berendsen thermostat with a coupling time of 1 ps and the Berendsen barostat105 with the same coupling time and a reference pressure of 1 bar. The resulting box size was 5.03 nm for all systems. The following final warm up runs with a length of 200 ns were conducted in NVT ensemble by the Nose–Hoover thermostat106 with the same parameters for the Berendsen thermostat at a temperature of 298 K as used above. The presented data have been obtained by NVT production runs with length of 300 ns. In addition, we also simulated a reference system in absence of spherical solutes. The parameters and the length of the simulation, respectively the equilibration protocol were identical to the values and the procedure described above. The final box length of the reference simulations was 5.05 nm.
4 Numerical results
4.1 Structural properties of the solution
The study of the radial distribution function around solutes gives insights into the internal structure of the solution and helps to identify the width and the position of the solvent shells. In terms of a binary solvent like ionic liquids, the contributions of both ionic species can be analyzed separately.With respect to the slow molecular relaxation of ionic liquids, we have performed warm up runs of 200 ns to ensure the presence of energetically stable and thermodynamically equilibrated molecular configurations. The calculated intermediate scattering function (data presented in the ESI†) further indicates the importance of long equilibration times. With regard to the obtained values, it can be clearly stated that the initial configuration was exponentially relaxed after 200 ns for length scales r ≤ 0.5 nm. In contrast, the presence of fully relaxed structures on longer length scales demands more equilibration time. However, the main aim of this article is given by the study of the properties and corresponding consequences of the local solvent environment within distances of 0.5 nm (which roughly corresponds to the first two solvent shells) such that our equilibration protocol is validated.
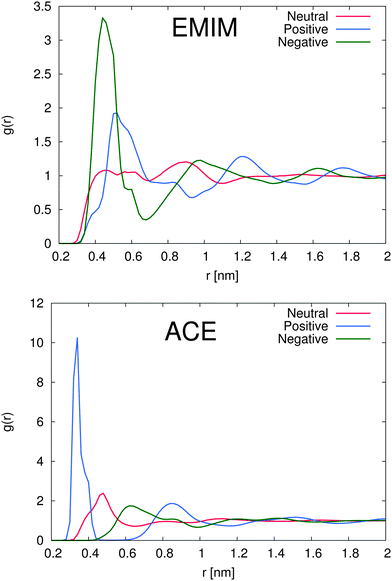
In order to study the properties of the solution, we present the radial distribution function for both ions around the differently charged solutes in Fig. 2. First we will discuss the solvation properties of a negatively charged sphere. For EMIM, it can be clearly seen that the first solvation shell around the negative solute is given for distances r ≈ 0.35–0.65 nm. The broad solvent shell can be related to the appearance of several configurational orientations of the EMIM molecules. We will come back to this point in the next subsection. In addition, we observe a distinct ordering behavior between the first EMIM and acetate shell with a strong depletion of EMIM ions at distances between 0.6 to 0.8 nm. Furthermore, the presence of pronounced shell structures even at distances larger than 1.5 nm becomes evident.
Instead, the solvent properties around the positively charged solute slightly differ. Notably, we found a pronounced peak value for the first EMIM shell around the positively charged sphere which corresponds to the second solvation shell between r ≈ 0.5–0.7 nm with a depletion gap for the acetate ions between r ≈ 0.45–0.6 nm. With respect to the location of the acetate ions for this system, it becomes evident that first a layer of acetate ions around the sphere is formed followed by the EMIM ions as the second solvation shell. Therefore, it can be concluded that electrostatic interactions between the solute and the acetate and also the EMIM ions are the general main driving force for the composition and the ordering of the first two solvation shells. A strongly pronounced layer behavior around the positively charged solute can be for example even identified for the second peaks in the EMIM and the acetate distribution function (r ≈ 0.6–1.1 nm for acetate ions and r ≈ 1.1–1.45 nm for EMIM ions) which validates the presence of an electrostatically induced ordering effect. In addition, the peak values of the radial distribution function for the first solvation shell of acetate ions around the positively charged solute are significantly larger compared to all other distribution functions, even for the EMIM ions around the negatively charged solute. We can relate this finding to the significantly smaller molecular size of the acetate ion compared to the EMIM ion. Therefore, the excluded volume effect of the acetate ions is less pronounced and more ions compared to EMIM can accumulate at the positively charged sphere within smaller distances.
A slightly pronounced ordering effect can be also identified for the neutral uncharged sphere. We find a small acetate peak around 0.5 nm with a diffuse EMIM distribution at the same distance and a recognizable second solvation shell of EMIM ions around 0.9 nm. Thus, we can conclude that the presence of solutes, although uncharged, generally results in the breakage of the isotropical order of the system in comparison to a bulk solution. It can be assumed, that mainly the occurrence of the first acetate peak around the uncharged solute induces the formation of the second solvation shell of EMIM ions by favorable electrostatic interactions. Hence, the entropic loss due to the formation of these shells and the resulting order is compensated by the enthalpic gain of electrostatic interactions between the EMIM and the acetate ion layers. More detailed insights into the conformational behavior of these layers will be presented in the next subsection. Nevertheless, with respect to the presented results, we have to conclude that each solute induces the formation of more or less distinct solvation shells which significantly perturb the solution structure. This behavior has been also assumed in a recent publication where it was proposed that the composition of ionic liquids at molecular interfaces strongly differs from bulk behavior in terms of a long-range order influence.39
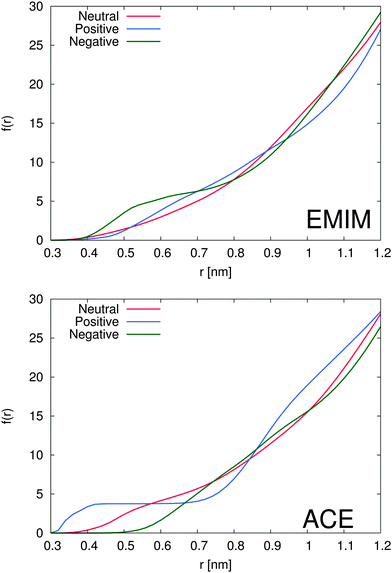
The total amount of accumulated ions can be calculated by the cumulative number distribution function f(r) according to eqn (2) which was independently computed for the EMIM and the acetate ions (Fig. 3). It becomes obvious that the most pronounced closed shell character can be observed for acetate ions around the positively charged solute with roughly 5 ions within distances of r ≤ 0.42 nm. In agreement with our previous results, we observe for acetate ions around the negatively charged solute a slightly pronounced second solvent shell (r ≈ 0.6–0.8 nm). The slight dominance of acetate ions around the uncharged solute compared to EMIM ions for distances r ≈ 0.4–0.8 nm can be also recognized by the presence of a small bump.
With respect to the maximum number of ions in the first solvent shell, we have found roughly 5 acetate ions within a distance of 0.42 nm around the positively charged solute and roughly 6 EMIM ions within a distance of 0.7 nm around the negatively charged solute. Therefore, the maximum packing density for acetate ions is larger which explains the high peak value for acetate ions around the positively charged solute in Fig. 2. Interestingly, the pronounced occurrence of closed and well-defined solvent shells which is evident for acetate ions around positively charged solutes is more or less absent for EMIM ions around negatively charged spheres. We can relate this finding to a broader orientational distribution of EMIM ions as it will be discussed in the next section.
In order to quantify the amount of structural organization, one can calculate the translational order parameter according to eqn (3) in addition to the corresponding excess entropies (eqn (4)). The obtained results which are presented in the ESI† validate the strong influence of positively and negatively charged solutes. Indeed, the highest order can be found for acetate ions around the positively charged solute which is also reflected by the corresponding results for the excess entropy. Our results further validate that the non-converging values for the excess entropies and the translational order parameter around the charged spheres indicate the occurrence of a long-range order perturbation effect induced by the spheres which is mainly electrostatically driven in its origin. This assumption can be validated with regard to the neutral solutes where the presence of converged values at finite distances is evident.
In addition, we have also calculated the conservative energetic contributions to the solvation behavior (data shown in the ESI†). Our results indicate that the positively charged sphere has the strongest electrostatic interactions with the environment. The short distance to the first acetate solvent shell as well as the corresponding high packing density results in the most favorable Coulomb interaction energy. The corresponding results for the EMIM ions around the negatively charged sphere are less favorable. Nevertheless, the overwhelming dominance of electrostatic interactions in contrast to smaller Lennard-Jones energies is demonstrated.
4.2 Orientational order parameters for the solvent shells
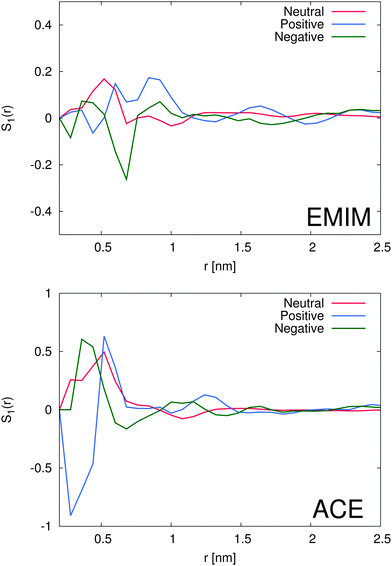
With regard to the orientational order parameter according to eqn (5), we have analyzed the distribution of the molecular configurations for both ionic species around the solutes. The results are presented in Fig. 4. It can be clearly seen that the charged solutes induce a strong conformational order behavior on distances of roughly 1.5 nm and beyond. Therefore, even the second solvation shells, independent of the ionic species, indicate a preferred orientational order behavior. Indeed, the orientational behavior of acetate ions around positively charged solutes is mostly pronounced with a single preferred configuration due to favorable electrostatic interactions with the solute. Furthermore, the different conformations of EMIM ions around negatively and positively charged solutes on distances r ≤ 1.2 nm, as they are also assumed to be responsible for the broad peaks of the radial distribution function (Fig. 2), become clearly evident. In addition, we also find a preferred orientational behavior for the acetate and the EMIM ions around the uncharged solute.In order to study the orientational configuration of the ions in the first and second solvation shell in more detail, we have calculated the probability distribution for the orientational order parameter P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) in Fig. 5. The distances for the evaluation of P(cos
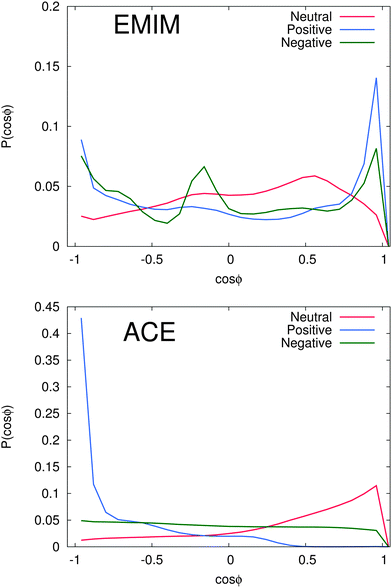
ϕ) in Fig. 5. The distances for the evaluation of P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) have been determined with respect to the results of Fig. 2. We decided to take the first and the second solvation shell into account which restricted the considered distance to the local minimum beyond the second solvent shell.
ϕ) have been determined with respect to the results of Fig. 2. We decided to take the first and the second solvation shell into account which restricted the considered distance to the local minimum beyond the second solvent shell.
As it was discussed above, we observe a more or less isoconfigurational orientation behavior for acetate ions around negatively charged solutes. A slight configurational preference for cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ ≈ 1 can be observed around neutral solutes. Hence, the negatively charged carboxylic group points away from the solute surface to maximize electrostatic interactions with the surrounding EMIM ions. The most expressed configurational order effect can be observed for acetate ions around positively charged solutes with P(cos
ϕ ≈ 1 can be observed around neutral solutes. Hence, the negatively charged carboxylic group points away from the solute surface to maximize electrostatic interactions with the surrounding EMIM ions. The most expressed configurational order effect can be observed for acetate ions around positively charged solutes with P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) ≈ −1 where the negatively charged mesomeric carboxyl group directly interacts with the solute. Thereby, we can clearly elucidate the presence of favorable electrostatic interactions between positively charged spheres and acetate ions as the most prominent reason for the induced structural order of the first solvation shell. Further analysis with additional angular orientational order parameters has also revealed the presence of edge-like configuration instead of a planar configurations relative to the solute. Therefore, the acetate ions nicely resemble the orientation of water molecules towards negatively charged surfaces.101
ϕ) ≈ −1 where the negatively charged mesomeric carboxyl group directly interacts with the solute. Thereby, we can clearly elucidate the presence of favorable electrostatic interactions between positively charged spheres and acetate ions as the most prominent reason for the induced structural order of the first solvation shell. Further analysis with additional angular orientational order parameters has also revealed the presence of edge-like configuration instead of a planar configurations relative to the solute. Therefore, the acetate ions nicely resemble the orientation of water molecules towards negatively charged surfaces.101
With regard to the EMIM configuration around neutral solutes, we also observe a broad angular distribution with a slight preference of configurations where the atom H1 (Fig. 1) is oriented towards the solute (P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) ≈ 0.5) as discussed above to minimize the distance to the negatively charged carboxylic group of the neighboring first solvent shell acetate ions (cf.Fig. 2). In addition, the strong orientational preference of three EMIM conformations around the negative solute, which results in a broadened first solvation shell (Fig. 2) becomes evident with regard to the three peaks at P(cos
ϕ) ≈ 0.5) as discussed above to minimize the distance to the negatively charged carboxylic group of the neighboring first solvent shell acetate ions (cf.Fig. 2). In addition, the strong orientational preference of three EMIM conformations around the negative solute, which results in a broadened first solvation shell (Fig. 2) becomes evident with regard to the three peaks at P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) ≈ −0.9, P(cos
ϕ) ≈ −0.9, P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) ≈ −0.2 and P(cos
ϕ) ≈ −0.2 and P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) ≈ 0.9. As it was also found for the acetate ion, the most pronounced configurations are given by edge-like conformations due to direct interaction of the solute with the H1 atom and the methyl group of EMIM. Therefore, it becomes obvious that the orientation of the N1 atom towards the solute is more favorable than the orientation with respect to the N2 atom and the ethyl group. This can be mainly related to steric reasons. A typical simulation snapshot for these configurations can be seen in Fig. 6. Interestingly, two EMIM conformations are strongly favored around positively charged solutes (P(cos
ϕ) ≈ 0.9. As it was also found for the acetate ion, the most pronounced configurations are given by edge-like conformations due to direct interaction of the solute with the H1 atom and the methyl group of EMIM. Therefore, it becomes obvious that the orientation of the N1 atom towards the solute is more favorable than the orientation with respect to the N2 atom and the ethyl group. This can be mainly related to steric reasons. A typical simulation snapshot for these configurations can be seen in Fig. 6. Interestingly, two EMIM conformations are strongly favored around positively charged solutes (P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) ≈ ±0.9). Here, the EMIM shell corresponds to the second solvation shell which is embedded between two acetate shells. Thus, EMIM ions that are more closely located to the first acetate shell orient differently (H1 pointing towards the solute) as those EMIM ions that are located more closely to the second acetate shell (H1 pointing away from the solute) which is in good agreement with the results of Fig. 4. All these results illustrate the high orientational order of the ionic species around the charged solutes. We observe a broad variety of preferred orientations, specifically for the EMIM cations, which are mainly induced by electrostatic interactions as well as unfavorable Lennard-Jones interactions with the solute or the embedding solvation shells.
ϕ) ≈ ±0.9). Here, the EMIM shell corresponds to the second solvation shell which is embedded between two acetate shells. Thus, EMIM ions that are more closely located to the first acetate shell orient differently (H1 pointing towards the solute) as those EMIM ions that are located more closely to the second acetate shell (H1 pointing away from the solute) which is in good agreement with the results of Fig. 4. All these results illustrate the high orientational order of the ionic species around the charged solutes. We observe a broad variety of preferred orientations, specifically for the EMIM cations, which are mainly induced by electrostatic interactions as well as unfavorable Lennard-Jones interactions with the solute or the embedding solvation shells.
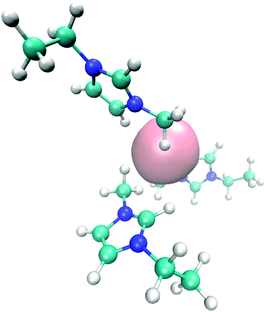 | ||
| Fig. 6 Molecular snapshot with typical EMIM orientation configurations in the first solvent shell around a negatively charged solute. | ||
4.3 Dynamic behavior of the solutes and the ionic liquids
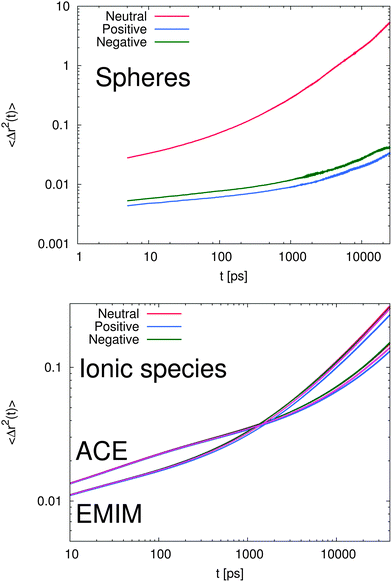
In order to study the dynamic behavior of the considered species in more detail, we present the mean-square displacement (MSD) of the center of mass for the solutes and the ionic liquids according to 〈Δr2(t)〉 = 〈(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cm(t) −
cm(t) − ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cm(0))2〉 in terms of the Einstein relation
cm(0))2〉 in terms of the Einstein relation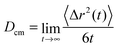 | (10) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) cm at different times in Fig. 7. It can be clearly seen that the MSD of the spheres (top of Fig. 7) strongly differs with respect to the charge of the sphere. Furthermore, it becomes evident that even the slope of the MSD shows significant deviations between the neutral and the charged solutes. In order to quantify this behavior, one can generally define a fractional MSD according to
cm at different times in Fig. 7. It can be clearly seen that the MSD of the spheres (top of Fig. 7) strongly differs with respect to the charge of the sphere. Furthermore, it becomes evident that even the slope of the MSD shows significant deviations between the neutral and the charged solutes. In order to quantify this behavior, one can generally define a fractional MSD according to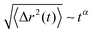 | (11) |
However, with regard to the results for the charged spheres in Fig. 7, the presence of a strong subdiffusive regime with values of α ∼ 0.07 at timescales t ≤ 2 ns is clearly evident. Here, we observe a strong anomalous behavior in which the local cage is very successful in pushing back the solutes into their original position. The value of α for the neutral sphere for times smaller than 100 ps is given by 0.18. Indeed, it can be clearly seen by the shorter transition time (t ≈ 200 ps) into the α regime for the neutral solute, that a less stable cage around the uncharged species is formed. With respect to the previous results, we can clearly state that the formation of a strong local ‘IL cage’ in presence of charged solutes which leads to the low values for α and the later transition times is mainly driven by electrostatic interactions. To validate this conclusion in more detail, it becomes also evident that the β-regime for charged spheres dominates on timescales up to 3–5 ns whereas the corresponding transition into the α-regime for the uncharged solute is even visible at timescales t ≥ 200 ps.
With respect to the corresponding diffusion behavior of the ionic liquid compounds (bottom of Fig. 7), it becomes evident that the charge of the sphere obeys a slight influence as compared to a reference system without solutes. Specifically the intrinsic difference between the positively and the negatively charged solute system is obvious for times t ≥ 1 ns. In addition, it can be seen that the diffusional behavior between acetate and EMIM ions strongly differs for times larger than 200 ps. Although it has been largely discussed that the dynamic properties of ionic liquids may be affected by the absence of polarization effects71,74 and some spurious artifacts of the CL&P force fields are known, the observed results allow us to draw some general qualitative conclusions.
First, it can be clearly seen that the caging effect for the charged spheres dominates the diffusional behavior. In contrast, the dynamic behavior of the IL species is only weakly perturbed by the solutes. Therefore, we can conclude that the solutes strongly interact with the local environment in terms of electrostatic interactions which build up a very long lasting cage structure. In absence of electrostatic interactions, the cage effect is weakened as the results for the uncharged solute imply.
In order to investigate the slight deviations between acetate and EMIM ions around the charged solute, we have evaluated the dipolar autocorrelation function and studied the influence of the ionic species in the first, respectively second solvation shell on the dynamics.
The results for the dipolar autocorrelation function Cμ(t) according to eqn (6) are presented in Fig. 8. It can be clearly seen that the dipolar relaxation behavior of EMIM and acetate ions strongly differs. Due to the smaller size of acetate ions, the dipolar relaxation time according to eqn (7) is roughly less than half of the order of EMIM ions. Slight differences for both ionic species with respect to the reference system without solutes can be observed for negative and neutral solutes. However, these differences are only slightly pronounced. In contrast, we observe a strong delay in the dipolar correlation times for both ionic liquid species around positively charged solutes. The reason for this finding can be mainly related to the strong electrostatic interactions with the positively charged sphere as they were discussed above. This conclusion becomes reasonable with regard to the slightly smaller MSDs for the system with the positively charged sphere due to the formation of a rigid, weakly rearranging solvent cage as the high electrostatic energy show (see ESI†).
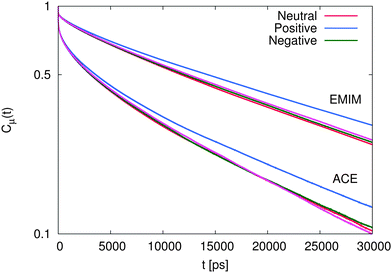 | ||
| Fig. 8 Dipolar autocorrelation function Cμ(t) according to eqn (6) for EMIM and acetate ions. The magenta lines denote the results for the reference system in absence of spherical solutes. | ||
With respect to the strength of the local cage effect and the relaxation times of the ionic species, we have also evaluated the binding lifetimes for the corresponding solvation shells. For this procedure, we have evaluated the width of the first two solvation shells in agreement with the procedure described for the computation of the orientational order parameter distribution above (Fig. 5). The corresponding results for the lifetimes of ACE (blue curve) and EMIM (black curve) are presented in Fig. 9. Here, we observe a decay on longer timescales for EMIM as well as acetate ions around the positively and the negatively charged solute compared to the uncharged sphere. Hence, the binding time is strongly influenced by electrostatic interactions. The general non-exponential decay at short time scales for all species can be related to a coupling between collective diffusional behavior as well as the contributions of independent molecular motion.88 In addition, we have also calculated the probability for the sphere to cover a distance less than 0.3 nm (red lines) in Fig. 9 with regard to the integrated eqn (9). The length scale of 0.3 nm represents the minimum size of the local IL cage with respect to the radial distribution functions shown in Fig. 2. The differences between the decay of the probability distribution and the lifetimes for all systems imply that the binding timescale for the ionic liquid species does not influence the dynamic behavior of the spheres. Hence, rearrangement effects in the local solvent cage are not responsible for the varying solute dynamics between the spheres as it was found for the MSD. Thus, the strength of the confining cage is reflected by the pronounced and well-order structure around the charged solutes, irrespective of restructuring effects of the cage itself.
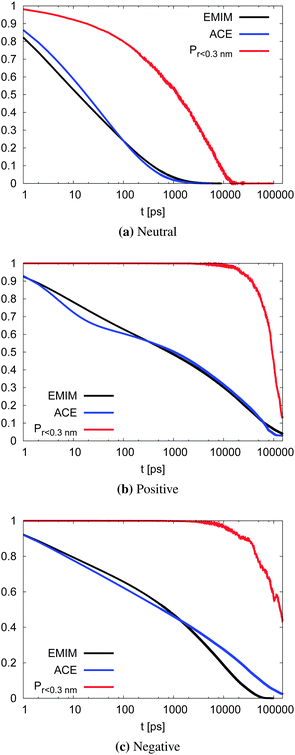 | ||
| Fig. 9 Binding lifetime function Cb(t) and the probability for the neutral (top), positively charged (middle) and the negatively charged sphere (bottom) to move less than 0.3 nm. | ||
In order to estimate the relative binding strength between the ionic species and the solute, one can rely on standard transition theory with τb ∼ exp(ΔF*/kBT) to estimate the activation free energy ΔF* that is needed for the rearrangement of the solvation shells as it has been originally proposed for aqueous hydrogen bonds.109 In terms of our previous observations, it can be expected that ΔF* is strongly dominated by enthalpic contributions in terms of electrostatic interactions which are significantly more pronounced than entropic contributions. With regard to the above reported average binding lifetimes, it can be expected that the strongest activation binding free energy should be observed for acetate ions around positively charged solutes.
5 Summary and conclusion
We have performed atomistic molecular dynamics simulations of differently charged model spheres in 1-ethyl-3-methylimidazolium acetate to study the solvation properties at 298 K. The results clearly indicate a different solvation behavior for all considered solutes. Our main findings evidence the significantly stronger solvation of positively charged solutes due to a larger packing density in the first solvation shell. This finding can be mainly related to the molecular size of the acetate ions, which facilitates a tighter accumulation effect compared to the behavior of the corresponding EMIM cations around the negatively charged solute. Our results further evidence a long-range perturbation of the solvent on length scales r ≤ 2.5 nm and even beyond as it was validated by the translational order parameter and the excess entropies. Thus, we can clearly see that the local solvent order is strongly influenced in presence of charged solutes. This finding can be mainly related to the overwhelming dominance of electrostatic interactions of the first solvent shell with the solute. Our findings are in good agreement with previous results about the solvation of small molecules like methane, glucose or uncharged oligomers.32–35,37,38 The authors of these publications have often found a significant binding of the ionic liquid species to the charged groups of the solute which is mostly reflected by strong hydrogen bonds. Specifically smaller ionic liquid anions like chloride anions are known to form strong and long-lasting ionic bonds with the corresponding charged solute groups.32–35,37,38 The occurrence of a slightly ordered ionic liquid around uncharged solutes has been also discussed. Nevertheless, the results of our study indicate that these findings can be generalized without any specificity with regard to the considered solute.We have also investigated the local orientation of the ionic liquid compounds with respect to the solute surface. Our results indicate the presence of several favorable conformations of EMIM ions which significantly depend on the solute charge in contrast to the acetate ions, which indicate more or less preferred conformations.
In addition, we have also studied the dynamic properties of the systems where we have investigated the MSD of all species as well as the dipolar relaxation behavior of the ions. Based on the MSD we found an anomalous diffusional behavior for all the spheres. In contrast to the charged solutes, the length of this so-called anomalous diffusional regime is less pronounced for the uncharged sphere. Noteworthy, the presence of the positively charged sphere results in a significant retardation of the dynamical behavior of the system as the decay of the dipolar relaxation function Cμ(t) clearly shows. The probability function for the spheres to move on length scales smaller than 0.3 nm decays on different time scales compared to the binding time autocorrelation function. Thus, the diffusional behavior of the charged spheres is independent from the rearrangement of the solvation shells.
With regard to the analysis of the total energetic contributions, we are able to show that favorable electrostatic interactions significantly dominate the total conservative potential energy. Noteworthy, the most favorable interaction energy was observed for the positively charged solute. Based on these findings, we can conclude, that solutes where the smaller sized ionic species of the ionic liquid form the first solvent shell are favorably solvated. This can be explained by the higher ion packing density in the first solvation shell due to molecular size effects. Notably, the usage of this principle32,33,35,38 has lead to some successful results for the dissolution of glucose and other small solutes.
We hope that our study highlighted the subtle interplay between solute–solvent interactions in ionic liquids. With respect to the important idea of using novel, less hazardous solvents in terms of a ‘green chemistry’ approach, ionic liquids may represent a valuable, but nevertheless challenging alternative to traditional solvents. Over the next years, it can be assumed that the systematic study of ionic liquid or polyionic liquid effects110 may facilitate the steering of chemical reactions as well as the dissolution of apolar components among other benefits.
Acknowledgements
We thank Diddo Diddens, Anand Narayanan Krishnamoorthy, Christian Schröder, Marcello Sega and Florian Dommert for helpful discussions. We acknowledge the BMBF within the SafeBatt project (Förderkennzeichen: 03X4631N) and the Deutsche Forschungsgemeinschaft (DFG) via the cluster of excellence ‘Simulation Technology’ (EXC 310) for financial support.References
- M. Galiński, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580 CrossRef.
- M. Ishikawa, T. Sugimoto, M. Kikuta, E. Ishiko and M. Kono, J. Power Sources, 2006, 162, 658–662 CrossRef CAS.
- S. M. Zakeeruddin and M. Graetzel, Adv. Funct. Mater., 2009, 19, 2187–2202 CrossRef CAS.
- T. Welton, Chem. Rev., 1999, 99, 2071–2084 CrossRef CAS PubMed.
- R. D. Rogers and K. R. Seddon, Science, 2003, 302, 792–793 CrossRef PubMed.
- J. S. Wilkes, J. Mol. Catal. A: Chem., 2004, 214, 11–17 CrossRef CAS.
- J. D. Holbrey, W. M. Reichert, S. K. Spear, R. P. Swatloski, M. B. Turner and A. E. Visser, ACS Symposium Series, 2003 Search PubMed.
- P. Wasserscheid and W. Keim, Angew. Chem., 2000, 39, 3772–3789 CrossRef CAS.
- T. Yasuda and M. Watanabe, MRS Bull., 2013, 38, 560–566 CrossRef CAS.
- A. Matic and B. Scrosati, MRS Bull., 2013, 38, 533–537 CrossRef CAS.
- O. Borodin, G. D. Smith and W. Henderson, J. Phys. Chem. B, 2006, 110, 16879–16886 CrossRef CAS PubMed.
- O. Borodin, J. Phys. Chem. B, 2009, 113, 12353–12357 CrossRef CAS PubMed.
- Z. Li, G. D. Smith and D. Bedrov, J. Phys. Chem. B, 2012, 116, 12801–12809 CrossRef CAS PubMed.
- V. Lesch, S. Jeremias, A. Moretti, S. Passerini, A. Heuer and O. Borodin, J. Phys. Chem. B, 2014, 118, 7367–7375 CrossRef CAS PubMed.
- H. Ohno, Electrochemical aspects of ionic liquids, John Wiley & Sons, 2011 Search PubMed.
- K. R. Seddon, J. Chem. Technol. Biotechnol., 1997, 68, 351–356 CrossRef CAS.
- D. Bedrov, O. Borodin, Z. Li and G. D. Smith, J. Phys. Chem. B, 2010, 114, 4984–4997 CrossRef CAS PubMed.
- M. G. Del Pópolo, R. M. Lynden-Bell and J. Kohanoff, J. Phys. Chem. B, 2005, 109, 5895–5902 CrossRef PubMed.
- M. G. Del Pópolo, J. Kohanoff and R. M. Lynden-Bell, J. Phys. Chem. B, 2006, 110, 8798–8803 CrossRef PubMed.
- B. Bhargava and S. Balasubramanian, Chem. Phys. Lett., 2006, 417, 486–491 CrossRef CAS.
- E. W. Castner Jr, J. F. Wishart and H. Shirota, Acc. Chem. Res., 2007, 40, 1217–1227 CrossRef PubMed.
- H. Jin, G. A. Baker, S. Arzhantsev, J. Dong and M. Maroncelli, J. Phys. Chem. B, 2007, 111, 7291–7302 CrossRef CAS PubMed.
- H. Jin, X. Li and M. Maroncelli, J. Phys. Chem. B, 2007, 111, 13473–13478 CrossRef CAS PubMed.
- A. Samanta, J. Phys. Chem. Lett., 2010, 1, 1557–1562 CrossRef CAS.
- B. Qiao, C. Krekeler, R. Berger, L. Delle Site and C. Holm, J. Phys. Chem. B, 2008, 112, 1743–1751 CrossRef CAS PubMed.
- F. Dommert, J. Schmidt, B. Qiao, Y. Zhao, C. Krekeler, L. Delle Site, R. Berger and C. Holm, J. Chem. Phys., 2008, 129, 224501 CrossRef PubMed.
- D. Roy and M. Maroncelli, J. Phys. Chem. B, 2012, 116, 5951–5970 CrossRef CAS PubMed.
- A. Kaintz, G. Baker, A. Benesi and M. Maroncelli, J. Phys. Chem. B, 2013, 117, 11697–11708 CrossRef CAS PubMed.
- K. A. Maerzke, G. S. Goff, W. H. Runde, W. F. Schneider and E. J. Maginn, J. Phys. Chem. B, 2013, 117, 10852–10868 CrossRef CAS PubMed.
- T. Yago, Y. Ishii and M. Wakasa, J. Phys. Chem. C, 2014, 118, 22356–22367 CAS.
- C. Reichardt and T. Welton, Solvents and solvent effects in organicchemistry, John Wiley & Sons, 2011 Search PubMed.
- C. Hanke, N. Atamas and R. Lynden-Bell, Green Chem., 2002, 4, 107–111 RSC.
- Y. Shim, J. Duan, M. Choi and H. J. Kim, J. Chem. Phys., 2003, 119, 6411–6414 CrossRef CAS.
- Y. Shim, M. Y. Choi and H. J. Kim, J. Chem. Phys., 2005, 122, 044510 CrossRef CAS PubMed.
- T. G. Youngs, J. D. Holbrey, M. Deetlefs, M. Nieuwenhuyzen, M. F. Costa Gomes and C. Hardacre, ChemPhysChem, 2006, 7, 2279–2281 CrossRef CAS PubMed.
- D. Jeong, Y. Shim, M. Choi and H. J. Kim, J. Phys. Chem. B, 2007, 111, 4920–4925 CrossRef CAS PubMed.
- A. A. Padua, M. F. Costa Gomes and J. N. Canongia Lopes, Acc. Chem. Res., 2007, 40, 1087–1096 CrossRef CAS PubMed.
- T. Youngs, C. Hardacre and J. Holbrey, J. Phys. Chem. B, 2007, 111, 13765–13774 CrossRef CAS PubMed.
- C. Hardacre, J. D. Holbrey, M. Nieuwenhuyzen and T. G. Youngs, Acc. Chem. Res., 2007, 40, 1146–1155 CrossRef CAS PubMed.
- K. Shimizu, M. F. Costa Gomes, A. A. Paìdua, L. P. N. Rebelo and J. N. Canongia Lopes, J. Phys. Chem. B, 2009, 113, 9894–9900 CrossRef CAS PubMed.
- T. Pal and R. Biswas, J. Chem. Phys., 2014, 141, 104501 CrossRef PubMed.
- L. Xue, G. Tamas, E. Gurung and E. L. Quitevis, J. Chem. Phys., 2014, 140, 164512 CrossRef PubMed.
- R. M. Lynden-Bell, M. G. Del Popolo, T. G. Youngs, J. Kohanoff, C. G. Hanke, J. B. Harper and C. C. Pinilla, Acc. Chem. Res., 2007, 40, 1138–1145 CrossRef CAS PubMed.
- J. Vatamanu, O. Borodin, D. Bedrov and G. D. Smith, J. Phys. Chem. C, 2012, 116, 7940–7951 CAS.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed.
- Y. Shim, D. Jeong, S. Manjari, M. Y. Choi and H. J. Kim, Acc. Chem. Res., 2007, 40, 1130–1137 CrossRef CAS PubMed.
- D. Xiao, L. G. Hines Jr, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2009, 113, 4544–4548 CrossRef CAS PubMed.
- B. Ni and A. D. Headley, Chem. – Eur. J., 2010, 16, 4426–4436 CrossRef CAS PubMed.
- P. Ball, Chem. Rev., 2008, 108, 74–108 CrossRef CAS PubMed.
- J. Smiatek, A. Wohlfarth and C. Holm, New J. Phys., 2014, 16, 025001 CrossRef.
- A. S. Thomas and A. H. Elcock, J. Am. Chem. Soc., 2007, 129, 14887–14898 CrossRef CAS PubMed.
- A. Vishnyakov and A. V. Neimark, J. Chem. Phys., 2008, 128, 164902 CrossRef PubMed.
- M. N. Rodnikova, J. Mol. Liq., 2007, 136, 211–213 CrossRef CAS.
- C. N. Pace, S. Trevino, E. Prabhakaran and J. M. Scholtz, Philos. Trans. R. Soc. London, Ser. B, 2004, 359, 1225–1235 CrossRef CAS PubMed.
- M. Yaacobi and A. Ben-Naim, J. Phys. Chem., 1974, 78, 175 CrossRef CAS.
- N. M. Micaêlo and C. M. Soares, J. Phys. Chem. B, 2008, 112, 2566–2572 CrossRef PubMed.
- M. Klähn, G. S. Lim, A. Seduraman and P. Wu, Phys. Chem. Chem. Phys., 2011, 13, 1649–1662 RSC.
- M. Haberler, C. Schröder and O. Steinhauser, Phys. Chem. Chem. Phys., 2011, 13, 6955–6969 RSC.
- C. Byrne and N. Angell, J. Mol. Biol., 2008, 378, 707–714 CrossRef PubMed.
- P. Kumar and V. Awanish, RSC Adv., 2013, 3, 362–367 RSC.
- M. V. Fedorov and A. A. Kornyshev, J. Phys. Chem. B, 2008, 112, 11868–11872 CrossRef CAS PubMed.
- M. V. Fedorov, N. Georgi and A. A. Kornyshev, Electrochem. Commun., 2010, 12, 296–299 CrossRef CAS.
- N. Georgi, A. A. Kornyshev and M. V. Fedorov, J. Electroanal. Chem., 2010, 649, 261–267 CrossRef CAS.
- C. Merlet, M. Salanne, B. Rotenberg and P. A. Madden, J. Phys. Chem. C, 2011, 115, 16613–16618 CAS.
- C. Merlet, M. Salanne and B. Rotenberg, J. Phys. Chem. C, 2012, 116, 7687–7693 CAS.
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310 CrossRef CAS PubMed.
- K. Breitsprecher, P. Kosovan and C. Holm, J. Phys.: Condens. Matter, 2014, 26, 284108 CrossRef PubMed.
- K. Breitsprecher, P. Kosovan and C. Holm, J. Phys.: Condens. Matter, 2014, 26, 284114 CrossRef PubMed.
- T. Yan, C. J. Burnham, M. G. Del Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 11877–11881 CrossRef CAS.
- M. G. Del Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 1744–1752 CrossRef.
- T. Köddermann, D. Paschek and R. Ludwig, ChemPhysChem, 2007, 8, 2464–2470 CrossRef PubMed.
- J. Schmidt, C. Krekeler, F. Dommert, Y. Zhao, R. Berger, L. Delle Site and C. Holm, J. Phys. Chem. B, 2010, 114, 6150–6155 CrossRef CAS PubMed.
- C. Schröder and O. Steinhauser, J. Chem. Phys., 2010, 133, 154511 CrossRef PubMed.
- F. Dommert, K. Wendler, R. Berger, L. Delle Site and C. Holm, ChemPhysChem, 2012, 13, 1625–1637 CrossRef CAS PubMed.
- H. Yu and W. F. van Gunsteren, Comput. Phys. Commun., 2005, 172, 69–85 CrossRef CAS.
- O. Borodin, J. Phys. Chem. B, 2009, 113, 11463–11478 CrossRef CAS PubMed.
- E. J. Maginn, J. Phys.: Condens. Matter, 2009, 21, 373101 CrossRef CAS PubMed.
- A. R. Leach, Molecular modelling: principles and applications, Pearson Education, 2001 Search PubMed.
- I. Yokoyama, Phys. B, 1999, 269, 244–248 CrossRef CAS.
- P. Kumar, S. V. Buldyrev and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 22130–22134 CrossRef CAS PubMed.
- A. Baranyai and D. J. Evans, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 3817 CrossRef CAS.
- T. M. Truskett, S. Torquato and P. G. Debenedetti, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 993 CrossRef CAS.
- Z. Yan, S. V. Buldyrev and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 051201 CrossRef.
- R. Nettleton and M. Green, J. Chem. Phys., 1958, 29, 1365–1370 CrossRef CAS.
- D. K. Hore, D. S. Walker and G. L. Richmond, J. Am. Chem. Soc., 2008, 130, 1800–1801 CrossRef CAS PubMed.
- P. Kumar, G. Franzese, S. V. Buldyrev and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041505 CrossRef.
- G. Adam and J. H. Gibbs, J. Chem. Phys., 1965, 43, 139–146 CrossRef CAS.
- A. Luzar and D. Chandler, Nature, 1996, 379, 55–57 CrossRef CAS.
- L. Van Hove, Phys. Rev., 1954, 95, 249 CrossRef CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- J. M. Martinez and L. Martinez, J. Comput. Chem., 2003, 24, 819–825 CrossRef CAS PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- J. N. Canongia Lopes, J. Deschamps and A. A. H. Padua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- J. N. Canongia Lopes and A. A. H. Padua, J. Phys. Chem. B, 2006, 110, 19586–19592 CrossRef CAS PubMed.
- J. N. Canongia Lopes and A. A. H. Padua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
- J. N. Canongia Lopes, A. A. H. Padua and K. Shimizu, J. Phys. Chem. B, 2008, 112, 5039–5046 CrossRef CAS PubMed.
- J. N. C. Lopes and A. A. Padua, Theor. Chem. Acc., 2012, 131, 1–11 Search PubMed.
- M. Markowski, C. Czaplewski, A. Liwo and H. A. Scheraga, J. Phys. Chem. B, 2010, 114, 993–1003 CrossRef PubMed.
- J. Smiatek, J. Phys. Chem. B, 2014, 118, 771–782 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- H. Berendsen, J. Postma, W. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- B. Doliwa and A. Heuer, Phys. Rev. Lett., 1998, 80, 4915 CrossRef CAS.
- D. van der Spoel, P. J. van Maaren, P. Larsson and N. Timneanu, J. Phys. Chem. B, 2006, 110, 4393–4398 CrossRef CAS PubMed.
- J. Yuan, D. Mecerreyes and M. Antonietti, Prog. Polym. Sci., 2013, 38, 1009–1036 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp05312e |
| This journal is © the Owner Societies 2015 |