Open Access Article
Open Access ArticleStepwise alkyne insertion in Au(I) acetylides: influence of the nuclearity†
Juan
Cayuela-Castillo
 a,
Francisco J.
Fernández-de-Córdova
a,
Francisco J.
Fernández-de-Córdova
 a,
Matthew S.
See
a,
Matthew S.
See
 b,
Israel
Fernández
b,
Israel
Fernández
 *c and
Pablo
Ríos
*c and
Pablo
Ríos
 *a
*a
aInstituto de Investigaciones Químicas (IIQ), Departamento de Química Inorgánica, Centro de Innovación en Química Avanzada (ORFEO-CINQA), CSIC and Universidad de Sevilla, 41092 Sevilla, Spain. E-mail: prios1@us.es
bDepartment of Chemistry, University of California, Berkeley, Berkeley, CA 94720, USA
cDepartamento de Química Orgánica I and Centro de Innovación en Química Avanzada (ORFEO-CINQA), Facultad de Químicas, Universidad Complutense de Madrid, Madrid 28040, Spain. E-mail: israel@quim.ucm.es
First published on 13th February 2025
Abstract
The reaction between NHC-supported (NHC = N-heterocyclic carbene) gold(I) trimethylsilylacetylide complexes with NHC gold(I) hydroxide species renders different symmetrical homobimetallic Au complexes. These compounds readily undergo migratory insertion of DMAD (dimethyl acetylenedicarboxylate) at 25 °C to give the corresponding bimetallic enyne products. On the contrary, monometallic analogues require much more forcing conditions (excess of DMAD and temperature ≥110 °C) to give the same transformation. Experimental and computational studies reveal that the second metal fragment is responsible for the enhanced nucleophilicity of the reactive carbon atom of the acetylide C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond, which initially leads to a more favorable interaction with DMAD in the rate-determining step of an unprecedented, stepwise mechanism where the lability of the Au–C bonds plays an instrumental role. The enhanced reactivity displayed by the bimetallic species was leveraged in the insertion of other substrates such as heterocumulenes.
C bond, which initially leads to a more favorable interaction with DMAD in the rate-determining step of an unprecedented, stepwise mechanism where the lability of the Au–C bonds plays an instrumental role. The enhanced reactivity displayed by the bimetallic species was leveraged in the insertion of other substrates such as heterocumulenes.
Introduction
Since the first observation that cationic gold(I) complexes electrophilically activate unsaturated C–C bonds upon binding,1 the utilization of gold(I) in homogeneous catalysis has grown exponentially over the last couple of decades. The π-coordination renders the system susceptible to nucleophilic attack and has led to a myriad of organic transformations.2 This process typically requires a vacant position at the cationic gold(I) species for coordination of the π-substrate, which would imply that neutral, coordinatively saturated gold(I) complexes are, in principle, unreactive, according to this reactivity pattern. However, recent discoveries have demonstrated that these types of gold compounds can also undergo elementary steps typical of transition metals, such as oxidative addition, reductive elimination, and/or migratory insertion.3 In the latter case, only a few examples have been published.4 In 2007, Sadighi and co-workers described the reversible insertion of different internal alkynes into the gold–fluorine bond of SIPrAuF (SIPr = 1,3-bis(2,6-diisopropylphenyl)imidazolin-2-ylidene) to give the corresponding trans product.5 The proposed mechanism involves fluoride displacement by the alkyne followed by nucleophilic addition to the coordinated triple bond, thus explaining the trans orientation. Conversely, the first example of a syn insertion was reported by Amgoune and Bourissou, where phosphine-supported gold(I) silyl species yielded β-silyl vinylgold products in a stereo- and regioselective manner.6 Notably, replacing the phosphine fragment with an NHC ligand gave rise to the insertion product with opposite regioselectivity, presumably due to steric factors.7 Nonetheless, the majority of the examples described in the literature require electron-deficient alkynes such as DMAD for a successful migratory insertion event, some of which are summarized in Fig. 1. Indeed, IPrAuH (IPr = 1,3-bis(2,6-diisopropylphenyl)imidazol-2-ylidene) does not react with 3-hexyne or diphenylacetylene, but it cleanly reacts with DMAD, giving the corresponding vinylgold complex with a trans arrangement of the ester groups (Fig. 1A).8 This is unusual given that the rest of the examples exhibit a cis geometry. Based on kinetic and computational studies, Miqueu, Amgoune and Bourissou proposed a two-step mechanism for the DMAD insertion into Au–Si bonds, where the alkyne first coordinates to gold (π-complex) followed by a concerted cis insertion step (Fig. 1B). However, this species is accompanied by an approximately equal amount of the Au–P insertion product. This complex seems to be the result of phosphine dissociation, Michael addition to DMAD, and attack of the resulting phosphonium enolate to the gold silyl fragment.9 The non-innocent character of Au–P bonds in the insertion of alkynes was also reported by Kuniyasu and Kambe for (Ph3P)AuSPh species. Instead of observing the expected Au–S insertion product (in agreement with their previous results with Pd and Pt), the zwitterionic alkenylphosphorus species depicted in Fig. 1C was regioselectively obtained, attributed to a concerted inner-sphere attack of PPh3 to the alkyne moiety bound to gold.10 Similarly, Stockland Jr and co-workers observed Z-vinylgold formation upon DMAD insertion on gold(I) phosphite compounds (Fig. 1D).11 While all these examples provide detailed and useful information about alkyne insertion into Au–X (X = H or heteroatom) bonds, they are all restricted to monometallic gold(I) complexes. Considering the role of bimetallic species in catalysis,12 especially in the case of digold complexes,13 it seems necessary to develop dinuclear architectures to study the factors governing this elementary step in organogold systems. To this end, bimetallic gold acetylides supported by NHC ligands (NHC–Au–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Au–NHC) were chosen as platforms for this study. Dinuclear gold(I) acetylides have been known for several decades, and their photophysical properties have been studied in detail because of the interest in Cn-bridged multinuclear inorganic species from the point of view of molecular electronics and nonlinear optical materials.14 However, the reactivity of dinuclear gold(I) acetylides remains essentially underexplored, which sharply contrasts with lighter group 11 congeners such as Cu2C2, an active catalyst for a number of ethynylation processes (i.e., Reppe chemistry).15
C–Au–NHC) were chosen as platforms for this study. Dinuclear gold(I) acetylides have been known for several decades, and their photophysical properties have been studied in detail because of the interest in Cn-bridged multinuclear inorganic species from the point of view of molecular electronics and nonlinear optical materials.14 However, the reactivity of dinuclear gold(I) acetylides remains essentially underexplored, which sharply contrasts with lighter group 11 congeners such as Cu2C2, an active catalyst for a number of ethynylation processes (i.e., Reppe chemistry).15
Herein, we present the preparation and characterization of digold(I) acetylides and their reactivity with DMAD. While a subtle modification on the ligand scaffold results in different kinetics of insertion, a pronounced disparity in reaction rates is observed between bi- and monometallic complexes. A rationalization for this different behavior is provided based on Density Functional Theory (DFT) calculations, as well as an unprecedented, stepwise mechanism for the alkyne insertion into the Au–C bonds of the synthesized complexes. In light of the enhanced reactivity exhibited by the bimetallic species, a variety of substrates was also investigated.
Results and discussion
Synthesis and initial reactivity studies
Initial synthetic studies were carried out with gold(I) species supported by the IPr ligand. The utilization of IPrAuX species is based on their wide applicability, their ease of preparation,16 and the stronger bond of NHCs with gold compared to phosphine ligands. Similar to previous studies reported for copper(I) species,17 the introduction of a trimethylsilylacetylene fragment on gold would provide the C2 fragment together with a leaving group that can be displaced by an appropriate nucleophilic Au(I) synthon. This approach would constitute a modular synthetic pathway for bimetallic Au(I)-based acetylides, thus avoiding acetylene gas14 and opening the possibility of developing unsymmetrical complexes. Starting from chloride complex 116 (Scheme 1), addition of LiC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CSiMe3 in toluene resulted in the precipitation of LiCl together with the formation of a soluble alkynyl complex 3, which could be isolated as a colorless solid in 91% isolated yield. Diagnostic evidence for the formation of the desired product was observed by NMR (resonances at 0.05 and −25.8 ppm in the 1H and 29Si–1H HMBC spectra, respectively) and IR spectroscopy (νC
CSiMe3 in toluene resulted in the precipitation of LiCl together with the formation of a soluble alkynyl complex 3, which could be isolated as a colorless solid in 91% isolated yield. Diagnostic evidence for the formation of the desired product was observed by NMR (resonances at 0.05 and −25.8 ppm in the 1H and 29Si–1H HMBC spectra, respectively) and IR spectroscopy (νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C = 2054 cm−1). Additionally, crystals of 3 suitable for single-crystal X-ray diffraction were obtained from a n-pentane solution at −30 °C, allowing for the confirmation of the expected assignment (see ESI†). From complex 3, the formation of a bimetallic acetylide was pursued using IPrAuOH 518 so that the formation of Me3SiOH acts as a driving force in the transformation. Initially, no reaction takes place at 25 °C according to the 1H NMR spectrum of the reaction mixture. However, heating the solution to 100 °C for 15 h led to the complete consumption of both reagents in favor of a new symmetrical species, in line with the expected bimetallic complex 7 (Scheme 1). Structural confirmation came from single-crystal X-ray diffraction analysis of colorless crystals grown from diffusion of n-pentane into a benzene solution of 7 (Fig. 2). The solid-state structure exhibits an almost coplanar orientation of the IPr imidazole rings (∠N1–C2–C2′–N1′ = 12.7(3)°) and a linear arrangement along the acetylide axis (∠C2–Au1–C1 and ∠Au1–C1–C1′ = 175°). The Au1–C1 and C1–C1′ bond distances (1.991(3) and 1.194(3) Å, respectively) fall within the range observed for other bimetallic Au(I) acetylides.14 The centrosymmetric character of 7 leads to a silent νC
C = 2054 cm−1). Additionally, crystals of 3 suitable for single-crystal X-ray diffraction were obtained from a n-pentane solution at −30 °C, allowing for the confirmation of the expected assignment (see ESI†). From complex 3, the formation of a bimetallic acetylide was pursued using IPrAuOH 518 so that the formation of Me3SiOH acts as a driving force in the transformation. Initially, no reaction takes place at 25 °C according to the 1H NMR spectrum of the reaction mixture. However, heating the solution to 100 °C for 15 h led to the complete consumption of both reagents in favor of a new symmetrical species, in line with the expected bimetallic complex 7 (Scheme 1). Structural confirmation came from single-crystal X-ray diffraction analysis of colorless crystals grown from diffusion of n-pentane into a benzene solution of 7 (Fig. 2). The solid-state structure exhibits an almost coplanar orientation of the IPr imidazole rings (∠N1–C2–C2′–N1′ = 12.7(3)°) and a linear arrangement along the acetylide axis (∠C2–Au1–C1 and ∠Au1–C1–C1′ = 175°). The Au1–C1 and C1–C1′ bond distances (1.991(3) and 1.194(3) Å, respectively) fall within the range observed for other bimetallic Au(I) acetylides.14 The centrosymmetric character of 7 leads to a silent νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C stretch by IR spectroscopy, yet Raman measurements exhibit a strong peak at 2012 cm−1, in good agreement with phosphine-supported analogues.14 Reactivity studies were conducted with 7 and alkynes with different electronic properties (Scheme 2). An excess (4 equiv.) of 3-hexyne did not react with 7 after 16 h at 80 °C in C6D6 (Fig. S62†), which is in stark contrast to that observed by Sadighi and co-workers for Au–F species.5 On the other hand, acetylene gas (1.5 bar) cleanly reacts with 7 under similar (80 °C in C6D6) reaction conditions to selectively yield the terminal alkyne complex IPrAuCCH (9),19 confirmed by an independent synthesis using 1 and MgBrCCH (Fig. S63†). Although this reaction has not been explored in detail, the initial steps of this transformation might find their origin in the acidity of the acetylene C–H bonds20 and the increased electron density of the π-system of 7. Indeed, a related bimetallic Au(I) acetylide complex exhibits up to four T-shaped and orthogonal C–H⋯π interactions between the triple bond and the C–H bond of four CHCl3 molecules.14c The authors attributed these strong interactions to the acidity of the C–H bonds of the solvent and the electron richness of the alkyne provided by the donation of the gold atoms. Therefore, an electron-deficient alkyne such as DMAD was investigated next, based on the examples described in Fig. 1. Addition of DMAD to complex 7 in C6D6 at 25 °C resulted in the progressive formation of two new sets of signals in the 1H NMR spectrum for the IPr ligands in a 1
C stretch by IR spectroscopy, yet Raman measurements exhibit a strong peak at 2012 cm−1, in good agreement with phosphine-supported analogues.14 Reactivity studies were conducted with 7 and alkynes with different electronic properties (Scheme 2). An excess (4 equiv.) of 3-hexyne did not react with 7 after 16 h at 80 °C in C6D6 (Fig. S62†), which is in stark contrast to that observed by Sadighi and co-workers for Au–F species.5 On the other hand, acetylene gas (1.5 bar) cleanly reacts with 7 under similar (80 °C in C6D6) reaction conditions to selectively yield the terminal alkyne complex IPrAuCCH (9),19 confirmed by an independent synthesis using 1 and MgBrCCH (Fig. S63†). Although this reaction has not been explored in detail, the initial steps of this transformation might find their origin in the acidity of the acetylene C–H bonds20 and the increased electron density of the π-system of 7. Indeed, a related bimetallic Au(I) acetylide complex exhibits up to four T-shaped and orthogonal C–H⋯π interactions between the triple bond and the C–H bond of four CHCl3 molecules.14c The authors attributed these strong interactions to the acidity of the C–H bonds of the solvent and the electron richness of the alkyne provided by the donation of the gold atoms. Therefore, an electron-deficient alkyne such as DMAD was investigated next, based on the examples described in Fig. 1. Addition of DMAD to complex 7 in C6D6 at 25 °C resulted in the progressive formation of two new sets of signals in the 1H NMR spectrum for the IPr ligands in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, consistent with the unsymmetrical product 10 (Scheme 2). These resonances are accompanied by two new singlets at 3.1 and 3.5 ppm integrating for 3 protons each, which suggests the incorporation of 1 equiv. of DMAD into the unsymmetrical structure. The reaction can be accelerated by heating the mixture to 60 °C, leading to the full consumption of 7 in favor of the aforementioned signals of complex 10. Vapor diffusion of n-pentane into the reaction mixture at 25 °C afforded colorless crystals suitable for single-crystal X-ray analysis. Fig. 3 shows the solid-state structure of the insertion product 10, revealing a bimetallic enyne structure with a cis orientation of the IPrAu fragments and ester groups, in line with the majority of examples described in Fig. 1 (C–C bond distances (C1–C2 = 1.20(1) Å, C2–C3 = 1.442(8) Å, C3–C4 = 1.34(1)) and angles (∠C1–C2–C3 = 173.9(8)°, ∠C2–C3–C4 = 122.2(6)°)). Leveraging the synthetic strategy employed for the preparation of 7 (Scheme 1), the synthesis of a different bimetallic Au(I) acetylide complex was pursued. In order to evaluate the effect of the π-electron density on the insertion of DMAD, a minimal structural modification was carried out to modify the electronic properties of the NHC ligand while keeping the steric demand around the AuCCAu moiety unaltered. To this end, acetylide 8 was envisaged (Scheme 1).21 Complex 8 is identical to 7, yet the IPr backbone has been replaced by the saturated version SIPr, which would, in principle, increase the electron density of the C
1 ratio, consistent with the unsymmetrical product 10 (Scheme 2). These resonances are accompanied by two new singlets at 3.1 and 3.5 ppm integrating for 3 protons each, which suggests the incorporation of 1 equiv. of DMAD into the unsymmetrical structure. The reaction can be accelerated by heating the mixture to 60 °C, leading to the full consumption of 7 in favor of the aforementioned signals of complex 10. Vapor diffusion of n-pentane into the reaction mixture at 25 °C afforded colorless crystals suitable for single-crystal X-ray analysis. Fig. 3 shows the solid-state structure of the insertion product 10, revealing a bimetallic enyne structure with a cis orientation of the IPrAu fragments and ester groups, in line with the majority of examples described in Fig. 1 (C–C bond distances (C1–C2 = 1.20(1) Å, C2–C3 = 1.442(8) Å, C3–C4 = 1.34(1)) and angles (∠C1–C2–C3 = 173.9(8)°, ∠C2–C3–C4 = 122.2(6)°)). Leveraging the synthetic strategy employed for the preparation of 7 (Scheme 1), the synthesis of a different bimetallic Au(I) acetylide complex was pursued. In order to evaluate the effect of the π-electron density on the insertion of DMAD, a minimal structural modification was carried out to modify the electronic properties of the NHC ligand while keeping the steric demand around the AuCCAu moiety unaltered. To this end, acetylide 8 was envisaged (Scheme 1).21 Complex 8 is identical to 7, yet the IPr backbone has been replaced by the saturated version SIPr, which would, in principle, increase the electron density of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond.21 The trimethylsilylacetylide gold(I) precursor 4 was obtained in very good yield (88%) from the corresponding chloride complex 2. Then, bimetallic assembly was carried out by reaction with SIPrAuOH species 6 upon heating, as depicted in Scheme 1. Bimetallic acetylide 8 was isolated as colorless crystals in 84% yield after layering n-pentane over a THF solution of the complex at 25 °C. 1H NMR analysis of the isolated material agrees well with the expected product (Fig. S14†), and single-crystal X-ray diffraction analysis allows its identification in the solid state, as depicted in Fig. 4. Similar to species 7, complex 8 possesses a coplanar orientation of the imidazole moieties (∠N1–C2–C2′–N1′ = 1.8(2)°). Nevertheless, the longer C
C bond.21 The trimethylsilylacetylide gold(I) precursor 4 was obtained in very good yield (88%) from the corresponding chloride complex 2. Then, bimetallic assembly was carried out by reaction with SIPrAuOH species 6 upon heating, as depicted in Scheme 1. Bimetallic acetylide 8 was isolated as colorless crystals in 84% yield after layering n-pentane over a THF solution of the complex at 25 °C. 1H NMR analysis of the isolated material agrees well with the expected product (Fig. S14†), and single-crystal X-ray diffraction analysis allows its identification in the solid state, as depicted in Fig. 4. Similar to species 7, complex 8 possesses a coplanar orientation of the imidazole moieties (∠N1–C2–C2′–N1′ = 1.8(2)°). Nevertheless, the longer C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond distance in the solid-state structure (1.215(3) Å) and lower νC
C bond distance in the solid-state structure (1.215(3) Å) and lower νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C stretch (2003 cm−1, Raman spectroscopy) compared to 7 point to a slightly weaker triple bond (vide infra). 1H NMR analysis of the reaction mixture between 8 and DMAD reveals progressive transformation to an unsymmetrical species 11, as evidenced by the two sets of imidazole and ester resonances in a 1
C stretch (2003 cm−1, Raman spectroscopy) compared to 7 point to a slightly weaker triple bond (vide infra). 1H NMR analysis of the reaction mixture between 8 and DMAD reveals progressive transformation to an unsymmetrical species 11, as evidenced by the two sets of imidazole and ester resonances in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Further characterization experiments of 11 are in agreement with the insertion
of 1 equivalent of DMAD, similar to that observed for complex 7 (Fig. S20 and S21†)
1 ratio. Further characterization experiments of 11 are in agreement with the insertion
of 1 equivalent of DMAD, similar to that observed for complex 7 (Fig. S20 and S21†)
 | ||
| Fig. 2 Solid-state structure of bimetallic acetylide 7 (50% probability ellipsoids). H atoms are omitted and 2,6-diisopropylphenylgroups are represented as capped sticks for clarity. | ||
 | ||
| Fig. 3 Solid-state structure of bimetallic enyne 10 (50% probability ellipsoids). H atoms are omitted and 2,6-diisopropylphenylgroups are represented as capped sticks for clarity. | ||
 | ||
| Fig. 4 Solid-state structure of bimetallic acetylide 8 (50% probability ellipsoids). Most of the H atoms are omitted and 2,6-diisopropylphenylgroups are represented as capped sticks for clarity. | ||
Kinetic studies: ligand and nuclearity effects
In order to investigate further details of the DMAD insertion, kinetic studies were performed. Initial experiments were conducted in C6D6 with parent acetylide 7 under pseudo-first-order conditions ([DMAD] ≥ 10 equivalents), which indicate that the reaction is first-order with respect to the bimetallic complex (see ESI†). Determination of kobs at different temperatures (25, 30, 35 and 40 °C) and Eyring analysis afforded an activation enthalpy ΔH‡ = 18.1 (±0.3) kcal mol−1 and a negative activation entropy ΔS‡ = −15.0 (±1.0) cal mol−1 K−1, the latter suggesting an associative process in the rate-determining step (Fig. 5). The activation Gibbs free energy determined by this method is ΔG‡ (298 K) = 22.6 (±0.1) kcal mol−1. Within the pseudo-first order regime, the determination of kobs was carried out using different concentrations of DMAD. A linear correlation was observed after plotting kobsvs. [DMAD] (Fig. S78†), indicating that the reaction is first order in each component and suggesting a bimolecular mechanism (vide infra). Thus, the second order rate constant could be determined, with a value of k = 3.9 × 10−4 M−1 s−1. | ||
| Fig. 5 Selected results from kinetic analysis. (A) Plot of [X] vs. time (X = 7 or 8) at 25 °C. (B) Plot of ln[7] vs. time at different T values. (C) Eyring plot for 7 (ln(kobs/T) vs. 1/T). | ||
Whereas the activation parameters above are similar to those observed for a concerted insertion mechanism of DMAD in a Au(I) complex,9,10 computational evidence suggests this does not seem to be the case (vide infra). Similar experiments were conducted with bimetallic acetylide 8 (see ESI†). Complex 8 engages in a slower insertion reaction (Fig. 5A, purple trace), despite the stronger σ-donating character of the SIPr ligand, which suggests that π-backbonding from Au(I) to the NHC ligands is playing a non-negligible role.22 A ΔG‡ value of 23.2 (±0.1) kcal mol−1 was obtained from this kinetic analysis. These results are in agreement with the spectroscopic and crystallographic data described above regarding the strength of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond.
C bond.
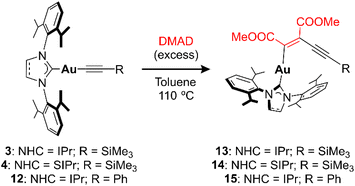
The examples reported in the literature for DMAD insertion on Au(I) are not appropriate for comparison due to the different nature of the ligands around the metal and the lack of bimetallic systems (Fig. 1). This prompted us to investigate the effect of the nuclearity on systems related to the synthesized dinuclear acetylides and compare the impact that one or two gold atoms may have on the insertion reaction. To this end, non-aryl complexes 3 and 4 (precursors to acetylides 7 and 8) and aromatic alkynyl complex IPrAuCCPh (12) were examined in the insertion of DMAD (Scheme 3). Gratifyingly, monometallic complexes 3, 4, and 12 insert DMAD in a similar fashion to the examples described above, yielding the corresponding Z-enyne products as the main species, as ascertained by multinuclear NMR and single-crystal X-ray diffraction studies (see ESI†). However, far more forcing experimental conditions were required for the reactions to reach completion. In all cases, an excess of DMAD had to be added and the reaction mixtures had to be heated up to 110 °C in toluene in order to show evolution. Kinetic studies were carried out with species 4 under pseudo-first-order conditions ([DMAD] ≥ 10 equivalents) in p-xylene-d10 at 120 °C, indicating that the insertion is first order in the Au(I) complex.23 At this temperature, kobs values similar to those observed for bimetallic complex 8 at 25 °C were obtained (Table S2†), along with a ΔG‡ (393 K) = 30.6 (±0.3) kcal mol−1. Therefore, these results suggest that the second NHC–Au fragment in the bimetallic acetylides greatly facilitates the insertion reaction in comparison to the monometallic analogues (Fig. 6).
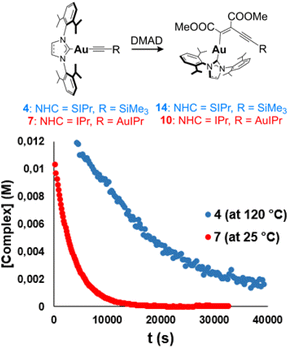 | ||
| Fig. 6 Comparison between bimetallic complex 7 and monometallic species 4: plot of [complex] vs. time. | ||
Extension of the scope
Based on the superior reactivity displayed by bimetallic acetylide complex 7, different reaction conditions and substrates were explored (Table S1†). First, DMAD and 3-hexyne were investigated under more forcing reaction temperatures, namely 150 °C (mesitylene as solvent) and 120 °C (toluene as solvent) respectively. While the former experiment resulted in the partial decomposition of the complex, the latter did not show any evolution by 1H NMR spectroscopy. Similarly, diphenylacetylene did not lead to any insertion event, as well as 1-phenylprop-1-yne (Ph–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Me). However, introduction of electron-withdrawing groups –COOMe on the para positions of the diphenylacetylene backbone resulted in reactivity with complex 7; however, multiple unidentified products were observed even at 25 °C. A similar outcome was obtained when using methyl 2-butynoate (Me–C
C–Me). However, introduction of electron-withdrawing groups –COOMe on the para positions of the diphenylacetylene backbone resulted in reactivity with complex 7; however, multiple unidentified products were observed even at 25 °C. A similar outcome was obtained when using methyl 2-butynoate (Me–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–COOMe) at 120 °C (Fig. S66 and S67†). Considering that the acidity of the methyl group might give rise to deprotonation processes and subsequent side-reactions, this fragment was replaced by a phenyl ring in methyl phenylpropiolate (Ph–C
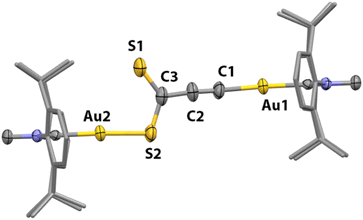
C–COOMe) at 120 °C (Fig. S66 and S67†). Considering that the acidity of the methyl group might give rise to deprotonation processes and subsequent side-reactions, this fragment was replaced by a phenyl ring in methyl phenylpropiolate (Ph–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–COOMe). Heating this reaction mixture in toluene to 120 °C selectively yielded insertion product 16 (Scheme 4), as determined by NMR spectroscopy. In addition, the regioselectivity of the insertion reaction was established by single-crystal X-ray diffraction analysis (see ESI†). Conversely, monometallic derivative 12 did not show any evolution under these conditions (10 equiv. of alkyne and 120 °C), which, again, manifests the beneficial role of the second metal in this type of reaction. As a matter of fact, only bimetallic compound 7 reacted with CS2 to give the monoinsertion product 17 (Scheme 4). The connectivity of 17 was ascertained by X-ray diffraction studies on crystals grown from vapor diffusion of diethyl ether into a MeCN solution of the complex (Fig. 7). The formation of a Au–S bond may be a driving force for this transformation, which motivated the exploration of a different, sulfur-containing substrate. Indeed, when electron-deficient 4-(trifluoromethyl)phenyl isothiocyanate (10 equiv.) was added to a toluene solution of 7, rapid (30 min) conversion to a new unsymmetrical species was observed at 25 °C by 1H NMR spectroscopy. Multinuclear NMR and IR spectroscopy and combustion analysis indicate that the product corresponds to the monoinsertion derivative 18 (Scheme 4). Heating the reaction mixture to 120 °C did not lead to clear, further reactivity as species 18 was still the main product after 17 h and the 19F{1H} NMR spectrum reveals the presence of numerous resonances, which suggests partial decomposition (Fig. S68†). Monometallic compound 12 also exhibited reactivity with 4-(trifluoromethyl)phenyl isothiocyanate, albeit at 120 °C using a 10-fold excess of reagent (when 1 equiv. was employed, ca. 20% conversion was observed after 3 days at 120 °C). Unfortunately, the high solubility of the product in apolar (n-pentane or hexamethyldisiloxane) and polar (MeCN or MeOH) solvents prevented its isolation from the excess of isothiocyanate, precluding its further characterization. Nonetheless, mass spectrometry analysis (Fig. S45†) points to a product with two equivalents of isothiocyanate per IPr ligand. Last, CO2 and N-N′-dicyclohexylcarbodiimide were also investigated, but they did not react with 7 or 12 under the experimental conditions tested.
C–COOMe). Heating this reaction mixture in toluene to 120 °C selectively yielded insertion product 16 (Scheme 4), as determined by NMR spectroscopy. In addition, the regioselectivity of the insertion reaction was established by single-crystal X-ray diffraction analysis (see ESI†). Conversely, monometallic derivative 12 did not show any evolution under these conditions (10 equiv. of alkyne and 120 °C), which, again, manifests the beneficial role of the second metal in this type of reaction. As a matter of fact, only bimetallic compound 7 reacted with CS2 to give the monoinsertion product 17 (Scheme 4). The connectivity of 17 was ascertained by X-ray diffraction studies on crystals grown from vapor diffusion of diethyl ether into a MeCN solution of the complex (Fig. 7). The formation of a Au–S bond may be a driving force for this transformation, which motivated the exploration of a different, sulfur-containing substrate. Indeed, when electron-deficient 4-(trifluoromethyl)phenyl isothiocyanate (10 equiv.) was added to a toluene solution of 7, rapid (30 min) conversion to a new unsymmetrical species was observed at 25 °C by 1H NMR spectroscopy. Multinuclear NMR and IR spectroscopy and combustion analysis indicate that the product corresponds to the monoinsertion derivative 18 (Scheme 4). Heating the reaction mixture to 120 °C did not lead to clear, further reactivity as species 18 was still the main product after 17 h and the 19F{1H} NMR spectrum reveals the presence of numerous resonances, which suggests partial decomposition (Fig. S68†). Monometallic compound 12 also exhibited reactivity with 4-(trifluoromethyl)phenyl isothiocyanate, albeit at 120 °C using a 10-fold excess of reagent (when 1 equiv. was employed, ca. 20% conversion was observed after 3 days at 120 °C). Unfortunately, the high solubility of the product in apolar (n-pentane or hexamethyldisiloxane) and polar (MeCN or MeOH) solvents prevented its isolation from the excess of isothiocyanate, precluding its further characterization. Nonetheless, mass spectrometry analysis (Fig. S45†) points to a product with two equivalents of isothiocyanate per IPr ligand. Last, CO2 and N-N′-dicyclohexylcarbodiimide were also investigated, but they did not react with 7 or 12 under the experimental conditions tested.
Mechanistic studies
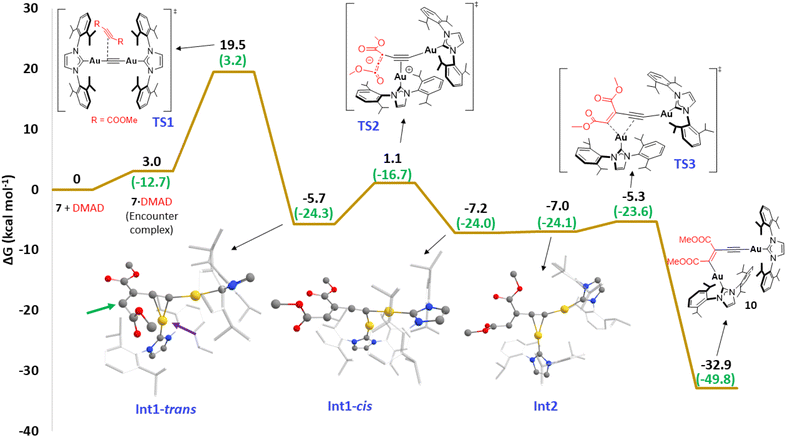
In order to understand the role of the second metal atom in the process, the reaction mechanism with DMAD was investigated by means of experimental and computational tools. Simple frontier molecular orbital (FMO) analysis of parent acetylide 7 and DMAD was performed on DFT-optimized structures24 to gather information related to the interaction between both compounds. As depicted in Fig. 8, the LUMO of DMAD consists of an antibonding combination of p orbitals of the triple bond, and the HOMO of 7 is mostly located on the acetylenic π-system with a clear contribution of the adjacent gold atoms. Thus, interaction between these two species would involve electron density donation from the alkyne in 7 to DMAD (i.e., a Michael-type nucleophilic addition), debilitating the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond of the organic fragment. This analysis suggests that blocking the π-system in 7 should inhibit DMAD insertion. For this reason, trinuclear complex 19 was synthesized by mixing 7 and IPrAuOTf in THF as shown in Fig. 9 (top). X-ray quality crystals of this material were obtained from the vapor diffusion of n-pentane into a THF solution of 19 at −30 °C, which allowed for the determination of its structure in the solid state (Fig. 9, bottom). As expected, the third IPrAu fragment establishes π-bonding with the triple bond, which leads to the bending of the AuCCAu axis, as judged by the ∠Au1–C1–C1′ and ∠Au1′–C1′–C1 angles ca. 164°. This deformation is likely caused by the steric demand of the three IPr ligands. Notably, a very slight elongation of the triple bond (1.226(5) Å) is observed compared to 7. Addition of DMAD to complex 19 does not show any evolution at 25 or 100 °C by 1H NMR spectroscopy, in line with the lack of availability of the C
C bond of the organic fragment. This analysis suggests that blocking the π-system in 7 should inhibit DMAD insertion. For this reason, trinuclear complex 19 was synthesized by mixing 7 and IPrAuOTf in THF as shown in Fig. 9 (top). X-ray quality crystals of this material were obtained from the vapor diffusion of n-pentane into a THF solution of 19 at −30 °C, which allowed for the determination of its structure in the solid state (Fig. 9, bottom). As expected, the third IPrAu fragment establishes π-bonding with the triple bond, which leads to the bending of the AuCCAu axis, as judged by the ∠Au1–C1–C1′ and ∠Au1′–C1′–C1 angles ca. 164°. This deformation is likely caused by the steric demand of the three IPr ligands. Notably, a very slight elongation of the triple bond (1.226(5) Å) is observed compared to 7. Addition of DMAD to complex 19 does not show any evolution at 25 or 100 °C by 1H NMR spectroscopy, in line with the lack of availability of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond in 19 (Fig. S64†). However, this observation also implies that a potential equilibrium 19 ↔ 7 + IPrAuOTf does not seem to be taking place since free acetylide 7 readily reacts with DMAD. ESI-MS supports this hypothesis since the mass spectrum only exhibits a parent ion peak with the expected m/z and isotope distribution pattern (Fig. S44†). On the other hand, the 1H NMR spectrum of 19 at 25 °C reveals only one set of resonances for all three IPr ligands (Fig. S39†), suggesting rapid exchange between the π and σ-bonding modes of the acetylide fragment. Variable temperature 1H NMR spectra were acquired in THF-d8 from 25 °C to −95 °C (Fig. S42†), and coalescence phenomena were observed at approximately −75 °C. Unfortunately, no slow exchange was observed within the temperature range determined by the solvent, which precluded the extraction of a rate constant. Nonetheless, a transition state connecting the structure depicted in Fig. 9 and a gem-digold acetylide species was found leading to a rather low barrier of 3.6 kcal mol−1, which is consistent with the observed fast exchange (Fig. S93†) and that proposed by Widenhoefer and co-workers.25 These findings highlight the labile character of the Au–C bonds in this type of complexes, which seems to be an essential feature in the mechanism proposed for the insertion of DMAD (vide infra). The mechanism of the reaction between 7 and DMAD was also explored by DFT methods. Starting from 7 and DMAD as energy reference, the first step of the mechanism involves the formation of the van der Waals encounter complex 7·DMAD, which lies 3.0 kcal mol−1 above the separate reactants due to entropic reasons. From this point, initial approaches involved approximation of DMAD to different regions of the acetylide complex via relaxed potential energy surface scans to find a concerted insertion process (e.g. formation of Au–C and C–C bonds in the same step), similar to those proposed by Amgoune and Bourissou9 or Kuniyasu and Kambe.10 All our attempts were fruitless in this regard; however, they led to a different, unprecedented stepwise mechanism depicted in Fig. 10. In the first step of this reaction profile, the HOMO of complex 7 interacts with the LUMO of DMAD viaTS1, a saddle point located 19.5 kcal mol−1 above the energy reference. This reaction is the rate-determining step of the entire process, with an activation Gibbs energy close to that determined experimentally (22.6 kcal mol−1). Likewise, the enthalpy difference of this barrier (15.9 kcal mol−1) is close to the value determined by 1H NMR spectroscopy (18.2 kcal mol−1). This key saddle point, TS1, is associated with both the approach of DMAD and the formation of what will be the single C–C bond in the enyne structure of 10. In this species, the C⋯C bond-forming distance is 2.05 Å, and DMAD is no longer linear based on C(O)–C–C angles of ≈134°, implying a marked sp2 hybridization of the carbon atoms (Fig. 11, top). This transition state leads to Int1-trans, which consists of a σ,π–digold complex, similar to those reported by Widenhoefer,25 Nolan26 and Echavarren.27 Based on this structure, this initial step can be viewed as the DMAD-promoted displacement of one IPrAu moiety from its σ-bond with the C22− fragment to the π-coordination in Int1-trans. The geometry of the latter species can be regarded as a zwitterionic structure with a cationic IPrAu group bound to the triple C
C bond in 19 (Fig. S64†). However, this observation also implies that a potential equilibrium 19 ↔ 7 + IPrAuOTf does not seem to be taking place since free acetylide 7 readily reacts with DMAD. ESI-MS supports this hypothesis since the mass spectrum only exhibits a parent ion peak with the expected m/z and isotope distribution pattern (Fig. S44†). On the other hand, the 1H NMR spectrum of 19 at 25 °C reveals only one set of resonances for all three IPr ligands (Fig. S39†), suggesting rapid exchange between the π and σ-bonding modes of the acetylide fragment. Variable temperature 1H NMR spectra were acquired in THF-d8 from 25 °C to −95 °C (Fig. S42†), and coalescence phenomena were observed at approximately −75 °C. Unfortunately, no slow exchange was observed within the temperature range determined by the solvent, which precluded the extraction of a rate constant. Nonetheless, a transition state connecting the structure depicted in Fig. 9 and a gem-digold acetylide species was found leading to a rather low barrier of 3.6 kcal mol−1, which is consistent with the observed fast exchange (Fig. S93†) and that proposed by Widenhoefer and co-workers.25 These findings highlight the labile character of the Au–C bonds in this type of complexes, which seems to be an essential feature in the mechanism proposed for the insertion of DMAD (vide infra). The mechanism of the reaction between 7 and DMAD was also explored by DFT methods. Starting from 7 and DMAD as energy reference, the first step of the mechanism involves the formation of the van der Waals encounter complex 7·DMAD, which lies 3.0 kcal mol−1 above the separate reactants due to entropic reasons. From this point, initial approaches involved approximation of DMAD to different regions of the acetylide complex via relaxed potential energy surface scans to find a concerted insertion process (e.g. formation of Au–C and C–C bonds in the same step), similar to those proposed by Amgoune and Bourissou9 or Kuniyasu and Kambe.10 All our attempts were fruitless in this regard; however, they led to a different, unprecedented stepwise mechanism depicted in Fig. 10. In the first step of this reaction profile, the HOMO of complex 7 interacts with the LUMO of DMAD viaTS1, a saddle point located 19.5 kcal mol−1 above the energy reference. This reaction is the rate-determining step of the entire process, with an activation Gibbs energy close to that determined experimentally (22.6 kcal mol−1). Likewise, the enthalpy difference of this barrier (15.9 kcal mol−1) is close to the value determined by 1H NMR spectroscopy (18.2 kcal mol−1). This key saddle point, TS1, is associated with both the approach of DMAD and the formation of what will be the single C–C bond in the enyne structure of 10. In this species, the C⋯C bond-forming distance is 2.05 Å, and DMAD is no longer linear based on C(O)–C–C angles of ≈134°, implying a marked sp2 hybridization of the carbon atoms (Fig. 11, top). This transition state leads to Int1-trans, which consists of a σ,π–digold complex, similar to those reported by Widenhoefer,25 Nolan26 and Echavarren.27 Based on this structure, this initial step can be viewed as the DMAD-promoted displacement of one IPrAu moiety from its σ-bond with the C22− fragment to the π-coordination in Int1-trans. The geometry of the latter species can be regarded as a zwitterionic structure with a cationic IPrAu group bound to the triple C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond (Fig. 10, purple arrow) and featuring a dicoordinate, sp2 carbanion (green arrow). From Int1-trans, the cationic [IPrAu]+ moiety can migrate to this sp2 carbon atom to yield the insertion product. However, this step would afford the E-enyne complex instead of the observed Z isomer. Expectedly, this migration is 10 kcal mol−1 more energy demanding (ΔG‡ = 5.4 kcal mol−1, Fig. S91†) than the analogous migration leading to the Z-product (vide infra) in accordance with the experimental observations. Therefore, an isomerization step from Int1-trans is necessary. This takes place through TS2, lying 1.1 kcal mol−1 above the energy reference, where a linear C(O)–C–C(C) arrangement (178.3 °C) is observed, which evolves to Int1-cis, 1.5 kcal mol−1 more stable than its trans isomer. This species possesses both ester groups in a cis orientation, and places both gold atoms in close contact (Au⋯Au distance of 3.11 Å) where metalophilic interactions might be present.28 These interactions might be involved in the stabilization of Int1-cis, unlike analogous intermediates where there is only one metal (Fig. S92†). Despite that, a different, almost isoenergetic conformer Int2 was located, which preorganizes the molecule for the final [IPrAu]+ migration step. The most noticeable change in this structure is the rotation of the DMAD fragment from Int1-cis (where both ester groups were located in a plane perpendicular to the [IPrAu]+ moiety) to Int2 (where the DMAD backbone and the gold atom are in the same plane). This arrangement facilitates the transition metal fragment migration from the C
C bond (Fig. 10, purple arrow) and featuring a dicoordinate, sp2 carbanion (green arrow). From Int1-trans, the cationic [IPrAu]+ moiety can migrate to this sp2 carbon atom to yield the insertion product. However, this step would afford the E-enyne complex instead of the observed Z isomer. Expectedly, this migration is 10 kcal mol−1 more energy demanding (ΔG‡ = 5.4 kcal mol−1, Fig. S91†) than the analogous migration leading to the Z-product (vide infra) in accordance with the experimental observations. Therefore, an isomerization step from Int1-trans is necessary. This takes place through TS2, lying 1.1 kcal mol−1 above the energy reference, where a linear C(O)–C–C(C) arrangement (178.3 °C) is observed, which evolves to Int1-cis, 1.5 kcal mol−1 more stable than its trans isomer. This species possesses both ester groups in a cis orientation, and places both gold atoms in close contact (Au⋯Au distance of 3.11 Å) where metalophilic interactions might be present.28 These interactions might be involved in the stabilization of Int1-cis, unlike analogous intermediates where there is only one metal (Fig. S92†). Despite that, a different, almost isoenergetic conformer Int2 was located, which preorganizes the molecule for the final [IPrAu]+ migration step. The most noticeable change in this structure is the rotation of the DMAD fragment from Int1-cis (where both ester groups were located in a plane perpendicular to the [IPrAu]+ moiety) to Int2 (where the DMAD backbone and the gold atom are in the same plane). This arrangement facilitates the transition metal fragment migration from the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond to the sp2 atom through TS3, only 1.7 kcal mol−1 above the reagents. This saddle point involves a 5-membered
metallacycle and directly affords the Z-enyne species 10, 32.9 kcal mol−1 more stable than acetylide 7 + DMAD reactants. Not surprisingly, an analogous mechanism was also found for monometallic species 12 (Fig. S92†), where the approach of DMAD is also the rate-determining step. Nonetheless, the Gibbs free energy barrier required for this key step is comparatively much higher (ΔG‡ = 27.4 kcal mol−1), in good agreement with the more forcing experimental conditions required for the reaction to occur. Moreover, the regioselectivity observed for complex 16 is in agreement with the proposed mechanism (see Fig. S94†). While the aforementioned computed profiles are consistent with the experimental results, further computational analysis was carried out to understand the factors behind the observed enhanced reactivity of the bimetallic system, i.e., why the second IPrAu fragment facilitates the insertion reaction to the extent described above. To this end, we first applied the Activation Strain Model (ASM)29 of reactivity to compare the initial step involving the addition of DMAD to both the parent bimetallic complex 7 and its monometallic counterpart 12. This analysis decomposes the electronic energy (ΔE) into two terms, namely the strain (ΔEstrain) that results from the distortion of the individual reactants and the interaction (ΔEint) between the deformed reactants along the reaction coordinate defined, in this case, by the C⋯C bond-forming distance. Fig. 11a shows the corresponding Activation Strain Diagrams (ASDs) from the initial stages of the transformation up to the respective transition states. From the data in Fig. 11a, it becomes evident that the lower barrier computed for the reaction involving 7 does not originate from the strain term, which is actually less destabilizing for the reaction involving the monometallic complex, but exclusively from the stronger interaction between the deformed reactants along the entire reaction coordinate. The origin of the computed stronger interaction for the 7 + DMAD reaction can be further analyzed by means of the Energy Decomposition Analysis (EDA) method.30 This approach involves decomposing the interaction ΔEint between the reactants into the following, physically meaningful energy terms: the classical electrostatic interaction (ΔVelstat), the Pauli repulsion (ΔEPauli) arising from the repulsion between occupied closed-shell orbitals of both deformed reactants, the orbital interaction (ΔEorb) that accounts for charge transfer and polarization, and the dispersion interactions (ΔEdisp) coming from dispersion forces. As depicted in Fig. 11b, which graphically shows the evolution of the EDA terms along the reaction coordinate from the initial stages of the processes up to the respective transition states, the stronger (i.e., more stabilizing) interaction between the reactants computed for the reaction involving the bimetallic system mainly results from both stronger electrostatic and orbital interactions, particularly at the transition state region. For instance, at the same consistent C⋯C bond-forming distance of 2.1 Å, ΔVelstat = −65.5 kcal mol−1 and ΔEorb = −64.1 kcal mol−1 for the reaction involving 7, whereas much lower values were computed for the analogous DMAD + 12 reaction (ΔVelstat = −53.2 kcal mol−1 and ΔEorb = −46.8 kcal mol−1). The stronger electrostatic interactions can be ascribed to the stronger polarization induced by the IPrAu fragment in 7 compared to the phenyl group in 12, as confirmed by the higher negative NBO-charge computed at the carbon atom adjacent to the reactive carbon (−0.55e vs. −0.14e, for 7 and 12, respectively).31
C bond to the sp2 atom through TS3, only 1.7 kcal mol−1 above the reagents. This saddle point involves a 5-membered
metallacycle and directly affords the Z-enyne species 10, 32.9 kcal mol−1 more stable than acetylide 7 + DMAD reactants. Not surprisingly, an analogous mechanism was also found for monometallic species 12 (Fig. S92†), where the approach of DMAD is also the rate-determining step. Nonetheless, the Gibbs free energy barrier required for this key step is comparatively much higher (ΔG‡ = 27.4 kcal mol−1), in good agreement with the more forcing experimental conditions required for the reaction to occur. Moreover, the regioselectivity observed for complex 16 is in agreement with the proposed mechanism (see Fig. S94†). While the aforementioned computed profiles are consistent with the experimental results, further computational analysis was carried out to understand the factors behind the observed enhanced reactivity of the bimetallic system, i.e., why the second IPrAu fragment facilitates the insertion reaction to the extent described above. To this end, we first applied the Activation Strain Model (ASM)29 of reactivity to compare the initial step involving the addition of DMAD to both the parent bimetallic complex 7 and its monometallic counterpart 12. This analysis decomposes the electronic energy (ΔE) into two terms, namely the strain (ΔEstrain) that results from the distortion of the individual reactants and the interaction (ΔEint) between the deformed reactants along the reaction coordinate defined, in this case, by the C⋯C bond-forming distance. Fig. 11a shows the corresponding Activation Strain Diagrams (ASDs) from the initial stages of the transformation up to the respective transition states. From the data in Fig. 11a, it becomes evident that the lower barrier computed for the reaction involving 7 does not originate from the strain term, which is actually less destabilizing for the reaction involving the monometallic complex, but exclusively from the stronger interaction between the deformed reactants along the entire reaction coordinate. The origin of the computed stronger interaction for the 7 + DMAD reaction can be further analyzed by means of the Energy Decomposition Analysis (EDA) method.30 This approach involves decomposing the interaction ΔEint between the reactants into the following, physically meaningful energy terms: the classical electrostatic interaction (ΔVelstat), the Pauli repulsion (ΔEPauli) arising from the repulsion between occupied closed-shell orbitals of both deformed reactants, the orbital interaction (ΔEorb) that accounts for charge transfer and polarization, and the dispersion interactions (ΔEdisp) coming from dispersion forces. As depicted in Fig. 11b, which graphically shows the evolution of the EDA terms along the reaction coordinate from the initial stages of the processes up to the respective transition states, the stronger (i.e., more stabilizing) interaction between the reactants computed for the reaction involving the bimetallic system mainly results from both stronger electrostatic and orbital interactions, particularly at the transition state region. For instance, at the same consistent C⋯C bond-forming distance of 2.1 Å, ΔVelstat = −65.5 kcal mol−1 and ΔEorb = −64.1 kcal mol−1 for the reaction involving 7, whereas much lower values were computed for the analogous DMAD + 12 reaction (ΔVelstat = −53.2 kcal mol−1 and ΔEorb = −46.8 kcal mol−1). The stronger electrostatic interactions can be ascribed to the stronger polarization induced by the IPrAu fragment in 7 compared to the phenyl group in 12, as confirmed by the higher negative NBO-charge computed at the carbon atom adjacent to the reactive carbon (−0.55e vs. −0.14e, for 7 and 12, respectively).31
In turn, the origin of the more stabilizing ΔEorb can be found by applying the Natural Orbital for Chemical Valence (NOCV)32 extension of the EDA method. Within this approach, the main orbital interactions contributing to the total ΔEorb term can be visualized and also quantified. As expected from our initial FMO analyses (vide supra), the EDA-NOCV method identifies the electron flow from the π(HOMO) of the metal complex to the π*(LUMO) of DMAD as the main orbital interaction in this transformation (Fig. 12). Notably, this π(HOMO) → π*(LUMO) molecular orbital interaction is significantly stronger, i.e., more stabilizing, for the process involving the bimetallic system (see the corresponding stabilizing energies computed at a consistent C⋯C bond-forming distance of 2.1 Å). Therefore, the ASM-EDA(NOCV) analysis suggests that the enhanced reactivity of the bimetallic system, compared to its monometallic counterpart, finds its origin in the significant polarization induced by the IPrAu fragment onto the reactive C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond which results in stronger electrostatic and orbital (π(HOMO) → π*(LUMO)) interactions with the DMAD reactant and ultimately, in the observed lower addition barrier.
C bond which results in stronger electrostatic and orbital (π(HOMO) → π*(LUMO)) interactions with the DMAD reactant and ultimately, in the observed lower addition barrier.
Conclusions
In summary, a modular synthetic strategy for the preparation of bimetallic Au(I) acetylides has been described. Whereas only symmetrical digold complexes have been explored in this work, this route opens the door to the development of unsymmetrical derivatives or heterobimetallic species, which is currently an ongoing research direction in our laboratory. The synthesized symmetrical digold acetylides and monometallic alkynyl analogues selectively insert DMAD to yield the corresponding Z enyne products; however, much more forcing conditions are necessary when only one metal is employed (110 °C vs. 25 °C). This pronounced disparity has been studied in detail through experimental and computational methods, leading to a stepwise mechanism, which differs from previously reported examples for insertion on gold(I) complexes. Two key aspects of this mechanism are evident: (1) the presence of a second gold fragment stabilizes both the transition state and intermediate species due to the increased electron donation to the alkyne fragment (although aurophilic contacts might also play a role in some of them (e.g.Int1-cis)). This supply of electron density facilitates the initial interaction with DMAD and subsequently keeps the cationic IPrAu moiety bound to the π-system. (2) Certain lability of the Au–C bonds is necessary so that DMAD can displace one IPrAu fragment from σ to π-coordination, and ease the migration of Au from sp to sp2 carbon atoms. The balance of these two aspects accounts for the mild conditions observed for the insertion reaction in the bimetallic complexes and provides new knowledge of the role that two metals play in the case of digold-mediated organic transformations.Data availability
The data supporting this article have been included as part of the ESI.† Deposition numbers 2372473–2372479 (for complexes 3, 7, 8, 10, 13, 15 and 19), 2407558 (for complex 16) and 2403953 (for complex 17) contain the supplementary crystallographic data for this paper. These data can be obtained free of charge viahttp://www.ccdc.cam.ac.uk/dat_request/cif, or by emailing E-mail: data_request@ccdc.cam.ac.uk, or by contacting the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.Author contributions
P. R. conceived of the idea. J. C.-C. and P. R. performed the experiments and analyzed the synthesis, reactivity and characterization data. Crystallographic characterization was performed by F. J. F.-C. and M. S. S. Computational analyses were performed by I. F. and P. R. I. F. and P. R. wrote and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Junta de Andalucía under project ProyExcel_00758. We are also grateful for financial support from grants PID2022-139318NB-I00 and RED2022-134331-T, funded by MICIU/AEI/10.13039/501100011033.Notes and references
- J. H. Teles, S. Brode and M. Chabanas, Angew. Chem., Int. Ed., 1998, 37, 1415–1418 CrossRef PubMed.
- (a) R. Dorel and A. M. Echavarren, Chem. Rev., 2015, 115, 9028–9072 CrossRef PubMed; (b) C. Praveen, Coord. Chem. Rev., 2019, 392, 1–34 CrossRef.
- M. Joost, A. Amgoune and D. Bourissou, Angew. Chem., Int. Ed., 2015, 54, 15022–15045 CrossRef PubMed.
- Some pioneering studies reported the reaction between alkynes and neutral gold complexes via mixed-valent Au(I)/Au(III) species instead of migratory insertion. See (a) C. M. Mitchell and F. G. A. Stone, J. Chem. Soc. D, 1970, 1263–1264 RSC; (b) C. J. Gilmore and P. Woodward, J. Chem. Soc. D, 1971, 1233–1234 RSC; (c) A. Johnson, R. J. Puddephatt and J. L. Quirk, J. Chem. Soc., Chem. Commun., 1972, 938–939 RSC; (d) C. M. Mitchell and F. G. A. Stone, J. Chem. Soc., Dalton Trans., 1972, 102–107 RSC; (e) J. A. J. Jarvis, A. Johnson and R. J. Puddephatt, J. Chem. Soc., Chem. Commun., 1973, 373–374 RSC; (f) A. Johnson and R. J. Puddephatt, J. Chem. Soc., Dalton Trans., 1977, 1384–1388 RSC; (g) A. Johnson and R. J. Puddephatt, J. Chem. Soc., Dalton Trans., 1978, 980–985 RSC.
- J. A. Akana, K. X. Bhattacharyya, P. Müller and J. P. Sadighi, J. Am. Chem. Soc., 2007, 129, 7736–7737 CrossRef PubMed.
- M. Joost, P. Gualco, S. Mallet-Ladeira, A. Amgoune and D. Bourissou, Angew. Chem., Int. Ed., 2013, 52, 7160–7163 CrossRef PubMed.
- M. Joost, N. Saffon-Merceron, A. Amgoune and D. Bourissou, Organometallics, 2019, 38, 3494–3497 CrossRef.
- E. Y. Tsui, P. Müller and J. P. Sadighi, Angew. Chem., Int. Ed., 2008, 47, 8937–8940 CrossRef PubMed.
- M. Joost, L. Estevez, S. Mallet-Ladeira, K. Miqueu, A. Amgoune and D. Bourissou, J. Am. Chem. Soc., 2014, 136, 10373–10382 CrossRef.
- H. Kuniyasu, T. Nakajima, T. Tamaki, T. Iwasaki and N. Kambe, Organometallics, 2015, 34, 1373–1376 CrossRef.
- C. L. Masonheimer, M. G. Atwood, S. E. Hartzell, E. A. Reph, R. D. Pike and R. Stockland Jr, Organometallics, 2021, 40, 2546–2556 CrossRef.
- See for example: (a) M. K. Karunananda and N. P. Mankad, J. Am. Chem. Soc., 2015, 137, 14598–14601 CrossRef; (b) A. C. Deacy, A. F. R. Kilpatrick, A. Regoutz and C. K. Williams, Nat. Chem., 2020, 12, 372–380 CrossRef.
- Selected examples: (a) W. E. Brenzovich Jr, D. Benitez, A. D. Lackner, H. P. Shunatona, E. Tkatchouk, W. A. Goddard III and F. D. Toste, Angew. Chem., Int. Ed., 2010, 49, 5519–5522 CrossRef; (b) A. Gómez-Suárez and S. P. Nolan, Angew. Chem., Int. Ed., 2012, 51, 8156–8159 CrossRef; (c) A. S. K. Hashmi, Acc. Chem. Res., 2014, 47, 864–876 CrossRef; (d) X. Zhao, M. Rudolph and A. S. K. Hashmi, Chem. Commun., 2019, 55, 12127–12135 RSC; (e) W. Wang, C.-L. Ji, K. Liu, C.-G. Zhao, W. Li and J. Xie, Chem. Soc. Rev., 2021, 50, 1874–1912 RSC; (f) Y. Jiang, Y. Wei, X.-Y. Tang and M. Shi, Chem.–Eur. J., 2015, 21, 7675–7681 CrossRef; (g) I. Abdellah, A. Poater, J.-F. Lohier and A.-C. Gaumont, Catal. Sci. Technol., 2018, 8, 6486–6492 RSC; (h) F. Christoffel, N. V. Igareta, M. M. Pellizzoni, L. Tiessler-Sala, B. Lozhkin, D. C. Spiess, A. Lledós, J.-D. Maréchal, R. L. Peterson and T. R. Ward, Nat. Catal., 2021, 4, 643–653 CrossRef; (i) S. Escayola, J. Poater, M. Ramos, J. A. Luque-Urrutia, J. Duran, S. Simon, M. Solà, L. Cavallo, S. P. Nolan and A. Poater, Appl. Organomet. Chem., 2021, 35, e6362 CrossRef.
- (a) R. J. Cross and M. F. Davidson, J. Chem. Soc., Dalton Trans., 1986, 411–414 RSC; (b) M. I. Bruce, K. R. Grundy, M. J. Liddell, M. R. Snow and E. R. T. Tiekink, J. Organomet. Chem., 1988, 344, C49–C52 CrossRef; (c) T. E. Müller, D. M. P. Mingos and D. J. Williams, J. Chem. Soc. Chem. Commun., 1994, 1787–1788 RSC; (d) T. E. Müller, S. W.-K. Choi, D. M. P. Mingos, D. Murphy, D. J. Williams and V. W.-W. Yam, J. Organomet. Chem., 1994, 484, 209–224 CrossRef; (e) C.-M. Che, H.-Yi. Chao, V. M. Miskowski, Y. Li and K.-K. Cheung, J. Am. Chem. Soc., 2001, 123, 4985–4991 CrossRef CAS PubMed; (f) H. Lang, S. Köcher, S. Back, G. Rheinwald and G. van Koten, Organometallics, 2001, 20, 1968–1972 CrossRef CAS; (g) W. Lu, N. Zhu and C.-M. Che, J. Organomet. Chem., 2003, 670, 11–16 CrossRef CAS; (h) R.-Y. Liau, A. Schier and H. Schimdbaur, Organometallics, 2003, 22, 3199–3204 CrossRef CAS; (i) T. N. Hooper, M. Green and C. A. Russell, Chem. Commun., 2010, 46, 2313–2315 RSC; (j) T. J. Feuerstein, M. Poß, T. P. Seifert, S. Bestgen, C. Feldmann and P. W. Roesky, Chem. Commun., 2017, 53, 9012–9015 RSC; (k) A. Grirrane, E. Álvarez, H. García and A. Corma, Chem.–Eur. J., 2020, 26, 8810–8818 CrossRef CAS.
- T. Bruhm, A. Abram, J. Häusler, O. Thomys and K. Köhler, Chem.–Eur. J., 2021, 27, 16834–16839 CrossRef PubMed.
- T. Scattolin, G. Tonon, E. Botter, S. G. Guillet, N. V. Tzouras and S. P. Nolan, Chem.–Eur. J., 2023, 29, e202301961 CrossRef PubMed.
- P. Ríos, M. S. See, R. C. Handford, J. K. Cooper and T. D. Tilley, Angew. Chem., Int. Ed., 2023, 62, e202310307 CrossRef PubMed.
- R. M. P. Veenboer, D. Gasperini, F. Nahra, D. B. Cordes, A. M. Z. Slawin, C. S. J. Cazin and S. P. Nolan, Organometallics, 2017, 36, 3645–3653 CrossRef.
- K. Klauke, S. Werner and F. Mohr, Eur. J. Inorg. Chem., 2018, 1053–1056 CrossRef.
- P. Pässler, W. Hefner, K. Buckl, H. Meinass, A. Meiswinkel, H.-J. Wernicke, G. Ebersberg, R. Müller, J. Bässler, H. Behringer and D. Mayer, Acetylene, in Ullmann's Encyclopedia of Industrial Chemistry, 2011, DOI:10.1002/14356007.a01_097.pub4.
- IPr and SIPr possess different electronic properties but similar %Vbur values. See (a) A. Gómez-Suárez, D. J. Nelson and S. P. Nolan, Chem. Commun., 2017, 53, 2650 RSC; (b) G. Meng, L. Kakalis, S. P. Nolan and M. Szostak, Tetrahedron Lett., 2019, 60, 378–381 CrossRef CAS for more information..
- L. Kuster, M. Bélanger-Bouliga, T. E. Shaw, T. Jurca, A. Nazemi and M. Frenette, Nanoscale, 2014, 16, 11052–11068 RSC.
- Species 4 showed the best behavior by 1H NMR spectroscopy under these conditions, as the overlap of resonances in the case of 3 and 12 prevented proper signal integration. The partial order in [DMAD] could not be established due to the error obtained when determining kobs values (see ESI† for more information).
- Computational details can be found in the ESI†.
- T. J. Brown and R. A. Widenhoefer, Organometallics, 2011, 30, 6003–6009 CrossRef CAS.
- A. Gómez-Suárez, S. Dupuy, A. M. Z. Slawin and S. P. Nolan, Angew. Chem., Int. Ed., 2013, 52, 938–942 CrossRef.
- S. Ferrer and A. M. Echavarren, Organometallics, 2018, 37, 781–786 CrossRef CAS.
- H. Schmidbaur, Gold Bull., 2000, 3, 3–10 CrossRef.
- (a) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967 RSC; (b) L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343 CAS; (c) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 ( Angew. Chem. , 2017 , 129 , 10204–10221 ) CrossRef CAS . See also; ; (d) I. Fernández, in Discovering the Future of Molecular Sciences, ed. B. Pignataro, Wiley-VCH, Weinheim, 2014, pp. 165–187 Search PubMed.
- For reviews on the EDA method, see: (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed; (b) M. von Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62 CAS; (c) I. Fernández, in Applied Theoretical Organic Chemistry, ed. D. J. Tantillo, World Scientific, New Jersey, 2018, pp. 191–226 Search PubMed.
- In 12, the computed NBO-charge at the carbon atom directly attached to the NHC ligand (i.e. reactive carbon) is −0.41e, again lower than that computed for the analogous carbon atom in compound 7.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2372473–2372479, 2403953 and 2407558. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc08227c |
| This journal is © The Royal Society of Chemistry 2025 |