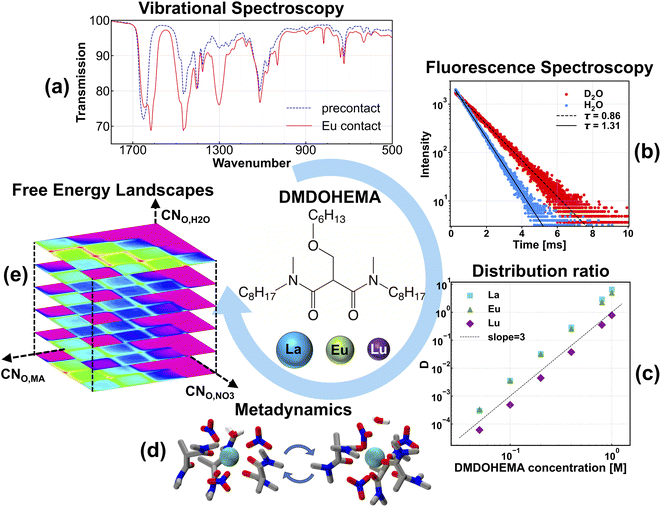
Open Access Article
Open Access ArticleMetadynamics investigation of lanthanide solvation free energy landscapes and insights into separations energetics†
Xiaoyu
Wang
 *a,
Allison A.
Peroutka
*a,
Allison A.
Peroutka
 a,
Dmytro V.
Kravchuk
a,
Jenifer C.
Shafer
a,
Dmytro V.
Kravchuk
a,
Jenifer C.
Shafer
 b,
Richard E.
Wilson
b,
Richard E.
Wilson
 a and
Michael J.
Servis
a and
Michael J.
Servis
 *a
*a
aChemical Sciences and Engineering Division, Argonne National Laboratory, 9700 S Cass Ave, Lemont, IL 60439, USA. E-mail: xiaoyu.wang@anl.gov; mservis@anl.gov
bDepartment of Chemistry, Colorado School of Mines, 1500 Illinois St., Golden, CO 80401, USA
First published on 26th September 2024
Abstract
Lanthanide ion solvation chemistry in nonaqueous phases is key to understanding and developing effective separation processes for these critical materials. Due to the complexity and inherent disorder of the solution phase, a comprehensive picture of the solvated metal ion is often difficult to generate solely from conventional spectroscopic approaches and electronic structure calculations, particularly in the extractant phase. In this work, we use classical molecular dynamics (MD) simulation with an advanced sampling technique, metadynamics, supplemented by experimental spectroscopy and speciation analysis, to measure lanthanide solvation free energy landscapes. We define coordination-based collective variables to probe the entire range of solvation configurations in the organic phase of lanthanum (La), europium (Eu), and lutetium (Lu) nitrate salts bound with a commonly used extractant, N,N′-dimethyl, N,N′-dioctylhexylethoxymalonamide (DMDOHEMA). The known lanthanide extraction trend of La ≈ Eu > Lu is readily explained by the measured free energy surfaces, which show consistent DMDOHEMA coordination from La to Eu, followed by loss of DMDOHEMA coordination from Eu to Lu. These simulations suggest how ligand crowding at the metal center can control selectivity, in this case resulting in the opposite extraction trend as observed with other conventional extractants, where the enthalpic contribution from increasing lanthanide charge density across the series dominates the extraction energetics. We also find that the presence of inner-sphere water, verified by time-resolved fluorescence, diversifies the accessible solvation structures. As a result, understanding solvation requires consideration of an entire thermodynamic ensemble, rather than the single dominant lowest-energy structure, as is often considered out of necessity in interpretation of spectroscopic data or in electronic structure-based ligand design approaches. In general, we demonstrate how metadynamics uniquely enables investigation of complex, multidimensional solvation energetic landscapes, and how it can explain selectivity trends where extraction is controlled by more complex mechanisms than simple charge density-based selectivity.
1 Introduction
Insights into the metal ion solvation environment in complex solutions, such as organic solvents used in chemical separations, are essential for understanding and designing more efficient solvent extraction (SX) processes employed in the increasingly critical separation of lanthanide elements.1 In a typical SX process, amphiphilic extractant ligands, often multidentate chelators, selectively bind to metal ions bringing them from the aqueous phase to the organic phase.2 A primary challenge is selectivity between chemically similar ions, as highlighted by the difficulty of intra-lanthanide separations,1,3 where the lanthanide contraction across the series leads to small increases in charge density. This is leveraged by extractants whose selectivity for the heavy lanthanides is dominated by the increased binding enthalpy to those more charge dense ions, such as widely used diglycolamides4,5 and phosphoric acids.6 To this end, traditional work in the field has focused on utilizing the metal-ion charge density and ligands' binding strength to suggest extractants with better separation performances. While straightforward, this strategy does not account for other potential selectivity drivers, such as solvent effects,7 ligands' intrinsic conformational energetics,8 and their crowding and steric effects around the lanthanide metal center. For example, while malonamide extractant head groups are chemically similar to diglycolamides, malonamides feature the opposite selectivity trend across the lanthanide series,6 due presumably to those other selectivity drivers. Similar opposite selectivity has been observed for ligands using macrocyclic structures to induce size preference for lighter lanthanides.9 However, in this study, we are interested in the case where this trend results from freely coordinated ligands. In general, more detailed understandings on ligands' crowding and steric effects, and the complexity of metal ion solvation environments is vital to designing better separation processes.One common route to understanding metal coordination is by inferring solution-phase solvation from the solid state using crystallography.10–15 Yet this approach has its limitations since the structural information obtained from the solid state does not always translate to metal speciation in solution. Vibrational spectroscopies, including infrared and Raman, are also employed to infer structural organization of the metal ion-ligand complexes.16–20 However, because of the complexity of the solution chemistry, uniquely attributing spectral features and peak shifts to particular species is difficult.19 Therefore, it is often not possible to draw satisfactory quantitative conclusions from vibrational spectroscopy. In addition to the aforementioned techniques, synchrotron-based extended X-ray absorption fine structure spectroscopy (EXAFS), often supplemented by molecular dynamics simulations, can directly probe the solvation environment.5,21–27 However, the disordered nature of the liquid state, and limitations of model fitting where the oxygen atoms of different ligands (anion, water, extractant) coordinate to metal ions at similar metal–oxygen distances, often result in significant ambiguity. This can result in total coordination numbers with uncertainties larger than 1,22,28 which is similar to the entire change in coordination number across the lanthanide series.15 Overall, these challenges in understanding lanthanide coordination, beyond size selectivity, fundamentally limit the design of separations with entropically dominated, ligand crowding-driven selectivity.
In this work, we combine classical MD simulations with experimental extraction and spectroscopy to provide a complete energetic landscape of the solvation environment for the trivalent lanthanide ion bound to a popular malonamide bidentate extractant—DMDOHEMA (denoted hereafter as MA for simplicity), whose molecular structure is shown in the inset in Fig. 1. By performing experimental spectroscopies and separation measurements, we confirm that the stoichiometry of La(III), Eu(III), and Lu(III) in the organic phase is maintained as Ln(MA)3(NO3)3 for all lanthanides. Ellis et al.22 combined EXAFS and time-resolved laser-induced fluorescence spectroscopy (TRLIFS) to reveal the total inner-sphere coordination number of oxygen sites and the number of coordinating water, respectively, ultimately concluding that a wide range of complexation configurations was possible. However, the specific ensemble, including a more detailed understanding of how ligands bind with the metal ion, such as mono- vs. bidentate for both extractant and anion, and inner- vs. outer-sphere water, remains unresolved. We hypothesize that the unique trend in selectivity for this system depends on these details. To this end, we carried out MD simulations with an advanced sampling technique, metadynamics (MetaD), to map out the entire free energy landscape of different possible coordination environments.
The reliability of the classical force field in MD simulation is an intrinsic challenge for modeling SX systems containing polarizing trivalent ions. In recent work by Duvail et al.,33 a pairwise additive, nonbonded potential for lanthanides was developed using Li et al.‘s methodology29–32 that includes a 1/r4 term in the 12-6-4 force field, representing ion–dipole interactions. Furthermore, by reparameterizing the 12-6-4 potential based on hydration free energy and aqueous phase EXAFS spectra. While not including the polarizability and charge transfer explicitly, their new model can accurately describe the lanthanide cations in both aqueous and organic media, including in the presence of DMDOHEMA and nitrate anion.23,33 In addition to the organic phase EXAFS spectra, the average Ln–O bond length described by this 12-6-4 potential also agrees with the DFT cluster calculations for the malonamide extractant.34
Interconversion between solvation structures is expected to be slow, where, for example, interconversion between MA head group conformations occurs on the nanosecond time scale even in the absence of the metal.35,36 Conversion between lanthanide ion solvation structures would be even slower, as we find below, and it would not be feasible to sample ergodically even with classical pairwise additive models. To address this, we combine this newly developed force field for trivalent lanthanide ions with advanced sampling, where we perform microseconds of MetaD MD simulations to explore, for the first time, the entire range of possible solvation configurations for the metal–ligand complexation. Our MD simulations not only reveal the importance of inner-sphere H2O, which has resulted in much more diverse coordination structures under the same stoichiometry, but, more importantly, they have also provided free energy landscapes in which all thermodynamically accessible solvation configurations and their relative free energies are reported. We use these free energy surfaces to explain the experimental separation performance across the lanthanide series, in which La(III) and Eu(III) show similar separation performances, while Lu(III) is much more difficult to extract by MA (La ≈ Eu > Lu) even though the coordination number in the organic phase is similar between Eu and heavier lanthanides.22 Our work demonstrates that, when complemented by experimental spectroscopies and extraction measurements, classical MD simulation with advanced sampling is a powerful tool to probe the metal solvation energetics in the organic phase, and can help design better lanthanide separations that rely on more complex mechanisms than simple charge density-driven extractant-metal electrostatics.
2 Result and discussion
First, to obtain information on the overall stoichiometry of the metal–ligand speciation, we perform the slope analysis on the extraction of La(III), Eu(III), and Lu(III) by MA in n-heptane, shown in Fig. 1(c). From there we can get an approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 stoichiometry of the metal–ligand for La(III), Eu(III), and Lu(III), which is consistent with the literature.37,38 As Fig. S1† has shown, slopes for all three lanthanides are slightly above 3, which is an indication that, although 1
3 stoichiometry of the metal–ligand for La(III), Eu(III), and Lu(III), which is consistent with the literature.37,38 As Fig. S1† has shown, slopes for all three lanthanides are slightly above 3, which is an indication that, although 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexation is the main speciation, a minority of 1
3 complexation is the main speciation, a minority of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 complexes could also form. This 1
4 complexes could also form. This 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 complex has been observed with DMDOHEMA extraction of a trivalent actinide.39 However, because we expect the speciation to be dominated by the 1
4 complex has been observed with DMDOHEMA extraction of a trivalent actinide.39 However, because we expect the speciation to be dominated by the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complex, we only consider this main complex without computing many other stoichiometries. Sampling over an additional collective variable representing the two possible numbers of extractants in the complex would roughly double the total computational time. While slope analysis can tell us the overall stoichiometry, more detailed information is still needed to explain how the extractant, anion and any potentially coextracted water bind to the metal center, including inner- and outer-sphere solvation.13,24,25,40 To verify inner-sphere solvation of the extractant and the nitrate anion, we use Fourier transform infrared (FTIR) spectroscopy to verify the binding of both MA and NO3− to Eu(III), as shown in Fig. 1(a). FTIR spectra have clearly shown a red shift at around 1650 cm−1 due to the binding of C
3 complex, we only consider this main complex without computing many other stoichiometries. Sampling over an additional collective variable representing the two possible numbers of extractants in the complex would roughly double the total computational time. While slope analysis can tell us the overall stoichiometry, more detailed information is still needed to explain how the extractant, anion and any potentially coextracted water bind to the metal center, including inner- and outer-sphere solvation.13,24,25,40 To verify inner-sphere solvation of the extractant and the nitrate anion, we use Fourier transform infrared (FTIR) spectroscopy to verify the binding of both MA and NO3− to Eu(III), as shown in Fig. 1(a). FTIR spectra have clearly shown a red shift at around 1650 cm−1 due to the binding of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups on MA to Eu(III). The appearance of multiple peaks corresponding to different denticity modes in the range of 700–1400 cm−1 suggests direct inner-sphere coordination of NO3− with Eu(III), which is consistent with results obtained from lanthanide-malonamide crystal structures in our previous work.15 Although these FTIR results do not differentiate between specific ligand denticities, we can still assert that both MA and NO3− are bound, to some extent, directly to the rare-earth metal ion. To determine whether any coextracted water remains in the inner sphere with the metal–ligand complex, we have performed TRLIFS to measure the lifetime of Eu in the organic phase; details of the TRLIFS measurement and raw lifetime data and fits can be found in the ESI.† Our lifetime measurements, shown in Fig. 1(b), have revealed that the number of coordinating H2O molecules per Eu(III) ranges from 0 to 0.64, suggesting that 0 or 1 inner-sphere H2O in MA extraction systems. These results are consistent with the literature on Eu(III) extraction with other malonamides in n-alkanes, where Sengupta et al. determined that there is 1 coordinating H2O molecule coordinating the metal.38 It is worth noting that, although TRLIFS can probe the number of inner-sphere H2O through Eu luminescence lifetime, the overall number of co-extracted H2O per metal-ion, and their locations, especially at the outer sphere location, are still not well-understood.
O groups on MA to Eu(III). The appearance of multiple peaks corresponding to different denticity modes in the range of 700–1400 cm−1 suggests direct inner-sphere coordination of NO3− with Eu(III), which is consistent with results obtained from lanthanide-malonamide crystal structures in our previous work.15 Although these FTIR results do not differentiate between specific ligand denticities, we can still assert that both MA and NO3− are bound, to some extent, directly to the rare-earth metal ion. To determine whether any coextracted water remains in the inner sphere with the metal–ligand complex, we have performed TRLIFS to measure the lifetime of Eu in the organic phase; details of the TRLIFS measurement and raw lifetime data and fits can be found in the ESI.† Our lifetime measurements, shown in Fig. 1(b), have revealed that the number of coordinating H2O molecules per Eu(III) ranges from 0 to 0.64, suggesting that 0 or 1 inner-sphere H2O in MA extraction systems. These results are consistent with the literature on Eu(III) extraction with other malonamides in n-alkanes, where Sengupta et al. determined that there is 1 coordinating H2O molecule coordinating the metal.38 It is worth noting that, although TRLIFS can probe the number of inner-sphere H2O through Eu luminescence lifetime, the overall number of co-extracted H2O per metal-ion, and their locations, especially at the outer sphere location, are still not well-understood.
Gathering the above experimental evidence is key to helping us design MD simulations. For each lanthanide, we initially pack a single 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Ln(III)
1 Ln(III)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MA
MA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3−
NO3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O using n-hexane as the solvent. We also note that the Karl Fischer titration has suggested that there are two co-extracted H2O per Eu(III) complex.37 By considering the TRLIFS lifetime, we can infer that the additional H2O molecules must stay in the outer sphere. Unfortunately, this dramatically expands the possible structures in our three dimensional collective variable. To minimize the number of simulations to run, we only include one water molecule in the complex and our water coordination collective variable considers only the case of 1 or 0 water molecules that coordinate directly to the metal ion. As our goal is to investigate the energetics of primary metal coordination, and our TRLIFS results preclude more than one coordinating water per Eu(III), we do not expect this necessary simplification to dramatically impact metal coordination. Because the metal–ligand complexation is driven by strong enthalpic interactions between the Lewis basic sites in the chelator and the cationic rare-earth metal ion center, such a hindrance prohibits rearrangement of the metal–ligand complex over simulation-accessible timescales, as has also been found in various MD simulation works.41–43 This necessitates the application of an advanced sampling technique to help the MD trajectory escape local minima and ensure complete sampling of the configurational space. Since the development of MetaD and its variant techniques,8,44–47 they have been widely applied as elegant ways to sample the entire free energy landscape with a careful selection of collective variables (CVs) in the configurational space. MetaD is a class of advanced sampling methods in which history-dependent Gaussian bias potentials are spawned to discourage the system from revisiting locations in the configurational space. The detailed underlying theory of MetaD is beyond the scope of this work; instead, we will only briefly discuss the definition of our CVs. As our definition of CVs should be able to account for various binding possibilities for ligands that can vary denticity under the same total metal–ligand speciation, we characterize the binding environment by the coordination number (CN) of ligand binding sites from each ligand type surrounding the lanthanide ion: oxygen atoms of NO3−, carbonyl oxygen in MA, and water oxygen. It is worth emphasizing that the CNs defined here the number of oxygen sites for a type of ligand, not simply the number of coordinating ligands. The natural way to define a CN is as a discrete step function, which cannot be used directly as a CV in the MetaD simulation. Here, we use the continuous switch function48 in eqn (1):
H2O using n-hexane as the solvent. We also note that the Karl Fischer titration has suggested that there are two co-extracted H2O per Eu(III) complex.37 By considering the TRLIFS lifetime, we can infer that the additional H2O molecules must stay in the outer sphere. Unfortunately, this dramatically expands the possible structures in our three dimensional collective variable. To minimize the number of simulations to run, we only include one water molecule in the complex and our water coordination collective variable considers only the case of 1 or 0 water molecules that coordinate directly to the metal ion. As our goal is to investigate the energetics of primary metal coordination, and our TRLIFS results preclude more than one coordinating water per Eu(III), we do not expect this necessary simplification to dramatically impact metal coordination. Because the metal–ligand complexation is driven by strong enthalpic interactions between the Lewis basic sites in the chelator and the cationic rare-earth metal ion center, such a hindrance prohibits rearrangement of the metal–ligand complex over simulation-accessible timescales, as has also been found in various MD simulation works.41–43 This necessitates the application of an advanced sampling technique to help the MD trajectory escape local minima and ensure complete sampling of the configurational space. Since the development of MetaD and its variant techniques,8,44–47 they have been widely applied as elegant ways to sample the entire free energy landscape with a careful selection of collective variables (CVs) in the configurational space. MetaD is a class of advanced sampling methods in which history-dependent Gaussian bias potentials are spawned to discourage the system from revisiting locations in the configurational space. The detailed underlying theory of MetaD is beyond the scope of this work; instead, we will only briefly discuss the definition of our CVs. As our definition of CVs should be able to account for various binding possibilities for ligands that can vary denticity under the same total metal–ligand speciation, we characterize the binding environment by the coordination number (CN) of ligand binding sites from each ligand type surrounding the lanthanide ion: oxygen atoms of NO3−, carbonyl oxygen in MA, and water oxygen. It is worth emphasizing that the CNs defined here the number of oxygen sites for a type of ligand, not simply the number of coordinating ligands. The natural way to define a CN is as a discrete step function, which cannot be used directly as a CV in the MetaD simulation. Here, we use the continuous switch function48 in eqn (1):
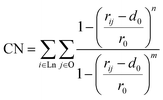 | (1) |
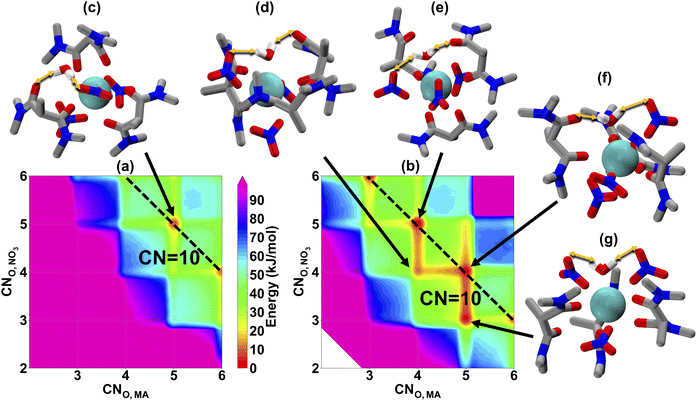
To investigate the organic phase solvation behavior, we ran 4 μs MD simulations using MetaD sampling. Since we have defined 3 CVs in the configurational space, the final energetic landscape is a 4D free-energy surface, which is hard to visualize. So, in Fig. 2, we show two separate slices of the free energy surfaces: one when it is in the outer-sphere (CNO,H2O = 0) (a) and one when water is directly bound to La(III) (CNO,H2O = 1) (b). As we have defined a CV on the CNO,H2O, solvation energetic landscapes in panel (a) and (b) can be compared directly on the same energetic scale. The first observation is that (b) (inner-sphere water) shows more accessible local minima at different coordination configurations, and the overall free energies are significantly lower than (a) (outer-sphere water). From the simulation result, this observation indicates that metal–ligand structures with inner-sphere water might be more stable, although we cannot verify with fluorescence for La(III). However, as our TRLIFS shows that water is likely to bind with Eu(III) directly, the larger ionic radius of La(III) will likely also promote inner-sphere water solvation. Another interesting observation is that the inner-sphere water enables a wider range of energetically accessible metal–ligand binding configurations, with representative structures shown in Fig. 2(d)–(g) suggesting that the inner-sphere water has an additional stabilization effect by forming hydrogen bonds (highlighted by orange arrows) to the nitrate anion and MA. In traditional DFT ligand design works, ligand conformations around the metal center are often optimized so that the enthalpic interaction between metal ions and ligands are maximized without explicit consideration of entropic contributions or entire ensembles of configurations, often favoring bidentate configurations. Recent work by Summers et al.49 significantly improves upon this approach by explicitly considering many DFT structures, which significantly improves the predictive capability of DFT studies. Here, we implement a different approach using MD simulation with MetaD to determine the relative free energies of the entire ensemble of accessible coordination environments. In doing so, we show that there is a great multitude of binding configurations that exist at CNO,MA = 4/5, with one or two monodentate MAs bound to La(III). Nitrate coordination is also a mixture of monodentate and bidentate motifs. These combine with the water to result in a total CN remains around 10, with some accessible 9-coordinate structures, which agrees with the experimental EXAFS spectra in the organic phase.22,23 Such an agreement also gives us extra confidence in this 12-6-4 lanthanide model and the MetaD MD simulation results.
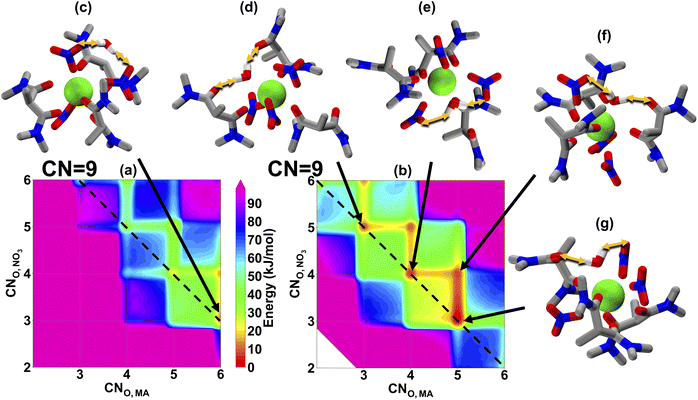
From La(III) to Eu(III), the MA shows nearly the same distribution ratio, which then begins to decrease significantly for the heavy lanthanides.6 In order to link this observation to organic phase solvation, we show the coordination free energy landscapes of Eu(III), Fig. 3, and Lu(III), Fig. 4. Eu(III) has shown a preferable CN of 9, with some accessible 10-coordinate structures, which is slightly smaller than that of La(III). This observation also agrees with the experimental EXAFS spectra.22,23 We also note that, just as with La(III), the water prefers to solvate the metal in the inner-sphere, consistent with the TRLIFS data, enabling a wider range of accessible solvation modes than when the water remains in the outer-sphere. By comparing Fig. 3 and 2, we can see that smaller ionic radius of Eu(III) results in a lower CN, but the stronger Eu(III)-MA interaction keeps the most favorable CNO,MA remaining at 4 and 5 (which is similar to La(III)), while CNO,NO3 decreases to compensate for the decreasing CN. In addition to the solvation behaviors in the organic phase, the increase in the hydration free energy of Eu(III) over La(III)33 results in a more difficult extraction from the aqueous phase to the organic phase for Eu(III). Therefore, we hypothesize that similar distribution ratios of La(III) and Eu(III) in Fig. 1(c) are the product of the persistent degree of MA coordination between these two lanthanides. We note that a direct evaluation of the binding strength for La(III) and Eu(III) cannot be concluded by comparing Fig. 2 and 3, as both maps are from two separation simulations and their reference states are different.
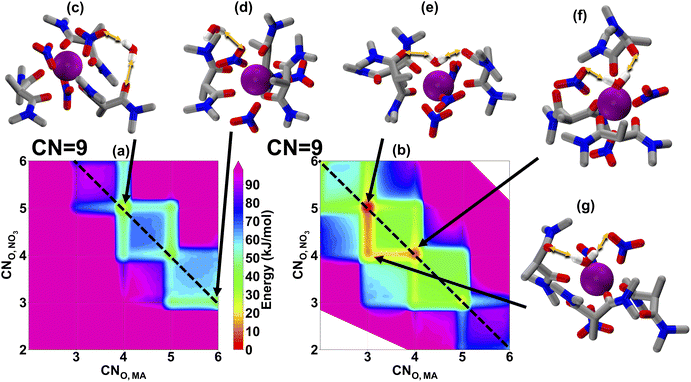
The distribution ratio for Lu(III) is an order of magnitude lower than Eu(III) and La(III), as shown in Fig. 1(c). To investigate this significant decrease in the distribution ratio and potentially link this to the organic phase solvation behavior, we sample the CN of Lu(III) under the same stoichiometry as La(III) and Eu(III), which has been shown in Fig. 4. Overall, there are fewer energetically accessible configurations for Lu(III) than for lighter lanthanides. Compared with CNO,MA = 4/5 for La(III) and Eu(III) when the water is in the inner sphere, the most preferable CNO,MA is at 3 or 4. This observation can be explained by the shrinking size of the ionic radius of Lu(III) limits MA coordination, even though we find the total coordination number is similar between Eu(III) and Lu(III). The stronger Lu(III)-ligand interaction is not enough to compensate for the smaller ionic size, as the binding between the Lu(III)-MA has to overcome increased ligand crowding. Therefore, the significant decrease in the Lu(III) distribution ratio can be attributed to the decrease in CNO,MA. Although the observation of bidentate nitrates with monodentate MA ligands for Lu(III) might seem counterintuitive given the bidentate nature of the extracant, this actually agrees with our prior crystallographic findings.15 There, N,N,N′,N′-tetramethylmalonamide with Lu(NO3)3 forms a 9-coordinate structure where the bidentate binding of the nitrates is retained at the expense of monodentate MA. Another interesting observation is that the water molecule strongly prefers to stay at the inner-sphere; there are more favorable and more diverse accessible coordination environments with inner-sphere water than when the water migrates to the outer sphere. Overall, our findings confirm the importance of obtaining the whole free-energy landscape of different solvation environments: although the stoichiometry of the metal–ligand complex remains the same, the detailed solvation configuration and its free energy can be drastically different, leading to various separation performances with MA.
All energetically accessible solvation configurations are listed in Table 1, along with the relative free energies estimated from the MetaD simulation. Error bars are estimated by taking the standard deviation of the relative free energy during the last 2 μs while the trajectory is reweighted to account for the dynamic change of the adaptive bias potentials in the well-tempered MetaD technique (details provided in the ESI†).47 While the exact energetic ordering of each state is not possible given the magnitude of the error bars relative to the total free energy differences between states, we can still identify states that are predicted to be thermodynamically accessible and therefore relevant to the separation process design.
| Metals | CNO,MA; CNO,NO3; CNO,H2O | Free energy (kJ mol−1) | ||
|---|---|---|---|---|
| a States taken as the references. | ||||
| La(III) | 5 | 4 | 1 | 0a |
| 4 | 5 | 1 | 0 ± 5 | |
| 5 | 3 | 1 | 2 ± 2 | |
| 3 | 6 | 1 | 3 ± 5 | |
| 5 | 5 | 0 | 8 ± 4 | |
| 4 | 4 | 1 | 10 ± 2 | |
| 6 | 4 | 0 | 11 ± 5 | |
| 6 | 3 | 1 | 12 ± 5 | |
| Eu(III) | 5 | 3 | 1 | 0a |
| 4 | 4 | 1 | 5 ± 5 | |
| 5 | 4 | 1 | 6 ± 1 | |
| 4 | 5 | 1 | 9 ± 4 | |
| 3 | 5 | 1 | 9 ± 2 | |
| 6 | 3 | 0 | 13 ± 5 | |
| 3 | 6 | 1 | 13 ± 1 | |
| Lu(III) | 3 | 5 | 1 | 0a |
| 4 | 4 | 1 | 8 ± 4 | |
| 3 | 4 | 1 | 13 ± 3 | |
3 Conclusion
In this work, we use the state-of-the-art MetaD advanced sampling technique using 4 μs trajectories, coupled with experimental data, to map out trivalent lanthanide ion solvation energetics in the organic phase of a separation system using a malonamide extractant. This extraction system shows a decrease in Ln extraction for the smaller, more charge-dense heavy lanthanides. As such effects are hard to predict simply by looking only at a single lowest energy configuration, our MetaD approach reveals how the complex solvation environment changes across the lanthanide series. We can readily explain the extraction trend La ≈ Eu > rbin Lu by a reduction of extractant coordination occurring between Eu and Lu, but not between La and Eu. Importantly, this demonstrates the extraction behavior is the result of the ligand arrangement around the complex, because we find that the total coordination number in the organic phase changes between La and Eu, and not between Eu and Lu. We find that the presence of inner-sphere water directly bound to the lanthanide ion, which then hydrogen bonds with excess oxygens of the coordinating extractant and nitrate anions, greatly diversifies the energetically accessible coordination configurations compared to those of outer-sphere water. Our findings show how to understand separation trends driven by ligand crowding, where traditional electronic structure methods or experimental spectroscopy are unable to capture the entire range of accessible solvation structures and their relative free energies. Overall, we believe that the classical MD simulation coupled with MetaD provides a powerful tool for studying complex metal ion solvation environments and for explaining and guiding the design of metal ion separations.Data availability
Data for this article, including simulation setups, experimental IR and fluorescence data, are available at Zenodo at https://doi.org/10.5281/zenodo.13124211.Author contributions
XW: conceptualization, methodology, formal analysis, investigation, writing – original draft, review & editing; AAP: formal analysis, investigation; DVK: writing – review & editing; REW: writing – review & editing; JCS: writing – review & editing; MJS: conceptualization, writing – original draft, review & editing, supervision, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division, Separation Science Program, under Contract DE-AC02-06CH11357 to UChicago Argonne, LLC, Operator of Argonne National Laboratory. AAP acknowledges the support of the Department of Energy, Basic Energy Science program, under contract number DE-SC0022217 and the U.S. Department of Energy, Office of Science, Office of Workforce Development for Teachers and Scientists, Office of Science Graduate Student Research (SCGSR) program. The SCGSR program is administered by the Oak Ridge Institute for Science and Education for the DOE under contract number DE-SC0014664. We gratefully acknowledge the computing resources provided on Improv, a high-performance computing cluster operated by the Laboratory Computing Resource Center at Argonne National Laboratory.References
- D. S. Sholl and R. P. Lively, Seven Chemical Separations to Change the World, Nature, 2016, 532, 435–437 CrossRef.
- K. R. Johnson, D. M. Driscoll, J. T. Damron, A. S. Ivanov and S. Jansone-Popova, Size selective ligand tug of war strategy to separate rare earth elements, JACS Au, 2023, 3, 584–591 CrossRef CAS.
- T. Cheisson and E. J. Schelter, Rare earth elements: Mendeleev's bane, modern marvels, Science, 2019, 363, 489–493 CrossRef CAS.
- A. A. Peroutka, S. S. Galley and J. C. Shafer, Elucidating the speciation of extracted lanthanides by diglycolamides, Coord. Chem. Rev., 2023, 482, 215071 CrossRef CAS.
- R. J. Ellis, D. M. Brigham, L. Delmau, A. S. Ivanov, N. J. Williams, M. N. Vo, B. Reinhart, B. A. Moyer and V. S. Bryantsev, “Straining” to separate the rare earths: how the lanthanide contraction impacts chelation by diglycolamide ligands, Inorg. Chem., 2017, 56, 1152–1160 CrossRef CAS.
- B. Gannaz, R. Chiarizia, M. R. Antonio, C. Hill and G. Cote, Extraction of lanthanides (III) and Am (III) by mixtures of malonamide and dialkylphosphoric acid, Solvent Extr. Ion Exch., 2007, 25, 313–337 CrossRef CAS.
- X. Wang, S. Nayak, R. E. Wilson, L. Soderholm and M. J. Servis, Solvent effects on extractant conformational energetics in liquid–liquid extraction: a simulation study of molecular solvents and ionic liquids, Phys. Chem. Chem. Phys., 2024, 26, 2877–2886 RSC.
- X. Wang and M. J. Servis, Using Metadynamics to Reveal Extractant Conformational Free Energy Landscapes, J. Phys. Chem. B, 2023, 128, 263–272 CrossRef.
- A. Hu, S. N. MacMillan and J. J. Wilson, Macrocyclic ligands with an unprecedented size-selectivity pattern for the lanthanide ions, J. Am. Chem. Soc., 2020, 142, 13500–13506 CrossRef CAS.
- E. Castellano and R. W. Becker, Structural studies of addition compounds of lanthanides with organic ligands. II. Lanthanum hexafluorophosphate and N, N, N’, N’-tetramethylmalonamide, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, 37, 1998–2001 CrossRef.
- G. Y. Chan, M. G. Drew, M. J. Hudson, P. B. Iveson, J.-O. Liljenzin, M. Skålberg, L. Spjuth and C. Madic, Solvent extraction of metal ions from nitric acid solution using N,N’-substituted malonamides. Experimental and crystallographic evidence for two mechanisms of extraction, metal complexation and ion-pair formation, J. Chem. Soc., Dalton Trans., 1997, 649–660 RSC.
- S. Okumura, T. Kawasaki, Y. Sasaki and Y. Ikeda, Crystal Structures of Lanthanoid (III)(Ln (III), Ln= Tb, Dy, Ho, Er, Tm, Yb, and Lu) Nitrate Complexes with N, N, N’, N’-Tetraethyldiglycolamide, Bull. Chem. Soc. Jpn., 2014, 87, 1133–1139 CrossRef CAS.
- M. R. Antonio, D. R. McAlister and E. P. Horwitz, An europium (III) diglycolamide complex: insights into the coordination chemistry of lanthanides in solvent extraction, Dalton Trans., 2015, 44, 515–521 RSC.
- X. Wang, L. Song, Q. Yu, Q. Li, L. He, X. Xiao, Q. Pan, Y. Yang and S. Ding, Complexation of a Nitrilotriacetate-Derived Triamide Ligand with Trivalent Lanthanides: A Thermodynamic and Crystallographic Study, Inorg. Chem., 2023, 62, 3916–3928 CrossRef CAS.
- D. Kravchuk, X. Wang, M. Servis and R. Wilson, Structural Trends and Vibrational Analysis of N,N,N′,N′-Tetramethylmalonamide Complexes Across the Lanthanide Series, 2023 Search PubMed.
- B. K. McNamara, G. J. Lumetta and B. M. Rapko, Extraction of europium (III) ion with tetrahexylmalonamides, Solvent Extr. Ion Exch., 1999, 17, 1403–1421 CrossRef.
- G. J. Lumetta, B. K. McNamara, B. M. Rapko and J. E. Hutchison, Complexation of uranyl ion by tetrahexylmalonamides: an equilibrium modeling and infrared spectroscopic study, Inorg. Chim. Acta, 1999, 293, 195–205 CrossRef CAS.
- P. Narayanan, K. R. Swami, T. Prathibha and K. Venkatesan, FTIR spectroscopic investigations on the aggregation behaviour of N, N, N’, N’-tetraoctyldiglycolamide and N, N-dioctylhydroxyacetamide in n-dodecane during the extraction of Nd (III) from nitric acid medium, J. Mol. Liq., 2020, 314, 113685 CrossRef CAS.
- E. Horwitz, D. Kalina and A. Muscatello, The extraction of Th (IV) and U (VI) by dihexyl-N, N-diethylcarbamoylmethylphosphonate from aqueous nitrate media, Sep. Sci. Technol., 1981, 16, 403–416 CrossRef CAS.
- A. A. Peroutka, X. Wang, M. J. Servis and J. C. Shafer, Influence of Aqueous Phase Acidity on Ln (III) Coordination by N, N, N’, N’-Tetraoctyldiglycolamide, Inorg. Chem., 2024, 63, 10466–10470 CrossRef CAS.
- R. J. Ellis and M. R. Antonio, Coordination structures and supramolecular architectures in a cerium (III)–malonamide solvent extraction system, Langmuir, 2012, 28, 5987–5998 CrossRef CAS.
- R. J. Ellis, Y. Meridiano, R. Chiarizia, L. Berthon, J. Muller, L. Couston and M. R. Antonio, Periodic behavior of lanthanide coordination within reverse micelles, Chem. - Eur. J., 2013, 19, 2663–2675 CrossRef CAS.
- R. J. Ellis, Y. Meridiano, J. Muller, L. Berthon, P. Guilbaud, N. Zorz, M. R. Antonio, T. Demars and T. Zemb, Complexation-Induced Supramolecular Assembly Drives Metal-Ion Extraction, Chem. - Eur. J., 2014, 20, 12796–12807 CrossRef CAS.
- D. M. Brigham, A. S. Ivanov, B. A. Moyer, L. H. Delmau, V. S. Bryantsev and R. J. Ellis, Trefoil-shaped outer-sphere ion clusters mediate lanthanide (III) ion transport with diglycolamide ligands, J. Am. Chem. Soc., 2017, 139, 17350–17358 CrossRef CAS.
- D. M. Driscoll, H. Liu, B. Reinhart, I. Popovs, V. Bocharova, S. Jansone-Popova, D.-e. Jiang and A. S. Ivanov, Noncoordinating Secondary Sphere Ion Modulates Supramolecular Clustering of Lanthanides, J. Phys. Chem. Lett., 2022, 13, 12076–12081 CrossRef CAS.
- R. C. Shiery, J. L. Fulton, M. Balasubramanian, M.-T. Nguyen, J.-B. Lu, J. Li, R. Rousseau, V.-A. Glezakou and D. C. Cantu, Coordination sphere of lanthanide aqua ions resolved with ab initio molecular dynamics and X-ray absorption spectroscopy, Inorg. Chem., 2021, 60, 3117–3130 CrossRef CAS.
- G. L. Licup, T. J. Summers, J. A. Sobrinho, A. de Bettencourt-Dias and D. C. Cantu, Elucidating the Structure of the Eu-EDTA Complex in Solution at Various Protonation States, Eur. J. Inorg. Chem., 2024, e202400042 CrossRef CAS.
- P. Lee, P. Citrin, P. t. Eisenberger and B. Kincaid, Extended x-ray absorption fine structure-its strengths and limitations as a structural tool, Rev. Mod. Phys., 1981, 53, 769 CrossRef CAS.
- P. Li and K. M. Merz Jr, Taking into account the ion-induced dipole interaction in the nonbonded model of ions, J. Chem. Theory Comput., 2014, 10, 289–297 CrossRef CAS.
- P. Li, L. F. Song and K. M. Merz Jr, Parameterization of highly charged metal ions using the 12-6-4 LJ-type nonbonded model in explicit water, J. Phys. Chem. B, 2015, 119, 883–895 CrossRef CAS.
- P. Li, L. F. Song and K. M. Merz Jr, Systematic parameterization of monovalent ions employing the nonbonded model, J. Chem. Theory Comput., 2015, 11, 1645–1657 CrossRef CAS.
- Z. Li, L. F. Song, P. Li and K. M. Merz Jr, Parametrization of Trivalent and Tetravalent Metal Ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models, J. Chem. Theory Comput., 2021, 17, 2342–2354 CrossRef CAS.
- M. Duvail, D. Moreno Martinez, L. Ziberna, E. Guillam, J.-F. Dufrêche and P. Guilbaud, Modeling Lanthanide Ions in Solution: A Versatile Force Field in Aqueous and Organic Solvents, J. Chem. Theory Comput., 2024 Search PubMed.
- C. Boehme, B. Coupez and G. Wipff, Interaction of M3+ lanthanide cations with diamide ligands and their thia analogues: a quantum mechanics study of monodentate vs bidentate binding, counterion effects, and ligand protonation, J. Phys. Chem. A, 2002, 106, 6487–6498 CrossRef CAS.
- M. J. Servis, M. Piechowicz and L. Soderholm, Impact of water extraction on malonamide aggregation: A molecular dynamics and graph theoretic approach, J. Phys. Chem. B, 2021, 125, 6629–6638 CrossRef CAS.
- M. J. Servis, B. Sadhu, L. Soderholm and A. E. Clark, Amphiphile conformation impacts aggregate morphology and solution structure across multiple lengthscales, J. Mol. Liq., 2022, 345, 117743 CrossRef CAS.
- Y. Meridiano, L. Berthon, S. Lagrave, X. Crozes, C. Sorel, F. Testard and T. Zemb, Correlation between aggregation and extracting properties in solvent extraction systems: extraction of actinides (III) and lanthanides (III) by a malonamide in non acidic media, 2008 Search PubMed.
- A. Sengupta, S. M. Ali and K. T. Shenoy, Understanding the complexation of the Eu3+ ion with TODGA, CMPO, TOPO and DMDBTDMA: Extraction, luminescence and theoretical investigation, Polyhedron, 2016, 117, 612–622 CrossRef CAS.
- P. Weßling, M. Trumm, A. Geist and P. J. Panak, Stoichiometry of An (iii)–DMDOHEMA complexes formed during solvent extraction, Dalton Trans., 2018, 47, 10906–10914 RSC.
- A. G. Baldwin, A. S. Ivanov, N. J. Williams, R. J. Ellis, B. A. Moyer, V. S. Bryantsev and J. C. Shafer, Outer-sphere water clusters tune the lanthanide selectivity of diglycolamides, ACS Cent. Sci., 2018, 4, 739–747 CrossRef CAS.
- T. D. N. Reddy, A. S. Ivanov, D. M. Driscoll, S. Jansone-Popova and D.-e. Jiang, Changes in nitrate binding with lanthanides in BLPhen complexes, J. Mol. Liq., 2023, 387, 122573 CrossRef CAS.
- D. Massey, C. D. Williams, J. Mu, A. J. Masters, R. Motokawa, N. Aoyagi, Y. Ueda and M. R. Antonio, Hierarchical Aggregation in a Complex Fluid- The Role of Isomeric Interconversion, J. Phys. Chem. B, 2023, 127, 2052–2065 CrossRef CAS.
- T. J. Summers, J. A. Sobrinho, A. de Bettencourt-Dias, S. D. Kelly, J. L. Fulton and D. C. Cantu, Solution Structures of Europium Terpyridyl Complexes with Nitrate and Triflate Counterions in Acetonitrile, Inorg. Chem., 2023, 62, 5207–5218 CrossRef CAS.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS.
- M. Iannuzzi, A. Laio and M. Parrinello, Efficient exploration of reactive potential energy surfaces using Car-Parrinello molecular dynamics, Phys. Rev. Lett., 2003, 90, 238302 CrossRef.
- A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: a smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100, 020603 CrossRef.
- P. Tiwary and M. Parrinello, A time-independent free energy estimator for metadynamics, J. Phys. Chem. B, 2015, 119, 736–742 CrossRef CAS.
- PLUMED: COORDINATION, https://www.plumed.org/doc-v2.9/user-doc/html/_c_o_o_r_d_i_n_a_t_i_o_n.html.
- T. Summers, M. Taylor, L. Augustine, J. Janssen, D. Perez, E. Batista and P. Yang, On the importance of configuration search to the predictivity of lanthanide selectivity, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-2112n.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05061d |
| This journal is © The Royal Society of Chemistry 2024 |