Tailoring the lasing modes in CH₃NH₃PbBr₃ perovskite microplates via micro-manipulation

Abstract

Laser emissions from perovskite microplates have been intensively studied recently. However, due to their relatively large sizes, most of them produced multiple lasing modes simultaneously. In order to improve the monochromaticity of perovskite microlasers without significantly affecting the output energy, here we demonstrate a simple way to tailor the number of lasing modes in a microcavity. By pushing an additional microplate to contact the lasing microplate, the number of lasing modes has been effectively reduced and single-mode laser operation has been achieved even though the size of the microplate is orders of magnitude larger than the lasing wavelengths. The corresponding extinction ratio can be as high as 11.8 dB. Our experimental results show that introducing the second microplate and the extremely narrow gain region play essential roles in achieving single-mode laser operation. We believe that our findings will be interesting for the applications of perovskite microdisk lasers.

---

1. Introduction

Due to the relatively small defect density, long carrier diffusion lengths, and large carrier mobility, lead halide perovskites have shown great potential in both solar cells and optoelectronic devices.^1–15 To date, a number of unique properties have been achieved in perovskite based devices. The light conversion coefficients of perovskite solar cells have been improved to above 20.1%,³ and the band of a single-crystal perovskite photon detector is as small as 20 nm.² Perovskite based micro- and nano-lasers are another type of prominent example.^5–15 In the past few years, various perovskite microlasers have been observed in different kinds of resonant systems, e.g. random lasers in thin films and whispering gallery modes in microspheres.¹³ Very recently, due to the better crystal quality, ultralow laser thresholds have been obtained from dimension reduced devices such as two-dimensional microplates^8–10 and one-dimensional nanowires by either single-photon pumping or two-photon excitation.^11,12,14 These achievements have promised the bright future of lead halide perovskites, especially in the “green gap” of conventional III-nitride and III-phosphides.⁵ However, as these devices have at least one dimension much larger than the lasing wavelength, most perovskite microplates and microwires produced multiple lasing modes, which strongly restricted their potential applications.

Monochromaticity is one of the key characteristics of lasers. In past decade achieving single-mode operation in laser systems has become a primary goal of cavity design, especially for the micro-sized laser that are too small to be tailored as conventional laser systems.^16–22 Several approaches have been developed to suppress the competing parasitic modes, by adding intracavity dispersive elements,¹⁶ reducing the cavity size,¹⁷ and spatially modulate the pumping and gain.¹⁸ Very recently, parity-time symmetry breaking^19,20 and mode coupling^21,22 have also been applied to control the lasing modes in microcavities. Single-mode operations with extinction ratios more than 15 dB have been demonstrated in either double disks or single cavity. All these progresses have significantly boosted the possibly practical applications of microlasers. Unfortunately, most of these techniques cannot be applied in the recently developed perovskite microdisk lasers due to their relatively low stabilities in most solutions.²³ Reducing the cavity size can improve the monochromaticity.¹⁴ But it will also reduce the total emission intensity.¹⁷ Here, by introducing an additional perovskite via micro-manipulation, the thresholds of different lasing modes in lasing microdisk have been significantly distinguished and single-mode laser operation has been achieved.

2. Experimental results and discussions

2.1 Synthesis of perovskite microplates

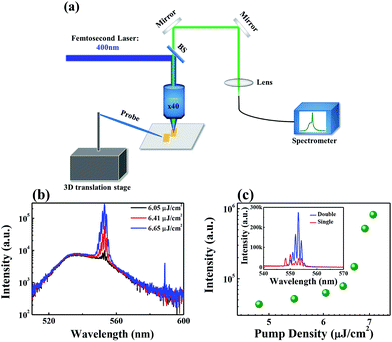
The perovskite microplates are synthesized by a simple one-step solution-processed method. Basically, equal volumes of solutions of CH₃NH₃Br (0.1 M) and PbBr₂ (0.1 M) in DMF (N,N-dimethylformamide) are mixed to achieve CH₃NH₃Br·PbBr₂ (0.05 M) solution. Then the CH₃NH₃Br·PbBr₂ solution is dip-casted onto a glass slide, which is placed onto a Teflon stage in a beaker containing dichloromethane (DCM). The beaker is sealed with a porous Parafilm (3M) to control the evaporation rate of solution. After 24 hours in room temperature, single-crystal CH₃NH₃PbBr₃ microplate can be achieved on the glass substrate.

Fig. 1(a) shows the scanning electron microscope (SEM) image of the synthesized perovskite microplates. Besides the numerous micro- & nano-wires, most of the microplates have rectangle shapes. The lengths and widths of rectangle microplates mostly range from a few micron to tens of micron (see ESI†). The thicknesses of microplates are usually below 1 micron. Fig. 1(b) shows the linear absorption and photoluminescence spectra of the synthesized perovskites. The absorption coefficient decreases quickly at wavelength around 535 nm and becomes saturated at shorter wavelength. This is a typical absorption spectrum and clearly shows the bandgap of CH₃NH₃PbBr₃ perovskite at E_g = 2.31 eV. The photoluminescence is a broad peak centered at 535 nm with full width at half maximum (FWHM) ∼24 nm. The photoluminescence and absorption spectra overlap in a large wavelength range.

Fig. 1 The synthesized perovskite microstructures. (a) Top view SEM image of the synthesized CH₃NH₃PbBr₃ perovskites. (b) The absorption spectrum (dashed line) and photoluminescence spectrum (solid line) of the perovskites.

2.2 Optical characterization of single microplate

Then we mount the samples under a home-made microscope system and study the optical properties under optical excitation. A Ti : sapphire regenerative amplifier (100 fs pulse width, 1k Hz repetition rate, and 800 nm) is frequency doubled by a BBO crystal and focused onto the top surface of the sample via a 40× objective lens. The emitted lights is collected by the same objective lens and coupled to a CCD (Princeton Instruments, PIXIS UV enhanced CCD) coupled spectrometer (Acton SpectroPro s2700) via a multimode fiber. The excitation beam spot on the samples is fixed at around 120 μm in diameters with most energy concentrated on the central. We first study the laser characteristics in a single microplate. Fig. 2(a) shows the top-view SEM image of the microplate (Disk-1). The lengths of long and short sides are 26.78 micron and 14.4 micron, respectively. Fig. 2(b) demonstrates the emission spectra at different pumping density. When the pumping power is small, a broad photoluminescence peak can be observed. Once the pumping power exceeds 6.1 μJ cm⁻², several sharp peaks appear and dominate the emission spectrum. During the emergence of discrete peaks, bright spots can be clearly seen at the edges of the microplate, clearly demonstrating the amplifications of perovskites (see the inset in Fig. 2(b)).

Fig. 2 Lasing action in single microplate. (a) Top-view SEM image of rectangle microplates. Here the left microplate is the initial one (marked as Disk-1) and the right microplate is the second one (marked as Disk-2) that is pushed to suppress the lasing mode. Two microplates closely contact each other. (b) The laser spectra from rectangle microplate at different pumping density. (c) The output power (dots) and linewidth (crosses) as a function of pumping density. (d) The lasing wavelength ranges of 10 different samples. The inset in (b) is the corresponding fluorescent microscope image at 6.41 μJ cm⁻². Different from (a), here we can clearly see that two microplates are well separated.

Fig. 2(c) shows the dependence of output intensity on the pumping density. With the increase of pumping density, a clear “S” shaped curve can be observed in the log–log plot. The slope quickly changes from ∼1 to ∼7 above 6.1 μJ cm⁻² and finally reaches the gain saturation. The superliner shows the transition from spontaneous emission to amplification. The crosses in Fig. 2(c) show the linewidths of the emission spectra. With the onset of sharp peaks, the linewidth quickly reduces from ∼28 nm to below 1 nm. All these phenomena confirm the lasing actions in microplate well and a threshold ∼6.1 μJ cm⁻² can be simply obtained. The measured perovskite microplates with good lasing properties in our experiment usually have relative small thickness (ranging from 300 nm to 600 nm). Therefore, the lasing modes can't be effectively supported along the vertical direction. All of the lasing modes in this manuscript are along the in-plane of the microplates.

The lasing modes from perovskite microplate have different mode spacings. The mode spacing of left two main peaks and their side small peaks is around 1.8 nm. From the equation for the mode spacing Δλ = λ²/(n − λdn/dλ)L, the calculated cavity length L is around 60 micron, which matches the length of diamond orbit in rectangle microplate well. In a similar process, the modes at relatively longer wavelength are determined as Fabry–Perot modes along the long side. In principle, two types of resonances are localized by different mechanisms. The diamond modes are confined by total internal reflection at four boundaries, whereas the Fabry–Perot modes are mainly reflected by two end-facets. In this sense, two types of lasing modes have the possibility to be separated experimentally.

Besides the lasing actions, it is also interesting to study the wavelength range of the lasing actions. As shown in Fig. 2(b), we define a parameter W to characterize the spectral range from the left laser peak to the right laser peak. We have measured totally ten samples. As shown in Fig. 2(d), the lasing wavelengths ranges slightly vary around 10 nm (from 5 nm to 15 nm). And all the lasing peaks are distributed around 553 nm (see the ESI†). The narrow lasing wavelength region corresponds to the range with maximal net gain (amplification–absorption). This region is formed because that the intrinsic absorption is quickly increased at shorter wavelength and the gain is reduced at the longer wavelength (see Fig. 1(b)).

2.3 Controlling the lasing modes in double microplates

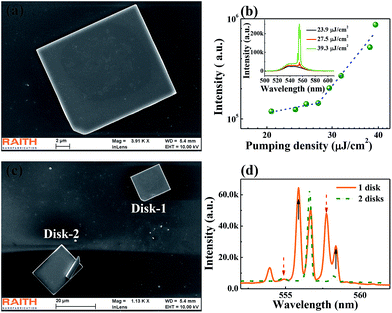
Then we start to consider the control of mode numbers in such large microplates. Because the sizes of microplates are usually around several microns to tens of microns, we can clearly see them with conventional microscope and thus tailor their relative positions via micromanipulation.¹⁴ Here we select one relatively thick microplate and gradually push it to the lasing disk in Fig. 2 by using a tapered fiber (see the schematic picture in Fig. 3(a)). The SEM image of the second microplate is also shown in Fig. 2(a) (Disk-2). It is also a rectangle microplate whose width and length are 17.7 micron and 35.59 micron, respectively. In our samples, the thick microplate has very low crystal quality and won't lase in optical experiment. Meanwhile, the pumping laser spot is still focused on the first microplate and the second microplate is un-pumped. These settings are applied to ensure that the lasing modes are entirely formed within the initial microplate in Fig. 2.

Fig. 3 Lasing action in double microplates. (a) Schematic picture of the micro-manipulation. (b) Logscale plot of the emission spectra from double microplates at different pumping density. (c) The dependence of output intensity and extinction ratio on the pumping density. Inset in (c) shows the laser spectra of single and double microplates. Here the pumping density is fixed at 6.65 μJ cm⁻².

Fig. 3(b) shows the emission spectrum when the second microplate is pushed close to the initial one. Similar to Fig. 2, a broad spontaneous emission peak has been observed at low pumping density. Once the pumping power is above 6.1 μJ cm⁻², lasing modes can be clearly observed at around 551 nm (see Fig. 3(b)). Different from the results in Fig. 2, here the left two peaks disappear and the spectrum completely consists of the Fabry–Perot modes in Fig. 2. Fig. 3(c) shows the output intensity as a function of pumping density. Similar to Fig. 2(c), a clear threshold behavior can be observed at around 6.1 μJ cm⁻². Meanwhile, we can also see the reduction of linewidth around 6.1 μJ cm⁻². Thus the lasing actions in double microplates can also be confirmed.

From the results in Fig. 3, we know that the mode number is decreased by adding the second microplate. This mode suppression is expected as the mechanisms of light confinements for two types of resonances are different. As shown in Fig. 2(a), the second microplate closely touches the right side of the first one. Then the total internal reflection at the right boundary of the first microplate is broken. Meanwhile, as two microplates have quite different thicknesses, strong scattering losses shall happen at the interface and exclude the possibility of forming resonances within two microplates simultaneously.²⁴ Consequently, the entire whispering gallery-like modes such as 4-bounce diamond modes and 6-bounce double-diamond modes are suppressed. On the contrary, the Fabry–Perot modes along the long side of rectangle can survive because they are almost independent on the reflection at the right side of the first microplate. This information can also be confirmed by the laser thresholds. Fig. 2(c) and Fig. 3(c) show that the thresholds of Fabry–Perot modes are almost the same. Interestingly, as the diamond modes are killed by the structure, all the pumped gain is used by the Fabry–Perot modes in double microplate. Therefore, the intensities of Fabry–Perot modes in double microplates are almost one order of magnitude higher than the ones in single microplate. As the perovskite microplate can only provide finite gain, the double microplates can thus efficiently utilize the gain in particular lasing mode.

2.4 Single-mode lasing action in double microplates

The results in Fig. 3 clearly demonstrate that the number of lasing modes can be controlled via the simple micro-manipulation. Considering the facts that the gain region is very narrow and the mode number can be significantly reduced, the single-mode operation is possible to be achieved in relatively small microplate that usually supports lasing modes with much larger free spectral range. To realize the single-mode operation, we select a relatively smaller microplate. Fig. 4(a) shows its top-view SEM image. Similar to the microplate in Fig. 2(a), it is also a rectangle cavity with length and width around 16.12 μm and 14 μm, respectively. When this single microplate is pumped by femtosecond laser, a broad emission peak can be observed. And it transits to sharp peak at higher pumping power (see inset in Fig. 4(b)). The output intensities have been plotted in Fig. 4(b) as a function of pumping density. Similar to above reports, the superliner slope above 28 μJ cm⁻² clearly shows the laser behaviors and confirms the lasing actions.

Fig. 4 Single-mode lasing action in contacted microplates. (a) The top-view SEM image of the perovskite microplate. The length and width of the microplate are 16.12 μm and 14 μm, respectively. (b) The dependence of output intensity on the pumping density. The inset shows the laser spectrum of the microplate under different pumping density. (c) The top-view SEM image of the second microplate (Disk-2). The initial microplate is also shown as Disk-1 in this figure. (d) The high resolution laser spectra of single microplate (solid line) and contacted microplates (dashed line). Here the pumping density is 39.3 μJ cm⁻².

Then we gradually push another microplate close to it. Fig. 4(c) shows the SEM image of the second microplate (Disk-2). The length and width of the second microplate are 20.83 μm and 15.59 μm, respectively. Similar to above setting, this microplate is not pumped in optical experiment and it won't lase experimentally to ensure all the lasing modes come from the initial microplate. The dashed line in Fig. 4(d) shows the emission spectra from double microplates. Similar to Fig. 3, the number of lasing modes is reduced by the second microplate. Remarkably, here only one lasing peak dominates the emission spectrum. The other modes of single microplate have been well suppressed. And the extinction ratio in Fig. 4(d) is about 11.8 dB. This means that single-mode operation has been obtained even though the cavity sizes are orders of magnitude larger than the lasing wavelengths.

The formation of the single-mode operation is also expected. While there are a number of lasing modes in single microplate (see solid line in Fig. 4(d)), they can be categorized to different groups by their mode spacings. The peaks marked by the upward arrows and downward arrows correspond to the modes along diamond orbit with different mode orders (with mode spacing around 2.6 nm). These lasing modes are thus confined by total internal reflection at four boundaries.^25–28 Once the second microplate contact the side of initial microplate, all these modes shall be suppressed. The peaks at 556.625 nm and 553.983 nm are considered as Fabry–Perot cavities modes. As only the mode at 556.625 nm exists in the laser spectrum of double microplates, these two modes should be Fabry–Perot modes along long side and short side of rectangle, respectively.

One may think that the Fabry–Perot resonances also can also generate multiple lasing modes, just as what we have observed in Fig. 3(c). Here we note that two effects play the key roles in mode selection. The mode spacing between Fabry–Perot modes along long side is around 3.75 nm. Meanwhile, the lasing wavelength range (W) in the inset of Fig. 4(b) is only 5.7 nm. Thus there are at most two Fabry–Perot modes in the laser spectrum. As the mode appears at 556.625 nm around the center of gain region, only one lasing mode has been obtained in our experiment. Of course, a microwire with similar length and gain spectral region can also form such kind of single-mode operation. However, as the gain material of microwire is much smaller than the microplate, the total output intensity is also quite lower than the microplate laser.

To confirm the dependence of single-operation on coupling between two microplates, we have also studied the evolution of laser spectrum by slightly changing the position of the second microplate. All the results are summarized in Fig. 5. When two microplates are widely separated at positon-1, only the upper disk (the initial lasing disk) shows bright spots on all four boundaries in the fluorescent microscope image. Consequently, multiple laser peaks can be observed in the laser spectrum. When two microplates are gradually pushed close to one another at positon-2, both the fluorescent image and laser spectrum are well kept. This is because that the separation distance is still much larger than the lasing wavelength (can be seen in the microscope image in Fig. 5(c)) and the mode interaction via evanescent waves can be neglected. Further pushing the second microplate to position-3 and position-4, where two microplates contact, significant changes can be observed. In the fluorescent microscope image, we can see that the positions of bright spots change from all four boundaries to left and right two boundaries. Meanwhile, the laser spectrum transits to single mode. The fluorescent microscope images also clear show that the single mode is formed by the refection at two end-facets, consistent with the above analysis well. To confirm that single-mode laser is formed by two contacted microplates instead of damaging the first one, we have further moved the second microplate. Once the second microplate is pushed to position-5, where two microplates are separated again, the laser spectrum changes back to multiple laser peaks. And the lasing wavelengths match the initial laser peak at positon-1 well. This shows that the laser spectrum can be recovered by moving away the second microplate. Therefore, our experimental results clearly show that placing an additional microplate can effectively control the mode numbers and even form single-mode operation in perovskite microplate.

Fig. 5 Formation of single-mode lasing action in contacted microplates. (a) The laser spectra of two microplates with different separation distance. (b)–(f) are the corresponding microscope images and fluorescent microscope images at position 1–5. Here the pumping density is 39.3 μJ cm⁻². The scale bar in (b)–(f) is 20 μm.

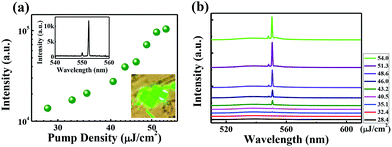
We note that tailoring the number of lasing modes through an additional microplate is quite robust in perovskite microplates. We have observed similar single-mode lasing action in a number of microplates with cavity sizes around 10–15 μm. Fig. 6 is another example of single-mode lasing emission via micro-manipulation. Similar to the above results, the clear superliner slope of the output intensity and narrow line width conform the lasing actions. Inset is the high resolution spectra at pumping density 51.3 μJ cm⁻². Fig. 6(b) is the detailed spectrum at different pump density. We can clearly see that one peak still dominates the lasing spectrum even under the strong excitations, indicating the single-mode lasing emission is not on account of the low pump density. What's more, the other samples with single-mode emission have also been summarized in the ESI.† Moreover, the whispering gallery-like modes are usually suppressed and only Fabry–Perot modes are left in above experiments. This is simply because these two types of resonances are much easier to be distinguished. Here we realize these experiments with a typical three-dimensional translation stage (resolution > 1 micron). In principle, any two types of resonances with different localization mechanisms can be separated by using the same method. Of course, much precise position control of the second microplate is required.

Fig. 6 Single-mode lasing emission of the coupled microplates. (a) The output intensity as a function of pump density. Inset is the high resolution spectra at 52.3 μJ cm⁻² and the corresponding fluorescent microscope image. (b) The detailed spectrum at different pump density.

3. Conclusions

In summary, we have studied the suppression of lasing modes in CH₃NH₃PbBr₃ perovskite microplate. As the perovskite is quite unstable, most of the current techniques in mode control cannot be applied. Here we simply contact the microplate with another microplate. We find that most of the lasing modes are suppressed and even single-mode lasing action can be easily obtained in a microplate more than 10 micron. Our experimental data show that the large mode spacing and extremely narrow gain region play the key role in the formation of single-mode laser emission. As this technique is not limited in Fabry–Perot resonances, we believe our finding can be further applied in other microcavities and will be interesting for the applications of lead halide perovskite microplate lasers.

Acknowledgements

This research is supported by National Nature Science Foundation of China under the Grant No. NSFC11374078. It is also supported by the Shenzhen peacock plan under the Grant No. KQCX20130627094615410 and the Shenzhen fundamental research plan under the Grant No. JCYJ20140417172417110, JCYJ20140417172417096. The authors also would like to thank the supports from Shenzhen Aerospace Micro- and Nano-Device Fabrication and Test Platform.

References

1. M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643.
2. Y. J. Yang, Q. F. Dong, Y. C. Shao, Y. B. Yuan and J. S. Huang, Nat. Photonics, 2015, 9, 679.
3. W. S. Yang, J. H. Noh, N. J. Jeon, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Science, 2015, 348, 1234.
4. M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506.
5. G. Xing, N. Mathews, S. S. Lim, N. Yantara, X. Liu, D. Sabba, M. Grazel, S. Mhaisalkar and T. C. Sum, Nat. Mater., 2014, 13, 476.
6. Z. K. Tan, R. S. Moghaddam, M. L. Lai, P. Docampo, R. Higler, F. Deschler, M. Price, A. Sadhanala, L. M. Pazos, D. Credgington, F. Hanusch, T. Bein, H. J. Snaith and R. H. Friend, Nat. Nanotechnol., 2014, 9, 687.
7. S. T. Ha, X. Liu, Q. Zhang, D. Giovanni, T. C. Sum and Q. Xiong, Adv. Opt. Mater., 2014, 2, 838.
8. J. Xing, X. F. Liu, Q. Zhang, S. T. Ha, W. W. Yuan, C. Shen, T. C. Sum and Q. Xiong, Nano Lett., 2015, 15, 4751.
9. Q. Liao, K. Hu, H. H. Zhang, X. D. Wang, J. N. Yao and H. B. Fu, Adv. Mater., 2015, 27, 3405.
10. Q. Zhang, S. T. Ha, X. Liu, T. C. Sum and Q. Xiong, Nano Lett., 2014, 14, 5595.
11. H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. Tuan Trinh, S. Jin and X.-Y. Zhu, Nat. Mater., 2015, 14, 636.
12. Z. Y. Gu, K. Y. Wang, W. Z. Sun, J. K. Li, S. Liu, Q. H. Song and H. Cao, Adv. Opt. Mater., 2016, 4, 472.
13. S. Yakunin, L. Protesescu, F. Krieg, M. I. Bodnarchuk, G. Nedelcu, M. Humer, G. De Luca, M. Fiebig, W. Heiss and M. V. Kovalenko, Nat. Commun., 2015, 6, 8056.
14. K. Y. Wang, Z. Y. Gu, S. Liu, J. K. Li, S. M. Xiao and Q. H. Song, Opt. Lett., 2016, 41, 555.
15. S. T. Ha, C. Shen, J. Zhang and Q. Xiong, Nat. Photonics, 2015, 10, 115.
16. A. Arbabi, S. M. Kamali, E. Arbabi, B. G. Greffin and L. L. Goddard, Opt. Express, 2015, 23, 5335.
17. Q. H. Song, H. Cao, S. T. Ho and G. S. Solomon, Appl. Phys. Lett., 2009, 94, 061109.
18. S. F. Liew, L. Ge, B. Redding, G. S. Solomon and H. Cao, Phys. Rev. A, 2015, 91, 043828.
19. L. Feng, Z. J. Wong, R. M. Ma, Y. Wang and X. Zhang, Science, 2014, 346, 972.
20. H. Hodaei, M. A. Miri, M. Heinrich, D. N. Christodoulides and M. Khajavikhan, Science, 2014, 346, 975.
21. L. Shang, L. Liu and L. Xu, Opt. Lett., 2008, 33, 1150.
22. M. Li, N. Zhang, K. Y. Wang, J. K. Li, S. M. Xiao and Q. H. Song, Sci. Rep., 2015, 5, 13682.
23. P. D. Yang, Nat. Mater., 2015, 14, 557.
24. Z. Y. Gu, S. Liu, S. Sun, K. Wang, Q. Lyu, S. Xiao and Q. H. Song, Sci. Rep., 2015, 5, 9171.
25. Y.-Z. Huang, K.-J. Che, Y.-D. Yang, S.-J. Wang, Y. Du and Z.-C. Fan, Opt. Lett., 2008, 33, 2170.
26. A. W. Poon, F. Courvoisier and R. K. Chang, Opt. Lett., 2001, 26, 632.
27. J. Wiersig, Phys. Rev. Lett., 2006, 97, 253901.
28. H. Long, Y. Z. Huang, Y. D. Yang, L. X. Zou, J. L. Xiao and Z. X. Xiao, Sci. China: Phys., Mech. Astron., 2015, 58, 114205.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra06415a

---