Open Access Article
Open Access ArticleA substrate descriptor based approach for the prediction and understanding of the regioselectivity in caged catalyzed hydroformylation†
Pim R.
Linnebank
 *a,
David A.
Poole
*a,
David A.
Poole
 a,
Alexander M.
Kluwer
b and
Joost N. H.
Reek
a,
Alexander M.
Kluwer
b and
Joost N. H.
Reek
 *ab
*ab
aHomogeneous, Supramolecular and Bio-Inspired Catalysis, Van’t Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: j.n.h.reek@uva.nl; p.r.linnebank@uva.nl
bInCatT B.V., Science Park 904, 1098 XH Amsterdam, The Netherlands
First published on 9th February 2023
Abstract
The use of data driven tools to predict the selectivity of homogeneous catalysts has received considerable attention in the past years. In these studies often the catalyst structure is varied, but the use of substrate descriptors to rationalize the catalytic outcome is relatively unexplored. To study whether this may be an effective tool, we investigated both an encapsulated and a non-encapsulated rhodium based catalyst in the hydroformylation reaction of 41 terminal alkenes. For the non-encapsulated catalyst, CAT2, the regioselectivity of the acquired substrate scope could be predicted with high accuracy using the Δ13C NMR shift of the alkene carbon atoms as a descriptor (R2 = 0.74) and when combined with a computed intensity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch vibration (IC
C stretch vibration (IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch) the accuracy increased further (R2 = 0.86). In contrast, a substrate descriptor approach with an encapsulated catalyst, CAT1, appeared more challenging indicating a confined space effect. We investigated Sterimol parameters of the substrates as well as computer-aided drug design descriptors of the substrates, but these parameters did not result in a predictive formula. The most accurate substrate descriptor based prediction was made with the Δ13C NMR shift and IC
C stretch) the accuracy increased further (R2 = 0.86). In contrast, a substrate descriptor approach with an encapsulated catalyst, CAT1, appeared more challenging indicating a confined space effect. We investigated Sterimol parameters of the substrates as well as computer-aided drug design descriptors of the substrates, but these parameters did not result in a predictive formula. The most accurate substrate descriptor based prediction was made with the Δ13C NMR shift and IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch (R2 = 0.52), suggestive of the involvement of CH–π interactions. To further understand the confined space effect of CAT1, we focused on the subset of 21 allylbenzene derivatives to investigate predictive parameters unique for this subset. These results showed the inclusion of a charge parameter of the aryl ring improved the regioselectivity predictions, which is in agreement with our assessment that noncovalent interactions between the phenyl ring of the cage and the aryl ring of the substrate are relevant for the regioselectivity outcome. However, the correlation is still weak (R2 = 0.36) and as such we are investigating novel parameters that should improve the overall regioselectivity outcome.
C stretch (R2 = 0.52), suggestive of the involvement of CH–π interactions. To further understand the confined space effect of CAT1, we focused on the subset of 21 allylbenzene derivatives to investigate predictive parameters unique for this subset. These results showed the inclusion of a charge parameter of the aryl ring improved the regioselectivity predictions, which is in agreement with our assessment that noncovalent interactions between the phenyl ring of the cage and the aryl ring of the substrate are relevant for the regioselectivity outcome. However, the correlation is still weak (R2 = 0.36) and as such we are investigating novel parameters that should improve the overall regioselectivity outcome.
Introduction
Enzymes have served as major sources of inspiration for synthetic chemists, as such systems offer levels of selectivity control unattainable using traditional transition metals. Through multiple interactions between the substrate and the enzyme, the regio-, enantio- and chemoselectivity can be controlled for otherwise unselective reactions. As such, several commonplace elements used by enzymes such as a confined space and/or noncovalent interactions have been consciously incorporated into the design of transition metal catalysts.1–15 This has been achieved by incorporating hydrogen bond donors and/or acceptors into the ligand structure to, similar to enzymes, achieve higher selectivity.1,12,13 Alternatively transition metal catalysts have been encapsulated into supramolecular cages to mimic the confined spaces commonly observed in enzymes and the application of encapsulated transition metal catalysts has led to impressive examples of selectivity control for several reactions.16–37Due to the complex shapes of encapsulated catalysts, a small variation in the substrate structure can lead to large variations in the overall catalytic outcome and the catalytic outcome of a single substrate cannot be easily extrapolated to other substrates. Despite this fact, the substrate scope is often not explored extensively in reports discussing encapsulated transition metal catalysts.17,28–31,38,39
To rationalize the catalytic outcome, often DFT calculations combined with analytical techniques are used to rationalize catalytic outcomes and predict the selectivity for novel substrates.40–47 To explain the catalytic outcomes using DFT calculations, all pathways need to be considered for every substrate. However, this is not feasible due to computational cost and computational resources required for large systems, such as when encapsulated transition metal catalysts are studied and/or large amounts of substrates are investigated. Because of this, the catalytic results are often only rationalized afterwards, and methods to predict how additional substrates would react often remain elusive. Therefore, it is desirable to find methods that circumvent elaborate DFT calculations, while being able to predict the catalytic outcome of a large substrate scope with reasonable accuracy.
Recently multivariate data driven approaches have been applied to predict the catalytic outcomes of catalyzed reactions.3,48–60 These methods have received considerable attention as these require less computational power while providing valuable information about catalytic systems studied. To be successful, these methods typically require large data sets. Most often catalyst descriptors are used to devise a mathematical model that accurately describes the catalytic outcome for a range of catalysts for a reaction using the same substrates (Fig. 1). However, substrate descriptors should also be applicable to rationalize the catalytic outcome of a large substrate scope. This would then lead to mechanistic insights as such an approach should demonstrate what substrate moieties affect the selectivity outcome, while the amount of computational resources required is lower as only the substrates have to be modeled.
In the hydroformylation reaction, syngas (H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO) is reacted with an alkene in the presence of a transition metal catalyst to form an aldehyde (Fig. 2). Since the aldehyde can add onto both sides of the alkene, a regio-isomeric mixture is typically formed and as such regioselectivity control is a longstanding challenge for this reaction.61–63
CO) is reacted with an alkene in the presence of a transition metal catalyst to form an aldehyde (Fig. 2). Since the aldehyde can add onto both sides of the alkene, a regio-isomeric mixture is typically formed and as such regioselectivity control is a longstanding challenge for this reaction.61–63
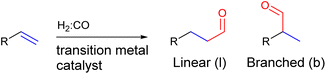 | ||
| Fig. 2 General scheme of the hydroformylation reaction showing that two regio-isomers of the aldehyde product can be formed. | ||
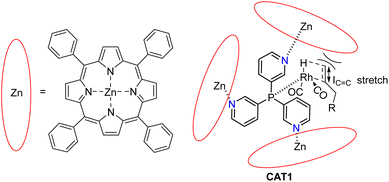
In our group we have reported an encapsulated hydroformylation catalyst based on rhodium using a ligand-template meta-tris pyridylphosphine (P(mPy3)) and three zinc-tetraphenylporphyrin (ZnTPP) building blocks (Scheme 1).19,20
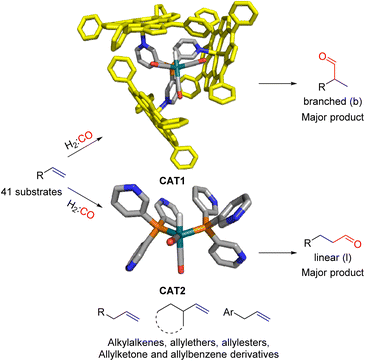 | ||
| Scheme 1 Substrate scope investigation of the encapsulated [Rh(H)(CO)3(P(mPy3(ZnTPP))3)] catalyst (CAT1) in the hydroformylation reaction of terminal alkenes. | ||
The cage formation relies on the selective coordination of the ZnTPP building blocks to the pyridine moieties of the ligand-template P(mPy3). [Rh(H)(CO)3(P(mPy3(ZnTPP))3)] was the active catalyst which formed under syngas (H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
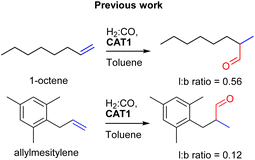
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO) conditions. This encapsulated catalyst offered unique regioselectivity in the hydroformylation reaction as this catalyst is able to convert terminal alkenes such as 1-octene to form an excess of the branched aldehyde (linear/branched ratio = 0.56) (Fig. 3). For internal alkenes, such as 2-octene, the innermost internal aldehyde (outermost/innermost ratio = 1/9) is dominantly formed.21
CO) conditions. This encapsulated catalyst offered unique regioselectivity in the hydroformylation reaction as this catalyst is able to convert terminal alkenes such as 1-octene to form an excess of the branched aldehyde (linear/branched ratio = 0.56) (Fig. 3). For internal alkenes, such as 2-octene, the innermost internal aldehyde (outermost/innermost ratio = 1/9) is dominantly formed.21
Recently, we evaluated the substrate scope of this caged catalyst ([Rh(H)(CO)3(P(mPy3(ZnTPP))3)] (CAT1)) using 41 terminal alkenes and compared the outcomes against an unencapsulated reference catalyst [Rh(H)(CO)2(P(mPy3))2] (CAT2) (Scheme 1).64 For all substrates investigated, CAT1 produces more branched product than CAT2. The degree of branched selectivity enhancement, however, significantly varies between substrates and no clear rationale was discovered for why certain substrates gave a significantly higher regioselectivity enhancement to the branched product than others (Fig. 3). To explain the catalytic outcomes using DFT calculations is not feasible due to computational cost and computational resources required due both to the size of CAT1 as well as the size of the substrate scope.22,65,66 We hypothesized that this data set could be used to apply a substrate descriptor based approach to uncover regioselectivity trends, which ultimately should lead to more insight into the cage effects induced by hydroformylation catalyst CAT1.
As descriptors, steric53 and electronic parameters54–56 as well as IR frequencies57 have been used. These have been successfully applied to predict catalyst properties for several different reactions including organocatalyzed52,58,59 and transition metal catalyzed reactions.53–57,60 Based on a limited parameter set, a mathematical model is constructed. This model shows which parameters, such as steric or noncovalent interactions, largely affect the outcome of the reaction and this allows for the a priori identification of substrates that react with high selectivity with a chosen catalyst as well as entries towards improved catalyst design. An effective substrate descriptor approach for the investigated substrate scope would provide an important tool for identifying substrates that can be converted with high selectivity with a chosen encapsulated transition metal catalyst. Additionally, this could significantly reduce the amount of experiments required to identify reactions that are practically applicable.
Results and discussion
To investigate whether a substrate descriptor approach was able to accurately predict the regioselectivity, we used the catalytic results of the encapsulated [Rh(H)(CO)3(P(mPy3(ZnTPP))3)] catalyst (CAT1) in the hydroformylation reaction of 41 terminal alkenes as a data set.64 As a reference, the catalytic results of an unencapsulated [Rh(H)(CO)2(P(mPy3))2] (CAT2) catalyst were used, which is the catalyst that is formed under the same conditions in the absence of the Zn–porphyrin building blocks. In all cases, two regioisomers were formed; the linear (l) and the branched (b) aldehyde product (Fig. 2). Using the linear/branched ratios of all entries, we calculated the relative reaction barriers (ΔΔE) for CAT1 and CAT2 based on the Boltzmann distribution with kB being the Boltzmann constant and T being the reaction temperature in Kelvin: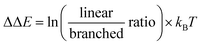 | (1) |
Modeling of a non-encapsulated reference catalyst
We commenced our studies by modeling the catalytic results of CAT2, the unencapsulated catalyst. This was done to create a benchmark and gain insight into what parameters govern the regioselectivity for non-encapsulated catalysts where substrate rotation is not limited. For the substrate parametrization, the catalytic outcomes of CAT2 were plotted against the polarization of alkene moieties of the substrates. It is well known that the polarization of the alkene plays a large role in determining the regioisomeric outcome in the hydroformylation reaction.61,62,67–69As a physical parameter, the difference between the 13C shift of the two olefinic carbon atoms (Δ13C shift) was used and correlated to the selectivity of the hydroformylation reaction with CAT2 (Fig. 4). In previous olefin insertion reactions, this has been identified as a descriptor that strongly correlates with the regioisomeric outcome.55,56,69 Plotting the regioselectivity (ΔΔE) against the Δ13C shift of all substrates evaluated shows a relatively strong correlation with CAT2, demonstrating that for the unencapsulated CAT2 the regioselectivity in the hydroformylation reaction can be predicted with a reasonable accuracy using the Δ13C shift as a substrate descriptor, in line with a previous report.69
 | ||
| Fig. 4 Plot of the experimental regioselectivity expressed in ΔΔE against the Δ13C shift for all substrates studied for the unencapsulated catalyst CAT2. | ||
To improve the accuracy of our predictions, we calculated the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C IR-stretch intensity (IC
C IR-stretch intensity (IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch) for all substrates using DFT calculations as this frequency was proven to be a useful descriptor that accurately predicts the selectivity for some other reactions.52,57,58,70 This was done by calculating the lowest energy structures and subsequently using the Amsterdam Density Functional (ADF) program.71–73 The B3LYP-D3(BJ)74–76 density functional was used together with a small core TZ2P basis set for both the geometry optimizations as well as the frequency calculations.
C stretch) for all substrates using DFT calculations as this frequency was proven to be a useful descriptor that accurately predicts the selectivity for some other reactions.52,57,58,70 This was done by calculating the lowest energy structures and subsequently using the Amsterdam Density Functional (ADF) program.71–73 The B3LYP-D3(BJ)74–76 density functional was used together with a small core TZ2P basis set for both the geometry optimizations as well as the frequency calculations.
ΔΔECAT2 = 0.038Δ13Cshift + 0.021IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch − 0.70 C stretch − 0.70 | (2) |
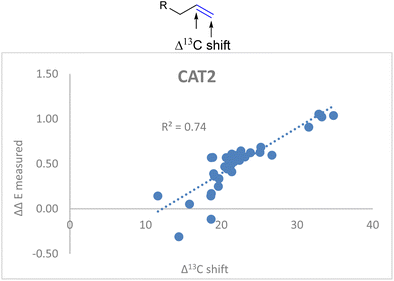
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch in the descriptor formula led to a strong correlation (R2 = 0.86) between the calculated and the observed regioselectivity (Fig. 5). The fact that the regioselectivity in the hydroformylation reaction can be predicted with high accuracy shows that the regioisomeric outcome with CAT2 is mostly governed by alkene polarization, as the IR intensity is mainly governed by the charge redistribution within the bond under specific vibrational transitions.77
C stretch in the descriptor formula led to a strong correlation (R2 = 0.86) between the calculated and the observed regioselectivity (Fig. 5). The fact that the regioselectivity in the hydroformylation reaction can be predicted with high accuracy shows that the regioisomeric outcome with CAT2 is mostly governed by alkene polarization, as the IR intensity is mainly governed by the charge redistribution within the bond under specific vibrational transitions.77
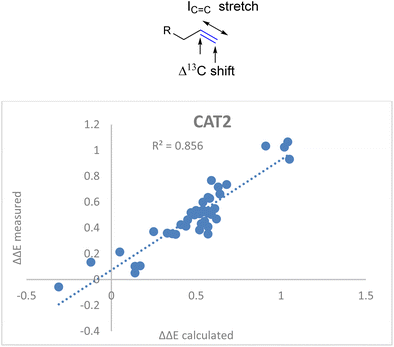 | ||
Fig. 5 Correlation plot of regioselectivity (ΔΔECAT2) predicted versus the experimentally obtained regioselectivity using the Δ13C shift and IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch substrate parameters as indicated in eqn (2). C stretch substrate parameters as indicated in eqn (2). | ||
Modeling of the encapsulated catalyst
Using the models of our non-encapsulated reference catalyst, CAT2, we pursued the modelling of CAT1. For all substrates evaluated, the encapsulated CAT1 provided more of the branched product than the unencapsulated CAT2. Therefore, a lower ΔΔE for all the reaction outcomes with CAT1 compared to CAT2 is obtained. With this energy value we subtracted the ΔΔE with CAT1 from the ΔΔE with CAT2 for every substrate which is a measure of the cage induced selectivity, coined the cage effect:| Cage effect = ΔΔECAT2 − ΔΔECAT1 | (3) |
Also for CAT1 the regioselectivity induced by the catalyst was plotted against the Δ13C shift (Fig. 6). Consistent with our expectations, the correlation was significantly less strong compared to CAT2 using the same parameter (0.35 vs. 0.74).
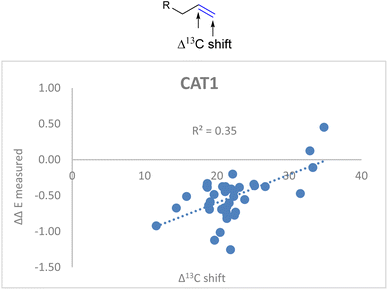 | ||
| Fig. 6 Plot of the experimental regioselectivity expressed in ΔΔE against the Δ13C shift for all substrates studied for the encapsulated catalyst CAT1. | ||
This is in line with the anticipated effect of the confined space around CAT1 as this interacts in a different way when the shape and/or the functional groups on the substrates are altered. Therefore, we hypothesized that models that account for the shape of the substrates could improve the predictive ability of our models. To obtain models that account for the shape of the substrates, we extended the substrate descriptors investigated to Sterimol parameters (Fig. 7), which are parameters that systematically account for the steric influence of the shape of the substrates as reported by Verloop et al.78 Previous work reported by Sigman et al. has shown that for several reactions such descriptors are useful to account for steric effects of functional groups.52–54,58
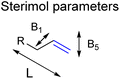 | ||
| Fig. 7 Sterimol parameters acquired to find stronger correlations between substrate properties and selectivity in hydroformylation displayed by CAT1. | ||
We investigated whether such simple steric parameters can account for the interactions such substrates experience with the inner compartment of caged catalyst CAT1. Using the DFT calculated structures of the substrates, we obtained Sterimol parameters. The Sterimol values consist of two width parameters (B1 and B5) and a length parameter (L). The different width parameters were calculated according to the profile of the substituent when viewed down the axis of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. B1 is defined as the minimum width perpendicular to the primary bond axis. This value generally describes the extent of branching at the first carbon center next to the C
C bond. B1 is defined as the minimum width perpendicular to the primary bond axis. This value generally describes the extent of branching at the first carbon center next to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. The B5 parameter describes the maximum width orthogonal to the same axis, which is a degree for how wide the substrate is. L is the total length of the substituent along the C
C bond. The B5 parameter describes the maximum width orthogonal to the same axis, which is a degree for how wide the substrate is. L is the total length of the substituent along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis.
C axis.
In the first instance, the substrate descriptor values were plotted against the regioselectivity of CAT1 and CAT2. The cage effect (expressed in ΔΔE) was also used and the overall R2 values for every parameter are presented in Fig. 8.
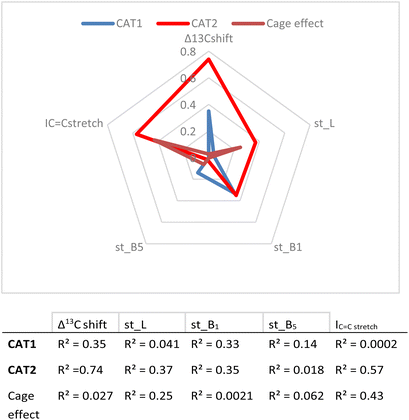 | ||
| Fig. 8 Correlation between descriptors and experimental results (given as R2 values) and a visual representation of parameters investigated. | ||
These values show that better correlations are observed for CAT2 than CAT1 for most substrate descriptors. B1 also correlates with the regioselectivity displayed by CAT1, however, construction of a multiparameter formula with B1 does not result in improved fitting results. The inspection of the substrate scope shows that the B1 parameter mostly reflects di-substitution (B1 ≈ 2.4) or mono-substitution (B1 ≈ 1.8) on the aliphatic carbon atom next to the alkene. However, di-substitution on this carbon atoms is also reflected strongly in Δ13C shift where disubstituted alkenes have a significantly higher Δ13C shift. This also results in a low orthogonality of this parameter to the Δ13C shift, which in turn is reflected by a low correlation between B1 and the cage effect.
Also, L, the substrate length parameter, and B5, the parameter that represents the maximum width of the substrate orthogonal to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, display low correlation values for both catalysts and do not provide useful handles to predict the regioselectivity displayed by these catalysts. Indeed, in our substrate scope investigation, some bulky substrates reacted with exceptionally high branched selectivity (e.g. allylmesitylene, l/b = 0.12) whereas other bulky substrates reacted with low branched selectivity (e.g. 3-(3,5-dimethylphenyl)-1-propene, l/b = 0.71) (Fig. 9), which exemplifies the limitations of employing Sterimol parameters for predicting the catalytic outcome with CAT1. Despite the low correlations observed, we explored correlation equations that included the Sterimol parameters. However, these did not yield significantly better correlations to describe the regioselectivity observed by CAT1 and CAT2 than the equation based on solely the Δ13C shift. This shows that the interactions of the substrates with the cage cannot be simply accounted for with the Sterimol parameters. Most likely, the cage effect of CAT1 involves the precise position of the substrate which is governed by steric hindrance in combination with noncovalent interactions.
C bond, display low correlation values for both catalysts and do not provide useful handles to predict the regioselectivity displayed by these catalysts. Indeed, in our substrate scope investigation, some bulky substrates reacted with exceptionally high branched selectivity (e.g. allylmesitylene, l/b = 0.12) whereas other bulky substrates reacted with low branched selectivity (e.g. 3-(3,5-dimethylphenyl)-1-propene, l/b = 0.71) (Fig. 9), which exemplifies the limitations of employing Sterimol parameters for predicting the catalytic outcome with CAT1. Despite the low correlations observed, we explored correlation equations that included the Sterimol parameters. However, these did not yield significantly better correlations to describe the regioselectivity observed by CAT1 and CAT2 than the equation based on solely the Δ13C shift. This shows that the interactions of the substrates with the cage cannot be simply accounted for with the Sterimol parameters. Most likely, the cage effect of CAT1 involves the precise position of the substrate which is governed by steric hindrance in combination with noncovalent interactions.
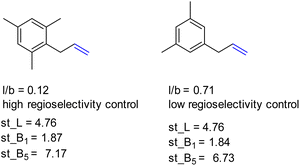 | ||
| Fig. 9 Bulky substrates both display high regioselectivity control as well as low regioselectivity control with CAT1 despite having similar Sterimol parameters. | ||
As the confined space around CAT1 resembles the active site of enzymes, we also explored substrate descriptors derived from computer-aided drug design (CADD) using RDKit (Fig. 10).79 The substrate descriptors investigated included Kappa shape indices (κ1, κ2, κ3),80,81 Chi shape indices (χ0n–3n, χ0v–3v),81 topological polar surface area (TPSA),82 eccentricity,83 plane of best fit (PBF),84 asphericity,85 sphericity, principal moments of inertia (PMI1, PMI2, PMI3, NPR1, NPR2), approximate surface area (LabuteASA), inertial shape factor (ISF),85 spherocity index,85 the number of rotatable bonds. Unfortunately, none of these substrate descriptors that we examined resulted in strong correlations for the regioselectivity outcomes of CAT1, CAT2, or the cage effect.
For the unencapsulated catalyst CAT2 the correlation function significantly improved when the IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch was included. Also, this descriptor correlated well with the cage effect (Fig. 8) and therefore this descriptor was also explored for cage catalyst CAT1. With the IC
C stretch was included. Also, this descriptor correlated well with the cage effect (Fig. 8) and therefore this descriptor was also explored for cage catalyst CAT1. With the IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch included as a substrate descriptor the overall fit for the selectivity displayed by CAT1 indeed improved (R2 = 0.35 vs. 0.52) (Fig. 11).
C stretch included as a substrate descriptor the overall fit for the selectivity displayed by CAT1 indeed improved (R2 = 0.35 vs. 0.52) (Fig. 11).
ΔΔECAT1 = 0.057Δ13Cshift − 0.031IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch − 1.28 C stretch − 1.28 | (4) |
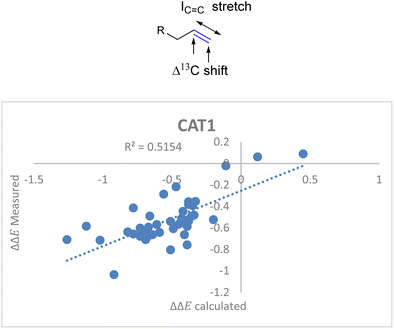 | ||
Fig. 11 Moderate correlation for catalytic outcome with CAT1 and the Δ13C shift and IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch substrate parameters. C stretch substrate parameters. | ||
Surprisingly, the IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch had an opposite sign in the correlation equation for CAT1 as a catalyst. The correlation equation for CAT1 shows that an increase in IC
C stretch had an opposite sign in the correlation equation for CAT1 as a catalyst. The correlation equation for CAT1 shows that an increase in IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch intensity enhances the selectivity for the branched product, whereas the correlation equation for CAT2 predicts that a higher IC
C stretch intensity enhances the selectivity for the branched product, whereas the correlation equation for CAT2 predicts that a higher IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch intensity enhances the selectivity for the linear product. A plausible explanation is that the alkene interacts with the aromatic planes of the walls of the cage as the alkene is in close proximity with the ZnTPP walls, which results in an altered IC
C stretch intensity enhances the selectivity for the linear product. A plausible explanation is that the alkene interacts with the aromatic planes of the walls of the cage as the alkene is in close proximity with the ZnTPP walls, which results in an altered IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch vibration (Fig. 12). Indeed, simple DFT calculations show that the intensity of the IC
C stretch vibration (Fig. 12). Indeed, simple DFT calculations show that the intensity of the IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch is affected in the proximity of an aromatic surface. The regioselectivity predictions are still significantly less accurate for CAT1 than CAT2 (R2 = 0.51 vs. 0.86), indicating that we didn’t capture the cage effect to its full extent yet. Therefore, it is still desirable to acquire substrate and/or substrate/catalyst descriptors for the substrate scope with CAT1 to construct a formula with higher accuracy.
C stretch is affected in the proximity of an aromatic surface. The regioselectivity predictions are still significantly less accurate for CAT1 than CAT2 (R2 = 0.51 vs. 0.86), indicating that we didn’t capture the cage effect to its full extent yet. Therefore, it is still desirable to acquire substrate and/or substrate/catalyst descriptors for the substrate scope with CAT1 to construct a formula with higher accuracy.
 | ||
| Fig. 12 Noncovalent interactions between the alkene moiety and aromatic plane of the cage affect the regioselectivity. | ||
Modeling of allylbenzene subsection with CAT1
Since we struggled to obtain parameters that accurately account for cage–substrate interactions for the entire substrate scope, we set out to acquire parameters with the allylbenzene subset (Fig. 13). | ||
| Fig. 13 Allylbenzene subset investigated to understand the noncovalent interactions between CAT1 and the substrates. | ||
We chose this subset as it is the largest subset investigated and there is a significant variation in the overall regioselectivity outcome with CAT1, while the alkene polarization is comparable for this substrate class. Furthermore, the difference in size between all the substrates does not explain the regioselectivity trends observed. Correlation equations have also been applied to a limited set of similar substrates in other reports.53,54,56,70 This is generally more facile as the catalyst–substrate interactions are generally more similar, making the construction of predictive formulae less complicated. Possibly, due to the diversity of the substrates investigated in this study, the construction of a general formula that accounts for all substrates evaluated is unsuccessful for CAT1. Therefore, better correlations might be obtained with models that only cover certain substrate classes. However, the added value of such models is lower as the formulae only apply to a single class of substrates.
If the alkene polarization (Δ13C shift) of all allylbenzene derivatives against measured ΔΔE is plotted, no correlation between the regioselectivity outcome and the alkene polarization of allylbenzene derivatives is observed (R = 0.011) (Fig. 14).
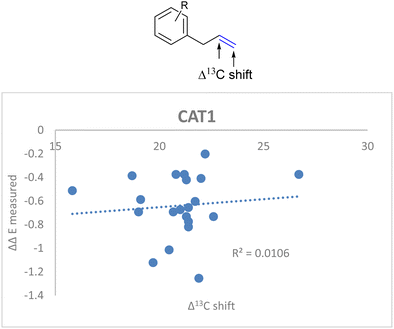 | ||
| Fig. 14 Weak correlation between the alkene polarization (represented by Δ13C shift) and the regioselectivity outcome of allylbenzene derivatives for CAT1. | ||
Since there was no correlation between the polarization of the alkenes and the overall regioselectivity outcome we investigated additional parameters to obtain a better correlation.
DFT calculations in previous reports show that the computed substrates (i.e. 2-octene and allylbenzene) display CH–π interactions with the porphyrin walls of the cage.22,64 Since the aryl ring of CAT1 interacted with the aryl ring of allylbenzene in a DFT study, we hypothesized that the charge of the aryl ring of the allylbenzene derivatives could provide a predictive parameter of the regioselectivity outcome as these interactions differ between substrates and are most likely responsible for the large differences in selectivity control, e.g., the regioselectivity differences between the allylbenzene type substrates (vide supra). Additionally, these substrates show interesting regioselectivity effects, where ortho and para substituents lead to an increased branched selectivity, whereas meta substituents lead to decreased branched selectivity. When combined with the aforementioned IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch we obtained a significantly better correlation when we included the average Voronoi deformation density (VDD) charge of the C3 and C5 positions of the aryl ring as an additional descriptor (Fig. 15, eqn (5)).86 This is in agreement with our previously reported assessment that noncovalent interactions between the aryl ring of the allylbenzene moiety and the aryl ring of the ZnTPP moiety of the catalyst affect the regioselectivity.22,64 It shows that a more negative charge on these positions lowers the ΔΔE, which leads to a higher branched selectivity.
C stretch we obtained a significantly better correlation when we included the average Voronoi deformation density (VDD) charge of the C3 and C5 positions of the aryl ring as an additional descriptor (Fig. 15, eqn (5)).86 This is in agreement with our previously reported assessment that noncovalent interactions between the aryl ring of the allylbenzene moiety and the aryl ring of the ZnTPP moiety of the catalyst affect the regioselectivity.22,64 It shows that a more negative charge on these positions lowers the ΔΔE, which leads to a higher branched selectivity.
ΔΔECAT1 = 0.062Δ13Cshift − 0.036IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch + 2.92VDDmeta + 1.30 C stretch + 2.92VDDmeta + 1.30 | (5) |
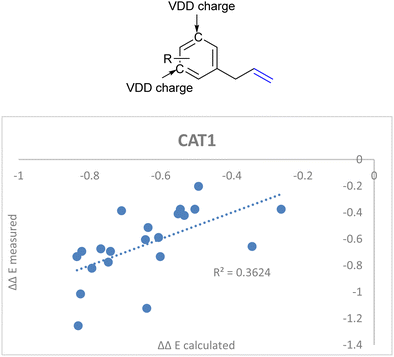 | ||
| Fig. 15 Improved regioselectivity prediction of the allylbenzene derivative substrate scope with the inclusion of VDD charges on the meta-carbon atoms of the aryl rings. | ||
Similar to the formula that covered the entire substrate scope evaluated, inclusion of the Sterimol or CADD derived descriptors did not result in a significant improvement of the predictivity of the constructed mathematical equations. Recently Sigman et al. reported a workflow to predict the selectivity of a class of cavity shaped C–H activation catalysts accurately.51 Several additional descriptors of the catalysts, coined SMART, were included to accurately predict the selectivity of these catalysts. The selectivity of the catalysts investigated in this study are also caused by confinement effects, similar to CAT1.
Conclusions
In this contribution we evaluated if substrate descriptors are useful to predict and understand the regioselectivity outcomes of a substrate scope in the hydroformylation reaction. To study this, an encapsulated catalyst CAT1 and an unencapsulated reference catalyst CAT2 were used to correlate the observed regioselectivity against equations based on different substrate descriptors. For the unencapsulated CAT2, a formula was constructed that described the catalytic outcome with high accuracy (R2 = 0.86) using the Δ13C shift of the alkenes and the IC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch as substrate descriptors. This is in agreement with our assertion that the outcome is mostly determined by the alkene polarization parameters and remote substituents do not significantly affect the catalytic outcome with this catalyst.
C stretch as substrate descriptors. This is in agreement with our assertion that the outcome is mostly determined by the alkene polarization parameters and remote substituents do not significantly affect the catalytic outcome with this catalyst.
A similar approach for the encapsulated catalyst CAT1 showed that the selectivity of the reaction was significantly more difficult to predict and it is clear that additional substrate parameters such as steric interactions between the substrates and the cage as well as noncovalent interactions play a role in determining the overall regioselectivity. Sterimol and molecular dynamics derived parameters were investigated in order to improve the model by accounting for the substrate size. However, the use of such parameters does not lead to improved models for prediction of the selectivity of the reaction. The models used did not account for the noncovalent interactions displayed between substrate moieties and the walls of the cages as well as the relative flexibility of the substrate. As such, we investigated correlation equations using the allylbenzene derivative substrates subset when reacted with CAT1 and found a significant improvement when we included the average VDD charge at the C3 and C5 positions of the allylbenzene derivatives. Despite this improvement, the accuracy of the formula predicting the regioselectivity was still low using these descriptors (R2 = 0.36). As such we are currently investigating additional parameters to be able to accurately predict the regioselectivity of substrates when reacted with CAT1.
Author contributions
PL conceived the project, wrote the manuscript and conducted the data analytical work. DP performed the CADD calculations. JR conceived the project, supervised the project and wrote the manuscript. AK helped write the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr Tristan Bereau and Dr Arghya Dutta are acknowledged for their assistance determining the Sterimol parameters and initial modelling.Notes and references
- J. N. H. Reek, B. de Bruin, S. Pullen, T. J. Mooibroek, A. M. Kluwer and X. Caumes, Chem. Rev., 2022, 122, 12308–12369 CrossRef CAS PubMed.
- S. H. A. M. Leenders, R. Gramage-Doria, B. de Bruin and J. N. H. Reek, Chem. Soc. Rev., 2015, 44, 433–448 RSC.
- F. D. Toste, M. S. Sigman and S. J. Miller, Acc. Chem. Res., 2017, 50, 609–615 CrossRef CAS PubMed.
- D. M. Vriezema, M. C. Aragonès, J. A. A. W. Elemans, J. J. L. M. Cornelissen, A. E. Rowan and R. J. M. Nolte, Chem. Rev., 2005, 105, 1445–1489 CrossRef CAS PubMed.
- M. Raynal, P. Ballester, A. Vidal-Ferran and P. W. N. M. van Leeuwen, Chem. Soc. Rev., 2014, 43, 1660–1733 RSC.
- M. Raynal, P. Ballester, A. Vidal-Ferran and P. W. N. M. van Leeuwen, Chem. Soc. Rev., 2014, 43, 1734–1787 RSC.
- M. J. Wiester, P. A. Ulmann and C. A. Mirkin, Angew. Chem., Int. Ed., 2011, 50, 114–137 CrossRef CAS PubMed.
- L. Catti, Q. Zhang and K. Tiefenbacher, Chem.–Eur. J., 2016, 22, 9060–9066 CrossRef CAS PubMed.
- R. J. Severinsen, G. J. Rowlands and P. G. Plieger, J. Inclusion Phenom. Macrocyclic Chem., 2020, 96, 29–42 CrossRef CAS.
- M. Morimoto, S. M. Bierschenk, K. T. Xia, R. G. Bergman, K. N. Raymond and F. D. Toste, Nat. Catal., 2020, 3, 969–984 CrossRef CAS.
- J. Meeuwissen and J. N. H. Reek, Nat. Chem., 2010, 2, 615–621 CrossRef CAS PubMed.
- P. Dydio and J. N. H. Reek, Chem. Sci., 2014, 5, 2135–2145 RSC.
- H. J. Davis and R. J. Phipps, Chem. Sci., 2017, 8, 864–877 RSC.
- L. J. Jongkind, X. Caumes, A. P. T. Hartendorp and J. N. H. Reek, Acc. Chem. Res., 2018, 51, 2115–2128 CrossRef CAS PubMed.
- S. S. Nurttila, P. R. Linnebank, T. Krachko and J. N. H. Reek, ACS Catal., 2018, 8, 3469–3488 CrossRef CAS PubMed.
- C. J. Brown, F. D. Toste, R. G. Bergman and K. N. Raymond, Chem. Rev., 2015, 115, 3012–3035 CrossRef CAS PubMed.
- T. Gadzikwa, R. Bellini, H. L. Dekker and J. N. H. Reek, J. Am. Chem. Soc., 2012, 134, 2860–2863 CrossRef CAS PubMed.
- C. García-Simón, R. Gramage-Doria, S. Raoufmoghaddam, T. Parella, M. Costas, X. Ribas and J. N. H. Reek, J. Am. Chem. Soc., 2015, 137, 2680–2687 CrossRef PubMed.
- V. F. Slagt, J. N. H. Reek, P. C. J. Kamer and P. W. N. M. van Leeuwen, Angew. Chem., Int. Ed., 2001, 40, 4271–4274 CrossRef CAS PubMed.
- V. F. Slagt, P. C. J. Kamer, P. W. N. M. van Leeuwen and J. N. H. Reek, J. Am. Chem. Soc., 2004, 126, 1526–1536 CrossRef CAS PubMed.
- M. Kuil, T. Soltner, P. W. N. M. van Leeuwen and J. N. H. Reek, J. Am. Chem. Soc., 2006, 128, 11344–11345 CrossRef CAS PubMed.
- V. Bocokić, A. Kalkan, M. Lutz, A. L. Spek, D. T. Gryko and J. N. H. Reek, Nat. Commun., 2013, 4, 2670 CrossRef PubMed.
- M. Jouffroy, R. Gramage-Doria, D. Armspach, D. Sémeril, W. Oberhauser, D. Matt and L. Toupet, Angew. Chem., Int. Ed., 2014, 53, 3937–3940 CrossRef CAS PubMed.
- X. Wang, S. S. Nurttila, W. I. Dzik, R. Becker, J. Rodgers and J. N. H. Reek, Chem.–Eur. J., 2017, 23, 14769–14777 CrossRef CAS PubMed.
- C. Gibson and J. Rebek, Org. Lett., 2002, 4, 1887–1890 CrossRef CAS PubMed.
- D. H. Leung, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2007, 129, 2746–2747 CrossRef CAS PubMed.
- D. H. Leung, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2006, 128, 9781–9797 CrossRef CAS PubMed.
- T. A. Bender, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2019, 141, 11806–11810 CrossRef CAS PubMed.
- M. Otte, P. F. Kuijpers, O. Troeppner, I. Ivanović-Burmazović, J. N. H. Reek and B. de Bruin, Chem.–Eur. J., 2014, 20, 4880–4884 CrossRef CAS PubMed.
- M. Otte, P. F. Kuijpers, O. Troeppner, I. Ivanović-Burmazović, J. N. H. Reek and B. de Bruin, Chem.–Eur. J., 2013, 19, 10170–10178 CrossRef CAS PubMed.
- P. F. Kuijpers, M. Otte, M. Dürr, I. Ivanović-Burmazović, J. N. H. Reek and B. de Bruin, ACS Catal., 2016, 6, 3106–3112 CrossRef CAS.
- M. L. Merlau, M. D. P. Mejia, S. T. Nguyen and J. T. Hupp, Angew. Chem., Int. Ed., 2001, 40, 4239–4242 CrossRef CAS PubMed.
- J. L. Suk, S. H. Cho, K. L. Mulfort, D. M. Tiede, J. T. Hupp and S. B. T. Nguyen, J. Am. Chem. Soc., 2008, 130, 16828–16829 CrossRef PubMed.
- P. Zhang, J. Meijide Suárez, T. Driant, E. Derat, Y. Zhang, M. Ménand, S. Roland and M. Sollogoub, Angew. Chem., Int. Ed., 2017, 56, 10821–10825 CrossRef CAS PubMed.
- R. Gramage-Doria, J. Hessels, S. H. A. M. Leenders, O. Tröppner, M. Dürr, I. Ivanović-Burmazović and J. N. H. Reek, Angew. Chem., Int. Ed., 2014, 53, 13380–13384 CrossRef CAS PubMed.
- Q.-Q. Wang, S. Gonell, S. H. A. M. Leenders, M. Dürr, I. Ivanović-Burmazović and J. N. H. Reek, Nat. Chem., 2016, 8, 225–230 CrossRef CAS PubMed.
- M. Guitet, P. Zhang, F. Marcelo, C. Tugny, J. Jiménez-Barbero, O. Buriez, C. Amatore, V. Mouriès-Mansuy, J.-P. Goddard, L. Fensterbank, Y. Zhang, S. Roland, M. Ménand and M. Sollogoub, Angew. Chem., Int. Ed., 2013, 52, 7213–7218 CrossRef CAS PubMed.
- S. S. Nurttila, W. Brenner, J. Mosquera, K. M. van Vliet, J. R. Nitschke and J. N. H. Reek, Chem.–Eur. J., 2019, 25, 609–620 CAS.
- V. F. Slagt, P. W. N. M. van Leeuwen and J. N. H. Reek, Angew. Chem., Int. Ed., 2003, 42, 5619–5623 CrossRef CAS PubMed.
- P. Dingwall, J. A. Fuentes, L. Crawford, A. M. Z. Slawin, M. Bühl and M. L. Clarke, J. Am. Chem. Soc., 2017, 139, 15921–15932 CrossRef CAS PubMed.
- Y. H. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Acc. Chem. Res., 2016, 49, 750–762 CrossRef CAS PubMed.
- L. Xu, M. Hilton and X. Zhang, J. Am. Chem. Soc., 2014, 136, 1960–1967 CrossRef CAS PubMed.
- Y. Dang, S. Qu, Z. X. Wang and X. Wang, J. Am. Chem. Soc., 2014, 136, 986–998 CrossRef CAS PubMed.
- M. J. Hilton, L. P. Xu, P. O. Norrby, Y. D. Wu, O. Wiest and M. S. Sigman, J. Org. Chem., 2014, 79, 11841–11850 CrossRef CAS PubMed.
- T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586 CrossRef CAS PubMed.
- T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311–1319 CrossRef CAS PubMed.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2019, 119, 2453–2523 CrossRef CAS PubMed.
- M. S. Sigman, K. C. Harper, E. N. Bess and A. Milo, Acc. Chem. Res., 2016, 49, 1292–1301 CrossRef CAS PubMed.
- A. R. Rosales, S. P. Ross, P. Helquist, P. O. Norrby, M. S. Sigman and O. Wiest, J. Am. Chem. Soc., 2020, 142, 9700–9707 CAS.
- J. J. Dotson, L. van Dijk, J. C. Timmerman, S. Grosslight, R. C. Walroth, F. Gosselin, K. Püntener, K. A. Mack and M. S. Sigman, J. Am. Chem. Soc., 2023, 145, 110–121 CrossRef CAS PubMed.
- R. C. Cammarota, W. Liu, J. Bacsa, H. M. L. Davies and M. S. Sigman, J. Am. Chem. Soc., 2022, 144, 1881–1898 CrossRef CAS PubMed.
- J. Werth and M. S. Sigman, J. Am. Chem. Soc., 2020, 142, 16382–16391 CrossRef CAS PubMed.
- K. C. Harper, S. C. Vilardi and M. S. Sigman, J. Am. Chem. Soc., 2013, 135, 2482–2485 CrossRef CAS PubMed.
- C. Zhang, C. B. Santiago, L. Kou and M. S. Sigman, J. Am. Chem. Soc., 2015, 137, 7290–7293 CrossRef CAS PubMed.
- T.-S. Mei, H. H. Patel and M. S. Sigman, Nature, 2014, 508, 340–344 CrossRef CAS PubMed.
- T. S. Mei, E. W. Werner, A. J. Burckle and M. S. Sigman, J. Am. Chem. Soc., 2013, 135, 6830–6833 CrossRef CAS PubMed.
- A. Milo, E. N. Bess and M. S. Sigman, Nature, 2014, 507, 210–214 CrossRef CAS PubMed.
- A. Milo, A. J. Neel, F. D. Toste and M. S. Sigman, Science, 2015, 347, 737–743 CrossRef CAS PubMed.
- A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, 1–11 CrossRef PubMed.
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190 CrossRef CAS PubMed.
- R. Franke, D. Selent and A. Börner, Chem. Rev., 2012, 112, 5675–5732 CrossRef CAS PubMed.
- P. W. N. M. van Leeuwen, C. P. Casey and G. T. Whiteker, Rhodium Catalyzed Hydroformylation, Kluwer Academic Publishers, Dordrecht, 2000 Search PubMed.
- M. Kranenburg, Y. E. M. van der Burgt, P. C. J. Kamer, P. W. N. M. van Leeuwen, K. Goubitz and J. Fraanje, Organometallics, 1995, 14, 3081–3089 CrossRef CAS.
- P. R. Linnebank, A. M. Kluwer and J. N. H. Reek, 2023, submitted.
- I. Jacobs, B. de Bruin and J. N. H. Reek, ChemCatChem, 2015, 7, 1708–1718 CrossRef CAS.
- P. R. Linnebank, A. M. Kluwer and J. N. H. Reek, ChemCatChem, 2022, 14, e202200541 CrossRef CAS.
- B. Breit, Top. Curr. Chem., 2007, 279, 139–172 CrossRef CAS.
- B. Breit and W. Seiche, Synthesis, 2001, 1–36 CrossRef CAS.
- Z. Yu, M. S. Eno, A. H. Annis and J. P. Morken, Org. Lett., 2015, 17, 3264–3267 CrossRef CAS PubMed.
- Z.-M. Chen, M. J. Hilton and M. S. Sigman, J. Am. Chem. Soc., 2016, 138, 11461–11464 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. J. Baerends, T. Ziegler, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, M. Franchini, ADF2017, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2017 Search PubMed.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- L. Dixit, Appl. Spectrosc. Rev., 1984, 20, 159–254 CrossRef CAS.
- A. Verloop, in Drug Design, Academic Press, New York, 1976 Search PubMed.
- RDKit: Open-Source Cheminformatics Software, http://www.rdkit.org, accessed Jan 2023 Search PubMed.
- L. B. Kier and L. H. Hall, Derivation and Significance of Valence Molecular Connectivity, J. Pharm. Sci., 1981, 70, 583–589 CrossRef CAS PubMed.
- L. H. Hall and L. B. Kier, Rev. Comput. Chem., 2007, 2, 367–422 Search PubMed.
- P. Ertl, in Molecular drug properties, 2007, pp. 111–126 Search PubMed.
- M. Petitjean, Applications of the Radius-Diameter Diagram to the Classification of Topological and Geometrical Shapes of Chemical Compounds, J. Chem. Inf. Comput. Sci., 1992, 32, 331–337 CrossRef CAS.
- N. C. Firth, N. Brown and J. Blagg, J. Chem. Inf. Model., 2012, 52, 2516–2525 CrossRef CAS PubMed.
- R. Todeschini and V. Consonni, in Handbook of Chemoinformatics, Wiley-VCH Verlag GmbH, Weinheim, Germany, 2008, pp. 1004–1033 Search PubMed.
- C. Fonseca Guerra, J. W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00023k |
| This journal is © The Royal Society of Chemistry 2023 |