Role of structural dimensionality in the magneto-chiral dichroism of chiral molecular ferrimagnets

Abstract

Here we report on magneto-chiral dichroism (MChD) detected with visible light on the chiral molecular ferrimagnet [{Cr^III(CN)₆}(Mn^IINH₂ala)₃]·3H₂O (X = S, R; NH₂ala = 2-aminoalanine). Single crystals suitable for magneto-chiral optical measurements were grown starting from enantiopure precursors. X-ray diffraction and magnetic measurements confirmed the 3D-helical structure of the material, its absolute configuration, and its ferrimagnetic ordering below 35 K. Absorption and MChD spectra were measured between 520 and 900 nm from room temperature down to 4 K. At 4 K the electronic spectrum features spin-allowed and spin-forbidden transitions of Cr^III centers and metal-to-metal charge transfer bands. The MChD spectra below the magnetic ordering temperature exhibit absolute configuration-dependent MChD signals, whose shape and intensity closely resamble that of a recently investigated 2D-layered chiral ferrimagnet featuring the same building blocks but different chiral ligands and a lower structural dimensionality. By comparing the temperature and magnetic field dependence of the MChD signals in these two chiral molecular ferrimagnets, we unravel the effect of structural dimensionality in MChD and provide chemical design criteria towards highly responsive magneto-chiral optical materials.

---

Matteo Atzori

Matteo Atzori is a CNRS researcher at the Laboratoire National des Champs Magnétiques Intenses (LNCMI – CNRS, Grenoble – France). During the PhD (University of Cagliari, Italy – University of Angers, France), he worked on chiral functional molecular materials showing magnetism and electrical conductivity. Then he worked on the quantum coherence properties of vanadium complexes at the University of Florence (Italy). Currently, he is investigating Magneto-Chiral Dichroism in chiral molecules and materials. Matteo won several awards, including the silver medal of the European Young Chemists’ Award 2018 of EuChemS, and has co-authored more than 40 publications and a book, Functional Molecular Materials.

Introduction

Magneto-chiral dichroism (MChD) represents the ability of chiral molecules and materials to enantioselectively and non-reciprocally absorb unpolarized light when placed in a magnetic field.^1,2 This phenomenon is particularly fascinating because it allows chiral systems to interact with an unpolarized light source thanks to the magnetic field, which is, as unpolarized light, a non-chiral physical entity.^3,4 However, as elegantly demonstrated by Laurence Barron in 1986, achiral physical entities can be combined into chiral ones to permit chiral interactions with chemical systems,^5–7 and MChD represents one of these phenomena. To be more specific, when two enantiomers of a chiral systems are placed in a magnetic field, a given enantiomer can potentially absorb more light than in zero field, generating a positive MChD signal. If this occurs, the other enantiomer will absorb less light than in zero field, providing a negative MChD signal.³ The intensity of this enantioselective differential absorption of light is equal in magnitude for the two enantiomers and provide mirrored MChD spectra, as for natural circular dichroism (NCD).⁸ At the same time, the intensity of the MChD signals is proportional to the magnetization of the sample,⁹ similarly to what observed in magnetic circular dichroism (MCD),^10,11 as a consequence of the intrinsic magnetization-related nature of both MChD and MCD.

It has been proposed, but not yet demonstrated that this light-matter interaction can be potentially used for the optical read-out of magnetic data in magneto-optical disks.^12–14 Compare to what is technologically established using circularly polarized light, the use of chiral materials can permit the replacement of polarized light by a simpler unpolarized light source. While the microscopic parameters that are at the basis of MCD spectral responses of magnetic materials are investigated since several decades,^10,11 those at the origin of MChD are not yet fully understood. This is principally related to two aspects. First, MChD has been experimentally demonstrated 25 years ago¹ but an intense research activity to understand which physico-chemical microscopic parameters are at the basis of this phenomenon started only recently.^14–23 The aim of these studies is to provide a fundamental understanding of MChD and to propose design principles to prepare highly MChD responsive chiral magnetic materials. Second, MChD is a cross effect between natural optical activity (NOA) and magnetic optical activity (MOA).^2,8 The respective contributions of these two complex phenomena are energy and chromophore dependent, making prediction and rationalization of MChD rather difficult.

We have recently reported the magnetic, optical and MChD investigation of a chiral molecular ferrimagnet formulated as [Mn^II(X-pnH)(H₂O)][Cr^III(CN)₆]·H₂O (X = S, R; pn = 1,2-propanediamine) (1), where the paramagnetic Mn^II and Cr^III ions are antiferromagnetically coupled at low temperatures through cyanide-bridging ligands.¹⁵ This interaction provides a long range ferrimagnetic ordering within the bidimensional layers that composes the crystal structure below a critical temperature T_c of 38 K.^24,25 Temperature and magnetic field dependent MChD signals were clearly observed in the visible range of the electromagnetic spectrum, and the most intense signals were associated to the spin-forbidden transitions of Mn^II, which was the only metal chromophore directly coordinated by a chiral ligand.¹⁵ Weaker signals were also evidenced for the spin-allowed transitions of Cr^III but their broadness and weak intensity do not permit to clearly assign them.

Interestingly, the authors that first reported the synthesis, magnetic and structural characterization of this 2D chiral ferrimagnet, also reported another chiral magnetic material formulated as [{Cr^III(CN)₆}(Mn^IINH₂ala)₃]·3H₂O (X = S, R; NH₂ala = 2-aminoalanine) (2).²⁶ This system was obtained using the same building blocks as for 1 with the only exception that the chiral 1,2-propanediamine ligand was substituted with chiral 2-aminoalanine. Despite the ligand change, the coordination environment around the Mn^II and Cr^III centres remains essentially similar, but the overall dimensionality of the crystal structure increases, going from a 2D-layered to a 3D-helical arrangement whose helicity is dictated by the absolute configuration of the chiral ligand.²⁶ Astonishingly, despites the increased dimensionality, 2 shows a very similar magnetic response with respect to 1, with a critical ordering temperature T_c of ca. 35 K.

These two systems constitute therefore an ideal case study to explore the role of structural dimensionality on the MChD response. Indeed, since the coordination environment remains very similar, as well as the magnitude of the magnetic interactions, by performing a temperature and magnetic field dependent MChD investigation one can understand the role of structural dimensionality on the overall MChD response.

Here we recall the main structural features and magnetic properties for the two compounds and we report a full optical and magneto-chiral optical investigation of 2 on oriented single crystals. Finally, we analyse and discuss the obtained results by comparing them to those previously obtained on 1 under the same conditions.

Results and discussion

Material preparation

Compound 2 was prepared according to what was already reported in the literature by reacting enantiopure 2-aminoalanine with MnCl₂·4H₂O and K₃[Cr^III(CN)₆].²⁶ Powder X-ray diffraction analysis performed on microcrystalline samples of 2-(S) and 2-(R) show a very good agreement with respect to the pattern calculated on the basis of the single crystal X-ray data (Fig. S1, ESI†). Slow diffusion (several weeks) of a slightly basic aqueous solution containing (S)- or (R)-2-aminoalanine and MnCl₂·4H₂O in a H₂O:isopropanol solution of K₃[Cr^III(CN)₆] provides orange-brown hexagonal-shape single crystals of 2-(S) or 2-(R) with a good optical quality, a key feature for quantitative measurements of MChD (Fig. S2, ESI†).

Molecular and crystal structure

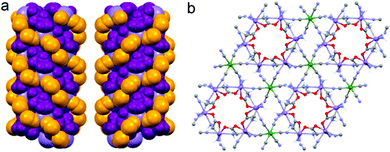
Although the crystal structure of compound 2 was already described,²⁶ here we recall the main features needed to follow the discussion on the magnetic and magneto-chiral optical properties, as well as for the comparison with the crystal structure of 1.

2 crystallizes in the hexagonal chiral space group P6₃ with triple-strand helical chains that develop along the c crystallographic axis. Left- and right-handed helical chirality is observed depending on the absolute configuration of the chiral ligand (R = left-handed, S = right-handed) (Fig. 1(a)). These helical chains are interconnected by hexacyanidochromate(III) building blocks (Fig. 1(b)).

Fig. 1 (a) View of the triple-strand infinite helical chains of 2. The left- and right helicity is dictated by the absolute configuration of the chiral ligand (purple). Cyanide ligands are represented in orange and the Mn^II ions are shown in violet. (b) View of a portion of the crystal structure of 2 along the c crystallographic axis. Color codes: violet, Mn^II; green, Cr^III; red, O; light-blue, N; gray, C; white, H.

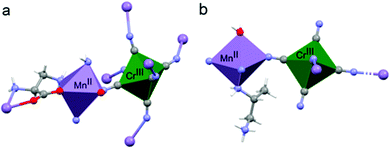
The coordination geometry around the Cr^III center slightly deviates from a pure octahedral O_h symmetry due to the coordination. Each of the six cyanide ligands of the [Cr^III(CN)₆]³⁻ moiety indeed bridges one Mn^II ion, inducing a slight radial distortion around the C₃ symmetry axis (Fig. 2(a)). The Mn^II ions are instead hexacoordinated by two cyanide ligand of two different [Cr^III(CN)₆]³⁻ moieties, and by two 2-aminoalanine ligands. Each 2-aminoalanine ligand bridges two Mn^II ions in a bidentate mode using its three different functional groups (Fig. 2(a)).

Fig. 2 View of a portion of the crystal structure of 2 (a) and 1 (b) where the coordination environment around the Mn^II and Cr^III ions is highlighted for the two compounds. In particular, the distortion of the metal polyhedra is shown. Color codes: violet, Mn^II; green, Cr^III; red, O; light-blue, N; gray, C; white, H.

One Mn^II ion is chelated through one oxygen of the carboxylate and the amino group in 2 position, forming a 5-membered chelate ring, and another Mn^II ion through one oxygen of the carboxylate and the amino group in 3 position forming a 6-membered chelate ring. Overall, four nitrogens and two oxygens surround each Mn^II ion. The resulting octahedron is distorted due to the bidentate coordination mode of the chiral ligand. This is further enhanced by the fact that two different chelate-ring are present. Indeed, both axial and radial distortion of the idealized octahedral geometry are observed (Fig. 2(a)).

As a brief reminder, 1 crystallizes in the orthorhombic chiral space group P2₁2₁2₁ with 2D layers of [Mn^II(X-pnH)(H₂O)][Cr^III(CN)₆] (X = S, R) units that develop in a squared fashion parallel to the ab plane (Fig. 3).¹⁵

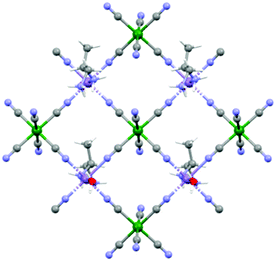Fig. 3 View of the squared 2D-layers of 1 that develops along the ab crystallographic plane. Color codes: violet, Mn^II; green, Cr^III; red, O; light-blue, N; gray, C; white, H.

Similarly to 2, the coordination geometry of the Cr^III center only slightly deviates from an octahedral symmetry due to the coordination (Fig. 2(b)). In this case, only four out of six cyanide ligands act as bridging ligands towards Mn^II centers. The Mn^II centers are hexacoordinated, with four cyanide ligands of four different [Cr^III(CN)₆]³⁻ moieties on the plane, one axial water molecule, and the amino group in 2 position of the chiral 1,2-propanediamine ligand that completes the coordination polyhedron. Also in this case, the Mn^II octahedron is both radially and axially distorted (Fig. 2(b)).

Overall, in both materials the coordination of the chiral ligands around the Mn^II ions induces the highest distortion of metal polyhedron while that of the Cr^III is only slightly affected. It is instructive to remember here that d–d transitions are formally forbidden and should not exhibit optical activity.^27,28 However, the coupling between the d-orbitals of the metal and the molecular orbitals of the ligand allows observation of optical activity. The rotary strength has been correlated to the degree of radial and axial distortion in mononuclear tris-chelated complexes by theoretical calculations.^27,28

Magnetic properties

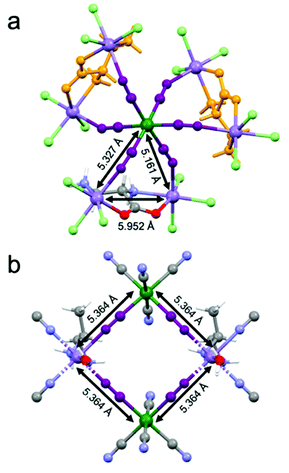
Magnetic measurements as a function of the temperature and the magnetic field have been performed on a microcrystalline sample of 2-(R). They confirm the magnetic behavior previously observed, in particular the ferrimagnetic ordering below 35 K (Fig. S3 and S4, ESI†).²⁶ It is important to recall here that 1 similarly shows ferrimagnetic ordering below 38 K. While 1 shows a square arrangement of paramagnetic ions with a well-defined super-exchange pathway for the magnetic interaction between Mn^II and Cr^III ions mediated by the cyanide ligands whose distance is 5.364 Å (Fig. 4(a)), the situation for 2 is more complex. Indeed, the paramagnetic ions are arranged in a heptanuclear unit where a central Cr^III ions interacts with six Mn^II ions (Fig. 4(b)). The super-exchange pathways between Cr^III and Mn^II are mediated by cyanide ligands and the distances are of 5.327 Å and 5.161 Å as two crystallographic independent Mn^II centers are present. At the same time, a super-exchange interaction between two Mn^II ions is ensured by the bridging chiral ligand. The intermetallic Mn^II⋯Mn^II distance is 5.952 Å, thus comparable to that of the Cr^III⋯Mn^II interaction.

Fig. 4 Super-exchange pathways between paramagnetic centers in 2 (a) and 1 (b) mediated by cyanide (purple) and chiral ligands (orange) with intermetallic distances. A ligand with usual color codes is shown for 2 in panel (a) to better highlights its coordination mode.

On the basis of the super-exchange theory, passing from four- to six-connected Cr^III centers while increasing the dimensionality from a 2D to a 3D structure, one could expect an increase of the ordering temperature.²⁹1 and 2 shows instead very similar magnetic ordering temperatures, thus suggesting that the more complex arrangement of the metal ions and competitive interactions between Mn^II⋯Mn^II and Cr^III⋯Mn^II in 2 compensate the potential gain in the ordering temperature value.^30,31

Optical properties

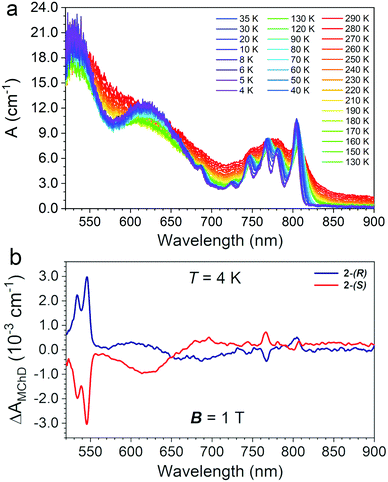
Single-crystals of 2 of ca. 1 mm × 0.8 mm × 0.8 mm (Fig. S2, ESI†) were used to record absorption spectra in transmission mode perpendicularly to the c crystallographic axis as a function of the temperature (290–4 K) in the 520–900 nm spectral range. The temperature variation of the absorption coefficient (A, cm⁻¹) is reported in Fig. 5(a).

Fig. 5 Temperature variation (see legend) of the absorption coefficient A (cm⁻¹) for an oriented single crystal of 2-(R) (a). ΔA at 4.0 K recorded on single crystals of 2-(R) and 2-(S) (see legend) oriented in the same direction (b).

The electronic spectrum at room temperature shows three broad absorption bands centred at ca. λ = 520, 640 and 780 nm, the latter more structured than the others (Fig. 5(a)). By lowering the temperature down to 4 K, the spectrum became better defined and distinct peaks appear. The two intense and broad absorption bands at ca. λ = 520 and 640 nm are assigned to the two low-energy spin-allowed d–d transitions of the octahedral Cr^III centres, ⁴T₁ ← ⁴A₂, and ⁴T₂ ← ⁴A₂, respectively, and the weak intensity peak at ca. 685 nm to the spin-forbidden transition, ²T₂ ← ⁴A₂. At low temperature the absorption at ca. λ = 780 nm appears as a series of narrow peaks that are assigned to a set of metal-to-metal charge transfer (MMCT) transitions.^24,25,32,33 The number and the nature of the observed transitions of 2 are similar to those observed for 1.¹⁵ However, some differences can be highlighted: (i) all bands are broader for 2 with respect to that of 1; (ii) 2 shows a high energy spin-allowed ⁴T₁ ← ⁴A₂ absorption that is red-shifted and more intense with respect that of 1; (iii) the spin-forbidden transitions of the high-spin Mn^II centres that were observed for 1 between 520 and 550 nm are masked in 2 by the red-shifted spin-allowed transition of the Cr^III centres. On the basis of the Tanabe-Sugano diagram for octahedral Cr^III complexes,³⁴ the energy of the lowest energy spin-allowed transition for Cr^III can be used to extract the value of the crystal field parameter Δ_O, 16100 cm⁻¹. The spin-forbidden ²T₂ ← ⁴A₂ transition is rather insensitive to the coordination environment, and indeed, its energy is not changed with respect to that of 1. However, the intensity of the high energy spin-allowed band, which is close to the saturation limit of the detector, do not allow an accurate determination of the λ_max, hence of the B Racah parameter for 2. For 1, the value of Δ_O/B was 37.¹⁵ Finally, the broadening of the MMCT bands in 2 compared to 1 is ascribed the presence of two different Mn^II sites bridged to the Cr^III center.

Magneto-chiral dichroism

MChD measurements on 2-(S) and 2-(R) were performed in transmission mode perpendicularly to the c crystallographic axis using the same single crystals used for absorption measurements. Measurements were performed in the temperature range 4.0–80 K with an alternating magnetic field B (Ω = 0.4 Hz) of ±1.0 T applied along the light propagation vector k. Fig. 5(b) shows a spectrum in the entire investigated range for the two enantiomers at T = 4.0 K, featuring multiple MChD signals. Measurements performed under the same conditions for 2-(S) and 2-(R) provide signals of opposite signs, resulting in mirror image spectra. The most intense and sharp MChD signals are observed in the λ = 520–550 nm range, followed by sharp signals of lower intensity at λ = 770 and 800 nm. A broad and derivative type MChD signal centred at λ = 650 nm of weak intensity is also observed. At first sight, following the band assignments of the absorption spectrum, the most intense MChD signals might be attributed to the ⁴T₁ ← ⁴A₂ spin-allowed transition of Cr^III. To confirm this, it is instructive to compare the low temperature MChD spectrum with that of 1.¹⁵ The MChD spectra of the two compounds show very similar features. Indeed, MChD signals are observed in the same spectral ranges, and show similar ΔA_MChD values. For both systems, the highest intensity signal is found at ca. λ = 545 nm, and provides values of ΔA_MChD of the order of 2.5–3.0 × 10⁻³ cm⁻¹, that of 2 only slightly higher than 1. Accordingly, such comparison contradicts the initial assignment of the most intense MChD signals to the ⁴T₁ ← ⁴A₂ spin-allowed transition of Cr^III, because the energy, shape and intensity of these MChD signals closely resemble those related to spin-forbidden transitions of the Mn^II chromophore in 1, suggesting the same assignment in 2. The signals of lower intensity at lower energy are associated to the MMCT bands, with a broadening of the signals clearly related to that of the originating absorption bands. Finally, though broader and weaker than the others, the MChD signal associated to the spin-allowed ⁴T₂ ← ⁴A₂ Cr^III transition in 2 has sufficiently high intensity to be clearly observed, while for 1 it was at the limit of the spectrometer capabilities.

Overall, this clearly suggests that the key factors that drive the MChD response in chiral magnetic materials are associated to (i) the nature of the chromophores, (ii) the nature of their electronic transitions, and (iii) the distortion of the coordination geometry of the chromophores induced by the chiral ligands, whereas the overall structural dimensionality, that is the relative position of the chromophores in the crystal structure and their connectivity, plays a minor role.

The temperature dependence of ΔA_MChD was investigated for the most intense MChD signals (520–560 nm) for both 2-(S) and 2-(R), and the results are reported in Fig. 6.

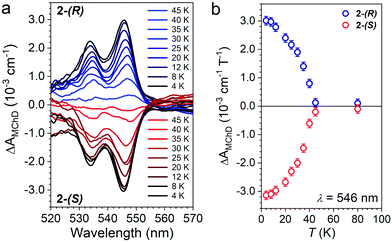Fig. 6 ΔA_MChD at different temperatures (see legend) for both 2-(R) and 2-(S) in the 520–570 nm range (a). Temperature dependence of ΔA_MChD at λ = 546 nm for both enantiomers (b).

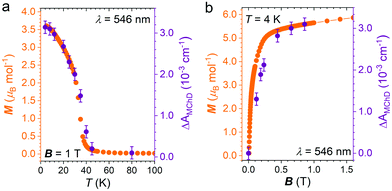
The strongest signal at λ = 546 nm is clearly observed up to 40 K, slightly above the ordering temperature of the material (T_c = 35 K), and then loses intensity. This behavior is in agreement with the proportionality of MChD with the magnetization of the sample.^9,15–17 Unfortunately, given the superposition of the Mn^II and Cr^III absorption bands in this energy region, a quantitative determination of the g_MChD cannot be performed. However, given the relative low intensity of ΔA_MChD with respect to what observed for other highly-responsive systems, the g_MChD should not exceed a few percent per Tesla.

To confirm that the enhancement of the MChD signal is driven by the spontaneous magnetization of the material, ΔA_MChD data were compared to magnetization data collected in the same conditions (Fig. 7).

Fig. 7 Temperature (a) and magnetic field (b) dependence of the ΔA_MChD signal at λ = 546 nm (B = 1.0 T, T = 4.0 K, respectively) for 2-(R) compared to field cooled magnetization data recorded in the same conditions.

Similarly to what observed for 1,¹⁵ magnetic and magneto-optical data for 2 shows the same temperature and magnetic field dependence, demonstrating the close correlation between the magneto-chiral optical response and the magnetization of the material.

Conclusions

In conclusion, we have investigated the optical and magneto-chiral optical properties of a chiral 3D ferrimagnet based on Mn^II and Cr^III ions. This chiral material provides MChD signals associated with the spin-forbidden transitions of Mn^II, MMCT bands and spin-allowed transition of Cr^III, the highest in intensity being the formers. The optical and MChD response as a function of energy, temperature and the magnetic field are very similar to that observed in a chiral 2D ferrimagnet based on the same chromophores and featuring similar coordinating building blocks. This clearly indicates that the immediate environment around the chromophores is a key factor in driving MChD in the visible region of the electromagnetic spectrum, while the dimensionality of the overall structural arrangement, that is the relative position of the chromophores in the crystal structure and their connectivity, does not play a crucial role. This provides a new clue for the design of efficient MChD responsive magneto-chiral optical materials. Chemists can indeed optimize the local chiral environment and the nature of the chromophores to enhance the intensity of the MChD and increase the magnetic ordering temperature by playing with the connectivity and nature of the magnetic centres and the nature of the bridging ligand. Synthetic efforts into these directions are currently underway in our laboratory.

Experimental

Synthesis

Compounds 2-(S) and 2-(R) were prepared following the procedure reported in the literature²⁶ starting from commercially available enantiopure ligands (S)- and (R)-2-aminoalanine (Tokyo Chemical Industry, >97%).

Powder X-ray diffractometry

Wide-Angle Powder X-Ray Diffraction (PXRD) patterns on polycrystalline samples of 2-(S) and 2-(R) were recorded with a Bruker Endevor D8 Advance DAVINCI diffractometer in a theta-theta configuration equipped with a linear detector. The scans were collected within the range 5–40° (2θ) using Cu-Kα radiation (λ = 1.540 Å). Simulated patterns were generated from the atomic coordinates of the single-crystal structure solutions using the Mercury CSD 3.5 software (copyright CCDC, https://www.ccdc.cam.ac.uk/mercury/)³⁵ using a FWHM (full width at half maximum) of 0.10 and a 2θ step of 0.025.

Magnetic measurements

Magnetization and susceptibility measurements were performed in the 4.0–300 K temperature range with an applied magnetic field of 1.0 T on polycrystalline samples of compound 2-(R) with mass of 13.10 mg by using a Quantum Design VSM-SQUID magnetometer. Hysteresis measurements were performed at T = 4 K on the same sample with applied external magnetic field between ±7 T. Susceptibility data were corrected for the sample holders previously measured using the same conditions and for the diamagnetic contributions as deduced by using Pascal's constant tables.³⁶

Magneto-chiral dichroism spectroscopy

MChD spectra were recorded with a home-made multichannel MChD spectrometer operating in the visible and near infrared spectral window (420–1600 nm) between 4.0 and 300 K with an alternating magnetic field B up to ±2 T. A detailed description of the measurement apparatus has been reported elsewhere.³⁷ MChD spectra were acquired on enantiopure single crystals of 2-(R) and 2-(S). The samples were mounted on a titanium sample holder over a 0.8 mm hole diameter centered with respect to a 1.0 mm diameter collimated beam. Measurements were performed in the 4.0–80 K range with an alternating magnetic field B = ±1.0 T and frequency Ω = 0.04 Hz. MChD spectra as a function of the magnetic field were recorded at T = 4.0 K for alternating magnetic fields of different amplitudes (0.0–1.0 T). The MChD signals were obtained at each temperature/field by recording, on average, 30.000 spectra with an integration time, t_int of 5 ms, every 10 ms. Unpolarized light was provided by Thorlabs broadband Tungsten–Halogen (Thorlabs SLS201L) for wide-range Vis-NIR measurements. The data were collected with a OPTOSKY detector equipped with a thermoelectric cooled sensor operating in the 420–1000 nm spectral region with a resolution of 16 bits. Each spectrum was correlated to a specific magnetic field value by a dual channel digitizer (Picoscope 5000B) acquiring simultaneously triggers from the spectrometer and the magnetic field from a Hall effect sensor placed in proximity of the sample. Data are then post-processed as a synchronous detection with a MatLab routine to obtain a MChD spectrum.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the French National Research Agency (ANR) through MONAFER (ANR-18-CE09-0032), and MaChiNaCo (ANR-19-CE09-0018) projects.

Notes and references

1. G. L. J. A. Rikken and E. Raupach, Nature, 1997, 390, 493–494.
2. L. D. Barron and J. Vrbancich, Mol. Phys., 1984, 51, 715–730.
3. M. Atzori, G. L. J. A. Rikken and C. Train, Chem. – Eur. J., 2020, 26, 9784–9791.
4. M. Atzori, C. Train, E. A. Hillard, N. Avarvari and G. L. J. A. Rikken, Chirality, 2021, 33, 844–857.
5. L. D. Barron, J. Am. Chem. Soc., 1986, 108, 5539–5542.
6. L. D. Barron, Chem. Rev., 1986, 15, 189.
7. L. D. Barron, Chem. Phys. Lett., 1986, 123, 423–427.
8. G. L. J. A. Rikken and E. Raupach, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 5081–5084.
9. C. Train, R. Gheorghe, V. Krstic, L.-M. Chamoreau, N. S. Ovanesyan, G. L. J. A. Rikken, M. Gruselle and M. Verdaguer, Nat. Mater., 2008, 7, 729–734.
10. P. J. Stephens, J. Chem. Phys., 1970, 52, 3489.
11. W. R. Mason, A Practical Guide to Magnetic Circular Dichroism Spectroscopy, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2007.
12. L. D. Barron, Nat. Mater., 2008, 7, 691–692.
13. J. R. Galán-Mascarós, Nat. Phys., 2015, 11, 7–8.
14. M. Ceolín, S. Goberna-Ferrón and J. R. Galán-Mascarós, Adv. Mater., 2012, 24, 3120–3123.
15. M. Atzori, I. Breslavetz, K. Paillot, K. Inoue, G. L. J. A. Rikken and C. Train, J. Am. Chem. Soc., 2019, 141, 20022–20025.
16. M. Atzori, K. Dhbaibi, H. Douib, M. Grasser, V. Dorcet, I. Breslavetz, K. Paillot, O. Cador, G. L. J. A. Rikken, B. le Guennic, J. Crassous, F. Pointillart and C. Train, J. Am. Chem. Soc., 2021, 143, 2671–2675.
17. M. Atzori, F. Santanni, I. Breslavetz, K. Paillot, A. Caneschi, G. L. J. A. Rikken, R. Sessoli and C. Train, J. Am. Chem. Soc., 2020, 142, 13908–13916.
18. M. Atzori, H. Ludowieg, M. Cortijo, I. Breslavetz, K. Paillot, P. Rosa, C. Train, J. Autschbach, E. A. Hillard and G. L. J. A. Rikken, Sci. Adv., 2021, 7, eabg2859.
19. K. Taniguchi, S. Kishiue, S. Kimura and H. Miyasaka, J. Phys. Soc. Jpn., 2019, 88, 93708.
20. K. Taniguchi, M. Nishio, S. Kishiue, P.-J. Huang, S. Kimura and H. Miyasaka, Phys. Rev. Mater., 2019, 3, 45202.
21. R. Sessoli, M.-E. Boulon, A. Caneschi, M. Mannini, L. Poggini, F. Wilhelm and A. Rogalev, Nat. Phys., 2015, 11, 69–74.
22. J. Goulon, A. Rogalev, F. Wilhelm, C. Goulon-Ginet, P. Carra, D. Cabaret and C. Brouder, Phys. Rev. Lett., 2002, 88, 237401.
23. D. Mitcov, M. Platunov, C. D. Buch, A. Reinholdt, A. R. Døssing, F. Wilhelm, A. Rogalev and S. Piligkos, Chem. Sci., 2020, 11, 8306–8311.
24. K. Inoue, K. Kikuchi, M. Ohba and H. Ōkawa, Angew. Chem., Int. Ed., 2003, 42, 4810–4813.
25. Y. Yoshida, K. Inoue, K. Kikuchi and M. Kurmoo, Chem. Mater., 2016, 28, 7029–7038.
26. H. Imai, K. Inoue, K. Kikuchi, Y. Yoshida, M. Ito, T. Sunahara and S. Onaka, Angew. Chem., Int. Ed., 2004, 43, 5618–5621.
27. F. E. Jorge, J. Autschbach and T. Ziegler, J. Am. Chem. Soc., 2005, 127, 975–985.
28. F. E. Jorge, J. Autschbach and T. Ziegler, Inorg. Chem., 2003, 42, 8902–8910.
29. M. Atzori and F. Artizzu, Functional Molecular Materials, Pan Stanford Publishing, 2018.
30. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006.
31. J.-P. Launay and M. Verdaguer, Electrons in Molecules, Oxford University Press, 2013.
32. A. B. P. Lever and S. A. Rice, Phys. Today, 1969, 22, 77.
33. Y.-S. Meng, O. Sato and T. Liu, Angew. Chem., Int. Ed., 2018, 57, 12216–12226.
34. Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766–779.
35. C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453–457.
36. G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532.
37. G. Kopnov and G. L. J. A. Rikken, Rev. Sci. Instrum., 2014, 85, 53106.

---

Footnote

† Electronic supplementary information (ESI) available: Additional figures. See DOI: https://doi.org/10.1039/d2tc01777f

---