Open Access Article
Open Access ArticleDiamond surface engineering for molecular sensing with nitrogen—vacancy centers
Erika
Janitz
,
Konstantin
Herb
,
Laura A.
Völker
 ,
William S.
Huxter
,
William S.
Huxter
 ,
Christian L.
Degen
and
John M.
Abendroth
,
Christian L.
Degen
and
John M.
Abendroth
 *
*
Department of Physics, ETH Zürich, Otto-Stern-Weg 1, 8093 Zürich, Switzerland. E-mail: jabendroth@phys.ethz.ch
First published on 1st September 2022
Abstract
Quantum sensing using optically addressable atomic-scale defects, such as the nitrogen-vacancy (NV) center in diamond, provides new opportunities for sensitive and highly localized characterization of chemical functionality. Notably, near-surface defects facilitate detection of the minute magnetic fields generated by nuclear or electron spins outside of the diamond crystal, such as those in chemisorbed and physisorbed molecules. However, the promise of NV centers is hindered by a severe degradation of critical sensor properties, namely charge stability and spin coherence, near surfaces (< ca. 10 nm deep). Moreover, applications in the chemical sciences require methods for covalent bonding of target molecules to diamond with robust control over density, orientation, and binding configuration. This forward-looking Review provides a survey of the rapidly converging fields of diamond surface science and NV-center physics, highlighting their combined potential for quantum sensing of molecules. We outline the diamond surface properties that are advantageous for NV-sensing applications, and discuss strategies to mitigate deleterious effects while simultaneously providing avenues for chemical attachment. Finally, we present an outlook on emerging applications in which the unprecedented sensitivity and spatial resolution of NV-based sensing could provide unique insight into chemically functionalized surfaces at the single-molecule level.
1 Introduction
Nuclear and electron spins within molecules provide invaluable handles with which to identify chemical structures and intermolecular interactions, allowing for visualization of physiological processes and biological matter for medical diagnostics. Moreover, observing the spin dynamics of transient reaction intermediates could provide new insights into spin-selective chemistries. Traditional methods for performing such characterizations include nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR) spectroscopy.1–4 Unfortunately, these conventional techniques commonly rely on large spin ensembles to overcome low thermal polarization and suffer from poor detection efficiency, which preclude the study of dilute spin samples.5–7 In addition, spatial resolution is hampered by the challenge of applying large magnetic gradients with nanoscale precision.8,9 Therefore, the grand goal of studying individual molecules (spins) requires a fundamentally different experimental approach.One such approach replaces traditional NMR and EPR detectors with single, individually addressable quantum spins, which are capable of detecting the minute magnetic fields generated by nuclei or unpaired electrons in nearby molecules.10,11 In particular, the nitrogen—vacancy (NV) center in diamond has emerged as a promising candidate sensor for molecular analysis due to its exquisite magnetic-field sensitivity, nanoscale spatial resolution, biocompatibility, and operational capacity under ambient conditions.12–20 Already in the context of chemical sensing, the atomic scale of such defects has been exploited to probe nanotesla magnetic fluctuations with nanoscale resolution,21,22 facilitating the study of dilute protein assemblies,23,24 DNA,25 and paramagnetic species26 with single NVs, as well as detection of NMR chemical shifts in proximal molecules.27–29 However, the weak dipolar fields generated by target spins decay rapidly with target—sensor separation, motivating the use of near-surface NVs and direct molecular functionalization of the diamond surface. In such cases, the exquisite sensitivity of the NV center presents a challenge in the presence of surface noise, which degrades charge stability and spin coherence for shallow defects.30,31 Thus, improving near-surface NV properties while simultaneously enabling chemical functionalization of the diamond surface represents a critical multidisciplinary challenge.
This Review begins with a tutorial-style introduction to the NV center electronic structure and sensing properties, focusing on detection of magnetic fields since it is the most prevalent sensing modality. We include a brief complementary summary of electric-field, strain, and temperature sensing, which may prove useful in future surface-chemistry characterization. We follow with a discussion of measurement sensitivity and other relevant figures of merit, elucidating which experimental parameters are most important for chemical characterization with shallow defects. Next, we explore the origins of instabilities that plague near-surface NV centers along with experimental progress toward mitigating these effects. Focus is given mainly to experiments on NV centers hosted in bulk diamond materials as opposed to scanning probe experiments and nanodiamonds, although, we note that many of the surface engineering techniques described here can be applied to those systems. Ultimately, applications in chemical sciences require precise and optimal placement of analytes on the diamond surface; we therefore highlight advances in chemical functionalization techniques that are compatible with near-surface NVs. This discussion is accompanied by a survey of measurement-based strategies for further improving detection sensitivities. Finally, we combine the aforementioned chemical toolbox and library of quantum control strategies to offer a perspective on untapped applications for NV-based quantum sensing of chemical systems.
2 Quantum sensing with the NV center
The NV center is the most widely used and best understood crystallographic defect in diamond.32 Its utility as a quantum sensor stems from a number of valuable properties: (i) atomic size, which provides nanoscale resolution, (ii) energetic coupling to a variety of physical quantities, (iii) long spin lifetimes (even at room temperature), (iv) coherent spin-state manipulation using microwave or optical fields, and (v) spin readout via spin-dependent fluorescence. In this section, we will introduce the NV center, discuss its basic sensing properties, and walk through several canonical sensing schemes with the goal of elucidating which sensor parameters are critical in the NV-sensing community.2.1 Physical and electronic structure of the NV center
The NV center comprises a substitutional nitrogen atom and adjacent vacancy occurring along the 〈111〉-family of crystallographic directions (Fig. 1a).16 Consequently, the NV center has threefold C3v symmetry, where the z-axis is typically defined along the nitrogen—vacancy bond and the x-axis points orthogonally towards one of the three carbons closest to the vacancy. In its neutral state, five electrons contribute to the net electronic spin; one from each of the three carbon dangling bonds and two from the nitrogen lone pair.33 When negatively charged by an additional electron, it develops a S = 1 spin character, which is essential for its use as a quantum sensor.16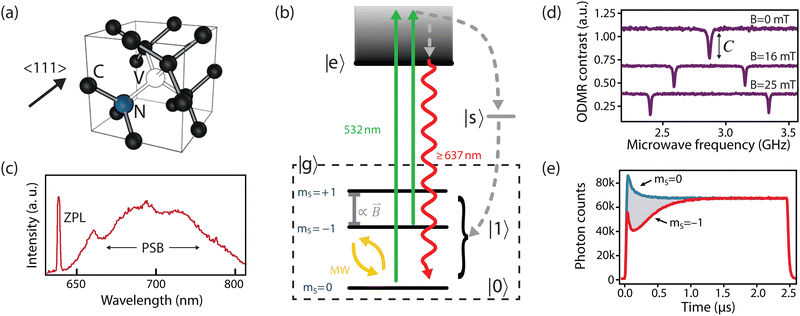 | ||
| Fig. 1 The NV center. (a) Crystallographic structure. (b) Simplified NV electronic structure including ground-state fine structure. (c) NV low-temperature emission spectrum. (d) Continuous-wave optically detected magnetic-resonance (CW ODMR) measurements corresponding to different on-axis DC magnetic fields (B0). Continuous optical and microwave excitation is applied to the NV and the microwave frequency is scanned across ground-state splitting. Dips in fluorescence with contrast C appear when the microwave frequency is resonant with the transitions between ms = 0 and ms = ±1. (e) Transient (time-resolved) spin-dependent fluorescence measurements for an NV center prepared in either the ms = 0 or ms = −1 spin states. (c) Adapted from ref. 34, Copyright 2006 Wiley-VCH Verlag GmbH & Co. KGaA. | ||
The relevant low-energy states of the NV lie within the band gap of diamond, hosting an electronic ground-state (|g〉) with orbital-singlet, spin-triplet character (Fig. 1b). This state couples to the environment according to the ground-state Hamiltonian,16,35 which can be written as
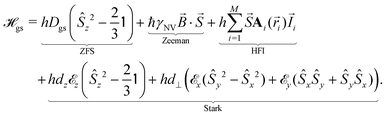 | (1) |
![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) = [Ŝx,Ŝy,Ŝz] are the spin-1 operators,
= [Ŝx,Ŝy,Ŝz] are the spin-1 operators, ![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) is the nuclear spin operator and
is the nuclear spin operator and 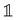 is the identity operator. The simplified Hamiltonian in eqn (1) is spanned by the three S = 1 spin states: |ms = 0〉, |ms = +1〉, and |ms = −1〉, and is grouped into four terms. First, there is a zero-field splitting (ZFS) term caused by electron spin–spin interaction, which shifts the |ms = ±1〉 states in energy by Dgs = 2.87 GHz relative to |ms = 0〉. The second term describes the Zeeman interaction for the |ms = ±1〉 states, which is used to lift their degeneracy in quantum sensing experiments (Section 2.3); most commonly, the anisotropy of the interaction is neglected and the energy splitting is given by the product of the gyromagnetic ratio of the NV center γNV and the strength of the magnetic field. Here, the gyromagnetic ratio is γNV = γe (1 + 357(74) ppm) = 2π × 28.0345(28) GHz T−1
is the identity operator. The simplified Hamiltonian in eqn (1) is spanned by the three S = 1 spin states: |ms = 0〉, |ms = +1〉, and |ms = −1〉, and is grouped into four terms. First, there is a zero-field splitting (ZFS) term caused by electron spin–spin interaction, which shifts the |ms = ±1〉 states in energy by Dgs = 2.87 GHz relative to |ms = 0〉. The second term describes the Zeeman interaction for the |ms = ±1〉 states, which is used to lift their degeneracy in quantum sensing experiments (Section 2.3); most commonly, the anisotropy of the interaction is neglected and the energy splitting is given by the product of the gyromagnetic ratio of the NV center γNV and the strength of the magnetic field. Here, the gyromagnetic ratio is γNV = γe (1 + 357(74) ppm) = 2π × 28.0345(28) GHz T−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) differing only slightly from the free electron value as typical for carbon-based materials.36–38 The third term of
differing only slightly from the free electron value as typical for carbon-based materials.36–38 The third term of 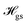 includes coherent coupling to M proximal nuclear spins via the hyperfine interaction (HFI). The hyperfine tensor Ai(
includes coherent coupling to M proximal nuclear spins via the hyperfine interaction (HFI). The hyperfine tensor Ai(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i) comprises a dipolar component and a contact contribution for nearby nuclear spins. Finally, the fourth term describes the coupling to both electric fields
i) comprises a dipolar component and a contact contribution for nearby nuclear spins. Finally, the fourth term describes the coupling to both electric fields ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) and strain
and strain ![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) ,
, 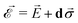 , which impact the NV center through electric dipole interaction, spin–spin interaction, and piezoelectric coupling (described by the tensor d), all of which distort the electron orbitals.35,39,239 Consequently, the three-dimensional structure (and C3v symmetry) of the NV necessitates a directional dependence on
, which impact the NV center through electric dipole interaction, spin–spin interaction, and piezoelectric coupling (described by the tensor d), all of which distort the electron orbitals.35,39,239 Consequently, the three-dimensional structure (and C3v symmetry) of the NV necessitates a directional dependence on 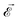 . The coupling is mediated via the ground-state electric susceptibility parameters of the NV center dz = 3.5 × 10−3 Hz (V m−1)−1
. The coupling is mediated via the ground-state electric susceptibility parameters of the NV center dz = 3.5 × 10−3 Hz (V m−1)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and d⊥ = 0.165 Hz (V m−1)−1.41 An additional perpendicular electric term (proportional to the coupling parameter
40 and d⊥ = 0.165 Hz (V m−1)−1.41 An additional perpendicular electric term (proportional to the coupling parameter 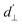 ) is omitted from eqn (1), as it can be ignored when
) is omitted from eqn (1), as it can be ignored when 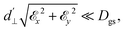 35 which is the case in most experiments.
35 which is the case in most experiments.
In addition, the NV center is optically addressable, with an excited state (|e〉, Fig. 1b) located 1.945 eV (637 nm) above the ground state. This state has spin-triplet, orbital-doublet character (see other reviews for a detailed description16,32,42,43) resulting in a fine structure containing six energy levels, which can be resolved under cryogenic conditions (T < 10 K).44 At elevated temperatures, these orbitals undergo rapid averaging caused by the dynamic Jahn–Teller effect,44,45 resulting in an effective three-level (spin-triplet) system at room temperature. In either case, decay from the NV excited state exhibits spin-dependent fluorescence (discussed in Section 2.2) that is exploited for spin-state readout in most NV-based quantum sensing schemes.
2.2 Photophysics and sensing properties
An ideal quantum sensor would offer mechanisms for coherent control of the sensor state, as well as methods for efficient state preparation and readout. Such a system can be realized within the NV ground state using the ms = 0 and one of the ms = ±1 states (hereafter generalized as |0〉 and |1〉, Fig. 1b) by applying a magnetic field along the z-axis to split the ms = ±1 energy levels (see Fig. 1d). Impressively, resonant microwave fields have been used to achieve universal quantum control within the ground-state manifold13 with fidelities exceeding 99%.46Furthermore, the NV center optical transitions can be leveraged for initializing and reading out the spin state.13,47 Excitation to the excited state is typically achieved using an off-resonant laser (usually ∼532 nm, see green arrows in Fig. 1b). The resulting NV fluorescence spectrum (radiative decay from the excited state to the ground state) comprises a zero phonon line (ZPL, 3% of emission)48 and a broad phonon sideband (PSB, 97% of emission) that extends to 800 nm49 (see red arrow in Fig. 1b and c). Such off-resonant schemes allow for spin preparation and readout using an intermediate singlet state (|s〉, see Fig. 1b): ms = ±1 spin projections are more likely to decay non-radiatively from the excited state into |s〉, from which there is a roughly equal probability to decay (non-radiatively) to any spin projection in the ground state (grey arrow in Fig. 1b).50,51 Consequently, continuous 532 nm optical illumination results in a net ground-state spin polarization into ms = 0.50 Such spin polarization is illustrated in Fig. 1e, where both spin states reach the same fluorescence levels after ∼1 μs of laser excitation. Moreover, this non-radiative decay process provides a readout mechanism for the spin state since it yields reduced fluorescence for ms ± 1 states with up to ∼40% contrast (Fig. 1d and e).52 The simplest experiment demonstrating this phenomenon is continuous-wave optically detected magnetic resonance (CW ODMR), in which microwave and laser excitation are applied simultaneously. When the microwave frequency is resonant the splittings between |ms = 0〉 and |ms = ±1〉, population is transferred and a reduction in fluorescence is observed (Fig. 1d).
The aforementioned preparation, control, and readout mechanisms for the NV offer a powerful toolbox for detection of environmental signals. In practice, sensing applications benefit from several additional experimental constraints: (i) proximity to the sensing target for increased signal and spatial resolution, (ii) long measurement times for maximizing signal integration and spectral resolution, and (iii) efficient mechanisms for spin preparation and readout of the sensor. In the following, we describe relevant sensing properties that are directly influenced by these experimental constraints.
First, we note that the signal strength and detection volume of an NV sensor scales sensitively with experimental geometry, namely with the NV–target distance d. Indeed, for high-spatial-resolution detection of rapidly decaying signals, this distance must be minimized through both the NV–interface distance and the interface–target distance. Thus, there has been significant effort toward deterministic fabrication of near-surface NVs for sensing applications, which are outlined in Section 3.1. Furthermore, diamond surface functionalization methods yielding minimal stand-off distance are discussed in detail in Section 4.
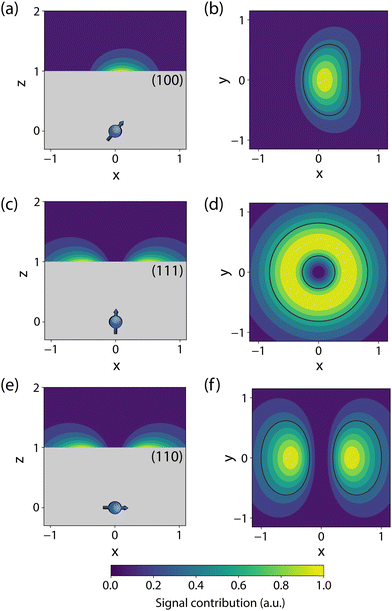
The sensor spatial resolution is parameterized by the NV sensing volume, which depends on the specific protocol used and the NV orientation,53 and scales as V = (0.98d)3 for a (100)-terminated diamond. Fig. 2 shows an example sensitivity profile for an echo-like variance detection scheme (protocol details in Section 2.3). The regions outlined in black contribute 50% of the B2rms signal (or equivalently 70% of Brms) for a monolayer of spins on the diamond surface. The specific details of the sensing scheme play an important role, e.g., for phase canceling effects. In general, such sensitivity maps can be obtained by numerically evaluating the signal contribution of a single spin at every location of the diamond surface for a given measurement protocol. In addition, these maps vary strongly with the NV-center crystallographic orientation and cut of the diamond (the surface plane), motivating careful consideration of the substrate.53
Next, the measurement time Tm impacts signal integration and spectral resolution, and is fundamentally limited by the spin lifetimes of the NV center (either T1, 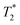 or T2 depending on the measurement sequence). The largest of these values is the spin–lattice relaxation lifetime T1 (also known as the longitudinal relaxation lifetime), which characterizes the time for the spin population to reach thermal equilibrium. Impressively, spin–lattice relaxation times within the ground-state manifold can reach a few milliseconds at room temperature54 and hours at 4 K.55 In contrast,
or T2 depending on the measurement sequence). The largest of these values is the spin–lattice relaxation lifetime T1 (also known as the longitudinal relaxation lifetime), which characterizes the time for the spin population to reach thermal equilibrium. Impressively, spin–lattice relaxation times within the ground-state manifold can reach a few milliseconds at room temperature54 and hours at 4 K.55 In contrast, 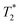 and T2 refer to the transverse relaxation or spin-coherence lifetimes, which are theoretically limited to 2T1 although they are typically much shorter.
and T2 refer to the transverse relaxation or spin-coherence lifetimes, which are theoretically limited to 2T1 although they are typically much shorter. 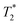 refers to the DC coherence decay time and T2 is used to indicate general, pulsed (AC) coherence decay times. Spin-coherence times of T2 > 1 ms at room temperature56 and T2 ∼ 1 s at 4 K55 have been achieved using multi-pulse experiments (see Section 5). In practice, low-frequency noise leads to faster dephasing, resulting in
refers to the DC coherence decay time and T2 is used to indicate general, pulsed (AC) coherence decay times. Spin-coherence times of T2 > 1 ms at room temperature56 and T2 ∼ 1 s at 4 K55 have been achieved using multi-pulse experiments (see Section 5). In practice, low-frequency noise leads to faster dephasing, resulting in 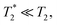 which limits the ability to measure DC signals.
which limits the ability to measure DC signals.
Furthermore, the spectral resolution Δf is an additional consideration for signals that may exhibit closely spaced resonances, such as detection of small chemical shifts, hyperfine couplings, or even spurious harmonics.57,58 For relatively simple sensing protocols, such as those described in the following section, Δf is limited by the coherence lifetime of the NV center and sensing protocol (Δf ∼ 1/T2). However, frequency resolution can be made arbitrarily small59,60 and it is possible to decouple the NV coherence time such that resolution is only constrained by the target spin coherence time,61,62 which can be significantly longer (see Section 5).
Next, the magnetic-field sensitivity improves for increased spin initialization fidelity. Off-resonant, optical spin polarization efficiency for deep NV centers depends on the applied laser power and can approach ∼80%.50 However, we note that this value can vary considerably for shallow defects due to charge instability.31 Promisingly, logic-based charge initialization (of the negative NV− state, see Section 3.2.1) has been employed to increase the average spin initialization fidelity of near-surface defects, with values approaching unity.31 Consequently, we ignore this quantity in subsequent calculations.
Finally, the readout fidelity F quantifies the ability to measure the spin state of the NV at the end of a single experiment, with F = 1 corresponding to an ideal, single-shot readout. This value varies considerably for different experimental conditions, and is therefore explored extensively in this text. Since quantum sensing experiments often employ repeated measurements for statistical averaging, a larger readout fidelity can speed up experiments significantly. For off-resonant readout, the fidelity is given by63,64
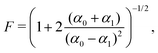 | (2) |
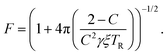 | (3) |
2.3 Magnetic sensing
The vast majority of NV sensing focuses on magnetic interactions owing primarily to its strong coupling constant (γNV), which impacts detection of external fields as well as the strength of the (dipolar) hyperfine interaction. In the following section, we will explore the sensitivities obtained for some of the simplest detection protocols, including DC and AC schemes with the Ramsey and spin-echo experiments, as well as T1 and T2 relaxation experiments. While these represent only a small fraction of possible sensing schemes, they illustrate which experimental parameters should be considered and optimized when implementing an NV sensor.For these examples, we simplify eqn (1) to include only contributions related to a small, time-dependent magnetic field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (t) and a relatively large magnetic-field bias B0 along the z-axis of the NV center, yielding
(t) and a relatively large magnetic-field bias B0 along the z-axis of the NV center, yielding
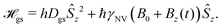 | (4) |
| e± = hDgs ± ħγNV (B0 + Bz(t)). | (5) |
In this Review, we consider a simplified sensor utilizing a two-level subspace spanned by the |ms = 0〉 and one of the |ms = ±1〉 states, resulting in the following effective Hamiltonian
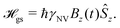 | (6) |
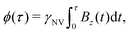 | (7) |
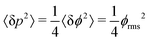 is measured.
is measured.
The SNR of slope-detection-based experiments is defined as SNR = δp/σp, where 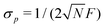 is a combination of the quantum projection noise for N experimental repetitions and the classical readout noise associated with the finite readout efficiency (described by F).10
is a combination of the quantum projection noise for N experimental repetitions and the classical readout noise associated with the finite readout efficiency (described by F).10
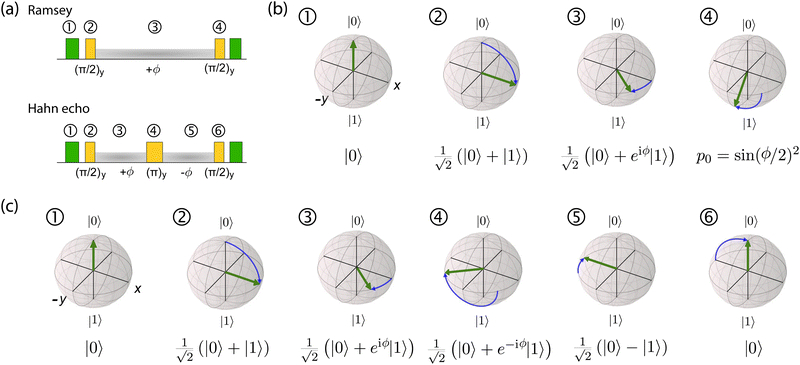
This analysis can be applied directly in determining the sensitivity of the Ramsey experiment,69 which is one of the simplest methods for determining a DC magnetic field of the form Bz(t) = BDC. Following eqn (7), such a field would result in an acquired phase of ϕ(τ) = γNVBDCτ (Fig. 3a). Subsequent conversion to NV population followed by slope detection yields δp = γNVτδBDC/2 with 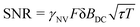 for a total experiment duration T = Nτ. The sensitivity can then be calculated as
for a total experiment duration T = Nτ. The sensitivity can then be calculated as 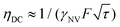 , which is optimized by maximizing the acquisition time τ. For the Ramsey experiment, τ is fundamentally limited to the natural dephasing time of the sensor spin
, which is optimized by maximizing the acquisition time τ. For the Ramsey experiment, τ is fundamentally limited to the natural dephasing time of the sensor spin 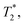 resulting in a minimum sensitivity of
resulting in a minimum sensitivity of
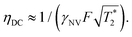 | (8) |
While Ramsey experiments are ideal for sensing DC fields, they are ill-suited for detection of signals that vary quickly compared to τ since the acquired phase is averaged away over the course of the measurement. For detection of AC magnetic fields, the canonical spin-echo experiment70 incorporates an intermediate (π)y pulse (Fig. 3b) that flips the spin, allowing for an effective reversal of the detected field Bz(t) according to
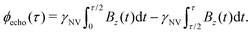 | (9) |
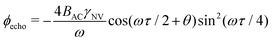 . This quantity is maximized for ω = 2π/τ and θ = 0, resulting in ϕecho = 2BACγNVτ/π. The sensitivity can then be calculated as
. This quantity is maximized for ω = 2π/τ and θ = 0, resulting in ϕecho = 2BACγNVτ/π. The sensitivity can then be calculated as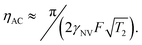 | (10) |
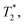 resulting in an improvement in slope-detection sensitivity of
resulting in an improvement in slope-detection sensitivity of 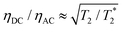 .
.
Similarly, the sensitivity for variance detection of an AC field can be calculated from 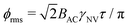 and SNR = 〈δp2〉/σp resulting in
and SNR = 〈δp2〉/σp resulting in
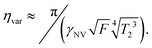 | (11) |
Complementing these widely used DC and AC measurement techniques, relaxometry71,72 offers a sensing modality for detecting magnetic and electric noise at ω01 = e±/ħ, the frequency splitting between |ms = 0〉 and |ms = ±1〉. While the Ramsey and spin-echo protocols operate in the 0 Hz (DC) to <1 GHz regimes, ω01 may exist in the few GHz regime, extending the frequency range over which NV sensors can be employed.73,74
In such experiments, the system is initialized to |0〉 and allowed to evolve for time τ. Subsequently, δp is measured, displaying an exponential decay as a function of time with rate
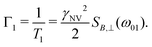 | (12) |
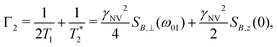 | (13) |
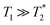 such that
such that 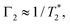 yielding the natural dephasing time observed in Ramsey experiments. Indeed, this decay rate can be thought of in terms of the rms phase previously mentioned in the context of variance detection, where ϕrms2 = 2Γτ. Moreover, extension of this technique with multi-pulse sequences (such as spin-echo or the dynamical decoupling sequences described in Section 5) enable measurements of SB,z for non-zero ω.77,78
yielding the natural dephasing time observed in Ramsey experiments. Indeed, this decay rate can be thought of in terms of the rms phase previously mentioned in the context of variance detection, where ϕrms2 = 2Γτ. Moreover, extension of this technique with multi-pulse sequences (such as spin-echo or the dynamical decoupling sequences described in Section 5) enable measurements of SB,z for non-zero ω.77,78
2.4 Electric sensing
Electric-field sensing with NV centers is possible through a piezoelectric coupling that produces a Stark shift in the NV resonance levels.32,35,39,79 While such schemes suffer from poor sensitivities (in comparison to magnetic detection), bulk and surface charge screening,80,81 and complications from strain interactions, electric-field sensing may prove useful for the chemical sciences. For example, the NV is capable of detecting surface electrons in this manner75,76 and has enabled the mapping of a single electron via its electric field from a distance of roughly 25 nm.82 Consequently, improved surface preparation techniques may enable sensing of electrons involved in various chemical processes. Additionally, measurements of local strain83 and local band bending80 would inform the fabrication of stable and shallow NV centers. Furthermore, electric-field sensing could complement magnetic sensing of surface molecules, providing a route to disentangle signal contributions from magnetic fields (arising from electron spins and currents) and electric fields (due to electron charge).An electric-field sensor can be realized using a single energy-level transition (Section 2.3) with a sensitivity defined similarly to those of magnetic-field protocols where the electric susceptibility parameters (dz and d⊥) serve the same purpose as the gyromagnetic ratio (γNV). With established techniques for sensing DC and AC electric fields with deeply implanted NV centers,41,84,85 current research efforts are focused on nanoscale sensing of external electric fields with shallow NV centers.86–88
In this section, we will highlight two common sensing schemes for measuring electric fields. Both schemes derive from a second order perturbation theory under the assumption of ħγNVBi ≪ hDgs and neglecting nuclear spin coupling.35,84 For simplicity, we also ignore contributions from strain; however, we note that in the high-strain limit 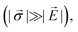 electric-field sensing is only possible along the strain direction.
electric-field sensing is only possible along the strain direction.
The first scheme for electric-field sensing requires a weak magnetic bias field along the z-axis of the NV center (B0 = Bz). In the presence of an electric field, the transition energies are
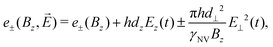 | (14) |
The second scheme employs a weak perpendicular magnetic bias field (B0 = B⊥ = (Bx2 + By2)1/2) on the NV center. In this configuration, the transition energies are
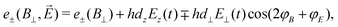 | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φB = By/Bx and tan
φB = By/Bx and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φE = Ey(t)/Ex(t)) allows for control over the electric-field detection axis through variation of φB.84 Since d⊥/dz ∼ 47, this detection scheme is significantly more sensitive to perpendicular electric fields; consequently, the Ez term is often excluded for simplicity.
φE = Ey(t)/Ex(t)) allows for control over the electric-field detection axis through variation of φB.84 Since d⊥/dz ∼ 47, this detection scheme is significantly more sensitive to perpendicular electric fields; consequently, the Ez term is often excluded for simplicity.
2.5 Additional sensing modalities
The NV center is susceptible to additional physical quantities through the dependencies of the Hamiltonian coupling terms; for example, the ZFS splitting is both a function of temperature and pressure (Dgs (T, P)).89,90 Consequently, careful attention must be taken to correctly attribute energy-level shifts that occur under non-ambient experimental conditions, e.g., elevated temperatures or pressures required for specific reactions or temperature changes resulting from exothermic and endothermic reactions.Lastly, it is also possible to utilize the excited-state coupling terms, which can greatly differ from those found in the ground-state Hamiltonian.16,39 Of particular note, the excited-state electric susceptibility parameters are much larger than those of the ground state, enabling significantly more sensitive electric-field detection.91 However, such techniques employ resonant optical pumping that is only possible at cryogenic temperatures, precluding general use.91
2.6 Experimental considerations
As an illustrative example, we explore the experimental considerations for the detection of a single nuclear spin external to the diamond using variance detection. The magnitude of the magnetic variance generated by the Larmor precession of a single nuclear spin at distance d from the NV is24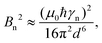 | (16) |
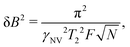 | (17) |
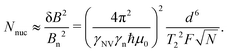 | (18) |
Eqn (18) scales with the sixth power of d, emphasizing the crucial importance of minimizing the NV–target distance. While the exact dependence of the magnetic-field strength on d varies for different target geometries (B2rms ∼ 1/d6 for a single spin, B2rms ∼ 1/d4 for a two-dimensional spin layer, and B2rms ∼ 1/d3 for a volume of spins),24,66,92 reducing this distance will always result in a larger field at the NV.
Eqn (18) also illustrates the effect of extending T2, which has inspired large bodies of work aimed at fabricating coherent, near-surface emitters (Section 3) in addition to development of sensing protocols for extending T2 by mitigating surface noise (Section 5).
Finally, improving the readout fidelity is another avenue for experimental optimization. For off-resonant excitation, the readout fidelity is limited by short readout times (TR ≈ 400 ns) due to the transient nature of the spin contrast (Fig. 1e), the low radiative emission rate of the NV (γ = 2π × 13 MHz), and poor optical collection efficiency (ξ ∼ 0.01 is typical for confocal measurements of bulk diamond). Such schemes are further limited for C < 1, resulting in an overall readout fidelity of only F ∼ 0.03 (eqn (2) and (3)). For such a low value, more than 500 experimental repetitions would be required to achieve SNR = 1. Encouragingly, several routes have been explored to increase off-resonant readout fidelity, including nuclear-spin-assisted techniques (obtaining F = 0.5)24 and spin-to-charge conversion93 with near-unity fidelity (F > 0.99).94 However, such protocols come at the expense of additional experimental overhead and significantly longer readout times.
The best combination of NV preparation and readout fidelities have been achieved using resonant excitation of spin-dependent optical transitions within the ZPL.95 Below 10 K, the ZPL transitions of such emitters can be spectrally resolved and optically cycled multiple times before spin flips occur. This cyclicity allows for spin-state readout via excitation and the subsequent presence or absence of corresponding emission, yielding F = 0.97.96,97 Meanwhile, a small degree of spin mixing within the excited state is used as a resource for spin preparation via resonant optical pumping, yielding near-perfect preparation efficiencies (99.8% into ms = 0).96 These techniques have been combined to demonstrate imaging of a 27-spin 13C cluster within a diamond substrate at cryogenic temperatures.98 Finally, access to resonant optical transitions can facilitate all-optical spin manipulation,99 albeit with substantially lower fidelity than microwave techniques due to spontaneous emission. Unfortunately, this set of techniques have largely relied on the exceptional optical stability of naturally occurring NV centers located microns below the diamond surface.100 Indeed, resonant excitation of near-surface NV centers is not possible due to instability of the ZPL frequency over time referred to as spectral diffusion.101,102 The asymmetry of the nitrogen and vacancy sites (Fig. 1a) leads to inequivalent electric dipole moments in the ground and excited states, which makes it extremely sensitive to electric-field noise on nearby surfaces. Such noise can cause spectral diffusion of the optical transition of many GHz,425 precluding spectral selectivity within the ZPL fine structure. Consequently, near-surface NV centers required for studying external targets rely on off-resonant excitation.
We conclude by noting that chemical sensing at diamond surfaces may be performed using either single NV centers or ensembles of shallow defects. Single emitters boast nanoscale spatial resolution but are limited in signal by their radiative emission rate γ and optical collection efficiency ξ.63,103 A reduction in excited-state lifetime can be achieved via coupling to an optical resonator structure,104 while higher optical collection efficiencies can be obtained using nanophotonic structures such as waveguides, lenses, cavities, or gratings.95,105–114
In contrast to single NV sensors, dense ensembles offer accelerated measurement times that scale with NNV, the number of NVs.10 Moreover, the sensitivity scales with 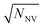 per unit time,10 with a best predicted sensitivity of ca.
per unit time,10 with a best predicted sensitivity of ca.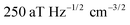 in the high-density limit.63 Higher density, however, may be accompanied by reduced coherence times that ultimately limit sensor utility.103,115 Furthermore, the efficient collection of fluorescence from ensembles of NV centers remains difficult; some nanofabricated structures that offer improvement for single NVs may not be suitable for ensembles. Still, alternative strategies that rely on absorptive and dispersive schemes could improve light collection from ensembles.116–119 Finally, we note that nanostructured diamond surfaces hosting high NV densities benefit from increased sensor—analyte contact area.120
in the high-density limit.63 Higher density, however, may be accompanied by reduced coherence times that ultimately limit sensor utility.103,115 Furthermore, the efficient collection of fluorescence from ensembles of NV centers remains difficult; some nanofabricated structures that offer improvement for single NVs may not be suitable for ensembles. Still, alternative strategies that rely on absorptive and dispersive schemes could improve light collection from ensembles.116–119 Finally, we note that nanostructured diamond surfaces hosting high NV densities benefit from increased sensor—analyte contact area.120
3 Surface influence on NV center stability
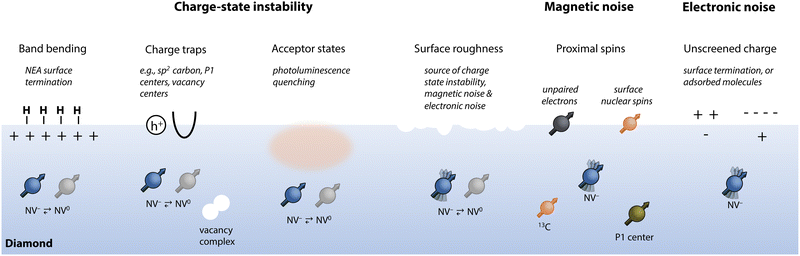
Achieving the excellent magnetic-field sensitivity and spatial resolution required for detecting single molecules necessitates shallow NV centers (i.e., depths < ca. 10 nm). Unfortunately, emitter optical and spin properties deteriorate within ca. 100 nm of the diamond surface,30 presenting a critical challenge. In this section, we introduce how shallow NV centers are typically generated and then detail the leading sources of their charge instability and spin dephasing (summarized in Fig. 4). Finally, we describe suitable surface terminations that have been theoretically and experimentally identified to promote preservation of NV center properties.3.1 Generation of shallow NV centers
Magnetic sensing of external targets necessitates fabrication processes that yield a deterministic density of shallow NVs with high spin coherence.121 Most commonly, NV-forming nitrogen atoms are incorporated into electronic-grade diamond through post-growth, blanket implantation,122–124 forming a randomly distributed, two-dimensional layer of impurities at a depth and density determined by the acceleration energy and fluence, respectively.125 In contrast, deterministic impurity placement can be achieved by performing implantation with a focused ion beam (FIB),126–129 or through a mask.130–133 In fact, a combination of shallow masked implantation and diamond overgrowth has been used to achieve high-precision placement for alternative defect centers.134 Subsequent high-temperature, high-vacuum annealing (ca. 800–880 °C) mobilizes vacancies created by implantation, which combine with nitrogen to form NV centers with varying efficiency.123,135–137 Unfortunately, the implantation and annealing processes can lead to formation of unwanted vacancy complexes that degrade coherence. This effect increases with implantation energy, but there is evidence that annealing at higher temperatures (i.e., 1000–1500 °C) can eliminate localized defects that degrade the spin and optical properties of emitters.138–141 Furthermore, Fermi-level engineering through co-doping with donor impurities may preclude the formation of vacancy chains.142An alternative strategy for defect formation is impurity incorporation during diamond growth via chemical vapor deposition (CVD) or high-pressure, high-temperature (HPHT) synthesis. In both cases, NV centers can be formed naturally from non-negligible native nitrogen levels. However, such defects occur at random positions within the diamond crystal, limiting their utility. In HPHT synthesis, higher nitrogen content is typically observed (up to hundreds of ppm) than during CVD growth, with varying densities related to the efficiency of nitrogen incorporation along different crystallographic growth directions.143,144 Conversely, nitrogen incorporation during CVD growth can localize emitters into a single growth layer (referred to as delta doping).145–149 Advantageously, deterministic introduction of nitrogen during the CVD growth process can allow for preferential alignment along one of the four possible crystallographic orientations.150–152 Such alignment is useful both for higher experimental throughput in single NV studies as well as for obtaining higher contrast in ensemble NV measurements. Following impurity incorporation, techniques such as electron irradiation,100,153–155 laser writing,156,157 or implantation with additional species153,158,159 can be used to generate the vacancies necessary for emitter formation through subsequent annealing.
3.2 Origins of instability
In this section, we explore physical phenomena leading to reduced measurement sensitivity for near-surface NV centers, namely charge instability and magnetic and electronic noise. | (19) |
Photoinduced charge conversion between the NV− and NV0 states can occur via one-photon (energy >2.6 eV) or two-photon (energy >1.946 eV) absorption processes that eject an electron into the conduction band of diamond.167 The reverse process, reduction of NV0 back to its negative state, may also occur via both one-photon (energy >2.94 eV) or two-photon (energy >2.156 eV) absorption processes by receiving an electron from the diamond valence band.167 Consequently, green laser excitation that is commonly used for spin preparation and readout results in unavoidable modulation between NV− and NV0, leading to a steady-state ζ ≈ 0.75.163,172,173 This value can be even smaller for NV ensembles,174 where tunneling between proximal NV centers and nearby nitrogen species may occur upon photoexcitation.175 Multicolor illumination with near-infrared light94,176,177 (resulting in spin-dependent charge transfer178,179), doping,180–182 and high laser powers183 provide possible routes to increase the relative population of NV−. Moreover, spin-dependent ionization of NV−versus NV0 states has been used as a resource for achieving single-shot spin readout.93,94,184
Proximal surfaces preferentially convert NV− to NV0 following photoionization since local electronic traps and acceptor states inhibit electron exchange between the NV and the diamond electronic bands (Fig. 4).31,185 Moreover, charge-state instability has also been observed in the dark (without photoexcitation), which is hypothesized to occur by tunneling to electron traps.31,167,186 Such non-optical discharge of NV− is exacerbated near surfaces, where primal sp2 carbon serves as an efficient charge trap.81,187
While it cannot account for all processes leading to NV-center destabilization,167,188,189 a band-bending model provides a simplified picture of how the NV− state is affected by surface proximity.190 An electric dipole layer at the surface, due to the terminating species or chemical adsorbates, can lead to accumulation of positive or negative charge at the diamond interface. In the case of hole accumulation, electrons are withdrawn from shallow NV centers, yielding the neutral charge state.191–193 This is captured by the electron affinity of the surface, defined as
| χ = Evac − ECBM, | (20) |
| Orientation | Reconstruction | Termination | Sample preparation | χ (eV) | Notes | Ref. |
|---|---|---|---|---|---|---|
| (100) | (1 × 1) | O | Theory | +3.91 | Ketone termination | 198 |
| O | Theory | +3.64 | Ketone termination | 199 | ||
| O | Theory | +2.63 | Ether termination | 198 | ||
| O | Theory | +2.61 | Ether termination | 199 | ||
| O | Thermal oxygen annealing | +2.14 | Single crystal | 30 | ||
| O | Chemically oxidized | +1.7 | Natural, single-crystal type IIb | 194 | ||
| O | Chemically oxidized | +1.0–1.45 | Natural, single-crystal type IIb | 200 | ||
| O | Thermal oxygen annealing | +0.54 | Homoepitaxial p-type CVD film | 201 | ||
| H | Hydrogenation via hot filament | ca. −0.4 | Natural, single-crystal type IIb | 206 | ||
| H | Theory | −3.4 | Dihydride termination | 202 | ||
| (2 × 1) | N | Theory | +3.46 | — | 203 | |
| F | Theory | +3.00 | — | 189 | ||
| F | Thermal dissociation of XeF2 | +2.56 | Single-crystal, boron-doped CVD | 204 | ||
| O | Theory | +2.40 | Ether termination | 189 | ||
| F | Theory | +2.13 | — | 198 | ||
| C | UHV annealing | +1.3 | Natural, single-crystal type IIb | 205 | ||
| C | Theory | +0.8 | — | 202 | ||
| C | UHV annealing | +0.75 | Natural, single-crystal type IIb | 200 | ||
| C | Theory | +0.61 | — | 198 | ||
| C | Theory | +0.51 | — | 199 | ||
| C | UHV annealing | +0.50 | Natural, single-crystal type IIb | 194 | ||
| H | Plasma hydrogenation | +0.19 | Homoepitaxial, p-type CVD film | 201 | ||
| H/F | Theory | −0.38 | 50% F coverage | 198 | ||
| O | Theory | −0.6 | Hydroxyl termination | 189 | ||
| H | Plasma hydrogenation | ca. −0.8 | Natural, single-crystal type IIb | 207 | ||
| H | Plasma hydrogenation | ≤−1.0 | Natural, single-crystal type IIb | 205 | ||
| H | Plasma hydrogenation | −1.3 | Natural, single-crystal type IIb | 194 | ||
| H | Theory | −1.7 | — | 189 | ||
| H | Theory | −1.96 | — | 198 | ||
| H | Theory | −2.05 | — | 199 | ||
| O | Theory | −2.13 | Hydroxl termination | 208 | ||
| H | UHV annealing | ca. −2.2 | Natural, single-crystal type IIb | 209 | ||
| H | Theory | −2.2 | Monohydride termination | 202 | ||
| (2 × 2) | H/O | Theory | +0.5 | Mixed H/O/OH termination | 189 | |
| H/N | Theory | +0.32 | 50% N coverage | 203 | ||
| — | O | Chemically oxidized | +0.92 | Single crystal | 30 | |
| (111) | (1 × 1) | O | Theory | +3.75 | — | 210 |
| N | Theory | +3.23 | — | 211 | ||
| F | Theory | +2.63 | — | 198 | ||
| C | Theory | +1.37 | — | 198 | ||
| H/F | Theory | +0.49 | 50% F coverage | 198 | ||
| H | Plasma hydrogenation | < 0 | Single crystal, first chemically oxidized | 200 | ||
| H | Hydrogenation via hot filament | ≤−0.7 | Natural, single-crystal type IIb | 212 | ||
| H | Plasma hydrogenation | ≤−0.9 | Natural, single-crystal type IIb | 205 | ||
| H | Plasma hydrogenation | −1.27 | Natural, single-crystal type IIb | 213 | ||
| H | Theory | −1.63 | — | 211 | ||
| H | Theory | −2.01 | — | 198 | ||
| H | Theory | −2.03 | — | 199 and 208 | ||
| (2 × 1) | O | Theory | +3.42 | Ketone termination | 210 | |
| F | Theory | +2.49 | — | 198 | ||
| O | Theory | +1.85 | Epoxy termination | 210 | ||
| C | UHV annealing | +1.5 | Natural, single-crystal type IIb | 205 | ||
| H/F | Theory | +0.52 | 50% F coverage | 198 | ||
| C | UHV annealing | +0.5 | Natural, single-crystal type IIb | 200 and 212 | ||
| C | UHV annealing | +0.38 | Natural, single-crystal type IIb | 213 | ||
| C | Theory | +0.35 | — | 199 and 208 | ||
| C | Theory | +0.32 | — | 198 | ||
| H | Theory | −2.19 | — | 198 | ||
| — | C | UHV annealing | +0.8 | Single crystal, graphitized surface | 213 | |
| (110) | (1 × 1) | F | Theory | +2.38 | — | 198 |
| C | Theory | +0.91 | — | 198 | ||
| C | Theory | +0.9 | — | 214 | ||
| H/F | Theory | +0.52 | 50% F coverage | 198 | ||
| H | Theory | −2.41 | — | 198 | ||
| (2 × 1) | H | Theory | +2.4 | — | 214 | |
| (113) | (2 × 1) | N | Theory | +3.56 | — | 215 |
| F | Theory | ca. +3.3 | — | 215 | ||
| O | Theory | +2.18 | Ether termination | 215 | ||
| O | Theory | −0.06 | Hydroxl termination | 215 | ||
| H | Theory | −1.80 | — | 215 |
The influence of a surface spin bath on shallow NV centers can be exploited as a useful probe of the local chemical environment,230,231 which has been widely used for chemical and biochemical sensing with NV centers both in bulk diamond and nanodiamond systems. For example, relaxometry measurements that do not require microwave irradiation can be used to characterize changes in T1 caused by e.g., proximal paramagnetic species,232 redox reactions,233 changes in pH,234 and radical production.235–237 Nevertheless, for highly sensitive techniques such as NMR spectroscopy, these sources of magnetic noise are often undesirable. Consequently, the optimization of diamond surface chemistries is a critical step toward realizing the full potential of NV sensing for dilute assemblies of external spins.
The influence of electric-field noise on the NV is thought to be comparatively minor,30 unless operating in a regime where the NV EPR frequencies exhibit anticrossings238 or in an off-axis magnetic field.84,239,240 However, in some cases, electric noise has been shown to dominate magnetic noise. Indeed, Kim et al. showed an almost factor-of-5 increase in T2 for shallow NV centers when bare diamond surfaces were coated in dielectric liquid to shield fluctuating surface charges.75 In contrast, the magnetic noise generated by dark spins was unaffected by the coating. In addition, Myers et al. used complementary double-quantum relaxometry measurements to differentiate between electric and magnetic noise sources, demonstrating that T1 was limited by surface electric-field noise at low magnetic fields.241
Moving forward, systematic investigations using multiple measurement techniques will be essential in optimizing surface preparations for attaching molecules of interest. For (bio)chemical sensing, functionalization with dense, highly charged, and mobile biomolecules contributes additional sources of electric-field noise and may pose a challenge for highly sensitive measurements. One solution would be to operate at large magnetic-field strengths; in addition, dielectric surface layers (e.g., solid- or solution-phase capping material) may mitigate electric-field-driven decoherence of shallow NV centers.75,242 Still, the choice of dielectric coating depends critically on the operational frequency range of the sensor242 and its compatibility with the analytes of interest. An as-yet unexplored strategy to shield near-surface NVs from fluctuating electric fields could leverage surface dipole control using self-assembled monolayers (SAMs).243,244 More generally, magnetic and electric noise sources from surface traps could be reduced using highly homogeneous chemical surface functionalization, which is detailed in Section 4.
3.3 Surface terminations for increasing NV stability
Common diamond CVD growth employs hydrogen gas, resulting in hydrogen termination of dangling bonds at interfaces.245,246 This termination induces a highly unfavorable NEA that destabilizes the NV− state. Furthermore, H termination is expected to introduce sub-bandgap states resulting in delocalization and loss of NV electrons upon photoexcitation.189 While hydrogen termination will naturally degrade when exposed to air, the systematic chemical control of diamond surfaces offers a solution to combat destabilization of shallow NV centers.189,247 Below, we summarize methods for tailoring the diamond surface termination and explore the resulting influence on NV-sensing properties. Subsequent chemical functionalization with molecular films of interest is described in Section 4.Theoretically, fully fluorinated surfaces are expected to yield favorable PEA. For example, (100)-cut diamonds, which are most commonly used, are estimated to have χ = 2.13–3.00 eV.189,198 Furthermore, (111) surfaces are theoretically predicted to have up to χ = 2.63 eV,198 while fluorinated (113) interfaces are estimated to yield ca. χ = 3.30 eV.215 In addition, recent density functional theory calculations suggest that this termination is also highly suitable for the less-studied (110) interface.198,258
Experimentally, fluorine termination has been achieved using several techniques. Rietwyk et al. utilized exposure to dissociated XeF2, measuring a PEA of χ = 2.56 eV for a (100) surface.204 In addition, Cui and Hu tested the influence of fluorine-terminated (100) diamond, prepared using a CF4 plasma (Fig. 5).259 Analysis with X-ray photoelectron spectroscopy revealed that a 5-minute exposure led to a ca. 3 nm-thick polymerized fluorocarbon on the surface. Moreover, charge-state-dependent NV fluorescence measurements revealed a higher ζ for fluorine-terminated diamond than for oxygen and hydrogen termination. Similar results were obtained for nanodiamonds treated with electron-beam-induced fluorination, which allows for highly localized surface modification.260 Finally, Osterkamp et al. demonstrated the stabilization of shallow (ca. 5 nm-deep) NVs using SF6 plasma exposure, enabling NMR signal detection from protons in immersion oil on the diamond surface.147
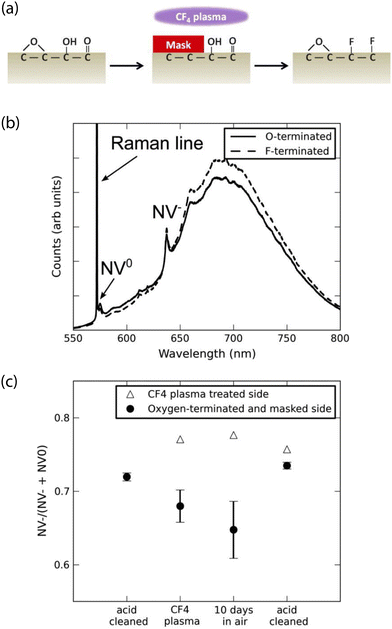 | ||
| Fig. 5 Characterization of the impact of fluorine-terminated diamond on shallow NV centers. (a) Schematic showing use of CF4 plasma to induce surface fluorination of oxygen-terminated diamond. (b) Representative photoluminescence spectra comparing oxygen- and fluorine-terminated surfaces. Zero-phonon lines (ZPL) of the NV0 and NV− are indicated. (c) Ratio of the NV− ZPL area to that of the sum of NV− ZPL and NV0 ZPL areas after different surface preparation conditions. Adapted with permission from ref. 259. Copyright 2013 AIP Publishing LLC. | ||
In contrast to these results, Ohashi et al. found that a brief (15 s) treatment with CF4 plasma led to permanent bleaching of ca. 30% of shallow NV centers.220 This experiment underlines the critical importance of reducing acceptor states and charge traps at the diamond surface, even for interfaces with large global PEA.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), and ether (C–O–C) groups, impact both χ and as the presence of deleterious sub-bandgap surface states. Such states may perturb the excited-state energy levels of nearby NV centers, impacting their charge stability.189 In addition, we note that different diamond surface planes may also strongly impact χ and the presence of surface states. Indeed, recent theoretical work by Li et al. suggests that the oxygenated (113) diamond surfaces may increase optical stability of near-surface NV centers compared to the commonly used (100)- and (111)-cut diamonds.215
O), and ether (C–O–C) groups, impact both χ and as the presence of deleterious sub-bandgap surface states. Such states may perturb the excited-state energy levels of nearby NV centers, impacting their charge stability.189 In addition, we note that different diamond surface planes may also strongly impact χ and the presence of surface states. Indeed, recent theoretical work by Li et al. suggests that the oxygenated (113) diamond surfaces may increase optical stability of near-surface NV centers compared to the commonly used (100)- and (111)-cut diamonds.215
Full termination with hydroxyl groups is theoretically predicted to yield NEA of χ = −0.6 eV and PEA of χ = 0.2 eV for (100) and (111) diamond surfaces, respectively,247 and may yield sub-bandgap states in the case of (100) surfaces.189 Similarly, carboxyl groups can introduce deep, localized acceptor states that quench NV luminescence.189 Moreover, ether-like bridges on oxidized (100) surfaces were theoretically calculated to induce a PEA of χ = 2.4–2.63 eV;189,198,199 however, photo-excited electrons from NV− may be trapped by such surfaces, resulting in blinking.189 Encouragingly, epoxy-oxidized (111) surfaces were recently predicted to have PEA of χ = 1.85 eV without generation of sub-bandgap states.210 Moving forward, it is likely that a combination of these terminators will be required to yield both optimal PEA and reduced surface states.189,261
In practice, oxygen termination results from the use of strongly oxidizing acids (e.g., piranha solution and “tri-acid” mixtures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H2SO4
1 H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HClO4
HClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HNO3),21,22,221,226,262,263 oxygen plasma,196,264–266 thermal annealing in an oxygen atmosphere,30,265,267 UV/ozone,268 or ozone treatments.269 Importantly, such treatments often result in a surface that is decorated by a mixture of oxygen containing functional groups. Various surface characterization methods can be used to distinguish between these terminal groups and to measure their influence on the surface electronic structure270 including X-ray photoelectron spectroscopy (XPS), ultraviolet photoelectron spectroscopy (UPS), near-edge X-ray absorption fine-structure (NEXAFS) spectroscopy, high-resolution electron-loss spectroscopy (HREELS), and Fourier-transform infrared (FTIR) spectroscopy. However, deterministic control over the relative ratio of these groups is not trivial, and different oxidation procedures yield variable compositions.271 Moreover, surface roughness and crystallographic orientation also influence the coverage.272,273 Finally, depending on how harsh the oxidation process is, some procedures may result in undesired graphitization.
HNO3),21,22,221,226,262,263 oxygen plasma,196,264–266 thermal annealing in an oxygen atmosphere,30,265,267 UV/ozone,268 or ozone treatments.269 Importantly, such treatments often result in a surface that is decorated by a mixture of oxygen containing functional groups. Various surface characterization methods can be used to distinguish between these terminal groups and to measure their influence on the surface electronic structure270 including X-ray photoelectron spectroscopy (XPS), ultraviolet photoelectron spectroscopy (UPS), near-edge X-ray absorption fine-structure (NEXAFS) spectroscopy, high-resolution electron-loss spectroscopy (HREELS), and Fourier-transform infrared (FTIR) spectroscopy. However, deterministic control over the relative ratio of these groups is not trivial, and different oxidation procedures yield variable compositions.271 Moreover, surface roughness and crystallographic orientation also influence the coverage.272,273 Finally, depending on how harsh the oxidation process is, some procedures may result in undesired graphitization.
Experimentally, surface oxidation treatments have consistently shown improvements in T2 times for near-surface NVs, as well as higher ζ both for bulk196,265 and nanodiamond materials.49,274 Fu et al. showed efficient conversion of NV0 to NV− for ca. 10–75 nm-deep emitters after annealing at 465 °C in an oxygen atmosphere (Fig. 6a).193 Moreover, Fávaro de Oliveira et al. observed a threefold increase in T2 following an O2 soft plasma exposure compared to tri-acid-cleaned surfaces (Fig. 6b).264 In addition, Yamano et al. demonstrated an improvement in Rabi oscillation contrast; the C = 0.14 observed for shallow NV centers in acid-cleaned diamond increased to C = 0.30 after UV/ozone treatment, further improving to C = 0.43 following oxygen thermal annealing (Fig. 6c).267 More recently, Sangtawesin et al. reported on the impact of thermal oxygen annealing on shallow NV-center spin coherence, along with complementary characterization of the surface morphology (Fig. 6d–f).30 They reported an up to a factor-of-four improvement in T2 for shallow NV centers compared to samples prepared with tri-acid cleaning alone. These improved properties were attributed to the formation of a highly ordered, predominantly ether-terminated surface. This ordering was facilitated by fabrication of extremely flat (100) surfaces with rms roughness of <0.4 nm. In contrast, Braunbeck et al. studied the impact of mechanical polishing and etching techniques on coherence times for shallow emitters and found minimal correlation with surface roughness.275 These findings suggest that the particular method of preparing flat diamond surfaces (i.e., etching, polishing, etc.) likely has a strong influence on the chemical termination.
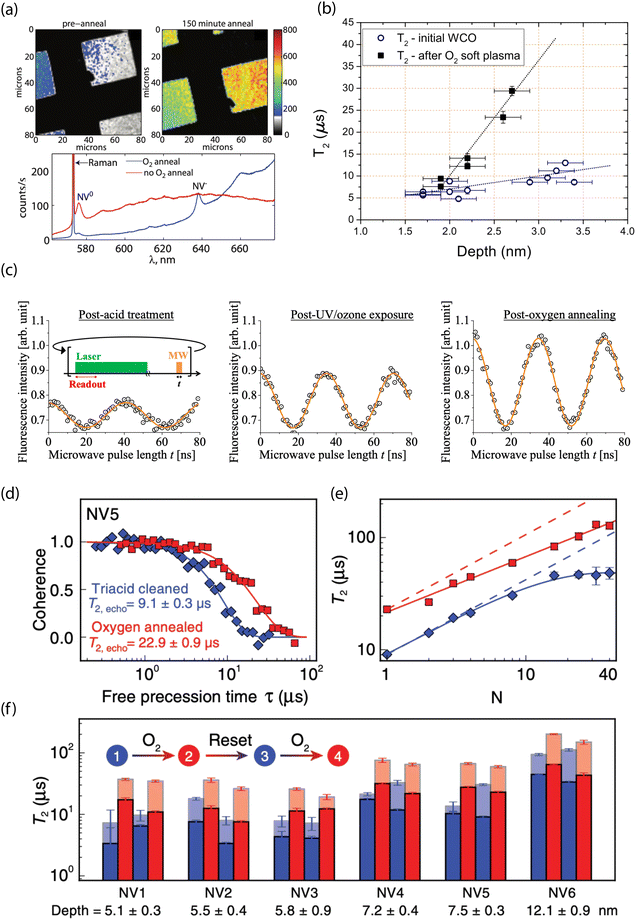 | ||
| Fig. 6 Experimental characterization of oxygen-terminated diamond for stabilizing shallow NV centers. (a) Confocal images (top) and photoluminescence spectra (bottom) before and after O2 thermal annealing of diamond surfaces containing shallow NV centers. (b) Hahn-echo spin coherence (T2) as a function of depth for NV centers before and after oxygen plasma exposure. (c) Representative Rabi oscillations for a single NV after acid treatment, after UV/ozone treatment, and following thermal annealing in O2. (d) T2 (Hahn echo) decay curves from the same NV center and (e) coherence time as a function of the number of dynamical decoupling pulses before (bue) and after (red) O2 thermal annealing. (f) Reversibility and reproducibility of O2 thermal annealing shown by comparing T2 from Hahn echo (opaque) and XY-8 (transparent). (a) Adapted with permission from ref. 193. Copyright 2010 American Institute of Physics. (b) Adapted with permission from ref. 264. Copyright 2015 AIP Publishing LLC. (c) Adapted with permission from ref. 267. Copyright 2017 The Japan Society of Applied Physics. (d)–(f) Adapted with permission from ref. 30. Copyright 2019 American Physical Society. | ||
In some cases, surface oxidation can have minimal impact on T2 while having a significant influence on T1 for shallow emitters. For example, Ohashi et al. observed no significant change in T2 after oxidation (compared to H-terminated surfaces after tri-acid cleaning) but observed a larger spread in relaxation times (T1 ≈ 0.54–4.2 ms after compared to T1 ≈ 2.7–3.8 ms before oxidation).220 Moreover, Tetienne et al. saw that thermal annealing in oxygen for 4 h at 465 °C had little influence on T2 and no effect on the average photoluminescence rate or Rabi contrast.276 In contrast, such annealing resulted in a two-order-of-magnitude reduction in T1 for some emitters; however, longer T1 times could be recovered after tri-acid cleaning. In summary, the experimental results reported for oxygenated diamond surfaces underline the complexity of the relevant spin and charge dynamics that impact shallow NV centers.
Theoretical results from Stacey et al. showed that (2 × 1)-reconstructed (100) surfaces that are fully terminated with nitrogen exhibit a PEA of χ = 3.46 eV, while (2 × 2)-reconstructed surfaces with 50/50 N/H termination exhibit a PEA of only χ = 0.32 eV (Fig. 7a).203 Furthermore, Chou et al. performed first-principles calculations of (111) diamond surfaces in which terminal carbon atoms could bind to a single hydrogen. With this model, they found that an over 50% substitution of C–H units by isovalent nitrogen led to PEA (Fig. 7b and c),211 with full nitrogen coverage resulting in χ = 3.23 eV. Interestingly, unlike the (100) and (111) surfaces, nitrogen termination of (113) diamond was proposed as unsuitable for NV sensing since surface-state mixing with the NV excited state would lead to photoionization.215
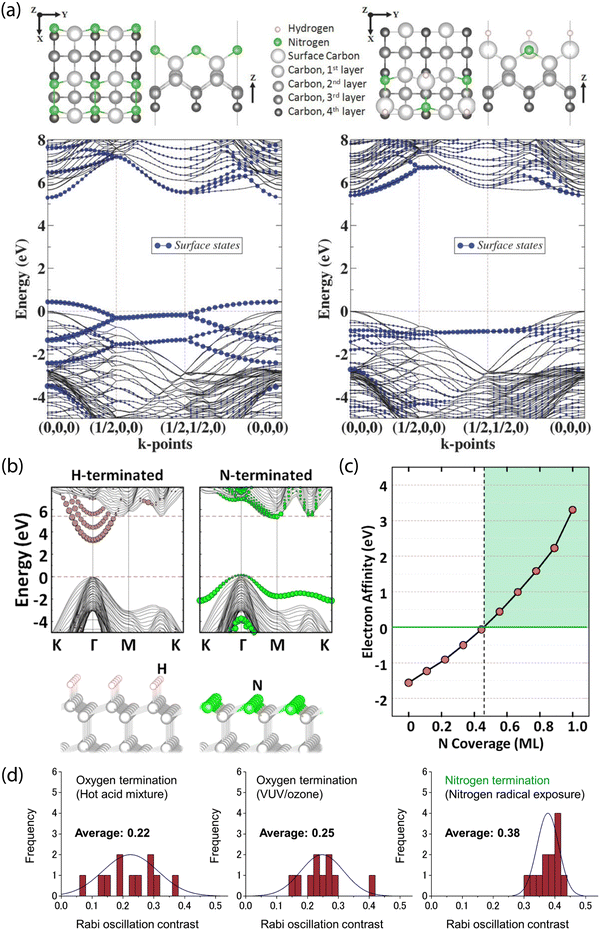 | ||
| Fig. 7 Theoretical prediction and experimental characterization of nitrogen-terminated diamond for near-surface NV stabilization. (a) Surface termination models and band structure calculations for fully N-terminated (left) and mixed N/H-terminated reconstructed (right) (100) diamond surfaces. Both cases show minimal leakage of surface states into the diamond bandgap. (b) Comparison of H- and N-terminated (111) diamond surfaces. Unlike the N-terminated surface, the H-termination introduces delocalized surface-related image states into the bandgap. (c) Electron affinity as a function of N coverage. (d) Analysis of charge stability for NV centers via Rabi oscillations; contrast is compared between oxygen-terminating treatments and after nitrogen termination using nitrogen radical exposure. (a) Adapted with permission from ref. 203. Copyright 2015 John Wiley & Sons, Inc. (b) and (c) Adapted with permission from ref. 211. Copyright 2017 American Chemical Society. (d) Adapted with permission from ref. 280. Copyright 2019 American Chemical Society. | ||
Experimentally, nitrogenation of diamond surfaces has been achieved using anodic polarization in liquid ammonia (requiring conductive, e.g., boron-doped diamond),281 plasma treatment with nitrogen (N2),203,282–285 ammonia (NH3),286–289 or mixed sources,281 radical beam exposure,280 and UV irradiation in NH3 gas.290 In these experiments, photoelectron spectroscopies including XPS, NEXAFS, and HREELS were used to probe the binding configuration of nitrogen atoms. The resulting nitrogen may be incorporated as nitrile (CN) groups, imines (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), single-bonded (C–N, N–N), or amine (NHx) species.
N), single-bonded (C–N, N–N), or amine (NHx) species.
In a recent study, Kawai et al. demonstrated the stabilization of the NV− charge state in shallow defects using nitrogen radical beam exposure (Fig. 7d).280 This method is suspected to produce diamond surfaces with a mixture of nitrogen terminations, as characterized by XPS and NEXAFS. Using this technique, the authors reported increased Rabi oscillation contrast compared to NV centers in oxygen-terminated diamond (prepared by hot acid treatment and VUV/ozone exposure). Furthermore, measured T2 values were comparable to prior reports on oxygen-terminated surfaces.291 Subsequently, 4–10 nm-deep emitters were used for NV-NMR detection of 1H spins in immersion oil.
Interestingly, nitrogenation can also impact the fractional coverage of sp2 and sp3 carbon, a phenomenon that is heavily dependent on the process parameters and diamond surface morphology. For example, a radio-frequency plasma based on a mixture of NH3/N2 diluted in H2 was shown to induce surface graphitization on polycrystalline, boron-doped diamond.281 In contrast, we recently showed that exposure of oxygen-terminated, single-crystalline (100) diamond surfaces to NH3 plasma resulted in a reduction of residual sp2 carbon, which may be linked to an observed increase in T2 for shallow NV centers.289
Moving forward, derivatization (e.g., of amines) enables complementary tests of chemical functionality. While the introduction of reactive amine functional groups enables facile attachment of molecules, fully amine-terminated diamond surfaces were experimentally shown to exhibit NEA,288 and are thus incompatible with near-surface NV centers. Therefore, mixed surface terminations are likely preferable to maintain NV stability while allowing for covalent molecular attachment.203,289
4 Surface functionalization for molecular sensing with NV centers
NV-center detection of external molecular targets requires both molecular immobilization on the diamond surface and preservation of emitter properties via the aforementioned techniques. While the detection of magnetic noise arising from electron292,293 and nuclear spins21,22,27–29,147,280,294 external to the diamond has been demonstrated, robust and deterministic functionalization of the diamond surface will prove critical for future experiments. Indeed, such functionalization could facilitate observation of, e.g., surface reactions, conformational changes in biomolecules, spin-dependent effects in charge transfer, and target binding to receptors (such as antibodies or aptamers). Moreover, directed and self-assembly of molecules on surfaces provides well-defined specificity and selectivity, as well as control over molecular orientation (e.g., the availability of binding sites or functional groups) and density, further motivating its development.Despite being widely regarded as chemically inert, numerous techniques exist to functionalize diamond surfaces, which are the focus of recent reviews.271,295 However, not all strategies for molecular attachment to diamond are compatible with high-quality, shallow NV centers; for example, electrochemical methods, such as diazonium grafting,296,297 require conductive (e.g., boron-doped) diamond. These substrates are typically incompatible with NV sensing experiments, which require ultra-high-purity substrates. In addition, while direct modification of hydrogen-terminated diamond is possible,298–302 it is not be suitable for charge stabilization of near-surface NV− since local band bending promotes the neutral charge state.196 In this section, we explore strategies for stable non-covalent and covalent grafting of molecules to diamond that are compatible with near-surface NV centers. In particular, we focus on covalent attachment for oxygen- and nitrogen-terminated surfaces, in addition to molecular self-assembly on oxide adhesion layers that are grown on diamond.
4.1 Noncovalent functionalization
One functionalization approach employs non-covalent attachment by physisorption, which is stabilized by, e.g., hydrogen-bond interactions or electrostatic attraction. Alternatively, large molecules of interest (e.g., proteins) could be immobilized within solid polymer matrices that restrict translational and rotational degrees of freedom. Indeed, such a route may prove useful for NV-NMR-based approaches for elucidation of structural information. Moreover, solid supports could take advantage of dielectric shielding to mitigate the impact of electronic noise on NV-center sensors.For example, Shi et al. used a polylysine matrix to immobilize mitotic arrest deficient-2 (MAD2) proteins that were modified with nitroxide spin labels.23 These molecules were drop-cast onto the diamond surface before freeze drying with liquid nitrogen (Fig. 8a and b).23 Shallow NV centers were subsequently used to monitor dilute densities of these proteins using EPR measurements. Notably, even though motion was restricted by the polylysine matrix, protein dynamics persisted on the millisecond time scale, resulting in spectral broadening of the EPR spectra. Consequently, improved surface functionalization and NV sensing schemes are required for detection of hierarchical ordering and conformational changes in biomolecules.
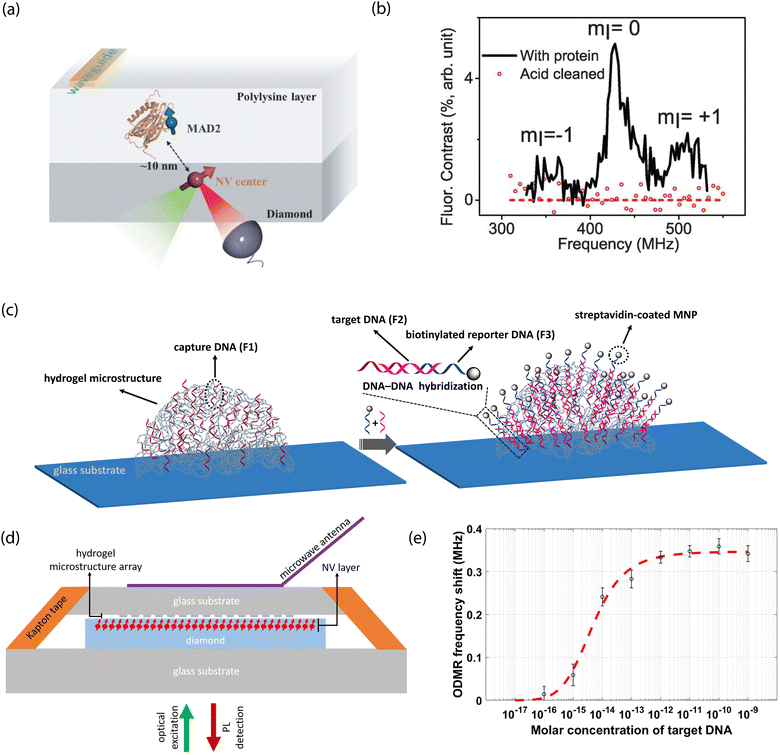 | ||
| Fig. 8 NV studies with non-covalently modified surfaces. (a) Schematic of proteins labeled with nitroxide spins and dispersed within a polylysine matrix layer on a diamond surface. (b) EPR spectrum characteristic of the nitroxide spin label tethered to proteins under study. Signals disappear after removal of the proteins from the surface. (c) Illustration of probe DNA immobilization in hydrogel microstructures on glass substrates and hybridization with complementary strands bound to magnetic nanoparticles. (d) Scheme for NV-center detection of magnetic fields arising from magnetic nanoparticles upon DNA capture. (e) Dose response curve of shifts in NV ODMR frequency for increasing concentration of target DNA. (a) and (b) Adapted with permission from ref. 23. Copyright 2015 American Association for the Advancement of Science. (c)–(e) Adapted with permission from ref. 303. Copyright 2021 National Academy of Science. | ||
Interestingly, Kayci et al. recently developed a sandwich bioassay that bypasses diamond functionalization in favor of modifying glass substrates with indexed droplets of hydrogel microstructures.303 These substrates are then brought into close proximity to a diamond containing near-surface NV centers for sensing (Fig. 8c–e).303 This approach relied on magnetic-nanoparticle-tagged DNA for nucleic acid detection; briefly, poly(ethylene glycol)diacrylate-based hydrogel microstructure networks were polymerized with acrylamide-functionalized oligonucleotides. Complementary target DNA (conjugated with magnetic nanoparticles) then hybridized with probe sequences, resulting in a modified NV ODMR signal. Three-dimensional hydrogel structures hosting bioreceptors could also be patterned directly on planar diamond substrates for applications necessitating direct diamond surface modification.
Overall, non-covalent functionalization is attractive due to the ease of achieving physisorption compared to chemisorption, particularly for diamond substrates where the density of functional groups may be limited. Nevertheless, under normal sensing conditions, desorption of physisorbed molecules occurs more readily than for covalently tethered species. Furthermore, non-specific binding may pose a significant issue when relying on non-covalent attachment methods alone.304
4.2 Covalent functionalization
In contrast to non-covalent techniques, chemisorption offers greater stability and control over molecular attachment to surfaces that exhibit well-defined chemical terminations. In practice, the optimal chemical modification procedure and starting diamond surface termination are dependent on the available functional groups of the target molecule. Fig. 9 highlights some selected pathways to functionalize oxygen- and nitrogen-terminated diamond surfaces, which are of great interest due to their compatibility with near-surface NV centers for sensing applications (see Section 3).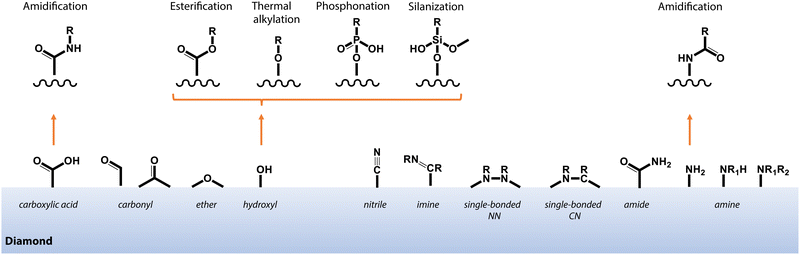 | ||
| Fig. 9 Schematic depiction of common functional groups at the surface of oxygen- and nitrogen-terminated diamond, and selected pathways for covalent functionalization as described in the main text. | ||
For example, Sushkov et al. employed a 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide (EDC)/N-hydroxysuccinimide (NHS) crosslinking chemistry to tether paramagnetic molecules composed of a gadolinium ion (Gd3+) chelated by an amine-terminated ligand to carboxylic-acid moieties on diamond (Fig. 10a and b).26 Co-localization of isolated molecules using single NV centers allowed for detection of an individual S = 7/2 electron spin from a (Gd3+) chelated molecule using T1 relaxometry. Lovchinsky et al. later used the same crosslinking chemistry to immobilize ubiquitin proteins via exposed carboxylic acid groups on the protein (Fig. 10c and d).24 This dilute attachment, in combination with enrichment of the protein with 2H and 13C, allowed the authors to detect proteins on the surface using single, shallow NV centers. Moving forward, more precise control over specific binding to orient proteins (e.g., antibodies), such as labeling with His-tags, or targeting thiolated cysteine residues, will prove highly useful. In particular, specific binding will enable subsequent target attachment to immobilized receptors, as well as positioning of active sites in close proximity to the surface.
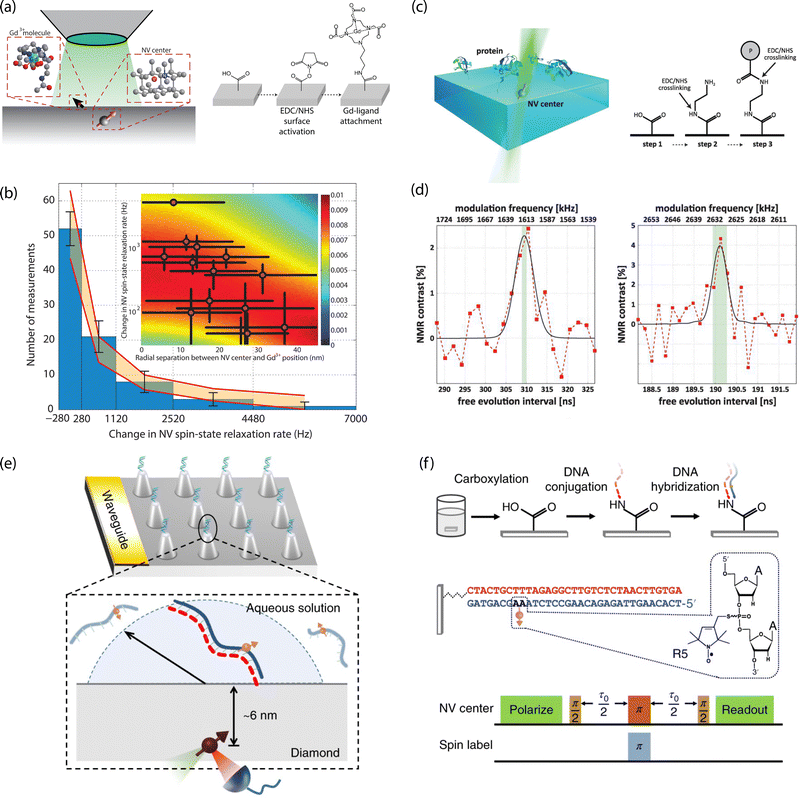 | ||
| Fig. 10 Characterization of chemically functionalized, oxygen-terminated diamond surfaces with shallow NV centers. (a) Schematic of single-electron-spin detection from isolated Gd3+-chelated molecules bound to carboxylic acids on the diamond surface. (b) Magnetic noise measurements from Gd3+-chelated molecules. (c) Schematic for probing isolated proteins by NMR detection with single NV centers (left) and chemical attachment strategy with EDC/NHS crosslinking (right). (d) 2H (left) and 13C (right) detection by NV-NMR of proteins enriched with 2H and 13C isotopes. (e) Schematic of diamond nanopillar arrays functionalized with DNA probes attached to carboxylic acid groups on the diamond surface. (f) Double electron–electron resonance (DEER) pulse sequence used for electron spin detection in hybridized complementary DNA strands. (a) and (b) Adapted with permission from ref. 26. Copyright 2014 American Chemical Society. (c) and (d) Adapted with permission from ref. 24. Copyright 2016 American Association for the Advancement of Science. (e) and (f) Adapted with permission from ref. 25. Copyright 2018 Springer Nature Limited. | ||
Oligonucleotide probes may also be tethered using readily available modifications to the ends of the sugar phosphate backbone. For example, Shi et al. functionalized carboxylic acid groups on diamond nanopillars hosting single NV centers with NH2-modified probe sequences. They subsequently detected hybridization with nitroxide-labeled complementary strands using EPR measurements (Fig. 10e and f).25
Finally, hydroxl groups can be used to attach molecules of interest by esterification307–310 and thermal alkylation.311 Moreover, hydroxl groups may serve as anchoring points for phosphonic acid headgroups,312 for silanization,313–315 or for precursor molecules in growth of capping films via atomic layer deposition (see Section 4.2.3). Starting with oxygen-annealed diamond substrates, Grotz et al. used silanization to covalently bind the 4-maleimido-TEMPO spin label.316 The authors employed DEER techniques to monitor Rabi nutations of surface-bound electron spins and measured the coupling strength between spin labels and NV-center probes. In addition, we demonstrated surface NMR detection using vapor-deposited trimethoxy(3,3,3-trifluoropropyl)silane, as well as (3-aminopropyl)trimethoxysilane, that were subsequently exposed to trifluoromethyl tags for amine-reactive crosslinking.289 In this work, signals from 19F spins were readily detected via NV NMR, however, multilayer film formation could not be ruled out. Generally, preventing multilayer formation or silane film degradation under aqueous conditions or air exposure is difficult and the mechanism for molecular assembly on oxidized surfaces is not fully understood. Still, silanization provides a facile route toward dense surface functionalization.
Recently, we introduced a strategy for direct chemical functionalization of terminal amine groups using mixed nitrogen- and oxygen-terminated (N/O) surfaces prepared using NH3 plasma following a thermal oxygen anneal.289 Importantly, short plasma exposure times (ca. 20 s) resulted in increased coherence times for NV centers <10 nm from the surface and significantly reduced background fluorescence from the diamond interface. Subsequent chemical functionalization of the mixed N/O-terminated diamond surfaces via highly generalizable amine-reactive crosslinking allowed for tunable molecular density and recyclable functionalization. Finally, NV-NMR measurements were used to detect surface-bound analytes with trifluoromethyl tags in the few-molecule (<200 molecules) regime. While promising, this approach is hampered by a decrease in the number of NV centers that exhibited ODMR signal for long NH3 plasma exposure times. The mechanism of this destabilization is not well understood, but may be linked to a concomitant increase of reactive amine groups that can contribute to NEA surfaces.288 Moving forward, situations requiring a high surface density of analytes crosslinked to surface-bound amine groups may benefit from co-doping with electron donors to aid in stabilizing the NV− state.142
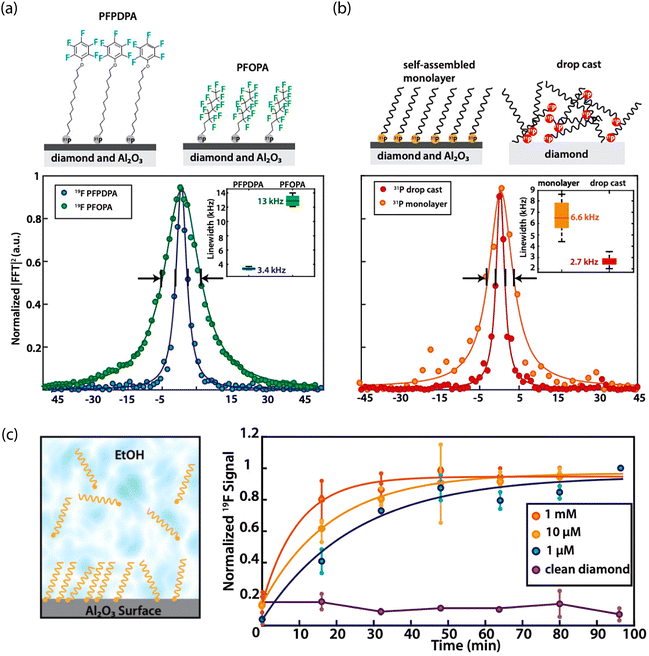 | ||
| Fig. 11 Surface NMR using ensembles of shallow NV centers to probe self-assembled monolayers (SAMs) on diamond capped with Al2O3. (a) Comparison of 19F resonance linewidth for SAMs of 1H,1H,2H,2H-perfluoroctanephosphonic acid (PFOPA) and 2-pentafluorophenoxydodecylphosphonic acid (PFPDPA). (b) Comparison of 31P resonance linewidth of SAMs of molecules containing phosphonate headgroups on Al2O3 capping layers vs. bare diamond surfaces. (c) SAM formation probed by monitoring increase in 19F resonance signal upon chemical binding of PFPDPA from ethanolic solutions. Adapted with permission from ref. 321. Copyright 2022 National Academy of Science. | ||
Similarly, Xie et al. used ca. 2-nm-thick ALD-grown Al2O3 adhesion layers on oxygen-terminated diamond to test surface functionalization, chemical stability, and preservation of shallow NV sensors (Fig. 12).322 Subsequent silanization of these layers enabled grafting of polyethylene glycol (PEG) moieties and attachment of proteins and DNA molecules. Functionalization with PEG molecules is promising as it yields highly biocompatible surfaces and minimizes non-specific binding.304,323 While ALD and functionalization resulted in decreased coherence times for shallow (2.3–11 nm deep) NV centers compared to pristine diamond surfaces, some NVs still exhibited coherence times of up to 100 μs, which are sufficiently long for quantum sensing experiments. Moreover, the authors showed that the Al2O3 layer can be removed by KOH, providing an easily recyclable NV-sensing platform.
 | ||
| Fig. 12 Surface functionalization of Al2O3-capped diamond and subsequent characterization of shallow NV properties. (a) Recyclable functionalization scheme showing Al2O3 growth by atomic layer deposition, silanization of the oxide film, and chemical attachment. (b) Illustration of biomolecule attachment on silanized surfaces. (c) Confocal fluorescence image showing near-surface NV centers characterized following surface modification. (d) Representative coherence time traces before and after functionalization for a 4.8-nm-deep NV center. Adapted with permission from ref. 322 Copyright 2022 National Academy of Science. | ||
In summary, these recent examples show the benefit of amorphous oxide capping layers for NV-center sensing of functionalized diamond surfaces. Specifically, ALD affords precise control of adhesion layer thickness, enables the formation of dense monolayer coverage of molecular adsorbates, and facilitates recyclable surfaces through removal and regrowth. Nevertheless, there are challenges that accompany this functionalization strategy; the adhesion layer leads to increased distance between the NV and target spin, resulting in decreased signal (see Section 2.3). Moreover, the spin and charge properties of shallow NV centers were observed to degrade with application of ALD layers. Indeed, depending on the stoichiometry of aluminum and oxygen in AlxOy films, the layers can induce unfavorable electron affinity.324 In addition, these films may also host paramagnetic defects leading to reduced T2 times.325,326
5 Measurement strategies to mitigate surface noise
In addition to the aforementioned materials optimization and surface chemistries, several strategies can be employed during measurement to mitigate the effects of noise on the NV center. Typically, such measurement sequences increase the sensor coherence time or realize a detection method that is immune to certain noise sources. While a complete overview of the methods for reducing the effects of noise via careful engineering of the measurement protocol (or measurement “hardenings”) is beyond the scope of this work, we point the reader towards dedicated review articles.10,43 In the following section, we discuss illustrative examples for combating unwanted surface effects through experimental sequences. Importantly, the improvements in sensitivity afforded by such techniques are complementary to the advanced surface chemistry discussed thus far.5.1 Dynamical decoupling
While dynamical decoupling (DD) sequences were not initially developed for sensing, they have proven exceptionally useful for detecting signals at the specific frequencies where they do not refocus the signal;10,78,221,327 a phenomenon known as “recoupling”.The simplest DD sequence is the Hahn-echo protocol,70 comprising a single π pulse that protects the NV center from dephasing caused by variations in the magnetic field that are slow compared to the experiment duration. The basic idea is illustrated in Fig. 3: any phase accumulation on the NV center caused by variations in B0 are refocused. Similarly, decoherence from magnetic-field fluctuations at higher frequencies can be mitigated by instead applying a train of π pulses, with the interpulse delay τ dictating the high-frequency cut off (1/τ) of the noise spectrum. In such cases, the magnetic field must remain constant over shorter interpulse delays to achieve a refocusing. As a result, dynamical decoupling protocols can substantially enhance observed coherence times; in contrast, the magnetic noise at f = 1/(2τ) is instead integrated.
This phenomenon can be exploited for sensing environmental noise via changes in coherence at specific frequencies, essentially using the NV as a magnetic spectrum analyzer. Such sequences have also been used in scanning probe experiments to detect signals originating from AC-modulated single spins,328 currents,329 magnetic gradients330,331 and electric fields.84 For noise with frequency f, refocusing will occur for sequences with τ = 1/(2f) as well as for harmonics τ′ = N/(2f), where N = 2n + 1. Moreover, DD sequences may exhibit spurious sub-harmonics for finite-width pulses dependent on the phase cycling.57
Sequences containing over 104 π pulses have been successfully applied to a target NV center,55,332 resulting in coherence times exceeding one second at cryogenic temperatures.55 It is therefore of crucial importance that DD sequences do not themselves introduce significant errors, necessitating either high-fidelity pulses46 or fault-tolerant sequences. For example, a significant reduction in error can be achieved using a scheme proposed by Meiboom and Gill,333 who adapted the Carr–Purcell (CP) sequence
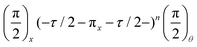 | (21) |
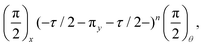 | (22) |
Such sequences have proven exceptionally useful for detecting, and even controlling, proximal nuclear spins. As with any other source of magnetic noise, DD sequences can very efficiently decouple the NV center from a bath of proximal spins if they are not also refocused by the DD pulses,55 which is typically the case due to the large zero-field splitting of the NV center. Additionally, DD protocols can impart back-action on coupled nuclear spins, which can be used as a resource for realizing coherent control over a multi-spin system.336,337 Encouragingly, recent efforts have made progress in designing DD sequences that refocus noise at only one frequency, suppressing spurious harmonics at the expense of a reduction in signal.338,339
5.2 Coherent driving of surface spins
Dynamical decoupling alone cannot mitigate noise from residual paramagnetic impurities (e.g., electron spins associated with dangling bonds at the surface or substitutional nitrogen centers) due to their fast Larmor precession at typical magnetic bias fields. However, if such spins have sufficiently long T1 times, one can combat noise by employing continuous, coherent driving of the spin bath.340,341 This complementary approach aims at engineering the spectral density of the magnetic noise generated by the electron spin bath itself. In practice, the bath spins are driven with Rabi frequency Ω, which leads to periodic modulation in the resulting noise at the NV location. Essentially, such driving shifts the center of the magnetic noise spectrum from f = 0 to f = Ω, which can reduce the spectral overlap with the NV measurement window,10 resulting in an increased NV coherence time. Noise can be reduced further by spectral engineering of the applied field342 or by using pulsed schemes.340,343Previously, such techniques have been used to reduce dephasing for NV-rich diamonds with large nitrogen content. However, coherent driving of the spin bath is applicable to any paramagnetic spins that exhibit sufficiently long T1 times, including nuclear spins. However, in this case, low nuclear gyromagnetic ratios pose a challenge in achieving high driving frequencies but also reduce the magnetic noise generated by such species.
5.3 Repetitive measurement and readout schemes
Often the sensor coherence time is insufficient for achieving the desired spectral resolution using standard DD protocols; in such cases, weak-measurement techniques may serve as a viable alternative.61,62 Such measurement schemes are appropriate only when coherent detection is possible (e.g., measuring coherently coupled nuclear spins) and involve applying sequential, weak measurements that result in limited back-action on the target spin. Since the NV center can be reinitialized between sequential measurements, the spectral resolution is no longer limited by the NV T2 time and instead by that of the target nuclear spin. Importantly, we note that the measurement sensitivity is still limited by the NV T2, motivating the use of highly coherent emitters.5.4 Double-quantum sensing
Most measurement protocols leverage only two of the three spin states within the ground-state manifold (|ms = 0〉 and |ms = ±1〉, see Section 2). In contrast, double-quantum protocols make use of the full spin-triplet subspace to obtain higher sensitivity. For example, in the Ramsey-like experiment shown in Fig. 3a, the first (π/2) pulse would be replaced by two pulses: a (π/2)y pulse on the |0〉 ↔ |−1〉 transition followed by a (−π)y pulse on the |0〉 ↔ |+1〉 transition. These rotations result in an equal superposition of both the |−1〉 and |+1〉 states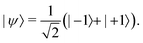 | (23) |
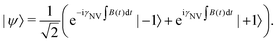 | (24) |
6 Emerging applications
The previously surveyed methods for diamond-surface functionalization could be used in concert with the exceptional sensitivity and spatial resolution of the NV to provide new approaches for molecular-level detection. Indeed, NV sensors could revolutionize many active areas of research since they operate at ambient conditions with minimal perturbation to the system of interest.346 In the following section, we highlight a selection of emerging applications within various fields of chemistry and biology that would benefit from (or necessitate) covalent attachment to a well-defined, functionalized diamond surface (summarized in Fig. 13), underscoring the immense potential of the NV-center sensing platform.6.1 Structure–function relationships in biomolecules
The potential for NV sensors to elucidate the structure of small to hierarchically more complex biomolecules (e.g., proteins) has been widely posited.17,23,24,347 While the first demonstration of NV-center NMR of external nuclear spins in chemical samples dates back to 2013,21,22 three-dimensional mapping of such spins within a molecule remains an outstanding challenge.Conventional solid-state NMR has made tremendous progress in structural analysis by employing fast magic-angle spinning (MAS)348 and high magnetic fields349 to achieve the exquisite spectral resolution required for detecting small chemical shifts. In contrast, NV center experiments are typically carried out at low applied magnetic field and MAS cannot (yet) be applied, precluding such detection. Nevertheless, NV centers could still be used to measure structure-function relationships in biomolecules via position-dependent hyperfine interactions with nuclear spins rather than chemical-shift differences.350,351 Furthermore, changes in the magnitude of magnetic noise detected from the Larmor precession of nuclear spin labels can serve as a proxy for conformational changes (e.g., opening of DNA hairpins).
Finally, optical pumping of the NV-center spin can provide a local, low-entropy source of nuclear-spin polarization that could provide complementary structural information to conventional NMR and EPR techniques. In such experiments, nuclear spins coupled to the NV center are polarized beyond the thermal limit by transferring polarization from the NV.352–355 Subsequently, the polarized spin bath can be detected classically (using NMR pick-up coils) or coherently using the NV center.61
6.2 Biosensing
The biocompatibility of diamond supports the use of NV centers for bio-sensing applications.356,357 To that end, the in vitro detection of viral RNA using NV centers was first demonstrated in 2020 using a lateral-flow format for HIV diagnosis.358 In this work, the presence of HIV-1-RNA caused immobilization of antibody functionalized nanodiamonds, which was subsequently observed via NV fluorescence readout. In addition, Li et al. proposed a sensing scheme for SARS-CoV-2 RNA that exploits T1 relaxation of NV centers in nanodiamonds.359 In analogy to earlier work on pH and redox sensing,360 they propose Gd3+ as a source for magnetic noise. Specifically, nanodiamonds could be coated with DNA strands containing electrostatically bound Gd3+; upon base-pair matching with the complementary viral RNA, the DNA molecules including Gd3+ complexes would be released from the diamond surface. This reaction would result in decreased noise and therefore longer relaxation times for near-surface NV centers.Notably, the majority of NV biosensing research has thus far leveraged nanodiamonds rather than bulk substrates, which can directly utilize many of the diamond surface preparation and functionalization strategies described in this Review. Further supported by significant advancements in production and purification of nanodiamonds, this alternate platform has seen application in biomedical sensing and imaging,361–365 drug delivery,366 and reaction monitoring,233,367 as discussed in recent reviews.346,368,369 Specifically, these experiments have monitored physiological variables, such as concentration of ions, radicals, and biomolecules, in addition to pH, temperature, and redox potential or forces.357 Informed by these efforts, bulk diamond substrates offer a complementary or alternative sensing platform for hosting NV centers with significantly improved spin properties. It is worth noting that motivations for chemical control of bulk surfaces may differ from those of nanodiamonds intended for studies of aggregation, protein corona formation, cellular uptake, and targeted delivery. In addition, alignment of the magnetic field required for NV-center experiments is simpler for bulk substrates than for randomly orientated nanocrystals.370,371 Nevertheless, both nano- and bulk-diamond platforms would benefit from improved NV-center properties and deterministic surface functionalization protocols, motivating progress in this field.
6.3 The radical-pair reaction
Radical pairs are reaction intermediates that either encounter each other in solution or are created simultaneously, usually by a chemical reaction such as homolytic bond cleavage or photo-induced electron transfer (e.g., in blue-light photoreceptive cryptochromes).372–374Research on radical pairs began in the late 20th century in the context of Chemically Induced Dynamic Nuclear Polarization (CIDNP)375 and Chemically Induced Dynamic Electron Polarization (CIDEP). Later, this research gained interest in the area of magnetic-field effects (MFE),376–378 including low-field effects with biological significance379,380 (e.g., magnetoreception in birds381,382). Currently, most radical-pair research focuses on spin-correlated states, which may be either a spin singlet or triplet state.383 Since radical recombination commonly occurs solely from the singlet state, the inter-conversion between singlet and triplet states, which is mainly driven by differences in Zeeman frequencies and hyperfine interactions with surrounding nuclei, is a crucial parameter for the chemical outcome.
Recently, Finkler et al. proposed to use the NV as a sensor for observing this radical-pair mechanism.384 In such an experiment, a nearby radical pair would experience an effective magnetic field (and therefore singlet-to-triplet conversion rate) that depends on the spin state of the NV sensor. An alternate strategy was introduced by Liu et al.385, who proposed to use the electric-field sensitivity of the NV to measure radical-pair recombination rates. Essentially, the charge-separated state of the pair generates a non-zero electric field at the NV position that vanishes upon recombination. Consequently, detection of this field would enable measurement of recombination rates at the single-molecule level. We note that both proposals rely on radical-pair generation in proximal molecules, which would benefit greatly from the advances in diamond functionalization discussed in this Review.
6.4 Chiral-induced spin selectivity
Chiral-induced spin selectivity (CISS) refers to enantioselective and electron spin-dependent transmission of electrons through chiral molecules and crystalline materials.386,387 While spin-selective electron transfer is typically associated with magnetic materials or those possessing substantial spin-orbit coupling, the discovery of the CISS effect suggests that organic molecules lacking inversion symmetry that are composed of low-atomic-weight building blocks may also be promising systems for spintronics applications.388 Since this discovery, experiments have revealed large asymmetry in the scattering probability of polarized photoelectrons traversing thin organized films of chiral organic molecules,388–392 observed spin selectivity in the conduction regime,393–396 and measured spin-dependent charge polarization within molecules and at surfaces.397–399 However, despite concurrent advances in theoretical models to describe this effect,400–406 questions remain regarding the role of spin coherence and the magnitude of spin polarization accompanying electron transport within chiral molecules. Moreover, the majority of CISS measurements have relied on ferromagnetic electrodes, which may perturb observed polarizations due to the interface between ferromagnetic surfaces and the chiral material.407–410Several recent proposals outline methods for studying CISS via magnetic-resonance experiments.411–413 Chiesa et al. described methods for detection through either asymmetry in the dipolar coupling between the sensor and the polarized spin or via polarization transfer from the polarized spin to the sensor.411 Meanwhile, Fay et al. suggested monitoring coherence associated with CISS in the presence of a magnetic field that is orthogonal to the chiral axis.412 Critically, proposed experiments necessitate well-aligned molecular assemblies. Moreover, application of conventional NMR and EPR measurements may be limited by the need for substantial magnetic fields and large spin ensembles. In contrast, NV centers present a promising method for detection of CISS locally at the nanoscale. Notably, NVs were used to indirectly probe CISS by Merzeida et al,414 who measured the magnetization orientation in a ferromagnetic layer that exhibited perpendicular anisotropy from chiral molecular adsorption. In future experiments, chiral molecules could be instead assembled directly on diamond surfaces, in close proximity to NV centers, with externally driven charge transfer to generate spin polarization.393,415–418 Adsorbed molecules supporting charge- and spin-polarized electrons would induce both electric and magnetic fields at the NV position, enabling new methods for characterization of CISS that could provide novel mechanistic insight.
6.5 Catalysis
As previously mentioned, solid-state NMR is a powerful tool for studying the structure of heterogeneous catalysts419 due to advancements in magnetic-field strength,349 fast MAS,348 and dynamic nuclear polarization (DNP).420 However, it is often unclear whether the relevant, active species are observed since the working conditions of most catalysts include either high temperatures or pressures, which differ dramatically from standard measurement conditions.421 Consequently, the development of techniques for variable temperature and pressure operando NMR422 are viewed as an important step towards in situ characterization of catalytic materials. Such schemes are still limited to probing sensitive NMR nuclei that are in high abundance. Moreover, the detection of active sites in supported single-site catalysts is not compatible with this technique since such studies rely on solid-effect DNP and therefore must be performed at liquid–nitrogen temperatures in frozen glassy matrices of radical solution.423 In contrast, the high pressure and temperature stability of diamond, in combination with exquisitely sensitive NV sensors, could enable detection of dilute, insensitive nuclear species at relevant catalytic working conditions. For such experiments, single-site catalysts would be prepared in the vicinity of NV sensor spins using a surface-organometallic chemistry.424 The conventional metal-oxide support (e.g., SiO2, Al2O3) could be replaced either by well-defined diamond surface terminations with controllable densities of anchoring sites (e.g., hydroxyls or amines) or by a thin layer of oxide.321 The latter option would utilize the original grafting chemistry at the cost of larger NV-sample distances, as exemplified in Fig. 13 for selected heterogeneous olefin-metathesis catalysts.424 Subsequently, structural changes resulting from catalytic reactions (e.g., loss of a ligand or change in oxidation state of the metal) would be detected using the NV center. Notably, while the large chemical-shift range and quadrupolar nature of many interesting NMR-active metals (e.g., 195Pt, 71Ga) are a major challenge in conventional NMR spectroscopy, they could serve as a resource for NV-center sensing.7 Outlook
NMR and EPR spectroscopy of molecules are powerful tools for elucidating details of chemical structure, intermolecular interactions, and chemical reactions. The experimental approach wherein traditional inductive detectors are replaced with NV centers in diamond has facilitated highly sensitive and localized spectroscopy, allowing for detection of electron and nuclear spins in external targets at the single- or few-spin level. Encouragingly, vast improvements in measurement sensitivity have been obtained through advances in diamond surface engineering that reduce charge instability and decoherence for shallow emitters. In addition, novel methods for chemical functionalization of diamond allows for deterministic, covalent attachment of target molecular species.Despite this impressive progress, additional experimental challenges must also be overcome. For instance, the stability of molecular films or of hierarchically ordered structures in biomolecules may be compromised by extended exposure to laser- and microwave-induced heating. Nevertheless, use of low laser power as well as reduced experimental duty cycles may help to prevent ablation of specifically bound molecules during extended measurement times. Likewise, reduced microwave duty cycles, or elimination of microwave sources entirely (e.g., for relaxometry measurements) can mitigate heating issues. In addition, current detection sensitivities necessitate long integration times, placing limits on reaction monitoring or tracking of transient paramagnetic intermediates. Greater control over molecular density, orientation, and binding configurations at diamond surfaces will circumvent rapid diffusion of analytes into and out of NV sensing volumes, allowing for longer measurements. Moreover, motional dynamics and thermal fluctuations in large molecules induce signal broadening, complicating the extraction of structural and functional information and localized imaging of surface spins. Depending on the sensing application, immobilization approaches that restrict motional degrees of freedom can be employed to reduce spectral broadening. Finally, despite the exquisite sensitivity and spatial resolution, NV-center spectroscopy cannot achieve the spectral resolution of conventional spectroscopy methods. Indeed, typical magnetic-field biases applied in NV experiments are on the order of ca. 10−3–10−1 T, compared to ca. 100–101 T in conventional NMR. Therefore, a 5 ppm 1H chemical shift, easily resolved in conventional NMR with an operating field strength of, e.g., 600 MHz, would result in an absolute shift of <1 Hz at 20 mT. However, novel NV approaches including homonuclear decoupling sequences,27 ensemble measurements,28 or hyperpolarization techniques29 provide promising paths forward.
In conclusion, advances in diamond surface engineering and chemical functionalization have facilitated landmark advances in nanoscale NMR and EPR using NV centers. Moving forward, the simultaneous immobilization of chemical analytes and preservation of NV sensing properties represents a critical step toward single-spin, coherent detection in chemically and biologically relevant systems. Efforts to overcome these challenges will benefit from the interdisciplinary nature of this research field, which lies at the intersection of surface chemistry, materials science, and quantum metrology. Motivated by the promise of new insights into molecular structure, spin transport, and reaction monitoring, the utility of NV-center sensing for the chemical sciences has only just begun to be realized.
Author contributions
Following CRediT definitions: conceptualization: E. J., K. H., L. A. V., W. S. H., C. L. D., J. M. A.; funding acquisition: C. L. D., J. M. A.; investigation: E. J., K. H., L. A. V., W. S. H., J. M. A.; project administration: J. M. A.; supervision: J. M. A.; validation: E. J., K. H., L. A. V., W. S. H., C. L. D., J. M. A.; visualization: E. J., K. H., L. A. V., J. M. A.; writing – original draft: E. J., K. H., L. A. V., W. S. H., J. M. A.; writing – review & editing: E. J., K. H., L. A. V., W. S. H., C. L. D., J. M. A.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Lilian Childress, Claire McLellan, Marius Palm, Romana Schirhagl, and Pol Welter for helpful comments and discussions. We gratefully acknowledge the Swiss National Science Foundation (SNSF) Ambizione Grant, “Quantum Coherence in Mirror-Image Molecules” [PZ00P2_201590], SNSF Project Grant No. 200020 175600, and funding through the SNSF NCCR QSIT, a National Centre of Competence in Research in Quantum Science and Technology, Grant No. 51NF40-185902 for support of this work. We also gratefully acknowledge the European Research Council through ERC CoG 817720 (IMAGINE) and the Advancing Science and TEchnology thRough dIamond Quantum Sensing (ASTERQIS) program, Grant No. 820394, of the European Commission. J. M. A. also acknowledges an ETH Career Seed Grant and E. J. acknowledges support from a Natural Sciences and Engineering Research Council of Canada (NSERC) postdoctoral fellowship (application number PDF-558200-2021).Notes and references
- R. R. Ernst, Angew. Chem., Int. Ed. Engl., 1992, 31, 805–823 CrossRef
.
-
A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, 2001 Search PubMed
.
- K. Wüthrich, Angew. Chem., Int. Ed., 2003, 42, 3340–3363 CrossRef PubMed
.
- M. M. Roessler and E. Salvadori, Chem. Soc. Rev., 2018, 47, 2534–2553 RSC
.
- G. Jeschke, A. Bender, H. Paulsen, H. Zimmermann and A. Godt, J. Magn. Reson., 2004, 169, 1–12 CrossRef CAS PubMed
.
- E. Terreno, D. D. Castelli, A. Viale and S. Aime, Chem. Rev., 2010, 110, 3019–3042 CrossRef CAS PubMed
.
- J. H. Lee, Y. Okuno and S. Cavagnero, J. Magn. Reson., 2014, 241, 18–31 CrossRef CAS PubMed
.
- C. L. Degen, M. Poggio, H. J. Mamin, C. T. Rettner and D. Rugar, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1313–1317 CrossRef CAS PubMed
.
- M. S. Grinolds, M. Warner, K. De Greve, Y. Dovzhenko, L. Thiel, R. L. Walsworth, S. Hong, P. Maletinsky and A. Yacoby, Nat. Nanotechnol., 2014, 9, 279–284 CrossRef CAS PubMed
.
- C. L. Degen, F. Reinhard and P. Cappellaro, Rev. Mod. Phys., 2017, 89, 035002 CrossRef
.
- G. Wolfowicz, F. J. Heremans, C. P. Anderson, S. Kanai, H. Seo, A. Gali, G. Galli and D. D. Awschalom, Nat. Rev. Mater., 2021, 6, 906–925 CrossRef CAS
.
- A. Gruber, A. Dräbenstedt, C. Tietz, L. Fleury, J. Wrachtrup and C. von Borczyskowski, Science, 1997, 276, 2012–2014 CrossRef CAS
.
- F. Jelezko, T. Gaebel, I. Popa, A. Gruber and J. Wrachtrup, Phys. Rev. Lett., 2004, 92, 076401 CrossRef CAS PubMed
.
- G. Balasubramanian, I. Y. Chan, R. Kolesov, M. Al-Hmoud, J. Tisler, C. Shin, C. Kim, A. Wojcik, P. R. Hemmer, A. Krueger, T. Hanke, A. Leitenstorfer, R. Bratschitsch, F. Jelezko and J. Wrachtrup, Nature, 2008, 455, 648–651 CrossRef CAS PubMed
.
- C. L. Degen, Appl. Phys. Lett., 2008, 92, 243111 CrossRef
.
- M. W. Doherty, N. B. Manson, P. Delaney, F. Jelezko, J. Wrachtrup and L. C. L. Hollenberg, Phys. Rep., 2013, 528, 1–45 CrossRef CAS
.
- R. Schirhagl, K. Chang, M. Loretz and C. L. Degen, Annu. Rev. Phys. Chem., 2014, 65, 83–105 CrossRef CAS PubMed
.
- D. B. Bucher, D. P. L. Aude Craik, M. P. Backlund, M. J. Turner, O. Ben Dor, D. R. Glenn and R. L. Walsworth, Nat. Protoc., 2019, 14, 2707–2747 CrossRef CAS PubMed
.
- T. Weggler, C. Ganslmayer, F. Frank, T. Eilert, F. Jelezko and J. Michaelis, Nano Lett., 2020, 20, 2980–2985 CrossRef CAS PubMed
.
- G. Wang, Y.-X. Liu, Y. Zhu and P. Cappellaro, Nano Lett., 2021, 21, 5143–5150 CrossRef CAS
.
- T. Staudacher, F. Shi, S. Pezzagna, J. Meijer, J. Du, C. A. Meriles, F. Reinhard and J. Wrachtrup, Science, 2013, 339, 561–563 CrossRef CAS PubMed
.
- H. J. Mamin, M. Kim, M. H. Sherwood, C. T. Rettner, K. Ohno, D. D. Awschalom and D. Rugar, Science, 2013, 339, 557–560 CrossRef CAS
.
- F. Shi, Q. Zhang, P. Wang, H. Sun, J. Wang, X. Rong, M. Chen, C. Ju, F. Reinhard, H. Chen, J. Wrachtrup, J. Wang and J. Du, Science, 2015, 347, 1135–1138 CrossRef CAS PubMed
.
- I. Lovchinsky, A. O. Sushkov, E. Urbach, N. P. de Leon, S. Choi, K. De Greve, R. Evans, R. Gertner, E. Bersin, C. Müller, L. McGuinness, F. Jelezko, R. L. Walsworth, H. Park and M. D. Lukin, Science, 2016, 351, 836–841 CrossRef CAS PubMed
.
- F. Shi, F. Kong, P. Zhao, X. Zhang, M. Chen, S. Chen, Q. Zhang, M. Wang, X. Ye, Z. Wang, Z. Qin, X. Rong, J. Su, P. Wang, P. Z. Qin and J. Du, Nat. Methods, 2018, 15, 697–699 CrossRef CAS
.
- A. O. Sushkov, N. Chisholm, I. Lovchinsky, M. Kubo, P. K. Lo, S. D. Bennett, D. Hunger, A. Akimov, R. L. Walsworth, H. Park and M. D. Lukin, Nano Lett., 2014, 14, 6443–6448 CrossRef CAS PubMed
.
- N. Aslam, M. Pfender, P. Neumann, R. Reuter, A. Zappe, F. F. de Oliveira, A. Denisenko, H. Sumiya, S. Onoda, J. Isoya and J. Wrachtrup, Science, 2017, 357, 67–71 CrossRef CAS
.
- D. R. Glenn, D. B. Bucher, J. Lee, M. D. Lukin, H. Park and R. L. Walsworth, Nature, 2018, 555, 351–354 CrossRef CAS
.
- N. Arunkumar, D. B. Bucher, M. J. Turner, P. TomHon, D. Glenn, S. Lehmkuhl, M. D. Lukin, H. Park, M. S. Rosen, T. Theis and R. L. Walsworth, PRX Quantum, 2021, 2, 010305 CrossRef
.
- S. Sangtawesin, B. L. Dwyer, S. Srinivasan, J. J. Allred, L. V. H. Rodgers, K. De Greve, A. Stacey, N. Dontschuk, K. M. O'Donnell, D. Hu, D. A. Evans, C. Jaye, D. A. Fischer, M. L. Markham, D. J. Twitchen, H. Park, M. D. Lukin and N. P. de Leon, Phys. Rev. X, 2019, 9, 031052 CAS
.
- D. Bluvstein, Z. Zhang and A. C. Bleszynski Jayich, Phys. Rev. Lett., 2019, 122, 076101 CrossRef CAS PubMed
.
- Á. Gali, Nanophotonics, 2019, 8, 1907–1943 Search PubMed
.
- A. Gali, M. Fyta and E. Kaxiras, Phys. Rev. B, 2008, 77, 155206 CrossRef
.
- F. Jelezko and J. Wrachtrup, Phys. Status Solidi A, 2006, 203, 3207–3225 CrossRef CAS
.
- M. W. Doherty, F. Dolde, H. Fedder, F. Jelezko, J. Wrachtrup, N. B. Manson and L. C. L. Hollenberg, Phys. Rev. B, 2012, 85, 205203 CrossRef
.
- E. Tiesinga, P. J. Mohr, D. B. Newell and B. N. Taylor, Rev. Mod. Phys., 2021, 93, 025010 CrossRef CAS
.
- S. Felton, A. M. Edmonds, M. E. Newton, P. M. Martineau, D. Fisher, D. J. Twitchen and J. M. Baker, Phys. Rev. B, 2009, 79, 075203 CrossRef
.
- K. Herb, R. Tschaggelar, G. Denninger and G. Jeschke, J. Magn. Reson., 2018, 289, 100–106 CrossRef CAS PubMed
.
- J. R. Maze, A. Gali, E. Togan, Y. Chu, A. Trifonov, E. Kaxiras and M. D. Lukin, New. J. Phys., 2011, 13, 025025 CrossRef
.
- E. V. Oort and M. Glasbeek, Chem. Phys. Lett., 1990, 168, 529–532 CrossRef
.
- J. Michl, J. Steiner, A. Denisenko, A. Bülau, A. Zimmermann, K. Nakamura, H. Sumiya, S. Onoda, P. Neumann, J. Isoya and J. Wrachtrup, Nano Lett., 2019, 19, 4904–4910 CrossRef CAS PubMed
.
- F. Jelezko and J. Wrachtrup, Phys. Status Solidi A, 2006, 203, 3207–3225 CrossRef CAS
.
- J. F. Barry, J. M. Schloss, E. Bauch, M. J. Turner, C. A. Hart, L. M. Pham and R. L. Walsworth, Rev. Mod. Phys., 2020, 92, 015004 CrossRef CAS
.
- K.-M. C. Fu, C. Santori, P. E. Barclay, L. J. Rogers, N. B. Manson and R. G. Beausoleil, Phys. Rev. Lett., 2009, 103, 256404 CrossRef PubMed
.
- J. Happacher, D. A. Broadway, J. Bocquel, P. Reiser, A. Jimenéz, M. A. Tschudin, L. Thiel, D. Rohner, M. L. G. Puigibert, B. Shields, J. R. Maze, V. Jacques and P. Maletinsky, Phys. Rev. Lett., 2022, 128, 177401 CrossRef CAS PubMed
.
- X. Rong, J. Geng, F. Shi, Y. Liu, K. Xu, W. Ma, F. Kong, Z. Jiang, Y. Wu and J. Du, Nat. Commun., 2015, 6, 8748 CrossRef CAS PubMed
.
- A. Dreau, M. Lesik, L. Rondin, P. Spinicelli, O. Arcizet, J.-F. Roch and V. Jacques, Phys. Rev. B, 2011, 84, 195204 CrossRef
.
- P. E. Barclay, K.-M. C. Fu, C. Santori, A. Faraon and R. G. Beausoleil, Phys. Rev. X, 2011, 1, 011007 Search PubMed
.
- L. Rondin, G. Dantelle, A. Slablab, F. Grosshans, F. Treussart, P. Bergonzo, S. Perruchas, T. Gacoin, M. Chaigneau, H.-C. Chang, V. Jacques and J.-F. Roch, Phys. Rev. B, 2010, 82, 115449 CrossRef
.
- L. Robledo, H. Bernien, T. van der Sar and R. Hanson, New J. Phys., 2011, 13, 025013 CrossRef
.
- G. Thiering and A. Gali, Phys. Rev. B, 2018, 98, 085207 CrossRef CAS
.
- The authors have experimentally observed several NV centers with C > 0.4 throughout their collective work.
- F. Bruckmaier, K. D. Briegel and D. B. Bucher, J. Magn. Reson. Open, 2021, 8-9, 100023 CrossRef
.
- A. Jarmola, V. M. Acosta, K. Jensen, S. Chemerisov and D. Budker, Phys. Rev. Lett., 2012, 108, 197601 CrossRef CAS PubMed
.
- M. H. Abobeih, J. Cramer, M. A. Bakker, N. Kalb, M. Markham, D. J. Twitchen and T. H. Taminiau, Nat. Commun., 2018, 9, 2552 CrossRef CAS PubMed
.
- E. D. Herbschleb, H. Kato, Y. Maruyama, T. Danjo, T. Makino, S. Yamasaki, I. Ohki, K. Hayashi, H. Morishita, M. Fujiwara and N. Mizuochi, Nat. Commun., 2019, 10, 3766 CrossRef CAS PubMed
.
- M. Loretz, J. M. Boss, T. Rosskopf, H. J. Mamin, D. Rugar and C. L. Degen, Phys. Rev. X, 2015, 5, 021009 Search PubMed
.
- J. M. Boss, K. Chang, J. Armijo, K. Cujia, T. Rosskopf, J. R. Maze and C. L. Degen, Phys. Rev. Lett., 2016, 116, 197601 CrossRef CAS PubMed
.
- J. M. Boss, K. S. Cujia, J. Zopes and C. L. Degen, Science, 2017, 356, 837–840 CrossRef CAS PubMed
.
- S. Schmitt, T. Gefen, F. M. Stürner, T. Unden, G. Wolff, C. Müller, J. Scheuer, B. Naydenov, M. Markham, S. Pezzagna, J. Meijer, I. Schwarz, M. Plenio, A. Retzker, L. P. McGuinness and F. Jelezko, Science, 2017, 356, 832–837 CrossRef CAS PubMed
.
- K. S. Cujia, J. M. Boss, K. Herb, J. Zopes and C. L. Degen, Nature, 2019, 571, 230–233 CrossRef CAS
.
- M. Pfender, P. Wang, H. Sumiya, S. Onoda, W. Yang, D. B. R. Dasari, P. Neumann, X.-Y. Pan, J. Isoya, R.-B. Liu and J. Wrachtrup, Nat. Commun., 2019, 10, 594 CrossRef CAS PubMed
.
- J. M. Taylor, P. Cappellaro, L. Childress, L. Jiang, D. Budker, P. R. Hemmer, A. Yacoby, R. Walsworth and M. D. Lukin, Nat. Phys., 2008, 4, 810–816 Search PubMed
.
- D. A. Hopper, H. J. Shulevitz and L. C. Bassett, Micromachines, 2018, 9, 437 Search PubMed
.
- R. P. Feynman, F. L. Vernon and R. W. Hellwarth, J. Appl. Phys., 1957, 28, 49–52 CrossRef CAS
.
- C. A. Meriles, L. Jiang, G. Goldstein, J. S. Hodges, J. Maze, M. D. Lukin and P. Cappellaro, J. Chem. Phys., 2010, 133, 124105 CrossRef PubMed
.
- M. Loretz, S. Pezzagna, J. Meijer and C. L. Degen, Appl. Phys. Lett., 2014, 104, 033102 CrossRef
.
- L. M. Pham, S. J. DeVience, F. Casola, I. Lovchinsky, A. O. Sushkov, E. Bersin, J. Lee, E. Urbach, P. Cappellaro, H. Park, A. Yacoby, M. Lukin and R. L. Walsworth, Phys. Rev. B, 2016, 93, 045425 CrossRef
.
- N. F. Ramsey, Phys. Rev., 1950, 78, 695–699 CrossRef CAS
.
- E. L. Hahn, Phys. Rev., 1950, 80, 580–594 CrossRef
.
-
R. J. Schoelkopf, A. A. Clerk, S. M. Girvin, K. W. Lehnert and M. H. Devoret, Qubits as Spectrometers of Quantum Noise, Springer, Netherlands, 2003, pp. 175–203 Search PubMed
.
- J. H. Cole and L. C. L. Hollenberg, Nanotechnology, 2009, 20, 495401 CrossRef
.
- L. T. Hall, J. H. Cole, C. D. Hill and L. C. L. Hollenberg, Phys. Rev. Lett., 2009, 103, 220802 CrossRef CAS PubMed
.
- L. T. Hall, P. Kehayias, D. A. Simpson, A. Jarmola, A. Stacey, D. Budker and L. C. L. Hollenberg, Nat. Commun., 2016, 7, 10211 CrossRef CAS PubMed
.
- M. Kim, H. J. Mamin, M. H. Sherwood, K. Ohno, D. D. Awschalom and D. Rugar, Phys. Rev. Lett., 2015, 115, 087602 CrossRef CAS PubMed
.
- R. Li, F. Kong, P. Zhao, Z. Cheng, Z. Qin, M. Wang, Q. Zhang, P. Wang, Y. Wang, F. Shi and J. Du, Phys. Rev. Lett., 2020, 124, 247701 CrossRef CAS PubMed
.
- S. Steinert, F. Ziem, L. T. Hall, A. Zappe, M. Schweikert, N. Götz, A. Aird, G. Balasubramanian, L. Hollenberg and J. Wrachtrup, Nat. Commun., 2013, 4, 1607 CrossRef CAS PubMed
.
- Y. Romach, C. Müller, T. Unden, L. J. Rogers, T. Isoda, K. M. Itoh, M. Markham, A. Stacey, J. Meijer, S. Pezzagna, B. Naydenov, L. P. McGuinness, N. Bar-Gill and F. Jelezko, Phys. Rev. Lett., 2015, 114, 017601 CrossRef CAS PubMed
.
- P. Tamarat, T. Gaebel, J. R. Rabeau, M. Khan, A. D. Greentree, H. Wilson, L. C. L. Hollenberg, S. Prawer, P. Hemmer, F. Jelezko and J. Wrachtrup, Phys. Rev. Lett., 2006, 97, 083002 CrossRef PubMed
.
- D. A. Broadway, N. Dontschuk, A. Tsai, S. E. Lillie, C. T.-K. Lew, J. C. McCallum, B. C. Johnson, M. W. Doherty, A. Stacey, L. C. L. Hollenberg and J.-P. Tetienne, Nat. Electron., 2018, 1, 502–507 CrossRef CAS
.
- A. Stacey, N. Dontschuk, J.-P. Chou, D. A. Broadway, A. K. Schenk, M. J. Sear, J.-P. Tetienne, A. Hoffman, S. Prawer, C. I. Pakes, A. Tadich, N. P. de Leon, A. Gali and L. C. L. Hollenberg, Adv. Mater. Interfaces, 2019, 6, 1801449 CrossRef
.
- F. Dolde, M. W. Doherty, J. Michl, I. Jakobi, B. Naydenov, S. Pezzagna, J. Meijer, P. Neumann, F. Jelezko, N. B. Manson and J. Wrachtrup, Phys. Rev. Lett., 2014, 112, 097603 CrossRef PubMed
.
- M. C. Marshall, R. Ebadi, C. Hart, M. J. Turner, M. J. H. Ku, D. F. Phillips and R. L. Walsworth, Phys. Rev. Appl., 2022, 17, 024041 CrossRef CAS
.
- F. Dolde, H. Fedder, M. W. Doherty, T. Nöbauer, F. Rempp, G. Balasubramanian, T. Wolf, F. Reinhard, L. C. L. Hollenberg, F. Jelezko and J. Wrachtrup, Nat. Phys., 2011, 7, 459–463 Search PubMed
.
- T. Iwasaki, W. Naruki, K. Tahara, T. Makino, H. Kato, M. Ogura, D. Takeuchi, S. Yamasaki and M. Hatano, ACS Nano, 2017, 11, 1238–1245 CrossRef CAS
.
- L. M. Oberg, M. O. de Vries, L. Hanlon, K. Strazdins, M. S. J. Barson, M. W. Doherty and J. Wrachtrup, Phys. Rev. Appl., 2020, 14, 014085 CrossRef CAS
.
- K. Bian, W. Zheng, X. Zeng, X. Chen, R. Stöhr, A. Denisenko, S. Yang, J. Wrachtrup and Y. Jiang, Nat. Commun., 2021, 12, 2457 CrossRef CAS PubMed
.
- M. S. J. Barson, L. M. Oberg, L. P. McGuinness, A. Denisenko, N. B. Manson, J. Wrachtrup and M. W. Doherty, Nano Lett., 2021, 21, 2962–2967 CrossRef CAS PubMed
.
- V. M. Acosta, E. Bauch, M. P. Ledbetter, A. Waxman, L.-S. Bouchard and D. Budker, Phys. Rev. Lett., 2010, 104, 070801 CrossRef CAS
.
- M. W. Doherty, V. V. Struzhkin, D. A. Simpson, L. P. McGuinness, Y. Meng, A. Stacey, T. J. Karle, R. J. Hemley, N. B. Manson, L. C. L. Hollenberg and S. Prawer, Phys. Rev. Lett., 2014, 112, 047601 CrossRef
.
- M. Block, B. Kobrin, A. Jarmola, S. Hsieh, C. Zu, N. L. Figueroa, V. M. Acosta, J. Minguzzi, J. Maze, D. Budker and N. Y. Yao, Phys. Rev. Appl., 2021, 16, 024024 CrossRef CAS
.
- T. Rosskopf, A. Dussaux, K. Ohashi, M. Loretz, R. Schirhagl, H. Watanabe, S. Shikata, K. M. Itoh and C. L. Degen, Phys. Rev. Lett., 2014, 112, 147602 CrossRef CAS
.
- B. J. Shields, Q. P. Unterreithmeier, N. P. de Leon, H. Park and M. D. Lukin, Phys. Rev. Lett., 2015, 114, 136402 CrossRef CAS PubMed
.
- D. A. Hopper, R. R. Grote, A. L. Exarhos and L. C. Bassett, Phys. Rev. B, 2016, 94, 241201 CrossRef
.
- L. Robledo, L. Childress, H. Bernien, B. Hensen, P. F. A. Alkemade and R. Hanson, Nature, 2011, 477, 574–578 CrossRef CAS PubMed
.
- B. Hensen, H. Bernien, A. E. Dréau, A. Reiserer, N. Kalb, M. S. Blok, J. Ruitenberg, R. F. L. Vermeulen, R. N. Schouten, C. Abellán, W. Amaya, V. Pruneri, M. W. Mitchell, M. Markham, D. J. Twitchen, D. Elkouss, S. Wehner, T. H. Taminiau and R. Hanson, Nature, 2015, 526, 682–686 CrossRef CAS
.
- P. C. Humphreys, N. Kalb, J. P. J. Morits, R. N. Schouten, R. F. Vermeulen, D. J. Twitchen, M. Markham and R. Hanson, Nature, 2018, 558, 268–273 CrossRef CAS PubMed
.
- M. H. Abobeih, J. Randall, C. E. Bradley, H. P. Bartling, M. A. Bakker, M. J. Degen, M. Markham, D. J. Twitchen and T. H. Taminiau, Nature, 2019, 576, 411–415 CrossRef CAS PubMed
.
- C. G. Yale, B. B. Buckley, D. J. Christle, G. Burkard, F. J. Heremans, L. C. Bassett and D. D. Awschalom, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 7595–7600 CrossRef CAS PubMed
.
- M. Ruf, M. IJspeert, S. van Dam, N. de Jong, H. van den Berg, G. Evers and R. Hanson, Nano Lett., 2019, 19, 3987–3992 CrossRef CAS
.
- C. Santori, P. E. Barclay, K.-M. C. Fu, R. G. Beausoleil, S. Spillane and M. Fisch, Nanotechnology, 2010, 21, 274008 CrossRef CAS
.
- L. Robledo, H. Bernien, I. van Weperen and R. Hanson, Phys. Rev. Lett., 2010, 105, 177403 CrossRef PubMed
.
- V. M. Acosta, E. Bauch, M. P. Ledbetter, C. Santori, K.-M. C. Fu, P. E. Barclay, R. G. Beausoleil, H. Linget, J. F. Roch, F. Treussart, S. Chemerisov, W. Gawlik and D. Budker, Phys. Rev. B, 2009, 80, 115202 CrossRef
.
- E. Janitz, M. K. Bhaskar and L. Childress, Optica, 2020, 7, 1232–1252 CrossRef
.
- B. J. M. Hausmann, M. Khan, Y. Zhang, T. M. Babinec, K. Martinick, M. McCutcheon, P. R. Hemmer and M. Lončar, Diamond Relat. Mater., 2010, 19, 621–629 CrossRef CAS
.
- J. P. Hadden, J. P. Harrison, A. C. Stanley-Clarke, L. Marseglia, Y.-L. D. Ho, B. R. Patton, J. L. O’Brien and J. G. Rarity, Appl. Phys. Lett., 2010, 97, 241901 CrossRef
.
- D. Riedel, D. Rohner, M. Ganzhorn, T. Kaldewey, P. Appel, E. Neu, R. J. Warburton and P. Maletinsky, Phys. Rev. Appl., 2014, 2, 064011 CrossRef CAS
.
- E. Neu, P. Appel, M. Ganzhorn, J. Miguel-Sánchez, M. Lesik, V. Mille, V. Jacques, A. Tallaire, J. Achard and P. Maletinsky, Appl. Phys. Lett., 2014, 104, 153108 CrossRef
.
- S. A. Momenzadeh, R. J. Stöhr, F. F. de Oliveira, A. Brunner, A. Denisenko, S. Yang, F. Reinhard and J. Wrachtrup, Nano Lett., 2015, 15, 165–169 CrossRef CAS PubMed
.
- L. Li, E. H. Chen, J. Zheng, S. L. Mouradian, F. Dolde, T. Schröder, S. Karaveli, M. L. Markham, D. J. Twitchen and D. Englund, Nano Lett., 2015, 15, 1493–1497 CrossRef CAS PubMed
.
- N. H. Wan, B. J. Shields, D. Kim, S. Mouradian, B. Lienhard, M. Walsh, H. Bakhru, T. Schröder and D. Englund, Nano Lett., 2018, 18, 2787–2793 CrossRef CAS
.
- D. Riedel, I. Söllner, B. J. Shields, S. Starosielec, P. Appel, E. Neu, P. Maletinsky and R. J. Warburton, Phys. Rev. X, 2017, 7, 031040 Search PubMed
.
- S.-W. Jeon, J. Lee, H. Jung, S.-W. Han, Y.-W. Cho, Y.-S. Kim, H.-T. Lim, Y. Kim, M. Niethammer, W. C. Lim, J. Song, S. Onoda, T. Ohshima, R. Reuter, A. Denisenko, J. Wrachtrup and S.-Y. Lee, ACS Photonics, 2020, 7, 2739–2747 CrossRef CAS
.
- D. J. McCloskey, N. Dontschuk, D. A. Broadway, A. Nadarajah, A. Stacey, J.-P. Tetienne, L. C. L. Hollenberg, S. Prawer and D. A. Simpson, ACS Appl. Mater. Interfaces, 2020, 12, 13421–13427 CrossRef CAS
.
- J. Choi, S. Choi, G. Kucsko, P. C. Maurer, B. J. Shields, H. Sumiya, S. Onoda, J. Isoya, E. Demler, F. Jelezko, N. Y. Yao and M. D. Lukin, Phys. Rev. Lett., 2017, 118, 093601 CrossRef PubMed
.
- D. Le Sage, L. M. Pham, N. Bar-Gill, C. Belthangady, M. D. Lukin, A. Yacoby and R. L. Walsworth, Phys. Rev. B, 2012, 85, 121202 CrossRef
.
- K. Jensen, N. Leefer, A. Jarmola, Y. Dumeige, V. M. Acosta, P. Kehayias, B. Patton and D. Budker, Phys. Rev. Lett., 2014, 112, 160802 CrossRef CAS
.
- H. Clevenson, M. E. Trusheim, C. Teale, T. Schröder, D. Braje and D. Englund, Nat. Phys., 2015, 11, 393–397 Search PubMed
.
- T. Wolf, P. Neumann, K. Nakamura, H. Sumiya, T. Ohshima, J. Isoya and J. Wrachtrup, Phys. Rev. X, 2015, 5, 041001 Search PubMed
.
- P. Kehayias, A. Jarmola, N. Mosavian, I. Fescenko, F. M. Benito, A. Laraoui, J. Smits, L. Bougas, D. Budker, A. Neumann, S. R. J. Brueck and V. M. Acosta, Nat. Commun., 2017, 8, 188 Search PubMed
.
- J. M. Smith, S. A. Meynell, A. C. Bleszynski Jayich and J. Meijer, Nanophotonics, 2019, 8, 1889–1906 Search PubMed
.
- J. Rabeau, P. Reichart, G. Tamanyan, D. N. Jamieson, S. Prawer, F. Jelezko, T. Gaebel, I. Popa, M. Domhan and J. Wrachtrup, Appl. Phys. Lett., 2006, 88, 023113 CrossRef
.
- S. Pezzagna, D. Rogalla, D. Wildanger, J. Meijer and A. Zaitsev, New J. Phys., 2011, 13, 035024 CrossRef
.
- J. O. Orwa, C. Santori, K. M. C. Fu, B. Gibson, D. Simpson, I. Aharonovich, A. Stacey, A. Cimmino, P. Balog, M. Markham, D. Twitchen, A. D. Greentree, R. G. Beausoleil and S. Prawer, J. Appl. Phys., 2011, 109, 083530 CrossRef
.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS
.
- J. Meijer, B. Burchard, M. Domhan, C. Wittmann, T. Gaebel, I. Popa, F. Jelezko and J. Wrachtrup, Appl. Phys. Lett., 2005, 87, 261909 CrossRef
.
- M. Lesik, P. Spinicelli, S. Pezzagna, P. Happel, V. Jacques, O. Salord, B. Rasser, A. Delobbe, P. Sudraud, A. Tallaire, J. Meijer and J.-F. Roch, Phys. Status Solidi A, 2013, 210, 2055–2059 CrossRef CAS
.
- S. Tamura, G. Koike, A. Komatsubara, T. Teraji, S. Onoda, L. P. McGuinness, L. Rogers, B. Naydenov, E. Wu, L. Yan, F. Jelezko, T. Ohshima, J. Isoya, T. Shinada and T. Tanii, Appl. Phys. Express, 2014, 7, 115201 CrossRef
.
- T. Schröder, M. E. Trusheim, M. Walsh, L. Li, J. Zheng, M. Schukraft, A. Sipahigil, R. E. Evans, D. D. Sukachev, C. T. Nguyen, J. L. Pacheco, R. M. Camacho, E. S. Bielejec, M. D. Lukin and D. Englund, Nat. Commun., 2017, 8, 15376 CrossRef
.
- D. M. Toyli, C. D. Weis, G. D. Fuchs, T. Schenkel and D. D. Awschalom, Nano Lett., 2010, 10, 3168–3172 CrossRef CAS PubMed
.
- P. Spinicelli, A. Dréau, L. Rondin, F. Silva, J. Achard, S. Xavier, S. Bansropun, T. Debuisschert, S. Pezzagna, J. Meijer, V. Jacques and J.-F. Roch, New J. Phys., 2011, 13, 025014 CrossRef
.
- I. Bayn, E. H. Chen, M. E. Trusheim, L. Li, T. Schröder, O. Gaathon, M. Lu, A. Stein, M. Liu, K. Kisslinger, H. Clevenson and D. Englund, Nano Lett., 2015, 15, 1751–1758 CrossRef CAS PubMed
.
- D. Scarabelli, M. Trusheim, O. Gaathon, D. Englund and S. J. Wind, Nano Lett., 2016, 16, 4982–4990 CrossRef CAS PubMed
.
- A. E. Rugar, H. Lu, C. Dory, S. Sun, P. J. McQuade, Z.-X. Shen, N. A. Melosh and J. Vuckovic, Nano Lett., 2020, 20, 1614–1619 CrossRef CAS PubMed
.
- P. Deák, B. Aradi, M. Kaviani, T. Frauenheim and A. Gali, Phys. Rev. B, 2014, 89, 075203 CrossRef
.
- A. G. Alekseev, V. N. Amosov, A. V. Krasil’nikov, S. N. Tugarinov, V. V. Frunze and A. Yu. Tsutskikh, Tech. Phys. Lett., 2000, 26, 496–498 CrossRef CAS
.
- D. J. Twitchen, M. E. Newton, J. M. Baker, T. R. Anthony and W. F. Banholzer, Phys. Rev. B, 1999, 59, 12900 CrossRef CAS
.
- B. Naydenov, F. Reinhard, A. Lämmle, V. Richter, R. Kalish, U. F. S. D’Haenens-Johansson, M. Newton, F. Jelezko and J. Wrachtrup, Appl. Phys. Lett., 2010, 97, 242511 CrossRef
.
- Y. Chu, N. P. de Leon, B. J. Shields, B. Hausmann, R. Evans, E. Togan, M. J. Burek, M. Markham, A. Stacey, A. S. Zibrov, A. Yacoby, D. J. Twitchen, M. D. Loncar, H. Park, P. Maletinsky and M. Lukin, Nano Lett., 2014, 14, 1982–1986 CrossRef CAS PubMed
.
- T. Yamamoto, T. Umeda, K. Watanabe, S. Onoda, M. L. Markham, D. J. Twitchen, B. Naydenov, L. P. McGuinness, T. Teraji, S. Koizumi, F. Dolde, H. Fedder, J. Honert, J. Wrachtrup, T. Ohshima, F. Jelezko and J. Isoya, Phys. Rev. B, 2013, 88, 075206 CrossRef
.
- J. Lang, S. Häußler, J. Fuhrmann, R. Waltrich, S. Laddha, J. Scharpf, A. Kubanek, B. Naydenov and F. Jelezko, Appl. Phys. Lett., 2020, 116, 064001 CrossRef CAS
.
- T. Lühmann, R. John, R. Wunderlich, J. Meijer and S. Pezzagna, Nat. Commun., 2019, 10, 4956 CrossRef PubMed
.
- M. Capelli, A. H. Heffernan, T. Ohshima, H. Abe, J. Jeske, A. Hope, A. D. Greentree, P. Reineck and B. C. Gibson, Carbon, 2019, 143, 714–719 CrossRef CAS
.
- T. Luo, L. Lindner, J. Langer, V. Cimalla, X. Vidal, F. Hahl, C. Schreyvogel, S. Onoda, S. Ishii, T. Ohshima, D. Wang, D. A. Simpson, B. C. Johnson, M. Capelli, R. Blinder and J. Jeske, New J. Phys., 2022, 24, 033030 CrossRef
.
- K. Ohno, F. J. Heremans, L. C. Bassett, B. A. Myers, D. M. Toyli, A. C. Bleszynski Jayich, C. J. Palmstrøm and D. D. Awschalom, Appl. Phys. Lett., 2012, 101, 082413 CrossRef
.
- K. Ohno, F. J. Heremans, C. F. de las Casas, B. A. Myers, B. J. Alemán, A. C. Bleszynski Jayich and D. D. Awschalom, Appl. Phys. Lett., 2014, 105, 052406 CrossRef
.
- C. Osterkamp, J. Lang, J. Scharpf, C. Müller, L. P. McGuinness, T. Diemant, R. J. Behm, B. Naydenov and F. Jelezko, Appl. Phys. Lett., 2015, 106, 113109 CrossRef
.
- J. C. Lee, D. O. Bracher, S. Cui, K. Ohno, C. A. McLellan, X. Zhang, P. Andrich, B. Alemán, K. J. Russell, A. P. Magyar, I. Aharonovich, A. Bleszynski Jayich, D. Awschalom and E. L. Hu, Appl. Phys. Lett., 2014, 105, 261101 CrossRef
.
- T. Jaffe, M. Attrash, M. K. Kuntumalla, R. Akhvlediani, S. Michaelson, L. Gal, N. Felgen, M. Fischer, J. P. Reithmaier, C. Popov, A. Hoffman and M. Orenstein, Nano Lett., 2020, 20, 3192–3198 CrossRef CAS PubMed
.
- J. Michl, T. Teraji, S. Zaiser, I. Jakobi, G. Waldherr, F. Dolde, P. Neumann, M. W. Doherty, N. B. Manson, J. Isoya and J. Wrachtrup, Appl. Phys. Lett., 2014, 104, 102407 CrossRef
.
- H. Ozawa, K. Tahara, H. Ishiwata, M. Hatano and T. Iwasaki, Appl. Phys. Express, 2017, 10, 045501 CrossRef
.
- T. Tatsuishi, K. Kanehisa, T. Kageura, T. Sonoda, Y. Hata, K. Kawakatsu, T. Tanii, S. Onoda, A. Stacey, S. Kono and H. Kawarada, Carbon, 2021, 180, 127–134 CrossRef CAS
.
- J. Martin, R. Wannemacher, J. Teichert, L. Bischoff and B. Köhler, Appl. Phys. Lett., 1999, 75, 3096–3098 CrossRef CAS
.
- B. Campbell and A. Mainwood, Phys. Status Solidi A, 2000, 181, 99–107 CrossRef CAS
.
- C. A. McLellan, B. A. Myers, S. Kraemer, K. Ohno, D. D. Awschalom and A. C. Bleszynski Jayich, Nano Lett., 2016, 16, 2450–2454 CrossRef CAS PubMed
.
- Y.-C. Chen, P. S. Salter, S. Knauer, L. Weng, A. C. Frangeskou, C. J. Stephen, S. N. Ishmael, P. R. Dolan, S. Johnson, B. L. Green, G. W. Morley, M. E. Newton, J. G. Rarity, M. J. Booth and J. M. Smith, Nat. Photonics, 2017, 11, 77–80 CrossRef CAS
.
- B. Sotillo, V. Bharadwaj, J. P. Hadden, M. Sakakura, A. Chiappini, T. T. Fernandez, S. Longhi, O. Jedrkiewicz, Y. Shimotsuma, L. Criante, R. Osellame, G. Galzerano, M. Ferrari, K. Miura, R. Ramponi, P. E. Barclay and S. M. Eaton, Sci. Rep., 2016, 6, 35566 CrossRef CAS
.
- F. Fávaro de Oliveira, S. A. Momenzadeh, D. Antonov, J. Scharpf, C. Osterkamp, B. Naydenov, F. Jelezko, A. Denisenko and J. Wrachtrup, Nano Lett., 2016, 16, 2228–2233 CrossRef PubMed
.
- F. Fávaro de Oliveira, S. A. Momenzadeh, D. Antonov, H. Fedder, A. Denisenko and J. Wrachtrup, Phys. Status Solidi A, 2016, 213, 2044–2050 CrossRef
.
- S. Felton, A. M. Edmonds, M. E. Newton, P. M. Martineau, D. Fisher and D. J. Twitchen, Phys. Rev. B, 2008, 77, 081201(R) CrossRef
.
- M. Pfender, N. Aslam, P. Simon, D. Antonov, G. Thiering, S. Burk, F. Fávaro de Oliveira, A. Denisenko, H. Fedder, J. Meijer, J. A. Garrido, A. Gali, T. Teraji, J. Isoya, M. W. Doherty, A. Alkauskas, A. Gallo, A. Grüneis, P. Neumann and J. Wrachtrup, Nano Lett., 2017, 17, 5931–5937 CrossRef CAS PubMed
.
- K. Y. Han, S. K. Kim, C. Eggeling and S. W. Hell, Nano Lett., 2010, 10, 3199–3203 CrossRef CAS
.
- G. Waldherr, J. Beck, M. Steiner, P. Neumann, A. Gali, T. Frauenheim, F. Jelezko and J. Wrachtrup, Phys. Rev. Lett., 2011, 106, 157601 CrossRef CAS
.
- X. Chen, C. Zou, Z. Gong, C. Dong, G. Guo and F. Sun, Light Sci.: Appl., 2015, 4, e230–e230 CrossRef CAS
.
- S. Baier, C. E. Bradley, T. Middelburg, V. V. Dobrovitski, T. H. Taminiau and R. Hanson, Phys. Rev. Lett., 2020, 125, 193601 CrossRef CAS PubMed
.
- S. Dhomkar, J. Henshaw, H. Jayakumar and C. A. Meriles, Sci. Adv., 2016, 2, e1600911 CrossRef PubMed
.
- S. Dhomkar, H. Jayakumar, P. R. Zangara and C. A. Meriles, Nano Lett., 2018, 18, 4046–4052 CrossRef CAS PubMed
.
- K. Beha, A. Batalov, N. B. Manson, R. Bratschitsch and A. Leitenstorfer, Phys. Rev. Lett., 2012, 109, 097404 CrossRef CAS PubMed
.
- A. Lozovoi, H. Jayakumar, D. Daw, G. Vizkelethy, E. Bielejec, M. W. Doherty, J. Flick and C. A. Meriles, Nat. Electron., 2021, 4, 717–724 CrossRef CAS
.
- Y. Doi, T. Makino, H. Kato, D. Takeuchi, M. Ogura, H. Okushi, H. Morishita, T. Tashima, S. Miwa, S. Yamasaki, P. Neumann, J. Wrachtrup, Y. Suzuki and N. Mizuochi, Phys. Rev. X, 2014, 4, 011057 CAS
.
- N. Mizuochi, T. Makino, H. Kato, D. Takeuchi, M. Ogura, H. Okushi, M. Nothaft, P. Neumann, A. Gali, F. Jelezko, J. Wrachtrup and S. Yamasaki, Nat. Photonics, 2012, 6, 299–303 CrossRef CAS
.
- N. Aslam, G. Waldherr, P. Neumann, F. Jelezko and J. Wrachtrup, New J. Phys., 2013, 15, 013064 CrossRef CAS
.
- X.-D. Chen, C.-L. Zou, F.-W. Sun and G.-C. Guo, Appl. Phys. Lett., 2013, 103, 013112 CrossRef
.
- N. B. Manson and J. P. Harrison, Diamond Relat. Mater., 2005, 14, 1705–1710 CrossRef CAS
.
- R. Giri, F. Gorrini, C. Dorigoni, C. E. Avalos, M. Cazzanelli, S. Tambalo and A. Bifone, Phys. Rev. B, 2018, 98, 045401 CrossRef CAS
.
- X.-D. Chen, S. Li, A. Shen, Y. Dong, C.-H. Dong, G.-C. Guo and F.-W. Sun, Phys. Rev. Appl., 2017, 7, 014008 CrossRef
.
- I. Meirzada, Y. Hovav, S. A. Wolf and N. Bar-Gill, Phys. Rev. B, 2018, 98, 245411 CrossRef CAS
.
- P. Ji and M. V. G. Dutt, Phys. Rev. B, 2016, 94, 024101 CrossRef
.
- R. P. Roberts, M. L. Juan and G. Molina-Terriza, Phys. Rev. B, 2019, 99, 174307 CrossRef CAS
.
- K. Groot-Berning, N. Raatz, I. Dobrinets, M. Lesik, P. Spinicelli, A. Tallaire, J. Achard, V. Jacques, J.-F. Roch, A. M. Zaitsev, J. Meijer and S. Pezzagna, Phys. Status Solidi A, 2014, 211, 2268–2273 CrossRef CAS
.
- Y. Doi, T. Fukui, H. Kato, T. Makino, S. Yamasaki, T. Tashima, H. Morishita, S. Miwa, F. Jelezko, Y. Suzuki and N. Mizuochi, Phys. Rev. B, 2016, 93, 081203(R) CrossRef
.
- T. Murai, T. Makino, H. Kato, M. Shimizu, T. Murooka, E. D. Herbschleb, Y. Doi, H. Morishita, M. Fujiwara, M. Hatano, S. Yamasaki and N. Mizuochi, Appl. Phys. Lett., 2018, 112, 111903 CrossRef
.
- F. Gorrini, C. Dorigoni, D. Olivares-Postigo, R. Giri, P. Aprà, F. Picollo and A. Bifone, ACS Appl. Mater. Interfaces, 2021, 13, 43221–43232 CrossRef CAS PubMed
.
- Q. Zhang, Y. Guo, W. Ji, M. Wang, J. Yin, F. Kong, Y. Lin, C. Yin, F. Shi, Y. Wang and J. Du, Nat. Commun., 2021, 12, 1529 CrossRef CAS PubMed
.
- S. Chakravarthi, C. Pederson, Z. Kazi, A. Ivanov and K.-M. C. Fu, Phys. Rev. B, 2021, 104, 085425 CrossRef CAS
.
- Z. Yuan, M. Fitzpatrick, L. V. H. Rodgers, S. Sangtawesin, S. Srinivasan and N. P. de Leon, Phys. Rev. Res., 2020, 2, 033263 CrossRef CAS
.
- R. G. Ryan, A. Stacey, K. M. O’Donnell, T. Ohshima, B. C. Johnson, L. C. L. Hollenberg, P. Mulvaney and D. A. Simpson, ACS Appl. Mater. Interfaces, 2018, 10, 13143–13149 CrossRef CAS
.
- C. Bradac, T. Gaebel, N. Naidoo, M. J. Sellars, J. Twamley, L. J. Brown, A. S. Barnard, T. Plakhotnik, A. V. Zvyagin and J. R. Rabeau, Nat. Nanotechnol., 2010, 5, 345–349 CrossRef CAS PubMed
.
- M. Kaviani, P. Deák, B. Aradi, T. Frauenheim, J.-P. Chou and A. Gali, Nano Lett., 2014, 14, 4772–4777 CrossRef CAS PubMed
.
- B. Grotz, M. V. Hauf, M. Dankerl, B. Naydenov, S. Pezzagna, J. Meijer, F. Jelezko, J. Wrachtrup, M. Stutzmann, F. Reinhard and J. A. Garrido, Nat. Commun., 2012, 3, 729 CrossRef PubMed
.
- T. Gaebel, M. Domhan, C. Wittmann, I. Popa, F. Jelezko, J. Rabeau, A. Greentree, S. Prawer, E. Trajkov, P. R. Hemmer and J. Wrachtrup, Appl. Phys. B, 2006, 82, 243–246 CrossRef CAS
.
- C. Santori, P. E. Barclay, K.-M. C. Fu and R. G. Beausoleil, Phys. Rev. B, 2009, 79, 125313 CrossRef
.
- K.-M. C. Fu, C. Santori, P. E. Barclay and R. G. Beausoleil, Appl. Phys. Lett., 2010, 96, 121907 CrossRef
.
- F. Maier, J. Ristein and L. Ley, Phys. Rev. B, 2001, 64, 165411 CrossRef
.
- J. A. Garrido, S. Nowy, A. Härtl and M. Stutzmann, Langmuir, 2008, 24, 3897–3904 CrossRef CAS PubMed
.
- M. V. Hauf, B. Grotz, B. Naydenov, M. Dankerl, S. Pezzagna, J. Meijer, F. Jelezko, J. Wrachtrup, M. Stutzmann, F. Reinhard and J. A. Garrido, Phys. Rev. B, 2011, 83, 081304(R) CrossRef
.
- A. N. Newell, D. A. Dowdell and D. H. Santamore, J. Appl. Phys., 2016, 120, 185104 CrossRef
.
- A. K. Tiwari, J. P. Goss, P. R. Briddon, N. G. Wright, A. B. Horsfall, R. Jones, H. Pinto and M. J. Rayson, Phys. Rev. B, 2011, 84, 245305 CrossRef
.
- J. Robertson and M. J. Rutter, Diamond Relat. Mater., 1998, 7, 620–625 CrossRef CAS
.
- P. K. Baumann and R. J. Nemanich, Surf. Sci., 1998, 409, 320–335 CrossRef CAS
.
- Y. M. Wang, K. W. Wong, S. T. Lee, M. Nishitani-Gamo, I. Sakaguchi, K. P. Loh and T. Ando, Diamond Relat. Mater., 2000, 9, 1582–1590 CrossRef CAS
.
- Z. Zhang, M. Wensell and J. Bernholc, Phys. Rev. B, 1995, 51, 5291–5296 CrossRef CAS
.
- A. Stacey, K. M. O'Donnell, J.-P. Chou, A. Schenk, A. Tadich, N. Dontschuk, J. Cervenka, C. Pakes, A. Gali, A. Hoffman and S. Prawer, Adv. Mater. Interfaces, 2015, 2, 1500079 CrossRef
.
- K. J. Rietwyk, S. L. Wong, L. Cao, K. M. O'Donnell, L. Ley, A. T. S. Wee and C. I. Pakes, Appl. Phys. Lett., 2013, 102, 091604 CrossRef
.
- L. Diederich, O. M. Küttel, P. Aebi and L. Schlapbach, Surf. Sci., 1998, 418, 219–239 CrossRef CAS
.
- T. P. Humphreys, R. E. Thomas, D. P. Malta, J. B. Posthill, M. J. Mantini, R. A. Rudder, G. C. Hudson, R. J. Markunas and C. Pettenkofer, Appl. Phys. Lett., 1997, 70, 1257–1259 CrossRef CAS
.
- C. Bandis and B. B. Pate, Surf. Sci., 1996, 350, 315–321 CrossRef CAS
.
- M. J. Rutter and J. Robertson, Phys. Rev. B, 1998, 57, 9241–9245 CrossRef CAS
.
- J. van der Weide, Z. Zhang, P. K. Baumann, M. G. Wensell, J. Bernholc and R. J. Nemanich, Phys. Rev. B, 1994, 50, 5803–5806 CrossRef CAS
.
- W. Shen, S. Shen, S. Liu, H. Li, Y. Zhang, Q. Zhang and Y. Guo, Carbon, 2021, 173, 485–492 CrossRef CAS
.
- J.-P. Chou, A. Retzker and A. Gali, Nano Lett., 2017, 17, 2294–2298 CrossRef CAS PubMed
.
- C. Bandis and B. B. Pate, Phys. Rev. B, 1995, 52, 12056–12071 CrossRef CAS PubMed
.
- J. B. Cui, J. Ristein and L. Ley, Phys. Rev. B, 1999, 59, 5847–5856 CrossRef CAS
.
- G. Kern and J. Hafner, Phys. Rev. B, 1997, 56, 4203–4210 CrossRef CAS
.
- S. Li, J.-P. Chou, J. Wei, M. Sun, A. Hu and A. Gali, Carbon, 2019, 145, 273–280 CrossRef CAS
.
- P. Balasubramanian, C. Osterkamp, Y. Chen, X. Chen, T. Teraji, E. Wu, B. Naydenov and F. Jelezko, Nano Lett., 2019, 19, 6681–6686 CrossRef CAS PubMed
.
- S. Ajisaka and Y. B. Band, Phys. Rev. B, 2016, 94, 134107 CrossRef
.
- P. Chrostoski, B. Barrios and D. H. Santamore, Phys. B: Condens. Matter, 2021, 605, 412767 CrossRef CAS
.
- B. K. Ofori-Okai, S. Pezzagna, K. Chang, M. Loretz, R. Schirhagl, Y. Tao, B. A. Moores, K. Groot-Berning, J. Meijer and C. L. Degen, Phys. Rev. B, 2012, 86, 081406(R) CrossRef
.
- K. Ohashi, T. Rosskopf, H. Watanabe, M. Loretz, Y. Tao, R. Hauert, S. Tomizawa, T. Ishikawa, J. Ishi-Hayase, S. Shikata, C. L. Degen and K. M. Itoh, Nano Lett., 2013, 13, 4733–4738 CrossRef CAS
.
- B. A. Myers, A. Das, M. C. Dartiailh, K. Ohno, D. D. Awschalom and A. C. Bleszynski Jayich, Phys. Rev. Lett., 2014, 113, 027602 CrossRef CAS
.
- W. Zhang, J. Zhang, J. Wang, F. Feng, S. Lin, L. Lou, W. Zhu and G. Wang, Phys. Rev. B, 2017, 96, 235443 CrossRef
.
- S. E. Lillie, D. A. Broadway, N. Dontschuk, A. Zavabeti, D. A. Simpson, T. Teraji, T. Daeneke, L. C. L. Hollenberg and J.-P. Tetienne, Phys. Rev. Mater., 2018, 2, 116002 CrossRef CAS
.
- M. Rollo, A. Finco, R. Tanos, F. Fabre, T. Devolder, I. Robert-Philip and V. Jacques, Phys. Rev. B, 2021, 103, 235418 CrossRef CAS
.
- A. M. Panich, A. I. Shames, H.-M. Vieth, E. Ösawa, M. Takahashi and A. Ya. Vul’, Eur. Phys. J. B, 2006, 52, 397–402 CrossRef CAS
.
- J. Tisler, G. Balasubramanian, B. Naydenov, R. Kolesov, B. Grotz, R. Reuter, J.-P. Boudou, P. A. Curmi, M. Sennour, A. Thorel, M. Börsch, K. Aulenbacher, R. Erdmann, P. R. Hemmer, F. Jelezko and J. Wrachtrup, ACS Nano, 2009, 3, 1959–1965 CrossRef CAS PubMed
.
- A. Laraoui, J. S. Hodges and C. A. Meriles, Nano Lett., 2012, 12, 3477–3482 CrossRef CAS PubMed
.
- X. Song, J. Zhang, F. Feng, J. Wang, W. Zhang, L. Lou, W. Zhu and G. Wang, AIP Adv., 2014, 4, 047103 CrossRef
.
- Z. Peng, J. Dallas and S. Takahashi, J. Appl. Phys., 2020, 128, 054301 CrossRef CAS
.
- J.-P. Tetienne, T. Hingant, L. Rondin, A. Cavaillès, L. Mayer, G. Dantelle, T. Gacoin, J. Wrachtrup, J.-F. Roch and V. Jacques, Phys. Rev. B, 2013, 87, 235436 CrossRef
.
- L. P. McGuinness, L. T. Hall, A. Stacey, D. A. Simpson, C. D. Hill, J. H. Cole, K. Ganesan, B. C. Gibson, S. Prawer, P. Mulvaney, F. Jelezko, J. Wrachtrup, R. E. Scholten and L. C. L. Hollenberg, New J. Phys., 2013, 15, 073042 CrossRef CAS
.
- M. Pelliccione, B. A. Myers, L. M. A. Pascal, A. Das and A. C. Bleszynski Jayich, Phys. Rev. Appl., 2014, 2, 054014 CrossRef CAS
.
- J. Barton, M. Gulka, J. Tarabek, Y. Mindarava, Z. Wang, J. Schimer, H. Raabova, J. Bednar, M. B. Plenio, F. Jelezko, M. Nesladek and P. Cigler, ACS Nano, 2020, 14, 12938–12950 CrossRef CAS PubMed
.
- T. Fujisaku, R. Tanabe, S. Onoda, R. Kubota, T. F. Segawa, F. T.-K. So, T. Ohshima, I. Hamachi, M. Shirakawa and R. Igarashi, ACS Nano, 2019, 13, 11726–11732 CrossRef CAS PubMed
.
- F. P. Martínez, A. C. Nusantara, M. Chipaux, S. K. Padamati and R. Schirhagl, ACS Sens., 2020, 5, 3862–3869 CrossRef PubMed
.
- L. Nie, A. C. Nusantara, V. G. Damle, M. V. Baranov, M. Chipaux, C. Reyes-San-Martin, T. Hamoh, C. P. Epperla, M. Guricova, P. Cigler, G. van den Bogaart and R. Schirhagl, Nano Lett., 2022, 22, 1818–1825 CrossRef CAS PubMed
.
- K. Wu, T. A. Vedelaar, V. G. Damle, A. Morita, J. Mougnaud, C. Reyes San Martin, Y. Zhang, D. P. van der Pol, H. Ende-Metselaar, I. Rodenhuis-Zybert and R. Schirhagl, Redox Biol., 2022, 52, 102279 CrossRef CAS PubMed
.
- P. Jamonneau, M. Lesik, J. P. Tetienne, I. Alvizu, L. Mayer, A. Dréau, S. Kosen, J.-F. Roch, S. Pezzagna, J. Meijer, T. Teraji, Y. Kubo, P. Bertet, J. R. Maze and V. Jacques, Phys. Rev. B, 2016, 93, 024305 CrossRef
.
- M. W. Doherty, J. Michl, F. Dolde, I. Jakobi, P. Neumann, N. B. Manson and J. Wrachtrup, New J. Phys., 2014, 16, 063067 CrossRef CAS
.
- M. S. J. Barson, L. M. Oberg, L. P. McGuinness, A. Denisenko, N. B. Manson, J. Wrachtrup and M. W. Doherty, Nano Lett., 2021, 21, 2962–2967 CrossRef CAS PubMed
.
- B. A. Myers, A. Ariyaratne and A. C. Bleszynski Jayich, Phys. Rev. Lett., 2017, 118, 197201 CrossRef CAS PubMed
.
- P. Chrostoski, H. R. Sadeghpour and D. H. Santamore, Phys. Rev. Appl., 2018, 10, 064056 CrossRef CAS
.
- J. C. Thomas, J. J. Schwartz, J. N. Hohman, S. A. Claridge, H. S. Auluck, A. C. Serino, A. M. Spokoyny, G. Tran, K. F. Kelly, C. A. Mirkin, J. Gilles, S. J. Osher and P. S. Weiss, ACS Nano, 2015, 9, 4734–4742 CrossRef CAS PubMed
.
- J. Kim, Y. S. Rim, Y. Liu, A. C. Serino, J. C. Thomas, H. Chen, Y. Yang and P. S. Weiss, Nano Lett., 2014, 14, 2946–2951 CrossRef CAS PubMed
.
- V. Seshan, D. Ullien, A. Castellanos-Gomez, S. Sachdeva, D. H. K. Murthy, T. J. Savenije, H. A. Ahmad, T. S. Nunney, S. D. Janssens, K. Haenen, M. Nesládek, H. S. J. van der Zant, E. J. R. Sudhölter and L. C. P. M. de Smet, J. Chem. Phys., 2013, 138, 234707 CrossRef CAS
.
- R. J. Nemanich, J. A. Carlisle, A. Hirata and K. Haenen, MRS Bull., 2014, 39, 490–494 CrossRef CAS
.
- J.-P. Chou and A. Gali, MRS Commun., 2017, 7, 551–562 CrossRef CAS
.
- C. Popov, W. Kulisch, S. Bliznakov, G. Ceccone, D. Gilliland, L. Sirghi and F. Rossi, Diamond Relat. Mater., 2008, 17, 1229–1234 CrossRef CAS
.
- A. Denisenko, A. Romanyuk, C. Pietzka, J. Scharpf and E. Kohn, Diamond Relat. Mater., 2010, 19, 423–427 CrossRef CAS
.
- C. J. Widmann, C. Giese, M. Wolfer, S. Kono and C. E. Nebel, Phys. Status Solidi A, 2014, 211, 2328–2332 CrossRef CAS
.
- Y.-F. Wang, W. Wang, J. Wei, B. Jiao, D. Xu, X. Chang, H. N. Abbasi, W. Song, G. Chen and H.-X. Wang, Carbon, 2021, 176, 83–87 CrossRef CAS
.
- A. Freedman, J. Appl. Phys., 1994, 75, 3112–3120 CrossRef CAS
.
- V. S. Smentkowski and J. T. Yates, Science, 1996, 271, 193–195 CrossRef CAS
.
- T. Ando, M. Nishitani-Gamo, R. E. Rawles, K. Yamamoto, M. Kamo and Y. Sato, Diamond Relat. Mater., 1996, 5, 1136–1142 CrossRef CAS
.
- J. B. Miller and D. W. Brown, Langmuir, 1996, 12, 5809–5817 CrossRef CAS
.
- J. B. Miller, Surf. Sci., 1999, 439, 21–33 CrossRef CAS
.
- J. Cai, A. Retzker, F. Jelezko and M. B. Plenio, Nat. Phys., 2013, 9, 168–173 Search PubMed
.
- W. Shen, G. Wu, L. Li, H. Li, S. Liu, S. Shen and D. Zou, Carbon, 2022, 193, 17–25 CrossRef CAS
.
- S. Cui and E. L. Hu, Appl. Phys. Lett., 2013, 103, 051603 CrossRef
.
- T. W. Shanley, A. A. Martin, I. Aharonovich and M. Toth, Appl. Phys. Lett., 2014, 105, 063103 CrossRef
.
- S. Lu, D. Fan, C. Chen, Y. Mei, Y. Ma and X. Hu, Carbon, 2020, 159, 9–15 CrossRef CAS
.
- A. O. Sushkov, I. Lovchinsky, N. Chisholm, R. L. Walsworth, H. Park and M. D. Lukin, Phys. Rev. Lett., 2014, 113, 197601 CrossRef CAS PubMed
.
- K. J. Brown, E. Chartier, E. M. Sweet, D. A. Hopper and L. C. Bassett, J. Chem. Health Saf., 2019, 26, 40–44 CrossRef
.
- F. Fávaro de Oliveira, S. A. Momenzadeh, Y. Wang, M. Konuma, M. Markham, A. M. Edmonds, A. Denisenko and J. Wrachtrup, Appl. Phys. Lett., 2015, 107, 073107 CrossRef
.
- M. Kim, H. J. Mamin, M. H. Sherwood, C. T. Rettner, J. Frommer and D. Rugar, Appl. Phys. Lett., 2014, 105, 042406 CrossRef
.
- S. Cui, A. S. Greenspon, K. Ohno, B. A. Myers, A. C. Bleszynski Jayich, D. D. Awschalom and E. L. Hu, Nano Lett., 2015, 15, 2887–2891 CrossRef CAS PubMed
.
- H. Yamano, S. Kawai, K. Kato, T. Kageura, M. Inaba, T. Okada, I. Higashimata, M. Haruyama, T. Tanii, K. Yamada, S. Onoda, W. Kada, O. Hanaizumi, T. Teraji, J. Isoya and H. Kawarada, Jpn. J. Appl. Phys., 2017, 56, 04CK08 CrossRef
.
- T. Teraji, Y. Garino, Y. Koide and T. Ito, J. Appl. Phys., 2009, 105, 126109 CrossRef
.
- F. Cataldo and A. P. Koscheev, Fuller. Nanotub. Carbon Nanostructures, 2003, 11, 201–218 CrossRef CAS
.
- F. Li, R. Akhvlediani, M. K. Kuntumalla and A. Hoffman, Appl. Surf. Sci., 2019, 465, 313–319 CrossRef CAS
.
- J. Raymakers, K. Haenen and W. Maes, J. Mater. Chem. C, 2019, 7, 10134–10165 RSC
.
- X. Wang, A. R. Ruslinda, Y. Ishiyama, Y. Ishii and H. Kawarada, Diamond Relat. Mater., 2011, 20, 1319–1324 CrossRef CAS
.
- V. Damle, K. Wu, O. De Luca, N. Ortí-Casañ, N. Norouzi, A. Morita, J. de Vries, H. Kaper, I. S. Zuhorn, U. Eisel, D. E. Vanpoucke, P. Rudolf and R. Schirhagl, Carbon, 2020, 162, 1–12 CrossRef CAS
.
- R. Tsukahara, M. Fujiwara, Y. Sera, Y. Nishimura, Y. Sugai, C. Jentgens, Y. Teki, H. Hashimoto and S. Shikata, ACS Appl. Nano Mater., 2019, 2, 3701–3710 CrossRef CAS
.
- G. Braunbeck, S. Mandal, M. Touge, O. A. Williams and F. Reinhard, Diamond Relat. Mater., 2018, 85, 18–22 CrossRef CAS
.
- J.-P. Tetienne, R. W. de Gille, D. A. Broadway, T. Teraji, S. E. Lillie, J. M. McCoey, N. Dontschuk, L. T. Hall, A. Stacey, D. A. Simpson and L. C. L. Hollenberg, Phys. Rev. B, 2018, 97, 085402 CrossRef CAS
.
- T. Pakornchote, A. Ektarawong, W. Busayaporn, U. Pinsook and T. Bovornratanaraks, Phys. Rev. B, 2020, 102, 075418 CrossRef CAS
.
- M. Gong, Q. Wang, N. Gao and H. Li, Diamond Relat. Mater., 2021, 120, 108601 CrossRef CAS
.
- W. Körner, R. Ghassemizadeh, D. F. Urban and C. Elsässer, Phys. Rev. B, 2022, 105, 085305 CrossRef
.
- S. Kawai, H. Yamano, T. Sonoda, K. Kato, J. J. Buendia, T. Kageura, R. Fukuda, T. Okada, T. Tanii, T. Higuchi, M. Haruyama, K. Yamada, S. Onoda, T. Ohshima, W. Kada, O. Hanaizumi, A. Stacey, T. Teraji, S. Kono, J. Isoya and H. Kawarada, J. Phys. Chem. C, 2019, 123, 3594–3604 CrossRef CAS
.
- N. Simon, C. Decorse-Pascanut, A. Gonçalves, D. Ballutaud, G. Charrier and A. Etcheberry, Diamond Relat. Mater., 2009, 18, 890–894 CrossRef CAS
.
- M. Chandran, M. Shasha, S. Michaelson and A. Hoffman, Appl. Phys. Lett., 2015, 107, 111602 CrossRef
.
- M. Chandran, M. Shasha, S. Michaelson, R. Akhvlediani and A. Hoffman, Phys. Status Solidi A, 2015, 212, 2487–2495 CrossRef CAS
.
- M. Attrash, M. K. Kuntumalla, S. Michaelson and A. Hoffman, J. Phys. Chem. C, 2020, 124, 5657–5664 CrossRef CAS
.
- M. Attrash, M. K. Kuntumalla, S. Michaelson and A. Hoffman, Surf. Sci., 2021, 703, 121741 CrossRef CAS
.
- S. Szunerits, C. Jama, Y. Coffinier, B. Marcus, D. Delabouglise and R. Boukherroub, Electrochem. Commun., 2006, 8, 1185–1190 CrossRef CAS
.
- Y. Coffinier, S. Szunerits, C. Jama, R. Desmet, O. Melnyk, B. Marcus, L. Gengembre, E. Payen, D. Delabouglise and R. Boukherroub, Langmuir, 2007, 23, 4494–4497 CrossRef CAS PubMed
.
- D. Zhu, J. A. Bandy, S. Li and R. J. Hamers, Surf. Sci., 2016, 650, 295–301 CrossRef CAS
.
- J. M. Abendroth, K. Herb, E. Janitz, T. Zhu, L. A. Völker and C. L. Degen, Nano Lett., 2022 DOI:10.1021/acs.nanolett.2c00533
.
- G.-J. Zhang, K.-S. Song, Y. Nakamura, T. Ueno, T. Funatsu, I. Ohdomari and H. Kawarada, Langmuir, 2006, 22, 3728–3734 CrossRef CAS
.
- R. Fukuda, P. Balasubramanian, I. Higashimata, G. Koike, T. Okada, R. Kagami, T. Teraji, S. Onoda, M. Haruyama, K. Yamada, M. Inaba, H. Yamano, F. M. Stürner, S. Schmitt, L. P. McGuinness, F. Jelezko, T. Ohshima, T. Shinada, H. Kawarada, W. Kada, O. Hanaizumi, T. Tanii and J. Isoya, New J. Phys., 2018, 20, 083029 CrossRef
.
- D. A. Simpson, R. G. Ryan, L. T. Hall, E. Panchenko, S. C. Drew, S. Petrou, P. S. Donnelly, P. Mulvaney and L. C. L. Hollenberg, Nat. Commun., 2017, 8, 458 CrossRef PubMed
.
- P. Wang, S. Chen, M. Guo, S. Peng, M. Wang, M. Chen, W. Ma, R. Zhang, J. Su, X. Rong, F. Shi, T. Xu and J. Du, Sci. Adv., 2019, 5, eaau8038 CrossRef CAS PubMed
.
- T. Staudacher, N. Raatz, S. Pezzagna, J. Meijer, F. Reinhard, C. A. Meriles and J. Wrachtrup, Nat. Commun., 2015, 6, 8527 CrossRef CAS PubMed
.
- S. Szunerits, C. E. Nebel and R. J. Hamers, MRS Bull., 2014, 39, 517–524 CrossRef CAS
.
- J. Wang, M. A. Firestone, O. Auciello and J. A. Carlisle, Langmuir, 2004, 20, 11450–11456 CrossRef CAS
.
- J. Pinson and F. Podvorica, Chem. Soc. Rev., 2005, 34, 429–439 RSC
.
- W. Yang, O. Auciello, J. E. Butler, W. Cai, J. A. Carlisle, J. E. Gerbi, D. M. Gruen, T. Knickerbocker, T. L. Lasseter, J. N. Russell, L. M. Smith and R. J. Hamers, Nat. Mater., 2002, 1, 253–257 CrossRef CAS PubMed
.
- A. Härtl, E. Schmich, J. A. Garrido, J. Hernando, S. C. R. Catharino, S. Walter, P. Feulner, A. Kromka, D. Steinmüller and M. Stutzmann, Nat. Mater., 2004, 3, 736–742 CrossRef
.
- B. M. Nichols, J. E. Butler, J. N. Russell and R. J. Hamers, J. Phys. Chem. B, 2005, 109, 20938–20947 CrossRef CAS PubMed
.
- P. E. Colavita, B. Sun, K.-Y. Tse and R. J. Hamers, J. Am. Chem. Soc., 2007, 129, 13554–13565 CrossRef CAS
.
- C. Stavis, T. L. Clare, J. E. Butler, A. D. Radadia, R. Carr, H. Zeng, W. P. King, J. A. Carlisle, A. Aksimentiev, R. Bashir and R. J. Hamers, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 983–988 CrossRef CAS PubMed
.
- M. Kayci, J. Fan, O. Bakirman and A. Herrmann, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2112664118 CrossRef CAS PubMed
.
- A. Frutiger, A. Tanno, S. Hwu, R. F. Tiefenauer, J. Vörös and N. Nakatsuka, Chem. Rev., 2021, 121, 8095–8160 CrossRef CAS
.
- X. Wang, Y. Ishii, A. R. Ruslinda, M. Hasegawa and H. Kawarada, ACS Appl. Mater. Interfaces, 2012, 4, 3526–3534 CrossRef CAS
.
- A. Wolcott, T. Schiros, M. E. Trusheim, E. H. Chen, D. Nordlund, R. E. Diaz, O. Gaathon, D. Englund and J. S. Owen, J. Phys. Chem. C, 2014, 118, 26695–26702 CrossRef CAS PubMed
.
- K. Ushizawa, Y. Sato, T. Mitsumori, T. Machinami, T. Ueda and T. Ando, Chem. Phys. Lett., 2002, 351, 105–108 CrossRef CAS
.
- P. Krysiński, Y. Show, J. Stotter and G. J. Blanchard, J. Am. Chem. Soc., 2003, 125, 12726–12728 CrossRef
.
- M. Wang, M. R. Das, M. Li, R. Boukherroub and S. Szunerits, J. Phys. Chem. C, 2009, 113, 17082–17086 CrossRef CAS
.
- L. Marcon, M. Wang, Y. Coffinier, F. Le Normand, O. Melnyk, R. Boukherroub and S. Szunerits, Langmuir, 2010, 26, 1075–1080 CrossRef CAS PubMed
.
- M. Hoeb, M. Auernhammer, S. J. Schoell, M. S. Brandt, J. A. Garrido, M. Stutzmann and I. D. Sharp, Langmuir, 2010, 26, 18862–18867 CrossRef CAS PubMed
.
- R. Caterino, R. Csiki, M. Wiesinger, M. Sachsenhauser, M. Stutzmann, J. A. Garrido, A. Cattani-Scholz, G. Speranza, S. D. Janssens and K. Haenen, ACS Appl. Mater. Interfaces, 2014, 6, 13909–13916 CrossRef CAS PubMed
.
- H. Notsu, T. Fukazawa, T. Tatsuma, D. A. Tryk and A. Fujishima, Electrochem. Solid-State Lett., 2001, 4, H1 CrossRef CAS
.
- R. Ohta, N. Saito, Y. Inoue, H. Sugimura and O. Takai, J. Vac. Sci. Technol., A, 2004, 22, 2005–2009 CrossRef CAS
.
- R. D. Akiel, X. Zhang, C. Abeywardana, V. Stepanov, P. Z. Qin and S. Takahashi, J. Phys. Chem. B, 2016, 120, 4003–4008 CrossRef CAS PubMed
.
- B. Grotz, J. Beck, P. Neumann, B. Naydenov, R. Reuter, F. Reinhard, F. Jelezko, J. Wrachtrup, D. Schweinfurth, B. Sarkar and P. Hemmer, New J. Phys., 2011, 13, 055004 CrossRef
.
- Q. Wang, A. Kromka, J. Houdkova, O. Babchenko, B. Rezek, M. Li, R. Boukherroub and S. Szunerits, Langmuir, 2012, 28, 587–592 CrossRef CAS PubMed
.
- J.-H. Yang, K.-S. Song, G.-J. Zhang, M. Degawa, Y. Sasaki, I. Ohdomari and H. Kawarada, Langmuir, 2006, 22, 11245–11250 CrossRef CAS PubMed
.
- D. Meziane, A. Barras, A. Kromka, J. Houdkova, R. Boukherroub and S. Szunerits, Anal. Chem., 2012, 84, 194–200 CrossRef CAS PubMed
.
- C. Müller, X. Kong, J.-M. Cai, K. Melentijević, A. Stacey, M. Markham, D. Twitchen, J. Isoya, S. Pezzagna, J. Meijer, J. F. Du, M. B. Plenio, B. Naydenov, L. P. McGuinness and F. Jelezko, Nat. Commun., 2014, 5, 4703 CrossRef
.
- K. S. Liu, A. Henning, M. W. Heindl, R. D. Allert, J. D. Bartl, I. D. Sharp, R. Rizzato and D. B. Bucher, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2111607119 CrossRef CAS PubMed
.
- M. Xie, X. Yu, L. V. H. Rodgers, D. Xu, I. Chi-Durán, A. Toros, N. Quack, N. P. de Leon and P. C. Maurer, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2114186119 CrossRef CAS PubMed
.
- T. L. Lasseter, B. H. Clare, N. L. Abbott and R. J. Hamers, J. Am. Chem. Soc., 2004, 126, 10220–10221 CrossRef CAS PubMed
.
- J. M. A. Beattie, J. P. Goss, M. J. Rayson and P. R. Briddon, Diamond Relat. Mater., 2019, 94, 137–145 CrossRef CAS
.
- H. Bluhm, J. A. Bert, N. C. Koshnick, M. E. Huber and K. A. Moler, Phys. Rev. Lett., 2009, 103, 026805 CrossRef PubMed
.
- N. Adelstein, D. Lee, J. L. DuBois, K. G. Ray, J. B. Varley and V. Lordi, AIP Adv., 2017, 7, 025110 CrossRef
.
- G. de Lange, Z. H. Wang, D. Ristè, V. V. Dobrovitski and R. Hanson, Science, 2010, 330, 60–63 CrossRef CAS PubMed
.
- M. S. Grinolds, S. Hong, P. Maletinsky, L. Luan, M. D. Lukin, R. L. Walsworth and A. Yacoby, Nat. Phys., 2013, 9, 215–219 Search PubMed
.
- M. Palm, W. Huxter, P. Welter, S. Ernst, P. Scheidegger, S. Diesch, K. Chang, P. Rickhaus, T. Taniguchi, K. Watanabe, K. Ensslin and C. Degen, Phys. Rev. Appl., 2022, 17, 054008 Search PubMed
.
- S. Hong, M. S. Grinolds, P. Maletinsky, R. L. Walsworth, M. D. Lukin and A. Yacoby, Nano Lett., 2012, 12, 3920–3924 CrossRef CAS PubMed
.
- W. S. Huxter, M. L. Palm, M. L. Davis, P. Welter, C.-H. Lambert, M. Trassin and C. L. Degen, Nat. Commun., 2022, 13, 3761 CrossRef CAS PubMed
.
- J. Zopes, K. Sasaki, K. S. Cujia, J. M. Boss, K. Chang, T. F. Segawa, K. M. Itoh and C. L. Degen, Phys. Rev. Lett., 2017, 119, 260501 CrossRef CAS PubMed
.
- S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS
.
- T. Gullion, D. B. Baker and M. S. Conradi, J. Magn. Reson., 1990, 89, 479–484 CAS
.
- A. M. Souza, G. A. Álvarez and D. Suter, Philos. Trans. R. Soc., A, 2012, 370, 4748–4769 CrossRef PubMed
.
- T. H. Taminiau, J. Cramer, T. van der Sar, V. V. Dobrovitski and R. Hanson, Nat. Nanotechnol., 2014, 9, 171–176 CrossRef CAS PubMed
.
- C. E. Bradley, J. Randall, M. H. Abobeih, R. Berrevoets, M. Degen, M. A. Bakker, M. Markham, D. Twitchen and T. H. Taminiau, Phys. Rev. X, 2019, 9, 031045 CAS
.
- Y. Romach, A. Lazariev, I. Avrahami, F. Kleißler, S. Arroyo-Camejo and N. Bar-Gill, Phys. Rev. Appl., 2019, 11, 014064 CrossRef CAS
.
- A. Lazariev, S. Arroyo-Camejo, G. Rahane, V. K. Kavatamane and G. Balasubramanian, Sci. Rep., 2017, 7, 6586 CrossRef PubMed
.
- G. de Lange, T. van der Sar, M. Blok, Z.-H. Wang, V. Dobrovitski and R. Hanson, Sci. Rep., 2012, 2, 382 CrossRef PubMed
.
- H. S. Knowles, D. M. Kara and M. Atatüre, Nat. Mater., 2013, 13, 21–25 CrossRef PubMed
.
- M. Joos, D. Bluvstein, Y. Lyu, D. Weld and A. Bleszynski Jayich, npj Quantum Information, 2022, 8, 47 CrossRef
.
- E. Bauch, C. A. Hart, J. M. Schloss, M. J. Turner, J. F. Barry, P. Kehayias, S. Singh and R. L. Walsworth, Phys. Rev. X, 2018, 8, 031025 CAS
.
- K. Fang, V. M. Acosta, C. Santori, Z. Huang, K. M. Itoh, H. Watanabe, S. Shikata and R. G. Beausoleil, Phys. Rev. Lett., 2013, 110, 130802 CrossRef PubMed
.
- H. J. Mamin, M. H. Sherwood, M. Kim, C. T. Rettner, K. Ohno, D. D. Awschalom and D. Rugar, Phys. Rev. Lett., 2014, 113, 030803 CrossRef CAS PubMed
.
- A. Mzyk, Y. Ong, A. R. Ortiz Moreno, S. K. Padamati, Y. Zhang, C. A. Reyes-San-Martin and R. Schirhagl, Anal. Chem., 2022, 94, 225–249 CrossRef CAS PubMed
.
- M. Kost, J. Cai and M. B. Plenio, Sci. Rep., 2015, 5, 11007 CrossRef CAS PubMed
.
- A. Böckmann, M. Ernst and B. H. Meier, J. Magn. Reson., 2015, 253, 71–79 CrossRef
.
- M. Callon, A. A. Malär, S. Pfister, V. Římal, M. E. Weber, T. Wiegand, J. Zehnder, M. Chávez, R. Cadalbert, R. Deb, A. Däpp, M.-L. Fogeron, A. Hunkeler, L. Lecoq, A. Torosyan, D. Zyla, R. Glockshuber, S. Jonas, M. Nassal, M. Ernst, A. Böckmann and B. H. Meier, J. Biomol. NMR, 2021, 75, 255–272 CrossRef CAS PubMed
.
- J. Zopes, K. Herb, K. S. Cujia and C. L. Degen, Phys. Rev. Lett., 2018, 121, 170801 CrossRef CAS PubMed
.
- K. S. Cujia, K. Herb, J. Zopes, J. M. Abendroth and C. L. Degen, Nat. Commun., 2022, 13, 1260 CrossRef CAS PubMed
.
- F. Shagieva, S. Zaiser, P. Neumann, D. B. R. Dasari, R. Stöhr, A. Denisenko, R. Reuter, C. A. Meriles and J. Wrachtrup, Nano Lett., 2018, 18, 3731–3737 CrossRef CAS PubMed
.
- P. Fernández-Acebal, O. Rosolio, J. Scheuer, C. Müller, S. Müller, S. Schmitt, L. McGuinness, I. Schwarz, Q. Chen, A. Retzker, B. Naydenov, F. Jelezko and M. Plenio, Nano Lett., 2018, 18, 1882–1887 CrossRef PubMed
.
- A. J. Healey, L. T. Hall, G. A. L. White, T. Teraji, M.-A. Sani, F. Separovic, J.-P. Tetienne and L. C. L. Hollenberg, Phys. Rev. Appl., 2021, 15, 054052 CrossRef CAS
.
- J.-P. Tetienne, L. T. Hall, A. J. Healey, G. A. L. White, M.-A. Sani, F. Separovic and L. C. L. Hollenberg, Phys. Rev. B, 2021, 103, 014434 CrossRef CAS
.
- G. Petrini, E. Moreva, E. Bernardi, P. Traina, G. Tomagra, V. Carabelli, I. P. Degiovanni and M. Genovese, Adv. Quantum Technol., 2020, 3, 2000066 CrossRef CAS
.
- T. Zhang, G. Pramanik, K. Zhang, M. Gulka, L. Wang, J. Jing, F. Xu, Z. Li, Q. Wei, P. Cigler and Z. Chu, ACS Sens., 2021, 6, 2077–2107 CrossRef CAS
.
- B. S. Miller, L. Bezinge, H. D. Gliddon, D. Huang, G. Dold, E. R. Gray, J. Heaney, P. J. Dobson, E. Nastouli, J. J. L. Morton and R. A. McKendry, Nature, 2020, 587, 588–593 CrossRef CAS PubMed
.
- C. Li, R. Soleyman, M. Kohandel and P. Cappellaro, Nano Lett., 2022, 22, 43–49 CrossRef CAS PubMed
.
- T. Rendler, J. Neburkova, O. Zemek, J. Kotek, A. Zappe, Z. Chu, P. Cigler and J. Wrachtrup, Nat. Commun., 2017, 8, 14701 CrossRef CAS PubMed
.
- P. Reineck, D. W. M. Lau, E. R. Wilson, K. Fox, M. R. Field, C. Deeleepojananan, V. N. Mochalin and B. C. Gibson, ACS Nano, 2017, 11, 10924–10934 CrossRef CAS PubMed
.
- L. P. McGuinness, Y. Yan, A. Stacey, D. A. Simpson, L. T. Hall, D. Maclaurin, S. Prawer, P. Mulvaney, J. Wrachtrup, F. Caruso, R. E. Scholten and L. C. L. Hollenberg, Nat. Nanotechnol., 2011, 6, 358–363 CrossRef CAS PubMed
.
- G. Kucsko, P. C. Maurer, N. Y. Yao, M. Kubo, H. J. Noh, P. K. Lo, H. Park and M. D. Lukin, Nature, 2013, 500, 54–58 CrossRef CAS PubMed
.
- A. Ermakova, G. Pramanik, J.-M. Cai, G. Algara-Siller, U. Kaiser, T. Weil, Y.-K. Tzeng, H. C. Chang, L. P. McGuinness, M. B. Plenio, B. Naydenov and F. Jelezko, Nano Lett., 2013, 13, 3305–3309 CrossRef CAS PubMed
.
- L. Nie, A. C. Nusantara, V. G. Damle, R. Sharmin, E. P. P. Evans, S. R. Hemelaar, K. J. van der Laan, R. Li, F. P. P. Martinez, T. Vedelaar, M. Chipaux and R. Schirhagl, Sci. Adv., 2021, 7, eabf0573 CrossRef CAS
.
- Y. Zhu, J. Li, W. Li, Y. Zhang, X. Yang, N. Chen, Y. Sun, Y. Zhao, C. Fan and Q. Huang, Theranostics, 2012, 2, 302–312 CrossRef CAS PubMed
.
- B. F. Bachman, Z. R. Jones, G. R. Jaffe, J. Salman, R. Wambold, Z. Yu, J. T. Choy, S. J. Kolkowitz, M. A. Eriksson, M. A. Kats and R. J. Hamers, Langmuir, 2021, 37, 9222–9231 CrossRef CAS
.
- M. D. Torelli, N. A. Nunn and O. A. Shenderova, Small, 2019, 15, 1902151 CrossRef CAS PubMed
.
- M. Barzegar Amiri Olia, P. S. Donnelly, L. C. L. Hollenberg, P. Mulvaney and D. A. Simpson, ACS Appl. Nano Mater., 2021, 4, 9985–10005 CrossRef CAS
.
- J. Holzgrafe, Q. Gu, J. Beitner, D. M. Kara, H. S. Knowles and M. Atatüre, Phys. Rev. Appl., 2020, 13, 044004 CrossRef CAS
.
- R. Igarashi, T. Sugi, S. Sotoma, T. Genjo, Y. Kumiya, E. Walinda, H. Ueno, K. Ikeda, H. Sumiya, H. Tochio, Y. Yoshinari, Y. Harada and M. Shirakawa, J. Am. Chem. Soc., 2020, 142, 7542–7554 CrossRef CAS
.
- J. R. Woodward, Prog. React. Kinet. Mech., 2002, 27, 165–207 CrossRef CAS
.
- T. Biskup, E. Schleicher, A. Okafuji, G. Link, K. Hitomi, E. D. Getzoff and S. Weber, Angew. Chem., Int. Ed., 2009, 48, 404–407 CrossRef CAS
.
- I. A. Solov’yov, T. Domratcheva and K. Schulten, Sci. Rep., 2013, 4, 3845 CrossRef
.
- H. R. Ward and R. G. Lawler, J. Am. Chem. Soc., 1967, 89, 5518–5519 CrossRef CAS
.
- U. E. Steiner and T. Ulrich, Chem. Rev., 1989, 89, 51–147 CrossRef CAS
.
- A. Buchachenko and R. G. Lawler, Acc. Chem. Res., 2017, 50, 877–884 CrossRef CAS PubMed
.
- U. E. Steiner, J. Schäfer, N. N. Lukzen and C. Lambert, J. Phys. Chem. C, 2018, 122, 11701–11708 CrossRef CAS
.
- C. R. Timmel, U. Till, B. Brocklehurst, K. A. Mclauchlan and P. J. Hore, Mol. Phys., 1998, 95, 71–89 CrossRef CAS
.
- A. R. O’Dea, A. F. Curtis, N. J. B. Green, C. R. Timmel and P. J. Hore, J. Phys. Chem. A, 2005, 109, 869–873 CrossRef
.
- H. J. Hogben, T. Biskup and P. J. Hore, Phys. Rev. Lett., 2012, 109, 220501 CrossRef
.
- P. J. Hore and H. Mouritsen, Annu. Rev. Biophys., 2016, 45, 299–344 CrossRef CAS PubMed
.
- S. M. Harvey and M. R. Wasielewski, J. Am. Chem. Soc., 2021, 143, 15508–15529 CrossRef CAS PubMed
.
- A. Finkler and D. Dasari, Phys. Rev. Appl., 2021, 15, 034066 CrossRef CAS
.
- H. Liu, M. B. Plenio and J. Cai, Phys. Rev. Lett., 2017, 118, 200402 CrossRef PubMed
.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Annu. Rev. Biophy., 2022, 51, 99–114 CrossRef PubMed
.
- C. D. Aiello, J. M. Abendroth, M. Abbas, A. Afanasev, S. Agarwal, A. S. Banerjee, D. N. Beratan, J. N. Belling, B. Berche, A. Botana, J. R. Caram, G. L. Celardo, G. Cuniberti, A. Garcia-Etxarri, A. Dianat, I. Diez-Perez, Y. Guo, R. Gutierrez, C. Herrmann, J. Hihath, S. Kale, P. Kurian, Y.-C. Lai, T. Liu, A. Lopez, E. Medina, V. Mujica, R. Naaman, M. Noormandipour, J. L. Palma, Y. Paltiel, W. Petuskey, J. C. Ribeiro-Silva, J. J. Saenz, E. J. G. Santos, M. Solyanik-Gorgone, V. J. Sorger, D. M. Stemer, J. M. Ugalde, A. Valdes-Curiel, S. Varela, D. H. Waldeck, M. R. Wasielewski, P. S. Weiss, H. Zacharias and Q. H. Wang, ACS Nano, 2022, 16, 4989–5035 CrossRef CAS
.
- K. Ray, S. P. Ananthavel, D. H. Waldeck and R. Naaman, Science, 1999, 283, 814–816 CrossRef CAS
.
- B. Göhler, V. Hamelbeck, T. Z. Markus, M. Kettner, G. F. Hanne, Z. Vager, R. Naaman and H. Zacharias, Science, 2011, 331, 894–897 CrossRef PubMed
.
- M. Kettner, V. V. Maslyuk, D. Nürenberg, J. Seibel, R. Gutierrez, G. Cuniberti, K.-H. Ernst and H. Zacharias, J. Phys. Chem. Lett., 2018, 9, 2025–2030 CrossRef CAS PubMed
.
- J. M. Abendroth, K. M. Cheung, D. M. Stemer, M. S. El Hadri, C. Zhao, E. E. Fullerton and P. S. Weiss, J. Am. Chem. Soc., 2019, 141, 3863–3874 CrossRef CAS PubMed
.
- D. M. Stemer, J. M. Abendroth, K. M. Cheung, M. Ye, M. S. El Hadri, E. E. Fullerton and P. S. Weiss, Nano Lett., 2020, 20, 1218–1225 CrossRef CAS PubMed
.
- J. M. Abendroth, N. Nakatsuka, M. Ye, D. Kim, E. E. Fullerton, A. M. Andrews and P. S. Weiss, ACS Nano, 2017, 11, 7516–7526 CrossRef CAS PubMed
.
- S. Mishra, A. K. Mondal, S. Pal, T. K. Das, E. Z. B. Smolinsky, G. Siligardi and R. Naaman, J. Phys. Chem. C, 2020, 124, 10776–10782 CrossRef CAS
.
- T. Liu, X. Wang, H. Wang, G. Shi, F. Gao, H. Feng, H. Deng, L. Hu, E. Lochner, P. Schlottmann, S. von Molnár, Y. Li, J. Zhao and P. Xiong, ACS Nano, 2020, 14, 15983–15991 CrossRef PubMed
.
- Y. Sang, S. Mishra, F. Tassinari, S. K. Karuppannan, R. Carmieli, R. D. Teo, A. Migliore, D. N. Beratan, H. B. Gray, I. Pecht, J. Fransson, D. H. Waldeck and R. Naaman, J. Phys. Chem. C, 2021, 125, 9875–9883 CrossRef CAS
.
- A. Kumar, E. Capua, M. K. Kesharwani, J. M. L. Martin, E. Sitbon, D. H. Waldeck and R. Naaman, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2474–2478 CrossRef CAS PubMed
.
- K. Banerjee-Ghosh, O. B. Dor, F. Tassinari, E. Capua, S. Yochelis, A. Capua, S.-H. Yang, S. S. P. Parkin, S. Sarkar, L. Kronik, L. T. Baczewski, R. Naaman and Y. Paltiel, Science, 2018, 360, 1331–1334 CrossRef CAS PubMed
.
- S. Ghosh, S. Mishra, E. Avigad, B. P. Bloom, L. T. Baczewski, S. Yochelis, Y. Paltiel, R. Naaman and D. H. Waldeck, J. Phys. Chem. Lett., 2020, 11, 1550–1557 CrossRef CAS PubMed
.
- S. Dalum and P. HedegÃÂ¥rd, Nano Lett., 2019, 19, 5253–5259 CrossRef CAS PubMed
.
- X. Yang, C. H. van der Wal and B. J. van Wees, Phys. Rev. B, 2019, 99, 024418 CrossRef CAS
.
- A. Ghazaryan, Y. Paltiel and M. Lemeshko, J. Phys. Chem. C, 2020, 124, 11716–11721 CrossRef CAS
.
- A. Dianat, R. Gutierrez, H. Alpern, V. Mujica, A. Ziv, S. Yochelis, O. Millo, Y. Paltiel and G. Cuniberti, Nano Lett., 2020, 20, 7077–7086 CrossRef CAS PubMed
.
- M. S. Zöllner, S. Varela, E. Medina, V. Mujica and C. Herrmann, J. Chem. Theory Comput., 2020, 16, 2914–2929 CrossRef
.
- J. Fransson, Nano Lett., 2021, 21, 3026–3032 CrossRef CAS PubMed
.
- J. Fransson, J. Phys. Chem. Lett., 2022, 13, 808–814 CrossRef CAS PubMed
.
- D. H. Waldeck, R. Naaman and Y. Paltiel, APL Mater., 2021, 9, 040902 CrossRef CAS
.
- Y. Liu, J. Xiao, J. Koo and B. Yan, Nat. Mater., 2021, 20, 638–644 CrossRef CAS PubMed
.
- S. Alwan and Y. Dubi, J. Am. Chem. Soc., 2021, 143, 14235–14241 CrossRef CAS
.
- C. Vittmann, R. K. Kessing, J. Lim, S. F. Huelga and M. B. Plenio, J. Phys. Chem. Lett., 2022, 13, 1791–1796 CrossRef CAS PubMed
.
- A. Chiesa, M. Chizzini, E. Garlatti, E. Salvadori, F. Tacchino, P. Santini, I. Tavernelli, R. Bittl, M. Chiesa, R. Sessoli and S. Carretta, J. Phys. Chem. Lett., 2021, 12, 6341–6347 CrossRef CAS PubMed
.
- T. P. Fay, J. Phys. Chem. Lett., 2021, 12, 1407–1412 CrossRef CAS PubMed
.
- J. Luo and P. J. Hore, New J. Phys., 2021, 23, 043032 CrossRef CAS
.
- I. Meirzada, N. Sukenik, G. Haim, S. Yochelis, L. T. Baczewski, Y. Paltiel and N. Bar-Gill, ACS Nano, 2021, 15, 5574–5579 CrossRef CAS
.
- J. M. Abendroth, D. M. Stemer, B. P. Bloom, P. Roy, R. Naaman, D. H. Waldeck, P. S. Weiss and P. C. Mondal, ACS Nano, 2019, 13, 4928–4946 CrossRef CAS PubMed
.
- J. H. Olshansky, M. D. Krzyaniak, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2019, 141, 2152–2160 CrossRef CAS PubMed
.
- M. J. Junge, M. A. Kordan and E. T. Chernick, J. Org. Chem., 2020, 85, 13793–13807 CrossRef CAS
.
- E. R. Lorenzo, J. H. Olshansky, D. S. D. Abia, M. D. Krzyaniak, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2021, 143, 4625–4632 CrossRef CAS PubMed
.
- C. Copéret, W.-C. Liao, C. P. Gordon and T.-C. Ong, J. Am. Chem. Soc., 2017, 139, 10588–10596 CrossRef
.
- B. Corzilius, Annu. Rev. Phys. Chem., 2020, 71, 143–170 CrossRef CAS PubMed
.
- A. V. Yakimov, D. Mance, K. Searles and C. Copéret, J. Phys. Chem. Lett., 2020, 11, 3401–3407 CrossRef CAS
.
- N. R. Jaegers, K. T. Mueller, Y. Wang and J. T. Hu, Acc. Chem. Res., 2020, 53, 611–619 CrossRef CAS PubMed
.
- A. J. Rossini, A. Zagdoun, M. Lelli, A. Lesage, C. Copéret and L. Emsley, Acc. Chem. Res., 2013, 46, 1942–1951 CrossRef CAS PubMed
.
- C. Copéret, M. Chabanas, R. P. Saint-Arroman and J.-M. Basset, Angew. Chem., Int. Ed., 2003, 42, 156–181 CrossRef PubMed
.
- A. Faraon, C. Santori, Z. Huang, V. M. Acosta and R. G. Beausoleil, Phys. Rev. Lett., 2012, 109, 033604 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2022 |