Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On thermodynamic inconsistencies in several photosynthetic and solar cell models and how to fix them†
David
Gelbwaser-Klimovsky
* and
Alán
Aspuru-Guzik

Department of Chemistry and Chemical Biology, Cambridge, MA 02138, USA. E-mail: dgelbwaser@fas.harvard.edu
First published on 26th October 2016
Abstract
We analyze standard theoretical models of solar energy conversion developed to study solar cells and photosynthetic systems. We show that assuming the energy transfer to the reaction center/electric circuit is through a decay rate or “sink”, contradicts the second law of thermodynamics. We put forward a thermodynamically consistent alternative by explicitly considering parts of the reaction center/electric circuit and by employing a Hamiltonian transfer. The predicted energy transfer by the new scheme differs from the one found using a decay rate, casting doubts on the validity of the conclusions obtained by models which include the latter.
Light-harvesting organisms and solar cells convert thermal photons from the Sun, into useful energy such as ATP or electric power.1–3 Understanding and improving these processes may lead to more efficient ways to produce clean energy.4 These systems are effectively heat engines5–9 because they transform a heat flow into power (useful energy). Therefore, they are constrained by the laws of thermodynamics4,10–16 which set a fundamental efficiency bound based on the distinction between the two forms of energy exchange: heat flow and power. These two are not interchangeable: in a cyclic process, power may be totally converted into heat flow, but the opposite is forbidden by the second law of thermodynamics.7,17,18
A key for understanding the efficiency and the power produced by solar cells and plants, is the development of microscopical models of energy absorption, transmission and storage. Recent researches have shown that effects such as environment assisted quantum transport,19–22 coherent nuclear motion,23,24 and quantum coherences,25–28 play an important role in the enhancement of energy conversion. The importance of some of these effects for energy transport have been experimentally proven in specific realizations such as genetically engineered excitonic networks,29 waveguides networks,30 Rydberg aggregates31 and electrical oscillators.32
For practical computational and theoretical reasons, models have been restricted to the study of specific subsystems. It is customary to study photosynthetic complexes coupled to “traps” or “sinks” that represent the reaction center (RC) where exciton dissociation occurs.19–22,32 Similar models have been employed for the study of solar cells and exciton absorption and transport.24–27,33,34
Here we show that if not careful, the introduction of sinks and traps leads to violations of the second law of thermodynamics. These violations are a reason of concern for the validity of the models that have been employed to date. To shed light on the issue and to provide a simple to understand situation, we introduce a toy model to study this approximation and put forward a thermodynamically consistent version of it. This model could be used as the basis for more elaborate solar cell and plant microscopic models. Finally, we show that the output power of the thermodynamically-consistent version of the model can differ substantially from the simple trap or sink models.
Second law of thermodynamics and solar energy conversion
The standard thermodynamic models for solar energy conversion are comprised by a system, S, that interacts with different thermal baths and transforms the solar energy into chemical energy or electric current. Here we analyze two types of models: donor–acceptor models, where S is composed of four to five levels. These models have been applied for studying solar cells26,27 as well as photosynthetic systems,25 (see Fig. 1a); a second type of models describe the celebrated Fenna–Matthews–Olson (FMO) complex models, where S includes seven bacteriochlorophyll, each of them described by a single energy state19–22,24,32–34 (see Fig. 1b). In both cases, the energy conversion process is composed of the following explicit or implicit steps: (i) Light absorption. The system, S, absorbs hot photons coming from the Sun. The temperature of the photon is Tabs and Jabs is the heat flow between the hot photons bath and S; (ii) Energy transfer. The absorbed energy is transmitted between different states of S. During this stage, some energy is lost through a heat current, Jloss, to a vibrational bath at room temperature Tloss (material photons for solar cells2,3 or protein modes for photosynthetic systems1); (iii) Power extraction. A decay rate that represents an irreversible energy flow to an external system, work reservoir. The latter is generally not explicitly considered. For photosynthetic models, this last stage involves the decay to a sink or trap, together with an energy transfer to the RC and its subsequent transformation into chemical energy. In the case of solar cells, the energy flow produced by the decay rate is the electric power that runs through the circuit. These models are fundamentally different from the ones used on ref. 29–32, where the sink or trap is explicitly described by a Hamiltonian as we do below.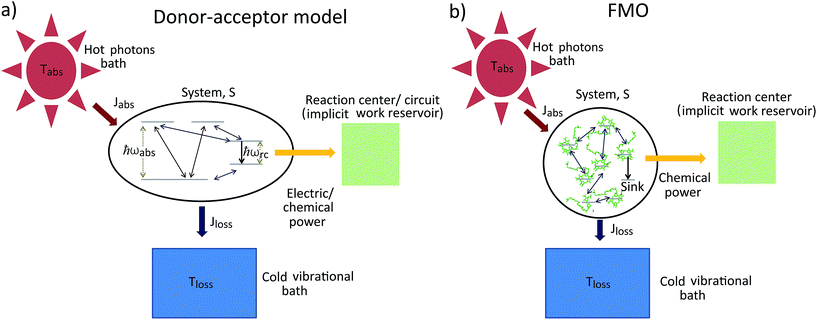 | ||
| Fig. 1 Solar energy conversion models: (a) donor–acceptor model; (b) FMO model. In both cases the allowed transitions are shown only for illustration purposes and may vary between different models. | ||
The dynamics of these systems is constrained by the second law of thermodynamics, through the entropy production inequality,8,35
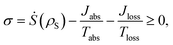 | (1) |
Ji = Tr[![[script L]](https://www.rsc.org/images/entities/char_e144.gif) i(ρS)H], i(ρS)H], | (2) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) i(ρS) is the evolution induced by the i-bath on S or excitation rate, and H is the system Hamiltonian which is equivalent to the excitation energy. For the heat currents, as wells as for the power, we use the sign convention that energy flowing to (from) S is positive (negative). Models with artificial sinks could be envisioned as systems that transfer energy to a zero-temperature bath. This could justify the addition of an extra term on the r.h.s of eqn (1) that would allow a 100% energy conversion efficiency. Nevertheless, solar cells and plants must obey the same thermodynamic bound as a heat engine operating between thermal baths at the temperatures of the Sun and the vibrational bath, which are 6000 K and 300 K, respectively, and therefore bounded to 95%. More elaborate models predict an even lower bound.4,10–16
i(ρS) is the evolution induced by the i-bath on S or excitation rate, and H is the system Hamiltonian which is equivalent to the excitation energy. For the heat currents, as wells as for the power, we use the sign convention that energy flowing to (from) S is positive (negative). Models with artificial sinks could be envisioned as systems that transfer energy to a zero-temperature bath. This could justify the addition of an extra term on the r.h.s of eqn (1) that would allow a 100% energy conversion efficiency. Nevertheless, solar cells and plants must obey the same thermodynamic bound as a heat engine operating between thermal baths at the temperatures of the Sun and the vibrational bath, which are 6000 K and 300 K, respectively, and therefore bounded to 95%. More elaborate models predict an even lower bound.4,10–16
In the case of a steady state flux of solar energy into S, the state of S on average does not change, and the second law, eqn (1), simplifies to
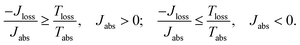 | (3) |
The donor/acceptor models studied in ref. 25–28, analyze the solar energy conversion at steady state. Their heat currents ratio has the form (see ESI-IA†):
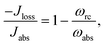 | (4) |
As shown in Fig. 2a, for 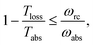 these models violate the second law of thermodynamics. Realistic model parameters may well fall outside of this range. This does not exclude the fact that the model is both inconsistent and potentially leading to artificial results. As we show below, the power predicted by a thermodynamically consistent model differs from the simple sink or trap models.
these models violate the second law of thermodynamics. Realistic model parameters may well fall outside of this range. This does not exclude the fact that the model is both inconsistent and potentially leading to artificial results. As we show below, the power predicted by a thermodynamically consistent model differs from the simple sink or trap models.
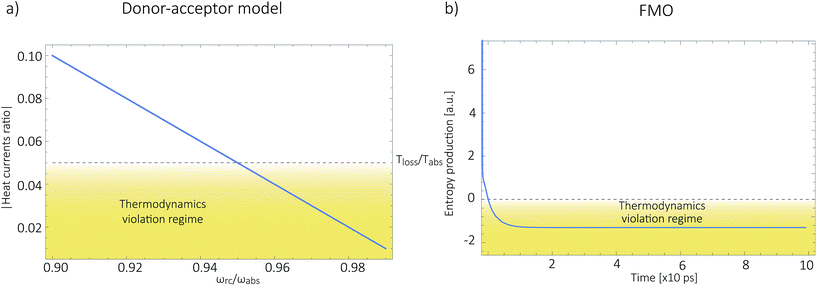 | ||
| Fig. 2 (a) Absolute value of the heat currents ratio as function of frequency ratio for the steady state models in ref. 25–28; (b) entropy production as a function of time for FMO models.19–22,24,32–34,37 In both graphs the shaded area represents a regime forbidden by thermodynamics laws. | ||
Next, we consider the standard sink or trap models of the FMO complex,19–22,24,32–34,37 governed by HFMO which includes the FMO sites, the vibrational bath and their interaction, as well as the transfer to the RC (see ESI-IB†). The later is a decay term (see Fig. 1b). In order to calculate the entropy production, eqn (1), we include the antenna and the solar thermal radiation.
The antenna is composed of around N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 absorbing pigments,38 and we model their collective effect as an effective monochromatic antenna of frequency ωant = 13
000 absorbing pigments,38 and we model their collective effect as an effective monochromatic antenna of frequency ωant = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 cm−1 or two level system (TLS), with a transition dipole moment
333 cm−1 or two level system (TLS), with a transition dipole moment 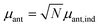 , where μant,ind ∼ 5 Debye, a typical value for a molecular transition dipole moment. Light absorption is governed by the antenna–radiation coupling, Hant–rad = μant|ant〉〈0| ⊗ Babs + h.c., where Babs is an operator on the thermal radiation bath, |ant〉 is the antenna excited state and |0〉 is the ground state. h.c. stands for the Hermitian conjugate. The FMO sites also interacts with the thermal radiation through the Hamiltonian,
, where μant,ind ∼ 5 Debye, a typical value for a molecular transition dipole moment. Light absorption is governed by the antenna–radiation coupling, Hant–rad = μant|ant〉〈0| ⊗ Babs + h.c., where Babs is an operator on the thermal radiation bath, |ant〉 is the antenna excited state and |0〉 is the ground state. h.c. stands for the Hermitian conjugate. The FMO sites also interacts with the thermal radiation through the Hamiltonian, 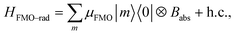 where |m〉 is the excited state of the FMO m site and μFMO = 5.44 Debye.39
where |m〉 is the excited state of the FMO m site and μFMO = 5.44 Debye.39
The transmission of the excitation from the antenna to the FMO is assisted by the vibrational degrees of freedom and described by
 | (5) |
Collecting everything together, the total Hamiltonian is
| HFMO + Hant + Hrad + Hant–FMO + Hant–rad + HFMO–rad, | (6) |
In this scenario, the dynamics outside the steady state is considered. For these models, there is not a simple analytical expression such as eqn (4), therefore we use a standard numeric simulation based on a Lindblad equation40–42 to calculate the dynamics governed by eqn (6) and together with eqn (2) we obtain S evolution and the heat currents Jabs(Jloss) between the FMO and the radiation (vibrational) baths. In Fig. 2b the entropy production, eqn (1), as function of time is presented, showing a violation of the second law of thermodynamics.
Thermodynamically-consistent model
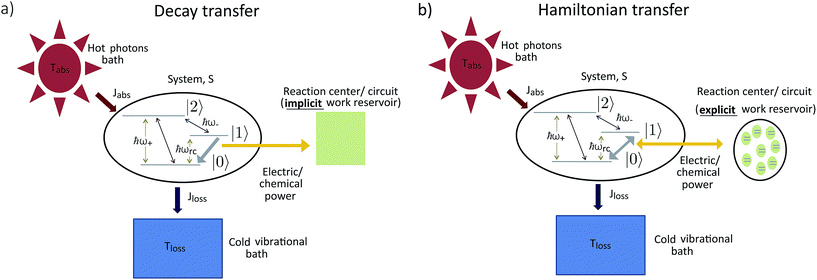
The assumption in the trap or sink models that the energy transfer to the RC/circuit is based solely on a relaxation process, introduces an inconsistency with thermodynamics, which is independent of the trap temperature, chemical potential or if it is modeled as an absorbing boundary by a non-Hermitian Hamiltonian. As it was shown in ref. 43, the later can be reformulated as an open quantum system. Even though physically the energy flow to the RC/circuit is power, a decay rate, or an absorbing boundary, effectively represents a heat flow. This is the root of the inconsistency. Here we use a toy model to clarify this point and put forward an alternative that could serve as basis to correctly model these systems. We compare between two possible energy transfers schemes to the RC/circuit: (i) standard decay; (ii) Hamiltonian transfer.For both schemes, S is a three level system as shown in Fig. 3. The absorption of a photon causes an excitation transfer between |0〉 and |2〉, whereas phonons are emitted by transitions from |2〉 to |1〉 to the vibrational bath. Finally, the cycle is closed by a transition between |1〉 and |0〉, and the energy difference is transferred to the RC/circuit. The S-bath Hamiltonian is HS + HB + HSB, where HB includes the photon and vibrational bath free Hamiltonian. Both baths are in thermal equilibrium at temperatures Tabs and Tloss, respectively. The S Hamiltonian is
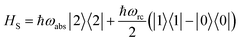 | (7) |
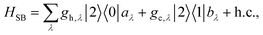 | (8) |
 | ||
| Fig. 3 A toy model used to study different energy transfer schemes: decay rate (left); Hamiltonian transfer (right). | ||
(i) Decay transfer. The standard relaxation scheme is a decay rate between |1〉 and |0〉,
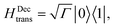 | (9) |
(ii) Hamiltonian transfer. An alternative to the model above is to explicitly include at least part of the RC/circuit, which plays the role of the work reservoir. In photosynthetic systems, the last stage on the reaction center is the transfer of electrons to the QB quinone, that once full, migrates to drive the production of ATP.44 This quinone is replaced by an empty one from a quinone pool. Inspired by this process, we construct a toy model of the work reservoir that could be a guideline for more complicated photosynthetic or solar cells models. It consists of a collection of independent and identical TLSs. Each of them represents a quinone in a photosynthetic system or an electrode site in a solar cell. The ground state corresponds to an empty quinone/site, and the excited state to a “full” quinone/site. Furthermore, we assume that there are always empty quinones/sites available to accept an electron. Thus, the number of quinones/sites, j, is always much larger than the number of electrons c†c, J ≫ c†c. This assumption is equivalent to the thermodynamic limit taken in the Holstein–Primakoff procedure,45,46 which allows to describe the collection of quinones/sites as a single harmonic oscillator (HO). Therefore, we can write the work reservoir and transfer Hamiltonian as (see ESI-IIB†)
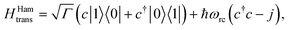 | (10) |
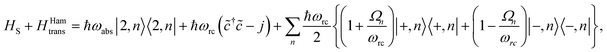 | (11) |
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) †(
†(![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ) is the creation (annihilation) operator in the new basis,
) is the creation (annihilation) operator in the new basis, 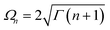 and
and | (12) |
In both schemes we use the standard Born–Markov approximation36 and write the Lindblad equations for (see ESI-II†): (i) Decay transfer scheme. The three level system, whose populations are given by ρi where i ∈ {0, 1, 2}; (ii) Hamiltonian transfer scheme. The three level system and the HO, whose populations are given by ρi,n where i ∈ {−, +, 2}. For both schemes, we analyze the energy transfer at the three level system steady state and assume that the zero temperature decay rates50 of the baths are equal to the transfer rate to the RC/circuit, Γh = Γc = Γ (see ESI-II†).
(i) Decay transfer. For this case the evolution equations in the interaction picture are (see ESI-IIA†)
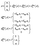 | (13) |
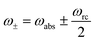 and ñabs(loss) = nabs(loss) + 1. The equations for the off-diagonal terms are decoupled from the populations and we assume that the off-diagonal terms are zero. The heat currents, eqn (2), at steady state are found using eqn (7) and (13),
and ñabs(loss) = nabs(loss) + 1. The equations for the off-diagonal terms are decoupled from the populations and we assume that the off-diagonal terms are zero. The heat currents, eqn (2), at steady state are found using eqn (7) and (13),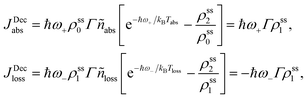 | (14) |
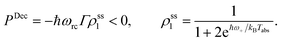 | (15) |
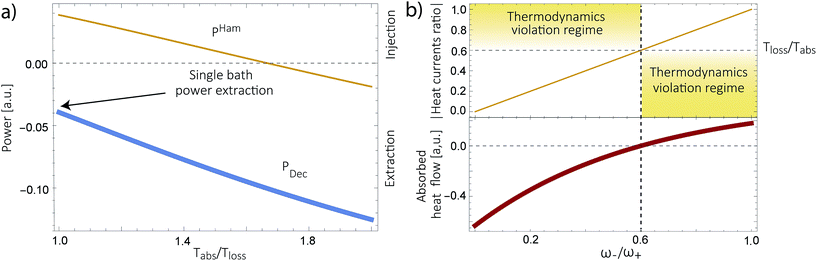
Power is always extracted (PDec < 0), even if the temperatures are the same, Tabs = Tloss. This is in contradiction with thermodynamics, which forbids cyclic power extraction in the presence of a single temperature. In combination, the temperature independence of the heat currents ratio and the positivity of JDecabs (eqn (3) and (4)), provides further evidence of the violation of thermodynamics,
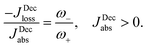 | (16) |
For 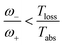 the model breaks the second law of thermodynamics, eqn (3).
the model breaks the second law of thermodynamics, eqn (3).
(ii) Hamiltonian transfer. For this case the evolution equations in the interaction picture for ρ2,n, ρ+,n and ρ−,n are (see ESI-IIB†)
 | (17) |
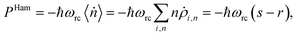 | (18) |
| JHamabs = ℏω+(s − r); JHamloss = −ℏω−(s − r), | (19) |
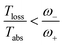 | (20) |
Fig. 4b shows the heat currents ratio of the Hamiltonian transfer scheme, which complies with the second law of thermodynamics (see eqn (3)). The thermodynamic violation regime splits due to the JHamabs sign change. Although for positive JHamabs the absolute value of the heat currents ratio should be larger than the temperatures ratio, for negative JHamabs it should be smaller. The lack of sign change for JDecabs prevents the splitting of the thermodynamic violation regime, placing the heat currents ratio in a thermodynamically forbidden region (see Fig. 2a).
Conclusions
We have analyzed several models used for describing energy absorption and transmission both in solar cells and in photosynthetic systems, such as the FMO complex. We have shown that the use of sinks, traps or any artificial relaxation process in order to describe the energy transfer to a further stage (the reaction center in photosynthetic systems or the electric circuit in a solar cell) introduces a contradiction with the second law of thermodynamics. This invalidates several models currently used to study solar energy conversion, casting doubts regarding their conclusions. These include the role of coherences, environment assisted quantum transport, coherent nuclear motion and the presence of quantum effects in photosynthesis, among others. We do not argue against the existence of those effects in the conversion of solar energy. But they should be verified using thermodynamically consistent models.We have further proposed how to correctly analyze these systems. We show this in a thermodynamically consistent toy model that explicitly describes parts of the RC/circuit and uses a Hamiltonian term to describe the energy transfer instead of a decay rate. The predicted transmitted energy greatly differs between these two alternatives (see Fig. 4a), highlighting the need to review the conclusions derived by thermodynamically inconsistent models.
Acknowledgements
We acknowledge Robert Alicki and Doran Bennett for useful discussions. We acknowledge the support from the Center for Excitonics, an Energy Frontier Research Center funded by the U.S. Department of Energy under award DE-SC0001088 (Solar energy conversion process). D. G.-K. also acknowledges the support of the CONACYT (Quantum thermodynamics).References
- R. E. Blankenship, Molecular mechanisms of photosynthesis, John Wiley & Sons, 2013 Search PubMed.
- J. Nelson, The physics of solar cells, World Scientific, 2003, vol. 1 Search PubMed.
- P. Würfel and U. Würfel, Physics of solar cells: from basic principles to advanced concepts, John Wiley & Sons, 2009 Search PubMed.
- R. E. Blankenship, D. M. Tiede, J. Barber, G. W. Brudvig, G. Fleming, M. Ghirardi, M. Gunner, W. Junge, D. M. Kramer and A. Melis, et al. , Science, 2011, 332, 805–809 CrossRef CAS PubMed.
- R. Alicki, D. Gelbwaser-Klimovsky and K. Szczygielski, J. Phys. A: Math. Theor., 2016, 49, 015002 CrossRef.
- M. Einax and A. Nitzan, J. Phys. Chem. C, 2014, 118, 27226–27234 CrossRef CAS.
- D. Kondepudi and I. Prigogine, Modern thermodynamics: from heat engines to dissipative structures, John Wiley & Sons, 2014 Search PubMed.
- D. Gelbwaser-Klimovsky, W. Niedenzu and G. Kurizki, Adv. At., Mol., Opt. Phys., 2015, 64, 329 Search PubMed.
- R. Kosloff, Entropy, 2013, 15, 2100–2128 CrossRef CAS.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- P. Landsberg and G. Tonge, J. Appl. Phys., 1980, 51, R1–R20 CrossRef CAS.
- R. S. Knox and W. W. Parson, Biochim. Biophys. Acta, Bioenerg., 2007, 1767, 1189–1193 CrossRef CAS PubMed.
- R. S. Knox, Biophys. J., 1969, 9, 1351 CrossRef CAS PubMed.
- W. W. Parson, Photochem. Photobiol., 1978, 28, 389–393 CrossRef CAS.
- R. T. Ross and M. Calvin, Biophys. J., 1967, 7, 595 CrossRef CAS PubMed.
- R. Alicki and D. Gelbwaser-Klimovsky, New. J. Phys., 2015, 17, 115012 CrossRef.
- D. Gelbwaser-Klimovsky, R. Alicki and G. Kurizki, EPL, 2013, 103, 60005 CrossRef CAS.
- D. Gelbwaser-Klimovsky and G. Kurizki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022102 CrossRef CAS PubMed.
- M. Mohseni, P. Rebentrost, S. Lloyd and A. Aspuru-Guzik, J. Chem. Phys., 2008, 129, 174106 CrossRef PubMed.
- P. Rebentrost, M. Mohseni, I. Kassal, S. Lloyd and A. Aspuru-Guzik, New. J. Phys., 2009, 11, 033003 CrossRef.
- M. B. Plenio and S. F. Huelga, New. J. Phys., 2008, 10, 113019 CrossRef.
- Y. Dubi, J. Phys. Chem. C, 2015, 119, 25252–25259 CrossRef CAS.
- V. I. Novoderezhkin, A. G. Yakovlev, R. Van Grondelle and V. A. Shuvalov, J. Phys. Chem. B, 2004, 108, 7445–7457 CrossRef CAS.
- N. Killoran, S. F. Huelga and M. B. Plenio, 2014, arXiv preprint arXiv:1412.4136.
- K. E. Dorfman, D. V. Voronine, S. Mukamel and M. O. Scully, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 2746–2751 CrossRef CAS PubMed.
- M. O. Scully, K. R. Chapin, K. E. Dorfman, M. B. Kim and A. Svidzinsky, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15097–15100 CrossRef CAS PubMed.
- C. Creatore, M. Parker, S. Emmott and A. Chin, Phys. Rev. Lett., 2013, 111, 253601 CrossRef CAS PubMed.
- F. Fassioli, A. Nazir and A. Olaya-Castro, J. Phys. Chem. Lett., 2010, 1, 2139–2143 CrossRef CAS.
- H. Park, N. Heldman, P. Rebentrost, L. Abbondanza, A. Iagatti, A. Alessi, B. Patrizi, M. Salvalaggio, L. Bussotti and M. Mohseni, et al. , Nat. Mater., 2016, 15, 211–216 CrossRef CAS PubMed.
- D. N. Biggerstaff, R. Heilmann, A. A. Zecevik, M. Gräfe, M. A. Broome, A. Fedrizzi, S. Nolte, A. Szameit, A. G. White and I. Kassal, Nat. Commun., 2016, 7, 11282 CrossRef CAS PubMed.
- D. Schönleber, A. Eisfeld, M. Genkin, S. Whitlock and S. Wüster, Phys. Rev. Lett., 2015, 114, 123005 CrossRef PubMed.
- R. d. J. León-Montiel, M. A. Quiroz-Juárez, R. Quintero-Torres, J. L. Domínguez-Juárez, H. M. Moya-Cessa, J. P. Torres and J. L. Aragón, Sci. Rep., 2015, 5, 17339 CrossRef PubMed.
- F. H. Alharbi and S. Kais, Renewable Sustainable Energy Rev., 2015, 43, 1073–1089 CrossRef.
- J. Cao and R. J. Silbey, J. Phys. Chem. A, 2009, 113, 13825–13838 CrossRef CAS PubMed.
- H. Spohn, J. Math. Phys., 1978, 19, 1227–1230 CrossRef.
- H.-P. Breuer and F. Petruccione, The theory of open quantum systems, Oxford university press, 2002 Search PubMed.
- F. Caruso, A. W. Chin, A. Datta, S. F. Huelga and M. B. Plenio, J. Chem. Phys., 2009, 131, 105106 CrossRef.
- S. Valleau, S. K. Saikin, D. Ansari-Oghol-Beig, M. Rostami, H. Mossallaei and A. Aspuru-Guzik, ACS Nano, 2014, 8, 3884–3894 CrossRef CAS PubMed.
- J. Adolphs and T. Renger, Biophys. J., 2006, 91, 2778–2797 CrossRef CAS PubMed.
- E. B. Davies, Commun. Math. Phys., 1974, 39, 91–110 CrossRef.
- V. Gorini, A. Kossakowski and E. C. G. Sudarshan, J. Math. Phys., 1976, 17, 821–825 CrossRef.
- G. Lindblad, Commun. Math. Phys., 1976, 48, 119–130 CrossRef.
- S. Selstø and S. Kvaal, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 065004 CrossRef.
- M. Jones, Biochem. Soc. Trans., 2009, 37, 400 CrossRef CAS PubMed.
- T. Holstein and H. Primakoff, Phys. Rev., 1940, 58, 1098 CrossRef.
- C. Emary and T. Brandes, Phys. Rev. A, 2004, 69, 053804 CrossRef.
- A. Mari, A. Farace and V. Giovannetti, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 175501 CrossRef.
- A. Levy, L. Diósi and R. Kosloff, Phys. Rev. A, 2016, 93, 052119 CrossRef.
- M. Bathaee and A. Bahrampour, Phys. Rev. E, 2016, 94, 022141 CrossRef CAS PubMed.
- G. Gordon, G. Bensky, D. Gelbwaser-Klimovsky, D. B. Rao, N. Erez and G. Kurizki, New. J. Phys., 2009, 11, 123025 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: (A) Dynamic equations for standar donor–acceptor models; (B) standard FMO models; (C) detailed derivation of dynamic equations for simple models for the RC/circuit. See DOI: 10.1039/c6sc04350j |
| This journal is © The Royal Society of Chemistry 2017 |