Negative ion photoelectron spectroscopy of P₂N₃⁻: electron affinity and electronic structures of P₂N₃˙

Abstract

We report here a negative ion photoelectron spectroscopy (NIPES) and ab initio study of the recently synthesized planar aromatic inorganic ion P₂N₃⁻, to investigate the electronic structures of P₂N₃⁻ and its neutral P₂N₃˙ radical. The adiabatic detachment energy of P₂N₃⁻ (electron affinity of P₂N₃˙) was determined to be 3.765 ± 0.010 eV, indicating high stability for the P₂N₃⁻ anion. Ab initio electronic structure calculations reveal the existence of five, low-lying, electronic states in the neutral P₂N₃˙ radical. Calculation of the Franck–Condon factors (FCFs) for each anion-to-neutral electronic transition and comparison of the resulting simulated NIPE spectrum with the vibrational structure in the observed spectrum allows the first four excited states of P₂N₃˙ to be determined to lie 6.2, 6.7, 11.5, and 22.8 kcal mol⁻¹ above the ground state of the radical, which is found to be a 6π-electron, ²A₁, σ state.

---

1. Introduction

Inspired by the unusual stability of the aromatic benzene molecule,^1–3 chemists have long sought other aromatic compounds. In the 1950s, cyclopentadienide (C₅H₅⁻, Cp⁻) was first synthesized.⁴ This anion has a planar five-membered ring, containing 6π electrons; so Cp⁻ fulfills the 4n + 2 Hückel rule for aromaticity.⁵ Indeed, Cp⁻ is the prototype of an aromatic, organic, anionic species, and it has become the primary building block of metallocenes.^6–10

It took about 30 years until, in the 1980s, cyclo-pentaphosphorus cyclo-P₅⁻, the all-phosphorus analog of C₅H₅⁻, was first prepared in alkali metal salts, MP₅ (M = Li, Na).^11–13 The cyclo-P₅⁻ ion also is found in the carbon-free metallocene complex (P₅TiP₅)²⁻,¹⁴ and in mixed-metallocene complexes Cp*MP₅ (Cp* = C₅Me₅; M = Fe, Ru),^12,13,15 as well as in nano-sized inorganic fullerene-like molecules.^16–19 Thus, the discovery of cyclo-P₅⁻ has greatly enriched metallocene chemistry and impacted supramolecular and capsule chemistry.

During the past three decades, researchers have sought other, all-inorganic, aromatic species. For example, N₂S₃²⁺,²⁰ N₃S₂⁺,²¹ and SN₂P₂,²² which are isolobal to cyclo-P₅⁻, have been identified; but N₂S₃²⁺ is not stable in solutions (N₂S₃²⁺), SN₂P₂ is only stable when isolated in an Ar matrix, and only N₃S₂⁺ has proven to be stable enough for isolation. Cyclo-N₅⁻, the first-row congener of cyclo-P₅⁻, has only been observed in the gas phase, where it can be formed via collision induced dissociation (CID) of a compound containing the N₅ unit^23,24 or its presence inferred via labeling studies of azide ion produced in the decomposition.^25,26

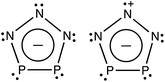
A recent report by Velian et al. of the successful synthesis of large amounts of a salt containing diphosphatriazolate (P₂N₃⁻, see Scheme 1) anion marks a breakthrough in synthetic phosphorus–nitrogen chemistry.^27,28 As a 6π-electron aromatic species with a planar five-membered ring, P₂N₃⁻ belongs to the set of (P_nN_5−n)⁻ (n = 0–5) anions, which, except for the n = 5 member of this series, have until now remained elusive. Considering the substantial enrichment of inorganic and organometallic chemistry made possible by the discovery of cyclo-P₅⁻, one may anticipate that the synthesis of bottleable P₂N₃⁻ will impact chemistry in a similar way. Thus, this all-inorganic, aromatic species may serve as an important link in inorganic chemistry that is missing no longer.

Scheme 1 Schematic depiction of P₂N₃⁻ and the lowest electronic state (²A₁) of P₂N₃˙.

Understanding the electronic structure of P₂N₃⁻ is a prerequisite to fully understanding its relationship to related compounds, such as C₅H₅⁻ and P₅⁻. One of the most fundamental aspects of these anions is, of course, their aromaticity;^29–31 and, as the prototypical aromatic anion, the electronic structure of C₅H₅⁻ has been relatively well studied. For example, the electron affinity (EA), Jahn–Teller coupling, and vibronic energies of C₅H₅⁻ and its neutral C₅H₅˙ radical have been investigated by negative ion photoelectron spectroscopy (NIPES),^32,33 electronic spectroscopy,³⁴ and ab initio calculations.^35,36 The cyclo-P₅⁻ ion and its heavier analogs, composed of As, Sb, and Bi, also have been studied by NIPES with the aid of electronic structure calculations.^37–39 All of these anions were found to have aromatic D_5h ring structures in their electronic ground states and to have π-MOs similar to those in C₅H₅⁻.

In light of the potential importance of P₂N₃⁻, we wanted to obtain detailed information about the electronic structure of this ion and of the neutral radical, formed by loss of an electron from the anion. Therefore, we produced the P₂N₃⁻ anion in the gas phase by electrospray ionization of an acetonitrile solution of a [Na-kryptofix-221] salt; and we characterized the electronic structures of P₂N₃⁻ and P₂N₃˙ by NIPES, with the help of high level ab initio calculations. We have shown previously that electrospray ionization has the ability to retain the solid-state structure of the molecules in the gas phase⁴⁰ and that NIPES is an excellent technique for investigating the electronic structures of cyclic organic molecules, such as (CO)_n,^41–43 (CS)₄,⁴⁴meta-benzoquinone (MBQ),⁴⁵ and 1,2,4,5-tetraoxatetramethylenebenzene (TOTMB).⁴⁶ In this paper we describe and analyze the NIPE spectra of P₂N₃⁻.

During the preparation of this manuscript, a paper by Jin et al. appeared, reporting calculations on the spectroscopy of P₂N₃⁻.⁴⁷ Of particular interest to us, their IP-EOM-CCSD calculations predicted that the vertical ionization energy (IE) of P₂N₃⁻ would be found to be 4.22 eV. We are thus able to compare this predicted value against the adiabatic value that we have measured and also against the vertical and adiabatic CCSD(T) values that we have computed.

2. Experimental methods

The NIPES experiments were performed with an apparatus⁴⁸ consisting of an electrospray ionization source, a cryogenic ion trap, and a magnetic-bottle time-of-flight (TOF) photoelectron spectrometer. A pure acetonitrile solution of [Na-kryptofix-221][P₂N₃]²⁷ was prepared in the glove box under a N₂ atmosphere and was transferred immediately into the electrospray ionization source, which was purged with N₂ to minimize the content of O₂ and moisture. The electrospray ionization conditions were optimized to make sure there was only one dominant mass peak at m/z = 104, i.e., P₂N₃⁻, in the mass spectrum. The anions generated were guided by quadrupole ion guides into an ion trap, where they were accumulated and cooled by collisions with cold buffer gas for 20–100 ms, before being transferred into the extraction zone of a TOF mass spectrometer. In the current study, the ion trap temperature was set to 20 K. The cooling of the anions to 20 K eliminated the possibility of the appearance of extra spectral peaks in the NIPE spectra, due to hot bands.⁴⁸

The P₂N₃⁻ anions were then mass selected, and decelerated before being photodetached. In the current study the wavelengths of the photodetachment lasers were 266 nm (4.661 eV) from a Nd:YAG laser, 193 nm (6.424 eV) from an ArF laser, and 157 nm (7.867 eV) from a F₂ excimer laser. The lasers were all operated at a 20 Hz repetition rate, with the ion beam off in alternating laser shots, thus allowing shot-to-shot background subtraction to be carried out. Photoelectrons were collected at ∼100% efficiency with the magnetic bottle and analyzed in a 5.2 m long electron flight tube.

The TOF photoelectron spectra were converted into electron kinetic energy spectra by calibration with the known NIPE spectra of I⁻, OsCl²⁻, and/or Cu(CN)₂⁻.⁴⁸ The electron binding energies (EBE) were obtained by subtracting the electron kinetic energies from the photon energies of the detaching lasers. The energy resolution was about 2%, i.e., ∼20 meV for 1 eV kinetic energy electrons.

3. Computational methodology

In order to help analyze the NIPE spectra of P₂N₃⁻, two different types of electronic structure calculations were performed. B3LYP⁴⁹ density functional theory (DFT) calculations and CCSD(T)⁵⁰ coupled-cluster ab initio calculations were both carried out. The aug-cc-pVTZ basis set⁵¹ was used for both types of calculations. The B3LYP geometry optimizations (including time-dependent⁵² B3LYP calculations on the 2²A₁ state of P₂N₃˙) and vibrational analyses were performed using the Gaussian09 suite of programs.⁵³ The CCSD(T) geometry optimizations and vibrational analyses were performed using the Molpro 10 program.⁵⁴

The program ezSpectrum⁵⁵ was used to compute the Franck–Condon factors (FCFs)⁵⁶ that were necessary, in order to simulate the vibrational progressions in the NIPE spectra of P₂N₃⁻. The NIPE spectra at 20 K were simulated, and no vibrational hot bands were seen in the simulations. In computing the FCFs for the simulations, the imaginary frequencies in the excited states of the neutral radical were treated as real frequencies; but the FCFs that were computed for these vibrational modes were zero; and, had they not been zero, we would have discarded them.

4. Results and discussion

4.1 The NIPE spectra of P₂N₃⁻

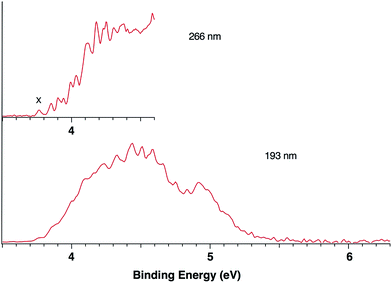
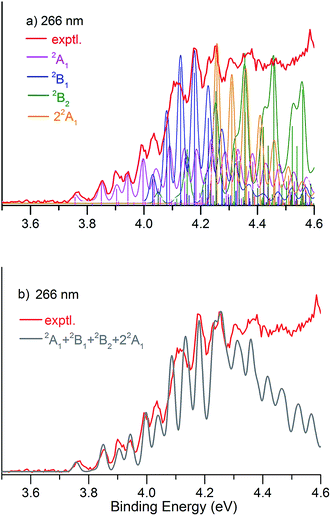
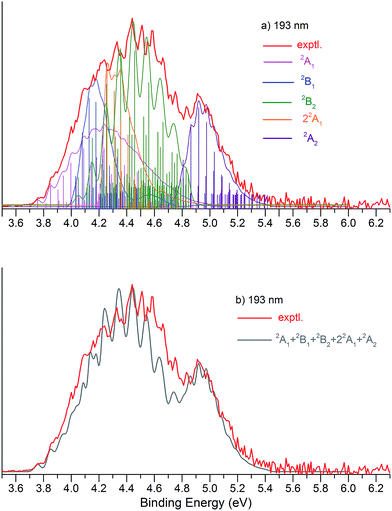
Fig. 1 presents the 20 K NIPE spectra of P₂N₃⁻ at 266 and 193 nm, respectively. The 157 nm NIPE spectrum shows almost the same spectral features in the electron binding energy (EBE) range of 3.7–5.5 eV as in the 193 nm spectrum, and is provided in Fig. S1 of the ESI.† However, much higher EBE features at around 7.0 and 7.6 eV can be seen in the 157 nm spectrum.

Fig. 1 The 20 K NIPE spectra of P₂N₃⁻ at 266 (4.661 eV) and 193 nm (6.424 eV), respectively. The origin of the band for what appears to be the first electronic state of P₂N₃˙ is labeled X in the 266 nm spectrum.

Partially resolved spectral features are seen at 266 nm in Fig. 1. The NIPE spectrum shows many rather closely-spaced peaks, suggesting that the spectrum probably contains multiple electronic state transitions and associated vibrational progressions. The adiabatic detachment energy (ADE) of P₂N₃⁻ (i.e., the EA of P₂N₃˙) is determined from the 0–0 transition (X) in the 266 nm NIPE spectrum in Fig. 1 to be 3.765 ± 0.010 eV.

The EA value of P₂N₃˙ is only slightly smaller than that of P₅˙, which was previously measured to have EA = 3.88 ± 0.03 eV,³⁹ but the EA value of P₂N₃˙ is much larger than that of C₅H₅˙, which has EA = 1.786 ± 0.020 eV.³² Significantly, the measured value of EA(P₂N₃˙) = 3.765 ± 0.010 eV, which is the adiabatic IE of the P₂N₃⁻ anion, is 0.45 eV lower than the predicted vertical IE of the anion, computed at the IP-EOM-CCSD level of theory.⁴⁷

4.2 The electronic structures of P₂N₃⁻ and P₂N₃˙

In order to help interpret the NIPE spectra of P₂N₃⁻, we carried out electronic structure calculations on both the P₂N₃⁻ anion and the neutral P₂N₃˙ radical. Fig. 2 shows the calculated geometry of P₂N₃⁻ at B3LYP/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels of theory. The calculated N–N bond lengths are in good agreement with those determined by X-ray diffraction in the solid salts;²⁷ but the calculated N–P and P–P bond lengths are both a little longer than those found in the salt. It should be noted that the two N–N and also the two P–N bond distances in the X-ray structure of P₂N₃⁻ are not the same, probably due to the packing effects in the crystal environment. However, the calculations predict a symmetric C_2v geometry to be an energy minimum for the gas-phase anion. The CCSD(T)/aug-cc-pVTZ geometries are also very close to those calculated by Jin et al.⁴⁷ at the same level of theory.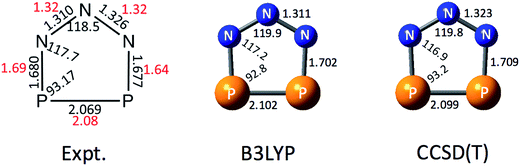

Fig. 2 Comparison of the X-ray structure of P₂N₃⁻ in [Na-kryptofix-221][P₂N₃] salt (major component in black, minor component in red)²⁷ with the calculated structures at B3LYP/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels of theory. Bond distances are in angstroms (Å) and bond angles are in degrees (°).

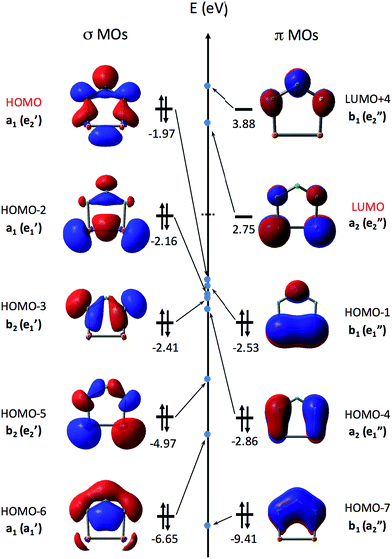
Fig. 3 shows the eight highest occupied molecular orbitals (HOMOs) and two virtual MOs of the ground state of P₂N₃⁻. These ten MOs, five π MOs and five σ MOs, are similar to those in P₅⁻.³⁹ Of course, substitution of three nitrogens for three phosphorus atoms in D_5h P₅⁻ reduces the symmetry to C_2v in P₂N₃⁻. Consequently, the degeneracy of four pairs of MOs in D_5h P₅⁻ (e′′₂, e′′₁, e′₂, and e′₁) is lifted. Nonetheless, occupation of the three low-lying valence π MOs – HOMO−1, HOMO−4, and HOMO−7 – by 6 electrons indicates that P₂N₃⁻ is aromatic, as was confirmed previously by NICS (Nucleus-Independent Chemical Shift) and QTAIM (Quantum Theory of Atoms in Molecules) calculations.²⁷

Fig. 3 The eight highest occupied molecular orbitals (HOMOs) and two lowest unoccupied molecular orbitals (LUMOs) of P₂N₃⁻, and their orbital energies, calculated at the B3LYP/aug-cc-pVTZ level of theory. [The LUMO+1, LUMO+2, and LUMO+3 are Rydberg MOs, formed from diffuse functions in the basis set]. The symmetry representation of each valence MO in C_2v P₂N₃⁻ is given; and next to it, in parenthesis, is the symmetry of the corresponding MO in D_5h P₅⁻. As indicated, the a₁ and b₂ orbitals of P₂N₃⁻ are σ MOs, and the b₁ and a₂ orbitals are π MOs.

Unlike the case of C₅H₅⁻, in which the five C–H σ MOs are all lower in energy than the three π MOs, the σ MOs in P₅⁻ (ref. 39) and in P₂N₃⁻ (Fig. 3) are comparable to the π MOs in energy. In fact, as shown in Fig. 3, the HOMO of P₂N₃⁻ is an a₁ σ MO, with considerable lone-pair character on the central nitrogen.

As shown in Table 1, the B3LYP and CCSD(T) calculations each find five low-lying electronic states of P₂N₃˙, three different σ states (1²A₁, ²B₂, and 2²A₁) and two different π states (²A₂ and ²B₁). In D_5h P₅˙ the 2²A₁ and ²B₂ σ states of P₂N₃˙ would be a degenerate pair of ²E′₁ states, and the π states of P₂N₃˙ would be a degenerate pair of ²E′′₁ states. Substitution of nitrogen for three phosphorus atoms of P₅˙ lifts the degeneracy of these states at the C_2v equilibrium geometry of P₂N₃˙, so that the two degenerate ²E′₁ σ states of P₅˙ differ in energy by ca. 7 kcal mol⁻¹ in P₂N₃˙, and the two degenerate ²E′′₁ π states of P₅˙ differ in energy by ca. 12 kcal mol⁻¹ in P₂N₃˙. The states nearest in energy to each other in P₂N₃˙, are ²B₁, a π state, and ²B₂, a σ state.

Table 1 Energies, with zero-point energy (ZPE) corrections in parenthesis, of the 1²A₁, ²B₁, ²B₂, ²A₂, and 2²A₁ states of P₂N₃˙, relative to the ¹A₁ state of P₂N₃⁻, computed at UB3LYP/aug-cc-pVTZ//UB3LYP/aug-cc-pVTZ and UCCSD(T)/aug-cc-pVTZ//UCCSD(T)/aug-cc-pVTZ level of theories

Molecule	Electronic state	Singly occupied MO	UB3LYP/aug-cc-pVTZ energies		UCCSD(T)/aug-cc-pVTZ energies
			in kcal mol^−1	in eV	in kcal mol^−1	in eV
a Energy minimum. b This state has an imaginary, out-of plane, b1 vibrational mode, because a b1 geometry distortion gives the ^2B1 excited state the same symmetry as the ^2A1 ground state. c This state has an imaginary, in-plane, b2 vibrational mode with both methods and an additional imaginary, out-of-plane, b1 mode with UCCSD(T). A b2 geometry distortion gives the ^2B2 excited state the same symmetry as the ^2A1 ground state. d This state has an imaginary, in-plane, b2 vibrational mode, because a b2 geometry distortion gives ^2A2 the same symmetry as ^2B1, the π state of lower energy. e The ZPE correction is not available, due to unsuccessful UCCSD(T) frequency analysis. f The excited ^2A1 state in which the unpaired electron occupies HOMO−2 in Fig. 3. UB3LYP vibrational analysis predicts an imaginary, in-plane b2 vibrational mode, because a b2 geometry distortion gives 2^2A1 the same symmetry as ^2B2, the σ excited state of lower energy. g The energy of this state, computed using time-dependent DFT at the TD-UB3LYP/aug-cc-pVTZ//TD-UB3LYP/aug-cc-pVTZ level of theory, is 101.5 kcal mol^−1 = 4.40 eV without ZPE correction. This energy is only 0.4 kcal mol^−1 lower than the value computed by a ground state UB3LYP calculation, in which the unpaired electron remained in the HOMO−2 σ MO during the geometry optimization. h UCCSD(T) geometry optimization leads to the 1^2A1 ground state. Therefore, a single point UCCSD(T) calculation at the UB3LYP/aug-cc-pVTZ optimized geometry was carried out, in order to obtain the UCCSD(T)/aug-cc-pVTZ energy of the 2^2A1 state.
P2N3^−	^1A1^a	None	0 (0)	0 (0)	0 (0)	0 (0)
P2N3˙	1^2A1^a	HOMO	82.9 (82.7)	3.59 (3.58)	86.4 (86.2)	3.75 (3.74)
	^2B1^b	HOMO−1	93.4 (91.4)	4.05 (3.96)	94.5 (93.3)	4.10 (4.05)
	^2B2^c	HOMO−3	94.8 (92.8)	4.11 (4.02)	96.4 (94.0)	4.18 (4.08)
	^2A2^d	HOMO−4	105.8 (104.9)	4.59 (4.55)	106.5 (^e)	4.62 (^e)
	2^2A1^f	HOMO−2	101.9 (101.5)^g	4.42 (4.40)^g	100.4^h	4.36^h

---

As shown in Table 1, both UB3LYP and UCCSD(T) methods predict that the ground state of neutral P₂N₃˙ is the ²A₁ state. It can be generated by removing one electron from the a₁ σ MO of P₂N₃⁻, which is the HOMO of the anion. The ²A₁ state retains 6π electrons, and is a σ radical.

The EA of the ²A₁ state of P₂N₃˙ is computed to be 3.74 eV at the UCCSD(T)/aug-cc-pVTZ level of theory, a value almost exactly the same as the EBE of the first resolved peak (3.765 ± 0.010 eV) in the 266 nm NIPE spectrum in Fig. 1. The excellent agreement between both the B3LYP and CCSD(T) calculations and the experimental value of the EA of P₂N₃˙ strongly suggests that the ground state of P₂N₃˙ is, indeed, the ²A₁ state, in which the unpaired electron occupies the a₁ σ MO.

As mentioned in the introduction, IP-EOM-CCSD/aug-cc-pVTZ calculations predict the vertical IE of P₂N₃⁻ to be 4.22 eV.⁴⁷ This value is 0.45 eV larger than the adiabatic IE of P₂N₃⁻ (which is, of course, the same as the adiabatic EA of P₂N₃˙) from the NIPE spectrum in Fig. 1. The reason for the large difference between the calculated and measured IEs could be due to the fact that 4.22 eV was computed to be the vertical IE of P₂N₃⁻; whereas the observed value of 3.765 eV is the adiabatic IE.

Since our calculated adiabatic IE of 3.74 eV is in excellent agreement with the measured value of 3.765 eV, we could test accurately whether or not there is, in fact, a large difference between the vertical and adiabatic IEs of P₂N₃⁻ by carrying out (U)CCSD(T)/aug-cc-pVTZ calculations of the vertical IE. The vertical IE that we obtained is 4.27 eV, which is 0.52 eV higher than our (U)CCSD(T)/aug-cc-pVTZ adiabatic value of 3.75 eV (without vibrational corrections) but only 0.05 eV higher than the IP-EOM-CCSD/aug-cc-pVTZ vertical IE that was computed by Jin et al.⁴⁷ The 0.52 eV difference between the vertical and adiabatic (U)CCSD(T)/aug-cc-pVTZ IEs and the small difference between the (U)CCSD(T)/aug-cc-pVTZ and IP-EOM-CCSD/aug-cc-pVTZ vertical IEs shows that almost all of the difference between the IP-EOM-CCSD/aug-cc-pVTZ vertical IE of 4.22 eV, calculated by Jin et al.,⁴⁷ and the experimental adiabatic IE of 3.765 eV, measured by us, is due to the large difference between the vertical and adiabatic IEs of P₂N₃⁻. The large geometry relaxation energy of ca. 0.5 eV on ionization is, presumably due to the fact that the electron lost occupies a σ bonding MO.

The three low-lying electronic states of C_2v P₂N₃˙ – ²B₁, ²B₂, and ²A₂ – that correspond to the three irreducible symmetry representations of the C_2v point group, other than A₁, can be generated by removing one electron from, respectively, the b₁ HOMO−1, b₂ HOMO−3, and a₂ HOMO−4 in P₂N₃⁻. Since these MOs are lower in energy than the HOMO in P₂N₃⁻, it would be expected that more energy is needed to detach an electron from these three MOs than from the a₁ HOMO in P₂N₃⁻. Therefore, the resulting three electronic states of P₂N₃˙, each of which places the unpaired electron in one of these three MOs, are expected to be higher in energy than the ²A₁ state. As shown in Table 1, calculations show that the ²B₁, ²B₂, and ²A₂ are, respectively, 7–11, 8–12, and 20–23 kcal mol⁻¹ higher in energy than the ²A₁ ground state of P₂N₃˙.

Removal of an electron from the HOMO−2 of P₂N₃⁻ generates a ²A₁ state, which has the same symmetry as the 1²A₁ ground state of the radical. Consequently, a time-dependent (TD)DFT calculation was necessary, in order to obtain the energy of the 2²A₁ state. Table 1 shows that a TD-UB3LYP/aug-cc-pVTZ//TD-UB3LYP/aug-cc-pVTZ calculation places the energy of the 2²A₁ state 18.6 kcal mol⁻¹ above the 1²A₁ ground state of the radical and 4.3 kcal mol⁻¹ below the ²A₂ state.

Starting from the TD-UB3LYP optimized geometry for the 2²A₁ state, we were able to do ground-state UB3LYP/aug-cc-pVTZ geometry optimization and frequency analysis on this state, using a wavefunction in which the unpaired electron was forced to occupy the HOMO−2 of Fig. 3. The ground-state UB3LYP calculation predicts an energy for the 2²A₁ state that is within 0.4 kcal mol⁻¹ of the energy obtained from the TD-UB3LYP calculation.

We also carried out UCCSD(T)/aug-cc-pVTZ//UB3LYP/aug-cc-pVTZ calculations on 2²A₁ that give a similar result. They predict that the 2²A₁ state is 14.0 kcal mol⁻¹ above the 1²A₁ ground state and 6.1 kcal mol⁻¹ below the ²A₂ state. Therefore, at both levels of theory, the 2²A₁ state is predicted to be the second highest energy state among the five lowest-lying states of P₂N₃˙ in Table 1.

The UCCSD(T) predicted EA values of the five lowest-lying states of P₂N₃˙ (3.74–4.62 eV) are all lower than the 193 nm photon energy (6.424 eV). Therefore, these five states are all potentially accessible by photodetachment of P₂N₃⁻, and they are very likely to be responsible for at least the first half of the spectral features in the range of 3.7–4.6 eV in the 193 nm spectrum of Fig. 1. The second half of the spectral features in the 4.6 – 5.5 eV range of the 193 nm spectrum could be due to still higher energy excited states of P₂N₃˙, or they could also be due to vibrational progressions belonging to the five lowest energy electronic states of P₂N₃˙.

4.3 Simulation of the vibrational progressions in the NIPE spectra

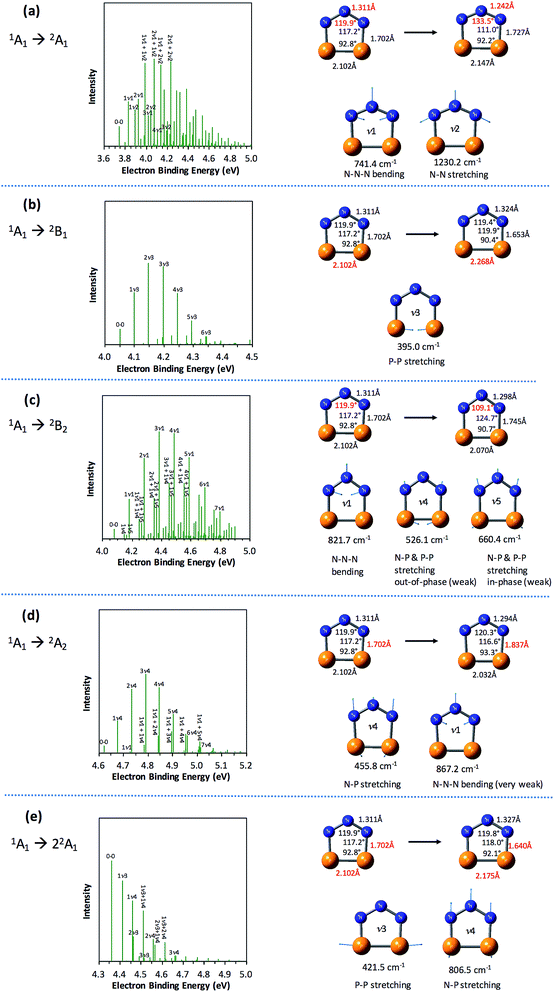
The partially resolved spectral features at 266 nm in Fig. 1 correspond to the transitions from the ground state of P₂N₃⁻ to the ground and excited states of P₂N₃˙, along with the vibrational excitations associated with the formation of each electronic state. Therefore, in order to assign all of the peaks in the 266 nm NIPE spectrum, we calculated the Franck–Condon factors (FCFs)⁵⁶ of transitions from the ¹A₁ ground state of P₂N₃⁻ to each of the five, lowest-lying electronic states of P₂N₃˙ (²A₁, ²B₁, ²B₂, ²A₂, and 2²A₁).

Fig. 4 shows the vibrational progressions, simulated using the UB3LYP geometries, frequencies and FCFs. The geometry changes and the active vibrational modes that yield the vibrational progressions for each transition are also shown in Fig. 4. Simulations using UCCSD(T) geometries, frequencies and FCFs gave very similar vibrational progression patterns as UB3LYP; and the UCCSD(T) stick spectra are provided in the ESI† of this manuscript.

Fig. 4 Simulated vibrational progressions (stick spectra) at 20 K for the formation of the five low-lying states of P₂N₃˙ from the ¹A₁ ground state of P₂N₃⁻, using UB3LYP geometries, frequencies and FCFs, and UCCSD(T) energies. Geometry changes (the most significant changes are highlighted in red) from the initial state of the anion to the target state of the radical and the active modes (with frequencies) for each of the five transitions are also shown. The assignments of the major peaks in the stick spectra are given.

As shown in Fig. 4, the electronic transitions from the ¹A₁ ground state of P₂N₃⁻ to the five low-lying states of P₂N₃˙ all feature weak 0–0 peaks, except for the transition to the 2²A₁ state, in which the 0–0 peak is the most intense. Nevertheless, all five transitions show long vibrational progressions. The reason is that, as shown in Fig. 4, the calculations reveal significant geometry changes for each of these electronic transitions in the NIPE spectrum of P₂N₃⁻.

For example, in the ¹A₁ → ²A₁ transition (Fig. 4a), one electron is removed from the a₁ HOMO of P₂N₃⁻ in Fig. 3. The HOMO contains N–N antibonding interactions, N–P and P–P bonding interactions, and a bonding interaction between non-nearest neighbor nitrogens. Removing one electron from this orbital leads to exactly the calculated geometrical changes that one would expect — shortening of the N–N bond lengths, lengthening of the N–P and P–P bonds, and expansion of the N–N–N bond angle.

Calculations show that the two most significant geometrical changes are shortening of the N–N bond length, from 1.311 to 1.242 Å, and expansion of the N–N–N bond angle from 119.9 to 133.5°. These large changes on going from the equilibrium geometry of P₂N₃⁻ to that of P₂N₃˙ are responsible for the calculated difference of 0.52 eV between the vertical and adiabatic IEs of the anion.

N–N–N bending (ν₁ = 741.4 cm⁻¹) and N–N stretching (ν₂ = 1230.2 cm⁻¹) are the two vibrational modes that create the most significant changes in, respectively, the N–N–N bond angle and the N–N bond length. These a₁ vibrational modes are active in the transition from the ¹A₁ ground state of the anion to the ²A₁ ground state of the neutral. The four most intense peaks in the long vibrational progression that is associated with the ¹A₁ → ²A₁ transition are due to coupled a₁ vibrational modes, involving both N–N–N bending and N–N stretching.

Analysis of the other four electronic transitions in Fig. 4b–e in a similar fashion shows that the most active a₁ vibrational modes in each of these transitions are P–P stretching (ν₃ = 395.0 cm⁻¹) in ¹A₁ → ²B₁, N–N–N bending (ν₁ = 821.7 cm⁻¹) in ¹A₁ → ²B₂, N–P stretching (ν₄ = 455.8 cm⁻¹) in ¹A₁ → ²A₂, and P–P stretching (ν₃ = 421.5 cm⁻¹) and N–P stretching (ν₃ = 806.5 cm⁻¹) in ¹A₁ → 2²A₁.

4.4 Simulation of the NIPE spectra of P₂N₃⁻

We simulated the experimental 266 and 193 nm NIPE spectra of P₂N₃⁻ by convoluting the UB3LYP calculated stick spectrum with Gaussian functions having full widths of 25 meV (for the 266 nm NIPE spectrum) and 55 meV (for the 193 nm spectrum) at half maxima for each stick. As shown in Figs. 5 and 6, after small adjustments of the UCCSD(T) calculated energies of the 0–0 bands for the five electronic states of P₂N₃˙, (+0.02 eV for ²A₁, −0.02 eV for ²B₁, −0.03 eV for ²B₂, −0.10 eV for 2²A₁, and +0.13 eV for ²A₂), the simulated NIPE spectra of P₂N₃⁻ match the experimental 266 and 193 nm spectra quite well.

Fig. 5 (a) UB3LYP/aug-cc-pVTZ simulated vibrational progressions (sticks) in the NIPE spectrum and the convoluted spectra, superimposed onto the experimental 266 nm NIPE spectrum (red). The UCCSD(T) predicted positions of the 0–0 bands have been slightly adjusted – 3.74 → 3.76 eV for ²A₁ (pink), 4.05 → 4.03 eV for ²B₁(blue), 4.08 → 4.05 eV for ²B₂ (green), 4.36 → 4.26 eV for 2²A₁ (orange) – to give a better match to the experimental spectrum. The convoluted spectrum, using Gaussian line shapes with 25 meV full widths at half maxima for each stick in the ²A₁, ²B₁, ²B₂, and 2²A₁ states is also shown. (b) The computed NIPE spectrum (grey), calculated from the sum of the convoluted contributions of the four doublet states in (a), superimposed on the experimental 266 spectrum (red).

Fig. 6 (a) UB3LYP/aug-cc-pVTZ simulated vibrational progressions (stick spectrum) and the convoluted spectra, superimposed onto the experimental 193 nm NIPE spectrum (red). The UCCSD(T) predicted positions of the 0–0 bands have been slightly adjusted, i.e., +0.02 eV (3.74 → 3.76 eV) for ²A₁ (pink), −0.02 eV (4.05 → 4.03 eV) for ²B₁(blue), −0.03 eV (4.08 → 4.05 eV) for ²B₂ (green), −0.10 eV (4.36 →4.26 eV) for 2²A₁ (orange) and +0.13 eV (4.62 → 4.75 eV) for ²A₂ (purple), in order to give a better match to the experimental spectrum. The convoluted spectrum, using Gaussian line shapes with 55 meV full widths at half maxima for each stick in ²A₁, ²B₁, ²B₂, 2²A₁, and ²A₂, is also shown. (b) The computed NIPE spectrum (grey), calculated from the sum of the convoluted contributions of the five doublets in (a), superimposed on the experimental 193 spectrum (red).

It should be noted that, starting near EBE > 4.3 eV, the 266 nm experimental spectral bands seem to sit on top of a background, which makes the spectral features in this region appear more intense than they would be if only direct detachment processes were involved. Resonant photodetachment⁵⁷ may give rise to an underlying band in this region, thus accounting for the differences between the experimental and simulated NIPE spectra in Fig. 5. Resonant photodetachment was previously used to explain the difference between the experimental and simulated NIPE spectra in our previous NIPES study of the TOTMB radical anion.⁴⁶

These small adjustments of the calculated 0–0 bands for formation of the five lowest electronic states of P₂N₃˙ give the EAs of these states of P₂N₃˙ as 3.76, 4.03, 4.05, 4.26, and 4.75 eV, respectively. We have also simulated the NIPE spectra by slightly different adjustments of the calculated 0–0 energies of the four excited states, and these simulations are presented in the ESI† of this manuscript. These simulated spectra all agree reasonably well with the experimental spectra, but the simulations shown in Figs. 5 and 6 give the best agreement.

Our confidence in the absolute energies assigned to the 0–0 bands of the excited states is about 0.05 eV (1 kcal mol⁻¹). Simulations using UCCSD(T) geometries, frequencies and FCFs gave similar vibrational patterns to the B3LYP simulations in Figs. 5 and 6. The UCCSD(T) stick spectra are provided in the ESI† of this manuscript.

In order to account for the variation of energy resolution of our TOF type photoelectron spectrometer in the photoelectron energy range of EBE = 3.8–4.4 eV, we also simulated the 266 nm NIPE spectrum, by convoluting the UB3LYP calculated stick spectrum with Gaussian functions having full widths of 20 and 30 meV at half maxima for each stick. These two simulated NIPE spectra, which are presented in the ESI† for this manuscript, gave fits to the experimental NIPE spectrum of the same quality as that in Fig. 5, which assumed a 25 meV energy resolution.

5. Conclusions

We report the NIPE spectra of P₂N₃⁻, an all-inorganic, aromatic species, which was recently isolated in bulk quantities as a salt. The NIPE spectra provide the measurement of the electron affinity (EA = 3.765 ± 0.010 eV) for the ground state of neutral P₂N₃˙. The NIPE spectra also indicate that other electronic states of P₂N₃˙ are quite close in energy to the ground state of this radical.

Ab initio electronic structure calculations and simulations, based on computed Franck–Condon factors (FCFs), reveal that the ground state of P₂N₃˙ is ²A₁, in which the unpaired electron occupies an a₁ σ MO. The first four excited states of P₂N₃˙ are ²B₁, ²B₂, 2²A₁, and ²A₂ with their energies calculated at the CCSD(T)/aug-cc-pVTZ level of theory to be 8.1, 10.0, 14.0, and 20.1 kcal mol⁻¹ above the ²A₁ ground state. Simulations of the NIPE spectrum of P₂N₃˙, based on the FCFs computed for formation of these five electronic states from the ¹A₁ ground state of the P₂N₃⁻ anion provide a reasonable fit to the peaks in the NIPE spectrum of the anion.

The results in this paper, obtained from a combination of experiments and calculations, contribute fundamental information about the electronic structures of P₂N₃⁻ and the P₂N₃˙ radical formed from it by photochemical electron detachment. This information is likely to prove useful in future investigations of P₂N₃⁻, P₂N₃˙, and their chemistry.

Conflict of interest

The authors declare no competing financial interest.

Acknowledgements

The NIPES research done at PNNL was supported by U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, the Division of Chemical Sciences, Geosciences, and Biosciences, and performed using EMSL, a national scientific user facility sponsored by DOE's Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory, which is operated by Battelle Memorial Institute for the DOE. The theoretical calculations at UNT were supported by Grant B0027 from the Robert A. Welch Foundation. The synthesis work of [Na-kryptofix-221][P₂N₃] was supported by the National Science Foundation under grant no. CHE-1362118. G.-L. Hou thanks Dr Shaoguang Zhang from PNNL for providing the dry and degassed acetonitrile.

References and notes

1. M. Faraday, Philos. Trans. R. Soc. London, 1825, 115, 440.
2. A. Kekuié, Justus Liebigs Ann. Chem., 1866, 137, 129.
3. I. I. Naumov and R. J. Hemley, Acc. Chem. Res., 2014, 47, 3551.
4. K. Ziegler, H. Froitzheim-Kuhlhorn and K. Hafner, Chem. Ber., 1956, 89, 434.
5. (a) E. Hückel, Z. Phys., 1931, 70, 204; (b) E. Hückel, Z. Phys., 1931, 72, 310; (c) E. Hückel, Z. Phys., 1932, 76, 628.
6. T. J. Kealy and P. L. Pauson, Nature, 1951, 168, 1039.
7. G. Wilkinson, M. Rosenblum, M. C. Whiting and R. B. Woodward, J. Am. Chem. Soc., 1952, 74, 2125.
8. E. O. Fischer and W. Pfab, Z. Naturforsch., B: J. Chem. Sci., 1952, 7, 377.
9. 1973 Nobel Prize in Chemistry, see http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1973/.
10. H. Werner, Angew. Chem., Int. Ed., 2012, 51, 6052.
11. M. Baudler, D. Düster and D. Ouzounis, Z. Anorg. Allg. Chem., 1987, 544, 87.
12. M. Baudler, S. Akpapoglou, D. Ouzounis, F. Wasgestian, B. Meinigke, H. Budzikiewicz and H. Münster, Angew. Chem., Int. Ed., 1988, 27, 280.
13. H. Grützmacher, Z. Anorg. Allg. Chem., 2012, 638, 1877.
14. E. Urnėžius, W. W. Brennessel, C. J. Cramer, J. E. Ellis and P. V. R. Schleyer, Science, 2002, 295, 832.
15. O. J. Scherer, Angew. Chem., Int. Ed. Engl., 1990, 29, 1104.
16. J. Bai, A. V. Virovets and M. Scheer, Science, 2003, 300, 781.
17. M. Scheer, A. Schindler, R. Merkle, B. P. Johnson, M. Linseis, R. Winter, C. E. Anson and A. V. Virovets, J. Am. Chem. Soc., 2007, 129, 13386.
18. M. Fleischmann, J. S. Jones, F. P. Gabbai and M. Scheer, Chem. Sci., 2015, 6, 132.
19. S. Heinl, E. Peresypkina, J. Sutter and M. Scheer, Angew. Chem., Int. Ed., 2015, 54, 13431.
20. W. V. F. Brooks, T. S. Cameron, S. Parsons, J. Passmore and M. J. Schriver, Inorg. Chem., 1994, 33, 6230.
21. S. Herler, P. Mayer, H. Nöth, A. Schulz, M. Suter and M. Vogt, Angew. Chem., Int. Ed., 2001, 40, 3173.
22. X. Zeng, H. Li, H. Sun, H. Beckers, H. Willner and H. F. Schaefer III, Angew. Chem., Int. Ed., 2015, 54, 1327.
23. A. Vij, J. G. Pavlovich, W. W. Wilson, V. Vij and K. O. Christe, Angew. Chem., 2002, 114, 3177.
24. T. Schroer, R. Haiges, S. Schneider and K. O. Christe, Chem. Commun., 2005, 1607.
25. R. N. Butler, J. M. Hanniffy, J. C. Stephens and L. A. Burke, J. Org. Chem., 2008, 73, 1354.
26. S. A. Perera, A. Gregušová and R. J. Bartlett, J. Phys. Chem. A, 2009, 113, 3197.
27. A. Velian and C. C. Cummins, Science, 2015, 348, 1001.
28. C. Hering-Junghans and E. Rivard, Angew. Chem., Int. Ed., 2015, 54, 10077.
29. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842.
30. A. I. Boldyrev and L.-S. Wang, Chem. Rev., 2005, 105, 3716.
31. R. Hoffmann, Am. Sci., 2015, 103, 18.
32. P. C. Engelking and W. C. Lineberger, J. Chem. Phys., 1977, 67, 1412.
33. T. Ichino, S. W. Wren, K. M. Vogelhuber, A. J. Gianola, W. C. Lineberger and J. F. Stanton, J. Chem. Phys., 2008, 129, 084310.
34. B. E. Applegate, T. A. Miller and T. A. Barckholtz, J. Chem. Phys., 2001, 114, 4855.
35. W. T. Borden and E. R. Davidson, J. Am. Chem. Soc., 1979, 101, 3771.
36. X. Zhou, D. A. Hrovat and W. T. Borden, J. Am. Chem. Soc., 2007, 129, 10785.
37. R. O. Jones, G. Ganteför, S. Hunsicker and P. Pieperhoff, J. Chem. Phys., 1995, 103, 9549.
38. T. P. Lippa, S.-J. Xu, S. A. Lyapustina, J. M. Nilles and K. H. Bowen, J. Chem. Phys., 1998, 109, 10727.
39. H.-J. Zhai, L.-S. Wang, A. E. Kuznetsov and A. I. Boldyrev, J. Phys. Chem. A, 2002, 106, 5600.
40. G.-L. Hou, H. Wen, K. Lopata, W.-J. Zheng, K. Kowalski, N. Govind, X.-B. Wang and S. S. Xantheas, Angew. Chem., Int. Ed., 2012, 51, 6356.
41. J.-C. Guo, G.-L. Hou, S.-D. Li and X.-B. Wang, J. Phys. Chem. Lett., 2012, 3, 304.
42. X. Bao, D. A. Hrovat, W. T. Borden and X.-B. Wang, J. Am. Chem. Soc., 2013, 135, 4291.
43. B. Chen, D. A. Hrovat, R. West, S. H. M. Deng, X.-B. Wang and W. T. Borden, J. Am. Chem. Soc., 2014, 136, 12345.
44. J. Zhang, D. A. Hrovat, Z. Sun, X. Bao, W. T. Borden and X.-B. Wang, J. Phys. Chem. A, 2013, 117, 7841.
45. B. Chen, D. A. Hrovat, S. H. M. Deng, J. Zhang, X.-B. Wang and W. T. Borden, J. Am. Chem. Soc., 2014, 136, 3589.
46. D. A. Hrovat, G.-L. Hou, X.-B. Wang and W. T. Borden, J. Am. Chem. Soc., 2015, 137, 9094.
47. Y. Jin, A. Perera and R. J. Bartlett, Chem. Phys. Lett., 2015, 640, 68.
48. X.-B. Wang and L.-S. Wang, Rev. Sci. Instrum., 2008, 79, 073108.
49. B3LYP is a combination of Becke’s 3-parameter hybrid exchange functional ( A. D. Becke, J. Chem. Phys., 1993, 98, 5648 ) with the electron correlation functional of Lee, Yang, and Parr ( C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 ).
50. (a) G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910; (b) K. Raghavachari, G. W. Trucks, J. A. Pople and M. H. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
51. (a) T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007; (b) R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
52. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454.
53. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
54. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, and M. Wang, MOLPRO, version 2010.1, a package of ab initio programs, see http://www.molpro.net.
55. V. A. Mozhayskiy and A. I. Krylov, ezSpectrum, version 3.0, see http://iopenshell.usc.edu/downloads.
56. (a) J. Franck, Trans. Faraday Soc., 1926, 21, 536; (b) E. Condon, Phys. Rev., 1926, 28, 1182.
57. J. Schiedt and R. Weinkauf, J. Chem. Phys., 1999, 110, 304.

---

Footnote

† Electronic supplementary information (ESI) available: The 20 K NIPE spectra of P₂N₃⁻ at 266, 193, and 157 nm (Fig. S1); simulations of vibrational progressions (stick spectra), using UCCSD(T) geometries, frequencies and FCFs (Fig. S2); the simulation of the NIPE spectra by adjusting the calculated 0–0 band positions for each electronic state, relative to the experiments (Figs. S3 and S4); the simulated 266 nm spectra with Gaussian functions of 20 and 30 meV full widths at half maxima (Figs. S5 and S6); coordinates and energies of calculated structures (Table S1); computed Franck–Condon factors (Table S2). See DOI: 10.1039/c5sc04667j

---