 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fitting a square peg in a round hole: parameterisation of quasi-spherical molecules employing the Mie potential†
Gustavo
Chaparro
 and
Erich A.
Müller
and
Erich A.
Müller
 *
*
Sargent Centre for Process Systems Engineering, Department of Chemical Engineering, Imperial College London, London, SW7 2AZ, UK. E-mail: e.muller@imperial.ac.uk
First published on 19th June 2025
Abstract
The parameterisation of the force field of a molecular system is essential for accurately describing and predicting macroscopic thermophysical properties. Here, we discuss three approaches to obtain the molecular parameters (σ, ε, and λr) of the Mie force field from experimental data for quasi-spherical molecules. The first approach is based on a classical strategy that considers fitting only to vapour–liquid equilibria data. The second approach entails a simultaneous fit to equilibrium properties and liquid shear viscosity. Finally, a third approach incorporates solid–fluid equilibrium data. The fitting procedure is facilitated by the use of recently published machine-learned equations of state for the Mie particle, which allows the prediction of thermophysical properties given a set of molecular parameters. The goodness-of-fit is assessed based on the deviations between calculated and experimental data. We also assess the behaviour of the thermal conductivity and speed of sound of the saturated liquid phase to evaluate the transferability of the molecular parameters to properties not used in the parametrisation. Apart from the singular case of monoatomic molecules, no single set of parameters can simultaneously describe the fluid phase equilibria, transport, and solid transition properties of quasi-spherical molecules. This result highlights the limitations of the Mie potential for modelling the thermophysical properties of small molecules. Therefore, a compromise must be made, either to achieve a good description of a specific set of properties or to attain modest accuracy across all phase space.
Design, System, ApplicationThe fitting of force field parameters to experimental thermophysical data typically relies solely on comparisons with vapour–liquid equilibrium data. We utilise physics-informed machine-learned equations of state to evaluate this classical approach against two alternative parameterisation strategies that incorporate either transport or solid-phase properties. Using the Mie forcefield as a benchmark, it is observed that for simple monoatomic substances, all schemes are essentially equivalent, yielding a good overall fit. However, for more complex molecules, the limitation of the Mie forcefield becomes evident, as no single set of parameters is seen to accurately and simultaneously predict all studied properties. These results highlight the need to develop more robust and detailed force fields for molecular modelling. |
1 Introduction
Accurately representing molecular interactions is key for describing and predicting the thermophysical properties of fluids through molecular dynamics (MD) simulations. While, in principle, the intermolecular forces can be resolved via the solution of the Schrödinger equations, we are still far from being able to apply these concepts to obtain accurate dispersion energies and comprehensively model fluid phases with accuracy. An accepted approach to circumvent this is to depict the intermolecular interactions via mathematical functions known as force fields. Historically, the development of force fields has relied on postulating semi-empirical equations that explicitly model non-bonded, bonded, angular, torsional, and electrostatic interactions.1–4 These arguably “simple” force fields provide a computationally efficient but incomplete representation of molecular interactions. While successful in many applications, their limitations must be acknowledged,5 especially when studying systems where polarisation, multi-body effects and detailed electrostatic interactions are significant. Recently, force fields based on machine-learning (data-driven) techniques6,7 have been developed to address these challenges. These include force fields based on artificial neural networks,8,9 Gaussian processes,10 and many-body expansions.11,12 Force fields can represent molecules at different resolutions: all-atom (AA), united-atom (UA), and coarse-grained (CG). In AA, all atoms in a molecule are explicitly accounted for, while in UA, small molecular groups are condensed into a single particle; for instance, by treating a –CH2– group as a single particle. Lastly, in CG, the molecular representation is simplified using larger fictitious particles that group multiple functional groups. CG force fields have been parametrised using experimental thermophysical properties13 and structural14,15 data. The CG approach simplifies the molecular representation, allowing the exploration of spatio-temporal scales closer to the macroscopic level.Regardless of the type of force field (i.e., classical or machine-learning-based) and its molecular resolution (AA, UA, or CG), its applicability depends on the selection of molecular parameters that, along with the state conditions (i.e., density, temperature, and composition), define a Hamiltonian that can be translated into macroscopic observables through molecular simulations and statistical thermodynamics. The appropriate parameterisation of the force field (i.e., the fitting of the molecular parameters) is crucial for its success in predicting thermophysical properties. The parameterisation of a given force field can follow either a bottom-up16,17 or a top-down13 approach. In bottom-up approaches, the force field is fitted to reproduce forces, bond distances, and angles from rigorous quantum mechanical calculations. This approach is also the ansatz of machine learning potentials that aim to bridge ab initio accuracy with larger scales.9,18 Conversely, the top-down approach directly optimises the molecular parameters to reproduce relevant experimental data. This method links a molecular model to its implied thermophysical properties and is the most efficient from an engineering and design perspective.
For the sake of conciseness, we shall henceforth discuss the parameterisation of the Mie potential, shown in eqn (1).
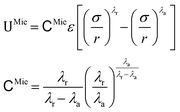 | (1) |
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) Mie is the interaction energy between two Mie particles, ε is the interaction energy well depth, σ is a characteristic length scale, which is loosely related to the effective particle diameter, and r is the centre-to-centre distance between two monomers. Finally, λr and λa are the exponents that control the steepness of the repulsive and attractive interactions, respectively. It has been shown that for describing fluid phase equilibria, the exponents of the Mie potential are conformal,19 implying that multiple combinations of the repulsive and attractive exponents can lead to the same macroscopic equilibrium properties. Following this, for simplicity, the attractive exponent is commonly set to 6 in agreement with the London theory for dispersion forces,20 resulting in what is sometimes referred to as the (λr, 6) Mie potential.21
Mie is the interaction energy between two Mie particles, ε is the interaction energy well depth, σ is a characteristic length scale, which is loosely related to the effective particle diameter, and r is the centre-to-centre distance between two monomers. Finally, λr and λa are the exponents that control the steepness of the repulsive and attractive interactions, respectively. It has been shown that for describing fluid phase equilibria, the exponents of the Mie potential are conformal,19 implying that multiple combinations of the repulsive and attractive exponents can lead to the same macroscopic equilibrium properties. Following this, for simplicity, the attractive exponent is commonly set to 6 in agreement with the London theory for dispersion forces,20 resulting in what is sometimes referred to as the (λr, 6) Mie potential.21
Although the fitting of force fields to experimental data seems a judicious approach, the details of how to proceed remain elusive: which properties should be targeted? Which ones provide the most information? How can one guarantee the robustness and transferability of the optimised parameters? A century ago, Lennard-Jones pioneered the answering of these questions by parameterising the Mie potential using a top-down approach, which led to the well-known Lennard-Jones (LJ) potential (i.e., ULJ = 4ε[(σ/r)12 − (σ/r)6]).22,23 He recognised that the molecular parameters of the Mie potential (or the LJ potential) could be fitted to either the second virial coefficient or the viscosity of a dilute argon gas. However, no unique set of parameters could be isolated: “… so it does not prove possible to obtain a molecular model which will simultaneously explain the two sets of experimental facts”.23 The results from Lennard-Jones already showed that even for simple molecules like argon, there are trade-offs with respect to which property to choose for fitting.24
Within a modern approach, one can target the simultaneous fitting of multiple thermophysical properties and larger data sets. Take, for example, the SAFT-γ Mie force field,13 a CG force field based on the Mie potential. The parameterisation of this force field is performed by invoking an analytical equation of state (the SAFT-VR-Mie EoS25), which accurately maps the force field parameters to macroscopic fluid phase equilibria. By using the equation of state as a surrogate of the underlying MD results, optimised molecular parameters that best fit the vapour–liquid equilibria over a broad range of state points can be effectively determined. The SAFT-γ Mie force field has since been successfully used to model equilibrium properties of alkanes,26 carbon dioxide,27 greenhouse gases,28 water,29 fluorinated compounds30,31 and polymers32–34 amongst others. However, limitations have been seen when attempting to employ the force fields to describe transport properties and to determine the triple point and onset of the solid phases.
In spite of its limitations, the above approach can be generalised by employing the corresponding states principle. Mejía et al.35 developed a corresponding states correlation that relies on the critical temperature (Tc), a saturated liquid density (ρl at Tr = 0.7) and the Pitzer acentric factor (ω = −1 − log10(Psat/Pc) at Tr = 0.7) to obtain the molecular parameters of homonuclear Mie chains. This approach, a.k.a. the M&M correlation, has been successfully applied to model the phase equilibria and interfacial properties of a diverse range of industrially relevant molecules, including alkanes, aromatics, gases, and solvents.36 Moreover, this corresponding states principle has been applied to 6000+ molecular fluids, whose parameters have been freely published in the Bottled SAFT webpage.37 Alternatively to the M&M correlation, Hoang et al.38 proposed a similar corresponding states correlation for homonuclear Mie chains. Interestingly, they proposed using the reduced liquid viscosity data point (η1 at Tr = 0.7) as an additional parameter into the correlation. This approach suggests that transport properties could be employed in addition to the volumetric equilibrium properties to obtain more robust and transferable molecular models.
That being said, this contribution focuses on the single-bead CG modelling of quasi-spherical molecules using the Mie potential, eqn (1). Three main parameterisation approaches are explored and compared. The first approach follows the classical strategy for parameterising force fields where only vapour–liquid equilibria and fluid data are considered. The second approach follows the corresponding states principle of Hoang et al.,38 where the liquid shear viscosity data is considered in addition to the VLE data. The third parameterisation approach includes solid–fluid data along with fluid phase equilibria. Details of the different parameterisation approaches and how the thermophysical properties are modelled are discussed in section 2, while the discussion of the results is given in section 3. Finally, the conclusions are summarised in section 4.
2 Multi-property parametrisation approaches
Quasi-spherical molecules can be described using the Mie potential, eqn (1). Upon setting the attractive exponent to 6, the Mie isotropic particle is fully specified by three molecular parameters (σ, ε, and λr). These molecular parameters must be fitted to experimental data for the potential to represent thermophysical properties.Here, we consider three parameterisation approaches to obtain the molecular parameters (σ, ε, λr) of the Mie potential. We formulate a general objective function as follows.
 | (2) |
| P VLE | ρ l,VLE | ΔHVLEb | P SLE | P SVE | ΔHSVEd | η | |
|---|---|---|---|---|---|---|---|
| a Thermophysical properties considered in the objective function (OF) are indicated by a “✓”. b Vapour–liquid equilibria (VLE) properties are also referred to as “vaporisation” properties. These include the vaporisation pressure (PVLE), saturated liquid density (ρl,VLE), and vaporisation enthalpy (ΔHVLE). VLE properties can be obtained either with the FE-ANN EoS40 or FE-ANN(s) EoS,41 based on eqn (3). c Solid–liquid equilibria (SLE) properties are also referred to as “melting” properties. Only the melting pressure (PSLE) is considered here. d Solid–vapour equilibria (SVE) properties are also referred to as “sublimation” properties. These include the sublimation pressure (PSVE) and sublimation enthalpy (ΔHSVE). SLE and SVE properties are obtained using the FE-ANN(s) EoS. e The shear viscosity (η) is modelled using the ANN-based models developed in ref. 42, based on eqn (6). | |||||||
| OF1 | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ |
| OF2 | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ |
| OF3 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
2.1 Experimental data acquisition
The objective functions based on eqn (2) require experimental data. Pseudo-experimental data is obtained from the NIST TRC database.43 The data reported by NIST have already been curated and fitted to accurate empirical functions. The use of the data sets provided by NIST provides advantages over the use of discrete experimental data sets. Not only is the pseudo-data smooth and devoid of outliers, but it is also “continuous” in nature and allows for evaluating properties over an extensive range of state points. Furthermore, the data is internally and thermodynamically consistent.Thermophysical properties under VLE conditions are generated within the range Tr = T/Tc ∈ [0.55, 0.95]. The VLE data includes saturation pressure, saturated liquid density, vaporisation enthalpy, and saturated liquid viscosity. In addition, the thermal conductivity and speed of sound of the saturated liquid phase are generated to assess the transferability of the molecular parameters to unseen thermophysical properties. Similarly, the melting pressure data is generated in the Tr = T/Tc ∈ [0.55, 1.1] range, and the sublimation pressure and enthalpies are generated in the Tr = T/Tc ∈ [0.45, 0.55] range. These constitute our database of experimental information.
2.2 Thermophysical properties modelling
To assess the objective functions, we are additionally required to evaluate the thermophysical properties corresponding to the Mie potential at a given state point as a function of the molecular parameters (σ, ε, and λr). The thermophysical properties of the Mie particle are modelled using physics-informed Free Energy Artificial Neural Networks (FE-ANNs). We employ the FE-ANN EoS40 that explicitly models the Helmholtz free energy of the Mie fluid and can predict the fluid phase properties and VLE with an accuracy that matches MD results. Similarly, we employ the FE-ANN(s) EoS41 that extends the framework to handle solid–fluid equilibria, such as SLE and SVE. The Helmholtz free energy is a convenient state function for computing thermophysical properties and phase equilibria, and the reader is referred to ref. 40, 41 and 44 for further details about Helmholtz free energy thermodynamics. The FE-ANN/FE-ANN(s) EoSs are formulated using reduced units, indicated by a “*” superscript. The framework can be used for actual molecules by converting the results into real units, as shown below. The reader is referred to section S.1 of the ESI† for further details about reduced units. | (3) |
 | (4) |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) Mie is defined in eqn (1). Then, the total Helmholtz free energy is obtained by adding residual Helmholtz free energy obtained from the FE-ANN EoS and the ideal gas contribution obtained from statistical thermodynamics.24
Mie is defined in eqn (1). Then, the total Helmholtz free energy is obtained by adding residual Helmholtz free energy obtained from the FE-ANN EoS and the ideal gas contribution obtained from statistical thermodynamics.24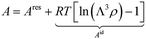 | (5) |
 ).
).
The second objective function (OF2) requires predicting the shear viscosity of the Mie fluid. For this purpose, we employ the artificial neural network (ANN)-based models for the transport properties of the Mie fluid reported in ref. 42. The recommended model for the shear viscosity (η) is based on an ANN and utilises a semi-log scale. This model is formulated using reduced units and can be converted into real units, as shown below.
 | (6) |
The behaviour of the speed of sound and the thermal conductivity will also be studied to assess the transferability of the optimised molecular parameters (σ, ε, λr) to other thermophysical properties. The speed of sound can be obtained by any EoS as follows.
 | (7) |
Here, w is the speed of sound (in m s−1), κT is the isothermal compressibility (in Pa−1) and CV and CP are obtained isochoric and the isobaric heat capacities (in J K−1 mol−1). The FE-ANN/FE-ANN(s) EoSs explicitly model the residual Helmholtz free energy and the ideal contribution can be accounted for analytically as shown in eqn (5). The isothermal compressibility is directly obtained from the Helmholtz free energy as κT = (∂ρ/∂P)T/ρ. It is recommended that the ideal and residual contributions for the heat capacities be considered separately.
| CV = CidV + CresV | (8a) |
| CP = CidP + CresP | (8b) |
Finally, the thermal conductivity is obtained from the recommended ANN-based model developed in ref. 42. This model uses reduced units and a semi-log scale. Therefore, the thermal conductivity of the Mie fluid is obtained as follows.
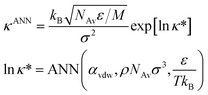 | (9) |
 | (10) |
 | (11) |
The ideal gas isochoric heat capacity is obtained from the correlations of the DIPPR project 801.46 The number of non-vibrational degrees of freedom of a molecule depends on its molecular structure. Monoatomic molecules have three non-vibrational degrees of freedom. Linear molecules, such as carbon monoxide, have five non-vibrational degrees of freedom. Non-linear molecules, like methane, have six non-vibrational degrees of freedom. The correction term κvib is small for liquid phases. For the molecules of interest of this work κvib/κANN ≲ 10−2. Finally, the thermal conductivity is obtained by adding eqn (9) and (10).
| κ = κANN + κvib | (12) |
2.3 Multi-start optimisation approach
The objective functions, based on eqn (2), are minimised to find suitable parameters (σ, ε, λr) to describe the phase behaviour of a given molecule. The objective function is minimised using the Nelder–Mead method50 included in the minimize function from the scipy.optimize Python library.51 The Nelder–Mead method, also known as the simplex method, is a derivative-free local minimisation algorithm capable of handling bounded optimisation. The optimised molecular parameters are highly dependent on the initial guess as the Nelder–Mead method can easily get stuck on a local solution of the optimisation surface. The optimisation could be initialised from molecular parameters obtained from the corresponding states principle correlations.35,38 However, these initial guesses can potentially bias the optimisation results. In order to find an optimal “global” set of molecular parameters, a multi-start optimisation approach using 32 initial guesses generated through Sobol' sequences52 is used here. This number of initial guesses was chosen to enhance the likelihood of reaching multiple local optimal solutions, from which the one with the lowest objective value is selected. The ranges of the initial guesses are detailed in Table 2. Furthermore, to operate in the validity region of the ANN-based models, the repulsive exponent is restricted to be in the λr ∈ [8, 34] range.3 Parameterisation results for quasi-spherical molecules
The molecular parameters of the Mie potential have been determined for representative quasi-spherical molecules. The selected molecules are sufficient to assess the limitations of the Mie potential and to provide insights into good practices for its parameterisation. The selected quasi-spherical molecules can be categorised into three major groups: monoatomic (argon, krypton, and xenon), linear (nitrogen and carbon monoxide), and tetrahedral (methane and tetrafluoromethane) molecules.The optimised molecular parameters and their corresponding deviations are summarised in Table 3. This table also includes the parameters predicted by the M&M35 and the Hoang et al.38 corresponding states correlations. Overall, it is evident from this table that the VLE can be modelled with low deviations (MAPE ≲ 5%) when it is the sole target data (i.e., OF1). It must be noted that the parameters obtained from this objective function are in good agreement with the M&M correlation. This similarity results from the M&M correlation using the critical temperature, acentric factor, and liquid density to predict molecular parameters that correctly predict the VLE conditions at Tr = 0.7. However, this correlation is parametrised to predict a correct density behaviour, and higher deviations (>10%) are observed for the saturation pressure (PVLE). This higher deviation in pressure is also observed from the parameters obtained in the correlation of Hoang et al.38 This correlation targets a correct density and shear viscosity behaviour. The objective of the parameters provided by this correlation is comparable to the ones obtained from using OF2.
a Thermophysical properties included in the objective functions are coloured with a light grey background. Refer to eqn (2) and Table 1 for further details about OF1, OF2, and OF3.
b The objective functions are optimised using pseudo-experimental data obtained from the NIST TRC.43
c The reported Mean Absolute Percentage Error (MAPE) is obtained as  . The reported MAPE include the vaporisation pressure (PVLE), saturated liquid density (ρl,VLE), vaporisation enthalpy (ΔHVLE), melting pressure (PSLE), sublimation pressure (PSVE), sublimation enthalpy (ΔHSVE), shear viscosity (η), thermal conductivity (κ), and speed of sound (w).
d The smallest MAPE deviations per component are highlighted in bold.
e
σ, ε/kB, and λr are the molecular parameters of the Mie potential, eqn (1). λa is set to 6. σ is reported in Angstroms (1 Å = 10−10 meters) and ε/kB is reported in Kelvin.
f No MAPE is reported for the sublimation pressure and enthalpy when the pseudo-experimental data is below the validity of the FE-ANN(s) EoS, i.e., T* < 0.6.
g The predicted thermal conductivity is obtained as in eqn (12) which is based on eqn (9) and (10).
h The modelled thermal conductivity and speed of sound use the ideal gas heat capacities correlations from the DIPPR project 801.46
i Molecular parameters obtained from the M&M35 and Hoang et al.38 correlations are based on the corresponding states principle. The M&M correlation relies on the critical temperature, acentric factor, and liquid density at Tr = 0.7. The correlation of Hoang et al.38 additionally uses the saturated liquid viscosity at Tr = 0.7. . The reported MAPE include the vaporisation pressure (PVLE), saturated liquid density (ρl,VLE), vaporisation enthalpy (ΔHVLE), melting pressure (PSLE), sublimation pressure (PSVE), sublimation enthalpy (ΔHSVE), shear viscosity (η), thermal conductivity (κ), and speed of sound (w).
d The smallest MAPE deviations per component are highlighted in bold.
e
σ, ε/kB, and λr are the molecular parameters of the Mie potential, eqn (1). λa is set to 6. σ is reported in Angstroms (1 Å = 10−10 meters) and ε/kB is reported in Kelvin.
f No MAPE is reported for the sublimation pressure and enthalpy when the pseudo-experimental data is below the validity of the FE-ANN(s) EoS, i.e., T* < 0.6.
g The predicted thermal conductivity is obtained as in eqn (12) which is based on eqn (9) and (10).
h The modelled thermal conductivity and speed of sound use the ideal gas heat capacities correlations from the DIPPR project 801.46
i Molecular parameters obtained from the M&M35 and Hoang et al.38 correlations are based on the corresponding states principle. The M&M correlation relies on the critical temperature, acentric factor, and liquid density at Tr = 0.7. The correlation of Hoang et al.38 additionally uses the saturated liquid viscosity at Tr = 0.7.
|
|---|

|
Using OF1 (or the M&M correlation) provides a good description of the VLE. However, the overfitting of the VLE phase envelope commonly comes at the cost of increasing the repulsions and interaction energy of the Mie potential. As will be shown later in Fig. 3–5, the apparent excellent agreement with the experiments stems from extending the validity range of a fluid EoS to regions below the triple temperature where a solid phase would exist. This overfitting, in itself, is not problematic if only fluid properties are considered, but it has implications if one wishes to transfer the model to other thermophysical properties. For example, an erroneous prediction of triple points will substantially influence viscosity predictions, which are known to rise exponentially as one approaches solid-phase conditions.53
The ratio between the critical (Tc) and triple (Ttr) points for the selected molecules is illustrated in Fig. 1. From this figure, it is apparent that Tc/Ttr is accurately represented for monoatomics when using only VLE data. However, including data on shear viscosity (OF2) or solid–fluid equilibria (OF3) data is essential to more effectively predict this ratio for polyatomic molecules. The proposed parameterisation approaches can also predict other transport properties, such as the self-diffusivity coefficient. As shown in Fig. S.5 in the ESI,† the self-diffusivity can be accurately predicted by the three different objective functions as long as the stable fluid region is correctly predicted (i.e., correct Tc/Ttr ratio). This behaviour results from the dependence of the self-diffusivity on the molecular size (related to σ) for non-associating molecules. This result has been observed in the early13 and recent54 parameterisation of the SAFT-γ force field and implies that this property is not determinant when parameterising coarse-grained force fields that ignore explicit polar moments and electrostatics. These general observations set the stage for the main discussion below, which explains how achieving acceptable fits for certain properties comes at the price of producing unreliable representations of others. The discussion will be presented below based on the aforementioned molecular groups (i.e., monoatomic, linear, and tetrahedral molecules). Further results for molecules not covered in this section are available in section S.2 of the ESI.†
 | ||
| Fig. 1 Critical and triple temperature ratio of selected quasi-spherical molecules. Grey bars with diagonal hatch refer to the value obtained from the NIST TRC database.43 Blue bars with a circle pattern refer to the values obtained from OF1 (VLE only). Orange bars with a star pattern refer to the values obtained from OF2 (VLE + shear viscosity). Green with a dotted pattern refers to the values obtained from OF3 (VLE + SLE + SVE). | ||
3.1 Monoatomic molecules
Three monoatomic molecules are considered here: argon (Ar), krypton (Kr), and xenon (Xe). In Table 3, we show how the fitted characteristic parameters of each molecule are similar regardless of which objective function is used. Consequently, the deviations of each thermophysical property fall within the same ranges. Nevertheless, interesting insights emerge when considering transport properties or solid–fluid equilibria data. It can be seen that including the shear viscosity in the objective function (OF2) tends to reduce the deviations in the properties related to SLE and SVE. It is understood that the shear viscosity and the description of the solid phase are sensitive to short distances between molecules where the repulsive part of an interaction potential becomes relevant. Thus, improving the description of one property benefits the other. It can further be noted that the molecular parameters obtained can correctly predict the thermal conductivity and speed of sound of these molecules. The thermal conductivity is accurately predicted for argon and xenon (MAPE κ ≲ 4%). The thermal conductivity for krypton, however, is predicted with higher deviations, on the order of 15%. Similarly, the Mie potential can predict the speed of sound with relative errors in the range of 5% for these spherical molecules. The speed of sound serves as a stringent test for a set of molecular parameters, as it depends on multiple derivatives of the Helmholtz free energy. Moreover, the speed of sound can be accurately measured,55,56 enabling an assessment of the limitations of the molecular model and its parameters.The results of Table 3 are best interpreted graphically. The phase equilibria and selected thermophysical properties results of argon are illustrated in Fig. 2. Similar figures for krypton and xenon can be found in the ESI.†Fig. 2 takes into account the three sets of parameters along with two possible modelling approaches. Fig. 2(a)–(c) depict the phase equilibria results modelled solely with fluid-phase data. Generally, good agreement can be noted with the reference VLE data when using the OF1 and OF2 parameterisation approaches. Fig. 2(d)–(f) examine the same set of molecular parameters but using the FE-ANN(s) EoS. This EoS broadens the prediction to encompass the entire phase diagram, including VLE, SLE, SVE, and the triple point. It can be observed that even when solid-phase data are excluded from the parameterisation, all modelling approaches converge to predict a similar phase envelope, equilibrium pressure, and enthalpy of phase change. These sets of parameters also accurately predict the triple temperature, which is marked by a solid black line in the figures.
 | ||
| Fig. 2 Selected thermophysical properties argon. (a) and (d) Phase envelope. (b) and (e) Clapeyron plot. (c) and (f) Enthalpy of phase change. (g) Speed of sound. (h) Shear viscosity. (i) Thermal conductivity. (a)–(c) Phase equilibria modelled using the FE-ANN EoS developed ref. 40. (d)–(g) Phase equilibria and speed of sound modelled using the FE-ANN(s) EoS developed in ref. 41. FE-ANN/FE-ANN(s) EoSs are based on eqn (3). (h) and (i) The shear viscosity and thermal conductivity are modelled using the ANN-based models developed ref. 42, based on eqn (6) and (12). Dashed blue lines and symbols refer to results using parameters optimised with OF1 (VLE only). Dotted orange lines and symbols refer to results using parameters optimised with OF2 (VLE + shear viscosity). Solid green lines and symbols refer to results using parameters optimised with OF3 (VLE + SLE + SVE). Refer to eqn (2) and Table 1 for further details about the objective functions. Filled circle is the critical point. Filled square is the triple point. Pseudo-experimental data obtained from NIST TRC.43 Upright triangles are VLE data, diamonds are SLE data, and downward triangles are SLE data. For reference, the solid black line refers to the triple temperature. | ||
The results for the speed of sound, shear viscosity and thermal conductivity of saturated liquid argon are presented in Fig. 2(g)–(i). Similarly to the phase equilibria results, the three parameterisation approaches accurately predict these thermophysical properties. These findings further confirm that the Mie potential can model the thermophysical properties of simple monoatomics with precision. Notably, the optimal repulsive exponents for these molecules are closer to the value of 13–13.5 than to the “classical” value of 12 employed in the LJ model.
3.2 Linear molecules
While the various parameterisation choices did not play a significant role in determining the molecular parameters of noble gases, a different scenario unfolds as the underlying molecules become more complex. This section will discuss the effects of the parameterisation approach on small linear molecules, such as nitrogen (N2) and carbon monoxide (CO). From the results shown in Table 3 for these molecules, it can be observed that the VLE properties are better predicted with OF1 albeit at the cost of increased repulsiveness (↑λr) and energy (↑ε) of the interactions. The size parameter, σ, which is closely related to the liquid density, remains consistent across the three parameterisation approaches. Including the shear viscosity (OF2) or solid (OF3) data in the optimisation results in a decrease in the repulsive exponent and interaction energy of the potential with these two properties targeting molecular parameters in the same direction. It can be observed that there is a trade-off regarding which properties are better suited to adjust simple pairwise potentials. A more accurate description of a transport property compromises the description of equilibrium properties. Furthermore, the melting pressure cannot be accurately modelled using the Mie potential if the fluid phase is to be accurately described. Presumably, the coarse-grained approximation overlooks structural effects that influence the conformation of the crystal phase, as well as the friction between molecules that affects the transport properties. These results indicate that the coarse-grained approximation is, in most cases, overfitted to a single property, and extrapolation to other properties must be approached with caution.The results are presented for nitrogen in Fig. 3. Fig. 3(a)–(c) illustrate the VLE results using the fluid FE-ANN EoS. A good agreement can be observed for the VLE phase envelope, vaporisation pressure, and vaporisation enthalpy using OF1 or OF2. However, it is important to note that the fluid FE-ANN EoS is stretched to predict VLE at conditions below the triple temperature. In a molecular simulation context, the Mie particle exhibits coexistence between a fluid and a solid phase in those conditions. In Fig. 3(d)–(f), the entire phase diagram is modelled using the FE-ANN(s) EoS with different parameter sets. These figures clearly demonstrate that the triple point predicted by the parameters obtained from OF1 is above some experimental VLE data points. Under those conditions, the VLE is unstable, and the Mie particle exhibits SVE. Incorporating the shear viscosity or solid phase data reduces the repulsive exponent and interaction energy of the Mie potential and, consequently, lowers the triple point. The parameters from OF2 and OF3 model the VLE similarly to those from OF1, but they provide a better description of the triple point, SLE and SVE. It is noteworthy that the order of magnitude of the melting pressure (∼103 MPa) is considerably higher than that of the vaporisation (∼10−1 MPa) and sublimation pressures (∼10−3 MPa). Although the molecular parameters obtained from OF3 predict the correct melting pressure trend, the reported relative errors are significant (∼50%). Ultimately, the differences in the various molecular parameters result in noticeably distinct SLE densities. This information could be helpful in distinguishing optimal molecular parameters; however, this data is not available from the NIST TRC correlations.43
 | ||
| Fig. 3 Phase equilibria modelling of nitrogen. (a) and (d) Phase envelope. (b) and (e) Clapeyron plot. (c) and (f) Enthalpy of phase change. (g) Speed of sound. (h) Shear viscosity. (i) Thermal conductivity. (a)–(c) Phase equilibria modelled using the FE-ANN EoS developed ref. 40. (d)–(g) Phase equilibria and speed of sound modelled using the FE-ANN(s) EoS developed in ref. 41. FE-ANN/FE-ANN(s) EoSs are based on eqn (3). (h) and (i) The shear viscosity and thermal conductivity are modelled using the ANN-based models developed ref. 42, based on eqn (6) and (12). Dashed blue lines and symbols refer to results using parameters optimised with OF1 (VLE only). Dotted orange lines and symbols refer to results using parameters optimised with OF2 (VLE + shear viscosity). Solid green lines and symbols refer to results using parameters optimised with OF3 (VLE + SLE + SVE). Refer to eqn (2) and Table 1 for further details about the objective functions. Filled circle is the critical point. Filled square is the triple point. Pseudo-experimental data obtained from NIST TRC.43 Upright triangles are VLE data, diamonds are SLE data, and downward triangles are SLE data. For reference, the solid black line refers to the triple temperature. | ||
The liquid speed of sound results of Nitrogen are shown in Fig. 3(g). It is observed here that the three parameterisation approaches led to a similar description of this property. However, it should be noted that the described ranges for these properties depend on the predicted critical and triple points. For the case of the shear viscosity, shown in Fig. 3(h), it can be observed that including properties related to the repulsive branch of the force field enhances the accurate description of this property. In this instance, the parameters from OF2 and OF3 exhibit a similar behaviour. This finding contrasts with the observations for the thermal conductivity, illustrated in Fig. 3(i). These results graphically illustrate the trade-offs inherent in the coarse-grained modelling approach, specifically regarding which properties to fit (in this case, shear viscosity or thermal conductivity). Similar conclusions can be drawn from the analysis of the data for carbon monoxide, which is included in section S.2 of the ESI.†
3.3 Tetrahedral molecules
This final section will analyse the limitations of the Mie potential in modelling tetrahedral molecules such as methane (CH4) and tetrafluoromethane (CF4). These molecules are often considered as isotropic spheres in UA or CG representations. The results for these two molecules are shown in Fig. 4 and 5, respectively. When only considering the VLE information using the fluid FE-ANN EoS, figures (a) to (c), there is a clear and excellent match to the phase envelope, saturation pressure, and vaporisation enthalpy. Results such as these have led to the claims that the Mie force field holds an advantage over the LJ model, in that the use of the additional parameter (λr) allows for a quantitative description of the fluid phase equilibria.28 This is certainly the case, but the apparent success emerges from an overestimation of the repulsions and interaction energies of the force field. In the case of tetrafluoromethane, the optimisation programme reaches the upper limit of the FE-ANN EoS with λr = 34. The overfitting of the VLE properties is evident when analysing the high deviations of the shear viscosity and melting pressure in Table 3. As with the case of linear molecules, the use of overfitted parameters unphysically predicts VLE in regions below the triple point. | ||
| Fig. 4 Phase equilibria modelling of methane. (a) and (d) Phase envelope. (b) and (e) Clapeyron plot. (c) and (f) Enthalpy of phase change. (g) Speed of sound. (h) Shear viscosity. (i) Thermal conductivity. (a)–(c) Phase equilibria modelled using the FE-ANN EoS developed ref. 40. (d)–(g) Phase equilibria and speed of sound modelled using the FE-ANN(s) EoS developed in ref. 41. FE-ANN/FE-ANN(s) EoSs are based on eqn (3). (h) and (i) The shear viscosity and thermal conductivity are modelled using the ANN-based models developed ref. 42, based on eqn (6) and (12). Dashed blue lines and symbols refer to results using parameters optimised with OF1 (VLE only). Dotted orange lines and symbols refer to results using parameters optimised with OF2 (VLE + shear viscosity). Solid green lines and symbols refer to results using parameters optimised with OF3 (VLE + SLE + SVE). Refer to eqn (2) and Table 1 for further details about the objective functions. Filled circle is the critical point. Filled square is the triple point. Pseudo-experimental data obtained from NIST TRC.43 Upright triangles are VLE data, diamonds are SLE data, and downward triangles are SLE data. For reference, the solid black line refers to the triple temperature. | ||
 | ||
| Fig. 5 Phase equilibria modelling of tetrafluoromethane. (a) and (d) Phase envelope. (b) and (e) Clapeyron plot. (c) and (f) Enthalpy of phase change. (g) Speed of sound. (h) Shear viscosity. (i) Thermal conductivity. (a)–(c) Phase equilibria modelled using the FE-ANN EoS developed ref. 40. (d)–(g) Phase equilibria and speed of sound modelled using the FE-ANN(s) EoS developed in ref. 41. FE-ANN/FE-ANN(s) EoSs are based on eqn (3). (h) and (i) The shear viscosity and thermal conductivity are modelled using the ANN-based models developed ref. 42, based on eqn (6) and (12). Dashed blue lines and symbols refer to results using parameters optimised with OF1 (VLE only). Dotted orange lines and symbols refer to results using parameters optimised with OF2 (VLE + shear viscosity). Solid green lines and symbols refer to results using parameters optimised with OF3 (VLE + SLE + SVE). Refer to eqn (2) and Table 1 for further details about the objective functions. Filled circle is the critical point. Filled square is the triple point. Pseudo-experimental data obtained from NIST TRC.43 Upright triangles are VLE data, diamonds are SLE data, and downward triangles are SLE data. For reference, the solid black line refers to the triple temperature. | ||
The effect of the various choices of parameters in the predicted phase diagram is shown in subfigures (d) to (i). For the case of Methane, Fig. 4, it observed that when including solid phase (OF3) or shear viscosity (OF2) data the correct behaviour for the VLE is retained with an improvement on the prediction of the triple point, SLE and SVE. Both OF2 and OF3 objective functions lead to lower repulsions and interaction energies of the system and similar molecular parameters. In this context, it is observed that incorporating a thermophysical property related to the repulsive interactions benefits the description of the phase diagram and transport properties. This result is also observed for linear molecules and aligns with the corresponding states methodology proposed by Hoang et al.38
For the case of tetrafluoromethane, Fig. 5, the limitations of the Mie potential are further unveiled. In Fig. 5(d)–(f), it is shown how the highly repulsive parameters (i.e., λr = 34) obtained from OF1 lead to a phase diagram where a considerable part of the experimental VLE data points are below the triple line. Below this temperature, the Mie particle will exhibit a solid phase. Moreover, when incorporating solid (OF3) or shear viscosity (OF2) data, there is no set of parameters that can adequately describe all properties (hence the title of this manuscript). It must be noted that all these parameter sets fail to describe the triple temperature of tetrafluoromethane. It is not a surprise that other thermophysical properties, such as the speed of sound, Fig. 5(g), and thermal conductivity, Fig. 5(i), are not described correctly either. Tetrafluoromethane (CF4), similar to methane (CH4), is a non-polar molecular. However, the fluorine atoms in CF4 are highly electronegative and larger than the hydrogen atoms in CH4. The fluoride atoms in CF4 can lead to strong local polar moments, an overall octopolar moment and steric effects that a simple single-bead coarse-grained model seems incapable of taking into account. These results align with the findings of Bell57 that suggested including these polar moments in an EoS to improve the description of derivative data of refrigerants.
4 Conclusions
This manuscript highlights the limitations of the Mie potential for modelling quasi-spherical molecules. The molecules studied include monoatomic (e.g., argon, krypton, and xenon), linear (e.g., nitrogen and carbon monoxide), and tetrahedral (e.g., methane and tetrafluoromethane) molecules. While other pseudo-spherical molecules could have been included, the results obtained are to a large extent repetitive. These molecules were parameterised using three approaches. The first parameterisation approach relied solely on vapour–liquid equilibria data. The second parameterisation approach took into account the liquid shear viscosity and the vapour–liquid equilibria data. Finally, the third parameterisation approach included solid–fluid (solid–liquid and solid–vapour) equilibrium data in addition to the vapour–liquid equilibria data.It has been found that a single set of parameters can accurately describe the entire range of properties for simple monoatomic molecules, such as argon, krypton, and xenon. An optimal set of parameters is encountered regardless of the thermophysical properties used to parameterise the Mie potential. The expected simple nature of noble gases, described as isotropic particles with a fixed repulsion and dispersion, most likely contributes to this result. However, the limitations of the Mie potential become evident beyond these simple cases. For linear and tetrahedral molecules, the numerical solution of the parameterisation overfits the vapour–liquid equilibrium when it is the sole target property. Notably, this approach is a customary parametrisation strategy in SAFT-like EoSs25,39 and leads to a displacement of the triple point, resulting in a region of the VLE phase envelope that is unstable (frozen) as it lies below the triple temperature. This behaviour is ignored when using the EoS in the context of fluid phases, but it will lead to incorrect phase behaviour when deployed in a molecular simulation. Furthermore, this suboptimal parameterisation leads to a poor description of other thermophysical properties, particularly transport properties. In contrast to noble gases, which interact solely through simple repulsion and van der Waals forces, polyatomic molecules can exhibit additional anisotropic inter- and intramolecular interactions. Examples include dipolar and higher polar moments, polarisation effects, and steric effects caused by molecular geometry. These interactions are not accounted for when modelling a polyatomic molecule using a coarse-grained approach with a single bead per molecule.
In contrast to the exclusive use of VLE data, the proposed parameterisation approaches suggest that incorporating properties such as shear viscosity and/or solid–fluid equilibria data results in a different set of molecular parameters. The inclusion of these properties in the parameterisation influences the interaction energy and repulsive exponent of the molecular model. This stems from the fact that both of these properties are strongly affected by short-range interactions. Shear viscosity relates to the friction between molecules, which is pertinent at short distances. Likewise, the solid phase and crystal structure directly relate to relatively short-distance steric packing. In contrast, vapour–liquid equilibria is a consequence of the interplay between repulsive and attractive interactions. This interplay can be characterised by multiple sets of roughly equivalent molecular parameters that correctly describe the VLE region.19 This multiplicity (and ultimate mathematical global minimum in the parameter search) is not a guarantee that the parameters will extrapolate effectively to other thermophysical properties. For this reason, we advise to include properties related to the repulsions of the system when parameterising force fields. This observation aligns with the corresponding states methodology proposed by Hoang et al.,38 which takes the shear viscosity into account in the force field parametrisation.
Incidentally, the use of viscosity or solid properties in the overall fit reduce the rather large repulsive exponent (λr > 20) obtained when “force-fitting” large or polar molecules to VLE. The apparent success of UA force fields based on the Mie potential in describing both fluid phase equilibria and transport properties,58,59 despite being fitted only to VLE, seems to be aided by a fortunate choice of a conservative repulsive exponent within the range of 14–16. We conjecture that more robust and transferable parameter sets could be obtained by incorporating information such as viscosity, triple point data, or similar that directly pertains to the repulsive branch of the potential.
In summary, we have found that
• Relying exclusively on VLE as the target property in the objective function carries a risk of “overfitting” the Mie potential. This seemingly “optimal” parameterisation does not guarantee that other thermophysical properties can be accurately modelled or transferred. A clear sign of overfitting, as well as of an inadequate molecular model, is the shift of the triple point, which reduces the effective VLE region predicted by the model compared to experimental data.
• The parametrisation based exclusively on VLE data does not sufficiently quantify system repulsions. We propose a compromise parameterisation that we believe offers greater robustness than solely concentrating on VLE data. We recommend including a property that is significantly influenced by these short-range interactions, such as viscosity or solid-phase data, in the force field parameterisation. The limited effectiveness of VLE modelling in this context highlights the shortcomings of the molecular model or force field employed (which is the reasoning behind the manuscript's running title). Often, the Mie model's parameter set cannot simultaneously account for all properties.
As an end note, we highlight that the parameterisation approaches presented in this manuscript rely on physics-informed artificial neural networks to model thermophysical properties. These thermophysical property models are equations of state derived directly from discrete molecular simulation data and physics-inspired constraints employing machine learning techniques. They serve as reliable surrogates for molecular simulation results and represent promising paths for parameterising force fields using a top-down approach. It should be noted that the observations made in this manuscript are limited to simple spherical geometries and London-like dispersive interactions. Future work will focus on extending the framework to incorporate additional molecular geometries and interactions.
Data availability
Data and Python scripts to reproduce the results of this article are found in the following repository: https://github.com/gustavochm/Square-Peg-Mie.Author contributions
Gustavo Chaparro: conceptualization (equal), data curation (lead), formal analysis (equal), investigation (lead), methodology (equal), software (lead), validation (equal), writing – original draft (lead) Erich A. Müller: conceptualization (lead), funding acquisition (lead), formal analysis (equal), investigation (equal), methodology (equal), supervision (lead), validation (equal), writing – review & editing (equal).Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. C. acknowledges the support provided by the President's Ph.D. Scholarship (Imperial College London). Computations were performed using the Imperial College Research Computing Service (DOI: https://doi.org/10.14469/hpc/2232).Notes and references
- G. C. Maitland, Intermolecular forces: Their origin and determination, Clarendon Pr, Oxford, 1981 Search PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- A. Hemmen and J. Gross, J. Phys. Chem. B, 2015, 119, 11695–11707 CrossRef CAS PubMed.
- M. J. Tillotson, N. I. Diamantonis, C. Buda, L. W. Bolton and E. A. Müller, Phys. Chem. Chem. Phys., 2023, 25, 12607–12628 RSC.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- J. Behler and G. Csányi, Eur. Phys. J. B, 2021, 94, 142 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118 CrossRef CAS PubMed.
- V. L. Deringer, D. M. Proserpio, G. Csányi and C. J. Pickard, Faraday Discuss., 2018, 211, 45–59 RSC.
- D. P. Kovács, C. V. D. Oord, J. Kucera, A. E. A. Allen, D. J. Cole, C. Ortner and G. Csányi, J. Chem. Theory Comput., 2021, 17, 7696–7711 CrossRef PubMed.
- D. P. Kovács, I. Batatia, E. S. Arany and G. Csányi, J. Chem. Phys., 2023, 159, 044118 CrossRef PubMed.
- E. A. Müller and G. Jackson, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 405–427 CrossRef PubMed.
- K. R. Hadley and C. McCabe, J. Phys. Chem. B, 2010, 114, 4590–4599 CrossRef CAS PubMed.
- T. C. Moore, C. R. Iacovella and C. McCabe, J. Chem. Phys., 2014, 140, 224104 CrossRef PubMed.
- T. G. A. Youngs, M. G. Del Pópolo and J. Kohanoff, J. Phys. Chem. B, 2006, 110, 5697–5707 CrossRef CAS PubMed.
- J. Jin, A. J. Pak, A. E. P. Durumeric, T. D. Loose and G. A. Voth, J. Chem. Theory Comput., 2022, 18, 5759–5791 CrossRef CAS PubMed.
- F. L. Thiemann, P. Rowe, E. A. Müller and A. Michaelides, J. Phys. Chem. C, 2020, 124, 22278–22290 CrossRef CAS.
- N. Ramrattan, C. Avendaño, E. Müller and A. Galindo, Mol. Phys., 2015, 113, 932–947 CrossRef CAS.
- F. London, Trans. Faraday Soc., 1937, 33, 8b RSC.
- J. Fischer and M. Wendland, Fluid Phase Equilib., 2023, 573, 113876 CrossRef CAS.
- J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 441–462 CAS.
- J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477 CAS.
- T. M. Reed and K. E. Gubbins, Applied statistical mechanics: thermodynamic and transport properties of fluids, McGraw-Hill, 1973 Search PubMed.
- T. Lafitte, A. Apostolakou, C. Avendaño, A. Galindo, C. S. Adjiman, E. A. Müller and G. Jackson, J. Chem. Phys., 2013, 139, 154504 CrossRef PubMed.
- S. Rahman, O. Lobanova, G. Jiménez-Serratos, C. Braga, V. Raptis, E. A. Müller, G. Jackson, C. Avendaño and A. Galindo, J. Phys. Chem. B, 2018, 122, 9161–9177 CrossRef CAS PubMed.
- C. Avendaño, T. Lafitte, A. Galindo, C. S. Adjiman, G. Jackson and E. A. Müller, J. Phys. Chem. B, 2011, 115, 11154–11169 CrossRef PubMed.
- C. Avendaño, T. Lafitte, C. S. Adjiman, A. Galindo, E. A. Müller and G. Jackson, J. Phys. Chem. B, 2013, 117, 2717–2733 CrossRef PubMed.
- O. Lobanova, C. Avendaño, T. Lafitte, E. A. Müller and G. Jackson, Mol. Phys., 2015, 113, 1228–1249 CrossRef CAS.
- P. Morgado, O. Lobanova, E. A. Müller, G. Jackson, M. Almeida and E. J. M. Filipe, Mol. Phys., 2016, 114, 2597–2614 CrossRef CAS.
- C. Herdes, E. Forte, G. Jackson and E. A. Müller, Adsorpt. Sci. Technol., 2016, 34, 64–78 CrossRef CAS.
- G. Jiménez-Serratos, C. Herdes, A. J. Haslam, G. Jackson and E. A. Müller, Macromolecules, 2017, 50, 4840–4853 CrossRef.
- M. Fayaz-Torshizi and E. A. Müller, Mol. Syst. Des. Eng., 2021, 6, 594–608 RSC.
- M. Fayaz-Torshizi and E. A. Müller, Macromol. Theory Simul., 2022, 31, 2100031 CrossRef CAS.
- A. Mejía, C. Herdes and E. A. Müller, Ind. Eng. Chem. Res., 2014, 53, 4131–4141 CrossRef.
- C. Herdes, T. S. Totton and E. A. Müller, Fluid Phase Equilib., 2015, 406, 91–100 CrossRef CAS.
- Å. Ervik, A. Mejía and E. A. Müller, J. Chem. Inf. Model., 2016, 56, 1609–1614 CrossRef PubMed.
- H. Hoang, S. Delage-Santacreu and G. Galliero, Ind. Eng. Chem. Res., 2017, 56, 9213–9226 CrossRef CAS.
- V. Papaioannou, T. Lafitte, C. Avendaño, C. S. Adjiman, G. Jackson, E. A. Müller and A. Galindo, J. Chem. Phys., 2014, 140, 054107 CrossRef PubMed.
- G. Chaparro and E. A. Müller, J. Chem. Phys., 2023, 158, 184505 CrossRef CAS PubMed.
- G. Chaparro and E. A. Müller, Commun. Phys., 2024, 7, 406 CrossRef.
- G. Chaparro and E. A. Müller, J. Phys. Chem. B, 2024, 128, 551–566 CrossRef CAS PubMed.
- P. Linstrom, NIST Chemistry WebBook, NIST Standard Reference Database 69, 1997, http://webbook.nist.gov/chemistry/.
- M. L. Michelsen and J. M. Mollerup, Thermodynamic models: fundamentals & computational aspects, Tie-Line Publications, Holte, 2nd edn, 2007 Search PubMed.
- D. B. Newell, F. Cabiati, J. Fischer, K. Fujii, S. G. Karshenboim, H. S. Margolis, E. De Mirandés, P. J. Mohr, F. Nez, K. Pachucki, T. J. Quinn, B. N. Taylor, M. Wang, B. M. Wood and Z. Zhang, Metrologia, 2018, 55, L13–L16 CrossRef CAS.
- W. Wilding, R. L. Rowley and J. L. Oscarson, Fluid Phase Equilib., 1998, 150–151, 413–420 CrossRef.
- G. Galliero and C. Boned, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061202 CrossRef PubMed.
- B. E. Poling, J. M. Prausnitz and J. P. O'Connell, Properties of Gases and Liquids, McGraw-Hill Education, 5th edn, 2020 Search PubMed.
- Z. Liang and H.-L. Tsai, Mol. Phys., 2010, 108, 1707–1714 CrossRef CAS.
- F. Gao and L. Han, Comput. Optim. Appl., 2012, 51, 259–277 CrossRef.
- P. Virtanen, et al. , Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- I. Sobol', USSR Comput. Math. Math. Phys., 1967, 7, 86–112 CrossRef.
- L. Zheng, J. M. Trusler, F. Bresme and E. A. Müller, Fluid Phase Equilib., 2019, 496, 1–6 CrossRef CAS.
- J. Šlepavičius, A. Patti and C. Avendaño, Phys. Fluids, 2025, 37, 017129 CrossRef.
- K. Meier and S. Kabelac, Rev. Sci. Instrum., 2006, 77, 123903 CrossRef.
- C. Wedler and J. P. M. Trusler, J. Chem. Eng. Data, 2023, 68, 1305–1312 CrossRef CAS PubMed.
- I. Bell, Proceedings of the 20th International Refrigeration and Air Conditioning Conference, West Lafayette, IN, United States, 2024 Search PubMed.
- R. A. Messerly, M. C. Anderson, S. M. Razavi and J. R. Elliott, Fluid Phase Equilib., 2019, 483, 101–115 CrossRef CAS.
- M. Fischer, G. Bauer and J. Gross, Ind. Eng. Chem. Res., 2020, 59, 8855–8869 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Includes details about reduced Mie units and further modelling results of quasi-spherical molecules. See DOI: https://doi.org/10.1039/d5me00048c |
| This journal is © The Royal Society of Chemistry 2025 |
