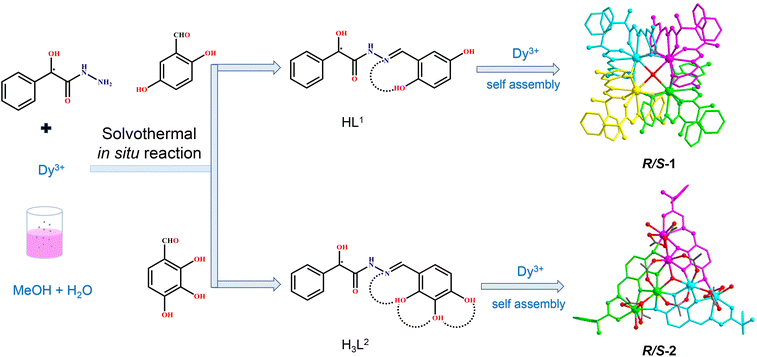
Coordination site manipulation of the annular growth mechanism to assemble chiral lanthanide clusters with different shapes and magnetic properties†
Bing-Fan
Long
a,
Shui
Yu
a,
Zhong-Hong
Zhu
 *a,
Yun-Lan
Li
a,
Fu-Pei
Liang
*ab and
Hua-Hong
Zou
*a,
Yun-Lan
Li
a,
Fu-Pei
Liang
*ab and
Hua-Hong
Zou
 *a
*a
aSchool of Chemistry and Pharmaceutical Sciences, State Key Laboratory for Chemistry and Molecular Engineering of Medicinal Resources/Key Laboratory for Chemistry and Molecular Engineering of Medicinal Resources (Ministry of Education of China), Collaborative Innovation Center for Guangxi Ethnic Medicine, School of Chemistry and Pharmaceutical Sciences, Guangxi Normal University, Guilin 541004, P. R. China. E-mail: 18317725515@163.com; liangfupei@glut.edu.cn
bGuangxi Key Laboratory of Electrochemical and Magnetochemical Functional Materials, College of Chemistry and Bioengineering, Guilin University of Technology, Guilin 541004, P. R. China. E-mail: gxnuchem@foxmail.com
First published on 29th September 2022
Abstract
Chiral lanthanide clusters provide a platform for molecular-based materials with coordination between chirality and magnetism and exhibit great application prospects in the fields of three-dimensional displays, magneto-optical memories, and spintronic devices. To date there is no reliable self-assembly rule for the directional design of chiral lanthanide clusters with specific shapes and functions. Further, we are the first to achieve the directional construction of chiral lanthanide clusters with different shapes and magnetic properties by regulating the hydroxyl coordination sites at different positions on the ligands by manipulating the annular growth mechanism. Specifically, we carried out the reaction of R/S-mandelic acid hydrazide, 2,5-dihydroxybenzaldehyde and DyCl3·6H2O with methanol and water as mixed solvents under solvothermal conditions at 80 °C to obtain mutual enantiomers tetranuclear chiral lanthanide clusters R/S-1. In R/S-1, first, two HL1 ligands captured one Dy(III) ion to form a template unit Dy(L1)2, and following this, four Dy(L1)2 template units were well-ordered and arranged at the four vertices of the square, which were induced by a bridge anion μ4-O2−, to undergo the annular growth mechanism to form square-shaped clusters R/S-1. Replacing 2,5-dihydroxybenzaldehyde with 2,3,4-trihydroxybenzaldehyde in the reaction system, hexanuclear chiral clusters R/S-2 were obtained. Changing the hydroxyl coordination sites enabled one H3L2 ligand to capture two Dy(III) ions, forming a template unit Dy2L2, following which three Dy2L2 were connected by a μ3-OH− bridge anion along the annular growth to form a triangular pyramid-shaped hexanuclear chiral lanthanide cluster R/S-2. Circular dichroism spectra indicated that R/S-1 and R/S-2 were two pairs of enantiomers. Magnetic studies showed that the R-1 chiral cluster was a typical single-molecule magnet under a zero dc field, and it exhibited a distinct double relaxation behavior. To the best of our knowledge, this is one of the rare examples of chiral lanthanide clusters with double relaxation behavior. This work provides an effective method for the directional construction of chiral lanthanide clusters with different connections and shapes and opens up a new horizon for the design and synthesis of multifunctional materials with magneto-optical applications.
Introduction
Chirality is a fundamental property of nature that plays a very vital role in connecting micro and macro molecules, and it is closely related to the origin of life.1–3 The formation of biological macromolecules in nature, such as the double helix structure of DNA, nucleic acids and proteins of their hierarchical structure is all derived from the regulation of chirality.4–6 However, the study of these chiral macromolecules is very complicated and difficult to effectively elaborate through specific single crystal structures.7–9 Therefore, there is an urgent need to develop some simple and effective simplified models to facilitate the exploration of the formation process of chiral macromolecules. Chiral nanoclusters with precise structural connections and compositions as simplified models have established an efficient platform for the study of complex chiral compounds.10–12 In addition, chiral nanoclusters have shown wide application prospects in asymmetric catalysis, enantioselective recognition, circularly polarized luminescent materials, biomimetic chemistry, molecular magnetism, etc.13–18 In 2017, Cui et al. reported a chiral porous octahedral cage, which can serve as an efficient asymmetric supramolecular catalyst and achieve high catalytic activity and high selectivity.19 In 2021, Zhou et al. prepared a chiral dodecanuclear lanthanide double-shell porous coordination cage and extended its use for the selective separation of racemic enantiomers.20 Chiral lanthanide clusters as an important part of chiral nanoclusters have both chirality and magnetism and have shown great application prospects in magnetic chiral dichroism (MchD), circularly polarized luminescence (CPL), second harmonic generation (SHG) and other aspects.21–23 In 2019, Tong et al. reported a pair of dinuclear chiral erbium-based single-molecule magnets and studied their magnetic structure relationship.24Due to the variable coordination numbers, weak stereochemical bias and kinetic instability of lanthanide ions, research on the formation process and self-assembly mechanism of lanthanide clusters has been slow.25–27 Although the exploration of the self-assembly mechanism of lanthanide clusters is still at the initial stage, we have made a series of progresses in this field.28–37 In 2018, we were the first to use HRESI-MS to track the self-assembly process of triangular-shaped dysprosium clusters with toroidal magnetic moments.28 Furthermore, we were the first to use crystallography combined with the HRESI-MS technique to trace the formation mechanism of the high-nuclearity lanthanide cluster Dy10 with double relaxation behavior.29 In 2020, the ligand chelation method was first proposed to construct the largest double cage-like cluster Dy60 and its intermediate Dy30 was obtained.30 In addition, we achieved the construction of the caged lanthanide cluster Dy14 using strong hydrogen bonding of the dish-shaped cluster precursors and achieved a highly selective photo-response to heavy metal ions in the solution.31 In 2021, we were the first to propose the out-to-in growth mechanism to guide the directional construction of a series of 16 nuclear dish-like lanthanide clusters, and under the guidance of the above mechanism, a series of different types of lanthanide clusters were obtained by changing the reaction conditions.32 Such as crown-shaped high-nucleation lanthanide cluster Dy34etc.33 Recently, we have successfully constructed the largest series of brucite-like dysprosium-based nanoclusters of Dy19 under solvothermal reactions, and proposed their possible assembly mechanisms as the in-plane growth mechanism or planer epitaxial growth mechanism.38 The introduction of chirality into lanthanide clusters will complicate the formation process. Therefore, the research on the formation process and self-assembly mechanism of chiral lanthanide clusters is still blank.
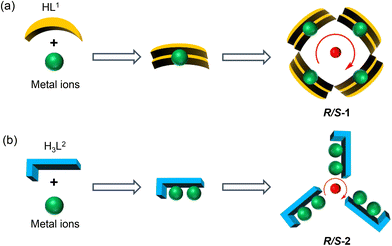
Herein, two pairs of chiral lanthanide clusters R/S-1 (Scheme 1a) and R/S-2 (Scheme 1b), which are enantiomers of each other, were obtained by controlling the coordination sites of acylhydrazone ligands and reaction with Dy(III) ions under solvothermal conditions. Specifically, the chiral R/S-mandelic acid hydrazide, 2,5-dihydroxybenzaldehyde, and DyCl3·6H2O were used as raw materials, and with MeOH and H2O as mixed solvents were reacted under solvothermal conditions to obtain square-shaped chiral clusters R/S-1 by the assembly of eight R/S-HL1 ligand molecules and four Dy(III) ions. After replacing 2,5-dihydroxybenzaldehyde with 2,3,4-trihydroxybenzaldehyde with more aggregated coordination sites, a pair of triangular pyramidal chiral hexanuclear lanthanide clusters R/S-2 were obtained. The regulation of the coordination sites of the reaction starting materials leads to the formation of the template units of the two pairs of enantiomers with different structural connections (Dy(L1)2 and Dy2L2), and then the different template units form chiral clusters with different shapes through the annular growth mechanism. To the best of our knowledge, this is the first time that chiral lanthanide clusters with different linkages and shapes have been constructed by regulating the coordination sites on the ligands. Magnetic studies showed that R-1 was a single-molecule magnet with double relaxation behaviors under zero fields, and R-2 had obvious frequency-dependent behaviors under zero fields. This work provides a vivid example for the design and synthesis of chiral lanthanide clusters and opens a door for the directed synthesis of multifunctional materials with magneto-optical applications.
Results and discussion
Structural analysis of R/S-1 and R/S-2
Accurately weighed R/S-mandelic acid hydrazide (0.1 mmol, 0.0166 g), 2,5-dihydroxybenzaldehyde (0.1 mmol, 0.0138 g) and DyCl3·6H2O (0.5 mmol, 0.1885 g) were reacted in the mixed solvents of methanol and water (0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
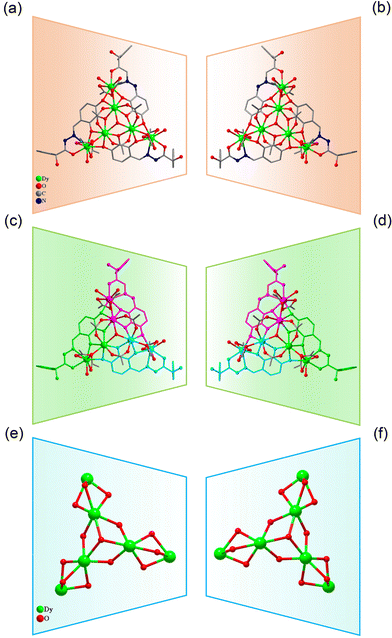
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 mL) under solvothermal conditions at 80 °C, which gave rise to a light green bulk crystal R/S-1. Single-crystal XRD (SCXRD) data indicated that the R/S-1 crystallized in the orthorhombic space group I222 (Table S1†). The structures of R-1 and S-1 were a pair of enantiomeric structures and R-1 was discussed in detail. To be specific, the structure framework of R-1 contains four Dy(III) ions, eight deprotonated R-(E)-N′-(2,5-dihydroxybenzylidene)-2-hydroxy-2-phenyl-2λ3-ethanehydrazide (R-(L1)−) ligands, one bridged anion μ4-O2−, two peripherally free Cl− anions, eight peripherally free MeOH molecules and twelve peripherally free H2O molecules. The molecular formula of R-1 was [Dy4(L1)8(μ4-O)]·2Cl·xCH3OH·yH2O (R-1: x = 8, y = 12; S-1: x = 3, y = 7) (Fig. 1a and b). The independent unit of R-1 consists of one Dy(III) ion and two deprotonated R-(L1)− ligands. First, the two R-(L1)− ligand units chelated one Dy(III) ion in a crossover pattern, forming a Dy(L1)2 fragment (Fig. 3a, S-1 shown in Fig. S1a†). Subsequently, the four Dy(L1)2 units arranged on the four vertices of the square by an annular arrangement and are further bridged by an anion μ4-O2− to form a square-shaped tetranuclear dysprosium cluster R-1 (Fig. 1c and d). The {Dy/O} nuclei of R-1 exhibited a square arrangement (Fig. 1e and f). Furthermore, the eight ligands R-(L1)− in the cluster R-1 exhibited the same coordination pattern: μ2-η1:η1:η2 (Fig. 3b, S-1 shown in Fig. S1b†). All the metal center Dy(III) ions were in a ninth-coordinated O7N2 coordination environment by the R-(L1)− ligands and the bridged anion μ4-O2−. The coordination configuration of the metal center Dy(III) ion was calculated using SHAPE software to be a capped square antiprism (CSAPR-9) (Fig. 3c, S-1 shown in Fig. S1c, and Tables S6 and S7†).39 The structural analysis showed that the bond lengths between Dy–O and Dy–N in R/S-1 were in the normal range (Tables S2 and S3†).
0.4 mL) under solvothermal conditions at 80 °C, which gave rise to a light green bulk crystal R/S-1. Single-crystal XRD (SCXRD) data indicated that the R/S-1 crystallized in the orthorhombic space group I222 (Table S1†). The structures of R-1 and S-1 were a pair of enantiomeric structures and R-1 was discussed in detail. To be specific, the structure framework of R-1 contains four Dy(III) ions, eight deprotonated R-(E)-N′-(2,5-dihydroxybenzylidene)-2-hydroxy-2-phenyl-2λ3-ethanehydrazide (R-(L1)−) ligands, one bridged anion μ4-O2−, two peripherally free Cl− anions, eight peripherally free MeOH molecules and twelve peripherally free H2O molecules. The molecular formula of R-1 was [Dy4(L1)8(μ4-O)]·2Cl·xCH3OH·yH2O (R-1: x = 8, y = 12; S-1: x = 3, y = 7) (Fig. 1a and b). The independent unit of R-1 consists of one Dy(III) ion and two deprotonated R-(L1)− ligands. First, the two R-(L1)− ligand units chelated one Dy(III) ion in a crossover pattern, forming a Dy(L1)2 fragment (Fig. 3a, S-1 shown in Fig. S1a†). Subsequently, the four Dy(L1)2 units arranged on the four vertices of the square by an annular arrangement and are further bridged by an anion μ4-O2− to form a square-shaped tetranuclear dysprosium cluster R-1 (Fig. 1c and d). The {Dy/O} nuclei of R-1 exhibited a square arrangement (Fig. 1e and f). Furthermore, the eight ligands R-(L1)− in the cluster R-1 exhibited the same coordination pattern: μ2-η1:η1:η2 (Fig. 3b, S-1 shown in Fig. S1b†). All the metal center Dy(III) ions were in a ninth-coordinated O7N2 coordination environment by the R-(L1)− ligands and the bridged anion μ4-O2−. The coordination configuration of the metal center Dy(III) ion was calculated using SHAPE software to be a capped square antiprism (CSAPR-9) (Fig. 3c, S-1 shown in Fig. S1c, and Tables S6 and S7†).39 The structural analysis showed that the bond lengths between Dy–O and Dy–N in R/S-1 were in the normal range (Tables S2 and S3†).
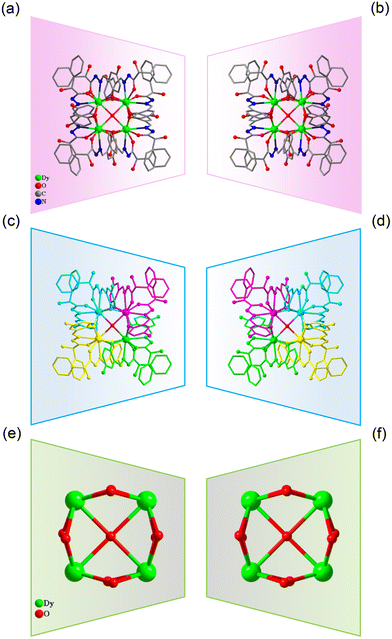 | ||
| Fig. 1 Structure of R/S-1 (a and b); four Dy(L1)2 fragments of R/S-1 (c and d); and cluster core connection (e and f). | ||
 | ||
| Fig. 2 Structure of R/S-2 (a and b); three Dy2L2 fragments of R/S-2 (c and d); and cluster core connection (e and f). | ||
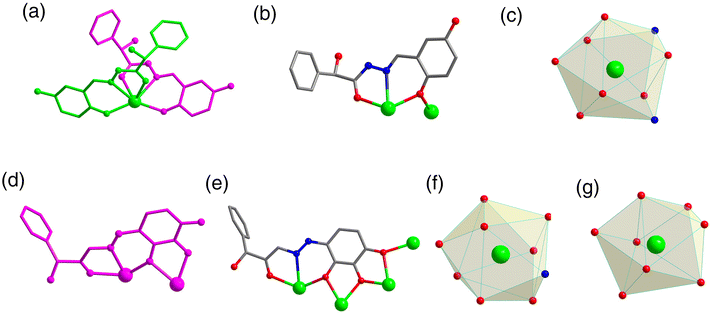 | ||
| Fig. 3 The asymmetric unit of R-1 (a) and R-2 (d); ligand coordination mode of R-1 (b) and R-2 (e); and coordination polyhedron around the Dy(III) ions of R-1 (c) and R-2 (f and g). | ||
When we replaced 2,5-dihydroxybenzaldehyde with 2,3,4-trihydroxybenzaldehyde (0.1 mmol, 0.0154 g), the metal salt was changed to Dy(OAc)3·4H2O (0.5 mmol, 0.2058 g) under the same reaction conditions and two yellow bulk crystals R/S-2 were obtained. SCXRD results showed that the clusters R-2 and S-2 were a pair of enantiomers crystallized in the monoclinic system I2 space group (Table S1†). Here, the structure of R-2 was discussed in detail. The R-2 was composed of six Dy(III) ions, three R-deprotonated(E)-2-hydroxy-2-phenyl-N′-(2,3,4-trihydroxybenzylidene)-2λ3-ethanehydrazide (R-(L2)3−) ligands, one bridged anion μ3-OH−, nine terminally coordinated OAc−, three terminally coordinated H2O molecules, one peripherally free H3O+ ion, six peripherally free MeOH molecules and three peripherally free H2O molecules. The molecular formula of R-2 was [Dy6(L2)3(μ3-OH)(OAc)9(H2O)3]·H3O·xCH3OH·yH2O (R-2: x = 6, y = 3; S-2: x = 4, y = 2) (Fig. 2a and b). The smallest asymmetric unit of R-2 consists of two Dy(III) ions and one deprotonated organic ligand R-(L2)3−. Interestingly, we regulated the position of the hydroxyl coordination sites on the reaction starting materials. That is, the change from 5-hydroxyl to 3-hydroxyl resulted in more concentrated chelation sites for R-(L2)3−. Therefore, R-(L2)3− can effectively capture two Dy(III) ions to form a Dy2L2 template unit at the initial stage of the reaction (Fig. 3d, S-2 shown in Fig. S1d†). Furthermore, the added coordination sites of 4-hydroxyl on the R-(L2)3− ligand can further bridge the Dy2L2 template unit of another molecule, finally forming a triangular pyramid-shaped hexanuclear cluster R-2 (Fig. 2c and d). The cluster core {Dy/O} of R-2 contains three Dy2O5 connected by an anion μ3-OH− (Fig. 2e and f). The three ligands in the cluster R-2 had the same coordination mode as μ4-η1:η1:η2:η2:η2 (Fig. 3e, S-2 shown in Fig. S1e†). The metal center Dy(III) ions had two different coordination environments. The metal center Dy1 was surrounded by an O8N1 coordination environment formed by R-(L2)3−, OAc− and terminally coordinated H2O molecules and its coordination configuration was calculated using SHAPE to be a capped square antiprism (CSAPR-9) (Fig. 3f, S-2 shown in Fig. S1f†). The Dy2 was surrounded by an O8 coordination environment formed by R-(L2)3−, OAc− and bridged anion μ4-O2− and its coordination configuration was biaugmented trigonal prism (BTPR-8) (Fig. 3g, S-2 shown in Fig. S1g, and Tables S8 and S9†). The structural analysis showed that the bond lengths between Dy–O and Dy–N in R/S-2 were in the normal range (Tables S4 and S5†).
The clusters R/S-1 (Fig. S2a†) and R/S-2 (Fig. S2b†) were two pairs of enantiomers, so they have similar infrared absorption peaks. The test results showed that they all have characteristic absorption peaks including ν(HO–H) of the water molecule, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N of the imine group (–C
N of the imine group (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–), C
N–), C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C
N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of the aromatic ring, and C–O of the phenolic hydroxyl group.40 The thermogravimetric curves of R/S-1 and R/S-2 showed that the frameworks were stable up to 180 °C, after which they quickly collapsed. From 35 to 170 °C, the weight loss of R-1 was 13.42%, which corresponds to eight free MeOH molecules and twelve free H2O molecules (theoretical, 13.09%) (Fig. S3a†). The weight loss of S-1 was 6.87% from 35 to 170 °C, which corresponds to three free MeOH molecules and seven free H2O molecules (theoretical, 6.59%) (Fig. S3b†). From 35 to 180 °C, the weight loss of R-2 was 11.85%, which corresponds to six free MeOH molecules and four free H2O molecules and three terminally coordinated H2O molecules (theoretical, 13.25%) (Fig. S3c†). For the S-2, the weight loss rate was 9.52% over the range 35–180 °C, which corresponds to the loss of four free MeOH molecules, three free H2O molecules and three terminally coordinated H2O molecules (theoretical, 8.69%) (Fig. S3d†). Powder X-ray diffraction (PXRD) patterns of R/S-1 and R/S-2 (Fig. S4†) agreed well with simulated patterns calculated from SCXRD data, indicating phase purity in all crystalline samples.
C of the aromatic ring, and C–O of the phenolic hydroxyl group.40 The thermogravimetric curves of R/S-1 and R/S-2 showed that the frameworks were stable up to 180 °C, after which they quickly collapsed. From 35 to 170 °C, the weight loss of R-1 was 13.42%, which corresponds to eight free MeOH molecules and twelve free H2O molecules (theoretical, 13.09%) (Fig. S3a†). The weight loss of S-1 was 6.87% from 35 to 170 °C, which corresponds to three free MeOH molecules and seven free H2O molecules (theoretical, 6.59%) (Fig. S3b†). From 35 to 180 °C, the weight loss of R-2 was 11.85%, which corresponds to six free MeOH molecules and four free H2O molecules and three terminally coordinated H2O molecules (theoretical, 13.25%) (Fig. S3c†). For the S-2, the weight loss rate was 9.52% over the range 35–180 °C, which corresponds to the loss of four free MeOH molecules, three free H2O molecules and three terminally coordinated H2O molecules (theoretical, 8.69%) (Fig. S3d†). Powder X-ray diffraction (PXRD) patterns of R/S-1 and R/S-2 (Fig. S4†) agreed well with simulated patterns calculated from SCXRD data, indicating phase purity in all crystalline samples.
As for R/S-1, first, two HL1 ligand molecules captured one Dy(III) ion, forming the template unit Dy(L1)2. And then four Dy(L1)2 template units were well-ordered arranged at the four vertices of the square to form a square-like tetranuclear cluster R/S-1 by a bridged anion μ4-O2− (Scheme 2a). In the process of R/S-1 formation, the template unit Dy(L1)2 undergoes a hydrolysis-induced annular growth mechanism to form the final product. When we changed the coordination sites on the aldehyde, the original 5-hydroxyl was changed to 3-hydroxyl, which resulted in more aggregation of the coordination sites on the ligand. One H3L2 ligand molecule can capture two Dy(III) ions, forming the template unit Dy2L2. Furthermore, the above-mentioned multiple template units Dy2L2 were then bridged by an anion μ3-OH− to form triangular pyramid-like hexanuclear clusters R/S-2 (Scheme 2b). In a word, we obtained template units with different linkages by regulating the coordination sites of ligands and achieved the manipulation of the annular growth mechanism to construct chiral lanthanide clusters with different shapes and linkages.
CD spectra analysis of R/S-1 and R/S-2
The chiral optical activity and enantiomeric characteristics of clusters R/S-1 and R/S-2 were verified by circular dichroism (CD) spectra in methanol. The CD signal peaks of the two enantiomers at a concentration of 0.1 g L−1 in the range of 200–500 nm presented a nearly perfect mirror symmetry (Fig. 4b and d). The results indicated that R-1 displayed a strong positive Cotton effect at 242 and 303 nm, a weak positive Cotton effect at 273 nm and a strong negative Cotton effect at 221 nm, while S-1 showed opposite signals at the same wavelength to form a mirror image, indicating that R-1 and S-1 were a pair of enantiomers. The CD signals of R/S-2 were different from those of the R/S-1 due to the significant difference in self-assembled structure. The R-2 exhibited a strong positive Cotton effect at 354 nm and 273 nm, a weak negative Cotton effect at 240 nm and a strong negative Cotton effect at 215 nm, while S-2 showed opposite signals at the same wavelength, confirming that the R-2 and S-2 were a pair of enantiomers. In combination with the absorption spectrum analysis, the R/S-1 had three strong absorption peaks at 380 nm, 288 nm and 256 nm, which were attributed to the n–π* transition of the imino group on the ligands and the π–π* transition of the aromatic group (Fig. 4a). The R/S-2 had a strong absorption peak at 364 nm, which was attributed to the n–π* transition of the imino group and the π–π* transition of the aromatic group, while a weak shoulder peak at 271 nm was attributed to the π–π* transition on the ligands (Fig. 4c).41,42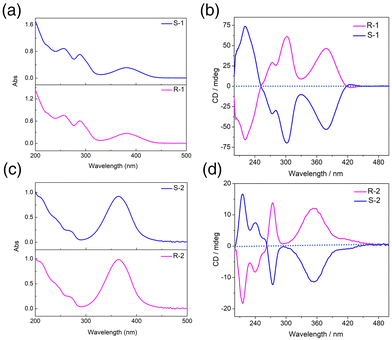 | ||
| Fig. 4 The UV-vis absorption spectra of clusters R/S-1 (a) and R/S-2 (c). CD spectra of clusters R/S-1 (b) and R/S-2 (d). | ||
Magnetic analysis of clusters R/S-1 and R/S-2
The variable-temperature molar magnetic susceptibility of clusters R/S-1 and R/S-2 was measured from 300 K to 2 K under an external dc magnetic field of 0.1 T.43–47 The χmT values of clusters R-1, S-1, R-2 and S-2 were 55.17, 55.95, 85.13 and 85.96 cm3 mol−1 K at 300 K, respectively, which were close to expected values (6H15/2, S = 5/2, g = 4/3, J = 15/2, L = 5) (Fig. S5a, S8a, S5b and S8b†). The χmT values of clusters R-1 and S-1 reached minimum values of 46.69 cm3 mol−1 K and 50.92 cm3 mol−1 K at 14 K, which can be attributed to the thermal depopulation of the excited Stark sublevels of Dy(III) ions. Then the R-1 increased to 49.75 cm3 mol−1 K and the S-1 reached 53.94 cm3 mol−1 K at 2 K, which can be attributed to a weak ferromagnetic interaction. For the R-2 and S-2, the χmT values decreased and reached the minimum values of 42.44 cm3 mol−1 K and 44.37 cm3 mol−1 K at 2 K, which was likely due to the presence of intermolecular weak antiferromagnetic coupling. The magnetization versus magnetic field plots of clusters R/S-1 and R/S-2 in the applied field of 0–7 T and temperature range of 2–5 K, respectively. The magnetization of clusters R-1, S-1, R-2 and S-2 was 18.92, 17.75, 27.16 and 34.23Nβ, respectively. The nonoverlapping M versus HT−1 graph revealed the existence of significant magnetic anisotropy which may be attributed to the strong crystal field effect (Fig. S5c, S8c, S5d and S8d†). Furthermore, the hysteresis loops of clusters R-1, S-1, R-2 and S-2 were not obvious at 2 K which may be caused by the strong quantum tunneling effect of Dy(III) ions (Fig. S6a, S9a, S6b and S9b†).To further study the magnetic relaxation dynamics of clusters R/S-1 and R/S-2, we conducted alternating current (AC) magnetization under zero dc field at different temperatures in the frequency range of 10–999 Hz. The results indicated that the in-phase (χ′) and out-of-phase (χ′′) AC susceptibilities of R-1 and S-1 had obvious frequency and temperature dependence, which confirmed that R-1 and S-1 showed slow magnetic relaxation behavior. Also the out-of-phase signal had a distinct peak of R-1 and S-1, and with the increase of frequency, the peak gradually shifted to the high temperature region, which was a typical feature of SMMs (Fig. 5a and S10a†). The field-dependence of magnetic dynamics was monitored at 2 K (Fig. S11a and S11b†) for R-1 and S-1, respectively. The field-dependence of the relaxation time τ indicates that the relaxation rate decreases to a minimum under the applied dc field of 1000 Oe (Fig. S11c and S11d†). Therefore, 1000 Oe was selected as an optimum external dc field for further measurements of R-1 and S-1. We found that the quantum tunneling effect can be suppressed. Both in-phase and out-of-phase signals of clusters R-1 and S-1 showed obvious peaks (Fig. S11e and S11f†). For the R-2 and S-2, only a slight frequency-dependent behavior was observed, and no obvious peak was observed with the decreasing temperature, which might be caused by the fast quantum tunneling effect of the clusters R-2 and S-2 at low temperature (Fig. 5c and S13a†). When a certain external field was applied, the quantum tunneling effect might be suppressed. Therefore, the R-2 and S-2 were tested under 1000 Oe external dc field. In order to study the magnetic behavior of R-2 and S-2 under 1000 Oe dc fields, the in-phase and out-of-phase AC susceptibilities were plotted as a function of temperature (χ′/χ′′ vs. T) (Fig. S7a and S13b†) and frequency (χ′/χ′′ vs. v), respectively (Fig. S7b and S7c†). The results showed that the in-phase and out of phase only showed slight frequency dependence, no peak. Although an external field of 1000 Oe was applied, the experimental results showed that the in-phase and out of phase signals of R-2 and S-2 were not significantly different from under zero field, confirming that R-2 and S-2 had no field effect, and only exhibited frequency-dependent behavior.
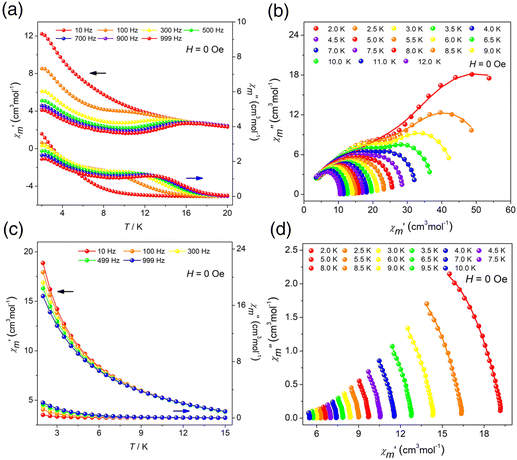 | ||
| Fig. 5 Temperature-dependent χ′ and χ′′ AC susceptibilities under 0 Oe dc fields for R-1 (a) and R-2 (c); and Cole–Cole plots for R-1 (b) and R-2 (d). | ||
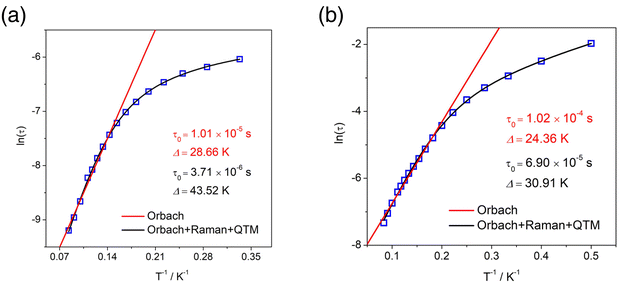
To explore the relaxation process of R-1 and S-1, the Cole–Cole diagram between 2 K and 12 K was fitted and the fitting values were basically consistent with the generalized Debye model. The R-1 and S-1 presented two semicircular shapes, exhibiting double relaxation processes, namely the fast relaxation phase (FR, with a relatively short relaxation time) and the slow relaxation phase (SR, with a relatively long relaxation time) (Fig. 5b and S10b†).29,48 The ln(τ/s) vs. T−1 curve for the cluster R-1 was also plotted from these fitting results. The temperature-dependent relaxation time was analyzed by assuming the thermal activation process according to the Arrhenius law τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ueff/kBT). At high temperatures, we applied an Orbach relaxation process (τ−1 = τ0−1
exp(Ueff/kBT). At high temperatures, we applied an Orbach relaxation process (τ−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/kBT) to best fit obtained Ueff = 28.66 K, τ0 = 1.01 × 10−5 s for the FR phase (Fig. 6a) and Ueff = 24.36 K, τ0 = 1.02 × 10−4 s for the SR phase (Fig. 6b), respectively. In addition, in order to adapt to a larger temperature range, the fitting process should include multiple relaxation processes, such as the Orbach process (τ0−1
exp(−Ueff/kBT) to best fit obtained Ueff = 28.66 K, τ0 = 1.01 × 10−5 s for the FR phase (Fig. 6a) and Ueff = 24.36 K, τ0 = 1.02 × 10−4 s for the SR phase (Fig. 6b), respectively. In addition, in order to adapt to a larger temperature range, the fitting process should include multiple relaxation processes, such as the Orbach process (τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/kBT)), Raman (CTn), direct relaxation process (AHmT) and quantum tunneling process (QTM); the direct relaxation process can be ignored for the slow relaxation behaviors at zero field. So, we considered multinomial relaxation processes (τ−1 = τ0−1
exp(−Ueff/kBT)), Raman (CTn), direct relaxation process (AHmT) and quantum tunneling process (QTM); the direct relaxation process can be ignored for the slow relaxation behaviors at zero field. So, we considered multinomial relaxation processes (τ−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/kBT) + τQTM−1 + CTn) to fit R-1 over all of the temperatures, and we obtained Ueff = 43.52 K, τ0 = 3.71 × 10−6 s for the FR phase (Fig. 6a) and Ueff = 30.91 K, τ0 = 6.90 × 10−5 s for the SR phase (Fig. 6b), respectively.49,50 The Cole–Cole plots for the R-2 at 0 Oe and 1000 Oe dc fields are shown in Fig. 5d and S7d;† since the R-2 had no field effect, it cannot be fitted. Magnetic analysis showed that R-1 had more obvious SMM behavior than R-2. The ln(τ/s) vs. T−1 curve for the cluster S-1 is shown in Fig. S12a and S12b.†
exp(−Ueff/kBT) + τQTM−1 + CTn) to fit R-1 over all of the temperatures, and we obtained Ueff = 43.52 K, τ0 = 3.71 × 10−6 s for the FR phase (Fig. 6a) and Ueff = 30.91 K, τ0 = 6.90 × 10−5 s for the SR phase (Fig. 6b), respectively.49,50 The Cole–Cole plots for the R-2 at 0 Oe and 1000 Oe dc fields are shown in Fig. 5d and S7d;† since the R-2 had no field effect, it cannot be fitted. Magnetic analysis showed that R-1 had more obvious SMM behavior than R-2. The ln(τ/s) vs. T−1 curve for the cluster S-1 is shown in Fig. S12a and S12b.†
Conclusion
In summary, we induced the formation of template units with different linkages through the change of hydroxyl coordination sites at different positions on the ligands and realized the directional construction of two pairs of chiral lanthanide clusters R/S-1 and R/S-2 with different shapes and magnetic properties by hydrolysis manipulating the annular growth mechanism. The template unit formed in the initial stage of the reaction is crucial for the design and synthesis of chiral clusters. Two HL1 ligands co-chelate one Dy(III) ion to form a mononuclear template unit Dy(L1)2. The above template units are pulled by a bridge anion μ4-O2− and assembled to form square-shaped clusters R/S-1 through the annular growth mechanism. The change of the hydroxyl coordination sites enables the H3L2 ligand to capture two Dy(III) ions and to form the template unit Dy2L2. The above three Dy2L2 are assembled along the annular arrangement by the traction of the bridge anion μ3-OH− to form triangular pyramidal hexanuclear clusters R/S-2. Magnetic studies showed that the chiral clusters R-1 and S-1 exhibited obvious single-molecule magnet behavior with double relaxation behavior under zero dc field. To the best of our knowledge, this is one of the rare examples of chiral lanthanide clusters with double relaxation behavior. The R-2 and S-2 have distinct frequency-dependent behavior under zero dc field. This work provides a vivid example for the design and synthesis of chiral lanthanide clusters, and for the first time, the self-assembly process is regulated by the design of coordination sites to induce the formation of chiral lanthanide clusters with different shapes. Furthermore, this work opens a door for the directional construction of specific chiral clusters, which opens a new horizon for the design and synthesis of multifunctional materials with magneto-optical applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (22075058 and 22061005).References
- P. Peluso and B. Chankvetadze, Recognition in the Domain of Molecular Chirality: From Noncovalent Interactions to Separation of Enantiomers, Chem. Rev., 2022, 122, 13235–13400 CrossRef CAS PubMed.
- D. P. Glavin, A. S. Burton, J. E. Elsila, J. C. Aponte, J. C. Aponte and J. P. Dworkin, The Search for Chiral Asymmetry as a Potential Biosignature in our Solar System, Chem. Rev., 2020, 120, 4660–4689 CrossRef CAS PubMed.
- X. L. Zhao, S. Q. Zang and X. Y. Chen, Stereospecific interactions between chiral inorganic nanomaterials and biological systems, Chem. Soc. Rev., 2020, 49, 2481–2503 RSC.
- G. Z. Kong, M. Y. Xiong, L. Liu, L. Hu, H.-M. Meng, G. L. Ke, X.-B. Zhang and W. H. Tan, DNA origami-based protein networks: from basic construction to emerging applications, Chem. Soc. Rev., 2021, 50, 1846–1873 RSC.
- M. S. Xiao, W. Lai, T. T. Man, B. B. Chang, L. Li, A. R. Chandrasekaran and H. Pei, Rationally Engineered Nucleic Acid Architectures for Biosensing Applications, Chem. Rev., 2019, 119, 11631–11717 CrossRef CAS PubMed.
- F. De Fazio, D. Misatziou, Y. R. Baker, O. L. Muskens, T. Brown and A. G. Kanaras, Chemically modified nucleic acids and DNA intercalators as tools for nanoparticle assembly, Chem. Soc. Rev., 2021, 50, 13410–13440 RSC.
- G. X. Y. Huang, X. C. Zhan, C. Zeng, K. Liang, X. C. Zhu, Y. Y. Zhao, P. Wang, Q. F. Wang, Q. Zhou, Q. H. Tao, M. H. Liu, J. L. Lei, C. Y. Yan and Y. G. Shi, Cryo-EM structure of the inner ring from the Xenopus laevis nuclear pore complex, Cell Res., 2022, 32, 451–460 CrossRef CAS PubMed.
- R. Bai, R. X. Wan, L. Wang, K. Xu, Q. F. Zhang, J. L. Lei and Y. G. Shi, Structure of the activated human minor spliceosome, Science, 2021, 371, 1220 Search PubMed.
- X. C. Zhu, G. X. Y. Huang, C. Zeng, X. C. Zhan, K. Liang, Q. K. Xu, Y. Y. Zhao, P. Wang, Q. F. Wang, Q. Zhou, Q. H. Tao, M. H. Liu, J. L. Lei, C. Y. Yan and Y. G. Shi, Structure of the cytoplasmic ring of the Xenopus laevis nuclear pore complex, Science, 2022, 376, 1177 CrossRef PubMed.
- X.-Z. Li, C.-B. Tian and Q.-F. Sun, Coordination-Directed Self-Assembly of Functional Polynuclear Lanthanide Supramolecular Architectures, Chem. Rev., 2022, 122, 6374–6458 CrossRef CAS PubMed.
- S.-J. Hu, X.-Q. Guo, L.-P. Zhou, D.-N. Yan, P.-M. Cheng, L.-X. Cai, X.-Z. Li and Q.-F. Sun, Guest-Driven Self-Assembly and Chiral Induction of Photofunctional Lanthanide Tetrahedral Cages, J. Am. Chem. Soc., 2022, 144, 4244–4253 CrossRef CAS PubMed.
- Y. Y. Zhou, H. F. Li, T. Y. Zhu, T. Gao and P. F. Yan, A Highly Luminescent Chiral Tetrahedral Eu4L4(L′)4 Cage: Chirality Induction, Chirality Memory, and Circularly Polarized Luminescence, J. Am. Chem. Soc., 2019, 141, 19634–19643 CrossRef CAS PubMed.
- J. J. Jiao, C. X. Tan, Z. J. Li, Y. Liu, X. Han and Y. Cui, Design and Assembly of Chiral Coordination Cages for Asymmetric Sequential Reactions, J. Am. Chem. Soc., 2018, 140, 2251–2259 CrossRef CAS PubMed.
- Y.-J. Hou, K. Wu, Z.-W. Wei, K. Li, Y.-L. Lu, C.-Y. Zhu, J.-S. Wang, M. Pan, J.-J. Jiang, G.-Q. Li and C.-Y. Su, Design and Enantioresolution of Homochiral Fe(II)-Pd(II) Coordination Cages from Stereolabile Metalloligands: Stereochemical Stability and Enantioselective Separation, J. Am. Chem. Soc., 2018, 140, 18183–18191 CrossRef CAS PubMed.
- Y. B. Tan, Y. Okayasu, S. Katao, Y. Nishikawa, F. Asanoma, M. Yamada, J. Yuasa and T. Kawai, Visible Circularly Polarized Luminescence of Octanuclear Circular Eu(III) Helicate, J. Am. Chem. Soc., 2020, 142, 17653–17661 CrossRef CAS PubMed.
- J. Wang, Z.-H. Zhu, M.-W. Chen, Q.-A. Chen and Y.-G. Zhou, Catalytic BiomimeticAsymmetric Reduction of Alkenes and Imines Enabled by Chiral and Regenerable NAD(P)H Models, Angew. Chem., Int. Ed., 2019, 58, 1813–1817 CrossRef CAS PubMed.
- K. Wang, F. Ma, D. D. Qi, X. Chen, Y. X. Chen, Y.-C. Chen, H.-L. Sun, M.-L. Tong and J. Z. Jiang, Chiral bis(phthalocyaninato) terbium double-decker compounds with enhanced single-ion magnetic behavior, Inorg. Chem. Front., 2018, 5, 939–943 RSC.
- Z. H. Zhu, C. Zhao, T. T. Feng, X. D. Liu, X. Ying, X.-L. Li, Y.-Q. Zhang and J. K. Tang, Air-Stable Chiral Single-Molecule Magnets with Record Anisotropy Barrier Exceeding 1800 K, J. Am. Chem. Soc., 2021, 143, 10077–10082 CrossRef CAS PubMed.
- C. X. Tan, J. J. Jiao, Z. J. Li, Y. Liu, X. Han and Y. Cui, Design and Assembly of a Chiral Metallosalen-Based Octahedral Coordination Cage for Supramolecular Asymmetric Catalysis, Angew. Chem., Int. Ed., 2018, 57, 2085–2090 CrossRef CAS PubMed.
- C. F. Zhu, H. T. Tang, K. K. Yang, Y. Fang, K.-Y. Wang, Z. F. Xiao, X. Wu, Y. G. Li, J. A. Powell and H.-C. Zhou, Homochiral Dodecanuclear Lanthanide “Cage in Cage” for Enantioselective Separation, J. Am. Chem. Soc., 2021, 143, 12560–12566 CrossRef CAS PubMed.
- J. H. Zhang, L. X. Dai, A. M. Webster, W. T. K. Chan, L. E. Mackenzie, R. Pal, S. L. Cobb and G.-L. Law, Unusual Magnetic Field Responsive Circularly Polarized Luminescence Probes with Highly Emissive Chiral Europium(III) Complexes, Angew. Chem., Int. Ed., 2021, 60, 1004–1010 CrossRef CAS PubMed.
- X. Wang, S.-Q. Wang, J.-N. Chen, J.-H. Jia, C. Wang, K. Paillot, I. Breslavetz, L.-S. Long, L.-S. Zheng, G. L. J. A. Rikken, C. Train, X.-J. Kong and M. Atzori, Magnetic 3d-4f Chiral Clusters Showing Multimetal Site Magneto-Chiral Dichroism, J. Am. Chem. Soc., 2022, 144, 8837–8847 CrossRef CAS PubMed.
- F. Gendron, S. Di Pietro, L. Abad Galán, F. Riobé, V. Placide, L. Guy, F. Zinna, L. Di Bari, A. Bensalah-Ledoux, Y. Guyot, G. Pilet, F. Pointillart, B. Baguenard, S. Guy, O. Cador, O. Maury and B. Le Guennic, Luminescence, chiroptical, magnetic and ab initio crystal-field characterizations of an enantiopure helicoidal Yb(III) complex, Inorg. Chem. Front., 2021, 8, 914–926 RSC.
- M. Feng, B.-H. Lyu, M.-H. Wang, W.-W. Wu, Y.-C. Chen, G.-Z. Huang, W.-Q. Lin, S.-G. Wu, J.-L. Liu and M.-L. Tong, Chiral Erbium(III) Complexes: Single-Molecule Magnet Behavior, Chirality, and Nuclearity Control, Inorg. Chem., 2019, 58, 10694–10703 CrossRef CAS PubMed.
- M.-H. Du, L.-Q. Chen, L.-P. Jiang, W.-D. Liu, L.-S. Long, L.-S. Zheng and X.-J. Kong, Counterintuitive Lanthanide Hydrolysis-Induced Assembly Mechanism, J. Am. Chem. Soc., 2022, 144, 5653–5660 CrossRef CAS PubMed.
- H. Zheng, M.-H. Du, S.-C. Lin, Z.-C. Tang, X.-J. Kong, L.-S. Long and L.-S. Zheng, Assembly of a Wheel-Like Eu24Ti8 Cluster under the Guidance of High-Resolution Electrospray Ionization Mass Spectrometry, Angew. Chem., Int. Ed., 2018, 57, 10976–10979 CrossRef CAS PubMed.
- W. M. Huang, W. M. Chen, Q. X. Bai, Z. Zhang, M. Feng and Z. P. Zheng, Anion-Guided Stepwise Assembly of High-Nuclearity Lanthanide Hydroxide Clusters, Angew. Chem., Int. Ed., 2022, 61, e202205385 CAS.
- Z.-H. Zhu, X.-F. Ma, H.-L. Wang, H.-H. Zou, K.-Q. Mo, Y.-Q. Zhang, Q.-Z. Yang, B. Li and F.-P. Liang, A triangular Dy3 single-molecule toroic with high inversion energy barrier: magnetic properties and multiple-step assembly mechanism, Inorg. Chem. Front., 2018, 5, 3155–3162 RSC.
- H.-L. Wang, X.-F. Ma, J.-M. Peng, Z.-H. Zhu, B. Li, H.-H. Zou and F.-P. Liang, Tracking the Stepwise Formation of the Dysprosium Cluster (Dy10) with Multiple Relaxation Behavior, Inorg. Chem., 2019, 58, 9169–9174 CrossRef CAS PubMed.
- Z.-R. Luo, H.-L. Wang, Z.-H. Zhu, T. Liu, X.-F. Ma, H.-F. Wang, H.-H. Zou and F.-P. Liang, Assembly of Dy60 and Dy30 cage-shaped nanoclusters, Commun. Chem., 2020, 3, 1–9 CrossRef.
- Z.-H. Zhu, J.-M. Peng, H.-L. Wang, H.-H. Zou and F.-P. Liang, Assembly Mechanism and Heavy Metal Ion Sensing of Cage-Shaped Lanthanide Nanoclusters, Cell Rep. Phys. Sci., 2020, 1, 100165 CrossRef CAS.
- H.-L. Wang, T. Liu, Z.-H. Zhu, J.-M. Peng, H.-H. Zou and F.-P. Liang, A series of dysprosium clusters assembled by a substitution effect-driven out-to-in growth mechanism, Inorg. Chem. Front., 2021, 8, 2136–2143 RSC.
- Y.-L. Li, H.-L. Wang, Z.-H. Zhu, F.-P. Liang and H.-H. Zou, Giant Crown-Shaped Dy34 Nanocluster with High Acid-Base Stability Assembled by an out-to-in Growth Mechanism, Inorg. Chem., 2022, 61, 10101–10107 CrossRef CAS PubMed.
- Z.-R. Luo, H.-H. Zou, Z.-L. Chen, B. Li, K. Wang and F.-P. Liang, Triethylamine-templated nanocalix Ln12 clusters of diacylhydrazone: crystal structures and magnetic properties, Dalton Trans., 2019, 48, 17414–17421 RSC.
- Y.-L. Li, H.-L. Wang, Z.-H. Zhu, J. Li, H.-H. Zou and F.-P. Liang, A Series of High-Nuclear Gadolinium Cluster Aggregates with a Magnetocaloric Effect Constructed through Two-Component Manipulation, Inorg. Chem., 2021, 60, 16794–16802 CrossRef CAS PubMed.
- K.-Q. Mo, Z.-H. Zhu, H.-L. Wang, X.-F. Ma, J.-M. Peng, H.-H. Zou, J. Bai and F.-P. Liang, Substituents lead to differences in the formation of two different butterfly-shaped NiII2DyIII2 clusters: structures and multistep assembly mechanisms, Dalton Trans., 2019, 48, 16641–16649 RSC.
- H.-L. Wang, J.-M. Peng, Z.-H. Zhu, K.-Q. Mo, X.-F. Ma, B. Li, H.-H. Zou and F.-P. Liang, Step-by-Step and Competitive Assembly of Two Dy(III) Single-Molecule Magnets with Their Performance Tuned by Schiff Base Ligands, Cryst. Growth Des., 2019, 19, 5369–5375 CrossRef CAS.
- J.-M. Peng, H.-L. Wang, Z.-H. Zhu, J. Bai, F.-P. Liang and H.-H. Zou, Series of the Largest Dish-Shaped Dysprosium Nanoclusters Formed by In Situ Reactions, Inorg. Chem., 2022, 61, 6094–6100 CrossRef CAS PubMed.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Shape maps and polyhedral interconversion paths in transition metal chemistry, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- H.-L. Wang, T. Liu, Z.-H. Zhu, J.-M. Peng, H.-H. Zou and F.-P. Liang, pH manipulates the assembly of a series of dysprosium clusters with subtle difference, Inorg. Chem. Front., 2021, 8, 3134–3140 RSC.
- C.-M. Liu, R. Sun, B.-W. Wang, F. Wu, X. Hao and Z. Shen, Homochiral Ferromagnetic Coupling Dy2 Single-Molecule Magnets with Strong Magneto-Optical Faraday Effects at Room Temperature, Inorg. Chem., 2021, 60, 12039–12048 CrossRef CAS PubMed.
- M. H. Cui, L. P. Yang, F. C. Li, L. M. Zhou, Y. L. Song, S.-M. Fang, C.-M. Liu and X.-L. Li, Multifunctional DyIII Enantiomeric Pairs Showing Enhanced Photoluminescences and Third-Harmonic Generation Responses through the Coordination Role of Homochiral Tridentate N,N,N- Pincer Ligands, Inorg. Chem., 2021, 60, 13366–13375 CrossRef CAS PubMed.
- F.-S. Guo, A. K. Bar and R. A. Layfield, Main Group Chemistry at the Interface with Molecular Magnetism, Chem. Rev., 2019, 119, 8479–8505 CrossRef CAS PubMed.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J.-K. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, Strong Axiality and Ising Exchange Interaction Suppress Zero-Field Tunneling of Magnetization of an Asymmetric Dy2 Single-Molecule Magnet, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed.
- P. Zhang, L. Zhang, C. Wang, S. F. Xue, S.-Y. Lin and J. K. Tang, Equatorially Coordinated Lanthanide Single Ion Magnets, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- J. F. Wu, S.-Y. Lin, S. Shen, X.-L. Li, L. Zhao, L. Zhang and J. K. Tang, Probing the magnetic relaxation and magnetic moment arrangement in a series of Dy4 squares, Dalton Trans., 2017, 46, 1577–1584 RSC.
- Z.-H. Zhu, H.-F. Wang, S. Yu, H.-H. Zou, H.-L. Wang, B. Yin and F.-P. Liang, Substitution Effects Regulate the Formation of Butterfly-Shaped Tetranuclear Dy(III) Cluster and Dy-Based Hydrogen-Bonded Helix Frameworks: Structure and Magnetic Properties, Inorg. Chem., 2020, 59, 11640–11650 CrossRef CAS PubMed.
- H.-F. Wang, Z.-H. Zhu, J.-M. Peng, B. Yin, H.-L. Wang, H.-H. Zou and F.-P. Liang, Multifunctional Binuclear Ln(III) Complexes Obtained via In Situ Tandem Reactions: Multiple Photoresponses to Volatile Organic Solvents and Anticounterfeiting and Magnetic Properties, Inorg. Chem., 2020, 59, 13774–13783 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2194449–2194452. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qi01711c |
| This journal is © the Partner Organisations 2022 |