Room temperature lithium superionic conductivity in high entropy oxides

Abstract

Impedance spectroscopy measurements evidence superionic Li⁺ mobility (>10⁻³ S cm⁻¹) at room temperature and fast ionic mobility for Na⁺ (5 × 10⁻⁶ S cm⁻¹) in high entropy oxides, a new family of oxide-based materials with the general formula (MgCoNiCuZn)_1−x−yGa_yA_xO (with A = Li, Na, K). Structural investigations indicate that the conduction path probably involves oxygen vacancies.

---

Introduction

Constant electrification of many devices (from the connected watch to the electric car) and their parallel need for longer energetic autonomy require the development of high efficiency batteries.¹ In this field, all-solid-state technology has many advantages over conventional commercial cells.^2,3 Indeed, without liquid electrolyte, devices are safer and also comply with current environmental standards. Moreover, in the microelectronic domain, all-solid-state microbatteries are thin, bendable and can be produced with a customizable shape for a better integration into small devices (as smart cards/labels, computers etc.). However, usual solid electrolytes are not sufficiently conductive to allow ultrafast charge/discharge rates (which are crucial for high power applications). Indeed, in lithium based, thin film microbatteries, for example, the largest internal resistance of the cell comes from the LiPON (lithium phosphorous oxy-nitride) solid electrolyte (whose ionic conductivity at 25 °C is around 2 × 10⁻⁶ S cm⁻¹).⁴

The search for new fast ionic conductors, at room temperature, is thus of critical interest for manufacturing high power batteries.^5–14

It has been shown recently that the entropic contribution to the Gibbs free energy can be used to stabilize new oxide phases, similarly to the situation that occurs in high entropy alloys. In particular, a rock salt structure was observed for entropy-stabilized (Mg, Cu, Ni, Co, Zn)O with a random occupation of the cation sites.¹⁵ Following this pioneering study, we showed that these compounds (hereafter called HEOx, from high entropy oxides) exhibit promising dielectric properties, with a colossal dielectric constant (CDC) observed in a wide frequency range.¹⁶ Moreover, we showed that the cations in “undoped” (Mg, Cu, Ni, Co, Zn)O can be substituted by Li⁺ ions, with an intrinsic charge compensation mechanism, or combinations of +1 and +3 elements, with a self-charge compensation between the substituents, while keeping the rock salt structure. As such, the number of phases that can be synthesized in this system is impressive. Interestingly, the charge compensation mechanism that occurs in the case of the substitution by +1 elements could involve oxygen vacancies, thus providing a possible diffusion pathway for lithium or sodium. In this report, we show that Li and Na substituted HEOx exhibit very large values of ionic conductivity, which makes them among the best oxide-based Li conductors.

Results and discussions

As mentioned in our previous report,¹⁶ all the samples belonging to the series (Mg, Co, Ni, Cu, Zn)_1−xLi_xO and (Mg, Co, Ni, Cu, Zn)_1−2xLi_xGa_xO obtained after air-quenching from 1000 °C are single phase with a rock salt structure. Moreover, they are stable in ambient conditions and can be handled without particular care, as exemplified in Fig. S1† which shows a comparison of the XRD patterns of as-synthesized (Mg, Co, Ni, Cu, Zn)O and of the same sample after being kept for one month in laboratory conditions, and after 24 h in water. As Na⁺ is much larger than both Li⁺ and the average ionic radius of the divalent cations used here (r_Na⁺ = 1.02 Å in an octahedral environment as compared to r_M²⁺ = 0.72–0.74 Å (ref. 17)), Na⁺ might have been too large to substitute for the divalent cations while maintaining the rock salt structure. However, the XRD patterns confirm that the samples belonging to the series (Mg, Co, Ni, Cu, Zn)_1−xNa_xO are also single phase with a rock salt structure (see Fig. S2a and b†). In our previous report, we showed that the partial substitution of cations in (Mg, Co, Ni, Cu, Zn)O by Li⁺ led to a significant decrease of the lattice parameter, following Vegard's law. The ionic radius of Li⁺ in an octahedral configuration is slightly larger than the average ionic radius of the divalent cations, therefore the decrease of the lattice parameters with Li⁺ doping indicated that a charge compensation mechanism occurred. This mechanism involves the formation of Co³⁺ and/or oxygen vacancies, as confirmed by XPS measurements.¹⁶ In the case of the substitution by Na⁺, the decrease of the lattice parameter is strongly reduced, which is consistent with the much larger ionic radius of Na⁺ compared to that of Li⁺. However, the lattice parameter still decreases even for the case of Na doping, which confirms that oxygen vacancies are involved (at least in part) in the charge compensation mechanism. Indeed, if the formation of Co³⁺ were solely involved, the lattice parameter should increase, as the average ionic radius of Na⁺ and Co³⁺ (0.78 Å in the case of the smaller low-spin Co³⁺) is larger than the average ionic radius of the divalent cations of the parent structure (0.73 Å in the case of the larger high-spin Co²⁺). The same conclusion can be drawn for the case of the substitution by Li⁺, as the decrease of the lattice parameter is larger than would be expected assuming a charge compensation mechanism solely by Co³⁺ formation, even by considering the ionic radius of low-spin Co³⁺. In the case of the samples belonging to the series (Mg, Co, Ni, Cu, Zn)_1−2xLi_xGa_xO, the lattice parameter is slightly smaller than the one observed in the undoped sample, consistent with the average ionic radius of Li⁺ and Ga³⁺ being slightly smaller than those of the divalent cations. The fact that the lattice parameter of Li–Ga co-doped samples is larger than that observed in the series (Mg, Co, Ni, Cu, Zn)_1−xLi_xO for the same Li fractions¹⁶ suggests that (at least a proportion of) the oxygen vacancies present in the (Mg, Co, Ni, Cu, Zn)_1−xLi_xO samples have been suppressed when co-substituting by Ga³⁺. Indeed as the ionic radius of Ga³⁺ is significantly smaller than the average ionic radius of the divalent cations, a smaller lattice parameter would be expected for (Mg, Co, Ni, Cu, Zn)_1−2xLi_xGa_xO as compared to (Mg, Co, Ni, Cu, Zn)_1−xLi_xO if the oxygen vacancy concentration remained constant. In the case of (Mg, Co, Ni, Cu, Zn)_0.95K_0.05O, the lattice parameter is slightly larger than that observed in the undoped sample, which is consistent with the larger ionic radius of K⁺ (1.38 A).

Chemical analysis (see Experimental section) showed that the sample composition is close to the nominal value; typical values for cation compositions in the (Mg : Co : Ni : Cu : Zn) series are 0.95 : 1 : 1.1 : 1.05 : 0.95 whereas the alkali ion composition is slightly lower than the nominal composition, due to loss by evaporation during heat treatment at high temperature, as listed in Table 1. To summarize, (Mg, Co, Ni, Cu, Zn)_1−xA_xO (A = Li, Na, K) have been successfully synthesized and they crystallize in a rock-salt structure, with a charge compensation mechanism that involves oxygen vacancies, whereas the concentration of such oxygen vacancies is probably very limited in (Mg, Co, Ni, Cu, Zn)_1−2xLi_xGa_xO due to the self-charge compensation mechanism between Li⁺ and Ga³⁺.

Table 1 Ionic conductivity and activation energies for HEOx samples

HEOx, nominal	HEOx, exp	σ i (S cm^−1) at 20 °C	σ i (S cm^−1) at 80 °C	E a (eV)
0% A		3 × 10^−8	1.5 × 10^−7	0.24
A = Li
x = 0.02	0.02(1)	3 × 10^−8	8 × 10^−7	0.49
x = 0.08		1.5 × 10^−7	6 × 10^−7	0.21
x = 0.10	0.09(1)	2 × 10^−7	2 × 10^−6	0.34
x = 0.16		8 × 10^−6	1 × 10^−5	0.10
x = 0.20		3 × 10^−4	7 × 10^−4	0.12
x = 0.25	0.23(2)	3 × 10^−4	1 × 10^−3	0.18
x = 0.33	0.29(3)	1 × 10^−3	4 × 10^−3	0.20
A = Na
x = 0.02		1 × 10^−7	5 × 10^−4	0.58
x = 0.05		4 × 10^−7	7 × 10^−4	0.42
x = 0.10	0.08(2)	5.5 × 10^−6	1 × 10^−3	0.10
x = 0.15	0.14(2)	6 × 10^−6	1 × 10^−3	0.10
A = K
x = 0.05		8 × 10^−9	—	—
A = Li–Ga
x = 0.025 Li, 0.025 Ga		3 × 10^−8	—	—
x = 0.05 Li, 0.05 Ga		2 × 10^−10	—	—
x = 0.075 Li, 0.075 Ga		1 × 10^−10	—	—

---

Determination of the electronic conductivity of the HEOx samples

The evolution of the current density, during a 1 V potential step during 2 days with blocking electrodes, is presented in Fig. S3.† The first part is characterized by an important current decrease and is mainly due to the displacement of the ions or defects in the electrolyte. Then, once all ions are blocked at the interfaces and ionic transport has ended, a residual steady current corresponding to the sole electronic flow is measured in the last part of the curve.

An evaluation of the electronic conductivity was made for the samples with 0% Li and 30% Li. It is worth noting that both samples exhibit the same behaviour, which demonstrates that the Li content of the material has no effect on the electronic conductivity.

The stabilized current value (around 2 nA, for both HEOx samples) corresponds to the leakage current through the materials, and depends on the electronic conductivity of the sample. The electronic conductivity can be estimated from the following equation:

σ_e = eI/SΔE (1)

where e is the material thickness, S is the active surface, ΔE is the applied voltage, and I is the residual current intensity measured after 2 days. In our case, eqn (1) gives: σ_e = 2 × 10⁻⁹ S cm⁻¹, therefore we can conclude that these materials are electronical insulators.

Determination of the ionic conductivity of the HEOx samples

By using a Pt/HEOx/Pt cell configuration, the HEOx resistance, R_e, and capacitance, Q_e, were extracted from the impedance data by fitting the spectra (Fig. 1 shows selected samples; fitted spectra are shown in Fig. S8†). Fitting was performed using the classical R + R_e//Q_e + C electrical equivalent circuit shown in the inset of Fig. 1, where Q stands for a constant phase element (CPE), which takes the non-ideality of the capacitor into account (Z_CPE = 1/Q(jω)^α). Indeed, in the case of Li, Na or K-substituted HEOx, the metal–insulator–metal (MIM) behaviour is assumed to be the consequence of the displacement of free ionic charges (A⁺) in a static insulator host. This host matrix induces an electrical resistance to the motion of the A⁺ species. Then, the formation of a charge gradient gives rise to a capacitive phenomenon at the same time. The simultaneity of these two mechanisms can therefore be modelled by a resistance in parallel with a capacitance. Finally, the accumulation of charges at the blocking HEOx/Pt interfaces induces a pure capacitance behaviour, which can be easily observed in the low frequency range.^18–20

Fig. 1 Impedance spectra for HEOx samples with different contents of Li at 20 °C in the configuration Pt/HEOx/Pt. The inset shows the circuit model used for fitting.

Due to the high dielectric constant values of the HEOx family of compounds, especially at very low frequencies (see Fig. S5 and S6† and our previous work¹⁶), the space charge accumulation at the HEOx/blocking electrode interfaces is high, leading to a corresponding small impedance and a peculiar shape to the end part of the spectra (the imaginary part tends to zero instead of infinity). The difference between the blocking and non-blocking characters of the metal electrodes (Pt or Li) can be clearly seen in Fig. S5–S7.† Fitted plots are shown in Fig. S8 and S9.†

It is possible to calculate the ionic conductivity σ_i and the permittivity ε_r of each HEOx sample as a function of the alkali content. Moreover, EIS measurements over a temperature range (−20 °C to 80 °C), showed that the ionic conductivity follows the Arrhenius' law systematically. This allowed the determination of the corresponding activation energies, listed in Table 1 (Arrhenius plots are shown in Fig. S10†).

The activation energies do not exhibit any clear trend with respect to the fraction of the alkaline element, except for a decrease when going from low A⁺ fractions to high ones. This means that several distinct mechanisms could be involved. For low doping fractions, A⁺ ions and oxygen vacancies might be isolated, whereas they could form clusters for the highest fractions of dopant. Best fits are always obtained in the temperature window 20–80 °C, which is another indication that ionic mobility in these compounds is probably quite complex and may involve different mechanisms that are sensitive to both composition (oxygen vacancies) and temperature but with different trends.

In order to investigate the electrical properties of HEOx samples in a wide range of frequencies and temperatures, it is also possible to use the complex ionic conductivity, σ*, and the complex dielectric permittivity, ε*. This method allows the separation of the bulk conductivity and the electrode effect of the MIM cells, and makes it straightforward to observe the frequency dependence (and domain) of the ionic conductivity and permittivity.

σ* = [Y′(ω) + jY′′(ω)] = σ′(ω) + jσ′′(ω) (2)

where e is the sample thickness, S is the active surface, ω is the pulsation (ω = 2πf), Y′(ω) is the real part of the admittance, and Y′′(ω) is the imaginary part of the admittance (Y = 1/Z) and

ε* = σ*/jωε₀ = ε′(ω) − jε′′(ω) (3)

where ε₀ is the vacuum permittivity constant.

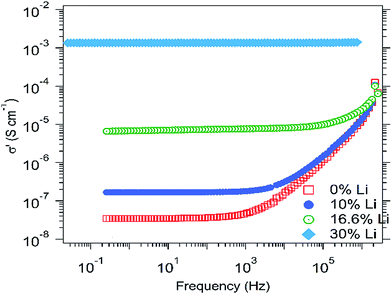
Finally, both complex conductivity and permittivity can be extracted from these two equations, and their respective real parts can be plotted as a function of the frequency in order to obtain the ionic conductivity curve and the dielectric permittivity curve, at different temperatures. Fig. 2 shows the ionic conductivity for HEOx 2% Li (Fig. S4–S6† show the results for undoped HEOx).

Fig. 2 Ionic conductivity of 2% Li doped HEOx at various temperatures.

According to the literature^21,22 these spectra can be divided into three parts. The high and medium frequency zones are mainly governed by the ionic motion in the material. For instance, at higher frequencies, the conductivity increases very rapidly while the permittivity reaches a stable limit (see Fig. S4–S6†), corresponding to a relaxed system without an electric field. Here, the ions tend to move non-randomly by carrying along their neighbours, in the manner of a jelly material.

In the medium frequency region, the conductivity is constant and corresponds to the calculated values (Table 1). Then, from high to medium frequencies, the permittivity curves exhibit a smooth and stable slope until reaching a limit, where suddenly the value noticeably increases. This point corresponds to the relative dielectric constant (ε′_r) of the HEOx material.

The low frequency region is governed by the electrode polarization. Indeed, with a low frequency perturbation signal, lithium ions tend to accumulate at the interface with the blocking electrodes, leading to a depletion of positive charges on the opposite metallic electrodes (platinum). This gives a drastic fall of the ionic conductivity and leads to a large polarization of the MIM cell.

Non-blocking MIM cells have also been built (A/HEOx/A, where A = Li, Na or K metal). Examples of the corresponding Nyquist plots are shown in Fig. 3 and dielectric permittivity evolution is shown in Fig. S6 and S7.† Theoretically, depending on the nature of the terminal electrodes (blocking or non-blocking), the behaviour of the material is different and the corresponding equivalent electrical circuit must take into account the interfacial processes. That is why, when platinum (blocking) electrodes are used, the equivalent circuit shows a terminal capacitor to take into account the polarization due to the accumulation of mobile ions at the interfaces (as previously mentioned), whereas when lithium (non-blocking) electrodes are used, the equivalent circuit exhibits a terminal R//C circuit to model the charge transfer process due to the exchange of lithium species through the interface.^23,24

Fig. 3 Nyquist plots for Li/HEOx/Li samples, measured at 20 °C. The inset shows the curves for 16.6% and 30% Li and the circuit model used for fitting.

Experimentally, on these Nyquist diagrams, we find again the R//Q relaxation due to the ionic conductivity and, as expected, at low frequencies, all diagrams systematically end on the real axis, which is consistent with the pure resistive behaviour of an ionic conductor where moving ions are not blocked at the interfaces. The low frequency region is no longer governed by the electrode polarization. Indeed, with a low frequency perturbation signal, alkali ions no longer accumulate at the interface with the metal electrodes since a redox reaction becomes possible: A⁺ + e⁻ = A. This can also be evidenced with the permittivity evolution at low frequencies (for Li containing samples, there is no increase, contrary to platinum blocking electrodes, Fig. S7†). However, this final process is less likely to be limiting compared to the first one (bulk ionic conductivity) and the corresponding resistance (R_tc) can be neglected since it represents here systematically less than 1% of the total resistance (R₂ + R_tc).

The influence of lithium content in HEOx materials on the observed CDC values has been already discussed in another paper.¹⁶ Here, we will focus on the effect of the alkali content on the ionic conductivity properties. However, we underline that the CDC exhibited by these materials can still be observed at high frequencies and that the largest values are observed in Li-free samples. This shows that the CDC behaviour cannot solely be explained by the ionic conductor character of these materials.

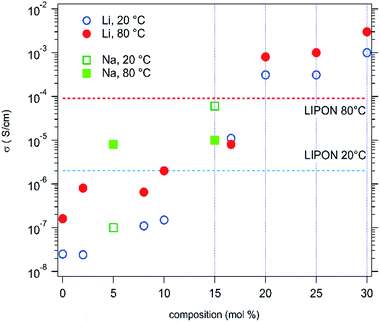
It is interesting to note that the conductivity increases with the lithium content in the materials (Fig. 4). At 20 °C, ionic conduction starts from 2 × 10⁻⁸ S cm⁻¹ with 0% Li and exceeds 1 × 10⁻³ S cm⁻¹ with 30% Li. These values are much larger than the electrical conductivity determined previously (σ_e = 2 × 10⁻⁹ S cm⁻¹), which shows that these materials are (almost) pure ionic conductors and that electrical leakage current can be neglected.

Fig. 4 Ionic conductivity of Li doped samples at room temperature.

Evolution is the same for sodium doped HEOx materials. The results, obtained for both alkali series, at 20 °C and 80 °C, are summarized in Fig. 5. The values usually observed for a LiPON solid conductor have also been reported for comparison. Thus, it can be seen that a better ionic conduction, at room temperature, is available with 16.6% Li. Much more interestingly, the room temperature Li⁺ conductivity of the compound with Li > 20% exceeds the ionic conductivity of LiPON by 2 orders of magnitude. At 80 °C the ionic conductivity values of the Li > 20% samples are still at least one order of magnitude larger than that exhibited by LiPON. This makes this new family of materials very attractive for applications as solid electrolytes.

Fig. 5 Ionic conductivities for Li and Na doped HEOx samples.

However, due to larger activation energies of LiPON only the compounds with more than 20% Li exhibit higher conductivities than LiPON at 80 °C. This probably originates from the ion conduction mechanism in these compounds, which do not exhibit a crystal structure with layers or channels.

For a better understanding of the ionic conduction mechanism, we performed 2 sets of experiments:

-A simultaneous substitution of the compounds with the same amount of lithium and gallium in order to compensate for the charge defaults inside the solid matrix (i.e. the decrease in the oxygen vacancies).

-A substitution with potassium instead of sodium or lithium (the ionic radius of potassium is larger than that of an oxygen vacancy, avoiding cationic conduction through such defaults).

The ionic conductivities for both sets of experiments are shown in Fig. 6. This sheds more light on the conduction mechanism since, for both sets, the conduction is systematically lower than that of 0% Li (σ < 2 × 10⁻⁸ S cm⁻¹), demonstrating that (small) alkali ions (Li and Na) are probably moving through the oxygen vacancies that have been created in the solid matrix by their incorporation during the synthesis, for charge compensation, as mentioned above. Potassium ions are likely too big to move through these vacancies (which explains the low conductivity measured) and a high gallium content prevents oxygen vacancies from being formed, which consequently leads to lower conductivity for the lithium ions in the co-doped material (Fig. 6).

Fig. 6 Ionic conductivity for 5% K and Li/Ga doped samples at 20 °C.

In these conditions, we show that a larger amount of alkali in the host matrix, leading to a larger number of oxygen vacancies (charge defaults), probably creates percolating channels. These voids (or channels) are better linked as the number of oxygen vacancies increases (which is also correlated with the estimated activation energies, Table 1) and are adequate for lithium or sodium ion motion, leading to fast ionic conductivity.

Experimental details

Synthesis

(Mg, Co, Ni, Cu, Zn)_1−xLi_xO, (Mg, Co, Ni, Cu, Zn)_1−xNa_xO, (Mg, Co, Ni, Cu, Zn)_1−2xLi_xGa_xO and (Mg, Co, Ni, Cu, Zn)_0.95K_0.05O samples were synthesized from binary oxides and carbonates, MgO, Co₃O₄, Ni₂O₃, CuO, ZnO, Ga₂O₃, Li₂CO₃, Na₂CO₃ and K₂CO₃.

Mg, Co, Ni, Cu, Zn cations were mixed in equimolar ratios. The starting powders, in stoichiometric amounts, were mechanically ground using a Fritsch Pulverisette 7 Premium Line with agate balls and vials at 250 rpm for 60 min. The resulting mixtures were then uniaxially pressed into 12 × 3 × 3 mm³ pellets under a pressure of 250 MPa, and were then heat treated at 1000 °C in air for 12 h before air quenching. The geometrical density of the samples was in the 75–80% range.

Characterisation

Room temperature X-ray diffraction (XRD) patterns were collected using a Panalytical X'Pert diffractometer with a Ge(111) incident monochromator (Cu-K_α1 radiation) and X'celerator detector. The resulting diffraction patterns were refined using FULLPROF software.²⁵

Chemical analysis was performed by inductively coupled plasma optical emission spectrometry (ICP-OES) using a Varian VISTA axial spectrometer. X-ray fluorescence analysis was performed by using a Panalytical MiniPal instrument equipped with a Rh X-ray tube.

The conduction properties of the materials were determined using a MIM cell configuration. First, platinum (Pt) was chosen as a chemically/electrochemically inert metal, able to lead to good blocking conditions. In this Pt/HEOx/Pt configuration, only the ion transport in the bulk (ionic conductivity) and the charge accumulation at the solid/solid interfaces (capacitance) are expected to contribute to the impedance spectra. Then, the same alkali metal (A) as contained in the HEOx sample was chosen as a non-blocking electrode. In this A/HEOx/A configuration, only the ion transport in the bulk (ionic conductivity) and the charge transfer at the solid/solid interfaces (redox reactions) are expected to contribute to the impedance spectra.

Electrochemical impedance spectroscopy (EIS) measurements were performed on two-probe MIM cells with a 500 mV AC perturbation in the frequency range from 2 MHz to 200 mHz (MMates 7260 Impedancemeter), at various temperatures between −20 °C and 100 °C (with 20 °C steps and a heating rate of 1 °C min⁻¹) in a Binder climatic chamber (accuracy ± 1 °C).

The cells were systematically kept at the chosen temperature for 15 min for stabilization before starting the EIS measurements. EIS spectra (normalized to sample dimensions which were typically S = 20 to 30 mm² and about 1 mm thickness) were fitted using the Zplot software (Scribner).

The electronic conductivity of the HEOx materials was determined by imposing a steady voltage of 1 V for 2 days (VMP3 BioLogic) to a Pt/HEOx/Pt cell and measuring the stabilized current flowing through the cell. This procedure allows the elimination of the transient contribution due to ionic transport.

Conclusions

High entropy oxides substituted with monovalent cations have been successfully synthesized. These new materials are superionic Li⁺ and fast-ionic Na⁺ conductors, with Li⁺ ionic conductivity that exceeds 10⁻³ S cm⁻¹ at room temperature. This value, which is more than 2 orders of magnitude larger than that encountered in LiPON and among the largest ever observed in oxides,^26,27 makes this new family of materials very promising for applications as solid state electrolytes, for example in all-solid-state batteries. The comparison of the ionic conductivities of Li⁺, Na⁺ and K⁺, together with those of low-oxygen-vacancy Li/Ga co-doped compounds, indicates that the ionic conduction probably occurs through the oxygen vacancies that are created by a charge compensation occurring when a monovalent element is introduced in the pristine compound. This shows that larger ionic conductivity values could probably be obtained by optimizing the concentration or ordering of oxygen vacancies as well as the size of the divalent cations in the compound.

Acknowledgements

We thank Dr Diana Dragoe (ICMMO) and Mr Remy Pires (ICMPE, Thiais) for chemical analysis, and acknowledge Tassadit Nait (ICMMO) for her help with sample elaboration.

Notes and references

1. G. Crabtree, Nature, 2015, 526, S92.
2. J. Motavalli, Nature, 2015, 526, S96.
3. L. Sebastian and J. Gopalakrishnan, J. Mater. Chem., 2003, 13, 433.
4. G. Nagasubramanian and D. H. Doughty, J. Power Sources, 2004, 136, 395.
5. P. G. Bruce, Chem. Commun., 1997, 1817.
6. C. Mariappan and G. Govindaraj, Solid State Ionics, 2005, 176, 1311.
7. M. Zahir, R. Olazcuaga and P. Hagenmuller, Mater. Lett., 1984, 2, 234.
8. A. Jolley, G. Cohn, G. T. Hitz and E. D. Wachsman, Ionics, 2015, 21, 3031.
9. X. Yu, J. B. Bates, G. E. Jellison Jr and F. X. Hart, J. Electrochem. Soc., 1997, 144, 524.
10. M. Nisula, Y. Shindo, H. Koga and M. Karppinen, Chem. Mater., 2015, 27, 6987.
11. M. Monchak, T. Hupfer, A. Senyshyn, H. Boysen, D. Chernyshov, T. Hansen, K. G. Schell, E. C. Bucharsky, M. J. Hoffmann and H. Ehrenberg, Inorg. Chem., 2016, 55, 2941.
12. W. S. Tang, M. Matsuo, H. Wu, V. Stavila, W. Zhou, A. A. Talin, A. V. Soloninin, R. V. Skoryunov, O. A. Babanova, A. V. Skripov, A. Unemoto, S.-I. Orimo and T. J. Udovic, Adv. Energy Mater., 2016 DOI:10.1002/aenm.201502237.
13. Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026.
14. J. R. Peet, C. M. Widdifield, D. C. Apperley, P. Hodgkinson, M. R. Johnson and I. R. Evans, Chem. Commun., 2015, 51, 17163.
15. C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J.-P. Maria, Nat. Commun., 2015, 6, 8485.
16. D. Bérardan, S. Franger, D. Dragoe, A. K. Meena and N. Dragoe, Phys. Status Solidi RRL, 2016, 10, 328–333.
17. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
18. N. Suzuki, S. Shirai, N. Takahashi, T. Inaba and T. Shiga, Solid State Ionics, 2011, 191, 49.
19. J. Bates, Solid State Ionics, 1992, 53, 647.
20. J. B. Bates, N. J. Dudney, G. R. Gruzalski, R. A. Zuhr, A. Choudhury and C. F. Luck, J. Power Sources, 1993, 43, 103.
21. J. C. Dyre, P. Maass, B. Roling and D. L. Sidebottom, Rep. Prog. Phys., 2009, 72, 46501.
22. J. R. Dygas, Solid State Ionics, 2005, 176, 2065.
23. J. Bauerle, J. Phys. Chem. Solids, 1969, 30, 2657.
24. R. D. Armstrong, T. Dickinson and J. Turner, J. Electroanal. Chem., 1973, 44, 157.
25. J. Rodriguez-Carvajal, Phys. B, 1993, 192, 55.
26. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140.
27. J. W. Fergus, J. Power Sources, 2010, 195, 4554.

---

Footnote

† Electronic supplementary information (ESI) available: Selected powder XRD data, Nyquist plots, EIS data, complex permittivity and ionic conductivity results. See DOI: 10.1039/c6ta03249d

---