Application of independent component analysis, principal component regression and partial least squares methodologies for the simultaneous potentiometric titration of some amino acids
A. Hakan Aktaş* and
Sermin Göksu Karagöz
Department of Chemistry, Faculty of Science & Art, Süleyman Demirel University, 32260, Isparta, Turkey. E-mail: hakanaktas@sdu.edu.tr
First published on 18th July 2016
Abstract
Potentiometric titration and chemometric methods were applied to the simultaneous determination of the four amino acids, alanine (ALA), phenylalanine (PHE), leucine (LEU) and lysine (LYS). The applied chemometric techniques are multivariate methods including principal component regression (PCR), partial least squares (PLS) and independent component analysis (ICA) methods. The developed methods were validated and successfully applied to the simultaneous determination of ALA, PHE, LEU and LYS in chicken samples. The assay results obtained using the chemometric methods were statistically compared to those of the HPLC method and good agreement was observed.
1 Introduction
The intensive development of biotechnology in various branches of industry, in particular, in the production of new medical research or biological fluids, or food additives containing amino acids, calls for a rapid procedure for simultaneous determination of amino acids. An analytical problem comprises the development of procedures for separating amino acid mixtures and quantitatively determining concentrations of individual components in solution.The simultaneous determination of different amino acids in solution is very important in diverse fields such as food chemistry, biochemistry and pharmaceutical formulations. Several kinds of samples are produced, and their amino acid contents, their chemical form, and the matrix of samples can be very different. There are various analytical techniques to determinate amino acids, including potentiometry,1–3 spectrophotometry,4–7 capillary electrophoresis,8–11 and liquid chromatography.12–16 High-performance liquid chromatography is favored method for amino acid analysis. Post-column fluorescent labeling reagents such as ninhydrin,17,18 dansyl chloride,19 and o-phtaldialdehyde (OPA),20,21 are developed for the HPLC analysis of different amino acids by using fluorescence detector. This method is accurate and reproducible; however, some drawbacks such as low sensitivity, long run times, and high instrument expenses make the post-column derivatization method unsuitable in many cases. For these samples, a simple and efficient way other than the expensive and time consuming HPLC methods, for the simultaneous determination of different amino acids will be useful.
The potentiometric titration method is all the time used for determining concentration of single amino acid in solution, but can barely be used for the simultaneous determination of several amino acids in the mixture.22,23 The potentiometric titration method corresponds to one of the more traditional areas of analytical chemistry, and they also have improved upon the application of chemometric techniques. For potentiometric titration, the application of chemometrics was first introduced by Lindberg and Kowalski24 for the simultaneous analysis of acids with partial least squares regression. Later on, several papers have been published using partial least squares (PLS), classical least squares (CLS) and principle component regression (PCR) calibration methods of acid–base titration,25 potentiometric precipitation titration26 and complexometric titration.27 In another example, an artificial neural network (ANN) model was applied to potentiometric titration data for the resolution of polybasic acid mixtures by Shamsipur et al.28 Additionally, we have studied a mixture of acid29 and mixtures thereof drugs30 in these studies.
The fast independent component analysis (fast-ICA) is a well-known linear modeling method;31,32 it is known for its computational complexity and precision prediction.33,34 It has been used in different areas, such as for: the interpretation of analytical responses from medicinal samples,35 kinetic spectrometric determination of antioxidants in fruit samples,36 image processing,37 monitoring of statistical results and resolution of overlapping spectra.38
Although there are many chemometric study the literature, there is no study about ICA, PCR and PLS chemometric methods for potentiometric determination of amino acids. The aim of the study were to develop a potentiometric titration method for the simultaneous analysis of some amino acids in foods, to investigate several chemometrics methods, including the ICA data pre-treatment algorithm, for the construction of the best performing calibration and prediction model and to compare the performance of the selected chemometric prediction model for the prediction of the some amino acids with results obtained from HPLC analysis.
2 Chemometric model
2.1 Independent component analysis (ICA) and its algorithms
ICA is a signal processing technique whose goal is to express a set of m measured variables x1, x2, …, xm as linear combinations of d (d ≤ m) statistically independent component variables s1, s2, …, sd.39 The relationship among the variables is captured by| X = AS + E | (1) |
| Ŝ = WX | (2) |
Many ICA algorithms are available for processing analytical chemistry data. For example, fast-ICA, infomax ICA, joint approximate diagonalization of eigen matrices (JADE), kernel ICA (KICA) and mean field ICA (MF-ICA). The fast-ICA algorithm was chosen in this work because it was demonstrated to be robust and fast to calculate.
3 Experimental
3.1 Reagent and solutions
The accuracy of amino acid analysis is highly dependent on the integrity of the samples. Cleaning up of all surfaces of the sample contact is so important hence purity of all reagents were ensured. Alanine, phenylalanine, leucine, lysine and OPA standard solution were purchased from Sigma Chemical Company. HPLC-grade acetonitrile and methanol were obtained from Merck, ultrapure water was generated using a Milli-Q water purification system. All other chemicals were of the purest grade available commercially.OPA reagent was prepared 24 h before use by dissolving 27 mg o-phtaldialdehyde in 500 μL ethanol. After that 5 mL of 0.1 M sodium tetraborate (Na2B4O7·10H2O) (pH 9.5) was added, followed by 50 μL 2-mercaptoethanol. The mixture was properly mixed and stored in a tightly closed container in the dark. The OPA reagent can be kept for several days with periodic additions of 20 μL 2-mercaptoethanol to maintain the yield of OPA amino acid derivatives.41
All the solutions were prepared in 0.1 M potassium chloride to keep the ionic strength constant. The calibration of the electrode system was done potentiometrically by Gran's method.42
3.2 Apparatus
The titrations were conducted in batch mode with magnetic stirrer and the glass vessels, which were standard equipments. Measurement of pH were carried out with a Mettler Toledo MPC 227 Microprocessor pH meter by using a combined pH electrode was used. All experiments were performed at room temperature about 25 °C ± 0.1 °C. The HPLC analyses were carried out using Shimadzu class LC-vp HPLC system with class SCL-10Avp software, a pump (LC-10Advp), an auto sampler (SIL-10Advp, 70 vial Model Rack 7), photodiode array detector (SPD-M 10Avp) (PDAD), column oven (CT0 10Avp) and gas removing unit (DGU 14A). The column used was a Zorbax Eclipse C18 column 5 μm 4.6 × 250 mm. The flow rate was maintained at 2.0 mL min−1, and the injection volume was 20 μL.3.3 Preparation of chicken samples
Taken as a whole chicken, sliced 1–2 mm thick samples prior to analysis, then approximately 2 × 2 mm in size were ready to break down the analysis. Sliced-shredded chicken samples were placed into jars and maintained 4 °C.4.0 grams of chicken and 40 mL of 0.1 N HCl were blended for 45 seconds at 4 °C using a ultra turrax homogenizer. The extract was then transferred to a 100 mL volumetric flask, and the jar was rinsed at least three times with enough 0.1 N HCl. Homogenized samples were stored for 12 hours at 4 °C. The content of the flask was transferred to a centrifuge tube and centrifuged at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 50 min at 4 °C. The supernatant was used for the analysis after filtration with a 0.20 μm membrane filter. Chromatograms of the resulting solutions were plotting as time versus detector response. When necessary, filtered sample extracts were stored in a freezer at −20 °C.
000 rpm for 50 min at 4 °C. The supernatant was used for the analysis after filtration with a 0.20 μm membrane filter. Chromatograms of the resulting solutions were plotting as time versus detector response. When necessary, filtered sample extracts were stored in a freezer at −20 °C.
3.4 Potentiometric titration procedure
The determination of amino acids in synthetic real samples were nominated by titration, using NaOH solution as titrant, according to the criteria endorsed by IUPAC.43For this purpose, an estimated amount of solution at the same conditions as temperature, ionic strength and solvent composition (hereafter will be called background solution) was placed in a double-walled, thermo stated vessel. The potential was allowed to stabilize after each addition of acid or base and then value was used to obtain the standard potential of the cell called Eo. The electrode was immersed in background solution and titrated with a strong base in the same experimental conditions of ionic strength and solvent composition. In order to verify determination of Eo accurately, in general, 18 or 20 additions were enough. In second step, an aliquot of sample containing between 4 and 36 ppm of the amino acids (alone or in mixtures) was titrated by sodium hydroxide. For real sample; an amount volume of food sample was added to the cell and titrated by base.
3.5 Classical HPLC method
The multiwavelength chromatograms a for ALA 20–36 μg mL−1, for PHE 8–24 μg mL−1, for LEU 4–20 μg mL−1 and for LYS 8–24 μg mL−1 and for IS 20 μg mL−1 were plotted by using diode array detector obtained at the five wavelengths. The detector responses were measured in terms of peak area. Amino acids were derivatives with OPA and detected by a diode array detector. To 50 μL of amino acid standard or diluted sample supernatant was added 100 μL of OPA, followed by thorough mixing using a vortex. The OPA reagent and sample are in contact for precisely 2 min prior to the injection. After derivatization, an amount equivalent to 20 μL of each sample was injected on a Zorbax Eclipse-AAA column, 5 μm, 150 × 4.6 mm (Agilent), at 40 °C, with detection at λ = 338 nm. In fact several mobile phase and other chromatographic conditions were found to be suitable for the separation and determination of ALA, PHE, LEU and LYS in their mixtures. Mobile phase A was 15 mM NaH2PO4, adjusted to pH 7.8 with 10 N NaOH, while mobile phase B was acetonitrile/methanol/water (45/45/10 v/v/v). The separation was obtained at a flow rate of 2 mL min−1 with a gradient program. Retention times were 21.0 min for ALA, 28.1 min for PHE, 28.5 min for LYS, 33.0 min for LEU and 26.3 min for IS (Fig. 1).For the calibration, the ratios of the peak areas ALA/IS, PHE/IS, LEU/IS and LYS/IS were computed by using the values achieved for the give five wavelengths set 326 nm, 330 nm, 334 nm, 338 nm and 342 nm that shown Table 1.
| No. | Training set, μg mL−1 | The ratio peak area (ALA/IS) | The ratio peak area (PHE/IS) | The ratio peak area (LEU/IS) | The ratio peak area (LYS/IS) | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ALA | PHE | LEU | LYS | IS | 326 | 330 | 334 | 338 | 342 | 326 | 330 | 334 | 338 | 342 | 326 | 330 | 334 | 338 | 342 | 326 | 330 | 334 | 338 | 342 | |
| 1 | 20 | 8 | 4 | 8 | 20 | 1.3404 | 1.3294 | 1.3157 | 1.3065 | 1.3049 | 0.2901 | 0.2923 | 0.2948 | 0.2961 | 0.2968 | 0.2208 | 0.2226 | 0.2238 | 0.2258 | 0.2272 | 0.1942 | 0.1915 | 0.1879 | 0.1838 | 0.1809 |
| 2 | 24 | 12 | 8 | 12 | 20 | 1.5874 | 1.5743 | 1.5555 | 1.5474 | 1.5465 | 0.4235 | 0.4275 | 0.4315 | 0.4343 | 0.4355 | 0.4042 | 0.4051 | 0.4063 | 0.4071 | 0.4078 | 0.3260 | 0.3229 | 0.3158 | 0.3092 | 0.3076 |
| 3 | 28 | 16 | 12 | 16 | 20 | 1.8552 | 1.8414 | 1.8252 | 1.8137 | 1.8101 | 0.5654 | 0.5696 | 0.5743 | 0.5777 | 0.5795 | 0.5890 | 0.5898 | 0.5904 | 0.5912 | 0.5926 | 0.4742 | 0.4699 | 0.4613 | 0.4519 | 0.4466 |
| 4 | 32 | 20 | 16 | 20 | 20 | 2.1050 | 2.0790 | 2.0652 | 2.0542 | 2.0498 | 0.7153 | 0.7199 | 0.7222 | 0.7258 | 0.7267 | 0.7546 | 0.7552 | 0.7561 | 0.7578 | 0.7582 | 0.6345 | 0.6297 | 0.6180 | 0.6062 | 0.6034 |
| 5 | 36 | 24 | 20 | 24 | 20 | 2.3922 | 2.3706 | 2.3430 | 2.3302 | 2.3298 | 0.8423 | 0.8654 | 0.8506 | 0.8536 | 0.8554 | 0.9365 | 0.9370 | 0.9376 | 0.9391 | 0.9411 | 0.7791 | 0.7751 | 0.7620 | 0.7499 | 0.7416 |
The calculated linear regression functions and statistical parameters were shown in Table 2. The correlation of coefficients of regression equations were generally higher than 0.99. The slope and correlation coefficient values for the classical HPLC calibration graphs at 338 nm were found suitable than those at the wavelengths. For this reason, calculated calibration equations chosen for analyzed procedure of four amino acids.
| Amino acid | λ nm | Equation | r | Sa | LOD (μg mL−1) | LOQ (μg mL−1) |
|---|---|---|---|---|---|---|
| a Sa: standard error of intercept, C: concentration (μg mL−1), A: peak area, r: regression coefficient. | ||||||
| ALA | 326 | A = 0.0655C + 0.0212 | 0.9994 | 0.0272 | 0.6048 | 1.8327 |
| 330 | A = 0.0647C + 0.0280 | 0.9990 | 0.0334 | 0.7531 | 2.2820 | |
| 334 | A = 0.0649C + 0.0258 | 0.9994 | 0.0257 | 0.5868 | 1.7782 | |
| 338 | A = 0.0639C + 0.0224 | 0.9995 | 0.0240 | 0.5436 | 1.6474 | |
| 342 | A = 0.0638C + 0.0209 | 0.9994 | 0.0267 | 0.6018 | 1.8236 | |
| LEU | 326 | A = 0.0445C + 0.0465 | 0.9997 | 0.0062 | 0.4326 | 1.3109 |
| 330 | A = 0.0445C + 0.0483 | 0.9997 | 0.0060 | 0.4230 | 1.2818 | |
| 334 | A = 0.0444C + 0.0496 | 0.9997 | 0.0058 | 0.4106 | 1.2444 | |
| 338 | A = 0.0444C + 0.0510 | 0.9998 | 0.0052 | 0.3721 | 1.1276 | |
| 342 | A = 0.0445C + 0.0519 | 0.9997 | 0.0055 | 0.3919 | 1.1876 | |
| LYS | 326 | A = 0.0370C − 0.1097 | 0.9999 | 0.0113 | 0.7518 | 2.2781 |
| 330 | A = 0.0368C − 0.1197 | 0.9999 | 0.0189 | 0.7621 | 2.3094 | |
| 334 | A = 0.0363C − 0.1111 | 0.9989 | 0.0118 | 0.7982 | 2.4186 | |
| 338 | A = 0.0357C − 0.1114 | 0.9988 | 0.0122 | 0.8395 | 2.5441 | |
| 342 | A = 0.0354C − 0.1109 | 0.9988 | 0.0120 | 0.8318 | 2.5205 | |
| PHE | 326 | A = 0.0349C + 0.0089 | 0.9994 | 0.0083 | 0.5814 | 1.7617 |
| 330 | A = 0.0360C + 0.0005 | 0.9996 | 0.0095 | 0.4615 | 1.3984 | |
| 334 | A = 0.0351C + 0.0138 | 0.9996 | 0.0072 | 0.4951 | 1.5003 | |
| 338 | A = 0.0352C + 0.0149 | 0.9995 | 0.0085 | 0.5200 | 1.5757 | |
| 342 | A = 0.0352C + 0.0154 | 0.9996 | 0.0070 | 0.4911 | 1.4882 | |
4 Results and discussion
In the conventional acid–base titration system, the endpoints are routinely determined by indicators. But, for acid mixtures when the ΔpK between any two acids is less than 3–4 logarithmic units, the titration curve will be overlapped and it will make the determination of endpoint more difficult. These four amino acid pK values used in this study are given in Table 3.44 As can be seen in Table 3 that pK of all four species are extremely close and much less than 3–4 units. In the conventional titration method, the titration curve of these amino acids will be overlapped and affected each other. Under these conditions, multivariate calibration methods could be used to the pH titration for the simultaneous determination of amino acids in mixtures and offer the advantage of eliminating preliminary separation steps.| pK1 | pK2 | |
|---|---|---|
| Amino acid | (α-COOH) | (α-NH3+) |
| Alanine | 2.4 | 9.9 |
| Phenylalanine | 2.2 | 9.2 |
| Leucine | 2.3 | 9.7 |
| Lysine | 2.2 | 9.3 |
4.1 Chemometric analysis of synthetic amino acids mixtures
Fig. 2 shows the titration curves of the synthetic amino acids in mixtures. It can be seen that there are highly overlapping curves, hence, the determination of each amino acid is not possible by traditional method. The results of ICA, PCR and PLS were obtained by potentiometric titration.The multivariate calibration process requires a training data set, with the inclusion of the known concentration of each amino acids and the corresponding pH titration spectrum of that sample. Then some of the multivariate calibration techniques such as PCR or PLS were applied to construct a mathematical model. The established model can be efficiently used to predict the concentrations of unknown mixtures. The calibration sets for multivariate calibration were prepared according to orthogonal array design.25 A four-level orthogonal array design method, denoted by OA16(44), was selected in this work in order to obtain maximum information on each amino acids from the calibration procedure. The main advantage of this design method is that a large amount of quantitative information of components to be analyzed can be extracted by using only a few experimental trials.
A four-level orthogonal array design, which was used for the construction of a calibration set that total twenty samples, and the concentration matrix was expressed as C(20 × 4). The concentration levels were in ranges of 20–36, 8–24, 4–20 and 8–24 μg mL−1 for alanine, phenylalanine, leucine and lysine, respectively. Each of the calibration samples were submitted to perform the potentiometric titration according to the experimental procedure described in section potentiometric titration procedure, pH data matrix denoted by A(20 × 21) was then obtained. To verify the established chemometric models, another unknown set of mixtures of 20 amino acids were prepared and submitted to potentiometric titration measurements as above, and a data matrix of this verification set, Aunknown(20 × 21), was also obtained.
Thus, the fast-ICA was used for data pre-treatment on the above data sets, and initially, the input data was quantized with the use of the fixed-point toolbox in STATISTICA, which reconstructed the matrices A(calibration) and Aunknown(verification) and then produced two new matrices, MICA(n × i) and MICAunknown(n × i), where n is the sample number of calibration or prediction set (i stands for fixed-point numbers). It is important to select the optimal number of fixed-points for the fast-ICA, so that preferential results can be obtained. MICA(n × i) was then used to established calibration models were then used in PCR and PLS methods. These models were then applied for the prediction of the confirmation samples (the MICAunk matrix data). Later on three different types of chemometric model, ICA-PLS, PLS and PCR, were applied for the prediction of amino acids with the use of the above data matrix.
PCR and PLS are factor analysis method, based on a two-stage procedure; a calibration step, in which a mathematical model is built by using component concentrations and spectral data from a set of references, followed by a prediction step in which the model is used to calculate the concentrations unknown sample from its spectrum. These methods are also called “factor methods” because they transform the original variables into a smaller number of orthogonal variables called factors or principal components (PCs), which are linear combinations of the original variables. When multivariate calibration approaches are applied in spectrophotometric multicomponent analysis, a relationship between spectral and concentration data from reference samples, representing the variables of the system, is established. A new matrix constituted by the new variables PCs and scores is built. The calculation of this new matrix is planned by algorithm specific to the regression method adopted. The most used regression method is PLS in calibration methods. The theory of such techniques has been fully described by several authors.45–48
The predictive applicability of a model can be defined in various ways. The most general expressions is the root mean square error of validation (RMSEV), which is given by following equation:
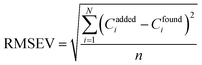 | (3) |
| RMSEV | RMSEC | r | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Fast-ICA/PLS | PCR | PLS | Fast-ICA/PLS | PCR | PLS | Fast-ICA/PLS | PCR | PLS | |
| ALA | 0.12 | 0.27 | 0.28 | 0.28 | 0.55 | 0.46 | 0.9966 | 0.9664 | 0.9801 |
| PHE | 0.09 | 0.13 | 0.09 | 0.21 | 0.44 | 0.16 | 0.9982 | 0.9758 | 0.9968 |
| LEU | 0.07 | 0.14 | 0.20 | 0.18 | 0.36 | 0.37 | 0.9998 | 0.9769 | 0.9837 |
| LYS | 0.05 | 0.06 | 0.28 | 0.24 | 0.40 | 0.42 | 0.9954 | 0.9812 | 0.9830 |
In Table 4, r is defined as the correlation between substituent concentrations and shows the potentiometric respond effects relating to the constituent of interest. The r values obtained in the method fast-ICA/PLS close to 1 mean to no interference was coming from the other constituents in this set of synthetic mixtures.
Another value is the root mean square error of calibration (RMSEC) and the calculation of this value was realized using following equation:
 | (4) |
Prediction results for the three chemometric methods (Table 4), clearly demonstrate that three methods performed similarly. Presumably, on the basis of the RMSEV and RMSEC, when the potentiometric data were pretreated by the fast-ICA and then submitted to PLS analysis, the prediction performance was better. Here by, this calibration model was chosen for the simultaneous determination of the four amino acids in chicken samples.
4.2 Analysis of amino acids in chicken samples
To investigate the performance of the analytical method with random samples, several fresh chicken samples were purchased locally and analyzed for the four amino acids with the aid of the fast-ICA data pretreatment and the PLS method. The chicken pretreatment procedure was previously described Section 3.3 preparation of chicken samples. The results obtained with the use analytical method were compared with those from the HPLC reference analysis in Table 5.| ALA (μg g−1) | PHE (μg g−1) | LEU (μg g−1) | LYS (μg g−1) | |||||
|---|---|---|---|---|---|---|---|---|
| Fast-ICA/PLS | Classical HPLC | Fast-ICA/PLS | Classical HPLC | Fast-ICA/PLS | Classical HPLC | Fast-ICA/PLS | Classical HPLC | |
| a SD: standard deviation, RSD: relative standard deviation. | ||||||||
| 1 | 1460 | 1474 | 438 | 440 | 310 | 321 | 524 | 532 |
| 2 | 1466 | 1484 | 440 | 448 | 302 | 328 | 520 | 515 |
| 3 | 1462 | 1478 | 438 | 451 | 312 | 332 | 518 | 519 |
| Mean | 1463 | 1479 | 439 | 446 | 308 | 327 | 521 | 522 |
| SD | 3.05 | 5.03 | 1.15 | 5.69 | 5.29 | 5.57 | 3.05 | 8.89 |
| RSD | 0.21 | 0.34 | 0.26 | 1.27 | 1.72 | 1.70 | 0.59 | 1.70 |
5 Conclusions
A rapid, sensitive method for the simultaneous determination of four amino acids in chicken samples were developed with the use of potentiometric titration. The results indicated that the analytical method, simple and cheaper produced substantially improved analytical results for chicken samples in comparison to those produced by the common HPLC technique. Although the HPLC method is more specific than the chemometric spectrophotometric methods, HPLC methods need expensive equipment and materials such as columns and HPLC grade solvents. Chemometric methods are less expensive methods and they do not require sophisticated instrumentation and any prior separation step. This can be considered a superiority of these chemometric techniques over HPLC. On the other hand chemometric methods need software for resolution and determination of active ingredients in the mixtures. The chemometric methods could be proposed as powerful procedure for the simultaneous analysis of multicomponent mixtures in which the potentiometric spectra of the active compounds overlap each other.Acknowledgements
The authors would like to acknowledge financially supported by Süleyman Demirel University Research Foundation (Project No. 2054-D-09).References
- S. S. Khaloo, M. K. K. Amini, S. Tangestaninejad, S. Shahrokhian and R. Kia, J. Iran. Chem. Soc., 2004, 1, 128 CrossRef CAS.
- M. H. Moustafa, Ass. Univ. Bull. Environ. Res., 2005, 8, 81 Search PubMed.
- A. Martovic, S. C. Stefenovic and N. Radic, J. Chem. Metrol., 2008, 2, 1 Search PubMed.
- D. A. M. Zaia, K. C. L. Ribas and C. T. B. V. Zaia, Talanta, 1999, 50, 1003 CrossRef CAS PubMed.
- G. Fang and N. Liu, Anal. Chim. Acta, 2001, 445, 245 CrossRef CAS.
- C. Yin, Y. Shen, S. Liu, Q. Yin, W. Gua and Z. Pan, Comput. Chem., 2001, 25, 239 CrossRef CAS PubMed.
- M. H. Sorauaddin, M. R. Rashid, E. G. Kalhor and K. E. Zeynali, Il Farmaco, 2005, 60, 451 CrossRef PubMed.
- N. Novatchev and U. Holzgrabe, J. Pharm. Biomed. Anal., 2001, 26, 779 CrossRef CAS PubMed.
- W. J. M. Underberg and J. C. M. Waterval, Electrophoresis, 2002, 23, 3922 CrossRef CAS PubMed.
- M. Jaworsko, Z. Szulinsko and M. Wilk, J. Chromatogr. A, 2003, 993, 165 CrossRef.
- Q. Qu, X. Tang, C. Wang, G. Yong, X. Hu, X. Lu, Y. Liu, S. Li and C. Yan, Anal. Chim. Acta, 2006, 576, 212 CrossRef PubMed.
- F. R. Antoine, C. I. Wei, R. C. Littell, B. P. Quinn, A. D. Hogle and M. R. Marshall, Food Chem. Toxicol., 2001, 66, 72 CAS.
- R. I. Khan, R. Onodera, M. R. Amin and N. Mohammed, Amino Acids, 2002, 22, 167 CrossRef CAS PubMed.
- R. W. Peace and G. S. Gilani, J. AOAC Int., 2005, 88, 877 CAS.
- M. P. Bartolomeo and F. Maisana, J. Biomol. Tech., 2006, 17, 131 Search PubMed.
- E. Barrado, J. A. Rodriguez and V. Castrillejo, Talanta, 2009, 78, 672 CrossRef CAS PubMed.
- J. Le Boucher, C. Charret, C. C. Lucas, J. Giboudeau and L. Cynober, Clin. Chem., 1997, 43, 1421 CAS.
- M. Zhao, Y. Ma, L. L. Dai, D. L. Zhang, J. H. Li, W. X. Yuan, Y. L. Li and H. J. Zhou, Food Anal. Methods, 2013, 6, 69 CrossRef.
- H. P. Chen, L. Chen, Y. M. Wei and Y. L. Zheng, Chin. J. Anal. Chem., 2005, 33, 1689 CAS.
- M. Roth and A. Hompai, J. Chromatogr., 1973, 83, 353 CrossRef CAS PubMed.
- P. Linderoth and K. Mopper, Anal. Chem., 1979, 51, 1667 CrossRef.
- T. Michalowski, M. Toporek and M. Rymanowski, Talanta, 2005, 65, 1241 CrossRef CAS PubMed.
- Y. N. Ni and S. Kokot, Anal. Chim. Acta, 2008, 626, 130 CrossRef CAS PubMed.
- W. Lindberg and B. Kowalski, Anal. Chim. Acta, 1988, 206, 125 CrossRef CAS.
- Y. N. Ni, Anal. Chim. Acta, 1998, 367, 145 CrossRef CAS.
- Y. N. Ni and A. G. Wu, Anal. Chim. Acta, 1999, 390, 117 CrossRef CAS.
- Y. Zhang, J. Sun, X. T. Yu and T. H. Li, Chin. J. Anal. Chem., 2005, 33, 1764 CAS.
- M. Shamsipur, B. Hemmateenejad and M. Akhond, Anal. Chim. Acta, 2002, 461, 147 CrossRef CAS.
- A. H. Aktaş and S. Yaşar, Acta Chim. Slov., 2004, 51, 273 Search PubMed.
- A. H. Aktaş and G. P. Ertokuş, J. Serb. Chem. Soc., 2008, 73, 87 CrossRef.
- A. Hyvärinen, P. O. Hoyer and M. Inki, Neural Comput., 2001, 13, 1527 CrossRef PubMed.
- A. Hyvärinen, IEEE Trans. Neural Network., 1999, 10, 626 CrossRef PubMed.
- A. Hyvärinen and E. Oja, Neural Comput., 1997, 9, 1483 CrossRef.
- L. De Lathauwer, B. De Moor and J. Vandewalle, J. Chemom., 2000, 14, 123 CrossRef CAS.
- S. Makeig, Science, 2002, 295, 690 CrossRef CAS PubMed.
- R. Sun, Y. Wang, Y. Ni and S. Kokot, Spectrochim. Acta, Part A, 2014, 122, 529 CrossRef CAS PubMed.
- S. Javidi, C. C. Took and D. P. Mandic, IEEE Trans. Neural Network., 2011, 22, 1967 CrossRef PubMed.
- J. M. Lee, C. K. Yoo and I. B. Lee, Process Contr., 2004, 15, 467 CrossRef.
- A. Palazoğlu, X. Yan and C. Tong, Chemom. Intell. Lab. Syst., 2014, 135, 141 CrossRef.
- A. Hyvärinen and E. Oja, Neural Networks, 2000, 13, 411 CrossRef.
- M. H. Joseph and C. A. Marsden, A Practical Approach, ed. C. K. Lim, IRL, Oxford, U.K., 1986, pp. 13–28 Search PubMed.
- G. Gran, Analyst, 1952, 7, 661 RSC.
- P. R. Mussini, T. Mussini and S. Rondinini, Pure Appl. Chem., 1997, 69, 1007 CrossRef CAS.
- R. K. Murray, D. K. Granner, P. A. Mayes and V. M. Rodwell, Harper's Illustrated Biochemistry, Lange medical Books/McGraw-Hill, 26th edn, 2003, pp. 15–17 Search PubMed.
- J. Zupan and J. Gastreiger, Neural Networks in Chemistry and Drug Design, VCH, 1993 Search PubMed.
- H. Wold, Research Paper in Statistics, Wiley, New York, 1996 Search PubMed.
- E. Dinç, D. Balenau, G. Ioele, M. De Luca and G. Ragno, J. Pharm. Biomed. Anal., 2008, 48, 1471 CrossRef PubMed.
- M. De Luca, F. Oliveria and G. Ragno, Chemom. Intell. Lab. Syst., 2009, 96, 14 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |


