Interactions of Pt nanoparticles with molecular components in polymer electrolyte membrane fuel cells: multi-scale modeling approach†
Giuseppe F. Brunelloa,
Ji Hye Leeb,
Seung Geol Lee*b,
Ji Il Choia,
David Harveyc and
Seung Soon Jang*ade
aComputational NanoBio Technology Laboratory, School of Materials Science and Engineering, Georgia Institute of Technology, 771 Ferst Drive NW, Atlanta, GA 30332-0245, USA. E-mail: SeungSoon.Jang@mse.gatech.edu; Fax: +1-404-894-9140; Tel: +1-404-385-3356
bDepartment of Organic Material Science and Engineering, Pusan National University, 2, Busandaehak-ro 63beon gil, Geumjeong-gu, Busan 46241, Republic of Korea. E-mail: seunggeol.lee@pusan.ac.kr; Fax: +82-51-512-8175; Tel: +82-51-510-2412
cBallard Power Systems, 9000 Glenlyon Parkway, Burnaby, BC V5J 5J8, Canada
dInstitute for Electronics and Nanotechnology, Georgia Institute of Technology, Atlanta, GA, USA
eParker H. Petit Institute for Bioengineering and Bioscience, Georgia Institute of Technology, Atlanta, GA, USA
First published on 18th July 2016
Abstract
In this study, a three-phase interfacial system of a fuel cell is simulated using a multi-scale simulation approach consisting of quantum mechanical density functional theory and molecular dynamics simulations. Through these simulations, the structural and transport properties of the three-phase system are investigated. The molecular interactions among the components of the three-phase interfacial system are examined by density functional theory and parameterized for potential energy functions of force field. First, we investigate the interactions of the Pt clusters with various molecules as a function of distance using the density functional theory method with dispersion correction. Based on the results of these calculations, a non-bonded interaction curve is built for each Pt–molecule pair. Such non-bonded interaction curves are reproduced by potential energy functions with optimized parameters. Based on these investigations, we develop a force field to describe the structures and transport properties of the Nafion–Pt–carbon (graphite) three-phase interfacial system using molecular dynamics simulations.
Introduction
There has been strong interest in nanosized metal particles, owing to their engineering importance,1 which stems from their distinctly different properties compared to the bulk phase. This size-dependent difference in properties is also valid for various transition metals.2 In particular, despite their high price, Pt nanoparticles are considered as the catalyst of choice for fuel cells owing to their excellent catalytic activities. Therefore, theoretical and computational investigations3 as well as experimental studies4 have been performed extensively to obtain a fundamental understanding on the size-dependent properties of Pt nanoparticles, with the aim of maximizing the benefits from the use of such precious metals.Compared to experimental methods, theoretical and computational approaches may have a unique advantage in tackling small systems with dimensions of nanometer-scale. In the latter methods, the atomic structures and corresponding properties are examined directly. Lee et al.3g investigated Pt2 molecules using Kramers restricted ab initio calculations and determined that dynamic and non-dynamic electron correlation effects are required to obtain reliable spectroscopic data. Varga et al.3a found that relativistic effects should be considered in order to calculate accurate binding energy values for diatomic molecules of heavy metals using relativistic density functional theory (DFT). Grönbeck and Andreoni3b studied neutral and anionic Pt clusters of various shapes up to Pt5 using SLDA and BLYP. Based on their DFT calculations, they found that 3-D geometries are unfavorable up to Pt5 clusters. Similarly, through a DFT study on 70 Pt clusters of various sizes and shapes using PW91 and plane wave basis set, Xiao and Wang3e found that the planar shape is preferred for small clusters of up to 9 atoms. In addition, they found that the layered Pt clusters are very stable compared to closed-packed spherical shapes. This observation has also been validated by several research groups.3f,5 However, by examining the effect of spin–orbit interactions on Ptn (n = 4–6) using B3LYP, Sebetci6 reported that the 3-D geometries are energetically preferred, which conflicts with previous reports.3b,d,e,5 Using BPW91 and effective core potential, Aprà and Fortunelli3d reported that Ptn (n = 13, 38, and 55) starts developing metallic characteristics and Pt55 favors the icosahedral geometry (Ih), whereas Pt13 favors the D4h geometry. Chepulskii and Curtarolo7 calculated the energies of various common Pt nanoparticle shapes as a function of size up to 400 atoms using various GGA functionals and plane wave basis set. From such large cluster calculations, they found that the surface energy depends on the lattice parameters. They also suggested that the bulk surface energies are valid only for nanoparticles with diameters greater than 1.46–1.57 nm.
Although there are numerous studies on Pt nanoparticles, the interaction of Pt nanoparticles with other molecular species has received relatively little attention. This may be mostly due to the difficulties associated with experimentally probing molecular interactions at the nanometer scale. Langenbach et al.8 found that water molecules are adsorbed on Pt (111) surfaces via oxygen using IR-reflection and UV-photoemission, and Michaelides et al.9 confirmed that water adsorption occurs on the on-top sites of the Pt (111) surface using PW91 and plane wave basis set. Huang and Balbuena10 used molecular dynamic (MD) simulations to study Pt nanoparticles with spherical and cubic shapes containing 256–260 atoms on graphite. They found that in the case of nanoparticles, a melting-like structural transformation is observed at a temperature that is much lower (∼1000 K) than the bulk melting temperature (2045.15 K).
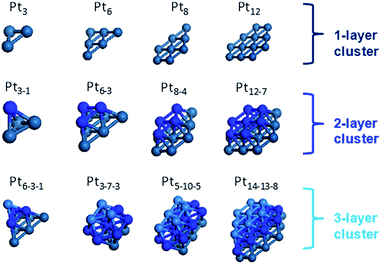
Thus, our primary objective in this simulation study is to model the Pt nanoparticle with various molecular species in a polymer electrolyte membrane fuel cell (PEMFC) and to elucidate the detailed interactions between the main components of PEMFC. First, we used density functional theory (DFT) to study Pt nano-clusters as used in PEMFCs. We tested the various Pt nanoparticles to obtain their most probable energy state with normalized cohesive energy (NCE) calculations. Based on these results, we developed a coordination number (CN) model to evaluate the energy of a cluster. Our model correctly predicted the energy of various facets of Pt surface. The CN model captures the surface energy reasonable well, especially for the (111) surface. Consequently, we have probed the various moieties of the electrolyte with Pt (111) surface to obtain the interaction, position and conformation of the adsorbed species. From this, we developed a force field for use in molecular dynamics (MD) simulations describing the three-phase interface (Pt–graphite–electrolyte) of the PEMFC system. Using the newly developed a force field, we successfully described diffusion of oxygen in three-phase model which contains a Pt cluster on top of graphite.
Computational details
In order to investigate the electronic structures and interactions of Pt nanoparticle with various sizes and shapes, we used spin-unrestricted density functional theory (DFT) through Jaguar11 by employing three widely used functionals, namely M06,12 PBE,13 and B3LYP14 with LACVP** basis set containing 6-31G** and LANL2DZ effective core basis sets15 (Fig. 1). We also used spin-unrestricted periodic DFT through CASTEP16 and DMol3 (ref. 17) implemented in Materials Studio18 with PBE functional and plane wave basis set. All the geometries shown in Fig. 1 are optimized by DFT calculations. The electronic structure of the Pt particles depends on both the size as well as the shape of the particles. Consequently, different clusters have different multiplicities and energy values. For such DFT calculations, we started with an initial guess value for the spin state, using the method described by the spin guesser from Goddard.19 Then, we simulated various multiplicities around this initial guess until we arrived at the lowest energy value, which turned out that various functionals agree with the multiplicity showing the lowest energy.From these results, we found that that the stability of the Pt nanoparticle increases with increasing the particle size, and that the two-layer and three-layer Pt nanoparticles have nearly the same stability to each other. Using this information, we selected a highly stable model of Pt nanoparticles to develop a force field describing the interaction between the Pt nanoparticles and molecules. To obtain force fields describing the interaction of the molecular species with Pt, we optimized the force field parameters in the Morse potential to reproduce the DFT energies and structures.
After developing a force field for the Nafion–Pt interactions, we built a model for the three-phase system of the PEMFC for the MD simulation. For the MD simulations, we utilized the DREIDING force field20 and F3C water model,21 which have been used widely to describe hydrated polymeric systems such as hydrogels,22 fuel cells,23 epoxy molding compounds,24 and so on. The total energy (Etotal) is calculated using eqn (1):
| Etotal = EvdW + EQ + Ebond + Eangle + Etorsion + Einversion | (1) |
Results and discussion
Analysis of Pt nanoclusters
In order to obtain the most probable energy state, we performed spin-unrestricted calculations with various spin multiplicities. The results of these calculations are presented in Fig. 2. Here, the relative energies are calculated with respect to the minimum energy value (i.e., energy deviation from the minimum energy) and the optimal spin state is defined as the spin state resulting in the minimum energy value. After specifying the minimum energy value of Pt nanoparticles with the optimal spin state, we calculated the normalized cohesive energy (NCE) using eqn (2):| NCE = [E(PtX–Y–Z[m]) − n × E(Pt)]/n | (2) |
In Fig. 3, we summarize the NCEs calculated for the Pt nanoparticles shown in Fig. 1. First of all, it is commonly observed from the calculations involving three different functionals that the NCE decreases as a function of the number of Pt atoms in a nanoparticle, approaching the experimental NCE value for bulk Pt (−5.85 eV).28 This implies that the stability of the Pt nanoparticles increases with increase in the particle size. Although the general trend of NCE is the same regardless of the functional used in this study, it should be noted that the NCE values themselves are different depending on the functionals used and may be ranked in the following order: NCE (PBE) < NCE (M06) < NCE (B3LYP). In other words, PBE results in the most stable NCE value, whereas B3LYP yields the least stable NCE for the same Pt nanoparticle.
 | ||
| Fig. 3 Change in the normalized cohesive energy (NCE) at various layers as a function of the number of Pt atoms in a cluster. The NCE values of the Pt clusters are higher than that of bulk Pt. | ||
Another observation from Fig. 3 is that the two- and three-layer Pt nanoparticles have nearly the same stability and the data points from these nanoparticles appear to be identical for each functional. On the other hand, the single-layer nanoparticles are relatively less stable with higher NCE values, since the Pt atoms in the single-layer model lack the coordination with the neighboring atoms. From these results, we presume that the two-layer model with a high number of Pt atoms as well as three-layer model would be sufficient for describing the Pt nanoparticles with any given number of Pt atoms. Thus, our result appears in agreement with Sebetci's findings.6 Using this information, we selected a highly stable model of Pt nanoparticles to develop a force field describing the interaction between the Pt nanoparticles and molecules.
Coordination number (CN) model for Pt nanoparticles
Based on the DFT calculations for various Pt nanoparticles, we developed a model to evaluate the energy of the Pt nanoparticles based on their size and shape. For this purpose, we counted the number of Pt atoms corresponding to each CN for all the Pt nanoparticle models in Fig. 1. The example in Fig. 4(a) shows that four Pt atoms in Pt6–3–1 nanoparticle have CN of 3 while six Pt atoms have CN of 6. After determining the number of Pt atoms for each CN, we calculated the atomic cohesive energy for each CN ((ACE)CN) in eqn (3) using the least-squares method:
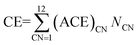 | (3) |
 | ||
| Fig. 4 Pt nanoparticles have atoms with various coordination numbers (CNs): (a) model of the Pt6–3–1 nanoparticle, which has 4 Pt atoms with CN = 3 and 6 Pt atoms with CN = 6; (b) change in atomic cohesive energy of Pt as a function of CN reported in Table 1. | ||
However, in Fig. 4(b), it is also important to note the deviations in the values of (ACE)CN from the dashed line, particularly for lower CN values. The dashed line between CN = 0 and CN = 12, which predicts the stability of the Pt atoms, increases linearly as a function of CN on the assumption that each bond has a constant strength regardless of the number of bonds. However, such negative deviation from the dashed line indicates that the bond strength is not constant. Rather, it decreases as a function of CN. In other words, the characteristics of bond between two Pt atoms depend on the number of the neighboring Pt atoms. This interpretation could be clearly confirmed by plotting ACE/CN as a function of CN, which is shown in Fig. 4(b). The contribution of individual Pt–Pt bonds to ACE is most significant for CN = 1, and becomes weaker with increasing CN.
In order to validate the CN model in eqn (3) with the ACE contributions of each CN in Table 1, we calculated the surface energy with various facets using the CN model. As shown in Table 2, we compared the surface energies calculated using the CN model with the values reported in the literature.7,29 For this purpose, we calculated the surface energies for several different facets such as (111), (100), and (730) as shown in Fig. 5. Although the surface energies for the (100) and (730) surfaces calculated from the CN model slightly deviate from the reported surface energy values, in general, the CN model captures the surface energy reasonably well, especially for the (111) surface (Table 2).
| CN | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Energy (eV) | −0.93 | −1.77 | −2.29 | −2.91 | −2.64 | −2.72 |
| CN | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|
| Energy (eV) | −3.13 | −4.41 | −4.76 | −4.82 | −4.90 | −5.80 |
 | ||
| Fig. 5 Various facets of Pt surfaces: (a) (111) direction; (b) (100) direction; (c) (730) direction. The colors are used to clarify the structural repetition of the atomic layers. | ||
Force field development
To obtain force fields describing the interaction of the molecular species with Pt, we used the Morse potential whose parameters obtained are summarized in Table 3. These parameters were developed with a pragmatic approach in mind, namely that the force field would include all the DFT interaction energies.| Pairs | D (kcal mol−1) | R0 (Å) | γ |
|---|---|---|---|
| O(H2O)–Pt | 2.500 | 2.416 | 11.648 |
| H(H2O)–Pt | 1.364 | 3.054 | 9.830 |
| O(H3O+)–Pt | 6.433 | 3.473 | 7.746 |
| H(H3O+)–Pt | 0.231 | 1.609 | 12.000 |
| O(O2)–Pt | 0.429 | 3.470 | 7.024 |
| C(Nafion)–Pt | 0.338 | 4.476 | 13.789 |
| F(Nafion)–Pt | 0.205 | 3.674 | 5.995 |
| Oether(Nafion)–Pt | 0.409 | 3.470 | 7.024 |
| S(Nafion)–Pt | 3.041 | 3.413 | 14.672 |
| OSO3(Nafion)–Pt | 2.351 | 2.511 | 5.144 |
| C(graphite)–Pt | 0.118 | 4.421 | 7.887 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 468 Da and ten sulfonate groups per chain, whose equivalent weight is ∼1100. The number of water molecules was 2240 (λ = 14, 14 water molecules per sulfonate group).
468 Da and ten sulfonate groups per chain, whose equivalent weight is ∼1100. The number of water molecules was 2240 (λ = 14, 14 water molecules per sulfonate group).
In our previous study,30 we analyzed the surface of Pt nanoparticles and the distribution of O2 molecules in a three-phase interfacial system using Connolly surface analysis and the pair correlation function, respectively. It was found that ∼60% of the surface of Pt nanoparticles is available for electrochemical reaction in the three-phase interfacial system. We also found that O2 molecules tend to be located around the Nafion phase rather than the water phase.
The diffusion of O2 molecules in the three-phase system is another interesting property of PEMFCs, because the transport of O2 molecules would affect the performance of PEMFC. The mean square displacement (MSD) of O2 molecules in the three-phase system was obtained from the last 5 ns of the NPT MD simulations at 353 K (Fig. 6(b)) to calculate the diffusion coefficients (D) defined in eqn (4)
 | (4) |
Conclusions
In this study, we characterized the relationship between the CN and energy of the Pt particles. This understanding would be useful in the preparation of model structures with various numbers of Pt atoms in a three-phase system. Our CN-based model of stable Pt particles is suitable for predicting the ACE of a Pt particle consisting of n atoms in any arbitrary shape. We also developed a force field describing the interactions between Pt particle and other components such as graphite, Nafion, water, hydronium, and oxygen in the three-phase system by optimizing the parameters of potential energy functions to reproduce the structures and energies from the DFT calculations. The force field developed in this study can be used to perform extensive MD simulations to investigate the structures and transport in the three-phase interfacial system.Acknowledgements
This research was supported by Ballard via the Department of Energy (DOE) grant No. DE-EE0000466. This research was also supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2015M1A2A2057129).Notes and references
- (a) K. Koga, T. Ikeshoji and K. Sugawara, Phys. Rev. Lett., 2004, 92, 115507 CrossRef PubMed; (b) Y. Sun and Y. Xia, Science, 2002, 298, 2176 CrossRef CAS PubMed; (c) R. Sardar, A. M. Funston, P. Mulvaney and R. W. Murray, Langmuir, 2009, 25, 13840 CrossRef CAS PubMed; (d) S. Link, C. Burda, B. Nikoobakht and M. A. El-Sayed, J. Phys. Chem. B, 2000, 104, 6152 CrossRef CAS.
- (a) G. Hodes, Adv. Mater., 2007, 19, 639 CrossRef CAS; (b) M. J. Yacaman, J. A. Ascencio, H. B. Liu and J. Gardea-Torresdey, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2001, 19, 1091 CrossRef CAS.
- (a) S. Varga, B. Fricke, H. Nakamatsu, T. Mukoyama, J. Anton, D. Geschke, A. Heitmann, E. Engel and T. Bastug, J. Chem. Phys., 2000, 112, 3499 CrossRef CAS; (b) H. Grönbeck and W. Andreoni, Chem. Phys., 2000, 262, 1 CrossRef; (c) J. Wang, G. Wang and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035418 CrossRef; (d) E. Aprà and A. Fortunelli, J. Phys. Chem. A, 2003, 107, 2934 CrossRef; (e) L. Xiao and L. Wang, J. Phys. Chem. A, 2004, 108, 8605 CrossRef CAS; (f) W. Q. Tian, M. Ge, B. R. Sahu, D. Wang, T. Yamada and S. Mashiko, J. Phys. Chem. A, 2004, 108, 3806 CrossRef CAS; (g) D.-K. Lee, G.-H. Jeung and Y. S. Lee, Int. J. Quantum Chem., 2009, 109, 1975 CrossRef CAS.
- (a) W. Eberhardt, P. Fayet, D. M. Cox, Z. Fu, A. Kaldor, R. Sherwood and D. Sondericker, Phys. Rev. Lett., 1990, 64, 780 CrossRef CAS PubMed; (b) Z. L. Wang, J. M. Petroski, T. C. Green and M. A. El-Sayed, J. Phys. Chem. B, 1998, 102, 6145 CrossRef CAS; (c) M. B. Airola and M. D. Morse, J. Chem. Phys., 2002, 116, 1313 CrossRef CAS.
- (a) M. N. Huda, M. K. Niranjan, B. R. Sahu and L. Kleinman, Phys. Rev. A, 2006, 73, 053201 CrossRef; (b) K. Bhattacharyya and C. Majumder, Chem. Phys. Lett., 2007, 446, 374 CrossRef CAS.
- A. Sebetci, Phys. Chem. Chem. Phys., 2009, 11, 921 RSC.
- R. V. Chepulskii and S. Curtarolo, ACS Nano, 2011, 5, 247 CrossRef CAS PubMed.
- E. Langenbach, A. Spitzer and H. Lüth, Surf. Sci., 1984, 147, 179 CrossRef CAS.
- A. Michaelides, V. A. Ranea, P. L. de Andres and D. A. King, Phys. Rev. Lett., 2003, 90, 216102 CrossRef CAS PubMed.
- S.-P. Huang and P. B. Balbuena, Mol. Phys., 2002, 100, 2165 CrossRef CAS.
- Jaguar, v7.5, Schrödinger, LLC, New York, 2008 Search PubMed.
- (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS; (b) Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849 CrossRef CAS PubMed.
- (a) J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533 CrossRef CAS; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299 CrossRef CAS.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508 CrossRef CAS.
- Materials Studio, v5.0, Accelrys Software Inc., San Diego, 2009 Search PubMed.
- (a) J. Kua and W. A. Goddard, J. Phys. Chem. B, 1998, 102, 9481 CrossRef CAS; (b) J. Kua and W. A. Goddard, J. Phys. Chem. B, 1999, 103, 2318 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897 CrossRef CAS.
- M. Levitt, M. Hirshberg, R. Sharon, K. E. Laidig and V. Daggett, J. Phys. Chem. B, 1997, 101, 5051 CrossRef CAS.
- (a) S. G. Lee, G. F. Brunello, S. S. Jang and D. G. Bucknall, Biomaterials, 2009, 30, 6130 CrossRef CAS PubMed; (b) S. G. Lee, G. F. Brunello, S. S. Jang, J. H. Lee and D. G. Bucknall, J. Phys. Chem. B, 2009, 113, 6604 CrossRef CAS PubMed; (c) S. G. Lee, W. Koh, G. F. Brunello, J. I. Choi, D. G. Bucknall and S. S. Jang, Theor. Chem. Acc., 2012, 131, 1206 CrossRef; (d) S. G. Lee, T. A. Pascal, W. Koh, G. F. Brunello, W. A. Goddard III and S. S. Jang, J. Phys. Chem. C, 2012, 116, 15974 CrossRef CAS.
- (a) G. Brunello, S. G. Lee, S. S. Jang and Y. Qi, J. Renewable Sustainable Energy, 2009, 1, 033101 CrossRef; (b) G. F. Brunello, W. R. Mateker, S. G. Lee, J. I. Choi and S. S. Jang, J. Renewable Sustainable Energy, 2011, 3, 043111 CrossRef.
- (a) S. G. Lee, J. I. Choi, W. Koh, S. S. Jang, J. Kim and G. Kim, IEEE Trans. Compon., Packag., Manuf. Technol., 2011, 1, 1533 CrossRef CAS; (b) S. G. Lee, S. S. Jang, J. Kim and G. Kim, IEEE Trans. Adv. Packag., 2010, 33, 333 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637 CrossRef CAS.
- (a) S. Nose, Mol. Phys., 1984, 52, 255 CrossRef CAS; (b) S. Nose, J. Chem. Phys., 1984, 81, 511 CrossRef CAS; (c) S. Nose, Mol. Phys., 1986, 57, 187 CrossRef CAS.
- D. R. Lide, CRC handbook of chemistry and physics, CRC Press, Inc., Boca Raton, FL, 71st edn, 2005 Search PubMed.
- (a) N. E. Singh-Miller and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235407 CrossRef; (b) H. Iddir, V. Komanicky, S. Ogut, H. You and P. Zapol, J. Phys. Chem. C, 2007, 111, 14782 CrossRef CAS; (c) S. Baud, C. Ramseyer, G. Bihlmayer, S. Blugel, C. Barreteau, M. C. Desjonqueres, D. Spanjaard and N. Bernstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235423 CrossRef; (d) J. L. F. Da Silva, C. Stampfl and M. Scheffler, Surf. Sci., 2006, 600, 703 CrossRef CAS; (e) G. Boisvert, L. J. Lewis and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1881 CrossRef CAS.
- G. F. Brunello, J. I. Choi, D. A. Harvey and S. S. Jang, ECS Trans., 2012, 50, 155 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra09274h |
| This journal is © The Royal Society of Chemistry 2016 |