Taming the diffusiophoretic convective instability in colloidal suspensions

Abstract

A suspension of Brownian colloidal particles stabilised against aggregation is expected to be stable against convection when its density decreases monotonically with height. Surprisingly, a recent experimental investigation has shown that when colloidal particles are dispersed uniformly in a solvent with a stabilising stratification of a molecular solute, the system develops a convective instability under generic conditions [Anzivino et al., J. Phys. Chem. Lett., 2024, 15, 9030]. This instability arises because the solute concentration gradient induces an upward diffusiophoretic motion of the colloidal particles, triggering a diffusiophoretic convective instability (DCI). In this work, we investigate the stability of a colloidal suspension against convection in the presence of a stable density stratification of the sample, under different initial conditions. In particular, we study the condition where both the colloid and the molecular solute are initially localized in the lower half of the sample prior to merging with the upper half made of pure water. This is unlike the previously studied setup where the colloid was initially present also in the upper half, suspended in water. We show that only when the concentration of glycerol exceeds a fairly large threshold value of approximately 0.3 w/w the system develops the convective instability. Hence, this new setup offers the possibility to tame DCI by changing the initial conditions. We model the experimental results by numerically solving the nonlinear double diffusion equations in the presence of a diffusiophoretic coupling to determine the time evolution of the base state of the system. The theoretical analysis allows us to elucidate the physical reason for the existence of the threshold value of the glycerol concentration and to establish that the interactions between the colloidal particles do not play a significant role in the DCI.

---

1 Introduction

The gravitational stability of colloidal particles dispersed in a liquid under isothermal conditions is affected by several processes acting both at the microscopic and macroscopic scales, including sedimentation, aggregation, and convection. In the absence of these processes, the thermal energy keeps the particles distributed uniformly inside the liquid; conversely, when such processes are present, instabilities may arise within the liquid. The stability of particles against sedimentation is characterised by the dimensionless Peclet number Pe = ua/D_c, where u is the settling velocity, D_c is the diffusion coefficient and a is the radius of a particle. Large particles with Pe ≫ 1 sediment in the presence of gravity, giving rise to a partial demixing of the colloidal dispersion, while small particles with Pe ≪ 1 remain indefinitely distributed almost uniformly.¹ When the concentration is large enough to enable the interaction between the particles, this can lead to their aggregation and to the precipitation of the aggregates. The stability against aggregation is characterised by the interparticle potential between two particles. In the presence of a potential barrier much larger than k_BT the aggregation of particles through Diffusion Limited and Reaction Limited aggregation processes is prevented and the colloidal suspension is stable against aggregation.² In the presence of a convective flow, also particles with a large energy barrier ≫k_BT can be made to aggregate.³ Finally, even in the case of small Brownian particles stabilised against aggregation, their spatial distribution determines the stability of the suspension against convection. When the suspension is characterised by a density profile increasing monotonically with height, the top denser layers can sink into the lighter bottom layers giving rise to solutal convection.⁴ This occurs when the solutal Rayleigh numberexceeds a critical value which depends on the boundary conditions.^5,6 Here Δz is the thickness of the layer associated with an unstable density difference Δρ, g is the gravity acceleration, and η is the shear viscosity of the solvent.

When the system is prepared in a configuration where all these processes capable of triggering convective instability can be ruled out, one would expect that gravity does not have any influence on the stability of the colloidal suspension. This is the case for example of a suspension of small Brownian particles stabilised against aggregation and dispersed in a fluid with a gravitationally stable density stratification of a molecular solute. In contrast, we have shown recently that under these conditions, when the particles are dispersed uniformly in a solution in the presence of a concentration gradient of a molecular solvent, they undergo a transient diffusiophoretic convective instability.⁷ A simple understanding of the conditions leading to the development of the instability has been achieved by investigating numerically the time evolution of the base state of the system, which represents the state where the fluid is at rest with a known density profile before any perturbation occurs. The investigation of the time evolution of the base state by means of simulations has provided convincing evidence that this peculiar instability is determined by the diffusiophoretic transport of nanoparticles induced by the gradient ∇c of the molecular solute. Under the action of ∇c, diffusiophoresis determines a drift of each particle with velocity u ∝ ∇c.⁸ The diffusiophoretic mass flux determines a local inversion of the initially stable density profile of the colloidal suspension. When the solutal Rayleigh number associated with this density stratification reaches the threshold convection sets in. In the case of a uniform distribution of particles, transient convection is observed quite generally in a wide range of volume fraction concentrations of nanoparticles 1% < ϕ < 8% and of the mass fractions of glycerol 5% < c < 56%.

In this work, we investigate the emergent behaviors in a suspension of Brownian colloidal particles dispersed in a solvent with a gradient of a molecular solute. We are interested in the possibility of taming the diffusiophoretic instability by varying the initial conditions, where the molecular solvent determines a strong stabilising density profile that should inhibit the onset of convection. Here we address whether a different initial distribution of nanoparticles could stabilise the system against convection. The initial condition where a top layer of water is superimposed to a bottom layer of water–glycerol–nanoparticles is of particular relevance because in this case both the glycerol and the nanoparticles contribute initially to the gravitational stabilisation of the system. To allow for a comparison with the results obtained with a uniform distribution of particles we use the combinations of (ϕ₀, c₀) adopted in the uniform case, the only difference being that initially the top phase does not contain any nanoparticle but just water. The systematic exploration of the parameter space allows us to investigate the stability of the colloidal suspension for any combination (ϕ₀, c₀) and to map a stability diagram as a function of these parameters. The computational solution of the equations describing the base state of the system allows us to determine the time evolution of the density profile of the colloidal suspension before convection sets in. In the absence of a diffusiophoretic contribution to the mass flux of nanoparticles, the equations for ϕ and c are decoupled and the density profile remains stable indefinitely. Conversely, when diffusiophoresis is incorporated into the equations, the accumulation of nanoparticles determined by the diffusiophoretic flow can lead to the formation of a gravitationally unstable layer in the density profile. The numerical determination of the time evolution of the solutal Rayleigh number of the density profile allows us to determine the combinations of parameters (ϕ₀, c₀) where the system becomes unstable.

Although the diffusiophoretic behavior of a single particle is well understood,^8–10 recently the investigation of the role of diffusiophoresis in determining emerging behavior in colloidal suspensions, including self organisation and collective phenomena, is attracting increasing interest. This surge of interest is determined by the increasing awareness that the role of diffusiophoresis could be more widespread than expected in natural and artificial systems.^11,12 Indeed, very recent work has shown the important role played by it in outstanding problems such as the origin of the sharpness of Turing patterns observed in nature in biological species like the Ornate Boxfish and Jewel Moray Eel.¹³ Moreover, the similarity with the chemotaxis of living microorganisms has suggested that the self-diffusiophoresis of active colloidal particles can be used as a model for the collective behavior of active matter driven by chemical gradients.^14,15 The breadth of these concepts has been transferred to other disciplines, including the social sciences. The mathematical framework for diffusiophoresis and chemotaxis has been very recently applied to human population dynamics, providing insight into migration patterns influenced by resource availability, safety, and social factors, with potential applications for studying climate change-driven population shifts.¹⁶

2 Methods

2.1 Sample

The sample consists of two liquid phases that are brought into contact at the beginning of the experiment. The top phase is always pure demineralised water. The bottom phase is a suspension of silica nanoparticles with a diameter of 22 nm (Ludox TMA) and a volume fraction ϕ₀, dispersed in a mixture of water and glycerol with a weight fraction c₀. To investigate systematically the stability of the system, we explored all the 32 possible combinations (ϕ₀, c₀), where ϕ₀ = 1, 2, 4, and 8% and c₀ = 5, 7, 10, 14, 20, 28, 40, and 56%.

2.2 Experimental setup

The experimental setup is designed to study the evolution in time of a horizontal interface between two miscible liquids that at the initial time has a minimum amount of perturbations. To obtain a sharp and unperturbed interface, we used a liquid bridge cell.¹⁷ Two microscope glass slides were prepared, each with a 37 μl drop. The drop on the bottom slide contained the water–glycerol–Ludox mixture, while the drop on the top slide contained only water. The two slides were positioned horizontally so that the two drops faced each other as shown in Fig. 1(a). A 0.95 mm thick rubber spacer with a central hole for the drop was placed on the lower slide. Using a mechanical system, the upper slide can be lowered enough to rest on the rubber spacer. The contact allows the formation of a liquid bridge with an interface between the two liquids which, after rapid settling, becomes sharp and free of visible disturbances.

Fig. 1 Schematic representation of (a) the liquid bridge cell operation and (b) the shadowgraph optical setup. (a) A droplet of water and a droplet of the water–glycerol–ludox mixture are deposited on two separate microscope slides and kept apart (top panel). For t > 0, the two droplets are brought into contact, forming a liquid bridge (bottom panel). Over time, the two liquid phases diffuse into each other. (b) Shadowgraph optical setup: light emitted by an LED is collimated using an achromatic doublet (lens A), passes vertically through the liquid bridge cell, and is demagnified by a second lens (lens B) onto a CMOS camera.

After bringing the droplets into contact, the refractive index variations in the fluid are recorded with a camera. All the components are aligned vertically (Fig. 1b) and kept fixed to an optical column. The light source at the bottom of the column is a super-luminescent diode from SUPERLUM (SLD). The diode emits high-intensity light radiation of wavelength λ = 670 ± 13 nm and is coupled to an optical fiber. The SLD Current and Temperature Controller operating console which powers the diode makes it possible to regulate the light intensity. The diode is mounted on a support which allows it to be micro-metrically shifted. An achromatic doublet of focal length f = 20 cm (lens A, Fig. 1b) is placed at distance f from the diode and collects and collimates the diverging rays. The lens is followed by the sample cell fixed 29.5 cm above, and by a second achromatic doublet (lens B, Fig. 1b) with focal length f = 5.0 cm that reduces the image size by a factor of 0.5 on a camera placed at a distance of 7.5 cm at the top of the column. Lens B conjugates the plane of the sensor with a plane located at a defocusing distance z = 4.0 cm from the sample. Each component is mounted on a support that allows its fine movement necessary for a good alignment.

2.3 Image processing

A suitable method to characterize the onset of instability is to determine the time evolution of the relative variance of images defined as follows:where I(x, t) is the luminous intensity of the pixel at position x = (x, y), while 〈I(x, t)〉 is the average of the luminous intensities computed over all the pixels in the image.¹⁸ The variance quantifies the contrast of the image, where dark regions are associated with low colloid concentration and light regions with high concentration. Qualitatively, this translates into the fact that, in the presence of a convective pattern, the variance is larger than that in a stable phase where the distribution of colloids is homogeneous. By evaluating the variance for each image in a given sequence, it is possible to graph its trend as a function of time, thus highlighting the onset of a convective instability.¹⁹ This procedure is rather robust and does not require an accurate selection of a region of interest covered by the sample. In fact, it works very well even when the images include the regions surrounding the sample. The reason behind its reliability is that, since we are interested in the time evolution of the variance, the regions where the sample is not present provide a static contribution to it and do not contribute to its variations.

2.4 Computational methods

We supplement the experimental investigation with a theoretical analysis of the conditions leading to the evolution of the base state of the system towards an instability. Since the geometry of the experimental sample can be approximated with a cylinder of height h = 0.95 mm and diameter d ≫ h, we introduce a 1D reference system with the ẑ-axis pointing upward. Following standard treatments, the equation for the evolution of the concentration profile c(z, t) of the water–glycerol mixture according to ref. 4 is:

The diffusion coefficient D_s of the mixture and its density ρ depend on the concentration c of glycerol. In the concentration range of interest in this study they are well approximated by the linear relations D_s(c) = D_0s + εc and ρ(c) = ρ₀ + βc, where D_0s = D_s(0) = 1.025 × 10⁻⁵ cm² s⁻¹ is the diffusion coefficient of the water glycerol mixture in the limit of infinite dilution, ε = −1.308 × 10⁻⁵ cm² s⁻¹, ρ₀ = 0.997 g cm⁻³ is the density of pure water and β = 0.230 g cm⁻³.²⁰

The equation for the diffusion of the colloidal particles can be written as follows

where ϕ is the volume fraction of the colloidal particles, and D_c = k_BT/(6πηa) is the Stokes–Einstein diffusion coefficient of the colloid. Here, k_B is the Boltzmann constant, a is the radius of the colloidal particles, and η is the shear viscosity of the mixture. The diffusion coefficient D_c in general depends on the concentration of glycerol c through the shear viscosity η. In the case of the water–glycerol mixture investigated in this study the dependence of η on c can be expressed by the empirical formula where η_w and η_g are the shear viscosity of pure water and glycerol, respectively, and is a weighting exponent, with dimensionless constants χ = 0.705 and ξ = 2.²¹

The second term between square brackets in eqn (4) represents the diffusiophoretic flow of colloidal particles induced by the gradient of the molecular solute. In writing eqn (4), we have adopted the formalism where the diffusiophoretic coefficient α is dimensionless. In our simulations, α is a free parameter, but in ref. 7 it has been proved reasonable to assume α ≈ D_s/D_c ≈ 100 as long as the colloid volume fraction in the system is small, that is when the inter-colloid interaction is negligible. This finding is consistent with observations reported within the context of colloid diffusiophoresis driven by the concentration gradient of an electrolyte.²²

Since the bottom and top walls of our experimental setup can be assumed as impermeable, we apply the Neumann boundary conditions (∂c/∂z)_z=0 = (∂c/∂z)_z=h = 0 and (∂ϕ/∂z)_z=0 = (∂ϕ/∂z)_z=h = 0 to eqn (3) and (4). For any combination of ϕ₀ and c₀, we solve numerically the system of eqn (3) and (4) using the PDE solver of Matlab 2023 and obtain the time evolution of the concentration profile c(z, τ) of glycerol and ϕ(z, τ) of the colloid. Crucial to understand if the system evolves towards an instability is to monitor the vertical variation of the density profile ρ. For any pair c(z, τ) and ϕ(z, τ), the corresponding profile of the fluid density can be expressed as⁷

ρ(c, ϕ) = ρ₀ + (ρ_L − ρ₀)ϕ + β(1 − ϕ)c, (5)

where ρ_L = 2.2 g cm⁻³ is the density of a single colloidal particle. If, at a certain time, the density profile ρ of the suspension has developed a local minimum ρ_min at height z_min, followed by a local maximum ρ_max at height z_max > z_min, gravity acts to pull denser fluid parcels between z_min and z_max from top to bottom. By contrast, the suspension remains gravitationally stable in case ρ is always a monotonically decreasing function of z. To characterize the stability of the density profile we adopt the seminal approach proposed by Howard to investigate the onset of boundary layer convection.²³ Basically, in the case of a growing boundary layer one can determine a Rayleigh number associated with it and estimate when it exceeds a threshold value. As stated by Howard, this approach “is right in spirit” and, although not strictly rigorous, provides the right orders of magnitude of the quantities involved in the process. For the suspension of colloidal particles investigated by us, the stability of the density profile can be quantified by means of the solutal Rayleigh number defined in eqn (1). The suspension undergoes convection only in case Ra_S reaches a threshold value whose precise value depends on the system under consideration. In our case, we use the value associated with isothermal and free boundary conditions.^6,24 Although this choice of the critical Rayleigh number is arbitrary because in our system the boundary conditions change in time and are not well defined, it allows us to establish an order of magnitude estimate of in line with the spirit of the method proposed by Howard.

3 Results and discussion

3.1 Experimental results

For each of the 32 possible combinations of (ϕ₀, c₀), we collected a sequence of shadowgraph images, starting from the initial event when the two droplets were brought into contact. In all of the experiments, perturbations appeared immediately after the droplets merged to form a liquid bridge and rapidly faded away in a time of the order of 20–30 s because of the strong gravitational stabilisation determined by the density profile of the colloidal suspension and of the glycerol solution.

Inspection of the time evolution of the images, accompanied by the related graph of the time evolution of the variance, allowed us to identify two major classes of behavior, schematically shown in Fig. 2. The first class is represented by the samples that remained stable (Fig. 2a). In this case, the appearance of perturbations when the droplets are brought into contact is accompanied by a sudden increase of the relative variance (Fig. 2c orange line), followed by a rapid monotonic decrease and by a long phase where the images do not show the appearance of convective patterns and the variance remains constant. This regime is compatible with a diffusive mixing of water, glycerol, and colloidal particles. In fact, under the conditions adopted for these experiments, from the macroscopic point of view, the diffusion process is homogeneous in the horizontal direction, because the only variations of the concentration are due to the stratification of the sample in the vertical direction. Since the light beam propagates in the direction parallel to the concentration gradients, diffusive remixing does not produce any variation in the contrast of the images. The second class of behavior is represented by the samples that exhibited the onset of a transient convective instability (Fig. 2b). Here, after a sudden increase and decrease in the variance when the droplets come into contact, the sequence of images shows the appearance of cellular patterns, accompanied by a gradual increase of the relative variance (Fig. 2 blue line), which reaches a peak in a time of the order of a few hundred seconds and then gradually decreases back to a value compatible with the absence of perturbations. Interestingly, from a comparison of the patterns shown in Fig. 2a and b at time t = 0 one can appreciate that the initial perturbations determined by the mechanical shock induced by the merging of the two droplets are stronger in the stable case of panel (a). This is due to the fact that initially the gravitational stabilisation determined by the stable stratification of glycerol is much weaker in the case of panel (a), due to the smaller gradient of glycerol in comparison to that of panel (b).^4,25

Fig. 2 (a) Image sequence collected for a stable configuration with c₀ = 14% and ϕ₀ = 1.0%: transient disturbances appear shortly after the droplets are brought into contact at t = 0, and rapidly fade away for t > 80 s leaving place to a stable state. (b) Onset of solutal convection in a sample with c₀ = 56% and ϕ₀ = 4.0%: the perturbations generated after contact at t = 0 last a few seconds, and are less pronounced than in (a) as a consequence of the strong gravitational stabilisation determined by the glycerol and colloid concentration gradients. The initial short transient is first followed by a stable phase (t < 180 s), then by the development of a convective instability peaking at t = 250 s, and finally, by another stable phase (t > 500 s). (c) Temporal evolution of the relative variance for both measurements shown in (a) (orange) and (b) (blu). X markers indicate the variance values for the images presented in (a) and (b). The spatial scale in (a) and (b) corresponds to the scale bar of 0.6 cm in (a).

A systematic classification of the stability of the sample allows us to build a diagram mapping the stability of the system for all the combinations of (ϕ₀, c₀) (Fig. 3). The diagram is characterised by a broad stable region for small concentrations of glycerol, independently of the concentration of colloid. Increasing the concentration of glycerol at fixed ϕ₀ determines the transition into a region of instability for values of c₀ larger than . At each fixed value of ϕ₀, the transition occurs within a different range of concentrations of glycerol.

Fig. 3 Stability diagram, highlighting the existence of two distinct regions: a stable region (orange) and an unstable region (blue). The spline lines mark the boundaries of a threshold strip (green) in which, for each ϕ₀, the threshold value of c₀ lies.

3.2 Computational results

To achieve a basic understanding of the stability of the system, we first linearised eqn (3) and (4) and solved them with the method described in ref. 7 to determine when the density profile develops a local inversion, leading to the development of a diffusiophoretic convective instability. By adopting this procedure, we are able to obtain a threshold of the instability in the range of values of (ϕ₀, c₀) compatible with the experimental results shown in Fig. 3 only by assuming that the diffusiophoretic coefficient α exhibits a strong dependence on the volume fraction of the colloid ϕ. More in detail, reproducing the experimental results at ϕ₀ = 1%, 2%, 4%, and 8% requires assuming that α = 175, 125, 75, and 50, respectively. In a previous publication, we have speculated that this marked dependence of α on ϕ₀ could be due to the fact that the diffusiophoretic coupling in eqn (4) does not take into account the interactions between colloidal particles.⁷ In this work we bring this hypothesis to a critical test and check whether solving the nonlinear eqn (3) and (4) allows one to obtain results compatible with a single value of α, irrespective of the concentration of the colloid.

We solve numerically the nonlinear eqn (3) and (4) and determine the concentration and density profiles for each combination of (ϕ₀, c₀). Examples of these profiles are shown in Fig. 4 for two meaningful cases where the sample is stable (panels a–c, ϕ₀ = 0.01, c₀ = 0.2) and unstable (panels d–f, ϕ₀ = 0.01, c₀ = 0.4).

Fig. 4 Vertical profiles of glycerol mass fraction c/c₀ (a) and (d), colloid volume fraction ϕ/ϕ₀ (b) and (e) and densitys ρ/ρ₀ − 1 computed viaeqn (5) (c) and (f) at several times t (see the legend). Profiles of c and ϕ have been obtained by solving eqn (3) and 4 at fixed diffusiophoretic coupling α = 125, with initial conditions ϕ₀ = 0.01, c₀ = 0.2 (a)–(c) leading to a gravitationally stable configuration, and ϕ₀ = 0.01, c₀ = 0.4 (d)–(f), leading to an unstable configuration. The insets of panels (c) and (f) show the temporal evolution of the density profile in the region 0 ≤ z/h ≤ 0.5, at times t = 633, 700, 970 s. In this interval of time, ρ starts displaying a critical local inversion of its slope in case c₀ = 0.4 (f) while no critical inversion occurs in the case c₀ = 0.2 (c).

At t = 0 the system is in its initial configuration: both the glycerol and the colloids lie on the bottom of the sample and are absent from the top (Fig. 4(a), (b), (d) and (e)). The corresponding ρ decreases monotonically as a function of z, and the system is consequently gravitationally stable (Fig. 4(c) and (f)). At t > 0 glycerol starts to freely diffuse upwards. Whether or not the system undergoes an instability strongly depends on the value of c₀. In case c₀ is small, the upward diffusion of colloids is weakly affected by the glycerol concentration gradient (Fig. 4(b)). Correspondingly, the density profile ρ decreases monotonically as a function of z for any time t > 0 (Fig. 4(c)) and the system remains always gravitationally stable. By contrast, when c₀ is large, the glycerol concentration gradient determines an upward diffusiophoretic flux of colloids (Fig. 4(e)) which has relevant repercussions on the density profile of the suspension. For t ≥ 700 s, ρ starts displaying a local inversion of its slope, which becomes critical when 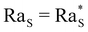(Fig. 5(a)). Remarkably, the diffusiophoretic-induced migration of colloidal particles mostly occurs within the bottom region of the sample (the inset of Fig. 4(b) and (e)). As a consequence, the local minimum and maximum developed by the suspension density profiles lie within the bottom region of the sample (the inset of Fig. 4(c) and (f)). While the maximum ρ_max develops around z_max/h ≈ 0.4 and remains roughly located at this height as a function of time, the position z_min of the minimum ρ_min moves towards the bottom wall z ≈ 0 when the system approaches the threshold for convection. Consequently, the variation Δz ≡ z_max − z_min is always quite large. In particular, Δz is typically one order of magnitude larger than the variation Δρ ≡ ρ_max − ρ_min, and therefore is mainly responsible for the increase of Ra_s.

Fig. 5 (a)–(d) Time evolution of the solutal Rayleigh number associated with the density profile of the base state (Fig. 4) for the four volume fractions ϕ₀ of the colloid. When Ra_s exceeds the threshold value (dashed line), the system becomes unstable against convection. In each panel, the Rayleigh number is calculated numerically at three glycerol concentrations c₀ (see the legend in a). For each value of ϕ₀, we adjusted the value of the diffusiophoretic coefficient α until the curves in panels (a)–(d) reproduced the experimentally observed treshold of the instability (Fig. 3). Panel (e) shows for each concentration of colloid ϕ₀ the range of values of α compatible with the range of values of c₀ observed experimentally where the threshold of the instability falls. The black points indicate the α values used to compute Ra_s in panels a–d.

For each fixed value of ϕ₀, this analysis allows us to determine the range of values of c₀ where the system becomes unstable. This is achieved by calculating the time evolution of the solutal Rayleigh number Ra_s to assess whether it reaches the critical value 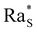(Fig. 5). Within this procedure, the diffusiophoretic coefficient α is a free parameter, and we adjust its value until the system becomes unstable in a range of values of c₀ compatible with the one observed experimentally (Fig. 3). We find that an agreement between the experimental and computational results is achieved when α ≈ 125 at ϕ₀ = 1%, 2%, and α = 105 at ϕ₀ = 4%, 8% (Fig. 5(e)). This is a remakable finding, because it shows that including the nonlinear terms in the equations for the base state of the system allows us to obtain results fully consistent with a value of α of the order of D_w/D_c. and strongly suggests that the interactions between colloidal particles do not significantly affect the diffusiophoretic process in the range of concentrations explored by us.

3.3 Discussion

The stability diagram shown in Fig. 3 provides clear evidence that the diffusiophoretic convective instability reported in ref. 7 can be tamed using an initial condition where both the colloid and the molecular solute are initially localized in the bottom half of the system (while the upper half is pure water), and both contribute to the gravitational stabilization of the sample. Adjusting the concentrations of glycerol and colloid, we identify distinct stable and unstable regions, the instability threshold being primarily determined by the glycerol concentration c₀. Notably, choosing c₀ below this threshold completely suppresses the instability. This emergence of a threshold is a novel result, absent in the previous study with an initially uniform colloid distribution.⁷ The threshold represents a balance between two competing effects: the gravitational stabilization due to the stratified density profile and the destabilization caused by the diffusiophoretic accumulation of particles. Interestingly, both effects depend linearly on the glycerol concentration gradient ∇c. As a result, varying ∇c alone should not alter the balance between these two competing effects, meaning the system should remain consistently in the stable or unstable region of the stability diagram, independently of c₀. The existence of a threshold suggests an underlying non-linear dependence on ∇c, which is not immediately apparent. To uncover the physical mechanism behind this unexpected behavior, it is worth analysing in more detail the computational results in comparison to the experimental ones, performing a critical discussion of the differences between the case of an initially uniform colloid distribution and the one discussed in this work, where the colloid is initially accumulated in the bottom phase.

The computational results show that at the beginning of the process the glycerol concentration gradient is different from zero only in the small region close to the center z/h = 0.5 of the sample. Within this same region, the concentration of colloid undergoes an abrupt decrease from ϕ₀ to 0. As a consequence, the diffusiophoretic flux ∼ϕ(z)∇c(z) is initially very weak and there is almost no induced migration of the colloids. Under these conditions, the density profile monotonically decreases as a function of z. As a consequence of the diffusion of glycerol, its concentration gradient gradually extends to a wider region of the sample. When it extends to a region close to the bottom of the sample, the migration of colloids becomes significant. However, the gradient has become weaker, such that only if it is strong enough at the beginning of the process, the migration is able to generate a local inversion of the density profile. This scenario may provide a physical explanation for the experimentally observed threshold of c₀ below which convection is inhibited. Quite interestingly, it is different from the one found in ref. 7. There, as a consequence of the initial uniform distribution of colloids, the diffusiophoretic induced migration starts soon when the glycerol concentration gradient is the strongest and the sample becomes always unstable.

4 Conclusions

In this work we have investigated the stability against convection of a suspension of Brownian particles dispersed in a mixture of water–glycerol. When a bottom horizontal layer of the solution is brought into contact with a top layer of pure water, the two layers should mix through a double diffusive process because any convective motion is inhibited by the stable density profile determined by the stratification of the molecular solvent and of the colloidal particles. This stability should increase by increasing the concentration of the colloid and that of the molecular solute. In contrast, we observe that increasing the concentration of glycerol above a threshold leads invariably to the onset of a transient solutal convective instability. We model the time evolution of the base state of the system by means of two coupled equations for the diffusion of glycerol and that of the colloid. In the absence of the coupling between the equations the system remains gravitationally stable indefinitely, until it reaches equilibrium. Instead, when a diffusiophoretic coupling term is introduced in the equation for the diffusion of the colloid, the system can undergo a local inversion of the density profile. We have investigated numerically the stability of the base state determined by this local inversion and shown that it depends critically on the initial concentration of the molecular solute and on the value of the diffusiophoretic coefficient α. The good agreement between the experimental and theoretical results provides compelling evidence that a diffusiophoretic convective instability is triggered in the presence of a large gradient of glycerol, notwithstanding the fact that this gradient contributes at the same time to the gravitational stabilisation of the system. We have discussed how this instability can be prevented by reducing the concentration of glycerol. Our results are of wide relevance for the fundamental understanding of the gravitational stability of a colloidal suspension dispersed in a multicomponent mixture, with potential implication for biological and geological systems, for the spread of pollutants and for the industrial processing of colloidal materials.^12,26 Moreover, the understanding of the behavior of complex fluids at various gravitational levels is becoming increasingly important for the exploration of space, where the ability to control the stability and the processing of complex fluids needed for food, fuels, healthcare and fabrication represents a strategic factor.²⁷ Within this context, the understanding of the stability of multi-component fluids undergoing cross-diffusion and diffusiophoresis represents a challenging and yet largely unexplored front of research.²⁸ Beyond these applicative aspects, several recent works have provided compelling evidence that a fundamental investigation of the emergent behavior determined by diffusiophoresis in colloids could serve as a model for natural processes such as pattern formation in the hide of animals,¹³ and for a fundamental understanding of more complex dynamical systems where the migration of entities is driven by a gradient of resources,¹⁵ including the chemotaxis of microorganisms and the spread of human populations.¹⁶

Author contributions

S. Castellini: software, validation, formal analysis, investigation, data curation, writing – review and editing, and visualization; C. Anzivino: software, validation, formal analysis, investigation, data curation, writing – original draft, and visualization; C. Marietti: software, validation, and investigation; M. Carpineti: methodology, resources, writing – original draft, and supervision; A. Zaccone: conceptualization, methodology, formal analysis, resources, writing – review and editing, supervision, project administration, and funding acquisition; and A. Vailati: conceptualization, methodology, formal analysis, resources, writing – original draft, supervision, project administration, and funding acquisition.

Data availability

The data that support the findings of this study, including image sequences and the C++ and python codes are openly available on the Zenodo repository [https://doi.org/10.5281/zenodo.14216894].

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank B. Alessio and K. Xhani for useful discussion. This work is partially supported by the European Space Agency (ESA) in the framework of the “Giant fluctuations”, NESTEX and “Sedimenting Colloids” projects, and by the Italian Space Agency (ASI) through the projects “Gravitationally TApping Colloids in Space (GTACS) – Sedimenting Colloids” (Number 2023-19-U.0) and “Non-Equilibrium Phenomena in Soft Matter and Complex Fluids (NESTEX)” (Number 2023-20-U.0). A. Z. gratefully acknowledges funding from the European Union through Horizon Europe ERC Grant number: 101043968 “Multimech”, from US Army Research Office through contract nr. W911NF-22-2-0256, and from the Niedersächsische Akademie der Wissenschaften zu Göttingen in the frame of the Gauss Professorship program.

Notes and references

1. R. Piazza, Rep. Prog. Phys., 2014, 77, 056602.
2. M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. C. Ball, R. Klein and P. Meakin, Nature, 1989, 339, 360–362.
3. A. Zaccone, H. Wu, D. Gentili and M. Morbidelli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 051404.
4. L. Landau and E. Lifshitz, Fluid Mechanics, Elsevier Science, vol. 6, 2013.
5. J. K. Platten and J. C. Legros, Convection in Liquids, Springer, Berlin, Germany, 2011.
6. S. Messlinger, W. Schöpf and I. Rehberg, Int. J. Heat Mass Transfer, 2013, 62, 336–349.
7. C. Anzivino, K. Xhani, M. Carpineti, S. Verrastro, A. Zaccone and A. Vailati, J. Phys. Chem. Lett., 2024, 15, 9030–9036.
8. J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99.
9. B. Derjaguin, G. Sidorenkov, E. Zubashchenko and E. Kiseleva, Kolloidnyj Zurnal, 1947, 9, 335–347.
10. J. L. Anderson, M. E. Lowell and D. C. Prieve, J. Fluid Mech., 1982, 117, 107–121.
11. D. Velegol, A. Garg, R. Guha, A. Kar and M. Kumar, Soft Matter, 2016, 12, 4686–4703.
12. S. Shin, Phys. Fluids, 2020, 32, 101302.
13. B. M. Alessio and A. Gupta, Sci. Adv., 2023, 9, eadj2457.
14. H. Stark, Acc. Chem. Res., 2018, 51, 2681–2688.
15. A. Ganguly, B. M. Alessio and A. Gupta, Front. Sens., 2023, 4, 1.
16. B. M. Alessio and A. Gupta, A Reaction-Diffusion-Chemotaxis Model for Human Population Dynamics over Fractal Terrains, arXiv, 2023, preprint, arXiv:2310.07185 DOI:10.48550/arXiv.2310.07185.
17. F. Giavazzi, G. Savorana, A. Vailati and R. Cerbino, Soft Matter, 2016, 12, 6588–6600.
18. R. Cerbino, S. Mazzoni, A. Vailati and M. Giglio, Phys. Rev. Lett., 2005, 94, 064501.
19. P. Fruton, A. Nauruzbaeva, H. Bataller, C. Giraudet, A. Vailati and F. Croccolo, Phys. Rev. Fluids, 2023, 8, 023503.
20. A. Bouchaudy, C. Loussert and J. Salmon, AIChE J., 2017, 64, 358–366.
21. N.-S. Cheng, Ind. Eng. Chem. Res., 2008, 47, 3285–3288.
22. A. Gupta, S. Shim and H. A. Stone, Soft Matter, 2020, 16, 6975–6984.
23. L. N. Howard, Applied Mechanics, Springer Berlin Heidelberg, 1966, pp. 1109–1115.
24. L. Rayleigh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1916, 32, 529–546.
25. P. G. Righetti, A. Bossi, M. Giglio, A. Vailati, T. Lyubimova and V. A. Briskman, Electrophoresis, 1994, 15, 1005–1013.
26. M. Alipour, Y. Li, H. Liu and A. A. Pahlavan, Diffusiophoretic transport of colloids in porous media, arXiv, 2024, preprint, arXiv:2411.14712 DOI:10.48550/arXiv.2411.14712.
27. A. Vailati, H. Bataller, M. M. Bou-Ali, M. Carpineti, R. Cerbino, F. Croccolo, S. U. Egelhaaf, F. Giavazzi, C. Giraudet, G. Guevara-Carrion, D. Horváth, W. Köhler, A. Mialdun, J. Porter, K. Schwarzenberger, V. Shevtsova and A. D. Wit, npj Microgravity, 2023, 9, 1.
28. A. Vailati, B. Šeta, M. Bou-Ali and V. Shevtsova, Int. J. Heat Mass Transfer, 2024, 229, 125705.

---